§2 矢量的表示及其应用
矢量知识

r i r j r k
矢量的有向线段表示方法: 矢量的有向线段表示方法: 作图时,用有方向的线段表示矢量。 作图时,用有方向的线段表示矢量。 线段的长度按一定比例表示矢量的大小, 线段的长度按一定比例表示矢量的大小, 线段的方向表示矢量的方向。 线段的方向表示矢量的方向。
r A r B
矢量的一个重要性质- 矢量的一个重要性质-矢量平移的不变性 把矢量在空间平移, 把矢量在空间平移,矢量的大小和方向 都不会因平移而改变。 都不会因平移而改变。
r r r B C 的方向垂直于A、 两矢量所决定的平
面,其指向由右手螺旋法则确定。 其指向由右手螺旋法则确定。
矢 量 矢 积 图 示 法
r C r C
r B
r C
θ
r A
v Ax、Ay、Az 表示矢量 A在直角坐标系三
个坐标轴的投影(坐标分量 ,可正可负。 个坐标轴的投影 坐标分量),可正可负。 坐标分量 矢量大小与三个坐标分量的关系: 矢量大小与三个坐标分量的关系:
A= A + A + A
2 x 2 y
2 z
பைடு நூலகம்
r A方向由该矢量与三个坐标轴的夹角
(方向角 确定 方向角)确定 方向角
Cx = Ax + Bx
2 2 2 Cy = Ay + By C = Cx +Cy +Cz Cz = A + Bz z
r C
方向由三个方向角确定
( ) ( ) r r cosγ = cos( C • k) = C
r r cosα = cos C • i = Cx C r r cosβ = cos C • j = Cy C
z
C
矢量简介

i i j j k k 1 i j j k k i 0
②分量式表示点积
C AB
(Axi Ay j Azk ) (Bxi By j Bzk )
Ax Bx Ay By Az Bz BA
2.叉乘:矢积
C AB
大小:C ABsin
方向:垂直于 A 和 B 组成的
平面,满足右手螺旋法则--
由 A 经由小于180°转向B 时
大拇指伸直时所指的方向。
B
B sin
A
i i 0, j j 0, k k 0
i j k, jk i,k i j
C AB
(Axi Ay j Azk )(Bxi By j Bzk )
(AyBz Az By )i (AzBx AxBz ) j (AxBy AyBx )k
Ax
Bx
i
Ay By j B A
Az
Bz
k
即:叉乘不满足交换律。
六、矢量函数的求导和积分
A(t) Axi Ay j Azk
dA dAx i dAy j dAz k dt dt dt dt
大小: C m A
方向:m>0 与 A 同向;
m<0,与 A 反向。
五、矢量运算的点乘与叉乘
1.点乘:标积
B
C AB
Acos
B cos
ABcos
①点乘的结果为标量(如力 A 与位移点乘得功)
i i j j k k 1
i j j k k i 0
d2A dt 2
矢量PPT课件

( Ay Bz Az By )iˆ ( Az Bx Ax Bz ) ˆj ( Ax By Ay Bx )kˆ
iˆ iˆ ˆj ˆj kˆ kˆ 0
iˆ ˆj kˆ, kˆ iˆ ˆj, ˆj kˆ iˆ
ˆj iˆ kˆ,iˆ kˆ ˆj, kˆ ˆj iˆ
– 结合律(associative law): (A+B)+C=A+(B+C)
三、矢量的加法和减法 (vector addition and subtraction)
4.两矢量的减法:
– 定义: C=A-B=A+(-B) 即两矢量A和B的矢量差C可看成为矢量A和矢量(-B)的矢量和
– 运算方法: • 平行四边形法则:以A和(-B)为邻边做平行四边形,其对角线 即为矢量差C • 三角形法则:将A和B的矢尾相接,由B的矢端向A的矢端做矢 量,则该矢量即为矢量差C
• 直角坐标系下n个矢量的求和
–
n个矢量:
A1
,
A2
,,
An
–
每个矢量都可分解成矢量投影式
Ai
Aixiˆ
Aiy
ˆj
Aiz kˆ
– 和矢量:
A
Axiˆ
Ay
ˆj
Az kˆ
A
n
Ai
n
( Aixiˆ Aiy ˆj Aiz kˆ)
i 1
i 1
n
n
n
( Aix )iˆ ( Aiy ) ˆj ( Aiz )kˆ
t 0 t
➢ 方向:当t0时,A的极限方向,沿A(t)的矢端曲线的切线且指向时
• 把一个矢量分解成若干个分矢量之和,可能采取的分解方式有无
限规多定个矢,量如A 果在规某定一了直 三角个坐正标交系分的量xy的z轴方上向分,解则,分则解z可是表唯示一成的。如, A A1 A2 A3
第2点 区分矢量与标量,理解位移与路程
第2点区分矢量与标量,理解位移与路程高中阶段的物理量分为两类:一类是有大小、有方向的物理量,称为矢量;另一类是有大小、没有方向的物理量,称为标量.两类物理量在表达、运算、比较等方面都是不同的.1.矢量和标量(1)矢量:既有大小又有方向的物理量.如:力、速度、位移等.①矢量可以用带箭头的线段表示,线段的长度表示矢量的大小,箭头的指向表示矢量的方向.②同一直线上的矢量,可用正、负表示方向.若矢量与规定的正方向相同,则为正;若矢量与规定的正方向相反,则为负.(2)标量:只有大小没有方向的物理量.如:长度、质量、温度等.①有些标量也带正、负号,但标量的正、负号与矢量的正、负号意义是不同的,它不表示方向.对于不同的标量,正、负号的意义也是不同的,如:温度的正、负表示比零摄氏度高还是低,电荷量的正、负表示是正电荷还是负电荷.②标量的运算遵从算术法则.(3)大小比较:①比较两个矢量大小时比较其绝对值即可;②比较两个标量大小时,需比较其代数值.2.位移和路程(1)位移:表示质点位置变化的物理量,是由初位置指向末位置的有向线段.线段的长度表示位移的大小,有向线段的指向表示位移的方向.(2)路程:物体运动轨迹的长度,它不表示质点位置的变化.路程和位移的比较:路程位移区别描述质点实际运动轨迹的长度描述质点位置的变化有大小,无方向既有大小,又有方向与质点的运动路径有关与质点的运动路径无关,只由初、末位置决定联系都是描述质点运动的空间特征都与一段时间相关,是过程量一般来说,位移的大小不等于路程,只有质点做单向直线运动时,位移的大小才等于路程.因此,质点运动过程中的位移大小总是小于或等于路程对点例题 某学生参加课外体育活动,他在一个半径为R 的圆形跑道上跑步,从O 点沿圆形跑道逆时针方向跑了4.75圈到达A 点,求它通过的位移和路程.思路点拨 位移是矢量,求某一过程的位移,既要求出大小,还要标明方向.描述物体在平面内的曲线运动时,需要建立平面直角坐标系.当物体做曲线运动时,其位移的大小与路程是不相等的,且路程大于位移的大小.解题指导 如图所示,有向线段OA 即为该学生通过的位移x =R 2+R 2=2R ,位移方向与x 轴的夹角为φ=45°.通过的路程为s =4×2πR +34×2πR =192πR . 答案 见解题指导如图1所示为中国古代的太极图,图中大圆的半径为R ,圆心在O 点,AC 是直径,中央“S ”型部分是两个半径均为R 2的半圆.某人晨练时按此图自A 点出发,沿图中箭头所示路径ABCOA 前进,第一次返回A 点的过程中,他的路程和位移大小分别是( )图1A.0,0B.0,2πRC.2πR,0D.2πR,2πR 答案 C解析 位移由初位置指向末位置,质点沿半径为R 的半圆运动,当质点由A 点运动到C 点再返回A 点,位移大小等于0,路程等于ABC 的半个圆弧长加上中央两个小半圆弧长之和,等于2πR ,故C 正确.A 、B 、D 错误.。
矢量基本知识

Ax Ay
Bx By
y
C
C
2 x
C
2 y
arctan
Cy Cx
C
A
B
By Ay
Ax
Bx
x
四、矢量的标积矢积
1、矢量的标积(点积、点乘)
A B ABcos 为A与B的夹角
若B为单位矢量,A B为A在B方向的投影。
其大小为
dA dt
dAx dt
2
dAy dt
2
dAz dt
2
矢量函数求导法则
(设A与B均为t的函数)
(1)
d
(A B)
dA
dB
dt
dt dt
(2)
d
[ f (t)B]
B
df
f (t) dB
矢量加法满足:
交换律:A B B A
结合律:A
(B
C)
(A
B)
C
式中各个矢量均相对同一个参照系
(2) 数乘
大小
A
C方向
C A
0 0
C平行于A
C平行于 A
三、矢量的分解 任一个矢量都可以分解为任意多个分矢 量如:
dt
dt
dt
(3)
d
(A B)
A
主矢知识点总结

主矢知识点总结矢量是一个重要的概念,在物理学、数学、工程学等各个领域都有广泛的应用。
矢量是一个同时包含大小和方向信息的量,它可以用来描述物理量的运动、力的方向和大小、电场的方向和强度等。
本文将从数学、物理和工程角度总结矢量的基本概念和相关知识点。
一、矢量的基本概念1.1 矢量的定义矢量是指具有大小和方向的物理量。
在数学上,矢量通常用箭头表示,并且箭头所指方向表示矢量的方向,箭头的长度表示矢量的大小。
1.2 矢量的表示矢量可以用不同的方式表示,最常见的表示方法有点表示、分量表示和矩阵表示。
点表示是将矢量的起点和终点坐标表示出来;分量表示是将矢量在坐标轴上的投影表示出来;矩阵表示是将矢量表示为一个列向量。
1.3 矢量的运算矢量的运算包括加法、减法、数量乘法和点积等。
矢量的加法是将两个矢量的对应分量相加;减法是将一个矢量减去另一个矢量;数量乘法是将一个矢量的每个分量都乘以一个实数;点积是将两个矢量的对应分量相乘再相加。
1.4 矢量的性质矢量具有平行四边形法则、共线性、可加性等性质。
平行四边形法则指出两个矢量的和等于构成这两个矢量的两条边的平行四边形的对角线。
二、矢量的物理应用2.1 力的矢量表示在物理学中,力是一个矢量量,它包含有大小和方向的信息。
力的方向对物体的运动方向和速度有重要的影响。
2.2 运动的矢量表示在描述物体的运动时,使用矢量来表示物体的位移、速度和加速度。
位移的方向和大小都可以用矢量来表示,速度是位移对时间的导数,加速度是速度对时间的导数。
2.3 矢量叠加原理矢量叠加原理是指当一个物体同时受到多个力的作用时,可以将这些力的矢量相加得到合力的矢量。
2.4 矢量的分解矢量的分解是指将一个矢量分解为相互垂直的两个分量的过程。
这个过程在解析力学和物体的平衡问题中经常用到。
三、工程中的矢量应用3.1 电场的矢量表示在电学中,电场是一个矢量量,它包含有方向和大小的信息。
电场矢量可以用来描述电荷粒子受到的力和电场的分布情况。
矢量在物理学中都有哪些应用?

矢量在物理学中都有哪些应用?一、力学中的矢量应用1. 矢量表示位移和速度:在力学中,矢量经常用来描述物体的位移和速度。
例如,我们可以用一个位移矢量来表示物体从起始位置到结束位置的移动。
同时,速度矢量可以告诉我们物体在某一时刻的速度大小和方向。
2. 力矢量的分解:力矢量在物理学中起着至关重要的作用。
通过将力矢量进行分解,我们可以获得力的分量,可以更好地理解力对物体的作用效果。
这种分解技术被广泛应用于静力学和动力学的问题求解中。
二、光学中的矢量应用1. 光的偏振:在光学中,矢量常常用于描述光的偏振现象。
偏振是光波在传播过程中振动方向的特性。
通过使用矢量来描述光的偏振,我们可以更好地理解光波的振动状态和传播方向。
2. 矢量光束:在激光器中,通常会生成矢量光束。
矢量光束不仅可以描述光的强度分布,还可以描述光的偏振方向。
这种矢量光束的特性在许多光学应用中都具有重要意义,例如光通信和激光加工等领域。
三、电磁学中的矢量应用1. 电场和磁场矢量:电磁学是研究电和磁的相互作用的学科。
在电磁学中,通过使用矢量来描述电场和磁场,我们可以更好地表示它们的强度和方向。
这样,我们可以更准确地研究电磁现象,例如电磁感应和电磁波传播等。
2. 电流矢量和电流密度:电流矢量用于描述电流的大小和方向。
而电流密度矢量则用于描述单位面积上电流的分布情况。
这些矢量在电路分析和电磁场计算中经常被广泛应用。
综上所述,矢量在物理学中拥有广泛而重要的应用。
从力学到光学、再到电磁学,矢量为我们理解和解决物理学问题提供了强有力的工具。
通过学习和掌握矢量的概念和应用方法,我们可以更好地理解物质世界的运动和相互作用。
高中物理矢量

高中物理矢量物理学家薛定谔提出的波动理论,与爱因斯坦的相对论共同推动了20世纪的物理学发展。
在物理学中,矢量又称为向量。
它是实数的一种推广。
它可以表示一个物体上任意两点之间的距离。
它也可以表示力、位移、速度、加速度等等。
在电磁学里,矢量就代表了所有的场,无论是有形的还是无形的。
矢量可以用有限数量的点来表示,也可以用无限数量的线段来表示。
矢量和标量相互转化,矢量和矢量相加仍然是矢量。
1。
在空间中,矢量的大小和方向都是不变的。
矢量的长度用符号“ s”表示,单位是米;高度用符号“ h”表示,单位是米;重力用符号“ g”表示,单位是牛顿。
矢量的大小和方向用大写字母表示。
2。
正交和斜交:两条直线在同一平面内如果不垂直(即两条直线不成一条直线),这两条直线互相正交或斜交,其夹角的正切记为cos (θ)。
注意:①同一平面内的两条直线是互相正交或互相斜交的;②同一平面内垂直于同一条直线的两条直线互相正交或互相斜交。
2。
在矢量乘法中,两个矢量的叉积等于两个矢量的矢积。
例如,两个矢量的叉积可以表示为a*b=ab,其中a=-b。
矢量叉积的运算规则:①一个矢量的叉积等于这个矢量的长度乘以这个矢量的指向,即;②一个矢量的叉积还等于这个矢量的大小乘以它的模,即。
3。
速度矢量:矢量表示一个物体沿着一个方向(在该方向上投影)的机械运动的快慢。
速度的方向可以是向前,向后,向左,向右,向上,向下,向东,向西,向南,向北。
速度的单位是米/秒。
速度的大小用大写字母表示。
4。
位移矢量:位移表示一个物体(或几个物体)相对于另外一个物体在某个参考面上(或地面上)的位置的变化。
位移的方向可以是前后,左右,上下,也可以是内外,里外。
位移的大小用大写字母表示。
4。
加速度矢量:加速度表示一个物体(或几个物体)的速度的变化率。
加速度的方向可以是向前,向后,向左,向右,向上,向下,向东,向西,向南,向北。
加速度的单位是米/秒。
加速度的大小用大写字母表示。
矢量运算

z
y
x
分别为矢量
和x,y,z轴的夹角,其中两个是独立的。
三. 矢量的和与差
1. 和
1) 图形法 三角形法则: 平行四边形法则: 2) 解析法
2. 差:
1)图形法
2)解析法
四. 矢量的标积(点乘)
1. 矢量的点乘是标量 ( 为两矢量的夹角) 2. 解析表示
3. 性质:
五. 矢量的矢积(叉乘)
二. 矢量的表示
1. 文字表示: 印刷体:加粗的字符 书写:顶部加箭头 2. 图形表示:
带有箭头的有向线段。箭头表示矢量方向, 线段的长短表示 矢量大小。
3. 单位矢量表示:
A
的大小,即
方向同 大小为1的矢量,即单位矢量。
4. 直角坐标系中的解析表示:
矢量表示: ----三坐标轴正向单位矢量。 大小: 方向余弦:
1. 矢量的叉乘是矢量
大小: 方向:右手螺旋 2. 矢矢量的导数
1. 一般表示法:
2. 解析表示法:
七. 矢量的积分
若:
则:
矢量及其运算
一. 标量和矢量 二. 矢量的表示 三. 矢量的和与差 四. 矢量的标积(点乘) 五. 矢量的矢积(叉乘) 六. 矢量的导数 七. 矢量的积分
一. 标量和矢量
1. 标量: 定义:只有大小没有方向的物理量。 例如:长度、质量、时间、能量、温度、压强等。 2. 矢量:
定义:既有大小又有方向的物理量。 例如:速度、加速度、力、动量等。
矢量(计算机术语)(一)

矢量(计算机术语)(一)引言概述:矢量是计算机领域常用的术语,用于表示具有大小和方向的量。
它在多个领域具有广泛应用,包括图形处理、物理模拟、数据分析等。
本文将从几个方面介绍矢量的定义、表示方法、常见操作以及其在计算机科学中的应用。
正文:1. 矢量的定义及表示方法:- 矢量是具有大小和方向的量,常用箭头表示,箭头的长度表示矢量大小,箭头的方向表示矢量方向。
- 数学上,矢量可以表示为包含坐标或分量的有序数组,如(x, y, z),每个坐标或分量表示在对应轴上的长度。
2. 矢量的运算:- 矢量加法:两个矢量相加的结果是一个新的矢量,其大小等于两个矢量的大小之和,方向由两个矢量的方向决定。
- 矢量的大小:根据矢量的坐标或分量计算出其长度,常用欧氏距离公式计算。
- 矢量的方向:可以用角度或方向向量表示,常用正弦和余弦函数计算。
- 矢量减法:两个矢量相减的结果是一个新的矢量,其大小等于两个矢量的大小之差,方向由两个矢量的方向决定。
- 矢量乘法:矢量与标量的乘法结果是一个新的矢量,其大小等于原矢量的大小乘以标量的值,方向与原矢量相同。
3. 矢量的常见操作:- 点乘:两个矢量的点乘结果是一个标量,它等于两个矢量的大小之积乘以它们之间的夹角的余弦值。
- 叉乘:两个矢量的叉乘结果是一个新的矢量,它的大小等于两个矢量大小之积乘以它们之间的夹角的正弦值,方向与两个矢量所在平面的法向量垂直。
4. 矢量的应用:- 图形处理:矢量图形是以矢量为基础的图形表示方法,能够无损地缩放和变换图形,并且文件大小相对较小。
- 物理模拟:在物理模拟中,矢量用于表示力、速度、加速度等物理量,能够更准确地描述物体的运动规律。
- 数据分析:在数据分析领域,矢量用于表示特征向量,从而用于聚类、分类和降维等数据分析任务。
- 机器学习:矢量在机器学习算法中广泛应用,例如支持向量机、神经网络等,用于表示输入和输出的数据集以及模型参数。
5. 矢量的优缺点:- 优点:能够准确表示大小和方向,在计算机科学中应用广泛,具有较高的数学描述能力。
矢量分析的知识点总结

矢量分析的知识点总结一、矢量的定义和表示1.1 矢量的定义矢量是指在空间中具有大小和方向的量,它可以用来表示物理量的大小和方向,如力、速度等。
矢量通常用箭头表示,箭头的长度表示矢量的大小,箭头的方向表示矢量的方向。
1.2 矢量的表示矢量可以用不同的方式表示,常见的表示方法有坐标表示和分量表示。
坐标表示是指用矢量所在空间的坐标系来表示矢量,分量表示是指将矢量在坐标系中的投影表示为一组数值。
1.3 矢量的运算矢量的运算包括加法、减法、数量乘法和点乘等。
加法和减法的运算结果是一个新的矢量,数量乘法是指将矢量的长度进行缩放,点乘是指将两个矢量的长度和夹角进行运算得到一个标量。
二、矢量的微积分2.1 矢量的导数矢量的导数是指对矢量的每个分量分别求导,得到的是一个新的矢量。
矢量的导数在物理学中有着广泛的应用,如速度、加速度等物理量都可以用矢量的导数来表示。
2.2 矢量场矢量场是指在空间中的每个点都有一个矢量与之对应的场,它可以用来描述流体的速度场、电场、磁场等。
矢量场的微积分可以用来研究矢量场的性质和行为。
2.3 曲线积分曲线积分是指对沿着曲线的矢量场进行积分,得到的是一个标量。
曲线积分在物理学中有着重要的应用,如对力沿着曲线的功的计算等。
2.4 曲面积分曲面积分是指对矢量场在曲面上的投影进行积分,得到的是一个标量。
曲面积分在物理学中也有着广泛的应用,如对电场在闭合曲面上的通量计算等。
三、矢量分析的应用3.1 物理学中的应用矢量分析在物理学中有着广泛的应用,如在力学中用于描述力、速度、加速度等物理量;在电磁学中用于描述电场、磁场等物理量。
3.2 工程学中的应用矢量分析在工程学中也有很多应用,如在流体力学中用于描述流体的速度场、压力场等;在航空航天工程中用于描述飞行器的运动状态、姿态等。
3.3 计算机科学中的应用矢量分析在计算机科学中也有着重要的应用,如在图形学中用于描述图像的旋转、平移等运动;在机器学习中用于描述数据的特征、相似度等。
矢量相关物理知识点总结

矢量相关物理知识点总结矢量是描述物理量的一种数学工具,它可以用来表示物理量的大小和方向。
在物理学中,矢量被广泛应用于描述力、速度、加速度、位移等物理量。
在本文中,我们将总结矢量相关的物理知识点,包括矢量的基本概念、矢量的运算、矢量的坐标表示、以及矢量在物理学中的应用等内容。
一、矢量的基本概念1. 矢量的定义矢量是具有大小和方向的物理量,通常用有向线段来表示。
在数学上,矢量可以表示为箭头,箭头的长度表示矢量的大小,箭头的方向表示矢量的方向。
矢量在物理学中有着广泛的应用,例如表示力、速度、加速度、位移等物理量。
2. 矢量的性质矢量有三个基本性质:大小、方向和起点。
矢量的大小表示为矢量的模,通常用|A|表示;矢量的方向表示为矢量的方向角,通常用θ表示。
起点是矢量的起始位置,通常用A表示。
3. 矢量的分解矢量可以分解为两个或多个分量矢量,分量矢量的和等于原始矢量。
矢量的分解可以帮助我们理解矢量的性质和运算规律。
二、矢量的运算1. 矢量的加法矢量的加法满足平行四边形法则,即两个矢量的和等于这两个矢量构成的平行四边形的对角线。
在坐标表示下,矢量的加法可以表示为A+B=(Ax+Bx, Ay+By)。
2. 矢量的减法矢量的减法可以看作是矢量的加法的逆运算,即A-B=A+(-B)。
在坐标表示下,矢量的减法可以表示为A-B=(Ax-Bx, Ay-By)。
3. 矢量的数量积矢量的数量积又称为点积或内积,表示为A·B,是两个矢量的模的乘积乘以它们的夹角的余弦值。
数量积的结果是一个标量,表示为A·B=|A||B|c osθ。
4. 矢量的向量积矢量的向量积又称为叉积或外积,表示为A×B,是两个矢量的模的乘积乘以它们的夹角的正弦值,并且方向垂直于这两个矢量所在的平面。
向量积的结果是一个矢量。
三、矢量的坐标表示1. 矢量的坐标分量矢量在笛卡尔坐标系中可以表示为一个有序实数对(x,y),其中x表示矢量在x轴上的分量,y表示矢量在y轴上的分量。
高一月考物理知识点矢量

高一月考物理知识点矢量物理学中的矢量是一个非常重要且基础的概念,在高一的物理学习中也是一个重要的知识点。
本文将对高一物理学中关于矢量的基本概念、运算规则和常见应用进行详细介绍。
一、矢量的基本概念1. 什么是矢量?矢量是具有大小和方向的物理量。
与矢量相对的是标量,标量只有大小没有方向,如时间、温度等。
而矢量可以表示力、速度、位移等需要同时考虑大小和方向的物理量。
2. 矢量的表示方法矢量可以使用箭头表示,箭头的长度表示矢量的大小,箭头的方向表示矢量的方向。
在文字表示中,通常用粗体小写字母表示,如a、a,或者用带箭头的小写字母表示,如→a、→a。
3. 矢量的分解任何一个矢量都可以分解为两个或多个分量。
如果一个矢量a 在某一方向上的分量为a₁,那么矢量a可以写成a=a₁+a₂,其中a₂为与a₁正交的方向上的分量。
二、矢量的运算规则1. 矢量的加法矢量的加法满足三角形法则。
如果有两个矢量a和a,将它们的起点放在一起,然后将它们的箭头相连,将连接的箭头作为新矢量的箭头,该箭头的起点就是新矢量的起点,终点就是新矢量的终点。
新矢量的大小等于两个原始矢量大小的矢量和。
2. 矢量的减法矢量的减法可以看作是矢量加法的反向操作。
如果有两个矢量a和a,将矢量a颠倒方向,然后将其起点与矢量a的起点放在一起,将它们的箭头相连,连接的箭头即为新矢量的箭头。
新矢量的终点就是矢量a的终点。
新矢量的大小等于两个原始矢量大小的矢量差。
3. 矢量的数量积矢量的数量积,也称为点积,是通过乘法运算得到一个标量。
数量积的结果等于两个矢量之间的夹角的余弦值乘以它们的大小。
4. 矢量的矢量积矢量的矢量积,也称为叉积,是通过乘法运算得到一个新的矢量。
矢量积的结果的大小等于两个原始矢量的大小与它们之间夹角的正弦值相乘,方向垂直于原始矢量所在的平面。
三、矢量的常见应用1. 力的合成在物理学中,力是一个矢量。
当一个物体同时受到多个力的作用时,可以使用矢量的加法规则将各个力合成为一个合力,从而求解物体的运动状态。
第一章 矢量

矢量用坐标分量表示
z
A ex Ax ey Ay ez Az
Ax A cos Ay A cos
Az
A
Ay
y
Ax O
x Az A cos A A(ex cos ey cos ez cos )
P
(1,1,1)
而该点的梯度值为
P (2 x)2 (2 y) 2 (1) 2
3
(1,1,1)
显然,梯度 P 描述了P点处标量函数 的最大变化率, 即最大的方向导数,故 恒成立。 P l P
1.4 矢量场的通量与散度
1. 矢量线 概念:矢量线是这样的曲线,其上每一 点的切线方向代表了该点矢量场
M
的方向。 意义:形象直观地描述了矢量场的空间分
布状态。 矢量线方程:
dr r r dr
O
矢量线
F
dx dy dz Fx ( x, y, z ) Fy ( x, y, z ) Fz ( x, y, z )
2. 矢量场的通量 问题:如何定量描述矢量场的大小? 引入通量的概念。 通量的概念
1. 标量场的等值面 等值面: 标量场取得同一数值的点在空 间形成的曲面。 意义: 形象直观地描述了物理量在空间 的分布状态。 等值面方程: u ( x, y, z ) C 等值面的特点: • 常数C 取一系列不同的值,就得到一系列 不同的等值面,形成等值面族; • 标量场的等值面充满场所在的整个空间; • 标量场的等值面互不相交。
概念: u el u | ,其中 el l max
u 取得最大值的方向 l
高中数学矢量知识点总结

高中数学矢量知识点总结1. 矢量的表示方法矢量可以用不同的表示方法来进行表述。
最常见的两种表示方法是坐标法和分解法。
在坐标法中,一个矢量可以表示为一个有序数对(a, b)。
在分解法中,一个矢量可以被分解成两个垂直方向的分量。
2. 矢量的加法和减法对于矢量的加法,可以利用平行四边形法则,将两个矢量放在一起,然后通过平行四边形的对角线来求和。
对于矢量的减法,可以利用加法的逆运算来进行计算。
3. 矢量的数量积和向量积数量积也叫点积,是两个矢量的数量乘积再乘以他们的夹角的余弦值。
向量积也叫叉积,是两个矢量的乘积然后再乘以他们的夹角的正弦值。
4. 矢量的模长和方向角矢量的模长是指矢量的大小。
它可以通过勾股定理来求解。
方向角是指矢量与坐标轴的夹角。
5. 矢量的坐标变换在平面直角坐标系中,一个矢量的坐标变换可以通过坐标轴的变换来进行。
6. 矢量的线性运算矢量具有线性性质,即对于任意的实数a和b,有a(u+v)=au + av和a(bv)=(ab)v。
7. 矢量的共线与共面如果存在一个非零数k,使得矢量a = k*v,则矢量a与v共线。
如果在同一平面上有n个矢量和它们的线性组合也在同一平面上,则这些矢量共面。
8. 矢量的投影一个矢量在另一个矢量上的投影可以通过数量积来求解。
9. 矢量的基本定理矢量存在的基本定理是矢量可以通过两个非零矢量的线性组合来构成。
10. 空间直角坐标系下矢量的数量积与向量积在三维空间中,矢量的数量积和向量积的计算方式与二维空间有所不同。
11. 空间直角坐标系下矢量的坐标变换空间直角坐标系下,矢量的坐标变换也有所不同,需要考虑三个方向的变化。
12. 平面上直线的方程矢量可以用来表示平面上的直线的方程,通过矢量的运算可以求解直线的交点等问题。
总的来说,矢量是一种重要的数学工具,它在几何、物理等领域都有广泛的应用。
熟练掌握矢量知识可以帮助我们更好地理解和解决数学和物理问题。
关于矢量的总结

关于矢量的总结矢量,即向量,是物理学与数学中常用的概念。
它具有方向和大小,并可以用箭头来表示。
矢量在各个学科中都有广泛的应用,例如力学、物理学、工程学、计算机图形学等。
下面将对矢量的定义、性质、运算法则以及应用进行详细的总结。
一、矢量的定义与性质1. 定义:矢量是一个有向线段,它具有大小和方向。
用加粗的小写字母表示,例如 a、b。
2. 大小:矢量的大小是指矢量的长度,用绝对值表示,例如|a|。
3. 方向:矢量的方向由与其平行的无数直线所组成的集合表示。
4. 自由矢量与固定矢量:自由矢量表示一个具有大小和方向的箭头,可以平行移动而不改变其性质;固定矢量表示一个固定在空间中的点,它具有大小和方向,但不能平行移动。
5. 等于矢量:如果两个矢量的大小及方向都相等,则称它们是等于矢量,用等号表示,例如 a = b。
6. 相反矢量:如果两个矢量的大小相等,方向相反,则称它们是相反矢量,用负号表示,例如 -a。
7. 单位矢量:大小为1的矢量称为单位矢量,用小写的带一个“^”的字母表示,例如 a^。
二、矢量的运算法则1. 矢量的加法:矢量的加法满足交换律和结合律,即 a + b = b + a,(a + b) + c = a + (b + c)。
2. 矢量的减法:矢量的减法可以看作是加上相反矢量,即 a - b = a + (-b)。
3. 数量积(点积):数量积是指两个矢量的乘积与它们夹角的余弦值的乘积,记作a·b,其结果是一个标量。
4. 向量积(叉积):向量积是指两个矢量的乘积与它们夹角的正弦值的乘积,记作a×b,其结果是一个矢量。
5. 数量积和向量积的运算法则:数量积满足分配律和交换律,a·(b + c) = a·b + a·c,a·b = b·a;向量积不满足交换律,a×b = -b×a。
6. 混合积:混合积是指三个矢量的乘积的结果,记作(a×b)·c,其结果是一个标量,它表示一个平行六面体的体积。
矢量的表示与应用

矢量的表示与应用矢量是物理学和数学中一个重要的概念,它用于表示带有大小和方向的量。
矢量的表示方式有多种,常见的有几何矢量、向量和坐标矢量等。
矢量的应用也非常广泛,涵盖了物理学、工程学、计算机图形学等多个领域。
下面将详细介绍矢量的表示与应用。
一、矢量的表示1. 几何矢量几何矢量是最常见的矢量表示方式之一。
它通过一个起点和一个终点来表示一个矢量,起点表示矢量的作用点,终点表示矢量的方向和大小。
几何矢量可以用箭头表示,箭头的长度表示矢量的大小,箭头的方向表示矢量的方向。
2. 向量向量是数学中常用的矢量表示方式。
向量可以用一个有序数对表示,例如(3, 4),其中第一个数表示矢量在x轴上的分量,第二个数表示矢量在y轴上的分量。
向量还可以用加粗的字母表示,例如a表示一个向量。
3. 坐标矢量坐标矢量是一种在坐标系中表示矢量的方式。
坐标矢量的表示方法与向量类似,但是它更加具体和精确。
坐标矢量可以用一个有序数对表示,例如(3, 4),其中第一个数表示矢量在x轴上的坐标,第二个数表示矢量在y轴上的坐标。
二、矢量的应用1. 物理学中的矢量在物理学中,矢量被广泛应用于描述物理量的大小和方向。
例如,速度是一个矢量,它既有大小又有方向。
通过矢量的加法和减法,可以计算出物体的合速度。
另外,力也是一个矢量,它既有大小又有方向。
通过矢量的分解和合成,可以计算出物体所受的合力。
2. 工程学中的矢量在工程学中,矢量被广泛应用于描述力、力矩、速度、加速度等物理量。
工程师可以利用矢量的性质,计算物体所受的合力、合力矩、合速度、合加速度等。
这些计算可以帮助工程师设计和优化各种结构和机械系统。
3. 计算机图形学中的矢量在计算机图形学中,矢量被广泛应用于描述图形的形状和位置。
通过矢量的平移、旋转和缩放等操作,可以实现图形的变换和动画效果。
矢量图形还可以利用矢量的性质进行高效的存储和渲染,使得图形在不同分辨率下保持清晰和流畅。
4. 其他领域中的矢量应用除了物理学、工程学和计算机图形学,矢量还被广泛应用于其他领域。
大学物理课件矢量的基本概念

大学物理课件矢量的基本概念大学物理课件:矢量的基本概念一、引言在大学物理课程中,矢量是一个基本且重要的概念。
矢量在物理学中具有广泛的应用,如力学、电磁学、热力学等领域。
为了更好地理解物理现象和解决实际问题,我们需要掌握矢量的基本概念、运算规则及其应用。
二、矢量的定义矢量,又称向量,是一种既有大小又有方向的物理量。
与标量不同,标量只有大小,没有方向。
例如,温度、质量、时间等都是标量,而速度、加速度、力等都是矢量。
三、矢量的表示矢量可以用箭头表示,箭头的长度表示矢量的大小,箭头的方向表示矢量的方向。
在二维平面内,矢量可以表示为从原点出发的有向线段;在三维空间中,矢量可以表示为从原点出发的有向线段或箭头。
四、矢量的运算规则1. 矢量的加法两个矢量的加法遵循平行四边形法则。
即将两个矢量的起点放在同一点,以这两个矢量为邻边作平行四边形,第三个顶点所对应的矢量即为这两个矢量的和。
2. 矢量的减法矢量的减法可以看作是矢量的加法,即 a b = a + (-b)。
其中,-b 表示与 b 大小相等、方向相反的矢量。
3. 矢量的数乘矢量的数乘是指将一个矢量与一个实数相乘。
数乘的结果是一个新的矢量,其大小为原矢量的大小与实数的乘积,方向与原矢量相同(实数为正)或相反(实数为负)。
4. 矢量的点乘矢量的点乘,又称数量积、内积,是指两个矢量的乘积。
点乘的结果是一个标量,其大小等于两个矢量大小的乘积与它们夹角余弦值的乘积。
5. 矢量的叉乘矢量的叉乘,又称向量积、外积,是指两个矢量的乘积。
叉乘的结果是一个新的矢量,其大小等于两个矢量大小的乘积与它们夹角正弦值的乘积,方向垂直于原矢量所在的平面,遵循右手定则。
五、矢量的应用1. 力的合成与分解在力学中,力是一种矢量。
多个力的合成与分解遵循矢量的加法与减法规则。
力的合成可以帮助我们求出多个力的合力,力的分解可以将一个力分解为多个分力。
2. 速度与加速度在运动学中,速度和加速度都是矢量。
§2 矢量的表示及其应用
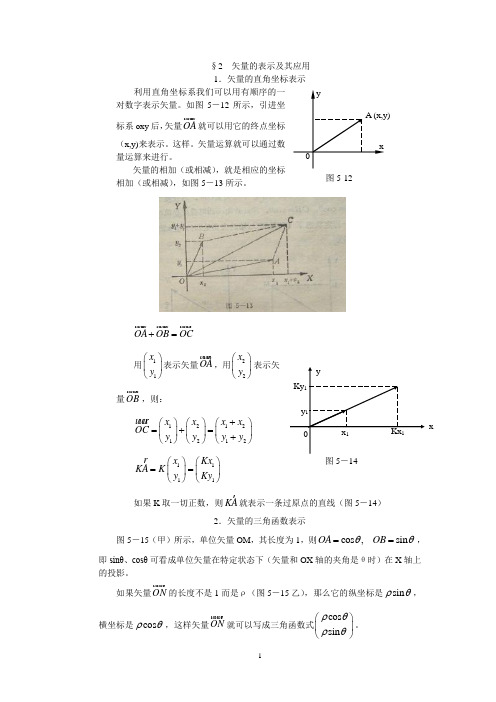
§2 矢量的表示及其应用 1.矢量的直角坐标表示利用直角坐标系我们可以用有顺序的一对数字表示矢量。
如图5-12所示,引进坐标系oxy 后,矢量OA 就可以用它的终点坐标(x,y)来表示。
这样。
矢量运算就可以通过数量运算来进行。
矢量的相加(或相减),就是相应的坐标相加(或相减),如图5-13所示。
OA OB OC +=用11x y ⎛⎫⎪⎝⎭表示矢量OA ,用22x y ⎛⎫⎪⎝⎭表示矢量OB ,则:12121212x x x x OC y y y y +⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭1111x Kx KA K y Ky ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭如果K 取一切正数,则KA 就表示一条过原点的直线(图5-14)2.矢量的三角函数表示图5-15(甲)所示,单位矢量OM ,其长度为1,则cos ,sin OA OB θθ==,即sinθ、cosθ可看成单位矢量在特定状态下(矢量和OX 轴的夹角是θ时)在X 轴上的投影。
如果矢量ON 的长度不是1而是ρ(图5-15乙),那么它的纵坐标是sin ρθ,横坐标是cos ρθ,这样矢量ON 就可以写成三角函数式cos sin ρθρθ⎛⎫⎪⎝⎭。
图5-12x图5-14在解决实际问题时,我们又常常把一个矢量沿相互垂直的坐标轴分解,或者用“一个矢量在另一个矢量的投影”这样的语言。
如图5-16所示,将矢量A 沿X 轴和Y 轴分解,x A 和y A 是矢量A 在X 轴和Y 轴方向上的分矢量,因为坐标轴的方向已确定,所以分矢量x A 和y A 只要用数值和和正负号就可以把它们的大小和方向完全表示出来。
这样我们就可以省去矢量符号而简单地把它们写成A X 和A Y ,A X 和A Y 叫做分量,显然:cos ,sin x y A A A A θθ==由于分量是标量而不是矢量(分量的正负表示分矢量的方向跟指定的方向相同或相反)因此,在X 轴和Y 轴方向上运算时,就可以把矢量运算转化为代数运算或三角运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 矢量的表示及其应用 1.矢量的直角坐标表示利用直角坐标系我们可以用有顺序的一对数字表示矢量。
如图5-12所示,引进坐标系oxy 后,矢量OA 就可以用它的终点坐标(x,y)来表示。
这样。
矢量运算就可以通过数量运算来进行。
矢量的相加(或相减),就是相应的坐标相加(或相减),如图5-13所示。
OA OB OC +=用11x y ⎛⎫⎪⎝⎭表示矢量OA ,用22x y ⎛⎫⎪⎝⎭表示矢量OB ,则:12121212x x x x OC y y y y +⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭1111x Kx KA K y Ky ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭如果K 取一切正数,则KA 就表示一条过原点的直线(图5-14)2.矢量的三角函数表示图5-15(甲)所示,单位矢量OM ,其长度为1,则cos ,sin OA OB θθ==,即sinθ、cosθ可看成单位矢量在特定状态下(矢量和OX 轴的夹角是θ时)在X 轴上的投影。
如果矢量ON 的长度不是1而是ρ(图5-15乙),那么它的纵坐标是sin ρθ,横坐标是cos ρθ,这样矢量ON 就可以写成三角函数式cos sin ρθρθ⎛⎫⎪⎝⎭。
图5-12x图5-14在解决实际问题时,我们又常常把一个矢量沿相互垂直的坐标轴分解,或者用“一个矢量在另一个矢量的投影”这样的语言。
如图5-16所示,将矢量A 沿X 轴和Y 轴分解,x A 和y A 是矢量A 在X 轴和Y 轴方向上的分矢量,因为坐标轴的方向已确定,所以分矢量x A 和y A 只要用数值和和正负号就可以把它们的大小和方向完全表示出来。
这样我们就可以省去矢量符号而简单地把它们写成A X 和A Y ,A X 和A Y 叫做分量,显然:cos ,sin x y A A A A θθ==由于分量是标量而不是矢量(分量的正负表示分矢量的方向跟指定的方向相同或相反)因此,在X 轴和Y 轴方向上运算时,就可以把矢量运算转化为代数运算或三角运算。
图5-17中的ON 是OA 矢量在矢量OB 上的投影,ON 的大小(ON )是OA 的大小(OA )乘上OA 和OB 的夹角的余弦。
即c o s O N O A θ=。
3.矢量的复数表示如图5-18所示,我们以X 轴为实轴,y 轴为虚轴,这两个坐标轴组成复平面,每个复数(a bi +)都可用复平面上的一个点M 表示(这个点的横坐标为a ,纵坐标是b )也可以用连接为O 、M 的有向线段(O 为起点,M 为终点(即矢量OM 来表示)因此,矢量OM 可以写成复数表示式:OM a bi =+(复数的实部与虚部相当于矢量的乙图5-15 AAx A图5-16O图5-17图5-18x, y 的分量)同样利用三角函数,矢量OM 还可写成复数的三角函数式:()cos sin cos sin OM i i ρθρθρθθ=+=+由图5-18可见,矢量OM 的长度为:OM ρ==由X 轴转到OM 矢量的角度arctan baθ称为幅角。
此外利用数学上的尤拉公式:()cos sin j e i θρρθθ=+,复数OM 又可写成为指数形式:j OM e θρ=必须指出:复数虽然是“一个数”,但具有“大小”和“方向”这两个要素,因此我们把复数作为描写矢量或刻划只有大小和相位的数量(如谐振量)的工具。
例5-5用计算法解例4-7。
例4-7 水流向东,速率为2km/h ,汽船以8km/h 的航速在向东偏北600的方向航行。
一位旅客在甲板上散步,速度为1km/h ,面向正西北。
求旅客对岸的速度。
解:令X 轴指向正东,Y 轴指向正北,建立直角坐标系oxy ,将各速度矢量的起点移至坐标原点,作矢量图(图5-19)用A A x y ⎛⎫⎪⎝⎭表示矢量V 水对岸,用B B x y ⎛⎫⎪⎝⎭表示矢量V 船对水,用C C x y ⎛⎫⎪⎝⎭表示矢量V 人对船。
依速度合成规律,有:V V V V C A B C A B A B C A B C x x x x x x y y y y y y ++⎛⎫⎛⎫⎛⎫⎛⎫++= ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭人对岸水对岸船对水人对船=++=00cos60cos13512816 5.3222A B C x x x v v v ++=+=+⨯-⨯=-=水对岸船对水人对船+00sin 60sin135817.6222A B C y y y v v ++=+=⨯+⨯==船对水水对船 ∴9.2(km/h)v 水对岸V水对岸与X 轴所成的夹角为:0/7.6tan 1.4345565.3A B C A B C x x x y y y θθ++==++向东偏北。
例5-6在加速行驶的火车上固定一斜面,斜面倾角为θ(图5-20),有一物体静止在斜面上,如果火车的加速度小于某一值a 0,物体就会下滑。
设物体和斜面间的静摩擦因数为μ0,推导a 0的表达式。
解:选斜面上的物体为研究对象,物体受三个力的作用:重力mg ,竖直向下;斜面对它的支持力N ,与斜面垂直向上,静摩擦力f ,沿斜面向上(当加速度为a 0时,有最大静摩擦力0m f N μ=⋅)解法一:选取加速度a 0的方向为X 轴正向,与之垂直的方向为Y 轴方向建立直角坐标系。
将mg 、N 、f 沿X 、Y 两个方向分解(见图5-21)得:()sin ,cos ,()0cos ,sin ,sin cos cosx mx m x y my m y xm yN N f f mg N N f f mg mgFN f FN f θθθθθθθ==-====-=-=+∑∑根据牛顿第二定律有:0xyFma F==∑∑即:0sin cos m N f ma θθ-= ...... (1) cos sin 0m N f mg θθ+-= (2)解(1)、(2)两方程得:000sin cos cos sin a g θμθθμθ-=+解法二:斜面是物体的支承面,取沿斜面方向和垂直斜面方向为直角坐标系的方位,将N 、mg 、f 进行分解(见图5-22),得:00cos x a a θ= 00sin y a a θ=根据牛顿第二定律有:00x x yyF ma Fma ==∑∑即:00sin cos (1)cos sin (2)m mg f ma N mg ma θθθθ-=-=解(1)、(2)两式得:000sin cos cos sin a g θμθθμθ-=+ 说明:本例是在分析物体受力情报基础上,根据力的独立性作用原理(每个力都能各自独立产生相应的效应的效果),在受力体的适当的位置建立直角坐标系,把所有作用于物体上的外力沿两条互相垂直的坐标轴分解,然后利用代数方法将各分量叠加(各分量的正负由坐标轴的取向决定),最后依图5-20图5-21图5-22a据牛顿第二定律列出方程。
在X 轴方向上:Xx Fma =∑ 在Y 轴方向上:YY Fma =∑上述方法称为正交分解法,其主要优点在于:将力和加速度的矢量运算转化为代数运算。
若要求合力F ,则F合,a 合F 合与X 轴的正向的夹角arctanyxFFθ=∑∑,这样就可用直角三角形色股定理替换三角形的余弦定理进行计算。
正交分析法在解决动力学问题中有重要作用。
坐标轴的选取需根据物体的运动的特点,一般取加速度方向和垂直于加速度方向(或沿运动方向和垂直于运动方向)。
例5-7如图5-23所示,金属矩形框架放在水平位置上,可动边cd 可在框架上无摩擦地滑动。
已知cd 的质量m=0.05kg ,边长L =0.50m,匀强磁场的B =0.50T,方向斜向上与框架平面成150且与线框边AB ,CD 垂直,整个框架电阻R =0.20欧,问当cd 的滑动速度达到多大时,它才对框架AD ,BC 边没有压力。
解:如图5-24所示,由于cd 边以速度V 运动时切割了磁感应线,产生由d 向c 的感应电动势:线框中的感应电流:sin BLv I RRεα==cd 所受的磁场力F 垂直于导线cd 和磁感应强度B 所决定的平面,且:sin BLv F BIL BLRα== 将力F 沿直方向和水平 方向正交分解:2cos cos ()F F F βαβα===由此,导线cd 在竖直方向上受三个力:重力G ,弹力N ,磁场分力FeBr2,(平面图如图5-25所示)为了使cd 对线框没有压力(即N =0),必须有:2F mg =即:22sin cos B L v mg Rαα=l 图5-23即:()()2222220.050.20106.4(/)sin 20.50.500.5mgR v m s B L α⨯⨯⨯===⨯⨯ 例5-8证明质点作匀速圆周运动时,它在直径上的投影作简谐振动地,并写出其投影在任意时刻的位移、速度和加速度的表达式。
证明:图5-26所示,设质点以匀角速度ω在半径为r 的圆周上逆时针运动,并设当t=0时质点在M 0处,半径为OM 0,与X 轴的夹角为ф,经时间t 后,质点到达M 点,半径OM 与X 轴的夹角为t ωφ+,M 点在X 轴(即直径CB )上的投影为M /,它离开圆心O 的位移/OM 是矢量OM 在X 轴上的投影,其大小:()/cos OM OM t ωφ=+即:()cos x r t ωφ=+ …… (1) 根据圆周运动的规律,质点在M 处的线速度的大小:v r ω=,沿切线方向,加速度的大小为2a r ω=,方向指向圆心。
M /既然是M 在X 轴上的投影,那么M /的速度V /、加速度a 应分别是M 点的速度V 和a /在X 轴的投影, 即:()()/cos sin 2v v t r t πωφωωφ⎡⎤=-+=+⎢⎥⎣⎦∵V /的方向与X 轴的取向相反,()/sin v r t ωωφ∴=-+ (2)()()/2cos cos a a t r t ωφωωφ=+=+∵a /的方向与X 轴的取向相反,()/2cos a r t ωωφ∴=-+ (3)以(1)代入(3)得:/2a x ω=- …… (4)(负号表示加速度的方向与位移的方向相反)(4)式表明投影M /的运动是简谐振动。
(1)、(2)、(3)式告诉我们,投影M /的位移、速度和加速度都是时间t 的正弦或余弦函数。
说明:因为匀速园周运动的质点在直径上的投影的运动是简谐振动,因此我们可借助于匀速园周运动来研究简谐振动。
M 点所描绘的圆称为M /点的简谐振动的参考圆。
例5-9如图5-27所示,质量为m ,带电量为+q 的带电粒子,从坐标原点O 沿Y 轴正方向以速度V 射入磁感应强度为B 的匀强磁场和电场强度为E 的匀强电场中,B 、E 的方向均平行于Z 轴的方向。
当带电粒子第一次XOZ 平面内的挡板OACD 上的小孔M 射出时,试求带电粒子的位移OM 。
