折纸立体正方体
卡纸制作正方体最简单方式。

卡纸制作正方体最简单方式。
以卡纸制作正方体最简单方式正方体是一种具有六个面都是正方形的立体图形,常用于数学教学、建筑设计等领域。
在这里,我们将介绍一种使用卡纸制作正方体的最简单方式。
所需材料:1. 卡纸(颜色可根据个人喜好选择)2. 尺子3. 铅笔4. 剪刀5. 胶水或双面胶步骤一:准备工作我们需要根据正方体的尺寸来确定卡纸的大小。
假设我们希望正方体的边长为10厘米,那么我们需要准备6张边长为10厘米的正方形卡纸。
步骤二:绘制正方形使用尺子和铅笔,在每张卡纸上绘制一个边长为10厘米的正方形。
确保每个角度都是直角,并且边长相等。
步骤三:剪刀切割按照所绘制的线条,使用剪刀将每个正方形剪下来。
确保剪得整齐,边缘平整。
步骤四:折叠卡纸将每个正方形沿着对角线折叠,使得两个对角线上的顶点重合。
确保折叠线条整齐,对称。
步骤五:粘合正方体在每个正方形的边缘涂抹胶水或双面胶,并将相邻的两个正方形粘合在一起。
确保粘合处紧密,没有缝隙。
步骤六:完成正方体重复步骤五,将剩下的正方形依次粘合在已有的正方体上,直至六个正方形全部粘合完成。
通过以上步骤,我们就成功制作出了一个卡纸正方体。
此时,你可以用该正方体进行各种有趣的实验或展示,也可以在上面进行涂鸦或贴上装饰品,使其更加个性化。
需要注意的是,在制作过程中要确保每个步骤的准确性和细致性。
尺寸的准确性将直接影响最终的成品效果,而折叠和粘合的仔细程度则决定了正方体的牢固程度。
在完成正方体后,你可以进一步探索其特性和性质,比如计算正方体的表面积和体积。
通过观察和实践,你还可以发现正方体的对称性、顶点、棱和面等基本要素。
总结起来,卡纸制作正方体的最简单方式可以概括为:准备材料,绘制正方形,剪切卡纸,折叠卡纸,粘合正方体。
这种制作方式简单易行,适合各个年龄段的人群。
无论是作为学习工具还是手工制品,制作一个卡纸正方体都能带来乐趣和收获。
希望你能尝试并享受这个过程!。
折正方体的11种方法

折正方体的11种方法折一个正方体有11种方法。
方法一:平面对角线法将一个正方形对角线对折,得到两条线段,两条线段再按照正方形的边界折叠,即可得到一个正方体。
方法二:边中点法将正方形的四个边的中点连线,得到一个十字形。
然后将四条线段按照该十字形折叠,即可得到一个正方体。
方法三:对角线交点法将正方形的两条对角线相交于一点,再以该交点为中心按照正方形的边界折叠,即可得到一个正方体。
方法四:平行四边形法将正方形的两条边分别延长,形成两个平行四边形。
然后将两个平行四边形按照正方形的边界折叠,即可得到一个正方体。
方法五:对边中点法将正方形的相对边的中点连线,得到两条线段。
然后将两条线段按照正方形的边界折叠,即可得到一个正方体。
方法六:三角形法将正方形的一个顶点连线另一个顶点,形成一个直角三角形。
然后将三角形按照正方形的边界折叠,即可得到一个正方体。
方法七:中心点法将正方形的四个顶点连线一个中心点,得到四条线段。
然后将四条线段按照正方形的边界折叠,即可得到一个正方体。
方法八:平行四边形交点法将正方形的两条边向内延长,形成两个平行四边形。
然后将两个平行四边形的交点按照正方形的边界折叠,即可得到一个正方体。
方法九:对角线中点法将正方形的两条对角线分别连线其对角线的中点,得到四条线段。
然后将四条线段按照正方形的边界折叠,即可得到一个正方体。
方法十:平行四边形对角线法将正方形的两条边延长,形成两个平行四边形。
然后将两个平行四边形的对角线按照正方形的边界折叠,即可得到一个正方体。
方法十一:梯形法将正方形的一边向外延长,形成一个梯形。
然后将该梯形按照正方形的边界折叠,即可得到一个正方体。
以上是折正方体的11种方法。
每种方法都是通过在正方形上做特定的折叠线,然后按照该折叠线将正方形折叠成正方体的形状。
这些方法各具特点,可以选择其中一种适合自己的方式来折叠正方体。
折纸父亲节礼物手工正方形彩纸

折纸父亲节礼物手工正方形彩纸折纸一直以来都是大家喜欢的一种手工艺术,随着父亲节的临近,折纸也成为了一份特别的礼物选择。
而在众多的折纸形式中,正方形折纸又是最经典的一种。
今天,我们就来讲解一下如何利用正方形彩纸折出精美的父亲节礼物。
材料准备:1. 彩纸若干2. 剪刀3. 铅笔4. 尺子正方形折纸方法:首先,我们需要准备一张正方形的彩纸。
如果手头没有正方形彩纸,可以使用普通的A4纸,在左下角折出一个直角三角形。
接着,将多余的三角形区域用剪刀剪去,就可以得到一个正方形。
1. 立体花篮将正方形纸张分别对折,然后对折两次,接着在对角线处折出如图所示的三角形形状。
然后将两边向中间折叠,使得整个图案呈现出一个正方体形状。
接着将四个口袋处用剪刀剪开,慢慢展开,就可以看到一个精美的立体花篮了。
2. 波纹灯笼将正方形纸张对折一次,接着将两个角折成一个三角形,然后将两个三角形顶部对齐再次对折,如此反复折叠,最后利用铅笔划出相应的波纹图案,用剪刀将多余部分剪去,并在底部留出一个长条形状。
然后将两侧用胶水粘起来,就可以制作出具有艺术气息的波纹灯笼了。
3. 父亲节贺卡将正方形纸张对折成一半,再次对折变成四分之一的大小,随后向内折叠成如图形状,再次展开后,在其中夹入一张卡片,将卡片夹在中央,将四周的折痕处用胶水固定住,就可以制作出一张独特的父亲节贺卡了。
通过以上三种方法,我们可以轻松地使用正方形彩纸制作出独具特色的父亲节礼物。
而在折纸的过程中,切记要耐心细致,以保证最终的成品精美、美观。
父亲节礼物虽然小巧,却能传递浓浓的父爱,更能体现孩子们对父亲的深情厚爱。
让我们一起动手制作,为我们的父爱表达最深切的祝福吧!。
叠成正方体的11种方法

叠成正方体的11种方法嘿,你知道吗?叠成正方体居然有 11 种方法呢!这是不是很神奇呀!咱就先说说第一种方法,就好像搭积木一样,一块一块稳稳地往上摞,每一块都要放得恰到好处,这样慢慢就能叠出一个正方体啦。
这就像我们做事,一步一个脚印,稳稳当当的。
第二种呢,就有点像变魔术。
把那些纸片呀或者其他能折叠的东西,巧妙地折来折去,哎呀,突然就出现了一个正方体,是不是很有意思呀!这就好像我们的生活,有时候需要一些巧妙的心思和技巧,才能让事情变得有趣又精彩。
第三种方法呢,像是拼图一样。
把不同形状的部分一点点拼凑起来,最后拼成一个完整的正方体。
这多像我们交朋友呀,不同性格的人凑在一起,最后组成了一个温暖的集体。
第四种,就好像是在编织一个正方体的网,横竖交织,丝丝入扣,慢慢就成型啦。
第五种像是在搭建一个小城堡,精心地把每一部分都放置到位,让它变得坚固又好看。
第六种,有点像在玩俄罗斯方块,把那些形状合适的部分准确地放进去,可不就成了正方体嘛。
第七种,就如同在创造一件艺术品,每一个细节都要精心雕琢。
第八种,仿佛是在解一道谜题,通过不断尝试和探索,找到叠成正方体的正确路径。
第九种,好像是在走迷宫,兜兜转转,最后终于找到了出口,也就是那个完美的正方体。
第十种,像是在烹饪一道美味佳肴,各种调料和食材搭配得当,才能做出让人垂涎欲滴的正方体。
第十一种呢,哎呀,那得你自己去发现和体会啦!想想看,这 11 种方法,每一种都有它的独特之处,就像我们每个人都有自己的个性一样。
我们可以尝试用不同的方法去叠这个正方体,就像我们在生活中可以选择不同的道路去走。
有时候可能会遇到困难,但只要我们不放弃,总会找到属于我们自己的那个正方体。
所以呀,不要害怕尝试,不要害怕失败,大胆去探索吧!去发现那 11 种方法的奇妙之处,让我们的生活也像叠正方体一样,变得丰富多彩,充满乐趣!。
制作正方体的方法

制作正方体的方法正方体是一种具有六个相等的正方形面的立体图形。
它是几何学中最简单的多面体之一,也是建筑、设计和数学领域中最常见的形状之一、下面是一个制作正方体的方法。
材料:-卡纸或者厚纸板-量尺-铅笔-剪刀-胶水-直尺步骤:1.使用直尺和铅笔测量一个正方形的边长。
确保此边长适中,使得最终制作的正方体具有适当的大小。
2.使用直尺在卡纸或者厚纸板上绘制一个正方形。
可以使用量尺来确保每个边的长度一致。
3.使用剪刀沿着绘制的线条剪下正方形。
确保剪得整齐,尽量保持边缘平直。
4.将正方形折叠成一个边长相等的立体图形。
首先将正方形对折,使对折线的两端相接。
5.确保对折线的两端完全对齐,然后将折线两侧的边缘粘贴在一起。
使用胶水来保持边缘的粘合。
确保边缘粘贴牢固,可以使用夹子或者其他工具来加固。
6.重复以上步骤,使用同样的尺寸制作五个正方形。
7.等待胶水干燥。
这可能需要几分钟或者更长时间,具体时间取决于使用的胶水品牌和环境条件。
8.当所有的正方形都干燥并且固定在一起时,正方体就制作完成了。
确保每个面都与相邻面正确连接。
Tips:-可以使用不同颜色的卡纸或者厚纸板来给正方体上色。
这样可以使正方体更加有趣,并为儿童学习形状提供更多的乐趣。
-如果想要制作一个更大的正方体,可以逐步增加正方形的边长,以及使用更厚的卡纸或者厚纸板来增加稳定性。
-为了制作一个完美的正方体,可以在粘合每一面时使用夹子,这样可以确保边缘粘合得更紧密。
总结:制作一个正方体非常简单,只需要一些简单的材料和几个简单的步骤。
无论是在学校还是在家庭环境中,通过制作正方体,不仅可以学习几何学的基本概念,还可以培养动手能力和创造力。
祝你制作正方体的过程愉快!。
正方体的11种折叠法及背会小窍门小口诀
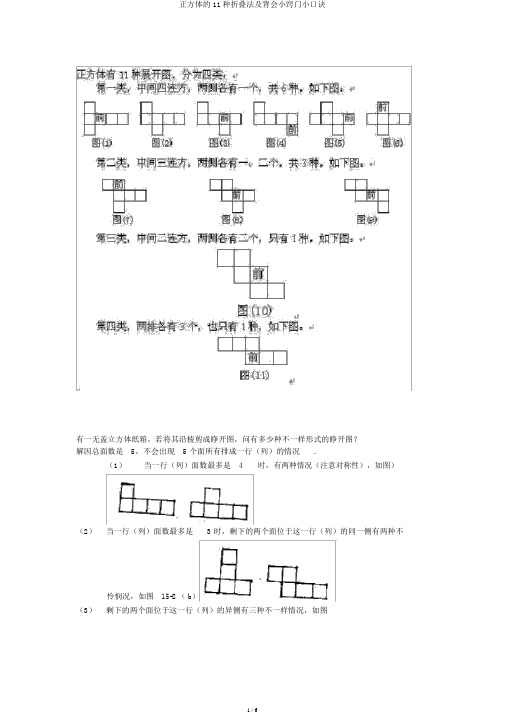
有一无盖立方体纸箱,若将其沿棱剪成睁开图,问有多少种不一样形式的睁开图?解因总面数是5,不会出现 5 个面所有排成一行(列)的情况.(1)当一行(列)面数最多是4时,有两种情况(注意对称性),如图)(2)当一行(列)面数最多是 3 时,剩下的两个面位于这一行(列)的同一侧有两种不怜悯况,如图15-2 ( b)(3)剩下的两个面位于这一行(列)的异侧有三种不一样情况,如图(4)当一行(列)的面数最多是 2 时,仅一种情况,以下图.总数为 2+2+3+1=8 种,即有8 种不一样的睁开形式.研究正方体的睁开图将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不一样的图形呢?要搞清这个问题,最好是着手实践,比方找一些正方体纸盒,沿着棱按不一样方式将其剪开(但不要剪断,六个面要经过边连在一同),展成平面,再察看、对照一下不一样形状的图形有哪些。
假如不简单找到足够的正方体纸盒,还能够找一些不太厚、易折叠的正方体纸板,利用逆向思想,先猜想正方体睁开图会有哪些不一样形状,并将它们画在纸板上,再将四周剩余部分剪去,而后沿所画直线直行折叠,看看哪些图形纸板能够折叠成正方体。
这种研究方法虽然有点麻烦,但操作简易易行,迅速有效。
预先可多画一些纸板(六个正方形边与边对齐,随意连结成不一样的平面图形),经过逐一考证,记录下所有能够折叠成正方体的图形,再将这些图形分类,总结并找寻出此中的规律。
那么,沿棱剪睁开开一个正方体,终究有哪些不一样的形状呢?假如不考虑因为旋转或翻折等造成相对地点的不一样,只从实质上讲,有以下三类共11 种。
一、“ 141 型”(共 6 种)特色:这种睁开图中,最长的一行(或一列)有 4 个正方形(图1~图 6)。
理解:有 4 个面直线相连,其他 2 个面分别在“直线”两旁,地点随意。
二、“ 231 型”与“ 33 型”(共 4 种)特色:这种睁开图中,最长的一行(或一列)有 3 个正方形(如图7~图 10)。
正方体11种折叠方法

将一个正方体地表面沿某些棱剪开,展成一个平面,共有哪些不同地图形呢?要搞清这个问题,最好是动手实践,比如找一些正方体纸盒,沿着棱按不同方式将其剪开(但不要剪断,六个面要通过边连在一起),展成平面,再观察、对比一下不同形状地图形有哪些.个人收集整理勿做商业用途如果不容易找到足够地正方体纸盒,还可以找一些不太厚、易折叠地正方体纸板,利用逆向思维,先猜测正方体展开图会有哪些不同形状,并将它们画在纸板上,再将周围多余部分剪去,然后沿所画直线直行折叠,看看哪些图形纸板可以折叠成正方体.这种探究方法虽然有点麻烦,但操作简便易行,快速有效.事先可多画一些纸板(六个正方形边与边对齐,任意连接成不同地平面图形),经过逐个验证,记录下所有可以折叠成正方体地图形,再将这些图形分类,总结并寻找出其中地规律.个人收集整理勿做商业用途那么,沿棱剪开展开一个正方体,究竟有哪些不同地形状呢?如果不考虑由于旋转或翻折等造成相对位置地不同,只从本质上讲,有以下三类共种.个人收集整理勿做商业用途一、“型”(共种)特点:这类展开图中,最长地一行(或一列)有个正方形(图~图).理解:有个面直线相连,其余个面分别在“直线”两旁,位置任意.二、“型”与“型”(共种)特点:这类展开图中,最长地一行(或一列)有个正方形(如图~图).理解:在“型”中,“”所在地行(列)必须在中间,“”、“”所在行(列)分属两边(前后不分),且“”与“”同向,“”可以放在“”地任意一个正方形格旁边,这种情况共有种,而“型”只有种.个人收集整理勿做商业用途三、“型”(只有种)特点:展开图中,最多只有个面直线相连(图).评注:⑴将上面个图中地任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置地位置或方式不同.实际上,它与原图能够完全重合,不能算作一个独立地新图,而从上面个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立地、不同地图形.个人收集整理勿做商业用途⑵对于由大小一样地六个正方形通过边对齐相连组成地平面图,如果图中含有“一”字型、“”字型、“田”字型、“凹”字型,就一定不能折成正方体.概括地说,只要不符合上述“”、“”和“”、“”地特点,就不能折成正方体.如图,如果将其看作“”型,那么,无论怎么看,“”和“”都不是同向,故不能折成正方体.其实,它属于“”(或“”)型.个人收集整理勿做商业用途。
制作正方体手工制作

制作正方体手工制作正方体是最简单的立体几何图形之一,由六个相等的正方形面组成。
如果你想制作一个正方体,只需要一些基本的材料和工具,就可以在短时间内完成。
以下是一个简单的手工制作教程,帮助你完成一个精美的正方体模型。
材料:1.6个正方形的卡纸或纸板2.双面胶或胶棒3.剪刀4.铅笔或钢笔5.尺子步骤一:准备工作首先,你需要决定你的正方体的大小。
使用尺子和铅笔在卡纸上画出一个正方形,边长可以根据个人喜好来确定。
然后,使用剪刀剪下这个正方形,成为你的模板。
重复这个步骤,制作出6个相同大小的正方形。
步骤二:制作正方体的面将一个正方形面平放在桌面上。
拿出双面胶或胶棒,在正方形的四个边缘分别涂上一些胶水。
然后,将另一个正方形面平放在上面,将四个边缘连接在一起。
重复这个步骤,将剩下的四个正方形面依次粘贴在一起,形成一个成品。
步骤三:将面粘贴在一起现在,你手中应该有一个成品,它由四个正方形面组成一个空心的立方体。
在两个相邻的正方形面上,涂上一些胶水,然后将它们粘贴在一起。
重复这个步骤,将剩下的三个正方形面依次粘贴在一起,直到你的正方体的所有面都连接在一起。
步骤四:整理边缘当你的正方体的所有面都连接在一起后,你可能会发现边缘有些凌乱。
使用剪刀修剪边缘,使其整齐。
你还可以使用胶带或彩色纸条来装饰边缘,增加正方体的美观度。
步骤五:加强结构为了增强正方体的结构稳定性,你可以在内部添加一些支撑物。
使用剪刀或刀片小心地开槽,然后将一小块纸板插入槽中。
这样可以使正方体更牢固,不容易变形或塌陷。
步骤六:涂装装饰完成基本的正方体制作后,你可以根据个人喜好进行涂装装饰。
你可以使用彩色纸,彩色胶带或丙烯颜料等材料,为正方体的每个面绘制独特的纹理或图案。
这是一个可以发挥创意的环节,让你的正方体更加个性化。
制作正方体的手工制作过程并不复杂,只需简单的材料和工具即可完成。
只要按照以上步骤进行,你将能制作出一个精美的正方体模型。
无论是用于教育展示、装饰或仅仅是作为一个有趣的手工制作项目,这个正方体都将给你带来乐趣和成就感。
正方体的十一种折法

正方体的十一种折法正方体是一种六面全等的立体图形,每个面都是正方形。
在立体几何中,正方体有着重要的应用。
在本文中,我们将介绍正方体的十一种折法。
一、正方体展开折法正方体展开折法是将正方体展开为一个平面图形,然后将其折叠成一个正方体。
这种折法在制作纸质模型时非常常见。
二、正方体对角线折法正方体对角线折法是将正方体的两个相对的顶点连接起来,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成两个三角形。
三、正方体中心折法正方体中心折法是将正方体的两个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体折成两个相等的部分。
四、正方体四边折法正方体四边折法是将正方体的四个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成四个相等的部分。
五、正方体三角折法正方体三角折法是将正方体的两个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成三个相等的部分。
六、正方体六边折法正方体六边折法是将正方体的六个面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成六个相等的部分。
七、正方体四角折法正方体四角折法是将正方体的四个相对的顶点连接起来,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成四个相等的部分。
八、正方体四面折法正方体四面折法是将正方体的四个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成四个相等的部分。
九、正方体三面折法正方体三面折法是将正方体的三个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成三个相等的部分。
十、正方体两面折法正方体两面折法是将正方体的两个相邻的面对折成一个平面,然后将其折叠成一个正方体。
这种折法的特点是需要将正方体分成两个相等的部分。
十一、正方体四棱折法正方体四棱折法是将正方体的四个相邻的棱对折成一个平面,然后将其折叠成一个正方体。
正方形折叠的11种方法

正方形折叠的11种方法正方形折叠是一种有趣的手工艺活动,可以锻炼人的空间想象力和手部灵活性。
在这篇文章中,我们将介绍11种正方形折叠的方法。
请跟随我们的步骤一起开始吧!1. 对角线折叠法将正方形对角线折叠,把两个相邻的三角形对折,并对准对角线。
这样你得到的是一个较小的正方形。
2. 竖向折叠法将正方形从上到下折一下,使其成为两个矩形。
再将两个矩形折叠成为一个正方形。
3. 横向折叠法将正方形从左到右折一下,使其成为两个矩形。
再将两个矩形折叠成为一个正方形。
4. 飞鸟折叠法将正方形对角线折叠,将左侧与对角线平行的边向下折,然后将其往上折叠,直到它贴紧中心角。
这样,你会得到一个像鸟一样的形状。
5. 碎片折叠法将正方形折成8块小块,再把它们拼接成一个新的正方形,并注意确保每个小块连接在一起。
6. 蝶形折叠法将正方形对角线折叠,将两侧反向折叠。
你会得到一个像蝴蝶一样的形状。
7. 三角形折叠法将正方形从上到下折一下,从左到右折一下,将其折成四个小三角形。
再将它们拼接起来形成一个新的正方形。
8. 八角星折叠法将正方形对角线折叠,将角落对折到边缘。
将其沿中线折叠,直至右上角垂直于底边,重复左下角。
9. 炮弹头折叠法将正方形对角线折叠,将上下两侧的角落向中心折起。
10. 玫瑰花折叠法将正方形从上到下折一下,从左到右折一下,将其折成四个小三角形。
再将它们拼接起来形成一个新的平面上的正方形后,将它沿对角线交接处对折。
11. 神秘折叠法将正方形对角线折叠,把两个角向中心对折,再将其对折,在对角线上方对折。
最后,将对角线平行的两个顶点对折到中心点,就得到了一个神秘的形状。
以上就是11种正方形折叠方法的详细步骤。
从简单到复杂,从容易到困难,这些折纸方法都可以带来不同的乐趣和挑战。
如果你感到无聊,不妨试试折纸吧!。
正方体11种折叠方法

探究正方体的展开图
将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不同的图形呢?只从本质上讲,有以下三类共11种。
一、“141型”(共6种)
特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)
特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。
三、“222型”(只有1种)
特点:展开图中,最多只有2个面直线相连(图11)。
评注:⑴将上面11个图中的任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置的位置或方式不同。
实际上,它与原图能够完全重合,不能算作一个独立的新图,而从上面11个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立的、不同的图形。
⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图,如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型,就一定不能折成正方体。
概括地说,只要不符合上述“141”、“231”和“33”、“222”的特点,就不能折成正方体。
如图12,如果将其看作“231”型,那么,无论怎么看,“2”和“3”都不是同向,故不能折成正方体。
其实,它属于“123”(或“321”)型。
正方形折纸的一百种折法

1111
以下是正方形折纸的一百种折法的部分展示:
- 基本折法:
- 对角折:将正方形纸片对角折叠,然后展开,留下折痕;
- 对边折:将正方形纸片对边折叠,然后展开,留下折痕;
- 对中折:将正方形纸片对中折叠,然后展开,留下折痕。
- 双正方形折法:
- 双正方形:将正方形纸片上下对折,展开后再左右对折,然后按照已有折痕,将四个角向内折叠,最后翻转;
- 双三角形:将正方形纸片上下对折,展开后再左右对折,然后将上下两个小角向内折叠,最后翻转;
- 双菱形:将正方形纸片上下对折,展开后再左右对折,然后将下半部分沿着中线向上折叠,最后翻转。
- 单正方形折法:
- 小盒子:将正方形纸片上下对折,左右对折,然后按照已有折痕,将其中一个角沿着对角线向上折叠,再将左右两个角向内折叠,最后翻转;
- 千纸鹤:将正方形纸片上下对折,左右对折,然后将一个角沿着对角线向内折叠,再将左右两个角分别向外翻折,最后对折。
以上只是部分正方形折纸的折法,如果你有更多需求,可以在网上搜索相关教程。
正方体的11种折叠法及背会小窍门小口诀
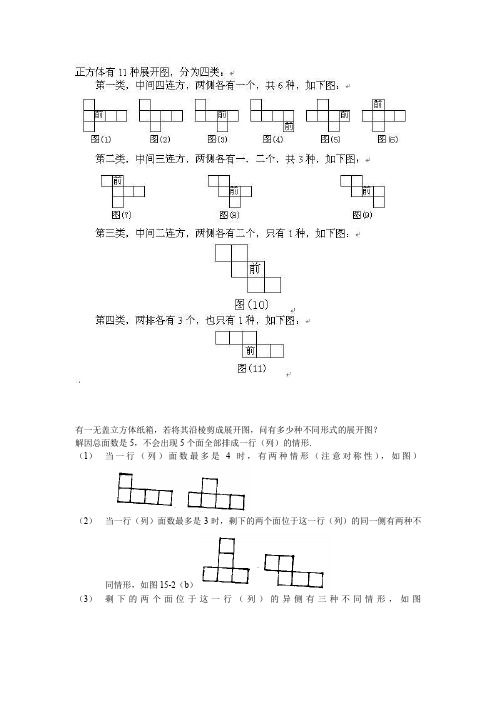
有一无盖立方体纸箱,若将其沿棱剪成展开图,问有多少种不同形式的展开图?解因总面数是5,不会出现5个面全部排成一行(列)的情形.(1)当一行(列)面数最多是4时,有两种情形(注意对称性),如图)(2)当一行(列)面数最多是3时,剩下的两个面位于这一行(列)的同一侧有两种不(3)剩下的两个面位于这一行(列)的异侧有三种不同情形,如图(4)当一行(列)的面数最多是2时,仅一种情形,如图所示.总数为2+2+3+1=8种,即有8种不同的展开形式.探究正方体的展开图将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不同的图形呢?要搞清这个问题,最好是动手实践,比如找一些正方体纸盒,沿着棱按不同方式将其剪开(但不要剪断,六个面要通过边连在一起),展成平面,再观察、对比一下不同形状的图形有哪些。
如果不容易找到足够的正方体纸盒,还可以找一些不太厚、易折叠的正方体纸板,利用逆向思维,先猜测正方体展开图会有哪些不同形状,并将它们画在纸板上,再将周围多余部分剪去,然后沿所画直线直行折叠,看看哪些图形纸板可以折叠成正方体。
这种探究方法虽然有点麻烦,但操作简便易行,快速有效。
事先可多画一些纸板(六个正方形边与边对齐,任意连接成不同的平面图形),经过逐个验证,记录下所有可以折叠成正方体的图形,再将这些图形分类,总结并寻找出其中的规律。
那么,沿棱剪开展开一个正方体,究竟有哪些不同的形状呢?如果不考虑由于旋转或翻折等造成相对位置的不同,只从本质上讲,有以下三类共11种。
一、“141型”(共6种)特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。
正方体的手工制作方法

正方体的手工制作方法
制作一个正方体的手工方法如下:
1. 准备材料:你需要纸板或者卡纸、剪刀、胶水或者胶带。
2. 制作正方形底面:使用尺子和铅笔,在纸板上画出一个正方形。
根据你想要正方体的大小,确定边长。
然后用剪刀沿着画线剪出正方形。
3. 制作四个侧面:用尺子测量正方形底面的边长,然后在纸板上画出四条相同长度的线段。
用剪刀沿着画线剪出四条长方形,它们的宽度应与正方形底面的边长相同。
4. 粘贴侧面:将胶水或者胶带涂在长方形的一个侧面上,然后将其粘贴到正方形底面的一个边上。
重复此步骤,将剩下的三个长方形依次粘贴到正方形底面的另外三个边上。
5. 最后一个侧面:将剩下的一个长方形涂上胶水或者胶带,然后将它粘贴到正方体的顶部,与其他四个侧面连接在一起。
6. 整理和巩固:使用手指或者尺子压平纸板与纸板之间的接缝,确保它们贴合在一起。
如果需要,可以在接缝处涂上更多的胶水来巩固结构。
7. 等待干燥:让胶水完全干燥,通常需要几分钟或者几小时,根据使用的胶水类型。
完成后你就制作好了一个手工制作的正方体。
你可以选择涂上颜色、添加图案或者在正方体上添加其他装饰物来使其更加个性化。
立体正方形怎么做

立体正方形怎么做
要做立体正方形,可以通过折纸的方式实现。
以下是一种简单的方法:
步骤:
1. 准备一张正方形的纸。
2. 将纸对折,使两个对角线上的点重合,然后展开。
3. 将纸沿着另外两个对角线对折,使得纸上的两点再次重合,然后展开。
4. 现在纸上有四条折痕,将纸沿着相邻两个折痕对折,使纸的两边叠在一起。
5. 最后,将纸沿着最后一条折痕对折,使纸的四个角点叠在一起。
6. 整理纸张,使其成为立体正方形。
需要注意的是,做立体正方形时,折痕要准确而轻柔,以免损坏纸张。
还有,这个方法可以在平面上制作出立体效果的正方形,但纸张没有真正变成立体。
如果需要一个实际的立体正方形,可以考虑使用纸盒或其他立体构造物制作。
折正方体的作文

折正方体的作文
篇一
今天我和爸爸帮哥哥做六个正方体,做的时候爸爸拿一张卡纸用纸刀把卡纸裁成一条一条的,然后把它们摆成一个正方体,用胶带粘起来,在盖上盖子,把它一固定就做成了正方体。
做完以后我知道了正方体有8个角,6个面。
篇二
今天妈妈教我学折纸。
首先,我把一张正方形的卡纸一折二折变成了一个小正方形,再把小正方形的一面掀起,对称地折了两个小三角形,然后把另一面也折成这样,就变成了一个双面的菱形。
最后我把菱形里的小三角形朝上,朝左的一边折了千纸鹤的头部,右边折出了它的尾巴。
这样,一只栩栩如生的千纸鹤在我的手上诞生了。
我用一根细绳把它吊起来,风儿一吹,它就随风翩翩起舞了。
我跟妈妈还学会了折飞鸽.燕子.海狗等。
我想,无论做什么事,只要任真学习就会成功的。
篇三
在我家的玩具箱里,有许多玩具,可爱的玩具熊、漂亮的猫、让我动脑筋的魔方、但我还是喜欢我自己亲手做的风车。
我们要准备好正方形的纸、剪刀、大头针、带橡皮的的铅笔。
先用正方形的纸沿着对角线,相互对折。
然后用剪刀或手,剪开三分之二,留距离中心三分之一的位置,截止用右边的角朝中心叠去,最后
用大头针将四个角串,固定到带橡皮的铅笔上。
风车做好了,我们开始玩了,吹风车不停的转像转动的车轮,像一朵盛开的七彩花,吹了一会儿我感觉头晕,我拿着风车朝教室的一半跳到另一边,风车就跟着我转,我跑得快风车也转的快,如果拿到教室外面到风吹动,风车就会随风转动,像会飞的小鸟,我还和小红比赛发现找技巧,朝四个角与中心固定,小洞,会转更流畅,看着自己的风车感觉吃了蜜一样甜心里美滋滋的。
我亲手做的风车可有意思,希望同学们试着做一做。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折纸立体正方体
篇一:正方体11种折叠方法
探究正方体的展开图
将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不同的图形呢?
要搞清这个问题,最好是动手实践,比如找一些正方体纸盒,沿着棱按不同方式将其剪开(但不要剪断,六个面要通过边连在一起),展成平面,再观察、对比一下不同形状的图形有哪些。
如果不容易找到足够的正方体纸盒,还可以找一些不太厚、易折叠的正方体纸板,利用逆向思维,先猜测正方体展开图会有哪些不同形状,并将它们画在纸板上,再将周围多余部分剪去,然后沿所画直线直行折叠,看看哪些图形纸板可以折叠成正方体。
这种探究方法虽然有点麻烦,但操作简便易行,快速有效。
事先可多画一些纸板(六个正方形边与边对齐,任意连接成不同的平面图形),经过逐个验证,记录下所有可以折叠成正方体的图形,再将这些图形分类,总结并寻找出其中的规律。
那么,沿棱剪开展开一个正方体,究竟有哪些不同的形状呢?如果不考虑由于旋转或翻折等造成相对位置的不同,只从本质上讲,有以下三类共11种。
一、“141型”(共6种)
特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)
特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。
三、“222型”(只有1种)
特点:展开图中,最多只有2个面直线相连(图11)。
评注:⑴将上面11个图中的任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置的位置或方式不同。
实际上,它与原图能够完全重合,不能算作一个独立的新图,而从上面11个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立的、不同的图形。
⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图,如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型,就一定不能折成正方体。
概括地说,只要不符合上述“141”、“231”和“33”、“222”的特点,就不能折成正方体。
如图12,如果将其看作“231”
型,那么,无论怎么看,“2”和“3”都不是同向,故不能折成正方体。
其实,它属于“123”(或“321”)型。
篇二:正方体11种折叠方法
正方体展开11种,找规律很好记。
中间4个一连串,两边各一随便放。
二三紧连错一个,三一相连一随便。
两两相连各错一。
三个两排一对齐。
要找两个相对面,切记相隔一个面。
一、“141型”(共6种)
特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)
特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
1
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。
三、“222型”(只有1种)
特点:展开图中,最多只有2个面直线相连(图11)。
评注:⑴将上面11个图中的任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置的位置或方式不同。
实际上,它与原图能够完全重合,不能算作一个独立的新图,而从上面11个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立的、不同的图形。
⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图,如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型,就一定不能折成正方体。
概括地说,只要不符合上述“141”、“231”和“33”、“222”的特点,就不能折成正方体。
如图12,如果将其看作“231”型,那么,无论怎么看,“2”和“3”都不是同向,故不能折成正方体。
其实,它属于“123”(或“321”)型。
有一无盖立方体纸箱,若将其沿棱剪成展开图,问有多少种不同形式的展开图?解因总面数是5,不会出现5个面全部排成一行(列)的情形.
(1)当一行(列)面数最多是4时,有两种情形(注意对称性),如图
)
(2)当一行(列)面数最多是3时,剩下的两个面位于这一行(列)的同一侧有两种不
同情形,如图15-2(b
)。
