matlab控制系统传递函数模型
控制系统MATLAB仿真基础

系统仿真§ 4.1控制系统的数学模型1、传递函数模型(tranfer function)2、零极点增益模型(zero-pole-gain)3、状态空间模型(state-space)4、动态结构图(Simulink结构图)一、传递函数模型(transfer fcn-----tf)1、传递函数模型的形式传函定义:在零初始条件下,系统输出量的拉氏变换C(S)与输入量的拉氏变换R(S)之比。
C(S) b1S m+b2S m-1+…+b mG(S)=----------- =- --------------------------------R(S) a1S n + a2S n-1 +…+ a nnum(S)= ------------den(S)2、在MATLAB命令中的输入形式在MATLAB环境中,可直接用分子分母多项式系数构成的两个向量num、den表示系统: num = [b1, b2, ..., b m];den = [a1, a2, ..., a n];注:1)将系统的分子分母多项式的系数按降幂的方式以向量的形式输入两个变量,中间缺项的用0补齐,不能遗漏。
2)num、den是任意两个变量名,用户可以用其他任意的变量名来输入系数向量。
3)当系统种含有几个传函时,输入MATLAB命令状态下可用n1,d1;n2,d2…….。
4)给变量num,den赋值时用的是方括号;方括号内每个系数分隔开用空格或逗号;num,den方括号间用的是分号。
3、函数命令tf( )在MATLAB中,用函数命令tf( )来建立控制系统的传函模型,或者将零极点增益模型、状态空间模型转换为传函模型。
tf( )函数命令的调用格式为:圆括号中的逗号不能用空格来代替sys = tf ( num, den ) [G= tf ( num, den )]其中,函数的返回变量sys或G 为连续系统的传函模型;函数输入参量num和den分别为系统的分子分母多项式的系数向量。
《自动控制原理》MATLAB中的传递函数模型实验

《自动控制原理》MATLAB中的传递函数模型实验一、实验目的1、熟练运用matlab软件,求解控制系统数学模型2、掌握传递函数在matlab中的表达方法3、掌握matlab求解拉氏变换和反变换4、掌握matlab求系统极值点和零点判断系统稳定性二、实验仪器Matlab2014b版三、实验原理(一)MATLAB中的传递函数模型传递函数在matlab中的表达方法控制系统的传递函数模型为:在MATLAB中,分子/分母多项式通过其系数行向量表示,即:num = [b0 b1 … bm]den = [a0 a1 … an]此时,系统的传递函数模型用tf函数生成,句法为:sys=tf(num, den) 其中,sys为系统传递函数。
如:num = [1 5 0 2]; den = [2 3 15 8];则:sys=tf(num, den)输出为:Transfer function:若控制系统的模型形式为零极点增益形式:此时,系统的传递函数模型用zpk函数生成,句法为:sys=zpk(z, p, k)。
zpk函数也可用于将传递函数模型转换为零极点增益形式,句法为:zpksys=zpk(sys)如:z=[-0.5 -1 -3]; p=[1 -2 -1.5 -5]; k=10;sys=zpk(z, p, k)传递函数的转换[num,den]=zp2tf(z,p,k)[z,p,k]=tf2zp(num,den)实际系统往往由多个环节通过串联、并联及反馈方式互连构成。
MATLAB提供的三个用于计算串联、并联及反馈连接形成的新系统模型的函数。
series函数计算两子系统串联后的新系统模型。
句法:sys = series(sys1, sys2)sys1, sys2分别为两子系统模型parallel函数计算两子系统并联后的新系统模型。
句法: sys = parallel(sys1, sys2)feedback函数计算两子系统反馈互联后的新系统模型。
matlab 传递函数零极点模型零极点相消

专题:MATLAB传递函数零极点模型及零极点相消1. 介绍MATLAB是一种用于高级技术计算和科学工程应用的计算机语言和交互式环境。
在控制系统工程方面,MATLAB被广泛应用于分析和设计传递函数模型。
传递函数模型是控制系统工程中常用的一种模型,通过分析传递函数的零极点特性可以帮助工程师理解系统的动态特性并进行系统设计和优化。
2. 传递函数零极点模型传递函数是控制系统中描述信号输入与输出之间关系的数学模型。
一般的传递函数模型可以表示为:\[G(s) = \frac{Y(s)}{U(s)} = \frac{b_m s^m + b_{m-1} s^{m-1} + ... + b_1 s + b_0}{a_n s^n + a_{n-1} s^{n-1} + ... + a_1 s + a_0}\]其中,\(Y(s)\)为系统的输出信号,\(U(s)\)为系统的输入信号,\(s\)为复变量,\(m\)和\(n\)分别为输出和输入的次数,\(b_m, b_{m-1}, ..., b_0\)和\(a_n, a_{n-1}, ..., a_0\)分别为系统的系数。
3. 零极点分析传递函数的零极点可以通过MATLAB进行分析和计算。
零点是传递函数的分子多项式为零的根,极点是传递函数的分母多项式为零的根。
零点和极点的位置决定了系统的动态特性,例如稳定性、频率响应和阶跃响应等。
3.1 零点的计算在MATLAB中,可以使用函数`zero`来计算传递函数的零点。
对于一个传递函数\(G(s) = \frac{s+1}{s^2+2s+1}\),可以通过以下命令计算其零点:```G = tf([1 1], [1 2 1]);z = zero(G)```3.2 极点的计算类似地,可以使用函数`pole`来计算传递函数的极点。
对于上述的传递函数,可以通过以下命令计算其极点:```p = pole(G)```4. 零极点相消零极点相消是控制系统设计中的一个重要概念。
用matlab建立传递函数模型

用matlab建立传递函数模型使用MATLAB建立传递函数模型在控制系统的设计和分析中,传递函数模型是一个重要的工具。
它可以帮助我们理解系统的动态行为,并提供一种有效的方式来设计控制器。
在本文中,我们将介绍如何使用MATLAB来建立传递函数模型,并展示如何利用该模型进行系统分析和控制器设计。
传递函数模型是一种数学模型,用于描述线性时不变系统的输入和输出之间的关系。
它可以表示为一个分子多项式除以一个分母多项式的比值。
在MATLAB中,我们可以使用tf函数来创建传递函数模型。
我们需要准备一个分子多项式和一个分母多项式。
这些多项式的系数可以通过实验数据或系统参数估计得到。
然后,我们可以使用tf 函数将这些多项式转换为传递函数模型。
例如,如果我们有一个二阶系统,其传递函数模型为:G(s) = (b0*s^2 + b1*s + b2) / (a0*s^2 + a1*s + a2)其中,b0、b1、b2是分子多项式的系数,a0、a1、a2是分母多项式的系数。
在MATLAB中,我们可以使用以下代码创建传递函数模型:b = [b0, b1, b2]; % 分子多项式的系数a = [a0, a1, a2]; % 分母多项式的系数G = tf(b, a); % 创建传递函数模型创建传递函数模型后,我们可以使用MATLAB提供的各种函数来进行系统分析和控制器设计。
例如,我们可以使用step函数来绘制系统的阶跃响应,使用bode函数来绘制系统的频率响应,使用pole 函数来计算系统的极点等等。
MATLAB还提供了一些用于控制器设计的工具箱,如Control System Toolbox和Robust Control Toolbox。
这些工具箱中包含了各种用于系统分析和控制器设计的函数和工具,可以帮助我们更方便地进行控制系统的设计和分析工作。
使用MATLAB建立传递函数模型是一种强大的工具,可以帮助我们理解系统的动态行为,并进行控制器设计。
matlab里控制系统的三种数学模型的转换

在MATLAB中,控制系统的建模和分析是非常重要的。
控制系统的数学模型是描述系统行为的数学表示,可以用来进行模拟、分析和设计控制系统。
在控制系统中,常见的数学模型包括积分-微分模型、状态空间模型和传递函数模型。
接下来,我将按照深度和广度的要求,对这三种数学模型进行全面评估,并据此撰写一篇有价值的文章。
1. 积分-微分模型在控制系统中,积分-微分模型是一种常见的数学表示方法。
它由两部分组成:积分部分和微分部分。
积分部分描述了系统的累积效应,微分部分描述了系统的瞬时响应。
这种模型常用于描述惯性较大、响应缓慢的系统,例如机械系统和电气系统。
在MATLAB中,可以使用积分-微分模型来进行系统建模和仿真,以分析系统的稳定性和性能指标。
2. 状态空间模型状态空间模型是另一种常见的控制系统数学表示方法。
它由状态方程和输出方程组成,用来描述系统的状态变量和外部输入之间的关系。
状态空间模型适用于描述多变量、多输入多输出系统,例如飞行器、汽车控制系统等。
在MATLAB中,可以使用状态空间模型来进行系统分析和设计,包括系统的稳定性、可控性和可观性分析,以及控制器设计和系统性能评价。
3. 传递函数模型传递函数模型是控制系统中最常用的数学表示方法之一。
它用传递函数来描述系统的输入和输出之间的关系,其中传递函数是输入信号和输出信号的比值。
传递函数模型适用于描述单输入单输出系统,例如电路系统、机械系统等。
在MATLAB中,可以使用传递函数模型进行系统分析和设计,包括频域分析、极点和零点分析,以及控制器设计和系统稳定性评估。
总结回顾:在本文中,我按照深度和广度的要求对MATLAB中控制系统的三种数学模型进行了全面评估。
我从积分-微分模型入手,介绍了其构成和适用范围。
我转而讨论了状态空间模型,阐述了其在多变量系统中的重要性。
我详细介绍了传递函数模型,强调了其在单输入单输出系统中的广泛应用。
在文章的我共享了对这三种数学模型的个人观点和理解,指出了它们在控制系统中的重要性和实用性。
matlab 控制系统仿真

摘要MATLAB语言是一种十分有效的工具,能容易地解决在系统仿真及控制系统计算机辅助设计领域的教学与研究中遇到的问题,它可以将使用者从繁琐的底层编程中解放出来,把有限的宝贵时间更多地花在解决科学问题上。
MATLAB GUI 是MATLAB的人机交互界面。
由于GUI本身提供了windows基本控件的支持,并且具有良好的事件驱动机制,同时提供了MATLAB数学库的接口,所以GUI 对于控制系统仿真的平台设计显得十分合适。
GUI对于每个用户窗口生成.fig和.m 文件。
前者负责界面的设计信息,后者负责后台代码的设计。
本文所做的研究主要是基于MATLAB GUI平台,结合控制系统基础理论和MATLAB控制系统工具箱,实现了用于控制系统计算机辅助分析与设计的软件。
本软件主要功能:实现传递函数模型输入、状态方程模型输入、模型装换、控制系统稳定性分析、系统可观性可控性判断,绘制系统奈奎斯特图、波特图、根轨迹图以及零极点分布图。
在继续完善的基础上能够用于本科自动控制原理教程的教学实验和一般的科学研究。
关键词:控制系统;MATLAB GUI;计算机辅助设计AbstractMATLAB language is a very effective tool,and can be easily resolved in the system simulation and control system of teaching in the field of computer-aided design and research problems,it could be the bottom of the user from tedious programming liberate the limited spend more valuable time to solve scientific problems.The MATLAB GUI is the interactive interface.As the GUI itself provides the basic control windows support,and has a good mechanism for event-driven,while providing the MATLAB Math Library interface,the GUI for control system simulation platform for the design of it is suitable. GUI window generated for each user. Fig and.M file. The former is responsible for the design of the interface information,which is responsible for the design of the background code.Research done in this article is mainly based on MATLAB GUI platform,the basis of combination of control system theory and MATLAB Control System Toolbox,the realization of control systems for computer-aided analysis and design software. The main functions of the software: the realization of transfer function model input,the state equation model input,the model fitted for the control system stability analysis,system observability controllability judgments、rendering the system Nyquist diagram、Bode plots、root locus and Pole-zero distribution. While continuing to improve based on the principle of automatic control can be used for undergraduate teaching course experiments and scientific research in general.Key words:Control System;MATLAB GUI; Computer-assistant design目录第1章概述 (1)1.1 论文选题背景和意义 (1)1.2 计算机辅助分析与设计在控制系统仿真中的发展现状 (1)1.3 本文主要内容 (3)第2章控制系统与MATLAB语言 (4)2.1 控制系统理论基础 (4)2.2 MATLAB语言与控制系统工具箱 (5)第3章 MATLAB GUI简介及应用 (9)3.1 MATLAB GUI (9)3.2 软件设计步骤 (10)第4章仿真系统测试与演示 (16)4.1 控制系统的模型输入 (16)4.2 控制系统的稳定性分析 (19)4.3 控制系统可控可观性分析 (20)4.4 控制系统频率响应 (23)4.5 控制系统时域响应 (27)4.6 控制系统根轨迹绘制 (28)结论 (31)参考文献 (32)致谢 (33)第1章概述1.1 论文选题背景和意义自动控制原理是自动控制专业和自动化专业的主要课程之一,是研究自动控制技术的基础理论课,是必修的专业基础课程。
用matlab建立传递函数模型

用matlab建立传递函数模型用MATLAB建立传递函数模型在现代控制系统中,传递函数模型是一种常用的数学模型,用于描述信号在系统中的传递过程。
传递函数模型可以帮助我们理解和分析系统的动态特性,并为控制系统的设计和优化提供基础。
在本文中,我们将介绍如何使用MATLAB建立传递函数模型,并展示其在实际应用中的一些例子。
让我们明确传递函数的定义。
传递函数是输入和输出之间的关系,通常用分子多项式和分母多项式的比值来表示。
在MATLAB中,可以使用tf函数来创建传递函数对象。
例如,创建一个传递函数模型为G(s) = (s+1)/(s^2+2s+1)的对象,可以使用以下代码:G = tf([1 1],[1 2 1]);在这个例子中,分子多项式的系数为[1 1],分母多项式的系数为[1 2 1]。
tf函数会自动将这些系数转换为传递函数对象。
有了传递函数对象后,我们可以使用MATLAB的控制系统工具箱来进行各种分析和设计。
例如,我们可以使用step函数来绘制系统的单位阶跃响应曲线。
以下是一个绘制传递函数对象G的单位阶跃响应曲线的例子:step(G);除了绘制单位阶跃响应曲线外,MATLAB还提供了许多其他功能来分析和设计控制系统。
例如,我们可以使用bode函数来绘制系统的频率响应曲线,使用nyquist函数来绘制系统的奈奎斯特曲线,使用margin函数来计算系统的增益裕度和相位裕度等。
这些功能都可以帮助我们更好地理解和优化控制系统。
除了基本的传递函数模型外,MATLAB还支持复杂的系统建模和分析。
例如,我们可以使用串联、并联和反馈等操作来组合多个传递函数模型,以建立更复杂的系统模型。
此外,MATLAB还支持离散系统建模和分析,以及状态空间模型的建立和分析。
除了传递函数模型外,MATLAB还提供了其他类型的数学模型和工具,以满足不同的应用需求。
例如,MATLAB的神经网络工具箱可以用于建立和训练神经网络模型,MATLAB的图像处理工具箱可以用于图像处理和分析等。
MATLAB进行控制系统频域分析

一、基于MATLAB 的线性系统的频域分析基本知识(1)频率特性函数)(ωj G 。
设线性系统传递函数为:nn n n m m m m a s a s a s a b s b s b s b s G ++⋅⋅⋅++++⋅⋅⋅++=---1101110)( 则频率特性函数为:nn n n m m m m a j a j a j a b j b j b j b jw G ++⋅⋅⋅++++⋅⋅⋅++=---)()()()()()()(1101110ωωωωωω 由下面的MATLAB 语句可直接求出G(jw )。
i=sqrt (—1) % 求取—1的平方根GW=polyval (num ,i*w )./polyval(den ,i*w )其中(num ,den )为系统的传递函数模型。
而w 为频率点构成的向量,点右除(./)运算符表示操作元素点对点的运算.从数值运算的角度来看,上述算法在系统的极点附近精度不会很理想,甚至出现无穷大值,运算结果是一系列复数返回到变量GW 中。
(2)用MATLAB 作奈魁斯特图。
控制系统工具箱中提供了一个MATLAB 函数nyquist( ),该函数可以用来直接求解Nyquist 阵列或绘制奈氏图。
当命令中不包含左端返回变量时,nyquist ()函数仅在屏幕上产生奈氏图,命令调用格式为:nyquist(num ,den) nyquist (num,den ,w) 或者nyquist(G) nyquist(G,w ) 该命令将画出下列开环系统传递函数的奈氏曲线: )()()(s den s num s G = 如果用户给出频率向量w ,则w 包含了要分析的以弧度/秒表示的诸频率点。
在这些频率点上,将对系统的频率响应进行计算,若没有指定的w 向量,则该函数自动选择频率向量进行计算。
w 包含了用户要分析的以弧度/秒表示的诸频率点,MATLAB 会自动计算这些点的频率响应。
当命令中包含了左端的返回变量时,即:[re,im ,w]=nyquist (G )或[re ,im,w ]=nyquist (G ,w ) 函数运行后不在屏幕上产生图形,而是将计算结果返回到矩阵re 、im 和w 中。
MATLAB控制系统各种仿真例题(包括simulink解法)

一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ,T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5)); GTransfer function:s^3 + 4 s + 2 ------------------------------------------------------ s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]); H=tf(num,den,'Ts',0.1)Transfer function: z^2 + 0.56 ----------------------------- z^3 - 1.2 z^2 + 1.19 z - 0.992. 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点,并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ,T=0.05s>>z=[-1-j -1+j]; p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain: 8 (s^2 + 2s + 2) -------------------------- s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6]; p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846) ------------------------- (z-0.122)Sampling time: 0.05>>pzmap (H )二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
matlab pi控制传递函数

matlab pi控制传递函数
在MATLAB中,我们可以使用控制系统工具箱来处理和分析控制
系统的传递函数。
要创建一个传递函数模型,可以使用tf函数,该
函数的语法是tf(num,den),其中num和den分别是传递函数的分
子和分母多项式的系数。
例如,要创建一个传递函数G(s) =
(s+2)/(s^2+3s+5),可以使用以下代码:
num = [1 2];
den = [1 3 5];
G = tf(num,den);
接下来,如果要设计一个PI控制器来控制这个传递函数,可以
使用控制系统工具箱中的pid函数。
pid函数的语法是pid(Kp,Ki),其中Kp是比例增益,Ki是积分增益。
例如,要设计一个PI控制器,可以使用以下代码:
Kp = 1;
Ki = 1;
C = pid(Kp,Ki);
然后,可以使用feedback函数将传递函数和控制器连接起来,
形成闭环控制系统。
feedback函数的语法是feedback(sys1,sys2),其中sys1是传递函数,sys2是控制器。
例如,将传递函数G和控
制器C连接起来,可以使用以下代码:
T = feedback(GC,1);
最后,可以使用step函数来绘制系统的阶跃响应图。
例如,使
用以下代码来绘制系统的阶跃响应图:
step(T);
这样就可以在MATLAB中使用PI控制器来控制给定的传递函数。
当然,在实际应用中,还需要根据具体的控制要求和系统特性来调
整控制器的参数,以达到理想的控制效果。
MATLAB应用-传递函数与画图

用MATLAB求系统的零点、极点 及特征多项式
• 部分分式展开
n−1 +⋅⋅⋅+bn−1s +bn M(s) num b0sn +bs 1 = = 考虑传递函数:N(s) den a sn +asn−1 +⋅⋅⋅+a s +a 0 1 n−1 n
带有选项的曲线绘制命令的调用格式: plot(x1,y1,s1,x2,y2,s2,…)
用MATLAB绘制二维图形
• 子图的命令
MATLAB允许将一个图形窗口按矩阵形式分成多个子 窗口,分别显示多个图形,需要用到subplot( )函数。 该函数把一个图形窗口分割成m*n个子绘图区域。调 用格式:subplot (m, n, k) 例如:subplot(4,3,6)表示将窗口分割成4*3个部 分,在第6 个部分上绘制图像。 通过参考数 k 可以调用各个绘图区域,子绘图区域按 注意:MATLAB最多允许9*9的分割。 行从左到右从上到下编号。
10s + 5 G2 ( s ) = s
H (s) =
1 0.01s + 1
用MATLAB建立传递函数模型
• 多项式模型TF和零极点模型ZPK的转换 • TF对象转换成ZPK对象 调用格式为:G1=zpk(G) 例
6.8s 2 + 61.2 s + 95.2 G (s) = 4 s + 7.5s 3 + 22 s 2 + 19.5s
用MATLAB建立传递函数模型
• 多项式模型—TF对象(单入—单出系统) 线性时不变(LTI)系统的传递函数模型:
Matlab下的控制系统描述

》num=[0 0 -2;0 -1 -5;1 2 0];den=[1 6 11 6]; 》[A,B,C,D]=tf2ss(num,den) 》A= -6 -11 -6 B= 1 C= 0 0 -2 D= 0 1 0 0 0 0 -1 -5 0 0 1 0 0 1 2 0 0
3)系统的零极点增益模型:
状态空间实现与相似变换函数 ss 状态空间实现 ssbal (与 balance 有关)用对角相似变换矩阵对状态 空间模型进行平衡化,有利于提高计算精度. balreal :输入/输出平衡实现,可用于模型降阶. minreal :最小实现 或零极相消.对传递函数模型进行 零极相消;对状态空间模型则消去不可控或 不可观状态. ctrbf : 可控阶梯型 obsvf :可观阶梯型 以上函数的详细说明参见pdf帮助文档.
对线性定常系统,式中s的系数均为常数,且a1不等于零, 这时系统在MATLAB中可以方便地由分子和分母系数构成的 两个向量唯一地确定出来,这两个向量分别用num和den 表示. num=[b1,b2,…,bm,bm+1] den=[a1,a2,…,an,an+1] 注意:它们都是按s的降幂进行排列的. 应用 TF 函数可以创建传递函数模型.
模型变换注意事项
用法举例: 1)已知系统状态空间模型为:
》A=[0 1; -1 -2]; B=[0;1]; 》C=[1,3]; D=[1]; 》[num,den]=ss2tf(A,B,C,D,iu) %iu用来指定第n个输入,当只有一个输入时可忽略. 》num=1 5 2; den=1 2 1; 》[z,p,k]=ss2zp(A,B,C,D,iu) 》z= -4.5616 p= -1 k=1 -0.4384 -1
结构体可看作是MATLAB下的小型数据库.有关结构体 的内容可参见 Help 浏览器中的 Matlab/programing and data types/structures and arrays 类和对象的概念是面向对象程序设计的基础.类的 概念是结构体的拓展.对象是指类的一个实例. 在此我们只介绍类和对象的使用,没有涉及内部构造与 编程方法,有关内容可参考Help 浏览器中的 Matlab/programing and data types/Matlab classes and Objects 针对传递函数,状态空间,零极点增益和 FRD 等系 统描述方式,MATLAB 控制系统工具箱提供了四种专门的 数据结构(LTI objects),称作 TF,SS,ZPK,FRD 对象.
用matlab建立传递函数模型

用matlab建立传递函数模型
建立传递函数模型是控制系统设计中的重要步骤之一。
在matlab 中,我们可以使用Transfer Function模块来建立传递函数模型。
本文将介绍如何使用matlab建立传递函数模型。
我们需要打开matlab软件,并在命令窗口中输入“tf”命令,即可打开Transfer Function模块。
在Transfer Function模块中,我们可以输入传递函数的分子和分母多项式系数,以建立传递函数模型。
例如,假设我们要建立一个传递函数模型为:
G(s) = (s+1)/(s^2+2s+1)
其中,s为复变量。
我们可以将分子和分母多项式系数输入到matlab中,如下所示:
num = [1 1];
den = [1 2 1];
其中,num表示分子多项式系数,den表示分母多项式系数。
输入完毕后,我们可以使用“tf”命令来建立传递函数模型,如下所示: G = tf(num, den);
建立完传递函数模型后,我们可以使用“step”命令来绘制系统的阶跃响应曲线,如下所示:
step(G);
绘制出的阶跃响应曲线如下图所示:
从图中可以看出,系统的阶跃响应曲线呈现出一定的超调量和振荡现象,这是由于系统的极点位置导致的。
如果需要改善系统的性能,我们可以通过调整传递函数的分子和分母多项式系数来改变系统的极点位置,从而达到优化系统性能的目的。
使用matlab建立传递函数模型是控制系统设计中的重要步骤之一。
通过建立传递函数模型,我们可以分析系统的性能特点,并通过调整传递函数的分子和分母多项式系数来改善系统的性能。
MATLAB控制系统的仿真
C R
x1 x2
0 1
L
u
L
y [1
0]
x1 x2
[0]u
•
x Ax bu
y CT x du
• 没有良好的计算工具前:系统建立、变换、分析、设 计、绘图等相当复杂。
• MATLAB控制系统软件包以面向对象的数据结构为基 础,提供了大量的控制工程计算、设计库函数,可以 方便地用于控制系统设计、分析和建模。
Transfer function:
s+1 ------------s^2 + 5 s + 6
Matlab与系统仿真
22
应用——系统稳定性判断
系统稳定性判据: 对于连续时间系统,如果闭环极点全部在S平面左半平面,
则系统是稳定的;
若连续时间系统的全部零/极点都位于S左半平面, 则系统是——最小相位系统。
Matlab与系统仿真
38
4.2 动态特性和时域分析函数
(一)动态特性和时域分析函数表 (二)常用函数说明 (三)例子
Matlab与系统仿真
39
(一)动态特性和时域分析函数表 ——与系统的零极点有关的函数
表8.6前部分p263
Matlab与系统仿真
40
——与系统的时域分析有关的函数
Matlab与系统仿真
Matlab与系统仿真
8
4.1 控制工具箱中的LTI对象
Linear Time Invariable
(一)控制系统模型的建立 (二)模型的简单组合 (三)连续系统和采样系统变换(*略)
Matlab与系统仿真
9
(一)控制系统模型的建立
➢ MATLAB规定3种LTI子对象:
• Tf 对象—— 传递函数模型 • zpk 对象—— 零极增益模型 • ss 对象—— 状态空间模型
MATLAB的控制系统数学建模

赵广元.MATLAB与控制系统仿真实践,
北京航空航天大学出版社,2009.8.
在线交流,有问必答
8
后我们所讨论的系统主要以线性定常连续系 统为主。
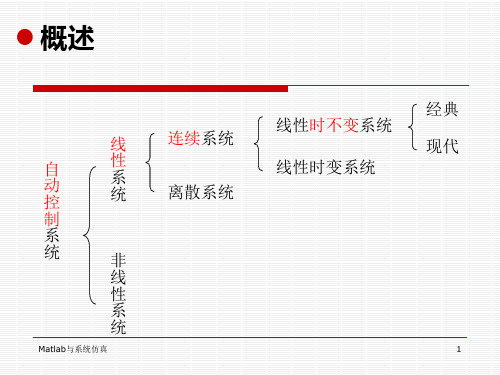
(2)线性定常离散系统: 离散系统指系统的某处或多处的信号
为脉冲序列或数码形式。这类系统用差分 方程(difference equations)来描述。 (3)非线性系统:
方式2:
>> s=tf(‘s’)
%定义Laplace算子
Transfer function:
s >> G=10*(2*s+1)/s^2/(s^2+7*s+13) %直接给出系统传递函
数表达式
Transfer function:
20 s + 10
s^4 + 7 s^3 + 13 s^2
--------------------
赵广元.MATLAB与控制系统仿真实践,
北京航空航天大学出版社,2009.8.
在线交流,有问必答
10
控制系统的传递函数模型
MATLAB与控制系统仿真实践,
北京航空航天大学出版社,2009.8.
在线交流,有问必答
12
本节主要内容
系统传递函数模型简述 传递函数的MATLAB相关函数 10.1.3 建立传递函数模型实例
北京航空航天大学出版社,2009.8.
在线交流,有问必答
7
原理要点——系统分类
按系统性能分:
线性系统和非线性系统;连续系统和 离散系统;定常系统和时变系统;确定系 统和不确定系统。
(1)线性连续系统: 用线性微分方程式(differential equations)
实验二用MATLAB建立传递函数模型

《自动控制原理》实验指导书北京科技大学自动化学院控制科学与工程系2013年4月目录实验一典型系统的时域响应和稳定性分析 (1)实验二用MATLAB建立传递函数模型 (5)实验三利用MATLAB进行时域分析 (13)实验四线性定常控制系统的稳定分析 (25)实验五利用MATLAB绘制系统根轨迹 (29)实验六线性系统的频域分析 (37)实验七基于MATLAB控制系统频域法串联校正设计 (51)附录1 MATLAB简介 (58)附录2 SIMULINK简介 (67)实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
图1-1(2) 对应的模拟电路图:如图1-2所示。
图1-2(3) 理论分析系统开环传递函数为:G(s)=?开环增益:K=?先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确地1-1中的参数。
0?T =, 1?T =,1?K = ?K ⇒=系统闭环传递函数为:()?W s =其中自然振荡角频率:?n ω=;阻尼比:?ζ=。
2.典型的三阶系统稳定性分析(1) 结构框图:如图1-3所示。
图1-3(2) 模拟电路图:如图1-4所示。
图1-4(3) 理论分析系统的开环传函为:()()?G s H s =系统的特征方程为:1()()0G s H s +=。
(4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 S 2 S 1 S 0为了保证系统稳定,第一列各值应为正数,因此可以确定系统稳定K值的范围系统临界稳定K系统不稳定K值的范围四、实验步骤1)将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
实验一 基于Matlab的控制系统仿真

实验一 基于Matlab 的控制系统模型姓名 学号 班级一、实验目的1) 熟悉Matlab 的使用环境,学习Matlab 软件的使用方法和简单编程方法。
2) 学习使用Matlab 软件进行拉氏变换和拉式反变换的方法。
3) 学习使用Matlab 软件建立、转换连续系统数学模型的方法。
4) 学习使用Matlab 软件分析控制系统稳定性的方法。
二、实验原理1. 拉氏变换和反拉氏变换(1) 拉氏变换syms a w tf1=exp(-a*t)laplace(f1)f2=2laplace(f2)f3=t*exp(-a*t)laplace(f3)f4=sin(w*t)laplace(f4)f5=exp(-a*t)*cos(w*t)laplace t-t (f5)(2) 拉氏反变换syms s a wf 1=1/silaplace(f 1)f 2=1/(s+a)ilaplace(f 2)f 3=1/s^2ilaplace(f 3)f 4=w/(s^2+w^2)ilaplace(f 4)f 5=1/(s*(s+2)^2*(s+3))ilaplace(f 5)…2. 控制系统模型的建立和转化传递函数模型:112m112+()+m m n n nb s b s b num G s den a s a s b --++==++……零极点增益模型:1212()()()()()()()m ns z s z s z G s k s p s p s p ---=---(1) 建立系统传递函数模型22(1)()(2)(3)56s s s sG s s s s s ++==++++num=[1,1,0]den=[1,5,6]Gs1=tf(num,den)(2) 建立系统的零极点模型z=[0,-1]p=[-2,-3]k=[1]Gs1=zpk(z,p,k)(3) 传递函数模型转化为零极点模型num=[1,1,0]den=[1,5,6]Gs1=tf(num,den)[z,p,k]=tf2zp(num,den)Gs2=zpk(z,p,k)(4) 零极点模型转化为传递函数模型z=[0,-1]p=[-2,-3]k=[1]Gs1=zpk(z,p,k)[num,den]=zp2tf(z',p',k)Gs2=tf(num,den)3. 用Matlab 进行传递函数部分分式展开5434321139+52s+26()1035+50s+241 2.530.5 1s+4s+3s+2s+1num s s s G s den s s s ++==++-=++++num=[1 11 39 52 26]den=[1 10 35 50 24][r,p,k]=residue(num,den)4. 连续系统稳定性分析已知传递函数,试求该系统的闭环极点并判断系统的稳定性。
matlab中的tfest函数

【matlab中的tfest函数:全面解析】在matlab中,tfest函数是一个非常重要的工具,它用于估计连续时间线性系统的传递函数模型。
本文将从简单到复杂的角度,全面解析tfest函数的使用方法、原理和实际应用。
1. tfest函数的基本介绍tfest函数是matlab控制系统工具箱中的一个函数,用于利用时间域数据来估计连续时间线性系统的传递函数模型。
这个函数在工业控制系统、信号处理领域、自动化领域等方面有着广泛的应用。
在matlab 中,我们可以通过tfest函数来拟合传递函数模型,从而对系统进行建模和分析。
2. tfest函数的使用方法在使用tfest函数时,首先需要准备好时间域数据。
这些数据可以是实际测量得到的系统响应,也可以是仿真或实验得到的数据。
我们需要指定传递函数模型的阶数和类型。
接下来,通过调用tfest函数,传入时间域数据和传递函数类型等参数,即可得到估计的传递函数模型。
举个例子,假设我们有一组输入-输出数据,我们可以通过以下代码来估计系统的传递函数模型:```sys_est = tfest(data, n, m);```其中,data是时间域数据,n是传递函数的分子阶数,m是传递函数的分母阶数。
通过这样简单的调用,我们就可以得到一个估计的传递函数模型sys_est。
3. tfest函数的原理tfest函数的原理是基于最小二乘法来进行参数估计。
它使用输入-输出数据来拟合传递函数模型,从而找到最优的参数。
在这个过程中,tfest函数会进行参数的优化和模型的拟合,以最大程度地符合实际数据的变化规律。
4. tfest函数的实际应用tfest函数在实际应用中有着广泛的用途。
在控制系统设计中,我们可以利用tfest函数来进行系统辨识和建模,从而设计出更加准确和高效的控制策略。
在信号处理领域,tfest函数可以用来拟合信号的频率响应特性,实现信号的分析和处理。
5. 个人观点和理解对于tfest函数,我个人认为它是一个非常强大的工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB及
控制系统仿真
实验
班级:智能0702
姓名:刘保卫
学号: 06074053(18)
实验四控制系统数学模型转换及MATLAB实现
一、实验目的
熟悉MATLAB 的实验环境。
掌握MATLAB 建立系统数学模型的方法。
二、实验内容
(注:实验报告只提交第2 题)
1、复习并验证相关示例。
(1)系统数学模型的建立
包括多项式模型(Transfer Function,TF),零极点增益模型(Zero-Pole,ZP),状态空间模型
(State-space,SS);
(2)模型间的相互转换
系统多项式模型到零极点模型(tf2zp),零极点增益模型到多项式模型(zp2tf),状态空间模
型与多项式模型和零极点模型之间的转换(tf2ss,ss2tf,zp2ss…);
(3)模型的连接
模型串联(series),模型并联(parallel),反馈连接(feedback)
2、用MATLAB 做如下练习。
(1)用2 种方法建立系统的多项式模型。
程序如下:
%建立系统的多项式模型(传递函数)
%方法一,直接写表达式
s=tf('s')
Gs1=(s+2)/(s^2+5*s+10)
%方法二,由分子分母构造
num=[1 2];
den=[1 5 10];
Gs2=tf(num,den)
figure
pzmap(Gs1)
figure
pzmap(Gs1)
grid on
运行结果:
易知两种方法结果一样
Transfer function:
s
Transfer function:
s + 2
--------------
s^2 + 5 s + 10
Transfer function:
s + 2
--------------
s^2 + 5 s + 10
(2)用2 种方法建立系统的零极点模型和多项式模型。
程序如下:
%方法一
s=tf('s')
Gs1=10*(s+1)/((s+1)*(s+5)*(s+10))
% zpk模型
ZPK=zpk(Gs1)
%方法二
% tf模型
num=[10 10];
den=conv([1 1],conv([1 5],[1 10]));
Gs2=tf(num,den)
% zpk模型
ZPK=zpk(Gs2)
figure
pzmap(Gs1)
figure
pzmap(Gs1)
grid on
运行结果:
易知两种方法结果一样
Transfer function:
s
Transfer function:
10 s + 10
------------------------
s^3 + 16 s^2 + 65 s + 50
Zero/pole/gain:
10 (s+1)
------------------
(s+10) (s+5) (s+1)
Transfer function:
10 s + 10
------------------------
s^3 + 16 s^2 + 65 s + 50
Zero/pole/gain:
10 (s+1)
------------------
(s+10) (s+5) (s+1)
(3)如图,已知G(s)和H(s)两方框对应的微分方程是:
且初始条件为零。
试求传递函数C(s)/R(s)及E(s)/R(s)。
程序如下:
%求微分方程的传递函数C(s)/R(s),E(s)/R(s)
%求Gs=Cs/Rs
n1=[20];
d1=[6 10];
Gs=tf(n1,d1)
%求Hs=Bs/Cs
n2=[10];
d2=[20 5];
Hs=tf(n2,d2)
% C(s)/R(s)
sys=feedback(Gs,Hs)
% E(s)/R(s)=(Es/Cs)*(Cs/Rs)
ER=sys/Gs
运行结果:
Transfer function:
20
-------- % Gs=Cs/Rs
6 s + 10
Transfer function:
10
-------- % Hs=Bs/Cs
20 s + 5
Transfer function:
400 s + 100
--------------------- % C(s)/R(s)
120 s^2 + 230 s + 250
Transfer function:
2400 s^2 + 4600 s + 1000
------------------------ % E(s)/R(s)=(Es/Cs)*(Cs/Rs) 2400 s^2 + 4600 s + 5000。
