船舶静力学作业题答案
大连理工大学考研专业课 船舶静力学课后习题答案

Statics of the ShipExercise响砂山月牙泉第一章复习思考题1.船舶静力学研究哪些内容?2.在船舶静力学计算中,坐标系统是怎样选取的? 3.作图说明船体的主尺度是怎样定义的?其尺度比的主要物理意义如何?4.作图说明船形系数是怎样定义的?其物理意义如何?试举一例说明其间的关系。
5.对船体近似计算方法有何要求?试说明船舶静力学计算中常用的近似计算法有哪几种?其基本原理、适用范围以及它们的优缺点。
复习思考题6.提高数值积分精确度的办法有哪些?并作图说明梯形法、辛浦生法对曲线端点曲率变化较大时如何处理?以求面积为例,写出其数值积分公式。
7.分别写出按梯形法,辛浦拉法计算水线面面积的积分公式,以及它们的数值积分公式和表格计算方法。
(5,8,-1) 法、(3,10,-1)法的适用范围。
8.写出计算水线面面积的漂心位置和水线面面积对x 轴y轴的惯性矩的积分公式。
并应用求面积的原理写出其数值积分公式和表格计算方法。
复习思考题9.如何应用乞贝雪夫法?试以九个乞贝雪夫坐标,写出求船舶排水体积的具体步骤。
10.说明积分曲线、重积分曲线与原曲线的关系.并以水线面面积曲线为例说明积分曲线、重积分曲线的应用。
Exercise 1-1已知: L=155m,B=18m,d=7.1m,V=10900m 3,Am=115m 2, Aw=1980m 2求:Cb=V/LBd=10900/(155Cb=V/LBd=10900/(155**1818**7.1)=0.550 Cp=V/Lam=10900/(155 Cp=V/Lam=10900/(155**115)=0.62 Cw=Aw/BL=19800/(18 Cw=Aw/BL=19800/(18**155)=0.710 Cm=Am/Bd=115/(18 Cm=Am/Bd=115/(18**7.1)=0.900 Cvp=V/Awd=10900/(1980 Cvp=V/Awd=10900/(1980**7.1)=0.775 某海洋客船L=155m ,B=18m ,d=7.1m ,V=10900m3,Am=115m 2,Aw=1980m 2。
船舶静力学习题答案

Exercise 1-3
某内河驳船的水下体积V=4400m3,吃水d=2.6m,方形系数Cb=0.815,水线面系 数Cw=0.882,求水线面面积Aw。
已知:Cb=0.815;Cw=0.882;V=4400t 解:Cvp=Cb/Cw=0.815/0.882=0.924
∵Cvp=V/(Aw.d) ∴Aw=V/(Cvp.d)=4400/(0.924*2.6)=1831.5 m2
Exercise 1-1
∵Am=πr2/2 Aw=2*0.2*4r*r=4r2 V=1/3(πr2)*2r=2/3 πr3
∴Cm=Am/(2r*r)= π/4=0.785 Cp=V/(1/2πr2*4r)= 1/3=0.333 Cwp=Aw /(4r*2r)= 1/2=0.500 Cb=V/(4r*2r*r)=π/12=0.261 Cvp=V/(4r2*r)=π/6=0.522
船舶静力学作业
船舶静力学习题答案
响砂山月牙泉
Exercise 1-1
1-1 两相等的正圆锥体在底部处相连接,每个锥体的高等于其底部直径.这个组 合体浮于水面,使其两个顶点在水表面上,试绘图并计算: (1)中横剖面系数Cm,(2)纵向棱形系数Cp, (3)水线面系数Cw,(4)方形系数Cb。
V=(A *h)/3 d
Exercise 1-4源自各站型值:Bx2
y2[1(0.5L)2]
序
0
1
2
3
4
5
6
7
8
9
10
x -30
-24
-18
-12
-6
0
6
12
18
24
30
y
0
1.512 2.688 3.528 4.032 4.2 4.032 3.528 2.688 1.512
_船舶静力学课后习题答案

A=δφ[∑yi-(y0-yn)/2]=0.524*(3.723-0)=1.956
2.辛浦森法:
Exercise 1-8
2.辛普森法:
半宽yi 辛普森数 乘积
0 0 1 0
30 0.5 4 2
60 0.866 2 1.732
90 1 4 4
120 0.866 2 1.732
150 0.5 4 2
180 0 1 0
Exercise 2-1
计算如图所示浮船坞水线面的有效面积对倾斜轴xx和
yy的惯性矩。巳知坞长L=75m,坞宽B=21m,b=2.2m。
Ixx=2{1/12*75*2.23 +(75*2.2)[(21-2.2)/2]2} =2(66.55+165*9.42)
= 29291.9m
4
Iyy=2*1/12*2.2*753
Exercise 1-2
∵Am=πr2/2
Aw=2*0.2*4r*r=4r2 V=1/3(πr2)*2r=2/3 πr3
∴Cm=Am/(2r*r)= π/4=0.785
Cp=V/(1/2πr2*4r)= 1/3=0.333
Cwp=Aw /(4r*2r)= 1/2=0.500 Cb=V/(4r*2r*r)=π/12=0.261 Cvp=V/(4r 2 *r)=π/6=0.522
∴Aw=V/(Cvp.d)=4400/(0.924*2.6)=1831.5 m2
Exercise 1-7
某军舰 L=92m;B=9.1m;d=2.9m;Cb=0.468;Cm=0.814 求排水体积V、舯横剖面面积、纵向棱形系数。 解:V=Cb.LBd=0.468*92*9.1*2.9=1136.25 m3 Am=Cm.Bd=0.814*9.1*2.9=21.48 m2 Cp=Cb/Cm=0.468/0.814=0.575
船舶静力学课后复习题答案

Statics of the Ship响砂山月牙泉第一章复习思考题1.船舶静力学研究哪些内容?2.在船舶静力学计算中,坐标系统是怎样选取的?3.作图说明船体的主尺度是怎样定义的?其尺度比的主要物理意义如何?4.作图说明船形系数是怎样定义的?其物理意义如何?试举一例说明其间的关系。
5.对船体近似计算方法有何要求?试说明船舶静力学计算中常用的近似计算法有哪几种?其基本原理、适用范围以及它们的优缺点。
复习思考题6.提高数值积分精确度的办法有哪些?并作图说明梯形法、辛浦生法对曲线端点曲率变化较大时如何处理?以求面积为例,写出其数值积分公式。
7.分别写出按梯形法,辛浦拉法计算水线面面积的积分公式,以及它们的数值积分公式和表格计算方法。
(5,8,-1) 法、(3,10,-1)法的适用范围。
8.写出计算水线面面积的漂心位置和水线面面积对x轴y轴的惯性矩的积分公式。
并应用求面积的原理写出其数值积分公式和表格计算方法。
复习思考题9.如何应用乞贝雪夫法?试以九个乞贝雪夫坐标,写出求船舶排水体积的具体步骤。
10.说明积分曲线、重积分曲线与原曲线的关系.并以水线面面积曲线为例说明积分曲线、重积分曲线的应用。
Exercise 1-1已知: L=155m,B=18m,d=7.1m,V=10900m3,Am=115m2,Aw=1980m2求:Cb=V/LBd=10900/(155*18*7.1)=0.550Cp=V/Lam=10900/(155*115)=0.62Cw=Aw/BL=19800/(18*155)=0.710Cm=Am/Bd=115/(18*7.1)=0.900Cvp=V/Awd=10900/(1980*7.1)=0.775某海洋客船L=155m,B=18m,d=7.1m,V=10900m3,Am=115m22。
试求Cb, Cp, Cw, Cm, Cvp。
Exercise 1-2两相等的正圆锥体在底部处相连接,每个锥体的高等于其底部直径.这个组合体浮于水面,使其两个顶点在水表面上,试绘图并计算:(1)中横剖面系数Cm,(2)纵向棱形系数Cp,(3)水线面系数Cw,(4)方形系数Cb。
20秋大工《船舶与海洋工程静力学》在线作业1答案

1.[1,4,2,4,2,...,2,4,1]是()的辛氏乘数。
A.辛浦生第一法B.辛浦生第二法答案:A2.基平面与中线面的交线称为()。
A.基线B.水线C.纵剖线D.横剖线答案:A3.某船水线面按照船长分为4等分,等分间距l=0.5m,其等分点处半宽分别为3,4,5,4.5,3.5(单位m),用梯形法算水线面面积为多少平方米?()A.6B.10C.8.375D.16.75答案:D4.基平面与中线面的交线称之为()。
A.基线B.设计水线C.中纵剖线D.中横剖线答案:A5.推进器的研究属于()的研究。
A.船舶稳性B.船舶浮性C.船舶快速性D.船舶操纵性答案:C6.下列哪些需要在型线图的纵剖线图上画出的有?()A.龙骨线B.首尾轮廓线C.甲板边线D.舷墙顶线答案:ABCD7.属于操纵性研究对象的是()。
A.推进器B.船舶航行时所遭受的阻力C.保证操纵性的设备舵D.船舶本身对操纵性能的影响答案:CD8.干舷F的大小与下列哪些因素有关?()A.型深DB.吃水dC.船长LD.甲板及其敷料的厚度答案:ABD9.平均吃水=()+()/2。
应填入的选项为()。
A.设计吃水B.首吃水C.尾吃水D.干舷答案:BC10.下列哪些需要在型线图的纵剖线图上画出的有哪些?()A.龙骨线B.首尾轮廓线C.甲板边线D.舷墙顶线答案:ABCD11.军舰通常以通过尾轮廓和满载水线交点的垂线作为尾垂线。
()A.错误B.正确答案:A12.乞贝雪夫法可用于坐标不间距相等的情形。
()A.错误B.正确答案:B13.中横剖面系数表示水线面的肥瘦程度。
()A.错误B.正确答案:A14.乞贝雪夫法不可用于坐标不间距相等的情形。
()A.错误B.正确答案:A15.中站面是船体的对称面。
()A.错误B.正确答案:A16.在船舶静力学中,型线图和型值表是计算船体形状各项参数和静水力性能的主要依据。
()A.错误B.正确答案:B17.船舶尺度比与船舶性能、强度以及经济性等有密切关系。
船舶静力学复习题答案

船舶静力学复习题答案
1. 船舶在静水中的平衡条件是什么?
答:船舶在静水中的平衡条件是船舶所受的浮力等于其重力,且浮力
作用线通过船舶的重心。
2. 船舶的排水量是如何定义的?
答:船舶的排水量是指船舶完全浸入水中时排开的水的质量。
3. 船舶的重心位置对船舶稳定性有何影响?
答:船舶的重心位置越低,船舶的稳定性越好。
重心位置过高会导致
船舶稳定性降低,容易发生倾覆。
4. 船舶的浮心位置是如何确定的?
答:船舶的浮心位置可以通过船舶水线面和浮力作用线的交点来确定。
5. 船舶的初稳性高度是如何计算的?
答:船舶的初稳性高度可以通过浮心位置与重心位置之间的垂直距离
来计算。
6. 船舶的横倾角如何影响船舶的稳定性?
答:船舶的横倾角越大,船舶的稳定性越差。
当横倾角超过一定限度时,船舶可能会发生倾覆。
7. 船舶的纵倾角如何影响船舶的浮力分布?
答:船舶的纵倾角会影响船舶的浮力分布,导致船舶前后部分的浮力
不平衡,从而影响船舶的稳定性和操纵性。
8. 船舶的横稳心是如何定义的?
答:船舶的横稳心是指船舶在横倾状态下,浮力作用线与船舶重心连
线的交点。
9. 船舶的纵稳心是如何定义的?
答:船舶的纵稳心是指船舶在纵倾状态下,浮力作用线与船舶重心连
线的交点。
10. 船舶的稳性曲线图是如何绘制的?
答:船舶的稳性曲线图是通过在横坐标上表示横倾角,在纵坐标上表
示相应的复原力矩,绘制出一系列的稳定曲线来表示船舶的稳定性能。
船舶静力学作业题答案解析

1-1 某海洋客船船长L=155m ,船宽B=18.0m ,吃水d =7.1m,排水体积▽=10900m 3,中横剖面面积A M =115m 2,水线面面积A W =1980m 2,试求:(1)方形系数C B ;(2)纵向菱形系数C P ;(3)水线面系数C WP ;(4)中横剖面系数C M ;(5)垂向菱形系数C VP 。
解:(1)550.01.7*0.18*15510900==⋅⋅∇=d B L C B (2)612.0155*11510900==⋅∇=L A C M P (3)710.0155*0.181980==⋅=L B A C W WP (4)900.01.7*0.18115==⋅=d B A C M M (5)775.01.7*198010900==⋅∇=d A C W VP 1-3 某海洋客货轮排水体积▽=9750 m 3,主尺度比为:长宽比L/B=8.0, 宽度吃水比B/d=2.63,船型系数为:C M =0.900,C P =0.660,C VP =0.780,试求:(1)船长L;(2)船宽B ;(3)吃水d ;(4)水线面系数C WP ;(5)方形系数C B ;(6)水线面面积A W 。
解: C B = C P* C M =0.660*0.900=0.594 762.0780.0594.0===VP B WP C C C d B L C B ⋅⋅∇=又因为所以:B=17.54m L=8.0B=140.32m d=B/2.63=6.67m 762.0=WP CC B =0.594 06.187467.6*780.09750==⋅∇=d C A VP W m 21-10 设一艘船的某一水线方程为:()⎥⎦⎤⎢⎣⎡-±=225.012L x B y 其中:船长L=60m ,船宽B=8.4m ,利用下列各种方法计算水线面积: (1) 梯形法(10等分); (2) 辛氏法(10等分)(3) 定积分,并以定积分计算数值为标准,求出其他两种方法的相对误差。
船舶静力学课后题集答案解析

1- 1某海洋客船船长L=155m ,船宽B=18.0m ,吃水d =7.1m, 排水体积^ =10900m 3,中横剖面面积 A M =115m 2,水线面面积A w =1980m 2,试求:(1)方形系数C B ; (2)纵向菱形系数C P ; (3)水线面系数C WP ;(4)中横剖面系数C M ; (5)垂向菱形系数C VP 。
1-3某海洋客货轮排水体积^ =9750 m 3,主尺度比为:长宽比 L/B=8.0,宽度吃水比 B/d=2.63,船型系数为:C M =0.900 ,C P =0.660, C VP =0.780,试求:(1)船长 L;(2)船宽 B ;(3)吃水 d ;(4)水 线面系数C WP ; ( 5)方形系数C B ; (6)水线面面积A w 。
解: C B = C P * C M =0.660*0.900=0.594C B 0.594 C WP0.762C VP 0.780又因为C B7^^ L=8.0B d=7^所以:B=17.54mL=8.0B=140.32m解:(1) C B10900 155*18.0*7.10.55010900115*1550.612(3) 0.7101150.90018.0* 7.110900 1980*7.10.7751980 18.0*155 C WPd=B/2.63=6.67m C WP0.7621-10设一艘船的某一水线方程为:y 1云右其中:船长L=60m ,船宽B=8.4m ,利用下列各种方法计算水线面 积:(1) 梯形法(10等分); (2) 辛氏法(10等分)(3) 定积分,并以定积分计算数值为标准,求出其他两种方法的相 对误差。
解:y — 1 x 2中的“ + ”表示左舷半宽值,“-”表示右20.5L舷半宽值。
因此船首尾部对称,故可只画出左舷首部的1/4水线面进 行计算。
2则:y 4.2 1 —,将左舷首部分为10等分,则l =30/10=3.0m。
船舶静力学作业题答案

1-1 某海洋客船船长L=155m ,船宽B=18.0m ,吃水d =7.1m,排水体积▽=10900m 3,中横剖面面积A M =115m 2,水线面面积A W =1980m 2,试求:(1)方形系数C B ;(2)纵向菱形系数C P ;(3)水线面系数C WP ;(4)中横剖面系数C M ;(5)垂向菱形系数C VP 。
解:(1)550.01.7*0.18*15510900==⋅⋅∇=d B L C B (2)612.0155*11510900==⋅∇=L A C M P (3)710.0155*0.181980==⋅=L B A C W WP (4)900.01.7*0.18115==⋅=d B A C M M (5)775.01.7*198010900==⋅∇=d A C W VP 1-3 某海洋客货轮排水体积▽=9750 m 3,主尺度比为:长宽比L/B=8.0, 宽度吃水比B/d=2.63,船型系数为:C M =0.900,C P =0.660,C VP =0.780,试求:(1)船长L;(2)船宽B ;(3)吃水d ;(4)水线面系数C WP ;(5)方形系数C B ;(6)水线面面积A W 。
解: C B = C P* C M =0.660*0.900=0.594 762.0780.0594.0===VP B WP C C C d B L C B ⋅⋅∇=又因为所以:B=17.54m L=8.0B=140.32m d=B/2.63=6.67m 762.0=WP CC B =0.594 06.187467.6*780.09750==⋅∇=d C A VP W m 2 1-10 设一艘船的某一水线方程为:()⎥⎦⎤⎢⎣⎡-±=225.012L x B y 其中:船长L=60m ,船宽B=8.4m ,利用下列各种方法计算水线面积: (1) 梯形法(10等分); (2) 辛氏法(10等分)(3) 定积分,并以定积分计算数值为标准,求出其他两种方法的相对误差。
船舶静力学试题2004答案

2003年春季船舶静力学(2004年6月考试)A卷标准答案及评分标准一、(共40分,每小题4分)名词解释【分析】考察学生对基本概念的掌握程度【标准答案】1.船型系数船型系数是表示船体部分面积或体积肥瘦程度的无因次系数,包括水线面系数、中横剖面系数、方形系数和菱形系数等。
2.设计水线设计水线是指船舶处于设计状态时船体型表面和水面的交线,设计水线和船舶的性能具有密切的关系。
3.纵倾值船舶首尾吃水之差,常用来表示船舶的纵倾。
4.设计排水量对于民船,设计排水量是指满载排水量,军船的设计排水量指正常排水量。
5.初稳心高当船舶的横倾角很小时,任意倾角下的浮力作用线都通过稳心,中心到稳心的距离称为稳心高(初稳心高)。
初稳心高是用来衡量船舶初稳心的主要参数。
6.每厘米纵倾力矩使船舶纵倾值改变1厘米所需要的力矩。
7.稳性消失角船舶静稳性曲线上除原点以外复原力矩等于零的点(复原力矩从正值变为负值的临界点)所对应的横倾角。
8.稳性衡准数船舶最小倾覆力矩和风压力矩的比值,是衡量船舶稳性的重要基本参数之一。
9.分舱因数为了满足不同船舶抗沉性的要求,规范规定采用分舱因素来决定许用舱长,分舱因素是一个小于1的系数。
N舱制船的分舱因素F为1/(N+1)<F 1/N10.可浸长度为了保证船舶(一舱)破损后的的水线不超过规定的界限线(甲板边线76mm),船舱的最大许可长度。
二.共(10分)【分析】考察学生对新普生法的理解和掌握程度【标准答案】证明:假设曲线可以用抛物线近似代替y = ax2+bx+c当x = -l时,y0 = al2-bl + c当x = 0时,y1 = c当x = l时,y2 = al2 + bl + c曲线下面积cl al dx c bx ax A l l 232)(32+=++=⎰- 若将面积A 表示为坐标值的函数210y y y A γβα++=比较两式可得)4(3210y y y l A ++=三.计算题(10分)【分析】浮性是船舶的基本属性之一,本题考察学生对浮性的理解和基本知识的应用【标准答案】解:根据T2和T3时的吃水以及水线面面积随吃水变化的线性假定可得T 3<T<T 2时船舶水线面面积的变化关系230380)5.4(5.45.5148018601480)(332323-=---+=---+=T T T T T T A A A A W W W W 为了满足吃水要求,船舶应卸下的载荷为 ton dT T dT A p TT W 375.1245)230380(35.56.411=-==⎰⎰ρ四、计算题(10分)【分析】船舶的初稳性和浮态的计算应用十分广泛,本题考察学生对初稳性和浮态计算的的理解和应用【标准答案】解:卸载后,船舶吃水变化量为m TPC p T 1846.05.6100120100-=⨯-==δ 考虑到卸载以后船舶减少了一个自由液面,卸载后船舶的初稳心高mp lb GM z T T p p GM M G 2.2)1201100(126159.0)86.180.021846.00.2(120110012086.1)(12)2(33=-⨯⨯⨯+-----=+∆+--++∆+='ρδ 船舶的横倾角167.02.2)1201100(3120)(2/tan -=⨯-⨯-='+∆=M G p pb φ ︒-=48.9φ船舶的横倾角为左倾9.48︒。
船舶静力学课后习题答案

=2+165* =
Iyy=2*1/12**753 = m4
Exercise 2-1
或 者:
Ixx=
∫2 BB2/b2 y2Ldy
Iyy
x2bdx
Exercise 2-2
某挖泥船的水线面如图,其中 L=30m, B=, l=12m, b=, l1=2m, l2=, b1=, b2=。求该水线面面积及形心坐标。
Exercise 1-10
B 各站型值: y=± [1
2
x2 2]
序 0 1 2 3 4 5 6 7 8 9 10
x -30 -24 -18 -12 -6 0 6 12 18 24 30
y0
0
6
4
2
0
-30
-24
-18
-12
-6
0
6
12
18
24
30
精确解:
Exercise 1-10
dx
Exercise 1-10
梯形法:
V=L/10*(Σy-ε) =100/10*(0++++++++++0) =3418 m3
Myoz=L/10*(Σxy-ε) =100/10*(-5*0-4****+0*
Xb= Myoz/V=100/3418= m
辛氏 1 法:
+1*+2*+3*+4*+5*0)*10=100 m4
V=L/30*(Σy) =100/30*(0+4*+2*+4*+2*+4* +2*+4*+2*+4*+0)=3433 m3
船舶静力学A 答案

一、名词解释(共30分)1. 横稳性高与纵稳性高横稳性高:船舶横倾某一小角度φ时,重力作用点G 和横稳心M 之间的距离GM ; 纵稳性高:船舶纵倾某一小角度θ时,重力作用点G 和横稳心L M 之间的距离L GM 。
2. 船长的三种定义①、总长OA L :自船首最前端至船尾最后端的水平距离; ②、垂线间长PP L :艏垂线FP 与艉垂线AP 之间的水平距离;③、设计水线长WL L :设计水线在首柱前缘和尾柱后缘之间的水平距离。
3. 漂心与浮心漂心:水线面WL 的形心; 浮心:设计水线长与垂线间长设计水线长WL L :设计水线在首柱前缘和尾柱后缘之间的水平距离; 垂线间长PP L :艏垂线FP 与艉垂线AP 之间的水平距离。
4. 干舷5.6. 浮态与浮态参数浮态:船舶浮于静水的平衡状态称为浮态,包括:正浮、横倾、纵倾和任意浮态; 浮态参数:吃水、横倾角和纵倾角。
二、 简答题(共40分)1. 在中横剖面上标注:型宽、型深、吃水、基线、干舷。
(8分)得分2. 简述:水线面系数、中横剖面系数、方形系数、棱形系数、垂向棱形系数,并说明各自的意义。
(8分)水线面系数WP C :/WP W C A LB =,大小表示水线面的肥瘦程度;中横剖面系数M C :/M M C A Bd =,大小表示水线以下的中横剖面的肥瘦程度; 方形系数B C :/B C LBd =∇,大小表示船体水下体积的肥瘦程度; 菱形系数p C :/p M C LA =∇,大小表示排水体积沿船长方向的分布情况; 垂向菱形系数Vp C :/Vp W C dA =∇,大小表示排水体积沿吃水方向的分布。
3. 简述船体型线图的组成及各自的文字表述。
(8分)①、横剖线图:用一组平行于中站面的剖面剖切船体,得到与船体型表面的一系列交线为横剖线图②、半宽水线图:用一组平行于水线面的剖面剖切船体,得到与船体一侧型表面的一系列交线为半宽水线图③、纵剖线图:用一组平行于中线面的剖面剖切船体,得到与船体型表面的一系列交线为纵剖线图4. 简述:稳性、稳心、稳心半径、稳性高。
船舶静力学试题及答案

船舶静力学试题及答案一、综合填空题(每题3分共30分)1.水线面系数表达式为(CWP=AW/LB ),含义是(与基平面平行的任一水线面的面积与由船长、型宽构成的长方形面积之比);2.辛浦生第一法的辛氏乘数为(1,4,1 ),第二法的辛氏乘数为(1,3,3,1 );3.写出三心(浮心、重心和稳心的垂向坐标之间的关系,即稳性高GM等于(GM=BM+KB-KG);4.称为(引起纵倾1cm的纵倾力矩),其中L为(船长),D为(排水量),GML为(纵稳性高);5.船舶处于横倾状态时,用参数(吃水d )和(横倾角φ)表示该浮态;6.水线面面积曲线是以(各吃水处水线面面积)为横坐标,以(吃水)为纵坐标所绘制的一条曲线,它与纵轴所围成的面积表示(某一吃水下的排水体积)的大小,其形状反映了(船舶排水体积)沿(吃水方向)的分布情况;7.船舶的横稳心高与横稳性高是不同的概念,横稳性高表示的是(横稳心和重心)之间的距离,而横稳心高表示的是(横稳心和浮心)之间的距离;8.称为(初稳心半径),它表示的是(横稳心和浮心)两点之间的距离,其中IT 为(水线面积对于纵向中心轴线的横向惯性矩),Ñ为(排水体积);9.储备浮力是指(满载水线以上主体水密部分的体积);它对船舶的(稳性、抗沉性和淹湿性)有很大影响;10.大倾角静稳性臂公式l = lb - lg中lb称为(形状稳性臂)lg称为(重量稳性臂)。
二、简答题(每题8分共40分)1、抗沉性计算中,根据船舱进水情况可将船舱分为三类舱,分别作出简略介绍。
答:在抗沉性计算中,根据船舱进水情况,.可将船舱分为下列三类。
第一类舱:舱的顶部位于水线以下,船体破损后海水灌满整个舱室,但舱顶未破损,因此舱内没有自由液面.双层底和顶盖在水线以下的舱柜等属于这种情况。
第二类舱:进水舱未被灌满,舱内的水与船外的海水不相联通,有自由液面。
为调整船舶浮态而灌水的舱以及船体破洞已被堵塞但水还没有抽干的舱室都属于这类情况。
船舶静力学 答案

《船舶静力学》答案一、简答题 (本题共4小题,满分20分)1.船舶的浮态有哪几种,以及各种浮态的参数表达?答:(1)正浮。
横倾角=0,纵倾角=0,首尾吃水相等(2)横倾。
横倾角不等于0,纵倾角=0,首尾吃水相等(3)纵倾。
横倾角=0,纵倾角不等于0,首尾吃水不等(4)任意浮态。
横倾角不等于0,纵倾角不等于0,首尾吃水不等。
2.什么是邦戎曲线?利用邦戎曲线图,如何计算任意纵倾水线下的排水体积和浮心位置?答:将各站处的横剖面面积曲线和各站处的横剖面面积矩曲线绘制在同一张图上,此图称为邦戎曲线。
利用邦戎曲线的计算步骤:(1)根据首尾吃水在邦戎曲线图上做出倾斜水线。
(2)根据倾斜水线与各站垂线的交点作平行于基线的直线,分别与各站横剖面面积曲线,Moy曲线的交点量出对应的横剖面面积及静矩的大小。
(3)利用横剖面面积曲线沿纵向积分求解排水体积及浮心纵向坐标,利用横剖面面积矩曲线沿纵向积分求解排水体积的垂向坐标。
3.何谓船舶稳性?答:船舶在外力作用下偏离其平衡位置而倾斜,当外力消失后,能自行恢复到原来平衡位置的能力。
4.什么是稳性横截曲线?答:计算4-5根水线下不同横倾角时的排水体积和ls浮力作用线到假定重心的水平距离,然后以ls为纵坐标,排水体积为横坐标绘制对应不同横倾角的ls曲线图,该图称为稳性横截曲线图。
二、填空题 (本题共10小题,满分20分)1.通常选用的船长有总长、垂线间长、设计水线长。
2.纵倾状态的浮态一般用首吃水和尾吃水或平均吃水和纵倾角来表示。
3.根据船舶任一水线下的横剖面面积曲线,可以求出该水线下的排水体积和浮心纵向坐标。
4.船舶在动力作用下倾斜产生的最大倾斜角称为动倾角。
船舶的动稳性是以复原力矩做的功来表达的。
5.计算抗沉性的两种方法:增加重量法和损失浮力法6.棱形系数是指船体水线以下的型排水体积与由相对应的中横剖面面积、船长L 所构成的棱形体积之比。
7.首垂线是通过设计水线与首柱前缘的交点所作的垂线。
船舶静力学习题答案

Exercise 3-1*
某长方形起重船的主要尺寸:船长L=15m,B=9m,型深 D=2m,起重船主体重p1=56t,其重心高度KG1=0.85 m, 船的上层建筑重p2=78t,重心高度KG2=7.5m,水的重量密 度为ω=1.025t/m3,试计算:(1)横稳性高GM,(2)纵 稳性高GML。
Exercise 1-2*
某海洋客货轮排水体积V=9750m3,长宽比L/B=8,宽 度吃水比B/d=2.63,船型系数Cm=0.9, Cp=0.66, Cvp= 0.78, 试求:(1)船长L;(2)船宽B;(3)吃水d;(4)水线 面系数Cw;(5)方形系数Cb;(6)水线面面积Aw。 解:Cp=V/CmBdL=V/CmB(B/2.63)(8B)=2.63V/8CmB3
∴B=((9750*2.63)/(8*0.66*0.9))1/3=17.54m
L=8*17.54=140.32m d=17.54/2.63=6.67m
Cb=Cm.Cp=0.9*0.66=0.594
Cw=Cb/Cvp=0.594/0.78=0.762 Aw=0.762*140.32*175.54=1875.44m2
Xb= Myoz/V=160/3433=0.046 m Cp=V/AmL= 3433/57.31/100=0.599
Exercise 2-3
某船的一个煤舱长为24m,自尾至首各横剖面面积为 5.7,8.7,11.3,10.1,8.8(单位m2)这些剖面的形心在 基线以上的高度分别为3.7,3.5,3.3,3.5,3.6(单位 m)。剖面之间的间距为6m。设煤舱的积载因数(每吨 煤所占体积m3)为1.56m3/t。试列表计算:(1)该船载 煤吨数,(2)该舱的重心位置(基线以上距离及距煤 舱尾舱壁的距离)。 15
本船舶静力学A 答案
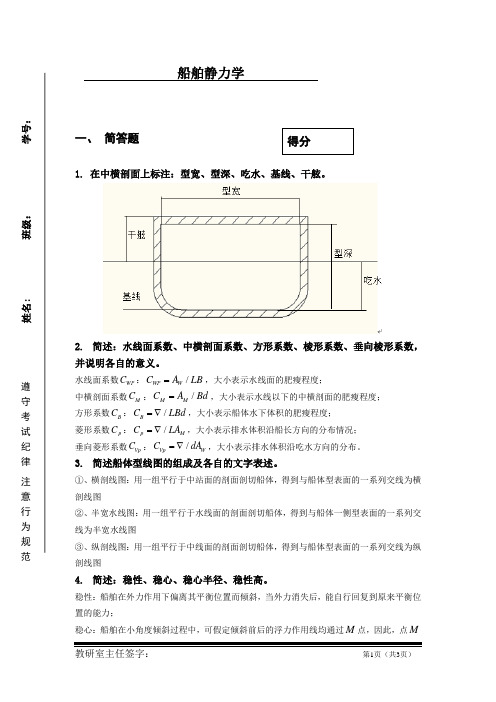
船舶静力学一、 简答题1. 在中横剖面上标注:型宽、型深、吃水、基线、干舷。
2. 简述:水线面系数、中横剖面系数、方形系数、棱形系数、垂向棱形系数,并说明各自的意义。
水线面系数WP C :/WP W C A LB =,大小表示水线面的肥瘦程度;中横剖面系数M C :/M M C A Bd =,大小表示水线以下的中横剖面的肥瘦程度; 方形系数B C :/B C LBd =∇,大小表示船体水下体积的肥瘦程度; 菱形系数p C :/p M C LA =∇,大小表示排水体积沿船长方向的分布情况; 垂向菱形系数Vp C :/Vp W C dA =∇,大小表示排水体积沿吃水方向的分布。
3. 简述船体型线图的组成及各自的文字表述。
①、横剖线图:用一组平行于中站面的剖面剖切船体,得到与船体型表面的一系列交线为横剖线图②、半宽水线图:用一组平行于水线面的剖面剖切船体,得到与船体一侧型表面的一系列交线为半宽水线图③、纵剖线图:用一组平行于中线面的剖面剖切船体,得到与船体型表面的一系列交线为纵剖线图4. 简述:稳性、稳心、稳心半径、稳性高。
稳性:船舶在外力作用下偏离其平衡位置而倾斜,当外力消失后,能自行回复到原来平衡位置的能力;稳心:船舶在小角度倾斜过程中,可假定倾斜前后的浮力作用线均通过M 点,因此,点M得分姓名: 班级: 学号:遵守 考 试 纪 律 注 意 行 为 规 范称为稳心;稳心半径:浮心和稳心之间的距离; 稳性高:重心与稳心之间的距离。
5. 简述:什么是邦戎曲线?在型线图各站线上,以吃水为纵坐标,相应的横剖面面积及其对基平面的力矩为横坐标绘制的两组曲线。
三、计算题1. 已知某船设计水线面半宽尺寸,船长220米,求 1)梯形法求水线面面积;(15) 2)辛普生第一法求水线面面积;(15)站号12345678910水线半宽y(m) 0.0 6.3 8.6 9.2 9.4 9.0 8.1 6.7 4.6 2.4 0.2答: 1、梯形法 站号 水线半宽 乘数 面积乘积 0 0 0.5 0 1 6.3 1 6.3 2 8.6 1 8.6 3 9.2 1 9.2 4 9.4 1 9.4 5 9.0 1 9.0 6 8.1 1 8.1 76.716.7得分X8 4.6 1 4.69 2.4 1 2.410 0.2 0.5 0.1总和64.4水线面面积:2*22*64.4=2833.62m;2、辛普生第一法站号水线半宽乘数面积乘积0 0 0.5 01 6.32 12.62 8.6 1 8.63 9.2 2 18.44 9.4 1 9.45 9.0 2 186 8.1 1 8.17 6.7 2 13.48 4.6 1 4.69 2.4 2 4.810 0.2 0.5 0.1总和98m水线面面积:2*2/3*22*98=2874.72。
船舶静力学第四章习题答案
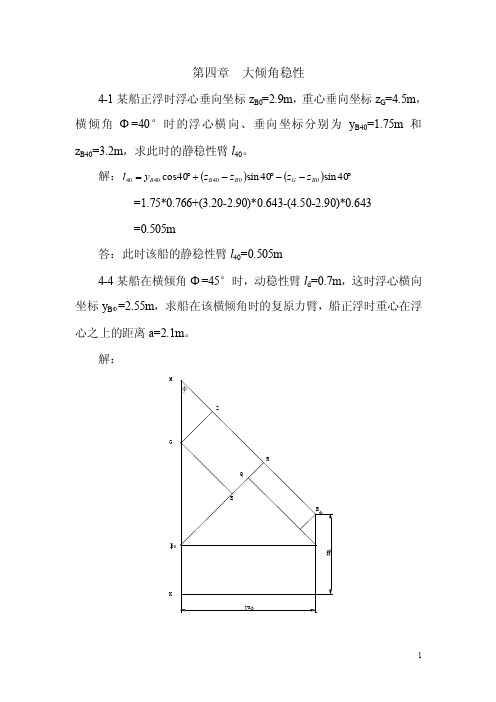
第四章 大倾角稳性4-1某船正浮时浮心垂向坐标z B0=2.9m ,重心垂向坐标z G =4.5m ,横倾角Φ=40°时的浮心横向、垂向坐标分别为y B40=1.75m 和z B40=3.2m ,求此时的静稳性臂l 40。
解:()()︒--︒-+︒=40sin 40sin 40cos 00404040B G B B B z z z z y l =1.75*0.766+(3.20-2.90)*0.643-(4.50-2.90)*0.643 =0.505m答:此时该船的静稳性臂l 40=0.505m4-4某船在横倾角Φ=45°时,动稳性臂l d =0.7m ,这时浮心横向坐标y B Φ=2.55m ,求船在该横倾角时的复原力臂,船正浮时重心在浮心之上的距离a=2.1m 。
动稳性臂的几何意义为:()G B KB z y G B G B zB l B B d 0000cos sin cos ---+=-=φφφφφφ即0.7=2.1*22+2.55*22-()0KB z B -φ*22-2.1 解得:()0KB z B -φ=0.69m()φφφφφsin sin cos 00G B KB z y l B B --+==2.55*22+0.69*22-2.1*22 =0.806m答:该船此状态的复原力臂l =0.806m 。
4-5某船在横倾角Φ=30°时的复原力臂l =2.60m ,动稳性臂l d =0.73m ,重心在龙骨以上高度z g =10.58m ,正浮时重心在浮心以上的高度a=5.99m ,求Φ=30°时浮心在龙骨以上的高度。
解:又∵()φφφφφsin sin cos 00G B KB z y l B B --+=即:()50.0*99.550.0*59.4866.0*60.2--+=φφB B z y ② 将式①②联立解得06.6=φB z ,61.5=φB y答:Φ=30°时浮心在龙骨以上的高度m z B 06.630=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1某海洋客船船长L=155m,船宽B=18。
0m,吃水d=7。
1m,排水体积▽=10900m3,中横剖面面积A M=115m2,水线面面积A W=1980m2,试求:
(1)方形系数C B;(2)纵向菱形系数CP;(3)水线面系数CWP;(4)中横剖面系数C M;(5)垂向菱形系数CVP。
解:(1)
(2)
(3)
(4)
(5)
1—3某海洋客货轮排水体积▽=9750m3,主尺度比为:长宽比L/B=8。
0,宽度吃水比B/d=2、63,船型系数为:C M=0、900,C P=0、660,C VP=0.780,试求:(1)船长L;(2)船宽B;(3)吃水d;(4)水线面系数CWP;(5)方形系数C B;(6)水线面面积A W。
解: CB= CP* C M=0。
660*0。
900=0.594
L=8、0B d=
所以:B=17、54m L=8.0B=140、32m
d=B/2.63=6、67m
CB=0、594m2
1-10 设一艘船得某一水线方程为:
其中:船长L=60m,船宽B=8。
4m,利用下列各种方法计算水线面积:
(1)梯形法(10等分);
(2)辛氏法(10等分)
(3)定积分,并以定积分计算数值为标准,求出其她两种方法得相对误差。
解:中得“+”表示左舷半宽值,“-”表示右舷半宽值。
因此船首尾部对称,故可只画出左舷首部得1/4水线面进行计算。
则:,将左舷首部分为10等分,则l=30/10=3。
0m。
梯形法:总与∑yi=30。
03,修正值(y0+y10)/2=2。
10,修正后∑`=27、93
解:(1)梯形法(10等分)
=4*3。
0*(30。
03-2.10)=12.0*27。
93=335。
16m2
(2)辛氏法(10等分)
(3)定积分计算
各计算方法得相对误差:
梯形法:
辛氏法:
2—13 某船由淡水进入海水,必须增加载荷P=175t,才能使其在海水中得吃水与淡水中得吃水相等。
求增加载重后得排水量。
解:∴
∴△海=△淡+P=7000、00+175、00=7175.00t
另解:水得密度变化引起得吃水得变化为
增加载荷P引起得吃水得变化为
则=0
解得
∴△海=△淡+P=7000、00+175.00=7175、00t
2-15 某内河客货船得尺度与要素如下:吃水d=2、40m,方形系
数CB=0。
654,水线面系数C W
P=0。
785,假定卸下货物重量P=8%排水量。
求船舶得平均吃水(设在吃水变化范围内船舷就是垂直得)。
解:∵在吃水变化范围内船舷就是垂直得
∴在该范围内水线面面积A W就是常数、
∴
3-3某巡洋舰得排水量△=10200t,船长L=200m,当尾倾为1.3m时,水线面面积得纵向惯性矩I L=420*104m4,重心得纵向坐标x G=—4。
23m,浮心得纵向坐标x B=-4.25m,水得重量密度。
试
解:
答:
3—1
坐标xF=4.0m。
今在船上装载120t得货物。
问货物装在何处才能使船得首吃水与尾吃水相等。
解:按题意要求最终得首尾吃水应相等,即
设货物应装在(x,y,z)处,则装货后首尾吃水应满足:
,即(1)
(2)
(3) (4)
将式(2)、(3)、(4)代入式(1)中得:
代入数值得:
()()75*100*1000.4*1200.420.1008.475*100*1000.4*1200.420.1002.4-⎪⎭
⎫ ⎝⎛+-=-⎪⎭⎫ ⎝⎛-+x x 解得: x =41、5m
答:应将货物放在(41、5,0,z)处。
3—14 已知某长方形船得船长L=100m,船宽B=12m,吃水d =6m,重心垂向坐标z G =3。
6m,该船得中纵剖面两边各有一淡水舱,其尺度为:长l=10m,宽b=6m,深a=4m 、在初始状态两舱都装满了淡水。
试求:(1)在一个舱内得水耗去一半时船得横倾角;
(2)如果消去横倾,那们船上x=8m,y=-4m 处得60t 货物应移至何处?
解:
本题为卸载荷,设该船为内河船、 预备数据: 水耗去半舱得重量: ,∴为小量载荷装卸。
m B L P d 1.00
.12*0.100*0.10
.1201-=-=⋅⋅=
ωδ平均吃水的变化: ⎪⎭
⎫
⎝⎛--+
+∆+
=GM z d d P P GM M G M G P g 111111112δ:后的卸去 自由液面要素:
m GM M G M G M G 349.1025.0374.1111111=-=+='
'δ:新的
(1) 假设右舷舱得淡水耗去一半: (左倾)
假设左舷舱得淡水耗去一半: (右倾)
(2)假设右舷舱得淡水耗去一半,,则P 应移到y 2处,使船横倾角: 即:, (向右舷移)
假设左舷舱得淡水耗去一半,,则:
()()m P
y P Py y g 0.100
.600.3(*)0.1204*0.601
12-=----=
-=
(向左舷移)
因本船B =12、0m,y=-4。
0m,故将P向左舷移到-10、0m不成立。
答:(1)(左倾)或(右倾)
(2)应将P 向右舷移动到y=2.0m 处。
3—15 已知某内河船得主要尺度与要素为:船长L=58m,船宽B =9.6m,首吃水dF =1.0m,尾吃水d A =1。
3m,方形系数CB =0、72,纵稳性高,为了通过浅水航道,必须移动船内得某些货物,使船处于平浮状态,假定货物从尾至首最大得移动距离为l =28.0m,求必须移动得货物重量、
解:设需移动得货物重量为P 、 由题意知原始状态: ,
t d B L C M B 0.46115.1*6.9*0.58*72.0*0.1==⋅⋅⋅⋅=∆ω
为使船处于平浮状态,则应使船产生相反得纵倾值-t: 即
解得:P =5、54t
答:需移动得重量P=5、54t、
4-1某船正浮时浮心垂向坐标zB0=2、9m,重心垂向坐标z G
=4.5m,横倾角Φ=40°时得浮心横向、垂向坐标分别为y B 40=1、75m 与z B40=3、2m,求此时得静稳性臂l 40。
解:
=1。
75*0、766+(3。
20-2。
90)*0。
643-(4、50-2。
90)*0、643
=0。
505m
答:此时该船得静稳性臂l 40=0、505m
4-6一艘排水量△=1000t 得干货船之静稳性曲线值如下:
求:(1)Φ=55°时得动稳性臂;
(2)当船得重心升高0、25m 后损失得稳性范围。
解:(1)
抛物线内插求得(2)
(2)在静力作用下得极限倾覆力矩;
(3)应用梯形法进行动稳性曲线得计算,并以适当比例绘制动稳性曲线;
(4)船在正浮时得极限动倾角及极限倾覆力矩;
(5)船在最大摆幅Φ0=15°时得极限动倾角及极限倾覆力矩。
解:(1)由曲线图可量得极限静倾角Φmax≈33、0°
(2)由曲线图可量得最大静稳性臂lmax≈0.48m
则静力作用下得极限倾覆力矩为:
(3)梯形法计算:
静、动稳性曲线图如下:
则Φ0=15°时船得极限倾覆力矩:。
