参数计算
如何进行参数计算(四参数高程拟合)?

如何进行参数计算(四参数高程拟合)?定义:四参数是指两个平面坐标系之间的平移(DX、DY),旋转(α),缩放参数(κ)。
四参数是RTK常用的一种坐标转换模式,通过四参数完成WGS84平面到当地平面的转换,通过高程拟合完成WGS84椭球高到当地水准的拟合。
要求:至少两个任意同一坐标系的坐标(通用方法)使用环境:适用于大部分的普通工程测量,工程放样简要步骤1)仪器工作模式设置2)采集控制点坐标3)求解参数4)坐标检核计算参数的详尽流程1、设置基站与移动站(可以选择手机卡或者电台模式),使移动台最终达到固定解;2、采集控制点坐标(如“交186”与“y265”为控制点)在碎部测量中,分别对控制点进行“交186”和“y265”采集坐标(使用平滑采集对控制点进行采集),分别保存为“交186”与“y265”。
3、求解参数1)进入参数求解界面2)、添加控制点对如图操作,分别添加“交186”与“y265”两个点对。
其中源点为刚才采集的坐标,目标点为控制点的已知坐标(需要自己手动添加,或者提前输到控制点库中,再调用)。
3)计算参数点击计算,得到“四参数+高程拟合”的结果点击应用后,即可完成操作。
A为高程固定差改正的差值。
注意:尺度的数据为0.999……或者1.000……4、进行坐标检核找一个控制点进行碎部测量(最好找第三个控制点),对比采集的(N,E,Z)与已知坐标(N,E,Z)检核坐标的正确性。
注意:1、这里的“四参数+高程拟合”计算是针对于基站而言的。
在计算“四参数+高程拟合”之前,必须保证坐标系统中的基准面的“转换模型”,平面转换的“转换模型”,高程拟合“转换模型”均为“无”;2、一个项目只能求解一次参数计算,或者说一个项目求参数前,必须满足前一点条件;3、计算参数的两个点数据必须是接收同一个基站信号采集的固定解坐标;用于计算参数的两个点的已知坐标必须是同一个坐标系统,即计算的尺度(k)为0.999……或者1.000……。
铣床参数公式计算
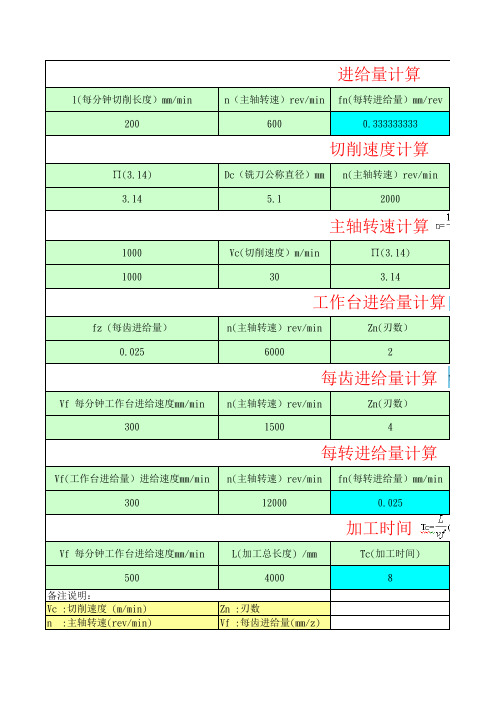
l(每分钟切削长度)mm/min
n(主轴转速)rev/min fn(每转进给量)mm/rev
200
600
0.333333333
切削速度计算
∏(3.14)
Dc(铣刀公称直径)mm n(主轴转速)rev/min
3.14
5.120Leabharlann 0主轴转速计算1000
Vc(切削速度)m/min
∏(3.14)
1000
Vf(工作台进给量)进给速度 mm/min 300
fz(每齿进给量)mm/min 0.05
Vc(切削速度)m/min 32.028
n(主轴转速)rev/min 955.4140127
间
削速度v、进给量f和切削深度ap,
2.进给量f: 进给量是指工件或刀具每转一周,刀具与工件之间沿进给方向的相对位移。 铣削时,由于铣刀是多齿刀具,所以规定了每齿的进给量af,单位是mm/z。
3.切削深度: 铣削时,这是指待加工表面与已加工表面的垂直距离,单位为mm。
算
计算 计算 量计算
计算 计算
1000 1000
Dc(铣刀公称直径)mm 10
30
3.14
工作台进给量计算
fz (每齿进给量)
n(主轴转速)rev/min
Zn(刃数)
0.025
6000
2
每齿进给量计算
Vf 每分钟工作台进给速度mm/min 300
n(主轴转速)rev/min
Zn(刃数)
1500
4
每转进给量计算
Vf(工作台进给量)进给速度mm/min n(主轴转速)rev/min fn(每转进给量)mm/min
300
12000
网络时间参数计算
2020/5/14
四.关键线路的确定方法: 1.分析线路进行确定; 2.通过计算时间参数进行确定; 3.破圈法:
关键线路走最长的线路,逢圈保留最长线路。 例如以下两例:
2020年5月14日星期四
建筑施工组织与管理
10
2020年5月14日星期四
建筑施工组织与管理
3
2-4工序:LS2-4=[ LS4-7,LS5-9]min-5=[8,11]min-5=3;
2-3工序:LS2-3=5-3=2;
2-6工序:LS2-6=9-4=5;
1-2工序:LS1-2=[ LS2-3,LS2-4,LS2-6]min-2
=[2,3,5]min-2=0
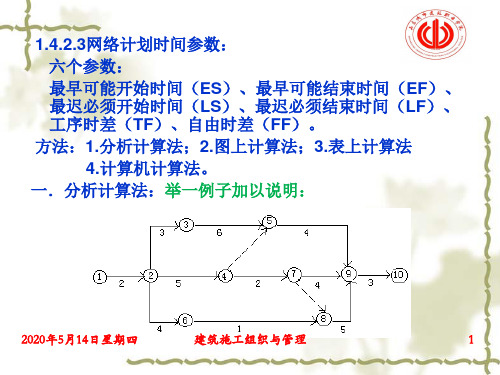
1.4.2.3网络计划时间参数:
六个参数:
最早可能开始时间(ES)、最早可能结束时间(EF)、 最迟必须开始时间(LS)、最迟必须结束时间(LF)、 工序时差(TF)、自由时差(FF)。
方法:1.分析计算法;2.图上计算法;3.表上计算法
4.计算机计算法。
一.分析计算法:举一例子加以说明:
2020年5月14日星期四
通过以上原理可以得到: ESjk=[ESji+tij]max=[ EFij]max。
3.计算最迟必须开始时间(LS): 逆算:LSij=T-[∑tjk]max-tij=[LSjk]min- tij 9-10工序:LS9-10=18-3=15; 5-9工序:LS5-9=15-4=11; 7-9工序:LS7-9=15-4=11; 8-9工序;LS8-9=15-5=10; 4-7工序:LS4-7=[ LS7-9,LS8-9]min-2=[11,10]min-2=8; 6-8工序:LS6-8=10-1=9; 3-5工序:LS3-5=11-6=5;
加工参数计算公式

加工参数计算公式
加工参数计算公式是指在机械加工中,根据不同的加工要求,计算出需要使用的各种加工参数的公式。
这些参数包括切削速度、进给量、切削深度等,它们直接影响着加工的效率、质量和安全性。
1. 切削速度计算公式:
Vc=π×D×n/1000
其中,Vc为切削速度,D为刀具直径,n为主轴转速。
单位为m/min。
2. 进给量计算公式:
f=Z×n×fz
其中,f为进给量,Z为齿数,n为主轴转速,fz为每齿进给量。
单位为mm/min。
3. 切削深度计算公式:
ae=Kt×fz×Z
其中,ae为切削深度,Kt为切削力系数,fz为每齿进给量,Z 为齿数。
单位为mm。
4. 切削宽度计算公式:
ap=ae×tanα
其中,ap为切削宽度,ae为切削深度,α为刀具前角。
单位为mm。
以上是常用的加工参数计算公式,不同的加工过程和材料会有所不同,需要根据具体情况进行调整和计算。
在使用计算公式时,需要注意单位的换算,保证计算结果的准确性。
计算参数的方法

计算参数的方法
计算参数的方法取决于具体的参数类型和问题背景。
以下是一些常见的参数计算方法:
1. 平均值:对于一组数据,计算所有数值的和,然后除以数据的数量,得到平均值。
2. 中位数:将一组数据从小到大排列,如果数据数量为奇数,则中位数是中间的数值;如果数据数量为偶数,则中位数是中间两个数值的平均值。
3. 标准差:用于衡量数据的离散程度。
标准差的计算公式为:标准差 = sqrt((1/N) Σ((x_i - μ)^2)),其中N是数据数量,x_i是每个数据点,μ是平均值。
4. 相关性系数:用于衡量两个变量之间的线性关系。
相关性系数的取值范围为-1到1,1表示完全正相关,-1表示完全负相关,0表示无相关性。
5. 回归系数:在回归分析中,用于衡量自变量对因变量的影响程度。
回归系数的计算公式为:回归系数 = (因变量的变化量 / 自变量的变化量) / (数据点的总数)。
这些参数的计算方法可以帮助我们了解数据的特征和关系,从而更好地解决实际问题。
请根据具体情况选择适当的参数计算方法。
四参数计算公式

四参数计算公式
四参数计算公式是指用四个参数(三个平移参数和一个旋转角度)来描述两个坐标系之间的变换关系的数学公式。
这四个参数分别是平
移向量x、y、z,以及旋转角度r。
四参数计算公式的表达式如下:
X' = X cos(r) - Y sin(r) + x
Y' = X sin(r) + Y cos(r) + y
Z' = Z + z
其中,(X, Y, Z)是原坐标系的坐标,(X', Y', Z')是目标坐标系
的坐标。
适当拓展:四参数计算公式是地图配准常用的一种方法。
在GIS
领域中,常使用四参数模型对不同坐标系统的地图进行转换。
例如,
在地图投影过程中,通过四参数计算公式实现坐标坐标系之间的转换,可以使地图数据在不同坐标系下的比较和分析成为可能。
同时,在车
辆导航、无人机遥感等领域也有广泛的应用。
参数的计算公式范文

参数的计算公式范文
1.工程领域参数的计算公式:
-电阻:R=ρL/A,其中ρ为电阻率,L为电阻长度,A为电阻截面积。
-功率:P=VI,其中V为电压,I为电流。
-速度:v=d/t,其中d为距离,t为时间。
-加速度:a=(v-u)/t,其中v为末速度,u为初速度,t为时间。
-压力:P=F/A,其中F为力,A为受力面积。
2.经济学中的参数计算公式:
-利润:利润=总收入-总成本。
-税收:税收=利润×税率。
-平均收益率:平均收益率=(资本收益-资本损失)/投资金额。
-实际利率:实际利率=名义利率-通货膨胀率。
3.统计学中的参数计算公式:
-平均值:平均值=总和/观察次数。
-方差:方差=(观察值-平均值)的平方的总和/观察次数。
-标准差:标准差=方差的平方根。
-相关系数:相关系数=协方差/(标准差1×标准差2)。
4.物理学中的参数计算公式:
-质量:质量=密度×体积。
-加速度:加速度=力/质量。
-能量:能量=力×距离。
-频率:频率=1/周期,其中周期为一个完整振动所需的时间。
需要注意的是,参数的计算公式可能会受到实际情况和假设条件的影响,应根据具体问题和背景进行选择和使用。
另外,计算方法也会因不同学科的发展和创新而不断改变,可能会有新的公式被提出和应用。
在实际问题中,应当结合具体条件和背景选择合适的计算方法,以得到准确和有意义的结果。
双代号网络计参数的计算(节点计算法)

制定标准与规范
01
制定统一的参数计算标准与规范,促进项目管理中参数计算的
普及。
培训与教育
02
加强相关人员的培训和教育,提高项目管理团队对参数计算的
认识和应用能力。
案例研究与经验分享
03
开展案例研究,分享成功经验,推动参数计算在项目管理中的
广泛应用。
参数计算与其他管理方法的融合与集成
与进度管理结合
将参数计算与进度管理方法相结合,实现项目进度与资源优化配 置。
实例二
针对不同工作,计算其总时差和自由 时差,分析其对工期的影响。
参数计算注意事项
注意事项一
确保所有工作的持续时间输入正确,避免因数 据错误导致计算结果不准确。
注意事项二
注意区分总时差和自由时差的概念,避免混淆。
注意事项三
在计算总时差和自由时差时,应考虑工作之间的逻辑关系,确保计算的正确性。
03
计算公式
总时差=紧后工作的最早开始时间-本 工作的最早完成时间;自由时差=本 工作的最早完成时间-本工作的最早开 始时间。
步骤
确定各节点的最早开始时间和最晚开 始时间,计算各工作的总时差和自由 时差,确定关键线路和关键工作。
参数计算实例
实例一
以某工程双代号网络计划为例,计算 各工作的总时差和自由时差,确定关 键线路和关键工作。
与风险管理整合
将参数计算与风险管理方法整合,提高项目风险应对能力。
与成本管理集成
将参数计算与成本管理相结合,实现项目成本的有效控制。
感谢您的观看
THANKS
在双代号网络计划中,节点表示工作或事件,箭线表示工作 之间的逻辑关系。节点计算法通过分析节点的时间参数,来 计算整个网络计划的关键线路和总工期。
时间参数的计算方法

时间参数的计算方法时间参数是数学中的一个重要概念,表示时间的一个度量单位。
在物理学、工程学、计算机科学等领域中,时间参数都有着广泛的应用。
本文将介绍时间参数的计算方法,并探讨其在实际应用中的重要性。
一、时间参数的定义时间参数是指时间的一个度量单位,通常用秒或分钟表示。
国际单位制(SI)中的时间参数为秒,其定义为地球自转一周所需的时间。
分钟也是由秒定义的,定义为地球自转一次所需的时间。
二、时间参数的计算方法时间参数的计算方法主要有两种:公历法和农历法。
1. 公历法公历法是利用公历定义时间参数的方法。
公历法将地球公转一周的时间称为一年,即365.2422天。
因此,一个世纪的天数为365.2422天/4年=91.4375天。
时间参数的秒数等于天数除以1000。
例如,2023年2月23日是公历2023年2月23日,其时间参数为69天19小时47分16秒。
2. 农历法农历法是利用农历定义时间参数的方法。
农历法将地球自转一周的时间称为一年,即365.2422天。
因此,一个世纪的天数为365.2422天/12年=31.5768天。
时间参数的秒数等于天数除以1000。
例如,2023年2月23日是农历2023年正月初一,其时间参数为6天16小时21分46秒。
三、时间参数在实际应用中的作用时间参数在实际应用中有着重要的作用。
以下是几个例子:1. 天气预报:时间参数可以用来预测天气的时间差,从而更准确地进行天气预报。
2. 天文学:时间参数可以用来测量天体的运动轨迹,例如测量恒星的亮度、距离和运动速度等。
3. 生物学:时间参数可以用来测量生物生长、代谢等过程的时间差,从而研究生物节律等方面的问题。
4. 工程学:时间参数可以用来设计、优化工程系统,例如设计高效的时钟系统、计算时间延迟等。
时间参数的计算方法和其在实际应用中的作用,可以帮助我们更好地理解和应用数学和自然科学知识。
参数的计算

参数的计算
参数的计算是指根据已知条件,通过特定的公式或方法,推导出未知参数的值。
在数学、物理、化学等学科中,参数的计算是非常重要的一部分。
在数学中,我们经常需要计算各种函数的参数,如一次函数、二次函数、三次函数等。
这些函数的参数包括斜率、截距、抛物线的对称轴等,通过计算这些参数,我们可以确定函数的性质,进而解决一系列相关问题。
在物理学中,参数的计算尤为重要。
例如在力学中,我们需要计算物体的速度、加速度、功、能量等参数,以便分析物体的运动规律、能量转化等问题。
在热学中,我们需要计算物体的温度、热容、热传导等参数,以便分析物体的热力学性质。
在化学中,参数的计算也是必不可少的。
例如在化学反应中,我们需要计算反应的速率常数、平衡常数等参数,以便预测反应的进程和结果。
在化学分析中,我们需要计算各种物质的浓度、摩尔质量等参数,以便准确测定物质的含量和性质。
综上所述,参数的计算在各个学科中都具有重要的应用价值,是各种研究工作中不可或缺的一部分。
- 1 -。
时间参数的计算方法

时间参数的计算方法时间是我们生活中不可或缺的一部分,我们需要准确地计算时间来安排日程、规划生活。
在计算时间参数时,我们可以使用一些简单而有效的方法。
本文将介绍几种常用的时间参数计算方法,帮助读者更好地理解和应用时间。
一、计算时间差计算时间差是常见的时间参数计算方法之一。
当我们想要知道两个时间点之间的时间差时,可以使用该方法。
首先,我们需要确定两个时间点的具体时间,例如一个事件发生的开始时间和结束时间。
接下来,我们可以使用减法来计算时间差,即结束时间减去开始时间。
最后,我们可以将时间差表示为小时、分钟、秒等单位,以更好地理解时间差的大小。
二、计算时间间隔计算时间间隔也是常用的时间参数计算方法之一。
当我们需要确定两个事件之间的时间间隔时,可以使用该方法。
首先,我们需要确定两个事件发生的具体时间点。
然后,我们可以使用减法来计算时间间隔,即第二个事件的时间减去第一个事件的时间。
最后,我们可以将时间间隔表示为小时、分钟、秒等单位,以更好地理解时间间隔的大小。
计算时间点是一种常见的时间参数计算方法。
当我们知道一个事件发生的时间间隔和起始时间点时,可以使用该方法。
首先,我们需要确定一个起始时间点,例如当前的时间。
然后,我们可以根据时间间隔来计算具体的时间点,即将时间间隔加上起始时间点。
最后,我们可以得到目标时间点的具体时间。
四、计算时间周期计算时间周期是一种常用的时间参数计算方法。
当我们需要确定一个事件发生的周期时,可以使用该方法。
首先,我们需要确定一个起始时间点,例如当前的时间。
然后,我们可以根据周期的大小来计算具体的时间点,即将周期的时间加上起始时间点。
最后,我们可以得到周期的具体时间。
五、计算时间进度计算时间进度是一种常见的时间参数计算方法。
当我们需要确定一个事件的进度时,可以使用该方法。
首先,我们需要确定事件的起始时间点和结束时间点。
然后,我们可以根据当前的时间来计算事件的进度,即当前时间减去起始时间点再除以事件的总时间差。
三坐标参数计算公式

三坐标参数计算公式在直角坐标系中,一个点的坐标可以由其在三个坐标轴上的投影来表示,即(x,y,z)。
其中,x表示点在x轴上的投影,y表示点在y轴上的投影,z表示点在z轴上的投影。
在三维空间中,两点之间的距离可以通过勾股定理来计算。
假设点A 的坐标为(x1,y1,z1),点B的坐标为(x2,y2,z2),则两点之间的距离d可以计算为:d = sqrt((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)在三维空间中,两个向量的夹角可以通过向量的点乘和模长来计算。
假设向量A的坐标为(x1,y1,z1),向量B的坐标为(x2,y2,z2),则两向量之间的夹角θ可以计算为:θ = arccos((x1*x2 + y1*y2 + z1*z2) / (sqrt(x1^2 + y1^2 + z1^2) * sqrt(x2^2 + y2^2 + z2^2)))在三维空间中,平面上三个点组成的三角形的面积可以通过向量的叉乘来计算。
假设点A的坐标为(x1,y1,z1),点B的坐标为(x2,y2,z2),点C的坐标为(x3,y3,z3),则三角形ABC的面积S可以计算为:S=0.5*,(x2-x1,y2-y1,z2-z1)×(x3-x1,y3-y1,z3-z1)在三维空间中,由四个点组成的四面体的体积可以通过向量的混合积来计算。
假设点A的坐标为(x1,y1,z1),点B的坐标为(x2,y2,z2),点C 的坐标为(x3,y3,z3),点D的坐标为(x4,y4,z4),则四面体ABCD的体积V可以计算为:V=1/6*,(x2-x1,y2-y1,z2-z1)·(x3-x1,y3-y1,z3-z1)×(x4-x1,y4-y1,z4-z1)以上是一些常用的三坐标参数计算公式,可以用于在三维空间中进行点的定位、距离的计算、角度的计算、面积的计算和体积的计算等。
这些公式在工程、物理、几何、计算机图形学等领域有广泛的应用。
动力学参数计算流程

动力学参数计算流程一、引言动力学参数计算是研究物体运动的重要方法之一,通过计算物体在运动过程中的力学特性,可以更好地理解和预测物体的运动行为。
本文将介绍动力学参数计算的基本流程,并以人类视角进行叙述,使读者能够深入理解这一过程。
二、动力学参数计算的基本流程1. 收集数据:在进行动力学参数计算之前,首先需要收集相关的数据。
这些数据可以是物体的质量、速度、加速度等基本信息,也可以是与物体运动相关的外部力或约束条件等。
2. 建立数学模型:根据收集到的数据,需要建立相应的数学模型来描述物体的运动。
数学模型可以是基于物理原理的方程组,也可以是基于统计学的概率模型等。
3. 求解方程:根据建立的数学模型,可以利用数值计算方法或解析解法求解方程,得到物体在运动过程中的各种参数。
这些参数可以包括物体的位置、速度、加速度、动能、势能等。
4. 分析结果:得到动力学参数后,需要对结果进行分析和解释。
可以通过绘制图表、计算相关指标等方式来分析物体的运动特性,比如速度曲线、加速度变化等。
5. 验证模型:在完成动力学参数计算后,需要对模型的准确性进行验证。
可以通过实验数据对比、与已有理论模型对比等方式来验证模型的可靠性和精确度。
6. 应用和推广:动力学参数计算的结果可以应用于各种领域,比如运动控制、工程设计、物体仿真等。
通过将动力学参数计算的方法推广应用,可以更好地理解和应用物体运动的规律。
三、结论通过动力学参数计算的流程,我们可以更好地理解和预测物体的运动行为。
通过收集数据、建立数学模型、求解方程、分析结果、验证模型和应用推广等步骤,可以得到物体在运动过程中的各种参数,并应用于实际问题中。
动力学参数计算的方法不仅在科学研究中具有重要意义,也在工程实践中发挥着重要作用。
相信通过不断的研究和应用,我们可以更好地理解和掌握物体运动的规律,推动科学技术的发展。
(完整版)网络时间参数计算(节点计算法)

(2)其他节点 其他节点i的最迟时间LTi 为:
式中 LTj ——工作i-j的箭头节点的最
迟时间。
ETi LTi
i
ETj LTj
j
3、由节点时间计算工作i-j的时间参数
(1)最早时间 工作i-j最早开始时间ESi-j等于该工作
开始节点的最早时间:ESi-j =ETi 工作i-j最早完成时间EFi-j等于该工作
9 I(2)
18 18
H(2)
20 20
10
(三)利用节点时间参数推导
工作时间参数 LFi-j =LTj
3 3 0 6 6 6 6 0 14 14 14 14 0
6 60 3 B(3)
6 93
00 000 3 3690
330
1
2
A(3)
6 95
C(3)
69 3 69 0
4
363
14 14 0
D(8)
6 11
18
9 I(2)
20
10
C(3)
4
8
F(4)
6
11
H(2)
(一)节点最早时间ETi
1.起始节点的最早时间,如无规定,定为0;
2.其他节点的最早时间按“顺箭头相加, 箭头相碰取大值”计算。 计算工期Tc=ETn ,当网络计划未规定要 求工期Tr时, Tp=Tc
(二)节点最迟时间LTi
--在不影响计划工期的情况下,以该节点为
节点计算法
ETi LTi
i
ETj LTj
j
3
7
B(3)
D(8)
G(4)
1
2
A(3)
C(3)
5
6
E(5)
时间参数计算

位置:课程学习>第八章>第三节第三节 网络时间参数计算网络时间参数包括事件的时间参数和活动的时间参数。
一、事件时间参数计算事件时间是一个瞬时的概念,在时间轴上是一个点,它包括事件最早可能发生时间、事件最迟必须发生时间和事件时差。
在网络图中,节点与事件对应。
起始节点表示项目开始事件,这一事件的发生,表示项目最早可以进行的活动开始;终止节点表示项目完成事件,这一事件的发生,表示最后进行的活动完成。
中间节点表示终止在该节点的箭线所代表的活动完成和从该节点发出的箭线所代表的活动开始这一事件。
(一)事件最早可能发生时间(Early time ,()ET j )事件最早可能发生时间是指从相应节点发出的箭线所代表的活动可能开始的最早时间,或相应节点接受的箭线所代表的活动可能完成的最早时间;事件最早可能发生时间从网络图的起始节点开始,按节点编号顺向计算,直到网络图的终止节点为止。
一般假定网络图的起始节点最早开始时间为零,即(1)0ET =。
其余节点最早可能发生时间可按下式计算:{}()m a x ()(,)E T j E T i t i j =+ 式中,i 和j 分别代表箭尾事件和箭头事件;t(i,j)为活动(i ,j)所需时间。
(二)事件最迟必须发生时间(Late time ,()LT i )事件最迟必须发生时间是指从相应节点接受的箭线所代表的活动完成的最迟时间或相应节点发出的箭线所代表的活动开始的最迟时间。
节点最迟必须发生时间的计算从网络图的终止节点开始,按节点编号逆向计算,直到网络图的起始节点为止。
由于事件本身不消耗时间,所以网络终止节点的最迟必须发生时间可以等于它的最早可能发生时间。
即()()LT n ET n =,其余节点最迟必须发生时间可按下式计算:{}()min ()(,)LT i LT j t i j =-(三)事件时差()S i()()()S i LT i ET i =-(四)关键路线关键路线从起始节点到终止节点顺序地将所有事件时差为零的节点连接起来的路线。
圆锥体基本参数的计算(精)

圆锥体基本参数的计算
一、圆锥体的基本参数
圆锥体的基本参数有:大端直径D,小端直径d,圆锥体轴向长度L,锥角a,锥度C。
如图1:
图1 圆锥面的基本参数
二、圆锥体基本参数的计算公式
(一)锥度的计算公式
根据锥度的概念有锥度的计算公式如下:
C=(D-d)/L=2tan(α/2)
(二)圆锥体基本参数的计算
在锥度的计算公式中。
包含了圆锥体的所有基本参数,只要已知其中三个参数,就可根据此公式推导出其它基本参数的计算公式。
如:
1.已知锥度C、小端直径d、锥长L,则锥体大端直径D=CL+d
2.已知锥度C、大端直径D、锥长L,则锥体小端直径d=D-CL
3.已知锥度C、大端直径D、小端直径d,则锥长L=(D-d)/C
4.已知锥度C,则锥角a=2arctan(c/2)
5.已知小端直径d、锥长L,大端直径D,则锥角a=2arctan[(D-d)/2L]
三、计算例题
图2中,已知锥体的大端直径D=80mm,小端直径d=50mm,锥度C=1/3,求锥体长度L。
图2
解:根据公式L=(D-d)/C 代入数据得: L=(80-50)/1/3=90mm。
电路设计之参数计算

电路设计之参数计算电路设计是电子工程中的重要环节,涉及到参数计算是设计过程中的一项基础工作。
参数计算是指根据电路设计的要求和特定的电子元器件的参数,计算出电路中各个元件的数值。
本文将从电阻、电容和电感三个方面,介绍电路设计中常用的参数计算方法。
电阻是电子电路中最基本的元件之一,用于控制电流的大小和流向。
在电路设计中,我们需要根据电路的要求和电源提供的电压,计算出电阻的阻值。
电阻的阻值单位是欧姆(Ω),常用的计算公式是R=V/I,其中R表示电阻的阻值,V表示电源提供的电压,I表示电流的大小。
例如,当我们需要设计一个电流为1A的电路,电源提供的电压为5V,那么可以通过计算得到电阻的阻值为5Ω。
电容是电子电路中常见的元件,用于储存和释放电荷。
在电路设计中,我们需要根据电路的要求和电源提供的电压,计算出电容的容值。
电容的容值单位是法拉(F),常用的计算公式是C=Q/V,其中C 表示电容的容值,Q表示电容器所储存的电荷量,V表示电容器所加的电压。
例如,当我们需要设计一个容值为10μF的电容器,电源提供的电压为10V,那么可以通过计算得到电容的容值为10μF。
电感是电子电路中常用的元件,用于储存和释放磁能。
在电路设计中,我们需要根据电路的要求和电源提供的电流,计算出电感的感值。
电感的感值单位是亨利(H),常用的计算公式是L=Φ/I,其中L表示电感的感值,Φ表示电感器所储存的磁通量,I表示电流的大小。
例如,当我们需要设计一个感值为1H的电感器,电源提供的电流为1A,那么可以通过计算得到电感的感值为1H。
除了电阻、电容和电感的参数计算,电路设计中还涉及到其他一些参数的计算,如功率、频率等。
功率的计算公式是P=VI,其中P表示功率,V表示电压,I表示电流。
频率的计算公式是f=1/T,其中f表示频率,T表示周期。
根据电路设计的要求,我们可以根据这些公式计算出相应的数值。
电路设计中的参数计算是设计过程中的基础工作,根据电路的要求和特定的电子元器件的参数,计算出电路中各个元件的数值。
线路参数计算方法

输入:电压等级(kV)110线路长度(km)28.7000导线的材质铝单根导线的标称截面积(m m2)240测试时的环境温度(℃)0每相导线的根数(根)单根导线架空地线及回路数有架空地线的双回线路输入:电压等级(kV)110线路长度(km)28.7000导线的材质铜单根导线的标称截面积(m m2)300测试时的环境温度(℃)020℃时的直流电阻(Ω/km)0.07541+jX1总 长度的零序电阻(Ω)总 长度的零序电抗(Ω)0+jX0二、电缆线路的参数计算:三、架空、电缆混合线路的参数计算:先按照架空线路、电缆线路分别计算一、架空线路的参数计算:输出:单位长度的正(负)序电阻(Ω/km)0.1218总 长度的正(负)序电阻(Ω)3.4957单位长度的正(负)序电抗(Ω/km)0.4000总 长度的正(负)序电抗(Ω)11.4800R1+jX13.4957+j11.4800正(负)序阻抗角度(度)73.06单位长度的零序电阻(Ω/km)0.3654总 长度的零序电阻(Ω)10.4870单位长度的零序电抗(Ω/km)1.2000总 长度的零序电抗(Ω)34.4400R0+jX010.4870+j34.4400零序阻抗角度(度)73.06输出:单位长度的正(负)序电阻(Ω/km)0.0696总 长度的正(负)序电阻(Ω)1.9975单位长度的正(负)序电抗(Ω/km)0.1800总 长度的正(负)序电抗(Ω)5.1660R1+jX11.9975+j5.1660正(负)序阻抗角度(度)68.86单位长度的零序电阻(Ω/km)0.6960总 长度的零序电阻(Ω)19.9752单位长度的零序电抗(Ω/km)0.0626总 长度的零序电抗(Ω)1.7966R0+jX019.9752+j1.7966零序阻抗角度(度)5.14总 长度的正(负)序电阻(Ω)5.4932总 长度的正(负)序电抗(Ω)16.6460R1+jX116.646+j5.4932正(负)序阻抗角度(度)71.74总 长度的零序电阻(Ω)30.4622总 长度的零序电抗(Ω)36.2366R0+jX030.4622+j36.2366零序阻抗角度(度)49.95。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Z
2
I
2 B
R2
Z
2
I
2 B
RB
2Z
2
I
2 R
RR
RB 为导条电阻;
RR 为相邻导条间的端环电阻.
于是 :
R2
RB
2RR (IB IR )2
RB
2RR 2
,
由于 IB 2sin 2sin p 2p
IR
2
Z2 Z2
于是 :
R2
RB
Z
2 2
RR
2 2 p2
(
lB AB
电机的电气参数
(一)直流电机电气参数:
励磁绕组电阻Rf、励磁绕组电感Lf;
电枢绕组电阻Ra、电枢绕组电感La;
(二)交流同步电机电气参数:
励磁绕组电阻Rf、励磁绕组电感Lf; 电枢绕组电阻Ra、直轴电枢反应电抗xd 交轴电枢反应电抗xq、电枢漏抗x1δ
(三)交流异步(感应)电机 电气参数:
转子绕组电阻R2、转子漏抗x2δ 定子绕组电阻R1、定子励磁电抗xm 定子漏抗x1δ
电流的频率很低集肤效应忽略不计。
3、笼型转子电阻的计算 指折算到定子方面的转子每相电阻。折算系数如下:
K m1 ( N1Kdp1 )2 m2 N2Kdp2
把笼型转子绕组当作一个对称多相绕组,其相数等于槽数即 导条数,每相的导条数为1。于是:
Kdp2 1,
N2
1 2
,
m2 Z2
各导条电流的有效值是相等的,相邻导条之间的相位差为相邻 两槽间的电角度α。
同步电机电枢绕组的每相电阻的计算和感应电机的算式一样。
§4-2绕组电抗的一般计算方法
绕组电抗分为两类:1、主电抗;2、漏电抗。通常把它们表示
成标么值的形式。例如,标么值表示的绕组漏抗等于:
x•
x U N
I N x U N
,式中U N , I N为电机的额定相电压 ,相电流
IN
电抗的计算方法有两种:
对于凸极式同步电机,显然,由于气隙不均匀,则对应于不 同气隙尺寸下的主电抗值是不同的。根据双反应理论,把主电抗 分为直轴的电枢反应电抗和交轴的电枢反应电抗。
直轴电枢反应电抗等于X ad kd X m
交轴电枢反应电抗等于X aq kq X m
式中,系数Kd与Kq由曲线图查得。
对于隐极式同步电机,由于电机气隙基本上均匀,因此电枢 反应电抗不分成直轴与交轴,即:
m
2
K
2 dp1
q ef
为主磁路的比磁导.
从公式可以看出,感应电机的主电抗或励磁电抗Xm,主要与 绕组的每相匝数N、电枢的轴向长度lef及极距与气隙之比τ/δ有关。
进一步分析表明:
若线负荷A 2mNIN1 N ;
D
以及B
N
E1 4K Nm f Kdp
因此,选用较大的A和较小的Bδ将使电机的主电抗变大。
由于集肤效应,使交流电阻较直流电阻值大。交流电阻值按下式
计算:
R0 K'FR
式中 K'F为电阻的增加系数
一、直流电机 直流电机电枢绕组的电阻可按下式计算:
Ra
N a lc Ac (2a)2
Nalc 1 Ac (2a) 2a
式中 Na为绕组的总导体数 ;
lc为线圈的平均半匝长 ;
Ac为导体截面积 ;
2a为并联支路数 ;
基准工作温度时导体的 电阻率.
二、感应电机 1、定子绕组每相电阻可按下式计算:
R1
K
' F
2 N1lc Ac1a1
式中 N1为绕组的每相串联匝数; lc为线圈的平均半匝长;
Ac1为导体截面积;
a1为相绕组的并联支路数;
2、绕线式转子电阻计算 计算公式同上,但系数KF’取1,因为在正常运行时,转子
磁链 : m1 1Kdp1N 0
2m
p
(NKdp1)2 I
2
lef
ef
பைடு நூலகம்
A
X
iA 2I cos(t)
Lm m1
2I
Xm
2fLm
2f
m1
2I
4 f0
m
(NK dp1)2 p
lef
ef
式中0 4 107 H / m
上式也可写成如下形式:
Xm
4f0
N2 pq
lef m
, 式中m
2p
Z2
同理,转子端环各段中的电流有效值也相等,相邻两段中的电流 相位差也等于α。
导条电流与端环电流之间的关系:
如图所示,导条电流IB等于相邻两端电流IR之差。由相量图可得:
IR
IB
2 sin
2
计算每相电阻时,可用接成星形的电阻来替代接成多边形的端环 电阻。如图所示。等效的相电阻R2的电损耗应等于原来笼型转子绕组 的电损耗即:
计算主电抗时假定:1)电枢槽部导体中的电流集中在槽中心 线上;2)μ=∞;3)槽开口的影响用气隙系数来计及。
由电枢电流所建立的气 隙基波磁密为 :
B 1
0H1
0
F1
ef
,
式中ef 有效气隙长 , F1为每极基波磁势幅值
F1
2m
p
NK dp1I
1.35
NK dp1I p
磁通 : 1
2
B 1lef
1)磁链法
对任何一个电路的电抗可以写成: X L
因此,在一定频率之下,电抗的计算归结为对电路的电感L的计算。
而电感又可以表示为 : L
i
则电感的计算又可归结为对磁链的计算。
2、能量法
§4-3 主电抗的计算
主电抗即为相应于基波磁场或相应于同时交链定、转子绕组 的主磁场的电抗,属于主电抗。
在感应电机中,又将主电抗称为励磁电抗;在同步电机中, 则称为电枢反应电抗。
Z
2 2
2 2 p2
DR )
Z2 AR
(
lB AB
Z2 DR
2P2 AR
)
lB , AB为导条的长度和面积 ; DR , AR为端环的平均直径和截 面积
折算到定子方面的每相转子电阻为:
R2' R2 K
三、同步电机
R2
m1 m2
( N1kdp1 N 2 K dp2
)2
R2
4m1 ( N1K dp1 )2 Z2
§4-1 绕组电阻的计算
直流电阻可按下式计算:
R l
A0 电阻率与温度有关,当温度为15C时铜的ρ 0.0175 106 Ω.m
在电机通常的运行范围内, 温度t时的电阻率ρt可按下式进行换算 : ρt ρ15[1 α(t t15 )]
α为导体电阻的温度系数. 对于铜α 0.004/C
按国家标准GB755-81的规定,各绝缘等级的基准工作温度为: 对于A级、E级、B级绝缘的基准工作温度为75℃; 对于F级、H级绝缘的基准工作温度为:115℃。
Xa Xm
§4-4 漏电抗的计算
漏电抗即为漏磁场对应的电抗。绕组的漏电抗分为:1)槽漏抗;2)
谐波漏抗;3)齿顶漏抗;4)端部漏抗等四个部分。
上述四个部分的漏抗全部相加即得总的漏抗值。
漏抗的公式可以表示为 : X
4f0
N2 pq
lef
s t E 因此,漏抗的计算归结为相应的比漏磁导λ的计算。
