初中数学二次函数压轴题
中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案

中考数学总复习《二次函数压轴题(面积问题)》专题训练-附含答案学校:___________班级:___________姓名:___________考号:___________1.如图,在平面直角坐标系中,抛物线2y ax x c =-+与y 轴交于点()0,4A -,与x 轴交于点()4,0B ,连接AB .(1)求抛物线的解析式.(2)P 是AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点C ,过点P 作PD x ⊥轴于点D .①求PC PD +的最大值.①连接PA ,PB ,是否存在点P ,使得线段PC 把PAB 的面积分成3:5两部分?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2.综合与探究如图1,抛物线212y x bx c =-++经过点(4,0)B 和(0,2)C ,与x 轴的另一个交点为A ,连接AC ,BC .(1)求该抛物线的解析式及点A 的坐标;(2)如图1,点D 是线段AC 的中点,连接BD .点E 是抛物线上一点,若ABE BCD S S =△△,设点E 的横坐标为x ,请求出x 的值;(3)试探究在抛物线上是否存在一点P ,使得45PBO OBC ∠+∠=︒?若存在,请直接写出点P 的坐标;若不存在,请说明理由.3.如图抛物线2y ax bx c =++经过点()1,0A -,点()0,3C ,且OB OC =.(1)求抛物线的解析式及其对称轴;(2)点D 、E 是直线1x =上的两个动点,且1DE =,点D 在点E 的上方,求四边形ACDE 的周长的最小值.(3)点P 为抛物线上一点,连接CP ,直线CP 把四边形CBPA 的面积分为3:5两部分,求点P 的坐标.4.已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ,与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 和DB ,判断BCD △的形状并说明理由;(3)在对称轴右侧抛物线上找一点P ,使得P 、D 、C 构成以PC 为底边的等腰三角形,求出点P 的坐标及此时四边形PBCD 的面积.5.如图,抛物线214y x bx c =-++与x 轴交于点,A B 两点(点A 在点B 的右侧),点()()8,02,0A B -、,与y 轴交于点C .(1)求抛物线的解析式; (2)点D 为抛物线的顶点,过点D 作DE AC ∥交抛物线于点E ,点P 为抛物线上点,D E 之间的一动点,连接,,,,AC AE AP CE CP ,线段,AP CE 交于点G ,记CPG △的面积为1,S AEG △的面积为2S ,且12S S S =-,求S 的最大值及此时点P 的坐标;(3)在(2)的条件下,将拋物线沿射线AC 方向平移5个单位长度后得到新抛物线,点Q 是新拋物线对称轴上一动点,在平面内确定一点R ,使得以点P Q B R 、、、为顶点的四边形是矩形.直接写出所有符合条件的点R 的坐标.6.如图,有一个长为30米的篱笆,一面利用墙(墙的最大可用长度18a =米)围成的中间隔有一道篱笆的长方形花圃设花圃的宽AB 为x 米,面积为y 平方米.(1)求y 与x 的函数关系式,并直接写出自变量x 的取值范围;(2)如何设计才能使长方形花圃面积最大;并求其最大面积.7.如图,过原点的抛物线212y x bx c =-++与x 轴的另一个交点为A ,且抛物线的对称轴为直线2x =,点B 为顶点(1)求抛物线的解析式(2)如图(1),点C 为直线OB 上方抛物线上一动点,连接AB,BC 和AC ,线段AC 交直线OB 于点E ,若CBE △的面积为1S ,ABE 的面积为2S ,求12S S 的最大值 (3)如图(2),设直线()20y kx k k =-≠与抛物线交于D ,F 两点,点D 关于直线2x =的对称点为D ,直线D F '与直线2x =交于点P ,求证:BP 的长是定值.8.抛物线2y x bx c =-++经过点A ,B ,C ,已知()1,0A -和()0,3C .(1)求抛物线的解析式及顶点E 的坐标;(2)点D 在BC 上方的抛物线上.①如图1,若CAB ABD ∠=∠,求点D 的坐标;①如图2,直线BD 交y 轴于点N ,过点B 作AD 的平行线交y 轴于点M ,当点D 运动时,求CBD AMNS S △△的最大值及此时点D 的坐标. 9.在平面直角坐标系中,O 为坐标原点,抛物线244y ax ax =-+交x 轴于点A 、B (A 左B右),交y 轴于点C ,直线123y x =-+,经过B 点,交y 轴于点D .(1)如图1,求a 的值;(2)如图2,点P 在第一象限内的抛物线上,过点A 、B 作x 轴的垂线,分别交直线PD 于点E 和F ,若PF DE =,求点P 的坐标;(3)如图3,在(2)的条件下,点Q 在第一象限内的抛物线上,过点Q 作QH DP ⊥于点H ,交直线BD 于点R ,连接EQ 和ER ,当QE ER =时,求ERQ △的面积.10.已知抛物线213222y x x =-++与x 轴交于B 、C 两点(点B 在点C 的左侧),与y 轴交于点A .(1)判断ABC 的形状,并说明理由.(2)设点(,)P m n 是抛物线在第一象限部分上的点,过点P 作PH x ⊥轴于H ,交AC 于点Q ,设四边形OAPC 的面积为S ,求S 关于m 的函数关系式,并求使S 最大时点P 的坐标和QHC △的面积;(3)在(2)的条件下,点N 是坐标平面内一点,抛物线的对称轴上是否存在点M ,使得以P 、C 和M 、N 为顶点的四边形是菱形,若存在,写出点M 的坐标,并选择一个点写出过程,若不存在,请说明理由.11.已知,如图,在平面直角坐标系中,点O 为坐标原点,直线6y x =+与x 轴相交于点B ,与y 轴交于点C ,点A 是x 轴正半轴上一点,且满足2tan 3ACO ∠=.(1)若抛物线2y ax bx c =++经过A 、B 和C 三点,求抛物线的解析式;(2)若点M 是第二象限内抛物线上的一个动点,过点M 作MP y ∥轴,交BC 于点P ,连接OP ,在第一象限内找一点Q ,过点Q 作⊥OQ OP 且OQ OP =,连接PQ ,MQ ,设MPQ 的面积为S ,点P 的横坐标为t ,求S 与t 的函数关系式,并直接写出自变量的取值范围;(3)在(2)的条件下,设PQ 与y 轴相交于点R ,若53=PR PC 时,求点P 的坐标. 12.已知抛物线22y ax ax c =-+过点()10A -,和()03C ,,与x 轴交于另一点B .(1)求抛物线的解析式;(2)若抛物线的顶点为D ,在直线BC 上方抛物线上有一点P (与D 不重合),BCP 面积与BCD △面积相等,求点P 的坐标;(3)若点E 为抛物线对称轴上一点,在平面内是否存在点F ,使得以E 、F 和B 、C 为顶点的四边形是菱形,若存在,请直接写出F 点的坐标;若不存在,请说明理由.13.如图,抛物线过点()08D ,,与x 轴交于()20A -,,()40B ,两点.(1)求抛物线的解析式;(2)若点C 为二次函数的顶点,求BCD S △.14.如图,O 为平面直角坐标系坐标原点,抛物线22y ax ax c =-+经过点()6,0B ,点()0,6C 与x 轴交于另一点A .(1)求抛物线的解析式;(2)D 点为第一象限抛物线上一点,连接AD 和BD ,设点D 的横坐标为t ,ABD △的面积为S ,求S 关于t 的函数解析式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,P 为第四象限抛物线上一点,连接PA 交y 轴于点E ,点F 在线段BC 上,点G 在直线AD 上,若1tan 2DAO ∠=,四边形BEFG 为菱形,求点P 的坐标. 15.已知抛物线2()20y ax x c a =++≠与x 轴交于点(1,0)A -和点B ,与直线3y x =-+交于点B 和点C ,M 为抛物线的顶点,直线ME 是抛物线的对称轴.(1)求抛物线的解析式及点M 的坐标;(2)点P 为直线BC 上方抛物线上一点,连接PB ,PC ,当PBC 的面积取最大值时,求点P 的坐标.参考答案:1.(1)2142y x x =-- (2)① PC PD +取得最大值254 ① 53,2⎛⎫- ⎪⎝⎭或 316,2⎛⎫+- ⎪⎝⎭2.(1)213222y x x =-++ (1,0)-; (2)3172+或3172-或3332+或3332- (3)存在,517(,)39--或113(,)39-3.(1)故抛物线的表达式为:223y x x =-++,函数的对称轴为:1x =;(2)10113++(3)()4,5-或()8,45-4.(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3,四边形PBCD 的面积为45.(1)213442y x x =-++ (2)S 的最大值为1,()4,6P(3)()7,3或()5,3-6.(1)2330S x x =-+ 410x ≤<;(2)当宽AB 为5米,长15BC =米时,长方形花圃的最大面积为75平方米.7.(1)2122y x x =-+ (2)188.(1)()1,4(2)①()2,3D ;①CBD AMN S S △△的最大值为916,此时315,24D ⎛⎫ ⎪⎝⎭9.(1)13a =- (2)()4,4P(3)1010.(1)直角三角形(2)244S m m =-++ (2,3)P 1QHC S =(3)存在,点M 坐标为3651(,)22+或3651(,)22-或333(,)22或333(,)22-或31(,)22,理由见解析11.(1)211642=--+y x x (2)()2396042S t t t =---<< (3)()()124,2,2,4P P --12.(1)223y x x =-++(2)()23P ,(3)存在,点F 的坐标为()417,或()417-,或()2314-+,或()2314--,13.(1)228y x x =-++(2)614.(1)211642y x x =-++ (2)2553042S t t =-++ (3)()8,6P -15.(1)抛物线的解析式为223y x x =-++,点M 的坐标为(1,4)(2)315,24P ⎛⎫ ⎪⎝⎭。
中考数学二次函数压轴题16道
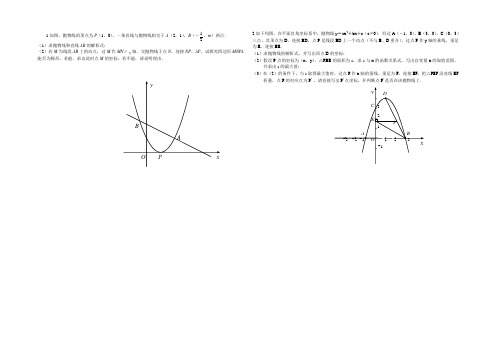
1.如图,抛物线的顶点为P (1,0),一条直线与抛物线相交于A (2,1),B (-21,m )两点.(1)求抛物线和直线AB 的解析式;(2)若M 为线段AB 上的动点,过M 作MN ∥y 轴,交抛物线于点N ,连接NP 、AP ,试探究四边形MNP A 能否为梯形,若能,求出此时点M 的坐标;若不能,请说明理由.2.如下列图,在平面直角坐标系中,抛物线y =ax2+bx +c (a ≠0).经过A (-1,0)、B (3,0)、C (0,3)三点,其顶点为D ,连接BD ,点P 是线段BD 上一个动点(不与B 、D 重合),过点P 作y 轴的垂线,垂足为E ,连接BE .(1)求抛物线的解析式,并写出顶点D 的坐标;(2)假设P 点的坐标为(x ,y ),△PBE 的面积为s ,求s 与x 的函数关系式,写出自变量x 的取值范围,并求出s 的最大值;(3)在(2)的条件下,当s 取得最大值时,过点P 作x 轴的垂线,垂足为F ,连接EF ,把△PEF 沿直线EF折叠,点P 的对应点为P ′ ,请直接写出P ′点坐标,并判断点P ′是否在该抛物线上.3.如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.(1)求这条抛物线的解析式;(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;(3)探究:若点Q是抛物线对称轴上的点,是否存有这样的点Q,使△QBC成为等腰三角形,若存有,请直接写出所有符合条件的点Q的坐标;若不存有,请说明理由.4.已知:如下列图,关于x的抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0),点B(6,0),与y 轴交于点C.(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q.是否存有以A、M、P、Q为顶点的平行四边形?假设存有,请直接写出点Q的坐标;假设不存有,请说明理由.5.如图,矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上,A (-3,0),过点C 的直线y =-2x +4与x 轴交于点D ,二次函数y =-21x2+bx +c 的图象经过B 、C 两点. (1)求B 、C 两点的坐标; (2)求二次函数的解析式;(3)若点P 是CD 的中点,求证:AP ⊥CD ;(4)在二次函数的图象上是否存有这样的点M ,使以A 、P 、C 、M 为顶点的四边形为矩形?若存有,求出点M 的坐标;若不存有,请说明理由.6.已知:抛物线y =ax2+bx +c (a ≠0)的对称轴为x =-1,与x 轴交于A 、B 两点,与y 轴交于点C ,其中A (-3,0)、C (0,-2).(1)求这条抛物线的函数表达式.(2)已知在对称轴上存有一点P ,使得△PBC 的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE ∥PC 交x 轴于点E ,连接PD 、PE .设CD 的长为m ,△PDE 的面积为S .求S 与m 之间的函数关系式.试说明S 是否存有最大值,若存有,请求出最大值;若不存有,请说明理由.7.如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.(1)求A、B、C三点的坐标.(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.(3)在x轴上方的抛物线上是否存有一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存有,请求出M点的坐标;否则,请说明理由.8.如图,抛物线y=ax2+bx-3与x轴交于A,B两点,与y轴交于C点,且经过点(2,-3a),对称轴是直线x=1,顶点是M.(1)求抛物线对应的函数表达式;(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存有这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存有,请求出点P的坐标;若不存有,请说明理由;(3)设直线y=-x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E 三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)当E是直线y=-x+3上任意一点时,(3)中的结论是否成立?(请直接写出结论)9.如图,已知抛物线y=ax2+bx+c与y轴交于点A(0,3),与x轴分别交于B(1,0)、C(5,0)两点.(1)求此抛物线的解析式;(2)若点D为线段OA的一个三等分点,求直线DC的解析式;(3)若一个动点P自OA的中点M出发,先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A.求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.10.如图,在平面直角坐标系中,以点A(-3,0)为圆心、5为半径的圆与x轴相交于点B、C两点(点B在点C的左边),与y轴相交于D、M两点(点D在点M的下方).(1)求以直线x=-3为对称轴、且经过D、C两点的抛物线的解析式;(2)若点P是这条抛物线对称轴上的一个动点,求PC+PD的取值范围;(3)若点E为这条抛物线对称轴上的点,则在抛物线上是否存有这样的点F,使得以点B、C、E、F 为顶点的四边形是平行四边形?若存有,求出点F的坐标;若不存有,说明理由.11.如图,已知抛物线y=ax2+bx-4与直线y=x交于点A、B两点,A、B的横坐标分别为-1和4.(1)求此抛物线的解析式.(2)若平行于y轴的直线x=m(0<m<5+1)与抛物线交于点M,与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示).(3)在(2)的条件下,连接OM、BM,是否存有m的值,使得△BOM的面积S最大?若存有,请求出m 的值,若不存有,请说明理由.12.如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存有P点,使得以A、P、M为顶点的三角形与△OAC相似?若存有,请求出符合条件的点P的坐标;若不存有,请说明理由;(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.13. 如图(1),抛物线42y x x =+-与y 轴交于点A ,E (0,b )为y 轴上一动点,过点E 的直线y x b =+与抛物线交于点B 、C .b ;若不存有,说明理由.14.如图,已知抛物线212y x bx c x =++与轴交于点A (-4,0)和B (1,0)两点,与y 轴交于C 点. (1)求此抛物线的解析式;(2)设E 是线段AB 上的动点,作EF ∥AC 交BC 于F ,连接CE ,当△CEF 的面积是△BEF 面积的2倍时,求E 点的坐标;(3)若P 为抛物线上A 、C 两点间的一个动点,过P 作y 轴的平行线,交AC 于Q ,当P 点运动到什么位置时,线段PQ 的值最大,并求此时P 点的坐标.x15.如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点. (1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存有点P ,使四边形POP /C 为菱形?若存有,请求出此时点P 的坐标;若不存有,请说明理由.(3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.16.在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(30)-,,若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线2x =-.(1)求直线AC 及抛物线的函数表达式;(2)假如P 是线段AC 上一点,设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆,且:2:3ABP BPC S S ∆∆=,求点P 的坐标;(3)设Q 的半径为l ,圆心Q 在抛物线上运动,则在运动过程中是否存有Q 与坐标轴相切的情况?若存有,求出圆心Q 的坐标;若不存有,请说明理由.并探究:若设⊙Q 的半径为r ,圆心Q 在抛物线上运动,则当r 取何值时,⊙Q 与两坐轴同时相切?。
2022年中考数学复习之二次函数压轴题40个问题

中考复习之二次函数压轴40个问题主要题型:1.二次函数之面积问题2.二次函数之特殊三角形的存在性问题3.二次函数之特殊四边形的存在性问题4.二次函数之线段最值问题5.二次函数之角度问题题目:如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D第1问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D.求二次函数的解析式;解:设:设二次函数解为y=a(x+1)(x-3)将(0,3)代入得a=-1,故二次函数解析式为y=-x2+2x +3第2问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1.顶点为D1.判断∆BCD的形状;解:D(1,4),B(3,0),C(0,3),方法一:BC=32,CD=2,BD=25,BC2+CD2=BD2,故∆BCD是直角三角形;方法二:KCD =1,KBC=-1,KCD∙KBC=-1,故CD⊥CB,所以∆BCD是直角三角形;yxBCAODyxBCAODyxBCAODyxBCAOD第3问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1.顶点为D, 2. 四边形ABDC 的面积解:BC:y =-x +3,铅垂法:E(1,2)DE=2,S BCD ∆=21∙2∙3=3 S ABDC 四=21∙4∙3+3=9第4问:如图,抛物线与x 轴交于A 、B 两点,与y 交于点C,OB=OC=3,OA=1,顶点为D, 1. P 为直线BC 上方抛物线上一点,求∆PBC 面积最大值及P 点坐标;解:方法一:设P(m,-m+2m+3)S PBC ∆=21∙3∙[-m 2+2m+3-(m+3)] =23(-m 2+3m),当m=23时,S 有最大值,此时P(23,415)S m ax =827 方法二:平移BC 至抛物线相切时,面积可取最大值设切线为y =-x +n,与抛物线y =-x 2+2x+3联立得x2-3x +n -3=0,∆=0,n=23,y =415,故P(23,415)S m ax =827y xBCAODy xBCAODEy xBCAOD第5问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D5点M 为BC 上方抛物线上一点,过点M 作y 轴的平行线交BC 于点N,求MN 的最大值;解:设点M(m,-m 2+2m+3),BC:y =-x +3,则点N(m,-m+3)MN=-m 2+2m+3-(-m+3)=-m 2+3m 当m=23时,MN m ax =49第6问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OC=3,OA=1,顶点为D, 6. 在对称轴上找一点P,使∆ACP 的周长最小,并求出最小值解:点A 、B 关于对称轴对称,连接BP,则BP=AP,PA+PC=PB+PC,当点B 、P 、C 三点共线时,可取最小值,此时P(1,2),∆ACP 周长的最小值为10+32第7问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点E,使∆BDE 为直角三角形,求出E 点坐标, 方法一:y xBCAOPDy xBCAODy xNBCAODMy xBCAOD P1.DE ⊥BE 时,设E(0,m)易知∆DEF~∆EBO,OE DF =BO EF ,即m 1=34m-,m=3或1,故E 1(0,1)、E 2(0,3)2. DE ⊥DB 时,设E(0,m)易知∆DEN~∆BDM,BM DN =DM EN ,即m 1=34m -,m=27故E ;(0,27)3. DB ⊥BE 时,设E(0,m),易知∆DBF~∆BEG,BG DF =EG BF ,即m -2=34,m=-23,故E 4(0,-23)第8问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点F,使∆BDF 为等腰三角形,求出F 点坐标;2. BD=DF,设F(0,m),22)4()01(m -+-=25,m=4+9 或4-19,F 1(0,4+19);F 2(0,4-19)yxFBCAODExyN MBCAODExy GFEBCAODxy BCAODF2.BD=BF,设F(0,m),22)0()03(m -+-=25,m=±11,F 1(0,11),F 2(0,-11)3.DF=BF,设F(0,m),22)0()03(m -+-=22)4()01(m -+-,m=1,F 4(0,1)第9问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 求抛物线上一点N,使S ABN ∆=S ABC ∆;解:设N 点的坐标(m,n),则∆ABC 与∆ABN 底相同,故n=±3,-m 2+2m+3=3或者-m 2+2m+3=3得m 1=0,m 2=2,m 3=1-7,m 4=1+7,N(0,3),(2,3),(1-7,-3),(1+7,-3)第10问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D, 1. 在抛物线上找一点Q,使S BDQ ∆=S AOC ∆解:设Q(m,-m 2+2m+3),S AOC ∆=23,BD :y =-2x +6,铅垂高QS=|-m 2+2m+3-(-2m+6)| S BDQ ∆=|-m 2+2m+3-(-2m+6)|∙21∙1=23得m=0或4Q(0,3),(4,-5),xBCAODFBCAOD FBCAODFBCAODN第11问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.在抛物线上找一点E,使BE 平分∆ABC 的面积; 解:BE 平分∆ABC 的面积,故BE 经过AC 的中点,AC 中点(-21,23),BE:y =-73x +79; 与抛物线联立得-x 2+2x +3=-73+79x =-74或722,E(-74;4919)或(722;491849)第12问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA =1,顶点为D 1.在对称轴上找一点M,使|MB -MC|取最大值,并求出最大值;解:点B 关于对称轴对称的点A,连接MA,则MB=MA,MA -MC<AC, 当点A 、C 、M 共线时,|MB -MA|m ax =AC=10, AC:y =3x x +3,M(1,6)第13问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 、N 为对称轴上的两点(M 在N 点上方),且MN=1,求四边形ACNM 周长的最小值; 解:A 关于对称轴对称的点B,连接BN,则BN=AN,将点向下平移1个单位得C’、N,则C’N=CM, 故CM+BN=C’N+BN,当C’、N 、B 共线时,取最小值(CM+BN)m in =13,故ACNM 周长得最小值为1+10+13BCAODQABCODEABCODM第14问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 在抛物线对称轴上,在抛物线上找一点F,使得点四边形ACFE 为平行四边形; 解:设E(1,m)F(n,-n 2+2n+3),A(-1,0),C(0,3),A 平行至点C 与E 平移至点F, n=1+1=2,m+3=-n 2+2n+3,m=0,故E(1,0)F(2,3)第15问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 为y 轴上一点,在坐标平面内找一点N,使A 、C 、M 、N 为顶点的四边形为菱形; 解:当 ACM 为等腰三角形时,问题转化为等腰三角形问题 1.ACNM 为菱形时,M(0,3),N(1,0),2.AMCN 为菱形时,M(0,34),N(-1,35),3.ACMN 为菱形时,M(0,3+10),N(-1,10)ABCODMNABCODM NC'ABCODEFABCODMN ABCONDM4.ACMN 为菱形时,M(0,3-10),N(-1,-10)第16问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 为x 轴上一点,以BE 为边的正方形BEFG ; 另一点G 在抛物线上,求点F 坐标;设E(m,0)则EF=|-m 2+2m+3|由EF=EB 得3-m=|-m 2+2m+3|,m=0或m=-2故F(0,3)或F(-2,-5)第17问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是抛物线上任意一点,过点P 作PE ⊥y 轴于点E,交直线BC 于点G ;过点G 作GF ⊥x 轴,连接EF,求EF 的最小值;连接OG,则OG=EF,当OG ⊥BC 时,OG 最小,即EF 最小,故EF m in =233x C,OB=OC=3,OA=1,顶点为D1.M 在抛物线上CB 上方一点过点M 作y 轴的平行线,交BC 于点E,则ME 的最大值是多少? 解:设M(m,-m 2+2m+3),BC :y =-x +3,E(m,3-m),ME=-m 2+2m+3-(3-m)=-m 2+3m,当m=23ABCONDMABCNODMGCABO EFF CABOE GFEGCABOPFEGCABOP时,ME m ax =49第19问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.求一点P,使∠POC=∠PCO ; 解:点P 在OC 得垂直平分线上,-x2+2x +3=23,x =1±210P 1(1-210,23)P 2(1+210,23)第20问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.E(2,-2),M 为x 轴上一点,且∠EMO=∠CMO ; 1.M 在右侧时,易知∆CMO~∆EMG,设M(m,0)则有2-m m =23,m=6 2.M 在左侧时,同理易知∆CMO~∆EMG ,m m --2=23,m=6(舍) 第21问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是直线y =x 上的动点,当直接y =x 平分∠APB 时,求点P 的坐标; 如图,∆PAO ≅∆PEO,此时OE=OA=1,故E(0,-1),EB :y =31x -1,与y =x 得x =-23,P(-23,-23) ECABOMPPCABOCABOEMG第22问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,且∠ABP=∠CBD,求P 坐标;解:C(0,3)D(1,4)B(3,0)tan ∠CBD=31,故tan ∠PBO=31,OE=1或者OF=1,PB :y =-31x +1或y 且=31x -1,联立可得P 1(-32,911)P 2(-23,-23)第23问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.在抛物线上找一点P,使∠ACP=450;方法1:∠OCB=∠ACP=450,得∠ACO=∠ECB,故tan ∠ECB=31,作EH ⊥BC,设BH=m,则EH=m;CH=3m,故4m=32,m=423,E(23,0)故CE:y =-2x +3,联立得P(4,-5) 方法2:由12345模型得tan ∠ECO=21得E(23,0)第24问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 在抛物线上,∠DBP=450; 由tan ∠CBD=31,∠CBD+∠CBP=450,而∠PBO+∠CBP=450,故tan ∠PBO=31,BP:y =-31x +1,P(-32,911) ECABOPPEFCABODPPHECABOPDP第25问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,∠PCB=150,求点P 的坐标;解:由∠BCO=450得∠PCO=30或∠PCO=600,故PC:y =-3x +3或y =-33x +3联立得P(2+3,-23)P(2+33,3328-)第26问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.直线y =31x -1与y 轴交于点E,求∠EBC -∠CBD ; 由tan ∠DBC=tan ∠EBO=31,故∠EBC -∠CBD=450第27问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.过点P(3,0)作直线与抛物线交于F 、G 、FM 、GN 分别垂直于x 轴,求PM,PN ;设F(1x ,1y )G(2x ,2y ),直线y =k (x +3)与抛物线y =-2x +2x +3联立得2x +(k -2)x +3k -3=0;1x +2x =2-k ,1x •2x =3k -3,PM •PN=(1x +3)(2x +3)=1x •2x +3(1x +2x )+9=12CABOPDPPF CABODPEECABODENMGFCABOPD第28问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DP 是第一象限抛物线上,PE ⊥AB,求BEAE的值,若PE 2=AE •BE,求P 点坐标 设P(m,-m 2+2m+3),AE=m+1,BE=3-m,BE AE =mm -+31,(m+1)(3-m)=(-m 2+2m+3)2得m=1+3,P(1+3,1)第29问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,N(0,-1),求23BM+MN 的最小值, 过点B 作I ⊥x 轴,MH ⊥I,∠MBH=600,MH=23BM,23BM+MN=MH+MN,当N 、M 、H 共线且垂直于I 时取最值(23BM+MN)min=3第30问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求21BM+OM 的最小值 过点B 作I:y =3x -33,MH ⊥I,∠MBH=300,MH=21BH,21BH+OM=MH+OM,当Q 、M 、H共线且垂直于I 时取最值(21BM+MN )min=233xy EBCAOPxy BCA O MN H第31问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求22BM+OM 的最小值 过点B 作I,I 与直线MN 夹角450,MH ⊥I,∠MBH=450,MH=22BM,22BM+OM=MH+OM,当Q 、M 、H 共线且垂直于I 时取最值两着色三角形相似,得cos150=426,(21BM +MN)min=423-63第32问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D在AB 上是否存在点M,使CM+21BM 取最小值. 过点B 作I,I 与x 轴夹角为300,MH=21BM,21BM+CM=MH+CM,当C 、M 、H 共线且垂直于I 时取最值(21BM+CM)min=2333+第33问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为Dxy BCAMO Hxy BCAMOHxy BCAO M EHM 是抛物线上一点,作MH ⊥x 轴,交BC 于点E,当ME:EH=3:2时,求M 点的横坐标, 设M(m,-m 2+2m+3),则E(m,3-m),ME=-m 2+2m+3-(3-m),EH=3-m,ME:EH=3:2 即有-m 2+2m+3-(3-m)=23(3-m) m=23第34问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于顶点为D P 是抛物线上一点,且∠PAB=2CBD,求P 点坐标. tan ∠CBD=31,tan ∠PAB=tan2∠CBD=43(12345模型) 设P(m,-m 2+2m+3)(1)tan ∠PAB=1322+++-m m m =43,m=49,P(49,1639)(2)tan ∠PAB=1322+--m m m =43,m=415,P(415,1657)第35问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(1)证明:M 上任意一点到直线y =417距离等于到F 点的距离, M(m,-m 2+2m+3),MH=417-(-m 2+2m+3)=m 2-2m+45MF=222)41532()1(-++-+-m m m =m 2-2m+45,故MH=MF xyEBCAOMHxy BCAODPP第36问:如图,抛物线与x 轴交于、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(2)证明:N(2,-1)M 为抛物线上一点,求NM+MF 的最小值 由(1)可知MF=MH,故NM+MF=MN+MH,(NM+MF)min=421第37问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D ∠BAC 的角平分线交y 轴于点M,绕点M 作直线I,与x 轴交于点E,与A 交于点F,求证:AE 1+AF 1为定值 过点M 、F 、C 作x 轴的平行线,交AC 于点G,交AM 于点H 、I ,易知:∆AEM~∆HFM,∆AFH~∆ACI,AO GM =AC CG ,CI GM =AC AG ,相加得AO GM +CI GM =AC CG +ACAG=1 即有AO 1+AC 1=GM 1,同理可得AE 1+AF 1=GM1=1+1010第38问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D P 为第四象限抛物线上一点,且tan ∠APC=21,求出点P 的坐标; 过点C 作CE ⊥AC,取一点E 使CE=2AC,过点C 作MN||x 轴,作A M ⊥MN 、EN ⊥MN,易知∆ACM~∆CEN,CN=6,EN=2,E(6,1),P 为以AE 为直径的圆与抛物线的交点AE 的中点F,F(25,21) xy BCOFMHxy BCNOFMHA过点易知AE HF AFACGM AO =CG AC ,GM CI =AGAC,GM AO +GM CI =CG AC +AGAC =1即有1AO +1AC =1GM,同1AE +1AF =1GM =11010xy H G FEMBCOIPF=225,设P(m,-m 2+2m+3),PF 2=(m -25)2+(-m 2+2m+325)2=225m=255,y =2531--,P(255,2531--)第39问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 直线y =x -3与抛物线交于点P,在x 轴正半轴上找一点E,使tan(∠PBO+∠PEO)=25 在x 轴上找一点F,使tan ∠HPF=25,∠HPF=450+∠BPH=∠PBO+∠PEO=450+∠PEO, 故∠BPF=∠PEO,故∆BEP~∆BPF,BP BE =BF BP ,即253-m =21525,m -3=320,m=329故E(329,0)第40问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 对称轴与BC 交于点E,在直线BC 上找一点P,使∆ABP 与∆DEB 相似,∠BED=1350=∠ABP,故P 在CB 的延长线上,DE=2,BE=22,AB=3,1.当∆EDB~∆BAP,AB DE =BP EB ,即42=BP22,BP=42,P(7,-4) 2.∆EDB~∆BPA 时,BP=22,P(5,-2)AxyN MPFEBCOAH PE FAxyIHEBCODP 1P 2。
2023年九年级数学中考专题:二次函数综合压轴题(面积问题)(含简单答案)

2023年九年级数学中考专题:二次函数综合压轴题(面积问题)1.如图,二次函数25y ax bx =++的图象经过点(1,8),且与x 轴交于A 、B 两点,与y 轴交于点C ,其中点(1,0)A -,M 为抛物线的顶点.(1)求二次函数的解析式; (2)求MCB △的面积;(3)在坐标轴上是否存在点N ,使得BCN △为直角三角形?若存在,求出点N 的坐标;若不存在,请说明理由.2.如图,抛物线212y x bx c =-++(b 、c 为常数)经过()4,0A 和()0,4B 两点,其顶点为C .(1)求该抛物线的表达式及其顶点坐标;(2)若点M 是拋物线上第一象限的一个动点.设ABM 的面积为S ,试求S 的最大值; (3)若抛物线222y mx mx m =-++与线段AB 有两个交点,直接写出m 的取值范围. 3.如图,抛物线22(0)y ax ax c a =-+>与y 轴交于点C ,与x 轴交于A ,B 两点,点A 在点B 左侧.点A 的坐标为(1,0),3OC OA -=.(1)求抛物线的解析式;(2)在直线BC 下方的抛物线上是否存在一点P ,使得PBC 的面积等于ABC 面积的三分之二?若存在,求出此时OP 的长;若不存在,请说明理由.(3)将直线AC 绕着点C 旋转45︒得到直线l ,直线l 与抛物线的交点为M (异于点C ),求M 点坐标.4.如图1,抛物线24y ax bx a =+-经过()10A -,,()04C ,两点,与x 轴交于另一点B .(1)求抛物线和直线BC 的解析式;(2)如图2,点P 为第一象限抛物线上一点,是否存在使四边形PBOC 面积最大的点P ?若存在,求出点P 的坐标;若不存在,请说明理由;(3)如图3,若抛物线的对称轴EF (E 为抛物线顶点)与直线BC 相交于点F ,M 为直线BC 上的任意一点,过点M 作MN EF ∥交抛物线于点N ,以E ,F ,M ,N 为顶点的四边形能否为平行四边形?若能,请求出点N 的坐标;若不能,请说明理由. 5.如图,抛物线24y ax bx =+-与x 轴交于点()2,0A -,()4,0B ,与y 轴交于点C ,顶点为D .(1)求抛物线的解析式和顶点D 的坐标;(2)动点P ,Q 以相同的速度从点O 同时出发,分别在线段,OB OC 上向点B ,C 方向运动,过点P 作x 轴的垂线,交抛物线于点E . ①当四边形OQEP 为矩形时,求点E 的坐标;①过点E 作EM BC ⊥于点M ,连接,PM QM ,设BPM △的面积为1S ,CQM 的面积为2S ,当PE 将BCE 的面积分成1:3两部分时,请直接写出12S S 的值. 6.如图,抛物线2(0)y ax bx c a =++≠与x 轴相交于A ,B 两点,抛物线的对称轴为直线=1x -,其中点A 的坐标为(3,0)-.(1)求点B 的坐标;(2)已知1a =,C 为抛物线与y 轴的交点,求抛物线的解析式; (3)若点P 在抛物线上,且4POCBOCSS=,求点P 的坐标;(4)设点Q 是线段AC 上的动点,过点Q 作QD y 轴交抛物线于点D ,求线段QD 长度的最大值.7.如图,在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于()30A -,,()10B ,两点,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △的面积最大时,求点P 的坐标;(3)Q 是x 轴上一动点,M 是第二象限内抛物线上一点,若以A ,C ,M ,Q 为顶点的四边形是平行四边形,直接写出点Q 的坐标.8.如图,直线132y x =-+交y 轴于点A ,交x 轴于点C ,抛物线214y x bx c =-++经过点A ,点C ,且交x 轴于另一点B .(1)直接写出点A ,点B ,点C 的坐标及抛物线的解析式;(2)在直线AC 上方的抛物线上有一点M ,求四边形ABCM 面积的最大值及此时点M 的坐标;(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A '',若线段O A ''与抛物线只有一个公共点,请结合函数图象,求m 的取值范围.9.如图,已知抛物线与x 轴交于()1,0A - 、()4,0B 两点,与y 轴交于点()0,3C .(1)求抛物线的解析式; (2)求直线BC 的函数解析式;(3)在抛物线上,是否存在一点P ,使PAB 的面积等于ABC 的面积?若存在,求出点P 的坐标;若不存在,请说明理由.10.如图,抛物线26y ax bx =++与x 轴交于点()6,0B ,()2,0C -,与y 轴交于点A ,点P 是线段AB 上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P 运动到什么位置时,PAB 的面积最大?(3)过点P 作x 轴的垂线,交线段AB 于点D ,再过点P 作PE x ∥轴交抛物线于点E ,连接DE .是否存在点P ,使PDE △为等腰直角三角形?若存在,求点P 的坐标;若不存在,请说明理由.11.如图,直线l :112y x =-+与x 轴,y 轴分别交于点B ,C ,经过B ,C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A .(1)求该抛物线的解析式;(2)若点P 在直线l 下方的抛物线上,过点P 作PD ①x 轴交l 于点D ,PE ①y 轴交l 于点E ,求PD PE +的最大值;(3)若点P 在直线l 下方的抛物线上,F 为直线l 上的点,以A ,B ,P ,F 为顶点的四边形能否构成平行四边形?若能,直接写出点F 的坐标;若不能,请说明理由. 12.已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B ,(1)求抛物线的解析式;(2)设C ,D 分别是x 轴、y 轴上的两个动点.①当四边形ABCD 的周长最小时,在图1中作直线CD ,保留作图痕迹并直接写出直线CD 的解析式;①点()(),>0P m n m 是直线y x =上的一个动点,Q 是OP 的中点,以PQ 为斜边按图2所示构造等腰Rt PQR △.在①的条件下,记PQR 与COD △的公共部分的面积为S ,求S 关于m 的函数关系式,并求S 的最大值.13.抛物线24y x x =-与直线y x =交于原点O 和点B , 与x 轴交于另一点A , 顶点为D .(1)填空: 点B 的坐标为___________, 点D 的坐标为___________.(2)如图1 , 连结OD P ,为x 轴上的动点, 当以O D P ,,为顶点的三角形是等腰三角形时, 请直接写出点P 的坐标;(3)如图2, M 是点B 关于拋物线对称轴的对称点, Q 是拋物线上的动点, 它的横坐标为 (05)m m <<, 连结MQ BQ MQ ,,与直线OB 交于点E . 设BEQ 和BEM △的面积分别为1S 和2S , 设12S t s =, 试求t 关于m 的函数解析式并求出t 的最值. 14.如图,二次函数的图象经过点()10A -,,()30B ,,()03C -,,直线22y x =-与x 轴、y 轴交于点D ,E .(1)求该二次函数的解析式(2)点M 为该二次函数图象上一动点.①若点M 在图象上的B ,C 两点之间,求DME 的面积的最大值. ①若MED EDB ∠∠=,求点M 的坐标.15.如图,在平面直角坐标系中,抛物线24y ax bx =+-与x 轴交于()2,0A -,B 两点,其对称轴直线2x =与x 轴交于点D .(1)求该抛物线的函数表达式为______;(2)如图1,点P 为抛物线上第四象限内的一动点,连接CD ,PB ,PC ,求四边形BDCP 面积最大值和点P 此时的坐标;(3)如图2,将该抛物线向左平移得到抛物线y ',当抛物线y '经过原点时,与原抛物线的对称轴相交于点E ,点F 为抛物线y '对称轴上的一点,点M 是平面内一点,若以点A ,E ,F ,M 为顶点的四边形是以AE 为边的菱形,请直接写出满足条件的点M 的坐标______.16.如图,已知抛物线2y x bx c =++与x 轴交于点()21,0A m -和点()2,0B m +,与y 轴交于点C ,对称轴轴为直线=1x -.(1)求抛物线的解析式;(2)点P 是直线AC 上一动点,过点P 作PQ y ∥轴,交抛物线于点Q ,以P 为圆心,PQ 为半径作P ,当P 与坐标轴相切时,求P 的半径;(3)直线()340y kx k k =++≠与抛物线交于M ,N 两点,求AMN 面积的最小值.17.如图,在平面直角坐标系中,抛物线23y ax bx =+-与x 轴交于两点()1,0A -和()3,0B ,与y 轴交于点C ,抛物线上有一动点P ,抛物线的对称轴交x 轴于点E ,连接EC ,作直线BC .(1)求抛物线的解析式;(2)若点P 为直线BC 上方抛物线上一动点时,连接,PB PC ,当23EBC PBC S S =△△时,求点P 坐标;(3)如果抛物线的对称轴上有一动点Q ,x 轴上有一动点N ,是否存在四边形PQCN 是矩形?若存在,在横线上直接写出点N 的坐标,若不存在,请说明理由. 18.如图,直线122y x =-+交y 轴于点A ,交x 轴于点C ,抛物线214y x bx c=-++经过点A ,点C ,且交x 轴于另一点B .(1)直接写出点A ,点B ,点C 的坐标及抛物线的解析式;(2)在直线AC 上方的抛物线上有一点M ,求三角形ACM 面积的最大值及此时点M 的坐标;(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90︒得到线段O A '',若线段O A ''与抛物线只有一个公共点,请结合函数图象,求m 的取值范围(直接写出结果即可).参考答案:1.(1)245y x x =-++; (2)15(3)存在,点N 的坐标为(5,0)-或(0,5)-或(0,0).2.(1)2142y x x =-++,91,2⎛⎫⎪⎝⎭(2)S 的最大值为4 (3)2m ≥或1249m -<≤-3.(1)抛物线的解析式为2=23y x x -- (2)不存在这样的点P , (3)M 点坐标是(45),或315()24-,4.(1)抛物线的解析式:234y x x =-++;直线BC 的解析式为4y x =-+;(2)当()26P ,时,四边形PBOC 面积最大; (3)能,点N 的坐标为52124⎛⎫ ⎪⎝⎭,或724⎛- ⎝或724⎛- ⎝.5.(1)2142y x x =--,91,2D ⎛⎫- ⎪⎝⎭.(2)①(-;①1215S S =或1279S S =6.(1)(1,0) (2)223y x x =+- (3)(4,21)或()4,5- (4)947.(1)224233y x x =--+(2)3(2P -,5)2(3)(5,0)-或(1,0)-8.(1)03A (,),20B -(,),60C (,),抛物线解析式为:2134y x x =-++; (2)3a =时,四边形ABCM 面积最大,其最大值为754,此时M 的坐标为153,4⎛⎫⎪⎝⎭;(3)当3m -≤≤-33m ≤≤时,线段O A ''与抛物线只有一个公共点.9.(1)239344y x x =-++(2)334y x =-+(3)存在,点P 的坐标为:()13,3P ,23P ⎫-⎪⎪⎝⎭,33P ⎫-⎪⎪⎝⎭10.(1)21262y x x =-++(2)153,2P ⎛⎫ ⎪⎝⎭(3)点P 坐标为()46,或()55.11.(1)2512y x x =-+ (2)3(3)13,2⎛⎫- ⎪⎝⎭或1(1,)212.(1)21119424y x x =-++(2)①4y x =-+;①当02m <≤时,218PQRSm =;当823m <≤时,27448S m m =-+-;当843m ≤≤时,21244S m m =-+;S 的最大值为:47答案第3页,共3页 13.(1)()5,5;()2,4-;(2)点P的坐标为()或()-或()4,0或()5,0; (3)()2150566t m m m =-+<<,当52m =时,t 的最大值为2524.14.(1)该二次函数的解析式是()()21323y x x x x =+-=--;(2)①DME 的面积的最大值为52;①点M的坐标为⎝⎭或()12--.15.(1)214433y x x =-- (2)PBDC S 四边形的最大值为17,此时点P 的坐标为()3,5-(3)⎛ ⎝⎭或⎛ ⎝⎭或⎛- ⎝⎭或8,⎛- ⎝⎭16.(1)223y x x =+-(2)2或4(3)817.(1)2=23y x x --(2)⎝⎭或⎝⎭ (3)存在,⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭18.(1)()0,2A ,()2,0B -,()4,0C ,211242y x x =-++ (2)2,()2,2(3)34m -≤≤-或32m -+≤。
二次函数与几何综合压轴题(原卷版)-2024年中考数学

二次函数与几何综合压轴题几乎所有的地方都把二次函数与几何综合压轴题作为中考压轴题。
1.(2023·青海·中考真题)如图,二次函数2y x bx c =−++的图象与x 轴相交于点A 和点()1,0C ,交y 轴于点()0,3B .(1)求此二次函数的解析式;(2)设二次函数图象的顶点为P ,对称轴与x 轴交于点Q ,求四边形AOBP 的面积(请在图1中探索); (3)二次函数图象的对称轴上是否存在点M ,使得△AMB 是以AB 为底边的等腰三角形?若存在,请求出满足条件的点M 的坐标;若不存在,请说明理由(请在图2中探索).2.(2023·内蒙古·中考真题)如图,在平面直角坐标系中,抛物线2y x bx c =−++与x 轴的交点分别为A 和()10B ,(点A 在点B 的左侧),与y 轴交于点()0,3C ,点P 是直线AC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,过点P 作x 轴平行线交AC 于点E ,过点P 作y 轴平行线交x 轴于点D ,求PE PD +的最大值及点P 的坐标;(3)如图2,设点M 为抛物线对称轴上一动点,当点P ,点M 运动时,在坐标轴上确定点N ,使四边形PMCN 为矩形,求出所有符合条件的点N 的坐标.3.(2023·海南·中考真题)如图1,抛物线2y x bx c =++交x 轴于A ,()3,0B 两点,交y 轴于点()0,3C −.点P 是抛物线上一动点.(1)求该抛物线的函数表达式;(2)当点P 的坐标为()1,4−时,求四边形BACP 的面积;(3)当动点P 在直线BC 上方时,在平面直角坐标系是否存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形?若存在,请求出点Q 的坐标;若不存在,请说明理由;(4)如图2,点D 是抛物线的顶点,过点D 作直线DH y ∥轴,交x 轴于点H ,当点P 在第二象限时,作直线PA ,PB 分别与直线DH 交于点G 和点I ,求证:点D 是线段IG 的中点.4.(2023·西藏·中考真题)在平面直角坐标系中,抛物线2y x bx c =−++与x 轴交于()30A −,,()10B ,两点,与y 轴交于点C .(1)求抛物线的解析式;(2)如图甲,在y 轴上找一点D ,使ACD 为等腰三角形,请直接写出点D 的坐标;(3)如图乙,点P 为抛物线对称轴上一点,是否存在P 、Q 两点使以点A ,C ,P ,Q 为顶点的四边形是菱形?若存在,求出P 、Q 两点的坐标,若不存在,请说明理由.5.(2023·四川甘孜·中考真题)已知抛物线2y x bx c =++与x 轴相交于()10A −,,B 两点,与y 轴相交于点()03C −,.(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,PBC 的面积与ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ′,试探究,是否存在满足条件的点E ,使得点P ′恰好落在直线BC 上,如果存在,求出点P ′的坐标;如果不存在,请说明理由.6.(2023·四川达州·中考真题)如图,抛物线2y ax bx c ++过点()()()1,0,3,,00,3A B C −.(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.7.(2023·四川巴中·中考真题)在平面直角坐标系中,抛物线2(0)y ax bx c a ++≠经过点(1,0)A −和(0,3)B ,其顶点的横坐标为1.(1)求抛物线的表达式.(2)若直线x m =与x 轴交于点N ,在第一象限内与抛物线交于点M ,当m 取何值时,使得AN MN +有最大值,并求出最大值.(3)若点P 为抛物线2(0)y ax bx c a ++≠的对称轴上一动点,将抛物线向左平移1个单位长度后,Q 为平移后抛物线上一动点.在(2)的条件下求得的点M ,是否能与A 、P 、Q 构成平行四边形?若能构成,求出Q 点坐标;若不能构成,请说明理由.8.(2023·四川眉山·中考真题)在平面直角坐标系中,已知抛物线2y ax bx c ++与x 轴交于点()()3,0,1,0A B −两点,与y 轴交于点()0,3C ,点P 是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PD DB的值最大时,求点P 的坐标及PD DB 的最大值; (3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将PCM △沿直线PC 翻折,当点M 的对应点'M 恰好落在y 轴上时,请直接写出此时点M 的坐标.9.(2023·四川内江·中考真题)如图,在平面直角坐标系中,抛物线2y ax bx c ++与x 轴交于()4,0B ,()2,0C −两点.与y 轴交于点()0,2A −.(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求与12PK PD +的最大值及此时点P 的坐标; (3)在抛物线的对称轴上是否存在一点M ,使得MAB △是以AB 为一条直角边的直角三角形:若存在,请求出点M 的坐标,若不存在,请说明理由.10.(2023·湖北黄冈·中考真题)已知抛物线212y x bx c =−++与x 轴交于,(4,0)A B 两点,与y 轴交于点(0,2)C ,点P 为第一象限抛物线上的点,连接,,,CA CB PB PC .(1)直接写出结果;b =_____,c =_____,点A 的坐标为_____,tan ABC ∠=______;(2)如图1,当2PCB OCA ∠=∠时,求点P 的坐标; (3)如图2,点D 在y 轴负半轴上,OD OB =,点Q 为抛物线上一点,90QBD ∠=°,点E ,F 分别为BDQ △的边,DQ DB 上的动点,QE DF =,记BE QF +的最小值为m . ①求m 的值;②设PCB 的面积为S ,若214S m k =−,请直接写出k 的取值范围.11.(2023·湖北武汉·中考真题)抛物线21:28=−−C y x x 交x 轴于,A B 两点(A 在B 的左边),交y 轴于点C .(1)直接写出,,A B C 三点的坐标;(2)如图(1),作直线()04=<<x t t ,分别交x 轴,线段BC ,抛物线1C 于,,D E F 三点,连接CF .若BDE 与CEF △相似,求t 的值;(3)如图(2),将抛物线1C 平移得到抛物线2C ,其顶点为原点.直线2y x =与抛物线2C 交于,O G 两点,过OG 的中点H 作直线MN (异于直线OG )交抛物线2C 于,M N 两点,直线MO 与直线GN 交于点P .问点P 是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.12.(2023·湖南郴州·中考真题)已知抛物线24y ax bx ++与x 轴相交于点 1,0A ,()4,0B ,与y 轴相交于点C .(1)求抛物线的表达式;(2)如图1,点P 是抛物线的对称轴l 上的一个动点,当PAC △的周长最小时,求PAPC的值; (3)如图2,取线段OC 的中点D ,在抛物线上是否存在点Q ,使1tan 2QDB ∠=若存在,求出点Q 的坐标;若不存在,请说明理由.且与直线:1l y x =−−交于D E 、两点(点D 在点E 的右侧),点M 为直线l 上的一动点,设点M 的横坐标为t .(1)求抛物线的解析式.(2)过点M 作x 轴的垂线,与拋物线交于点N .若04t <<,求NED 面积的最大值.(3)抛物线与y 轴交于点C ,点R 为平面直角坐标系上一点,若以B C M R 、、、为顶点的四边形是菱形,请求出所有满足条件的点R 的坐标.在此抛物线上,其横坐标分别为,2(0)m m m >,连接AP ,AQ .(1)求此抛物线的解析式.(2)当点Q 与此抛物线的顶点重合时,求m 的值.(3)当PAQ ∠的边与x 轴平行时,求点P 与点Q 的纵坐标的差.(4)设此抛物线在点A 与点P 之间部分(包括点A 和点P )的最高点与最低点的纵坐标的差为1h ,在点A 与点Q 之间部分(包括点A 和点Q )的最高点与最低点的纵坐标的差为2h .当21h h m −=时,直接写出m 的值.15.(2023·青海西宁·中考真题)如图,在平面直角坐标系中,直线l 与x 轴交于点()6,0A ,与y 轴交于点()0,6B −,抛物线经过点A ,B ,且对称轴是直线1x =.(1)求直线l 的解析式; (2)求抛物线的解析式;(3)点P 是直线l 下方抛物线上的一动点,过点P 作PC x ⊥轴,垂足为C ,交直线l 于点D ,过点P 作PM l ⊥,垂足为M .求PM 的最大值及此时P 点的坐标.16.(2023·湖南·中考真题)如图,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于C 点,其中()10B ,,()0,3C .(1)求这个二次函数的表达式;(2)在二次函数图象上是否存在点P ,使得PAC ABC S S =△△?若存在,请求出P 点坐标;若不存在,请说明理由;(3)点Q 是对称轴l 上一点,且点Q 的纵坐标为a ,当QAC △是锐角三角形时,求a 的取值范围.17.(2023·辽宁营口·中考真题)如图,抛物线()210y ax bx a +−≠与x 轴交于点 1,0A 和点B ,与y 轴交于点C ,抛物线的对称轴交x 轴于点()3,0D ,过点B 作直线l x ⊥轴,过点D 作DE CD ⊥,交直线l 于点E .(1)求抛物线的解析式;(2)如图,点P 为第三象限内抛物线上的点,连接CE 和BP 交于点Q ,当57BQ PQ =时.求点P 的坐标; (3)在(2)的条件下,连接AC ,在直线BP 上是否存在点F ,使得DEF ACD BED ∠=∠+∠?若存在,请直接写出点F 的坐标;若不存在,请说明理由.18.(2023·湖南湘西·中考真题)如图(1),二次函数25y ax x c =−+的图像与x 轴交于()4,0A −,(),0B b 两点,与y 轴交于点()0,4C −.(1)求二次函数的解析式和b 的值.(2)在二次函数位于x 轴上方的图像上是否存在点M ,使13BOM ABC S S =△△?若存在,请求出点M 的坐标;若不存在,请说明理由.(3)如图(2),作点A 关于原点O 的对称点E ,连接CE ,作以CE 为直径的圆.点E ′是圆在x 轴上方圆弧上的动点(点E ′不与圆弧的端点E 重合,但与圆弧的另一个端点可以重合),平移线段AE ,使点E 移动到点E ′,线段AE 的对应线段为A E ′′,连接E C ′,A A ′,A A ′的延长线交直线E C ′于点N ,求AA CN′的值.19.(2023·辽宁盘锦·中考真题)如图,抛物线23y ax bx ++与x 轴交于点()10A −,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式.(2)如图1,点Q 是x 轴上方抛物线上一点,射线QM x ⊥轴于点N ,若QM BM =,且4tan 3MBN ∠=,请直接写出点Q 的坐标.(3)如图2,点E 是第一象限内一点,连接AE 交y 轴于点D ,AE 的延长线交抛物线于点P ,点F 在线段CD 上,且CF OD =,连接FA FE BE BP ,,,,若AFE ABE S S =△△,求PAB 面积.20.(2023·重庆·中考真题)如图,在平面直角坐标系中,抛物线22y ax bx ++过点()1,3,且交x 轴于点()1,0A −,B 两点,交y 轴于点C .(1)求抛物线的表达式;(2)点P 是直线BC 上方抛物线上的一动点,过点P 作PD BC ⊥于点D ,过点P 作y 轴的平行线交直线BC 于点E ,求PDE △周长的最大值及此时点P 的坐标;(3)在(2)中PDE △周长取得最大值的条件下,将该抛物线沿射线CB M 为平移后的抛物线的对称轴上一点.在平面内确定一点N ,使得以点A ,P ,M ,N 为顶点的四边形是菱形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.21.(2023·四川广安·中考真题)如图,二次函数2y x bx c =++的图象交x 轴于点A B ,,交y 轴于点C ,点B 的坐标为()1,0,对称轴是直线=1x −,点P 是x 轴上一动点,PM x ⊥轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的解析式.(2)若点P 在线段AO 上运动(点P 与点A 、点O 不重合),求四边形ABCN 面积的最大值,并求出此时点P 的坐标.(3)若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M 、N C Q 、、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.22.(2023·湖北十堰·中考真题)已知抛物线28y ax bx ++过点()4,8B 和点()8,4C ,与y 轴交于点A .(1)求抛物线的解析式;(2)如图1,连接,AB BC ,点D 在线段AB 上(与点,A B 不重合),点F 是OA 的中点,连接FD ,过点D 作DE FD ⊥交BC 于点E ,连接EF ,当DEF 面积是ADF △面积的3倍时,求点D 的坐标;(3)如图2,点P 是抛物线上对称轴右侧的点,(),0H m 是x 轴正半轴上的动点,若线段OB 上存在点G (与点,O B 不重合),使得GBP HGP BOH ∠=∠=∠,求m 的取值范围.23.(2023·四川·中考真题)如图1,在平面直角坐标系中,已知二次函数24y ax bx ++的图象与x 轴交于点()2,0A −,()4,0B ,与y 轴交于点C .(1)求抛物线的解析式;(2)已知E 为抛物线上一点,F 为抛物线对称轴l 上一点,以B ,E ,F 为顶点的三角形是等腰直角三角形,且90BFE ∠=°,求出点F 的坐标; (3)如图2,P 为第一象限内抛物线上一点,连接AP 交y 轴于点M ,连接BP 并延长交y 轴于点N ,在点P 运动过程中,12OM ON +是否为定值?若是,求出这个定值;若不是,请说明理由.24.(2023·黑龙江绥化·中考真题)如图,抛物线21y ax bx c =++的图象经过(6,0)A −,(2,0)B −,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ⊥于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?25.(2023·四川德阳·中考真题)已知:在平面直角坐标系中,抛物线与x 轴交于点(4,0)A −,(2,0)B ,与y 轴交于点(0,4)C −.(1)求抛物线的解析式;(2)如图1,如果把抛物线x 轴下方的部分沿x 轴翻折180°,抛物线的其余部分保持不变,得到一个新图象.当平面内的直线6y kx =+与新图象有三个公共点时,求k 的值; (3)如图2,如果把直线AB 沿y 轴向上平移至经过点D ,与抛物线的交点分别是E ,F ,直线BC 交EF 于点H ,过点F 作FG CH ⊥于点G ,若DF HG=F 的坐标.26.(2023·辽宁锦州·中考真题)如图,抛物线2y bx c ++交x 轴于点()1,0A −和B ,交y 轴于点(C ,顶点为D .(1)求抛物线的表达式;(2)若点E 在第一象限内对称右侧的抛物线上,四边形ODEB 的面积为E 的坐标;(3)在(2)的条件下,若点F 是对称轴上一点,点H 是坐标平面内一点,在对称轴右侧的抛物线上是否存在点G ,使以E ,F ,G ,H 为顶点的四边形是菱形,且60EFG ∠=°,如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.27.(2023·辽宁鞍山·中考真题)如图1,抛物线253y ax x c =++经过点()3,1,与y 轴交于点()0,5B ,点E 为第一象限内抛物线上一动点.(1)求抛物线的解析式.(2)直线243y x =−与x 轴交于点A ,与y 轴交于点D ,过点E 作直线EF x ⊥轴,交AD 于点F ,连接BE .当BE DF =时,求点E 的横坐标.(3)如图2,点N 为x 轴正半轴上一点,OE 与BN 交于点M .若OE BN =,3tan 4BME ∠=,求点E 的坐标.28.(2023·辽宁丹东·中考真题)抛物线24y ax bx +−与x 轴交于点()4,0A −,()2,0B ,与y 轴交于点C .(1)求抛物线的表达式;(2)如图,点D 是抛物线上的一个动点,设点D 的横坐标是()42m m −<<,过点D 作直线DE x ⊥轴,垂足为点E ,交直线AC 于点F .当D ,E ,F 三点中一个点平分另外两点组成的线段时,求线段DF 的长;(3)若点P 是抛物线上的一个动点(点P 不与顶点重合),点M 是抛物线对称轴上的一个点,点N 在坐标平面内,当四边形CMPN 是矩形邻边之比为1:2时,请直接写出点P 的横坐标.。
二次函数压轴题(含答案)
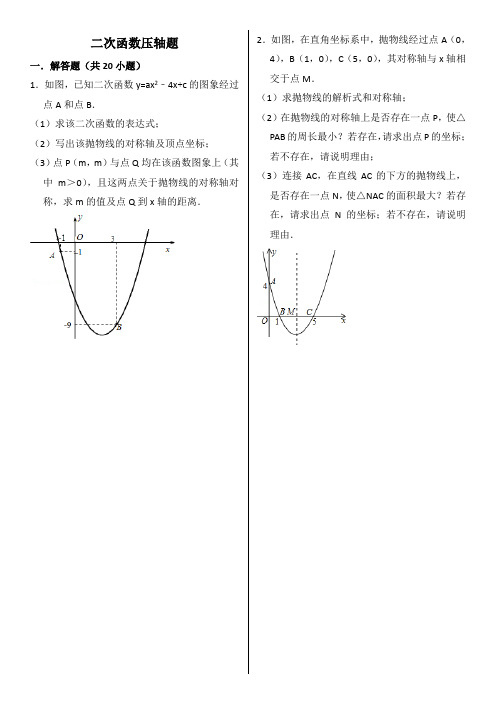
二次函数压轴题一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.3.已知二次函数y=x2﹣2mx+m2﹣1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.19.如图,已知抛物线y=(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+b与抛物线的另一交点为D.(1)若点D的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k 的值;(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?20.如图,抛物线y=﹣x2+bx+c与直线y=x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求抛物线的解析式;(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.二次函数压轴题参考答案一.解答题(共20小题)1.如图,已知二次函数y=ax2﹣4x+c的图象经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.解:(1)将x=﹣1,y=﹣1;x=3,y=﹣9,分别代入y=ax2﹣4x+c得,解得,∴二次函数的表达式为y=x2﹣4x﹣6.(2)对称轴为直线x=2;顶点坐标为(2,﹣10).(3)将(m,m)代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6,解得m1=﹣1,m2=6.∵m>0,∴m1=﹣1不合题意,舍去.∴m=6,∵点P与点Q关于对称轴x=2对称,∴点Q到x轴的距离为6.2.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.解:(1)根据已知条件可设抛物线的解析式为y=a (x﹣1)(x﹣5),把点A(0,4)代入上式得:a=,∴y=(x﹣1)(x﹣5)=x2﹣x+4=(x﹣3)2﹣,∴抛物线的对称轴是:直线x=3;(2)P点坐标为(3,).理由如下:∵点A(0,4),抛物线的对称轴是直线x=3,∴点A关于对称轴的对称点A′的坐标为(6,4)如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.设直线BA′的解析式为y=kx+b,把A′(6,4),B (1,0)代入得,解得,∴y=x ﹣,∵点P 的横坐标为3,∴y=×3﹣=, ∴P (3,).(3)在直线AC 的下方的抛物线上存在点N ,使△NAC 面积最大.设N 点的横坐标为t ,此时点N (t ,t 2﹣t +4)(0<t <5),如图2,过点N 作NG ∥y 轴交AC 于G ;作AD ⊥NG 于D ,由点A (0,4)和点C (5,0)可求出直线AC 的解析式为:y=﹣x +4,把x=t 代入得:y=﹣t +4,则G (t ,﹣t +4), 此时:NG=﹣t +4﹣(t 2﹣t +4)=﹣t 2+4t ,∵AD +CF=CO=5, ∴S △ACN =S △ANG +S △CGN=AD ×NG+NG ×CF=NG•OC=×(﹣t 2+4t )×5=﹣2t 2+10t=﹣2(t ﹣)2+,∴当t=时,△CAN 面积的最大值为,由t=,得:y=t 2﹣t +4=﹣3,∴N (,﹣3).3.已知二次函数y=x 2﹣2mx +m 2﹣1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.解:(1)∵二次函数的图象经过坐标原点O (0,0),∴代入二次函数y=x 2﹣2mx +m 2﹣1,得出:m 2﹣1=0,解得:m=±1,∴二次函数的解析式为:y=x 2﹣2x 或y=x 2+2x ; (2)∵m=2,∴二次函数y=x 2﹣2mx +m 2﹣1得:y=x 2﹣4x +3=(x ﹣2)2﹣1,∴抛物线的顶点为:D (2,﹣1), 当x=0时,y=3,∴C 点坐标为:(0,3), ∴C (0,3)、D (2,﹣1);(3)当P 、C 、D 共线时PC +PD 最短,过点D 作DE ⊥y 轴于点E , ∵PO ∥DE ,∴=,∴=,解得:PO=,∴PC +PD 最短时,P 点的坐标为:P (,0).4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C (0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.解:(1)依题意得:,解之得:,∴抛物线解析式为y=﹣x2﹣2x+3∵对称轴为x=﹣1,且抛物线经过A(1,0),∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,得,解之得:,∴直线y=mx+n的解析式为y=x+3;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)设P(﹣1,t),又∵B(﹣3,0),C(0,3),∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1=,t2=;综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).5.如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.解:(1)令y=0,解得x1=﹣1或x2=3∴A(﹣1,0)B(3,0)将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3∴C(2,﹣3)∴直线AC的函数解析式是y=﹣x﹣1;(2)设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1)E(x,x2﹣2x﹣3)∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x ﹣3)=﹣x2+x+2=﹣(x ﹣)2+,∴当时,PE的最大值=;(3)存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+,0),F4(4﹣,0).①如图,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+,3),由于直线GF 的斜率与直线AC的相同,因此可设直线GF 的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+.因此直线GF与x 轴的交点F的坐标为(4+,0);④如图,同③可求出F的坐标为(4﹣,0).综合四种情况可得出,存在4个符合条件的F点.6.如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点.(Ⅰ)求抛物线的解析式;(Ⅱ)在抛物线的对称轴上有一点P,使PA+PC 的值最小,求点P的坐标.(Ⅲ)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.解:(Ⅰ)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,﹣)三点在抛物线上,∴,解得.∴抛物线的解析式为:y=x2﹣2x ﹣;(Ⅱ)∵抛物线的解析式为:y=x2﹣2x ﹣,∴其对称轴为直线x=﹣=﹣=2,连接BC,如图1所示,∵B(5,0),C(0,﹣),∴设直线BC的解析式为y=kx+b(k≠0),∴,解得,∴直线BC的解析式为y=x ﹣,当x=2时,y=1﹣=﹣,∴P(2,﹣);(Ⅲ)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.如图2所示,①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣),∴N1(4,﹣);②当点N在x轴上方时,如图,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,∴△AN2D≌△M2CO(ASA),∴N2D=OC=,即N2点的纵坐标为.∴x2﹣2x ﹣=,解得x=2+或x=2﹣,∴N2(2+,),N3(2﹣,).综上所述,符合条件的点N的坐标为(4,﹣),(2+,)或(2﹣,).7.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y 轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.解:(1)将B、C 两点的坐标代入得,解得:;所以二次函数的表达式为:y=x2﹣2x﹣3(2)存在点P,使四边形POP′C为菱形;设P点坐标为(x,x2﹣2x﹣3),PP′交CO于E若四边形POP′C是菱形,则有PC=PO;连接PP′,则PE⊥CO于E,∵C(0,﹣3),∴CO=3,又∵OE=EC,∴OE=EC=∴y=;∴x2﹣2x﹣3=解得x1=,x2=(不合题意,舍去),∴P点的坐标为(,)(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2﹣2x﹣3),设直线BC的解析式为:y=kx+d,则,解得:∴直线BC的解析式为y=x﹣3,则Q点的坐标为(x,x﹣3);当0=x2﹣2x﹣3,解得:x1=﹣1,x2=3,∴AO=1,AB=4,S四边形ABPC=S△ABC+S△BPQ+S△CPQ=AB•OC+QP•BF +QP•OF==当时,四边形ABPC的面积最大此时P点的坐标为,四边形ABPC的面积的最大值为.8.如图,对称轴为x=﹣1的抛物线y=ax2+bx+c (a≠0)与x轴相交于A、B两点,其中点A 的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC,求点P 的坐标.②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2.将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.∴点P的坐标为(4,21)或(﹣4,5);②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D 点坐标为(x,x2+2x﹣3),QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x +)2+,∴当x=﹣时,QD 有最大值.9.如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.解:(1)将A(1,0),B(﹣3,0)代y=﹣x2+bx+c 中得,∴.∴抛物线解析式为:y=﹣x2﹣2x+3;(2)存在.理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称,∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小,∵y=﹣x2﹣2x+3,∴C的坐标为:(0,3),直线BC解析式为:y=x+3,Q点坐标即为,解得,∴Q(﹣1,2);(3)存在.理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0),∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO ﹣,若S四边形BPCO 有最大值,则S△BPC就最大,∴S四边形BPCO=S△BPE+S直角梯形PEOC,=BE•PE +OE(PE+OC)=(x+3)(﹣x2﹣2x+3)+(﹣x)(﹣x2﹣2x+3+3)=,当x=﹣时,S四边形BPCO最大值=,∴S△BPC最大=,当x=﹣时,﹣x2﹣2x+3=,∴点P 坐标为(﹣,).10.如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.解:(1)∵抛物线与y轴交于点C(0,3),∴设抛物线解析式为y=ax2+bx+3(a≠0),根据题意,得,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)存在.由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为直线x=1.①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据两点间距离公式,得x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,即y=4﹣x.又P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,解得x1=,x2=<1,应舍去,∴x=,∴y=4﹣x=,即点P 坐标为.②若以CD为一腰,∵点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3).∴符合条件的点P 坐标为或(2,3).(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB=,CD=,BD=,∴CB2+CD2=BD2=20,∴∠BCD=90°,设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,∵CF=DF=1,∴∠CDF=45°,由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),∴DM∥BC,∴四边形BCDM为直角梯形,由∠BCD=90°及题意可知,以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在.综上所述,符合条件的点M的坐标为(2,3).11.如图,直线y=x+2与抛物线y=ax2+bx+6(a ≠0)相交于A (,)和B(4,m),点P 是线段AB上异于A、B的动点,过点P作PC ⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n ﹣)2+,∵PC>0,∴当n=时,线段PC 最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A (,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A (,)关于对称轴x=2的对称点C,则点C在抛物线上,且C (,).当x=时,y=x+2=.∴P2(,).∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).12.如图,在平面直角坐标系xOy中,A、B为x 轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;(3)当△BDM为直角三角形时,求m的值.解:(1)y=mx2﹣2mx﹣3m=m(x﹣3)(x+1),∵m≠0,∴当y=0时,x1=﹣1,x2=3,∴A(﹣1,0),B(3,0);(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:,解得,故C1:y=x2﹣x﹣.如图:过点P作PQ∥y轴,交BC于Q,由B、C的坐标可得直线BC的解析式为:y=x﹣,设P(x ,x2﹣x ﹣),则Q(x,x ﹣),PQ=x ﹣﹣(x2﹣x﹣)=﹣x2+x,S△PBC=S△PCQ+S△PBQ =PQ•OB=×(﹣x2+x)×3=﹣(x ﹣)2+,当x=时,S△PBC有最大值,Smax=,×()2﹣﹣=﹣,P(,﹣);(3)y=mx2﹣2mx﹣3m=m(x﹣1)2﹣4m,顶点M坐标(1,﹣4m),当x=0时,y=﹣3m,∴D(0,﹣3m),B(3,0),∴DM2=(0﹣1)2+(﹣3m+4m)2=m2+1,MB2=(3﹣1)2+(0+4m)2=16m2+4,BD2=(3﹣0)2+(0+3m)2=9m2+9,当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,解得m=﹣1(∵m<0,∴m=1舍去);②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,解得m=﹣(m=舍去).综上,m=﹣1或﹣时,△BDM为直角三角形.13.如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.(1)点M(填M或N)能到达终点;(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.解:(1)点M.(2)经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t,∵A(4,0),C(0,4),∴AO=CO=4,∵∠AOC=90°,∴∠BCA=∠MAQ=45°,∴QN=CN=3﹣t∴PQ=1+t,∴S△AMQ=AM•PQ=(4﹣2t)(1+t)=﹣t2+t+2.∴S=﹣t2+t+2=﹣t2+t ﹣++2=﹣(t ﹣)2+,∵0≤t≤2∴当时,S的值最大.(3)存在.设经过t秒时,NB=t,OM=2t则CN=3﹣t,AM=4﹣2t∴∠BCA=∠MAQ=45°①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高∴PQ是底边MA的中线∴PQ=AP=MA∴1+t=(4﹣2t)∴t=∴点M的坐标为(1,0)②若∠QMA=90°,此时QM与QP重合∴QM=QP=MA∴1+t=4﹣2t∴t=1∴点M的坐标为(2,0).14.如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).(1)求抛物线的函数表达式;(2)若点P在抛物线上,且S△AOP=4S△BOC,求点P的坐标;(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得,解得.故该抛物线的解析式为:y=﹣x2﹣2x+3.(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).∵S△AOP=4S△BOC,∴×3×|﹣x2﹣2x+3|=4××1×3.整理,得(x+1)2=0或x2+2x﹣7=0,解得x=﹣1或x=﹣1±2.则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2,﹣4)或(﹣1﹣2,﹣4);(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,得,解得.即直线AC的解析式为y=x+3.设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD 有最大值.15.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.解:(1)把A(2,0)、B(0,﹣6)代入y=﹣+bx+c,得:解得,∴这个二次函数的解析式为y=﹣+4x﹣6.(2)∵该抛物线对称轴为直线x=﹣=4,∴点C的坐标为(4,0),∴AC=OC﹣OA=4﹣2=2,∴S△ABC =×AC×OB=×2×6=6.16.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,∴OB=3OA=3.∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1,∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).代入解析式为,解得:.∴抛物线的解析式为y=﹣x2﹣2x+3;(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,∴对称轴l=﹣=﹣1,∴E点的坐标为(﹣1,0).如图,当∠CEF=90°时,PE:CE=2:1,CO:OD=3:1,此时△CEF与△COD不相似.当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.∴,∴MP=3EM.∵P的横坐标为t,∴P(t,﹣t2﹣2t+3).∵P在第二象限,∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,∴﹣t2﹣2t+3=﹣(t﹣1)(t+3),解得:t1=﹣2,t2=﹣3(因为P与C重合,所以舍去),∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.∴P(﹣2,3).∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);②设直线CD的解析式为y=kx+b,由题意,得,解得:,∴直线CD的解析式为:y=x+1.设PM与CD的交点为N,则点N的坐标为(t,t+1),∴NM=t+1.∴PN=PM﹣NM=﹣t2﹣2t+3﹣(t+1)=﹣t2﹣+2.∵S△PCD=S△PCN+S△PDN,∴S△PCD=PN•CM +PN•OM=PN(CM+OM)=PN•OC=×3(﹣t2﹣+2)=﹣(t +)2+,∴当t=﹣时,S△PCD的最大值为.17.如图,抛物线y=﹣x2+bx+c与x轴交于点A (﹣1,0),B(5,0)两点,直线y=﹣x+3与y轴交于点C,与x轴交于点D.点P是x 轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.方法一:解:(1)将点A、B坐标代入抛物线解析式,得:,解得,∴抛物线的解析式为:y=﹣x2+4x+5.(2)∵点P的横坐标为m,∴P(m,﹣m2+4m+5),E(m,﹣m+3),F(m,0).∴PE=|y P﹣y E|=|(﹣m2+4m+5)﹣(﹣m+3)|=|﹣m2+m+2|,EF=|y E﹣y F|=|(﹣m+3)﹣0|=|﹣m+3|.由题意,PE=5EF,即:|﹣m2+m+2|=5|﹣m+3|=|m+15|①若﹣m2+m+2=m+15,整理得:2m2﹣17m+26=0,解得:m=2或m=;②若﹣m2+m+2=﹣(m+15),整理得:m2﹣m﹣17=0,解得:m=或m=.由题意,m的取值范围为:﹣1<m<5,故m=、m=这两个解均舍去.∴m=2或m=.(3)假设存在.作出示意图如下:∵点E、E′关于直线PC对称,∴∠1=∠2,CE=CE′,PE=PE′.∵PE平行于y轴,∴∠1=∠3,∴∠2=∠3,∴PE=CE,∴PE=CE=PE′=CE′,即四边形PECE′是菱形.当四边形PECE′是菱形存在时,由直线CD解析式y=﹣x+3,可得OD=4,OC=3,由勾股定理得CD=5.过点E作EM∥x轴,交y轴于点M,易得△CEM ∽△CDO,∴,即,解得CE=|m|,∴PE=CE=|m|,又由(2)可知:PE=|﹣m2+m+2|∴|﹣m2+m+2|=|m|.①若﹣m2+m+2=m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣;②若﹣m2+m+2=﹣m,整理得:m2﹣6m﹣2=0,解得m1=3+,m2=3﹣.由题意,m的取值范围为:﹣1<m<5,故m=3+这个解舍去.当四边形PECE′是菱形这一条件不存在时,此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,∴P(0,5)综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)方法二:(1)略.(2)略.(3)若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC 轴对称.∴点D关于直线PC的对称点D′也在y轴上,∴DD′⊥CP,∵y=﹣x+3,∴D(4,0),CD=5,∵OC=3,∴OD′=8或OD′=2,①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴,∴2t2﹣7t﹣4=0,∴t1=4,t2=﹣,②当OD′=2时,D′(0,﹣2),设P(t,﹣t2+4t+5),∵PC⊥DD′,∴K PC×K DD′=﹣1,∴=﹣1,∴t1=3+,t2=3﹣,∵点P是x轴上方的抛物线上一动点,∴﹣1<t<5,∴点P的坐标为(﹣,),(4,5),(3﹣,2﹣3).若点E与C重合时,P(0,5)也符合题意.综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣,),(4,5),(3﹣,2﹣3)18.如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC 交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A 两点)上平行移动,分别交x轴于点E,交CD 于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴,解得,∴抛物线的解析式为y=﹣x2+x+4;(2)设直线AC的解析式为y=kx+b,∵A(3,0),点C(0,4),∴,解得,∴直线AC的解析式为y=﹣x+4.∵点M的横坐标为m,点M在AC上,∴M点的坐标为(m ,﹣m+4),∵点P的横坐标为m,点P在抛物线y=﹣x2+x+4上,∴点P的坐标为(m ,﹣m2+m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F 为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,若以P、C、F为顶点的三角形和△AEM相似,P点在F上,PF=﹣m2+m+4﹣4=﹣m2+m.情况:①若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣m+4),∵m≠0且m≠3,∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM为直角三角形;②若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM为等腰三角形.综上所述,存在这样的点P使△PFC与△AEM相。
中考二次函数压轴题经典例题

中考二次函数压轴题经典例题
题目一:(2018年山东济南中考)已知函数y=ax²-8x+c(a≠0),当a=1或4时,函数的值都大于0。
问c的取值范围是多少?
解:根据题意,设a=1时,y=x²-8x+c > 0,则c > 8²/4=16,且当a=4时,
y=4x²-8x+c > 0,则c > (8/4)²=4。
因此,c的取值范围是c>16。
题目二:(2018年上海中考)已知二次函数y=-3x²+a+b,其图象经过点(2,3),求a和b的值。
解:将点(2,3)代入函数y=-3x²+a+b,可以得到3=-3*4+a+b,所以a+b=15。
因为题目中没有给出更多信息,所以只能求出a和b的和,不能求出a和b的具体值。
以上都是有关二次函数在中考中的经典压轴题。
二次函数在中考数学中占有相当重要的地位,要求学生熟练掌握二次函数的识别、画图、对称轴、最值等方面的知识,并能灵活运用这些知识解答实际问题。
中考数学二次函数压轴题

中考数学二次函数压轴题
一道典型的中考数学二次函数压轴题如下:
某种植物的数量随时间变化的规律可以用函数模型表示为:$y = -2x^2 + 8x + 3$,其中$y$表示植物的数量(单位:个),$x$表示时间(单位:月)。
(1)求植物数量在何时达到最大值?
(2)在上述最大值时,植物的数量是多少?
解答:
(1)由函数模型$y = -2x^2 + 8x + 3$可以看出,这是一个抛物线函数,开口向下。
而抛物线的最高点就是最大值的点。
最高点的横坐标$x$可以通过求解二次函数的顶点来得到。
二次函数的顶点公式为:$x = -\frac{b}{2a}$。
对于函数模型$y = -2x^2 + 8x + 3$,其中$a = -2$,$b = 8$,$c = 3$。
将这些值带入顶点公式,得到$x = -
\frac{8}{2 \cdot (-2)} = 2$。
所以,植物数量在$x = 2$时达到最大值。
(2)将$x = 2$代入函数模型$y = -2x^2 + 8x + 3$中,得到
$y = -2 \cdot 2^2 + 8 \cdot 2 + 3 = 11$。
所以,在最大值时,植物的数量为11个。
中考压轴题-二次函数综合(八大题型+解题方法)——冲刺2024年中考数学考点押题(全国通用)(解析)

中考压轴题-二次函数综合 (八大题型+解题方法)1、求证“两线段相等”的问题:借助于函数解析式,先把动点坐标用一个字母表示出来;然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题:由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题:先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题:方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题:1点到直线的距离中的常数问题:“抛物线上是否存在一点,使之到定直线的距离等于一个 固定常数”的问题:先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题:“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题:先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题:用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题:先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题:① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题:由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题:在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题:① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”:方法1:先利用两点间的距离公式求出定线段的长度;然后再利用上面3的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2:过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到)()(左(定)右(定)下(动)上(动)动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题:先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”:由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题: 有两种常见解决的方案:方案一:连接一条对角线,分成两个三角形面积之和;方案二:过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题: 两个定三角形是否相似:(1)已知有一个角相等的情形:运用两点间的距离公式求出已知角的两条夹边,看看是否成比例 若成比例,则相似;否则不相似;(2)不知道是否有一个角相等的情形:运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似:(1)已知有一个角相等的情形:先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形:这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题:首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况;若某边为腰,有两种情况;若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题:这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有:①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题:若夹直角的两边与y轴都不平行:先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是:过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点:先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题;反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题:题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或y轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题:此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论:1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离:点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式:若A 11,x y ,B 2,2x y , 则AB=目录:题型1:存在性问题 题型2:最值问题 题型3:定值问题 题型4:定点问题题型5:动点问题综合 题型6:对称问题 题型7:新定义题 题型8:二次函数与圆题型1:存在性问题1.(2024·四川广安·二模)如图,抛物线2y x bx c =−++交x 轴于()4,0A −,B 两点,交y 轴于点()0,4C .(1)求抛物线的函数解析式.(2)点D 在线段OA 上运动,过点D 作x 轴的垂线,与AC 交于点Q ,与抛物线交于点P ,连接AP 、CP ,求四边形AOCP 的面积的最大值.(3)在抛物线的对称轴上是否存在点M ,使得以点A 、C 、M 为顶点的三角形是直角三角形?若存在,请求出点M【答案】(1)234y x x =−−+;(2)四边形AOCP 的面积最大为16;(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.【分析】本题主要考查了二次函数综合,熟练掌握用待定系数法求解函数解析式的方法和步骤,以及二次函数的图象和性质,是解题的关键. (1)把()4,0A −,()0,4C 代入2y x bx c =−++,求出b 和c 的值,即可得出函数解析式; (2)易得182AOCSOA OC =⋅=,设()2,34P t t t −−+,则(),4Q t t +,求出24PQ t t =−−,则()()212282ACP C A S PQ x x t =⋅−=−++,根据四边形AOCP 的面积()22216ACP AOCS St =+=−++,结合二次函数的增减性,即可解答;(3)设3,2M m ⎛⎫− ⎪⎝⎭,根据两点之间距离公式得出232AC =,22254AM m =+,229(4)4CM m =+−,然后分情况根据勾股定理列出方程求解即可.【解析】(1)解:把()4,0A −,()0,4C 代入2y x bx c =−++得:01644b c c =−−+⎧⎨=⎩,解得:34b c =−⎧⎨=⎩,∴该二次函数的解析式234y x x =−−+;(2)解:∵()4,0A −,()0,4C ,∴4,4OA OC ==,∴1144822AOC S OA OC =⋅=⨯⨯=△,设直线AC 的解析式为4y kx =+, 代入()4,0A −得,044k =−+,解得1k =,∴直线AC 的解析式为4y x =+, 设()2,34P t t t −−+,则(),4Q t t +,∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++,∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++,∵20−<,∴当2t =−时,四边形AOCP 的面积最大为16; (3)解:设3,2M m ⎛⎫− ⎪⎝⎭,∵()4,0A −,()0,4C ,∴2224432AC =+=,2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭,()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭,当斜边为AC 时,AM CM AC 222+=,即()2225943244m m +++−=,整理得:24150m m ++=,无解;当斜边为AM 时,222AC CM AM +=,即2292532(4)44m m ++−=+,解得:112m =;∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时,222AC AM CM +=,即2225932(4)44m m ++=+−, 解得:52m =−;∴35,22M ⎛⎫−− ⎪⎝⎭综上:点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.2.(2024·内蒙古乌海·模拟预测)如图(1),在平面直角坐标系中,抛物线()240y ax bx a =+−≠与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为()1,0−,且OC OB =,点D 和点C 关于抛物线的对称轴对称.(1)分别求出a ,b 的值和直线AD 的解析式;(2)直线AD 下方的抛物线上有一点P ,过点P 作PH AD ⊥于点H ,作PM 平行于y 轴交直线AD 于点M ,交x 轴于点E ,求PHM 的周长的最大值;(3)在(2)的条件下,如图2,在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似?如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.【答案】(1)1a =,3b =−,=1y x −−(2)4+(3)存在,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用,掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式,列出PM 的长与a 的函数关系式是解题的关键.(1)先求得C 的坐标,从而得到点B 的坐标,设抛物线的解析式为()()14y a x x =+−,将点C 的坐标代入求解即可;先求得抛物线的对称轴,从而得到点()3,4D −,然后可求得直线AD 的解析式=1y x −−;(2)求得45BAD ∠=︒,接下来证明PMD △为等腰直角三角形,所当PM 有最大值时三角形的周长最大,设()2,34P a a a −−,()1M a −−,则223PM aa =−++,然后利用配方可求得PM 的最大值,最后根据MPH△的周长(1PM=求解即可;(3)当90EGN ∠=︒时,如果OA EG OC GN = 或OA GNOC EN =时,则AOC ∽EGN △,设点G 的坐标为(),0a ,则()2,34N a a a −−,则1EG a =−,234NG aa =−++,然后根据题意列方程求解即可.【解析】(1)点A 的坐标为()1,0−,1OA ∴=.令0x =,则4y =−,()0,4C ∴−,4OC =,OC OB =Q , 4OB ∴=,()4,0B ∴,设抛物线的解析式为()()14y a x x =+−,将0x =,4y =−代入得:44a −=−,解得1a =,∴抛物线的解析式为234y x x =−−;1a ∴=,3b =−; 抛物线的对称轴为33212x −=−=⨯,()0,4C −,点D 和点C 关于抛物线的对称轴对称,()3,4D ∴−;设直线AD 的解析式为y kx b =+.将()1,0A −、()3,4D −代入得:034k b k b −+=⎧⎨+=−⎩,解得1k =−,1b =-,∴直线AD 的解析式=1y x −−;(2)直线AD 的解析式=1y x −−,∴直线AD 的一次项系数1k =−,45BAD ∴∠=︒. PM 平行于y 轴,90AEP ∴∠=︒,45PMH AME ∴∠=∠=︒.MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=. 设()2,34P a a a −−,则(),1M a a −−, 则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+.∴当1a =时,PM 有最大值,最大值为4.MPH ∴的周长的最大值(414=⨯=+(3)在直线EP 的右侧、x 轴下方的抛物线上存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似;理由如下:设点G 的坐标为(),0a ,则()2,34N a a a −−①如图2.1,若OA EG OC GN = 时,AOC ∽EGN △. 则 211344a a a −=−++,整理得:280a a +−=.得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭; ②如图2.2,若OA GN OC EN =时,AOC ∽NGE ,则21434a a a −=−++,整理得:2411170a a −−=,得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭, 综上所述,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭. 3.(2024·重庆·一模)如图,在平面直角坐标系中,抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B ,与y 轴交于点C ,连接BC ,AC .(1)求抛物线的表达式;(2)P 为直线BC 上方抛物线上一点,过点P 作PD BC ⊥于点D ,过点P 作PE x 轴交抛物线于点E,求4+PD PE 的最大值及此时点P 的坐标; (3)点C 关于抛物线对称轴对称的点为Q ,将抛物线沿射线CAy ',新抛物线y '与y 轴交于点M ,新抛物线y '的对称轴与x 轴交于点N ,连接AM ,MN ,点R 在直线BC 上,连接QR .当QR 与AMN 一边平行时,直接写出点R 的坐标,并写出其中一种符合条件的解答过程.【答案】(1)2y x x =++(2)当154t =时,PE的最大值,15,416P ⎛ ⎝⎭, (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(.【分析】(1)利用待定系数法求抛物线解析式即可;(2)先求得2y x =2x =,过点P 作PG x ⊥轴交BC 于点F ,利用勾股定理求得BC ==DPF OBC ∽,得PF DP BC OB =即PF PD=,从而得PF =,求出设直线BC的解析式后,设2,P t ⎛+ ⎝,则,F t ⎛+ ⎝,从而2PF =+,当点P在E 点右侧时()424PE t t t =−−=−,从而得2154t ⎫=−⎪⎝⎭,利用二次函数的性质即可求解;当点P 在E 点左侧时:442PE t t t =−−=−时,同理可求.然后比较4+PE 的最大值即可得出答案. (3)先求得1OA=,OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ,过点P 作PW ⊥直线2x =,则AOC PWH ∽,得1OA OC AC WP HW PH ====,进而得平移后的抛物线2y x +'=,从而求得()1,0N,M ⎛ ⎝⎭,然后分QR AM ∥,QR MN ∥,QR AN ∥三种情况,利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解.【解析】(1)解:∵抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B 两点,代入坐标得:02550a b a b ⎧−=⎪⎨+=⎪⎩,解得:a b ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线的函数表达式为255y x x =−++(2)解:∵)2225555y x x x =−+=−−+,∴2y x =2x=,顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ,当0x =时,200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴,PD BC ⊥,x 轴y ⊥轴,∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒,,∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽,∴PF DP BC OB =即PF PD =,∴PF PD =∴44+PD PE =PF +PE ,设直线BC :y kx b =+,把(C ,()5,0B 代入得:05k b b =+⎧⎪=,解得5k b ⎧=−⎪⎨⎪=⎩, ∴直线BC:y =设2,P t ⎛ ⎝,则,F t ⎛+ ⎝,∴22PF ⎛⎛=−+=+ ⎝⎝,∵2y x =2x =,PE x 轴,∴24,E t ⎛−+ ⎝当点P 在E 点右侧时:()424PE t t t =−−=−,当24PE t =−时:∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时,的最大值∴2151544⎛⎫= ⎪⎝⎭,∴154P ⎛ ⎝⎭; 当点P 在E 点左侧时:442PE t t t =−−=−时,∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭, ∴当54t =时,的最大值.2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭,∵> 综上所诉,当点P 在E 点右侧时:即154t =时,的最大值,154P ⎛ ⎝⎭, (3)解:设直线AC :y mx n =+,把()1,0A −,(C , ∴1OA =,OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P , 过点P 作PW ⊥直线2x =,则AOC PWH ∽,∴1OA OC AC WP HW PH ====∴1PW =,HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭,∴平移后的抛物线)22155555y x x x =−−+=−++', ∴()1,0N令0x =,y '=,∴M ⎛ ⎝⎭ 如图,当QR AM ∥时,设直线AM 的解析式为:y px q =+,把M ⎛ ⎝⎭,()1,0A −代入得:0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩, ∴直线AM的解析式为:y =, ∴设直线QR的解析式为:y x n =∵(C ,Q 和C 关于2x =对称,∴(Q把(Q代入5y x n =+45n +,解得n =,∴直线QR的解析式为:y = 联立直线QR的解析式y =与直线BC:y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩,解得3x y =⎧⎪⎨=⎪⎩,∴R ⎛ ⎝⎭ 同理可得:当QR MN ∥时,6,5R ⎛− ⎝⎭ 当QR AN ∥时,(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(. 【点睛】本题考查待定系数法求抛物线解析式,勾股定理,抛物线的性质,抛物线平移,一次函数的平移,相似三角形的判定及性质,图形与坐标,掌握待定系数法求抛物线解析式,抛物线的性质,抛物线平移,相似三角形的判定及性质,图形与坐标,利用辅助线画出准确图形是解题关键.题型2:最值问题4.(2024·安徽合肥·二模)在平面直角坐标系中,O 为坐标原点,抛物线23y ax bx =+−与x 轴交于()1,0A −,()3,0B 两点,与y 轴交于点C ,连接BC .(1)求a ,b 的值;(2)点M 为线段BC 上一动点(不与B ,C 重合),过点M 作MP x ⊥轴于点P ,交抛物线于点N . (ⅰ)如图1,当3PA PB=时,求线段MN 的长; (ⅱ)如图2,在抛物线上找一点Q ,连接AM ,QN ,QP ,使得PQN V 与APM △的面积相等,当线段NQ 的长度最小时,求点M 的横坐标m 的值.【答案】(1)1a =,2b =−(2)(ⅰ)2MN =;(ⅱ)m 的值为32或12【分析】本题考查诶粗函数的图象和性质,掌握待定系数法和利用函数性质求面积是解题的关键.(1)运用待定系数法求函数解析式即可;(2)(ⅰ)先计算BC 的解析式,然后设(),3M m m −,则3PM PB m ==−,1PA m =+,根据题意得到方程133m m +=−求出m 值,即可求出MN 的长;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况,根据勾股定理解题即可.【解析】(1)由题意得309330a b a b −−=⎧⎨+−=⎩,解得12a b =⎧⎨=−⎩;(2)(ⅰ)当0x =时,3y =−,∴()0,3C −,设直线BC 为3y kx =−,∵点()3,0B ,∴330k −=,解得1k =,∴直线BC 为3y x =−,设(),3M m m −,则3PM PB m ==−,1PA m =+, ∵3PA PB =, ∴133m m +=−,解得2m =,经检验2m =符合题意,当2m =时,222233y =−⨯−=−, ∴3PN =,31PM PB m ==−=,∴2MN =;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,PQN V 的面积为()21232m m QR −++⋅,APM △的面积为()()1312m m −+,∴()()()211233122m m QR m m −++⋅=−+,解得1QR =;当点Q 在PN 的左侧时,如图1,Q 点的横坐标为1m QR m −=−,纵坐标为()()2212134m m m m −−⨯−−=−,∴R 点的坐标为()2,4m mm−,∵N 点坐标为()2,23m mm −−,∴32RN m =−,∴()22231NQ m =−+,∴当32m =时,NQ 取最小值;当点Q 在PN 的右侧时,如图2,Q 点的横坐标为1m QR m +=+,纵坐标为()()2212134m m m +−⨯+−=−,∴R 点的坐标为()2,4m m−,∵N 点的坐标为()2,23m mm −−,∴21RN m =−, ∴()222211NQ m =−+,∴当12m =时,NQ 取最小值.综上,m 的值为32或12.。
初中数学二次函数相关的压轴题(含答案)
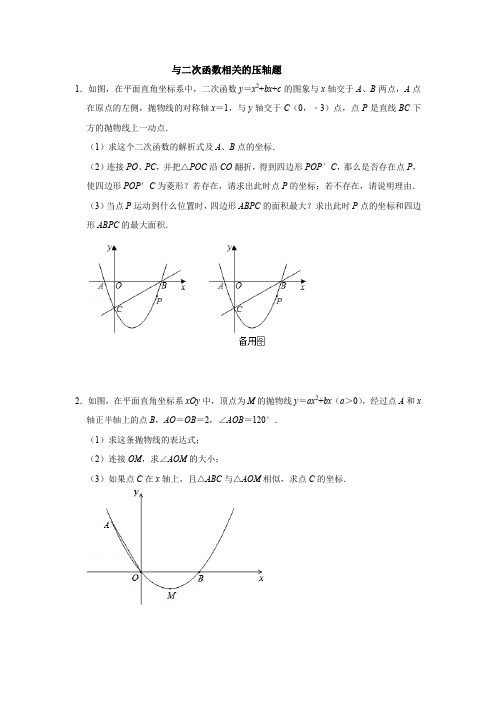
与二次函数相关的压轴题1.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,抛物线的对称轴x=1,与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的解析式及A、B点的坐标.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.2.如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x 轴正半轴上的点B,AO=OB=2,∠AOB=120°.(1)求这条抛物线的表达式;(2)连接OM,求∠AOM的大小;(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.3.如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x 轴正半轴上的点B,AB=BO=2,∠AOB=30°.(1)求这条抛物线的表达式;(2)连结OM,求∠AOM的大小;(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.4.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求抛物线的函数解析式.(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.5.如图,已知抛物线经过原点O,顶点A(2,2),且与直线y=x﹣4交于B、C.(1)求抛物线的解析式及C点的坐标;(2)求证:AB⊥BC;(3)若点N为x轴上一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O、M、N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.1.解:(1)函数的对称轴为:x=﹣=1,解得:b=﹣2,故抛物线的表达式为:y=x2﹣2x﹣3,令y=0,则x=﹣1或3,故点A、B的坐标分别为:(﹣1,0)、(3,0);(2)存在,理由:如图1,四边形POP′C为菱形,则yP=﹣OC=﹣,即y=x2﹣2x﹣3=﹣,解得:x=1(舍去负值),故点P(1+,﹣);(3)过点P作PH∥y轴交BC于点P,由点B、C的坐标得,BC的表达式为:y=x﹣3,设点P(x,x2﹣2x﹣3),则点H(x,x﹣3),ABPC的面积S=S△ABC+S△BCP=×AB×OC+×PH×OB=×4×3+×3×(x﹣3﹣x2+2x+3)=﹣x2﹣x+6,∵<0,故S有最大值为,此时点P(,﹣).【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.2.解:(1)过点A作AE⊥y轴于点E,∵AO=OB=2,∠AOB=120°,∴∠AOE=30°,∴OE=,AE=1,∴A点坐标为:(﹣1,),B点坐标为:(2,0),将两点代入y=ax2+bx得:,解得:,∴抛物线的表达式为:y=x2﹣x;(2)过点M作MF⊥OB于点F,∵y=x2﹣x=(x2﹣2x)=(x2﹣2x+1﹣1)=(x﹣1)2﹣,∴M点坐标为:(1,﹣),∴tan∠FOM==,∴∠FOM=30°,∴∠AOM=30°+120°=150°;(3)当点C在点左侧时,则∠BAC=150°,而∠ABC=30°,此时∠C=0°,故此种情况不存在;当点C在B点右侧时,∵AO=OB=2,∠AOB=120°,∴∠ABO=∠OAB=30°,∴AB=2EO=2,当△ABC1∽△AOM,∴=,∵MO==,∴=,解得:BC1=2,∴OC1=4,∴C1的坐标为:(4,0);当△C2BA∽△AOM,∴=,∴=,解得:BC2=6,∴OC2=8,∴C2的坐标为:(8,0).综上所述,△ABC与△AOM相似时,点C的坐标为:(4,0)或(8,0).【点评】此题主要考查了锐角三角函数的应用以及待定系数法求二次函数解析式和相似三角形的性质等知识,利用分类讨论思想以及数形结合得出是解题关键.3.解:(1)如图1,过点A作AH⊥x轴,垂足为H.∵AB=BO,∴∠∠OAB=∠AOB=30°,∴∠ABH=60°,在Rt△ABH中,AB=2,∴BH=1,AH=,∴A(3,),∵抛物线与x轴交于O、B(2,0)两点,设y=ax(x﹣2),代入点A(3,),可得a=,∴抛物线的表达式为=;(2)由,得抛物线的顶点M的坐标为(1,﹣),∴,∴∠BOM=30°,∴∠AOM=60°;(3)由A(3,),、B(2,0)、M(1,﹣),∵AH⊥x轴,∠AOB=30°,∴AO=2AH=,∵M(1,﹣),∠BOM=30°,∴,∴,当点C在点B左侧时,∠ABC=120°,△AMO中不可能出现120°的角,不存在满足条件的点;当点C在点B右侧时,∵∠ABC=∠AOM=60°,∴△ABC与△AOM相似,存在两种情况:①如图2,当时,.此时C(,0);②如图3,当时,BC=3BA=3×2=6.此时C(8,0).综上所述,C点的坐标为(,0)或(8,0).【点评】本题考查了待定系数法求二次函数解析式、特殊角的三角函数、解直角三角形、相似三角形的判定与性质等知识点,有一定综合性,难度适中.第(3)问注意分类讨论.分类讨论之前,可先通过分析排除不存在的情况,使解答过程得以简化.8.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得:,解得:,故抛物线函数解析式为:y=x2+2x;(2)∵AO为平行四边形的一边,∴DE∥AO,DE=AO,∵A(﹣2,0),∴DE=AO=2,∵四边形AODE是平行四边形,D在对称轴x=﹣1的右侧,D点横坐标为:﹣1+2=1,代入抛物线解析式得y=3,∴D的坐标为(1,3);(3)在y轴上存在点P,使得△POC与△BOF相似,理由如下:由y=x2+2x,顶点C的坐标为(﹣1,1),∵tan∠BOF==1,∴∠BOF=45°,当点P在y轴的负半轴时,tan∠COP==1,∴∠COP=45°,∴∠BOF=∠COP,设BC的解析式为y=kx+b(k≠0),∵图象经过B(﹣3,3),C(﹣1,﹣1)∴,∴,∴y=﹣2x﹣3;令y=0,则x=﹣1.5.∴F(﹣1.5,0),∴OB=3,OF=1.5,OC=,①当△POC∽△FOB时,则=,即=,∴OP=,∴P(0,﹣);②当△POC∽△BOF时,∴=,∴OP=4,∴P(0,﹣4),∴当△POC与△BOF相似时,点P的坐标为(0,﹣)或(0,﹣4).【点评】本题考查了二次函数的综合,涉及了相似三角形的判定与性质、待定系数法求二次函数解析式及平行四边形的性质,解答本题关键是分类讨论思想的运用,难度较大.4.(1)解:∵顶点坐标为(2,2),∴设抛物线解析式为y=a(x﹣2)2+2,又抛物线过原点,∴0=a(0﹣2)2+2,解得a=﹣,∴抛物线解析式为y=﹣(x﹣2)2+2,即y=﹣x2+2x,联立抛物线和直线解析式可得,解得或,∴B(4,0),C(﹣2,﹣6);综上所述,抛物线解析式为y=﹣x2+2x,C点的坐标是(﹣2,﹣6);(2)证明:由A(2,2),B(4,0),C(﹣2,﹣6)得到:AB2=(4﹣2)2+(0﹣2)2=8,BC2=(﹣2﹣4)2+(﹣6﹣0)2=72,AC2=(﹣2﹣2)2+(﹣6﹣2)2=80.∴AC2=AB2+BC2,∴∠ABC=90°,∴AB⊥BC;(3)解:假设存在满足条件的点N,设N(x,0),则M(x,﹣x2+2x),∴ON=|x|,MN=|﹣x2+2x|,由(2)知,AB=2,BC=6,∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,∴当△ABC和△MNO相似时,有=或=.①当=时,∴=,∵当x=0时M、O、N不能构成三角形,∴x≠0,解得x=或x=,此时N点坐标为(,0)或(,0);②当=时,=,解得x=﹣2或x=10,此时N点坐标为(﹣2,0)或(10,0),综上,满足条件的N点,其坐标为(,0)或(,0)或(﹣2,0)或(10,0).【点评】本题考查了二次函数综合题,涉及知识点有待定系数法确定函数解析式、图象的交点问题、直角三角形的判定、勾股定理及逆定理、相似三角形的性质及分类讨论等.在(1)中注意顶点式的运用,在(3)中设出N、M的坐标,利用相似三角形的性质得到关于坐标的方程是解题的关键,注意相似三角形点的对应.本题考查知识点较多,综合性较强,难度较大.。
二次函数解答压轴题(共62题)(学生版)-2023年中考数学真题分项汇编(全国通用)

二次函数解答压轴题(62题)一、解答题1(2023·浙江绍兴·统考中考真题)已知二次函数y=-x2+bx+c.(1)当b=4,c=3时,①求该函数图象的顶点坐标.②当-1≤x≤3时,求y的取值范围.(2)当x≤0时,y的最大值为2;当x>0时,y的最大值为3,求二次函数的表达式.2(2023·浙江·统考中考真题)已知点-m,0和3m,0在二次函数y=ax2+bx+3(a,b是常数,a≠0)的图像上.(1)当m=-1时,求a和b的值;(2)若二次函数的图像经过点A n,3且点A不在坐标轴上,当-2<m<-1时,求n的取值范围;(3)求证:b2+4a=0.3(2023·浙江嘉兴·统考中考真题)在二次函数y=x2-2tx+3(t>0)中,(1)若它的图象过点(2,1),则t的值为多少?(2)当0≤x≤3时,y的最小值为-2,求出t的值:(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上,且a<b<3,求m的取值范围.4(2023·浙江杭州·统考中考真题)设二次函数y=ax2+bx+1,(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:x⋯-10123⋯y⋯m1n1p⋯(1)若m=4,求二次函数的表达式;(2)写出一个符合条件的x的取值范围,使得y随x的增大而减小.(3)若在m、n、p这三个实数中,只有一个是正数,求a的取值范围.5(2023·湖南常德·统考中考真题)如图,二次函数的图象与x轴交于A-1,0,B5,0两点,与y轴交于点C,顶点为D.O为坐标原点,tan∠ACO=1 5.(1)求二次函数的表达式;(2)求四边形ACDB的面积;(3)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.6(2023·山东烟台·统考中考真题)如图,抛物线y=ax2+bx+5与x轴交于A,B两点,与y轴交于点C,AB=4.抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D,与x轴交于点E.(1)求直线AD及抛物线的表达式;(2)在抛物线上是否存在点M,使得△ADM是以AD为直角边的直角三角形?若存在,求出所有点M的坐标;若不存在,请说明理由;(3)以点B为圆心,画半径为2的圆,点P为⊙B上一个动点,请求出PC+1PA的最小值.27(2023·江苏苏州·统考中考真题)如图,二次函数y=x2-6x+8的图像与x轴分别交于点A,B(点A 在点B的左侧),直线l是对称轴.点P在函数图像上,其横坐标大于4,连接PA,PB,过点P作PM⊥l,垂足为M,以点M为圆心,作半径为r的圆,PT与⊙M相切,切点为T.(1)求点A,B的坐标;(2)若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等,且⊙M不经过点3,2,求PM长的取值范围.8(2023·山东东营·统考中考真题)如图,抛物线过点O0,0,矩形ABCD的边AB在线段,E10,0OE上(点B在点A的左侧),点C,D在抛物线上,设B t,0,当t=2时,BC=4.(1)求抛物线的函数表达式;(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离.9(2023·内蒙古通辽·统考中考真题)在平面直角坐标系中,已知抛物线y=ax2+83x+c a≠0与x轴交于点A1,0和点B,与y轴交于点C0,-4.(1)求这条抛物线的函数解析式;(2)P是抛物线上一动点(不与点A,B,C重合),作PD⊥x轴,垂足为D,连接PC.①如图,若点P在第三象限,且tan∠CPD=2,求点P的坐标;②直线PD交直线BC于点E,当点E关于直线PC的对称点E 落在y轴上时,请直接写出四边形PECE 的周长.10(2023·四川自贡·统考中考真题)如图,抛物线y=-43x2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C.(1)求抛物线解析式及B,C两点坐标;(2)以A,B,C,D为顶点的四边形是平行四边形,求点D坐标;(3)该抛物线对称轴上是否存在点E,使得∠ACE=45°,若存在,求出点E的坐标;若不存在,请说明理由.11(2023·四川达州·统考中考真题)如图,抛物线y =ax 2+bx +c 过点A -1,0 ,B 3,0 ,C 0,3 .(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出△PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B 、C 、M 、N 为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.12(2023·四川泸州·统考中考真题)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+2x+c与坐标轴分别相交于点A,B,C0,6三点,其对称轴为x=2.(1)求该抛物线的解析式;(2)点F是该抛物线上位于第一象限的一个动点,直线AF分别与y轴,直线BC交于点D,E.①当CD=CE时,求CD的长;②若△CAD,△CDE,△CEF的面积分别为S1,S2,S3,且满足S1+S3=2S2,求点F的坐标.13(2023·全国·统考中考真题)如图,在平面直角坐标系中,抛物线y=-x2+2x+c经过点A(0,1).点P,Q在此抛物线上,其横坐标分别为m,2m(m>0),连接AP,AQ.(1)求此抛物线的解析式.(2)当点Q与此抛物线的顶点重合时,求m的值.(3)当∠PAQ的边与x轴平行时,求点P与点Q的纵坐标的差.(4)设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为h1,在点A与点Q之间部分(包括点A和点Q)的最高点与最低点的纵坐标的差为h2.当h2-h1=m时,直接写出m的值.14(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线y=14x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B3,0,C0,-3.(1)求该抛物线的表达式;(2)点P是直线AC下方抛物线上一动点,过点P作PD⊥AC于点D,求PD的最大值及此时点P的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.15(2023·四川凉山·统考中考真题)如图,已知抛物线与x轴交于A1,0两点,与y轴交于和B-5,0点C.直线y=-3x+3过抛物线的顶点P.(1)求抛物线的函数解析式;(2)若直线x=m-5<m<0与抛物线交于点E,与直线BC交于点F.①当EF取得最大值时,求m的值和EF的最大值;②当△EFC是等腰三角形时,求点E的坐标.16(2023·四川成都·统考中考真题)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+c经过点P (4,-3),与y轴交于点A(0,1),直线y=kx(k≠0)与抛物线交于B,C两点.(1)求抛物线的函数表达式;(2)若△ABP是以AB为腰的等腰三角形,求点B的坐标;(3)过点M(0,m)作y轴的垂线,交直线AB于点D,交直线AC于点E.试探究:是否存在常数m,使得OD⊥OE始终成立?若存在,求出m的值;若不存在,请说明理由.17(2023·安徽·统考中考真题)在平面直角坐标系中,点O是坐标原点,抛物线y=ax2+bx a≠0经过点A3,3,对称轴为直线x=2.(1)求a,b的值;(2)已知点B,C在抛物线上,点B的横坐标为t,点C的横坐标为t+1.过点B作x轴的垂线交直线OA于点D,过点C作x轴的垂线交直线OA于点E.(ⅰ)当0<t<2时,求△OBD与△ACE的面积之和;(ⅱ)在抛物线对称轴右侧,是否存在点B,使得以B,C,D,E为顶点的四边形的面积为32若存在,请求出点B的横坐标t的值;若不存在,请说明理由.18(2023·浙江金华·统考中考真题)如图,直线y =52x +5与x 轴,y 轴分别交于点A ,B ,抛物线的顶点P 在直线AB 上,与x 轴的交点为C ,D ,其中点C 的坐标为2,0 .直线BC 与直线PD 相交于点E .(1)如图2,若抛物线经过原点O .①求该抛物线的函数表达式;②求BEEC的值.(2)连接PC ,∠CPE 与∠BAO 能否相等?若能,求符合条件的点P 的横坐标;若不能,试说明理由.19(2023·湖南·统考中考真题)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于C点,其中B1,0.,C0,3(1)求这个二次函数的表达式;(2)在二次函数图象上是否存在点P,使得S△PAC=S△ABC若存在,请求出P点坐标;若不存在,请说明理由;(3)点Q是对称轴l上一点,且点Q的纵坐标为a,当△QAC是锐角三角形时,求a的取值范围.20(2023·四川遂宁·统考中考真题)在平面直角坐标系中,O 为坐标原点,抛物线y =14x 2+bx +c 经过点O (0,0),对称轴过点B (2,0),直线l 过点C 2,-2 ,且垂直于y 轴.过点B 的直线l 1交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线l 1下方的抛物线上一动点,连接PQ 、PO ,其中PO 交l 1于点E ,设△OQE 的面积为S 1,△PQE 的面积为S 2.求S2S 1的最大值.21(2023·四川眉山·统考中考真题)在平面直角坐标系中,已知抛物线y =ax 2+bx +c 与x 轴交于点A -3,0 ,B 1,0 两点,与y 轴交于点C 0,3 ,点P 是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PDDB的值最大时,求点P 的坐标及PDDB的最大值;(3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将△PCM 沿直线PC 翻折,当点M 的对应点M '恰好落在y 轴上时,请直接写出此时点M 的坐标.22(2023·江西·统考中考真题)综合与实践问题提出:某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,D为AC上一点,CD=2,动点P 以每秒1个单位的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF设点P的运动时间为ts,正方形DPEF的而积为S,探究S与t的关系(1)初步感知:如图1,当点P由点C运动到点B时,①当t=1时,S=.②S关于t的函数解析式为.(2)当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象请根据图象信息,求S关于t的函数解析式及线段AB的长.(3)延伸探究:若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等.①t1+t2=;②当t3=4t1时,求正方形DPEF的面积.23(2023·新疆·统考中考真题)【建立模型】(1)如图1,点B 是线段CD 上的一点,AC ⊥BC ,AB ⊥BE ,ED ⊥BD ,垂足分别为C ,B ,D ,AB =BE .求证:△ACB ≌△BDE ;【类比迁移】(2)如图2,一次函数y =3x +3的图象与y 轴交于点A 、与x 轴交于点B ,将线段AB 绕点B 逆时针旋转90°得到BC 、直线AC 交x 轴于点D .①求点C 的坐标;②求直线AC 的解析式;【拓展延伸】(3)如图3,抛物线y =x 2-3x -4与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于C点,已知点Q (0,-1),连接BQ .抛物线上是否存在点M ,使得tan ∠MBQ =13,若存在,求出点M 的横坐标.24(2023·甘肃武威·统考中考真题)如图1,抛物线y=-x2+bx与x轴交于点A,与直线y=-x交于点B4,-4在y轴上.点P从点B出发,沿线段BO方向匀速运动,运动到点O时停止.,点C0,-4(1)求抛物线y=-x2+bx的表达式;(2)当BP=22时,请在图1中过点P作PD⊥OA交抛物线于点D,连接PC,OD,判断四边形OCPD 的形状,并说明理由.(3)如图2,点P从点B开始运动时,点Q从点O同时出发,以与点P相同的速度沿x轴正方向匀速运动,点P停止运动时点Q也停止运动.连接BQ,PC,求CP+BQ的最小值.25(2023·四川乐山·统考中考真题)已知x 1,y 1 ,x 2,y 2 是抛物C 1:y =-14x 2+bx (b 为常数)上的两点,当x 1+x 2=0时,总有y 1=y 2(1)求b 的值;(2)将抛物线C 1平移后得到抛物线C 2:y =-14(x -m )2+1(m >0).探究下列问题:①若抛物线C 1与抛物线C 2有一个交点,求m 的取值范围;②设抛物线C 2与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线C 2的顶点为点E ,△ABC 外接圆的圆心为点F ,如果对抛物线C 1上的任意一点P ,在抛物线C 2上总存在一点Q ,使得点P 、Q 的纵坐标相等.求EF 长的取值范围.26(2023·内蒙古·统考中考真题)如图,在平面直角坐标系中,抛物线y =-x 2+3x +1交y 轴于点A ,直线y =-13x +2交抛物线于B ,C 两点(点B 在点C 的左侧),交y 轴于点D ,交x 轴于点E .(1)求点D ,E ,C 的坐标;(2)F 是线段OE 上一点OF <EF ,连接AF ,DF ,CF ,且AF 2+EF 2=21.①求证:△DFC 是直角三角形;②∠DFC 的平分线FK 交线段DC 于点K ,P 是直线BC 上方抛物线上一动点,当3tan ∠PFK =1时,求点P 的坐标.27(2023·上海·统考中考真题)在平面直角坐标系xOy中,已知直线y=34x+6与x轴交于点A,y轴交于点B,点C在线段AB上,以点C为顶点的抛物线M:y=ax2+bx+c经过点B.(1)求点A,B的坐标;(2)求b,c的值;(3)平移抛物线M至N,点C,B分别平移至点P,D,联结CD,且CD∥x轴,如果点P在x轴上,且新抛物线过点B,求抛物线N的函数解析式.28(2023·江苏扬州·统考中考真题)在平面直角坐标系xOy中,已知点A在y轴正半轴上.(1)如果四个点0,0中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象、-1,1、1,1、0,2上.①a=;②如图1,已知菱形ABCD的顶点B、C、D在该二次函数的图象上,且AD⊥y轴,求菱形的边长;③如图2,已知正方形ABCD的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究n-m是否为定值.如果是,求出这个值;如果不是,请说明理由.(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数,且a>0)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.29(2023·湖南岳阳·统考中考真题)已知抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,B两点,交y 轴于点C0,3.(1)请求出抛物线Q1的表达式.(2)如图1,在y轴上有一点D0,-1,点E在抛物线Q1上,点F为坐标平面内一点,是否存在点E,F使得四边形DAEF为正方形?若存在,请求出点E,F的坐标;若不存在,请说明理由.(3)如图2,将抛物线Q1向右平移2个单位,得到抛物线Q2,抛物线Q2的顶点为K,与x轴正半轴交于点H,抛物线Q1上是否存在点P,使得∠CPK=∠CHK?若存在,请求出点P的坐标;若不存在,请说明理由.30(2023·湖南永州·统考中考真题)如图1,抛物线y =ax 2+bx +c (a ,b ,c 为常数)经过点F 0,5 ,顶点坐标为2,9 ,点P x 1,y 1 为抛物线上的动点,PH ⊥x 轴于H ,且x 1≥52.(1)求抛物线的表达式;(2)如图1,直线OP :y =y 1x 1x 交BF 于点G ,求S △BPG S △BOG的最大值;(3)如图2,四边形OBMF 为正方形,PA 交y 轴于点E ,BC 交FM 的延长线于C ,且BC ⊥BE ,PH =FC ,求点P 的横坐标.31(2023·山东枣庄·统考中考真题)如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与轴交于点D.(1)求该抛物线的表达式;(2)若点H是x轴上一动点,分别连接MH,DH,求MH+DH的最小值;(3)若点P是抛物线上一动点,问在对称轴上是否存在点Q,使得以D,M,P,Q为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.32(2023·湖北随州·统考中考真题)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC 于点M,交x轴于点N.(1)直接写出抛物线和直线BC的解析式;(2)如图2,连接OM,当△OCM为等腰三角形时,求m的值;(3)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.33(2023·四川内江·统考中考真题)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 与x 轴交于B 4,0 ,C -2,0 两点.与y 轴交于点A 0,-2 .(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求与12PK +PD 的最大值及此时点P 的坐标;(3)在抛物线的对称轴上是否存在一点M ,使得△MAB 是以AB 为一条直角边的直角三角形:若存在,请求出点M 的坐标,若不存在,请说明理由.34(2023·湖南·统考中考真题)已知二次函数y =ax 2+bx +c a >0 .(1)若a =1,c =-1,且该二次函数的图像过点2,0 ,求b 的值;(2)如图所示,在平面直角坐标系Oxy 中,该二次函数的图像与x 轴交于点A x 1,0 ,B x 2,0 ,且x 1<0<x 2,点D 在⊙O 上且在第二象限内,点E 在x 轴正半轴上,连接DE ,且线段DE 交y 轴正半轴于点F ,∠DOF =∠DEO ,OF =32DF .①求证:DO EO=23.②当点E 在线段OB 上,且BE =1.⊙O 的半径长为线段OA 的长度的2倍,若4ac =-a 2-b 2,求2a +b 的值.35(2023·山西·统考中考真题)如图,二次函数y =-x 2+4x 的图象与x 轴的正半轴交于点A ,经过点A 的直线与该函数图象交于点B 1,3 ,与y 轴交于点C .(1)求直线AB 的函数表达式及点C 的坐标;(2)点P 是第一象限内二次函数图象上的一个动点,过点P 作直线PE ⊥x 轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①当PD =12OC 时,求m 的值;②当点P 在直线AB 上方时,连接OP ,过点B 作BQ ⊥x 轴于点Q ,BQ 与OP 交于点F ,连接DF .设四边形FQED 的面积为S ,求S 关于m 的函数表达式,并求出S 的最大值.36(2023·湖北武汉·统考中考真题)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边),交y 轴于点C.(1)直接写出A,B,C三点的坐标;(2)如图(1),作直线x=t0<t<4,分别交x轴,线段BC,抛物线C1于D,E,F三点,连接CF.若△BDE 与△CEF相似,求t的值;(3)如图(2),将抛物线C1平移得到抛物线C2,其顶点为原点.直线y=2x与抛物线C2交于O,G两点,过OG的中点H作直线MN(异于直线OG)交抛物线C2于M,N两点,直线MO与直线GN交于点P.问点P是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.37(2023·湖北宜昌·统考中考真题)如图,已知A(0,2),B(2,0).点E位于第二象限且在直线y=-2x 上,∠EOD=90°,OD=OE,连接AB,DE,AE,DB.(1)直接判断△AOB的形状:△AOB是三角形;(2)求证:△AOE≌△BOD;(3)直线EA交x轴于点C(t,0),t>2.将经过B,C两点的抛物线y1=ax2+bx-4向左平移2个单位,得到抛物线y2.①若直线EA与抛物线y1有唯一交点,求t的值;②若抛物线y2的顶点P在直线EA上,求t的值;③将抛物线y2再向下平移,2(t-1)2个单位,得到抛物线y3.若点D在抛物线y3上,求点D的坐标.38(2023·湖南郴州·统考中考真题)已知抛物线y=ax2+bx+4与x轴相交于点A1,0,与y,B4,0轴相交于点C.(1)求抛物线的表达式;(2)如图1,点P是抛物线的对称轴l上的一个动点,当△PAC的周长最小时,求PAPC的值;(3)如图2,取线段OC的中点D,在抛物线上是否存在点Q,使tan∠QDB=12若存在,求出点Q的坐标;若不存在,请说明理由.39(2023·湖北黄冈·统考中考真题)已知抛物线y =-12x 2+bx +c 与x 轴交于A ,B (4,0)两点,与y 轴交于点C (0,2),点P 为第一象限抛物线上的点,连接CA ,CB ,PB ,PC .(1)直接写出结果;b =,c =,点A 的坐标为,tan ∠ABC =;(2)如图1,当∠PCB =2∠OCA 时,求点P 的坐标;(3)如图2,点D 在y 轴负半轴上,OD =OB ,点Q 为抛物线上一点,∠QBD =90°,点E ,F 分别为△BDQ 的边DQ ,DB 上的动点,QE =DF ,记BE +QF 的最小值为m .①求m 的值;②设△PCB 的面积为S ,若S =14m 2-k ,请直接写出k 的取值范围.40(2023·湖南·统考中考真题)如图,在平面直角坐标系中,抛物线y=ax2+x+c经过点A-2,0和点B4,0,且与直线l:y=-x-1交于D、E两点(点D在点E的右侧),点M为直线l上的一动点,设点M 的横坐标为t.(1)求抛物线的解析式.(2)过点M作x轴的垂线,与拋物线交于点N.若0<t<4,求△NED面积的最大值.(3)抛物线与y轴交于点C,点R为平面直角坐标系上一点,若以B、C、M、R为顶点的四边形是菱形,请求出所有满足条件的点R的坐标.41(2023·四川·统考中考真题)如图1,在平面直角坐标系中,已知二次函数y=ax2+bx+4的图象与x 轴交于点A-2,0,B4,0,与y轴交于点C.(1)求抛物线的解析式;(2)已知E为抛物线上一点,F为抛物线对称轴l上一点,以B,E,F为顶点的三角形是等腰直角三角形,且∠BFE=90°,求出点F的坐标;(3)如图2,P为第一象限内抛物线上一点,连接AP交y轴于点M,连接BP并延长交y轴于点N,在点P运动过程中,OM+12ON是否为定值?若是,求出这个定值;若不是,请说明理由.42(2023·山东聊城·统考中考真题)如图①,抛物线y=ax2+bx-9与x轴交于点A-3,0,,B6,0与y轴交于点C,连接AC,BC.点P是x轴上任意一点.(1)求抛物线的表达式;(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;(3)如图②,当点P m,0从点A出发沿x轴向点B运动时(点P与点A,B不重合),自点P分别作PE∥BC,交AC于点E,作PD⊥BC,垂足为点D.当m为何值时,△PED面积最大,并求出最大值.43(2023·湖北荆州·统考中考真题)已知:y关于x的函数y=a-2x+b.x2+a+1(1)若函数的图象与坐标轴有两个公共点,且a=4b,则a的值是;(2)如图,若函数的图象为抛物线,与x轴有两个公共点A-2,0,B4,0,并与动直线l:x=m(0<m<4)交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为S1,△CDE 的面积为S2.①当点P为抛物线顶点时,求△PBC的面积;②探究直线l在运动过程中,S1-S2是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.44(2023·福建·统考中考真题)已知抛物线y=ax2+bx+3交x轴于A1,0,B3,0两点,M为抛物线的顶点,C,D为抛物线上不与A,B重合的相异两点,记AB中点为E,直线AD,BC的交点为P.(1)求抛物线的函数表达式;(2)若C4,3,D m,-3 4,且m<2,求证:C,D,E三点共线;(3)小明研究发现:无论C,D在抛物线上如何运动,只要C,D,E三点共线,△AMP,△MEP,△ABP中必存在面积为定值的三角形.请直接写出其中面积为定值的三角形及其面积,不必说明理由.45(2023·山东·统考中考真题)如图,直线y=-x+4交x轴于点B,交y轴于点C,对称轴为x=32的抛物线经过B,C两点,交x轴负半轴于点A.P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.(1)求抛物线的解析式;(2)若0<m<32,当m为何值时,四边形CDNP是平行四边形?(3)若m<32,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m 的值;若不存在,请说明理由.46(2023·山东·统考中考真题)已知抛物线y =-x 2+bx +c 与x 轴交于A ,B 两点,与y 轴交于点C 0,4 ,其对称轴为x =-32.(1)求抛物线的表达式;(2)如图1,点D 是线段OC 上的一动点,连接AD ,BD ,将△ABD 沿直线AD 翻折,得到△AB D ,当点B 恰好落在抛物线的对称轴上时,求点D 的坐标;(3)如图2,动点P 在直线AC 上方的抛物线上,过点P 作直线AC 的垂线,分别交直线AC ,线段BC 于点E ,F ,过点F 作FG ⊥x 轴,垂足为G ,求FG +2FP 的最大值.47(2023·辽宁大连·统考中考真题)如图,在平面直角坐标系中,抛物线C 1:y =x 2上有两点A 、B ,其中点A 的横坐标为-2,点B 的横坐标为1,抛物线C 2:y =-x 2+bx +c 过点A 、B .过A 作AC ∥x 轴交抛物线C 1另一点为点C .以AC 、12AC 长为边向上构造矩形ACDE .(1)求抛物线C 2的解析式;(2)将矩形ACDE 向左平移m 个单位,向下平移n 个单位得到矩形A C D E ,点C 的对应点C 落在抛物线C 1上.①求n 关于m 的函数关系式,并直接写出自变量m 的取值范围;②直线A E 交抛物线C 1于点P ,交抛物线C 2于点Q .当点E 为线段PQ 的中点时,求m 的值;③抛物线C 2与边E D 、A C 分别相交于点M 、N ,点M 、N 在抛物线C 2的对称轴同侧,当MN =2103时,求点C 的坐标.48(2023·湖南张家界·统考中考真题)如图,在平面直角坐标系中,已知二次函数y=ax2+bx+c的图象与x轴交于点A-2,0.点D为线段BC上的一动点. 和点B6,0两点,与y轴交于点C0,6(1)求二次函数的表达式;(2)如图1,求△AOD周长的最小值;(3)如图2,过动点D作DP∥AC交抛物线第一象限部分于点P,连接PA,PB,记△PAD与△PBD的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.49(2023·黑龙江绥化·统考中考真题)如图,抛物线y1=ax2+bx+c的图象经过A(-6,0),B(-2,0),C (0,6)三点,且一次函数y=kx+6的图象经过点B.(1)求抛物线和一次函数的解析式.(2)点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的E,F两点是否存在?如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.(3)将抛物线y1=ax2+bx+c的图象向右平移8个单位长度得到抛物线y2,此抛物线的图象与x轴交于M,N两点(M点在N点左侧).点P是抛物线y2上的一个动点且在直线NC下方.已知点P的横坐标为PD有最大值,最大值是多少?m.过点P作PD⊥NC于点D.求m为何值时,CD+1250(2023·四川南充·统考中考真题)如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于A-1,0,B3,0两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)如图2,抛物线顶点为D,对称轴与x轴交于点E,过点K1,3的直线(直线KD除外)与抛物线交于G,H两点,直线DG,DH分别交x轴于点M,N.试探究EM⋅EN是否为定值,若是,求出该定值;若不是,说明理由.51(2023·四川宜宾·统考中考真题)如图,抛物线y=ax2+bx+c与x轴交于点A-4,0,且经、B2,0过点C-2,6.(1)求抛物线的表达式;(2)在x轴上方的抛物线上任取一点N,射线AN、BN分别与抛物线的对称轴交于点P、Q,点Q关于x轴的对称点为Q ,求△APQ 的面积;(3)点M是y轴上一动点,当∠AMC最大时,求M的坐标.52(2023·四川广安·统考中考真题)如图,二次函数y=x2+bx+c的图象交x轴于点A,B,交y轴于点C,点B的坐标为1,0,对称轴是直线x=-1,点P是x轴上一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的解析式.(2)若点P在线段AO上运动(点P与点A、点O不重合),求四边形ABCN面积的最大值,并求出此时点P 的坐标.(3)若点P在x轴上运动,则在y轴上是否存在点Q,使以M、N、C、Q为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.。
初中数学二次函数压轴题集锦(50道含解析)

1.如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C 坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t的取值范围.3.如图,在平面直角坐标系中,点A在抛物线y=﹣x2+4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当△PBE的面积最大时,求PH+HF+FO的最小值;(3)在(2)中,PH+HF+FO取得最小值时,将△CFH绕点C顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.4.如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.5.如图,在平面直角坐标系xOy中,以直线x=对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.(1)求抛物线的函数表达式;(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若=,且△BCG与△BCD面积相等,求点G的坐标;(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.6.如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.7.抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.(1)直接写出抛物线L的解析式;(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.8.在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.(Ⅰ)当抛物线经过点A时,求顶点P的坐标;(Ⅱ)若点P在x轴下方,当∠AOP=45°时,求抛物线的解析式;(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.9.如图1,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.(1)当t=2时,线段PQ的中点坐标为;(2)当△CBQ与△PAQ相似时,求t的值;(3)当t=1时,抛物线y=x2+bx+c经过P,Q两点,与y轴交于点M,抛物线的顶点为K,如图2所示,问该抛物线上是否存在点D,使∠MQD=∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.10.如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.(1)当x=2时,求⊙P的半径;(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到的距离等于到的距离的所有点的集合.(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C 的右侧,请利用图②,求cos∠APD的大小.11.已知顶点为A抛物线经过点,点.(1)求抛物线的解析式;(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.12.在平面直角坐标系xOy中(如图).已知抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;(2)求线段CD的长;(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.13.如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).(1)直接写出这两个二次函数的表达式;(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标14.小贤与小杰在探究某类二次函数问题时,经历了如下过程:求解体验:(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b=,顶点坐标为,该抛物线关于点(0,1)成中心对称的抛物线表达式是.抽象感悟:我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y′,则我们又称抛物线y′为抛物线y的“衍生抛物线”,点M为“衍生中心”.(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y′,若这两条抛物线有交点,求m的取值范围.问题解决:(3)已知抛物线y=ax2+2ax﹣b(a≠0)①若抛物线y的衍生抛物线为y′=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a、b的值及衍生中心的坐标;②若抛物线y关于点(0,k+12)的衍生抛物线为y1,其顶点为A1;关于点(0,k+22)的衍生抛物线为y2,其顶点为A2;…;关于点(0,k+n2)的衍生抛物线为y n,其顶点为A n…(n为正整数).求A n A n+1的长(用含n的式子表示).15.如图,已知抛物线y=ax2+bx(a≠0)过点A(,﹣3)和点B(3,0).过点A作直线AC∥x轴,交y轴于点C.(1)求抛物线的解析式;(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D.连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;=S△AOQ?若存在,求出点Q的坐标;若不存在,请说明理由.(3)抛物线上是否存在点Q,使得S△AOC16.如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.(1)求线段AD的长;(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.17.如图①,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且与y 轴交于点C.(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.(1)若点P的横坐标为﹣,求△DPQ面积的最大值,并求此时点D的坐标;(Ⅱ)直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.18.已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(﹣,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.19.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=DE.①求点P的坐标;②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.20.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有;②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形“十字形”.(填“是”或“不是”)(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB ﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD 的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;①=;②=;③“十字形”ABCD的周长为12.21.如图1,抛物线y 1=ax 2﹣x +c 与x 轴交于点A 和点B (1,0),与y 轴交于点C (0,),抛物线y 1的顶点为G ,GM ⊥x 轴于点M .将抛物线y 1平移后得到顶点为B 且对称轴为直线l 的抛物线y 2.(1)求抛物线y 2的解析式;(2)如图2,在直线l 上是否存在点T ,使△TAC 是等腰三角形?若存在,请求出所有点T 的坐标;若不存在,请说明理由;(3)点P 为抛物线y 1上一动点,过点P 作y 轴的平行线交抛物线y 2于点Q ,点Q 关于直线l 的对称点为R ,若以P ,Q ,R 为顶点的三角形与△AMG 全等,求直线PR 的解析式.22.如图,已知直线y=﹣2x +4分别交x 轴、y 轴于点A 、B ,抛物线过A ,B 两点,点P 是线段AB 上一动点,过点P 作PC ⊥x 轴于点C ,交抛物线于点D .(1)若抛物线的解析式为y=﹣2x 2+2x +4,设其顶点为M ,其对称轴交AB 于点N .①求点M 、N 的坐标;②是否存在点P ,使四边形MNPD 为菱形?并说明理由;(2)当点P 的横坐标为1时,是否存在这样的抛物线,使得以B 、P 、D 为顶点的三角形与△AOB 相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.23.如图,抛物线y=ax 2+bx 经过△OAB 的三个顶点,其中点A (1,),点B (3,﹣),O 为坐标原点.(1)求这条抛物线所对应的函数表达式;(2)若P (4,m ),Q (t ,n )为该抛物线上的两点,且n <m ,求t 的取值范围;(3)若C 为线段AB 上的一个动点,当点A ,点B 到直线OC 的距离之和最大时,求∠BOC 的大小及点C 的坐标.24.如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.(1)求抛物线C1的表达式;(2)直接用含t的代数式表示线段MN的长;(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.25.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=x 与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F 的距离总是相等,求定点F的坐标.26.如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(﹣4,0)、B(2,0),交y轴于点C (0,6),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标,若不存在请说明理由.27.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.(1)求抛物线的函数表达式;(2)求点D的坐标;(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M,N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.28.如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.(1)求a,b的值.(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,△OBP的面积为S,记K=.求K关于m的函数表达式及K的范围.29.抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C 绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M30.综合与探究如图,抛物线y=x﹣4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.31.如图,二次函数y=﹣+bx+2的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是;(2)设直线PB与直线AC相交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.32A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.33.如图,已知二次函数y=ax2﹣(2a﹣)x+3的图象经过点A(4,0),与y轴交于点B.在x轴上有一动点C(m,0)(0<m<4),过点C作x轴的垂线交直线AB于点E,交该二次函数图象于点D.(1)求a的值和直线AB的解析式;(2)过点D作DF⊥AB于点F,设△ACE,△DEF的面积分别为S1,S2,若S1=4S2,求m的值;(3)点H是该二次函数图象上位于第一象限的动点,点G是线段AB上的动点,当四边形DEGH是平行四边形,且▱DEGH周长取最大值时,求点G的坐标.34.已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.35.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣5交y轴于点A,交x轴于点B(﹣5,0)和点C(1,0),过点A作AD∥x轴交抛物线于点D.(1)求此抛物线的表达式;(2)点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,求△EAD的面积;(3)若点P是直线AB下方的抛物线上一动点,当点P运动到某一位置时,△ABP的面积最大,求出此时点P的坐标和△ABP的最大面积.36.已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(﹣,0).(1)求抛物线F的解析式;(2)如图1,直线l:y=x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);(3)在(2)中,若m=,设点A′是点A关于原点O的对称点,如图2.①判断△AA′B的形状,并说明理由;②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.37.直线y=﹣x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣x2+2mx﹣3m经过点A,交x 轴于另一点C,连接BD,AD,CD,如图所示.(1)直接写出抛物线的解析式和点A,C,D的坐标;(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t 秒.PQ交线段AD于点E.①当∠DPE=∠CAD时,求t的值;②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.38.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.(1)求m、n的值及该抛物线的解析式;(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.39.如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为(用含m的代数式表示);(2)求△ABC的面积(用含a的代数式表示);(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.40.如图1,在平面直角坐标系xOy中,已知点A和点B的坐标分别为A(﹣2,0),B(0,﹣6),将Rt △AOB绕点O按顺时针方向分别旋转90°,180°得到Rt△A1OC,Rt△EOF.抛物线C1经过点C,A,B;抛物线C2经过点C,E,F.(1)点C的坐标为,点E的坐标为;抛物线C1的解析式为.抛物线C2的解析式为;(2)如果点P(x,y)是直线BC上方抛物线C1上的一个动点.①若∠PCA=∠ABO时,求P点的坐标;②如图2,过点P作x轴的垂线交直线BC于点M,交抛物线C2于点N,记h=PM+NM+BM,求h与x的函数关系式,当﹣5≤x≤﹣2时,求h的取值范围.41.如图,抛物线y=ax2+bx+c与两坐标轴相交于点A(﹣1,0)、B(3,0)、C(0,3),D是抛物线的顶点,E是线段AB的中点.(1)求抛物线的解析式,并写出D点的坐标;(2)F(x,y)是抛物线上的动点:①当x>1,y>0时,求△BDF的面积的最大值;②当∠AEF=∠DBE时,求点F的坐标.42.如图,在平面直角坐标系中,矩形ABCD的对称中心为坐标原点O,AD⊥y轴于点E(点A在点D的左侧),经过E、D两点的函数y=﹣x2+mx+1(x≥0)的图象记为G1,函数y=﹣x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.(1)当点A的横坐标为﹣1时,求m的值;(2)求L与m之间的函数关系式;(3)当G2与矩形ABCD恰好有两个公共点时,求L的值;(4)设G在﹣4≤x≤2上最高点的纵坐标为y0,当≤y0≤9时,直接写出L的取值范围.43.已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.(1)求抛物线的解析式;(2)若MN与直线y=﹣2x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:①求证:BC平分∠MBN;②求△MBC外心的纵坐标的取值范围.44.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y轴交于点C(0,4).(1)求抛物线的解析式;(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF 的最大值;(3)点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,直接写出点D的坐标;②若△BCD是锐角三角形,直接写出点D的纵坐标n的取值范围.45.如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+分别与y 轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.46.如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.(1)求抛物线的解析式;(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H 作HF⊥x轴于点F,求矩形GEFH的最大面积;(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.47.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.48.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线与x轴交于A、B两点,与y 轴交于C点,其中A(1,0),C(0,3).(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.49.在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM 面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.50.如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.(1)求线段OC的长度;(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.答案解析一.解答题(共50小题)1.如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C 坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.【分析】(1)根据待定系数法即可求得;(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标;(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求=S△ABN﹣S△BMN得MD=(n+2),然后根据S△AMN得出关于n的二次函数,根据函数解析式求得即可.【解答】解:(1)∵二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),∴,解得.∴抛物线表达式:y=﹣x2+x+4;(2)△ABC是直角三角形.令y=0,则﹣x2+x+4=0,解得x1=8,x2=﹣2,∴点B的坐标为(﹣2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形.(3)∵A(0,4),C(8,0),∴AC==4,①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).(4)如图,AB==2,BC=8﹣(﹣2)=10,AC==4,∴AB2+AC2=BC2,∴∠BAC=90°.∴AC⊥AB.∵AC∥MN,∴MN⊥AB.设点N的坐标为(n,0),则BN=n+2,∵MN∥AC,△BMN∽△BAC∴=,∴=,BM==,MN==,AM=AB﹣BM=2﹣=∵S△AMN=AM•MN=××=﹣(n﹣3)2+5,当n=3时,△AMN面积最大是5,∴N点坐标为(3,0).∴当△AMN面积最大时,N点坐标为(3,0).【点评】本题是二次函数的综合题,解(1)的关键是待定系数法求解析式,解(2)的关键是勾股定理和逆定理,解(3)的关键是等腰三角形的性质,解(4)的关键是三角形相似的判定和性质以及函数的最值等.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t的取值范围.【分析】(1)根据点A、B、C三点的坐标作出△ABC,利用“闭距离”的定义即可得;(2)由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段,再分别求得经过(1,﹣1)和(﹣1,﹣1)时k的值即可得;(3)分⊙T在△ABC的左侧、内部和右侧三种情况,利用“闭距离”的定义逐一判断即可得.【解答】解:(1)如图所示,点O到△ABC的距离的最小值为2,。
中考数学二次函数-经典压轴题及详细答案

中考数学二次函数-经典压轴题及详细答案一、二次函数1.已知二次函数223y ax ax =-+的最大值为4,且该抛物线与y 轴的交点为C ,顶点为D .(1)求该二次函数的解析式及点C ,D 的坐标;(2)点(,0)P t 是x 轴上的动点,①求PC PD -的最大值及对应的点P 的坐标;②设(0,2)Q t 是y 轴上的动点,若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点,求t 的取值范围.【答案】(1)2y x 2x 3=-++,C 点坐标为(0,3),顶点D 的坐标为(1,4);(2)①最,P 的坐标为(3,0)-,②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】(1)先利用对称轴公式x=2a 12a--=,计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;(2)根据三角形的三边关系:可知P 、C 、D 三点共线时|PC-PD|取得最大值,求出直线CD 与x 轴的交点坐标,就是此时点P 的坐标;(3)先把函数中的绝对值化去,可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ 过点(0,3),即点Q 与点C 重合时,两图象有一个公共点,当线段PQ 过点(3,0),即点P 与点(3,0)重合时,两函数有两个公共点,写出t 的取值;②线段PQ 与当函数y=a|x|2-2a|x|+c (x≥0)时有一个公共点时,求t 的值;③当线段PQ 过点(-3,0),即点P 与点(-3,0)重合时,线段PQ 与当函数y=a|x|2-2a|x|+c (x <0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t 的取值.【详解】解:(1)∵2a x 12a-=-=, ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4,∴抛物线过点()1,4.得a 2a 34-+=,解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3,顶点D 的坐标为()1,4.(2)①∵PC PD CD -≤,∴当P,C,D 三点在一条直线上时,PC PD -取得最大值.连接DC 并延长交y 轴于点P ,PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入,得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+,将()P t,0,()Q 0,2t 的坐标代入,可得线段PQ 所在直线的方程为y 2x 2t =-+.(1)当线段PQ 过点()3,0-,即点P 与点()3,0-重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时t 3=-. ∴当t 3≤-时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (2)当线段PQ 过点()0,3,即点Q 与点C 重合时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点,此时3t 2=. 当线段PQ 过点()3,0,即点P 与点()3,0重合时,t 3=,此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. (3)将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥,并整理,得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=,解得7t 2=. ∴当7t 2=时,线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述,t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】 本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.2.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式;()2求ABC V 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC V 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-V 当时,有最大值,点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【解析】【分析】(1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC V 的面积计算拆分为APF CPF S S +V V 即可.【详解】()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-,又∵函数图象经过点()6,0A -,∴20(62)4a =-+-解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-; ()2∵点C 是函数2134y x x =+-的图象与y 轴的交点, ∴点C 的坐标是()0,3-,又当0y =时,有21304y x x =+-=, 解得16x =-,22x =,∴点B 的坐标是()2,0, 则11831222ABC S AB OC =⋅=⨯⨯=V ; ()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+,∵直线AC 过点()6,0A -,()0,3C -,∴603k b b -+=⎧⎨-=⎩, 解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅V V V2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S V 有最大值274, 此时点P 的坐标是153,4P ⎛⎫-- ⎪⎝⎭. 【点睛】本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF 最大进行理解.3.如图,已知抛物线2y ax bx c =++经过A (-3,0),B (1,0),C (0,3)三点,其顶点为D ,对称轴是直线l ,l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求△PBC 周长的最小值;(3)如图(2),若E 是线段AD 上的一个动点( E 与A 、D 不重合),过E 点作平行于y 轴的直线交抛物线于点F ,交x 轴于点G ,设点E 的横坐标为m ,△ADF 的面积为S . ①求S 与m 的函数关系式;②S 是否存在最大值?若存在,求出最大值及此时点E 的坐标; 若不存在,请说明理由.【答案】(1)2y x 2x 3=--+.(2)3210.(3)①2S m 4m 3=---.②当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2).【解析】【分析】(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可.(2)根据BC 是定值,得到当PB+PC 最小时,△PBC 的周长最小,根据点的坐标求得相应线段的长即可.(3)设点E 的横坐标为m ,表示出E (m ,2m+6),F (m ,2m 2m 3--+),最后表示出EF 的长,从而表示出S 于m 的函数关系,然后求二次函数的最值即可.【详解】解:(1)∵抛物线2y ax bx c =++经过A (-3,0),B (1,0),∴可设抛物线交点式为()()y a x 3x 1=+-.又∵抛物线2y ax bx c =++经过C (0,3),∴a 1=-.∴抛物线的解析式为:()()y x 3x 1=-+-,即2y x 2x 3=--+.(2)∵△PBC 的周长为:PB+PC+BC ,且BC 是定值.∴当PB+PC 最小时,△PBC 的周长最小.∵点A 、点B 关于对称轴I 对称,∴连接AC 交l 于点P ,即点P 为所求的点.∵AP=BP ,∴△PBC 的周长最小是:PB+PC+BC=AC+BC.∵A (-3,0),B (1,0),C (0,3),∴2,10.∴△PBC 的周长最小是:3210.(3)①∵抛物线2y x 2x 3=--+顶点D 的坐标为(﹣1,4),A (﹣3,0),∴直线AD 的解析式为y=2x+6∵点E 的横坐标为m ,∴E (m ,2m+6),F (m ,2m 2m 3--+)∴()22EF m 2m 32m 6m 4m 3=--+-+=---. ∴()22DEF AEF 1111S S S EF GH EF AG EF AH m 4m 32m 4m 32222∆∆=+=⋅⋅+⋅⋅=⋅⋅=⋅---⋅=---.∴S 与m 的函数关系式为2S m 4m 3=---.②()22S m 4m 3m 21=---=-++,∴当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2).4.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x 元.求:(1)房间每天的入住量y (间)关于x (元)的函数关系式;(2)该宾馆每天的房间收费p (元)关于x (元)的函数关系式;(3)该宾馆客房部每天的利润w (元)关于x (元)的函数关系式;当每个房间的定价为每天多少元时,w 有最大值?最大值是多少?【答案】(1)y=60-10x ;(2)z=-110x 2+40x+12000;(3)w=-110x 2+42x+10800,当每个房间的定价为每天410元时,w 有最大值,且最大值是15210元.【解析】 试题分析:(1)根据题意可得房间每天的入住量=60个房间﹣每个房间每天的定价增加的钱数÷10;(2)已知每天定价增加为x 元,则每天要(200+x )元.则宾馆每天的房间收费=每天的实际定价×房间每天的入住量;(3)支出费用为20×(60﹣10x ),则利润w =(200+x )(60﹣10x )﹣20×(60﹣10x ),利用配方法化简可求最大值.试题解析:解:(1)由题意得: y =60﹣10x (2)p =(200+x )(60﹣10x )=﹣2110x +40x +12000 (3)w =(200+x )(60﹣10x )﹣20×(60﹣10x ) =﹣2110x +42x +10800 =﹣110(x ﹣210)2+15210 当x =210时,w 有最大值.此时,x +200=410,就是说,当每个房间的定价为每天410元时,w 有最大值,且最大值是15210元.点睛:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题主要考查的是二次函数的应用,难度一般.5.如图①,在平面直角坐标系xOy 中,抛物线y=ax 2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y 轴交于点C.(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x 轴,并沿x 轴左右平移,直尺的左右两边所在的直线与抛物线相交于P 、 Q 两点(点P 在点Q 的左侧),连接PQ ,在线段PQ 上方抛物线上有一动点D ,连接DP 、DQ.①若点P 的横坐标为12-,求△DPQ 面积的最大值,并求此时点D 的坐标; ②直尺在平移过程中,△DPQ 面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.【答案】(1)抛物线y=-x 2+2x+3;(2)①点D ( 31524,);②△PQD 面积的最大值为8【解析】分析:(1)根据点A 、B 的坐标,利用待定系数法即可求出抛物线的表达式;(2)(I )由点P 的横坐标可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,过点D 作DE ∥y 轴交直线PQ 于点E ,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-x+54),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+6x+72,再利用二次函数的性质即可解决最值问题; (II )假设存在,设点P 的横坐标为t ,则点Q 的横坐标为4+t ,进而可得出点P 、Q 的坐标,利用待定系数法可求出直线PQ 的表达式,设点D 的坐标为(x ,-x 2+2x+3),则点E 的坐标为(x ,-2(t+1)x+t 2+4t+3),进而即可得出DE 的长度,利用三角形的面积公式可得出S △DPQ =-2x 2+4(t+2)x-2t 2-8t ,再利用二次函数的性质即可解决最值问题.详解:(1)将A (-1,0)、B (3,0)代入y=ax 2+bx+3,得:309330a b a b -+⎧⎨++⎩==,解得:12a b -⎧⎨⎩==, ∴抛物线的表达式为y=-x 2+2x+3.(2)(I )当点P 的横坐标为-12时,点Q 的横坐标为72, ∴此时点P 的坐标为(-12,74),点Q 的坐标为(72,-94). 设直线PQ 的表达式为y=mx+n ,将P(-12,74)、Q(72,-94)代入y=mx+n,得:17247924m nm n⎧-+⎪⎪⎨⎪+-⎪⎩==,解得:154mn-⎧⎪⎨⎪⎩==,∴直线PQ的表达式为y=-x+54.如图②,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+54),∴DE=-x2+2x+3-(-x+54)=-x2+3x+74,∴S△DPQ=12DE•(x Q-x P)=-2x2+6x+72=-2(x-32)2+8.∵-2<0,∴当x=32时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(32,154).(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,∴点P的坐标为(t,-t2+2t+3),点Q的坐标为(4+t,-(4+t)2+2(4+t)+3),利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,∴S△DPQ=12DE•(x Q-x P)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.∵-2<0,∴当x=t+2时,△DPQ的面积取最大值,最大值为8.∴假设成立,即直尺在平移过程中,△DPQ面积有最大值,面积的最大值为8.点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、三角形的面积以及二次函数的最值,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数表达式;(2)(I)利用三角形的面积公式找出S△DPQ=-2x 2+6x+72;(II )利用三角形的面积公式找出S △DPQ =-2x 2+4(t+2)x-2t 2-8t .6.在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(含答案)

2024年中考数学高频压轴题训练——二次函数压轴题(角度问题)(1)求抛物线的解析式;(2)抛物线上是否存在点,使P存在,请说明理由.(1)求该抛物线的函数表达式;(2)在直线上是否存在点,使说明理由.(3)为第一象限内抛物线上的一个动点,且在直线,垂足为,以点为圆心,,且不经过点l C P PM l ⊥M M 2PAB PT S =V M e (4.如图,已知顶点为的抛物线与x 轴交于A ,B 两点,且.(1)求点B 的坐标;(2)求二次函数的解析式;(3)作直线,问抛物线上是否存在点M ,使得,若存在,求出点M 的坐标;若不存在,请说明理由.5.如图,抛物线与x 轴交于A 、B 两点,,,与y 轴交于点C ,连接.()0,6C -()20y ax b a =+≠OC OB =()20y ax b a =+≠CB ()20y ax b a =+≠15MCB ∠=︒24y ax bx =+-()2,0A -()8,0B AC BC 、(1)求抛物线的解析式;(2)求证:;(3)点P 在抛物线上,且,求点P的坐标.6.如图,在平面直角坐标系中,已知抛物线与x 轴交于、两点,与y 轴交于点C ,连接.(1)求抛物线的解析式;(2)在对称轴上是否存在一点M ,使,若存在,请求出点M 的坐标;若不存在,请说明理由;(3)若点P 是直线下方的抛物线上的一个动点,作于点D ,当的值最大时,求此时点P 的坐标及的最大值.∠=∠ACO ABC PCB ACO ∠=∠()230y ax bx a =+-≠()3,0A ()1,0B -AC MCA MAC ∠=∠AC PD AC ⊥PD PD(1)试求抛物线的解析式;(2)点P 是直线下方抛物线上一动点,当的面积最大时,求点P 的坐标;(3)若M 是抛物线上一点,且,请直接写出点M 的坐标.BC BCP V MCB ABC ∠=∠(1)求此抛物线的解析式;(2)点E 是AC 延长线上一点,的平分线CD 交⊙于点D ,连接BD ,求点D 的坐标;(3)在(2)的条件下,抛物线上是否存在点P ,使得?如果存在,请求出点P 的坐标;如果不存在,请说明理由.9.综合与实践:如图,抛物线与x 轴交于点和点,与y 轴交于点C ,连接,点D 在抛物线上.(1)求抛物线的解析式;(2)小明探究点D 位置时发现:如图1,点D 在第一象限内的抛物线上,连接,,面积存在最大值,请帮助小明求出面积的最大值;(3)小明进一步探究点D 位置时发现:点D 在抛物线上移动,连接,存在BCE ∠O 'PDB CBD ∠=∠22y ax bx =++()1,0A -()4,0B BC BD CD BCD △BCD △CD(1)求抛物线的解析式.(2)如图1,过点D 作轴,垂足为M ,点P 在直线P 作,,求的最大值,以及此时点(3)将原抛物线沿射线方向平移个单位长度,在平移后的抛物线上存在点得,请写出所有符合条件的点G 的横坐标,并写出其中一个的求解过DM x ⊥PE AD ⊥PF DM ⊥2PE PF +CA 5245CAG ∠=︒(1)填空:___________,___________;(2)点为直线上方抛物线上一动点.①连接、,设直线交线段于点,求的最大值;②过点作于点,连接,是否存在点,使得中的,若存在,求出点的坐标;若不存在,请说明理由.(1)求抛物线的解析式;b =c =D AC BC CD BD AC E DE EBD DF AC ⊥F CD D CDF V 2DCF BAC ∠=∠D(1)求抛物线的解析式;(2)抛物线上是否存在点D ,使得?若存在,求出所有点不存在,请说明理由;(3)如图2,点E 是点B 关于抛物线对称轴的对称点,点F 是直线OB 动点,EF 与直线OB 交于点G .设和的面积分别为值.DOB OBC ∠=∠BFG V BEG V S14.如图,在平面直角坐标系中,点为坐标原点,抛物线与轴交于、两点且点,,与轴的负半轴交于点,.(1)求此抛物线的解析式;(2)在(1)的条件下,连接,点为直线下方的抛物线上的一点,过点作交于点,交直线于点,若,求点的坐标.(3)在(1)的条件下,点为该抛物线的顶点,过点作轴的平行线交抛物线于另一点,过点作于点,该抛物线对称轴右侧的抛物线上有一点,连接交于点,当时,求的度数.15.已知抛物线与轴相交于点,,与轴相交于点.O 2y x bx c =++x A B (3B 0)y C OB OC =AC P BC P PQ AC ∥AB Q BC D PD DQ =P D C x R R RH AB ⊥H M DM RH Q 2MQ RQ =MQH ∠24y ax bx =++x ()1,0A ()4,0B y C参考答案:的值最大时,此时,。
中考数学二次函数压轴题集锦(50道含解析)

中考二次函数专项训练1.如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t 的取值范围.3.如图,在平面直角坐标系中,点A在抛物线y=﹣x2+4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当△PBE的面积最大时,求PH+HF+FO的最小值;(3)在(2)中,PH+HF+FO取得最小值时,将△CFH绕点C顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.4.如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M 的坐标.5.如图,在平面直角坐标系xOy中,以直线x=对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.(1)求抛物线的函数表达式;(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若=,且△BCG与△BCD面积相等,求点G的坐标;(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.6.如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.7.抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.(1)直接写出抛物线L的解析式;(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.8.在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx ﹣2m(m是常数),顶点为P.(Ⅰ)当抛物线经过点A时,求顶点P的坐标;(Ⅱ)若点P在x轴下方,当∠AOP=45°时,求抛物线的解析式;(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.9.如图1,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.(1)当t=2时,线段PQ的中点坐标为;(2)当△CBQ与△PAQ相似时,求t的值;(3)当t=1时,抛物线y=x2+bx+c经过P,Q两点,与y轴交于点M,抛物线的顶点为K,如图2所示,问该抛物线上是否存在点D,使∠MQD=∠MKQ?若存在,求出所有满足条件的D的坐标;若不存在,说明理由.10.如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.(1)当x=2时,求⊙P的半径;(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到的距离等于到的距离的所有点的集合.(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.11.已知顶点为A抛物线经过点,点.(1)求抛物线的解析式;(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN ∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.12.在平面直角坐标系xOy中(如图).已知抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求这条抛物线的表达式;(2)求线段CD的长;(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.13.如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).(1)直接写出这两个二次函数的表达式;(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标14.小贤与小杰在探究某类二次函数问题时,经历了如下过程:求解体验:(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b=,顶点坐标为,该抛物线关于点(0,1)成中心对称的抛物线表达式是.抽象感悟:我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y′,则我们又称抛物线y′为抛物线y的“衍生抛物线”,点M为“衍生中心”.(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y′,若这两条抛物线有交点,求m的取值范围.问题解决:(3)已知抛物线y=ax2+2ax﹣b(a≠0)①若抛物线y的衍生抛物线为y′=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a、b的值及衍生中心的坐标;②若抛物线y关于点(0,k+12)的衍生抛物线为y1,其顶点为A1;关于点(0,k+22)的衍生抛物线为y2,其顶点为A2;…;关于点(0,k+n2)的衍生抛物线为y n,其顶点为A n…(n为正整数).求A n A n+1的长(用含n的式子表示).15.如图,已知抛物线y=ax2+bx(a≠0)过点A(,﹣3)和点B(3,0).过点A作直线AC∥x轴,交y轴于点C.(1)求抛物线的解析式;(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D.连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;(3)抛物线上是否存在点Q,使得S△AOC =S△AOQ?若存在,求出点Q的坐标;若不存在,请说明理由.16.如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C 为顶点,直线y=x+m经过点A,与y轴交于点D.(1)求线段AD的长;(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.17.如图①,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且与y轴交于点C.(1)求抛物线的表达式;(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.(1)若点P的横坐标为﹣,求△DPQ面积的最大值,并求此时点D的坐标;(Ⅱ)直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.18.已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(﹣,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.19.如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=DE.①求点P的坐标;②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.20.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有;②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形“十字形”.(填“是”或“不是”)(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;①=;②=;③“十字形”ABCD的周长为12.21.如图1,抛物线y1=ax2﹣x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.(1)求抛物线y2的解析式;(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.22.如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;②是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.23.如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,),点B (3,﹣),O为坐标原点.(1)求这条抛物线所对应的函数表达式;(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.24.如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.(1)求抛物线C1的表达式;(2)直接用含t的代数式表示线段MN的长;(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.25.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M 到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.26.如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A(﹣4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标,若不存在请说明理由.27.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.(1)求抛物线的函数表达式;(2)求点D的坐标;(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M,N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.28.如图,抛物线y=ax2+bx(a≠0)交x轴正半轴于点A,直线y=2x经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.(1)求a,b的值.(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m,△OBP的面积为S,记K=.求K关于m的函数表达式及K的范围.29.抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC 交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC 的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.30.综合与探究如图,抛物线y=x﹣4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE ∥AC交x轴于点E,交BC于点F.(1)求A,B,C三点的坐标;(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.31.如图,二次函数y=﹣+bx+2的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是;(2)设直线PB与直线AC相交于点M,是否存在这样的点P,使得PM:MB=1:2?若存在,求出点P的横坐标;若不存在,请说明理由;(3)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由.32.如图,在平面直角坐标系中,二次函数y=(x﹣a)(x﹣3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C 作直线CP⊥x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.33.如图,已知二次函数y=ax2﹣(2a﹣)x+3的图象经过点A(4,0),与y 轴交于点B.在x轴上有一动点C(m,0)(0<m<4),过点C作x轴的垂线交直线AB于点E,交该二次函数图象于点D.(1)求a的值和直线AB的解析式;(2)过点D作DF⊥AB于点F,设△ACE,△DEF的面积分别为S1,S2,若S1=4S2,求m的值;(3)点H是该二次函数图象上位于第一象限的动点,点G是线段AB上的动点,当四边形DEGH是平行四边形,且▱DEGH周长取最大值时,求点G的坐标.34.已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.35.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣5交y轴于点A,交x轴于点B(﹣5,0)和点C(1,0),过点A作AD∥x轴交抛物线于点D.(1)求此抛物线的表达式;(2)点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,求△EAD 的面积;(3)若点P是直线AB下方的抛物线上一动点,当点P运动到某一位置时,△ABP的面积最大,求出此时点P的坐标和△ABP的最大面积.36.已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(﹣,0).(1)求抛物线F的解析式;(2)如图1,直线l:y=x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);(3)在(2)中,若m=,设点A′是点A关于原点O的对称点,如图2.①判断△AA′B的形状,并说明理由;②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.37.直线y=﹣x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣x2+2mx ﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.(1)直接写出抛物线的解析式和点A,C,D的坐标;(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q 在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.①当∠DPE=∠CAD时,求t的值;②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.38.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.(1)求m、n的值及该抛物线的解析式;(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.39.如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为(用含m的代数式表示);(2)求△ABC的面积(用含a的代数式表示);(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.40.如图1,在平面直角坐标系xOy中,已知点A和点B的坐标分别为A(﹣2,0),B(0,﹣6),将Rt△AOB绕点O按顺时针方向分别旋转90°,180°得到Rt△A1OC,Rt△EOF.抛物线C1经过点C,A,B;抛物线C2经过点C,E,F.(1)点C的坐标为,点E的坐标为;抛物线C1的解析式为.抛物线C2的解析式为;(2)如果点P(x,y)是直线BC上方抛物线C1上的一个动点.①若∠PCA=∠ABO时,求P点的坐标;②如图2,过点P作x轴的垂线交直线BC于点M,交抛物线C2于点N,记h=PM+NM+BM,求h与x的函数关系式,当﹣5≤x≤﹣2时,求h的取值范围.41.如图,抛物线y=ax2+bx+c与两坐标轴相交于点A(﹣1,0)、B(3,0)、C (0,3),D是抛物线的顶点,E是线段AB的中点.(1)求抛物线的解析式,并写出D点的坐标;(2)F(x,y)是抛物线上的动点:①当x>1,y>0时,求△BDF的面积的最大值;②当∠AEF=∠DBE时,求点F的坐标.42.如图,在平面直角坐标系中,矩形ABCD的对称中心为坐标原点O,AD⊥y 轴于点E(点A在点D的左侧),经过E、D两点的函数y=﹣x2+mx+1(x≥0)的图象记为G1,函数y=﹣x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.(1)当点A的横坐标为﹣1时,求m的值;(2)求L与m之间的函数关系式;(3)当G2与矩形ABCD恰好有两个公共点时,求L的值;(4)设G在﹣4≤x≤2上最高点的纵坐标为y0,当≤y0≤9时,直接写出L的取值范围.43.已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.(1)求抛物线的解析式;(2)若MN与直线y=﹣2x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:①求证:BC平分∠MBN;②求△MBC外心的纵坐标的取值范围.44.如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(4,0),与y 轴交于点C(0,4).(1)求抛物线的解析式;(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值;(3)点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,直接写出点D的坐标;②若△BCD是锐角三角形,直接写出点D的纵坐标n的取值范围.45.如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+分别与y轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.46.如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.(1)求抛物线的解析式;(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.47.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.48.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线与x轴交于A、B两点,与y轴交于C点,其中A(1,0),C(0,3).(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.49.在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C(0,2)和点D (4,﹣2).点E是直线y=﹣x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.50.如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.(1)求线段OC的长度;(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC 面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.一.解答题(共50小题)1.如图1,已知二次函数y=ax 2+x +c (a ≠0)的图象与y 轴交于点A (0,4),与x 轴交于点B 、C ,点C 坐标为(8,0),连接AB 、AC .(1)请直接写出二次函数y=ax 2+x +c 的表达式;(2)判断△ABC 的形状,并说明理由;(3)若点N 在x 轴上运动,当以点A 、N 、C 为顶点的三角形是等腰三角形时,请写出此时点N 的坐标;(4)如图2,若点N 在线段BC 上运动(不与点B 、C 重合),过点N 作NM ∥AC ,交AB 于点M ,当△AMN 面积最大时,求此时点N 的坐标.【分析】(1)根据待定系数法即可求得;(2)根据抛物线的解析式求得B 的坐标,然后根据勾股定理分别求得AB 2=20,AC 2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC 是直角三角形. (3)分别以A 、C 两点为圆心,AC 长为半径画弧,与x 轴交于三个点,由AC 的垂直平分线与x 轴交于一个点,即可求得点N 的坐标;(4)设点N 的坐标为(n ,0),则BN=n +2,过M 点作MD ⊥x 轴于点D ,根据三角形相似对应边成比例求得MD=(n +2),然后根据S △AMN =S △ABN ﹣S △BMN 得出关于n 的二次函数,根据函数解析式求得即可.【解答】解:(1)∵二次函数y=ax 2+x +c 的图象与y 轴交于点A (0,4),与x 轴交于点B 、C ,点C 坐标为(8,0), ∴,解得.∴抛物线表达式:y=﹣x2+x+4;(2)△ABC是直角三角形.令y=0,则﹣x2+x+4=0,解得x1=8,x2=﹣2,∴点B的坐标为(﹣2,0),由已知可得,在Rt△ABO中AB2=BO2+AO2=22+42=20,在Rt△AOC中AC2=AO2+CO2=42+82=80,又∵BC=OB+OC=2+8=10,∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形.(3)∵A(0,4),C(8,0),∴AC==4,①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4,0)或(8+4,0)③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).(4)如图,AB==2,BC=8﹣(﹣2)=10,AC==4,∴AB2+AC2=BC2,∴∠BAC=90°.∴AC⊥AB.∵AC∥MN,∴MN⊥AB.设点N的坐标为(n,0),则BN=n+2,∵MN∥AC,△BMN∽△BAC∴=,∴=,BM==,MN==,AM=AB﹣BM=2﹣==AM•MN∵S△AMN=××=﹣(n﹣3)2+5,当n=3时,△AMN面积最大是5,∴N点坐标为(3,0).∴当△AMN面积最大时,N点坐标为(3,0).【点评】本题是二次函数的综合题,解(1)的关键是待定系数法求解析式,解(2)的关键是勾股定理和逆定理,解(3)的关键是等腰三角形的性质,解(4)的关键是三角形相似的判定和性质以及函数的最值等.2.对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离“,记作d(M,N).已知点A(﹣2,6),B(﹣2,﹣2),C(6,﹣2).(1)求d(点O,△ABC);(2)记函数y=kx(﹣1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t 的取值范围.【分析】(1)根据点A、B、C三点的坐标作出△ABC,利用“闭距离”的定义即可得;(2)由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段,再分别求得经过(1,﹣1)和(﹣1,﹣1)时k的值即可得;(3)分⊙T在△ABC的左侧、内部和右侧三种情况,利用“闭距离”的定义逐一判断即可得.【解答】解:(1)如图所示,点O到△ABC的距离的最小值为2,∴d(点O,△ABC)=2;(2)y=kx(k≠0)经过原点,在﹣1≤x≤1范围内,函数图象为线段,当y=kx(﹣1≤x≤1,k≠0)经过(1,﹣1)时,k=﹣1,此时d(G,△ABC)=1;当y=kx(﹣1≤x≤1,k≠0)经过(﹣1,﹣1)时,k=1,此时d(G,△ABC)=1;∴﹣1≤k≤1,∵k≠0,∴﹣1≤k≤1且k≠0;。
中考数学最新二次函数压轴训练

二次函数压轴题(一)1.如图,函数y=﹣x2+x+c(﹣2020≤x≤1)的图象记为L1,最大值为M1;函数y=﹣x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.(1)当c=1时,求M1,M2的值;(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;(3)若M1,M2的差为,直接写出c的值.2.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).(1)若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1,求实数m的最小值.3.如图,抛物线y=﹣x2+2x+3存在正实数m,n(m<n),当m≤x≤n时,恰好满足,求m,n的值.4.已知二次函数y=x2+3x﹣4是否在对称轴的同侧存在实数m、n(m<n),当m≤x≤n时,y的取值范围为≤y≤?若存在,求出m,n的值;若不存在,说明理由.5.已知抛物线y=﹣x2+(﹣2m﹣1)x﹣2m(﹣2<m<2),直线l:y=px+q(0<p<q).(1)若该抛物线与y轴交点的纵坐标为3,求该抛物线的顶点坐标;(2)若该抛物线经过点(t,4),且对任意实数x,不等式﹣x2+(﹣2m﹣1)x﹣2m≤4都成立;当p≤x≤q时,恰好有,求直线l的解析式.6.已知抛物线y=﹣2x2+(b﹣2)x+(c﹣2020)(b,c为常数).(1)若抛物线的顶点坐标为(1,1),求b,c的值;(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;(3)在(1)的条件下,存在正实数m,n(m<n),当m≤x≤n时,恰好≤≤,求m,n的值.二次函数压轴题(二)1.抛已知抛物线y=ax2+bx+c(a≠0)(1)若该抛物线与x轴交于两点,其中一个点的坐标为(2,0),对称轴为直线x=﹣1,求该抛物线与x轴的另一个交点的坐标;(2)在(1)的条件下,M(m,n)为抛物线上的一点,若M关于原点的对称点M1也在该抛物线上,求m的值;(3)当a=1时,若抛物线上的点P(p,q)满足﹣1≤p≤1时,1≤q≤5+b,求b,c的值.2.已知抛物线y=(2m﹣1)x2+(m+1)x+3(m为常数).(1)若该抛物线经过点(1,m+7),求m的值;(2)若抛物线上始终存在不重合的两点关于原点对称,求满足条件的最大整数m;3.物线y=tx2﹣16tx+48t(t为常数,t<0)与x轴交于A,B两点(点A在点B左侧),与y 轴交于点C.(1)点A的坐标是,点B的坐标是;(2)若该抛物线经过点(h,),且对于任意实数x,不等式tx2﹣16tx+48t≤恒成立,求t的值4.已知m=,抛物线y=(x﹣4)(x﹣12),上任意一点P(x0,y0)总有n+≥﹣4my02﹣12y0﹣50成立,求实数n的最小值.5.已知二次函数y=ax2+bx+c(a≠0).(1)若b=1,a=﹣c,求证:二次函数的图象与x轴一定有两个不同的交点;(2)若a<0,c=0,且对于任意的实数x,都有y≤1,求4a+b2的取值范围;(3)若函数图象上两点(0,y1)和(1,y2)满足y1•y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.6.规定:我们把一个函数关于某条直线或者某点作对称后形成的新函数,称之为原函数的“对称函数”.(1)已知一次函数y=﹣2x+3的图象,求关于直线y=﹣x的对称函数的解析式;(2)已知二次函数y=ax2+4ax+4a﹣1的图象为C1;①求C1关于点R(1,0)的对称函数图象C2的函数解析式;②若两抛物线与y轴分别交于A、B两点,当AB=16时,求a的值;(3)若直线y=﹣2x﹣3关于原点的对称函数的图象上的存在点P,不论m取何值,抛物线y=mx2+(m﹣)x﹣(2m﹣)都不通过点P,求符合条件的点P的坐标.7.已知:关于x的方程mx2﹣3(m﹣1)x+2m﹣3=0.(1)求证:m取任何实数,方程总有实数根;(2)若二次函数y1=mx2﹣3(m﹣1)x+2m﹣3的图象关于y轴对称;①求二次函数y1的解析式;②已知一次函数y2=2x﹣2,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≥y2均成立;(3)在(2)条件下,若二次函数y3=ax2+bx+c的图象经过点(﹣5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≥y3≥y2均成立,求二次函数y3=ax2+bx+c的解析式.。
二次函数难题压轴题中考精选

二次函数难题压轴题中考精选(含答案)第一部分:试题1.如图,二次函数c x y +-=221的图象经过点D ⎪⎭⎫ ⎝⎛-29,3,与x 轴交于A 、B 两点.⑴求c 的值;⑵如图①,设点C 为该二次函数的图象在x 轴上方的一点,直线AC 将四边形ABCD 的面积二等分,试证明线段BD 被直线AC 平分,并求此时直线AC 的函数解析式; ⑶设点P 、Q 为该二次函数的图象在x 轴上方的两个动点,试猜想:是否存在这样的点P 、Q ,使△AQP ≌△ABP ?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)2.(2010福建福州)如图,在△ABC 中,∠C =45°,BC =10,高AD =8,矩形EFPQ 的一边QP 在BC 边上,E 、F 两点分别在AB 、AC 上,AD 交EF 于点H . (1)求证:AH AD =EFBC;(2)设EF =x ,当x 为何值时,矩形EFPQ 的面积最大?并求其最大值;(3)当矩形EFPQ 的面积最大时,该矩形EFPQ 以每秒1个单位的速度沿射线QC 匀速运动(当点Q 与点C 重合时停止运动),设运动时间为t 秒,矩形EFFQ 与△ABC 重叠部分的面积为S ,求S 与t 的函数关系式.3.(2010福建福州)如图1,在平面直角坐标系中,点B 在直线y =2x 上,过点B 作x 轴的垂线,垂足为A ,OA =5.若抛物线y =16x 2+bx +c 过O 、A 两点.(1)求该抛物线的解析式;(2)若A 点关于直线y =2x 的对称点为C ,判断点C 是否在该抛物线上,并说明理由; (3)如图2,在(2)的条件下,⊙O 1是以BC 为直径的圆.过原点O 作⊙O 1的切线OP ,P 为切点(点P 与点C 不重合).抛物线上是否存在点Q ,使得以PQ 为直径的圆与⊙O 1相切?若存在,求出点Q 的横坐标;若不存在,请说明理由4.(2010江苏无锡)如图,矩形ABCD 的顶点A 、B 的坐标分别为(-4,0)和(2,0),BC =23.设直线AC 与直线x =4交于点E .(1)求以直线x =4为对称轴,且过C 与原点O 的抛物线的函数关系式,并说明此抛物线一定过点E ;(2)设(1)中的抛物线与x 轴的另一个交点为N ,M 是该抛物线上位于C 、N 之间的一动点,求△CMN 面积的最大值.x=4xyEDCBA O(第2题)(图1) (图2)5.(2010湖南邵阳)如图,抛物线y =2134x x -++与x 轴交于点A 、B ,与y 轴相交于点C ,顶点为点D ,对称轴l 与直线BC 相交于点E ,与x 轴交于点F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年中考数学冲刺复习资料:二次函数压轴题
面积类
1.如图,已知抛物线经过点 A (- 1 , 0)、B (3, 0)、C (0, 3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B , C重合),过M作MN // y轴交抛物线于 N,若点M 的横坐标为m,请用m的代数式表示 MN的长.
(3 )在(2)的条件下,连接 NB、NC,是否存在口,使厶BNC的面积最大?若存在,求
2 .如图,抛物线产曲'-亨疋- 2 (且芒0)的图象与x轴交于A、B两点,与y轴交于C 点,已知B点坐标为(4, 0).
(1) 求抛物线的解析式;
(2) 试探究△ ABC的外接圆的圆心位置,并求出圆心坐标;
(3) 若点M是线段BC下方的抛物线上一点,求△ MBC的面积的最大值,并求出此时 M
平行四边形类
3. 如图,在平面直角坐标系中,抛物线y=x2+mx+ n经过点
A (3, 0)、
B (0,- 3),点P
是直线AB上的动点,过点 P作x轴的垂线交抛物线于点 M,设点P的横坐标为t.
(1)分别求出直线 AB和这条抛物线的解析式.
(2)若点P在第四象限,连接 AM、BM,当线段PM最长时,求△ ABM的面积.
(3)是否存在这样的点 P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
4. 如图,在平面直角坐标系中放置一直角三角板,其顶点为 A (0, 1), B ( 2, 0), O ( 0,
0),将此三角板绕原点 0逆时针旋转90°得到△ A B O.
(1 )一抛物线经过点 A'、B'、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是
否存在点P,使四边形PBA B的面积是△ A B O面积4倍?若存在,请求出 P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形 PB A B是哪种形状的四边形?并写出四边形PB A B 的两条性质.。
