高考立体几何知识点详细总结
高中立体几何知识点总结

一、空间点、线、面的位置关系1.1 点与点•点的定义:空间中的任意一点。
•点的坐标表示:a⃗=(a x,a y,a z)。
1.2 直线与直线•直线的定义:无限延伸的平面内的所有点。
•直线的方程表示:r⃗=(x,y,z),其中Ax+By+Cz+D=0。
1.3 直线与平面•直线的平面方程表示:r⃗=(x,y,z),其中Ax+By+Cz+D=0。
•直线与平面的交点表示:设直线上的点为P(x0,y0,z0),则有Ax0+ By0+Cz0+D=0。
1.4 平面与平面•平面的定义:无限延伸的平面内的所有点。
•平面的方程表示:r⃗=(x,y,z),其中Ax+By+Cz+D=0。
1.5 平面与空间体•平面与空间体的交线表示:设空间体上的点为P(x0,y0,z0),则有Ax0+By0+Cz0+D=0。
二、空间几何体2.1 柱体•柱体的定义:底面为圆形或矩形,顶面与底面平行的空间几何体。
•柱体的体积公式:V=底面积×高。
2.2 锥体•锥体的定义:底面为圆形或三角形,顶点在底面内的空间几何体。
•锥体的体积公式:V=1底面积×高。
32.3 球体•球体的定义:所有点与球心等距的空间几何体。
•球体的体积公式:V=4πR3。
32.4 空间四边形•空间四边形的定义:四个顶点在空间中的四边形。
•空间四边形的面积公式:S=12|a⃗×b⃗⃗|,其中a⃗和b⃗⃗为四边形的两条对角线。
三、空间角的计算3.1 线线角•线线角的定义:两条直线之间的夹角。
•线线角的计算公式:θ=arccos(|a⃗⃗⋅b⃗⃗||a⃗⃗||b⃗⃗|),其中a⃗和b⃗⃗为两条直线的方向向量。
3.2 线面角•线面角的定义:直线与平面之间的夹角。
•线面角的计算公式:θ=arccos(|n⃗⃗⋅a⃗⃗||n⃗⃗||a⃗⃗|),其中n⃗⃗为平面的法向量,a⃗为直线的方向向量。
3.3 面面角•面面角的定义:两个平面之间的夹角。
•面面角的计算公式:θ=arccos(|n⃗⃗1⋅n⃗⃗2||n⃗⃗1||n⃗⃗2|),其中n⃗⃗1和n⃗⃗2为两个平面的法向量。
高中数学立体几何知识点总结(详细)

高中数学立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形1.3 棱柱的面积和体积公式ch S =直棱柱侧(c 是底周长,h 是高)S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形; 正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高) 正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
高考立体几何知识点总结(详细)

高考立体几何知识点总结(一)空间几何体的表面积与体积空间几何体的表面积棱柱、棱锥的表面积:各个面面积之和圆柱的表面积 :222S rl r ππ=+圆锥的表面积:2Srl r ππ=+ 圆台的表面积:22S rl r Rl R ππππ=+++球的表面积:24S R π= 扇形的面积公式2211=36022n R S lr r πα==扇形(其中l 表示弧长,r 表示半径,α表示弧度) 空间几何体的体积柱体的体积 :V S h =⨯底锥体的体积 :13V S h =⨯底 台体的体积 : 1)3V S S S S h =++⨯下下上上(球体的体积:343V R π= (四)空间几何体的三视图和直观图正视图:光线从几何体的前面向后面正投影,得到的投影图。
侧视图:光线从几何体的左边向右边正投影,得到的投影图。
俯视图:光线从几何体的上面向右边正投影,得到的投影图。
3、线面平行:(1)判定定理:(2)性质定理:4、线面垂直(1)如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面。
判定定理:性质定理:(2)垂直于同一平面的两直线平行。
★1.5 三垂线定理及其逆定理5、面面平行(1)判定定理:一个平面内的两条相交直线分别平行于另一个平面,这两个平面平行。
(2)性质定理:两个平行平面被第三个面所截,两条交线互相平行 6、面面垂直: (1)一个平面经过另一个平面的垂线,这两个平面互相垂直。
判定定理:性质定理:(2)7、空间角(1)异面直线所成的角: o o 900≤<α;(2)线面所成的角:是斜线与它在平面内的射影所成的角。
范围090o o α≤≤(3)二面角:关键是找出二面角的平面角。
方法有:①定义法;②三垂线定理法;③垂面法;二面角的平面角的范围:0180o o α≤<;向量法一、运用法向量求空间角向量法求空间两条异面直线a, b 所成角θ,只要在两条异面直线a, b 上各任取一个向量图2-7 斜线定理''AA BB 和,则角<','AA BB >=θ或π-θ,因为θ是锐角,所以cos θ=''''AA BB AA BB ⋅⋅, 不需要用法向量。
高中数学—立体几何知识点总结(精华版)

立体几何知识点一.基本概念和原理:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)(规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°])斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直。
a和一个平面内的任意一条直线都垂直,就说直线a和平面互相垂直.直线a叫平面的垂线,平面叫做直线a的垂面。
直,那么这条直线垂直于这个平面。
如果两条直线同垂直于一个平面,那么这两条直线平行。
如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
面,那么这两个平面平行。
如果两个平行平面同时和第三个平面相交,则交线平行。
8.(1)二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
高中数学立体几何知识点归纳总结

③正棱锥中六个元素,即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边
长一半,构成四个直角三角形;如上图: SOB, SOH, SBH, OBH 为直角三角形
3.3 侧面展开图:正 n 棱锥的侧面展开图是有 n 个全等的等腰三角形组成的;
3.4
面积、体积公式:S
正棱锥侧=
1 2
ch
,S
正棱锥全=
推论 2:两条相交直线确定一个平面. 图形语言:
推论 3:两条平行直线确定一个平面. 图形语言:
用途:用于确定平面;
公理 3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线两个
平面的交线.
用途:常用于证明线在面内,证明点在线上.
图形语言:
符号语言:
形语言,文字语言,符号语言的转化:
2.3 侧面展开图:圆柱的侧面展开图是以底面周长和 母线长为邻边的矩形.
A
O
B
2.4 面积、体积公式:
C'
轴
轴截面
C
侧面
底面
S = 圆柱侧 2 rh ;S = 圆柱全 2 rh 2 r2 ,V 圆柱=S 底 h= r2h 其中 r 为底面半径,h 为圆柱高
3.棱锥
3.1 棱锥——有一个面是多边形,其余各 面是有一个公共顶点的三角形,由这些
母线 l
轴
h
侧面
轴截面
A
r O
B 底面
S
我们把截面与底面之间的部分称为棱台.
5.2 正棱台的性质: ①各侧棱相等,各侧面都是全等的等腰梯形; ②正棱台的两个底面以及平行于底面的截面是 正多边形; ③ 如右图:四边形 O`MNO,O`B`BO 都是直角梯 形
高中立体几何基础知识点全集(图文并茂)

立体几何知识点整理姓名:一.直线和平面的三种位置关系:1. 线面平行l符号表示:2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量和向量共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,ln⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,mlα方法二:用面面垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m ,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量和向量的数量积为0,则m l ⊥。
三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒ (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理) 余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
高中数学—立体几何知识点总结(精华版)

立体几何知识点一.根本概念和原理:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)〔规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°]〕斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直。
a和一个平面内的任意一条直线都垂直,就说直线a和平面互相垂直.直线a叫平面的垂线,平面叫做直线a的垂面。
直,那么这条直线垂直于这个平面。
如果两条直线同垂直于一个平面,那么这两条直线平行。
如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
面,那么这两个平面平行。
行。
8.〔1〕二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
二面角的取值范围为[0°,180°]〔2〕二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
高中数学立体几何知识点归纳总结

高中数学立体几何学问点归纳总结一、立体几何学问点归纳第一章空间几何体(一)空间几何体的构造特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的构造特征1.棱柱1.1棱柱——有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形;③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA=++②(理解)长方体的一条对角线1AC与过顶点A的三条棱所成的角分别是αβγ,,,那么222cos cos cos1αβγ++=,222sin sin sin2αβγ++=;③(理解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面绽开图:正n 棱柱的侧面绽开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面绽开图:圆柱的侧面绽开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
高中数学立体几何知识点总结(全)

高中数学立体几何知识点总结(全)垂直直线:两条直线的夹角为90度。
XXX.三.点与平面的位置关系点在平面上:点在平面内部;点在平面外:点在平面的一侧;点在平面上方或下方:需要指定一个方向向量,点在平面的哪一侧就取决于该方向向量与平面法向量的夹角。
四.直线与平面的位置关系直线在平面上:直线的每一点都在平面上;直线在平面内部:直线与平面没有交点;直线与平面相交:直线与平面有且只有一个交点;直线平行于平面:直线与平面没有交点,且方向向量与平面法向量垂直。
改写后:一、空间几何体的三视图空间几何体的三视图包括正视图、侧视图和俯视图。
其中,正视图是指从几何体的前面向后面正投影得到的投影图,反映了物体的高度和长度;侧视图是指从几何体的左面向右面正投影得到的投影图,反映了物体的高度和宽度;俯视图是指从几何体的上面向下面正投影得到的投影图,反映了物体的长度和宽度。
在三视图中,长对正,高平齐,宽相等是反映长、宽、高特点的简洁表述。
二、空间几何体的直观图斜二测画法是一种用于绘制空间几何体直观图的方法。
基本步骤包括建立适当的直角坐标系xOy,建立斜坐标系x'O'y',并画出对应图形。
在直观图中,已知图形平行于X轴的线段画成平行于X'轴,长度不变;已知图形平行于Y轴的线段画成平行于Y'轴,长度变为原来的一半。
直观图与原图形的面积关系是直观图面积为原图形面积的四分之一。
三、空间几何体的表面积与体积圆柱、圆锥、圆台的侧面积分别为2πrl、πrl和πr(l+R),其中r表示底面半径,l表示母线长度,R表示上底面半径。
圆柱、圆锥、圆台的体积分别为Sh、S/3h和S(h/3),其中S为底面积,h为高度。
球的表面积和体积分别为4πR²和(4/3)πR³。
四、点、直线、平面之间的位置关系平面的基本性质包括三条公理,分别是公理1、公理2和公理3.直线与直线的位置关系有相交、平行和垂直;点与平面的位置关系有在平面上、在平面内部、在平面外部、在平面上方或下方;直线与平面的位置关系有在平面上、在平面内部、相交和平行。
高中数学立体几何知识点归纳总结

高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形; ③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222cos cos cos 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
高考立体几何知识点总结

高考立体几何知识点总结一、基本概念1.点、线、面、立体的定义与性质。
2.点线面的共面与异面判定方法。
3.直线与平面的位置关系。
二、棱柱1.棱柱的定义与性质。
2.平行截面与全等截面。
3.正棱柱的性质:底面形状与面数关系、对角线的长度关系。
4.斜棱柱的性质:母线、准线、侧面积、表面积、体积的计算公式。
三、棱锥1.棱锥的定义与性质。
2.正棱锥的性质:底面形状与面数关系、高线的长度、母线、准线、侧面积、表面积、体积的计算公式。
3.斜棱锥的性质:底面形状与面数关系、高线的长度、母线、准线、侧面积、表面积、体积的计算公式。
四、平面与立体的位置关系1.点到平面的距离。
2.点到直线的距离。
3.线沿直线的平行线、垂线、倾斜线的条件与性质。
4.点到立体的距离。
五、体积与表面积计算1.平面图形的面积计算。
2.立体图形的表面积计算。
3.立体图形的体积计算。
六、球与球内切关系1.球的定义与性质。
2.球内接关系与判定方法。
3.共切、内切球的性质及条件。
七、圆锥与圆台1.圆锥的定义与性质。
2.圆台的定义与性质。
3.正圆锥、正圆台的性质:母线、准线、侧面积、表面积、体积的计算公式。
4.斜圆锥、斜圆台的性质:母线、准线、侧面积、表面积、体积的计算公式。
八、立体几何的应用1.立体几何在建筑设计中的应用。
2.立体几何在工程测量中的应用。
3.立体几何在物体的表面积和体积计算中的应用。
以上是高考立体几何的知识点总结。
掌握这些知识点可以帮助学生在高考中更好地应对立体几何问题,提高解题的能力与准确性。
希望同学们能够认真复习并进行大量的练习,熟练掌握这些知识点,取得优异的成绩!。
高考立体几何知识点总结(详细)
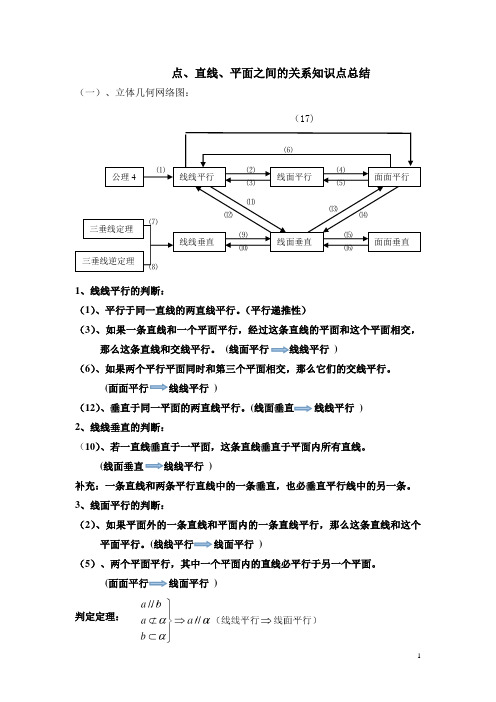
点、直线、平面之间的关系知识点总结(一)、立体几何网络图:(17)1、线线平行的判断:(1)、平行于同一直线的两直线平行。
(平行递推性)(3)、如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(线面平行)(6)、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
( )(12)、垂直于同一平面的两直线平行。
(线面垂直 线线平行 ) 2、线线垂直的判断:(10)、若一直线垂直于一平面,这条直线垂直于平面内所有直线。
(线面垂直 )补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。
3、线面平行的判断:(2)、如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
(线面平行 )(5)、两个平面平行,其中一个平面内的直线必平行于另一个平面。
( 线面平行 )判定定理:性质定理:4、线面垂直的判断:⑼如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⒃如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面。
判定定理:性质定理:(1)若直线垂直于平面,则它垂直于平面内任意一条直线。
即:(2)垂直于同一平面的两直线平行。
即:★判断或证明线面垂直的方法⑴利用定义,用反证法证明。
⑵利用判定定理证明。
⑶一条直线垂直于平面而平行于另一条直线,则另一条直线也垂直与平面。
⑷一条直线垂直于两平行平面中的一个,则也垂直于另一个。
⑸如果两平面垂直,在一平面内有一直线垂直于两平面交线,则该直线垂直于另一平面。
5、面面平行的判断:⑷一个平面内的两条相交直线分别平行于另一个平面,这两个平面平行。
⒀垂直于同一条直线的两个平面平行。
6、面面垂直的判断:⒂一个平面经过另一个平面的垂线,这两个平面互相垂直。
2024年高考数学立体几何知识点总结

2024年高考数学立体几何知识点总结立体几何是数学中的一个重要分支,也是高考数学中的重要内容之一。
在高考中,立体几何的知识点主要包括空间几何、立体图形的面积与体积等方面。
下面是对2024年高考数学立体几何知识点的总结,供考生参考。
一、空间几何1. 空间几何中的点、线、面的概念和性质。
点是没有长度、宽度和高度的,只有位置的大小,用字母表示。
线是由一组无限多个点构成的集合,用两个点的字母表示。
面是由无限多条线构成的,这些线共面且没有相交或平行关系。
2. 空间几何中的垂直、平行等概念和性质。
两条线在同一平面内,如果相交角为90°,则称两线垂直。
两条线没有相交关系,称两线平行。
3. 点到直线的距离的计算。
点到直线的距离等于该点在直线上的正交投影点的距离。
二、立体图形的面积与体积1. 立体图形的分类和性质。
立体图形包括球体、圆柱体、圆锥体、棱柱体、棱锥体等。
各种立体图形具有不同的性质,如球体表面上每一点到球心的距离都相等。
2. 立体图形的面积计算。
(1)球体的表面积计算公式:S = 4πr²,其中r为球的半径。
(2)圆柱体的侧面积计算公式:S = 2πrh。
(3)圆柱体的全面积计算公式:S = 2πrh + 2πr²。
(4)圆锥体的侧面积计算公式:S = πrl,其中r为圆锥底面半径,l为斜高。
(5)棱柱体的侧面积计算公式:S = ph,其中p为棱柱底面周长,h为高。
3. 立体图形的体积计算。
(1)球体的体积计算公式:V = 4/3πr³,其中r为球的半径。
(2)圆柱体的体积计算公式:V = πr²h。
(3)圆锥体的体积计算公式:V = 1/3πr²h。
(4)棱柱体的体积计算公式:V = ph。
(5)棱锥体的体积计算公式:V = 1/3Bh,其中B为底面积,h为高。
三、立体几何的一般理论1. 点、线、面的位置关系。
在空间中,点、线、面可以相互相交、平行、垂直等。
高考数学立体几何知识点梳理

高考数学立体几何知识点梳理关键信息:1、立体几何基本概念与公理点、线、面的位置关系三公理及推论2、直线与平面的位置关系直线与平面平行直线与平面垂直3、平面与平面的位置关系平面与平面平行平面与平面垂直4、空间几何体棱柱棱锥棱台圆柱圆锥圆台球5、空间几何体的表面积与体积表面积公式体积公式6、空间向量在立体几何中的应用空间向量的坐标表示空间向量的数量积利用空间向量证明位置关系利用空间向量求空间角11 立体几何基本概念与公理111 点、线、面的位置关系点是空间中最基本的元素,线是由无数个点组成的,面是由无数条线组成的。
点动成线,线动成面。
直线与平面的位置关系有:直线在平面内、直线与平面平行、直线与平面相交。
平面与平面的位置关系有:平行、相交。
112 三公理及推论公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
公理 2:过不在一条直线上的三点,有且只有一个平面。
公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
推论 1:经过一条直线和这条直线外一点,有且只有一个平面。
推论 2:经过两条相交直线,有且只有一个平面。
推论 3:经过两条平行直线,有且只有一个平面。
21 直线与平面的位置关系211 直线与平面平行判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行。
212 直线与平面垂直定义:如果一条直线与平面内任意一条直线都垂直,那么这条直线与这个平面垂直。
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
性质定理:垂直于同一个平面的两条直线平行。
31 平面与平面的位置关系311 平面与平面平行判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
312 平面与平面垂直定义:两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
立体几何知识点总结高考

立体几何知识点总结高考1. 立体几何基本概念(1)点、线、面、体的概念立体几何中的基本概念有点、线、面、体等。
点是没有大小、只有位置的几何图形,用大写字母表示;线是由无限多个点连在一起形成的,具有长度的图形,用小写字母表示;面是由无限多个线构成的,具有面积的图形,用小写字母加上一个尖角字母表示;体是由无限多个面构成的,具有体积的图形,用大写字母加上一个倒三角字母表示。
(2)平行线、垂直线平行线是在同一个平面内,既不相交也不相交的直线,用平行线符号“||”表示;垂直线是两条直线相交的两条线段的夹角为90度。
(3)平面与直线的位置关系平面与直线的位置关系有相交、平行、重合等。
2. 空间几何图形的性质(1)点、线、面、体的性质点没有面积,没有长度;线有长度,但没有面积;面有面积,但体积为零;体有体积,具有长度、宽度和高度。
(2)平行线的性质平行线的性质包括对顶角相等,内错角相等等。
3. 空间几何图形的计算(1)立体图形的表面积和体积立体图形的表面积和体积是对立体几何知识点的重点掌握内容。
包括长方体、正方体、圆柱体、圆锥体、球体等的表面积和体积的计算方法。
(2)空间几何图形的相似性空间几何图形的相似性是指两个或两个以上的几何图形的形状和大小都相同,称为相似图形。
在计算中,可利用相似三角形的性质进行计算。
4. 空间几何图形的展开(1)立体图形的展开立体图形的展开是将一个立体图形展开成平面图形的过程。
对不同的立体图形有不同的展开方式和规则,需要灵活运用。
5. 线段和角的表示(1)线段的表示线段是由两个端点所确定的一段直线。
用两个大写字母表示。
(2)角的表示角是由两条射线分界的平面角色,用三个字母表示,其中中间字母是角的顶点。
6. 平面几何图形和立体几何图形的关系平面几何图形和立体几何图形在空间中是相互联系、相互影响的。
在图形的计算和应用中,需要注意两者之间的转化和联系。
以上就是对高考立体几何知识点的总结,掌握这些知识可以帮助学生在高考数学中取得更好的成绩。
高中立体几何知识点总结

高中立体几何知识点总结高中立体几何知识点总结一、基本概念1. 立体图形:具有长度、宽度、高度三个方向的图形。
2. 空间:指有长度、宽度、高度三个方向的范围。
3. 空间几何体:由面与面之间的关系形成的几何体。
4. 立体几何体:在三维空间内有一定形状的几何体。
5. 交角:指两个面之间的夹角。
6. 平面角:指两个不同面的交线之间的夹角。
7. 侧面:多面体的略为平行于底面的面。
8. 正视角:指从正方向看角度。
9. 支干线:连接多边形顶点及其相邻点构成的线段。
10. 垂线(高线):从顶点引垂直于底面的线段。
11. 轴线:对称图形中的对称轴线。
12. 垂线高度定理:三角形内任意一点到三角形三边所引垂线的长度乘积等于该点到三边的距离乘积。
二、立体几何体的相关知识1. 立方体:六个相等的正方形构成的多面体,具有对称性。
2. 正方体:六面均为正方形的立体几何体。
3. 矩形:四边形的内角为直角的平行四边形。
4. 梯形:在同一平面上,两边平行的四边形。
5. 圆锥:底面为圆形,侧面为一条斜面向尖端(顶点)推出去的几何体。
6. 圆柱:底面为圆形,侧面为两个平行圆面及连接它们的矩形面构成的几何体。
7. 球体:由三维空间内的所有离一个固定点的距离小于等于一个固定值的点构成的点集。
三、平面几何图形在立体几何的应用1. 投影:三维物体在平面上的投影。
2. 平面几何图形的面积、周长:将平面几何图形投射到立体几何体上进行计算。
3. 平面几何图形的旋转:平面几何图形在平面上进行旋转。
四、平行四边形的相关知识1. 平行四边形的定义:有两组的对边平行的四边形。
2. 平行四边形的性质:① 对角线互相平分;② 对角线互相垂直;③对角线长相等。
3. 平行四边形的面积计算公式:S=底×高或S=对角线之积的一半。
五、多面体的相关知识1. 多面体的定义:有多个面的立体几何体。
2. 多面体的性质:①多面体的各面之间是通过一些棱连接的。
② 一个多面体的棱数、点数和面数之间有一个简单的关系:棱数加面数等于点数加2。
高中数学立体几何知识点

高中数学立体几何知识点(大全)一、【空间几何体结构】1.空间结合体:如果我们只考虑物体占用空间部分的形状和大小,而不考虑其它因素,那么由这些物体抽象出来的空间图形,就叫做空间几何体。
2.棱柱的结构特征:有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边互相平行,由这些面围成的图形叫做棱柱。
棱柱(1):棱柱中,两个相互平行的面,叫做棱柱的底面,简称底。
底面是几边形就叫做几棱柱。
(2):棱柱中除底面的各个面。
(3):相邻侧面的公共边叫做棱柱的侧棱。
(4):侧面与底面的公共顶点叫做棱柱的顶点棱柱的表示:用表示底面的各顶点的字母表示。
如:六棱柱表示为ABCDEF-A’B’C’D’E’F’3.棱锥的结构特征:有一个面是多边形,其余各面都是三角形,并且这些三角形有一个公共定点,由这些面所围成的多面体叫做棱锥。
棱锥4.圆柱的结构特征:以矩形的一边所在直线为旋转轴,其余边旋转形成的面所围成的旋转体叫做圆柱。
圆柱(1):旋转轴叫做圆柱的轴。
(2):垂直于轴的边旋转而成的圆面叫做圆柱的底面。
(3):平行于轴的边旋转而成的曲面叫做圆柱的侧面。
(4):无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示,如:圆柱O’O(注:棱柱与圆柱统称为柱体)5.圆锥的结构特征:以直角三角形的一条直角边所在直线为旋转轴, 两余边旋转形成的面所围成的旋转体叫做圆锥。
圆锥(1):作为旋转轴的直角边叫做圆锥的轴。
(2):另外一条直角边旋转形成的圆面叫做圆锥的底面。
(3):直角三角形斜边旋转形成的曲面叫做圆锥的侧面。
(4):作为旋转轴的直角边与斜边的交点。
(5):无论旋转到什么位置,直角三角形的斜边叫做圆锥的母线。
圆锥可以用它的轴来表示。
如:圆锥SO(注:棱锥与圆锥统称为锥体)二、【棱台和圆台的结构特征】1.棱台的结构特征:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台。
棱台(1):原棱锥的底面和截面分别叫做棱台的下底面和上底面。
高考立体几何知识点总结(详细)

高考立体几何知识点总结一、空间几何体(一)空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二)几种空间几何体的结构特征1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类图1-1 棱柱棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体底面是四边形底面是平行四边形侧棱垂直于底面底面是矩形底面是正方形棱长都相等性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等;Ⅱ、两底面是全等多边形且互相平行;Ⅲ、平行于底面的截面和底面全等;1.3棱柱的面积和体积公式(是底周长,是高)S直棱柱表面 = c·h+ 2S底V棱柱 = S底·h2 、棱锥的结构特征2.1 棱锥的定义(1)棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:(为底周长,为斜高)ABCDPOH体积:(为底面积,为高)正四面体:对于棱长为正四面体的问题可将它补成一个边长为的正方体问题。
对棱间的距离为(正方体的边长)正四面体的高()正四面体的体积为()正四面体的中心到底面与顶点的距离之比为()3 、棱台的结构特征3.1 棱台的定义:用一个平行于底面的平面去截棱锥,我们把截面和底面之间的部分称为棱台。
高考数学立体几何知识点总结精选全文完整版

可编辑修改精选全文完整版高考数学立体几何知识点总结(1)棱柱:定义:有两个面互相平行,别的各面都是四边形,且每相邻两个四边形的大众边都互相平行,由这些面所围成的几多体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各极点字母,如五棱柱或用对角线的端点字母,如五棱柱几多特性:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥定义:有一个面是多边形,别的各面都是有一个大众极点的三角形,由这些面所围成的几多体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各极点字母,如五棱锥几多特性:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比即是极点到截面隔断与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各极点字母,如五棱台几多特性:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的极点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,别的三边旋转所成的曲面所围成的几多体几多特性:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
(5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几多体几多特性:①底面是一个圆;②母线交于圆锥的极点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几多特性:①上下底面是两个圆;②侧面母线交于原圆锥的极点;③侧面展开图是一个弓形。
(7)球体:定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几多体几多特性:①球的截面是圆;②球面上恣意一点到球心的隔断即是半径。
2024年高考数学立体几何知识点总结

2024年高考数学立体几何知识点总结高考数学中的立体几何,是考查考生对空间图形的认识和理解,以及解决问题的能力。
以下是2024年高考数学立体几何的主要知识点总结:一、立体几何的基本概念1. 空间直角坐标系:了解三维空间的坐标系,掌握在空间直角坐标系下求两点之间距离和判定点与多面体关系的方法。
2. 几何体的分类与特征:了解各种几何体的定义、特征和性质,包括点、直线、平面、多面体等,熟悉各种几何体的命名和常见几何体的特征。
二、多面体与球的性质1. 正多面体:熟悉正多面体的定义、性质和相关定理,如正四面体、正六面体、正八面体等的性质,掌握计算正多面体的体积和表面积的方法。
2. 欧拉定理:了解欧拉定理的内容和证明思路,应用欧拉定理求解相应问题。
3. 球的性质:了解球的定义、性质和相关定理,如球面上的点和圆应用球的性质进行计算。
三、立体空间的位置关系1. 空间几何体的位置关系:了解空间几何体之间的位置关系,包括平行与垂直关系、相交与平面关系、点在立体内部与外部的关系等。
2. 空间向量的应用:熟悉空间向量的概念、性质和运算,掌握使用空间向量判断几何体的位置关系的方法。
四、立体几何中的投影1. 投影的概念与性质:了解投影的基本概念和性质,包括平行投影和斜投影的性质,熟悉使用投影解决几何问题的方法。
2. 截痕法与截面应用:掌握截痕法求解几何问题的基本思路和方法,熟练运用截痕法和截面方法解决立体几何问题。
五、向量运算在立体几何中的应用1. 向量投影的应用:了解向量投影的概念和性质,应用向量投影解决立体几何中的相关问题。
2. 向量混合积和向量积的应用:掌握向量混合积和向量积的定义和性质,应用向量混合积和向量积求解相关问题。
六、空间坐标系中的方向余弦与方向角1. 方向余弦的概念与性质:了解方向余弦的概念和性质,掌握方向余弦在立体几何中的应用方法。
2. 方向角的概念与计算:了解方向角的定义和计算方法,熟练求解立体几何中与方向角相关的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八、立体几何一、立体几何网络图:(1)线线平行的判断:⑴平行于同一直线的两直线平行。
⑶如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
⑹如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
⑿垂直于同一平面的两直线平行。
(2)线线垂直的判断:⑺在平面的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
⑻在平面的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
⑽若一直线垂直于一平面,这条直线垂直于平面所有直线。
补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。
(3)线面平行的判断:⑵如果平面外的一条直线和平面的一条直线平行,那么这条直线和这个平面平行。
⑸两个平面平行,其中一个平面的直线必平行于另一个平面。
(4)线面垂直的判断:⑼如果一直线和平面的两相交直线垂直,这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⒃如果两个平面垂直,那么在—个平面垂直于交线的直线必垂直于另—个平面。
(5)面面平行的判断:⑷一个平面的两条相交直线分别平行于另一个平面,这两个平面平行。
⒀垂直于同一条直线的两个平面平行。
(6)面面垂直的判断:⒂一个平面经过另一个平面的垂线,这两个平面互相垂直。
二、其他定理:(1)确定平面的条件:①不公线的三点;②直线和直线外一点;③相交直线;(2)直线与直线的位置关系:相交;平行;异面;直线与平面的位置关系:在平面;平行;相交(垂直是它的特殊情况);平面与平面的位置关系:相交;;平行;(3)等角定理:如果两个角的两边分别平行且方向相同,那么这两个角相等;如果两条相交直线和另外两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等;(4)射影定理(斜线长、射影长定理):从平面外一点向这个平面所引的垂线段和斜线段中,射影相等的两条斜线段相等;射影较长的斜线段也较长;反之,斜线段相等的射影相等;斜线段较长的射影也较长;垂线段比任何一条斜线段都短。
(5)最小角定理:斜线与平面所有直线所成的角中最小的是与它在平面射影所成的角。
(6)异面直线的判定:①反证法;②过平面外一点与平面一点的直线,和平面不过该点的直线是异面直线。
(7)过已知点与一条直线垂直的直线都在过这点与这条直线垂直平面。
(8)如果—直线平行于两个相交平面,那么这条直线平行于两个平面的交线。
(9)如果两个相交平面都垂直于第三个平面,那么它们的交线也垂直于第三个平面。
三、唯一性定理:(1)过已知点,有且只能作一直线和已知平面垂直。
(2)过已知平面外一点,有且只能作一平面和已知平面平行。
(3)过两条异面直线中的一条能且只能作一平面与另一条平行。
四、空间角的求法:(所有角的问题最后都要转化为解三角形的问题,尤其是直角三角形)(1)异面直线所成的角:通过直线的平移,把异面直线所成的角转化为平面相交直线所成o;的角。
异面直线所成角的围:o注意:若异面直线中一条直线是三角形的一边,则平移时可找三角形的中位线。
有的还可以通过补形,如:将三棱柱补成四棱柱;将正方体再加上三个同样的正方体,补成一个底面是正方形的长方体。
(2)线面所成的角:①线面平行或直线在平面:线面所成的角为o0; ②线面垂直:线面所成的角为o90;③斜线与平面所成的角:围oo;即也就是斜线与它在平面的射影所成的角。
(3)二面角:关键是找出二面角的平面角。
方法有:①定义法;②三垂线定理法;③垂面法;注意:还可以用射影法:SS 'cos =θ;其中θ为二面角βα--l 的大小,S 为α的一个封闭几何图形的面积;'S 为α的一个封闭几何图形在β射影图形的面积。
一般用于解选择、填空题。
五、距离的求法:(1)点点、点线、点面距离:点与点之间的距离就是两点之间线段的长、点与线、面间的距离是点到线、面垂足间线段的长。
求它们首先要找到表示距离的线段,然后再计算。
注意:求点到面的距离的方法:①直接法:直接确定点到平面的垂线段长(垂线段一般在二面角所在的平面上); ②转移法:转化为另一点到该平面的距离(利用线面平行的性质); ③体积法:利用三棱锥体积公式。
(2)线线距离:关于异面直线的距离,常用方法有: ①定义法,关键是确定出b a ,的公垂线段;②转化为线面距离,即转化为a 与过b 而平行于a 的平面之间的距离,关键是找出或构造出这个平面;③转化为面面距离;(3)线面、面面距离:线面间距离面面间距离与线线间、点线间距离常常相互转化; 六、常用的结论:(1)若直线l 在平面α的射影是直线l ',直线m 是平面α经过l 的斜足的一条直线,l 与l '所成的角为1θ,l '与m 所成的角为2θ, l 与m 所成的角为θ,则这三个角之间的关系是21cos cos cos θθθ=; (2)如何确定点在平面的射影位置:①Ⅰ、如果一个角所在平面外一点到角两边距离相等,那么这点在平面上的射影在这个角的平分线上;Ⅱ、经过一个角的顶角引这个角所在平面的斜线,如果斜线和这个角的两边夹角相等,那么斜线上的点在平面上的射影在这个角的平分线所在的直线上; Ⅲ、如果平面外一点到平面上两点的距离相等,则这一点在平面上的射影在以这两点为端点的线段的垂直平分线上。
②垂线法:如果过平面外一点的斜线与平面的一条直线垂直,那么这一点在这平面上的射影在过斜足且垂直于平面直线的直线上(三垂线定理和逆定理);③垂面法:如果两平面互相垂直,那么一个平面任一点在另一平面上的射影在这两面的交线上(面面垂直的性质定理);④整体法:确定点在平面的射影,可先确定过一点的斜线这一整体在平面的射影。
(3)在四面体ABCD 中:①若AD BC CD AB ⊥⊥,,则BD AC ⊥;且A 在平面BCD 上的射影是BCD ∆心。
②若AD AC AB ==,则A 在平面BCD 上的射影是BCD ∆的外心。
③若A 到BD CD BC ,,边的距离相等,则A 在平面BCD 上的射影是BCD ∆的心。
(4)异面直线上两点间的距离公式:若异面直线所成的角为θ,它们公垂线段'AA 的长为d ,在b a ,上分别取一点F E ,,设m E A =',n AF =;则θcos 2222mn n m d EF ±++=(如果AF E '∠为锐角,公式中取负号,如果AF E '∠为钝,公式中取正号)七、多面体: (1)棱柱:①定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
棱柱斜棱柱直棱柱正棱柱;四棱柱平行六面体直平行六面体长方体正四棱柱正方体。
②性质:Ⅰ、侧面都是平行四边形; Ⅱ、两底面是全等多边形;Ⅲ、平行于底面的截面和底面全等;对角面是平行四边形;Ⅳ、长方体一条对角线长的平方等于一个顶点上三条棱的长的平方和。
③面积:ch S =直棱柱侧(c 是底周长,h 是高) ④体积:d S Sh V 侧面棱柱21==(S 为底面积,h 为高,d 为已知侧面与它对棱的距离) (2)棱锥:①定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面围成的几棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形 底面是正多边形侧棱垂直于底面侧棱不垂直于底面bα aA ’AF E ’ Eθ何体叫做棱锥;正棱锥:底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥; ②性质:Ⅰ、平行于底面的截面和底面相似,截面的边长和底面的对应边边长的比等于截得的棱锥的高与原棱锥的高的比; 它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比; Ⅱ、正棱锥性质:各侧面都是全等的等腰三角形;通过四个直角三角形POH Rt ∆,POB Rt ∆,PBH Rt ∆,BOH Rt ∆实现边,高,斜高间的换算 ③面积:'21ch S =正棱锥(c 为底周长,'h 为斜高) ④体积:Sh V 31=棱锥(S 为底面积,h 为高)(3)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
对棱间的距离为a 22(正方体的边长) 正四面体的高a 36(正方体体对角线l 32=) 正四面体的体积为32a (正方体小三棱锥正方体V V V 314=-) 正四面体的中心到底面与顶点的距离之比为3:1(正方体体对角线正方体体对角线:l l 2161=) 外接球的半径为a 6(是正方体的外接球,则半径正方体体对角线l 21=) 切球的半径为a 6(是正四面体中心到四个面的距离,则半径正方体体对角线l 61=)(4)正多面体:①定义:每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的多面体叫做正多面体。
ABC D POH222121VF m m m n n n E +++=+++=(i n 表示各个面上的棱数,i m 表示过各个顶点的棱数)八、球(1)定义:①球面:半圆以它的直径为旋转轴,旋转所成的曲面。
②球体:球面所围成的几何体。
(2)性质:①任意截面是圆面(经过球心的平面,截得的圆叫大圆,不经过球心的平面截得的圆叫小圆)两点的球面距离,是指经过球面上这两点的大圆在这两点间的一段劣弧的长。
②球心和截面圆心的连线垂直于截面,并且22d R r -=,其中R 为球半径,r 为截面半径,d 为球心的到截面的距离。
(3)面积公式:24R S π=球面(R 为球半径); (4)体积公式:334R V π=球(R 为球半径)。
