【实验报告】控制系统的串联校正
自动控制原理实验报告 线性系统串联校正

武汉工程大学实验报告专业自动化班号组别指导教师陈艳菲姓名同组者三、实验结果分析1.开环传递函数为)1(4)(+=s s s G 的系统的分析及其串联超前校正:(1)取K=20,绘制原系统的Bode 图: 源程序代码及Bode 图: num0=20; den0=[1,1,0]; w=0.1:1000;[gm1,pm1,wcg1,wcp1]=margin(num0,den0); [mag1,phase1]=bode(num0,den0,w); [gm1,pm1,wcg1,wcp1] margin(num0,den0) grid;运行结果: ans =Inf 12.7580 Inf 4.4165分析:由结果可知,原系统相角裕度r=12.75800,c ω=4.4165rad/s ,不满足指标要求,系统的Bode 图如上图所示。
考虑采用串联超前校正装置,以增加系统的相角裕度。
确定串联装置所需要增加的超前相位角及求得的校正装置参数。
),5,,45(0000c m c Φ=Φ=+-=Φ令取为原系统的相角裕度εγγεγγ mm ϕϕαsin 1sin 1-+=将校正装置的最大超前角处的频率 作为校正后系统的剪切频率 。
则有: αωωω1)(0)()(lg 2000=⇒=c c c c j G j G j G即原系统幅频特性幅值等于 时的频率,选为c ω。
根据m ω=c ω ,求出校正装置的参数T 。
即αωc T 1=。
(2)系统的串联超前校正:源程序代码及Bode图:num0=20;den0=[1,1,0];w=0.1:1000;[gm1,pm1,wcg1,wcp1]=margin(num0,den0);[mag1,phase1]=bode(num0,den0,w);[gm1,pm1,wcg1,wcp1]margin(num0,den0)grid;e=5; r=50; r0=pm1;phic=(r-r0+e)*pi/180;alpha=(1+sin(phic))/(1-sin(phic));[il,ii]=min(abs(mag1-1/sqrt(alpha)));wc=w( ii);T=1/(wc*sqrt(alpha));numc=[alpha*T,1];denc=[T,1];[num,den]=series(num0,den0,numc,denc);[gm,pm,wcg,wcp]=margin(num,den);printsys(numc,denc)disp('校正之后的系统开环传递函数为:');printsys(num,den)[mag2,phase2]=bode(numc,denc,w);[mag,phase]=bode(num,den,w);subplot(2,1,1);semilogx(w,20*log10(mag),w,20*log10(mag1),'--',w,20*log10(mag2),'-.');grid; ylabel('幅值(db)');title('--Go,-Gc,GoGc');title(['校正前:幅值裕量=',num2str(20*log10(gm1)),'db','相位裕量=',num2str(pm1),'0']);subplot(2,1,2); semilogx(w,phase,w,phase1,'--',w,phase2,'-',w,(w-180-w),':');grid; ylabel('相位(0)'); xlabel('频率(rad/sec)');title(['校正后:幅值裕量=',num2str(20*log10(gm)),'db','相位裕量=',num2str(pm),'0']);运行结果:ans =Inf 12.7580 Inf 4.4165num/den =0.31815 s + 1--------------0.062352 s + 1校正之后的系统开环传递函数为:num/den =6.363 s + 20------------------------------0.062352 s^3 + 1.0624 s^2 + s分析:由结果可知,校正环节的传递函数为(0.31815 s + 1)/(0.062352 s + 1),校正后系统的开环传递函数为(6.363 s + 20)/(0.062352 s^3 + 1.0624 s^2 + s),系统的Bode图如上图所示。
自动控制原理实验报告(控制系统串联校正)

自动控制原理实验报告(控制系统串联校正)自动控制原理实验报告学院机械工程及自动化学院专业方向机械工程及自动化班级16学号1学生姓名自动控制与测试教学实验中心实验三控制系统串联校正实验目的了解和掌握串联校正的分析和设计方法。
研究串联校正环节对系统稳定性及过渡过程的影响。
实验内容设计串联超前校正,并验证。
设计串联滞后校正,并验证。
实验原理系统结构如下图所示:图SEQ 图\* ARABIC 1 控制系统结构图图中GC图SEQ 图\* ARABIC 2 控制系统模拟电路图未加校正时Gc(s)=1加串联超前校正时G给定a=2.44,T=0.26,则GCs=0.63s+10.26s+1 QUOTE加串联滞后校正时G给定b=0.12,T=83.33,则G在实验中,选取,通过Simulink模拟器产生模拟信号与实验采集的实测数据进行对比,分析实验结果,验证自动控制理论。
实验设备HHMN-1型电子模拟机一台。
PC机一台。
数字式万用表一块。
实验步骤熟悉HHMN-1电子模拟机的使用方法。
将各运算放大器接成比例器,通电调零。
断开电源,按照系统结构图和传递函数计算电阻和电容的取值,并按照模拟线路图搭接线路,不用的运算放大器接成比例器。
将D/A1与系统输入端Ui连接,将A/D1与系统输出端Uo 连接(此处谨慎连接,不可接错)。
在Windows XP桌面用鼠标双击“自控原理实验”图标后进入实验软件系统,在项目中选择“实验三”。
分别完成不加校正,加入超前校正,加入滞后校正的实验。
观察实验结果,绘制实验结果图形。
用MATLAB绘制以上三种情况时系统的波特图,完成实验报告。
实验结果原系统原系统阶跃响应曲线如下图SEQ 图\* ARABIC 3原系统时域阶跃响应曲线其阶跃响应性能参数如下σTT44.0389%0.16955.5645表格1 原系统阶跃响应性能参数原系统Bode图如下图SEQ 图\* ARABIC 4原系统Bode图超前校正系统超前校正系统阶跃响应曲线如下图SEQ 图\* ARABIC 5超前校正系统时域阶跃响应曲线超前校正后,系统阶跃响应性能参数如下σTT22.1411%0.04761.9845表格2 超前校正系统阶跃响应曲线超前校正系统Bode图如下图SEQ 图\* ARABIC 6超前校正系统Bode图滞后校正系统滞后校正系统阶跃响应曲线如下图SEQ 图\* ARABIC 7滞后校正系统时域阶跃响应曲线滞后校正后,系统阶跃响应性能参数如下σTT20.6731%2.358014.5420表格3 滞后校正系统阶跃响应性能参数滞后校正后系统Bode图如下图SEQ 图\* ARABIC 8滞后校正系统Bode图截止频率和稳定裕度计算在命令窗口输入相关命令,在得到的图形中读出系统的相角裕度γ、截止频率ωc项目系统项目系统γ/°ω原系统281.88超前校正47.42.38滞后校正54.80.449结果分析超前校正实验结果分析首先从系统频率特性曲线Bode图可以看出,经过超前校正后的系统在校正点处的性能有所改善。
自动控制实验报告五-连续系统串联校正

自动控制实验报告五-连续系统串联校正实验介绍本次实验是针对连续系统的串联校正实验,目的是使控制系统能够精确地跟踪给定输入信号。
具体地,要求通过串联校正的方式,将系统的稳态误差控制在一个很小的范围内。
为此,本次实验将对校正器进行串联配置,然后测试系统并进行基本的数据分析。
实验原理首先,需要明确串联校正的概念。
所谓串联校正,就是将校正器和系统连接起来,以提高控制系统的性能。
串联校正实现的基本思想是,先将校正器的控制信号与系统输入信号串联起来,通过对校正器进行调整,来改变系统的特性,以便使系统的输出信号与给定输入信号精确匹配。
具体来说,要完成串联校正,需要如下步骤:1.测量系统的开环特性,并进行基本的分析。
2.将校正器和系统进行串联,校正器的输出信号作为输入信号,系统的输出信号作为反馈信号。
3.根据反馈信号调整校正器的参数,使系统具有更好的稳态性能。
4.再次测量系统的闭环特性,检验串联校正后的效果。
具体的实现步骤和公式可参考连续系统校正实验报告。
实验过程实验步骤1.首先进行系统的稳态误差测量,记录输出信号与给定信号之间的稳态误差。
2.将校正器与系统进行串联,根据实验要求设定校正器的参数。
3.测试校正后的系统,记录输出信号与给定信号之间的稳态误差,与前一次进行对比。
实验结果实验结果如下表所示:测量项目原始系统校正后系统稳态误差0.2 0.02由上表可知,经过串联校正后,系统的稳态误差从0.2减少到了0.02,已经达到了实验的预期。
实验通过本次实验,我们掌握了连续系统的串联校正方法,了解了校正器与系统的串联关系,掌握了相应的实验操作和数据分析技术。
同时,我们还了解了校正器的参数调整对系统运行性能的影响,并进一步提高了自己的实际操作能力。
自动控制原理实验报告-线性系统串联校正设计

实验五线性系统串联校正设计实验原理:(1)串联校正环节原理串联校正环节通过改变系统频率响应特性,进而改善系统的动态或静态性能。
大致可以分为(相位)超前校正、滞后校正和滞后-超前校正三类。
超前校正环节的传递函数如下Tαs+1α(Ts+1),α>1超前校正环节有位于实轴负半轴的一个极点和一个零点,零点较极点距虚轴较近,因此具有高通特性,对正频率响应的相角为正,因此称为“超前”。
这一特性对系统的穿越频率影响较小的同时,将增加穿越频率处的相移,因此提高了系统的相位裕量,可以使系统动态性能改善。
滞后校正环节的传递函数如下Tαs+1Ts+1,α<1滞后校正环节的极点较零点距虚轴较近,因此有低通特性,附加相角为负。
通过附加低通特性,滞后环节可降低系统的幅值穿越频率,进而提升系统的相位裕量。
在使系统动态响应变慢的同时提高系统的稳定性。
(2)基于Baud图的超前校正环节设计设计超前校正环节时,意图让系统获得最大的超前量,即超前网络的最大相位超前频率等于校正后网络的穿越频率,因此设计方法如下:①根据稳态误差要求确定开环增益。
②计算校正前系统的相位裕度γ。
③确定需要的相位超前量:φm=γ∗−γ+(5°~12°) ,γ∗为期望的校正后相位裕度。
④计算衰减因子:α−1α+1= sin φm。
此时可计算校正后幅值穿越频率为ωm=−10lgα。
⑤时间常数T =ω√α。
(3)校正环节的电路实现构建待校正系统,开环传递函数为:G(s)=20s(s+0.5)电路原理图如下:校正环节的电路原理图如下:可计算其中参数:分子时间常数=R1C1,分母时间常数=R2C2。
实验记录:1.电路搭建和调试在实验面包板上搭建前述电路,首先利用四个运算放大器构建原系统,将r(t)接入实验板AO+和AI0+,C(t)接入AI1+,运算放大器正输入全部接地,电源接入±15V,将OP1和OP2间独立引出方便修改。
基于另外两运算放大器搭建校正网络,将所有电容值选为1uF,所有电阻引出方便修改。
自动控制串联校正实验报告
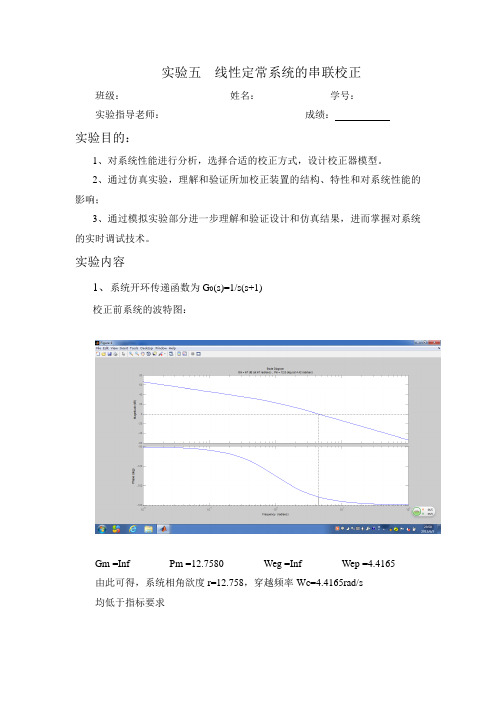
实验五线性定常系统的串联校正班级:姓名:学号:实验指导老师:成绩:实验目的:1、对系统性能进行分析,选择合适的校正方式,设计校正器模型。
2、通过仿真实验,理解和验证所加校正装置的结构、特性和对系统性能的影响;3、通过模拟实验部分进一步理解和验证设计和仿真结果,进而掌握对系统的实时调试技术。
实验内容1、系统开环传递函数为G0(s)=1/s(s+1)校正前系统的波特图:Gm =Inf Pm =12.7580 Weg =Inf Wep =4.4165由此可得,系统相角欲度r=12.758,穿越频率Wc=4.4165rad/s均低于指标要求校正前闭环系统的单位阶跃响应曲线:由图可得,校正前系统的单位阶跃响应参数如下:最大超调量为70%,调整时间为Ts=5.78s.源程序代码如下:num = [20];den = [1 1 0];g = tf(num,den)Nyquist(g)bode(g)margin(g)[Gm,Pm,Weg,Wep] = Margin(g)gf = feedback(g,1)step(gf)2、经过理论计算得到校正器模型:Gc(s)=(0.38s+1)/(0.046s+1)校正后系统的波特图为Gm =Inf Pm =59.1872 Weg =Inf Wep =7.5393 校正后的系统相角欲度为r=59.1872,穿越角频率Wc=7.5393rad/s,符合性能指标要求。
校正前后系统的波特图比较:校正后闭环系统的单位阶跃响应由图可得,校正后闭环系统的单位阶跃响应参数如下:最大超调量为15%,调整时间Ts=0.744s。
系统的稳定性和快速性得到了提高。
源程序代码如下:num = [20]den = [1 1 0]g0 = tf(num,den)gc = tf([0.38 1],[0.046 1]);g = g0 * gc;Bode(g,g0)margin(g)[Gm,Pm,Weg,Wep] = margin(g)gf = feedback(g,1);figure;step(gf)3、模拟部分3.1 根据给定的实验模型搭接校正前的模拟电路图根据传递函数绘制系统模拟电路图,搭接后系统传递函数为G0(s)=19.6/s*(s+1)在试验台上搭接模拟电路完毕后,使用模拟示波器观测校正前系统的阶跃响应,其响应曲线如下图所示:从图中可以看出,模拟校正前网络的阶跃响应参数为:最大超调量为68.6%,调整时间为Ts=6.185s3.2 搭建校正后系统的模拟电路图,校正环节传递函数为:Gc(s)=(0.47s+1)/(1+0.039s)在试验台上搭接校正器的模拟电路后,并引入原系统,用模拟示波器观测校正后系统的阶跃响应,其响应曲线如图所示:由图可知,校正后系统阶跃响应参数如下:最大超调量为:9%,调整时间Ts=0.344s。
北航自动控制原理实验三:控制系统串联校正

本次实验通过设计串联超前校正和串联滞后校正装置研究了串联校正环节对系统稳定性及过渡过程的影响,从直观的角度认识了串联校正环节的作用及超前校正和滞后校正的不同之处,对理论学习有一定的帮助。
附:实验数据,
成绩
自动控制原理
实验报告
院(系)名称
专业名称
学生学号
学生姓名
指导老师
2015年12月
实验二
实验时间
一、实验目的
1.了解和掌握串联校正的分析和设计方法。
2.研究串联校正环节对系统稳定性及过渡过程的影响。
二、实验内容
1.单位负反馈系统的开环传递函数为 ,进行半实物实时仿真,研究其时域性能,同时从频域分析系统稳定性。
2.电子模拟机
3.万用表
4.测试导线
五、实验步骤
1.正确连接电路,分别完成不加校正、加入超前校正、加入滞后校正的实验。在系统模型上的“Manual Switch”处可设置系统是否加入校正环节,在“ ”处可设置校正环节的传递函数。
2.绘制以上三种情况时系统的波特图。
3.采用示波器“Scope”观察阶跃响应曲线。观测试验结果,记录实验数据,绘制实验结果图形,完成实验报告。
图3-1系统结构图
其中 为校正环节,可放置在系统模型中来实现,也可使用模拟电路的方式由模拟机实现。
2.系统模拟电路如图3-2所示。
图3-2系统模拟电路图
取 , , , , 。
3.未加校正时, 。
4.加串联超前校正时, 。
取 , ,则 。
5.加串联滞后校正时, 。
取 , ,则 。
四、实验设备
1.数字计算机
2.针对以上系统,设计串联超前校正装置 ,使系统的相稳定裕度 ,并进行半实物实时仿真验证,研究其时域性能,同时从频域分析系统稳定性。
自控实验报告控制系统串联校正

自动控制原理实验报告(III)一、实验名称:控制系统串联校正二、实验目的1. 了解和掌握串联校正的分析和设计方法。
2. 研究串联校正环节对系统稳定性及过渡过程的影响。
三、实验内容1. 设计串联超前校正,并验证。
2. 设计串联滞后校正,并验证。
四、实验原理1. 系统结构如图3-1图3-1其中Gc(s) 为校正环节,可放置在系统模型中来实现,也可使用模拟电路的方式由模拟机来实现。
2. 系统模拟电路如图3-2图3-2各电阻电容取值R3=2MΩ R4=510KΩ R5=2MΩC1=0.47μF C2=0.47μF3. 未加校正时Gcs=14. 加串联超前校正时Gcs=aTs+1Ts+1 (a >1)给定 a = 2.44 , T = 0.26 , 则 Gcs=0.63s+10.26s+15. 加串联滞后校正时Gcs=bTs+1Ts+1(0<b<1)给定b = 0.12 , T = 83.33, 则Gcs=10s+183.33s+1五、数据记录未加校正超前校正滞后校正ts实测值/s 5.90 2.3515.24 ts理论值/s 5.41 1.9215.14γ/°25.546.855.7ωc/rad∙s-1 2.11 2.430.48(1)未加校正(2)超前校正(3)滞后校正3. 系统波特图(1)未加校正环节系统开环传递函数Gs=4s2+s(2)串联超前校正系统开环传递函数Gs=2.52s+40.26s3+1.26s2+s(3)串联滞后校正系统开环传递函数Gs=40s+483.33s3 + 84.33s2+s六、数据分析1、无论是串入何种校正环节,或者是否串入校正环节,系统最终都会进入稳态,即三个系统都是稳定系统。
2、超前校正:系统比未加校正时调节时间短,即系统快速性变好了,而且超调量也减小了。
从频率角度来看,戒指频率减小,相位稳定域度增大,系统稳定性变好。
3、滞后校正:系统比未加校正时调节时间长,即系统快速性变差了,但是超调量减小了很多,甚至比加串联超前校正时的超调还小。
【实验报告】控制系统的串联校正

实验名称:控制系统串联校正目录(一)实验目的 (3)(二)实验内容 (3)(三)实验设备 (3)(四)实验原理 (3)(五)实验结果 (4)(六)数据分析的 (7)附页: (9)Matlab模拟波特图程序: (9)图片目录图片1 系统结构图 (3)图片2 系统模拟电路 (3)图片3 无校正阶跃响应曲线 (4)图片4 无校正时波特图 (5)图片5 超前校正阶跃响应曲线 (5)图片6 超前校正时波特图 (6)图片7 滞后校正阶跃响应曲线 (6)图片8 滞后校正波特图 (7)表格目录表格1 稳定裕度和截止频率 (7)表格2 阶跃响应数据 (7)控制系统串联校正(一) 实验目的(1) 了解和掌握串联校正的分析和设计方法;(2) 研究串联校正环节对系统稳定性及过度过程的影响;(二) 实验内容(1) 设计串联超前校正,并验证; (2) 设计串联超前校正,并验证;(三) 实验设备(1) HMNN 电子模拟机一台 (2) PC 机一台 (3) 万用表一块(四) 实验原理图片 1 系统结构图其中()C G s 为校正环节,在本实验中利用系统模型实现; 不加校正环节时,系统的开环传递函数为:4()(1)G s s s =+图片 2 系统模拟电路K1 T1 K2 T2 K3(1) 未加校正环节时()1C G s =(2) 加串联超前校正环节时,传递函数: 1()1C TsG s Tsα+=+,其中: 2.55α=,0.26T =:10.63()10.26C sG s s+=+ (3) 加串联止滞后校正环节时,传递函数: 1()1C bTsG s Ts+=+,其中:0.12b =,83.33T =:110()183.33C sG s s+=+根据系统模型,可以达到系统参数的计算方法:12/113125/425231K R R T R C K R R T R C K ==⨯==⨯= (五) 实验结果(1) 由系统参数的计算公式可以得到(在实际电路中,略去由第一个和最后一个运算放大器构成的放大电路):512142503111R M C uf R K R M C uf=Ω==Ω=Ω=(2) 不加校正时的阶跃响应曲线和波特图图片 3 无校正阶跃响应曲线(3)加入超前校正时的阶跃响应曲线和波特图图片 5 超前校正阶跃响应曲线(4)加入滞后校正时的阶跃响应曲线和波特图图片7 滞后校正阶跃响应曲线根据波特图仿真结果可得:表格 1 稳定裕度和截止频率计算(六)数据分析的时频域分析:(1)由实际获得的阶跃响应实验数据可以得到:表格 2 阶跃响应数据所列时间已减去阶跃响应的0.5s延迟;w附近的区段,考察系统的平稳性和(2)利用中频段开环对数幅频特性曲线在截止频率c快速性(过渡过程);A)无反馈环节:利用开环传递函数,可以得到系统的转折频率为1rad/s,即在w大于转折频率的情况下,开环幅频特性曲线斜率近似为-40db/dec(中频段),由获得的无反馈条件下阶跃响应曲线(图3)和上表(表2)可以看出,系统振荡性较强,虽然振荡衰减,w与调节之间见的反比关系,此时截止频率大小在三个系统但超调量较大,同时考虑c中处于中间,而获得的实际调节时间数据也验证了这种关系。
控制系统的串联校正

实验四 控制系统的串联校正一、 实验目的1、了解比例微分(PD )和比例积分(PI )及比例积分微分(PID )校正在控制系统中的作用。
2、观察比较校正前后控制系统的时域动态品质。
二、 实验原理与线路1、某随动系统的方块图如图4—1:图4—1 某随动系统的方块图模拟线路图如图4—2:图4—2 某随动系统的模拟电路图图4—2中参数为:T=0.1~1S ,K=100a ~1000a ,a 为W 的衰减系数。
不加校正系统的特征方程为:TS 2+S+K=0其特征根为共轭复根,故稳定性很差,而加入比例微分校正后,则稳定储备大为改善。
11)(12++=s T s T s W j其中 T2=0.05 秒, T1=0.005秒。
实验四用SIMULINK仿真如下:校正前后系统的仿真图校正前系统的阶跃响应曲线校正后系统的阶跃响应曲线2. 某随动系统的方块图如图4—3:图4—3 某随动系统的方块图模拟线路图如图4—4: 图4—4中:其特征方程为:利用波德图和代数稳定判据,可分析出其稳定储备很差,进一步提高a ,系统会自振荡,而加入比例积分校正后,系统则成为稳定的系统。
100,515,101.0100221==⨯==⨯=K mS F K T mS F K T μμ0)(221321=++++αK s s T T s T T图4—4 某随动系统的模拟电路图3.某系统的方块图如图4—5:图4—5 某系统的方块图模拟线路图如图4—6:图4—6 某系统的模拟电路图图4—6中:a 为W 点的衰减系数。
显然,利用波德图和代数稳定判据,可分析出上述参数很难使系统稳定,而加入比例积分微分校正后,则稳定储备大为改善,品质可以满足要求。
比例积分微分(PID )校正的传递函数如下:三﹑实验内容及步骤1. 按给定的或自己设计的模拟线路接线,观察未加校正系统(模拟线路中K 打开时)的阶跃响应过渡过程,并与理论计算相比较。
并将实验结果记录在相应的实验记录表中。
自动控制原理线性系统串联校正实验报告五..

武汉工程大学实验报告专业 电气自动化 班号 指导教师 姓名 同组者 无实验名称 线性系统串联校正实验日期 第 五 次实验 一、 实验目的1.熟练掌握用MATLAB 语句绘制频域曲线。
2.掌握控制系统频域范围内的分析校正方法。
3.掌握用频率特性法进行串联校正设计的思路和步骤。
二、 实验内容1.某单位负反馈控制系统的开环传递函数为)1()(+=s s Ks G ,试设计一超前校正装置,使校正后系统的静态速度误差系数120-=s K v ,相位裕量050=γ,增益裕量dB K g 10lg 20=。
解:取20=K ,求原系统的相角裕度。
num0=20; den0=[1,1,0]; w=0.1:1000;[gm1,pm1,wcg1,wcp1]=margin(num0,den0); [mag1,phase1]=bode(num0,den0,w);[gm1,pm1,wcg1,wcp1] margin(num0,den0) grid; ans =Inf 12.7580 Inf 4.4165 由结果可知,原系统相角裕度7580.12=r ,srad c /4165.4=ω,不满足指标要求,系统的Bode 图如图5-1所示。
考虑采用串联超前校正装置,以增加系统的相角裕度。
1010101010幅值(d b )--Go,-Gc,GoGcM a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , P m = 12.8 deg (at 4.42 rad/sec)Frequency (rad/sec)图5-1 原系统的Bode 图由),3,8.12,50(00000c m c Φ=Φ=+-=Φ令取为原系统的相角裕度εγγεγγ,mm ϕϕαsin 1sin 1-+=可知:e=3; r=50; r0=pm1;phic=(r-r0+e)*pi/180;alpha=(1+sin(phic))/(1-sin(phic)) 得:alpha = 4.6500[il,ii]=min(abs(mag1-1/sqrt(alpha)));wc=w( ii); T=1/(wc*sqrt(alpha)); num0=20; den0=[1,1,0]; numc=[alpha*T,1]; denc=[T,1];[num,den]=series(num0,den0,numc,denc); [gm,pm,wcg,wcp]=margin(num,den); printsys(numc,denc) disp('校正之后的系统开环传递函数为:');printsys(num,den) [mag2,phase2]=bode(numc,denc,w); [mag,phase]=bode(num,den,w); subplot(2,1,1);semilogx(w,20*log10(mag),w,20*log10(mag1),'--',w,20*log10(mag2),'-.'); grid; ylabel('幅值(db)'); title('--Go,-Gc,GoGc'); subplot(2,1,2); semilogx(w,phase,w,phase1,'--',w,phase2,'-',w,(w-180-w),':'); grid; ylabel('相位(0)'); xlabel('频率(rad/sec)');title(['校正前:幅值裕量=',num2str(20*log10(gm1)),'db','相位裕量=',num2str(pm1),'0';'校正后:幅值裕量=',num2str(20*log10(gm)),'db','相位裕量=',num2str(pm),'0'])1010101010-100-5050幅值(d b )--Go,-Gc,GoGc1010101010-200-150-100-50050相位(0)频率(rad/sec)图5-2 系统校正前后的传递函数及Bode 图 num/den = 0.35351 s + 1-------------- 0.076023 s + 1校正之后的系统开环传递函数为:num/den = 7.0701 s + 20 -----------------------------0.076023 s^3 + 1.076 s^2 + s 系统的SIMULINK 仿真:校正前SIMULINK 仿真模型:单位阶跃响应波形:校正后SIMULINK仿真模型:单位阶跃响应波形:分析:由以上阶跃响应波形可知,校正后,系统的超调量减小,调节时间变短,稳定性增强。
自动控制实验五线性定常系统的串联校正

自动控制实验实验五线性定常系统的串联校正姓名: 学号: 班级:实验指导老师: __________________ 成绩: ____________________一、实验目的1 对系统性能进行分析, 选择合适的校正方式, 设计校正器模型。
2 通过仿真实验, 理解和验证所加校正装置的结构、特性和对系统性能的影响;3 通过模拟实验部分进一步理解和验证设计和仿真的结果, 进而掌握对系统的实时调试技术。
二、实验内容1 对未加校正装置时系统的性能进行分析, 根据性能要求进行校正器模型的理论设计2 Matlab仿真(1)观察校正前系统的时域、频域性能。
(2)观察校正后系统的时域、频域性能。
(3)对比1.2中结果分析校正器性能, 在保证校正效果的前提下并根据实验台实际参数进行校正器模型调整。
3 模拟实验。
(1)搭接校正前的系统模拟电路。
(2)搭接校正器模拟电路(3)验证是否满足设计要求。
三、实验数据或曲线1 MATLAB仿真部分选取实验题目三系统模型g0=tf([20],[1 1 0]);Bode(g0)gf=feedback(g0,1);step(gf)gc=tf([0.38 1],[0.05 1]);g=g0*gc;Bode(g0,g)gcf=feedback(g,1);step(gcf)校正前系统伯德图由图可知系统的性能不满足性能要求, 考虑采用串联超前校正。
阶跃响应曲线校正后系统的伯德图校正器模型(0.4s+1)/(0.05s+1),由图知系统的性能均满足性能要求, 校正器模型合理。
校正后闭环系统的阶跃响应曲线从校正前后系统的阶跃响应曲线上显示的参数可见, 系统的性能得到了改善。
2 模拟部分校正前系统的阶跃响应曲线校正后系统的阶跃响应曲线四、实验结论控制系统设计的思路之一就是在原系统特性的基础上, 对原特性加以校正, 使之达到要求的性能指标。
常用的串联校正装置有超前校正、滞后校正和超前滞后校正装置。
串联系统校正实验报告

3.3线性系统的校正与状态分析 3.3.1频域响应发串联超前校正-实验目的1. 了解和掌握超前校正的原理。
2. 掌握利用闭环和开环的对数副频和相频特性完成超前校正网络的参数的计算。
3. 掌握在被控系统中如何串入超前校正网络,构成性能满足指标的新系统的方法。
二实验内容及步骤1. 观察被控系统的闭环和开环的对数副频和相频特性、幅值穿越频率、相位余度,按校正后系统的相位余度要 求,设计矫正参数,构成矫正后系统。
2. 观察校正前后的时域特性曲线,并测量校正后的相位余度、超调量、峰值时间。
3. 按实验要求改变相位余度要求,计算相关参数填入实验报告。
(1)未校正系统的时域特性曲线的测试未校正系统图如下。
本实验用B5作为信号发生器,OUT 输出施加于被测系统的输入端 Ui 。
观察OUT 从0V到2.5V 时被测系统的时域特性。
实验步骤: ① 按表格接线。
② 在显示与功能选择(D1)单元中,选择“矩形波”。
③ 量程开关S2置下,调节“设定电位器1 ”,使脉宽>3秒。
④ 调节B5单元的“矩形波调幅”使电位器矩形波输出电压=2.5V 。
⑤ 运行、观察、记录:运行LABACT 软件,选择对应的模拟电路的构成,选择线性系统的校正,用 CH1观察系统输出信号待波形完后后用游标测量超调量、峰值时间、调节时间。
超调量=56.4%、峰值时间tp=0.32S(2)未校正系统的频域特性的测试本实验用D/A 转换单元(B2 )作为信号发生器,实验开始后,频率特性扫描点设置”表中根据自己的需要 填入各个扫描点的频率, OUT2输出施加于被测系统的输入项r (t ),然后分别测试被测系统的输出信号的闭环对数幅值的相位。
实验接线如下表所示② 运行、观察、记录:运行LABACT 软件,选择对应的模拟电路的构成,选择二阶系统,在弹出的“频率特性扫描点设置”表中 根据自己的需要填入各个扫描点的频率,本试验选择0.1Hz 为分辨率。
在未校正系统的相频特性曲线上测 得为校系统的相位余度 丫 =18.9 °穿越频率 Wc=9.4rad/s(3) 超前校正网络的设计① 在未校正系统模拟电路的开环性频特性曲线上侧得未校正系统的相位余度 丫 =18.9 °。
控制实验报告四线性系统串联校正

控制实验报告四线性系统串联校正式子中ωn =√50=7.07,ξ=1ωn =0.141, 因此,未加矫正装置时系统的超调量为63%,调节时间为4s ,静态速度误差系数K V 等于该Ⅰ型系统的开环增益为25,单位是1/s 。
2、串联校正的目标(1)超调量M P ≤25%(2)调节时间(过渡过程时间)t s ≤1s (3)校正后系统开环增益(静态速度误差系数)K V 25 1/s3、从对超调量要求可以得到 2125p M e ξ--=≤% ,于是有 0.4ξ> 。
由41s nt ξω=≤s 可以得到4n ωξ≥。
因为要求K V 25 1/s ,故令校正后开环传递函数仍包含一个积分环节,且放大系数为25。
设串联校正装置的传递函数为D (s ),则加串联校正后系统的开环传递函数为 25()()()(0.51)D s G s D s s s =+ 采用相消法,令0.51()1s D s Ts +=+ (其中T 为待确定参数),可以得到加校正后系统的闭环传递函数为 2()()25()1()()D s G s T W s D s G s s s T T==+++ 对校正后二阶系统进行分析,可以得到 225n T ω= 21n T ξω=综合考虑校正后的要求,取 T =0.05s ,此时 22.36n ω= 1/s,0.45ξ=,它们都能满足校正目标要求。
最后得到校正环节的传递函数为0.51()0.051s D s s +=+ 4、加校正后的模拟电路图如下所示:5、实验图像下图为未加矫正环节的实验图像(其坐标单位为1000ms/div ),可以看到系统超调量较大,调节时间很长,大概取4格坐标格,即约为4s ,最后的误差较难看出。
下图是校正后的实验图像(其坐标单位为400ms/div ),可以看出系统超调量明显减小,并且在这个图像中可以估计台调节时间为1.5格即0.6s ,说明满足要求,校正装置起到了预期的作用。
串联校正实验报告(3篇)

第1篇一、实验目的1. 了解串联校正的基本原理和设计方法。
2. 掌握利用串联校正装置改善系统性能的方法。
3. 通过实验验证串联校正对系统动态性能的影响。
二、实验原理串联校正是一种常用的控制系统设计方法,通过在系统的输入端或输出端添加校正装置,来改善系统的动态性能和稳态性能。
本实验主要研究串联校正对系统相位裕度和增益裕度的影响。
三、实验器材1. 控制系统实验平台2. 信号发生器3. 示波器4. 信号调理器5. 校正装置(如PID控制器、滤波器等)6. 计算机及仿真软件四、实验步骤1. 搭建实验系统:根据实验要求搭建控制系统实验平台,包括被控对象、校正装置和测量装置。
2. 设置实验参数:设置被控对象和校正装置的参数,如PID参数、滤波器参数等。
3. 进行开环实验:通过信号发生器向系统输入不同频率的正弦信号,利用示波器观察系统的输出响应,记录系统的相位裕度和增益裕度。
4. 进行闭环实验:将系统切换到闭环状态,再次输入正弦信号,观察系统的输出响应,记录系统的相位裕度和增益裕度。
5. 分析实验结果:比较开环和闭环实验结果,分析串联校正对系统性能的影响。
五、实验结果与分析1. 开环实验结果:通过开环实验,可以得到系统的相位裕度和增益裕度,以及系统的频率响应曲线。
2. 闭环实验结果:通过闭环实验,可以得到系统的相位裕度和增益裕度,以及系统的频率响应曲线。
3. 分析结果:- 当校正装置的参数设置合理时,系统的相位裕度和增益裕度会得到改善,从而提高系统的稳定性。
- 串联校正可以有效地抑制系统的振荡和超调,提高系统的响应速度。
- 串联校正对系统的稳态误差也有一定的影响,需要根据实际需求进行调整。
六、实验结论1. 串联校正是一种有效的控制系统设计方法,可以改善系统的动态性能和稳态性能。
2. 通过合理设置校正装置的参数,可以有效地提高系统的稳定性、响应速度和稳态精度。
3. 在实际应用中,需要根据被控对象和系统的具体要求,选择合适的校正装置和参数。
自动控制原理线性系统串联校正实验报告五

武汉工程大学实验报告专业电气自动化班号指导教师姓名同组者无
SIMULINK仿真模型:
单位阶跃响应波形:
分析:由以上阶跃响应波形可知,校正后,系统的超调量减小,调节时间变短,稳定性
单位阶跃响应:
单位阶跃响应:
分析:由以上仿真结果知,校正后,系统由不稳定变为稳定,系统的阶跃响应波形由发散
单位阶跃响应:
单位阶跃响应:
由以上仿真结果知,校正后,系统由不稳定变为稳定,系统的阶跃响应波形由发要求:正文用小四宋体,1.5倍行距,图表题用五号宋体,图题位于图下方,表题位于表上方。
自动控制实验报告五-连续系统串联校正

实验五连续系统串联校正一、实验目的1. 加深理解串联校正装置对系统动态性能的校正作用。
2. 对给定系统进行串联校正设计,并通过模拟实验检验设计的正确性。
二、实验仪器1.EL-AT-III型自动控制系统实验箱一台2.计算机一台三、实验内容1.串联超前校正(1)系统模拟电路图如图5-1,图中开关S断开对应未校情况,接通对应超前校正。
图5-1 超前校正电路图图5-1 超前校正电路图(2)系统结构图如图5-2图5-2 超前校正系统结构图图中Gc1(s)=22(0.055s+1)Gc2(s)=0.005s+12.串联滞后校正(1)模拟电路图如图5-3,开关s断开对应未校状态,接通对应滞后校正。
图5-3 滞后校正模拟电路图(2)系统结构图示如图5-4图5-4 滞后系统结构图图中Gc1(s)=1010(s+1)Gc2(s)=11s+13.串联超前—滞后校正(1)模拟电路图如图5-5,双刀开关断开对应未校状态,接通对应超前—滞后校正。
图5-5 超前—滞后校正模拟电路图(2)系统结构图示如图5-6。
图5-6超前—滞后校正系统结构图图中 Gc1(s)=66(1.2s+1)(0.15s+1)Gc2(s)=(6s+1)(0.05s+1)四、实验步骤1.启动计算机,在桌面双击图标 [自动控制实验系统] 运行软件。
2.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进行实验。
超前校正:3.连接被测量典型环节的模拟电路(图5-1)。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将将纯积分电容两端连在模拟开关上。
检查无误后接通电源。
4.开关s放在断开位置。
-5.在实验项目的下拉列表中选择实验五[五、连续系统串联校正]。
鼠标单击按钮,弹出实验课题参数设置对话框。
在参数设置对话框中设置相应的实验参数后鼠标单击确认等待屏幕的显示区显示实验结果,并记录超调量 p和调节时间ts。
控制系统的串联校正

接入超前校正装置,记录加超前校正后系统的单位阶跃响应曲线。
去掉超前校正网络,接入迟后校正网络,记录系统的单位阶跃响应曲线。
共 3 页指导教师签名
去掉迟后校正网络,接入迟后一超前网络,记录系统的单位阶跃响应曲线。
四、实训小结
)画出系统及校正环节的仿真模型。
)当系统开环增益K=10时,未加校正和分别加上三种校正方案后系统的单位阶跃响应曲线,从曲线上求,分析校正的作用,并指出哪种校正方案使系统的动态性能最好?
共 3 页指导教师签名。
自控实验报告-连续系统串联校正

实验二连续系统串联校正一、实验目的观察串联超前、滞后、滞后超前校正对改善系统性能的作用;学习串联校正的基本设计方法;观测超前、滞后、滞后超前三种校正方式的作用。
二、实验内容(1) 已知系统开环传递函数:()100(0.11)(0.011)o G s s s s =++模拟线路图如图1所示,图1 不加校正时的模拟电路图原系统的截止频率满足210010.1c ω=,解得31.62/c rad s ω=,其bode 图如图2图2 不加校正时的系统bode 图(2) 要求原系统经过超前校正后满足100v K =,40c rad ω≥,35%σ≤。
因为原系统已经能够满足速度误差系数100v K =,设超前校正的传递函数11lead Ts G Ts α+=+。
要求截止角频率40c rad ω≥,不妨取45/c rad s ω=,原系统在c ω处产生的相角arg(j )191.70c ω=- ,为了使系统有至少30°的相角裕量。
取arg((j )(j ))50lead c o c G G ωω= 又(j )(j )1lead c o c G G ωω=解得0.033,0.0027T T α==即0.03310.00271lead s G s +=+。
本次实验采用的超前系统传递函数为:0.041()0.0041c s G s s +=+图3超前校正部分自身的bode图其模拟线路图如图4所示:图4超前校正的电路图经过校正后的电路bode 图为:图5加入超前校正后电路的bode 图(3) 原系统经过滞后校正后100v K =,5c rad ω≥,40%σ≤。
设滞后校正装置的传递函数为:11lag Ts G Ts β+=+取截至角频率7/c rad s ω= 则有()()1lag c o c G j G j ωω= 不妨取10.2 1.4/c rad s Tω== 可以解得:=12.01T β即系统的滞后校正的传递函数可以取0.714112.011lag s G s +=+本次实验给出的滞后装置的传递函数为:0.51()8.51c s G s s +=+滞后部分的伯德图图6滞后校正部分自身的bode 图其模拟线路图如图7所示:图7加滞后校正的电路图电路的bode 图如图所示:图8加入滞后校正后的电路bode 图(4)原系统经过滞后超前校正后100v K =,20c rad ω≥,10%σ≤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称:控制系统串联校正
目录
(一)实验目的 (3)
(二)实验内容 (3)
(三)实验设备 (3)
(四)实验原理 (3)
(五)实验结果 (4)
(六)数据分析的 (7)
附页: (9)
Matlab模拟波特图程序: (9)
图片目录
图片1 系统结构图 (3)
图片2 系统模拟电路 (3)
图片3 无校正阶跃响应曲线 (4)
图片4 无校正时波特图 (5)
图片5 超前校正阶跃响应曲线 (5)
图片6 超前校正时波特图 (6)
图片7 滞后校正阶跃响应曲线 (6)
图片8 滞后校正波特图 (7)
表格目录
表格1 稳定裕度和截止频率 (7)
表格2 阶跃响应数据 (7)
控制系统串联校正
(一) 实验目的
(1) 了解和掌握串联校正的分析和设计方法;
(2) 研究串联校正环节对系统稳定性及过度过程的影响;
(二) 实验内容
(1) 设计串联超前校正,并验证; (2) 设计串联超前校正,并验证;
(三) 实验设备
(1) HMNN 电子模拟机一台 (2) PC 机一台 (3) 万用表一块
(四) 实验原理
图片 1 系统结构图
其中()C G s 为校正环节,在本实验中利用系统模型实现; 不加校正环节时,系统的开环传递函数为:
4
()(1)
G s s s =
+
图片 2 系统模拟电路
K1 T1 K2 T2 K3
(1) 未加校正环节时()1C G s =
(2) 加串联超前校正环节时,传递函数: 1()1C Ts
G s Ts
α+=
+,其中: 2.55α=,0.26T =:
10.63()10.26C s
G s s
+=
+ (3) 加串联止滞后校正环节时,传递函数: 1()1C bTs
G s Ts
+=+,其中:0.12b =,83.33T =:
110()183.33C s
G s s
+=
+
根据系统模型,可以达到系统参数的计算方法:
12/113125/425231
K R R T R C K R R T R C K ==⨯==⨯= (五) 实验结果
(1) 由系统参数的计算公式可以得到(在实际电路中,略去由第一个和最后一个运算放
大器构成的放大电路):
512142503111R M C uf R K R M C uf
=Ω
==Ω=Ω=
(2) 不加校正时的阶跃响应曲线和波特图
图片 3 无校正阶跃响应曲线
(3)加入超前校正时的阶跃响应曲线和波特图图片 5 超前校正阶跃响应曲线
(4)加入滞后校正时的阶跃响应曲线和波特图图片7 滞后校正阶跃响应曲线
根据波特图仿真结果可得:
表格 1 稳定裕度和截止频率
计算
(六)数据分析的
时频域分析:
(1)由实际获得的阶跃响应实验数据可以得到:
表格 2 阶跃响应数据
所列时间已减去阶跃响应的0.5s延迟;
w附近的区段,考察系统的平稳性和(2)利用中频段开环对数幅频特性曲线在截止频率
c
快速性(过渡过程);
A)无反馈环节:利用开环传递函数,可以得到系统的转折频率为1rad/s,即在w大于转折频率的情况下,开环幅频特性曲线斜率近似为-40db/dec(中频段),由获得的无反馈条
件下阶跃响应曲线(图3)和上表(表2)可以看出,系统振荡性较强,虽然振荡衰减,
w与调节之间见的反比关系,此时截止频率大小在三个系统但超调量较大,同时考虑
c
中处于中间,而获得的实际调节时间数据也验证了这种关系。
同时,根据频率特性曲线可以计算出:相稳定裕度=28degree,模稳定裕度=3507,相对较小,利用理论分析的结论可知,稳定裕度(包括模稳定裕度和相稳定裕度)相对较小意味着超调量大,振荡性强;
B)超前校正环节:通过表1可以看到,通过超前校正,系统的稳定裕度得到了大大增加,
w与调节时间间的反比关系,通同时截止频率相对无校正环节时也有所上升,考虑到
c
w较大,则调节时间较小;稳定裕度较大,对应阶跃故理论分析可以得到:此时对于
c
相应超调量也应该较小,震荡较弱。
参考实际时域阶跃响应曲线(图5)和表2,此时超调量和调节时间相比于无反馈时都明显减小,同时系统的振荡性也得到明显减弱,符合上段理论分析的结果。
w相对最小,但稳定裕度最大,可以得到理论分析结果C)滞后校正环节:参考表1,此时
c
w成反比),系统的为:此时在时域的阶跃响应,调节时间应在三个系统中最长(因与
c 平稳性好,对应超调量最小,振荡最弱。
参考实际时域阶跃响应曲线(图7)和表2,此时系统无振荡,超调量为19.75%是三个系统中最小的,但调节时间最长,此结果符合理论分析的预期。
(3)数据分析总结:
综合第(2)条中分析得到的结论,并结合课本理论知识,对加入超前及之后校正环节给系统阶跃响应带来的影响总结如下:
合理的设置校正环节,能对系统的平稳性和快速性有所改善,不同的校正环节改善情况各不相同;
对超前环节,通过增大截止频率和稳定裕度,能够在一定程度上改善系统的稳定性,同时对快速性的提高也有所帮助;
对滞后环节,能够增大稳定裕度,但会减小系统的截止频率,因此,滞后校正是通过牺牲快速性来换取稳定性和振荡性的改善。
附页:
(1)Matlab模拟波特图程序:w=logspace(-2,3,200);
num=[2.52 4];
den=[0.26 1.26 1 0];
g=tf(num,den);
[x,y,w]=bode(g,w);
margin(x,y,w);。
