《电力电子技术》课后答案
电力电子技术第二版课后答案

【复习思考】1.1电力电子技术的任务是什么?答:电力电子技术的根本任务是实现电能的变换、控制和调节。
1.2根据电能变换种类的不同,电力电子变换电路分为哪几种类型?各自的作用是什么?答:根据电能变换种类的不同,电力电子变换电路分为直流-直流变换、直流-交流变换、交流-直流变换、交流-交流变换四种类型。
直流-直流变换的作用是将一种直流电变换为另一固定或可调电压的直流电的电路;直流-交流变换的作用是使直流变成可调的交流电,而且可输出连续可调的工作频率;交流-直流变换的作用是将交流电变换为固定或可调的直流电的电路;交流-交流变换的作用是将交流电的参数(幅值、频率等)加以转换。
1.3信息电子技术和电力电子技术的相同和不同点分别是什么?控制理论在电力电子技术中有什么作用?答:电力电子技术和信息电子技术的相同点:①从器件的制造技术上讲两者同根同源,都是采用半导体材料制成,而且两者大多数的制造工艺也是一致的。
①两者电路的分析方法也基本一致。
电力电子技术和信息电子技术的不同点:①电力电子技术变换的是“电力”,所处理的电能功率一般是“大功率”,但也可以处理“小功率”;信息电子技术变换的是“信息”,一般处理的是“小功率”。
①在信息电子技术中的电子器件既可处于放大状态,也可处于开关状态;而在电力电子技术中为了避免功率损耗过大,电力电子器件总是工作在开关状态。
电力电子技术实质上是将现代电子技术和控制技术引入到传统电力技术领域实现电力变换和控制,可以看作弱电控制强电的技术,是弱电和强电之间的接口。
而控制理论则是实现这种接口的强有力的纽带。
1.4电力电子器件的发展分为哪几个阶段?答:电力电子技术的发展可以根据电力电子器件的发展分为4个阶段:第一个阶段:电子管、汞弧整流器等非半导体器件为主的史前期;第二个阶段:晶闸管时代;第三个阶段:全控型器件时代;第四个阶段:复合/新型器件时代。
【复习思考】2.1电力二极管属于哪种类型的控制器件?在电力电子电路中有哪些用途?答:电力二极管属于不可控型、双极性器件;用途:可作为整流、续流、保护元件用。
《电力电子技术》习题答案第四版

《电力电子技术》习题答案(第四版_ 1.电力电子技术的基本原理是什么?答:电力电子技术是指通过电子器件将
电能进行控制和转换的技术。
其基本原理是利用半导体器件的导通和截止特性,通过控制电流和电压的方向和大小,实现对电能的调节和转换。
2.什么是电力电子器件?答:电力电子器件是用于电力电子技术中的半导体
器件,常见的有晶闸管、二极管、MOSFET、IGBT等。
这些器件具有导通和截止的特性,可以实现对电能的控制和转换。
3.请简述晶闸管的工作原理。
答:晶闸管是一种双向可控的半导体开关器
件。
其工作原理是通过控制晶闸管的控制极,将其导通或截止。
当控制极施加一个触发脉冲时,晶闸管的阳极和阴极之间的电流将开始流动,晶闸管处于导通状态;当没有触发脉冲时,晶闸管处于截止状态。
4.什么是PWM调制技术?答:PWM调制技术是一种通过改变脉冲宽度的方式
来实现对电能的调节。
通过改变脉冲的宽度,可以改变电平的平均值,从而实现对电能的调节。
PWM调制技术广泛应用于电力电子领域,如变频调速、电力供应等。
5.请简述逆变器的工作原理。
答:逆变器是一种将直流电能转换为交流电能
的电力电子设备。
其工作原理是通过控制器控制晶闸管等开关器件的导通和截止,将直流电源的电压和电流转换为交流电压和电流。
逆变器广泛应用于太阳能发电、电动汽车等领域。
电力电子课后答案(整理版)

电力电子技术课后习题答案 第2章 电力电子器件1. 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:u AK >0且u GK >0。
2. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸管由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
3. 图1-43中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I 1、I 2、I 3。
π4π4π25π4a)b)c)图1-43图1-43 晶闸管导电波形解:a) I d1=π21⎰ππωω4)(sin t td I m =π2m I (122+)≈0.2717 I m I 1=⎰ππωωπ42)()sin (21t d t I m =2m I π2143+≈0.4767 I m b) I d2 =π1⎰ππωω4)(sin t td I m =πmI (122+)≈0.5434 I m I 2 =⎰ππωωπ42)()sin (1t d t I m =2m I π2123+≈0.898 I m c) I d3=π21⎰2)(πωt d I m =0.25I mI 3 =⎰202)(21πωπt d I m =0.5I m4. 上题中如果不考虑安全裕量,问100A 的晶闸管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(AV) =100A 的晶闸管,允许的电流有效值I =157A ,由上题计算结果知a) I m1≈4767.0I≈329.35, I d1≈0.2717 I m1≈89.48b) I m2≈6741.0I≈232.90, I d2≈0.5434 I m2≈126.56c) I m3=2 I = 314, I d3=41I m3=78.55. GTO 和普通晶闸管同为PNPN 结构,为什么GTO 能够自关断,而普通晶闸管不能? 答:GTO 和普通晶闸管同为PNPN 结构,由P 1N 1P 2和N 1P 2N 2构成两个晶体管V 1、V 2,分别具有共基极电流增益1α和2α,由普通晶闸管的分析可得,1α+2α=1是器件临界导通的条件。
电力电子技术课后答案pdf版

pd
y
第1章
1. 使晶闸管导通的条件是什么?
电力电子器件
答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。 或:uAK>0 且 uGK>0。 2. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断? 答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持 电流。 要使晶闸管由导通变为关断, 可利用外加电压和外电路的作用使流过晶闸管的电流降 到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。 3. 图 1-43 中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为 Im,试计算各波形的电流平均值 Id1、Id2、Id3 与电流有效值 I1、I2、I3。
目 录
第1章 第2章 第3章 第4章 第5章 第6章 第7章 第8章
电力电子器件 ········································································· 1 整流电路 ·················································································· 4 直流斩波电路 ······································································· 20 交流电力控制电路和交交变频电路 ·································· 26 逆变电路 ················································································ 31 PWM 控制技术 ····································································· 35 软开关技术············································································ 40 组合变流电路 ······································································· 42
《电力电子技术》课后答案完整版

GTO电压、电流容量大,适用于大功率场合,具有电导调制效应,其通流能力很强。电流关断增益很小,关断时门极负脉
冲电流大,开关速度低,驱动功率大,
驱动电路复杂,开关频率低。
电力
MOSFET
开关速度快,输入阻抗高,热稳定性好,所需驱动功率小且驱动电路简单,工作频率高,不存在二次击穿问题。通态电阻大,通态损耗大,电流容量
d I ,并画出d u与d i波形。
解: ︒=0α时,在电源电压2u的正半周期晶闸管导通时,负载电感L储能,在晶闸管开始导通时刻,负载电流为零。在电源电压2u的负半周期,负载电感L释放能量,晶闸管继续导通。因此,在电源电压2u的一个
周期里,以下方程均成立:
t U dt
di L
d
ωsin 22=考虑到初始条件:当0=t ω时0=d i可解方程得:
αα+两个等效晶体管过饱和而导通;121<
αα+不能维持饱和导通而关断。GTO之所以能够自行关断,而普通晶闸管不能,是因为GTO与普通晶闸管在设计和工艺方面有以下几点
图1-43晶闸管导电波形
不同:1多元并联集成结构使每个GTO元阴极面积很小,门极和阴极间的距离大为缩短,2P区的横向电阻很小,显著减小了横向压降效应,从而使从门极抽出较大的电流成为可能;
对于电感负载;~(απα+期问,单相全波电路中1VT导逼,单相全控桥电路中1VT、4VT导通,输出电压均与电源电压2U相等;2~(απαπ++期间,单相全波电路中2VT导通,单相全控桥电路中2VT、3VT导通,输出波形等于2U -。
可见,两者的输出电压相同,加到同样的负载上时,则输出电流也相同。
2.3单相桥式全控整流电路,V U 1002=,负载中Ω=20R ,L值极大,当︒=30α时,要求:①作出d u、
(完整版)《电力电子技术(第二版)》课后习题及解答

《电力电子技术》习题及解答第1章思考题与习题1.1晶闸管的导通条件是什么? 导通后流过晶闸管的电流和负载上的电压由什么决定?答:晶闸管的导通条件是:晶闸管阳极和阳极间施加正向电压,并在门极和阳极间施加正向触发电压和电流(或脉冲)。
导通后流过晶闸管的电流由负载阻抗决定,负载上电压由输入阳极电压U A决定。
1.2晶闸管的关断条件是什么?如何实现?晶闸管处于阻断状态时其两端的电压大小由什么决定?答:晶闸管的关断条件是:要使晶闸管由正向导通状态转变为阻断状态,可采用阳极电压反向使阳极电流I A减小,I A下降到维持电流I H以下时,晶闸管内部建立的正反馈无法进行。
进而实现晶闸管的关断,其两端电压大小由电源电压U A决定。
1.3温度升高时,晶闸管的触发电流、正反向漏电流、维持电流以及正向转折电压和反向击穿电压如何变化?答:温度升高时,晶闸管的触发电流随温度升高而减小,正反向漏电流随温度升高而增大,维持电流I H会减小,正向转折电压和反向击穿电压随温度升高而减小。
1.4晶闸管的非正常导通方式有哪几种?答:非正常导通方式有:(1) I g=0,阳极电压升高至相当高的数值;(1) 阳极电压上升率du/dt 过高;(3) 结温过高。
1.5请简述晶闸管的关断时间定义。
答:晶闸管从正向阳极电流下降为零到它恢复正向阻断能力所需的这段时间称为关断时间。
即gr rr q t t t +=。
1.6试说明晶闸管有哪些派生器件?答:快速晶闸管、双向晶闸管、逆导晶闸管、光控晶闸管等。
1.7请简述光控晶闸管的有关特征。
答:光控晶闸管是在普通晶闸管的门极区集成了一个光电二极管,在光的照射下,光电二极管电流增加,此电流便可作为门极电触发电流使晶闸管开通。
主要用于高压大功率场合。
1.8型号为KP100-3,维持电流I H =4mA 的晶闸管,使用在图题1.8所示电路中是否合理,为什么?(暂不考虑电压电流裕量)图题1.8答:(a )因为H A I mA K V I <=Ω=250100,所以不合理。
(完整word版)电力电子技术.课后习题答案.南航.丁道宏

第一章第1章 思考题与习题1.1晶闸管的导通条件是什么? 导通后流过晶闸管的电流和负载上的电压由什么决定? 答:晶闸管的导通条件是:晶闸管阳极和阳极间施加正向电压,并在门极和阳极间施加正向触发电压和电流(或脉冲)。
导通后流过晶闸管的电流由负载阻抗决定,负载上电压由输入阳极电压U A 决定。
1.2晶闸管的关断条件是什么? 如何实现? 晶闸管处于阻断状态时其两端的电压大小由什么决定?答:晶闸管的关断条件是:要使晶闸管由正向导通状态转变为阻断状态,可采用阳极电压反向使阳极电流I A 减小,I A 下降到维持电流I H 以下时,晶闸管内部建立的正反馈无法进行。
进而实现晶闸管的关断,其两端电压大小由电源电压U A 决定。
1.3温度升高时,晶闸管的触发电流、正反向漏电流、维持电流以及正向转折电压和反向击穿电压如何变化?答:温度升高时,晶闸管的触发电流随温度升高而减小,正反向漏电流随温度升高而增大,维持电流I H 会减小,正向转折电压和反向击穿电压随温度升高而减小。
1.4晶闸管的非正常导通方式有哪几种?答:非正常导通方式有:(1) I g =0,阳极电压升高至相当高的数值;(1) 阳极电压上升率du/dt 过高;(3) 结温过高。
1.5请简述晶闸管的关断时间定义。
答:晶闸管从正向阳极电流下降为零到它恢复正向阻断能力所需的这段时间称为关断时间。
即gr rr q t t t +=。
1.6试说明晶闸管有哪些派生器件?答:快速晶闸管、双向晶闸管、逆导晶闸管、光控晶闸管等。
1.7请简述光控晶闸管的有关特征。
答:光控晶闸管是在普通晶闸管的门极区集成了一个光电二极管,在光的照射下,光电二极管电流增加,此电流便可作为门极电触发电流使晶闸管开通。
主要用于高压大功率场合。
1.8型号为KP100-3,维持电流I H =4mA 的晶闸管,使用在图题1.8所示电路中是否合理,为什么?(暂不考虑电压电流裕量)图题1.8答:(a )因为H A I mA K VI <=Ω=250100,所以不合理。
(完整版)电力电子技术(王兆安第五版)课后习题全部答案

电力电子技术2-1与信息电子电路中的二极管相比,电力二极管具有怎样的结构特点才使得其具有耐受高压和大电流的能力?答:1.电力二极管大都采用垂直导电结构,使得硅片中通过电流的有效面积增大,显著提高了二极管的通流能力。
2.电力二极管在P区和N区之间多了一层低掺杂N区,也称漂移区。
低掺杂N区由于掺杂浓度低而接近于无掺杂的纯半导体材料即本征半导体,由于掺杂浓度低,低掺杂N区就可以承受很高的电压而不被击穿。
2-2. 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:uAK>0且uGK>0。
2-3. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
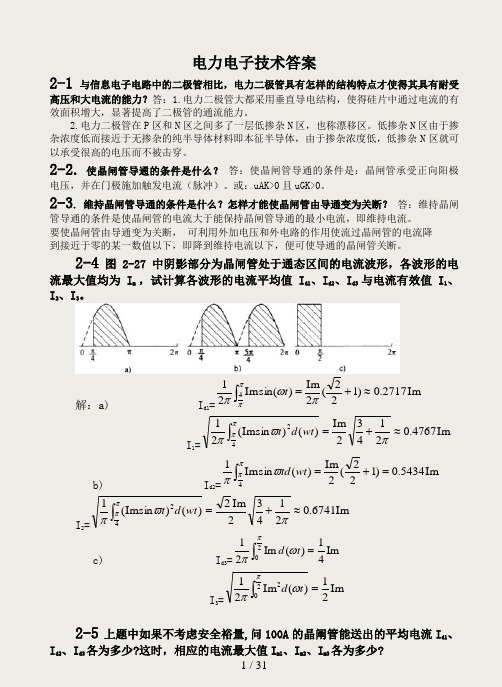
2-4 图2-27中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I1、I2、I3。
解:a) I d1=Im2717.0)122(2Im)(sinIm214≈+=⎰πωπππtI1=Im4767.021432Im)()sin(Im2142≈+=⎰πϖπππwtdtb) I d2=Im5434.0)122(2Im)(sinIm14=+=⎰wtd tππϖπI2=Im6741.021432Im2)()sin(Im142≈+=⎰πϖπππwtdtc) I d3=⎰=2Im41)(Im21πωπtdI3=Im21)(Im2122=⎰tdωππ2-5上题中如果不考虑安全裕量,问100A的晶阐管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(AV)=100A的晶闸管,允许的电流有效值I=157A,由上题计算结果知a) I m135.3294767.0≈≈IA, I d1≈0.2717I m1≈89.48A b) I m2,90.2326741.0A I≈≈I d2A I m 56.1265434.02≈≈c) I m3=2I=314 I d3=5.78413=m I2-6 GTO 和普通晶闸管同为PNPN 结构,为什么GTO 能够自关断,而普通晶闸管不能?答:GTO 和普通晶阐管同为PNPN 结构,由P1N1P2和N1P2N2构成两个晶体管V1、V2,分别具有共基极电流增益1α和2α,由普通晶阐管的分析可得,121=+αα是器件临界导通的条件。
电力电子技术(王兆安第五版)课后习题全部答案精编版

电力电子技术2-1与信息电子电路中的二极管相比,电力二极管具有怎样的结构特点才使得其具有耐受高压和大电流的能力?答:1.电力二极管大都采用垂直导电结构,使得硅片中通过电流的有效面积增大,显著提高了二极管的通流能力。
2.电力二极管在P区和N区之间多了一层低掺杂N区,也称漂移区。
低掺杂N区由于掺杂浓度低而接近于无掺杂的纯半导体材料即本征半导体,由于掺杂浓度低,低掺杂N区就可以承受很高的电压而不被击穿。
2-2. 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:uAK>0且uGK>0。
2-3. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
2-4 图2-27中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I1、I2、I3。
解:a) I d1=Im2717.0)122(2Im)(sinIm214≈+=⎰πωπππtI1=Im4767.021432Im)()sin(Im2142≈+=⎰πϖπππwtdtb) I d2=Im5434.0)122(2Im)(sinIm14=+=⎰wtd tππϖπI2=Im6741.021432Im2)()sin(Im142≈+=⎰πϖπππwtdtc) I d3=⎰=2Im41)(Im21πωπtdI3=Im21)(Im2122=⎰tdωππ2-5上题中如果不考虑安全裕量,问100A的晶阐管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(AV)=100A的晶闸管,允许的电流有效值I=157A,由上题计算结果知a) I m135.3294767.0≈≈IA, I d1≈0.2717I m1≈89.48Ab) I m2,90.2326741.0A I≈≈I d2A I m 56.1265434.02≈≈c) I m3=2I=314 I d3=5.78413=m I2-6 GTO 和普通晶闸管同为PNPN 结构,为什么GTO 能够自关断,而普通晶闸管不能?答:GTO 和普通晶阐管同为PNPN 结构,由P1N1P2和N1P2N2构成两个晶体管V1、V2,分别具有共基极电流增益1α和2α,由普通晶阐管的分析可得,121=+αα是器件临界导通的条件。
电力电子技术.课后习题答案.南航.丁道宏

第一章第1章 思考题与习题1.1晶闸管的导通条件是什么? 导通后流过晶闸管的电流和负载上的电压由什么决定? 答:晶闸管的导通条件是:晶闸管阳极和阳极间施加正向电压,并在门极和阳极间施加正向触发电压和电流(或脉冲)。
导通后流过晶闸管的电流由负载阻抗决定,负载上电压由输入阳极电压U A 决定。
1.2晶闸管的关断条件是什么? 如何实现? 晶闸管处于阻断状态时其两端的电压大小由什么决定?答:晶闸管的关断条件是:要使晶闸管由正向导通状态转变为阻断状态,可采用阳极电压反向使阳极电流I A 减小,I A 下降到维持电流I H 以下时,晶闸管内部建立的正反馈无法进行。
进而实现晶闸管的关断,其两端电压大小由电源电压U A 决定。
1.3温度升高时,晶闸管的触发电流、正反向漏电流、维持电流以及正向转折电压和反向击穿电压如何变化?答:温度升高时,晶闸管的触发电流随温度升高而减小,正反向漏电流随温度升高而增大,维持电流I H 会减小,正向转折电压和反向击穿电压随温度升高而减小。
1.4晶闸管的非正常导通方式有哪几种?答:非正常导通方式有:(1) I g =0,阳极电压升高至相当高的数值;(1) 阳极电压上升率du/dt 过高;(3) 结温过高。
1.5请简述晶闸管的关断时间定义。
答:晶闸管从正向阳极电流下降为零到它恢复正向阻断能力所需的这段时间称为关断时间。
即gr rr q t t t +=。
1.6试说明晶闸管有哪些派生器件?答:快速晶闸管、双向晶闸管、逆导晶闸管、光控晶闸管等。
1.7请简述光控晶闸管的有关特征。
答:光控晶闸管是在普通晶闸管的门极区集成了一个光电二极管,在光的照射下,光电二极管电流增加,此电流便可作为门极电触发电流使晶闸管开通。
主要用于高压大功率场合。
1.8型号为KP100-3,维持电流I H =4mA 的晶闸管,使用在图题1.8所示电路中是否合理,为什么?(暂不考虑电压电流裕量)图题1.8答:(a )因为H A I mA K VI <=Ω=250100,所以不合理。
《电力电子技术(第二版)》习题答案

《电力电子技术》习题及解答第1章 思考题与习题1.1晶闸管的导通条件是什么? 导通后流过晶闸管的电流和负载上的电压由什么决定? 答:晶闸管的导通条件是:晶闸管阳极和阳极间施加正向电压,并在门极和阳极间施加正向触发电压和电流(或脉冲)。
导通后流过晶闸管的电流由负载阻抗决定,负载上电压由输入阳极电压U A 决定。
1.2晶闸管的关断条件是什么? 如何实现? 晶闸管处于阻断状态时其两端的电压大小由什么决定?答:晶闸管的关断条件是:要使晶闸管由正向导通状态转变为阻断状态,可采用阳极电压反向使阳极电流I A 减小,I A 下降到维持电流I H 以下时,晶闸管内部建立的正反馈无法进行。
进而实现晶闸管的关断,其两端电压大小由电源电压U A 决定。
1.3温度升高时,晶闸管的触发电流、正反向漏电流、维持电流以及正向转折电压和反向击穿电压如何变化?答:温度升高时,晶闸管的触发电流随温度升高而减小,正反向漏电流随温度升高而增大,维持电流I H 会减小,正向转折电压和反向击穿电压随温度升高而减小。
1.4晶闸管的非正常导通方式有哪几种?答:非正常导通方式有:(1) I g =0,阳极电压升高至相当高的数值;(1) 阳极电压上升率du/dt 过高;(3) 结温过高。
1.5请简述晶闸管的关断时间定义。
答:晶闸管从正向阳极电流下降为零到它恢复正向阻断能力所需的这段时间称为关断时间。
即gr rr q t t t +=。
答:快速晶闸管、双向晶闸管、逆导晶闸管、光控晶闸管等。
1.7请简述光控晶闸管的有关特征。
答:光控晶闸管是在普通晶闸管的门极区集成了一个光电二极管,在光的照射下,光电二极管电流增加,此电流便可作为门极电触发电流使晶闸管开通。
主要用于高压大功率场合。
1.8型号为KP100-3,维持电流I H =4mA 的晶闸管,使用在图题1.8所示电路中是否合理,为什么?(暂不考虑电压电流裕量)图题1.8答:(a )因为H A I mA K VI <=Ω=250100,所以不合理。
电力电子技术(第五版)课后习题全部答案
电力电子技术答案2-1与信息电子电路中的二极管相比,电力二极管具有怎样的结构特点才使得其具有耐受高压和大电流的能力?答:1.电力二极管大都采用垂直导电结构,使得硅片中通过电流的有效面积增大,显著提高了二极管的通流能力。
2.电力二极管在P区和N区之间多了一层低掺杂N区,也称漂移区。
低掺杂N区由于掺杂浓度低而接近于无掺杂的纯半导体材料即本征半导体,由于掺杂浓度低,低掺杂N区就可以承受很高的电压而不被击穿。
2-2.使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:uAK>0且uGK>0。
2-3. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸管由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
2-4图2-27中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为Im ,试计算各波形的电流平均值Id1、Id2、Id3与电流有效值I1、I2、I3。
解:a) Id1=Im2717.0)122(2Im)(sinIm214≈+=⎰πωπππtI1=Im4767.021432Im)()sin(Im2142≈+=⎰πϖπππwtdtb) Id2=Im5434.0)122(2Im)(sinIm14=+=⎰wtd tππϖπI 2=Im6741.021432Im2)()sin(Im142≈+=⎰πϖπππwtdtc) Id3=⎰=2Im41)(Im21πωπtdI3=Im21)(Im2122=⎰tdωππ2-5上题中如果不考虑安全裕量,问100A的晶阐管能送出的平均电流I d1、Id2、Id3各为多少?这时,相应的电流最大值Im1、Im2、Im3各为多少?解:额定电流I T(AV)=100A 的晶闸管,允许的电流有效值I=157A,由上题计算结果知a) I m135.3294767.0≈≈I A, I d1≈0.2717I m1≈89.48A b) I m2,90.2326741.0A I ≈≈ I d2A I m 56.1265434.02≈≈c) I m3=2I=314 I d3=5.78413=m I2-6 GTO和普通晶闸管同为PNPN 结构,为什么GTO 能够自关断,而普通晶闸管不能?答:GTO 和普通晶阐管同为PNPN 结构,由P1N1P2和N1P2N2构成两个晶体管V1、V2,分别具有共基极电流增益1α和2α,由普通晶阐管的分析可得,121=+αα是器件临界导通的条件。
电力电子技术课后习题全部答案

第2章电力电子器件1.1 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正相阳极电压,并在门极施加触发电流(脉冲)。
或者U AK >0且U GK>01.2 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
1.3 图1-43中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I1、I2、I3。
解:a) I d1=Im2717.0)122(2Im)(sinIm214≈+=⎰πωπππtI1=Im4767.021432Im)()sin(Im2142≈+=⎰πϖπππwtdtb) I d2=Im5434.0)122(2Im)(sinIm14=+=⎰wtd tππϖπI2=Im6741.021432Im2)()sin(Im142≈+=⎰πϖπππwtdtc) I d3=⎰=2Im41)(Im21πωπtdI3=Im21)(Im2122=⎰tdωππ1.4.上题中如果不考虑安全裕量,问100A的晶阐管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(A V)=100A的晶闸管,允许的电流有效值I=157A,由上题计算结果知a) I m135.3294767.0≈≈IA, I d1≈0.2717I m1≈89.48Ab) I m2,90.2326741.0AI≈≈I d2AIm56.1265434.02≈≈c) I m3=2I=314 I d3=5.78 413=mI1.9.试说明IGBT、GTR、GTO和电力MOSFET各自的优缺点。
解:对ⅠGBT、GTR、GTO和电力MOSFET的优缺点的比较如下表:1.10什么是晶闸管的额定电流?答:晶闸管的额定电流就是它的通态平均电流,国标规定:是晶闸管在环境温度为40℃和规定的冷却状态下,稳定结温不超过额定结温所允许的最大工频正弦半波电流的平均值。
《电力电子技术》(科学出版社_程汉湘编著)习题答案

《电力电子技术》(科学出版社_程汉湘编著)习题答案2-1.一个开关器件的数据表的详细开关时间如下(对应图2.7(a))所示固定感应开关的线性特性):t ri =100ns ,t fv =50ns ,t rv =100ns ,t fi =200ns 。
试计算当频率范围为25~100khz 时的开关能量损失,并绘图。
假设图2.7(a)的电路中U d =300V ,I 0=4A 。
解:(1)先求出25s f kHz =时的开关能量损失T P 1)开关损耗:由: 7()150 1.510c on ri fv t t t ns s -=+==?7()300310c off rv fi t t t ns s -=+==? 4()() 4.510s on off t tc tc s -=+=?得:470113004 2.510 4.5106.7522s d S s P U I f t w-===2)导通损耗:000on on on on s sU Vt P U I f t =∴==3)关断损耗:01 4.52offd s off P U I f t w=开关的平均能量损耗: 6.75T s o n s P P P P w =+== 开关损耗如图2-1(2)同理:当100s f K H z =时: 1)开关损耗:由: 7()150 1.510c on ri fv t t t ns s -=+==?7()300310c off rv fi t t t ns s -=+==? 4()() 4.510s on off t tc tc s -=+=?570113004110 4.5102722s d S s P U I f t w-===2)导通损耗:000on on on on s sU Vt P U I f t =∴==3)关断损耗:01182offd s off P U I f t w=开关的平均能量损耗: 27T s on s P P P P w =+== 开关损耗如图2-2图2-1 图2-22-2.在下图的开关电路中,有U d =300V ,f V =100kHz ,R =75Ω。
电力电子技术答案第五版全

电子电力课后习题答案第一章电力电子器件使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管蒙受正相阳极电压,并在门极施加触发电流(脉冲)。
或许 U AK >0 且 U GK>0保持晶闸管导通的条件是什么?如何才能使晶闸管由导通变为关断?答:保持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即保持电流。
1.3 图 1- 43 中暗影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为 Im,试计算各波形的电流均匀值 I d1、 I d2、I d3与电流有效值 I 1、I 2、 I 3。
14 Im sin( t)Im ( 21)0.2717 Im解: a)I d1222=1(Im sin t) 2 d ( wt)Im31I1=242421Im sin td( wt )Im21)0.5434 Im(b)I d2=4221(Im sin t) 2 d ( wt) 2 Im31I 2=424212 Im d (t)1 Imc)I d3=20412 Im 2 d (t )1 ImI3=2021.4. 上题中假如不考虑安全裕量, 问 100A 的晶阐管能送出的均匀电流I d1、 I d2、I d3各为多少 ?这时,相应的电流最大值I m1、 I m2、I m3各为多少 ?解:额定电流 I T(AV) =100A的晶闸管,同意的电流有效值I=157A, 由上题计算结果知a)Ib)I m1m2IIA,I232.90 A,Id1d20.5434 Im1m 2126.56 A1I m3c)m3Id3=4 I =2I=3141.5.GTO 和一般晶闸管同为PNPN构造 , 为何 GTO能够自关断 , 而一般晶闸管不可以 ?答: GTO和一般晶阐管同为PNPN构造,由 P1N1P2和 N1P2N2构成两个晶体管 V1、 V2,分别拥有共基极电流增益 1 和 2 ,由一般晶阐管的剖析可得, 1 2 1 是器件临界导通的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 电力电子器件2. 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:u AK >0且u GK >0。
3. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断?答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸管由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
4. 图1-43中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I π4π4π25π4a)b)c)图1-43图1-43 晶闸管导电波形解:a)I d1=π21⎰ππωω4)(sin t td I m =π2m I (122+)≈0.2717 I mI 1=⎰ππωωπ42)()sin (21t d t I m =2mI π2143+≈0.4767 I m b) I d2 =π1⎰ππωω4)(sin t td I m =πm I (122+)≈0.5434 I m I 2 =⎰ππωωπ42)()sin (1t d t I m =22m I π2143+≈0.6741I m c)I d3=π21⎰20)(πωt d I m =41 I mI 3 =⎰22)(21πωπt d I m =21 I m5. 上题中如果不考虑安全裕量,问100A 的晶闸管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(AV) =100A 的晶闸管,允许的电流有效值I =157A ,由上题计算结果知a) I m1≈4767.0I≈329.35, I d1≈0.2717 I m1≈89.48b)I m2≈6741.0I ≈232.90,I d2≈0.5434 I m2≈126.56 c) I m3=2 I = 314,I d3=41 I m3=78.56. GTO 和普通晶闸管同为PNPN 结构,为什么GTO 能够自关断,而普通晶闸管不能?答:GTO 和普通晶闸管同为PNPN 结构,由P 1N 1P 2和N 1P 2N 2构成两个晶体管V 1、V 2,分别具有共基极电流增益1α和2α,由普通晶闸管的分析可得,1α+2α=1是器件临界导通的条件。
1α+2α>1,两个等效晶体管过饱和而导通;1α+2α<1,不能维持饱和导通而关断。
GTO 之所以能够自行关断,而普通晶闸管不能,是因为GTO 与普通晶闸管在设计和工艺方面有以下几点不同:1) GTO 在设计时2α较大,这样晶体管V 2控制灵敏,易于GTO 关断;2) GTO 导通时的1α+2α更接近于1,普通晶闸管1α+2α≥1.15,而GTO 则为1α+2α≈1.05,GTO 的饱和程度不深,接近于临界饱和,这样为门极控制关断提供了有利条件;3) 多元集成结构使每个GTO 元阴极面积很小,门极和阴极间的距离大为缩短,使得P 2极区所谓的横向电阻很小,从而使从门极抽出较大的电流成为可能。
第3章 整流电路1. 单相半波可控整流电路对电感负载供电,L =20mH ,U 2=100V ,求当α=0︒和60︒时的负载电流I d ,并画出u d 与i d 波形。
解:α=0︒时,在电源电压u 2的正半周期晶闸管导通时,负载电感L 储能,在晶闸管开始导通时刻,负载电流为零。
在电源电压u 2的负半周期,负载电感L 释放能量,晶闸管继续导通。
因此,在电源电压u 2的一个周期里,以下方程均成立:t U ti Lωsin 2d d 2d= 考虑到初始条件:当ωt =0时i d =0可解方程得:)cos 1(22d t L U i ωω-=⎰-=πωωωπ202d )(d )cos 1(221t t LU I=LU ω22=22.51(A)u d 与i d 的波形如下图:当α=60°时,在u 2正半周期60︒~180︒期间晶闸管导通使电感L 储能,电感L 储藏的能量在u 2负半周期180︒~300︒期间释放,因此在u 2一个周期中60︒~300︒期间以下微分方程成立:t U ti Lωsin 2d d 2d= 考虑初始条件:当ωt =60︒时i d =0可解方程得:)cos 21(22d t L U i ωω-=其平均值为)(d )cos 21(2213532d t t L U I ωωωπππ-=⎰=L U ω222=11.25(A)此时u d 与i d 的波形如下图:3.单相桥式全控整流电路,U2=100V,负载中R=2Ω,L值极大,当α=30°时,要求:①作出u d、i d、和i2的波形;②求整流输出平均电压U d、电流I d,变压器二次电流有效值I2;③考虑安全裕量,确定晶闸管的额定电压和额定电流。
解:①u d、i d、和i2的波形如下图:②输出平均电压U d、电流I d,变压器二次电流有效值I2分别为U d=0.9 U2 cosα=0.9×100×cos30°=77.97(V)I d=U d/R=77.97/2=38.99(A)I2=I d=38.99(A)③晶闸管承受的最大反向电压为:2U2=1002=141.4(V)考虑安全裕量,晶闸管的额定电压为:U N=(2~3)×141.4=283~424(V)具体数值可按晶闸管产品系列参数选取。
流过晶闸管的电流有效值为:I VT=I d∕2=27.57(A)晶闸管的额定电流为:I N=(1.5~2)×27.57∕1.57=26~35(A)具体数值可按晶闸管产品系列参数选取。
5.单相桥式全控整流电路,U2=200V,负载中R=2Ω,L值极大,反电势E=100V,当α=45︒时,要求:①作出u d、i d和i2的波形;②求整流输出平均电压U d、电流I d,变压器二次侧电流有效值I2;③考虑安全裕量,确定晶闸管的额定电压和额定电流。
解:①u d、i d和i2的波形如下图:②整流输出平均电压U d、电流I d,变压器二次侧电流有效值I2分别为U d=0.9 U2 cosα=0.9×200×cos45°=127.26(A)I d=(U d-E)/R=(127.26-100)/2=13.63(A)I2=I d=13.63(A)③晶闸管承受的最大反向电压为:2U2=2002=282.8(V)流过每个晶闸管的电流的有效值为:I VT=I d ∕2=9.64(A)故晶闸管的额定电压为:U N=(2~3)×282.8=566~848(V)晶闸管的额定电流为:I N=(1.5~2)×9.64∕1.57=9~12(A)晶闸管额定电压和电流的具体数值可按晶闸管产品系列参数选取。
11.三相半波可控整流电路,U 2=100V ,带电阻电感负载,R =5Ω,L 值极大,当α=60︒时,要求:① 画出u d 、i d 和i VT1的波形; ② 计算U d 、I d 、I dT 和I VT 。
解:①u d 、i d 和i VT1的波形如下图:ωti u②U d 、I d 、I dT 和I VT 分别如下U d =1.17U 2cos α=1.17×100×cos60°=58.5(V )I d =U d ∕R =58.5∕5=11.7(A ) I dVT =I d ∕3=11.7∕3=3.9(A ) I VT =I d ∕3=6.755(A )12.在三相桥式全控整流电路中,电阻负载,如果有一个晶闸管不能导通,此时的整流电压u d 波形如何?如果有一个晶闸管被击穿而短路,其他晶闸管受什么影响?答:假设VT 1不能导通,整流电压u d 波形如下:假设VT 1被击穿而短路,则当晶闸管VT 3或VT 5导通时,将发生电源相间短路,使得VT 3、VT 5也可能分别被击穿。
13.三相桥式全控整流电路,U 2=100V ,带电阻电感负载,R =5Ω,L 值极大,当α=60︒时,要求:① 画出u d 、i d 和i VT1的波形;② 计算U d 、I d 、I dT 和I VT 。
解:①u d 、i d 和i VT1的波形如下:i②U d 、I d 、dT VT U d =2.34U 2cos α=2.34×100×cos60°=117(V )I d =U d ∕R =117∕5=23.4(A ) I DVT =I d ∕3=23.4∕3=7.8(A ) I VT =I d ∕3=23.4∕3=13.51(A )15.三相半波可控整流电路,反电动势阻感负载,U 2=100V ,R =1Ω,L =∞,L B =1mH ,求当α=30︒时、E =50V 时U d 、I d 、γ 的值并作出u d 与i VT1和i VT2的波形。
解:考虑L B 时,有:U d =1.17U 2cos α-ΔU d ΔU d =3X B I d ∕2π I d =(U d -E )∕R解方程组得:U d =(πR 1.17U 2cos α+3X B E )∕(2πR +3X B )=94.63(V )ΔU d =6.7(V ) I d =44.63(A )又∵αcos -)cos(γα+=2B d X I ∕6U 2即得出︒=0.752+cos(γ)30换流重叠角γ=41.28°- 30°=11.28°u d、i VT1和i VT2的波形如下:ii26.使变流器工作于有源逆变状态的条件是什么?答:条件有二:①直流侧要有电动势,其极性须和晶闸管的导通方向一致,其值应大于变流电路直流侧的平均电压;②要求晶闸管的控制角α>π/2,使U d为负值。
29.什么是逆变失败?如何防止逆变失败?答:逆变运行时,一旦发生换流失败,外接的直流电源就会通过晶闸管电路形成短路,或者使变流器的输出平均电压和直流电动势变为顺向串联,由于逆变电路内阻很小,形成很大的短路电流,称为逆变失败或逆变颠覆。
防止逆变失败的方法有:采用精确可靠的触发电路,使用性能良好的晶闸管,保证交流电源的质量,留出充足的换向裕量角β等。
30.单相桥式全控整流电路、三相桥式全控整流电路中,当负载分别为电阻负载或电感负载时,要求的晶闸管移相范围分别是多少?答:单相桥式全控整流电路,当负载为电阻负载时,要求的晶闸管移相范围是0 ~ 180︒,当负载为电感负载时,要求的晶闸管移相范围是0 ~ 90︒。
