打印版 山东专升本高数2016真题
山东专升本真题及答案

山东专升本真题及答案一、选择题(每题2分,共20分)1. 下列哪个选项不是山东专升本考试的科目?A. 数学B. 英语C. 历史D. 物理答案:C2. 山东专升本考试的总分是多少分?A. 300分B. 400分C. 500分D. 600分答案:C3. 根据山东专升本考试规定,考生在考试中作弊将受到什么处罚?A. 警告B. 取消本次考试成绩C. 禁止参加下一年考试D. 终身禁止参加考试答案:B4. 山东专升本考试的报名费是多少?A. 100元B. 200元C. 300元D. 400元答案:B5. 山东专升本考试的考试时间通常安排在每年的哪个月份?A. 3月B. 6月C. 9月D. 12月答案:B二、填空题(每题2分,共20分)6. 山东专升本考试的报名通常在考试前的______个月进行。
答案:27. 考生在参加山东专升本考试时,必须携带的证件是______和身份证。
答案:准考证8. 山东专升本考试的合格分数线一般由______确定。
答案:教育厅9. 考生在山东专升本考试中,如果对成绩有异议,可以在成绩公布后的______个工作日内提出复核申请。
答案:510. 山东专升本考试的录取工作通常在______月份完成。
答案:8三、简答题(每题10分,共30分)11. 简述山东专升本考试的报名流程。
答案:考生首先需要在规定的时间内登录报名系统,填写个人信息并上传照片,然后选择考试科目和考点,缴纳报名费,最后打印准考证。
12. 山东专升本考试的考试内容主要包括哪些方面?答案:考试内容主要包括公共基础课和专业课两部分,公共基础课通常包括数学、英语等科目,专业课则根据考生报考的专业方向而定。
13. 如何准备山东专升本考试?答案:考生需要根据考试大纲复习相关知识点,参加模拟考试以熟悉考试流程和题型,合理安排复习时间,保持良好的心态。
四、论述题(每题30分,共30分)14. 论述山东专升本考试对考生未来发展的意义。
答案:略(考生需根据个人理解和观点进行论述)五、案例分析题(每题30分,共30分)15. 假设你是一名即将参加山东专升本考试的考生,你的朋友因为家庭原因无法参加考试,请你给出建议帮助他解决这个问题。
首发2016年度高等考试山东卷文科数学精编题及答案解析

首发2016年高考山东卷文科数学真题及答案2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤.参考公式:如果事件A,B互斥,那么P(A+B)=P(A)+P(B).第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()UA B =(A ){2,6} (B ){3,6}(C ){1,3,4,5}(D ){1,2,4,6}(2)若复数21iz =-,其中i 为虚数单位,则z = (A )1+i(B )1−i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是 (A )56(B )60(C )120(D )140(4)若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4(B )9(C )10(D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33(B )12π3 (C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,内,则“直线a 和直线b 相交”是“平面α和平面相交”的(A )充分不必要条件(B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件 (7)已知圆M :2220(0)x y ay a 截直线0x y 所得线段的长度是22M与圆N :22(1)1x y (-1)的位置关系是(A )内切(B )相交(C )外切(D )相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )bc a b A ,则A =(A )3π4(B )π3(C )π4(D )π6(9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= (A )-2 (B )-1(C )0 (D )2(10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是 (A )sin y x =(B )ln y x =(C )e x y =(D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
(精校版)2016年山东文数高考试题文档版(word含答案)

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:如果事件A,B 互斥,那么P(A+B)=P(A)+P(B).第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B ð=(A ){2,6} (B ){3,6} (C ){1,3,4,5} (D ){1,2,4,6}(2)若复数21i z =-,其中i 为虚数单位,则z = (A )1+i (B )1−i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60 (C )120 (D )140(4)若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4(B )9(C )10(D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33(B )12+π33(C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的(A )充分不必要条件(B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(7)已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是22,则圆M 与圆N :22(1)1x y +-=(-1)的位置关系是(A )内切(B )相交(C )外切(D )相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ==-,则A =(A )3π4(B )π3(C )π4(D )π6(9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= (A )-2 (B )-1(C )0 (D )2(10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是学科&网(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
2016年普通高等学校招生全国统一考试数学(理)山东卷
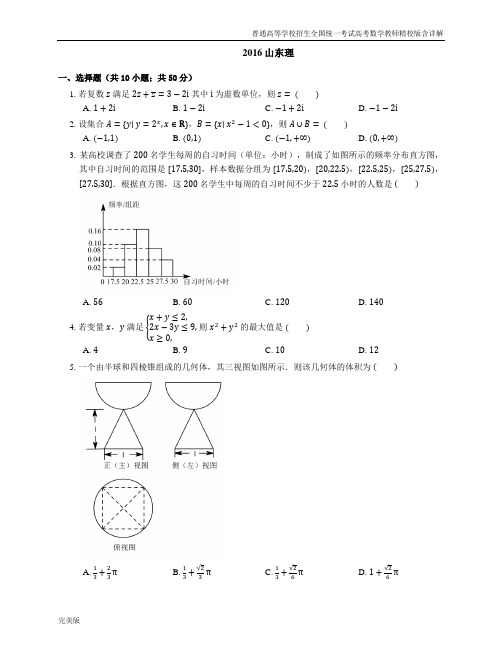
2016山东理一、选择题(共10小题;共50分)1. 若复数z满足2z+z=3−2i其中i为虚数单位,则z= A. 1+2iB. 1−2iC. −1+2iD. −1−2i2. 设集合A=y y=2x,x∈R,B=x x2−1<0,则A∪B= A. −1,1B. 0,1C. −1,+∞D. 0,+∞3. 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是17.5,30,样本数据分组为17.5,20,20,22.5,22.5,25,25,27.5,27.5,30.根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是 A. 56B. 60C. 120D. 1404. 若变量x,y满足x+y≤2,2x−3y≤9,x≥0,则x2+y2的最大值是 A. 4B. 9C. 10D. 125. 一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为 A. 13+23π B. 13+23π C. 13+26π D. 1+26π6. 已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b相交”是“平面α和平面β相交”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件7. 函数f x=3sin x+cos x 3cos x−sin x 的最小正周期是 A. π2B. π C. 3π2D. 2π8. 已知非零向量m,n满足4m=3n,cos<m,n>=13.若n⊥tm+n,则实数t的值为 A. 4B. −4C. 94D. −949. 已知函数f x的定义域为R.当x<0时,f x=x3−1;当−1≤x≤1时,f−x=−f x;当x>12时,f x+12=f x−12.则f6= A. −2B. −1C. 0D. 210. 若函数y=f x的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f x具有T性质.下列函数中具有T性质的是 A. y=sin xB. y=ln xC. y=e xD. y=x3二、填空题(共5小题;共25分)11. 执行如图的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为.12. 若 ax2x 5的展开式中x5的系数是−80,则实数a=.13. 已知双曲线E1:x2a2−y2b2=1a>0,b>0,若矩形ABCD的四个顶点在E1上,AB,CD的中点为E1的两个焦点,且2 AB =3 BC ,则E1的离心率是.14. 在−1,1上随机地取一个数k,则事件“直线y=kx与圆x−52+y2=9相交”发生的概率为.15. 已知函数f x= x ,x≤m,x2−2mx+4m,x>m,其中m>0,若存在实数b,使得关于x的方程f x=b有三个不同的根,则m的取值范围是.三、解答题(共6小题;共78分)16. 在△ABC中,角A,B,C的对边分别为a,b,c,已知2tan A+tan B=tan Acos B +tan Bcos A.(1)证明:a+b=2c;(2)求cos C的最小值.17. 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆Oʹ的直径,FB是圆台的一条母线.(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;(2)已知EF=FB=12AC=23,AB=BC.求二面角F−BC−A的余弦值.18. 已知数列a n的前n项和S n=3n2+8n,b n是等差数列,且a n=b n+b n+1.(1)求数列b n的通项公式;(2)令c n=a n+1n+1b n+2,求数列c n的前n项和T n.19. 甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是34,乙每轮猜对的概率是23;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:(1)“星队”至少猜对3个成语的概率;(2)“星队”两轮得分之和为X的分布列和数学期望EX.20. 已知f x=a x−ln x+2x−1x2,a∈R.(1)讨论f x的单调性;(2)当a=1时,证明f x>fʹx+32对于任意的x∈1,2成立.21. 平面直角坐标系xOy中,椭圆C:x2a +y2b=1a>b>0的离心率是32,抛物线E:x2=2y的焦点F是C的一个顶点.(1)求椭圆C的方程;(2)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的两点A,B,线段AB 的中点为D,直线OD与过P且垂直于x轴的直线交于点M.(i)求证:点M在定直线上;(ii)直线l与y轴交于点G,记△PFG的面积为S1,△PDM的面积为S2,求S1的最大值及取得S2最大值时点P的坐标.答案第一部分 1. B 【解析】设z =a +b i ,则2z +z =3a +b i =3−2i ,故a =1,b =−2,则z =1−2i . 2. C 【解析】A = y y >0 ,B = x −1<x <1 ,则A ∪B = x x >−1 .3. D 【解析】由频率分布直方图知,自习时间不少于22.5小时的有200× 0.16+0.08+0.04 ×2.5=140人.4. C 【解析】不等式组表示的可行域是以A 0,−3 ,B 0,2 ,C 3,−1 为顶点的三角形区域,x 2+y 2表示点 x ,y 到原点距离的平方,最大值必在顶点处取到,经验证最大值 OC 2=10.5. C【解析】由三视图可知,上面是半径为 22的半球,体积为V 1=12×43π×223=2π6,下面是底面积为1,高为1得四棱锥,体积V 2=13×1×1=13.6. A 【解析】直线a 与直线b 相交,则α,β一定相交,若α,β相交,则a ,b 可能相交,也可能平行.7. B 【解析】f x =2sin x +π6 ×2cos x +π6 =2sin 2x +π3 ,故最小正周期T =2π2=π.8. B【解析】由4 m =3 n ,可设 m =3k , n =4k k >0 ,又n ⊥ tm +n ,所以n ⋅ tm +n =n ⋅tm +n ⋅n=t m ⋅ n cos <m ,n >+ n2=t ×3k ×4k ×13+ 4k2=4tk 2+16k 2=0,所以t =−4. 9. D【解析】当x >12时,由f x +12 =f x −12 ,得f x +1 =f x ,所以当x >12时,f x 是周期为1的周期函数, 从而f 6 =f 1 .又因为当−1≤x ≤1时,f −x =−f x , 所以f 1 =−f −1 =− −1 3−1 =2. 10. A【解析】当y =sin x 时,yʹ=cos x ,cos0⋅cos π=−1,所以在函数y =sin x 图象存在两点x =0,x =π使条件成立,则 A 正确;函数y =ln x ,y =e x ,y =x 3的导数值均非负,不符合题意. 第二部分 11. 3【解析】第一次循环:a =1,b =8;第二次循环:a =3,b =6;第三次循环:a =6,b =3;满足条件,结束循环,此时,i =3. 12. −2【解析】因为T r+1=C5r ax25−rx r=C5r a5−r x10−5r,所以由10−52r=5⇒r=2,因此C52a5−2=−80⇒a=−2.13. 2【解析】易得A c,b 2a ,B c,−b2a,所以 AB =2b2a, BC =2c,由2 AB =3 BC ,c2=a2+b2得离心率e=2或e=−12(舍去),所以离心率为2.14. 34【解析】直线y=kx与圆x−52+y2=9相交,需要满足圆心到直线的距离小于半径,d=1+k2<3,解得−34<k<34,而k∈−1,1,所以发生的概率322=34.15. 3,+∞【解析】由题意画出函数图象如下图,要满足存在实数b,使得关于x的方程f x=b有三个不同的根则4m−m2<m解得m>3,即3,+∞.第三部分16. (1)由题意知2sin Acos A +sin Bcos B=sin Acos A cos B+sin Bcos A cos B,化简得2sin A cos B+sin B cos A=sin A+sin B,即2sin A+B=sin A+sin B.因为A+B+C=π,所以sin A+B=sinπ−C=sin C.从而sin A+sin B=2sin C.由正弦定理得a+b=2c.(2)由1知c=a+b2,所以cos C=a 2+b2−c22ab=a2+b2− a+b222ab=38ba+ab−14≥12,当且仅当a=b时,等号成立.故cos C的最小值为12.17. (1)设FC的中点为I,连接GI,HI,在△CEF中,因为G是CE的中点,所以GI∥EF,又EF∥OB,所以GI∥OB,在△CFB中,因为H是FB的中点,所以HI∥BC,又HI∩GI=I,BC,OB交于点B,所以平面GHI∥平面ABC,因为GH⊂平面GHI,所以GH∥平面ABC.(2)解法一:连接OOʹ,则OOʹ⊥平面ABC,又AB=BC,且AC是圆O的直径,所以BO⊥AC.以O为坐标原点,建立如图所示的空间直角坐标系O−xyz,由题意得B 0,23,0,C −23,0,0,过点F作FM垂直OB于点M,所以FM= FB2−BM2=3,可得F 0,3,3.故BC= −23,−23,0,BF=0,−3,3.设m=x,y,z是平面BCF的一个法向量.由m⋅BC=0, m⋅BF=0,可得−23x−23y=0,−3y+3z=0,可得平面BCF的一个法向量m= −1,1,33.因为平面ABC的一个法向量n=0,0,1,所以cos⟨m,n ⟩=m ⋅nm n =77.所以二面角F−BC−A的余弦值为77.解法二:连接OOʹ,过点F作FM⊥OB于点M,则有FM∥OOʹ,又OOʹ⊥平面ABC,所以FM⊥平面ABC,可得FM=2−BM2=3,过点M作MN垂直BC于点N,连接FN,可得FN⊥BC,从而∠FNM为二面角F−BC−A的平面角.又AB=BC,AC是圆O的直径,所以MN=BM sin45∘=62,从而FN=422,可得cos∠FNM=77.所以二面角F−BC−A的余弦值为77.18. (1)当n≥2时,a n=S n−S n−1=6n+5.当n=1时,a1=S1=11,代入上式适合,所以a n=6n+5n∈N∗;设数列b n的公差为d,则a1=b1+b2, a2=b2+b3,即11=2b1+d, 17=2b1+3d,解得b1=4, d=3,所以b n=3n+1.(2)由1知c n=a n+1n+1b n+2n=3n+1⋅2n+1.由T=c1+c2+c3+⋯+c n,得T n=32×22+3×23+4×24+⋯+n+12n+1,所以2T n=32×23+3×24+4×25+⋯+n+12n+2.以上两式两边相减,得−T n=32×22+23+24+⋯+2n+1−n+12n+2=34+42n−1−n+12n+2=−3n⋅2n+2.所以T n=3n⋅2n+2.19. (1)记事件A:“甲第一轮猜对”,记事件B:“乙第一轮猜对”,记事件C:“甲第二轮猜对”,记事件D:“乙第二轮猜对”,记事件E:“星队至少猜对3个成语”.由题意,E=ABCD++++由事件的独立性和互斥性,P E=P ABCD+P ABCD +P ABCD +P ABCD +P ABCD=P A P B P C P D+P A P B P C P D+P A P B P C P D+P A P B P C P D+P A P B P C P D=34×23×34×23+2×14×23×34×23+×34×13×34×23=2 3 .所以“星队”至少猜对3个成语的概率为23.(2)由题意,随机变量X的可能取值为0,1,2,3,4,6.由事件的独立性与互斥性得P X=0=14×13×14×13=1144,P X=1=2×34×13×14×13+14×23×14×13=10144=572,P X=2=34×13×34×13+34×13×14×23×+14×23×34×13×+14×23×14×23=25144,P X=3=34×23×14×13+14×13×34×23=112,P X=4=2×34×23×34×13+34×23×14×23=512,P X=6=34×23×34×23=14,可得随机变量X的分布列为x012346P1525151所以数学期望EX=0×1144+1×572+2×25144+3×112+4×512+6×14=236.所以EX=236.20. (1)f x的定义域为0,+∞;fʹx=a−ax −2x+2x=ax2−2⋅x−1x,(1)当a≤0时,若x∈0,1,fʹx>0,函数f x单调递增;x∈1,+∞,fʹx<0,函数f x单调递减.(2)当a>0时,fʹx=a x−1 x+ax−ax3.若0<a<2,则2a >1,所以当x∈0,1或2a,+∞ 时,fʹx>0,函数f x单调递增;当1,2a时,fʹx<0,函数f x单调递减;若a=2时,2a=1,fʹx≥0,函数f x单调递增;若a>2,则0<2a <1,所以当x∈0,2a或1,+∞时,fʹx>0,函数f x单调递增;当2a,1时,fʹx<0,函数f x单调递减.综上所述:当a≤0时,函数f x在0,1上单调递增;函数f x在1,+∞上单调递减.当0<a<2时,函数f x在0,1和2a ,+∞ 上单调递增;函数f x在1,2a上单调递减;当a=2时,函数f x在0,+∞上单调递增;当a>2,函数f x在0,2a 和1,+∞上单调递增;函数f x在2a,1上单调递减.(2)由(1)知a=1时,f x−fʹx=x−ln x+2x−12−1−1−22+23=x−ln x+3x+1x2−2x3−1, x∈1,2,令g x=x−ln x, x=3x +1x2−2x3−1,则f x−fʹx=g x+ x,由gʹx=x−1x≥0,可得g x≥g1=1,当且仅当x=1时取等号;又 ʹx=−3x 2−2x+6x4,设φx=−3x2−2x+6,则φx在1,2上单调递减,且φ1=1,φ2=−10,所以在1,2上存在x0使得x∈1,x0时,φx>0;x∈x0,2时,φx<0;所以函数 x在1,x0上单调递增;在x0,2上单调递减;由于 1=1, 2=12,因此 x≥ 2=12,当且仅当x=2取等号,所以f x−fʹx>g1+ 2=32,即f x>fʹx+32对于任意的x∈1,2恒成立.21. (1)由题意知: a2−b2a =32,解得a=2b.普通高等学校招生全国统一考试高考数学教师精校版含详解完美版 因为抛物线E 的焦点为F 0,12 ,所以a =1,b =12, 所以椭圆的方程为x 2+4y 2=1.(2)(i )设P m ,m 22 m >0 ,由x 2=2y 可得yʹ=x ,所以直线l 的斜率为m ,其直线方程为y −m 22=m x −m ,即y =mx −m 22. 设A x 1,y 1 ,B x 2,y 2 ,D x 0,y 0 ,联立方程组y =mx −m 22,x 2+4y 2=1. 消去y 并整理可得4m 2+1 x 2−4m 3x +m 4−1=0,故由其判别式Δ>0,可得0<m < 2+ 5且x 1+x 2=4m 34m +1, 故x 0=x 1+x 22=2m 34m 2+1,代入y =mx −m 22可得y 0=−m 224m +1, 因为y 0x 0=−14m ,所以直线OD 的方程为y =−14m x .联立 y =−14m x ,x =m ,可得点M 的纵坐标为y =−14, 即点M 在定直线y =−14上. (ii )由(i )知直线l 的方程为y =mx −m 22, 令x =0得y =−m 22,所以G 0,−m 22 , 又P m ,m 22 ,F 0,12 ,D 2m 34m +1,−m 224m +1 ,所以 S 1=12 GF m =14m m 2+1 , S 2=12 PM ⋅ m −x 0 =m 2m 2+1 28 4m 2+1 , 所以S 12=2 4m 2+1 m 2+1 2 2, 令t =2m 2+1,则S 1S 2= 2t−1 t +1 t 2=−1t 2+1t +2, 因此当1t =12,即t =2时,S1S 2最大,其最大值为94,此时m = 22满足Δ>0, 所以点P 的坐标为22,14 ,因此S 1S 2的最大值为94,此时点P 的坐标为 22,14 .。
2016年专升本真题试卷.doc

2016年专升本真题试卷.doc姓名:____________________________身份证号:____________________________1、协议背景11 本协议旨在规范和明确关于2016 年专升本真题试卷的相关事宜。
2、试卷的所有权与版权21 2016 年专升本真题试卷的所有权归相关考试主管部门或授权机构所有。
22 未经授权,任何个人或机构不得擅自复制、传播、出售或以其他方式侵犯试卷的版权。
3、试卷的使用目的31 试卷仅用于合法的教育和研究目的。
32 使用者不得将试卷用于商业盈利或非法活动。
4、试卷的获取与保管41 试卷的获取应通过合法合规的途径,如官方发布、授权的教育机构提供等。
42 获得试卷后,使用者应妥善保管,确保试卷不被泄露、丢失或损坏。
5、试卷的使用限制51 不得对试卷进行修改、篡改或伪造。
52 禁止在未经授权的情况下将试卷内容用于出版、发表或在公开场合展示。
6、保密义务61 使用者应对试卷的内容保密,不得向无关人员透露试卷的任何信息。
62 在使用过程中,应采取合理的措施防止试卷内容的泄露。
7、法律责任71 任何违反本协议的行为都将承担相应的法律责任,包括但不限于民事赔偿、行政处罚甚至刑事责任。
72 若因违反协议导致相关考试主管部门或授权机构遭受损失,违约方应承担全部赔偿责任。
8、协议的变更与终止81 本协议的内容如有变更,将以书面形式通知使用者。
82 在出现以下情况时,本协议将自动终止:821 使用者违反本协议的任何条款。
822 相关法律法规发生变化,导致本协议无法继续履行。
9、争议解决91 如因本协议产生任何争议,双方应首先通过友好协商解决。
92 若协商不成,任何一方均可向有管辖权的人民法院提起诉讼。
10、其他条款101 本协议构成双方关于 2016 年专升本真题试卷使用的完整协议,并取代之前的任何口头或书面协议。
102 本协议的解释和执行均应遵循相关法律法规的规定。
2016年专升本高数试卷Word版

浙江省2016 年选拔优秀高职高专毕业生进入本科学习统一考试高等数学请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用 2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
一、选择题: 本大题共5小题,每小题4分,共 20分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设x x x f -=][)(,则为)(x f ().(A )有界函数 (B )偶函数 (C )奇函数 (D )周期函数2. 则,),(x ,0)x (f 上可导,且],[在)(设00b a b a x f ∈='(A )()为函数的极值0x f(B )()处连续x x 在0='x f(C )()处可微x x 为0=x f(D )()为函数的拐点)(,x 00x f 3 ()1f 13f 1 2.(0)1,xf ()f x dx '''====⎰设,()则 (A )2 (B )3(C )0 (D )1 4. 的收敛半径为则级数,b 0若实数1n ∑∞=+<<n n nb ax a(A )a (B )b (C )a+b (D )b-a 5. 则其特解形式为,sin y 微分方程x x y y =+'+'' (A ))cos sin (xx b x a + (B )]cos )(sin )[(x d cx x b ax x +++ (C )x d cx x b ax cos )(sin )(+++ (D ))cos sin )((x d x c b ax ++非选择题部分注意事项:1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2.在答题纸上作图,可先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
(完整word版)2016年山东高考数学(文科)试题及答案(word版),推荐文档

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:如果事件A,B 互斥,那么P(A+B)=P(A)+P(B).第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B U ð=(A ){2,6} (B ){3,6} (C ){1,3,4,5} (D ){1,2,4,6}(2)若复数21i z =-,其中i 为虚数单位,则z = (A )1+i (B )1−i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60 (C )120 (D )140(4)若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4(B )9(C )10(D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33(B )123 (C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的(A )充分不必要条件(B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(7)已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是M 与圆N :22(1)1x y +-=(-1)的位置关系是(A )内切(B )相交(C )外切(D )相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ==-,则A =(A )3π4(B )π3(C )π4(D )π6 (9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= (A )-2 (B )-1(C )0 (D )2(10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
可打印2016年理数高考真题(山东+四川+新课标Ⅰ卷-含答案)

3. 第Ⅱ卷必须用 0.5 毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能 写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。 不按以上要求作答的答案无效。
(C) (1, ) (D) (0, )
(3)某高校调查了 200 名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中 自习时间的范围是[17.5,30] ,样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30] .根据直方图,
第Ⅱ卷(共 100 分) 二、填空题:本大题共 5 小题,每小题 5 分,共 25 分。
(11)执行右边的程序框图,若输入的 a,b 的值分别为 0 和 9,则输出的 i 的值为________.
(12)若(ax2+ 1 )5 的展开式中 x5 的系数是—80,则实数 a=_______. x
(13)已知双曲线
绝密★启用前 2016 年普通高等学校招生全国统一考试(山东卷) 理科数学
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 4 页。满分 150 分。考试用时 120 分钟。考试结束后,将将本试 卷和答题卡一并交回。 注意事项:
1.答卷前,考生务必用 0.5 毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和 试卷规定的位置上。
2
(18)(本小题满分 12 分)
已知数列
a n
的前 n 项和 Sn=3n2+8n,
b n
是等差数列,且 an bn bn1.
2016年山东省专升本考试高等数学真题试卷(含答案)

I 二 I~I : I : 口 一、选择题(本大题共 5 小题,每小题 3 分,共 15 分)
___
5 A
二、填空题(本大题共 5 小题,每小题 3 分,共 15 分)
1. 12兀
2. e
3. 3
4. 15
5. 发散
三、解答题(本大题共 7 小题,每小题 6 分,共 42 分,解答应写出文字说明、证明过程
=
ln
X
1
...
+ ,J;_万平了
…...
2
分
= -ln(x +.fx2+i) = -fCx) ......... 2 分
所以y = ln(x +.j;.了了1) 为奇函数......... 1 分
2. 证... ; .. ,1 分 2
使得f.!1 f (x)dx = /(c)(l - -1) ......... 2 分
·150·
i 』二c-,二.二-::c一c~c---:=::-~:::::::cc::c, —-三三亏- -- - - ----
山东省专升本考试公共课历年真题及解析·高等数学
4. 解:由伈f(x)dx = arcsinx + c,
通过求导可得xf(x) = 1 ...... …2 分 �
即上-= X�, ••••••••• z 分 f(x)
·:y垂直于&, ... r. a= o…...... 2分一
恤
:即.:;t(=P髻-..应.)....a.=..p1.分芘-应. a= o, ... ·-:1分
应a
厮 =P..:. 彗 a.......... z分
2. 解:根据公式: A=;f02巴 lsinx - cosxl dx.... ·令.... z分
2016年山东高考数学(文科)试题及答案(word版)

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤.参考公式:如果事件A,B互斥,那么P(A+B)=P(A)+P(B).第I卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}===,则()U A BA B=U(A){2,6}(B){3,6}(C){1,3,4,5}(D){1,2,4,6}(2)若复数21i z =-,其中i 为虚数单位,则z = (A )1+i (B )1−i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60 (C )120 (D )140(4)若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4(B )9(C )10(D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33(B )123 (C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,内,则“直线a 和直线b 相交”是“平面α和平面相交”的(A )充分不必要条件(B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(7)已知圆M :2220(0)x y ay a 截直线0x y 所得线段的长度是M 与圆N :22(1)1x y (-1)的位置关系是(A )内切(B )相交(C )外切(D )相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )bc a b A ,则A =(A )3π4(B )π3(C )π4(D )π6 (9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= (A )-2 (B )-1(C )0 (D )2(10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
(完整word版)2016年山东高考数学(文科)试题及答案(word版)(2),推荐文档

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:如果事件A,B 互斥,那么P(A+B)=P(A)+P(B).第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B U ð=(A ){2,6} (B ){3,6} (C ){1,3,4,5} (D ){1,2,4,6}(2)若复数21i z =-,其中i 为虚数单位,则z = (A )1+i (B )1−i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60 (C )120 (D )140(4)若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4(B )9(C )10(D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33(B )123 (C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的(A )充分不必要条件(B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(7)已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是M 与圆N :22(1)1x y +-=(-1)的位置关系是(A )内切(B )相交(C )外切(D )相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ==-,则A =(A )3π4(B )π3(C )π4(D )π6 (9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)= (A )-2 (B )-1(C )0 (D )2(10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
2016年全国普通高等学校招生统一考试文科数学试题(山东卷word解析版)

2016年全国普通高等学校招生统一考试文科科数学试题(山东卷)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释) 1.设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B ð=(A ){2,6} (B ){3,6} (C ){1,3,4,5} (D ){1,2,4,6}【答案】A【解析】试题分析:由已知,{13,5}{3,4,5}{1,3,4,5}A B ⋃=⋃=,,所以(){1,3,4,5U U C A B C ⋃==,选A.考点:集合的运算2.若复数21iz =-,其中i 为虚数单位,则z = (A )1+i (B )1−i (C )−1+i (D )−1−i【答案】B【解析】试题分析:22(1)1,11(1)(1)i z i z i i i i +===+∴=---+,选B. 考点:1.复数的运算;2.复数的概念.3.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60 (C )120 (D )140【答案】D【解析】试题分析:由频率分布直方图知,自习时间不少于22.5小时的有200(0.160.080.04) 2.5⨯++⨯=,选D. 考点:频率分布直方图4.若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则x 2+y 2的最大值是(A )4 (B )9 (C )10 (D )12考点:简单线性规划5.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )12+π33 (B)1+π33(C)1+π36 (D)1+π66.已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的(A )充分不必要条件(B )必要不充分条件(C )充要条件(D )既不充分也不必要条件7.已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是则圆M 与圆N :22(1)1x y +-=(-1)的位置关系是(A )内切 (B )相交 (C )外切 (D )相离8.ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ==-,则A=(A )3π4(B )π3 (C )π4 (D )π6 9.已知函数f (x )的定义域为R.当x <0时,f (x )=x 3-1;当-1≤x ≤1时,f (-x )= —f (x );当x >12时,f (x+12)=f (x —12).则f (6)= (A )-2 (B )-1(C )0 (D )210.若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释) n 的值为3,则输出的S 的值为_______.12.观察下列等式:22π2π4(sin )(sin )12333--+=⨯⨯; 2222π2π3π4π4(sin )(sin )(sin )(sin )2355553----+++=⨯⨯; 2222π2π3π6π4(sin )(sin )(sin )(sin )3477773----+++⋅⋅⋅+=⨯⨯; 2222π2π3π8π4(sin )(sin )(sin )(sin )4599993----+++⋅⋅⋅+=⨯⨯; ……照此规律,222π2π3π2π(s i n )(2121n n n n ---+++⋅+++_________. 13.已知向量a=(1,–1),b=(6,–4).若a ⊥(ta+b ),则实数t 的值为________.14.已知双曲线E :22x a –22y b =1(a>0,b>0).矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB|=3|BC|,则E 的离心率是_______.15.已知函数f (x )=2,,24,,x x m x mx m x m ⎧≤⎪⎨-+>⎪⎩其中m>0.若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是_______.三、解答题(题型注释) .参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x ,y.奖励规则如下:①若3xy ≤,则奖励玩具一个;②若8xy ≥,则奖励水杯一个;③其余情况奖励饮料一瓶.假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.(Ⅰ)求小亮获得玩具的概率;(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.17.设2()π)sin (sin cos )f x x x x x =--- .(Ⅰ)求()f x 得单调递增区间;(Ⅱ)把()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数()y g x =的图象,求π()6g 的值. 18.在如图所示的几何体中,D 是AC 的中点,EF ∥DB.(Ⅰ)已知AB=BC ,AE=EC.求证:AC ⊥FB ;(Ⅱ)已知G,H 分别是EC 和FB 的中点.求证:GH ∥平面ABC.19.已知数列{}n a 的前n 项和238n S n n =+,{}n b 是等差数列,且1n n n a b b +=+. (Ⅰ)求数列{}n b 的通项公式; (Ⅱ)令1(1)(2)n n n nn a c b ++=+.求数列{}n c 的前n 项和n T . 20.设f (x )=xlnx –ax 2+(2a –1)x ,a ∈R.(Ⅰ)令g (x )=f'(x ),求g (x )的单调区间;(Ⅱ)已知f (x )在x=1处取得极大值.求实数a 的取值范围.21.已知椭圆C:错误!未找到引用源。
(完整版)2016年山东高考数学(文科)试题及答案(word版)

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟.考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2。
第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
参考公式:如果事件A ,B 互斥,那么P (A+B)=P (A)+P (B ).第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B = (A ){2,6} (B ){3,6}(C){1,3,4,5} (D){1,2,4,6}(2)若复数21iz =-,其中i 为虚数单位,则z = (A )1+i(B )1−i (C)−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17。
5,30],样本数据分组为[17.5,20),[20,22.5),[22。
5,25),[25,27。
5),[27。
5,30)。
根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A)56 (B)60 (C)120 (D)140(4)若变量x,y满足2,239,0,x yx yx+≤⎧⎪-≤⎨⎪≥⎩则x2+y2的最大值是(A)4(B)9(C)10(D)12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示。
2016山东卷高考数学(理)试题----2016高考真题word版

绝密★启用前2016年普通高等学校招生全国统一考试(山东卷)理科数学本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤.参考公式:如果事件A,B互斥,那么P(A+B)=P(A)+P(B).第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的(1)若复数z 满足232i,z z +=- 其中i 为虚数单位,则z =(A )1+2i (B )1-2i (C )12i -+ (D )12i --(2)设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B = (A )(1,1)- (B )(0,1) (C )(1,)-+∞ (D )(0,)+∞(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30] ,样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30] .根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是(A )56 (B )60(C )120 (D )140(4)若变量x ,y 满足2,239,0,x y x y x ì+?ïïïï-?íïï锍ïî则22x y +的最大值是(A )4 (B )9 (C )10 (D )12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A )1233+π (B )1233+π (C )1236+π (D )216+π (6)已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件(7)函数f (x )=(3sin x +cos x )(3cos x –sin x )的最小正周期是(A )2π(B )π (C )23π (D )2π(8)已知非零向量m ,n 满足4│m │=3│n │,cos<m ,n >=13.若n ⊥(t m +n ),则实数t 的值为(A )4 (B )–4 (C )94 (D )–94(9)已知函数f (x )的定义域为R .当x <0时,3()1f x x =- ;当11x -≤≤ 时,()()f x f x -=-;当12x > 时,11()()22f x f x +=- .则f (6)= (A )−2(B )−1(C )0(D )2(10)若函数y =f (x )的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y =f (x )具有T 性质.下列函数中具有T 性质的是(A )y =sin x (B )y =ln x (C )y =e x (D )y =x 3第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
(精校版)2016年山东理数高考试题文档版(word含答案)

绝密★启用前2016年普通高等学校招生全国统一考试(山东卷)理科数学本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页。
满分150分。
考试用时120分钟。
考试结束后,将将本试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,在选涂其他答案标号。
答案写在试卷上无效。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题直接填写答案,解答题应写出文字说明、证明过程或演算步骤.参考公式:如果事件A,B 互斥,那么P(A+B)=P(A)+P(B).如果事件A ,B 独立,那么P(AB)=P(A)·P(B)第Ⅰ卷(共50分)一、 选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的(1)若复数z 满足232i,z z +=-其中i 为虚数单位,则z =( )(A )1+2i (B )1-2i (C )12i -+ (D )12i -- (2)设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B =( ) (A )(1,1)- (B )(0,1) (C )(1,)-+∞ (D )(0,)+∞(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30] .根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )(A)56 (B)60 (C)120 (D)140(4)若变量x,y满足2,239,0,x yx yxì+?ïïïï-?íïï锍ïî则22x y+的最大值是()(A)4 (B)9 (C)10 (D)12(5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()(A)1233+π(B )1233+π(C )1236+π(D )216+π(6)已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b相交”是“平面α和平面β相交”的()(A)充分不必要条件(B)必要不充分条件学.科.网(C)充要条件(D)既不充分也不必要条件(7)函数f (x )=(3sin x +cos x )(3cos x –sin x )的最小正周期是( )(A )2π(B )π (C )23π(D )2π (8)已知非零向量m ,n 满足4│m │=3│n │,cos<m ,n >=13.若n ⊥(t m +n ),则实数t 的值为( ) (A )4 (B )–4 (C )94(D )–94(9)已知函数f (x )的定义域为R .当x <0时,3()1f x x =-;当11x -≤≤时,()()f x f x -=-;当12x >时,11()()22f x f x +=- .则f (6)= ( ) (A )−2(B )−1(C )0(D )2(10)若函数y =f (x )的图象上存在两点,学科.网使得函数的图象在这两点处的切线互相垂直,则称y =f (x )具有T 性质.下列函数中具有T 性质的是( )(A )y =sin x (B )y =ln x (C )y =e x (D )y =x 3第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
2016年山东高考数学(文科)试题及答案(word版)

2016年普通高等学校招生全国统一考试(山东卷)数学(文科)参考公式: 如果事件A,B 互斥,那么P(A+B)=P(A)+P(B). 第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,3,4,5,6},{1,3,5},{3,4,5}U A B ===,则()U A B ð= (A ){2,6} (B ){3,6} (C ){1,3,4,5} (D ){1,2,4,6}(2)若复数21iz =-,其中i 为虚数单位,则z = (A )1+i (B )1−1−i i (C )−1+i (D )−1−i(3)某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20), [20,22.5), [22.5,25),[25,27.5),[27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是小时的人数是(A )56 (B )60 (C )120 (D )140 (4)若变量x ,y 满足2,239,0,x y x y x +£ìï-£íï³î则x 2+y 2的最大值是的最大值是(A )4(B )9(C )10(D )12 (5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为则该几何体的体积为(A )12+π33(B )12+π33(C )12+π36(D )21+π6(6)已知直线a ,b 分别在两个不同的平面α,b 内,则“直线a 和直线b 相交”是“平面α和平面b 相交”的(A )充分不必要条件(B )必要不充分条件)必要不充分条件 (C )充要条件)充要条件 (D )既不充分也不必要条件)既不充分也不必要条件(7)已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是22,则圆M 与圆N :22(1)1x y +-=(-1-1))的位置关系是的位置关系是 (A )内切(B )相交(C )外切(D )相离)相离(8)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ==-,则A = (A )3π4(B )π3(C )π4(D )π6(9)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x—12).则f(6)= (A )-2 (B )-1 (C )0 (D )2 (10)若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,使得函数的图象在这两点处的切线互相垂直,则称则称()y f x =具有T 性质.下列函数中具有T 性质的是性质的是 (A )sin y x =(B )ln y x =(C )e xy =(D )3y x =第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分。
