模式识别实验二、贝叶斯分类参数估计matlab代码

合集下载

贝叶斯分类器MATLAB经典程序

function Bayes2%为了提高实验样本测试的精度，故采用多次模拟求平均值的方法N=input('实验模拟次数N(N最好为奇数)＝');Result(1:3,1:3)=0; %判别矩阵的初始化for k=1:N %控制程序模拟次数N%生成二维正态分布的样本2 X N 维的矩阵X1=mvnrnd([1 2],[4 0;0 6],300)'; %2 X NX2=mvnrnd([5 3],[5 0;0 1],200)';X3=mvnrnd([4 7],[2 0;0 9],500)'; %样本程序%---------------------------------------------------%%测试样本X10=mvnrnd([1 2],[4 0;0 6],100)'; %2 X NX20=mvnrnd([5 3],[5 0;0 1],100)';X30=mvnrnd([4 7],[2 0;0 9],100)';%先验概率P(1)=length(X1)/(length(X1)+length(X2)+length(X3));P(2)=length(X2)/(length(X1)+length(X2)+length(X3));P(3)=length(X3)/(length(X1)+length(X2)+length(X3));%计算相关量cov(X)：协方差矩阵Ave:均值%--------------------------------------------------------%W1=-1/2*inv(cov(X1')); W2=-1/2*inv(cov(X2')); W3=-1/2*inv(cov(X3'));%Ave1=(sum(X1')/length(X1))';Ave2=(sum(X2')/length(X2))';Ave3=(sum(X3')/length(X3))';%计算平均值(2维列向量)w1=inv(cov(X1'))*Ave1;w2=inv(cov(X2'))*Ave2;w3=inv(cov(X3'))* Ave3;%2w10=-1/2*Ave1'*inv(cov(X1'))*Ave1-1/2*log(det(cov(X1')))+log(P(1 ));w20=-1/2*Ave2'*inv(cov(X2'))*Ave2-1/2*log(det(cov(X2')))+log(P(2 ));w30=-1/2*Ave3'*inv(cov(X3'))*Ave3-1/2*log(det(cov(X3')))+log(P(3 ));%-----------------------------------------------------------%for i=1:3for j=1:100if i==1g1=X10(:,j)'*W1*X10(:,j)+w1'*X10(:,j)+w10;g2=X10(:,j)'*W2*X10(:,j)+w2'*X10(:,j)+w20;g3=X10(:,j)'*W3*X10(:,j)+w3'*X10(:,j)+w30;if g1>=g2&g1>=g3Result(1,1)=Result(1,1)+1;elseif g2>=g1&g2>=g3Result(1,2)=Result(1,2)+1;%记录误判情况elseResult(1,3)=Result(1,3)+1;%记录误判情况endelseif i==2g1=X20(:,j)'*W1*X20(:,j)+w1'*X20(:,j)+w10;g2=X20(:,j)'*W2*X20(:,j)+w2'*X20(:,j)+w20;g3=X20(:,j)'*W3*X20(:,j)+w3'*X20(:,j)+w30;if g2>=g1&g2>=g3Result(2,2)=Result(2,2)+1;elseif g1>=g2&g1>=g3Result(2,1)=Result(2,1)+1;elseResult(2,3)=Result(2,3)+1;endelseg1=X30(:,j)'*W1*X30(:,j)+w1'*X30(:,j)+w10;g2=X30(:,j)'*W2*X30(:,j)+w2'*X30(:,j)+w20;g3=X30(:,j)'*W3*X30(:,j)+w3'*X30(:,j)+w30;if g3>=g1&g3>=g2Result(3,3)=Result(3,3)+1;elseif g2>=g1&g2>=g3Result(3,2)=Result(3,2)+1;elseResult(3,1)=Result(3,1)+1;endendendendend%画出各样本的分布情况subplot(2,1,1)plot(X1(1,:),X1(2,:),'r.','LineWidth',2),hold onplot(X2(1,:),X2(2,:),'go','LineWidth',2),hold onplot(X3(1,:),X3(2,:),'b+','LineWidth',2),hold ontitle('训练样本分布情况')legend('训练样本1','训练样本2','训练样本3') subplot(2,1,2)plot(X10(1,:),X10(2,:),'r.','LineWidth',2),hold onplot(X20(1,:),X20(2,:),'go','LineWidth',2),hold onplot(X30(1,:),X30(2,:),'b+','LineWidth',2),hold ontitle('测试样本分布情况')legend('测试样本1','测试样本2','测试样本3')%由于多次循环后存在小数，根据实际情况判别矩阵须取整%如果N为偶数，可能出现小数为0.5的情况，此时将无法更加准确判断矩阵Result=Result/N %判别矩阵，反映Bayes的判别效果for i=1:length(Result)if round(sum(Result(i,:)-fix(Result(i,:))))==1[m,n]=find(max(Result(i,:)-fix(Result(i,:)))==(Result(i,:)-fix(Result( i,:))));n=min(n);%存在小数点相同的情况随即选取一个for j=1:length(Result)if j==nResult(i,j)=fix(Result(i,j))+1;elseResult(i,j)=fix(Result(i,j));endendelseif round(sum(Result(i,:)-fix(Result(i,:))))==2[m,n1]=find(max(Result(i,:)-fix(Result(i,:)))==(Result(i,:)-fix(Resul t(i,:))));[m,n2]=find(min(Result(i,:)-fix(Result(i,:)))==(Result(i,:)-fix(Result (i,:))));n1=min(n1);n2=min(n2);%如果有存在小数点相同的情况,随即选取一个for j=1:length(Result)if j==n1Result(i,j)=fix(Result(i,j))+1;elseif j==n2Result(i,j)=fix(Result(i,j));elseResult(i,j)=fix(Result(i,j))+1;endendelsecontinue,endend总结的来说，我们都知道，只要有意义，那么就必须慎重考虑。

贝叶斯的matlab程序

Bayes判别matlab源程序2008年07月15日星期二 22:11在分类判别中，bayes判别的确具有明显的优势，与模糊，灰色，物元可拓相比，判别准确率一般都会高些，而BP神经网络由于调试麻烦，在调试过程中需要人工参与，而且存在明显的问题，局部极小点和精度与速度的矛盾，以及训练精度和仿真精度间的矛盾，等，尽管是非线性问题的一种重要方法，但是在我们项目中使用存在一定的局限，基于此，最近两天认真的研究了bayes判别，并写出bayes判别的matlab程序，与spss非逐步判别计算结果一致。

现对外共享下：clear;clc;yangben=[1 4.1 70 1.8 2.1 1.3 6.61 4.4 78 2.2 1.9 1.5 2.81 2.8 84 1.6 2.7 1.6 10.61 6.4 882 2.3 1.2 8.32 8.2 74 3.7 1.9 1.1 2.92 10.2 81 3.5 1.8 1.7 2.72 14.2 70 2.9 2 0.9 3.22 9.8 78 2.5 1.9 0.7 3.42 16.6 92 6.5 2.4 0.6 33 19.4 50 8.2 1.1 1.5 3.23 22.6 46 9.8 1.1 0.8 3.53 23.8 35 8.8 1.5 1.3 4.3];g=3;[m,n]=size(yangben); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for i=1:ggroupNum(i)=0;group(i)=0;for j=1:mif yangben(j,1)==igroup(i)=group(i)+1;endendif i==1groupNum(i)=group(i);elsegroupNum(i)=groupNum(i-1)+group(i);endendgroupgroupNum; %计算分类个数数组%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%GroupMean=[];for i=1:gif i==1low=1;up=groupNum(i);elselow=groupNum(i-1)+1;up=groupNum(i);endmatrix=yangben(low:up,:);MatrixMean=mean(matrix); %各分类组平均值GroupMean=[GroupMean;MatrixMean];for i=low:upfor j=2:nC(i,j-1)=yangben(i,j)-MatrixMean(j); endendendCGroupMeanV=C'*C/(m-g);V_inv=inv(V) %对矩阵V求逆GroupMean=GroupMean(:,2:n)Q1=GroupMean*V_invfor i=1:glnqi(i)=log(group(i)/m);tmp=GroupMean(i,:);Q2(i)=lnqi(i)-0.5*tmp*V_inv*tmp';endlnqiQ2b=[3.2 70 2.3 2.1 1.6 2.82 88 1.6 1.5 1.2 3.28.2 69 2.9 1.7 0.9 3.121.1 43 5.6 0.8 0.6 2.723.6 85 8.3 1.5 1.1 3.3]; % 判别的样本[u,v]=size(b)result=[]for i=1:ux=b(i,:)y=Q1*x'+Q2'result=[result y]; endresult。

贝叶斯预测模型及matlab代码

贝叶斯预测模型及matlab代码
贝叶斯预测模型是一种基于概率统计的方法，用于预测未来事件的可能性。

在贝叶斯预测模型中，事件的概率是随着时间和数据的变化而变化的。

贝叶斯预测模型的应用领域非常广泛，例如气象预测、金融风险评估、医疗诊断等。

在 MATLAB 中，可以使用贝叶斯统计工具箱来进行贝叶斯预测模型的构建和求解。

以下是一个简单的示例，展示如何在 MATLAB 中使用贝叶斯统计工具箱构建一个二分类的贝叶斯预测模型:
```matlab
% 加载数据
data = load("data.mat");
% 构建二元分类的贝叶斯预测模型
model = buildBaggingModel(data, "投资决策");
% 求解模型参数
[alpha, beta, gamma, lambda] =
estimateModelParams(model);
% 预测新数据
newData = load("newData.mat");
prediction = predict(model, newData);
```
在上述示例中，我们首先使用 MATLAB 内置的数据集`data.mat`来进行模型构建和参数求解。

然后，我们使用`predict()`函数对新
数据进行预测，结果保存在`prediction`变量中。

贝叶斯预测模型的构建和求解需要一定的数学知识和编程技能。

对于初学者来说，可以查阅贝叶斯统计工具箱的文档和教程，进一步学习贝叶斯预测模型的构建和求解。

贝叶斯分类器的matlab实现

贝叶斯分类器的matlab实现贝叶斯分类原理：1) 在已知P(Wi)，P(X|Wi)(i=1,2)及给出待识别的X的情况下，根据贝叶斯公式计算出后验概率P(Wi|X) ;2) 根据1)中计算的后验概率值，找到最大的后验概率，则样本X属于该类举例：解决方案：但对于两类来说，因为分母相同，所以可采取如下分类标准：%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%By Shelley from NCUT，April 14th 2011%Email:*********************%此程序利用贝叶斯分类算法，首先对两类样本进行训练，%进而可在屏幕上任意取点，程序可输出属于第一类，还是第二类%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%clear;close all%读入两类训练样本数据load data%求两类训练样本的均值和方差u1=mean(Sample1);u2=mean(Sample2);sigm1=cov(Sample1);sigm2=cov(Sample2);%计算两个样本的密度函数并显示x=-20:0.5:40;y= -20:0.5:20;[X,Y] = meshgrid(x,y);F1 = mvnpdf([X(:),Y(:)],u1,sigm1);F2 = mvnpdf([X(:),Y(:)],u2,sigm2);P1=reshape(F1,size(X));P2=reshape(F2,size(X));figure(2)surf(X,Y,P1)hold onsurf(X,Y,P2)shading interpcolorbartitle('条件概率密度函数曲线'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%以下为测试部分%利用ginput随机选取屏幕上的点（可连续取10个点）%程序可根据点的位置自动地显示出属于那个类%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%pw1=0.4;pw2=0.6;figure(1)plot(Sample1(:,1),Sample1(:,2),'r.')hold onplot(Sample2(:,1),Sample2(:,2),'b.')for i=1:10[u,v]=ginput(1);plot(u,v,'m*');P1=pw1*mvnpdf([u,v],u1,sigm1);P2=pw2*mvnpdf([u,v],u2,sigm2);hold allif(P1>P2)disp('it belong to the first class');elsedisp('it belong to the second class');end;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%结果示意：两个样本的密度函数曲线：测试结果：命令窗口中显示：it belong to the first classit belong to the second classit belong to the second classit belong to the first classit belong to the first classit belong to the first classit belong to the first classit belong to the first classit belong to the first classit belong to the first class分析可知在第一类周围有八个随机的测试点，在第二类周围有两个随机的测试点，与命令窗口中的结果相符合。

贝叶斯分类器代码

clc;clear all;close all;%训练集SampleMark={'咳嗽','头晕','体温','流感'}Sample={'是','是','正常', '否';....'是','是','高', '是';....'是','是','非常高','是';....'否','是','正常', '否';....'否','否','高', '否';....'否','是','非常高','是';....'是','否','高', '是';....'否','是','正常', '否';....}%流感为是的与否的两类子集IsFlu=Sample(strmatch('是',Sample(:,4)),:);NotFlu=Sample(strmatch('否',Sample(:,4)),:);%先验概率N1=size(IsFlu,1);N2=size(NotFlu,1);Pw1=N1/(N1+N2);Pw2=N2/(N1+N2);%咳嗽似然度%采用m-估计，计算各属性先验概率x1=size(strmatch('是',Sample(:,1)),1);x2=size(strmatch('否',Sample(:,1)),1);p1=x1/(x1+x2);p2=x2/(x1+x2);n1=size(strmatch('是',IsFlu(:,1)),1);n2=size(strmatch('否',IsFlu(:,1)),1);PXwi(1,1:2)=[(n1+1)/(n1+n2+p1) (n2+1)/(n1+n2+p2)]; n1=size(strmatch('是',NotFlu(:,1)),1);n2=size(strmatch('否',NotFlu(:,1)),1);PXwi(2,1:2)=[(n1+1)/(n1+n2+p1) (n2+1)/(n1+n2+p2)]; %头晕似然度%采用m-估计，计算各属性先验概率x1=size(strmatch('是',Sample(:,2)),1);x2=size(strmatch('否',Sample(:,2)),1);p1=x1/(x1+x2);p2=x2/(x1+x2);n1=size(strmatch('是',IsFlu(:,2)),1);n2=size(strmatch('否',IsFlu(:,2)),1);PXwi(1,3:4)=[(n1+1)/(n1+n2+p1) (n2+1)/(n1+n2+p2)]; n1=size(strmatch('是',NotFlu(:,2)),1);n2=size(strmatch('否',NotFlu(:,2)),1);PXwi(2,3:4)=[(n1+1)/(n1+n2+p1) (n2+1)/(n1+n2+p2)];%体温似然度%采用m-估计，计算各属性先验概率x1=size(strmatch('正常',Sample(:,3)),1);x2=size(strmatch('高',Sample(:,3)),1);x3=size(strmatch('非常高',Sample(:,3)),1);p1=x1/(x1+x2+x3);p2=x2/(x1+x2+x3);p3=x3/(x1+x2+x3);n1=size(strmatch('正常',IsFlu(:,3)),1);n2=size(strmatch('高',IsFlu(:,3)),1);n3=size(strmatch('非常高',IsFlu(:,3)),1);PXwi(1,5:7)=[(n1+p1)/(n1+n2+n3+p1) (n2+p2)/(n1+n2+n3+p2) (n3+p3)/(n1+n2+n3+p3)]; n1=size(strmatch('正常',NotFlu(:,3)),1);n2=size(strmatch('高',NotFlu(:,3)),1);n3=size(strmatch('非常高',NotFlu(:,3)),1);PXwi(2,5:7)=[(n1+p1)/(n1+n2+n3+p1) (n2+p2)/(n1+n2+n3+p2) (n3+p3)/(n1+n2+n3+p3)]; %似然度矩阵PXwi_Mark={'是','否','是','否','正常','高','非常高'}PXwi%测试样列，预测是否流感Test={'否','是','非常高'}%计算后验概率PwiX=PXwi(:,2).*PXwi(:,3).*PXwi(:,7);if 1==find(PwiX==max(PwiX))fprintf('是否流感：是\n');elsefprintf('是否流感：否\n');end。

贝叶斯突变检测matlab代码

贝叶斯突变检测是一种用于检测时变信号中突变点的统计方法。

通过计算信号的边际概率分布和条件概率分布，可以判断信号的突变点位置和突变幅度。

在Matlab中，可以通过编写代码来实现贝叶斯突变检测算法。

下面将介绍在Matlab中编写贝叶斯突变检测代码的方法。

1.引入必要的工具包在编写贝叶斯突变检测代码之前，首先需要引入Matlab中必要的工具包。

可以使用Matlab中提供的统计工具箱和信号处理工具箱来实现贝叶斯突变检测算法。

通过引入这些工具包，可以方便地使用其中的函数和工具来进行统计分析和信号处理。

2.生成测试信号在编写贝叶斯突变检测代码之前，首先需要生成一个测试信号，用于验证算法的有效性。

可以通过Matlab中提供的随机信号生成函数来生成一个包含突变点的时变信号。

生成的测试信号应包括正常段和突变段，以便在后续的贝叶斯突变检测中进行分析。

3.编写贝叶斯突变检测算法接下来，可以根据贝叶斯突变检测的原理和算法，在Matlab中编写相应的代码。

贝叶斯突变检测算法主要包括如下步骤：- 计算信号的边际概率分布和条件概率分布- 判断突变点的位置和突变幅度- 生成检测结果在编写代码时，需要充分利用Matlab中提供的统计分析和概率模型相关的函数，以及信号处理相关的函数，来实现贝叶斯突变检测算法的各个步骤。

还需要考虑代码的效率和可维护性，以便在实际应用中能够方便地进行调试和优化。

4.验证算法的有效性编写完贝叶斯突变检测代码后，需要对算法的有效性进行验证。

通过使用生成的测试信号，可以将生成的检测结果与实际的突变点进行对比，从而验证贝叶斯突变检测算法的准确性和可靠性。

如果检测结果与实际突变点吻合较好，则说明算法的实现是正确的。

5.优化和改进在验证算法的有效性之后，还可以对贝叶斯突变检测代码进行优化和改进。

可以考虑使用并行计算来加速算法的运行速度，或者使用更高效的数值计算方法来提高算法的准确性和稳定性。

还可以考虑在实际应用中对算法进行进一步的调试和优化，以适应不同类型和规模的信号数据。

贝叶斯预测模型及matlab代码

贝叶斯预测模型及matlab代码贝叶斯预测模型是一种基于贝叶斯定理的统计模型，用于对未知数据进行概率预测。

它采用先验知识和观测数据来更新概率分布，从而得到后验概率分布，进而进行预测。

贝叶斯预测模型的基本思想是将待预测事件看作是参数的函数，通过对参数的不确定性进行建模，得到预测结果的概率分布。

这种模型的优点是能够根据先验知识进行灵活的概率推断，同时也可以不断更新模型以适应新的数据。

在贝叶斯预测模型中，常用的方法有朴素贝叶斯分类器和贝叶斯网络。

朴素贝叶斯分类器假设特征之间相互独立，通过计算后验概率来进行分类。

贝叶斯网络则是通过有向无环图来表示变量之间的依赖关系，通过联合概率分布来进行推断和预测。

下面是一个简单的贝叶斯预测模型的matlab代码示例，用于预测某种疾病的发病率：```matlab% 假设有两个特征变量，年龄和家族史% 分别定义它们的概率分布age = [1 2 3]; % 年龄分别为1岁、2岁和3岁age_prob = [0.2 0.5 0.3]; % 对应的概率分布family_history = [0 1]; % 无家族史和有家族史family_history_prob = [0.7 0.3]; % 对应的概率分布% 假设发病率是年龄和家族史的函数% 定义发病率的条件概率表disease_prob_given_age_family_history = [0.1 0.9; % 年龄1岁，无家族史和有家族史的发病率0.3 0.7; % 年龄2岁，无家族史和有家族史的发病率0.5 0.5 % 年龄3岁，无家族史和有家族史的发病率];% 分别计算不同情况下的预测概率% 假设要预测的是年龄为2岁，有家族史的情况下的发病率age_index = 2;family_history_index = 2;prediction_prob = age_prob(age_index) *family_history_prob(family_history_index) *disease_prob_given_age_family_history(age_index,family_history_index);% 输出预测概率disp(['预测的发病率为：' num2str(prediction_prob)]);```这段代码演示了如何使用贝叶斯预测模型来预测疾病的发病率。

变分贝叶斯matlab代码

变分贝叶斯matlab代码以下是一个简单的变分贝叶斯（Variational Bayesian）的MATLAB 代码示例：matlab.% 假设我们有一个观测数据集X，其中包含N个样本，每个样本有D个特征。

% 我们的目标是通过变分贝叶斯推断模型的参数。

% 设置参数。

N = 100; % 样本数量。

D = 2; % 特征数量。

K = 3; % 潜在变量数量。

% 生成观测数据集X.X = randn(N, D);% 初始化模型参数。

alpha0 = 1; % 先验参数alpha的初始值。

beta0 = 1; % 先验参数beta的初始值。

m0 = zeros(D, 1); % 先验参数m的初始值。

W0 = eye(D); % 先验参数W的初始值。

% 迭代更新变分参数。

maxIter = 100; % 最大迭代次数。

tol = 1e-6; % 收敛容忍度。

alpha = alpha0;beta = beta0;m = m0;W = W0;for iter = 1:maxIter.% 更新变分参数q(u)。

Sn_inv = alpha eye(K) + beta X' X;Sn = inv(Sn_inv);mn = beta Sn X' (X m);% 更新变分参数q(lambda)。

gamma = alpha + N/2;lambda = beta + 0.5 sum((X m).^2 + diag(X Sn X'));% 更新变分参数q(alpha)。

alpha = alpha0 + N/2;% 更新变分参数q(W)。

W_inv = W0_inv + beta X' X + beta mn mn';W = inv(W_inv);% 更新变分参数q(beta)。

beta = beta0 + N/2;% 检查是否收敛。

if abs(alpha alpha_old) < tol && abs(beta beta_old) < tol && norm(m m_old) < tol && norm(W W_old) < tol.break;end.% 更新旧值。

贝叶斯分类器的MATLAB实现

贝叶斯分类器的MATLAB实现贝叶斯分类器是⼀种简单的模式分类器，它是以特征值的统计概率为基础的，简单的讲，例如已知两个类w1和w2，⼀个未知样本x，这⾥说的未知，就是不知道它属于w1类还是属于w2类，然后根据统计⽅法分别计算得到x属于w1类的概率，即P（w1|x）和属于w2类的概率，即P（w2|x），如果P（w1|x）> P（w2|x），则x属于w1，反之则属于w2。

其matlab代码如下：clear;%clc;n=100;m1=0;m2=0;num1=0;%⽤于计数num2=0;%⽤于计数num3=0;%⽤于计数num4=0;%⽤于计数mu1=[1 3];sigma1=[1.5 0;0 1];r1=mvnrnd(mu1,sigma1,n);%⽣成模式类1mu2=[3 1];sigma2=[1 0.5;0.5 2];r2=mvnrnd(mu2,sigma2,n);%⽣成模式类2subplot(1,2,1);plot(r1(:,1),r1(:,2),'ro',r2(:,1),r2(:,2),'b*');title('图1：两个模式类各⽣成个100正态分布的随机数⼆维散点图');p1=normpdf(r1(:,1),mu1(:,1),sqrt(1.5));p2=normpdf(r1(:,1),mu2(:,1),1);p3=normpdf(r2(:,1),mu1(:,1),sqrt(1.5));p4=normpdf(r2(:,1),mu2(:,1),1);for i=1:1:100if (p1(i)*0.5)>=(p2(i)*0.5)%进⾏模式判别num1=num1+1;m1=m1+1;a1(m1,:)=r1(i,:);%分到模式类1elsenum2=num2+1;m2=m2+1a2(m2,:)=r1(i,:);%分到模式类2endif (p3(i)*0.5)<=(p2(i)*0.5)num3=num3+1;m1=m1+1;a1(m1,:)=r2(i,:);%分到模式类1elsenum4=num4+1;m2=m2+1;a2(m2,:)=r2(i,:);%分到模式类2endendsubplot(1,2,2);plot(a1(:,1),a1(:,2),'ro',a2(:,1),a2(:,2),'b*');title('图2：以第⼀特征分量对200个样本分类');运⾏结果如下图所⽰：从运⾏结果可看出，模式类1的⼀些样本点被错误分到模式类2，模式类2的⼀些样本点被错误分到模式类1，也就是说，贝叶斯分类器的分类正确率不⾼。

matlab朴素贝叶斯分类算法代码

matlab朴素贝叶斯分类算法代码朴素贝叶斯分类算法是一种基于贝叶斯定理的统计学习方法，常用于分类和文本分类问题。

以下是一个简单的 MATLAB 朴素贝叶斯分类算法的示例代码，演示如何使用MATLAB 的统计工具箱（Statistics and Machine Learning Toolbox）进行朴素贝叶斯分类：% 生成示例数据data = randn(100, 2); % 两个特征的随机数据labels = randi([1, 2], 100, 1); % 两类标签（1或2）% 划分训练集和测试集idx = randperm(100);trainData = data(idx(1:70), :);trainLabels = labels(idx(1:70));testData = data(idx(71:end), :);testLabels = labels(idx(71:end));% 训练朴素贝叶斯分类器nbClassifier = fitcnb(trainData, trainLabels);% 在测试集上进行预测predictedLabels = predict(nbClassifier, testData);% 评估分类器性能accuracy = sum(predictedLabels == testLabels) / numel(testLabels);disp(['分类器准确率：', num2str(accuracy * 100), '%']);这个例子中，我们首先生成了一些随机的二维数据，并为每个数据点分配了一个类标签。

然后，我们将数据分为训练集和测试集。

接着，使用 fitcnb 函数训练朴素贝叶斯分类器，并使用 predict 函数在测试集上进行预测。

最后，计算分类器的准确率。

请注意，这只是一个简单的演示，实际应用中你可能需要更复杂的数据集和特征工程。

贝叶斯算法定位matlab代码

贝叶斯算法定位matlab代码贝叶斯算法是一种基于数学统计方法的机器学习算法，在现代数据处理和模型构建中得到了广泛的应用。

当我们要完成一些复杂的编程任务时，往往需要用到这个算法。

而MATLAB作为一种方便快捷的数学计算工具，在机器学习中也拥有着广泛的应用。

本文将从以下几个方面介绍如何使用贝叶斯算法定位MATLAB代码。

一、了解贝叶斯算法的基本知识在进行定位MATLAB代码前，我们需要了解贝叶斯算法的基本知识。

贝叶斯算法是一种基于概率模型的算法，主要是根据已经有的经验数据来计算得出未知参数的概率分布。

其主要思想是在先验概率分布的基础上不断更新后验概率分布以进行推理和预测。

重点掌握以下几个概念：先验概率分布、似然函数、边缘概率分布和后验概率分布。

二、利用贝叶斯算法定位MATLAB代码1、基于多项式回归的贝叶斯优化方法多项式回归是一种常用的回归方法，常常用于处理非线性数据。

而贝叶斯优化方法则是在优化过程中不断地利用当前的经验数据来更新和修正模型参数，以实现更加准确的优化结果。

我们可以利用这种方法来优化MATLAB代码，在写程序时达到更加准确的预测效果。

（详见Bayesian Optimization Toolbox）2、利用贝叶斯网络进行程序优化贝叶斯网络是一种图模型，可以用于描述各种不同的随机变量之间的概率关系。

我们可以利用这种方法来对MATLAB代码进行优化，尤其是对于一些复杂的程序。

根据代码的复杂程度，可以选择不同的贝叶斯网络类型来建模。

（详见Bayesian Network Toolbox）3、利用贝叶斯分类算法进行错误检测在开发MATLAB代码时，常常会出现一些错误，如数组越界、类型不匹配等等。

我们可以利用贝叶斯分类算法来进行错误检测，减少程序运行时出现的崩溃或错误。

（详见Naive Bayes Classifier Toolbox）三、总结在本文中，我们介绍了如何利用贝叶斯算法定位MATLAB代码。

模式识别实验报告

实验一Bayes 分类器设计本实验旨在让同学对模式识别有一个初步的理解，能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识，理解二类分类器的设计原理。

1实验原理最小风险贝叶斯决策可按下列步骤进行：(1)在已知)(i P ω，)(i X P ω，i=1,…，c 及给出待识别的X 的情况下，根据贝叶斯公式计算出后验概率： ∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…，x(2)利用计算出的后验概率及决策表，按下面的公式计算出采取i a ,i=1,…，a 的条件风险∑==cj j jii X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…，a 进行比较，找出使其条件风险最小的决策k a ，即则k a 就是最小风险贝叶斯决策。

2实验内容假定某个局部区域细胞识别中正常（1ω）和非正常（2ω）两类先验概率分别为正常状态：P （1ω）=0.9；异常状态：P （2ω）=0.1。

现有一系列待观察的细胞，其观察值为x ：-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682 -1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 已知类条件概率密度曲线如下图：)|(1ωx p )|(2ωx p 类条件概率分布正态分布分别为（-2，0.25）（2,4）试对观察的结果进行分类。

3 实验要求1) 用matlab 完成分类器的设计，要求程序相应语句有说明文字。

2) 根据例子画出后验概率的分布曲线以及分类的结果示意图。

使用MATLAB进行参数估计与模型选择的方法

使用MATLAB进行参数估计与模型选择的方法在MATLAB中，有多种方法可以进行参数估计与模型选择，其中包括最小二乘法、最大似然估计、贝叶斯统计和交叉验证。

最小二乘法：最小二乘法是一种常见的参数估计方法，适用于线性模型。

在MATLAB中，可以使用`polyfit`函数进行最小二乘法估计。

该函数采用原始数据点的坐标和多项式的次数作为输入，并返回多项式系数。

```matlabx=[1,2,3,4,5];y=[1,4,9,14,24];degree = 2;coefficients = polyfit(x, y, degree);```最大似然估计：最大似然估计是一种参数估计方法，通过最大化观测数据的可能性来估计参数。

在MATLAB中，可以使用`mle`函数进行最大似然估计。

该函数要求用户提供一个自定义的似然函数，该函数将根据参数估计观测数据的可能性。

```matlabx=[1,2,3,4,5];startingVals = [0, 1];estimates = mle(y, 'pdf', likelihoodFunc, 'start', startingVals);```贝叶斯统计：贝叶斯统计是一种基于概率的模型选择方法，通过计算后验概率来进行模型选择和参数估计。

在MATLAB中，可以使用`bayeslm`函数进行贝叶斯线性回归的模型选择。

该函数采用原始数据点的坐标和响应变量作为输入，并返回具有最高后验概率的线性回归模型。

```matlabx=[1,2,3,4,5];y=[1,4,9,14,24];model = bayeslm(x, y);```交叉验证：交叉验证是一种常用的模型选择方法，通过将数据集分成训练集和测试集来评估模型的性能。

在MATLAB中，可以使用`cvpartition`函数将数据集分成训练集和测试集。

然后，可以使用交叉验证来选择模型，并使用测试集进行性能评估。

模式识别实验报告2_贝叶斯分类实验_实验报告(例)

t2=[t2,tt2];
end
plot(1:23,t2,'b','LineWidth',3);
%下面是bayesian_fun函数
functionf=bayesian_fun(t2,t1,W1,W2,w1,w2,w10,w20)
x=[t1,t2]';
f=x'*W1*x+w1'*x+w10- (x'*W2*x+w2'*x+w20);
%f=bayesian_fun.m
function f=bayesian_fun(t2,t1,W1,W2,w1,w2,w10,w20)
x=[t1,t2]';
f=x'*W1*x+w1'*x+w10 - (x'*W2*x+w2'*x+w20);
w10=-1/2 * u1'*S1tinv*u1 - 1/2 *log(det(S1t)) + log(pw1);
w20=-1/2 * u2'*S2tinv*u2 - 1/2 *log(det(S2t)) + log(pw2);
t2=[]
fort1=1:23
tt2 = fsolve('bayesian_fun',5,[],t1,W1,W2,w1,w2,w10,w20);
'LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0 1 0],...
'MarkerSize',10)

朴素贝叶斯二分类matlab代码

朴素贝叶斯分类器是一种常用的机器学习算法，它基于贝叶斯定理和特征条件独立假设来进行分类。

它在文本分类、垃圾邮件过滤、情感分析等领域有着广泛的应用。

本文将介绍如何使用Matlab实现朴素贝叶斯分类器进行二分类，并附上相应的代码示例。

一、朴素贝叶斯分类器原理简介1. 贝叶斯定理贝叶斯定理是基于条件概率的一个重要公式，在朴素贝叶斯分类器中扮演着核心的角色。

其数学表达式为：P(c|x) = P(x|c) * P(c) / P(x)其中，P(c|x)表示在给定特征x的条件下，类别c的概率；P(x|c)表示在类别c的条件下，特征x的概率；P(c)表示类别c的先验概率；P(x)表示特征x的先验概率。

2. 特征条件独立假设朴素贝叶斯分类器的另一个核心假设是特征条件独立假设，即假设每个特征相互独立。

虽然这个假设在现实中不一定成立，但在实际应用中，朴素贝叶斯分类器仍然表现出色。

二、朴素贝叶斯分类器二分类matlab代码示例在Matlab中，可以利用已有的函数库和工具箱来实现朴素贝叶斯分类器。

下面是一个简单的二分类示例代码：```matlab% 1. 准备数据data = [3.393533211,2.331273381,0;3.110073483,1.781539638,0;1.343808831,3.368360954,0;3.582294042,4.679179110,0;2.280362439,2.866990263,0;7.423436942,4.696522875,1;5.745051997,3.533989803,1;9.172168622,2.511101045,1;7.792783481,3.424088941,1;7.939820817,0.791637231,1;];% 2. 训练模型X = data(:, 1:2);Y = data(:, 3);model = fib(X, Y);% 3. 预测新样本new_sample = [8, 3];label = predict(model, new_sample);disp(['The label of the new sample is: ', num2str(label)]);```以上代码实现了一个简单的二分类朴素贝叶斯分类器。

贝叶斯分类matlab程序

贝叶斯分类matlab程序
贝叶斯分类是一种基于贝叶斯定理的统计分类方法，它被广泛
应用于模式识别、机器学习和数据挖掘领域。

在MATLAB中，你可以
使用内置的函数和工具箱来实现贝叶斯分类。

首先，你需要准备你的数据集。

假设你有一个包含特征和标签
的数据集，你可以使用MATLAB的数据导入工具来加载数据。

然后，
你可以将数据集分为训练集和测试集，以便在训练集上训练模型，
在测试集上评估模型性能。

接下来，你可以使用MATLAB的统计和机器学习工具箱中的函数
来实现贝叶斯分类。

你可以使用`fitcnb`函数来训练贝叶斯分类器，并使用`predict`函数来对新样本进行分类预测。

在训练分类器时，
你可以指定先验分布的类型（如正态分布、核密度估计等）以及其
他参数。

另外，你还可以通过交叉验证、网格搜索等技术来优化分类器
的性能，以及通过可视化工具来分析分类结果和模型性能。

在实现贝叶斯分类器时，还需要考虑数据预处理、特征选择、
模型评估等步骤，以确保模型的准确性和泛化能力。

总之，在MATLAB中实现贝叶斯分类器涉及数据准备、模型训练、参数调优和性能评估等多个步骤，需要综合运用MATLAB的数据处理、统计分析和机器学习工具箱中的函数和工具来完成。

希望这个回答
能够帮助到你。

模式识别matlab程序

模式识别的一些matlab程序最小错误率Bayes分类器的设计与检验clcclearX1=10000;MU1=2.0;SIGMA1=0.2;Y1=normrnd(MU1,SIGMA1,X1,1);X2=5000;MU2=1.0;SIGMA2=0.2;Y2=normrnd(MU2,SIGMA2,X2,1);Y=[Y1;Y2];Pw1=X1/(X1+X2);Pw2=X2/(X1+X2);T1=find(normpdf(Y1,MU1,SIGMA1)*Pw1>normpdf(Y1,MU2,SIGMA2)*Pw2); T2=find(normpdf(Y2,MU2,SIGMA2)*Pw2>normpdf(Y2,MU1,SIGMA1)*Pw1); et=(X1-length(T1)+X2-length(T2))/(X1+X2);t=fsolve('fun1',1);e=quadl('fun2',-10000,t)+quadl('fun3',t,10000);%fun1function e=fun1(x)MU1=2.0;SIGMA1=0.2;MU2=1.0;SIGMA2=0.2;e=normpdf(x,MU1,SIGMA1)*2/3-normpdf(x,MU2,SIGMA2)*1/3;%fun2function y=fun2(x)MU1=2.0;SIGMA1=0.2;MU2=1.0;SIGMA2=0.2;y=normpdf(x,MU1,SIGMA1)*2/3;%fun3function y=fun3(x)MU1=2.0;SIGMA1=0.2;MU2=1.0;SIGMA2=0.2;y=normpdf(x,MU2,SIGMA2)*1/3;窗函数法高斯分布clcclearload('TestData.mat')Y=[Y1;Y2];%hist([Y1;Y2],x)hn=0.01;x=0:0.01:3;%y=1/15000*sum(1/hn*normpdf((x-Y),MU,SIGMA));for i=1:3/0.01+1y(i)=1/15000*sum(1/hn*normpdf((x(i)-Y)/hn,0,1));endplot(x,y)hold onMU1=2.0;SIGMA1=0.2;MU2=1.0;SIGMA2=0.2;z=normpdf(x,MU1,SIGMA1)*2/3+normpdf(x,MU2,SIGMA2)*1/3; plot(x,z,'r')近邻法高斯分布clcclearload('TestData.mat')Y=[Y1;Y2];Y=sort(Y);x=0:0.01:3;kn=100;for i=1:3/0.01+1j=1;while1if abs(Y(j)+Y(j+kn-1)-2*x(i))<abs(Y(j+1)+Y(j+kn)-2*x(i)) break;elsej=j+1;endif j==15000-kn+1break;endendy(i)=kn/15000/(Y(j+kn-1)-Y(j));endplot(x,y)hold onMU1=2.0;SIGMA1=0.2;MU2=1.0;SIGMA2=0.2;z=normpdf(x,MU1,SIGMA1)*2/3+normpdf(x,MU2,SIGMA2)*1/3; plot(x,z,'r')Fisher线性变换clcclearX1=5;One1=ones(X1,1);SIGMA1=0.2;Y1=normrnd([One1.*2One1.*3],SIGMA1,X1,2);X2=5;One2=ones(X2,1);MU2=3.0;SIGMA2=0.2;Y2=normrnd([One2.*3,One2.*2],SIGMA2,X2,2);plot(Y1(:,1),Y1(:,2),'r*',Y2(:,1),Y2(:,2),'bo')m1=mean(Y1);m2=mean(Y2);S1=(Y1-One1*m1)'*(Y1-One1*m1);S2=(Y2-One2*m2)'*(Y2-One2*m2);sw=S1+S2;w=inv(sw)*(m1-m2)';Y=[Y1;Y2];z=Y*w;hold ont=z*w'/norm(w)^2;plot(t(:,1),t(:,2))for i=1:X1+X2plot([Y(i,1)t(i,1)],[Y(i,2)t(i,2)],'-.')endaxis([-13.5-13.5])grid一种基于最近邻优先的知识聚类算法clear allclcI=imread('InPut.bmp');M=rgb2gray(I);clear II=im2bw(M,254/255);clear MIgl=I;%进行第一次聚类Igl=process(Igl,7);subplot(1,2,1)subimage(I)subplot(1,2,2)subimage(Igl)%第一次…%第...次%processfunction Igl=process(I,r)[A B]=find(I==0);A=round(mean(A));B=round(mean(B));[X,Y]=FindNextPoint(I,A,B,0)[Gx,Gy,Igl]=FindGroupPoint(I,X,Y,r,0);%FindNextPointfunction[X,Y]=FindNextPoint(I,A,B,x);[a,b]=size(I);temp=max([A,B,a-A,b-B]);for i=1:tempQ=I(A-i:A+i,B-i:B+i);[X,Y]=find(Q==x);if length(X)~=0X=X(1)+A-i-1;Y=Y(1)+B-i-1;break;endend%FindGroupPointfunction[Gx,Gy,Igl]=FindGroupPoint(I,X,Y,r,x)Igl=I;while(1)temp=length(X);if(temp==0)Gx=0;Gy=0;break;endT=find(Igl==x);pp=length(T)[X,Y,Igl]=FindNearPoint(Igl,X,Y,r,x); end。

贝叶斯matlab

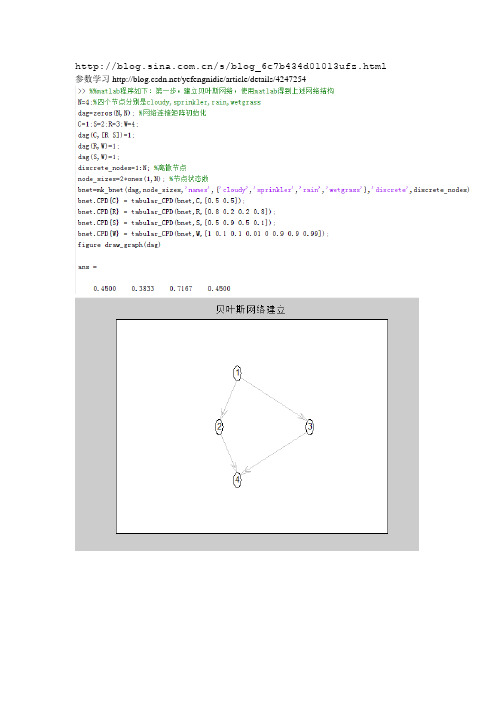
/s/blog_6c7b434d01013ufz.html 参数学习/yefengnidie/article/details/4247254参数学习实验：这里使用的例子依然是“草地潮湿原因模型”。

首先我先如上面实验那样建立好贝叶斯网bnet，并手动构造条件概率表CPT。

然后使用BNT里的函数sample_bnet(bnet)来产生nsamples 个数据样本，nsamples分别取值20，200，2000。

然后，再重新建立一个不知道条件概率表的贝叶斯网bnet2（结构和bnet相同），并把得到的样本作为训练集代入learn_params()函数进行学习，把学习到的条件概率表CPT2与手动构造的CPT进行了比较。

参数学习部分代码:nsamples = 20;samples = cell(N, nsamples);for i = 1:nsamplessamples(:,i) = sample_bnet(bnet);enddata = cell2num(samples);bnet2 = mk_bnet(dag,node_sizes,'discrete',discrete_nodes);seed = 0;rand('state',seed);bnet2.CPD{C} = tabular_CPD(bnet2,C);bnet2.CPD{S} = tabular_CPD(bnet2,S);bnet2.CPD{R} = tabular_CPD(bnet2,R);bnet2.CPD{W} = tabular_CPD(bnet2,W);bnet3 = learn_params(bnet2,data);实验结果：手动给出的CPT nsamples=20 nsamples=200 nsamples=2000BNT的结构学习及结果•福尔摩斯先生在他的办公室工作时接到了他邻居华生的电话。

华生告诉他：他的家里可能进了窃贼，因为他家的警铃响了被告知有窃贼闯入，福尔摩斯迅速开车回家。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

for i=21:40
ቤተ መጻሕፍቲ ባይዱ if(classify(i)~=2)
tne12=tne12+1;
end
end
tpe=(tne21+tne12)/40
test_classify=zeros((n1+n2),1); %测试样本值
for i=1:40
for i=1:(n1+n2)
g1(i) = (-0.5)*(xt(i,:)-us1)*invsigs1*(xt(i,:)-us1)'-log(2*pi)-0.5*log(ss1)+log(pw1);
g2(i) = (-0.5)*(xt(i,:)-us2)*invsigs2*(xt(i,:)-us2)'-log(2*pi)-0.5*log(ss2)+log(pw2);
classify=zeros((n1+n2),1); %理论值
for i=1:(n1+n2)
g1(i) = (-0.5)*(xt(i,:)-u1')*invsig1*(xt(i,:)-u1')'-log(2*pi)-0.5*log(s1)+log(pw1);
end
end
end
title('测试理论决策面')
subplot(2,2,4)
syms xs ys;
ggs = (-0.5)*[xs-us1(1),ys-us1(2)]*invsigs1*[xs-us1(1),ys-us1(2)]'-0.5*log(ss1)+log(pw1)-((-0.5)*[xs-us2(1),ys-us2(2)]*invsigs2*[xs-us2(1),ys-us2(2)]'-0.5*log(ss2)+log(pw2));
tclassify(i)=2;
end
end
tne21=0;%应该是1类，错分到2类的数目
tne12=0;%应该是2类，错分到1类的数目
for i=1:20
if(classify(i)~=1)
tne21=tne21+1;
end
end
ezplot(gg)
hold on
for i=1:40
if(i<=20)
if(tclassify(i)~=1)
plot(x1_test(i,:)-1,'r*');
else
plot(x1_test(i,:)-1,'ro');
end
end
end
title('理论决策面')
subplot(2,2,2)
syms xs ys;
ggs = (-0.5)*[xs-us1(1),ys-us1(2)]*invsigs1*[xs-us1(1),ys-us1(2)]'-0.5*log(ss1)+log(pw1)-((-0.5)*[xs-us2(1),ys-us2(2)]*invsigs2*[xs-us2(1),ys-us2(2)]'-0.5*log(ss2)+log(pw2));
g2(i) = (-0.5)*(x_test(i,:)-u2')*invsig2*(x_test(i,:)-u2')'-log(2*pi)-0.5*log(s2)+log(pw2);
if(g1(i)>g2(i))
tclassify(i)=1;
elseif(g1(i)<g2(i))
x1=mvnrnd(u1,d1,n1); %训练样本
x2=mvnrnd(u2,d2,n2);
xt=[x1;x2];
invsig1=inv(d1);
invsig2=inv(d2);
s1=abs(det(d1));
s2=abs(det(d2));
for i=1:20
if(test_classify(i)~=1)
teste21=sne21+1;
end
end
for i=21:40
if(test_classify(i)~=2)
sne12=sne12+1;
end
end
end
else
if(tclassify(i)~=2)
plot(x2_test(i-20,1)+3,x2_test(i-20,2),'b*'); %为了让1类和2类在图像上区分开
else
plot(x2_test(i-20,1)+3,x2_test(i-20,2),'bo');
g2(i) = (-0.5)*(xt(i,:)-u2')*invsig2*(xt(i,:)-u2')'-log(2*pi)-0.5*log(s2)+log(pw2);
if(g1(i)>g2(i))
classify(i)=1;
elseif(g1(i)<g2(i))
ezplot(ggs)
hold on
for i=1:n1+n2
if(i<=n1)
if(sclassify(i)~=1)
plot(x1(i,:)-1,'r*');
else
plot(x1(i,:)-1,'ro');
ezplot(gg)
hold on
for i=1:n1+n2
if(i<=n1)
if(classify(i)~=1)
plot(x1(i,:)-1,'r*');
else
plot(x1(i,:)-1,'ro');
if(classify(i)~=2)
ne12=ne12+1;
end
end
pe=(ne21+ne12)/(n1+n2)
us1=mean(x1) %参数估计
us2=mean(x2)
si1=zeros(2);
end
end
end
title('样本决策面')
subplot(2,2,3)
syms xx yy;
gg = (-0.5)*[xx-u1(1),yy-u1(2)]*invsig1*[xx-u1(1),yy-u1(2)]'-0.5*log(s1)+log(pw1)-((-0.5)*[xx-u2(1),yy-u2(2)]*invsig2*[xx-u2(1),yy-u2(2)]'-0.5*log(s2)+log(pw2));
invsigs1=inv(ds1);
invsigs2=inv(ds2);
ss1=abs(det(ds1));
ss2=abs(det(ds2));
x=xt(:,1);
y=xt(:,2);
[X,Y]=meshgrid(x,y);
g=zeros((n1+n2),2);
sclassify=zeros((n1+n2),1); %训练样本值
end
end
spe=(sne21+sne12)/(n1+n2)
tclassify=zeros((n1+n2),1); %测试理论值
for i=1:40
g1(i) = (-0.5)*(x_test(i,:)-u1')*invsig1*(x_test(i,:)-u1')'-log(2*pi)-0.5*log(s1)+log(pw1);
classify(i)=2;
end
end
ne21=0;%应该是1类，错分到2类的数目
ne12=0;%应该是2类，错分到1类的数目
for i=1:n1
if(classify(i)~=1)
ne21=ne21+1;
end
end
for i=n1+1:n1+n2
end
else
if(sclassify(i)~=2)
plot(x2(i-n1,1)+3,x2(i-n1,2),'b*'); %为了让1类和2类在图像上区分开
else
plot(x2(i-n1,1)+3,x2(i-n1,2),'bo');
for i=1:n1
si1=si1+(x1(i,:)-us1)'*(x1(i,:)-us1);
end
ds1=si1/n1
si2=zeros(2);
for i=1:n2
si2=si2+(x2(i,:)-us1)'*(x2(i,:)-us2);
end
ds2=si2/n2
test_pe=(sne21+sne12)/40
subplot(2,2,1)
syms xx yy;
gg = (-0.5)*[xx-u1(1),yy-u1(2)]*invsig1*[xx-u1(1),yy-u1(2)]'-0.5*log(s1)+log(pw1)-((-0.5)*[xx-u2(1),yy-u2(2)]*invsig2*[xx-u2(1),yy-u2(2)]'-0.5*log(s2)+log(pw2));
p1 = mvnpdf(x1, u1', d1);