第一部分 同位素地球化学原理解析
第六章 同位素地球化学-1

第六章同位素地球化学第一节基本概念一、同位素的定义核素:是由一定数量的质子(P)和中子(N)构成的原子核。
核素具有质量、电荷、能量、放射性和丰度5中主要性质。
.同位素:原子核内质子数相同而中子数不同的一类原子叫做同位素(isotope),他们处在周期表上的同一位置二、同位素的分类– 放射性同位素(radioactive isotope):原子核是不稳定的,它们能够白发地衰变成其他的同位素。
最终衰变为稳定的放射性成因同位素。
目前已知的放射性同位素达1200种左右,由于大部分放射性同位素的半衰期较短,目前已知自然界中存在的天然放射性同位素只有60种左右。
放射性同位素例子:238U→234Th+4He(α)+Q→206Pb;235U→207Pb;232Th→208Pb– 稳定同位素(stable isotope):原子核是稳定的,迄今还未发现它们能够自发衰变形成其他的同位素。
自然界中共有1700余种同位素,其中稳定同位素有260余种。
z轻稳定同位素,又称天然的稳定同位素,是核合成以来就保持稳定。
其特点是①原子量小,同—元素的各同位素间的相对质量差异较大;②轻稳定同位素变化主要原因是同位素分馏作用所造成的,其反应是可逆的。
如氢同位素(1H和2H)、氧同位素(16O和18O)、碳同位素(12C和13C)等。
z重稳定同位素,又称放射成因同位素(radiogenic isotope):稳定同位素中部分是由放射性同位素通过衰变后形成的稳定产物。
其特点是①原子量大,同—元素的各同位素间的相对质量差异小(0.7%~1.2%)环境的物理和化学条件的变化通常不导致重稳定同位素组成改变;②重稳定同位素变化主要原因是放射性同位素衰败引起,这种变化是单向的不可逆的。
如87Sr是由放射性同位素87Rb衰变而来的;三、同位素丰度同位素丰度(isotope abundance):可分为绝对丰度和相对丰度绝对丰度是指某一同位素在所有各种稳定同位素总量中的相对份额,常以该同位素与1H(取1H=1012)或28Si(取28Si=106)的比值表示。
第一章 同位素的基本概念和理论p
第一章 同位素的 基本概念和理论基础
同位素地球化学在解决地学领域问题的独到之处:
1)计时作用:每一对放射性同位素都是一只时钟,自地球形 成以来它们时时刻刻地,不受干扰地走动着,这样可以测定各 种地质体的年龄,尤其是对隐生宙的前寒武纪地层及复杂地质 体。 2)示踪作用:同位素成分的变化受到作用环境和作用本身的 影响,为此,可利用同位素成分的变异来指示地质体形成的环 境条件、机制,并能示踪物质来源。 3)测温作用:由于某些矿物同位素成分变化与其形成的温度 有关,为此可用来设计各种矿物对的同位素温度计,来测定成 岩成矿温度。 另外亦可用来进行资源勘查、环境监测、地质灾害防治等。
R = 重同位素丰度/轻同位素丰度
3.δ值:样品中两种稳定同位素的比值相对 于某种标准对应比值的千分差值: δ(‰)= ×1000
=[(R样品/R标准) -1]×1000
例如:硫同位素以迪亚布洛峡谷铁陨石中陨硫铁 的硫等标准(CDT),这个标准硫的34S/32S=0.0450045。 它的同位素组成相当于整个地球的平均硫同位素组 成。
传统与非传统稳定同位素
稳定同位素地球化学研究自然界稳定同位素的丰度及其变 化。稳定同位素丰度发生变化的主要原因是同位素的分馏 作用(fractionation),即轻同位素和重同位素在物质中 的分配发生了变化,使得一部分物质富集轻同位素,另一 部分物质富集重同位素。 一般传统稳定同位素研究限于质量数小于40的非金属元素 ,如氢(D/H)、碳(13C/12C)、氧(18O/16O和17O/16O)、 硫(34S/32S和33S/32S)和氮(15N/14N)等传统意义上的。 最新多接收等离子体同位素质谱技术(MC-ICPMS)已经 能够对一些过渡族金属元素的同位素分馏进行实验测定和 研究,这些金属和卤族元素的稳定同位素,如Li、Mg、 Cl、Ca、Cr、Fe、 Cu、Zn、Se和Mo等构成了非传统 稳定同位素研究的新领域。
01 同位素地球化学基本原理A

• 对于宇宙中元素的这种分布格局,E.M 布尔比奇等于1957年提出恒星核合成元 素理论来解释其成因,认为恒星演化遵 循如下的流程,并在不同阶段形成不同 核子数的核。其流程如下:
太阳系形成略图
恒 星 演 化 流 程 示 意 图
星际 气体
原始星
星际 中子星 黑洞 物质
白矮星
主序星
超新星 爆炸
红巨星
• 原子核的结合能除以核子数称平均结合
能,它反映原子核的稳定程度。平均结 合能越大,核子越难拆散;反之亦然。
• 通常而言,质量居中的核子的平均结合 能较大,它较轻核和重核稳定。
3,原子核的聚变和裂变
轻核聚合成较重的核叫聚变; 高温下的轻核聚变反应称热核反应; 重核裂解成两个以上中等质量的核称裂变。 聚变和裂变是获得核能的两种途径。 如:
7,p过程:质子捕获过程,形成低丰度 的同位素 8,x过程:合成D, Li, B等元素
6,地球上的天然核转变
地球上已知的天然核转变分两类: ①, 天然放射性同位素的衰变和裂变及其 诱发的核反应 ②, 宇宙射线引起的核反应 一般认为,地球内部不存在重要核反应, 而大气圈、水圈和岩石圈中存在着多种低能 核反应。
2,原子核的结合能
理论上,原子核的质量应确切地等于质子 和中子质量之和,但是实测发现却不是这样: 质子mH=1.007825原子单位 中子mn=1.008665原子单位
上二者之和为:2.016490 原子质量单位 实测2H核质量:2.014102原子质量单位
• 这种质子和中子结合成原子核时所减少的质 量叫质量亏损(△m)。 • 呈自由状态的核子(质子和中子)相互靠近 结合成原子核时所释放的能量叫结合能(△E)。 结合能与质量亏损遵循质能方程: • △E= △mc2
同位素地球化学1

§1.2 放射性衰变定律 放射性母体核素衰变成稳定子体产生的速率与任一时间t时的 原子数n成正比:
dn n dt
这里λ 是比例常数,它是每个放射性核素的特征值,称之为衰变 常数(以时间的倒数单位表示)。衰变常数表示了一给定放射性 原子在规定的时间内衰变的几率。dn/dt项是母体原子数的变化 率,为负是因为此变化率随时间减小。整理上式,我们得到:
沉积物埋藏和压实后,随后被抬升、褶皱与破裂,使得氧化性的 地下水活化和浓缩矿石形成宽度超过1m的几乎纯铀氧化物的矿 脉。 然而,作为反应堆运行,与现在的0.72%水平相比,在那时依 赖于更高的235U浓度(3%),在终止时间内通过α衰变,浓度减小 了。 裂变现象的地球化学证据:1.自裂变产生的元素丰度特征。如, 观测过量的稀土元素和象Zr这类的其它不活泼元素。碱金属和 碱土金属可能也是富集的,但随后通过淋滤被消去。2.一些元素 的特征同位素丰度仅能由裂变加以解释。
§1.3 分析技术
为了使用放射成因同位素作为定年工具与示踪剂,必须使用 先进、精确的仪器将不同质量的核素分离开,这种仪器就是现代 广泛使用的质谱计。在这种仪器中,使用扇形磁铁,使真空下离 子化的核素先通过高电压加速,然后在磁场中分离不同质荷比的 核素。
m 2V r 2 e H
2
因为产生的大多数离子是单电价的,不同的核素将被分成简 单的质量谱。每一个质量的相对丰度由其相应的离子电流(由法拉 第筒或电子倍增器捕获)确定。其它的质量分离方法(如四极杆、 飞行时间分析器)也可用于质量分析,但它们对于精确的同位素比 值测量很少广泛应用。
德国产的MAT261固体质谱计
德国产的MAT251稳定同位素质谱计
固体同位素分析前处理超纯实验室
固体同位素分析前处理超纯实验室
放射性同位素地球化学1(共86张PPT)

1.4 U-Th-Pb体系
地球化学性质(一)
• U和Th均属锕系元素,常为+4价,但在 地球表层条件下,U呈+6价;
• 由于较大的离子半径和高电价,U和Th 均表现为强不相容元素;
• +4价U、Th较稳定,但+6价的U可呈 UO22-溶于水而发生迁移;
地球化学性质(二)
• 除极少数情况下以沥青铀矿(uraninite, UO2)和硅酸钍矿(thorite)形式成独立矿 物外,多数条件下U和Th呈分散状分布 于造岩矿物中或集中于副矿物中(锆石、 独居石、磷灰石、榍石);
e 2) Nd= 0.25*T2-3T+8.5 (T in Ga)
3) eNd=
143Nd/ 144Nd - (143Nd/144Nd) CHUR (143Nd/144Nd) CHUR
×104
(143Nd/144Nd )CHUR = 0.512638;(147Sm/144Nd) CHUR = 0.1967
根本的数学关系与参数
206Pb = 206Pbi + 238U (el238t – 1) 207Pb = 207Pbi + 235U (el235t – 1)
208Pb = 208Pbi + 232Th (el232t – 1)
(1)对于低Pb高U的体系〔如锆石〕
(206Pb/ 238U)* = (el238t – 1) (207Pb/ 235U)* = (el235t – 1)
Rb-Sr等时线的形成
87Sr 86Sr
( ) 87Sr 86Sr o
a
b
87Rb 86Sr
c
to
Rb-Sr等时线的形成
87Sr 86Sr
地球化学研究中的同位素分析技术

地球化学研究中的同位素分析技术地球化学研究是研究地球和行星体中的元素组成、地球历史演化以及地球的生命起源和演化等问题的学科。
同位素分析技术在地球化学研究领域中起着重要作用。
同位素是同一元素的不同质量核素,具有不同的原子质量,通过同位素的测量,可以揭示地球和宇宙中的一些重要物理、化学和生物过程。
本文将介绍地球化学研究中常用的同位素分析技术。
一、同位素分析技术的原理同位素分析技术是基于同位素的相对丰度差异进行的一种分析方法。
同位素相对丰度的测量可以通过质谱仪、质光谱仪、中子活化分析等手段进行。
这些方法通过测量同位素的质量、电荷、光谱峰位置等特性,从而确定样品中不同同位素的相对含量。
二、同位素分析技术的应用1. 放射性同位素分析放射性同位素是一种具有放射性衰变性质的同位素,通过测量放射性同位素的衰变速率,可以推断出地质历史、地球年龄以及地球内部的物质循环过程。
常用的放射性同位素分析技术包括铀系列、钍系列和钾系列等。
2. 稳定同位素分析稳定同位素是指不发生放射性衰变的同位素。
稳定同位素分析常用于研究地球系统中的元素循环、生物地球化学循环以及古气候变化等问题。
例如,氧同位素分析技术可以用于研究古气候变化、古海洋生物演化等;碳同位素分析技术可以用于研究碳循环、生物地球化学循环等。
3. 稳定同位素示踪技术稳定同位素示踪技术是通过测量示踪物中同位素的相对含量变化来研究地质过程和环境变化的方法。
例如,氧同位素示踪技术可以用于研究水循环、地下水补给和河流水源等;硫同位素示踪技术可以用于研究硫的来源、硫循环以及硫化物的形成和分解等。
三、同位素分析技术的挑战和发展趋势同位素分析技术在地球化学研究中起着重要作用,但也存在一些挑战。
首先,同位素分析技术需要高精度的仪器设备和实验条件,成本较高。
其次,样品准备和分析过程中存在一定的干扰因素,影响测量的准确性和可重复性。
此外,某些同位素的测量范围和准确性仍然有待提高。
为了克服这些挑战,同位素分析技术正在不断发展。
地球化学 第四讲 同位素地球化学

② 同位素交换反应:就是在化学反应中反应物和生成物之间由 于物态、相态及化学键性质的变化,使轻重同位素分别富集在不 同分子中而发生分异,称同位素交换反应。(轻同位素易断裂) 例如:大气圈与水圈之间发生氧同位素交换反应
2H 2 18O16O2 2H 2 16O18O2
(0℃:α=1.074, :α=1.006)
Geochemistry
College of geological science & engineering, Shandong university of science & technology
问题:如何用δ求解αA-B=RA/RB αA-B=RA/RB=(δA+1)/(δB+1) 4、同位素富集系数:
③ 生物化学反应:动植物及微生物在生存过程中经常与介质交换 物质、并通过生物化学过程引起同位素分馏。 例如:植物通过光合作用,使12C更多地富集在有机体中,因此 生物成因地质体如煤、油、气等具有高的12C。生物成因的34S低。 (前生物时代碳质成因?)
Geochemistry
College of geological science & engineering, Shandong university of science & technology
Creativity
Geochemistry
College of geological science & engineering, Shandong university of science & technology
元素:具有相同质子数的核素称为元素。
同位素:具有相同质子数,不同中子数的一组核
Geochemistry
应用地球化学-4同位素地球化学

2020年7月22日星期三
中南大学彭建堂制作
1
同位素地球化学是研究自然体系中同位素的形成、丰度及 在自然作用中分馏和衰变的科学
研究思路:在地球系统作用过程形成宏观地质体的同时, 还发生了同位素成分的变异,这种变异记录了地球物质发 生的时间和形成条件。
同位素地球化学为研究地球或宇宙体的成因与演化,主要 包括地质时钟、地球热源、大气-海洋的相互作用、壳幔相 互作用及壳幔演化、成岩成矿作用、构造作用、古气候和 古环境记录等提供了重要的有价值的信息。
D2O更多残留于水体中。经过多次物理分馏,在一些地区 (如高纬度区),大气降水将形成最轻的水。
2020年7月22日星期三
中南大学彭建堂制作
17
e.g. 由于地球重力作用导致N同位素的扩散分异,大气高 空富集14N,而低层15N富集。 单向多次反复的物理过程中,同位素质量分馏效应 最明显。
2020年7月22日星期三
C+16O16O→C16O2 平衡常数为K1
C+16O18O→C16O18O 平衡常数为K2
实验测定:K1/K2=1.17
2020年7月22日星期三
中南大学彭建堂制作
19
③平衡分馏:在化学反应中,反应物和生成物之间由 于物态、相态、价态和化学键性质的变化,使轻、重 同位素分别富集于不同分子中而导致发生的分异。亦 称同位素交换反应。如:
中南大学彭建堂制作
21
若取某一给定样品的R值做标准,则可测定各地质样 品中R值与标准的绝对变差(δ):
δ(‰)=(R样-R标)/R标 × 1000 =( R样/ R标-1) × 1000
δ>0,样品比标准更富集;δ<0,比标准更贫化; δ=0,与标准具相同的同位素比值。
同位素地球化学1

I NTRODUCTION AND P HYSICS OF THE N UCLEUSI NTRODUCTIONIsotope geochemistry has grown over the last 40 years to become one of the most important fields in the Earth Sciences as well as in geochemistry. It has two broad subdivisions: radiogenic isotope geochemistry and stable isotope geochemistry. These subdivisions reflect the two primary reasons why the isotopes of some elements vary in nature: radioactive decay and chemical fractionation. One might recognize a third subdivision: cosmogenic isotope geochemistry, but this subdivision is perhaps better considered a part of radiogenic isotope geochemistry, since although cosmogenically produced isotopes are not products of radioactive decay, they are products of nuclear reactions.The growth in the importance of isotope geochemistry reflects its remarkable success in attacking fundamental problems of Earth Science, as well as problems in astrophysics and physics. Isotope geo-chemistry has played an important role in transforming geology from a qualitative, observational science to a modern quantitative one. To appreciate the point, consider the Ice Ages, a phenomenon that has fascinated geologist and layman alike for the past 150 years. The idea that much of the northern hemisphere was once covered by glaciers was first advanced by Swiss zoologist Louis Agas-siz in 1837. His theory was based on observations of geomorphology and modern glaciers. Over the next 100 years, this theory advanced very little, other than the discovery that there had been more than one ice advance. Isotopic studies in the last 40 years (and primarily in the past 20) have deter-mined the exact times of these ice ages and the exact extent of temperature change (about 3° or so cooler in temperate latitudes). Knowing the timing of these glaciations has allowed us to conclude that variations in the Earth’s orbital parameters (the Milankovitch parameters) and resulting changes in insolation have been the direct cause of these ice ages. Comparing isotopically deter-mined temperatures with CO2 concentrations in bubbles in carefully dated ice cores leads to the hy-pothesis that atmospheric CO2 plays and important role in amplifying changes in insolation. Care-ful U-Th dating of corals is now revealing the detailed timing of the melting of the ice sheet. Com-paring this with stable isotope geothermometry shows that melting lagged warming (not too surpris-ingly). Other recent isotopic studies have revealed changes in the ocean circulation system as the last ice age ended. Changes in ocean circulation may also be an important feedback mechanism af-fecting climate. Twenty years ago, all this was very interesting, but not very relevant. Today, it pro-vides us with critical insights into how the planet’s climate system works. With the current concern over potential global warming and greenhouse gases, this information is extremely ‘relevant’.Other examples of the impact of isotope geochemistry could be listed. The list would include such diverse topics as ore genesis, mantle dynamics, hydrology, and hydrocarbon migration, monitors of the cosmic ray flux, crustal evolution, volcanology, oceanic circulation, archeology and anthropology, environmental protection and monitoring, and paleontology. Indeed, there are few, if any, areas of geological inquiry where isotopic studies have not had a significant impact.One of the first applications of isotope geochemistry remains one of the most important: geochro-nology and cosmochronology: the determination of the timing of events in the history of the Earth and the Universe. The first ‘date’ was obtained by Boltwood in 1907, who determined the age of a uranium ore sample by measuring the amount of the radiogenic daughter of U, namely lead, present. Other early applications include determining the abundance of isotopes in nature to constrain models of the nature of the nucleus and models of nucleosynthesis (the origin of the elements). Work on the latter problem still proceeds. The usefulness of stable isotope variations as indicators of the condi-tions of natural processes was recognized by Harold Urey in the 1940’s.This course will touch on many, though not all, of these applications. Before discussing applica-tions, however, we must build a firm basis in the physical and chemical fundamentals.P HYSICS OF THE N UCLEUSEarly Development of Atomic and the Nuclear TheoryThat all matter consists of atoms was first proposed by John Dalton, an English school teacher, in 1806. Prout showed in 1815 that atomic weights were integral multiples of the mass of hydrogen.This observation was strong support for the atomic theory, though it was subsequently shown not to hold for all elements. J. J. Thomson developed the first mass spectrograph in 1906 and provided the answer as to why the Law of Constant Proportions did not always hold: those elements not having in-teger weights had several isotopes, each of which had mass that was an integral multiple of the mass of H. In the mean time, Rutherford had made another important observation: that atoms con-sisted mostly of empty space. This led to Bohr’s model of the atom, proposed in 1910, which stated that the atom consisted of a nucleus, which contained most of the mass, and electrons in orbit about it.It was nevertheless unclear why some atoms had different mass than other atoms of the same element. The answer was provided by W. Bothe and H. Becker of Germany and James Chadwick of England: the neutron. Bothe and Becker discovered the particle, but mistook it for radiation.Chadwick won the Nobel Prize for determining the mass of the neutron in 1932. Various other experiments showed the neutron could be emitted and absorbed by nuclei, so it became clear t h a tdiffering numbers of neutrons caused some atoms to be heavier than other atoms of the same element.This bit of history leads to our first basic observation about the nucleus:it consists of protons and neutrons.Some Definitions and UnitsBefore we consider the nucleus in more detail, let’s set out some defi-nitions:N : the number of neutrons, Z : the number of protons (this is the same as atomic number, since the number of protons dictates the chemical properties of the atom), A : Mass number (N+Z), M : Atomic Mass, I :Neutron excess number (I=N-Z). Iso-topes have the same number of pro-tons, but different numbers of neutrons; isobars have the same mass number (N+Z); isotones have the same number of neutrons but different number of protons.The basic unit of nuclear mass is the dalton (formerly known as the amu, or atomic mass unit), which is based on the mass 12C ≡12, that is,the mass of 12C is 12 daltons. The masses of atomic particles are:proton: 1.007593 daltons (oramu, atomic mass units) =1.6726231 x 10-27 kg neutron 1.008982 daltonsFigure 1.1 Neutron number vs. proton number for stable nu-clides.electron 0.000548756 daltons = 9.10093897 x 10-31 kgNucleons, Nuclei, and Nuclear ForcesFigure 1.1 is a plot of N vs. Z showing which nuclides are stable. A key observation in understand-ing the nucleus is that not all nuclides (combinations of N and Z) are stable. In other words, we cannot simply throw protons and neutrons (collectively termed nucleons) together and expect them to necessarily to form a nucleus. For some combinations of N and Z, a nucleus forms, but is unstable, with half-lives from >1015yrs to <10–12sec.An interesting observation from Figure 1.1 is that N ≈Z for stable nuclei. Thus a significant portion of the nucleus consists of protons, which obviously tend to repel each other by electrostatic force. Notice also that for small A, N=Z, for large A, N>Z. This is another important observation t h a t will lead to the first model of the nucleus.From the observation that nuclei exist at all, it is apparent that another force must exist that is stronger than coulomb repulsion at short distances. It must be negligible at larger distances, otherwise all matter would collapse into a single nucleus. This force, called the nuclear force, is a manifestation of one of the fundamental forces of nature (or a manifestation of the single force in nature if you prefer unifying theories), called the strong force. If this force is assigned a strength of 1, then the strengths of other forces are: electromagnetic 10-2; weak force 10-5; gravity 10-39 (we’ll discuss the weak nuclear force later). Just as electromagnetic forces are mediated by a particle, the photon, the nuclear force is mediated by the pion. The photon carries one quantum of electromagnetic force field; the pion carries one quantum of nuclear force field. A comparison of the relative strengths of the nuclear and electromagnetic forces as a function of distance is shown in Figure 1.2.Atomic Masses and Binding EnergiesThe carbon 12 atom consists of 6 neutrons, 6 protons and 6 electrons. But using the masses listed above, we find that the masses of these 18 particles do not add to 12 daltons, the mass of 12C. There is no mistake, they do not add up. What has happened to the extra mass? The mass has been converted to the energy binding the nucleons.It is a general physical principle that thelowest energy configuration is the most stable. We would expect that if 4He is stable relative to two free neutrons and two free protons, 4He must be a lower energy state compared to the free particles. If this is the case, then we can predict from Einstein's mass-energy equiva-lence:E = mc2 1.1that the 4He nucleus has less mass that 2 free neutrons and protons. It does in fact have less mass. From the principle that the lowest energy configurations are the most stable and the mass-energy equivalence, we should be able to predict the relative stability of various nuclei from their masses alone.We define the mass decrement of an atom as:d = W – M 1.210–410–510–610–710–810–910–10Distance, 10-12 cmV,ergsFigure 1.2. The nuclear and electromagnetic potential of a proton as a function of distance from the proton.where W is the sum of the mass of the constituent particles and M is the actual mass of the atom. For example, W for 4He is W = 2m p +2m n + 2m e = 4.034248 daltons. The mass of 4He is 4.003873 daltons, so d = 0.030375 daltons. Converting this to energy using Equ. 1.1 yields 28.28 MeV. This energy is known as the binding energy . Dividing by A,the mass number, or number of nu-cleons, gives the binding energy per nucleon , E b :E b =W –M Ac21.10This is a measure of nuclear stabil-ity: those nuclei with the largestbinding energy per nucleon are the most stable. Figure 1.3 shows E b as a function of mass. Note that the nucleons of intermediate mass tend to be the most stable. This distribution of binding energy is important to the life history of stars, the abundances of the elements, and radioactive decay, as we shall see.Some indication of the relative strength of the nuclear binding force can be obtained by comparing the mass decrement associated with it to that associated with binding an electron to a proton in a hydrogen atom. The mass decrement we calculated above for He is of theorder of 1%, 1 part in 102. The massdecrement associated with bindingan electron to a nucleus of the orderof 1 part in 108. So bonds between nucleons are about 106 times stronger than bonds between electrons and nuclei.The Liquid Drop ModelWhy are some combinations of N and Z more stable than others? The answer has to do with the forces between nucleons and how nucleons are organized within the nucleus. The structure and organi-zation of the nucleus are questions still being actively researched in physics, and full treatment is cer-tainly beyond the scope of this class, but we can gain some valuable insight to nuclear stability by considering two of the simplest models of nuclear structure. The simplest model of the nucleus is the liquid-drop model , proposed by Niels Bohr in 1936. This model assumes all nucleons in a nucleus have equivalent states. As its name suggests, the model treats the binding between nucleons as similar to the binding between molecules in a liquid drop. According to the liquid-drop model, the total bindingFigure 1.3 Binding energy per nucleon vs. mass number.Figure 1.4 Variation of surface, coulomb, and volume energy per nucleon vs. mass number.of nucleons is influenced by 4 effects: a volume energy, a surface energy, an excess neutron energy, and a coulomb energy. The variation of three of these forces with mass number and their total effect is shown in Figure 1.4.In the liquid drop model, the binding energy is given by the equation:B(A,I)= a 1A – a 2A 2/3 – a 3I 2/4A – a 4Z 2/4A 3 + d1.11where:a 1: heat of condensation (volume energy µA) = 14 MeV a 2: surface tension energy = 13 MeV a 3: excess neutron energy = 18.1 MeV a 4: coulomb energy = 0.58 MeVd : even-odd fudge factor. Binding energy greatest for even-even and smallest for odd-odd.Some of the nuclear stability rules above can be deduced from equation 1.11. Solutions for equation 1.11 at constant A, that is for isobars, result in a hyperbolic function of I, as illustrated in Figure 1.5.For odd A, one nuclei will lie at or near the bottom of this function (energy well). For even A,twoFigure 1.5 Graphical illustration of total binding energies of the isobars of mass number A= 81 (left) and A=80 (right). Energy values lie on parabolas, a single parabola for odd A and two parabolas for even A. Binding energies of the 'last'proton and 'last' neutrons are approximated by the straight lines in the lower part of the figure. After Suess (1987).curves result, one for odd-odd, and one for even-even. The even-even curve will be the one with the lower (more stable) one.Odd-Even Effects and Magic NumbersSomething that we have alluded to and which the liquid drop model does not explain well is the even-odd effect. This effect is illustrated in Table 1.1. Clearly, even combinations of nuclides are much more likely to be stable than odd ones. This is the first indication that the liquid drop model does not provide a complete description of nuclear stability. Another observation not explained by the liquid drop model is the so-called Magic Numbers. The Magic Numbers are 2, 8, 20, 28, 50, 82, and 126. Some observations about magic numbers:1. Isotopes and isotones with magic numbers are unusually common (i.e., there are a lot of differentnuclides in cases where N or Z equals a magic number).2. Magic number nuclides are unusually abundant in nature (high concentration of the nuclides).3. Delayed neutron emission in fission occurs in nuclei containing N*+1 (where N* denotes a magicnumber) neutrons.4. Heaviest stable nuclides occur at N=126 (and Z=83).5. Binding energy of last neutron or proton drops for N*+1.6. Neutron-capture cross sections for magic numbers are anomalously low.7. Nuclear properties (spin, magnetic moment, electrical quadrupole moment, metastable isomericstates) change when a magic number is reached.Table 1.1. Numbers of stable nuclei for odd and even Z and NZ N A number of stable nuclei number of very long-lived nuclei(Z + N)odd odd even45odd even odd503even odd odd553even even even16511The Shell Model of the NucleusThe state of the nucleus may be investigated in a number of ways. The electromagnetic spectra emitted by electrons is the principal means of investigating the electronic structure of the atom. B y analogy, we would expect that the electromagnetic spectra of the nucleus should yield clues to its structure, and indeed it does. However, the g spectra of nuclei are so complex that not much progress has been made interpreting it. Observations of magnetic moment and spin of the nucleus have been more useful (nuclear magnetic moment is also the basis of the nuclear magnetic resonance, or NMR, technique, used to investigate relations between atoms in lattices and the medical diagnostic technique nuclear magnetic imaging).Nuclei with magic numbers of protons or neutrons are particularly stable or ‘unreactive’. This is clearly analogous to chemical properties of atoms: atoms with filled electronic shells (the noble gases) are particularly unreactive. In addition, just as the chemical properties of an atom are largely dictated by the ‘last’ valence electron, properties such as the nucleus’s angular momentum and mag-netic moment can often be accounted for primarily by the ‘last’ odd nucleon. These observations sug-gest the nucleus may have a shell structure similar to the electronic shell structure of atoms, and leads to the shell model of the nucleus.In the shell model of the nucleus, the same general principles apply as to the shell model of the atom: possible states for particles are given by solutions to the Schrödinger Equation. Solutions to this equation, together with the Pauli Exclusion principle, which states that no two particles can have exactly the same set of quantum numbers, determine how many nucleons may occur in each shell. In the shell model, there are separate systems of shells for neutrons and protons. As do electrons, pro-tons and neutrons have intrinsic angular momentum, called spin, which is equal to 1/2h (h =h/2π, where h is Planck's constant and has units of momentum, h = 6.626 x 10-34 joule-sec). The total nuclear angular momentum, somewhat misleadingly called the nuclear spin, is the sum of (1) the intrinsic an-gular momentum of protons, (2) the intrinsic angular momentum of neutrons,and (3) the orbital angular momentum ofnucleons arising from their motion in thenucleus. Possible values for orbitalangular momentum are given by l , theorbital quantum number, which mayhave integral values. The total angular momentum of a nucleon in the nucleus is thus the sum of its orbital angular momentum plus its intrinsic angular momentum or spin: j = l ± 1/2. The plus or minus results because the spin angular momentum vector can be either in the same direction or opposite direction of the orbital angular momentum vector. Thus nuclear spin is related to the constituent nucleons in the manner shown in Table 1.2.Let’s now return to magic numbers and see how they relate to the shell model. The magic numbers belong to two different arithmetic series:N = 2, 8, 20, 40, 70, 112...N = 2, 6, 14, 28, 50, 82, 126...The lower magic numbers are part of the first series, the higher ones part of the second. The numbers in each series are related by their third differences (the differences between the differences between the differences). For example, for the first of the above series:28204070112Difference 612203042Difference 681012Difference 222This series turns out to be solutions to the Schrödinger equation for a three-dimensional harmonic os-cillator (Table 1.3). (This solution is different from the solution for particles in an isotropic Coulomb field, which describes electron shells).Table 1.3. Particles in a Three-Dimensional Harmonic Oscillator (Solution of Schrödinger Equation)Nl 010213j1/21/23/21/23/25/21/23/25/27/2State s +p -p +s +d -d +p -p +f -f +No.2242462468S 261220Total(2)(8)(20) (40)N is the shell number; No. gives the number of particles in the orbit, which is equal to 2j +1; S gives the number ofparticles in the shell or state, and total is the total of particles in all shells filled. Magic number fail to follow the progression of the first series because only the f state is available in the fourth shell.Magnetic MomentA rotating charged particle produces a magnetic field. A magnetic field also arises from the orbital motion of charged particles. Thus electrons in orbit around the nucleus, and also spinning about an in-ternal axis, produce magnetic fields, much as a bar magnet. The strength of a bar magnet may be mea-sured by its magnetic moment, which is defined as the energy needed to turn the magnet from a posi-tion parallel to an external magnetic field to a perpendicular position. For the electron, the spin magnetic moment is equal to 1 Bohr magneton (µe ) = 5.8 ¥ 10-9 ev/gauss. The spin magnetic moment of the proton is 2.79 nuclear magnetons, which is about three orders of magnitude less than the Bohr magneton (hence nuclear magnetic fields do not contribute significantly to atomic ones). Surprisingly,in 1936 the neutron was also found to have an intrinsic magnetic moment, equal to -1.91 nuclear magne-tons. Because magnetism always involves motion of charges, this result suggested there is a non-uni-Table 1.2. Nuclear Spin and Odd-Even Nuclides Number of Nucleons Nuclear Spin Even-Even 0Even-Odd 1/2, 3/2, 5/2, 7/2 ...Odd-Odd 1,3form distribution of charge on the neutron, which was an early hint that neutrons, and protons, werecomposite particles rather than elementary ones.Total angular momentum andmagnetic moment of pairs of protons cancel because the vectors of each member of the pair are aligned in opposite directions. The same holds true for neutrons. Hence even-even nuclei have 0 angular momentum and magnetic moment.Angular momentum, or nuclear spin,of odd-even nuclides can havevalues of 1/2, 3/2, 5/2, and non-zero magnetic moment (Table 1.2). Odd-odd nuclei have integer value of angular momentum or 'nuclear spin'.From this we can see that the angu-lar momentum and magnetic mo-ment of a nuclear are determined by the last nucleon added to the nu-cleus. For example, 18O has eight protons and 10 neutrons, and hence 0angular momentum and magnetic moment. Adding one proton to this nucleus transforms it to 19F, which has angular momentum of 1/2 and magnetic moment of ~2.79. For thisreason, the shell model is also sometimes called the single-parti-cle model, since the structure can be recognized from the quantum-mechanical state of the “last”particle (usually). This is a little surprising since particles are assumed to interact.The three-dimensional harmonic oscillator solution explains only the first three magic numbers;magic numbers above that belong to another series. This difference may be explained by assuming there is a strong spin-orbit interaction, resulting from the orbital magnetic field acting upon the spin magnetic moment. This effect is called the Mayer-Jensen coupling. The concept is that the energy state of the nucleon depends strongly on the orientation of the spin of the particle relative to the orbit, and that parallel spin-orbit orientations are energetically favored, i.e., states with higher values of j tend to be the lowest energy states. This leads to filling of the orbits in a somewhat differ-ent order; i.e., such that high spin values are energetically favored. Spin-orbit interaction also occurs in the electron structure, but it is less important.Pairing EffectsIn the liquid-drop model, it was necessary to add a term d , the even-odd effect. This arises from a 'pairing energy' that exists between two nucleons of the same kind. When proton-proton and neutron-neutron pairing energies are equal, the binding energy defines a single hyperbola as a function of I (e.g., Figure 1.4). When they are not, as is often the case in the vicinity of magic numbers, the hyper-bola for odd A splits into two curves, one for even Z, the other for even N. An example is shown in Figure 1.6. The empirical rule is: Whenever the number of one kind of nucleon is somewhat larger than a magic number, the pairing energy of this kind of nucleon will be smaller than the other kind.neutron excess number in the vicinity of N=50.Capture Cross-SectionsInformation about the structure and stability of nuclei can also be obtained from observations of the probability that a nucleus will capture an additional nucleon. This probability is termed the cap-ture-cross section, and has units of area. Neutron capture cross sections are generally of greater use than proton capture cross sections, mainly because they are much larger. The reason for this is simply that a proton must overcome the repulsive coulomb forces to be captured, whereas a neutron, being neu-tral, does not feel the electrostatic forces. Neutron-capture cross sections are measured in barns, which have units if 10-24 cm2, and are denoted by s. The physical cross-section of a typical nucleus (e.g., Ca) is of the order of 5 x 10-25 cm2, and increases somewhat with mass number (more precisely, R = r0A1/3, where A is mass number and r0 is the nuclear force radius, 1.4 x 10-13 cm). While many neutron capture cross sections are of the order of 1 barn, they vary from 0 (for 4He) to 105 for 157Gd, and are not simple functions of nuclear mass (or size). They depend on nuclear structure, being for example, gen-erally low at magic numbers of N. Capture cross-sections also dependent on the energy of the neutron, the dependence varying from nuclide to nuclide.Collective ModelA slightly more complex model is called the collective model. It is intermediate between the liq-uid-drop and the shell models. It emphasizes the collective motion of nuclear matter, particularly the vibrations and rotations, both quantized in energy, in which large groups of nucleons can partici-pate. Even-even nuclides with Z or N close to magic numbers are particularly stable with nearly per-fect spherical symmetry. Spherical nuclides cannot rotate because of a dictum of quantum mechanics that a rotation about an axis of symmetry is undetectable, and in a sphere every axis is a symmetry axis. The excitation of such nuclei (that is, when their energy rises to some quantum level above the ground state) may be ascribed to the vibration of the nucleus as a whole. On the other hand, even-even nuclides far from magic numbers depart substantially from spherical symmetry and the excita-tion energies of their excited states may be ascribed to rotation of the nucleus as a whole.R EFERENCES AND S UGGESTIONS FOR F URTHER R EADINGDickin, A. 1995. Radiogenic Isotope Geochemistry. Cambridge: Cambridge University Press.Faure, G. 1986. Principles of Isotope Geology. New York: Wiley & Sons.Suess, H. E. 1987. Chemistry of the Solar System. New York: John Wiley and Sons.。
地球化学第六章_同位素地球化学-放射性同位素

式中λ为衰变比例常数,简称衰变常数,dN/dt是任一时刻(t)时的衰变速率。 对上式积分得:
∫
t dN = −λ ∫ dt N0 N t0 N
设t=0时,放射性母体原子数为N0,得:lnN-lnN0=-λ t 化简得:
N=N0e
-λ t
,
该公式表示原子数为N0的放射性同位素, 与经过时间t后残存的母体原子数之间的关系。 设衰变产物的原子数为D*,当t=0时D=0,经过时间t的衰变反应,则, D*=N0-N 则,D*= N0(1-e ) or D= N(e -1) 如果一体系中,t=0 时的子体原子数为D0,则该体系子体原子总数为:
第六章 同位素地球化学 放射性同位素地球化学
第一节 放射性同位素地球化学基础
一、放射性衰变反应 1). α衰变 放射性母体同位素放出α粒子, 而转变为另一个新的子体核素。 α粒子由 2 个质子和 2 个中子组成,带正电荷+2。实际为 He 原子核。 衰变子体相对于母体来说,质子数和中子数各减少 2 ,同时质量数减少 4。
2
同位素及其衰变产物 (5)矿物岩石刚形成时只含某种放射性同位素,而不含与之有衰变关系的子体,或虽含一 部分子体但其数量可以估计 (6)对所测定的矿物、岩石的地球化学有相当可靠认识 2、同位素地质年代学所感兴趣的,是自然存在的为数不多的一些放射性同位素核素,主要 包括: – 具有非常慢的衰变速率的(如238U, 235U,232Th, 147Sm, 40K等)、 – 由长寿命放射性母体衰变产生的(如234U,230Th, 226Ra等)、 – 由天然核反应产生的(如14C, 10Be等)、以及由人工核试验产生的放射性同位素。 3、放射性同位素年龄的地质学含义 对同一地质体,选用不同的同位素测年方法,往往会得到不同的年龄值,它们所代表的 地质意义不同。 己有研究表明,对于一个缓慢冷却的岩体来说,不同矿物的封闭温度是不同的,不同的 同位素体系在同种矿物中的封闭温度也是不同的。 同位素年龄时钟是在低于封闭温度时才开 始启动的。 对于根据放射性同位素体系获得的地质年龄,Rollison(1993)划分出具有不同地质含义的 几种年龄: (1) 结晶年龄。对于火成岩体,矿物的结晶年龄记录了岩石的岩浆作用年龄。对于变质 岩体,如果变质矿物的结晶温度低于其封闭温度,则矿物一经形成,同位素时钟就 立即启动、开始记时,从而记录下变质岩结晶年龄。 (2) 冷却年龄。对于火成岩体,冷却年龄是指岩体固结之后的冷却过程中,达到矿物的 封闭温度时同位素时钟开始启动记录下来的年龄。对于变质岩体,矿物在变质高峰 期结晶生成,之后冷却过程中达到矿物的封闭温度时同位素时钟启动记录下来的年 龄。 (3) 变质年龄。很易与冷却年龄混淆,但它是指变质作用高峰期的年龄。变质年龄的确 定方法取决于变质作用的级别。对于低级变质作用,可选用封闭温度较高的某些特 定矿物来确定变质年龄; 对于高级变质作用, 则往往采用全岩的Rb-Sr或Sm-Nd同位 素体系来推断。 (4)地壳形成年龄。是指一个新的大陆地壳块体从地幔中分异出来的时间(O’Nions et al., 1983)。通常通过Sm-Nd模式年龄计算来获得。 (5)地壳滞留年龄。对来自大陆地壳块体剥蚀下来的沉积岩进行Sm-Nd同位素分析,可计 算获得一个地壳滞留年龄(tCR),反映地壳形成年龄。该年龄比地层沉积年龄值大。
同位素地球化学

C16O2 (气) +2H218O (液) ≒C18O2 (气) +2H216O (液) , 在 0℃:α=1.064, 23℃:α=1.059;327℃:α=1.014, 可见高温越高,α →1 。
地质体中共存相之间同位素分馏系数α可以通过实测两相δ值结 果用下列公式逼近:
3)半衰期与平均寿命 半衰期(T1/2):放射性母体同位素的原子数衰减到原有 数目的一半所需要的时间。特征常数 平均寿命:放射性母体同位素在衰变前所存在的平均时间。
4)放射性衰变的类型 单衰变 连续衰变与衰变系列:
一个放射性母体、若干个放射性中间子体和一个最终稳定 子体所形成的衰变链称衰变系列 分支衰变:放射性同位素同时存在两种或多种衰变方式, 形成不同的稳定子体。
αA-B=RA/RB=(1+δA/1000)/(1+δB/1000) lnαA-B=ln(1+δA/1000)-ln(1+δB/1000) 通常α是接近于1的数值,
α=1.00χ-1.0χ0 数学上可证明: 1000ln(1.00χ)≈χ
则下式是方便的近似计算式: 1000lnαA-B=δA-δB=ΔA-B 1000lnαA-B=1000ln(1+δA/1000)-1000ln(1+δB/1000)= δA-δB=ΔA-B (同位素分馏值)
1.02000
10.00 5.0
5.00
4.96
1.00498
20.00 15.0
5.00
4.91
1.00493
30.00 20.0
10.00 9.76
1.00980
地球化学的基本原理与研究方法

地球化学的基本原理与研究方法地球化学是研究地球各种元素、同位素在地球内外相互分配的科学,是研究地球层、地表、水体和大气中元素和同位素组成、分布和迁移规律的学科。
地球化学研究的主要内容包括物质来源、地球化学过程、地球化学时标以及地球化学计量等方面。
本文将介绍地球化学的基本原理与研究方法。
一、地球化学的基本原理地球化学研究以元素和同位素为研究对象,其基本原理可以概括为以下几点:1. 元素循环:地球上的元素在不同的地球系统之间进行循环。
例如,在岩石圈中,元素经历了岩浆作用、岩石风化和沉积作用等过程,不断地在地球系统中迁移和转化。
2. 同位素分馏:同位素分馏是地球化学中的重要现象。
同位素的分馏是指在地质、化学或生物过程中,不同同位素的分布比例发生变化。
通过研究同位素分馏过程,可以揭示地质、化学和生物时间尺度上的环境变化和地球演化过程。
3. 地球系统的开放性:地球系统是开放的,并与外部环境进行物质交换。
例如,大气中的的氧气可以通过生物作用与地壳中的氧发生反应形成氧化物。
这些交换过程对地球系统的物质组成和环境变化产生重要影响。
二、地球化学的研究方法地球化学研究方法是通过采集地球样品,利用实验室中的仪器设备对样品中的元素和同位素进行分析,来揭示地球化学特征和环境变化。
主要的研究方法包括:1. 野外样品采集:地球化学研究通常需要采集岩石、土壤、水体、大气等不同类型的地球样品。
采集样品的方法要求采集的样品具有代表性,以保证研究结果的可靠性。
2. 样品前处理:采集到的地球样品需要进行前处理,包括样品的破碎、磨粉、溶解等步骤。
这些前处理工作是为了获得样品中的溶液或粉末,以便进行后续的元素和同位素分析。
3. 元素分析:地球化学研究中常用的元素分析方法包括原子吸收光谱法、电感耦合等离子体质谱法和质谱法等。
这些方法可以对地球样品中的元素进行准确的定量和定性分析。
4. 同位素分析:同位素分析是地球化学研究中重要的手段,通过测量同位素的比例来研究地球化学过程。
地球化学中的同位素示踪和分析

地球化学中的同位素示踪和分析地球化学是研究地球化学元素地球内部和表层分布、地球化学过程及其规律的学科。
而同位素则是一种在化学和物理方面都具有重要意义的存在。
地球化学中的同位素示踪和分析,是通过同位素不同的浓度和比例来逐步研究地球物质的来源、演化和变化的过程。
在此过程中,地球化学家们可以获取大量有关地球构造、生物演化、古气候、古环境等重要信息。
本文将会探讨地球化学中的同位素示踪和分析的基本原理及其应用。
一、基本原理同位素是指具有相同原子序数(Z)但质量数(A)不同的原子。
同种元素的不同同位素,因为质量的差异而具有不同的化学特性和物理特性。
地球化学中,多数同位素其存在量非常稀少,可以利用现代分析技术对其进行测定,进而对地球物质进行示踪和分析。
在地球科学中,同位素示踪和分析的主要原理是利用同位素存在量不同的特性,对化学和地质过程进行追踪和研究。
具体而言,同位素示踪和分析是在分析样品中不同同位素存在量的基础上,研究样品来源、演化、变化等方面的科学方法。
地球化学中的同位素示踪可以分为两类,一种是稳定同位素示踪,另一种则是放射性同位素示踪。
稳定同位素示踪主要是利用稳定同位素在地球化学过程中不同的分馏效应,来推测样品中的某些地球化学过程,如元素演化,矿物相变,物种演化等。
放射性同位素示踪,则主要是利用放射性同位素的不同半衰期,来推测样品中年代和历史上某些事件的发生时间。
在同位素示踪的过程中,通常采用同位素比值的方法来获得与分析对象相关的信息。
同位素比值(R)是指两个同种元素不同同位素的存在量之比,可以根据比值的变化来推测样品中与分析对象相关的信息。
例如,碳同位素示踪就是利用炭素同位素比值中稳定同位素^13C和^12C的存在量差异,来推测样品中元素演化,动植物来源等信息。
二、应用地球化学中的同位素示踪和分析在地质学、生物学、气候学等领域都有着广泛的应用。
以下是一些常见的应用:1. 地球内部物质循环及元素分馏模型研究地球内部物质循环及元素分馏模型研究需要大量的岩石和矿物样品,利用稳定同位素的存在量差异,可以推测出岩石、矿物的成因和演化历史。
同位素地球化学

整理课件
14
地质学中经常采用的稳定同位素
❖ 1 H(D/H)
• 2 O(18O/16O)
❖ 3 S(34S/32S)
• 4 C(13C/12C)
❖ 5 Sr(87Sr/86Sr)
• 5 Nd(143Nd)
❖ 7 Pb(206Pb,207Pb,208Pb) • 8 N(15N/14N)
❖ 9 Si(32Si/30Si)
整理课件
18
6.1.1 同位素的基本内容
❖ 1. 核素和同位素 ❖ ① 什么叫核素?
❖ 由不同数量的质子和中子按一定结构组成 各种元素的原子核称为核素。
♣ 表示:A=N(neutron)+P(proton)
整理课件
19
② 核素性质
1)核素具有电荷 2)核素具有质量 3)核素具有丰度 4)核素具有能量 5) 核素具有放射性
第6章 同位素地球化学 PartⅠ
整理课件
1
整理课件
2
整理课件
3
同位素地球化学
它是研究地球和宇宙中核素的形成、丰度以 及在自然作用中分馏和衰变规律的科学。
整理课件
4
1. 同位素地球化学研究对象
自然界,尤其是地质作用和地质体中的
同位素丰度及其演化规律
整理课件
5
分支学科
➢宇宙同位素地球化学 ➢地幔同位素地球化学 ➢环境同位素地球化学 ➢考古同位素地球化学 ➢食品同位素地球化学 ➢水文同位素地球化学,等。
22
③ 同位素
❖ 具有相同质子数,不同数目中子数所组成的一 组核素称为同位素。
❖ 主要表现在以下方面:
♣ 实验测试技术不断完善和提高; ♣ 多元同位素体系的综合研究; ♣ 研究领域不断扩大; ♣ 各种新方法的出现 。
18-同位素地球化学PPT课件
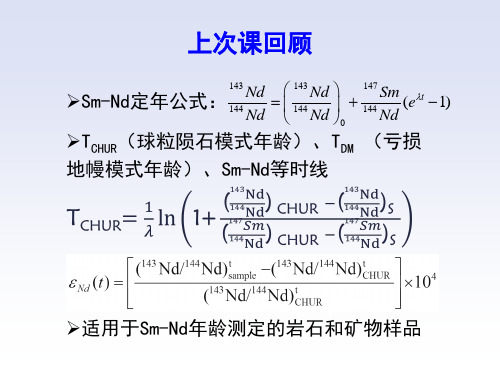
235U → 207Pb + 7 + 4 - + E
t1/2 = 704 106yr 2= 9.8485 10-10yr-1
232Th 228 Ra ...... 224 Ra 220 Rn ...... 212 Pb ...... 208 Pb
Pb Pb
207 204
Pb Pb
i
235U 204 Pb
(e235t
1)
208 Pb 204 Pb
208 204
Pb Pb
i
232Th (e232t 204 Pb
1)
11
U-Th-Pb同位素体系
由于U-Th-Pb体系可构成相互独立的衰变体系,原理上 对同一地质体进行同位素分析,可获得三个独立的年龄 值。如所分析样品符合等时线前提,238U-206Pb、235U207Pb、232Th-208Pb体系应该给出一致的年龄(相对误差 小于或等于10%);然而,由于U、Pb的易活动性,在 风化作用和低级变质作用,常可导致体系U-Pb同位素组 成不能保持封闭,往往得不到一致年龄,因此用等时线 法成功获得有意义年龄的实例相对有限。
20
谐和曲线
假如矿物形成于3.0Ga,则 其具谐和年龄的207Pb/235U、
206Pb/238U比值将分别为 18.1902和0.59249
21
如果样品铅丢失或铀获得,则坐标点落在一致曲线下方;
如果样品铅获得或铀丢失,则坐标点落在一致曲线上方.
若样品形成后丢失部分放射成因铅,随后又封闭,那么 一组经历相同的样品,在207Pb*/ 235U和 206Pb*/ 238U为横 纵坐标的图上的数据点就构成了一条直线,即不一致线。
01 同位素地球化学基本原理B

第二节 同位素的基本概念和 质谱分析
• 一、同位素的定义和物理化学性质 • 1,概念:
• 凡是原子核内质子数相同而中子数不同 的原子互称同位素。
• 同位素在元素周期表中占据同一位置,通常 记作:
•
A
X 或AXZ Z
• 其中X代表元素符号,Z为原子序数,A为质 量数。
• 除113Cd/113In外,A为奇数的稳定同位素不存 在。
• 相邻3个同量异位素中,中间放射性同位 素发生β-衰变时,该同位素同样具有k层 电子捕获。如: • • • •
40Ar←(k)←40 50Ti←(k)←50
K*→(β-)→40Ca La→(β-)→138Ce Lu→(β-)→176Hf
二、同位素丰度
• 某一元素中各同位素间的相对含量,即各同 位素所占的原子百分数,叫同位素丰度。 • 如铁的4个同位素丰度分别是:
• 5.89%,91.8%,2.1%,0.3%
• 原子核越稳定的同位素,丰度越高; • 原子序数较小的元素,通常有1种同位素 丰度占绝对优势; • 原子序数较大的元素,通常以2-3个同位 素为主。
• 利用质谱分析法测定同位素成分和丰度 的工作一般称为同位素的质谱分析。能 进行质谱分析的仪器叫质谱计。 • 目前所用质谱计是按尼尔(Nier,1940) 设计制造的。其构成和工作原理如下:
(一)质谱计的构成
• 1,进样系统:经过前处理的样品,制成气体、 液体或固体装入进样系统; • 2,离子源:将样品电离成带正电荷或负电荷 的离子,并将离子流加速,聚集成束;
三,同位素丰度规律
• 同位素丰度与核的稳定性有直接关系。 • 同位素丰度存在4个基本规律:
1,对称定则
地球化学课件raddioactive同位素地球化学

一、自然界引起同位素成分变化的原因
(一)核素的性质 1.什么叫核素? 由不同数量的质子和中子按一定结构组成各种元素
的原子核称为核素,任何一个核素都可以用A=P+N这 三个参数来表示。
而具有相同质子数,不同数目中子数所组成的一组 核素称为同位素。
O的质子数P=8,但中子数分别为8、9、10,因此 ,氧有质量数分别为16O、17O、18O三个同位素。
(三) 同位素成分的测定及表示方法
一般来说质量数A<209的同位素大部分是稳定的,只有少 数是放射性的,如14C,40K,87Rb;而质量数大于209的同位素 全部属于放射性同位素。
一种元素可由不同数量的同位素组成。自然界中 同位素最多的是Sn元素,有10个同位素:
112,114,115,116,117,118,119,120,122,124Sn 自然界也存在只有一种同位素单独组成的元素: Be、F、Na、Al、P等27种。其余大多数由2-5种同位素组 成。
(二) 同位素分类
从核素的稳定性来看,自然界存在两大类同位素: 一类是其核能自发地衰变为其它核的同位素,称为放射性同位 素; 另一类是其核是稳定的,到目前为止,还没有发现它们能够衰 变成其它核的同位素,称为稳定同位素。 然而,核素的稳定性是相对的,它取决于现阶段的实验技术对 放射性元素半衰期的检出范围,目前一般认为,凡是原子存在的 时间大于1017年的就称稳定同位素,反之则称为放射性同位素 。
(一) 核素的性质
(4)核素具有能量:原子核聚集高质量的粒子于一个极小的体积 内,因此,原子核内孕含着巨大的能量,即核能,也称“结合能”。 结合能越高核素越稳定;结合能低(如H、N、Li、Be及高质量 数 的核素)的核素不稳定。在核衰变过程中,一部分核能通过放射出 各种粒子及射线而被释放出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 同位素分馏效应
由质子数目相同,中子数目不同的同位素原子或化合物之间物 理化学性质上的差异(热力学性质,运动及反应速度上的差异等), 使得它们在自然界的各种地球化学作用过程中产生了同位素分馏。 根据分馏的性质和原因分为两大类型:热力学同位素分馏和动力学 同位素分馏。产生同位素分馏的各种作用统称为同位素分馏效应 (isotope fractionation efect)。
同位素分馏(isotope fractionation):是指一系统中,某元素的各 种同位素原子或分子以不同的比值分配到各种物质或物相中的作用。
同位素分馏系数(α)(isotope fractionation coefficient):某一组分 中两种同位素丰度之比与另一组分的相应比值之商。
AB
自然界物质的同位素交换,可以通过扩散、溶解-重新沉淀和微区化 学置换等方式来实现。交换可以在均质体系中进行,也可以在非均质体系 中进行。在均质体系中同位素交换速度快且容易接近或达到同位素平衡。
同位素交换及热力学同位素分馏特点
(1)同位素交换反应(isotope exchange reaction) :
(3)Slap(Standard light Antarctic Precipitation)南极原始的粒雪样品。 δD SMOW = -55.50‰,δ18O SMOW = -428.5±1‰; D/H=(89.02±0.05)×10-6, 18O/16O=1882.766×10-6。
(4) PDB(Pee Dee Belemnite)美国卡罗莱纳州白垩系Pee Dee组中拟箭 石制成的CO2,作为碳氧同位素标准。 PDB的 δ13CPDB=0‰,δ18OPDB=0‰;13C/12C=1123.72 ×10-6, 18O/16O=415.80 ×10-5。
(5) CDT(Canyon Diablo Troilite)美国亚利桑那州Comyon Diablo铁陨 石中陨硫铁相的硫同位素组成,34S/32S=0.0450045,δ34SCDT=0‰。 在不同类型的样品测定中,由于采用不同的标准样品得到不同的 δ值,如:水的δ18O值是相对于标准样品SMOW,而碳酸盐的δ18O值 是相对于PDB标准,在应用中要换算为相同标准。
2.1 热力学同位素分馏
因热力学原因,导致系统中轻、重同位素原子或分子在化合物或 物相之间发生重新分配,造成各化合物或物相中同位素组成的差异, 称之为热力学同位素分馏(isotope thermodynamic fractionation)。
热力学原因有两层含意:一是轻、重同位素原子或分子的热力学 性质不同,如它们的熵、焓、内能、热容等热力学参数存在着差异; 二是当环境因素(主要是温度)发生变化时,一个体系内的自由能 也会随之变化。当环境温度确定后,在不存在化学反应时,系统总 是通过同位素交换的方式,自动调整各化合物或物相的轻、重同位 素原子或分子的分配比,来降低系统的自由能(△E),实现系统的 稳定状态。当系统的△E为0,即同位素交换达到平衡时,系统的各 化合物或物相的同位素组成也随之确定,这时的同位素分馏,称为 热力学同位素平衡分馏。
δ值(δvalue) :指某一元素样品中的两种稳定同位素的比值相对于某 种标准样品对应比值的千分差值,即
δ= R样品 R标准 ×1000 (‰)
R标准
式中的R 代表样品、标准样品的同位素比值。
同位素组成(isotope composition):泛指各种物质同位素含量 (同位素丰度、同位素比值或δ值)的一种的称谓。
RA RB
同位素分馏系数定义为:
式中:RA为A物质的某种元素的同位素丰度之比;RB为B物质中同种元素的 同位素丰度之比。
同位素富集系数(△值)(isotope concentration coefficient) :用来表示两种物质间同一元素同位素组成差别 的程度。定义为:ΔA-B = δA-δB式中:δA和δB分别代表两种不 同物质同一元素的同位素组成。
同位素地球化学基本原理及应用 尹观
第一部分:同位素地球化学原理
一 . 同位素分馏理论基础
同位素、稳定同位素(stable isotope) 稳定同位素又分为轻(light mass)质量数元素的
稳定同位素和重(heav 同位素基本概念
同位素的表示方法: “mA”, A为某元素的符号, m为其质量数, m (质量数)=Z(质子数)+N(中子数)。例如:氢同位素:1H、D、 3H*(T);碳同位素:12C、13C、14 C*; 氧同位素:16O、17O、18O; 硫同位素:32S、33S、34S、36S;锶同位素:88Sr、87Sr、86Sr、84Sr。
同位素分馏系数(α)与δ值的关系
1.2 常用标准样品
(1)SMOW:标准平均海洋水,H、O 同位素国际标准。δD SMOW = 0‰,δ18O SMOW = 0‰;D/H=(157.6±0.3)×10-6, 18O/16O=(1993.4±2.5) ×10-6。
(2)V-SMOW(Vienna SMOW),经过蒸 馏后的海水。δD SMOW ≈0‰,δ18O SMOW≈0‰;D/H=(155.76±0.05)×10-6, 18O/16O=(2005.2±0.45) ×10-6。
同位素交换是热力学同位素分馏中的一种反应过程,它可用下列方程式
表示:
例如:
AX0+BX* AX*+BX0
同位素丰度(isotope abundance):指某种元素的各种同位素原子 数相对于其原子总数的百分比。
同位素比值(isotope ratio):指某种元素的两种同位素丰度之比。 与同位素丰度一样,它也是用来表示天然物质中同位素含量的一种 方式。习惯上把重质量数的同位素原子记作比值的分子,轻质量数 的同位素原子记作比值的分母。例如:氢同位素比值为D/H;氧同位 素比值为18O/16O;碳同位素比值为13C/12C;锶同位素比值为87Sr/86Sr 等。
