厦门大学材料学院 考研复试 材料测试方法 06 晶格常数的精确测定
highscore计算晶格常数

highscore计算晶格常数晶格常数是指晶体中晶胞的长度。
它是晶体中原子或离子的排列方式以及晶胞形状的重要参数,对于研究晶体的结构和性质具有重要意义。
计算晶格常数的方法有多种,下面将介绍其中几种常用的方法。
1.X射线衍射法X射线衍射是一种常用的计算晶格常数的方法。
X射线衍射谱能够提供晶体的结构信息,通过测定X射线衍射谱中的衍射角度,可以计算出晶格常数。
该方法适用于晶体具有明显的晶面衍射。
2.倍频晶格点法倍频晶格点法是一种结构测定常用的方法,通过测定晶体的衍射谱,可以获得晶格点的坐标。
然后利用晶格点的坐标进行计算,得到晶格常数。
该方法适用于晶体中存在不规则的晶格点。
3.粉末X射线衍射法粉末X射线衍射法是一种适用于粉末样品的方法。
通过测定粉末样品的X射线衍射谱,可以得到一系列的衍射峰。
然后利用布拉格方程进行计算,可以得到晶格常数。
该方法适用于粉末样品的结构分析。
4.光学显微镜法利用光学显微镜观察晶体的干涉条纹,可以得到晶体的晶胞参数。
通过测量干涉条纹的间距,可以计算出晶格常数。
该方法适用于具有明显干涉条纹的晶体。
5.晶体学衍射法晶体学衍射法是一种通过测量获得晶胞参数的方法。
通过测定晶体衍射的强度,可以得到晶体的结构信息。
然后利用晶体的结构信息进行计算,可以得到晶格常数。
该方法适用于具有完整的晶体衍射强度的晶体。
综上所述,计算晶格常数的方法主要包括X射线衍射法、倍频晶格点法、粉末X射线衍射法、光学显微镜法和晶体学衍射法。
这些方法各有特点,适用于不同类型的晶体。
同时,还可以结合其他的仪器和方法,如透射电子显微镜和散射仪器等,进行晶格常数的计算,以提高计算结果的准确度。
立方晶系晶格参数的精确测定 副本PPT课件

9 158.684 kα1 (444) 0.965795
48
0.543034 0.034205 0.034806
20
数据处理
第1题 采用外推法确定硅的精确的晶格参数
0.5436
0.5434
Lattice Parameter (nm)
0.5432
0.543 0.5428
a0=0.5430nm
0.5426
12
实验原理
❖ 外推法
●采用kα1 和kα2辐射时需要进行修正以求a,修正公式如下:
sin21
2
k1
2
k2
(sin2k2)
(1)
本实验中采用的是Cu Kα射线,其中 λα1=0.154056nm, λα2=0.154439nm
13
实验原理
❖ 最小二乘法
◆定义 最小二乘法是用数学方法从实验点出发寻求最佳直线
0.495
0.495
0.4949
0.4948
0.4948
0.4947
0.4947 0
0.02
0.04
0.06
0.08
0.1
cos2θ
0.12
0.14
0.16 26
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
1 67.080 kα1 0.848332 35 0.494766 0.151668 2 67.421 kα2 0.848354 35 0.494760 0.147423 3 69.061 kα1 0.872284 36 0.494847 0.127716 4 69.467 kα2 0.872632 36 0.494748 0.123023 5 79.794 kα1 0.968604 40 0.495000 0.031396 6 80.601 kα2 0.968509 40 0.495025 0.026670
厦门大学材料学院考研 材料分析与测试 必背

材料分析1.X射线的本质是什么?是谁首先发现了X射线,谁揭示了X射线的本质?答:X射线的本质是一种横电磁波?伦琴首先发现了X射线,劳厄揭示了X射线的本质?3.多重性因子的物理意义是什么?某立方晶系晶体,其{100}的多重性因子是多少?如该晶体转变为四方晶系,这个晶面族的多重性因子会发生什么变化?为什么?答:多重性因子的物理意义是等同晶面个数对衍射强度的影响因数叫作多重性因子。
某立方晶系晶体,其{100}的多重性因子是6?如该晶体转变为四方晶系多重性因子是4;这个晶面族的多重性因子会随对称性不同而改变。
5.透射电镜主要由几大系统构成? 各系统之间关系如何?答:四大系统:电子光学系统,真空系统,供电控制系统,附加仪器系统。
其中电子光学系统是其核心。
其他系统为辅助系统。
6.透射电镜中有哪些主要光阑? 分别安装在什么位置? 其作用如何?答:主要有三种光阑:①聚光镜光阑。
在双聚光镜系统中,该光阑装在第二聚光镜下方。
作用:限制照明孔径角。
②物镜光阑。
安装在物镜后焦面。
作用: 提高像衬度;减小孔径角,从而减小像差;进行暗场成像。
③选区光阑:放在物镜的像平面位置。
作用: 对样品进行微区衍射分析。
8.倒易点阵与正点阵之间关系如何? 画出fcc 和bcc 晶体的倒易点阵,并标出基本矢量a*, b*, c*。
答:倒易点阵与正点阵互为倒易。
1.决定X 射线强度的关系式是补充试说明式中各参数的物理意义?答:I0 为入射X 射线的强度;λ为入射X 射线的波长R 为试样到观测点之间的距离;V 为被照射晶体的体积Vc 为单位晶胞体积P 为多重性因子,表示等晶面个数对衍射强度的影响因子;F 为结构因子,反映晶体结构中原子位置、种类和个数对晶面的影响因子;φ(θ) 为角因子,反映样品中参与衍射的晶粒大小,晶粒数目和衍射线位置对衍射强度的影响;A(θ) 为吸收因子,圆筒状试样的吸收因子与布拉格角、试样的线吸收系数μl 和试样圆柱体的半径有关;平板状试样吸收因子与μ有关,而与θ角无关。
材料研究测试方法考核要点
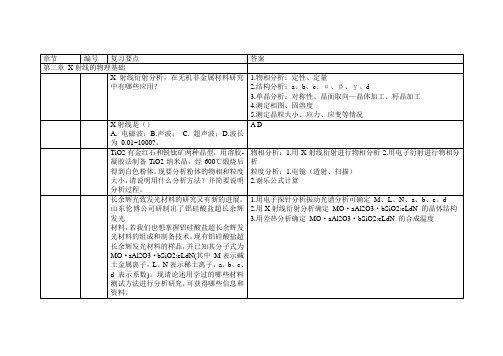
静电透镜:产生旋转对称等电位面的电极装置即为静电透镜,(1.5分)
磁透镜:产生旋转对称磁场的线圈装置称为磁透镜。
背散射电子和透射电子
背散射电子:电子射入试样后,受到原子的弹性和非弹性散射,有一部分电子的总散射角大于90o,重新从试样表面逸出,称为背散射电子。
透射电子:当试样厚度小于入射电子的穿透深度时,入射电子将穿透试样,从另一表面射出,称为透射电子。
(5).中点连线法:(1分)
(6).抛物线拟合法:适用于衍射峰线形漫散及双峰难分离的情况。(1分)
(7).重心法:干扰小,重复性好,但此法计算量大,宜配合计算机使用。(1分)
为什么说d值的数据比相对强度的数据更重要?
答:由于吸收的测量误差等的影响,相对强度的数值往往可以发生很大的偏差,而d值的误差一般不会太大。因此在将实验数据与卡片上的数据核对时,d值必须相当符合,一般要到小数点后第二位才允许有偏差。
A D
TiO2有金红石和锐钛矿两种晶型,用溶胶-凝胶法制备TiO2纳米晶,经600℃煅烧后得到白色粉体。现要分析粉体的物相和粒度大小,请说明用什么分析方法?并简要说明分析过程。
物相分析:1.用X射线衍射进行物相分析2.用电子衍射进行物相分析
粒度分析:1.电镜(透射、扫描)
2.谢乐公式计算
长余辉光致发光材料的研究又有新的进展,山东伦博公司研制出了铝硅酸盐超长余辉发光
章节
编号
复习要点
答案
第二章X射线的物理基础
X射线衍射分析,在无机非金属材料研究中有哪些应用?
1.物相分析:定性、定量
2.结构分析:a、b、c、α、β、γ、d
3.单晶分析:对称性、晶面取向—晶体加工、籽晶加工
4.测定相图、固溶度
厦门大学材料学院 考研复试 材料测试方法 04 物相定性分析

3 .PDF卡片索引
PDF卡片索引是一种能帮助实验者从数万张卡片中迅速查到 所需的PDF卡片工具书。由JCPDS编缉出的PDF卡片检索 手册有: Hanawalt无机物检索手册(Powder Diffraction File Search formlual Hanawalt Method Inorganic), 有机相检索手册(Powder Diffraction File Organic Phases Search Manual Hanawalt Alphabetical Formulae), 无机相字母索引(Powder Diffraction File Alqphabefiml Index lnorganic Phases) Fink无机索引(Fink lnorganic lndex To The Phases), Fink(Fink lnorganic lndex To The Powder iffraction File), 矿物检索手册(Mineral Powder Diffraction File Search Manual Chemical Name.Hanawalt.Fink.Mineral Name) 等品种。 这里仅以Hanawalt无机物数值索引和无机相字母索引为 例,简要地介绍其结构和使用
2)无机相字母索引
这种索引是按照物相英文名称的第一个字母为顺序编排条目。每个条 目占一横行。物相的英文名称写在最前面,其后,依次排列着化学式, 三强线的d值和相对强度,卡片编号,最后是参比强度(I/Ic)。例如
★Aluminum Oxide: 1Corundum Syn 1.608 10-173 1.00 Iron Oxide Fe2O3 Titanium Copper
06_第六讲_晶格常数的精确测定

如果令sin2θ代y,δ代x,A代α(α相当于
直线方程中α的系数),C代b,再参照正则方 程建立规则,可以列出柯亨法的正则方程
∑αsin2θ=A∑α2+C∑ αδ ∑δsin2θ=A∑αδ+C∑ δ2
y=a+bx
∑y= ∑ a+b ∑ x ∑ xy=a ∑ x+b ∑ x2
小结
熟悉点阵常数精确测定的基本原理 能用外推法和柯亨法测定常见晶体的点 阵常数
使∑Δy2为最小值的条件是
重排得: 0 a x ∑y= ∑ a+b ∑ ∑ xy=a ∑ x+b ∑ x2 为正则方程 y 2 Nhomakorabea和
y 2 b
0
通常是在sin 2θ关系上应用最小二乘法
为此,将布拉格方程平方并取对数,得: 2lgd=-lgsin2 θ+2lg(λ/2) 微分得2Δd/d=-Δsin2θ/sin2θ+2Δλ/λ 假定Δλ/λ为零,所以 2Δd/d=-Δsin2θ/sin2θ 代入Δd/d=Ksin2 ,φ=Kcos2θ得
二、求点阵常数的数学方法
(1)图解外推法 根据德拜-谢乐法中相机半径误差、底片收缩误差、试样偏心误差 的讨论可知,其综合误差为 Δ φS、R、C=( ΔS’ / S’ - ΔR/ R )+ΔXsinφcosφ/R Φ=90 °-θ, ΔΦ=-Δ θ,sin Φ =cos θ和 cos Φ =sin θ ,Δa/a=-cot θ Δθ
厦门大学材料学院 考研复试 材料测试方法 02 X射线的方向和强度
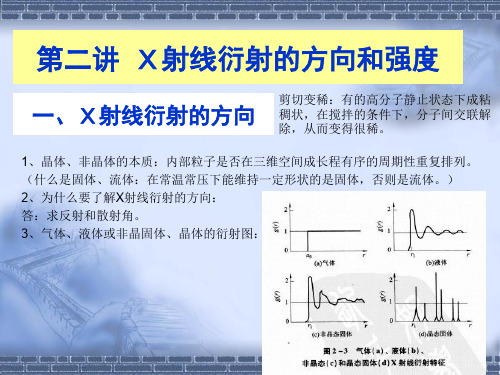
F =(a+ib)(a-ib)=a 2 +b2
e e
ix
n i
ix
2cos x,
=(-1) (n为整数)
n
e =e
-n i
1)简单晶胞
F=fe
2
2 i(0)
2
=f
F =f
000代入,结构因子不变 。与(hkl)无关,所有反 射有同值
2)底心斜方
F=fe
2 i ( 0)
fe
h k 2 i( + ) 2 2
i j
2 结构因子
• 结构因子:单位晶胞中所有原子散射波叠加的波 (structure factor )
Ab 一个晶胞内所有原子散射的相干散射波振幅 Fhkl= = Ae 一个电子散射的相干散射波振幅
• (hkl)晶面上原子相位[uvw]坐标 Φ=2π(hu+kv+lw)
Fhkl= f je
c、一个晶胞对X射线的散射(结构因子)
X射线对晶胞的作用
• 是晶胞中各原子散射波的叠加,同时晶体 的散射即为晶胞散射波的叠加 • 定义 r=x a+y b+z c
j j i j
• 原子坐标 • 相位:
Fhkl =
Eb Ee
j=
2
( rj s-s0)=2 ( rj
=ha*+kb*+kc*
( 1 1 cos 1 )(cos )( )= 2 = 2 sin 2 sin 2 sin 4sin cos
与极化因子结合,去掉常数1/8,得
1 cos 2 2 ()= 2 sin cos
c、吸收因子 r μe线吸收因子 圆柱试样: A() 平板试样: I= dI= I ab I 1/ 2 与θ无关 2 d、温度因子 讨论Bragg方程时,认为原子不动,而实际存在 热振动 RT:Al, Δd=0.017nm
材料分析方法复试题目(南理工各大材料学院可用)

《材料分析方法》复试考题一、解释下列名字的不同1、X射线衍射与电子衍射有何异同电子衍射与X射线衍射相比具有下列特点:1)电子波的波长比X射线短的多,在同样满足布拉格定律时,它的衍射角θ非常小,约为10-2rad, 而X射线衍射时, 最大角可接近π/2。
2)电子衍射操作时采用薄膜样品,薄膜样品的倒易阵点会沿样品的厚度方向延伸成杆状,于是,增加了倒易阵点和厄瓦尔德球相交的机会,结果使略微偏离布拉格条件的电子束也能发生衍射。
3)由于电子波的波长短,采用厄瓦尔德图解时,反射球的半径很大,在衍射角θ较小的范围内,反射球面可以近似看成一个平面. 可以认为,电子衍射产生的衍射斑点大致分布在一个二维倒易截面内.这个结果使晶体产生的衍射花样能比较直观地反映各晶面的位向,便于实际结构分析。
4)原子对电子的散射能力远高于它对X—射线的散射能力(约高出4个数量级),故电子衍射束的强度较大,摄取衍射花样时曝光时间仅需数秒钟。
2、特征x射线与连续x射线4、物相分析与成分分析二、说出下列检定所要用的手段(这个记不清了)1、测奥氏体成分含量直接比较法(定量)2、薄膜上1nm微粒的物相3、晶界的微量成分好像肯定俄歇谱仪4、忘了,反正就是XRD,透射电镜,扫描电镜,定性啊,定量啊什么的三、让你说明德拜照相法的衍射几何,还让画图四、给你一个图,让你说明二次电子成像的原理五、说明宏观应力测定的原理(没复习到,比较难)六、给你一个衍射斑点的图,告诉你体心立方好像,然后让你鉴别出点的指数七、给了一个15组数据的X射线衍射数据,还有3个PDF卡片,SiO2,α-Al2O3,β-Al2O3,然后让你说明这15组数据分别属于哪个物相,就是物相检定的一个实际操作。
2011复试材料分析方法回忆版一、简答题(40=5*4+10*2)1、连续X射线与特征X射线的特点连续X射线:1)X射线强度I沿着波长连续分布2)存在短波限λSWL3)存在最大强度对应的波长λm特征X射线波长对阳极靶材有严格恒定数值。
点阵常数的精确测量

南大学 接近 90°时,由 ∆θ 产生的 ∆d 也趋于零(见表 1);另一方面,较高角度程衍学射院的衍射角对晶
中 体
d
值的变化或差异更加敏感。所以,无论是为了精确测定晶胞参数或工者是为了比较结构参 与
数的差异或变化,原则表上1都当应该Δ尽θ可=能0使.0用1°高时角,度对衍于射不线材同的料衍数科射据学角。的晶面
院 晶面间距测材定料中科的系统误差进行分析。晶面间距 d 的测定准确度取决于衍射角的测定准确
度,可分学为两方面对此进行讨论。
学 大 工程 中南(1)衍射角的测量误差 ∆θ 与 d 值误差 ∆d 的关系
与 微分 Brag 方程可以得到: 科学∆d = −∆θ cotθ
料d
材 从上式可见,对于在较高角度下产生的衍射,同样大小的 ∆θ 值引起的 ∆d 值较小,当 θ
实验 3 点阵常数的精确测量
一、实验目的
1.掌握精确测量合金点阵常数的实验方法及数据处理方法。
2.熟悉晶体结构参数精密化处理的原理与方法。
3.了解 X 射线衍射法测量点阵常数的实验误差来源。
4.了解金属材料点阵常数变化与热处理制度的关系。
二、实验原理概述
院
1.晶胞参数的精确工测程定学
晶胞参数需由学已与知指标的晶面间距来计算,因此,如果要精确测定晶胞参数,首先要对
中南
式中 wi ——权重因子, wi =1/ Yi ;
Yoi , Yci ——步进扫描第 i 步的实测强度和计算强度。
使 M 值最小的过程也就是结构精修的过程。通过结构精修的方法精确计算点阵常数比 前两种方法可靠性大,操作简单,是近年来发展的新方法。 三、实验步骤与方法
1.采用步进扫描方式,测量金属粉末的点阵常数,实验条件为扫描范围 2θ=80-140 °, 步进宽度 0.01 °,步进时间 1s,晶体单色器,衍射束石墨单色器,接收狭缝 0.15°,发散狭 缝 0.30°。
厦门大学材料学院 考研复试 材料测试方法 08 TEM&SEM

3)供电控制系统
加速电压和透镜磁电流不稳定将会产生严重的色差 及降低电镜的分辨本领,所以加速电压和透镜电流 的稳定度是衡量电镜性能好坏的一个重要标准 透射电镜的电路主要由高压直流电源、透镜励磁电 源、偏转器线圈电源、电子枪灯丝加热电源,以及 真空系统控制电路、真空泵电源、照相驱动装置及 自动曝光电路等部分组成。 另外,许多高性能的电镜上还装备有扫描附件、能 谱议、电子能量损失谱等仪器
第二章 电Leabharlann 显微分析Electron Micro-Analysis
第三节
透射电镜(TEM)
透射电子显微镜是以波长很短的电子束 做照明源,用电磁透镜聚焦成像的一种具有 高分辨本领,高放大倍数的电子光学仪器。 测试的样品要求厚度极薄(几十纳米),以 便使电子束透过样品。
发展历史
※在电子光学微观分析仪器中,透射电镜历史久, 发展快,应用范围也最广泛 ※1932-1933,Ruska等制备第一台透射电子显微镜 后,透射电镜就已初步定型生产,并已达到分辨 率优于2nm的水平 ※到40年代末, 透射电镜的主体己基本定型。 ※由电子枪和两个聚光镜组成照明系统,产生一束 聚焦很细、亮度高、发散度小的电子束;由物镜、 中间镜和投影镜三个透镜组成三级放大的成像系 统; 给出分辨率优于lnm放大几十万倍的电子像。 透射电镜的发展带动了电子光学仪器和技术的发 展,在此基础上发展越来越多的高精尖仪器
R=L· tg2θ≈L· sin2θ≈2L· sinθ 可得 R/L=2sinθ=λ/d 电子衍射的基本公式:
R/L=λ/d
式中:R——衍射斑点距中心的距离 λ——电子波长,它与加速电压有关 L——镜筒长度,为定值
设:K=L· λ为相机常数,则
第六章 点阵常数的精确测定lpf

影响sinθ精度的关键因素 影响sinθ精度的关键因素 sinθ
由图可见, 由图可见,当θ角位于 低角度时, 低角度时,若存在一 的测量误差, △θ的测量误差,对应 的△sinθ的误差范围很 sinθ的误差范围很 角位于高角度 大;当θ角位于高角度 若存在同样△ 时,若存在同样△θ的 测量误差, 测量误差,对应的 sinθ的误差范围变小 的误差范围变小; △sinθ的误差范围变小; 当θ角趋近于90°时, 角趋近于90° 90 尽管存在同样大小的 的测量误差, △θ的测量误差,对应 sinθ的误差却趋近 的△sinθ的误差却趋近 于零。 于零
a- cos θ 图解外推法示意
2
这种外推法是在粗浅地分析误差时得出 的,在满足以下条件时才能得到较好的 结果。 1、在θ=60- 90°间有数目多、分布均匀 的衍射线; 2、至少有一条可靠的衍射线在80°以上
图解外推法
Nelson.J.B等用尝试法得 到了以上外推函数,它在 很广的θ范围内有较好的 直线性。后来Taylor.A等 从理论上证实了这一函数。
数学处理方法
图解外推法 最小二乘法
图解外推法
如果所测得的衍射线条θ 如果所测得的衍射线条θ角趋 90° 那么误差( a/a) 近90°,那么误差(△a/a)趋 近于0 近于0。 但是,要获得θ=90 θ=90° 但是,要获得θ=90°的衍射线 条是不可能的。 条是不可能的。于是人们考虑 采用“外推法”来解决问题。 采用“外推法”来解决问题。 所谓“外推法”是以θ 所谓“外推法”是以θ角为横 坐标,以点阵常数a为纵坐标; 坐标,以点阵常数a为纵坐标; 求出一系列衍射线条的θ 求出一系列衍射线条的θ角及 其所对应的点阵常数a 其所对应的点阵常数a;在所有 点阵常数a 点阵常数a坐标点之间作一条直 线交于θ=90 处的纵坐标轴上, θ=90° 线交于θ=90°处的纵坐标轴上, 从而获得θ=90 时的点阵常数, θ=90° 从而获得θ=90°时的点阵常数, 这就是精确的点阵常数。 这就是精确的点阵常数。
厦门大学材料学院 考研复试 材料测试方法 10 热分析

记录器 微伏放大器
CDR-1差动热分析仪
2.DSC仪的基本原理
热流型DSC:定量DTA
功率补偿型DSC:
S
Pt传感器
R
功率补偿型DSC仪的基本原理
热动态零位平衡原理 在程序控温过程中,始终保持试样和参比物温 度相同;保持R侧以给定的程序控温,通过变 化S侧的加热量来达到补偿的作用。 dH 记录热流率( dt )对T的关系曲线,得到DSC 曲线。 其它两种补偿方式 加热方式:外加热或内加热
T——试样自身的温度,但实际测量中,有时以参 比物温度表示,有时以炉温表示。 差热分析不能表征变化的性质。 差热分析本质上仍是一种动态量热。测得的结果 不同于热力学平衡条件下的测量结果。 试样与程序温度(以参比物温度表示)之间的温 度差比其它热分析方法更显著和重要。
5.DTA和DSC方法的比较
相似之处: 两种方法所测转变和热效应类似; 曲线形状(需注明方向)和定量校正方法相似; 主要差别: DTA(测定△T;无内加热问题,1500℃以上,可到 2400℃;重复性较差,分辨率不高,热量的定量较复 杂;定性或半定量;无机材料 ) DSC(测定热流率dH/dt;试样和参比物间无温差、 无热传递,热损失小,检测信号大;分辨率好、灵敏 度高;定量;有机、高分子及生物化学等领域)
DSC:在程控温度下,测定输入到物质和参比物 之间的功率差与温度的关系。
dH f T 或t dt
一、基本原理
1.传统DTA的基本原理 将试样S和参比物 R置于以一定速率加热 或冷却的相同温度状 态的环境中,记录下 试样和参比物之间的 温差△T,并对时间或 温度作图,得到DTA 曲线。
nbtin晶格常数

nbtin晶格常数1. 简介晶格常数是描述晶体结构的重要参数之一,它指的是晶体中原子或离子排列的周期性重复性。
nbtin晶格常数是指由铌(Nb)和锡(Sn)两种元素组成的铌锡合金(NbSn)的晶格常数。
nbtin合金具有重要的应用价值,例如在超导体、磁性材料和热电材料等领域。
研究nbtin晶格常数可以帮助我们更好地理解和掌握这些领域中的物理性质和现象。
2. 晶体结构nbtin合金的晶体结构是指铌和锡原子在晶体中的排列方式。
根据实验观测和理论计算,nbtin合金主要存在两种晶体结构:体心立方结构(BCC)和面心立方结构(FCC)。
2.1 体心立方结构(BCC)在体心立方结构中,铌原子和锡原子分别位于晶格的体心和顶点位置。
这种结构具有较高的对称性,而且相邻原子之间的距离相对较远。
nbtin合金的体心立方结构晶格常数通常用字母a表示。
2.2 面心立方结构(FCC)在面心立方结构中,铌原子和锡原子分别位于晶格的面心和顶点位置。
这种结构具有更高的对称性,相邻原子之间的距离相对较近。
nbtin合金的面心立方结构晶格常数通常用字母a表示。
3. nbtin晶格常数的测量方法测量nbtin晶格常数可以采用多种方法,以下是常用的几种方法:3.1 X射线衍射法X射线衍射是一种常用的测量晶格常数的方法。
通过将X射线照射到nbtin合金晶体上,根据衍射图样的特征可以计算出晶格常数。
这种方法需要使用X射线衍射仪器和相关的数据处理软件。
3.2 电子衍射法电子衍射是一种类似于X射线衍射的方法,但是使用的是电子束而不是X射线束。
这种方法通常需要使用透射电子显微镜(TEM)或扫描电子显微镜(SEM)等仪器进行测量。
3.3 中子衍射法中子衍射是一种利用中子束与晶体相互作用的方法。
中子具有较大的散射截面,可以用于研究晶体结构。
这种方法通常需要使用中子衍射仪器和相关的数据处理软件。
4. nbtin晶格常数的影响因素nbtin晶格常数受多种因素的影响,以下是一些常见的影响因素:4.1 温度温度是影响nbtin晶格常数的重要因素之一。
厦门大学-材料科学基础考研真题(2013-2018年)

厦门大学2013年招收攻读硕士学位研究生入学考试试题答案解析-材料科学基础真题一、名词解释(共15 分,每小题3 分)1.金属键2.置换式固溶体3.形变织构4.相律5.堆垛层错【考查重点】:这部分侧重考查基础知识和基本概念,答案一般在书本上都能找到,名词解释的回答要做适当展开,不能太过简单,但要达到点上,不能靠长篇大论模棱两可的答题。
【答案解析】:1.金属键:由金属中的自由电子与金属正离子相互作用所构成的键合称金属键。
2.置换式固溶体:当溶质原子溶入溶剂中形成固溶体时,溶质原子占据溶剂点阵的阵点,或者说溶质原子置换了溶剂点阵的部分溶剂原子,这种固溶体就称为置换固溶体。
3.形变织构:金属塑性变形到很大程度时,各个晶粒的滑移面和滑移方向都要向主形变方向转动,逐渐使多晶体中原来取向互不相同的各个晶粒在空间取向上呈现一定程度的规律性,这一现象称为择优取向,这种组织状态则称为形变织构。
4.相律:处于平衡状态的多元系中可能存在的相数可用吉布斯相律表示:f=C-P+2,式中f 为体系自由度数,C 为体系组元数,P 为相数,2 表示温度和压力两个变量,在常温下f=C-P+1。
5.堆垛层错:实际晶体中,密排面的正常堆垛顺序有可能遭到破坏和错排,错排可分为抽出型层错和插入型层错。
二、作图(13 分)在FCC 晶格中画出[110]、[211]晶向和(110)、(111)晶面,并分别画出这两个晶面上的原子排布,并标出原子的间距。
【考查重点】:作图题一般考查“固体结构”的相关知识点,应熟练掌握晶面和晶向指数的作图方法,立方和六方晶体作图方法,并能进行简单的分析应用。
三、作图(12 分)画出共晶系、包晶系、共析系和包析系相图的示意图,并写出相应的转变反应式。
【考查重点】:这是“二元系相图及其合金的凝固”章节中考查的相关知识点,需要考生熟练掌握二元系共晶(析)、包晶(析)相图的特点和画法,并能写出相应转变式。
【答案解析】:共晶系L→α+β 共析系γ→α+β包晶系L→α+β 包析系四、判断题(共15 分,每小题3 分)判断下列说法是否正确,并说明理由。
表层材料晶格常数的cbed方法精确表征

表层材料的晶格常数是其结构特征之一,对于理解和控制材料的性质具有重要意义。
传统的晶体学方法通常使用X射线衍射或电子衍射技术来测定晶格常数,然而这些方法在测量薄膜或纳米材料时存在一定的局限性。
近年来,倒向电子衍射(CBED)方法作为一种高分辨率的电子衍射技术,在表层材料晶格常数的测定方面得到了广泛的应用。
CBED方法利用透射电子显微镜(TEM)对晶格织构的特征进行研究,通过对电子在晶体中的多次散射进行模拟和分析,可以精确地测定出表层材料的晶格常数。
相比传统的X射线衍射技术,CBED方法具有更高的空间分辨率和敏感度,特别适用于薄膜、纳米材料和表面结构的研究。
CBED方法的精确表征表层材料的晶格常数主要包括以下几个方面:1. 晶格常数的测定精度。
CBED方法通过对电子衍射模式的分析,可以精确地确定表层材料的晶格常数,测定精度通常可达到0.1甚至更高。
2. 表层材料的晶体结构。
通过CBED方法可以获取表层材料的晶体结构信息,包括晶胞参数、晶面取向和晶格取向等,有助于深入理解材料的结构特征。
3. 薄膜和纳米材料的晶格畸变分析。
CBED方法可以有效地研究薄膜和纳米材料的晶格畸变,包括晶格扭转、晶格位错和晶格应变等,为材料的性能优化提供重要参考。
4. 表面结构的拓扑特征。
CBED方法还可以用于研究表层材料的表面拓扑结构,包括晶格面的原子排列、晶面形貌和晶界结构等,对材料的表面物理化学性质具有重要影响。
倒向电子衍射方法是一种精确表征表层材料晶格常数的高分辨率技术,具有广泛的应用前景。
通过CBED方法可以实现对表层材料微观结构特征的精确定量测定,为材料科学和工程领域的研究提供了强有力的工具和手段。
随着电子显微镜技术的不断发展和改进,CBED方法在表层材料研究中的应用前景将更加广阔。
基于倒向电子衍射方法的高分辨率特性和精确度,CBED方法在表层材料研究中已经成为一种不可或缺的工具。
其应用范围包括但不限于纳米材料、薄膜材料、表面结构、晶格畸变等方面,为材料科学和工程领域提供了强有力的支持。
晶胞参数精确测定

精确测量点阵参数的方法 一、德拜-谢乐法
测量Θ的误差 胶卷收缩 样品偏心 相机半径不正确 样品吸收造成的峰分歧
Bradley-Jay 函数
校正 cos 2Θ 引入外推函数
VS点阵参 数为线性
cos 2Θ cos 2Θ sin2Θ + Θ
Nelson-Riley 函数
对于一些少高角度衍射和小于60度的Θ都很有用 比前者更好
Sin2θ (Kα 1) 0.6875 8
hkl 331
a 0.4049 15
56.017 Kα
2
3
56.232 Kα
58.291 Kα
2
0.6910 5
0.7237 4
0.6876 3
0.7237 4
331
420
0.4049 00
0.4049 22
1
4
5
58.523 Kα
68.735 Kα
2
0.7273 5
晶体点阵参数精确测定
2009.9
为什么要精确测量?
晶胞参数是晶体的重要特征参数,随晶体成分 和外界条件(T,P等)而改变。 对键合能、理论密度精确计算、热膨胀系数、 固溶体类型、固溶度、原子间距、相平衡图、 材料应力等的测量很有用. 晶胞参数随各种条件的变化量很小,变化数量级 约为10-4 nm,精度要求万分之一~十万分之一。
A 0.0361895 C 7.8 107
求得的D值很小, 可知结果精确度会 很高 获得了高精 度的值!
a0 / 2 A 0.40491 nm
谢谢!
素质教育
• • • • 播种思想,收获行动 播种行动,收获习惯 习惯塑造品格(素质) 品格决定命运
晶格常数测定实验报告(3篇)

第1篇一、实验目的1. 了解X射线衍射(XRD)的基本原理和应用。
2. 掌握XRD法测定晶体晶格常数的方法。
3. 熟悉实验操作步骤,提高实验技能。
二、实验原理X射线衍射法是利用X射线照射晶体时,X射线与晶体中原子之间的相互作用,产生衍射现象,从而确定晶体结构的一种方法。
根据布拉格定律,衍射角θ与晶面间距d、入射波长λ之间的关系为:2dsinθ=nλ(n为整数)。
通过测定衍射角和入射波长,可以计算出晶体的晶格常数。
三、实验仪器与材料1. 仪器:X射线衍射仪、X射线发生器、样品台、数据采集卡、计算机等。
2. 材料:已知晶格常数的晶体样品(如NaCl、KCl等)、待测晶体样品、X射线靶材(如Cu靶)等。
四、实验步骤1. 样品准备:将待测晶体样品和已知晶格常数的晶体样品分别研磨成粉末,过200目筛,装入样品盒中。
2. 仪器调试:开启X射线衍射仪,调整X射线发生器、样品台和探测器等,使X 射线束垂直照射到样品上。
3. 数据采集:设置合适的衍射角度范围和步长,采集X射线衍射图谱。
4. 数据处理:利用X射线衍射仪自带的软件或相关数据处理软件,对采集到的X 射线衍射图谱进行分析,得到晶体衍射峰的位置、强度等信息。
5. 晶格常数计算:根据布拉格定律和采集到的衍射数据,计算出待测晶体的晶格常数。
五、实验结果与分析1. 样品A(已知晶格常数)的晶格常数计算:根据X射线衍射图谱,选取一个衍射峰(如2θ=20.56°,对应hkl=110),根据布拉格定律,计算得到晶面间距d=1.5405Å。
已知NaCl的晶格常数a=5.640Å,c=5.640Å,根据晶面间距与晶格常数的关系,计算得到a=5.640Å,c=5.640Å,与已知值相符。
2. 样品B(待测晶格常数)的晶格常数计算:根据X射线衍射图谱,选取一个衍射峰(如2θ=24.38°,对应hkl=200),根据布拉格定律,计算得到晶面间距d=1.8435Å。
厦门大学材料学院 材料科学基础 习题3
第三章作业
1. 若fcc 的Cu 中每500个原子会失去一个原子,其晶格常数为0.36153nm ,试求铜的密度。
2. 在铁中形成1mol 空位的能量为104.675KJ ,试计算从20℃升温之850℃时空位数目增加多少倍?
3.有两个被钉扎住的刃型位错A-B 和C-D ,他们的长度x 相等,且有相同的b 大小和方向(图3-1)。
每个位错都可看作F-R 位错源。
试分析在其增值过程中两者间的交互作用。
若能形成一个大的位错源,使其开动的τc 多大?若两位错b 相反,情况又如何?
图3-1
4.图3-6所示某晶体位错面上有一柏氏矢量为b 的位错环并收到一均匀切应力τ的作用,a)分析各段位错线所受力的大小并确定其方向;b)在τ作用下,若要使它在晶体中稳定不动,其最小半径为多大?
5、在面心立方晶体中有下述位错反应:101121111263a a a ⎡⎤⎡⎤⎡⎤→⎣⎦⎣⎦⎣⎦
+。
判断该反应能否进行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
尽管θ值趋近于90 °时的点阵常数的测试 精度较高,但是在实验过程中测量误差是 必然存在的,必须设法消除。
测量误差:系统误差和偶然误差 系统误差是由实验条件所决定的 偶然误差是由于测量者的主观判断错误及 测量仪表的偶然波动或干扰引起的
ቤተ መጻሕፍቲ ባይዱ
一、
德拜-谢乐法中系统误差的来源
德拜-谢乐法常用于点阵常数精确测 定,其系统误差的来源主要有: (1)相机半径误差 (2)底片收缩(或伸长) (3)试样偏心误差 (4)试样对X射线的吸收误差 (5)X射线折射误差
满足以下条件 (1)在θ=60 ° ~90°之间有数目多,分布均匀的衍射线。 (2)至少有一条很可靠的衍射线在80 °以上
外推法求纯铅的点阵常数
(2)最小二乘法(柯亨法)
两个物理量x和y呈直线关系即: y=a+bx
误差的平方和表达式 ∑Δy2=(a+bx1-y1)2+ (a+bx2-y2)2+…
使∑Δy2为最小值的条件是 y 2 0 重排得: a 和 ∑y= ∑ a+b ∑ x ∑ xy=a ∑ x+b ∑ x2 为正则方程
y 2 b
0
通常是在sin 2θ关系上应用最小二乘法
为此,将布拉格方程平方并取对数,得: 2lgd=-lgsin2 θ+2lg(λ/2) 微分得2Δd/d=-Δsin2θ/sin2θ+2Δλ/λ 假定Δλ/λ为零,所以 2Δd/d=-Δsin2θ/sin2θ 代入Δd/d=Ksin2φ=K’cos2θ得
问题: 每一个晶胞都有很多晶面,一个晶面对应 一条衍射线。哪一条衍射线确定的点阵常 数才是最接近真实值呢?即确定哪一个晶 面上衍射线的位置用于测试
☺由布拉格方程(2d sinθ =λ)可知,点阵常 数值的精确度取决于sinθ这个量的精确度, 而不是θ角测量的精确度。
θ-sin θ关系曲线(解析关系)
Δsin2θ=-2Ksin2θcos2θ=Dsin22θ
正则方程的确立是在布拉格方程上进行的, 各条衍射线的观察值sin 2θ有一定误差,且
误差值等于Dsin22 θ,现将这个误差加到平方形 式的布拉格方程中去, 对立方晶系 sin 2θ=λ2(h2+k2+l2)/4a02+ Dsin22 θ =Aα+Cδ 式中 A= λ2/ 4a02 α= h2+k2+l2 C= D/10 δ=10sin22 θ
如果令sin2θ代y,δ代x,A代α(α相当于
直线方程中α的系数),C代b,再参照正则方 程建立规则,可以列出柯亨法的正则方程
∑αsin2θ=A∑α2+C∑ αδ ∑δsin2θ=A∑αδ+C∑ δ2
y=a+bx
∑y= ∑ a+b ∑ x ∑ xy=a ∑ x+b ∑ x2
本讲小结
熟悉点阵常数精确测定的基本原理 了解测定晶格常数时产生误差的原因 了解消除德拜-谢乐法误差的基本方法 能够使用外推法和柯亨法测定常见晶体的点 阵常数
1.相机半径误差
ΔφR =φ表现-φ真实 =S’/4(R+ΔR)-S’/4R =-φΔR/ (R+ΔR) 实际上,ΔR总是很小的, 因此上式可以写成 ΔφR =- φ(ΔR/ R)
2.底片收缩误差
照相底片经冲洗、干 燥后,会发生收缩或 伸长,结果使衍射线 对之间的距离S’增大或 缩小成为S’+ ΔS’ ΔφR =φ表现-φ真实
从解析关系可以看出, θ和sinθ是一 个正弦曲线的关系
图中曲线显示,当θ越接近90°时, 对应于测量误差Δθ的Δsinθ值误差越 小
在90 °的角度范围内,由最大衍射 角线条计算出的点阵常数最精确
数学方法证明: 对方程 2d sinθ =λ进行微分 Δλ=2 sinθΔd+2dcosθΔθ 即Δd/d= Δλ/λ-cotθΔθ 如果不考虑波长λ的误差,则Δd/d=-cotθΔθ 对于立方晶系物质来说,由于Δd/d= Δa/a,因此, Δa/a=cotθΔθ 结论: 当Δθ一定时,采用高θ角的衍射线,面间距误差Δd/d将要 减小;当θ接近于90 °时误差将会趋近于零。
为A→C,B→D。 于是S’ 的误差为AC+BD=2DB≈2PN, 或S’ =2PN=2Δxsin2φ
因此试样偏心导致的误差为: ΔφC=φ(Δ S’/ S’ ) = φ(2Δxsin2 φ )/(4Rφ) =Δxsin φcos φ/R
注意到φ=(π/2-θ)的关系,于是立方晶系点阵 常数a的相对误差为 Δa/a=-cotθΔθ=-Δxcos2θ/R
于是:
Δd/d=-Δθcosθ/sinθ =Δφsinφ/cosφ =(-sinφ/cosφ)×[( ΔS’ / S’ - ΔR/ R )φ+ΔXsinφcosφ/R]
在背射区域中,当θ接近90 °时,φ很小,
可以运用近似关系式sin φ ≈φ,cos φ=1,于是 得 Δd/d=( ΔS’ / S’ - ΔR/ R+ ΔX/R)sin2 φ
3.试样偏心误差
试样的任何偏心都可以分解为沿入射线束的水平 位移Δx和垂直位移Δy两个分量 垂直位移Δy使衍射线对位置的相对变化为A→C, B→D。 当Δy很小时,AC和BD近乎相等,因此可以认为 垂直位移不会在S’ 中产生误差 上下垂直方向偏差都有一样的结果
水平位移Δx的存在,使衍射线条位置的相对变化
当θ接近90 °时,相机半径和底片收缩所造成的 点阵常数测算误差趋于零
不对称装片法或反装法的好处:
在实验工作中,采用不对称装片法或反装 法可以把底片收缩误差降至下限,因为对 应的背射线条在底片上仅相隔一个很短的 距离,因而底片收缩对其距离S’的影响极 小。 此外,用不对称装片法尚可求出相机有效 半径,以消除相机半径误差
在同一张底片中,由于每条衍射线的各种误差 来源相同,因而上式中括弧内的数值均属定值, 因此 Δd/d=Ksin2 φ=K’cos2θ
对立方晶系, Δd/d= Δa/a,因此立方晶系点阵 常数的相对误差与cos2θ成正比。
应用方法
1、获得衍射线的位置(各个特征晶面的位置)即θ角; 2、根据θ角算出a值和cos2θ值; 3、作出a- cos2θ关系直线; 4、根据拟合曲线并外推到cos2θ=0处,即θ为90度处 ,在 纵坐标a上即可得到真实点阵常数a
第六讲 点阵常数的精确测定
2011年03月24日
测定点阵常数的意义: 1.固溶体的研究:固溶体的晶格常数随溶质 的浓度而变化,可以根据晶格常数确定 某溶质的含量。 2.热膨胀系数测定:可以用高温相机通过 测定晶格常数来确定 3.内应力测定:内应力造成晶格的伸长或 者压缩。 4. 相变过程、晶体缺陷等:相变及晶体存 在缺陷,点阵常数都会发生变化。
练习题6
1、精确测定点阵常数为什么要选择高角度衍射线条?
2、外推法和最小二乘法测点阵常数的基本原理是什么? 3、测得铝在298℃不同衍射半角(θ)对应的晶面分别为:55.486- (331); 57.714-(420); 67.763-(422); 78.963- (333)。试用外推法求其点阵 常数(作图) 4、在单色X射线照射下,定轴转动的单晶体和多晶体的衍射图案是否相同? 5、在单色X射线照射下,面心立方多晶体(如Cu)产生一系列的衍射锥, 请问这些衍射锥都是有哪些晶面反射的?请按2θ由小到大的顺序写至 少写出8个晶面。 6、用数学(微分)的方法推导当衍射角接近90度时,测得晶格常数的误差 最小。 7、由相机半径、胶片伸缩、试样偏心引起的误差是多少? 8、德拜-谢乐法的误差如何校正?
二、求点阵常数的数学方法
(1)图解外推法 根据德拜-谢乐法中相机半径误差、底片收缩误差、试样偏心误差 的讨论可知,其综合误差为 Δ φS、R、C=( ΔS’ / S’ - ΔR/ R )+ΔXsinφcosφ/R Φ=90 °-θ, ΔΦ=-Δ θ,sin Φ =cos θ和 cos Φ =sin θ ,Δa/a=-cot θ Δθ
=( S’+ ΔS’ )/4R-S’/4R
= ΔS’ /4R = φ ΔS’ / S’
相机半径误差和底片收缩差具有相同的性质,可以 合并为:
ΔφR,S= ΔφR+ ΔφS =φ( ΔS’ / S’ - ΔR/ R)
立方晶系a的相对误差为: (Δa/a=-cotθΔθ)
Δa/a= ( ΔS’ / S’ - ΔR/ R)(π/2- θ )cot θ
4、德拜-谢乐法的误差校正方法
1.精密实验技术 (1)采用不对称装片法以消除由于底片和相机半径不精确 所产生的误差 (2)将试样轴高精度地对准相机中心,以消除试样偏心造 成的误差 (3)为了消除因试样吸收所产生的衍射线位移,可采用利 用背射衍射线和减小试样直径等措施 (4)对于直径为114.6mm或更大的相机,需要精密的比长 仪加以测定 (5)为了保证衍射线的清晰度不因曝光期间内晶格热胀冷 缩带来的影响,在曝光时间内必须将整个相机的温度变化 保持在±0.01℃以内。 2.提高实验人员的测量水平和技术
