习题10
《病理学》习题训练10

习题训练 10一、名词解释肿瘤:癌:肉瘤:异型性:癌前病变 :原位癌:二、填空题1.肿瘤的异型性表现为______和______。
2.肿瘤的生长方式有_____、_____、______。
3.肿瘤的扩散包括______和_______。
4.肿瘤的转移途径有______、______、_______。
癌的主要转移途径是______,肉瘤的主要转移途径是______。
5.良性肿瘤分化程度______,异型性______,与起源组织______。
生长速度______,呈______生长, ______包膜,与周围组织境界清楚, ______转移,手术切除后______复发,对机体影响较小,主要为局部______或______。
6.来源于上皮组织的恶性肿瘤称为______,来源于间叶组织的恶性肿瘤称为_______。
7.来源于造血组织的恶性肿瘤称______。
来源于骨组织的恶性肿瘤称______。
来源于脂肪组织的良性肿瘤称______。
来源于腺上皮的恶性肿瘤称______。
8.对肿瘤病人采取“三早”指的是______、______、_______。
9.肿瘤的实质是______,决定着肿瘤的_______。
10.肿瘤细胞异型性反映肿瘤组织的____程度,异型性越显著,_____越低。
三、单项选择题1.与肿瘤的颜色有关的是( )A 生长的部位B 组织的来源C 实质和间质的比例D 生长的速度 E瘤体的大小2. 肿瘤恶性程度的高低取决于( )A 肿瘤体积的大小B 肿瘤患者的临床表现C 肿瘤的生长速度D 肿瘤异型性E 肿瘤的形态3. 决定肿瘤性质的主要依据是( )A 肉眼改变B 生长速度 C临床表现D 镜下形态结构E 生长方式4. 癌前病变是指( )A 最终发展成癌的良性病变B 有癌变可能的良性病变C 原位癌D 溃疡病E 早期癌5. 下列哪项不属于恶性肿瘤的细胞形态特点( )A 瘤细胞核数目不一,形态不规则B 核大深染,核仁明显C 瘤细胞大小不一,形状不规则D 核质比增大E 瘤细胞与来源组织的细胞差异较小6. 下列哪项不属于肿瘤( )A 霍奇金病B 白血病C 血管瘤D 动脉瘤E 黑色素瘤7. 肉瘤的肉眼特点是( )A 灰白色,质硬,干燥B 灰红色,质软,湿润C 灰白色,质软,湿润D 灰红色,质硬,干燥E 灰白色,暗红色,质硬,湿润8. 癌的镜下特点是( )A 瘤细胞间多有网状纤维B 间质中血管丰富C 实质与间质交织排列D 实质细胞形成巢,间质围绕周围E 瘤细胞弥漫分布9. 下列哪项属于肿瘤的组织结构异型性( )A 瘤细胞失去正常的层次与排列B 核大,大小不等,核畸形C 核染色质分布不均,染色深D 病理性核分裂象E 瘤细胞大小不一,形状不规则10.下列哪项组织发生的肿瘤不能称为肉瘤( )A 软骨B 淋巴管C 脂肪D 胆管上皮E 纤维组织11.下列有关恶性肿瘤哪项是错误的( )A 分化程度高B 异型性大C 常见病理性核分裂象D 常有转移和复发E 对机体影响大12.机体细胞、组织从幼稚生长发育到成熟的过程,称为( )A 分化B 化生C 机化D 硬化E 老化13.下列哪项不是肉瘤的特点( )A 青少年多发B 属于来源于间叶组织的恶性肿瘤C 易发生血道转移D 质地较硬、灰白色E 肉瘤细胞呈弥漫分布14.恶性肿瘤生长方式是( )A 膨胀性生长B 外生性生长C 浸润性生长D 浸润性生长和外生性长E 加速性生长15.下列哪项不属于癌前病变( )A 慢性萎缩性胃炎B 十二指肠溃疡C 经久不愈的皮肤慢性溃疡D 粘膜白斑E 胃溃疡16.“癌症”是指( )A 泛指所有恶性肿瘤B 所有肿瘤的统称C 上皮组织发生的恶性肿瘤D 癌和肉瘤E 间叶组织来源的恶性肿瘤17.关于肿瘤性增生的特点下列不正确的是( )A 致瘤因素去除后生长停止B 具有异常的代谢和功能C 能遗传给子代细胞D 与机体不协调有害无益E 肿瘤细胞生长旺盛18.下列哪一项不符合良性肿瘤( )A 生长缓慢B 异型性小,核分裂象少见C 多呈浸润性生长D 不易转移E 多呈膨胀性生长19.肿瘤的分化程度低说明其( )A 异型性小B 生长缓慢C 不易转移D 恶性程度高E 继发改变少见20.肿瘤的异型性是指( )A 癌和肉瘤的不同B 瘤实质与间质的不同C 瘤细胞形态不一致D 肿瘤对机体的影响不同E 肿瘤与其来源组织之间在细胞形态和组织结构方面的差异21.纤维组织来源的恶性肿瘤,按命名原则应称为( )A 恶性纤维瘤B 纤维瘤C 纤维瘤恶变D 纤维肉瘤 B 纤维组织细胞瘤22.肉瘤的主要转移途径是( )A 直接蔓延B 血道转移C 淋巴道转移D 种植性转移E 自然管道扩散23.癌与肉瘤最根本的区别是( )A 生长方式不同B 发生年龄不同C 发生的部位不同D 组织来源不同E 转移途径不同24.肿瘤的扩散方式概括起来有( )A 浸润血管B 浸润淋巴管C 浸润器官全层D 直接蔓延和转移E 自然管道扩散25.下列哪种不属于良性肿瘤( )A 脂肪瘤B 纤维瘤 C黑色素瘤 D血管瘤 E 平滑肌瘤26.原位癌是指( )A 未发生转移的早期癌B 肉眼看不见的微小癌C 不同程度的非典型性增生D 是一种早期癌E 局部上皮全层癌变但未突破基底膜的早期癌27.X射线检查时,肿块周围出现毛刺样或放射状改变,是因为( )A 肿瘤呈外生性生长B 肿瘤呈膨胀性生长C 肿瘤呈浸润性生长D 肿瘤呈结节状E 肿瘤生长速度快28.肿瘤的本质是( )A 基因病B 组织损伤C 感染性局部D 炎症E 遗传性疾病29.某人患有癌症,穿刺取肝组织,镜下,发现有类肺样组织结构,细胞核多形,核质比大,则该患者患有( )A 肝癌B 肺癌C 肠癌D 食管癌E 胃癌30.下列肿瘤来源于上皮组织的是( )A 纤维瘤B 脂肪瘤C 血管瘤D 乳头状瘤E 平滑肌瘤四、多项选择题1.肿瘤性增生的特点有( )A 肿瘤细胞分化不成熟B 形态、代谢、功能异常C 生长旺盛D 相对无限制E 见于生理状态下细胞的更新和损伤的修复2.良性肿瘤的特点有( )A 分化程度低B 异型性小C 生长缓慢D 手术后很少复发E 多呈膨胀性生长3.下列哪些是癌的特点( )A 来源于上皮组织B 多见于40岁以后的成年人C 质地硬,色灰白D 癌细胞间多有网状纤维E 癌细胞多呈弥漫分布4.来源于间叶组织的肿瘤有( )A 纤维瘤B 血管瘤C 间皮瘤D 淋巴管瘤E 神经鞘瘤5.恶性肿瘤的转移途径有( )A 直接蔓延B 淋巴道转移C 种植性转移D 血道转移E 体液转移6.肿瘤浸润性生长的特点有( )A 肿瘤组织与正常组织界限不清B 生长过程中有完整包膜C 生长比较缓慢D 手术不易切除干净,术后易复发E 常为恶性肿瘤的生长方式7.肿瘤的异型性表现为( )A 肿瘤细胞核明显增大B 肿瘤细胞较正常细胞大C 细胞核与细胞质的比例变小D 可出现病理性核分裂E 肿瘤组织在空间排列方式上与其起源组织有差异8. 下列哪些不属于肿瘤( )A 动脉瘤B 室壁瘤C 结核瘤D 炎性假瘤E 黑色素瘤9. 以下哪些属于癌前病变( )A 慢性子宫颈糜烂B 慢性萎缩性胃炎C 乳腺纤维腺瘤D 肝硬化E 慢性溃疡性结肠炎10.下列属于恶性肿瘤的是( )A 葡萄胎B 黑色素瘤C 精原细胞瘤D 畸胎瘤E 淋巴瘤五、判断题1.肿瘤的生长速度与肿瘤细胞的分化程度,肿瘤的血液供应及机体的免疫反应有关。
数学分析习题集10复旦大学

4 − x2 ,
x −1 , x0 = 1; x +1 1+ x ⑼ ln , x0 = 0; 1− x
⑴
⑻ (1+x) ln (1-x), ⑽
e−x , x0 = 0。 1− x
1 , n2 Sn(x) = nx(1 - x)n , x x Sn(x) = ln , n n xn , Sn(x) = 1+ xn Sn(x) = (sin x)n , x2 +
1 n
(ii) x ∈ (1,+∞ ) ); (ii) x ∈ (1,+∞ ) ;
⑽ Sn(x) = (sin x) ,
1. 讨论下列函数序列在指定区间上的一致收敛性。
(i) x ∈ (0,1) , x ∈ (0,+∞ ) ; (i) x ∈ (−∞,+∞ ) , (i) x ∈ (0,1) , x ∈ ( −∞,+∞ ) ; x ∈ [0,1] ; (i) x ∈ (0,1) , (i) x ∈ (0,1) , x ∈ [0, π ] ; (i) x ∈ [0,1] ,
3n ⎛ x − 1 ⎞ ⑸ ∑ ⎜ ⎟ ; n =1 n ! ⎝ 2 ⎠
∞
n
ln 2 n n 2 ⑹ ∑ n x ; n=2 n
⑻
∞
⑺ ⑼
n! n x ; ∑ n n =1 n
∞
( n !) 2 n x ; ∑ n =1 ( 2n) !
∞
∑ (2n + 1)!!xn =1 ∞来自∞(2n )!!
n
。
2. 设 a>b>0,求下列幂级数的收敛域。
习
1. 求下列幂级数的收敛半径与收敛域。
护士执业资格考试习题及答案10精神障碍病人的护理

第十章第一节精神障碍症状学一、A11、I-不属于思维联想过程障碍的表现是A、思维奔逸B、思维破裂C、思维迟缓D、思维贫乏E、病理性赘述2、I-思维迟缓是A、痛症的典型症状B、强迫症的典型症状C、抑郁症的典型症状D、恐怖症的典型症状E、精神分裂症的:典型症状二、A21、I-患者女性,60岁,近一周来夜间出现行为紊乱,伴幻听,幻视,表情紧张,恐惧,白天卧床,自发言语较少,对夜间行为难以回忆,生活自理差,头颅CT示:顶枕叶片状梗死灶,考虑目前患者处于A、澹妄状态B、痴呆状态C、抑制状态D、木僵状态E、幻觉妄想状态2、I-患者男性,42岁,近一周突然兴奋,躁动不安,伤人毁物。
在药物治疗时易引起患者摔伤的因素是A、坠床B、不合作C、躁动不安D、变换体位E、药物不良反应3、I-患者在意识清楚情况下,头脑中涌现大量异己的思维,伴不自主感是A、强迫观念B、被动体验C、思维被插入D、强制性思维E、物理影响妄想4、1•患者女性,30岁,述自己经常听到一个声音在议论她,此症状为幻觉,真性幻觉和假性幻觉的区别是A、二者均缺乏客观刺激B、二者来源和感知方式不同C、二者感知的幻觉形象生动D、二者均是对客观事物的错误感受E、二者均是对客观事物的胡思乱想5、I-患者女性,一看到男性即不能自控地想是否要和他谈恋爱、结婚,明知不对也无法自控。
这种症状是A、见人恐怖B、钟情妄想C、强迫观念D、焦虑状态E、孤独状态6、1•患者男性,59岁,口中常常喃喃自语“我该死,我该死”。
每晚席地而卧,上盖一破单被。
此患者的症状属于A、被害妄想B、嫉妒妄想C、罪恶妄想D、夸大妄想E、物理影响妄想7、I-患者男性,36岁,一日起床后,悄声外出关门,即从窗缝中窥视尚在熟睡中的妻子,良久不动,旁人问其所为,其回答正在监视老婆是否与人有不轨行为。
此患者的症状属于A、关系妄想B、夸大妄想C、嫉妒妄想D、被害妄想E、物理影响妄想8、I-者女性,23岁,近一个月来一直觉得周围的任何东西都对她有特殊的喑示,如她走进办公室,就有人哼唱“你就像冬天里的一把火",意思是骂她勾引异性;她一上街,许多牌照中含有4的汽车开过来,就表示让她死。
基本逻辑门电路典型练习题10

基本逻辑门电路典型练习题101.监控系统控制电路如图所示,电键S闭合时,系统白天和晚上都工作;电键S断开时,系统仅晚上工作.在电路中虚框处分别接入光敏电阻(受光照时阻值减小)和定值电阻,则电路中,C是____________(选填“与门”、“或门”或“非门”),光敏电阻是__________(选填“A”或“B”)【答案】或门B【详解】由题意可知:S断开时监控系统晚上光线较暗时自动开始工作,白天光线不暗时不工作,所以滑动变阻器与光敏电阻相连,即光敏电阻是B;S闭合时,监控系统白天和晚上都能工作,所以电键S应与定值电阻相连,C中两个条件有一个满足就工作,所以C是或门.考点:逻辑电路.2.如图是一个应用某逻辑电路制作的简单车门报警电路图.图中的两个按钮S1、S2分别装在汽车的两道门上.只要其中任何一个开关处于开路状态,发光二极管(报警灯)就发光.则该逻辑电路是___门电路,并在图中画出这种门电路的符号;当S1、S2都闭合时,A、B的输入都为___,Y端输出为____;当S1断开时,___端的输入为1,Y端输出为____.(门电路有输入电压或有输出电压都记为1,无输入电压或无输出电压都记为0)【答案】或00A1【详解】驾驶员离开汽车后,两个车门均处于关闭状态,与两个车门对应的开关S1和S2均闭合,这时发光二极管不会发光报警.因为S1和S2闭合后,电流不通过发光二极管.当有其他人打开了某一个门时,S1或S2就处于断开状态,这时就有电流通过发光二极管,使其发光报警.可见,这一装置实际上是一个“或”门电路.. 当S1、S2都闭合时,A、B的输入都为0时,,Y端输出为0,当S1断开时,A端的输入为1,Y端输出为1考点:考查了逻辑电路的应用点评:关键是理解或门逻辑电路的特点3.逻辑电路在电子线路中有着重要的应用.某词学利用“非”门电路设计了一个路灯自动控制R,是一个光敏电阻,门电路.天黑了,让路灯自动接通;天亮了,让路灯自动熄灭,图中G与有光线照射时,光敏电阻的阻值会显着减小,R是可调电阻,起分压作用.“非”门电路能将输入的商电平转变为低电平,或将低电平转变为高电平,J为路灯总开关控制继电器,它在获得高电压时才启动(图中未画路灯电路)(1)当天黑时,G R变大还是变小?“非”门电路获得高电平还是低电平?J得到高电压还是低电压?(2)如果路灯的开关自动接通时天色还比较亮,现要调节自动控制装置,使得它在天色较黑时才会自动接通开关,应将R调大一些还是调小一些?【答案】(1)大,低,高(2)大【详解】(1)天黑时,光线减弱,光敏电阻RG变大,A端输入低电压,Y端输出高压信号,J得到高压,开始控制路灯工作。
京东考试练习题10

京东考试练习题10问题1:问:下列关于小智开启说法错误的是?答案:客服下班后,需要手动开启京东小智问题2:问:京挑客的通用计划可以暂停,可以修改佣金比例?答案:错误问题3:问:京东商品主图的数量有多少?答案:1--10张问题4:问:京东物流体系拥有几大物流网?答案:6大问题5:问:京东直播是否可以直播原石答案:不可以,一经发现永久封号问题6:问:哪个渠道依附于搜索端的展示内容渠道?答案:京挑细选问题7:问:商家在参加京东开放平台的促销活动前答案:不可以问题8:问:客户退货后,退回京东余额的时效是多久?答案:2-3个工作日问题9:问:哪个渠道依附于搜索的展示内容渠道?答案:京挑细选问题10:问:京东商城是否接受个体工商户的入驻申请?答案:不接受问题11:问:商家是否可以申请京东介入?答案:可以问题12:问:京腾魔方标签人群生效时间为几分钟?答案:3分钟问题13:问:违规商家接受国家法律法规的处罚后,是否可以免除京东开放平台对其违规行为的处理?.答案:否问题14:问:京东新业态展示包括?答案:京东到家问题15:问:消费者发起纠纷单后,纠纷单流转至商家端,如商家()小时未回复,则系统自动京东介入。
.答案:36问题16:问:商家未能按照《京东开放平台商家售后服务管理规则》的规定在有效时间内响应及处理消费者提交的售后服务申请的,每次扣多少分?答案:1分问题17:问:京东搜索的排名是基于?答案:SKU问题18:问:京东直投-腾讯资源-高级定向-用户行为兴趣定向—用户兴趣定向可以选择哪些?答案:类目问题19:问:下列哪种刀具不属于《京东禁发商品及信息管理规范》中禁止发布的商品?答案:B.未开刃的用于摆设装饰的工艺刀类问题20:问:品牌聚效账户搭建流程-京选店铺在计划中,设置计划类型为?答案:京选店铺问题21:问:王先生跟京东商城合作半年,但是由于个人原因不想跟京东商城继续合作,终止协议后王先生的平台使用费是否可以退回?答案:不可以问题22:问:选项中关于京豆使用用途描述错误的是?答案:京豆可用于购买超值商品:只使用京豆购买热销商品问题23:问:京小贷最长贷款期限是多久?答案:12个月问题24:问:下列关于保证金的说法,正确的是?答案:当卖家发生违约、违规行为时,京东可以依照与卖家签署的协议中相关约定及京东开放平台规则扣除相应金额的保证金作为违约金或给予买家的赔偿问题25:问:下列关于小智开启说法错误的是哪一个?答案:客服下班后,需要手动开启京东小智问题26:问:以下不属于京券使用要求的选项是?答案:全部商品都能使用问题27:问:哪种类型的商家投放京挑客时需要预充值?答案:POP问题28:问:如果商家对纠纷仲裁结果不满意,京东仲裁判责完成后()天内,商家可以提起申诉,超过()天,将无法提起申诉。
提高学习效果的10道习题

提高学习效果的10道习题学习是人类进步的关键,无论是在学校还是在工作中,我们都需要不断地学习新知识和技能。
然而,有时候我们在学习过程中会感到迷茫和困惑,不知道如何提高学习效果。
因此,我总结了10道习题,帮助你提高学习效果,让你更轻松地掌握知识和技能。
H1. 习题1:制定明确的学习目标在开始学习之前,你应该明确自己的学习目标。
制定明确的学习目标有助于你更有针对性地安排学习内容和时间。
例如,如果你想学习英语,你可以设定一个目标,比如每天学习30分钟,掌握一定的词汇和语法知识。
这样,你就可以更加专注地学习,并且有一个明确的方向。
H2. 习题2:分解学习任务有时候学习一个复杂的知识点或技能会让人感到无从下手。
为了解决这个问题,你可以将复杂的学习任务分解为若干个小的子任务。
这样做有两个好处:一方面,你可以更好地组织和管理学习内容;另一方面,你可以将一个复杂的任务变成一系列简单的任务,更容易理解和掌握。
H3. 习题3:制定学习计划学习计划对于提高学习效果非常重要。
一个好的学习计划可以帮助你合理安排学习时间和学习内容,避免拖延和浪费时间。
在制定学习计划时,你可以将学习任务分配到不同的时间段,确保每天都有固定的学习时间,并保持良好的学习习惯。
H4. 习题4:积极参与课堂无论是在学校还是在培训班,积极参与课堂是提高学习效果的关键。
你可以提问问题,与老师和同学进行交流,参加小组讨论等等。
通过积极参与课堂,你不仅可以加深对知识的理解,还可以加强与他人的互动,拓宽思路和观点。
H3. 习题5:自主学习除了参加课堂,自主学习也是提高学习效果的重要途径。
自主学习包括自主阅读、自主练习等等。
你可以选择适合自己的学习资源,如书籍、在线教程等,进行自主学习。
通过自主学习,你可以按照自己的节奏和兴趣进行学习,提高学习效果。
H4. 习题6:反思总结在学习过程中,经常进行反思总结是非常重要的。
你可以在学习之后花几分钟时间回顾学习内容,思考自己的理解和掌握程度,发现弱点和问题,并寻找解决方法。
应用概率统计习题十答案

应用概率统计习题十答案习题10答案10.1 设有3台机器生产规格相同的铝合金薄板.现从生产出的薄板中各取5块,测出厚度值,如下表机器(i) Ⅰ Ⅱ Ⅲ 2.36 2.57 2.58 2.38 2.53 2.64 厚度测量值 2.48 2.55 2.592.45 2.54 2.67 2.43 2.61 2.62 设各测量值服从同方差的正态分布,试分析各机器生产的薄板厚度有无显著差异(??0.05)?解: 原假设H0:?1??2??3对立假设H1:?i??ja?3 , ni?5 , n?15ST?0.12453 , SA?0.10533 , SE?ST?SA?0.01920 ST,SA,SE的自由度分别为14 , 2 , 12 方差分析表为:方差来源平方和自由度均方 F比因素A 0.10533 2 0.05267 32.92 误差E 0.01920 12 0.00160 总和T 0.12453 14由于??0.05,查表得F?(a?1,n?a)?F0.05(2,12)?3.89 又因为F?32.92?3.89?F0.05(2,12)故拒绝原假设H0,接受H1,说明薄板厚度有明显差异.10.4 设有一熟练工人,用4种不同的机器在6种不同的运转速度下生产同一种零件.各自记录1小时内生产的零件数,列在下表中.1速度 1 机器 1 2 3 4 42.5 39.5 40.2 41.3 2 39.3 40.1 40.5 42.2 3 39.6 40.541.3 43.5 4 39.9 42.3 43.4 44.2 5 42.9 42.5 44.9 45.9 6 43.6 43.1 45.1 42.3 (小数点后的数是根据最后1个零件完成的程度定出的)设各水平搭配下产量总体服从同方差的正态分布,试分析机器、运转速度对产量有无显著影响(??0.05)?解:此题为双因素无交互作用的试验原假设HA0:?1??2??3??4?0HB0:?1??2??3??4??5??6?0HA1:?i?0至少一个iHB1:?j?0至少一个j对立假设这里有a?3 b?6 ab?24ST?83.3383 , SA?16.3783 , SB?42.8083 , SE?24.1517 ST,SA,SB,SE的自由度分别为23,3,5,15 方差分析表为方差来源平方和自由度均方 F比机器A16.3783 3 5.45944 3.39 速度B 42.8083 58.56167 5.32 误差E 24.1517 15 1.61011 总和T83.3383 23由于??0.05 ,查表得F0.05(3,15)?3.29 , F0.05(5,15)?2.9又因为 FA?3.39?3.29, FB?5.32?2.9 故不同的机器不同的运转速度对产量有显著影响.210.5 取3种不同的导弹系统,4种不同类型的推进器,对某种燃料进行燃烧试验.每种组合下重复试验2次,测得燃烧速度的数值表如下表推进器导弹系统 B1 34.0,32.7 32.0,33.2 28.4,29.3 B2 30.1,32.8 30.2,29.8 27.3,28.9 B3 29.8,26.7 28.7,28.1 29.7,27.3 B4 29.0,28.9 27.6,27.8 28.8,29.1 A1 A2 A3 设各水平搭配下燃烧速度总体服从同方差的正态分布,试分析导弹系统、推进器类型及它们的交互作用对然烧速度有无显著影响(??0.05)?解:此题为双因素有交互作用的试验HA0:?1??2??3?0 原假设 HB0:?1??2??3??4?0HAB0:?ij?0i?1,2,3j?1,2,3,4HA1:?i?0至少一个i 备择假设 HB1:?j?0至少一个jHAB1:?ij?0至少一对i,j这里有a?3, b?4, n?2 , abn?24ST?91.6783,SA?14.5233,SB?40.0817,SA?B?22.1633,SE?14.9100 ST,SA,SB,SA?B,SE的自由度分别为23,2,3,6,12 方差分析表为方差来源平方和自由度均方 F比因素A 14.5233 2 7.2617 5.84 因素B 40.0817 3 13.3606 10.75 交互作用 22.1633 6 3.6939 2.97误差E 14.9100 12 1.2425 合计T 91.6783233由已知??0.05,查表得F0.05(2,12)?3.89,F0.05(3,12)?3.49,F0.05(6,12)?3.00又因为 FA?5.84?3.89,FB?10.75?3.49,FA?B?2.97?3 故导弹系统、推进器对燃烧速度有影响,交互作用无显著影响.4感谢您的阅读,祝您生活愉快。
大学物理课后习题详解(第十章)中国石油大学

根据高斯定理可得 方向由的正负确定
10-22 如图所示,在xOy平面内有与y轴平行、位于和处的两条无限长平 行均匀带电直线,电荷线密度分别为和。求z轴上任一点的电场强度。
[解] 无限长带电直线在线外任一点的电场强度 所以 P点的场强 由对称性知合场强的z方向分量为零,x方向分量 而
所以 方向指向x轴负方向 10-23 如图所示,在半径为R,体电荷密度为的均匀带电球体内点处放
所以 证毕。
10-27 电量q均匀分布在长为2l的细杆上,求在杆外延长线上与杆端距离 为a的点P的电势(以无穷远为零电势点)。 [解] 取如图所示的电荷元dq,,它在P点产生的电势为
则整个带电直线在P点产生的电势为
10-28 如图所示,在点电荷+q的电场中,若取图中点P处为电势零点, 则点M的电势为多少? [解] 取P点为电势零点,则M点电势为
10-10 如图所示,一厚度为b的无限大带电平板,其体电荷密度为 (0≤x≤b),式中k为正常量。求:(1)平板外两侧任一点和处的场强大小; (2)平板内任一点P处的电场强度; (3)场强为零的点在何处? [解] (1)过点作一圆柱体穿过无限大带电平板,由高斯定理
即 所以 因此平板外一点的场强与距平板的距离无关, (2)板内(即0≤x≤b区域) (3)若电场强度为0,则 此时,此即为场强为0的点。
10-1l 一半无限长的均匀带电直线,线电荷密度为。试证明:在通过带 电直线端点与直线垂直的平面上,任一点的电场强度 E的方向都与这直 线成45°角。 [解] 如图选择直角坐标系,在棒上取电荷元
它在过棒端的垂直面上任意点贡献场强为
由于
且
所以
总场强的分量为 它与负y方向的夹角是
10-12 一带电细线弯成半径为R的半圆形,线电荷密度,式中为一常 量,为半径R与x轴所成的夹角,如图所示。试求环心O处的电场强度。 [解] 取电荷元
人工智能基础(习题卷10)

人工智能基础(习题卷10)第1部分:单项选择题,共53题,每题只有一个正确答案,多选或少选均不得分。
1.[单选题]RPA在流程设计过程中,优先使用哪种方式设计流程 ()。
A)可视化控件操作B)图片识别C)手写代码答案:A解析:2.[单选题]大小为 1024X1024,灰度级别为 256 色的图像文件大小为( )。
A)1MBB)2MBC)6MBD)8MB答案:A解析:3.[单选题]Teacher(father(Zhan))的个体是 ()A)常量B)变量C)函数D)谓词答案:C解析:4.[单选题]循环神经网络适合处理的数据是()。
A)节点数据B)序列数据C)结构化数据D)图像数据答案:B解析:循环神经网络是一种用于处理序列数据的神经网络,相比一般的神经网络,他能 够处理序列变化的数据。
比如某个单词的意思会因为上文提到的内容不同而有不同的含义, RNN就能够很好地解决这类问题。
5.[单选题]外业调绘主要是通过影像调绘和( )两种作业方法。
其中影像调绘数据采用自空三自动匹配点粗纠正成数字正射影像图(DOM),并分块打印;线划图调绘采用采集成果数据回放图进行,作为作业调绘的底图。
( )A)线划图调绘B)手动调绘C)电脑调绘D)测量调绘答案:A解析:C)工作簿文件D)EXE文件答案:D解析:7.[单选题]建立一个模型,通过这个模型根据已知的变量值来预测其他某个变量值属于数据挖掘的哪一类任务?A)根据内容检索B)建模描述C)预测建模D)寻找模式和规则答案:C解析:8.[单选题]标准BP算法的目标是使训练集上的()最小。
A)累计方差B)累积误差C)累计协方差D)累积偏差GRU答案:B解析:9.[单选题]多分类学习中,最经典的三种拆分策略不包括( )。
A)一对一B)一对其余C)一对多D)多对多答案:A解析:多分类学习中,最经典的三种拆分策略包括一对多、多对多、一对其余。
10.[单选题]令N为数据集的大小[注:设训练样本(xi,yi),N即训练样本个数],d是输入空间的维数(注:d即向量无xi的维数)。
圆的面积练习题10
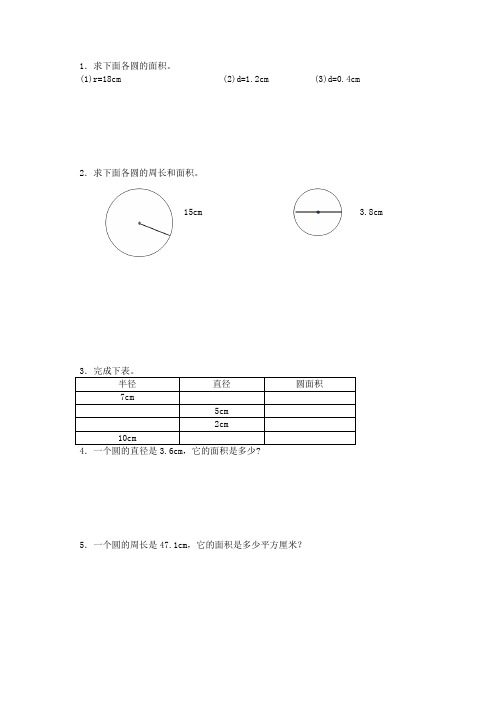
(1)r=18cm (2)d=1.2cm (3)d=0.4cm 2.求下面各圆的周长和面积。
15cm 3.8cm5.一个圆的周长是47.1cm,它的面积是多少平方厘米?(1)d=20cm (2)r=3.2cm (3)r=1.6cm 2.求下面各圆的周长和面积。
9cm 0.6cm5.一个圆的周长是72.22cm,它的面积是多少平方厘米?(1)d=16cm (2)r=1cm (3)r=3.6cm 2.求下面各圆的周长和面积。
13cm 0.6cm5.一个圆的周长是12.56cm,它的面积是多少平方厘米?(1)d=14cm (2)d=1.2cm (3)d=2.8cm 2.求下面各圆的周长和面积。
6cm 4.8cm5.一个圆的周长是56.52cm,它的面积是多少平方厘米?(1)r=20cm (2)r=1.4cm (3)d=2cm 2.求下面各圆的周长和面积。
4cm 4cm5.一个圆的周长是15.7cm,它的面积是多少平方厘米?(1)r=6cm (2)d=3.2cm (3)d=1.2cm 2.求下面各圆的周长和面积。
12cm 5cm5.一个圆的周长是34.54cm,它的面积是多少平方厘米?(1)d=6cm (2)d=0.4cm (3)d=2cm2.求下面各圆的周长和面积。
11cm 4.8cm5.一个圆的周长是34.54cm,它的面积是多少平方厘米?(1)d=2cm (2)d=2.4cm (3)r=0.4cm 2.求下面各圆的周长和面积。
2cm 4.2cm5.一个圆的周长是25.12cm,它的面积是多少平方厘米?(1)r=18cm (2)d=1.2cm (3)r=4cm2.求下面各圆的周长和面积。
1cm 0.6cm5.一个圆的周长是72.22cm,它的面积是多少平方厘米?(1)r=8cm (2)d=2.8cm (3)d=1.2cm 2.求下面各圆的周长和面积。
7cm 2.4cm5.一个圆的周长是21.98cm,它的面积是多少平方厘米?。
练习题10及参考答案

练习题10及参考答案1. 单项选择题(1)在声明一个结构体类型时系统分配给它的存储空间是。
A. 该结构体类型中第一个成员所需存储空间B. 该结构体类型中最后一个成员所需存储空间C. 该结构体类型中所有成员所需存储空间的总和D. 结构体类型本身并不占用存储空间,即系统并不给结构体类型分配存储空间【答】D(2)下列说法不正确的是。
A. 下列结构体声明时,占据了5个字节的空间struct stru{short int a;short int b;char c;}B. 结构体类型的成员名可以与程序中的变量名相同C. 结构体类型的成员可以是一个结构体变量D. 可以单独使用结构体变量中的成员,它的作用相当于普通变量【答】声明结构体类型时不占据内存空间。
本题答案为A。
(3)在定义一个结构体变量时系统分配给它的存储空间是。
A. 该结构体变量中第一个成员所需存储空间B. 该结构体变量中最后一个成员所需存储空间C. 该结构体变量中占用最大存储空间的成员所需存储空间D. 该结构体变量中所有成员所需存储空间的总和【答】D(4)下列说法正确的是。
A. 结构体类型的每个成员的数据类型必须是基本类型B. 结构体类型的每个成员的数据类型都相同,这一点与数组一样C. 在声明结构体类型时,其成员的数据类型不能是结构体本身D. 以上说法都不对【答】D(5)在定义一个共用体变量时系统分配给它的存储空间是。
A. 该共用体变量中第一个成员所需存储空间B. 该共用体变量中最后一个成员所需存储空间C. 该共用体变量中占用最大存储空间的成员所需存储空间D. 该共用体变量中所有成员所需存储空间的总和【答】C(6)以下关于枚举的叙述不正确的是。
A. 枚举变量只能取对应枚举类型的枚举元素表中元素B. 可以在定义枚举类型时对枚举元素进行初始化C. 枚举元素表中的元素有先后次序,可以进行比较D. 枚举元素的值可以是整数或字符串【答】D(7)以下关于typedef的叙述不正确的是。
大学法理学知识考试(习题卷10)

大学法理学知识考试(习题卷10)第1部分:单项选择题,共48题,每题只有一个正确答案,多选或少选均不得分。
1.[单选题]授权性法律规范的指引作用在于( )A)鼓励人们从事某种行为B)命令人们从事某种行为C)禁止人们从事某种行为D)防止人们从事某种行为答案:A解析:2.[单选题]"司法机关依法独立行使职权",这属于我国法律制度中的的( )A)法律编纂原则B)法律制定原则C)法律适用原则D)法律汇编原则答案:C解析:本题涉及法律原则。
司法机关依法行使职权的过程是我国的法律适用过程。
因此,这一原则就是法律适用的原则。
3.[单选题]下列选项中,属于规范性文件的有( )。
A)审判机关的判决B)立法机关的法律C)公安机关的逮捕证D)国家行政机关的裁决答案:B解析:法律规范与法律条文,二者是既有联系又有区别的两个概念。
法律规范是行为规则,而法律条文则是法律规范的外部表现形式,法律条文可以分为规范性条文和非规范性条文。
规范性条文是表述法律规范的条文,即规定具体权利、义务的条文。
非规范性条文是指并不具体设置权利、义务的条文,它是指适用法律规范的规定于社会生活中的行为所产生的具有法律效力的文件,如判决书、起诉书和行政决定书等。
非规范性法律文件与规范性法律文件最大的区别在于:非规范性法律文件只是针对具体的人和事,其法律效力只对特定的对象,没有普遍适用的规范性,不能反复适用;而规范性法律文件规定了人们普遍的权利义务,对一般人、一般事有效。
本题中A、C、D属于非规范性法律条文,故排除。
4.[单选题]关于中国法的渊源的历史演变错误的是()A)只有中国古代法的最早渊源都是从习惯法发展为成文法的。
B)公元前536年,郑国的执政子产“铸刑书”,这是中国最早公布的成文法。
C)中国历史上第一部完整的法典是战国时期李悝在诸侯国法 律基础上编制的《法经》。
D)民国时期形成了所谓的 “六法全书”,即宪法、民商法、民事诉讼法、刑法、刑事诉讼法和行政法。
数字10练习题小班

数字10练习题小班本文为小班学生设计的数字10练习题,旨在帮助学生熟悉数字10的认识、写法、比较和运算等方面的知识。
通过有趣的练习题,激发学生学习的兴趣,提高他们的数学能力。
以下是一些数字10的练习题,希望对小朋友们有所帮助!练习题一:认识数字101. 找出下图中表示数字10的图案。
(此处应插入一幅图)2. 用彩色纸剪出数字10的形状。
练习题二:数字10的写法1. 抄写下列数字,并写出数字10的中文拼音。
1、2、3、4、5、6、7、8、9、___2. 在铅笔盒里找出数字10。
练习题三:数字10的比较1. 用<、=或>将下列数字进行比较。
3 ___ 102. 把下列数字按从小到大的顺序排列。
5、7、10、2、9练习题四:数字10的运算1. 填空:10 - 5 = ___5 + ___ = 1010 - ___ = 72. 从1加到10,计算1+2+3+4+5+6+7+8+9+10的结果。
练习题五:数字10的拓展1. 写出数字10在日常生活中常见的应用场景。
2. 口算练习:快速计算出5个10相加的结果。
这些练习题既有认识数字10的基础题目,也有拓展与运用数字10的练习题,帮助小朋友深入学习和理解数字10的概念。
通过多样化的练习题,可以激发小朋友的学习兴趣,同时提高他们对数字10的认知和运用能力。
希望这些练习题能帮助小班的学生们更好地掌握数字10的知识,为他们以后的数学学习打下坚实的基础。
祝愿小朋友们在学习中取得进步,享受数学学习的乐趣!注:本文仅为示例,实际解答内容请根据具体情况编写。
第10章习题答案

第10章习题答案习题101.(1)图G 的度数列为2、2、3、3、4,则G 的边数是多少(2)3、3、2、3和5、2、3、1、4能成为图的度数列吗为什么(3)图G 有12条边,度数为3的结点有6个,其余结点的度数均⼩于3,问图G 中⾄多有⼏个结点为什么解 (1)设G 有m 条边,由握⼿定理得2m =∑∈Vv v d )(=2+2+3+3+4=14,所以G 的边数7条。
(2)由于这两个序列中有奇数个是奇数,由握⼿定理的推论知,它们都不能成为图的度数列。
(3) 由握⼿定理得∑∈Vv v d )(=2m =24,度数为3的结点有6个占去18度,还有6度由其它结点占有,其余结点的度数可为0、1、2,当均为2时所⽤结点数最少,所以应由3个结点占有这6度,即图G 中⾄多有9个结点。
2.若有n 个⼈,每个⼈恰有3个朋友,则n 必为偶数。
证明设1v 、2v 、…、n v 表⽰任给的n 个⼈,以1v 、2v 、…、n v 为结点,当且仅当两⼈为朋友时其对应的结点之间连⼀条边,这样得到⼀个简单图G 。
由握⼿定理知∑=nk kv d 1)(=3n 必为偶数,从⽽n 必为偶数。
3.判断下列各⾮负整数列哪些是可图化的哪些是可简单图化的 (1)(1,1,1,2,3)。
(2)(2,2,2,2,2)。
(3)(3,3,3,3)。
(4)(1,2,3,4,5)。
(5)(1,3,3,3)。
解由于⾮负整数列d =(d 1,d 2,…,d n )是可图化的当且仅当∑=ni i d 1≡0(mod 2),所以(1)、(2)、(3)、(5)能构成⽆向图的度数列。
(1)、(2)、(3)是可简单图化的。
其对应的⽆向简单图如图所⽰。
(5)是不可简单图化的。
若不然,存在⽆向图G 以为1,3,3,3度数列,不妨设G 中结点为1v 、2v 、3v 、4v ,且d(1v )=1,d(2v )=d(3v )=d(4v )=3。
⽽1v 只能与2v 、3v 、4v 之⼀相邻,设1v 与2v相邻,于是d(3v )=d(4v )=3不成⽴,⽭盾。
最新公路水运检测员考试习题及答案-习题10

精品文档试验检测检测员资格材料试验科目考试一、单项选择题(每题1分,共20题)1、下列有关水泥细度检测方法的描述中正确的是(C)。
A、比表面积的大小能够反映水泥某一粒径的粗细变化;B、筛析法以水泥通过标准筛的质量百分数表示水泥细度;C、比表面积的大小随水泥的颗粒粗细变化而变化;D、筛析法是代用方法,比表面积法是标准方法。
2、某地区夏季气候凉爽,冬季寒冷,且年降雨量较少,则该地区气候分区可能是(B)。
A、3—4—1;B、3—2—3;C、4—2—2;D、1—2—43、代表沥青与矿料之间结合程度的大小、抵御水破坏的性能是(A )。
A、粘附性;B、粘滞性;C、稠度;D、耐久性。
4、沥青延度试验过程中,有时要在水槽中加入食盐或酒精,其直接的目的是为了(B)。
A、调整沥青的密度;B、调整水的密度;C、保证试验的准确性;D、改善试验环境条件5、下列石料中与沥青粘附性最好的可能为(A)。
A、石灰岩;B、花岗岩;精品文档C、石英岩;D、砂岩;6、安定性试验的沸煮法主要是检验水泥中是否含有过量的(D )。
A、氧化钠;8、三氧化硫;C、游离氧化镁;D、游离氧化钙;7、下列各项水泥指标,当(D)不满足技术标准要求时,可判定水泥为废品。
A、细度;B、强度;C、终凝时间;D、初凝时间8、评价沥青混合料高温稳定性的试验方法是(A)。
A、车辙试验;B、薄膜烘箱试验;C、加热质量损失试验;D、残留稳定度试验9、粗集料密度试验中测定水温的原因是(B)。
A、修正不同温度下石料热胀冷缩的影响;B、修正不同温度下水密度变化产生的影响;C、不同水温下密度的计算公式不同;D、在规定的温度条件下试验相对简单;10、沥青混合料试件质量为1190g,高度为62.5mm,成型标准高度(63.5mm)的试件混合料的用量为(B)g。
A、1200;B、1209C、1171;D、118211、对某含有粘土粒的砂砾土进行颗粒分析试验,以便对其进行命名,已知小于0.074mm 颗粒的质量百分含量在5%左右,则最适合该土样的分析方法为(B)A、干筛法B、湿筛法C、比重计法D、移液管法12、土中的水可以分为(A)A、自由水与结合水B、重力水与结合水C、毛细水与重力水D、毛细水与结合水13、在进行含水量测试时,土中水的质量一般不包括(D)的质量A、弱结合水8、自由水C、强结合水D、毛细水14、利用“单轴固结仪法”做室内压缩试验时,如不需测定沉降速率,则其压缩稳定的标准时间是:(B)A、12小时B、24小时C、48小时D、96小时15、某土的细粒含量为96.2%, wP =28.1%, wL =50.0%则定名为(C)A、MLB、MHC、CLD、CH16、土的天然密度越大,干密度(B)A、不变B、不一定C、越大D、越小17、水泥稳定土在进行含水量测试时,烘箱起始温度应为:(D)A、室温B、65℃〜70℃C、75℃〜80℃D、105℃〜110℃18、密度测定时需进行两次平行试验,并求二者的算术平均值,但二者的平行差值不得大于(C),否则应重做A、0.01g/cm A3B、0.02g/cmA3C、0.03g/cmA3D、0.04g/cmA319、击实试验在结果整理时,若有超粒径的土颗粒,则(A)A、超粒径百分含量小于30%可以按规范公式进行修正B、超粒径百分含量小于20%可以按规范公式进行修正C、超粒径百分含量小于10%可以按规范公式进行修正D、不进行修正20、土样制备时需过0.5mm筛的试验为(C)A、击实试验B、压缩试验C、界限含水量试验D、剪切试验二、判断题(每题1分,共40题)21、采用间断级配配制的混凝土,虽然强度较高,但空隙率较大。
初级会计练习题10

初级会计练习题10一、选择题1、企业对于已经发出但不符合收入确认条件的商品,其成本应借记的科目是( )。
(2007年考题)A.在途物资B.发出商品C.库存商品D.主营业务成本【答案】B2、甲工业企业销售产品每件230元,若客户购买达到100件及以上的,可得到20元/件的商业折扣。
某客户2009年12月10日购买该企业产品100件,按规定现金折扣条件为2/10,1/20,n/30。
适用的增值税税率为17%。
该企业于12月16日收到该笔款项时,应给予客户的现金折扣为( )元。
(假定计算现金折扣时不考虑增值税)A. 714B. 0C. 210D. 420 【答案】 D【解析】应给予客户的现金折扣=(230-20)×100×2%=420(元)3、某企业2008年8月1日赊销一批商品,售价为120 000元(不含增值税),适用的增值税税率为17%。
规定的现金折扣条件为2/10,1/20,n/30,计算现金折扣时考虑增值税。
客户于2008年8月15日付清货款,该企业收款金额为( )元。
(2009年考题)A.118 800B.137 592C.138 996D.140 400【答案】 C【解析】该企业收款金额=120 000×(1+17%)×(1-1%)=138 996(元)。
注意:在此题目的分析中需要关注现金折扣计算的基础,即增值税是否考虑在内,题目条件已经明确告知,考试中要认真审核题目。
4、某企业某月销售商品发生商业折扣20万元、现金折扣15万元、销售折让25万元。
该企业上述业务计入当月财务费用的金额为( )万元。
(2008年考题)A.15B.20C.35D.45【答案】A【解析】本题目考核了商业折扣、现金折扣、销售折让的处理,三者中只有现金折扣在财务费用科目中体现,因此答案应该选择A。
5、甲公司本年度委托乙商店代销一批零配件,代销价款300万元。
本年度收到乙商店交来的代销清单,代销清单列明已销售代销零配件的50%,甲公司收到代销清单时向乙商店开具增值税发票。
习题10_交互式电子白板与多媒体CAI课件制作教程(第2版)_[共2页]
![习题10_交互式电子白板与多媒体CAI课件制作教程(第2版)_[共2页]](https://img.taocdn.com/s3/m/6039ea3c6294dd88d1d26bc4.png)
259 ④ 单击“图表/绘制新函数”菜单命令,弹出计算器,根据函数,输入变量和值,单击“确认”按钮后,得到如图10-45所示的抛物线。
图10-45 构造过程四
⑤ 分别拖动a 、m 、n ,观察抛物线形状变化。
例10-20 作椭圆函数图像。
具体操作方法如下。
① 作两个同心圆,圆心为O 。
② 选定O 点,单击“图表/定义原点”菜单命令,作
出坐标系。
③ 作射线OA ,交两圆于A 、B 点。
④ 过A 点作y 轴的平行线,过B 点作x 轴的平行线,
两线交于M 点。
⑤ 单击A 点,选择“编辑/操作类按钮/动画”菜单命
令,制作动画。
⑥ 单击M 点,选择“显示/追踪”菜单命令,单击“运
动点”按钮,跟踪M 点,如图10-46所示。
⑦ 调整大小圆关键点,可以看到不同形状的椭圆。
1.几何图形和几何体制作练习
(1)利用画射线工具绘制两条互相垂直的射线。
(2)绘制两个圆,其中一个圆过另一个圆的圆心。
(3)利用绘制中垂线的方法,绘制三角形的外接圆。
(4)利用平移选项,绘制两个全等三角形。
(5)绘制一个球体。
2.度量型课件制作练习
(1)验证切割线定理。
图10-46 椭圆函数图像的形成。
10习题与答案

问答题1.问:常见的齿轮传动失效有哪些形式?答:齿轮的常见失效为:轮齿折断、齿面磨损、齿面点蚀、齿面胶合、塑性变形等。
2.问:在不改变材料和尺寸的情况下,如何提高轮齿的抗折断能力?答:可采取如下措施:1)减小齿根应力集中;2)增大轴及支承刚度;3)采用适当的热处理方法提高齿芯的韧性;4)对齿根表层进行强化处理。
3.问:为什么齿面点蚀一般首先发生在靠近节线的齿根面上?答:当轮齿在靠近节线处啮合时,由于相对滑动速度低形成油膜的条件差,润滑不良,摩擦力较大,特别是直齿轮传动,通常这时只有一对齿啮合,轮齿受力也最大,因此,点蚀也就首先出现在靠近节线的齿根面上。
4.问:在开式齿轮传动中,为什么一般不出现点蚀破坏?答:开式齿轮传动,由于齿面磨损较快,很少出现点蚀。
5.问:如何提高齿面抗点蚀的能力?答:可采取如下措施:1)提高齿面硬度和降低表面粗糙度;2)在许用范围内采用大的变位系数和,以增大综合曲率半径;3)采用粘度高的润滑油;4)减小动载荷。
6.问:什么情况下工作的齿轮易出现胶合破坏?如何提高齿面抗胶合能力?答:高速重载或低速重载的齿轮传动易发生胶合失效。
措施为:1)采用角度变位以降低啮合开始和终了时的滑动系数;2)减小模数和齿高以降低滑动速度;3)采用极压润滑油;4)采用抗校核性能好的齿轮副材料;5)使大小齿轮保持硬度差;6)提高齿面硬度降低表面粗糙度。
7.问:闭式齿轮传动与开式齿轮传动的失效形式和设计准则有何不同?答:闭式齿轮传动:主要失效形式为齿面点蚀、轮齿折断和胶合。
目前一般只进行接触疲劳强度和弯曲疲劳强度计算。
开式齿轮传动:主要失效形式为轮齿折断和齿面磨损,磨损尚无完善的计算方法,故目前只进行弯曲疲劳强度计算,用适当增大模数的办法考虑磨损的影响。
8.问:硬齿面与软齿面如何划分?其热处理方式有何不同?答:软齿面:HB≤350,硬齿面:HB>350。
软齿面热处理一般为调质或正火,而硬齿面则是正火或调质后切齿,再经表面硬化处理。
法律硕士民法提高练习习题及答案10

一、单项选择题1.既属于不动产物权,又属于用益物权的是()。
A.典权B.质权C.抵押权D.权利质权2.既属于用益物权,又属于从物权的是()。
A.地上权B.留置权C.地役权D.权利质权3.甲、乙因房屋所有权引发争议,经仲裁机关裁决,乙获得了该房屋的所有权。
根据《物权法》的规定,房屋所有权的变动自()生效。
A.仲裁裁决生效时B.房屋所有权办理登记时C.房屋被乙实际占有时D.仲裁机构受理该案件时4.下列表述正确的是()。
A.甲从赵某处购房一套,物权自双方当事人签订买卖合同时发生变动B.乙继承其父房屋一套,物权自办理过户登记时发生变动C.钱某自建房屋一栋,物权自房屋建成并办理过户登记时发生变动D.丙、丁因房屋权属发生纠纷,法院判决房屋归丁,物权自法院判决生效时发生变动5.下列选项中,以登记作为物权取得的生效条件的是()。
A.甲用自己的房屋为周某设定抵押权B.乙在自己的宅基地上盖了一栋房屋C.丙在吴某的建设用地上设定地役权D.丁将自己的“奔驰”轿车卖给王某6.甲去世后,其子乙继承了其名下的房屋两间。
不久,乙将房屋卖给了丙。
则下列表述正确的是()。
A.乙取得房屋的方式为原始取得B.乙自继承开始时取得房屋的所有权C.丙取得房屋无须办理房屋过户登记D.乙和丙取得房屋都应办理过户登记7.根据《物权法》规定,下列登记不属于不动产物权登记类型的是()。
A.变动登记B.预售登记C.更正登记D.异议登记8.关于公示、公信原则的表述,错误的是()。
A.公信产生公示力B.公信是公示的补充C.公示、公信原则在于维护交易安全D.公示、公信原则是物权法的基本原则之一9.下列选项中,可以适用返还原物所有权的是()。
A.李某借给张某一台电脑,但因张某使用不善,电脑毁损、灭失B.陈某的自行车被范某偷走,范某将自行车送给赵某C.甲将古画交给乙保管,乙将古画卖给善意的丙D.丁答应赠给戊一台电脑,但迟迟不履行诺言10.甲将电脑租给乙使用,然后甲又出售给丙。
高等代数-李海龙-习题第10章群、环和域简介

第十章 群、环和域简介10.1 群1. 判断以下集合对于所给的运算来说哪些作成群,哪些不作成群: (1) 某一数域F 上全体n n ⨯矩阵的加法; (2) 全体正整数对于数的乘法;(3) {}2xx Z ∈对于数的乘法;(4){}01x R x ∈<≤对于数的乘法;(5) {}1,1-对于数的乘法. 解:(1) 设数域F 上全体n n ⨯矩阵的集合为()n M F ,对于矩阵的加法来说()n M F 作成一个加群.因为对任意,,()n A B C M F ∈,有1°()A B C ++=()A B C ++(加法结合律)2°()n M F 中存在零矩阵O ,使得对任意的A ∈()n M F ,有A O O A A +=+=3°对于A ∈()n M F ,有A -∈()n M F .使得()()A A A A O +-=-+=4°对于,A B ∈()n M F ,有A B B A +=+. (2) 全体正整数对于数的乘法不作成群.因为对于数的乘法来说,单位元是1,但是对于正整数a =2来说不存在正整数b 使得a ×b =1.(3) 集合{}2x M x Z =∈对于数的乘法作成阿贝尔群.因为1°对于12x ,22x,32x ∈M ,123,,x x x Z ∈,有312(22)2x x x ⨯⨯=1232x x x ++=3122(22)x x x ⨯⨯2°在M 中有021=,使得2x M ∈,有022x ⨯=022x ⨯=2x .3°对于2x M ∈,存在2xM -∈使得22x x -⨯=22x x -⨯=02=14°对于2,2x y M ∈,有22x y =2x y +=22y x.(4) 集合{}101M x R x =∈<≤对于数的乘法来说不作成群.因为1M 中的单位元是1,而对于12a =不存在1b M ∈,使得1a b ⨯=.(5) 集合{}1,1G =-对于数的乘法作成群〔阿贝尔群〕.因为对于G 任三个元素来说,结合律显然成立.再者G 有单位元1.对于G 中元素来说1(1)⨯-=(1)1-⨯=1-,并且1的逆元是1,1-的逆元是1-.2. 证明群中的指数规则〔1〕、〔2〕.证明:设G 是一个群,a G ∈,则1a G -∈,对于,m n ∈Z,如果0(0)m n <<或,设m m '=-, ()n n '=-或,并且注意当0n <时,对于a G ∈,有1()n n a a '-=.于是1°当0,0m n >>时,m nmna a aa aa ==m n a +;2°当0,0m n >=时,0mm na a aa a ==m a e =m a =m n a +,当0,0m n =>时,同理可证.;3°当0,0m n ><时,11n mm na a aa a a '--==111,,()(()),m n m n n m m n m n m n a a m n a a a a m n '-+'''------+'⎧=≥⎨'===<⎩; 4°当0,0m n <<时,1111m n m n a a a a a a ''----==1()m n a ''-+=11(())m na --+=m n a +. 所以对任意,m n ∈Z ,a G ∈都有m na a =m n a +,即〔1〕式成立.其次我们先证对于任意的m ∈Z ,a G ∈,都有1()m a -=1()ma -.∵1()m m a a -=1()m a a -=0()m a =me =e再由定义1()m m a a -=e ,根据G 中每一个元素的逆元的唯一性,∴1()m a -=1()m a -.以下证明等式〔2〕成立.1°当0,0m n >>时,()m na =()()()nmmma a a a a a =mn a2°当0,0m n ><时,()m n a =1[()]m n a '-=1[()]m n a '-=1()mn a '-=11[()]mn a --=mn a当0,0m n <>时,()m n a =1[()]m n a '-=1()m n a '-=11[()]mn a --=mn a .3°当0,0m n <<时,()m n a =1[()]m n a '-=11{[()]}m n a ''--=()m n a ''=m n a ''=mn a .综上所述所证,群G 中指数规则〔1〕、〔2〕成立. 3. 设{,,}G a b c =,G 的乘法由下面的表给出:ab c a a b c b b c a c ca b证明G 对于所给的乘法作成一个群.证明:根据G 的乘法表可知ab b ba ==,ac c ca ==,bc a cb ==,所以G 的乘法是可换的,以下证明G 对于乘法作成一个群.1°结合律成立.由于G 对于所给的乘法是可换的,对于结合律我们只要验证也容易验证以下的情况即可.()()ab c a bc =;()()aa b a ab =;()()aa c a ac =; ()()bb a b ba =;()()bb c b bc =;()()cc a c ca =; ()()cc b c cb =.其它情况由G 的乘法可换性,立即可以证得.2°G 中有单位元a ,使得对于G 中任意元素,,a b c ,都有aa a =,ab ba b ==,ac ca c ==3°G 中每一个元素都有逆元,a 的逆元是a ,〔因为aa a =〕,而b 的逆元是c ,c 的逆元是b ,〔因为bc cb a ==〕.所以G 对于所给的乘法作成一个〔可换〕群.4. 证明,一个群G 是阿贝尔群的充要条件是:对任意的,a b G ∈和任意的整数n ,都有 ()n n nab a b =.证明:必要性,已知群G 对乘法运算可换,且对结合律成立.设,a b G ∈,而n 是任意的整数,因为G 对指数规则〔1〕、〔2〕成立.故有()n ab =()()()ab ab ab =abab ab =22a b ab ab =…=n n a b .充分性,设,a b G ∈,而n 是整数,有()n n n ab a b =,令2n =,则有222()ab a b =,即()()ab ab =()a ba b =()()aa bb =()a ab b ,所以()a ba b =()a ab b ,在此等式两边左乘1a -以并右乘以1b -,得11()()()a a ba bb --=11()()()a a ab bb --,所以 ()e ba e =()e ab e ,即 ba =ab .所以G 是一个阿贝尔群.5. 证明,群G 的两个子群的交还是G 的一个子群. 证明:设1H ,2H 是群G 的两个子群,则12H H ≠∅〔至少有一个单位元e 〕.1°对于12,a b H H ∈则1,a b H ∈且2,a b H ∈,因为1H ,2H 是子群,所以1ab H ∈且2ab H ∈,所以12ab H H ∈;2°设12c H H ∈,则1c H ∈且2c H ∈因为1H ,2H 是子群,所以11c H -∈且12c H -∈,所以112c H H -∈,所以,由子群的定义可知,12H H 是G 的一个子群.6. 证明,n 维欧氏空间V 的全体正交变换作成V 上一般线性群()GL V 的一个子群,这个群称为V 上的正交群,用记号()O V 表示.证明:一般线性群()GL V 是指n 维欧氏空间V 上全体可逆线性变换的集合对V 上的线性变换与线性变换的乘法来说作成的群.因为正交变换是可逆的线性变换,且单位变换也是正交变换.所以()O V 是()GL V 的非空子集.任意两个正交变换的乘积也是正交变换,即乘法封闭. 正交变换的逆变换也是正交变换.所以,n 维欧氏空间V 的全体正交变换的集合()O V 是一般线性群()GL V 的一个子群. 7. 令a 是群G 中的一个元素,令{}n a a n 〈〉=∈,证明a 〈〉是G 的一个子群,称为由a生成的循环子群.特别,如果a 〈〉=G ,就称G 是由a 生成的循环子群.试各举出一个无限循环子群和有限循环子群的例子.证明:显然a a ∈〈〉,故a 〈〉非空,设,n m a a a ∈〈〉,,n m Z ∈,则n m n ma a a a +=∈〈〉;设n a ∈a 〈〉,则11()()n n na a a a ---==∈〈〉,所以a 〈〉是G 的一个子群.例1:设G Z =,运算是加法运算,则1G =〈〉是无限循环群. 例2:设{}70,1,2,3,4,5,6G Z ==运算是剩余类的“加法”,则1G =〈〉是由1生成的有限循环群,它只有7个元素.8. 令σ=1212n n i i i ⎛⎫⎪⎝⎭,设()A Mn F ∈,定义 ()A σ=111222121212n n n i i i n i i i n i i i n a a a a a a a a a ⎛⎫⎪ ⎪ ⎪⎪ ⎪⎝⎭就是对A 的行作置换σ所得的矩阵,令n ∑={}()n I S σσ∈,其中I 是n n ⨯单位矩阵,证明n∑作成(,)GL n F 的一个与n S 同构的子群. 证明:首先注意以下的几个事实: 1°设1(1,0,,0)ε=,2(0,1,,0)ε=,……,(0,0,,1)n ε=,由矩阵的乘法可知i j εε'=1,,0,i j i j=⎧⎨≠⎩〔,1,2,,i j n =〕2°集合n ∑={}()n I S σσ∈中的任一元素()I σ都是由n 阶单位矩阵I 的各行所给的假设干次的置换而得到,所以,每一个()I σ的每一行和每一列都是只有一个位置上的元素为1,其余位置上的元素全为0,并且||1I =.而()I σ都是由I 的各行经过对换而得到的所以|()|I σ=1±.3°容易计算,集合n∑={}()n I S σσ∈共有!n 个不同的元素,不妨设为:n∑={}12!,,,n I I I ;所以n ∑是群(,)GL n F 的一个非空子集.现在证明n ∑与n S 同构,由于n S 是一个群,所以n S 是(,)GL n F 的一个子群.(1) 集合n∑对(,)GL n F 的运算〔即矩阵乘法〕是封闭的.设1212n n i i i σ⎛⎫=⎪⎝⎭,1212n n j j j τ⎛⎫=⎪⎝⎭∈nS ,则()I σ和()I τ是n ∑的两个元素〔矩阵〕.因为I 的第1,2,…,n 行分别是n 维向量1ε,2ε,…,n ε,所以()I σ的第1,2,…,n 行分别是n 维向量1i ε,2i ε,…,niε,而()I τ的第1,2,…,n 行分别是n 维向量1jε,2jε,…,njε,由上述的事实2°可知()I τ的各列也是由一些单位向量所组成.设其在第1,2,…,n 列分别是n 维向量1kε,2kε,…,nkε,此处1k ,2k ,…,n k 是1,2,…,n 的某一个排列.设()I σ()I τ=A 〔A 是n n ⨯矩阵〕由矩阵的乘法可知A 的第s 行的各个元素分别是1s i k εε',2s i k εε',…,s n i k εε',由上述事实1°可知,这n 个数中只有一个t s k i =时才等于1,其余各数均为0,〔因为s i 是1,2,…,n 的某一个排列〕,这样矩阵A 的第s 行只有一个位置的元素是1,而其余位置的元素均为0,并且当s i 不同时,1的位置不同,令s =1,2,…,n 可知矩阵A 的各行各列的元素都只有一个位置的1,而其余位置的元素均为0,并且||A =|()()|I I στ=1±,所以nA ∈∑,即()I σ()I τn ∈∑.(2) 存在着n ∑到n S 的一个同构映射f . 如上所述,n ∑={}12!,,,n I I I ,设i I 是n ∑的任意一个矩阵,用i I 右乘n ∑的各个元素,得1i I I ,2i I I ,…,!i n I I ,因为n ∑对乘法是封闭的,所以它们仍是n ∑中!n 个不同的元素〔因为假设i k I I =i i I I ,由i I 的可逆性则有k I =i I 〕,这样我们得到一个n ∑元素之间的一个置换,i I τ=12!12!n i i n i I I I I I I I I I ⎛⎫⎪⎝⎭,所以我们定义n ∑到n S 的一个映射:ii I f I τ→.a ) f 是n ∑到n S 的一个双射.它显然是满射,现证是单射.设,i j nI I ∈∑,且i jI I ≠,则i I τ=12!12!n i i n i I I I I I I I I I ⎛⎫⎪⎝⎭≠j I τ=12!12!n j j n j I I I I I I I I I ⎛⎫⎪ ⎪⎝⎭,因为假设i t I I =j tI I ,t =1,2,…,n ,由n ∑中元素的可逆性,则有i I =jI 这与i jI I ≠矛盾,所以f 是n ∑到n S 的一个一一映射;b ) f 是n ∑到n S 的一个同构映射,设,i j nI I ∈∑,依f 的对应法则()i f I =i I τ,()j f I =j I τ,设i j kI I I =,则有:()i j f I I =()k f I =k I τ=12!12!n k k n k I I I I I I I I I ⎛⎫⎪⎝⎭=12!12!n i j j i j n i I I I I I I I I I I I I ⎛⎫⎪ ⎪⎝⎭=i j I I τ=()i f I ()j f I所以f 是n ∑到n S 的一个同构映射.所以n ∑和n S 同构,又由于n S 是群,因而n ∑也是群.且n ∑⊆(,)GL n F . 9. 设G 是一个群,a G ∈,映射:a x ax λ,x G ∈叫做G 的一个左平移.证明:(1) 左平移是G 到自身的一个双射;(2) 设,a b G ∈,定义a b a b λλλλ=〔映射的合成〕,则G 的全体左平移{}a a G λ∈对于这样的定义的乘法作成一个群G ';(3) G G '≅. 证明:(1) :a xax λ,x G ∈是G 到G 的一个双射.首先a λ是一个满射,因为对于任意的y G ∈,总存在一个1x a y G -=∈,使得ax y =,其次a λ的一个单射,因为12,x x G ∈,并且12x x ≠则12ax ax ≠.(2) G '是一个群.因为G '对映射的乘法是封闭的,且G '对映射的乘法满足结合律.另外,设e 是G 的单位元,则e λ是G '的单位元,对于a G λ'∈都有a λe λ=e λa λ=a λ.最后,设a G λ'∈,因为a G ∈,1a G -∈,所以存在一个映射1a G λ-'∈,使a λ1a λ-=1a λ-a λ=e λ,即G '中每一个元素a λ都有逆元1aλ-,所以G '是一个群.(3) G G '≅,作G 到G 的一个映射f :a a λ.容易证明f 是双射.且假设,a b G ∈,()f ab =ab λ=a λb λ=a b λλ=()f a ()f b .所以f 是G 到G 的一个同构映射,即G G '≅.10. 找出三次对称群3S 的一切子群.〔注意:要求证明你找出3S 的子群已经穷尽了的一切子群〕解:三次对称群3S ={}(1),(12),(13),(23),(123),(132)共六个元素.现在设H 是3S 的一个非空子集,如果H 要做3S 的子群,则H 必须对3S 的运算是封闭的;同时H 有(1)作为单位元,并且假设a H ∈则1a H -∈,而(1,2)的逆元是(1,2),(1,3)的逆元是(1,3),(2,3)的逆元是(2,3),(1,2,3)的逆元是(1,3,2).在3S 的一切非空子集中,可能构成3S 的子群的非空子集只有以下情况:1H ={}(1),2H =3S ,3H ={}(1),(12),4H ={}(1),(13),5H ={}(1),(23),6H ={}(1),(123),(132),7H ={}(1),(12),(123),(132),8H ={}(1),(13),(123),(132),9H ={}(1),(23),(123),(132),10H ={}(1),(12),(13),(123),(132),11H ={}(1),(12),(23),(123),(132), 12H ={}(1),(13),(23),(123),(132),13H ={}(1),(12),(13),14H ={}(1),(12),(23),15H ={}(1),(23),(13),16H ={}(1),(12),(13),(23),经检验,除1H ,2H ,3H ,4H ,5H ,6H ,可构成3S 的子群外,其余的子集都对乘法不封闭,所以不构成3S 的子群.10.2 剩余类加群1. 写出6Z 的加法表. 解:略.2. 证明:n Z 是循环群,并与n 次单位根群n U 同构.证明:设{},n Z +是模n 的剩余类加群,其元素有n 个:0,1,2,,,,1k n -,因为1111k k =+++=,这就是说n Z 中任意元k 皆是1的倍数,所以n Z 可由1生成,即n Z =1〈〉,故n Z 是循环群.又设n U 是n 次单位根群,则n U 是n 阶群,以ε表示n U 的一个单位原根,则n U ε=〈〉={}0121,,,,n εεεε-,作n Z 到n U 的一个映射:k f k ε,则f 显然是nZ 到n U 的一个双射.并且对于,n k l Z ∈都有()()()f k l f k f l +=+.1°假设k l n +<,则()()f k l f k l +=+=k l ε+=k lεε=()()f k f l ;2°假设k l n +≥,则(0)k l n s s n +=+≤≤,故有()()f k l f k l +=+=()f s =s ε=1s ε=n s εε=n s ε+=()()f k f l .所以f 是n Z 到n U 的一个同构映射,即n Z 与n U 同构. 3. 找到6Z 的所有子群. 解:已知{}60,1,2,3,4,5Z =,依习题习题10的方法,在加群6Z 中,0是单位元,1与5互为逆元,2与4互为逆元,3与3互为逆元.所以,可能构成6Z 的子群的集合有以下几个:{}10H =,2H =6Z ,{}30,3H =,{}40,2,4H =,{}50,2,3,4H =,{}60,1,5H =,{}70,1,3,5H =,经检验,1H ,2H ,3H ,4H 是6Z 的子群,其余子集均对运算不封闭,不能构成子群.因此,6Z 的一切子群有{}10H =,2H =6Z ,{}30,3H =,{}40,2,4H =.4. 证明,每一个有限群含有一个子群与某一个n Z 同构.证明:设G 是n 元有限群,e 是G 的单位元,a e ≠是G 中任意的元,作元素a 的非负整数幂:e =012,,,,,,,n k a a a a a ,因为G 是群,故上列这些元均是G 中的元素,又因为G是n 阶群,故上列元必有相同的.设s ka a =,且s k ≠,不妨设k s >,而k s m -=,所以0k s a a -==e ,即m a e =.我们把满足这一条件的最小正整数m 称为元a 的阶,显然,假设a的周期为m ,则m n ≤,〔否则G 有多于n 个元素,这与G 是n 阶群〕.令{}2,,,m H a a a e ==,因为m n ≤,所以H 是群G 的非空子集,现证H 是G 的子群,且m H Z ≅.1°H 是G 的子群.首先H 的元互不相同.因为假设1,l t m ≤≤,且l t ≠则l ta a ≠,〔假设l t a a =,设l t >,则l ta e -=,而l t m -<.这与m 是a 的阶矛盾〕.同时,H 对G 的乘法封闭.设,i j a a H ∈则有i j i j a a a +=,假设i j m +≤,则i j i ja a a H +=∈,假设i j m +>,则i j m p +=+,0p m <≤,则i j i j a a a +=m p p a a +==H ∈,其次H 有单位元m a e =,最后设k a H ∈,则1k m ≤≤.则必有正整数m k -,使得m k a H -∈,这时k m k m a a a e -==.所以H中任意一元k a H ∈都有逆元m ka H -∈.2°m H Z ≅.为了方便我们记0m a e a ==.作H 到n Z 的一个映射:k f k a ,显然f 是双射.设,m k l Z ∈,假设k l m +≤,则()()()()k l k lf k l f k l a a a f k f l ++=+===,假设k l m +>则设(0)k l m r r m +=+<<,则()()()r rf k l f k l f r a e a +=+===()()m r k l a a a f k f l +===所以f 是H 到n Z 的一个同构映射,即m H Z ≅.5. 设G 、H 是群,在{}(,),G H g h g G h H ⨯=∈∈中定义乘法:(,)(,)(,)g h g h gg hh ''''=,(,),(,)g h g h G H ''∈⨯.证明,G H ⨯按照这样的乘法来说作成一个群.证明:因为{}(,),G H g h g G h H ⨯=∈∈,G 、H 是两个群.1°G H ⨯对乘法封闭.设(,),(,)g h g h G H ''∈⨯,因G 、H 是群,故gg G '∈,hh H '∈,故(,)(,)(,)g h g h gg hh ''''=G H ∈⨯2°G H ⨯的乘法适合结合律,设11(,)g h G H ∈⨯,22(,)g h G H ∈⨯,33(,)g h G H ∈⨯,则123g g g G ∈,123h h h H ∈,又G 、H 是群,故123g g g G ∈,123h h h H ∈适合结合律.因此112233(,)[(,)(,)]g h g h g h=112323(,)(,)g h g g h h =123123(,)g g g h h h =121233(,)(,)g g h h g h =112233[(,)(,)](,)g h g h g h3°G H ⨯中有单位元12(,)e e ,其中设1e ,2e 分别是G 、H 的单位元.因为对于(,)g h G H ∈⨯,12(,)e e (,)g h •=12(,)e g e h =(,)g h ,12(,)(,)g h e e =12(,)ge he =(,)g h .4°G H ⨯中每个元(,)g h 都有逆元11(,)g h --,其中1g -,1h -分别是g G ∈,h H ∈的逆元.因为(,)g h 11(,)g h --=11(,)gg hh --= 12(,)e e ,11(,)g h --(,)g h =11(,)g g h h --=12(,)e e综上所证,{}(,),G H g h g G h H ⨯=∈∈对所定义的乘法(,)(,)(,)g h g h gg hh ''''=作成一个群.6. 写出22Z Z ⨯和23Z Z ⨯,证明,23Z Z ⨯6Z ≅ 证明:{}20,1Z =,{}30,1,2Z =,{}60,1,2,3,4,5Z =,22Z Z ⨯={}(0,0),(0,1),(1,0),(1,1),23Z Z ⨯={}(0,0),(0,1),(0,2),(1,0),(1,1),(1,2).以下证明23Z Z ⨯6Z ≅,因为6Z 是一个6阶循环群,而元素1的阶是6,故1可作为6Z 的生成元,在23Z Z ⨯中(1,1)的阶也是6,故(1,1)可以作为23Z Z ⨯的生成元,即23Z Z ⨯=(1,1)〈〉.所以23Z Z ⨯是6阶循环群.作6Z 到23Z Z ⨯的映射::1(1,1)0,1,2,3,4,5f k k k =,则在f 下,我们有:f 1(1,1),2(0,2),3(1,0),4(0,1),5(1,2),60(0,0)=,显然f 是双射.再对f 的(66)2⨯÷=16种情况逐一验证,知f 是一个同态映射,因而f 是6Z 到23Z Z ⨯同构映射,即23Z Z ⨯6Z ≅.7. 任何一个四阶循环群或者与4Z 同构,或者与22Z Z ⨯同构. 证明:设G 是任一四阶群,以下分两种情况讨论: (1) 假设G 是任一四阶循环群,则{}023,,,G a a e a a a =〈〉==,而{}40,1,2,3Z =.做4Z 到G 的映射:0,1,2,3kf ka k =,显然f 是双射,现设0,3k l ≤≤,假设3k l +≤,则()f k l +=()f k l +=k l a +=k l a a =()f k ()f l ,假设4k l +≥,则4(04)k l r r +=+≤<,则 ()f k l +=()f k l +=()f r =r a =r e a =4r a a =4r a +=k l a +=k l a a =()f k ()f l .所以f 是同构映射,即4G Z ≅(2) 假设{},,,G e a b c =不是循环群,则G 作为一个群,其乘法表为e a b c e e a b c a a e c b b b c e a cc b ae显然,{},,,G e a b c =非循环群,G 的非单位元的阶都是2,即2a e =,2b e =,2c e =,而22Z Z ⨯={}(0,0),(0,1),(1,0),(1,1),由2Z的运算性质可知,22Z Z ⨯的每个非单位元的阶也都是2.做G 到22Z Z ⨯的映射:(0,0)e ϕ,(0,1)a ,(1,0)b ,(1,1)c ,容易看出,映射ϕ是双射,再对ϕ的(44)2⨯÷=8种情况逐一验证,知ϕ是一个同态映射,所以映射ϕ是同构映射,即22G Z Z ≅⨯.10.3 环和域1. 证明,在一个交换环R 里,二项式定理()n a b +=11222n n n n n n a C a b C a b b --++++对于任意的,a b R ∈和正整数n 成立.证明:设,a b R ∈,我们对于正整数n 用数学归纳法来证明 1°当n=1时,1()a b +=a b +,命题成立;2°当n=2时,2()a b +=()()a b a b ++=22a ab ab b +++=222a ab b ++,命题成立;3°假定当n=k 时,命题成立,即有()k a b +=11222k k k k k k a C a b C a b b --++++成立,对于n=k+1时,我们有:1()k a b ++=()()k a b a b ++=11222()()k k k k k k a C a b C a b b a b --+++++ =11212()k k k k k k a C a b C a b ab +-++++1122231()k k k k k k a b C a b C a b b --++++++=11212111()k k k k k k aC a b C ab b +-+++++++,故结论成立.2. 设R 是一个环,并且对于加法来说R 作成一个循环群,证明R 是一个交换环. 证明:由题设存在元a 生成,使得{}R a na n Z =〈〉=∈.设12,a a R ∈,则11a n a =,22a n a =,12,n n Z ∈,有12a a =1()n a 2()n a =212n n a ,21a a =2()n a 1()n a =212n n a所以12a a =21a a ,即R 对乘法满足交换律,故R 是一个交换环.3. 证明,对于有单位元的环来说,加法适合交换律是环定义里其它条件是结果.〔提示:用两种方式展示()(11)a b ++〕证明:R 是一个有单位元1环,则由环定义中条件〔3〕可知()(11)a b ++=()1()1a b a b +++=a b a b +++=()a b a b+++,而()(11)a b ++=(11)(11)a b +++=a ab b+++=()a a b b+++,因此()a b a b +++=()a a b b +++,所以 b a +=a b +.4. 写出2Z 和7Z 的加法和乘法表. 解:略.5. 设R 是一个只有有限多个元的交换环,且R 没有零因子,证明R 是一个域. 证明:因为R 是一个只有有限多个元素的交换环,故可设12,,,n a a a R ∈是R 的全部非零元,这意味着这n 个元互不相同.设i a 是{}12,,,n G a a a =中之一,以i a 乘以{}12,,,n G a a a =的所有元得12,,,i i i n a a a a a a ,由于R 没有零因子,故这n 个元素仍是R 的非零元,且各不相同〔因为假设()i s i k a a a a s k =≠,由于R 没有零因子,故消去律成立,得到s k a a =与{}12,,,n G a a a =元素各不相同矛盾〕,所以12,,,i i i n a a a a a a 除去次序不同和12,,,n a a a 必完全相同.因此,对于这个i a ,必有一个k 存在〔1k n ≤≤〕使i k i a a a =〔因为如果不是这样,则12,,,i i i n a a a a a a 中没有一个等于i a ,这与12,,,i i i n a a a a a a 与12,,,na a a 完全相同矛盾〕,因为R 是一个交换环,所以k i i k i a a a a a ==.1°以下我们证明k a 是单位元.设.j a是G 的任一元,由以上证明知12,,,i i i n a a a a a a 除去次序不同和12,,,n a a a 必完全相同,所以必有i s a a =j a ,k j a a =k a ()i s a a =i s a a =j a ,再由R是一个交换环,知j k ja a a =,所以k a 是G 的单位元,记为k e a =是G 的单位元.2°以下证明G 中的元素都有逆元,为此我们对G 重新排序记为{}121,,,,n G e a a a -=,设r a 是G 任意元,以r a 乘以{}121,,,,n G e a a a -=中每一个元,得121,,,,r r r r n a e a a a a a a -,则由以上证明知121,,,,r r r r n a e a a a a a a -除去次序不同和12,,,n a a a 必完全相同,因而必有r t t r a a e a a ==.所以G 是一个可换群,所以R 是一个域.6. 设R 是一个环,a R ∈,如果存在一个正整数n ,使得0na =,就说a 是一个幂零元.证明,在一个交换环里,两个幂零元的和还是幂零元.证明:设,a b R ∈是两个幂零元,则有n ,m 是正整数,使得0n a =,0ma =,由本习题1,在交换环中二项式定理成立,故有()n m a b ++=11222n m n m n m n m n m n m a C a b C ab b ++-+-+++++++因为00n k n k k a a a a +===,00s m s m sb b b b +===,所以()n ma b ++=0,所以a b +是幂零元.7. 证明,在一个环R 中,以下两个条件等价: (i ) R 没有非零的幂零元;(ii )如果a R ∈,且20a =则0a =.证明:设〔ⅰ〕成立我们证明〔ⅱ〕成立.因为20a =,但是R 中没有非零幂零元,所以0a =.反之,设〔ⅱ〕成立我们证明〔ⅰ〕成立.设a R ∈是任一幂零元,则存在一个正整数n ,使得0na =,以下证明0a =,假设0a ≠,由〔ⅱ〕成立,则有20a ≠〔否则由假设20a =则0a =,矛盾〕,同理22()0a ≠,即40a ≠,如此继续下去,则有20ka ≠,1,2,k =,而当2k n >时,由已知有220k knn a aa -==,矛盾.所以,假设不成立,即〔ⅰ〕成立.8. 设R 与R '是环,:f R R '→是一个同态映射,证明, (i ) {}Im()()()f f R f a a R ==∈是R '的一个子环; (ii ){}()()0I Ker f a R f a ==∈=是R 的一个子环,并且对任意的r R ∈,a I ∈都有ra I ∈,如果R 与R '都有单位元,能不能断定(1)R f 是R '的单位元1R '?当f 是满射时,(1)R f 是R '的单位元1R '?证明:(i) 因为R 与R '是环,:f R R '→是一个同态映射,所以(0)0f '=〔此处0是R 的零元,0'是R '的零元〕,所以0Im()f '∈,又Im()()f f R R '=⊆,即Im()f 是R '的非空子集.所以对于(),()Im()f a f b f ∈,,a b R ∈,有()()()f a f b f a b -=-∈ Im()f .〔因为R 是环,,a b R ∈,所以a b R -∈〕,并且()()()Im()f a f b f ab f =∈.所以{}Im()()()f f R f a a R ==∈是R '的一个子环;(ii) 因为R 与R '是环,:f R R '→是一个同态映射,所以(0)0f R ''=∈,所以()Ker f ≠∅,设,()a b Ker f ∈,则()()0f a f b '==,于是()()()000f a b f a f b '''-=-=-=,所以()a b Ker f -∈,且()()()000f ab f a f b '''===,故()ab Ker f ∈,因此,{}()()0I Ker f a R f a ==∈=是R 的一个子环.对于r R ∈,a I ∈()Ker f =,则()()()()00f ra f r f a f r ''===,所以ra I ∈ ()Ker f =.如果R 与R '都有单位元,:f R R '→是一个同态映射,则(1)R f 不一定是R '的单位元1R ',例如{}20,1R Z ==,{}20,1R Z '==,作R R '→的映射:00,10f ,则显然:f R R '→是一个同态映射,但(1)0f =不是R '的单位元.如果f 是满射,(1)R f 是R '的单位元1R '.9. 设F 和F '是域,:f F F '→是同态映射,证明,或者()0f F =,或者f 是个单射,〔提示:利用第8题〔ⅱ〕证明()Ker f 或者等于零,或者等于F 〕.证明:因为F 和F '是域,:f F F '→是同态映射,所以F 和F '是环,由上题〔ⅱ〕知{}()()0Ker f a R f a =∈=是F 的一个子环〔域〕,以下分两种情况讨论:(i ) 假设{}()0Ker f =,则对于任意的,()a b Ker f ∈,有()()0f a f b '==,于是()()()000f a b f a f b '''-=-=-=,所以()a b Ker f -∈,但{}()0Ker f =,所以a b =,所以f 是个单射;(ii ) 假设{}()0Ker f ≠,则()Ker f 必有非零元素,设()a Ker f ∈并且0a ≠,又因为F 是域,所以a 在F 中必有逆元1a F -∈,由上题〔ⅱ〕知1()a a Ker f -∈,即1()e a a Ker f -=∈,设x 是F 中任意元素,再由〔ⅱ〕的结果可知:()xe x Ker f =∈,所以()F Ker f ⊆,而()Ker f F ⊆,所以()Ker f F =,当()Ker f F =时,Im()()0f f F ==.10. 证明,2阶实矩阵2()M R 的子集F =,a b a b R b a ⎧⎫⎛⎫⎪⎪∈⎨⎬ ⎪-⎪⎪⎝⎭⎩⎭作成一个与复数域同构的域.证明:首先证明F 是环2()M R 的一个子域.设a b A b a ⎛⎫= ⎪-⎝⎭,c d B d c ⎛⎫=⎪-⎝⎭是F 任意两个元素,其中a,b,c,d R ∈,则a b cd A B b a d c ⎛⎫⎛⎫-=- ⎪⎪--⎝⎭⎝⎭=a cb d b d ac --⎛⎫⎪-+-⎝⎭F∈,又当0B ≠时,c,d 不全为零,则22cd B c d dc ==+-0≠,所以1B -存在,且11cd B d c B --⎛⎫= ⎪⎝⎭,所以1B F -∈,于是11a b c d AB b a d c B--⎛⎫⎛⎫=⎪⎪-⎝⎭⎝⎭=1ac bd bc ad ad bc ac bd B+-⎛⎫ ⎪-+⎝⎭F ∈,所以F 是环2()M R 的一个子域,现在作复数域{}2,,1C a bi a b R i =+∈=-到F 的一个映射:a b f a bib a ⎛⎫+ ⎪-⎝⎭,显然,f 是C 到F 的一个双射.现在设()a b f a bi b a ⎛⎫+= ⎪-⎝⎭,()cd f c di dc ⎛⎫+=⎪-⎝⎭,则 [()()]f a bi c di +++=[()()]f a c b d i +++=()a cb d b d ac ++⎛⎫ ⎪-++⎝⎭a b c d b a d c ⎛⎫⎛⎫=+ ⎪ ⎪--⎝⎭⎝⎭=()()f a bi f c di +++.又 [()()]f a bi c di ++=[()()]f ac bd ad bc i -++=ac bd bc ad ad bc ac bd +-⎛⎫ ⎪-+⎝⎭ =a b c d b a d c ⎛⎫⎛⎫⎪⎪--⎝⎭⎝⎭.所以f 是C 到F 的同构映射,即F 作成一个与C 同构的域.11. 令Q 是有理数域,R 是一个环,而f ,g 都是Q 到环R 的环同态,证明,假设对任意整数n ,都有()()f n g n =则f g =.证明:由已知,来证明11()()f g nn =,假设11()()f g n n ≠,则 11()()()()f n f g n g n n ≠这与(1)(1)f g =,所以假设不成立,有11()()f g n n =. 再证明f g =.对于任意有理数mQn ∈,我们有 11()()()()()()m m f f m f g m g g n n n n ===,所以f g =.12. 证明,一切形如,,a bi c di a b R c di a bi ++⎛⎫∈ ⎪-+-⎝⎭的二阶复矩阵所成的集合作成一个环K ,这个环的每一个非零元素都有逆元,K 是不是域?证明:1°集合K 对于矩阵的加法和乘法都是封闭的.设 11111111a b i c d i A c d i a b i ++⎛⎫= ⎪-+-⎝⎭,22222222a b i c d i B c d i a b i ++⎛⎫= ⎪-+-⎝⎭K ∈, 则 1212121212121212()()()()()()()()a a b b i c c d d i A B c c d d i a a b b i ++++++⎛⎫+= ⎪-++++-+⎝⎭K ∈, 记 11111111a b i c d i A c d i a b i ++⎛⎫= ⎪-+-⎝⎭=αββα⎛⎫⎪-⎝⎭,22222222a b i c d i B c d i a b i ++⎛⎫= ⎪-+-⎝⎭=ξηηξ⎛⎫⎪-⎝⎭,则AB αβξηβαηξ⎛⎫⎛⎫=⎪⎪--⎝⎭⎝⎭=αξβηαηβξβξαηβηαξ⎛⎫-+⎪---+⎝⎭=()αξβηαηβξαηβξαξβη⎛⎫-+ ⎪ ⎪-+-⎝⎭K ∈; 2°零矩阵00000000i i O i i ++⎛⎫= ⎪-+-⎝⎭K ∈,且A O O A A +=+=; 3°设11111111a b i c d i A c d i a b i ++⎛⎫= ⎪-+-⎝⎭=αββα⎛⎫⎪-⎝⎭K ∈,则有逆元A -=αββα--⎛⎫⎪-⎝⎭K ∈,且()()A A A A O +-=-+=,4°所以K 作成一个环.且K 有单位元I .设A =αββα⎛⎫⎪-⎝⎭是任何一个非零元,则A=αββα-=ααββ+=22αβ+0≠.从而1A -=1Aαββα-⎛⎫ ⎪⎝⎭存在,但矩阵乘法不满足交换律,故K 不是域.13. 在15Z 中,找出适合方程21x =的一切元素.解:在15Z ={}0,1,2,3,4,5,6,7,8,9,10,11,12,13,14中,211(mod15)=,24161(mod15)==, 2111211(mod15)==,2141961(mod15)==.故在15Z 中, 适合方程21x =的元有1,4,11,14.14. 证明,一个特征为0的域一定含有一个与有理数域同构的子域;一个特征为0p >的域一定含有一个与pZ 同构的子域.证明:(i)设F 是特征为0的域,则F 含有单位元e ,所以对于任意整数n 来说,都有ne F ∈,令1{|}F ne n Z =∈,因为当且仅当0n =时,0ne =,所以,:n Z nne σ∀∈是Z 到1F 的双射,且显然是同构映射,令12{()()|,,0}F me ne m n Z n -=∈≠,则12F F F ⊆⊆.对mQ n ∀∈,规定1:()()mme ne nτ-,则τ是Q 到2F 的双射,且1212,m m Q n n ∀∈,1212()m m n n τ+=121212()m n n m n n τ+=1121212()()m n n m e n n e -+111122()()()()m e n e m e n e --=+=11()m n τ+22()mn τ11212121212121112112212()()()()()()()()()()m m m mm m e n n e n n n n m m m e n e m e n e n n ττττ---====所以2Q F ≅,所以2F 是域,且是F 的子域. (ii)设F 是一个特征为p >0的域, e 是F 的单位元,令1{0F =,,2,,(1)},ppe e e p e i Z =-∀∈,规定:iie σ,且是p Z 到的一个双射. ,p i j Z ∀∈且,0,,0j i kp r r p ij lp s s p +=+≤<=+≤<,故,i j r ij s +==则()()()i j r re kpe re i j e ie je σσ+==+=+=+()()()()ij s se lpe se ije ie je σσ===+==.所以,σ是pZ 到1F p 是素数,pZ 是域,所以1F 是的一个F 与pZ 同构的子域.15. 令2F Z =是仅含两个元素的域.[]F x 是F 上一元多项式环.(i)证明,21x x ++是[]F x 中唯一的二次不可约多项式.(ii)找出[]F x 中一切三次不可约多项式.解: (i)在[]F x 中二次多项式有222,1,x x x x ++,21x x ++,其中前三个多项式可约.因为0,1不是21x x ++的根,所以21x x ++是[]F x 中唯一的二次不可约.(ii) []F x 中三次多项式有3323332,,,1,x x x x x x x x x +++++,323321,1,1x x x x x x x +++++++.其中不可约多项式只有321x x ++和31x x ++。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 29 题: Windows xp系统正 确关机的 过程是( )。 A.在运行 Windows xp时直接 关机
B.关闭所 有运行程 序,选择 “开始” 按钮中“ 关闭系统 ”菜单, 在弹出的 对话框中 选择“关 闭计算机 ”项 C.先退到 Dos系 统,再下 电关机 D.关闭所 有任务栏 的窗口 后,直接 下电关机
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第5 题:关于 Windows 中注册表 的作用, 错误的说 法是 。 A.可以用 来保存财 务软件的 数据 B.可以保 存 Windows 应用程序 的设置信 息 C.保存硬 件配置信 息
D.保存用 户的信息
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 14 题: Windows XP是一个 多任务操 作系统, 这是指( ) A.可供多 个用户同 时使用 B.在同一 时间片中 运行多个 应用程序 C.可运行 很多种应 用程序 D.可同时 管理多种 资源
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 15 题:对 Windows XP,下述 正确的是 () A.回收站 和剪贴板 一样,是 内存中的 一个区域 B.只有对 当前活动 窗口才能 移动、改 变大小等 操作 C.一旦屏 幕保护开 始,原来 在屏幕上 的活动窗 口就关闭 了 D.桌面上 的图标, 不能按用 户的意愿 重新排列
正确答 案:C 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 17 题:在 Windowsx p系统桌 面上有一 个任务 栏,任务 栏上的“ En”图标 表示( ) 。 A.任务栏 的标识 B.某一窗 口的提示 符 C.没有任 何作用 D.输入法 转换图 标,说明 当前输入 方式为英 文
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 26 题:在 Windows xp系统 中,下列 叙述正确 的是( ) 。 A.利用鼠 标拖曳窗 口边框可 以改变窗 口的大小 B.利用鼠 标拖曳窗 口边框可 以移动窗 口
C.一个窗 口最大化 后不能再 改变 D.一个窗 口最小化 后不能立 即还原
正确答 案:C 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 23 题:假如 硬盘只有 一个分 区,在 Windows xp中格式 化硬盘的 操作( ) 。 A.能够进 行 B.部分能 进行 C.不能进 行 D.使用 Dos功能 可以进行
正确答 案:C 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
正确答 案:C 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 34 题:在 Windows xp桌面 上,( ) 。 A.不能创 建文件夹 B.不能创 建BMP图 像文件 C.不能创 建Word文 档 D.可以创 建Word空 文档
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
审计竞赛 练习十 (固定试 题) 第1部 分:单选 题() 第1 题:以下 关于菜单 的叙述 中,错误 的是( ) A.菜单分 为下拉菜 单和快捷 菜单 B.右击菜 单栏中的 某一菜 单,即可 得出下拉 菜单 C.单击带 省略号… 的菜单选 项后打开 一个对话 框 D.右击某 一位置或 选中的对 象,一般 均可得到 快捷菜单
第 24 题:用鼠 标直接运 行带有图 标的 Windows xp程序, 所要用的 操作是( )。 A.双击 B.单击 C.拖动 D.选中
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分
试题解 析:
第 25 题:在 Windows xp系统 中,在各 种中/英 文输入法 间切换是 按( )。 A.Ctrl+S hift键 B.Shift+ 空格键 C.Alt+Sh ift键 D.鼠标左 键单击输 入方式切 换按钮
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 27 题:在 Windows xp系统中 的可执行 程序文件 类型是( )。 A.prg B.sys C.app D.pif
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 28 题:在 Windows xp系统 中,当某 个应用程 序不再响 应用户的 操作时, 要弹出“ 关闭程序 ”对话框 需按( ) 。 A.Ctrl+A lt+Del键 B.Ctrl+S hift+Del 键 C.Ctrl+S hift+Tab 键 D.Ctrl+D el键
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第8 题:下面 文件系统 中,() 在 windowsx p系统中 不能直接 识别? A.NTFS B.FAT C.FAT32 D.EXT2
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第9 题:操作 系统可分 为。 A.单用户 、多用户 操作系统 B.单用户 、多用户 、网络操 作系统 C.网络操 作系统、 Unix操作 系统、多 用户操作 系统
正确答 案:A 用户答 案:
人工评 卷:错 误;得 分:0分 试题解 析:
第 22 题:以下 说法正确 的是( ) 。 A.Window s xp系统 提供标准 模式和 386模 式,提供 广域网络 管理功能 B.Window s xp系统 提供单任 务的并行 处理能力 C.Window s xp系统 提供网络 接口功能 D.文件管 理器 (Progra m Manager )是 Windows xp的核心
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 11 题:以下 关于用户 账户的描 述,不正 确的是( ) A.要使用 运行 WindowsX P的计算 机,用户 必须有自 己的账户 B.可以任 何成员的 身份登录 到计算 机,创建 新的用户 账户 C.使用控 制面板中 的“用户 和密码” 可以创建 新的用户 D.当将用 户添加到 某组后, 可以指派 给该组的 所有权限 授予这个 用户
试题解 析:
第 32 题:记事 本是用于 编辑( ) 文件的实 用程序。 A.ASCII 文本 B.批处理 C.扩展名 为doc的 D.数据库
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 33 题:在 Windows xp中,快 捷方式的 扩展名为 ( )。 A.sys B.bmp C.lnk D.ini
War e操作系 统、网络 操作系统 、单用户 操作系统
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 10 题:如果 要保证 windows 系统中文 件的信息 安全,最 可靠的手 段是? A.为 windows 设置用户 名和密码 B.设置文 件的访问 权限 C.设置文 件所在共 享目录的 访问权限 D.使用 windows 对文件进 行加密
第 35 题:设置 Windows xp用户名 和密码的 作用是( )。 A.防止别 人使用你 的计算机 B.防止别 人删除计 算机上的 文件 C.防止别 人在你的 计算机上 建立新用 户 D.保护自 己的个人 设置不被 修改
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
正确答 案:A
用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 20 题:在 Windows xp系统 中,刷新 当前窗口 的快捷键 ( )。 A.F2 B.F3 C.F4 D.F5
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 21 题:运行 Windows xp系统 时,首先 看到的是 ( )。 A.程序管 理器 B.文件管 理器 C.打印管 理器 D.PIF编 辑器
正确答 案:D
用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 18 题: Windowsx p的文件 系统是一 个基于( )的管理 系统。 A.桌面 B.文件 C.图标 D.文件夹
正确答 案:D 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 19 题:在 Windows xp系统 中,下列 正确的文 件名是( )。 A.test program. txt B.Lixiao wen|mulu 1 C.1.3 D.A? B.bos
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第2 题:在对 话框的组 成中,不 包含( ) A.菜单栏 B.选项卡 、命令按 钮 C.滑动块 、增量按 钮 D.单选钮 、复选框 、列表框 、文本框
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第 12 题:在 Windows XP系统工 具中,利 用( ) 可以将零 散的可用 空间连在 一片 A.系统还 原 B.磁盘清 理 C.备份 D.磁盘碎 片整理程 序
正解 析:
第3 题: Windows XP对磁盘 信息的管 理和使用 是以( )为单位 的 A.文件 B.盘片 C.字节 D.命令
正确答 案:A 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
第4 题:在 Windows XP中,用 “创建快 捷方式” 创建的图 标( ) A.只能是 单个文件 B.可以是 任何文件 和文件夹 C.只能是 可执行程 序或程序 组 D.只能是 程序文件 或文档文 件
正确答 案:B 用户答 案: 人工评 卷:错 误;得 分:0分 试题解 析:
