matlab课后习题答案第一章
MATLAB第一章作业答案

第一章 M A T L A B 概况与基本操作1.选择题(每题2分,共20分):(1)最初的MATLAB 核心程序是采用D 语言编写的。
A.PASCALB.CC.BASICD.FORTRAN(2)即将于2011年9月发布的MATLAB 新版本的编号为C 。
A.MATLAB 2011RaB.MATLAB 2011RbC.MATLAB R2011bD.MATLAB R2011a(3)在默认设置中,MATLAB 中的注释语句显示的颜色是B 。
A.黑色B.绿色C.红色D.蓝色(4)如果要以科学计数法显示15位有效数字,使用的命令是A 。
A.format long eB.format longC.format long gD.format long d(5)在命令窗口新建变量a 、b ,如果只查看变量a 的详细信息,使用的命令为A 。
A.whos aB.who aC.whoD.whos(6)如果要清除工作空间的所有变量,使用的命令为C 。
A.clearB.clear allC.两者都可D.两者都不可(7)在创建变量时,如果不想立即在命令窗口中输出结果,可以在命令后加上B 。
A.冒号B.分号C.空格D.逗号(8)如果要重新执行以前输入的命令,可以使用D 键。
A.下箭头↓B.右箭头→C.左箭头←D.上箭头↑(9)如果要查询函数det 的功能和用法,并显示在命令窗口,应使用命令C 。
A.docB.lookforC.helpD.三者均可(10)如果要启动Notebook 文档,下列D 操作是可行的。
A.在命令窗口输入notebook 命令B.在命令窗口输入notebook filename 命令C.在Word 中启动M-book 文档D.三者均可2.填空题(每空1分,共20分):(1)MATLAB 是matrix 和laboratory 两个单词前三个字母的组合,意为“矩阵实验室”,它的创始人是Cleve Moler 和Jack Little 。
MATLAB)课后实验答案[1]
![MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/edc54dcb58f5f61fb7366639.png)
实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5. 下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0.53再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下:123d4e56g9实验三 选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
(完整版)汽车理论课后作业答案MATLAB
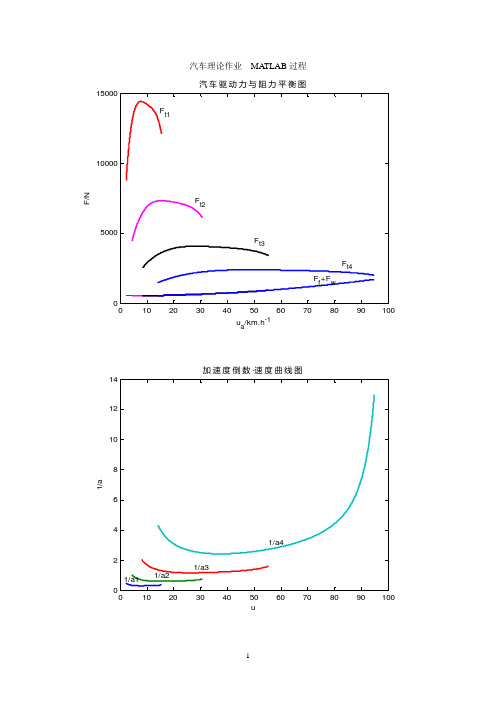
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序:《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知,他们无交点,u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档,较高转速(n取3401 ),最经济负荷(即90%负荷大约 46.9366Kw)行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间:(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间)因与题1.3第三问求法相同,这里不在累述,可直接有计算机求得:figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31)前轴利用附着系数为:gf zh b zL +=βϕ后轴利用附着系数为: ()gr zh a zL --=βϕ1空载时:g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。
数字图像处理及应用(MATLAB)第1章习题答案

第一章:习题与思考题参考答案1-1 什么是数字图像? 数字图像处理有哪些特点?数字图像是将连续的模拟图像经过离散化处理后变成计算机能够辨识的点阵图像。
数字图像处理具有以下特点:(1)处理精度高,再现性好。
(2)易于控制处理效果。
(3)处理的多样性。
(4)数字图像中各个像素间的相关性大,压缩的潜力很大。
(5)图像数据量庞大。
(6) 占用的频带较宽。
(7) 图像质量评价受主观因素的影响。
(8)图像处理技术综合性强。
1-2 数字图像处理的目的及主要内容。
一般而言,对图像进行处理主要有以下三个方面的目的(1) 提高图像的视感质量,以达到赏心悦目的目的。
(2) 提取图像中所包含的某些特征或特殊信息,以便于计算机分析。
(3) 对图像数据进行变换、编码和压缩,以便于图像的存储和传输。
数字图像处理的主要研究内容:根据其主要的处理流程与处理目标大致可以分为图像信息的描述、图像信息的处理、图像信息的分析、图像信息的编码以及图像信息的显示等几个方面。
如:图像数字化、图像增强、图像几何变换、图像复原、图像重建、图像隐藏、图像正交变换、图像编码、图像分析等。
1-3 数字图像处理的主要应用图像处理技术广泛用于众多的科学与工程领域,主要有:(1)生物医学领域中的应用(2)工业应用(3)遥感航天中的应用(4)军事、公安领域中的应用(5)其他应用,例如:图像的远距离通信;多媒体计算机系统及应用;服装试穿显示;办公自动化、现场视频管理1-4 在理想情况下获得一幅数字图像时,采样和量化间隔越小,图像的画面效果越好,当一幅图像的数据量被限定在一个范围内时,如何考虑图像的采样和量化使得图像的质量尽可能好。
一般,当限定数字图像的大小时, 为了得到质量较好的图像可采用如下原则: (1)对缓变的图像,应该细量化,粗采样,以避免假轮廓。
(2)对细节丰富的图像,应细采样,粗量化,以避免模糊(混叠)。
1-5 想想在你的工作和生活中,遇见过哪些数字化设备?它们的主要用途是什么?主要有以下几种数字化设备:(1) 图像采集卡通常图像采集卡安装于计算机主板扩展槽中,通过主机发出指令,将某一帧图像静止在存储通道中,即采集或捕获一帧图像,然后可对图像进行处理或存盘。
matlab课后习题答案(1-9章)

1 数字1.5e2,1.5e3 中的哪个与1500相同吗?1.5e32 请指出如下5个变量名中,哪些是合法的?abcd-2xyz_33chan a 变量ABCDefgh 2、5是合法的。
3 在MATLAB 环境中,比1大的最小数是多少? 1+eps4 设 a = -8 , 运行以下三条指令,问运行结果相同吗?为什么?w1=a^(2/3) w2=(a^2)^(1/3) w3=(a^(1/3))^2w1 = -2.0000 + 3.4641i ;w2 = 4.0000 ;w3 =-2.0000 + 3.4641i 5 指令clear, clf, clc 各有什么用处?clear 清除工作空间中所有的变量。
clf 清除当前图形。
clc 清除命令窗口中所有显示。
第二章1 说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”符号对象?3/7+0.1双; sym(3/7+0.1)符; sym('3/7+0.1') 符;; vpa(sym(3/7+0.1)) 符;2 在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是自由符号变量. sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)') symvar(sym('sin(w*t)'),1) w a z3 (1)试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
(2)试求二阶方程022=+-a ax x 在0>a 时的根。
(1)reset(symengine)syms x positive solve(x^3-44.5) ans =(2^(2/3)*89^(1/3))/2(2)求五阶方程022=+-a ax x 的实根 syms a positive %注意:关于x 的假设没有去除 solve(x^2-a*x+a^2)Warning: Explicit solution could not be found. > In solve at 83 ans =[ empty sym ]syms x clear syms a positivesolve(x^2-a*x+a^2) ans =a/2 + (3^(1/2)*a*i)/2 a/2 - (3^(1/2)*a*i)/24 观察一个数(在此用@记述)在以下四条不同指令作用下的异同。
matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装matlab时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即matlab选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
2.matlab操作方式桌面存有几个窗口?如何并使某个窗口瓦解桌面沦为单一制窗口?又如何将瓦解过来的窗口再次置放至桌面上?与其他计算机语言相比较,matlab语言注重的特点就是什么?matlab系统由那些部分共同组成?在matlab操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。
matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。
matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。
3.如何设置当前目录和搜寻路径,在当前目录上的文件和在搜寻路径上的文件存有什么区别?命令历史窗口除了可以观测前面键入的命令外,除了什么用途?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
命令历史窗口除了用作查阅以前键入的命令外,还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。
matlab课后习题及答案

第一章5题已知a=4.96,b=8.11,计算)ln(b a e b a +-的值。
解:clearclca=4.96;b=8.11;exp(a-b)/log(a+b)ans =0.01676题已知三角形的三边a=9.6,b=13.7,c=19.4,求三角形的面积。
提示:利用海伦公式area =))()((c s b s a s s ---计算,其中S=(A+B+C)/2.解:clearclca=9.6;b=13.7;c=19.4;s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c))s =21.3500第二章8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解:clearclcS=0;for i=0:1:63S=S+2^i;endSS =1.8447e+0199题分别用for 和while 循环结构编写程序,计算∑=-1001n 1n 2)(的值。
解:clearclcs=0;for n=1:100s=s+(2*n-1);endss =10000clearclcn=1;s=0;while n<=100s=s+(2*n-1);n=n+1;endss =10000第三章2题在同一坐标下绘制函数x ,,2x -,2x xsin(x)在()∏∈,0x 的曲线。
解:clearclcx=0:0.2:pi;y1=x;y2=x.^2;y3=-(x.^2);y4=x.*sin(x);plot(x,y1,'-',x,y2,'-',x,y3,'-',x,y4,'-')00.51 1.52 2.53-10-8-6-4-22468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2e x 5.0 、y2=sin(2∏x )的图形。
解:clearclcx=0:0.01:pi;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'b:',x,y2,'r--')00.51 1.52 2.53 3.5-1-0.50.511.52第四章1题对表达式f=3238641+++x x x 进行化简。
915204-MATLAB程序设计与应用-第1章 MATLAB系统环境_习题答案

第1章 MATLAB系统环境习题1一、选择题1.最初的MA TLAB核心程序是采用()语言编写的。
AA.FORTRAN B.C C.BASIC D.PASCAL2.2016年3月发布的MA TLAB版本的编号为()。
BA.MA TLAB 2016Ra B.MA TLAB R2016aC.MATLAB 2016Rb D.MA TLAB R2016b3.下列选项中能反应MA TLAB特点的是()。
DA.算法最优B.不需要写程序C.程序执行效率高D.编程效率高4.当在命令行窗口执行命令时,如果不想立即在命令行窗口中输出结果,可以在命令后加上()。
CA.冒号(:)B.逗号(,)C.分号(;)D.百分号(%)5.如果要重新执行以前输入的命令,可以使用()。
DA.左移光标键(←)B.右移光标键(→)C.下移光标键(↓)D.上移光标键(↑)6.MA TLAB命令行窗口中提示用户输入命令的符号是()。
BA.> B.>> C.>>> D.>>>>7.plot(x,y)是一条()命令。
CA.打印B.输出C.绘图D.描点8.以下两个命令行的区别是()。
A>> x=5,y=x+10>> x=5,y=x+10;A.第一个命令行同时显示x和y的值,第二个命令行只显示x的值B.第一个命令行同时显示x和y的值,第二个命令行只显示y的值C.第一个命令行只显示x的值,第二个命令行同时显示x和y的值D.第一个命令行只显示y的值,第二个命令行同时显示x和y的值9.下列命令行中,输出结果与其他3项不同的是()。
DA.>> 10+20+... B.>> ...30 10+20+30C.>> 10+20+30%5 D.>> %10+20+3010.下列选项中,不是MATLAB帮助命令的是()。
CA.lookfor B.lookfor –all C.search D.help二、填空题1.MA TLAB一词来自的缩写。
MATLAB第1-8章答案

第1章一、思考题4. (1) B=A(2:5,1:2:5)(2)A(7)=[](3) A=A+30(4)size(A)(5) t(find(t==0))=eps(6)t=reshape(x,3,4)(7)abs('matlab')(8)char(93)5. A=[97,67,34,10;-78,75,65,5;32,5,-23,-59;0,-12,54,7](1) B=A(1:3,:)C=A(:,1:2)D=A(2:4,3:4)E=B*C(2)A(find(A>=50 & A<=100))二、实验题1.x=-74/180*pi;y=-27/180*pi;sin(x*x+y*y)/sqrt(tan(abs(x+y)))+pi2.a=-3.0:0.1:3.0;exp(-0.3*a).*sin(a+0.3)3.x=[2,4;-0.45,5];log(x+sqrt(1+x.*x))/24. A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0]; (1)A*Bans =129 432 41977 -407 -1052402 591 12489A.*Bans =3 -108 13468 -360 518783 270 0(2) A^3ans =-28917 240246 -4368137883 -259101 27669171333 252504 38673A.^3ans =27 157464 839304 -91125 343658503 729000 3375(3)A/Bans =-5.8845 5.3549 -0.20286.3554 -5.6596 4.3293-6.6325 6.2078 9.0241B/Aans =30.2855 19.2643 -8.561433.4394 21.1547 -9.3974-0.7443 -0.3938 0.2830(4)[A,B]ans =3 54 2 1 -2 6734 -45 7 2 8 7487 90 15 9 3 0[A([1,3],:);B^2]ans =3 54 287 90 15600 183 -81684 282 72615 6 8255.a=1+2i;b=3+4i;c=exp(pi*i/6)c =0.8660 + 0.5000ic+a*b/(a+b)ans =1.6353 + 1.8462i第2章一、思考题3.s=0;for n=0:63s=s+2^n;enddisp(s)n=0:63;s=sum(2.^n)二、实验题1.x=input('输入一个四位整数:');y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,10)] z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)2.gh=input('输入工号');h=input('输入工时');dj=84;if h>120gz=dj*120+1.15*dj*(h-120);elseif h<60gz=dj*h-700;elsegz=dj*h;endformat bank;display([gh,gz])3.循环结构n=input('input n:');s=0;for k=1:ns=s+1/k^2;enddisplay(sqrt(s*6))向量运算n=input('input n:');k=1:n;display(sqrt(sum(1./k.^2)*6))4.y=0;k=0;while y<3k=k+1;y=y+1/(2*k-1);enddisplay([k-1,y-1/(2*k-1)])5.x0=0;x=1;k=0;a=input('a=');b=input('b=');while abs(x-x0)>=1e-5 && k<500x0=x;x=a/(b+x0);k=k+1;enddisplay([k,x]);display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);6.y=fun(40)/(fun(30)+fun(20))(1)函数文件fun.mfunction f=fun(n)f=n+log(n^2+5);(2)函数文件fun.mfunction f=fun(n)a=1:n;f=sum(a.*(a+1));第3章一、思考题4.t=0:0.01:1.5;y=sqrt(3)/2*exp(-4*t).*sin(4*sqrt(3)*t+pi/3);5.x=-10:0.01:10;y=linspace(-6,6,size(x,2))z=x.^3+3*x.*y.^2;plot3(x,y,z)6.x=100:100:400;y=100:100:400;z=[636,697,624,478;698,712,630,478;680,674,598,412;662,626,552,334]; [X,Y]=meshgrid(x,y);mesh(X,Y,z)二、实验题1.(1)x=-10:0.01:10;plot(x,x-x.^3/3/2)(2)plot(x,exp(-x.*x/2)/2/pi)(3)x=-8:0.01:8;plot(x,sqrt((64-x.*x)/2))(4)t=0:pi/100:6*pi;plot(t.*sin(t),t.*cos(t))2. (1)x1=linspace(0,1,100);y1=2*x1-0.5;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);plot(x1,y1,'r-',x,y,'b:');text(0.4,1,'y=2x-0.5');text(-0.4,0.5,'x=sin(3t)cos(t)');text(-0.4,0.3,'y=sin(3t)sin(t)');(2)subplot(1,2,1);scatter(x1,y1,10)title('y=2x-0.5');subplot(1,2,2);scatter(x,y,10)3.subplot(1,21);x=1:1:100; y=sin(1./x);plot(x,y)subplot(1,2,2);fplot('sin(1/x)',[1,100])4.subplot(2,2,1);bar(t,y);subplot(2,2,2);stairs(t,y);subplot(2,2,3);stem(t,y)subplot(2,2,4);semilogy(t,y);5.theta=linspace(-pi,pi,100);ro=5.*cos(theta)+4;polar(theta,ro);fi=linspace(0,2*pi,100);a=1r=a.*(1+cos(fi));polar(fi,r);6.t=0:pi/20:2*pi;x=exp(-t./20).*cos(t);y=exp(-t./20).*sin(t);z=t; plot3(x,y,z);t=0:0.01:1;x=t;y=t.^2;z=t.^3;plot3(x,y,z);7.x=-30:0.1:0;y=0:0.1:30;[x,y]=meshgrid(x,y);z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2); meshc(x,y,z);8.x=linspace(-3,3,100);y=linspace(-3,3,100);[x y]=meshgrid(x,y);fxy=-5./(1+x.^2+y.^2);i=find(abs(x)<=0.8 & abs(y)<=0.5);fxy(i)=NaN;surf(x,y,fxy)9.u=linspace(1,10,100);v=linspace(-pi,pi,100);[u,v]=meshgrid(u,v);x=3.*u.*sin(v);y=2.*u.*cos(v);z=4*u.^2;x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.^2;surf(x,y,z);shading interp;light('position',[1,0,1]);10.t=0:pi/100:2*pi;y=sin(t);comet(t,y)第4章一、思考题5.(1)A=eye(3);(2)C=100+(200-100)*rand(5,6);(3)D=1+sqrt(0.2)*randn(1,500);(4)E=ones(size(A));(5)A=A+30*eye(size(A));(6)B=diag(diag(A))二、实验题1.P=pascal(5);H=hilb(5);Dp=det(P);Dh=det(H);Kp=cond(P);Kh=cond(H);P矩阵的性能更好,因为Kp较小2.A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3]B=[3,pi/2,45;32,-76,sqrt(37);5,72,4.5e-4;exp(2),0,97]A1=diag(A);B1=diag(B);A2=triu(A);B2=triu(B);A3=tril(A);B3=tril(B);rA=rank(A);rB=rank(B);nA=norm(A);nb=norm(B);cA=cond(A);cB=cond(B);3.A=[31,1,0;-4,-1,0;4,-8,-2];[V,D]=eig(A);4.A=diag([-1,-1,-1,-1],-1)+diag([-1,-1,-1,-1],1)+diag([2,2,2,2,2]) b=[1,0,0,0,0]';x1=inv(A)*b;x2=A\b;[L,U]=lu(A);x3=U\(L\b);[Q,R]=qr(a);[Q,R]=qr(A);x4=R\(Q\b)R=chol(A);x5=R\(R'\b)5.B=sparse(A);x1=inv(B)*b;x2=B\b;[L,U]=lu(B);x3=U\(L\b);第5章一、思考题3.A=randn(10,5);mean(A)std(A)max(max(A))min(min(A))sum(A,2)sum(sum(A))sort(A,1)sort(A,2,'descend')二、实验题1.A=rand(1,30000);mean(A)std(A)max(A)min(A)size(find(A>0.5))/size(A)2.h=[466,715,950,1422,1635];w=[7.04,4.28,3.40,2.52,2.13];hh=[500,900,1500];ww=interp1(h,w,hh,'spline')3.x=linspace(1,10,50);y=log(x);f=polyfit(x,y,5);yy=polyval(f,x);plot(x,y,'r-',x,yy,'g.')4.N=64; % 采样点数T=5; % 采样时间终点t=linspace(0,T,N); % 给出N个采样时间ti(I=1:N) x=3*exp(-t); % 求各采样点样本值xdt=t(2)-t(1); % 采样周期f=1/dt; % 采样频率(Hz)X=fft(x); % 计算x的快速傅立叶变换XF=X(1:N/2+1); % F(k)=X(k)(k=1:N/2+1) f=f*(0:N/2)/N; % 使频率轴f从零开始plot(f,abs(F),'-*') % 绘制振幅-频率图xlabel('Frequency');ylabel('|F(k)|')5.(1)p1=[1 2 0 0 7];p2=[1 -2];p3=[1 0 0 5 1];p12=conv(p1,p2);p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3];roots(p)(2)A=[-1,4,3;2,1,5;0,5,6];Px=polyval(p,A)Pxm=polyvalm(p,A)6.(1)z=fzero('3*x-sin(x)+1',0)(2)建立函数文件myfun.mfunction F=myfun(X)x=X(1);y=X(2);F(1)=x*x+y*y-9;F(2)=x+y-1;在命令窗口中输入以下命令:x=fsolve(@myfun,[3,0]',optimset('Display','off')) 第6章一、思考题2.fx=inline('1./(1+x.^2)');[I,n]=quad(fx,-100000,100000,1e-3);[I,n]=quadl(fx,-100000,100000,1e-3);x=-100000:0.01:100000;y=1./(1+x.*x);trapz(x,y);3.(1)fx=inline('-2*y+2*x*x+2*x');[t,y]=ode23(fx,[0,0.5],1)(2)fx=inline('y-exp(x)*cos(x)');[t,y]=ode23(fx,[0,3],1)二、实验题1.for x=1:3fx=[x,x^2,x^3;1,2*x,3*x;0,2,6*x];diff(fx)end2.(1)x=0:0.01:1;y=x.^10+10.^x+1./log10(x);dy=diff(y)/0.01;(2)x=0:0.01:1;y=log(1+x);dy=diff(y,2)/0.01;plot(x(1:99),dy)3.(1)fx=inline('x.^2.*sqrt(2*x.*x+3)');quad(fx,1,5)(2)fx=inline('x./sin(x).^2');quad(fx,pi/4,pi/3)(3)fx=inline('abs(cos(x+y))');dblquad(fx,0,pi,0,pi)(4)syms x y ;fx=x*y;int(int(fx,y^2,y+2),-1,2)x 的积分区间为【0,2】时fx=inline('x.*y');dblquad(fx,0,2,-1,2)4.x=0.3:0.2:1.5;y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325]; trapz(x,y)5.(1)yp=inline('-(1.2+sin(10*x))*y');[t,y]=ode23(yp,[0,5],1);(2)令''3,,21y x y x y x ='==,则可写出原方程的状态方程形式:123233221sin 31)1(2cos 5cos x tx x t t t x x x x x +--++='='='⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'''t x x x t t t x x x cos 00)1(2cos 51sin 311000103212321 建立函数文件ztfun.mfunction y=ztfun(t,x)b=[0;0;cos(t)];y=[0,1,0;0,0,1;-1/(3+sin(t)),-1,5*cos(2*t)/(t+1)^2]*x+b; 解微分方程组[t,y]=ode23(@ztfun,[0,5],[1;0;2]);6.建立函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2)*y(3);-y(1)*y(3);-0.51*y(1)*y(2)];解微分方程组[t,y]=ode23(@ztfun,[0,5],[0;1;1])第7章一、思考题3.(1)数值积分fx=inline('exp(x).*(1+exp(x)).^2');quad(fx,0,log(2))符号积分f=sym('exp(x)*(1+exp(x))^2');v=int(f,0,log(2));eval(v)(2)略二、实验题1.A=sym('[1,2,3;x,y,z;3,2,1]')rank(A)inv(A)det(A)2.(1) y=sym('sqrt(x+sqrt(x+sqrt(x)))');y1=diff(y)y2=diff(y,'x',2)(2) syms x y;fxy=sin(x^2*y)*exp(-x^2-y);diff(diff(fxy,x),y)3.(1) syms xint(1/(1+x^4))(2) syms x tint((-2*x*x+1)/(2*x*x-3*x+1)^2,x,cos(t),exp(2*t)) 4.syms n xsymsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,inf)symsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,5)5.(1) syms xtaylor((exp(x)+exp(-x))/2,5,0)(2) syms a xtaylor(exp(-5*x)*sin(3*x+pi/3),5,a)6.(1)x=solve(sym('x^3+a*x+1=0'))(2) [x y]=solve(sym('sqrt(x^2+y^2)-100=0,3*x+5*y-8=0'))7. 方程转化为: π21'11't y y y y -=+=⎩⎨⎧符号解[y1,y11]=dsolve('Dy=y1,Dy1+y=1-t^2/pi','y(-2)=5,y1(-2)=5','t') 数值解编写函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2);1-t^2/pi-y(1)];在命令窗口输入以下命令[t,y]=ode45(@ztfun,[-2,7],[-5;5]);t=linspace(-2,7,49)y2=y8.[x,y]=dsolve('Dx=3*x+4*y,Dy=-4*x+3*y','x(0)=0,y(0)=1')。
matlab课后答案完整版

matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5(1)b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112(2)a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏,第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素,B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例:x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量(如y=2).底数也可以是标量(如x=2)5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、(1)y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1(1) x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505(2)x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6(3)x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456(4)t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81(2)subplot(1,2,1); >> scatter(x1,y1,10); >> title('y=2x-0.5'); >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图(分组) subplot(2,2,2);barh(t,'stack');%绘制柱形图(堆积) subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标,x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标,y 轴为常⽤对数刻度,x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、(1)theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); (2)x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、(1)t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468(2)t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、(1)、(2) p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、(1)z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串(空格也算)ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例:已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例:x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例:f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注:c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例:f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注:diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff (f3,x )表⽰z 对x 的偏导 diff (f3,y )表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ,b 之间的定积分eval (f1)计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。
MATLAB第一章作业答案

M A T L A B第一章作业答案(共5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章M A T L A B概况与基本操作1.选择题:(1)最初的MATLAB核心程序是采用A语言编写的。
(2)即将于2011年9月发布的MATLAB新版本的编号为D。
2011Ra 2011Rb R2011a R2011b(3)在默认设置中,MATLAB中的注释语句显示的颜色是D。
A.黑色B.蓝色C.红色D.绿色(4)如果要以科学计数法显示15位有效数字,使用的命令是B。
long long e long g long d(5)在命令窗口新建变量a、b,如果只查看变量a的详细信息,使用的命令为B。
a a(6)如果要清除工作空间的所有变量,使用的命令为 C 。
all C.两者都可 D.两者都不可(7)在创建变量时,如果不想立即在命令窗口中输出结果,可以在命令后加上D。
A.冒号B.逗号C.空格D.分号(8)如果要重新执行以前输入的命令,可以使用B键。
A.下箭头↓B.上箭头↑C.左箭头←D.右箭头→(9)如果要查询函数inv的相关信息,并显示在命令窗口,应使用命令A。
D.三者均可(10)如果要启动Notebook文档,下列D操作是可行的。
A.在命令窗口输入notebook命令B.在命令窗口输入notebook filename命令C.在Word中启动M-book文档D.三者均可2.填空题:(1)MATLAB是MATrix和LABoratory两个单词前三个字母的组合,意为“矩阵实验室”,它的创始人是Cleve Moler和Jack Little。
(2)在MATLAB的默认设置中,关键字显示的字体为蓝色,命令、表达式、计算结果显示的字体为黑色,字符串显示的字体为紫色,注释显示的字体为绿色,错误信息显示的字体为红色。
(3)在命令窗口中,输出结果显示为各行之间添加空行的命令为format compact,各行之间不添加空行的命令为format compact。
MATLAB课后题答案整理

第一章1.利用MATLAB 的帮助功能分别查询inv 、plot 、max 、round 等函数的功能及用法。
Help+函数2.简述MATLAB 的主要功能。
①数值计算和符号计算功能。
②绘图功能。
③编程语言功能。
④扩展功能。
3.help 命令和lookfor 命令有何区别?Help 命令只搜索出那些与关键字完全匹配的结果,lookfor 命令对搜索范围内的M 文件进行关键字搜索,条件比较宽松。
Lookfor 命令只对M 文件的第一行进行关键字搜索。
若在lookfor 命令后加上-all 选项,则可对M 文件进行全文搜索。
第二章1(1))1034245.01(26-⨯+⨯=ww=sqrt(2)*(1+0.34245*10^(-6)) w = 1.4142(2)ac b e abc c b a x ++-+++=)tan(22ππ,其中a=3.5,b=5,c=-9.8。
a=3.5;b=5;c=-9.8;x=(2*pi*a+(b+c)/(pi+a*b*c)-exp(2))/(tan(b+c)+a) x =0.9829(3)])48333.0()41[(22απβππα---=y ,其中α=3.32,β=-7.9。
a=3.32;b=-7.9;y=2*pi*a^2*((1-pi/4)*b-(0.8333-pi/4)*a) y = -128.4271(4))1ln(2122t t e z t ++=,其中t=]65.05312[--i 。
t=[2,1-3i;5,-0.65];z=0.5*exp(2*t)*log(t+sqrt(1+t.*t)) z = 1.0e+004 * 0.0048 + 0.0002i 0.0048 - 0.0034i1.58992.0090 - 1.3580i2.已知]023352138[],7613870451[--=--=B A 求下列表达式的值。
(1)B A 6+和I B A +-2。
matlab课后习题答案1到6章

欢迎共阅习题二1.如何理解“矩阵是MATLAB 最基本的数据对象”? 答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
(2) 删除矩阵A 的第7号元素。
答:A(7)=[](3) 将矩阵A 的每个元素值加30。
答:A=A+30;(4) 求矩阵A 的大小和维数。
答:size(A);ndims(A);(5) 将向量 t 的0元素用机器零来代替。
答:t(find(t==0))=eps; (6) 将含有12个元素的向量 x 转换成34⨯矩阵。
答:reshape(x,3,4); (7) 求一个字符串的ASCII码。
答:abs(‘123’); 或E 。
答:B=A(1:3,:); C=A(:,1:2); D=A(2:4,3:4);E=B*C;(2) 分别求E<D 、E&D 、E|D 、~E|~D 和find(A>=10&A<25)。
答:E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,11⎡⎤⎢⎥答:student(1).id='0001';student(1).name='Tom'; student(1).major='computer';student(1).grade=[89,78,67,90,86,85]; 8.建立单元矩阵B 并回答有关问题。
B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3); B{2,2}={12,34,2;54,21,3;4 ,23,67};(1)size(B)和ndims(B)的值分别是多少?答:size(B) 的值为2, 2。
ndims(B) 的值为2。
(2)B(2)和B(4)的值分别是(2)建立5×6随机矩阵A,其元素为[100,200]范围内的随机整数。
Matlab 第一章习题解答

4.>> help opsOperators and special characters.Arithmetic operators.plus - Plus +uplus - Unary plus +minus - Minus -uminus - Unary minus -mtimes - Matrix multiply *times - Array multiply .*mpower - Matrix power ^power - Array power .^mldivide - Backslash or left matrix divide \mrdivide - Slash or right matrix divide /ldivide - Left array divide .\rdivide - Right array divide ./kron - Kronecker tensor product kronRelational operators.eq - Equal ==ne - Not equal ~=lt - Less than <gt - Greater than >le - Less than or equal <=ge - Greater than or equal >=Logical operators.relop - Short-circuit logical AND &&relop - Short-circuit logical OR ||and - Element-wise logical AND &or - Element-wise logical OR |not - Logical NOT ~xor - Logical EXCLUSIVE ORany - True if any element of vector is nonzeroall - True if all elements of vector are nonzeroSpecial characters.colon - Colon :paren - Parentheses and subscripting ( ) paren - Brackets [ ]paren - Braces and subscripting { }punct - Function handle creation @punct - Decimal point .punct - Structure field access .punct - Parent directory ..punct - Continuation ...punct - Separator ,punct - Semicolon ;punct - Comment %punct - Invoke operating system command !punct - Assignment =punct - Quote 'transpose - Transpose .'ctranspose - Complex conjugate transpose 'horzcat - Horizontal concatenation [,]vertcat - Vertical concatenation [;]subsasgn - Subscripted assignment ( ),{ },.subsref - Subscripted reference ( ),{ },.subsindex - Subscript indexBitwise operators.bitand - Bit-wise AND.bitcmp - Complement bits.bitor - Bit-wise OR.bitmax - Maximum floating point integer.bitxor - Bit-wise XOR.bitset - Set bit.bitget - Get bit.bitshift - Bit-wise shift.Set operators.union - Set union.unique - Set unique.intersect - Set intersection.setdiff - Set difference.setxor - Set exclusive-or.ismember - True for set member.See also arith, relop, slash, function_handle.arithArithmetic operators.+ Plus.X + Y adds matrices X and Y. X and Y must have the samedimensions unless one is a scalar (a 1-by-1 matrix).A scalar can be added to anything.- Minus.X - Y subtracts matrix X from Y. X and Y must have the samedimensions unless one is a scalar. A scalar can be subtractedfrom anything.* Matrix multiplication.X*Y is the matrix product of X and Y. Any scalar (a 1-by-1 matrix) may multiply anything. Otherwise, the number of columns of X must equal the number of rows of Y..* Array multiplicationX.*Y denotes element-by-element multiplication. X and Ymust have the same dimensions unless one is a scalar.A scalar can be multiplied into anything.^ Matrix power.Z = X^y is X to the y power if y is a scalar and X is square. If y is aninteger greater than one, the power is computed by repeatedmultiplication. For other values of y the calculationinvolves eigenvalues and eigenvectors.Z = x^Y is x to the Y power, if Y is a square matrix and x is a scalar,computed using eigenvalues and eigenvectors.Z = X^Y, where both X and Y are matrices, is an error..^ Array power.Z = X.^Y denotes element-by-element powers. X and Ymust have the same dimensions unless one is a scalar.A scalar can operate into anything.RelopRelational operators.< > Relational operators.The six relational operators are <, <=, >, >=, ==, and ~=.A <B does element by element comparisons between A and Band returns a matrix of the same size with elements set to logical1 (TRUE) where the relation is true and elements set to logical 0(FALSE) where it is not. A and B must have the same dimensions(or one can be a scalar).& Element-wise Logical AND.A &B is a matrix whose elements are logical 1 (TRUE) where both A and B have non-zero elements, and logical 0 (FALSE) where either has a zero element. A and B must have the same dimensions (or one can be a scalar).&& Short-Circuit Logical AND.A &&B is a scalar value that is the logical AND of scalar A and B.This is a "short-circuit" operation in that MATLAB evaluates B onlyif the result is not fully determined by A. For example, if A equals0, then the entire expression evaluates to logical 0 (FALSE), regard-less of the value of B. Under these circumstances, there is no needto evaluate B because the result is already known.| Element-wise Logical OR.A |B is a matrix whose elements are logical 1 (TRUE) where eitherA orB has a non-zero element, and logical 0 (FALSE) where both have zero elements. A and B must have the same dimensions (or one canbe a scalar).|| Short-Circuit Logical OR.A ||B is a scalar value that is the logical OR of scalar A and B.This is a "short-circuit" operation in that MATLAB evaluates B onlyif the result is not fully determined by A. For example, if A equals1, then the entire expression evaluates to logical 1 (TRUE), regard-less of the value of B. Under these circumstances, there is no needto evaluate B because the result is already known.~ Logical complement (NOT).~A is a matrix whose elements are logical 1 (TRUE) where A has zero elements, and logical 0 (FALSE) where A has non-zero elements.xor Exclusive OR.xor(A,B) is logical 1 (TRUE) where either A or B, but not both, isnon-zero. See XOR.Relational operators.< > Relational operators.The six relational operators are <, <=, >, >=, ==, and ~=.A <B does element by element comparisons between A and Band returns a matrix of the same size with elements set to logical1 (TRUE) where the relation is true and elements set to logical 0(FALSE) where it is not. A and B must have the same dimensions(or one can be a scalar).& Element-wise Logical AND.A &B is a matrix whose elements are logical 1 (TRUE) where both A and B have non-zero elements, and logical 0 (FALSE) where either has a zero element. A and B must have the same dimensions (or one can be a scalar).&& Short-Circuit Logical AND.A &&B is a scalar value that is the logical AND of scalar A and B.This is a "short-circuit" operation in that MATLAB evaluates B onlyif the result is not fully determined by A. For example, if A equals0, then the entire expression evaluates to logical 0 (FALSE), regard-less of the value of B. Under these circumstances, there is no needto evaluate B because the result is already known.| Element-wise Logical OR.A |B is a matrix whose elements are logical 1 (TRUE) where eitherA orB has a non-zero element, and logical 0 (FALSE) where both have zero elements. A and B must have the same dimensions (or one canbe a scalar).|| Short-Circuit Logical OR.A ||B is a scalar value that is the logical OR of scalar A and B.This is a "short-circuit" operation in that MATLAB evaluates B onlyif the result is not fully determined by A. For example, if A equals1, then the entire expression evaluates to logical 1 (TRUE), regard-less of the value of B. Under these circumstances, there is no needto evaluate B because the result is already known.~ Logical complement (NOT).~A is a matrix whose elements are logical 1 (TRUE) where A has zeroelements, and logical 0 (FALSE) where A has non-zero elements.xor Exclusive OR.xor(A,B) is logical 1 (TRUE) where either A or B, but not both, isnon-zero. See XOR.SlashMatrix division.\ Backslash or left division.A\B is the matrix division of A into B, which is roughly thesame as INV(A)*B , except it is computed in a different way.If A is an N-by-N matrix and B is a column vector with Ncomponents, or a matrix with several such columns, thenX = A\B is the solution to the equation A*X = B computed byGaussian elimination. A warning message is printed if A isbadly scaled or nearly singular. A\EYE(SIZE(A)) produces theinverse of A.If A is an M-by-N matrix with M < or > N and B is a columnvector with M components, or a matrix with several such columns,then X = A\B is the solution in the least squares sense to theunder- or overdetermined system of equations A*X = B. Theeffective rank, K, of A is determined from the QR decompositionwith pivoting. A solution X is computed which has at most Knonzero components per column. If K < N this will usually notbe the same solution as PINV(A)*B. A\EYE(SIZE(A)) produces ageneralized inverse of A./ Slash or right division.B/A is the matrix division of A into B, which is roughly thesame as B*INV(A) , except it is computed in a different way.More precisely, B/A = (A'\B')'. See \../ Array right division.B./A denotes element-by-element division. A and Bmust have the same dimensions unless one is a scalar.A scalar can be divided with anything..\ Array left division.A.\B. denotes element-by-element division. A and Bmust have the same dimensions unless one is a scalar.A scalar can be divided with anything.function_FUNHANDLE = @FUNCTION_NAME returns a handle to the named function, FUNCTION_NAME. A function handle is a MATLAB value that provides a means of calling a function indirectly. You can pass functionhandles in calls to other functions (which are often called functionfunctions). You can also store function handles in data structures forlater use (for example, as Handle Graphics callbacks). A functionhandle is one of the standard MATLAB data types. Its class is'function_handle'.FUNHANDLE = @(ARGLIST)EXPRESSION constructs an anonymous function and returns a handle to that function. The body of the function, to theright of the parentheses, is a single MATLAB expression. ARGLIST is acomma-separated list of input arguments. Execute the function bycalling it by means of the returned function handle, FUNHANDLE. Formore information on anonymous functions, see "Types of Functions" inthe MATLAB Programming documentation.To call the function referred to by a function handle value, use ordinaryparenthesis notation. That is, specify the function handle variablefollowed by a comma-separated list of input arguments enclosed inparentheses. For example, HANDLE(ARG1, ARG2, ...). To call afunction_handle with no arguments, use empty parenthesis, e.g.,HANDLE().Example 2, below, shows how to make a call using a function handlethat has been passed as an argument.When you evaluate a function handle to a subfunction or privatefunction, that subfunction or private function is always executed whenthe function handle is called. When you evaluate a function handle toa built-in or ordinary function, an appropriate method may be selectedinstead of the built-in or ordinary function.With one exception, function handles can be manipulated and operated on inthe same manner as other MATLAB values, including assignment to variablesand inclusion in cells and structs. The exception is that you cannotconstruct a function_handle array. The reason is that the parenthesisnotation for values of this class is used to call a function, not toindex an array. To achieve the effect of an array of function handles,use cells, e.g., write "A = {@sin, @cos}" rather than "A = [@sin, @cos]".Of course, you need to index A with braces: "A{i}".Function handles enable you to:Pass a function reference to another function.Reduce the number of files that define your functions.Improve performance in repeated operations.Ensure reliability when evaluating functions.Note on Backward Compatibility:In R12 and R13, you could form arrays of function handles, and parenthesisnotation meant indexing into such an array. To call the function referredto by a function_handle value, you needed to use the FEVAL command. In R14,it is not necessary to use FEVAL (and this command will likely be deprecatedin a future release). Now, a function_handle variable, when followed by (...)'s,calls the associated function, and passes the arguments in parenthesis to it.This is faster than calling the function_handle using FEVAL.This change is not backward compatible, and R14 has a transitionstrategy that will leave almost all R12 & R13 programs working:o Constructing a non-scalar array of functions handles is only awarning, not an error.o Parenthesis notation on a non-scalar function handle meanssubscripting, just as in R13, while the same notation on scalarfunction handles means function call, as described above.Thus, incompatibility can arise only if you construct a scalar array offunction handles and actually index it, necessarily with an index of 1.Example 1 - Construct a handle, f, to the HUMPS function, and pass thishandle to FMINBND. (MATLAB maps a specific implementation of the HUMPS function to the handle f at the time the handle is created, and not atthe time f is called.)f = @humps;x = fminbnd(f,1,2);Example 2 - Call a function by means of the function handle, h, thatwas passed as an argument.function trigPlot(h, val)if isa(h, 'function_handle') % Verify that h is a function handle.A = h(val); % Call the function mapped to handle h.plot(A) % Plot the resulting data.endCall the function, passing the handle generated by @cos:trigPlot(@cos, -pi:0.01:pi)See also func2str, str2func, functions.Reference page in Help browserdoc function_handlehandleReference page in Help browserdoc function_handleFUNHANDLE = @FUNCTION_NAME returns a handle to the named function,FUNCTION_NAME. A function handle is a MATLAB value that provides ameans of calling a function indirectly. You can pass functionhandles in calls to other functions (which are often called functionfunctions). You can also store function handles in data structures forlater use (for example, as Handle Graphics callbacks). A functionhandle is one of the standard MATLAB data types. Its class is'function_handle'.FUNHANDLE = @(ARGLIST)EXPRESSION constructs an anonymous function and returns a handle to that function. The body of the function, to theright of the parentheses, is a single MATLAB expression. ARGLIST is acomma-separated list of input arguments. Execute the function bycalling it by means of the returned function handle, FUNHANDLE. Formore information on anonymous functions, see "Types of Functions" inthe MATLAB Programming documentation.To call the function referred to by a function handle value, use ordinaryparenthesis notation. That is, specify the function handle variablefollowed by a comma-separated list of input arguments enclosed inparentheses. For example, HANDLE(ARG1, ARG2, ...). To call afunction_handle with no arguments, use empty parenthesis, e.g.,HANDLE().Example 2, below, shows how to make a call using a function handlethat has been passed as an argument.When you evaluate a function handle to a subfunction or privatefunction, that subfunction or private function is always executed whenthe function handle is called. When you evaluate a function handle toa built-in or ordinary function, an appropriate method may be selectedinstead of the built-in or ordinary function.With one exception, function handles can be manipulated and operated on inthe same manner as other MATLAB values, including assignment to variablesand inclusion in cells and structs. The exception is that you cannotconstruct a function_handle array. The reason is that the parenthesisnotation for values of this class is used to call a function, not toindex an array. To achieve the effect of an array of function handles,use cells, e.g., write "A = {@sin, @cos}" rather than "A = [@sin, @cos]".Of course, you need to index A with braces: "A{i}".Function handles enable you to:Pass a function reference to another function.Reduce the number of files that define your functions.Improve performance in repeated operations.Ensure reliability when evaluating functions.Note on Backward Compatibility:In R12 and R13, you could form arrays of function handles, and parenthesisnotation meant indexing into such an array. To call the function referredto by a function_handle value, you needed to use the FEVAL command. In R14, it is not necessary to use FEVAL (and this command will likely be deprecatedin a future release). Now, a function_handle variable, when followed by (...)'s,calls the associated function, and passes the arguments in parenthesis to it.This is faster than calling the function_handle using FEVAL.This change is not backward compatible, and R14 has a transitionstrategy that will leave almost all R12 & R13 programs working:o Constructing a non-scalar array of functions handles is only awarning, not an error.o Parenthesis notation on a non-scalar function handle meanssubscripting, just as in R13, while the same notation on scalarfunction handles means function call, as described above.Thus, incompatibility can arise only if you construct a scalar array offunction handles and actually index it, necessarily with an index of 1.Example 1 - Construct a handle, f, to the HUMPS function, and pass thishandle to FMINBND. (MATLAB maps a specific implementation of the HUMPS function to the handle f at the time the handle is created, and not atthe time f is called.)f = @humps;x = fminbnd(f,1,2);Example 2 - Call a function by means of the function handle, h, thatwas passed as an argument.function trigPlot(h, val)if isa(h, 'function_handle') % Verify that h is a function handle.A = h(val); % Call the function mapped to handle h.plot(A) % Plot the resulting data.endCall the function, passing the handle generated by @cos:trigPlot(@cos, -pi:0.01:pi)See also func2str, str2func, functions.Reference page in Help browserdoc function_handle>> a=exp(1)a =2.7183>>>> A=piA =3.1416eπe=2.718282>> 2.718282^pians =23.1407>> 2.718282.^pians =23.1407πe>> pi^2.718282ans =22.4592或者 :>> pi.^2.718282ans =22.4592>>c=2.718282.^pi ; d=pi^2.718282 >>c<dans=>>c>dans=1>> rand(3,3)ans =0.8147 0.9134 0.2785 0.9058 0.6324 0.5469 0.1270 0.0975 0.9575>> A=rand(3,3)A =0.9649 0.9572 0.1419 0.1576 0.4854 0.4218 0.9706 0.8003 0.9157 >> A=rand(3,3);>> B=inv(A)B =-0.4740 3.7530 -3.3939 -1.3356 0.8875 0.3148 2.0968 -4.4272 3.9447 >> C=B*AC =1.0000 0.0000 0 -0.0000 1.0000 0.0000 0 -0.0000 1.0000 >> A=rand(3,3)A =0.3922 0.7060 0.0462 0.6555 0.0318 0.0971 0.1712 0.2769 0.8235 >> B=inv(A)B =0.0019 1.5730 -0.18561.4471 -0.8716 0.0217-0.4871 -0.0339 1.2457>> C=B*AC =1.0000 0 0.00000.0000 1.0000 00 -0.0000 1.0000>> D=B.*AD =0.0007 1.1106 -0.00860.9486 -0.0277 0.0021-0.0834 -0.0094 1.0258>> E=sqrt(C)>> F=abs(E)Short 3位整数4位小数的定点数>> format short>> A=rand(3,3)A =0.6948 0.0344 0.76550.3171 0.4387 0.79520.9502 0.3816 0.1869long 2位整数14位小数的定点数>> format long>> A=rand(3,3)A =0.489764395788231 0.709364830858073 0.679702676853675 0.445586********* 0.754686681982361 0.655098003973841 0.646313********* 0.276025076998578 0.162611735194631 short e 5个数字的浮点数,其中1位整数4位小数>> format short e>> A=rand(3,3)A =1.1900e-001 3.4039e-001 7.5127e-0014.9836e-0015.8527e-001 2.5510e-0019.5974e-001 2.2381e-001 5.0596e-001long e 16个数字的浮点数,其中1位整数15位小数short g 显示5个数字,自动选择定点数和浮点数>> format short g>> A=rand(3,3)A =0.69908 0.54722 0.257510.8909 0.13862 0.840720.95929 0.14929 0.25428long g显示15个数字,自动选择定点数和浮点数>> format long g>> A=rand(3,3)A =0.814284826068816 0.349983765984809 0.6160446761466390.243524968724989 0.196595250431208 0.4732888489027290.929263623187228 0.251083857976031 0.351659507062997 7.>> x=1:1:100;>> s=solve('x^2+sin(x)+ln(x)')s =-1.3901004146053480595845249400739-.98288867543926874105777377916614*i >>8.>> A=1;>> omega=4*pi;>> t=0:0.01:1;>> phi=0.1*pi;>> x=A*sin(omega*t+phi);>> plot(t,x)>> A=2;>> omega=[2*pi; 4*pi]; >> t=0:0.01:1;>> phi=0.1*pi;>> x=A*sin(omega*t+phi); >> plot(t,x)>> A=2;>> omega=[2*pi; 4*pi]; >> t=0:0.01:1;>> c=omega*t;>> phi=0.1*pi;>> x=A*sin(c+phi);>> plot(t,x(1,:),t,x(2,:))>> A=2;>> omega=[2*pi; 4*pi]; >> t=0:0.01:1;>> c=omega*t;>> phi=0.1*pi;>> x=A*sin(c+phi);>> plot(t,x(1,:),'r',t,x(2,:),'b')8、t=[0:0.1:2*pi];A1=5;A2=3;w1=2;w2=4;x1=A1*sin(w1*t+pi/3);x2=A2*sin(w2*t+pi/4);plot(t,x1,'-r',t,x2,'-b');01234567-5-4-3-2-1123459.1)>> 3+5i/(1+i)ans =5.5000 + 2.5000i2)>> sin(4+5*i)ans =-56.1623 -48.5025i3)>> 2.718282^(3+2*i)ans =-8.3585 +18.2637i4)>> 10^(3+2*i)ans =-1.0701e+002 -9.9426e+002i5)shx=(e x-e-x)/2chx=(e x+e-x)/2th= shx / chx>> (2.718282^(3+2*i)-2.718282^(-(3+2*i)))/2 ans =-4.1689 + 9.1545i10.>> A=[]A =[]>>>> B=zeros(3,3)B =0 0 00 0 00 0 0>> C=cell(3)C =[] [] [][] [] [][] [] []>>11.>> tril(ones(3,3),0) ans =1 0 01 1 01 1 1>> triu(ones(3,3),0) ans =1 1 10 1 10 0 1>> magic(3)ans =8 1 63 5 74 9 2>> tril(magic(3)) ans =8 0 03 5 04 9 2>> triu(magic(3)) ans =8 1 60 5 70 0 2or>> A=magic(3)A =8 1 63 5 74 9 2>> B=tril(A)B =8 0 03 5 04 9 2>> C=triu(A)C =8 1 60 5 70 0 2or>> A=magic(3)A =8 1 63 5 74 9 2>> B=tril(magic(3))B =8 0 03 5 04 9 2>> C=triu(magic(3))C =8 1 60 5 70 0 2 Exercise:1.>> A=magic(3)A =8 1 63 5 74 9 2 >> a=tril(A)a =8 0 03 5 04 9 2 >> b=triu(A)b =8 1 60 5 70 0 2b =8 1 60 5 70 0 2 2.>> c=sum(A)c =15 15 15 >> d=sum(A')d =15 15 15 >> sum(diag(A)) ans =15>> sum(diag(A')) ans =153.>> A=magic(3)A =8 1 63 5 74 9 2>> f=diag(A)f =852>> g=(A')g =8 3 4 1 5 9 6 7 24.>> h=fliplr(A)h =6 1 87 5 3 2 9 4>> i=flipud(A)i =4 9 2 35 7 8 1 6>> j=rot90(A)j =6 7 2 1 5 9 8 3 4 5.>> k=sort(A,1)k =3 1 24 5 68 9 7>> l=sort(A,2)l =1 6 83 5 72 4 96. ?a,b 对矩阵c,d,e dui 元素f,g 对矩阵h,i,j 对矩阵k 对矩阵12.>> A=[2 8 10; 11 3 7; 6 9 4]; >> B=[12 9 4; 5 2 21; 8 4 6]; >> C=A*BC =144 74 236203 133 149149 88 237>> A\Cans =12.0000 9.0000 4.0000 5.0000 2.0000 21.0000 8.0000 4.0000 6.0000>> C/Bans =2.0000 8.0000 10.0000 11.00003.0000 7.0000 6.0000 9.00004.0000>>>> D=A.*BD =24 72 4055 6 14748 36 2413.>> A=diag(1:4)A =1 0 0 00 2 0 00 0 3 00 0 0 4>> D=diag(1:5)D =1 0 0 0 0 02 0 0 0 0 03 0 0 0 0 04 0 0 0 0 0 5>> A=diag(1:3)A =1 0 00 2 00 0 3>> V=[1 2 3]V =1 2 3>> diag(V,1)ans =0 1 0 00 0 2 00 0 0 30 0 0 0>> diag(V,-1)ans =0 0 0 01 0 0 00 2 0 00 0 3 0>> diag(V,2)ans =0 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 13.>> A=diag(1:4)A =1 0 0 00 2 0 00 0 3 00 0 0 4>> D=diag(1:5)D =1 0 0 0 0 02 0 0 0 0 03 0 0 0 0 04 0 0 0 0 0 5>> A=diag(1:3)A =1 0 00 2 00 0 3>> V=[1 2 3]V =1 2 3>> diag(V,1)ans =0 1 0 00 0 2 00 0 0 30 0 0 0>> diag(V,-1)ans =0 0 0 01 0 0 00 2 0 00 0 3 0>> diag(V,2)ans =0 0 1 0 00 0 0 2 00 0 0 0 30 0 0 0 00 0 0 0 015.>> x1=[-1 0 1 -1];>> y1=[0 1 0 0];>> x2=[-1 0 1 -1];>> y2=[0 i 0 0];>> plot(x1,y1,'r:+',x2,imag(y2),'g:o')plot(x1,y1,'r:+','LineWidth',2, x2,imag(y2),'g:o','LineWidth',5)>> x1=[-1 0 1 -1];>> y1=[0 1 0 0];>> plot(x1,y1,'r:+','LineWidth',3)>> x2=[-1 0 1 -1];>> y2=[0 i 0 0];>> plot(x2,imag(y2),'g:O','LineWidth',5)>> x1=[-1 0 1 -1];>> y1=[0 1 0 0];>> x2=[-1 0 1 -1];>> y2=[0 i 0 0];plot(x1,y1,'r:+', x2,imag(y2),'g:O')1616.>> t=-10*pi:pi/250:10*pi;>> comet3(8*cos(t),4*sqrt(2)*sin(t),-4*sqrt(2)*sin(t))17>> fplot('cos(tan(pi*x))',[0 2*pi])fplot('cos(tan(pi*x))',[0 2*pi],'+-')>> fplot('cos(tan(pi*x))',[0 2*pi],'o')18>> ezplot('exp(y)+cos(x)/x+y=0',[-3,3])ezplot('exp(y)+cos(x)/x+y=0',[-4,4])>> ezplot('exp(y)+cos(x)/x+y=0')19 >> s=[0:8];t=[0:5*pi];>> [s,t]=meshgrid(s,t);>> x=exp(-s).*cos(t);>> y=exp(-s).*sin(t);>> z=t;>> surf(x,y,z)>> s=[0:1:8];t=[0:pi/60:5*pi];>> [s,t]=meshgrid(s,t);>> x=exp(-s).*cos(t);>> y=exp(-s).*sin(t);>> z=t;>> surf(x,y,z)20subplot(1,2,1);[X0,Y0,Z0]=sphere(20);X=2*X0;Y=3*Y0;Z=4*Z0+1;surf(X,Y,Z);axis equalsubplot(1,2,2)t=-1:0.1:1;[X,Y,Z]=cylinder(1+t.^2,20);%形成旋转曲面 surf(X,Y,Z);-2024-2220>> subplot(1,1,1);>> ellipsoid(0,0,1,2,3,4)>> [x,y,z]=ellipsoid(0,0,1,2,3,4); >> surf(x,y,z);>> [x,y,z]=ellipsoid(0,0,1,2,3,4); >> surf(x,y,z);>> colormap copper>> [x,y,z]=ellipsoid(0,0,1,2,3,4); >> surf(x,y,z);>> colormap copper>> t=[-1:0.1:1];>> [X,Y,Z]=cylinder(1+t.^2);>> [X,Y,Z]=ellipsoid(0,0,1,2,3,4); >> surf(X,Y,Z)21x=-5:0.1:5;y=0:0.1:10;[X,Y]=meshgrid(x,y); z=X.^2.*Y + sqrt(Y)./X; mesh(X,Y,z);>> ezmesh('x^2*y+sqrt(y)/x',[-5,5,0,10])>> ezsurf('x^2*y+sqrt(y)/x',[-5,5,0,10])。
matlab第一章习题集合及答案

MATLAB 多多练 赋值语句 例1-3:在命令窗口键入:1+2*3+6/2键入a=2;b=3;c=4;totle=a*b+c 例:当π+=1x 时,计算表达式 的值,并将结果赋给变量y ,然后显示出结果。
在MATLAB 命令窗口分别输入命令:x=sqrt(1+pi); y=(exp(x)+log(abs(sin(x)^2-sin(x*x))))/(x-5*i) %计算表达式的值变量的管理 例1-4:who;%显示目前工作空间的变量名whos %显示变量名,变量大小,数据类型等save myfilename %MATLAB 将产生一个名为myfilename.mat 的文件,文件中保存了当前工作空间的所有变量save mydata a b %MATLAB 将产生一个名为mydata.mat 的文件,文件中保存了当前工作空间的变量 a 和 b.clear %把当前工作空间清空22e ln sin sin 5x x x x i+--who %结果没有任何变量显示load myfilename %把文件myfilename.mat中的变量装入当前工作空间load mydata % 把mydata.mat中的内容装入MATLAB工作空间:数据的输出格式例1-5:x=215/6;format long; %16位十进制xformat short e; %五位十进制数加指数xformat long e; %16位十进制数加指数xformat hex %16位十六进制数xformat bank %两位小数xformat + %正、负或零xformat rat %分数近似xformat short %4位小数,默认格式xformat compact %紧凑格式xformat loose %默认格式x矩阵的生成例1-6:直接输入法:[1 2 3][1;2;3]x=[-1.3 sqrt(3) (1+2+3)/5*4]在命令窗口键入:A=[1 0 3 -1;2 1 0 2]键入:B=[4 1 0;-1 1 3;2 0 1;1 3 4]C=3+4i %输入复数D=[1+2i 3+4i;5+6i 7+8i]%输入复数[1 3;5 7]+[2 4;6 8]*i%输入复数*号不可少利用M文件建立矩阵例1-7(1)启动MATLAB的M-file编辑器,并输入待建矩阵mydata=[1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9;2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9;3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9];(2)把输入的内容保存(设文件名为matfund.m)。
MATLAB语言基础与应用(第二版)第1章 习题答案

第1章习题与答案1.1 MA TLAB桌面主要有哪些窗口构成?这些窗口主要功能是什么?请参考1.3节1.2计算下列表达式(1) 3+6 (2) sin(1+i)(3) (1+2i)×(2-i) (4) 2×4+3解答:(1) >> 3+6ans = 9(2) >> sin(1+i)ans = 1.2985 + 0.6350i(3) >> (1+2*i)*(2-i)ans = 4.0000 + 3.0000i(4) >> 2*4+3ans = 111.3借助“help”函数了解“meshgrid”函数的意义。
解答:>> help meshgridmeshgrid Cartesian grid in 2-D/3-D space[X,Y] = meshgrid(xgv,ygv) replicates the grid vectors xgv and ygv toproduce the coordinates of a rectangular grid (X, Y). The grid vectorxgv is replicated numel(ygv) times to form the columns of X. The gridvector ygv is replicated numel(xgv) times to form the rows of Y.[X,Y,Z] = meshgrid(xgv,ygv,zgv) replicates the grid vectors xgv, ygv, zgvto produce the coordinates of a 3D rectangular grid (X, Y, Z). The gridvectors xgv,ygv,zgv form the columns of X, rows of Y, and pages of Zrespectively. (X,Y,Z) are of size numel(ygv)-by-numel(xgv)-by(numel(zgv).[X,Y] = meshgrid(gv) is equivalent to [X,Y] = meshgrid(gv,gv).[X,Y,Z] = meshgrid(gv) is equivalent to [X,Y,Z] = meshgrid(gv,gv,gv).The coordinate arrays are typically used for the evaluation of functionsof two or three variables and for surface and volumetric plots.meshgrid and NDGRID are similar, though meshgrid is restricted to 2-Dand 3-D while NDGRID supports 1-D to N-D. In 2-D and 3-D the coordinates output by each function are the same, the difference is the shape of theoutput arrays. For grid vectors xgv, ygv and zgv of length M, N and Prespectively, NDGRID(xgv, ygv) will output arrays of size M-by-N whilemeshgrid(xgv, ygv) outputs arrays of size N-by-M. Similarly,NDGRID(xgv, ygv, zgv) will output arrays of size M-by-N-by-P whilemeshgrid(xgv, ygv, zgv) outputs arrays of size N-by-M-by-P.Example: Evaluate the function x*exp(-x^2-y^2)over the range -2 < x < 2, -4 < y < 4,[X,Y] = meshgrid(-2:.2:2, -4:.4:4);Z = X .* exp(-X.^2 - Y.^2);surf(X,Y,Z)Class support for inputs xgv,ygv,zgv:float: double, singleinteger: uint8, int8, uint16, int16, uint32, int32, uint64, int64 See also surf, slice, ndgrid.Overloaded methods:codistributed/meshgridgpuArray/meshgridReference page in Help browserdoc meshgrid1.4通过帮助浏览器窗口了解函数sin和cos。
matlab课后练习习题及答案详解

matlab课后习题及答案详解第1章MATLAB概论与其余计算机语言对比较,MATLAB语言突出的特色是什么?MATLAB拥有功能强盛、使用方便、输入简捷、库函数丰富、开放性强等特色。
MATLAB系统由那些部分构成?MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
安装MATLAB时,在选择组件窗口中哪些部分一定勾选,没有勾选的部分此后怎样补安装?在安装MATLAB时,安装内容由选择组件窗口中个复选框能否被勾选来决定,能够依据自己的需要选择安装内容,但基本平台(即MATLAB选项)一定安装。
第一次安装没有选择的内容在补安装时只要依据安装的过程进行,不过在选择组件时只勾选要补装的组件或工具箱即可。
MATLAB操作桌面有几个窗口?怎样使某个窗口离开桌面成为独立窗口?又怎样将离开出去的窗口从头搁置到桌面上?在MATLAB操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是封闭窗口的Close按钮,一个是能够使窗口成为独立窗口的Undock 按钮,点击Undock按钮就能够使该窗口离开桌面成为独立窗口,在独立窗口的view菜单中选择Dock,,菜单项就能够将独立的窗口从头防备的桌面上。
怎样启动M文件编写/调试器?在操作桌面上选择“成立新文件”或“翻开文件”操作时,M文件编写/调试器将被启动。
在命令窗口中键入edit命令时也能够启动M文件编写/调试器。
储存在工作空间中的数组能编写吗?怎样操作?储存在工作空间的数组能够经过数组编写器进行编写:在工作空间阅读器中双击要编写的数组名翻开数组编写器,再选中要改正的数据单元,输入改正内容即可。
命令历史窗口除了能够察看前方键入的命令外,还有什么用途?命令历史窗口除了用于查问从前键入的命令外,还能够直接履行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
怎样设置目前目录和搜寻路径,在目前目录上的文件和在搜寻路径上的文件有什么差别?目前目录能够在目前目录阅读器窗口左上方的输入栏中设置,搜寻路径能够经过选择操作桌面的file菜单中的SetPath菜单项来达成。
MATLAB习题答案(清华大学)

高等应用数学问题MATLAB 求解习题参考解答(薛定宇著)目录第1 章计算机数学语言概述2第2 章MATLAB 语言程序设计基础5第3 章微积分问题的计算机求解17第4 章线性代数问题的计算机求解29第5 章积分变换与复变函数问题的计算机求解43第6 章代数方程与最优化问题的计算机求解53第7 章微分方程问题的计算机求解71第8 章数据插值、函数逼近问题的计算机求解93第9 章概率论与数理统计问题的计算机求解114第10 章数学问题的非传统解法127第A章自由数学语言Scilab 简介136第1 章计算机数学语言概述1 在你的机器上安装MATLAB 语言环境,并键入demo 命令,由给出的菜单系统和对话框原型演示程序,领略MATLAB 语言在求解数学问题方面的能力与方法。
【求解】在MATLAB 提示符>> 下键入demo 命令,则将打开如图1-1 所示的窗口,窗口左侧的列表框可以选择各种不同组合的演示内容。
图1-1 MATLAB 演示程序界面例如,用户选择MATLAB ! Graphics ! Volume Vlsulization 演示,则将得出如图1-2 所示的演示说明,单击其中的Run this demo 栏目,则将得出如图1-3 所示的演示界面。
用户可以在该界面下按按钮,逐步演示相关内容,而实现这样演示的语句将在该程序界面的下部窗口中给出。
2 作者用MATLAB 语言编写了给出例子的源程序,读者可以自己用type 语句阅读一下源程序,对照数学问题初步理解语句的含义,编写的源程序说明由下表列出。
第1 章计算机数学语言概述3图1-2 MATLAB 演示程序界面举例序号文件名程序说明例1.1 c1ex1.m 利用MATLAB 的符号运算工具箱求解微分问题例1.2 c1ex2.m 分别利用MATLAB 的符号运算工具箱和数值运算功能求解多项式方程,其中用数值方法得出的结果有误差例1.3 c1ex3.m 分别利用MATLAB 的符号运算工具箱和数值运算功能计算Hilbert 矩阵的行列式,其中用数值方法得出的结果有很大误差例1.4 c1ex4.m 令x1 = y; x2 = y_,则可以将原来的二阶微分方程转换成一阶微分方程组,然后就可以求解微分方程的数值解了,原方程是非线性微分方程,故不存在解析解。
MATLAB习题参考答案(胡良剑

第一章 MATLAB 入门4、求近似解解:>> x=-2:0.05:2;y=x.^4-2.^x两个近似解:y1=f(-0.85)= -0.0328; y2=f(1.250)= 0.0630第二章 MATLAB 编程与作图1、 设x 是数组,求均值和方差解:函数文件如下:function [xx,s]=func1(x)n=length(x);xx=sum(x)/n;s=sqrt((sum(x.^2)-n*xx^2)/(n-1));命令窗口:>> x=[1 2 3 4 5];[xx,s]=func1(x)2、求满足的最小m 值 100)1ln(0>+∑=m n n s=0;n=0;while(s<=100)s=s+log(1+n);n=n+1;endn,s3、用循环语句形成Fibonacci 数列,....4,3,,12121=+===−−k F F F F F k k k 。
并验证极限2511+→−k k F F (提示:计算至两边误差小于精度1e-8为止) 解: 求Fibonacci 数列的函数文件:function f=fun(n)if n<=2f=1;elsef=fun(n-1)+fun(n-2);end验证极限的函数文件:function [k,a]=funTest(e)a=abs(1-(1+sqrt(5))/2);k=2;while(a>e)k=k+1;a=abs(fun(k)/fun(k-1)-(1+sqrt(5))/2);end命令行:>> [k,a]=funTest(10^-8)k =21a =9.7719e-009或者M 文件如下:clear; F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1; F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k4、分别用for 和while 循环结构编写程序,求出∑==610123i i K ,并考虑一种避免循环语句的程序设计,比较各种算法的运行时间。
