平行线辅助线练习题

合集下载

中考数学专题复习全等三角形之辅助线做平行线

中考数学专题复习全等三角形（辅助线做平行线）学校:___________姓名：___________班级：___________考号：___________评卷人得分一、单选题1．如图，△ABC是边长为4的等边三角形，点P在AB上，过点P作PE⊥AC，垂足为E，延长BC至点Q，使CQ＝P A，连接PQ交AC于点D，则DE的长为（）A．1B．1.8C．2D．2.52．如图，⊥ABC是边长为2的等边三角形，点P在AB上，过点P作PE⊥AC，垂足为E，延长BC到点Q，使CQ＝P A，连接PQ交AC于点D，则DE的长为（）A．0.5B．0.9C．1D．1.25评卷人得分二、填空题3．如图，四边形ABCD中，AC与BD相交于点O，且AC⊥BD，AC＝BD＝CD，点P 是⊥OCD角平分线的交点，点M是AB的中点，给出下列结论：⊥⊥CPD＝135°；⊥BA＝BP；⊥⊥P AC⊥⊥PDB；⊥S△ABP＝S△DCP；⊥PM＝12CD．其中正确的是___．（填序号）评卷人得分三、解答题4．如图，⊥ABC中，点D，E在边AB上，点F在边BC上，且AD＝AC，EF＝EC，⊥CEF＝⊥A，连接DF．（1）在图1中找出与⊥ACE相等的角，并证明；（2）求证：⊥BDF＝⊥EFC；（3）如图2，延长FD，CA交于点G，连接EG，若EG＝AG，DE＝kAE，求DG DF的值（用含k的代数式表示）．5．如图所示：ABC是等边三角形，D、E分别是AB及AC延长线上的一点，且BD CE=，连接DE交BC于点M．求让：MD ME=6．P为等边△ABC的边AB上一点，Q为BC延长线上一点，且P A＝CQ，连PQ交AC边于D．（1）证明：PD＝DQ．（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．7．P为等边⊥ABC的边AB上一点，Q为BC延长线上一点，且P A＝CQ，连PQ交AC 边于D．（1）证明：PD＝DQ．（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．8．如图，点P为等边⊥ABC的边AB上一点，Q为BC延长线上一点，AP=CQ，PQ交AC于D，(1)求证：DP=DQ；(2)过P作PE⊥AC于E，若BC=4，求DE的长．9．已知在等腰△ABC中，AB=AC，在射线CA上截取线段CE，在射线AB上截取线段BD，连接DE，DE所在直线交直线BC与点M．请探究：(1)如图（1），当点E在线段AC上，点D在AB延长线上时，若BD=CE，请判断线段MD和线段ME的数量关系，并证明你的结论．(2)如图（2），当点E在CA的延长线上，点D在AB的延长线上时，若BD=CE，则（1）中的结论还成立吗？如果成立，请证明；如果不成立，说明理由；(3)如图（3），当点E在CA的延长线上，点D在线段AB上（点D不与A，B重合），DE所在直线与直线BC交于点M，若CE＝2BD，请直接写出线段MD与线段ME的数量关系．10．读下面的题目及分析过程,并按要求进行证明．已知:如图,E是BC的中点,点A在DB上,且⊥BAE=⊥CDE,求证:AB=CD分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等．因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明．图(1):延长DE到F使得EF=DE图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F图(3):过C点作CF⊥AB交DE的延长线于F.参考答案：1．C【解析】【分析】过P作BC的平行线交AC于F，通过AAS证明PFD⊥QCD，得FD CD=，再由APF 是等边三角形，即可得出12DE AC=．【详解】解：过P作BC的平行线交AC于F，Q FPD∴∠=∠，ABC是等边三角形，60APF B∴∠=∠=︒，60AFP ACB∠=∠=︒，APF∴△是等边三角形，AP PF∴=，⊥CQ＝P A，⊥PF CQ=在PFD中和QCD中，FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD∴⊥()QCD AAS，FD CD∴=，PE AC⊥于E，APF是等边三角形，AE EF∴=，=AE DC EF FD ED∴+=+，12DE AC∴=，4AC=，2DE∴=，故选：C．【点睛】本题主要考查了等边三角形的判定与性质，全等三角形的判定与性质，作辅助线构造全等三角形是解题的关键．2．C【解析】【分析】过P作BC的平行线交AC于F，通过AAS证明PFD≌QCD，得FD CD=，再由APF 是等边三角形，即可得出12DE AC=．【详解】解：过P作BC的平行线交AC于F，Q FPD∴∠=∠，ABC是等边三角形，60APF B∴∠=∠=︒，60AFP ACB∠=∠=︒，APF∴是等边三角形，AP PF∴=，在PFD中和QCD中，FPD QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，PFD∴≌()QCD AAS，FD CD∴=，PE AC⊥于E，APF是等边三角形，AE EF ∴=，AE DC EF FD ∴+=+，12DE AC ∴=， 2AC =， 1DE ∴=，故选：C ．【点睛】本题主要考查了等边三角形的判定与性质，全等三角形的判定与性质，作辅助线构造全等三角形是解题的关键． 3．⊥⊥⊥⊥ 【解析】【分析】由角平分线的定义，可得⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°，进而即可判断⊥；先证ACP DCP ≌，可得APD △是等腰直角三角形，进而得PAC PDB ≌，即可判断⊥；过点A 作AN ⊥BP 交PM 的延长线于点N ，可得AMN BMP ≌，再证明APN PDC ≌，从而得PM ＝12CD ，即可判断⊥；由ABP APM BMP APM AMN APN S S S S S S +=+==，即可判断⊥．【详解】解：⊥AC ⊥BD ，点P 是⊥OCD 角平分线的交点，⊥⊥DOC =90°，⊥ODC +⊥OCD =90°，⊥CDP =12⊥CDO ，⊥DCP =12⊥DCO ， ⊥⊥CDP +⊥DCP =12⊥CDO +12⊥DCO =45°，⊥⊥CPD ＝180°-（⊥CDP +⊥DCP ）=135°，故⊥正确； ⊥CP ，DP 分别平分⊥DCO ，⊥CDO ， ⊥⊥DCP =⊥ACP ，⊥CDP =⊥BDP ， ⊥AC ＝CD ，PC =PC ， ⊥ACP DCP ≌，⊥AP =DP ，⊥CAP =⊥CDP =⊥BDP ，⊥APC =⊥DPC =135°， ⊥⊥DP A =360°-135°-135°=90°，⊥APD △是等腰直角三角形，又⊥AC =BD ，⊥CAP =⊥BDP，AP =DP ， ⊥PAC PDB ≌，故⊥正确； ⊥⊥DPB =⊥APC=135°，PB =PC ， ⊥⊥BPC =360°-135°-135°=90°，⊥BPC △是等腰直角三角形，找不到证明BA =BP 的条件，故⊥错误；过点A 作AN ⊥BP 交PM 的延长线于点N ，⊥⊥N =⊥BPM ，⊥P AN +⊥APB =180°， ⊥点M 是AB 的中点，即AM =BM ，又⊥⊥AMN =⊥BMP ， ⊥AMN BMP ≌，⊥MN =PM =12PN ，AN =PB =PC ，AMNBMPSS=，⊥⊥DP A =⊥BPC =90°， ⊥⊥APB +⊥DPC =180°，又⊥⊥P AN +⊥APB =180°， ⊥⊥P AN =⊥DPC ，又⊥AP =DP ，AN =PC ， ⊥APN PDC ≌，⊥CD =PN =2PM ，即：PM ＝12CD ，故⊥正确； ⊥APNPDCSS=，AMNBMPSS=，⊥ABPAPMBMPAPMAMNAPNS SSSSS+=+==，⊥ABPDCPSS=，故⊥正确．故正确的是⊥⊥⊥⊥．【点睛】本题主要考查全等三角形的判定和性质，平行线的性质，等腰直角三角形的判定和性质，熟练掌握中线倍长模型和旋转全等模型，是解题的关键． 4．（1）⊥DEF ＝⊥ACE ，证明见解析；（2）见解析；（3）k 【解析】【分析】（1）由三角形外角的性质可得出答案；（2）连接CD ，过点E 作AC 的平行线与CD 交于点M ，证明⊥DEF ⊥⊥MEC （SAS ），由全等三角形的性质可得出⊥EDF ＝⊥EMC ，证出⊥EMD ＝⊥EFC ，则可得出结论；（3）连接CD ，过点E 作AC 的平行线与CD 交于点M ，证明⊥EFG ⊥⊥ECD （ASA ），由全等三角形的性质可得出GF ＝DC ，证出GD ＝DM ，则根据平行线分线段成比例即可得出答案．【详解】解：（1）⊥DEF ＝⊥ACE ．证明：⊥⊥DEC 是⊥ACE 的外角， ⊥⊥DEC ＝⊥A +⊥ACE ， ⊥⊥DEC ＝⊥DEF +⊥CEF ， ⊥⊥DEC +⊥CEF ＝⊥A +⊥ACE ， ⊥⊥CEF ＝⊥A ， ⊥⊥DEF ＝⊥ACE ；（2）证明：连接CD ，过点E作AC 的平行线与CD 交于点M ，⊥AD ＝AC ，⊥⊥ADC＝⊥ACD，⊥EM⊥AC，⊥⊥EMD＝⊥ACD，⊥CEM＝⊥ACE，⊥⊥EDM＝⊥EMD，⊥DEF＝⊥CEM，⊥ED＝EM，又⊥EF＝EC，⊥⊥DEF⊥⊥MEC（SAS），⊥⊥EDF＝⊥EMC，⊥⊥BDF+⊥EDF＝⊥EMD+⊥EMC＝180°，⊥⊥BDF＝⊥EMC，⊥EM⊥AC，⊥⊥DEM＝⊥A，⊥⊥A＝⊥CEF，⊥⊥DEM＝⊥CEF，⊥⊥DEM中，⊥EMD＝1802DEM︒-∠，⊥FEC中，⊥EFC＝1802CEF︒-∠，⊥⊥EMD＝⊥EFC，⊥⊥BDF＝⊥EFC；（3）连接CD，过点E作AC的平行线与CD交于点M，⊥EG＝AG，⊥⊥GAE＝⊥GEA，⊥⊥DAC+⊥GAE＝⊥GEA+⊥GED＝180°，⊥⊥DAC＝⊥GED，⊥⊥CEF＝⊥DAC，⊥⊥DEG＝⊥CEF，⊥⊥DEG+⊥DEF＝⊥CEF+⊥DEF，即⊥GEF＝⊥DEC，⊥⊥DEF⊥⊥MEC，⊥⊥EFG＝⊥ECD，DF＝MC，又⊥EF＝EC，⊥⊥EFG⊥⊥ECD（ASA），⊥GF＝DC，⊥DC﹣MC＝GF﹣DF，即GD＝DM，⊥EM⊥AC，⊥DM DEk MC AE==，⊥GD DMk DF MC==．【点睛】本题考查了全等三角形的性质与判定，平行线分线段成比例，三角形的内角和定理，三角形的外角性质，添加辅助线证明三角形全等是解题的关键．5．见详解【解析】【分析】过点D作DE⊥AC，交BC于点E，根据等边三角形和平行线的性质得⊥MDE=⊥MEC，DE=CE，从而证明∆EMD≅∆CME，进而即可得到结论．【详解】过点D作DE⊥AC，交BC于点E，⊥ABC是等边三角形，⊥⊥B=⊥ACB=60°，⊥DE⊥AC，⊥⊥DEB=⊥ACB=60°，⊥MDE=⊥MEC，⊥BDE是等边三角形，⊥BD=DE，⊥DE=CE，又⊥⊥EMD=⊥CME，⊥∆EMD≅∆CME，⊥MDME =．【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理，添加辅助线，构造等边三角形和全等三角形，是解题的关键．6．（1）证明见解析；（2）DE＝3．【解析】【分析】（1）过点P作PF⊥BC交AC于点F；证出△APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明△PDF⊥⊥QDC，得出对应边相等即可；（2）过P作PF⊥BC交AC于F．同（1）由AAS证明△PFD⊥⊥QCD，得出对应边相等FD=CD，证出AE+CD=DE12=AC，即可得出结果．【详解】（1）如图1所示，点P作PF⊥BC交AC于点F．⊥⊥ABC是等边三角形，⊥⊥APF也是等边三角形，AP=PF=AF=CQ．⊥PF⊥BC，⊥⊥PFD=⊥DCQ．在△PDF和△QDC中，PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩，⊥⊥PDF⊥⊥QDC（AAS），（2）如图2所示，过P作PF⊥BC交AC于F．⊥PF⊥BC，△ABC是等边三角形，⊥⊥PFD=⊥QCD，△APF是等边三角形，⊥AP=PF=AF．⊥PE⊥AC，⊥AE=EF．⊥AP=PF，AP=CQ，⊥PF=CQ．在△PFD和△QCD中，PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩，⊥⊥PFD⊥⊥QCD（AAS），⊥FD=CD．⊥AE=EF，⊥EF+FD=AE+CD，⊥AE+CD=DE12=AC．⊥AC=6，⊥DE=3．【点睛】本题考查等边三角形的判定与性质、全等三角形的判定（AAS）与性质、平行线的性质，熟练掌握等边三角形的性质，解题的关键是掌握等边三角形的判定与性质、全等三角形的判定（AAS）与性质、平行线的性质，熟练掌握等边三角形的性质．7．（1）证明见解析；（2）DE＝3．【解析】【分析】（1）过点P作PF⊥BC交AC于点F；证出⊥APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明⊥PDF⊥⊥QDC，得出对应边相等即可；（2）过P作PF⊥BC交AC于F．同（1）由AAS证明⊥PFD⊥⊥QCD，得出对应边相等FD=CD，证出AE+CD=DE12=AC，即可得出结果．【详解】（1）如图1所示，点P作PF⊥BC交AC于点F．⊥⊥ABC是等边三角形，⊥⊥APF也是等边三角形，AP=PF=AF=CQ．⊥PF⊥BC，⊥⊥PFD=⊥DCQ．在⊥PDF和⊥QDC中，PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩，⊥⊥PDF⊥⊥QDC（AAS），⊥PD=DQ；（2）如图2所示，过P作PF⊥BC交AC于F．⊥PF⊥BC，⊥ABC是等边三角形，⊥⊥PFD=⊥QCD，⊥APF是等边三角形，⊥AP=PF=AF．⊥PE⊥AC，⊥AE=EF．⊥AP=PF，AP=CQ，⊥PF=CQ．在⊥PFD和⊥QCD中，PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩，⊥⊥PFD⊥⊥QCD（AAS），⊥FD=CD．⊥AE=EF，⊥EF+FD=AE+CD，⊥AE+CD=DE12=AC．⊥AC=6，⊥DE=3．【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．8．(1)详见解析(2)ED＝2【解析】【分析】（1）过P作PF⊥BQ，可得△APF为等边三角形，所以AP＝PF，再证△DCQ⊥⊥DFP，即可得PD＝DQ；（2）根据等腰三角形三线合一的性质可得AE＝EF，根据全等三角形对应边相等可得FD ＝CD，然后求出2DE=AC，代入数据进行计算即可得解．(1)证明：如图，过点P作PF⊥BC，则⊥DPF=⊥Q，⊥⊥ABC为等边三角形，⊥⊥APF是等边三角形，⊥AP=PF，又⊥AP=CQ，⊥PF=CQ，在△DPF和△DQC中，DPF QPDF QDC PF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，⊥⊥DPF⊥⊥DQC（AAS），⊥DP=DQ；(2)⊥⊥P AF为等边三角形，PE⊥AC，可得AE＝EF，由（1）知，⊥DPF⊥⊥DQC⊥FD＝CD，⊥AC＝AE＋EF＋FD＋CD，⊥AC＝2EF＋2FD＝2（EF＋FD）＝2ED，⊥AC＝BC＝4，⊥2ED＝4，⊥ED＝2．【点睛】本题考查了等边三角形的性质，全等三角形的判定与性质，等腰三角形三线合一的性质，作辅助线构造出等边三角形和全等三角形是解题的关键，也是本题的难点．9．(1)DM=EM．理由见详解；(2)成立，理由见详解；(3)MD=12ME．【解析】【分析】（1）DM=EM；过点E作EF//AB交BC于点F，然后利用平行线的性质和已知条件可以证明△DBM⊥⊥EFM，接着利用全等三角形的性质即可证明题目的结论；（2）成立；过点E作EF//AB交CB的延长线于点F，然后利用平行线的性质与已知条件可以证明△DBM⊥⊥EFM，接着利用全等三角形的性质即可证明题目的结论；（3）MD=12ME．过点E作EF//AB交CB的延长线于点F，然后利用平行线的性质和已知条件得到△DBM⊥⊥EFM，接着利用相似三角形的性质即可得到结论；(1)解：DM=EM；证明：过点E作EF//AB交BC于点F，⊥AB=AC，⊥⊥ABC=⊥C；又⊥EF//AB，⊥⊥ABC=⊥EFC，⊥⊥EFC=⊥C，⊥EF=EC．又⊥BD=EC，⊥EF=BD．又⊥EF//AB，⊥⊥ADM=⊥MEF．在△DBM和△EFM中BDM FEMBMD FMEBD EF∠=∠⎧⎪∠=∠⎨⎪=⎩，⊥⊥DBM⊥⊥EFM，⊥DM=EM．(2)解：成立；证明：过点E作EF//AB交CB的延长线于点F，⊥AB=AC，⊥⊥ABC=⊥C；又⊥EF//AB，⊥⊥ABC=⊥EFC，⊥⊥EFC=⊥C，⊥EF=EC．又⊥BD=EC，⊥EF=BD．又⊥EF//AB，⊥⊥ADM=⊥MEF．在△DBM和△EFM中BDE FEM BMD FME BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩⊥⊥DBM ⊥⊥EFM ；⊥DM =EM ；(3)解：过点E 作EF //AB 交CB 的延长线于点F ，⊥⊥DBM =⊥EFM ，⊥DMB =⊥EMF⊥⊥DBM ⊥⊥EFM ，⊥BD ：EF =DM ：ME ，⊥AB =AC ，⊥⊥ABC =⊥C ，⊥⊥F =⊥ABC ，⊥⊥F =⊥C ，⊥EF =EC ，⊥BD ：EC =DM ：ME =1：2，⊥MD =12ME ．【点睛】本题主要考查了三角形综合，涉及了等腰三角形性质和判定、全等三角形的判定与性质、相似三角形的判定和性质，利用平行构造全等三角形是解题关键．10．选择（1）（3）证明，证明见解析【解析】【分析】如图(1)延长DE 到F 使得EF=DE,证明△DCE⊥⊥FBE,得到⊥CDE=⊥F,BF=DC,结合题干条件即可得到结论;如图3,过C 点作CF⊥AB 交DE 的延长线于F,得到△ABE⊥⊥FCE,AB=FC,结合题干条件即可得到结论,【详解】如图(1)延长DE 到F 使得EF=DE在△DCE 和△FBE 中,EF DE DEC FEB BE EC =∠=∠=⎧⎪⎨⎪⎩⊥△DCE⊥⊥ FBE （SAS)⊥⊥CDE=⊥F,BF=DC⊥⊥BAE=⊥CDE⊥BF=AB⊥AB= CD如图3,过C 点作CF⊥AB 交DE 的延长线于F在△ABE 和△FCE 中B ECF BE ECBAE F ∠=∠=∠=∠⎧⎪⎨⎪⎩⊥△ABE⊥⊥ FCE(AAS),⊥AB=FC⊥⊥BAE=⊥CDE⊥⊥F=⊥CDE⊥CD=CF⊥AB=CD【点睛】此题考查全等三角形的判定与性质和等腰三角形的性质，解题关键在于利用三角形全等的性质证明。

平行线中常见作辅助线的技巧的九种类型

（ 2 ）如图 ① ，在 AB ∥ DE 的条件下，你能得出 ∠ B ， ∠BCD，∠D之间的数量关系吗？请说明理由．解：∠B＋∠BCD＋∠D＝360°.理由如下：因为CF∥AB，所以∠B＋∠BCF＝180°. 因为AB∥DE，所以CF∥DE. 所以∠FCD＋∠D＝180°. 所以∠B＋∠BCF＋∠FCD＋∠D＝180°＋ 180°，即∠B＋∠BCD＋∠D＝360°.
6．如图，AB∥DE，则∠BCD，∠B，∠D有何关系？为什么？
解：∠BCD＝∠B－∠D.理由如下：如图，过点C作CF∥AB，所以∠B＝∠BCF. 因为AB∥DE，CF∥AB，所以CF∥DE. 所以∠DCF＝∠D.所以∠B－∠D＝∠BCF－∠DCF. 因为∠BCD＝∠BCF－∠DCF，所以∠BCD＝∠B－∠D.
解：AB∥CD.理由如下：如图，连接 BD. 在三角形 BDE 中，∠1＋∠2＋∠E＝180°. 因为∠E＝∠3＋∠4，所以∠1＋∠2＋∠3＋∠4＝180°，即∠ABD＋∠CDB＝180°. 所以 AB∥CD.
2．【2020·攀枝花】如图，平行线AB，CD被直线EF所截，过点B作BG⊥EF于点G，已知∠1＝50°，则∠B＝（ C） A．20° B．30° C．40° D．50°
BS版平行线中常见作辅助线的技巧的九种
类型
提示：点击进入习题
1 见习题 2C 3 见习题 4 见习题
5 见习题 6 见习题 7 见习题 8 见习题 9 见习题
答案显示
1．如图，∠E＝∠B＋∠D，猜想AB与CD有怎样的位置关系，并说明理由．
【点拨】本题可通过连接 B，D 两点构造截线，进而利用平行线的判定说明 AB∥CD.
4 ．（ 1 ）如图 ① ，若 AB ∥ DE ， ∠ B ＝ 135° ， ∠ D ＝ 145°，求∠BCD的度数．

平行线中添辅助线的方法

平行线中添辅助线的方法平行线中常见的添辅助线的方法：(1) 在平行线内(或外)一点作直线的平行线；(2) 加截线(连接两点、延长线段相交)例：探究：(1) 、如图1,若AB//CD ，贝U/ B+Z D=Z E,你能说明为什么吗？(2) 、反之，若Z B+Z D=Z E,直线AB 与CD 有什么位置关系？请证明(3) 、若将点E 移至图2所示位置，此时之间有什么关系？请证明。

(4) 、若将点E 移至图3所示位置，情况又如何？(5) 、若将点E 移至图4所示位置，情况又如何？(6) 、在图5中，AB//CD ，Z B+Z D+Z F 与Z E+Z G 又有何关系？平行线拓展延伸题一、填空题1、如图，已知 AB// CD 若Z A=20°,Z E=35，则Z C 等于 ____________2、如图，I 1//I 2，Z 1=120°,Z 2=100°,则Z 3= _____________ 。

4、如图，AB // CD , 1 50°, 2 110°,则 3 _____________ 。

&如图，已知 AB// EF,Z BAC=p Z ACD=x Z CDE=y Z DEF=q 用 p 、q 、y 来表示x 得 _________________________________。

|2图1D、选择题如图1, AB// CD 且/ BAP=60 —a, / APC=45 + a,/ PCD=30 —a,则a =（A、10图1 B 、15BD图32、如图2, AB//CD，且 A 25 , C 45，贝U E的度数是（）A. 60B. 70C. 110D. 803、如图3,已知AB// CD则角a、B、丫之间的关系为（）A、a + B + Y =180°B、a — B + 丫=180°C、a + B —丫=180°D、a +B + Y =3605、如图，已知AB// EF,Z C=90，则a、B和r的关系是（）A、B = a + r B 、a + B + r =180 C、a + B — r =180 D 、B + r — a =180°三、解答题1如图所示，AB// ED, / B= 48° , / D= 42° ,证明：BCLCD（选择一种辅助线）B2、如图，若AB//CD 猜想/ A 、/ E 、/ D 之间的关系，并证明之4、如图，AB// CD / BE&85°，求/ ABE^Z EFC+/ FCD 勺度数5.已知 AB/ DE / ABC= 80°,/ CDE= 140一副三角板的旋转与边的平行问题1、如图1是一副三角尺拼成的图案:(1) 求/ EBC 的度数；(2) 将图1中的三角尺ABC 绕点B 旋转口度(0°VaV 90°)能否使/ ABE=2 / DBC 若能，求出/ EBC 的度数；若不能，说明理由•(图 2、图3供参考)F2、如图1,点0为直线AB上一点，过点0作射线0C使/ AOC60。

第3讲平行线辅助线(学生版)

第3讲平行线辅助线一、知识回顾：在解决平行线的问题时，当无法直接得到角的关系或两条线之间的位置关系时，通常借助辅助线来帮助解答，如何作辅助线需根据已知条件确定，辅助线的添加既可以产生新的条件，又能将题目中原有的条件联系在一起．一、加截线(连接两点或延长线段)1．如图，已知AB∥CD，∠ABF＝∠DCE.∠BFE与∠FEC有何关系？并说明理由．(第1题)【解析】：∠BFE＝∠FEC.理由一：连接BC，如图①.∵AB∥CD，∴∠ABC＝∠BCD(两直线平行，内错角相等)．又∵∠ABF＝∠DCE，∴∠ABC－∠ABF＝∠BCD－∠DCE，即∠FBC＝∠ECB.∴BF∥CE(内错角相等，两直线平行)．∴∠BFE＝∠FEC(两直线平行，内错角相等)．(第1题)理由二：延长AB，CE相交于点G，如图②.∵AB∥CD，∴AG∥CD.∴∠DCE＝∠G(两直线平行，内错角相等)．又∵∠ABF＝∠DCE，∴∠ABF＝∠G.∴BF∥CG(同位角相等，两直线平行)．∴∠BFE＝∠FEC(两直线平行，内错角相等)．二、过“拐点”作平行线a．“”形图2．如图，AB∥CD，P为AB，CD之间的一点，已知∠1＝32°，∠2＝25°，求∠BPC的度数．(第2题)【解析】：方法一：过点P作射线PN∥AB，如图①.∵AB∥CD，∴PN∥CD.∴∠4＝∠2＝25°.∵PN∥AB，∴∠3＝∠1＝32°.∴∠BPC＝∠3＋∠4＝57°.(第2题)方法二：过点P作射线PM∥AB，如图②.∵AB∥CD，∴PM∥CD.∴∠4＝180°－∠2＝180°－25°＝155°.∵AB∥PM，∴∠3＝180°－∠1＝180°－32°＝148°.∴∠BPC＝360°－∠3－∠4＝360°－148°－155°＝57°. 方法三：连接BC，略。

专题：平行线中作辅助线的方法(含答案)

专题：平行线中作辅助线的方法——形成思维定式，快速解题◆类型一含一个拐点的平行线问题1．(2017·南充中考)如图，直线a∥b，将一个直角三角尺按如图所示的位置摆放．若∠1＝58°，则∠2的度数为()A．30°B．32°C．42°D．58°第1题图第2题图2．(2017·潍坊中考)如图，∠BCD＝90°，AB∥DE，则∠α与∠β满足()A．∠α＋∠β＝180°B．∠β－∠α＝90°C．∠β＝3∠αD．∠α＋∠β＝90°3．阅读下列解题过程，然后解答后面的问题．如图①，已知AB∥CD，∠B＝35°，∠D＝32°，求∠BED的度数．解：过E作EF∥AB.∵AB∥CD，∴CD∥EF.∵AB∥EF，∴∠1＝∠B＝35°.又∵CD∥EF，∴∠2＝∠D＝32°，∴∠BED＝∠1＋∠2＝35°＋32°＝67°.如图②、图③，是明明设计的智力拼图玩具的一部分，现在明明遇到两个问题，请你帮他解决．(1)如图②，已知∠D＝30°，∠ACD＝65°，为了保证AB∥DE，∠A应多大？(2)如图③，要使GP∥HQ，则∠G，∠GFH，∠H之间有什么关系？【方法4】◆类型二含多个拐点的平行线问题4．如图，已知AB∥DE，∠ABC＝70°，∠CDE＝140°，则∠BCD的大小为【方法4】() A．20°B．30°C．40°D．70°第4题图第5题图5．如图，直线l1∥l2，∠α＝∠β，∠1＝40°，则∠2的度数为________．6．如图，给出下列三个论断：①∠B＋∠D＝180°；②AB∥CD；③BC∥DE.请你以其中两个论断作为已知条件，填入“已知”栏中，以剩余一个论断作为结论，填入“结论”栏中，使之成为一道由已知可得到结论的题目，并解答该题．已知：______________，结论：______________．解：7．如图①，AB∥CD，EOF 是直线AB，CD间的一条折线．【方法4】(1)试说明：∠EOF＝∠BEO＋∠DFO；(2)如果将折一次改为折两次，如图②，则∠BEO，∠EOP，∠OPF，∠PFC之间会满足怎样的数量关系？并说明理由．参考答案与解析1．B 2.B3．解：(1)∠A＝∠ACD－∠D＝35°.(2)过点F向右作FM∥PG.∵GP∥HQ，∴FM∥HQ，∴∠G＋∠MFG＝180°，∠H＋∠MFH＝180°，∴∠G＋∠GFH＋∠H＝360°.4．B解析：如图，过C向右作CM∥AB.∵AB∥DE，∴DE∥CM.∵∠ABC＝70°，∠CDE ＝140°，∴∠BCM＝70°，∠DCM＝180°－140°＝40°，∴∠BCD＝∠BCM－∠DCM＝70°－40°＝30°.5．140°解析：如图，延长AE交l2于点B.∵l1∥l2，∴∠3＝∠1＝40°.∵∠α＝∠β，∴AB∥CD，∴∠2＋∠3＝180°，∴∠2＝180°－∠3＝180°－40°＝140°.6．解：①②③∵AB∥CD，∴∠B＝∠C.又∵∠B＋∠D＝180°，∴∠C＋∠D＝180°，∴BC∥DE(答案不唯一)．7．解：(1)如图①，过O向左作OM∥AB，∴∠1＝∠BEO.∵AB∥CD，∴OM∥CD，∴∠2＝∠DFO，∴∠1＋∠2＝∠BEO＋∠DFO，即∠EOF＝∠BEO＋∠DFO.(2)∠EOP＋∠PFC＝∠BEO＋∠OPF.理由如下：如图②，过O向左作OQ∥AB，过P 向右作PN∥CD.∵AB∥CD，∴OQ∥PN∥AB∥CD，∴∠1＝∠BEO，∠2＝∠3，∠4＝∠PFC，∴∠1＋∠2＋∠PFC＝∠BEO＋∠3＋∠4，∴∠EOP＋∠PFC＝∠BEO＋∠OPF.。

平行线的判定及性质例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定（1）平行公理：经过直线外一点，有且只有一条直线与已知直线平行. （2）平行公理的推论：平行于同一条直线的两条直线. （3）在同一平面内，垂直于同一条直线的两条直线. （4）同位角相等，两直线平行. （5）内错角相等，两直线平行.（6）同旁内角互补，两直线平行.3、平行线的性质（1）两直线平行，同位角相等. （2）两直线平行，内错角相等.（3）两直线平行，同旁内角互补.二、【例题精讲】专题一：余角、补角、对顶角与三线八角例题1：∠A的余角与∠A的补角互为补角，那么2∠A是（）A．直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中，下列判断正确的是（）A.4对同位角，2对内错角，4对同旁内角B.4对同位角，2对内错角，2对同旁内角C.6对同位角，4对内错角，4对同旁内角D.6对同位角，4对内错角，2对同旁内角【活学活用2】如图2-82，下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是（）A.对顶角B.互余C.互补D相等例题2：如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角分别是_______.【活学活用4】如图，∠AOC +∠DOE +∠BOF = .专题二：平行线的判定例题3：如图，已知∠EFB+∠ADC=180°，且∠1=∠2，试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行，那么这样的平行棱共有 ( )A ．9对B ．16对 C.18对 D ．以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB.3、如图2-97,已知：∠1=∠2=，∠3=∠4，∠5=∠6.求证:AD ∥BC.4、如图2—101，若要能使AB ∥ED ，∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ，若a ∥b ，a ⊥c ，b ⊥d ，则c 、d 的位置关系为（） A.互相垂直 B ．互相平行 C.相交 D ．没有确定关系专题三：平行线的性质1、如图，110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行，则BOC ∠= . 2、如图，AB //CD ，BC //DE ，则∠B+∠D = .3、如图，直线AB 与CD 相交于点O ，OB 平分∠DOE .若60DOE ∠=，则∠AOC 的度数是 .4、如图，175,2120,375∠=∠=∠=，则4∠= .13 425、如图，//AB CD ，直线EF 分别交AB 、CD 于E 、F ，ED 平分BEF ∠，若172∠=，则2∠= .【例题讲解】例1：如图，已知：AD ∥BC, ∠AEF=∠B,求证：AD ∥EF 。

平行线(辅助线)(完整版)资料

平行线(辅助线)（完整版）资料(可以直接使用，可编辑优秀版资料，欢迎下载）解答题专项训练（5）——平行线（辅助线）1.如图，AB∥CD，∠B=72°，∠D=32°，求∠F的度数．2.如图，已知AB∥CD，且∠AEF=150°，∠DGF=60°．(1)试判断EF和FG的位置关系．(2)你能说明你的理由吗？3.已知：如图，AB∥CD，FE⊥AB于G，∠EMD=134°，求∠GEM的度数．4.如图，AB∥DC，增加折线条数，相应角的个数也会增多，∠B，∠E，∠F，∠G，∠D之间又会有何关系？5.如图，已知直线a∥b，直线m和直线a、b交于点C和D，点A在直线a上，点B在直线b上，点P在直线m上，且点A、B的位置不变，记∠PAC=α，∠APB=β，∠PBD=γ．（1）当点P在C、D之间运动时，问α、β、γ之间有什么数量关系？请说明理由．（2）当点P在C、D两点的外侧运动时（P点与点C、D 不重合），试探索α、β、γ之间的数量关系是______ （直接写出答案）．6.如图，AB∥CD，P为定点，E、F分别是AB、CD上的动点．（1）求证：∠P=∠BEP+∠PFD；（2）若M为CD上一点，MN交PF于N．证明：∠PNM=∠NMF+∠NFM；（说明：不能运用三角形内角和定理）（3）在（2）的基础上，若∠FMN=∠BEP，试说明∠EPF 与∠PNM的关系，并证明你的结论．7.如图，点A，B分别在直线CM，DN上，CM∥DN．（1）如图1，连接AB，则∠CAB+∠ABD= ______ 度（直接写出结果）；（2）如图2，点P1是直线CM、DN之间的一个点，连接AP1、BP1．求：∠CAP1+AP1B+∠P1BD的值（写出求解过程）；（3）如图3，点P1、P2是直线CM、DN之间的两个点，连接AP1、P1P2、P2B．求：∠CAP1+∠AP1P2+∠P1P2B+∠P2BD= ______ 度（直接写出结果）．8.如图，AB∥CD，直线a交AB、CD分别于点E、F，点M在EF上，p是直线CD上的一个动点，（点P不与F重合）（1）当点P在射线FC上移动时，如图（1），∠FMP+∠FPM=∠AEF成立吗？请说明理由．（2）当点P在射线FD上移动时，如图（2），∠FMP+∠FPM 与∠AEF有什么关系？说明你的理由．专题四平行线模型归纳基本模型归纳：基本模型的运用：基础过关：1.将两张矩形纸片如图所示摆放，的度数。

相似三角形中的辅助线及动点问题(经典题型)

C 中，AB⊥AC，AE⊥BC 于 E，D 在 AC 边上，若 BD=DC=EC=1，求 AC。
动点题型
1、如图正方形 ABCD 的边长为 2，AE=EB，线段 MN 的两端点分别在 CB、CD 上滑动，且 MN=1，当 CM 为何值时△AED 与以 M、N、C 为顶点的三角形相似？
一、作平行线
例 1. 如图， ABC 的 AB 边和 AC 边上各取一点 D 和 E，且使 AD＝AE，DE 延长线与 BC 延长线相交于 F，求证：
BF BD CF CE
例 2. 如图，△ABC 中，AB<AC，在 AB、AC 上分别截取 BD=CE，DE，BC 的延长线相交于点 F，证明：AB·DF=AC·EF。
1
三、作延长线例 5. 如图，在梯形 ABCD 中，AD∥BC，若∠BCD 的平分线 CH⊥AB 于点 H，BH=3AH，且四边形 AHCD 的面积为 21，求△HBC 的面积。
例 6. 如图，Rt ABC 中，CD 为斜边 AB 上的高，E 为 CD 的中点，AE 的延长线交 BC 于 F，FG AB 于 G，求证：FG =CF BF
A P H E D
B
C
1.如图，已知一个三角形纸片 ABC ， BC 边的长为 8， BC 边上的高为 6 ， B 和 C 都为锐角， M 为 AB 一动点（点 M 与点 A、B 不重合），过点 M 作 MN ∥ BC ，交 AC 于点 N ，在 △ AMN 中，设 MN 的长为 x ， MN 上的高为 h ．（1）请你用含 x 的代数式表示 h ．使 △ AMN 落在四边形 BCNM 所在平面，设点 A 落在平面的点为 A1 ， △ A1 MN （2）将 △ AMN 沿 MN 折叠，与四边形 BCNM 重叠部分的面积为 y ，当 x 为何值时， y 最大，最大值为多少？

七年级-人教版-数学-下册-[综合训练]第6课时--与平行线有关的辅助线问题

第6课时与平行线有关的辅助线问题
1．如图，已知AB∥CD，分别探索四个图形中∠P与∠A，∠C的关系，并从所得的四个关系中任选一个加以证明．
2．已知，直线AB∥CD．
（1）如图①，试说明∠AEF＋∠FGC＝∠BAE＋∠EFG＋∠GCD；
（2）如图②，∠AEF，∠FGH，∠HIC与∠BAE，∠EFG，∠GHI，∠ICD之间有什么关系？请直接写出结论．
参考答案
1．【答案】解：∠P与∠A，∠C的关系分别为：
题图①：∠P＝360°－∠A－∠C；
题图②：∠P＝∠A＋∠C；
题图③：∠P＝∠C－∠A；
题图④：∠P＝∠A－∠C．
现选题图①进行证明：如图，过点P作PQ∥AB，则PQ∥AB∥CD．
∵PQ∥AB∥CD，
∴∠A＋∠APQ＝180°，∠C＋∠CPQ＝180°．
∴∠APQ＝180°－∠A，∠CPQ＝180°－∠C．
∴∠APC＝∠APQ＋∠CPQ＝(180°－∠A)＋(180°－∠C)＝360°－∠A－∠C．2．【答案】解：（1）如图，过点E作EM∥AB，过点F作FN∥AB，过点G作GQ∥CD，
∵AB∥CD，
∴AB∥EM∥FN∥GQ∥CD．
∴∠BAE＝∠AEM，∠MEF＝∠EFN，∠NFG＝∠FGQ，∠QGC＝∠GCD．
∴∠AEF＝∠BAE＋∠EFN，∠FGC＝∠NFG＋GCD．
∵∠EFN＋∠NFG＝∠EFG，
∴∠BAE＋∠EFG＋∠GCD＝∠AEF＋∠FGC．
（2）∠AEF＋∠FGH＋∠HIC＝∠BAE＋∠EFG＋∠GHI＋∠ICD．。

七年级数学下册《平行线》练习题及答案(浙教版)

七年级数学下册《平行线》练习题及答案(浙教版)一、选择题1.如图，4根火柴棒形成象形“口”字，只通过平移火柴棒，原图形能变成的汉字是( )2.如图，下列各组角中，互为对顶角的是( )A.∠1和∠2B.∠1和∠3C.∠2和∠4D.∠2和∠53.如图，已知AB⊥BD，BC⊥CD，AD=a，CD=b，则BD的长的取值范围为（）A.大于bB.小于aC.大于b且小于aD.无法确定4.如图，下列说法正确的是( )A.∠1和∠B是同旁内角B.∠1和∠C是内错角C.∠2和∠B是同位角D.∠3和∠C同旁内角5.如图，在下列条件中，能判断AD∥BC的是( )A.∠DAC=∠BCAB.∠DCB+∠ABC=180°C.∠ABD=∠BDCD.∠BAC=∠ACD6.同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则c、d的位置关系为( )A.互相垂直B.互相平行C.相交D.没有确定关系7.长方体的每一对棱相互平行，那么这样的平行棱共有( )A.9对B.16对C.18对D.以上答案都不对8.如图，直线a∥b，将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置，其中A和C两点分别落在直线a和b上．若∠1=20°，则∠2的度数为( )A．20° B．30° C．40° D．50°9.如图，如果AB∥CD，CD∥EF，那么∠BCE等于( )A.∠1＋∠2B.∠2﹣∠1C.180°﹣∠2＋∠1D.180°﹣∠1＋∠210.如图，OA⊥OC，OB⊥OD，4位同学观察图形后分别说了自己的观点：甲：∠AOB＝∠COD；乙：∠BOC＋∠AOD＝180°；丙：∠AOB＋∠COD＝90°；丁：图中小于平角的角有6个；其中正确的结论是( )A.1个B.2个C.3个D.4个11.将一副三角板按如图放置，则下列结论：①如果∠2＝30°，则有AC∥DE；②∠BAE＋∠CAD＝180°；③如果BC∥AD，则有∠2＝45°；④如果∠CAD＝150°，必有∠4＝∠C.其中正确的有（）A.①②③B.①②④C.①③④D.①②③④12.学习了平行线后，小明想出了过已知直线外一点画这条直线的平行线的新方法，他是通过折一张半透明的纸得到的(如图①～④)：从图中可知，小明画平行线的依据有( )①两直线平行，同位角相等；②两直线平行，内错角相等；③同位角相等，两直线平行；④内错角相等，两直线平行.A.①②B.②③C.③④D.①④二、填空题13.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC ′＝.14.如图，直线AB，CD相交于点O，若∠AOC=90°，则AB与CD的位置关系是；若已知AB⊥CD，则∠AOC=∠COB=∠BOD=∠AOD= .15.如图所示，内错角共有____对．16.如图，利用直尺和三角尺过直线外一点画已知直线的平行线，这种画法依据的是.17.将如图1的长方形ABCD纸片沿EF折叠得到图2，折叠后DE与BF相交于点P.如果∠EPF＝70°，则∠PEF的度数为_________ .18.如图，直线l1∥l2，∠α＝∠β，∠1＝40°，则∠2＝_________．三、解答题19.如图，在Rt△ABC中，∠C=90°，AC=4cm ，BC=3cm ，将△ABC沿AB方向向右平移得到△DEF，若AE=8cm，DB=2cm．（1）求△ABC向右平移的距离AD的长．（2）求四边形AEFC的周长．20.如图，直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF；若∠AOE＝40°，求∠BOD的度数.21.如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？22.如图，△ABC中，∠ACB=90°，CD⊥AB，点D为垂足，点E，F分别在AC．AB边上且∠AEF=∠B．求证：EF∥CD．23.如图，BE平分∠ABD，DE平分∠BDC，DG平分∠CDF，且∠1＋∠2＝90°，试说明BE∥DG.24.如图1，已知△ABC，求证：∠A+∠B+∠C=180°．分析：通过画平行线，将∠A 、∠B 、∠C 作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法．证法1：如图1，延长BC 到D ，过C 画CE ∥BA ．∵BA ∥CE （作图2所知）∴∠B=∠1，∠A=∠2（两直线平行，同位角、内错角相等）．又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义）∴∠A+∠B+∠ACB=180°（等量代换）．如图3，过BC 上任一点F ，画FH ∥AC ，FG ∥AB ，这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗？请你试一试．25.已知AB ∥CD,∠ABE 与∠CDE 两个角的角平分线相交于点F.(1)如图1,若∠E ＝80°,求∠BFD 的度数.(2)如图2,若∠ABM ＝13∠ABF,∠CDM ＝13∠CDF,试写出∠M 与∠E 之间的数量关系并证明你的结论. (3)若∠ABM ＝1n ∠ABF,∠CDM ＝1n∠CDF,∠E ＝m °,请直接用含有n,m °的代数式表示出∠M.参考答案1.B2.A.3.C4.D5.A6.B7.C8.C9.C.10.C.11.D12.C13.答案为：5.14.答案为：垂直；90°.15.答案为：8.16.答案为：同位角相等，两直线平行.17.答案为：55°18.答案为：140°19.解：（1）3； (2)8+3+4+3=18.20.解：∵OA⊥OB(已知)∴∠AOB＝90°(垂直的定义)∵∠AOE＝40°(已知)∴∠BOE＝∠AOB-∠AOE＝90°-40°＝50°∵OC平分∠AOF(已知)∴∠BOD＝20°21.答案为：∠1和∠2是直线EF、DC被直线AB所截形成的同位角，∠1和∠3是直线AB、CD被直线EF所截形成的同位角．22.证明：∵∠ACB=90°∴∠B+∠A=90°∵CD⊥AB∴∠ADC=90°∴∠A+∠ACD=90°∴∠B=∠ACD∵∠AEF=∠B∴∠AEF=∠ACD∴EF∥CD．23.证明：∵∠1＋∠2＝90°(已知)∴△BDE中，∠E＝180°-(∠1＋∠2)＝90°∵ DE平分∠BDC，DG平分∠CDF(已知)∴∠EDG＝∠EDC＋∠CDG＝∴∠E＝∠EDG(等量代换)∴ BE∥DG (内错角相等，两直线平行)24.证明：如图3∵HF∥AC∴∠1=∠C∵GF∥AB∴∠B=∠3∵HF∥AC∴∠2+∠AGF=180°∵GF∥AH∴∠A+∠AGF=180°∴∠2=∠A∴∠A+∠B+∠C=∠1+∠2+∠3=180°（等量代换）．25.解：（1）如图，作EG∥AB，FH∥AB∵AB∥CD∴EG∥AB∥FH∥CD∴∠ABF＝∠BFH，∠CDF＝∠DFH，∠ABE＋∠BEG＝180°，∠GED＋∠CDE＝180°∴∠ABE＋∠BEG＋∠GED＋∠CDE＝360°∵∠BED＝∠BEG＋∠DEG＝70°∴∠ABE＋∠CDE＝290°∵∠ABF和∠CDF的角平分线相交于E∴∠ABF ＋∠CDF ＝145°∴∠BFD ＝∠BFH ＋∠DFH ＝145°；（2）∵∠ABM ＝13∠ABF ，∠CDM ＝13∠CDF ∴∠ABF ＝3∠ABM ，∠CDF ＝3∠CDM∵∠ABE 与∠CDE 两个角的角平分线相交于点F ∴∠ABE ＝6∠ABM ，∠CDE ＝6∠CDM∴6∠ABM ＋6∠CDM ＋∠E ＝360°∵∠M ＝∠ABM ＋∠CDM∴6∠M ＋∠E ＝360°．(3)由(2)结论可得2n ∠ABN ＋2n ∠CDM ＋∠E ＝360°，∠M ＝∠ABM ＋∠CDM 解得：∠M ＝n2m 360︒-︒．故答案为：∠M ＝n 2m 360︒-︒.。

人教版七年级数学下册第五章相交线与平行线第3节与角有关的辅助线暑假作业(部分含答案)

第3节与角有关的辅助线1.已知：如图，AB∥CD，∠1=135°，∠3=75°，则∠2的度数为（）A．45°B．75°C．30°D．105°第1题图第2题图2.已知：如图，∠BAC+∠C=180°，点E是CD上一点，且∠1=32°，∠AFE=110°，则∠FED的度数为（）A．78°B．64°C．55°D．60°3.如图，AB∥EF，∠BCD=90°，则∠α，∠β，∠γ的关系是（）A．∠β=∠α+∠γB．∠α+∠β+∠γ=180°C．∠α+∠β-∠γ=90°D．∠β+∠γ-∠α=90°4.已知：如图，AB∥CD，∠B=40°，∠D=20°，求∠BED的度数．5.已知：如图，AB∥CD．求证：∠1+∠3-∠2=180°．6.（1）①如图1所示，已知AB∥CD，∠ABC=60°，根据_____________________________，可得∠BCD=____________；②如图2所示，在①的条件下，若CM平分∠BCD，则∠BCM=_______；③如图3所示，在①②的条件下，若CN⊥CM，则∠BCN=__________．（2）尝试解决下面的问题：如图4所示，AB∥CD，∠B=40°，CN是∠BCE的平分线，CN⊥CM，求∠BCM的度数．7．如图（1），已知直线l1∥l2，且l3与l1、l2分别交于A、B两点，l4与l1、l2分别交于C、D两点，记∠ACP＝∠1，∠BDP＝∠2，∠CPD＝∠3，点P在线段AB上．（1）若∠1＝25°，∠2＝33°，则∠3＝；（2）猜想∠1，∠2，∠3之间的相等关系，并说明理由；（3）如图（2），点A在点B的南偏东23°方向，在点C的西南方向，利用（2）的结论，可知∠BAC＝；（4）点P在直线l3上且在A、B两点外侧运动时，其它条件不变，请直接写出∠1，∠2，∠3之间的相等关系．8．如图，已知AB∥CD，点C在点D的右侧，∠ADC＝70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB，CD之间．（1）如图1，点B在点A的左侧，若∠ABC＝60°，求∠BED的度数？（2）如图2，点B在点A的右侧，若∠ABC＝100°，直接写出∠BED的大小．9．小明同学在完成第10章的学习后，遇到了一些问题，请你帮助他．（1）图1中，当AB∥CD，试说明∠AEC＝∠BAE+∠DCE．（2）图2中，若∠AEC＝∠BAE+∠DCE，则AB∥CD吗？请说明理由．（3）图3中，AB∥CD，若∠BAE＝x°，∠AEF＝y°，∠EFD＝z°，∠FDC＝m°，则m ＝．（直接写出结果，用含x，y，z的式子表示）10．如图，∠BED＝∠B+∠D，猜想AB与CD有怎样的位置关系，并说明理由．11．直线AB∥CD，点P在其所在平面上，且不在直线AB，CD，AC上，设∠PAB＝α，∠PCD＝β，∠APC＝γ（α，β，γ，均不大于180°，且不小于0°）（1）如图1，当点P在两条平行直线AB，CD之间、直线AC的右边时试确定α，β，γ的数量关系；（2）如图2，当点P在直线AB的上面、直线AC的右边时试确定α，β，γ的数量关系；（3）α，β，γ的数量关系除了上面的两种关系之外，还有其他的数量关系，请直接写出这些．12．（1）读读做做：平行线是平面几何中最基本、也是非常重要的图形．在解决某些平面几何问题时，若能依据问题的需要，添加恰当的平行线，往往能使证明顺畅、简洁．请根据上述思想解决教材中的问题：如图①，AB∥CD，则∠B+∠D∠E（用“＞”、“＝”或“＜”填空）；（2）倒过来想：写出（1）中命题的逆命题，判断逆命题的真假并说明理由．（3）灵活应用如图②，已知AB∥CD，在∠ACD的平分线上取两个点M、N，使得∠AMN＝∠ANM，求证：∠CAM＝∠BAN．13．小华在学习“平行线的性质”后，对图中∠B，∠D和∠BOD的关系进行了探究：（1）如图1，AB∥CD，点O在AB，CD之间，试探究∠B，∠D和∠BOD之间有什么关系？并说明理由；小华添加了过点O的辅助线OM，并且OM∥CD请帮助他写出解答过程；（2）如图2，若点O在CD的上侧，试探究∠B，∠D和∠BOD之间有什么关系？并说明理由；（3）如图3，若点O在AB的下侧，试探究∠B，∠D和∠BOD之间有什么关系？请直接写出它们的关系式．14．已知AB∥CD，点E、F分别为两条平行线AB、CD上的一点，GE⊥GF于G．（1）如图1，直接写出∠AEG和∠CFG之间的数量关系；（2）如图2，连接GF，过点G分别作∠BGF和∠BGE的角平分线交AB于点K、H．GH⊥AB．①求∠HGK的度数；②探究∠CFG和∠BGF的数量关系并加以证明．15．已知射线AB平行于射线CD，点E、F分别在射线AB、CD上（1）如图1，若点P在线段EF上，若∠A＝25°，∠APC＝70°时，则∠C＝；（2）如图1，若点P在线段EF上运动（不包含E、F两点），则∠A、∠APC、∠C之间的等量关系是；（3）①如图2，若点P在线段FE的延长线上运动，则∠A、∠APC、∠C之间的等量关系是；②如图3，若点P在线段EF的延长线上运动，则∠A、∠APC、∠C之间的等量关系是；（4）请说明图2中所得结论的理由．16．如图，已知l1∥l2，线段MA分别与直线l1，l2交于点A，B，线段MC分别与直线l1，l2交于点C，D，点P在线段AM上运动（P点与A，B，M三点不重合），设∠PDB＝α，∠PCA＝β，∠CPD＝γ．（1）若点P在A，B两点之间运动时，若a＝25°，B＝40°，那么γ＝．（2）若点P在A，B两点之间运动时，探究α，β，γ之间的数量关系，请说明理由；（3）若点P在B，M两点之间运动时，α，β，γ之间有何数量关系？（只需直接写出结论）部分参考答案7．【解答】解：（1）∵l1∥l2，∴∠1+∠PCD+∠PDC+∠2＝180°，在△PCD中，∠3+∠PCD+∠PDC＝180°，∴∠3＝∠1+∠2＝58°，故答案为：58°；（2）∠1+∠2＝∠3，∵l1∥l2，∴∠1+∠PCD+∠PDC+∠2＝180°，在△PCD中，∠3+∠PCD+∠PDC＝180°，∴∠1+∠2＝∠3；（3）过A点作AF∥BE，如图1，则AF∥BE∥CD，则∠BAC＝∠ABE+∠ACD＝23°+45°＝68°；故答案为：68°；（4）当P点在A的外侧时，如图2，过P作PF∥l1，交l4于F，∴∠1＝∠FPC．∵l1∥l4，∴PF∥l2，∴∠2＝∠FPD∵∠CPD＝∠FPD﹣∠FPC∴∠3＝∠2﹣∠1．当P点在B的外侧时，如图3，过P作PG∥l2，交l4于G，∴∠2＝∠GPD ∵l 1∥l 2， ∴PG ∥l 1， ∴∠1＝∠CPG∵∠CPD ＝∠CPG ﹣∠GPD ∴∠3＝∠1﹣∠2．8．【解答】解：（1）如图1，过点E 作EF ∥AB ， ∵AB ∥CD ， ∴AB ∥CD ∥EF ，∴∠ABE ＝∠BEF ，∠CDE ＝∠DEF ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝60°，∠ADC ＝70°，∴∠ABE ＝∠ABC ＝30°，∠CDE ＝∠ADC ＝35°， ∴∠BED ＝∠BEF +∠DEF ＝30°+35°＝65°；（2）如图2，过点E 作EF ∥AB ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝100°，∠ADC ＝70°∴∠ABE ＝∠ABC ＝50°，∠CDE ＝∠ADC ＝35° ∵AB ∥CD ， ∴AB ∥CD ∥EF ，∴∠BEF＝180°﹣∠ABE＝180°﹣50°＝130°，∠CDE＝∠DEF＝35°，∴∠BED＝∠BEF+∠DEF＝180°﹣50°+35°＝165°．9．【解答】解：（1）过E作EM∥AB，∵AB∥CD，∴AB∥CD∥EM，∴∠BAE＝∠AEM，∠DCE＝∠CEM，∴∠AEC＝∠AEM+∠CEM＝∠BAE+∠DCE；（2）过E作EM∥AB，∵EM∥AB，∴∠BAE＝∠AEM，∵∠AEC＝∠BAE+∠DCE，∴∠DCE＝∠CEM，∴EM∥CD，∵AB∥EM，∴AB∥CD；（3）过E作EM∥AB，过F作FN∥AB，∵AB∥CD，∴AB∥CD∥EM∥FN，∴∠BAE＝∠AEM，∠FEM＝∠EFN，∠DFN＝∠CDF，∴∠BAE+∠EFN+∠DFN＝∠AEM+∠FEM+∠CDF，∴∠BAE+∠EFD＝∠AEF+∠CDF，∵∠BAE＝x°，∠AEF＝y°，∠EFD＝z°，∠FDC＝m°，∴x+z＝y+m，∴m＝x+z﹣y，故答案为：x+z﹣y．10．【解答】解：延长BE交CD于F．∵∠BED＝∠B+∠D，∠BED＝∠EFD+∠D，∴∠B＝∠EFD，∴AB∥CD．11．【解答】解：（1）如图1中，结论：γ＝α+β．理由：作PE∥AB，∵AB∥CD，∴PE∥CD，∴∠BAP＝∠APE，∠PCD＝∠CPE，∴∠APC＝∠APE+∠CPE＝∠BAP+∠PCD，∴γ＝α+β．（2）如图2中，结论：γ＝β﹣α．理由：作PE∥AB，∵AB∥CD，∴PE∥CD，∴∠BAP＝∠APE，∠PCD＝∠CPE，∴∠APC＝∠CPE﹣∠APE，∴γ＝β﹣α．（3）如图3中，有γ＝α﹣β．如图4中，有γ＝β﹣α．如图5中，有γ＝360°＝β﹣α．如图6中，有γ＝α﹣β．综上所述，γ＝α﹣β，γ＝β﹣α，γ＝360°﹣β﹣α．12．【解答】（1）解：过E作EF∥AB，如图①所示：则EF∥AB∥CD，∴∠B＝∠BEF，∠D＝∠DEF，∴∠B+∠D＝∠BEF+∠DEF，即∠B+∠D＝∠BED；故答案为：＝；（2）解：逆命题为：若∠B+∠D＝∠BED，则AB∥CD；该逆命题为真命题；理由如下：过E作EF∥AB，如图①所示：则∠B＝∠BEF，∵∠B+∠D＝∠BED，∠BEF+∠DEF＝∠BED，∴∠D＝∠BED﹣∠B，∠DEF＝∠BED﹣∠BEF，∴∠D＝∠DEF，∴EF∥CD，∵EF∥AB，∴AB∥CD；（3）证明：过点N作NG∥AB，交AM于点G，如图②所示：则NG∥AB∥CD，∴∠BAN＝∠ANG，∠GNC＝∠NCD，∵∠AMN是△ACM的一个外角，∴∠AMN＝∠ACM+∠CAM，又∵∠AMN＝∠ANM，∠ANM＝∠ANG+∠GNC，∴∠ACM+∠CAM＝∠ANG+∠GNC，∴∠ACM+∠CAM＝∠BAN+∠NCD，∵CN平分∠ACD，∴∠ACM＝∠NCD，∴∠CAM＝∠BAN．13．【解答】解：（1）∠BOD＝∠D+∠B，理由是：∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠DOB＝∠DOM+∠BOM＝∠B+∠D；（2）∠B＝∠BOD+∠D，理由是：过O作OM∥CD，∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠B＝∠BOM＝∠DOM+∠DOB＝∠D+∠DOB；（3）∠D＝∠DOB+∠B，理由是：过O作OM∥CD，∵AB∥CD，OM∥CD，∴AB∥CD∥OM，∴∠D＝∠DOM，∠B＝∠BOM，∴∠D＝∠DOM＝∠BOM+∠DOB＝∠B+∠DOB．14．【解答】解：（1）如图1中，结论：∠AEG+∠CFG＝90°．理由：作GH∥AB．∵AB∥CD，∴GH∥CD，∴∠AEG＝∠EGH，∠CFG＝∠HGF，∵EG⊥FG，∴∠EGF＝90°，∴∠AEG+∠CFG＝∠EGH+∠HGF＝∠EGF＝90°．（2）①如图2中，∵GH平分∠BGE，∴∠EGH＝∠BGH，∵GH⊥BE，∴∠GHB＝∠GHE＝90°，∴∠EGH+∠GEB＝90°，∠B+∠BGH＝90°，∴∠GEB＝∠B，∵GE⊥GF，∴∠EGF＝90°，∴∠EGH+∠FGH＝90°，∴∠FGH＝∠GEB＝∠B，∵∠HKG＝∠B+∠KGB，∠HGK＝∠HGL+∠KGL，∠KGB＝∠KGL，∴∠HKG＝∠HGK＝45°．②结论：∠CFG＝45°+∠BGF．理由：∵AB∥CD，∴∠ALG＝∠CFG，∵∠ALG＝∠LKG+∠KGL＝45°+∠BGF，∴∠CFG＝45°+∠BGF．15．【解答】解：（1）过P作PH∥CD，∴∠HPC＝∠C，∵AB∥CD，∴AB∥PH，∴∠A＝∠APH＝25°，∴∠HPC＝∠APC﹣∠APH＝70°﹣25°＝45°；（2）∠APC＝∠A+∠C；理由如下：过P作PH∥CD，∴∠HPC＝∠C，∵AB∥CD，∴AB∥PH，∴∠A＝∠APH，∴∠APC＝∠HPC+∠APH＝∠A+∠C；（3）①∠APC＝∠C﹣∠A，理由如下：过点P作PQ∥AB（如图2），∵AB∥CD，∴PQ∥CD，∴∠C＝∠CPQ，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠CPQ﹣∠APQ，∴∠APC＝∠C﹣∠A；②∠APC＝∠A﹣∠C．理由如下：过点P作PQ∥AB（如图3），∵AB∥CD，∴PQ∥CD，∴∠C＝∠CPQ，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠APQ﹣∠CPQ＝∠A﹣∠C，∴∠APC＝∠A﹣∠C．（4）过点P作PQ∥AB（如图2），∵AB∥CD，∴PQ∥CD，∵PQ∥AB，∴∠A＝∠APQ，∵∠APC＝∠CPQ﹣∠APQ，∴∠APC＝∠C﹣∠A．故答案为：45°，∠APC＝∠A+∠C，∠APC＝∠C﹣∠A，∠APC＝∠A﹣∠C．16．【解答】解：（1）∵AC∥BD，∴β+∠PCD+∠PDC+α＝180°，∵γ+∠PCD+∠PDC＝180°，∴γ＝α+β＝65°．故答案为：65°．（2）∵AC∥BD，∴β+∠PCD+∠PDC+α＝180°，∵γ+∠PCD+∠PDC＝180°，∴γ＝α+β＝（3）如图，当P在B，M之间时，∵AC∥BD，∴∠1＝β，∵∠1＝α+γ，∴β＝α+γ．。

相似三角形常用辅助线

A A C BD E F F， A . B D FA C E F
• 1、在△ABC中，D为AC上的一点，E为CB 延长线上的一点，BE=AD，DE交AB于F。
• 求证：EF×BC=AC×DF
.
1、证明：过D作DG∥BC交AB于G，则△DFG和△EFB相似，∴
DG DF BE EF
∵BE＝AD,∴
ED EC
CF FH FG BF
∴FG·FH=CF·BF
∵FG=FH ∴FG2=CF·BF
.
四、作中线
• 例7 如图，中，AB⊥AC，AE⊥BC于E，D 在AC边上，若BD=DC=EC=1，求AC。
.
解：取BC的中点M，连AM
∵ AB⊥AC ∴ AM=CM ∴ ∠1=∠C 又 BD=DC
Rt AE∽C Rt BAC
相交于F，求证：BF
B
CF
BD CE
G
D
证明：过点C作CG//FD交AB于G
小结：本题关键在于AD＝AE这个条件怎
样使用。由这道题还可以增加一种证明线
段相等的方法：相似、成比例。
A
EC
.
F
• 例2. 如Biblioteka ，△ABC中，AB<AC，在AB、 AC上分别截取BD=CE，DE，BC的延长线相交于点F，证明：AB·DF=AC·EF。
• 2、中，，AC=BC，P是AB上一点，Q是 PC上一点（不是中点），MN过Q且 MN⊥CP，交AC、BC于M、N，求证：
P:A P B C:M CN
.
2、证明：
过P作PE⊥AC于E，PF⊥CB于F，
则CEPF为矩形∴ PF //
EC
∵
A B45
RtAEP ∽ RtPFB

七年级-人教版-数学-下册-第6课时--与平行线有关的辅助线问题

G
H
则∠DCH＋∠CDE＝180°(两直线平行，同旁内角互补)． ∵∠CDE＝140°，∴∠DCH＝180°－∠CDE＝40°．
G
H
∵AB∥DE，∴AB∥GH(平行于同一条直线的两条直线平行)． ∴∠ABC＝∠BCH(两直线平行，内错角相等)． ∵∠ABC＝80°， ∴∠BCH＝80°． ∴∠BCD＝∠BCH－∠DCH＝40°．
解：如图，过点 C 作CG∥AB，过点 D 作DH∥EF．
1
G
2
3
H
4
∵AB∥EF，∴AB∥CG∥DH∥EF． ∴∠B＝∠1，∠2＝∠3，∠E＝∠4． ∵∠CDE＝∠3＋∠4，∠BCD＝∠1＋∠2＝90°， ∴∠B＋∠CDE－∠E＝∠1＋∠3＋∠4－∠4＝∠1＋∠2＝90°．
通过添加辅助线可将较复杂的几何图形转化为由平行线构成的基本图形，从而得到相关角之间的数量关系．
例3 如图，AB∥CD，P 为AB，CD 之间的一点，已知∠1＝ 34°，∠2＝26°，求∠BPC 的度数．
分析：此图不是我们所学过的“三线八角”的基本图形，需添加辅助线，把它转化成我们所熟悉的基本图形．
你能用多种方法添加辅助线解决此题吗？
3
4
N
解：方法 1：过点 P 作射线 PN∥AB，如图． ∵PN∥AB，∴∠3＝∠1＝34°． ∵AB∥CD，∴PN∥CD． ∴∠4＝∠2＝26°． ∴∠BPC＝∠3＋∠4＝60°．
例2 如图，若∠B＋∠D＋∠E＝360°，则 AB 与 CD 平行吗？为什么？
分析：过点 E 构造 AB 的平行线是解决此题的关键．可以先过点 E 作 AB 的平行线，再利用“两直线平行，同旁内角互补” 以及已知条件判断所作直线与 CD 平行，最后利用平行公理的推论得到 AB∥CD．

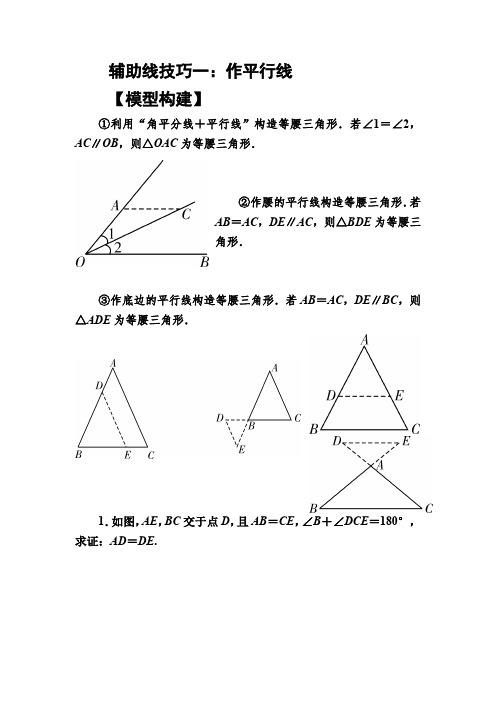
中考复习辅助线的添加----作平行线

辅助线技巧一：作平行线【模型构建】①利用“角平分线＋平行线”构造等腰三角形．若∠1＝∠2，AC∥OB，则△OAC为等腰三角形．②作腰的平行线构造等腰三角形．若AB＝AC，DE∥AC，则△BDE为等腰三角形．③作底边的平行线构造等腰三角形．若AB＝AC，DE∥BC，则△ADE为等腰三角形．1．如图，AE，BC交于点D，且AB＝CE，∠B＋∠DCE＝180°，求证：AD＝DE.证明：方法一：作AF∥CE交BC于点F，∴∠AFD＝∠ECD.∵∠B＋∠DCE＝180°，∴∠B＋∠AFD＝180°.而∠AFB＋∠AFD＝180°，∴∠B＝∠AFB.∴AB＝AF＝CE.∴可证△ADF≌△EDC.∴AD＝DE.方法二：作EF∥AB交BC的延长线于点F.可证EF＝CE＝AB，△ABD≌△EFD，∴AD＝DE.2．如图，等边△ABC中，D是边AC延长线上一点，延长BC 至E，使CE＝AD，DG⊥BE于G，求证：BG＝EG.证明：如答图，过点D作DF∥BE，交AB的延长线于F.∵△ABC是等边三角形，∴AB＝AC＝BC，∠ABC＝∠ACB＝∠AFD＝∠ADF＝∠A＝60°，∴△ADF是等边三角形，∴AD＝DF ＝AF，∴CD＝BF.∵AD＝CE，∴FD＝CE.∵∠DCE ＝∠ACB ＝60°，∴∠DFB ＝∠DCE .在△FBD 和△CDE 中，⎩⎪⎨⎪⎧CD ＝BF ，∠DFB ＝∠DCE ，FD ＝CE ，∴△FBD ≌△CDE (SAS)，∴DB ＝DE ，∴△BDE 是等腰三角形．∵DG ⊥BE 于G ，∴G 为BE 的中点，∴BG ＝EG .3．如图，△ABC 中，∠BAC ＝60°，∠C ＝40°，AP 平分∠BAC 交于BC 于点P ，BQ 平分∠ABC 交AC 于点Q .求证：AB ＋BP ＝BQ ＋AQ .证明：∵∠BAC ＝60°，∠C ＝40°，∴∠ABC ＝80°.∵BQ 平分∠ABC ，∴∠CBQ ＝12∠ABC ＝12×80°＝40°， ∴∠CBQ ＝∠C ，∴BQ ＝CQ ，∴BQ ＋AQ ＝CQ ＋AQ ＝AC ①，过点P 作PD ∥BQ 交CQ 于点D ，则∠CPD ＝∠CBQ ＝40°，∴∠CPD ＝∠C ＝40°，∴PD ＝CD ，∠ADP ＝∠CPD ＋∠C ＝40°＋40°＝80°.∵∠ABC ＝80°，∴∠ABC ＝∠ADP .∵AP 平分∠BAC ，∴∠BAP ＝∠DAP .∵在△ABP 与△ADP 中，∠ABP ＝∠ADP ，∠BAP ＝∠DAP ，AP ＝AP ， ∴△ABP ≌△ADP (AAS)，∴AB ＝AD ，BP ＝PD ，∴AB ＋BP ＝AD ＋PD ＝AD ＋CD ＝AC ②，由①②可得AB ＋BP ＝BQ ＋AQ .4.如图,在等腰Rt ABC 中，AC=BC,090ACB ∠=,D 是BC 的中点，E 是AB 延长线上的一点，且2BE=AB,求证：E CAD ∠=∠ 证明：如图，过点D 作DH//AB 交AC 于点H 。

湘教版七年级数学下册解题技巧专题：平行线中作辅助线的方法

解题技巧专题：平行线中作辅助线的方法◆类型一含一个拐点的平行线问题【方法17】1．(天门中考)如图，将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a，b上，如果∠2＝50°，那么∠1的度数为()A．10°B．20°C．30°D．40°第1题图第2题图2．如图，已知AB∥DE，∠ABC＝70°，∠CDE＝140°，则∠BCD的度数为()A．20°B．30°C．40°D．70°3．(金华中考)如图，已知AB∥CD，BC∥DE.若∠A＝20°，∠C＝120°，则∠AED的度数是________．第3题图第4题图4．如图，AB∥CD，∠A＝120°，∠1＝70°，则∠D的度数为________．5．小柯同学平时学习善于自己动手操作，以加深对知识的理解和掌握．学习了相交线与平行线的知识后，他又探索起来：如图，按虚线剪去长方形纸片的相邻两角，并使∠1＝115°，AB⊥CB于B，那么∠2的度数是多少呢？请你帮他计算出来．◆类型二含多个拐点的平行线问题【方法17】6．如图，直线l1∥l2，∠A＝125°，∠B＝85°，则∠1＋∠2＝()A．30°B．35°C．36°D．40°第6题图第7题图7．如图，直线l1∥l2，∠α＝∠β，∠1＝40°，则∠2＝________.8．如图，如果AB∥CD，则∠α，∠β，∠γ之间的关系为______________．第8题图9．★如图①，AB∥CD，EOF是直线AB，CD间的一条折线．(1)试说明：∠EOF＝∠BEO＋∠DFO；(2)如果将平行线间的1个拐点改为2个拐点，如图②，则∠BEO，∠EOP，∠OPF，∠PFC 之间会满足怎样的数量关系，请说明理由．参考答案与解析1．A2．B解析：如图，过C作CF∥DE，∴∠CDE＋∠DCF＝180°.∵∠CDE＝140°，∴∠DCF ＝40°.∵AB∥DE，∴CF∥AB，∴∠FCB＝∠ABC＝70°，∴∠BCD＝70°－40°＝30°.3．80° 4.50°5．解：过点B向左作BE∥AD.∵AD∥CF，∴AD∥BE∥CF，∴∠1＋∠ABE＝180°，∠2＋∠CBE＝180°，∴∠1＋∠2＋∠ABC＝360°.∵∠1＝115°，∠ABC＝90°，∴∠2＝360°－∠1－∠ABC＝155°.6．A解析：如图，作AC∥l1，BD∥l2，∴∠1＝∠3，∠2＝∠4.∵l1∥l2，∴AC∥BD，∴∠CAB＋∠ABD＝180°，∴∠3＋∠4＝125°＋85°－180°＝30°，∴∠1＋∠2＝30°.7．140°解析：如图，延长AE交l2于点B.∵l1∥l2，∴∠3＝∠1＝40°.∵∠α＝∠β，∴AB∥CD，∴∠2＋∠3＝180°，∴∠2＝180°－∠3＝180°－40°＝140°.8．∠α＋∠β－∠γ＝180°解析：如图，过点E作EF∥AB，∴∠α＋∠AEF＝180°.∵AB∥CD，∴EF∥CD，∴∠FED＝∠γ，∴∠AEF＝∠β－∠FED＝∠β－∠γ，∴∠α＋∠β－∠γ＝180°.9．解：(1)过点O作OM∥AB，如图①，∴∠1＝∠BEO.∵AB∥CD，∴OM∥CD，∴∠2＝∠DFO，∴∠1＋∠2＝∠BEO＋∠DFO，即∠EOF＝∠BEO＋∠DFO.(2)∠EOP＋∠PFC＝∠BEO＋∠OPF.理由如下：分别过点O，P作OM∥AB，PN∥CD，如图②.∵AB∥CD，∴OM∥PN∥AB∥CD，∴∠1＝∠BEO，∠2＝∠3，∠4＝∠PFC，∴∠1＋∠2＋∠PFC＝∠BEO＋∠3＋∠4，即∠EOP＋∠PFC＝∠BEO＋∠OPF.。

平行线分线段成比例(添辅助线)精编版

平行线分线段成比例(添辅助线)一、知识要点：1、平行线分线段成比例的基本图形；2、构造基本图形来解题。

二、例题简析及练习：例1、已知FD 与△ABC 的边AB 交于F ，与AC 交于E ，与BC 的延长线交于D ，且AF=CD ，求证：BC ABEF DE =练习1、已知如图BD=21CD ，求证：AC AFBE EF 2=例2、△ABC 中AF ∶FC=1∶2，G 是BF 的中点，AG 的延长线交BC 于E ，求BE:EC练习2、△ABC 中D 是BC 上的一点，AE ∶EC=3∶4，BD ∶DC=2∶3，求BF ∶FEA B C D E FC A B C GEF A B C E F例3、□ABCD 中，E 是AB 的中点，AF=21FD ，连接FE 交AC 于G ，求AG ∶AC练习3、已知，如图，△ABC 中，E 、F 分别为BC 的三等分点，D 为AC 的中点，BD 分别与AE 、AF 交于点M 、N ，求BM:MN:ND三、巩固练习：1、△ABC 中，AB=AC ，AD ⊥BC ，AP=PD 。

求证：1）PB=3PF ；2）如果AC=13，求AF 的长。

2、如图，D 、F 分别是△ABC 的边AB 、AC 上的点，且AD∶DB＝CF∶FA＝2∶3 连DF 交BC 的延长线于E.求EF∶FD.A B CDE F GN M FE D C B A A B C D FP3、已知OM ∶MP=ON ∶NR ，求证：△PQR 为等腰三角形。

4、直线截△ABC 的边AB 、BC 、AC 或其延长线于D 、E 、F ，求证：1=⋅⋅FACFEC BE DB AD5、在△ABC 中AC=BC ，F 为底边AB 上的一点，nmAF BF =，（n m ,为正数）。

取CF 的中点D ，连接AD 并延长交BC 于E 。

1）求ECBE的值；2）如果BE=2EC ，那么CF 所在的直线与边AB 有怎样的位置关系？证明你的结论。

全等辅助线方法2：作平行线

作平行线
1、如图，已知△ABC中，AB=AC, D为边AC延长线上一点，E为AB上一点，且BE=CD,连接DE交BC于点F,求证:DF=EF。

2、如图，等边三角形ABC的边长为10，D为AC边上任意一点，延长AB至点E,使BE=CD,连接DE交BC于点P.
（1）求证:DP=PE;
（2）过D点作DM⊥BC,作出图形并求BP的长。

3、如图，已知M是等边三角形ABD中边AB上任意一点(不与点A, B重合)，作∠DMN=60°,交△ABD的外角平分线于点N。

（1）求证:DM=MN.
（2）若点M在AB的延长线上，其余条件不变，结论"DM=MN"是否依然成立?请你画出图形并证明你的结论．
4、数学课上，王老师出示了如下框中的题目．
组长小明带领全组同学讨论，进行了如下探究，谢你一起完成．
（1）如图l，当点E为AB的中点时，试确定线段AE与DB的大小关系，井证明．
（2）如图2，当点E（点E不与点A、B重合）为线段AB上任意一点时，试确定线段AE与DB的大小关系，并证明．（提示：过点E作EF‖BC，交AC于点F）
（3）若点E在直线AB上，点D在CB的延长线上，且△ABC的边长为1，AE＝2．求出CD的长．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行线辅助线习题
2012/2/24
火箭式（铅笔式）结论________________ 鳄鱼式结论________________ 此结论非官方承认仅限在选择填空题使用，解答题请务必做出证明
E
A
B
C
D
1、如图1，AB ∥CD ，且∠BAP=60°-α，∠APC=45°+α，∠PCD=30°-α，则α=( ) A 、10° B 、15° C 、20° D 、30°
图1 图2 图3 2、如图2，CD AB //，且 25=∠A ， 45=∠C ，则E ∠的度数是（）
A. 60
B. 70
C. 110
D. 80
3、如图3，已知AB ∥CD ，则角α、β、γ之间的关系为（）
（A ）α+β+γ=1800 （B ）α—β+γ=1800 （C ）α+β—γ=1800 （D ）α+β+γ=3600
4、如图4，已知AB ∥CD,若∠A=20°，∠E=35°，则∠C 等于。

.
5、如图5，12//l l ，∠1=120°，∠2=100°，则∠3= 。

6、如图6，已知AC ∥ED ，∠C =26°，∠CBE =37°，则∠BED 的度数是。

图4 图5 图6
7.如图7所示,AB ∥CD,则∠A+∠E+∠F+∠C 等于_______
图
E
D C B A A B P
C D A B C D
E α β γ l 1
l 2
1
2 3 E
C
D
B
A
7
8．如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°则∠BED=__________.
图8 9、如图所示，AB∥ED，∠B＝48°,∠D＝42°, 证明：BC⊥CD。

（选择一种辅助线）
10、如图，若AB∥CD，猜想∠A、∠E、∠D之间的关系，并证明之。

11、如图，AB∥CD，∠BEF＝85°，求∠ABE＋∠EFC+∠FCD的度数。

12、如图，已知AB∥CD，∠1=100°，∠2=120°，求∠α。

13、已知AB
E
D
C
B
A
F
E
D
A B
C
2
1
F
E D
C
B
A
E
D
C
B
A
E
D
C
B
A。