(完整版)全等三角形难题超级好题汇总
全等三角形证明经典40题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 的长.解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:BC=ED ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
AD B C已知:∠1=∠2,CD=DE,EF如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
在BC上截取BF=AB,连接EF∵BE平分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE(SAS)∴∠A=∠BFE∵AB知:AB=CD,∠A=∠D,求证:∠B=∠C证明:设线段AB,CD所在的直线交于E,则:△AED是等腰三角形。
∴AE=DE而AB=CD∴BE=CE∴△BEC是等腰三角形∴∠B=∠C.是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB在AC上取点E,使AE=AB。
∵AE=ABBACDF21EAAP=AP∠EAP=∠BAE,∴△EAP≌△BAP∴PE=PB。
PC<EC+PE∴PC<(AC-AE)+PB∴PC-PB<AC-AB。
(完整版)初二数学全等三角形专题难题
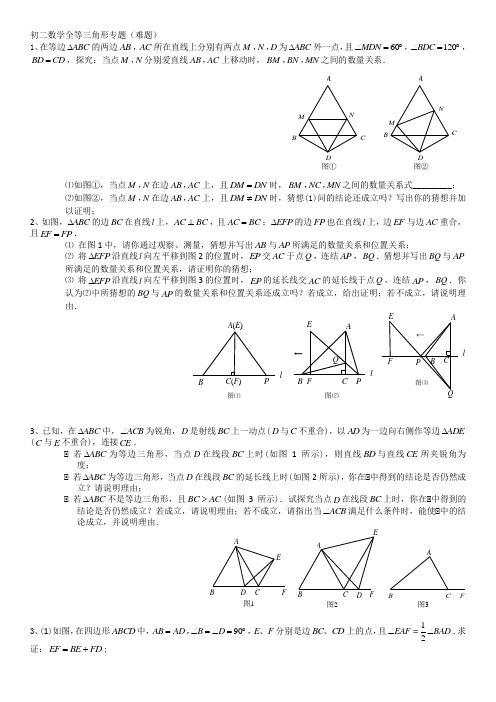
初二数学全等三角形专题(难题) 1、在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M N ,分别爱直线AB AC ,上移动时,BM BN MN ,,之间的数量关系.⑴如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________; ⑵如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的结论还成立吗?写出你的猜想并加以证明;2、如图,ABC ∆的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP ∆的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.⑴ 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;⑵ 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;⑶ 将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为⑵中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.3、已知,在ABC ∆中,ACB ∠为锐角,D 是射线BC 上一动点(D 与C 不重合),以AD 为一边向右侧作等边ADE ∆(C 与E 不重合),连接CE .⑴ 若ABC ∆为等边三角形,当点D 在线段BC 上时(如图1所示),则直线BD 与直线CE 所夹锐角为 度;⑴ 若ABC ∆为等边三角形,当点D 在线段BC 的延长线上时(如图2所示),你在⑴中得到的结论是否仍然成立?请说明理由;⑴ 若ABC ∆不是等边三角形,且BC AC >(如图3所示).试探究当点D 在线段BC 上时,你在⑴中得到的结论是否仍然成立?若成立,请说明理由;若不成立,请指出当ACB ∠满足什么条件时,能使⑴中的结论成立,并说明理由.3、(1)如图,在四边形ABCD 中,90AB AD B D =∠=∠=︒,,E F 、分别是边BC CD 、上的点,且12EAF =BAD ∠∠.求证:EF BE FD =+;图①M NDCBA图②MND CBA图⑴lPC (F )B A (E )图⑵Q ←lPFE C B A图⑶←QAEB CF Pl图1FED C B A图2B C D F AE图3B CFA(2) 如图在四边形ABCD 中,180AB AD B+D =∠∠=︒,,E F 、分别是边BC CD 、上的点,且12EAF BAD ∠=∠, (1)中的结论是否仍然成立?不用证明.(3) 如图,在四边形ABCD 中,AB AD =,180B ADC ∠+∠=︒,E F ,分别是边BC CD ,延长线上的点,且12EAF BAD ∠=∠, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.4、如图,已知⑴ABC 是等边三角形,E 是AC 延长线上一点,选择一点D ,使得⑴CDE 是等边三角形,如果M 是线段AD 的中点,N 是线段BE 的中点, 求证:⑴CMN 是等边三角形.(根据⑴ACD ⑴⑴BCE ,得出AD=BE ,AM=BN ;又⑴AMC ⑴⑴BNC ,可得CM=CN ,⑴ACM=⑴BCN ,证明⑴NCM=⑴ACB=60°即可证明⑴CMN 是等边三角形;)EFDCBAEFD CBAEFDCBA外角的平分线交于点N,DM与MN有怎样的数量关系?点M、N分别在AB、AC上,求AMN∆的周长.BMNM CBA。
(完整版)初二数学全等三角形专题难题

、如图,点M为正三角形ABD的边AB所在直线上的任意一点(点B除外),作60DMN,射线MN与DBA∠
N,DM与MN有怎样的数量关系?
、已知:如图,ABCD是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.
、如图所示,ABC是边长为1的正三角形,BDC是顶角为120的等腰三角形,以D为顶点作一个60的MDN,
、在等边ABC的两边AB,AC所在直线上分别有两点MND,,为ABC外一点,且60MDN,120BDC,
CD,探究:当点MN,分别爱直线ABAC,上移动时,BMBNMN,,之间的数量关系.
MN,在边ABAC,上,且DMDN时,BMNCMN,,之间的数量关系式_________;
MN,在边ABAC,上,且DMDN时,猜想(1)问的结论还成立吗?写出你的猜想并加
BMNMDCBA
3) 如图,在四边形ABCD中,ABAD,180BADC,EF,分别是边BCCD,延长线上的点,
1
EAFBAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量
、如图,已知⑴ABC是等边三角形,E是AC延长线上一点,选择一点D,使得⑴CDE是等边三角形,如果M是
AD的中点,N是线段BE的中点,
、如图,ABC的边BC在直线l上,ACBC,且ACBC;EFP的边FP也在直线l上,边EF与边AC重合,
EFFP.
在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
将EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP
将EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延线于点Q,连结AP,BQ.你
全等三角形难题(含答案)

全等三角形难题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形ADBCC∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 5. 证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
已知:∠1=∠2,CD=DE,EFBBA CDF2 1 E如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
在BC 上截取BF=AB ,连接EF ∵BE 平分∠ABC ∴∠ABE=∠FBE 又∵BE=BE∴⊿ABE ≌⊿FBE (SAS ) ∴∠A=∠BFE∵AB 知:ABDC BAFEABC DA14.P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB在AC上取点E,使AE=AB。
(完整word版)全等三角形难题(含答案),推荐文档

全等三角形难题(含答案)1.已知:AB=4, AC=2 D 是BC 中点,AD 是整数,求 AD解:延长AD 至U E,使AD=DE •/ D 是BC 中点 ••• BD=DC在^ ACD^n ^ BDE 中AD=DE/ BDE=Z ADCBD=DC••• AC=BE=2•••在△ ABE 中AB-BEv AE< AB+BE •/ AB=4即 4-2 v 2AD< 4+2 1v ADV 3••• AD=2延长CD 与 P,使D 为CP 中点。
连接 AP,BP •••DP=DC,DA=DB •••ACBP 为平行四边形又/ ACB=90•••平行四边形ACBP 为矩形2.已知:D 是AB 中点,/ ACB=90,求证: CD 1 -AB2••• AB=C P=1/2ABBC=DE / B=/ E ,/ C=/ D, F 是 CD 中点,求证:/ 仁/ 2证明:•/ BC=ED,CF=DF,/ BCF=/ EDF•••三角形BCF 全等于三角形 EDF (边角边)••• BF=EF, / CBF=/ DEF连接BE在三角形BEF 中,BF=EF••• / EBF=/ BEF•/ / ABC / AED••• / ABE=/ AEB •• AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,/ ABF=/ ABE+/ EBF=/ AEB+Z BEF=/ AEF•••三角形ABF 和三角形AEF 全等。
••• / BAF=/ EAF ( / 1 = / 2)。
4.已知:/ 仁/ 2, CD=DE EF//AB ,求证:EF=AC过C 作CG/ EF 交AD 的延长线于点GCG/ EF ,可得,/ EFD= CGDDE= DC/ FDE =/ GDC (对顶角)3.已知: 连接BF 和EFEF= CG/ CGD=/ EFD又,EF// AB•••/ CGD=/ 2 :.△ AGC为等腰三角形,AG= CG又EF = CG ••• EF= AC5.已知:AD平分/ BAC AC=AB+BD 求证:/ B=2/ C证明:延长AB取点E,使AE= AC连接DE•/ AD平分Z BAC• / EAD=/ CAD•AE= AC, AD= AD.△ A ED^A ACD (SAS• / E=/ C•AC= AB+BD• AE= AB+BD•AE= AB+BE• BD= BE• / BDE=/ E-/ ABC=/ E+Z BDE• / ABC= 2/ E• Z ABC= 2/ C6.已知:AC平分/ BAD CE丄AB, / B+Z D=180°,求证:AE=AD+BE证明:在AE上取F,使EF= EB,连接CF• CE 丄AB• / CEB=/ CEF= 90°•EB= EF, CE= CE,.△ CEB^A CEF• / B=/ CFE•/ B+/ »180°,/ CFE+/ CFA= 180• / CFAAC平分/ BAD./ DAC=/ FAC•AC= AC• △ ADC^A AFC( SAS• A» AF• AE= AF+ FE= AD+ BE12.如图,四边形ABCD中, AB// DC BE、CE分别平分/ ABC / BCD且点E在AD上。
各类型中高难度全等三角形125题(答案版)

1.已知:如图,AB ∥DE ,AC ∥DF ,BE =CF .求证:AB =DE .A DB EC F 【答案】∵ AB ∥ DE ,∴ ∠B =∠DEF∵AC ∥DF ,∴∠F =∠ACB∵ BE =CF ,∴ BE +EC =CF +EC 即 BC =EF∴∆ABC ≌∆DEF ,∴AB =DE .2.图中是一副三角板,45︒的三角板Rt ∆DEF 的直角顶点D 恰好在30︒的三角板Rt ∆ABC 斜边AB 的中点处,∠A = 30︒,∠E = 45︒,∠EDF =∠ACB = 90︒,DE 交AC 于点G ,GM ⊥AB 于M .(1)如图1,当DF 经过点C 时,作CN ⊥AB 于N ,求证:AM =DN .(2)如图2,当DF ∥AC 时,DF 交BC 于H ,作HN ⊥AB 于N ,(1)的结论仍然成立,请你说明理由.FCEGAM D N B图1ECFG HA B图2【答案】⑴ ∵ ∠A = 30︒,∠ACB = 90︒, D 是 AB 的中点,∴ BC =BD , ∠B = 60︒ ∴△BCD 是等边三角形.又∵CN ⊥DB ,∴DN =1DB ,2∵∠EDF = 90︒,∆BCD 是等边三角形.∴∠ADG = 30︒,而∠A = 30︒,∴GA =GD .∵ GM ⊥AB ,∴AM =1 AD 2又∵AD =DB ,∴AM =DN .⑵∵DF ∥AC ,∴∠BDF =∠A = 30︒,∠AGD =∠GDH = 90︒,∴∠ADG = 60︒.∵∠B = 60︒,AD =DB ,∴∆ADG ≌∆DBH ,∴AG =DH ,又∵∠BDF =∠A ,GM ⊥AB ,HN ⊥AB ,∴∆AMG ≌∆DNH .∴AM =DN .3.在正方形ABCD 中,AB 、BC 、CD 三边上分别有点E 、G 、F ,且EF ⊥DG .求证:EF =DG .⎨ ⎩ADA DEEM FFB G CBGC【答案】过点C 作 EF 的平行线,交 AB 于 M .易知CM = EF .从而证的∆BCM ≌ ∆CDG ,从而有 DG = CM ,故 EF = DG .4.在正方形 ABCD 中, E 、 F 、G 、 H 分别是 AB 、 BC 、CD 、 DA 边上的点,且 EG ⊥ FH ,求证: EG = FH .A HD A H N DGGEEMBF CBF C【答案】过点 E 作 EM ⊥ CD ,过点 F 作 FN ⊥ AD ,垂足分别为 M 、N . 由 EM ⊥ CD , FN ⊥ AD , EG ⊥ FH ,易得∠MEG = ∠NFH 因为 EM = BC , BC = CD , CD = NF ,所以 EM = NF 故∆EMG ≌ ∆NFH ,所以 EG = FH .5.∆ABC 中, ∠B = 90︒ , M 为 AB 上一点,使得 AM = BC , N 为 BC 上一点,使得CN = BM ,连 AN 、CM 交于 P 点.试求∠APM 的度数,并写出你的推理证明的过程.AMBN C【答案】∠APM 的度数为45︒证明过程如下:如图过点 M 作 AB 的垂线 MD ,使 MD = CN ,连接 DA 、 DN , 于是因为 MD ∥ CN 且 MD = CN ,所以四边形 MDNC 是平行四边形. 从而∠MDN = ∠MCN ,又因为CN = BM ,得到 DM = BM ,进而在∆MDA 与∆MBC 中, ⎧DM = BM ⎪∠DMA = ∠MBC = 90︒ , ⎪MA = BC PFP⎨ ⎩所以∆DMA ≌ ∆MBC ,这样 DA = MC ,而 MC = DN , 所以 DN = DA .又因为∠ADN = ∠ADM + ∠MDN= ∠ADM + ∠DAM = 90︒ , 所以得到∆ADN 是一个等腰直角三角形,所以∠AND = 45︒ ,利用 MC ∥ DN ,从而得到∠APM = ∠AND = 45︒ .ADB NC6.如图,在Rt ∆ABC 中, AB = AC ,AD ⊥ BC ,垂足为 D . E 、F 分别是CD 、AD 上的点,且CE = AF .如果∠AED = 62︒ ,那么∠DBF = .A【答案】28︒BDE7.E 、F 分别是正方形 ABCD 的 BC 、CD 边上的点,且 BE = CF .求证:AE ⊥ BF .ADF【答案】在∆ABE 和∆BCF 中⎧ AB = BC ⎪∠ABE = ∠BCF⎪BE = CF∴ ∆ABE ≌ ∆BCF BEC∴ ∠BAE = ∠CBF ∵ ∠BAE + ∠AEB = 90︒ ∴ ∠CBF + ∠AEB = 90︒ ∴ AE ⊥ BF8.E 、F 、G 分别是正方形 ABCD 的 BC 、CD 、AB 边上的点,GE ⊥ EF ,GE = EF .求证: BG + CF = BC .AD【答案】显然, ∆BEG ≌ ∆CFE ,GFBECM PC∴ BG = CE , BE = CF ∴ BG + CF = BC9.如图,矩形 ABCD 中, E 是 AD 上一点, CE ⊥ EF 交 AB 于 F 点,若 DE = 2 ,矩形周长为16 ,且CE = EF ,求 AE 的长.AEDFBC【答案】∵ FE ⊥ EC ,∴ ∠AEF + ∠DEC = 90︒ .∵ ∠AEF + ∠AFE = 90︒ , ∴ ∠AFE = ∠DEC .在三角形 AFE 与∆DEC 中, FE = CE , ∠A = ∠D = 90︒ , ∠AFE = ∠DEC , ∴ ∆AFE ≌ ∆DEC . ∴ AE = DC . ∵矩形周长为16 , ∴ AD + DC = 8 . ∵ AD = AE + DE ,∴且 DE = 2 .∴ 2 AE = 8 - DE . 即 AE = 3 .10.如图,已知∆ABC 中,∠ABC = 90︒,AB = BC ,三角形的顶点在相互平行的三条直线l 1 ,l 2 ,l 3 上,且l 1 ,l 2 之间的距离为2 ,l 2 ,l 3 之间的距离为3 ,则 AC 的长是 .Al 1 l 2【答案】2 Bl 311.两个全等的30︒ 、60︒ 的三角板 ADE 、 BAC ,如右下图所示摆放, E 、 A 、C 在一条直线上,连结 BD .取 BD 的中点 M ,连结 ME 、MC ,试判断∆EMC 的形状, 并说明理由.BMDEA C【解析】判断∆EMC 是等腰直角三角形.理由:如图,连结 AM .17MBA C∵ ∠DAE = 30︒ , ∠BAC = 60︒ ,∴ ∠DAB = 90︒ ∵ ∆ADE ≌ ∆BAC ,∴ AD = AB又∵ M 是 BD 的中点,∴ AM = DM = BM ∴ ∠ADM = ∠MAB = 45︒ ∴ ∠EDM = ∠EDA + ∠ADM = 60︒ + 45︒ = 105︒ ∴ ∠MAC = ∠MAB + ∠BAC = 45︒ + 60︒ = 105︒ ∴ ∠EDM = ∠MAC ∵ ED = CA ,∴ ∆EDM ≌ ∆CAM ∴ EM = CM , ∠DME = ∠AMC而∠DME + ∠EMA = 90︒ ,∴ ∠AMC + ∠EMA = 90︒ 即∠EMC = 90︒ ,∴ ∆EMC 是等腰直角三角形.12.已知等腰直角三角形 ABC , ∠C 为直角, M 为 BC 的中点. CD ⊥ AM .求证: ∠AMC = ∠DMB .求证: ∠AMC = ∠DMB .CA DB【答案】法一:如图,过 B 作 EB ⊥ BC ,交CD 延长线于 E .CE∵ ∠3 + ∠1 = 90︒ , ∠4 + ∠1 = 90︒ ,∴ ∠3 = ∠4 .又 AC = CB ,∴ Rt ∆CBE ≌ Rt ∆AMC ,∴ BE = CM , ∠5 = ∠1 . 又 BM = CM ,∴ BE = BM .∴ ∠MBD + ∠EBD = 90︒ ,而∠MBD = 45︒ ,∴ ∠EBD =∠MBD . 又 BD 为公共边,∴ ∆BED ≌ ∆BMD .∴ ∠5 = ∠2 .解法二:如图,作底边 AB 的高CE 交 AM 于 F ,则CE 亦为中线和角平分线,3 1 M4 2 ADB5 MDC ∴AE =CE =BE .又∠3 +∠CDE =∠4 +∠CDE = 90︒.∴∠3 =∠4 ,∴Rt∆DCE = Rt∆FAE ,∴AMA E D B=CE=2,∴∠EDF = 45︒=∠B ,故CM AC 1DF ∥BC .又 E 、M 为AB 、BC 的中点,∴连接EM ,则EM ∥AC .∴AC ⊥BC ,∴EM ⊥BC ,故EM ⊥DF .∴EM 为DF 的中垂线.∴∠FME =∠DME .而∠FME +∠1 =∠DME +∠2 = 90︒,∴∠1 =∠2 .解法三:如图,作CG =AG 的平分线CF 交AM 于F ,CA DB 则∠ACF =∠MCF = 45︒,即ACF =∠CBD = 45︒.∵AC ⊥BC ,C D ⊥AM ,∴∠CAF +∠CMF =∠BCD +∠CMF = 90︒.∴BM=1.AC 2又∠B =∠CAD ,∴∆ACF ≌∆CBD .∴CF =BD .又CM =BM ,∠MCF =∠MBD .∴∆CFM ≌∆BDM .∴∠FMC =∠DMB .解法四:如图,过D 作DG ⊥CB .CA∵∠B = 45︒,∴DG =BG .∵∠DCG +∠AMC =∠FAC +∠AMC = 90︒,∴∠DCG =∠FAC .∴∆DCG ∽∆MAC .∴DG∶CG =CM∶AC = 1∶2 ,则BG∶CG = 1∶2 .∵DG ∥AC ,∴BD∶AD = 1∶2 ,而BM∶AC = 1∶2 , B =∠CAD .∴∆BMD ∽∆ACD ,∴∠BMD =∠ACD .而∠ACD =MGM F3 1FM24AMC ,解法五:如图,延长CB 到 E ,使 BE = BC .连接 AE ,延长CD 交 AE 于G ,则 AC = BC = BE ,CE∴AM = CE = 2 .CM AC 1 ∴ Rt ∆ACM ∽ Rt ∆ECA .∴ ∠CAM = ∠E . ∵ ∠CAM + ∠ACF = 90︒ , ∠GCE + ∠ACF = 90︒ , ∴ ∠CAM = ∠GCE .即∠GCE = ∠E .∴ CG = GE . ∵ ∠CAE + ∠E = 90︒ , ∠ACG + ∠GCE = 90︒ ,∴ ∠CAE = ∠ACG ,∴ CG = AG ,从而 AG = GE .又∵ BC = BE ,所以 D 为∆AEC 的重心,∴ BD = 1.而 BM = 1 , ∠B = ∠CAD . AD 2AC 2∴ ∆BMD ∽ ∆ACD ,∴ ∠BMD =∠ACD . 而 ∠AMC = ∠ACF ,∴ ∠BMD = ∠AMC .解法六:如图,过 A 作 AH ⊥ AM ,与 BC 的延长交于 H .HD B∵ ∠1 + ∠2 = 90︒ , ∠1 + ∠AMC = 90︒ , ∴ ∠2 = ∠AMC , ∴ Rt ∆AHC ∽ Rt ∆MAC ,∴ HC = AC= 2 . AC MC而 AC = BC ,∴HC= 2 .BC∵ HA ∥ C D ,∴ AD = HC= 2 .BD BC又∵ AC BM = 2 , ∠CAD = ∠B ,∴ ∆ADC ∽ ∆BDM ,C MFFMAD BG而∠AMC = ∠ACD ,∴ ∠AMC = ∠BMD .解法七:如图,过 D 作 DE ⊥ BM ,垂足为 E .CA∵ ∠CAM + ∠CMA = 90︒ , ∠ECD + ∠CMA = 90︒ , ∴ ∠CAM = ∠ECD , ∴ Rt ∆CAM ∽ Rt ECD ,∴ DE = MC = 1 .CEAC2∵ ∠B = 45︒ , ∠DEB = 90︒ ,∴ DE = BE ,∴ BE = 1. CE 2设 ME = x ,CM = BE = a ,∴a - x = 1 ,∴ x = a. a + x 2 3∴ DE = BE = a - a = 2a ,∴ ME = 1 = MC,3 3 ∴ Rt ∆CAM ∽ Rt ∆EDM , ∴ ∠AMC = ∠BMD .DE 2 AC13.如图所示,已知在等腰直角三角形 ABC 中, ∠BAC 是直角, D 是 AC 上一点, AE ⊥ BD ,AE 的延长线交 BC 于 F ,若∠ADB = ∠FDC ,求证:D 是 AC 的中点.AFC【答案】过C 作CH 垂直于 AC 交 AF 延长线于 H 点;易证∆ABD ≌∆AHC , HC = AD ;进而证明∆FHC ≌∆FDC ,得到 HC = CD ,则 D 为 AC 中点.A14.如图所示,在等边∆ABC 中, DE ∥ BC , O 为∆ADE 的中心, M 为 BE 的中点, 求证OM ⊥ CM .M EDE【答案】如图所示,延长OM 至点 N ,使OM = MN ,连接OA 、OE 、OC 、 BN 、CN .AAD OEO N D EMMBCNB C因为OM = NM , BM = ME , ∠OME = ∠NMB , 故∆BMN ≌ ∆EMO ,则 BN = EO , ∠OEM =∠NBM . 因为 DE ∥ BC ,则∠DEB = ∠CBE , ∠OED = ∠CBN .因为O 为∆ADE 的中心,则OA = OE = BN , ∠OAE = ∠OED = 30︒ = ∠CBN . 因为 AC = BC ,故∆AOC ≌ ∆BNC ,从而OC = CN . 因为OM = MN ,故OM ⊥ CM .【点评】如果具备三角形相似的知识,我们就可以采取下面的解法. 如图所示,取 AE 的中点 N ,连接 MN 、OA 、ON 、OC . 因为O 为∆ADE 的中心,故∠OAN = 30︒ , OA =2ON . 因为 AN = NE , BM = EM ,故 AB = 2MN = AC .因为ON ⊥ AC , MN ∥ AB ,故∠MNE = 60︒ ,因为∠ONM = 30︒ ,故∆OAC ∽ ∆ONM ,∠OMN = ∠OCN ,则O 、M 、C 、N 四点共圆.因为ON ⊥ AC ,故OM ⊥ CM .15.已知 P 为等腰直角∆ABC 的斜边 AB 上任意一点, PE 、PF 分别为 AC 、BC 之垂线,垂足为 E 、 F . M 为 AB 之中点.则 E 、 M 、 F 组成等腰直角三角形.A ECF B【答案】解法一:如图,连接CM ,则CM 为 AB 之中线,亦为 AB 之高.P MAECFB∴ ∠CMA = 90︒ . ∵ ∠PEC = ∠PFC = ∠ECF = 90︒ , ∴ ECFP 为矩形,故 PE = CF . 又∵ ∠A = 45︒ ,∴ ∆AEP 为等腰直角三角形,∴ AE = PE .∴ AE = CF . 又∵ CM = AM , ∠MCF = ∠A = 45︒ , ∴ ∆AEM ≌ ∆CFM ,∴ ∠AME = ∠CMF , EM = FM . ∵ ∠CME + ∠AME = 90︒ ,∴ ∠CME + ∠CMF = 90︒ ,即∠EMF = 90︒ . ∴ ∆EMF 为等腰直角三角形. 解法二:如图,由 M 作 ME ' ⊥ AC , MF ' ⊥ BC ,则显然由于 M 为 AB 之中点, AC = BC , AC ⊥ BC ,AE E'CF F'B∴ ME 'CF ' 为正方形,故 ME ' = MF ' . 又设 ME ' 交 PF 于Q , 则∵ PE ⊥ AC , PF ⊥ BC ,∴ ∠EPF = ∠C = 90︒ .而∠PEE ' = ∠EE 'Q = 90︒ . ∴ EE 'QP 为矩形,故 EE ' = PQ . 同理 FF ' = QM .又∵ PF ∥ AC ,∴ ∠QPM = ∠A = 45︒ . ∴ ∆PQM 为等腰直角三角形, ∴ PQ = QM ,故 EE ' = FF ' .又 ME ' = MF ' , ∠EE 'M = ∠FF 'M = 90︒ . ∴ ∆EE 'M ≌ ∆FF 'M ,∴ ∠EME ' = ∠FMF ' , EM =FM . 又∠E 'MF + ∠FMF ' = 90︒ , ∴ ∠E 'MF + ∠EME ' = 90︒ .即∠EMF = 90︒ ,故∆MEF 为等腰直角三角形.解法三:如图,延长 FM 到Q ,使 MQ = FM ,连接 AQ .PMPMQ2 2 2 A QECFB∵ AM = BM ,∴ A 、 F 、 B 、Q 4 点组成平行四边形. ∴ AQ = FB , AQ ∥ FB .又∵ BC ⊥ AC ,∴ AQ ⊥ AC , ∴ ∠QAE = ∠FCE = 90︒ .又∵ PF ⊥ BC , ∠B = 45︒ ,∴ FP = FB .同理 EP = AE . ∵ ECFP 为矩形,∴ FP = CE , EP = CF ,故 AB .而CM ⊥ AB , ∴ AQ = CE , A E = CF . ∴ Rt ∆AEQ ≌ Rt ∆CFE . ∴ EQ = FE , ∠AQE = ∠CEF , ∠QEA = ∠EFC . ∵ ∠AQE + ∠QEA = 90︒ ,∴ ∠CEF + ∠QEA = 90︒ .故 PF= .QF∴ ∆FEQ 为等腰直角三角形.而 M 为底边之中点,所以∆EMF 亦为等腰直角三角形.解法四:如图,连接CM ,则因为 M 为 AB 之中点,所以CM ⊥ AB ,CM 平分∠ACB , 即∠MCB = 45︒ .由 F 向 MB 引垂线 FQ ,向CM 引垂线 FF ' ,显然 F 'FQM 为矩形.则 FF ' = MQ .AECFB又∵ ∆CF 'F 为等腰直角三角形, CF = 2FF ' = 2MQ . 又∵ PE ⊥ AC , PF ⊥ BC , AC ⊥ BC , ∴ ECFP 为矩形,故 EP = CF = 2MQ . 于是在Rt ∆EPF 和Rt ∆MQF 中, PF = FB =2QF , PF = , EP= ,∴ PF = EP ,QF MQQF MQ∴ ∆EPF ∽ ∆MQF ,故∠EFP =∠MFQ . 又∵ ∠PFM + ∠MFQ = 45︒ , ∵ ∠PFM + ∠EFP = 45︒ ,即 PF = BF .同理∠FEM = 45︒ , ∆EMF 为等腰直角三角形.PMPM QF'E解法五:如图,连接CP 、CM .AECFB∵ PF = BF , ∆ABC 为等腰直角三角形, ∴ ∠BPF = ∠BCM = 45︒ .∴ P 、C 、 F 、 M 4 点共圆.∴ ∠CMF = ∠CPF .又∵ ∠CPF = ∠CEF ,∴ ∠CEF = ∠CMF ,∴ E 、C 、 F 、 M 4 点共圆.∴ ∠MEF = ∠MCF = 45︒ , ∠MFE = ∠MCE = 45︒ ,∴ iEMF 是等腰直角三角形.16.长方形 ABCD 中, AB = 4 , BC = 7 , ∠BAD 的角平分线交 BC 于点 E , EF ⊥ ED 交 AB 于 F ,则 EF = .ADFBEC【解析】由 AB = 4 ,AE 平分∠BAD 可知 BE = AB = CD = 4 .由基本图可知∆BEF ≌∆CDE , 故 EF = DE又 BC = 7 , BE = 4 ,故CE = 3 .由勾股定理可知, DE = 5 . 从而可知 EF = 5 .【答案】517.如图,设∆ABC 和∆CDE 都是正三角形,且∠EBD = 62︒ ,则∠AEB A .124︒ B .122︒ C .120︒ D .118︒的度数是( )ABCD【答案】分析 既然题目这样问,说明这两个角之间必然能找到一定的联系. 解 易知∠ACE = ∠BCD , ∆AEC ≌ ∆BDC ,于是∠EAC = ∠DBC ,从而∠EBD = ∠CBD + ∠CBE = ∠EAC + ∠CBE ,在考虑到∠EAC + ∠AEC + ∠ACE + ∠CEB + ∠ECB + ∠EBD = 360,有:∠BEC + ∠AEC = 360 - 60 - 62 = 360 - ∠AEB 从而∠AEB = 122 ,选B 。
全等三角形难题集锦超级好

1.如图,已知等边△ABC ,P 在AC 延长线上一点,以PA 为边作等边△APE,EC 延长线交BP 于M ,连接AM,求证:(1)BP=CE ; (2)试证明:EM-PM=AM.2.已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图B E3.已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB ,连接AE CD ,. (1)求证:AGE DAC △≌△;(2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎样的三角形,试证明你的结论.CGAEDBF4、在ABC △中,2120AB BC ABC ==∠=,°,将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A BC A B 111△,交AC 于点E ,11A C 分别交AC BC 、于D F 、两点.如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系?并证明你的结论;ADBECF 1A1CADBECF 1A1C5. 如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .ABCD EF6已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°, EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.A EC F BD图1图3ADFECBADBCE 图2F7、已知AC//BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E.求证:AB=AC+BD.8.等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC.∠MDN=60°射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.DCBA9.如图1,BD 是等腰ABC Rt Δ的角平分线, 90=∠BAC .(1)求证BC =AB +AD ;(2)如图2,BD AF ⊥于F ,BD CE ⊥交延长线于E ,求证:BD =2CE ;10、如图,四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,AD+AB=2AE ,则∠B 与∠ADC 互补.为什么?ABCD FE 图2DBEAC图十一11如图,在△ABC 中∠ABC,∠ACB 的外角平分线交P.求证:AP 是∠BAC 的角平分线12、如图在四边形ABCD 中,AC 平分∠BAD ,∠ADC +∠ABC =180度,CE ⊥AD 于E ,猜想AD 、AE 、AB 之间的数量关系,并证明你的猜想,EBAC图2DCB13如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O ,求证:OE=OD14如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DC ,求证:BE=CF15如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
全等三角形难题集锦超级好题汇总

1.如图,已知等边△ABC ,P 在AC 延长线上一点,以PA 为边作等边△APE,EC 延长线交BP 于M ,连接AM,求证:(1)BP=CE ;(2)试证明:EM-PM=AM.2、点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,线段AN,MC 交于点E ,BM,CN 交于点F 。
求证:(1)AN=MB.(2)将△ACM 绕点C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,(1)中的结论是否依然成立 (3)AN与BM 相交所夹锐角是否发生变化。
3.已知,如图①所示,在ABC △和ADE △中,AB AC =,ADAE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.22题PB EAB A B N CNA4、如图1,以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断ABC △与AEG △面积之间的关系,并说明理由.5、如图所示,已知△ABC 和△BDE 都是等边三角形,且A 、B 、D 三点共线.下列结论:①AE=CD ;②BF=BG ;③HB 平分∠AHD ;④∠AHC=60°,⑤△BFG 是等边三角形;⑥FG ∥AD .其中正确的有( )A .3个B .4个C .5个D .6个6. 如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .AGFCBDE(图1)ABC DEF7、已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEFABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系请写出你的猜想,不需证明.8.已知AC 求证:AB=AC+BD.A E C FBD图1图3ADFECBADBCE 图2FDCBA9.如图1,BD 是等腰ABC Rt Δ的角平分线, 90=∠BAC .(1)求证BC =AB +AD ;(2)如图2,BD AF ⊥于F ,BD CE ⊥交延长线于E ,求证:BD =2CE ;10、已知,如图1,在四边形ABCD 中,BC >AB ,AD=DC ,BD 平分∠ABC 。
完整版)全等三角形难题题型归类及解析

完整版)全等三角形难题题型归类及解析1.在三角形ABC中,AD是角BAC的平分线,AE=AC,DE=2cm,BD=3cm,求BC的长度。
为了解决这个问题,我们可以利用角平分线的轴对称性,构造全等三角形ADE和ABC。
因为AE=AC,所以三角形ADE和三角形ABC的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠DAE=∠CAB,∠AED=∠ACB。
又因为AD是角BAC的平分线,所以∠DAE=∠EAC,因此∠CAB=2∠EAC。
设BC=x,则根据正弦定理可得:3/x=sin(2EAC)/sin(EAC),化简后得到x=6.2.在三角形ABC中,BD是角ABC的平分线,AB=BC,P在BD上,PM⊥AD于M,PN⊥CD于N,求解PM与PN 的关系。
首先,我们可以利用角平分线的性质,构造等腰三角形ABD和CBD。
因为AB=BC,所以三角形ABD和三角形CBD的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠BDA=∠BDC,∠ADB=∠CDB。
又因为BD是角ABC的平分线,所以∠ADB=∠BDC,因此∠BDA=∠CDB。
因此,三角形APM和三角形CPN是全等的。
因为全等三角形的对应边相等,所以PM=PN。
3.在三角形OAB中,P是角OAB的平分线上的一点,PC⊥OA于C,∠OAP+∠OBP=180°,OC=4cm,求解AO+BO的值。
我们可以利用角平分线的轴对称性,构造全等三角形OAC和OBC。
因为∠OAP+∠OBP=180°,所以∠AOP=∠BOP=90°。
因此,三角形OAP和三角形OBP是直角三角形。
设AO=x,BO=y,则根据勾股定理可得:x^2+PC^2=OP^2,y^2+PC^2=OP^2.又因为OC=4cm,所以PC=2cm。
将PC代入上面的两个式子中,得到x^2+y^2=OP^2-4.又因为三角形OAC和三角形OBC是全等的,所以x=y,因此2x^2=OP^2-4,即OP^2=2x^2+4.因此,AO+BO=2x=2√((OP^2-4)/2)=2√(2x^2)=2√(2y^2)=2√(2x^2+4)/2=2√(OP^2)/2=OP√2=2√6.4.在三角形ABC中,E在边AC上,且∠XXX∠ABC。
(完整)全等三角形难题及答案
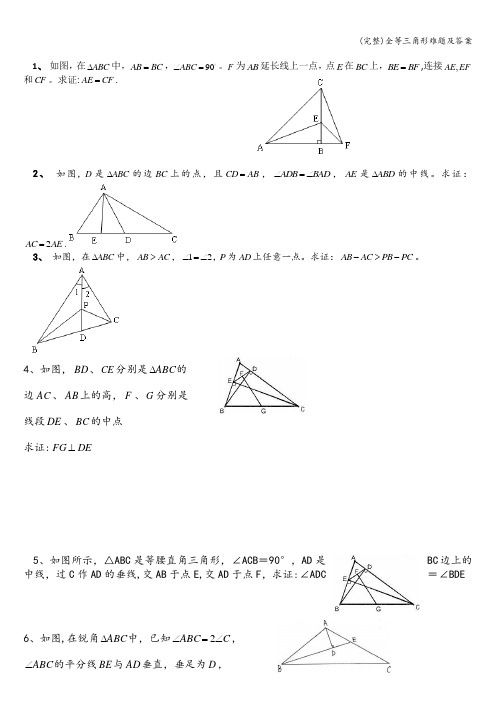
1、 如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =.2、 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =.3、 如图,在ABC ∆中,AB AC >,12∠=∠,P 为AD 上任意一点。
求证:AB AC PB PC ->-。
4、如图,BD 、CE 分别是ABC ∆的边AC 、AB 上的高,F 、G 分别是线段DE 、BC 的中点求证:DE FG ⊥5、如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E,交AD 于点F ,求证:∠ADC=∠BDE6、如图,在锐角ABC ∆中,已知C ABC ∠=∠2,ABC ∠的平分线BE 与AD 垂直,垂足为D ,若cm BD 4=,求AC 的长参考答案1、 思路分析:可以利用全等三角形来证明这两条线段相等,关键是要找到这两个三角形.以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置,而线段CF 正好是CBF ∆的边,故只要证明它们全等即可。
解答过程:90ABC ∠=,F 为AB 延长线上一点∴90ABC CBF ∠=∠=在ABE ∆与CBF ∆中AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴ABE CBF ∆≅∆(SAS)∴AE CF =。
解题后的思考:利用旋转的观点,不但有利于寻找全等三角形,而且有利于找对应边和对应角。
小结:利用三角形全等证明线段或角相等是重要的方法,但有时不容易找到需证明的三角形。
这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。
2、 思路分析:要证明“2AC AE =”,不妨构造出一条等于2AE 的线段,然后证其等于AC 。
全等三角形难题(含答案)
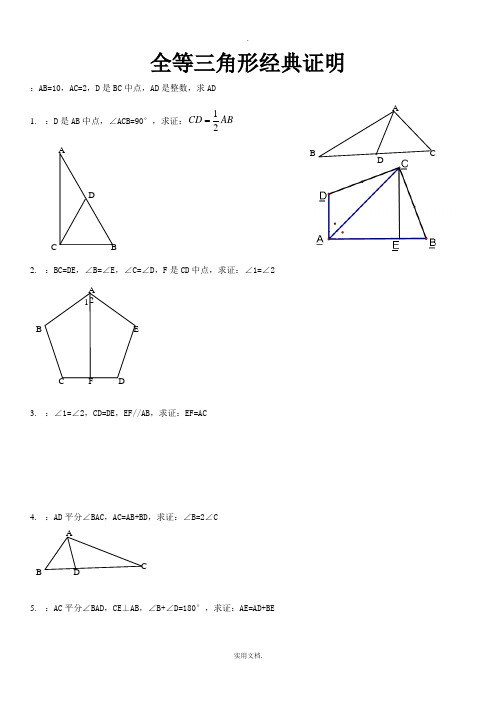
全等三角形经典证明:AB=10,AC=2,D 是BC 中点,AD 是整数,求AD1. :D 是AB 中点,∠ACB=90°,求证:12CD AB2. :BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23. :∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4. :AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5. :AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BEA BC DEF 21 DABC CDB AADBC6. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
7.:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C8、:AB=CD ,∠A=∠D ,求证:∠B=∠C9.〔5分〕如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC . 10.〔5分〕如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA 11.〔6分〕如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,假设AB =CD ,AF =CE ,BD 交DCB A F E A B CDAC 于点M .〔1〕求证:MB =MD ,ME =MF〔2〕当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?假设成立请给予证明;假设不成立请说明理由.12.〔7分〕:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, 〔1〕求证:△AED ≌△EBC .〔2〕观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.〔直接写出结果,不要求证明〕:/13.〔7分〕如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .14、〔10分〕如图:DF=CE ,AD=BC ,∠D=∠C 。
(完整版)全等三角形难题集锦超级好题汇总
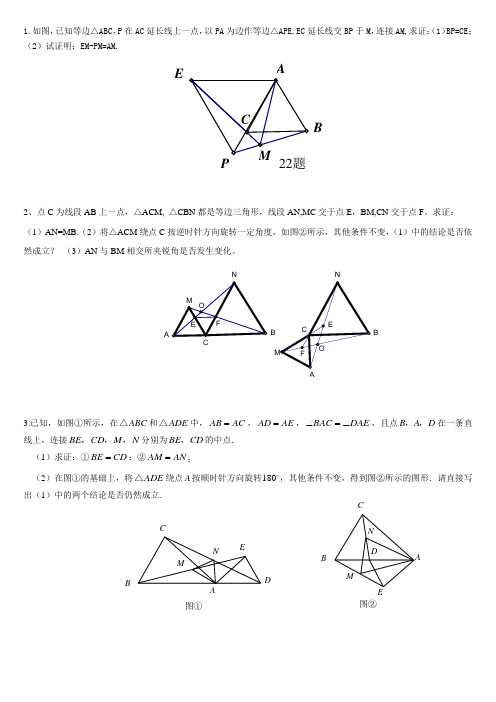
1.如图,已知等边△ABC ,P 在AC 延长线上一点,以PA 为边作等边△APE,EC 延长线交BP 于M ,连接AM,求证:(1)BP=CE ; (2)试证明:EM-PM=AM.2、点C 为线段AB 上一点,△ACM, △CBN 都是等边三角形,线段AN,MC 交于点E ,BM,CN 交于点F 。
求证: (1)AN=MB.(2)将△ACM 绕点C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,(1)中的结论是否依然成立? (3)AN 与BM 相交所夹锐角是否发生变化。
3.已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.22题PB EA B A B N CN 图①图②4、如图1,以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断ABC △与AEG △面积之间的关系,并说明理由.5、如图所示,已知△ABC 和△BDE 都是等边三角形,且A 、B 、D 三点共线.下列结论:①AE=CD ;②BF=BG ;③HB 平分∠AHD ;④∠AHC=60°,⑤△BFG 是等边三角形;⑥FG ∥AD .其中正确的有( ) A .3个 B .4个 C .5个 D .6个6. 如图所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .AG FC BDE (图1) ABCD EFDCB A7、已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.8.已知AC//BD,∠CAB 和∠DBA 的平分线EA 、EB 与CD 相交于点E. 求证:AB=AC+BD.9.如图1,BD 是等腰ABC Rt Δ的角平分线, 90=∠BAC .(1)求证BC =AB +AD ; (2)如图2,BD AF ⊥于F ,BD CE ⊥交延长线于E ,求证:BD =2CE ;A E C F BD图1图3ADFECBADBCE图2FAD FE图十一4321P A BC 10、已知,如图1,在四边形ABCD 中,BC >AB ,AD=DC ,BD 平分∠ABC 。
(完整版)全等三角形证明经典50题(含答案)
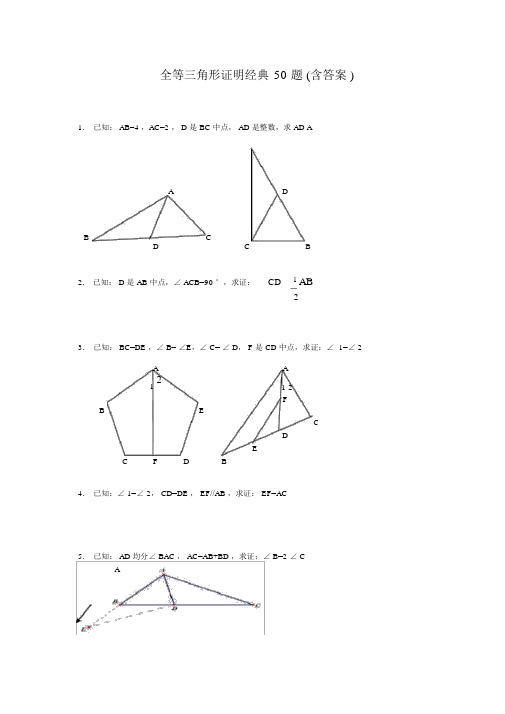
全等三角形证明经典50 题 (含答案 )1.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AA DB CD C B2. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB23.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A A1 21 2BFECDEC FD B4.已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=AC5.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CA6.已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
E DCFA B13.已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ C14.P 是∠ BAC 均分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB CAP DB15. 已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE16.已知, E 是 AB 中点, AF=BD , BD=5 , AC=7 ,求 DCDF A CE B18.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .19.如图, OM 均分∠ POQ ,MA ⊥ OP,MB⊥ OQ , A、 B 为垂足, AB 交 OM 于点 N.求证:∠ OAB=∠OBA20.( 5 分)如图,已知 AD ∥BC,∠ PAB 的均分线与∠ CBA 的均分线订交于 E, CE 的连线交AP 于 D .求证: AD +BC =AB.PACEDCD BA B21.如图,△ ABC 中, AD 是∠ CAB 的均分线,且AB=AC+CD,求证:∠ C=2∠ B22.( 6 分)如图①, E、F 分别为线段AC 上的两个动点,且DE ⊥AC 于 E, BF⊥AC 于 F ,若 AB=CD , AF=CE, BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点挪动到如图②的地点时,其他条件不变,上述结论可否建立?若建立请赐予证明;若不建立请说明原因.23.已知:如图,DC∥ AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添协助线的状况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE ODB C24.( 7 分)如图,△ ABC 中,∠ BAC=90 线垂直于过 C 点的直线于 E,直线 CE 交求证: BD =2CE.度, AB=AC, BD 是∠ ABC 的均分线, BD 的延伸BA 的延伸线于 F.FAED证明:B C25、如图: DF=CE, AD=BC,∠ D=∠ C。
(完整版)全等三角形难题集锦超级好题汇总,推荐文档

D
C
A
E
B
12、.如图,在△ABC 中∠ABC,∠ACB 的外角平分线交 P.求证:AP 是∠BAC 的角平分线
A
B
2 1
C
3 4
P
13、如图在四边形 ABCD 中,AC 平分∠BAD,∠ADC+∠ABC=180 度,一C一E⊥一 AD 于 E,猜想 AD、AE、AB 之间 E
D
的数量关系,并证明你的猜想,
② 如图 2,在正方形 ABCD 中,N 为 BC 边上任一点,CM 为正方形外角∠DCK 的平分线,若∠ANM=90°,则 AN=NM
③
如图 3,在正五边形 ABCDE 中,N 为 BC 边上任一点,CM 为正五边形外角∠DCK 的平分线,若∠ANM=108°,则
AN=NM
A M
B
NC
K
图1
E
A
1.如图,已知等边△ABC,P 在 AC 延长线上一点,以 PA 为边作等边△APE,EC 延长线交 BP 于 M,连接 AM,求证:(1)
BP=CE;
(2)试证明:EM-
PM=AM.
E
A
C
B
P M 22∠
2、点 C 为线段 AB 上一点,△ACM, △CBN 都是等边三角形,线段 AN,MC 交于点 E,BM,CN 交于点 F。求证: (1)AN=MB.(2)将△ACM 绕点 C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,(1)中的结论是否 依然成立? (3)AN 与 BM 相交所夹锐角是否发生变化。
B
M
B
O
P
E FD
E
FD
A N
图①
CA
图②
C
全等三角形难题(含答案)
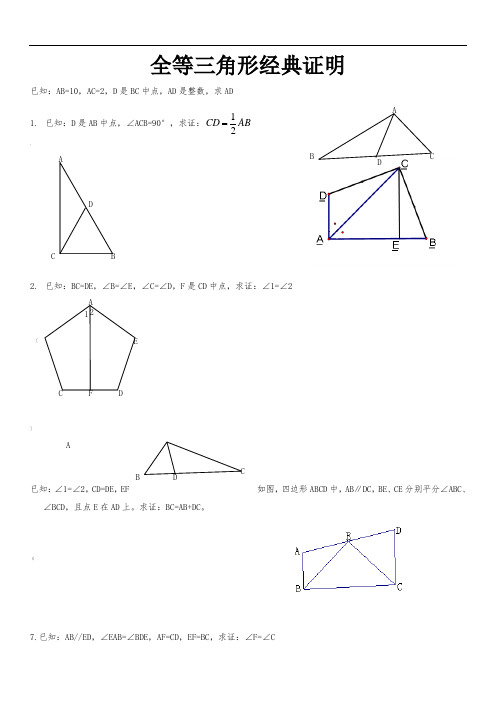
全等三角形经典证明已知:AB=10,AC=2,D 是BC 中点,AD 是整数,求AD1. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB,2. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2]已知:∠1=∠2,CD=DE ,EF如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
《7.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CA [CDEF 21 DABC CDBAADBC>8、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C9.(5分)如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .,10.(5分)如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA、11.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立若成立请给予证明;若不成立请说明理由.—12.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .D^BAFE AB C(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):【/13.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .&14、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
2024届初中数学重难点题型专项(全等三角形证明题)练习(附答案)

2024届初中数学重难点题型专项(全等三角形证明题)练习题型1:重叠边技巧①短边相等+重叠边=长边相等②长边相等-重叠边=短边相等1.(∙广东)如图,点A 、C 、F 、D 在同一直线上,AF=DC ,AB=DE ,BC=EF ,求证:∥AB DE .2.(∙重庆)已知点A 、E 、F 、C 在同一直线上,已知AD BC ∥,AD BC =,AE CF =,试说明BE 与DF 的关系.3.(∙湖北荆门)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.4.(∙甘肃)如图,AB∥CD,BN∥MD,点M、N在AC上,且AM=CN,求证:BN=DM.5.(∙新疆)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A =∠D,AF=DC.求证:(1)ABC≌△DEF;(2)BC∥EF.△题型2:重叠角技巧重叠角技巧: 小角相等+重叠角=大角相等大角相等-重叠角=小角相等∠=2∠,AB=AD.求证:△ABC≌△ADE.6.(∙福建∙福州)如图,AC=AE,17.(∙四川资阳)如图,在△ABC和△ADE中,AB=AD,∠B=∠D,1=2∠∠.求证:BC=DE.∠,求证:△ABC≌△ADE.8.如图,AB=AD,∠C=∠E,1∠=29.(雅礼)如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.∠∠.10.(∙四川达州)已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,1=2(1)求证:BD=CE;(2)求证:∠M=∠N.题型3:等角的余角相等技巧: ∠1+∠2=90,∠2+∠3=90, ∠1=∠3技巧:把全等三角形中一个三角形的两个锐角分别随意标上∠1、∠2,再从第二个三角形的两个锐角中挑一个和∠1或∠2互余的角标上∠3。
11.(∙甘肃)如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD, (1)求证:△ABD≌△CFD;(2)已知BC=7,AD=5,求AF的长.12.(∙辽宁沈阳)如图,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥于E ,AD CE ⊥于D , 2.5cm AD =,1.7cm DE =,求BE 的长.13.(长郡)如图,△ABC 中,∠ACB =90°,AC =BC ,E 是BC 边上的一点,连接AE ,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D .(1)求证:△ACE ≌△CBD ;(2)若BE =3,AB =6,求点E 到AB 的距离.14.(∙广东)如图,△ABC 中,AB =AC ,AD ⊥BC ,CE ⊥AB ,AE =CE .求证:(1)△AEF ≌△CEB ;(2)AF =2CD .15.(周南)(1)如图1,△ABC 中,∠BAC =90°,AB =AC ,AE 是过A 点的一条直线,且B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E ,求证:BD =DE +CE .(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.题型4:证两次全等的证明题16.如图,已知AB=DC,AE=DF,CE=BF.求证:AF=DE.17.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.求证:(1)△ACD≌△BEC;(2)CF⊥DE.18.如图1所示,点E、F在线段AC上,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为点E,F;DE,BF分别在线段AC的两侧,且AE=CF,AB=CD,BD与AC相交于点G.(1)求证:EG=GF;(2)若点E在F的右边,如图2时,其余条件不变,上述结论是否成立?请说明理由.题型5:旋转型全等(手拉手模型)19.(∙浙江)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,DC连接AE、DE、.(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求∠BDC的度数.20.(∙山东聊城)如图,在ABC 中,90ACB ∠= ,AC BC =,D 是AB 边上一点(点D 与A ,B 不重合),连接CD ,将线段CD 绕点C 按逆时针方向旋转90 得到线段CE ,连接DE 交BC 于点F ,连接BE . 1()求证:ACD △≌BCE ;2()当AD BF =时,求BEF ∠的度数.21.(∙湖南∙澧县)如图,四边形ABCD 中,对角线AC 、BD 交于点O ,AB =AC ,点E 是BD 上一点,且AE =AD ,EAD ∠=BAC,∠(1)求证:A ∠BD =ACD ∠;(2)若ACB ∠=65°,求BDC ∠的度数.22.(∙北京)如图,已知:△OAB ,△EOF 都是等腰直角三角形,∠AOB =90°,中,∠EOF =90°,连结AE 、BF .求证:(1)AE =BF ;(2)AE ⊥BF .23.(∙浙江)如图,点C 为线段BD 上一点,,ABC CDE △△都是等边三角形,AD 与CE 交于点,F BE 与AC 相交于点G .(1)求证:ACD BCE ≌;(2)求证:ACF BCG ≌求证:(1)AE =BF ;(2)AE ⊥BF .题型6:角平分线的性质与判定24.(∙北京)如图所示,在△ABC 中,C ∠=90°,AD 是BAC ∠的平分线,⊥DE AB 交AB 于点E ,点F 在AC 上,BD =DF .求证:(1)CF =EB ;(2)AB =AF +2EB .25.(∙广西北海)如图,⊥DE AB 于E ,⊥DF AC 于F,若BD=CD 、BE=CF ,(1)求证:AD 平分BAC ∠;(2)已知AC=20, BE=4,求AB 的长.求证:(1)AE =BF ;(2)AE ⊥BF .26.(∙浙江∙义乌)如图,已知AC 平分∠⊥BAD,CE AB 于E ,⊥CF AD 于F ,且BC=CD , (1)求证:△≌△BCE DCF(2)若AB=17,AD=9,求AE 的长.27.(∙甘肃平凉)如图,90B C ∠=∠=︒,M 是BC 的中点,DM 平分ADC ∠,求证:AM 平分DAB ∠.∠, 28.(∙北京)如图,在四边形ABCD中,BC>BA,AD=CD,BD平分ABC ∠∠.求证:A+C=180°29.(∙全国)在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.(1)若BE=CF,求证:AD是△ABC的角平分线.(2)若AD是△ABC的角平分线,求证:BE=CF.参考答案题型1:重叠边技巧①短边相等+重叠边=长边相等②长边相等-重叠边=短边相等1.(∙广东)如图,点A 、C 、F 、D 在同一直线上,AF=DC ,AB=DE ,BC=EF ,求证:∥AB DE .【答案详解】∵AF=DC ,∴AF ﹣FC=DC ﹣CF ,即AC=DF .在△ACB 和△DFE 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩,∴△≌△ACB DFE(SSS ),∴∠∠A=D ,∴∥AB DE .2.(∙重庆)已知点A 、E 、F 、C 在同一直线上,已知AD BC ∥,AD BC =,AE CF =,试说明BE 与DF 的关系.【答案详解】解:数量关系BE DF =,位置关系BE DF ∥.理由:∵AD BC ∥,∴∠A =∠C ,又AE CF = ,∴AE +EF =CF +EF ,即AF =CE ,在ADF 和CBE △中,AD BC A C AF CE =⎧⎪∠=∠⎨⎪=⎩,ADF ∴ ≌()CBE SAS △∴BE =DF ,∠BEF =∠DFE ,∴BE DF ∥.3.(∙湖北荆门)如图,点E 、F 在BC 上,BE =CF ,AB =DC ,∠B =∠C .求证:∠A =∠D .【答案详解】解∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE .在△ABF 和△DCE 中,AB DC B C BF CE =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△DCE , ∴∠A =∠D .4.(∙甘肃)如图,AB ∥CD ,BN ∥MD ,点M 、N 在AC 上,且AM =CN ,求证:BN =DM .【答案详解】解:∵AB ∥CD ,BN ∥MD ,∴∠A =∠C ,∠CMD =∠ANB ,∵AM =CN ,∴AM +MN =MN +CN ,即AN =MC ,在△ANB 和△CMD 中,∠A =∠C ,AN =MC ,∠ANB =∠CMF,∴△ANB ≌△CMD (ASA ),∴BN =MD .5.(∙新疆)如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB =DE ,∠A =∠D ,AF =DC .求证:△(1)ABC ≌△DEF ;(2)BC ∥EF .【答案详解】(1)证明:∵AF =DC ,∴AF +CF =DC +CF ,∴AC =DF ,∵在△ABC 和△DEF 中,AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS );(2)证明:由(1)知△ABC ≌△DEF ,∴∠BCA =∠EFD ,∴BC ∥EF .题型2:重叠角技巧重叠角技巧:①小角相等+重叠角=大角相等②大角相等-重叠角=小角相等6.(∙福建∙福州)如图,AC =AE ,1∠=2∠,AB =AD .求证:△ABC ≌△ADE .【答案详解】证明:∵∠∠1=2,12EAB EAB ∴∠+∠=∠+∠,即CAB EAD ∠=∠,在ABC 和ADE 中,{AC AECAB EAD AB AD=∠=∠=()ABC ADE SAS ∴≅ .7.(∙四川资阳)如图,在△ABC和△ADE 中,AB =AD ,∠B =∠D ,1=2∠∠.求证:BC =DE .【答案详解】证明:∵∠∠1=2,∵∠DAC +1=2+∠∠∠DAC ∴∠BAC =∠DAE ,在△ABC 和△ADE 中,B D AB AD BAC DAE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ADE ≌△ABC (ASA )∴BC =DE ,8.如图,AB =AD ,∠C =∠E ,1∠=2∠,求证:△ABC ≌△ADE .【解答】证明:∵∠1=2∠,∴∠1+∠EAC =2+∠∠EAC ,即∠BAC =∠DAE ,在△ABC 和△ADE 中,BAC DAE C E AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△ADE (AAS ). 9.(雅礼)如图,△ABC 和△ADE 都是等腰三角形,且∠BAC =90°,∠DAE =90°,B ,C ,D 在同一条直线上.求证:BD =CE .【解答】证明:∵△ABC 和△ADE 都是等腰直角三角形,∴AD =AE ,AB =AC ,又∵∠EAC =90°+∠CAD ,∠DAB =90°+∠CAD ,∴∠DAB =∠EAC ,∵在△ADB 和△AEC中,∴△ADB ≌△AEC (SAS ),∴BD =CE .10.(∙四川达州)已知△ABN 和△ACM 位置如图所示,AB =AC ,AD =AE ,1=2∠∠.(1)求证:BD =CE ;(2)求证:∠M=∠N .【答案详解】(1)证明:在△ABD 和△ACE 中,12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴BD =CE ;(2)证明:∵∠∠1=2,∴∠∠1+DAE =2+∠∠DAE ,即∠BAN =∠CAM ,由(1)知:△ABD ≌△ACE ,∴∠B =∠C ,在△ACM 和△ABN 中,C B AC AB CAM BAN ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ACM ≌△ABN (ASA ),∴∠M =∠N .题型3:等角的余角相等技巧: ∠1+∠2=90,∠2+∠3=90,∴∠1=∠3技巧:把全等三角形中一个三角形的两个锐角分别随意标上∠1、∠2,再从第二个三角形的两个锐角中挑一个和∠1或∠2互余的角标上∠3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 如图,已知等边△ ABC,P在AC延长线上一点,以PA为边作等边△ APE,EC延长线交BP于M,连接AM,求证:(1)BP=CE;(2)试证明:EM-PM=AM.3.已知,如图①所示,在△ABC和△ ADE中,AB AC,AD AE,BAC DAE ,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:① BE CD ;② AM AN ;2)在图①的基础上,将△ADE 绕点 A 按顺时针方向旋转180o,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立4、如图1,以△ ABC的边AB 、AC为边分别向外作正方形ABDE和正方形ACFG ,连结EG ,试判断△ABC与△AEG 面积之间的关系,并说明理由.2、点 C 为线段AB 上一点,△ ACM, △ CBN 都是等边三角形,线段AN,MC 交于点E,BM,CN交于点F。
求证:1)AN=MB. (2)将△ ACM 绕点 C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,1)中的结论是否依然成立?(3)AN 与BM 相交所夹锐角是否发生变化。
B图①CB图1)F7、已知 Rt △ ABC 中, AC BC ,∠C 90,D 为AB 边的中点, EDF 90°,EDF 绕 D 点旋转,它的两边分别交 AC 、 CB (或它们的延长线)于 E 、 F.1 当 EDF 绕 D 点旋转到 DE AC 于E时(如图1),易证S △DEF S △CEF S △ ABC .DEF CEF 2 ABC当 EDF 绕 D 点旋转到 DE 和 AC 不垂直时, 在图 2 和图 3 这两种情况下, 上述结论是否成立?若成立, 请给予证明;8. 已知 AC//BD, ∠CAB 和∠ DBA 的平分线 EA 、EB 与 CD 相交于点 E. 求证 :AB=AC+BD.5、如图所示,已知△ ABC 和△ BDE 都是等边三角形,且 A 、 HB 平分∠ AHD ;④∠ AHC=60 °,⑤△ BFG 是等边三角形;⑥ A .3个 B .4 个 C .5个 D .6 个B 、D 三点共线.下列结论:① AE=CD ;② BF=BG ;③ FG ∥AD .其中正确的有()6. 如图所示,△ ABC 是等腰直角三角形,∠ ACB =90°,AD 交 AD 于点 F ,求证:∠ ADC =∠ BDE .是 BC 边上的中线,过 C 作 AD 的垂线,交 AB 于点 E , 、 S △CEF 、 S △ABC 又有怎样的数量关系?请写出你的猜想,不需证明.图1若不成立,S △ DEF 图2图210、已知,如图1,在四边形ABCD 中,BC>AB,AD=DC,BD 平分∠ ABC 。
求证:∠ BAD+ ∠ BCD=180 °。
11、如图,四边形ABCD 中,AC平分∠ BAD ,CE⊥AB于E,AD+AB=2AE ,则∠ B与∠ ADC 互补.为什么?12、.如图,在△ ABC 中∠ ABC, ∠ ACB 的外角平分线交AE 、AB 之间的13、如图在四边形ABCD 中,数量关系,并证明你的猜想,图2B9. 如图1,BD 是等腰RtΔABC的角平分线,∠BAC=90(1)求证BC=AB+AD ;2)如图2,AF ⊥ BD于F,CE ⊥BD交延长线于E,求证:BD=2CE;ABA C F 而(1)中的其它条件不变B B M E EF DP O C A C 图① 图③ 图② E A D AMMMBBBKK K请问,你在 (1)中所得结论是否仍然成立? NC BAC 、∠BCA 的平分线, AD 、CE 相交于 NC,若∠ ANM=6°0 , 若∠ ANM=9°0 的平分线 ,若∠ ANM=10°8 请你证明以上三个命题; 如图1,在正三角形 ABC 中,N 为BC 边上任一点 ,CM 为正三角形外角∠ ACK 的平分线 如图 2,在正方形 ABCD 中,N 为 BC 边上任一点, CM 为正方形外角∠ DCK 的平分线, 如图 3,在正五边形 ABCDE 中,N 为BC 边上任一点 ,CM 为正五边形外角∠ DCK 则 AN=NM ,则 AN=NM ,则 AN=NM AN F D图3图1图214、如图所示,已知在△ AEC 中,∠ E=90°, AD 平分∠ EAC ,DF ⊥AC ,垂足为 F , DB=DC ,求证: BE=CFED N17.问题背景 ① ② ③ 16、△ABC 中,∠ BAC=60 °,∠ C=40°,AP 平分∠ BAC 交 BC 于 P ,BQ 平分∠ ABC 交 AC 于 Q ,求证:AB+BP=BQ+AQ 15、如图①, OP 是∠ MON 的平分线,请你利用该图形画一对以 OP 所在直线为对称轴的全等三角形。
请你参考这个 作全等三角形的方法,解答下列问题: (1)如图②,在△ ABC 中,∠ ACB 是直角,∠ B=60°, AD 、CE 分别是∠ 点 F 。
请你判断并写出 FE 与 FD 之间的数量关系; (2)如图③,在△ ABC 中,如果∠ ACB 不是直角 若成立,请证明;若不成立,请说明理由。
18.(1)如图,已知在正方形ABCD 中,M是AB的中点,E是AB延长线上一点,MN⊥DM 且交∠ CBE的平分线于N.试判定线段MD 与MN 的大小关系;(2)若将上述条件中的“ M 是AB 的中点”改为“ M 是AB上或AB 延长线上任意一点” ,其余条件不变.试问(1)中的结论还成立吗?如果成立,请证明;如果不成立,请说明理由.20..如图,已知△ ABC 中,AB=AC=6cm ,∠ B= ∠ C,BC=4cm ,点 D 为AB 的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.①若点Q 的运动速度与点P的运动速度相等,经过1秒后,△ BPD 与△ CQP是否全等,请说明理由;②若点Q 的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△ BPD 与△ CQP全等?(2)若点Q 以②中的运动速度从点C出发,点P以原来的运动速度从点则经过后,点P与点Q 第一次在△ ABC 的边上相遇?(在横线上直接写出答案,不必书写解题过程)21、已知△ ABC 为等边三角形,点 D 为直线BC 上的一动点(点 D 不与B、C 重合),以AD 为边作菱形ADEF (A、D、E、F按逆时针排列),使∠ DAF=60 °,连接CF.(1)如图1,当点 D 在边BC 上时,求证:① BD=CF ;② AC=CF+CD ;(2)如图2,当点 D 在边BC 的延长线上且其他条件不变时,结论AC=CF+CD 是否成立?若不成立,请写出AC 、CF、CD 之间存在的数量关系,并说明理由;(3)如图3,当点 D 在边BC 的延长线上且其他条件不变时,补全图形,并直接写出关系.19.如图,在△ ABC 中,∠ A=90垂足.求证:PE+PF=AB ., D 是AC 上的一点,B D=DC ,P是BC 上的任点,PE⊥BD,PF⊥AC,E、F 为B 同时出发,都逆时针沿△ ABC 三边运动,AC 、CF、CD 之间存在的数量22. ().如图1,在正方形ABCD 中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE ;②AF⊥DE.(不需要证明)(1)如图2,若点E、F不是正方形ABCD 的边BC、CD 的中点,但满足CE=DF.则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E、F分别在正方形ABCD 的边CB的延长线和DC 的延长线上,且CE=DF ,此时上面的结论①、② 是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.23、如图,△ ABC 中,∠ ACB =90°,AC =BC ,AE 是BC边上的中线,过C作CF⊥AE ,垂足为F,过B作BD⊥BC 交CF 的延长线于 D .25、如图,AD//BC ,AD=BC ,AE ⊥AD ,AF⊥AB ,且AE=AD ,AF=AB ,求证:AC=EF26、直线CD 经过BCA的顶点C,CA=CB .E、F 分别是直线CD 上两点,且BEC CFA24、.已知BE,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系1)若直线 CD 经过 BCA 的内部,且 E 、F 在射线 CD 上,请解决下面两个问题: ①如图 1,若 BCA 90 , 90 ,则 EF BE AF(填“ ”,“ ”或“ ”号);②如图 2,若 0o BCA 180o ,若使①中的结论仍然成立,则BCA ,请探究 EF 、与 BE 、 AF 三条线段的数量关系,并给予证明.分别交 AB 、AC 边于 M 、N 两点,连接 MN . 探究:线段 BM 、MN 、NC 之间的关系,并加以证明.28、.如图所示,已知△ ABC 中, AB=AC , D 是 CB 延长线上一点,∠ ADB=60 °, E 是 AD 上一点,且 DE=DB ,求证: AC=BE+BC29、在△ ABC 中, BD=DC ,ED ⊥ DF .求证: 与 BCA 应满足的关系是2)如图 3,若直线 CD 经过BCA的外部, 图2 图 327、如图①,△ ABC 是正三角形,△ BDC 是顶角∠ BDC =120°的等腰三角形,以 D 为顶点作一个 60 °角,角的两边图1。
