四年级奥数容斥原理
奥数四年级--容斥问题(二)

练 1.有30名运动员,其中18人会三级跳,16人 习 会撑杆跳高,10人三级跳远、撑杆跳高均不
会。既会三级跳远又会撑杆跳高的运动员有 多少名?
14名
练 2、操场上的学生排成10路纵队做操,毎路 习 纵队人数同样多,小明站在第四纵队,从排
头数他是第13个,从后往前数他是第8人。 操场上有多少人在做操?
200人
练 3、一个年级有120人爱好数学,100人爱好 习 语文,85人爱好美术,30人既爱好数学又爱
好语文,20人既爱好语文又爱好美术,35人 既爱好美术又爱好数学,有18人三门学科都 爱好。请问:这个年级中数学、语文、美术 三门学科中至少爱好一门学科的学生有多少 人?
238人
练 4、某班全体学生进行了数学、语文、英语 习 三个科目的测试,有8名学生在这三个科目
球、蓝球的学生人数分别为10人,10人,6 人,其中手中既有红球又有黄球的有3人, 既有黄球又有蓝球的有2人,既有蓝球又有 红球的有4人。已知全队每人手中都至少有 一种颜色的球,那么,手中三种颜色的球都 有的多少人?
3人
练 6、某班50名同学全部参加数学、语文、美 习 术三个课外兴趣小组,参加数学小组的有29
17人
18人
15人
求全班人数。
这道题目条件比较复杂,可以根据 题意画出示意图,以便形象直观地 显示他们之间的关系。 全班人数=至少有一个项目达到优 秀的人数+三个项目上都没有达到 优秀的人数
篮球15人 6人 短跑 17人
篮球 游泳 短跑 2人
6人 游泳 18人
6人
经 典 题 型
运用容斥定理 至少有一个项目达到优秀的人数=(短跑达 到优秀人数+游泳达到优秀人数+篮球达到 优秀人数)-(短跑、游泳达到优秀人数+ 游泳、篮球达到优秀人数+篮球、短跑达到 优秀人数)+短跑、游泳、篮球都达到优秀 的人数
小学四年级奥数 容斥原理

容斥原理在一些计数问题中,经常遇到有关集合元素个数的计算。
求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A∪B=A+B-A∩B (其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思;符号“∩”读作“交”,相当于中文“且”的意思。
),则称这一公式为包含与排除原理,简称容斥原理。
图示如下:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A∩B,即阴影面积。
1.先包含——A+B重叠部分A∩B计算了2次,多加了1次;2.再排除——A+B-A∩B把多加了1次的重叠部分A∩B减去。
A类、B类与C类元素个数的总和=A类元素的个数+B类元素个数+C类元素个数-既是A类又是B 类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数。
用符号表示为:A∪B∪C=A+B+C-A∩B-B∩C-A∩C+A∩B∩C图示如下:图中小圆表示A的元素的个数,中圆表示B的元素的个数,大圆表示C的元素的个数。
1.先包含——A+B+CA∩B、B∩C、C∩A重叠了2次,多加了1次。
2.再排除——A+B+C-A∩B-B∩C-A∩C重叠部分A∩B∩C重叠了3次,但是在进行A+B+C-A∩B-B∩C-A∩C计算时都被减掉了。
3.再包含——A+B+C-A∩B-B∩C-A∩C+A∩B∩C例1一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积。
例250名同学面向老师站成一行。
老师先让大家从左至右按1、2、3、…、49、50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。
问:现在面向老师的同学还有多少名?求1~2009这2009个自然数既不能被7整除又不能被41整除的自然数有多少个?例3在1到2004所有自然数中,既不是2的倍数又不是3和5的倍数的数有多少个?例4如图,已知甲乙丙三个圆的面积都是30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6,8,5,三个圆覆盖的总面积为73,求空白部分的面积。
小学奥数容斥原理教案

小学奥数容斥原理教课设计【篇一:四年级奥数讲义:容斥原理 (1)】四年级数学讲义奥数:容斥原理 (1)教课目的: 1、理解容斥原理,会绘图剖析此中关系,正确的找出答案。
2、培育学生的逻辑思想和数学思虑能力。
3、培育学生优异的书写习惯。
一、教课连接二、教课内容〔一〕知识介绍容斥问题波及到一个重要原理——包括与清除原理,也叫容斥原理。
即当两个计数局部有重复包括时,为了不重复计数,应从它们的和中清除重复局部。
容斥原理:对 n 个事物,假如采纳不一样的分类标准,按性质 a 分类与性质 b 分类〔如图〕,那么拥有性质 a 或性质 b 的事物的个数=na +nb -nab 。
〔二〕例题精讲 nanb例 1、一个班有 48 人,班主任在班会上问:“谁做完语文作业?请举手!〞有 37 人举手。
又问:“谁做完数学作业?请举手!〞有 42 人举手。
最后问:“谁语文、数学作业都没有做完?〞没有人举手。
求这个班语文、数学作业都达成的人数。
【思路导航】达成语文作业的有 37 人,达成数学作业的有 42 人,一共有 37+42=79 人,多于全班人数。
这是由于语文、数学作业都达成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以,这个班语文、数作业都达成的有: 79-48=31 人。
例 2、某班有 36 个同学在一项测试中,答对第一题的有 25 人,答对第二题的有 23 人,两题都答对的有 15 人。
问多少个同学两题都答得不对?【剖析与解答】答对第一题的有 25 人,两题都答对的有 15 人,能够求出只答对第一题的有 25-15=10 人。
又答对第二题的有23 人,用只答对第一题的人数,加上答对第二题的人数就获得起码有一题答对的人数: 10+23=33 人。
所以,两题都答得不对的有 36-33=3 人。
例 3、某班有 56 人,参加语文比赛的有 28 人,参加数学比赛的有27 人,假如两科都没有参加的有 25 人,那么同时参加语文、数学两科比赛的有多少人?【剖析与解答】要求两科比赛同时参加的人数,应先求出起码参加一科比赛的人数: 56-25=31 人,再求两科比赛同时参加的人数:28+27-31=24 人。
奥数四年级--容斥问题(一)
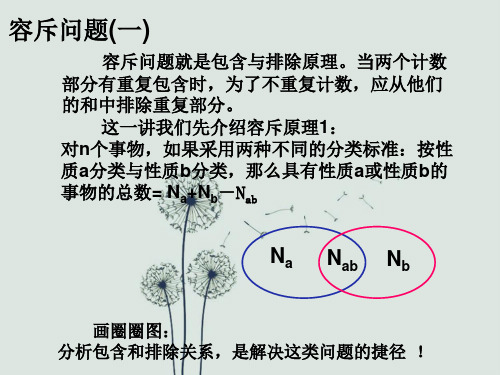
经 例2、有62名学生,其中会弹钢琴的有11人,会吹竖笛的有56人,
典 两样都不会的有4人,两样都会的有多少人?
题 依题意,画圈框图。
总人数62人
型 依图可知,会弹钢琴+会竖笛
=11+56=67人, 67 > 总人数62人
会弹钢琴的 会两样 会吹竖笛
有11人
?人
既不是5的倍数,也不是7的倍数??。
(3)求既是5的倍数又是7的倍数的数量: 1000÷35 = 28...20
总1--1000的自然数
(4)根据容斥原理: 是5或7的倍数的数有: 200+142-28=314
(5)既不是5,也不是7的倍数的: 1000-314=686
5的倍数 有200
5和7的 公倍数
容斥问题(一)
容斥问题就是包含与排除原理。当两个计数 部分有重复包含时,为了不重复计数,应从他们 的和中排除重复部分。
这一讲我们先介绍容斥原理1: 对n个事物,如果采用两种不同的分类标准:按性 质a分类与性质b分类,那么具有性质a或性质b的 事物的总数= Na+Nb-Nab
Na Nab Nb
画圈圈图: 分析包含和排除关系,是解决这类问题的捷径 !
48名
练 9、有一根36cm长的绳子,从一端开始每隔3 习 厘米做一个记号,每隔4厘米也做一个记号,
然后把标有记号的地方剪断。绳子共被剪成 了多少段?
18段
练 10、科技节那天,学校的科技室里展出了每 习 个年级学生的科技作品,其中有114件不是
一年级的,有96件不是二年级的,一、二年 级参展的作品共32件。其他年级参展的作品 共有多少件?
分析搞清数量关系,是解决数学问题的不二法门。
小学奥数全国推荐四年级奥数通用学案附带练习题解析答案43容斥原理(一)

年级四年级学科奥数版本通用版课程标题容斥原理(一)在计数时,必须注意无一重复,无一遗漏。
为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
有重叠的计数问题,即包含与排除问题。
研究这种问题通常需要画出示意图,这样的示意图又叫做文氏图(韦恩图),解决简单的两类或三类被计数事物之间的重叠问题时采用韦恩图会更加便捷、直接。
下面我们就用文氏图推导两个对象的容斥原理公式。
容斥原理一:如果被计数的事物有A、B两类,那么,A、B两类元素个数和=既是A 类又是B类的元素个数+A类或B类元素个数。
写成公式形式即:A+B=A∪B+A∩B(其中符号“”读作“并”,相当于“和”或者“或”的意思;符号“”读作“交”,相当于“且”的意思)。
包含与排除原理告诉我们,要计算两个集合A B、的并集A B的元素的个数,可分以下两步进行:第一步:分别计算集合A B、、的元素个数,然后加起来,即先求A B+(意思是把A B 各自的所有元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B=(意思是“排除”了重复计算的元素个数)。
例1一个班48人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了。
已知做完语文作业的有37人;做完数学作业的有42人。
这些人中语文、数学作业都完成的有多少人?分析与解:完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79(人),多于全班人数。
这是因为在统计做完语文作业的人数时语文、数学作业都完成的人数算了一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以这个班语文、数学作业都完成的有:79-48=31(人)。
四年级奥数-容斥原理初步(一)

【例3】(★★★) 网校老师组织理财培训,报名股票培训的有23人,报名基金培训的有 32人,两项都报名的有 都报名的有8人,两项都没有报名的有 都 有报名的有5人,那么网校老师 校老师 有多少人?
(★★★) 【改编】 网校组织40名老师参加趣味运动会,参加两人三脚项目的有26人,参 加拔河项目的有 有18人,两个项目都没参加的有 都 参 有6人,两个项目都参加 都参 的有多少人?
【例1】(★★) 网校老师共50人报名参加了羽毛球或乒乓球的训练,其中参加羽毛球 训练的有30人,参加乒乓球训练的有35人,请问:两个项目都参加的 有多少人?
容斥原理(一)
【例2】(★★★) 一个班 个班30人,完成作业的情况有三种:一种是完成语文作业没完成数 人 完成作业的情况有三种 种是完成语文作业没完成数 学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作 业都完成了 已知做完语文作业的有20人;做完数学作业的有23人。 业都完成了。已知做完语文作业的有 人 这些人只完成一种作业的有多少人?
1
【例4】(★★★) 【例5】(★★★) 网校老师60人组织春游。报名去香山的有37人,报名去鸟巢的有42人, 1~100中是2或5的倍数的数有多少个? 两个地点都没有报名的有 个地点都 有报名的有8人,那么只报名其中一个地点的有多少人? 报名其中 个地点的有多少
(★★★) 【改编】 1~100中既不是3的倍数,也不是4的倍数的数有多少个?
2
【例6】(★★★★) 写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数 的灯拉 次 关 第 次把编号是5的倍数的灯拉一次开关,那么亮着 的灯拉一次开关,第二次把编号是 的倍数的灯拉 次 关 亮着 的灯还有多少盏?
【例7】(★★★) 在游艺会上,有100名同学抽到了标签分别为1至100的奖券。按奖券标 签号发放奖 的规则如 签号发放奖品的规则如下:①标签号为 ①标签号为2的倍数,奖 的倍数 奖2支铅笔;②标签 支铅笔 ②标签 号为3的倍数,奖3只铅笔;③标签号既是2的倍数,又是3的倍数可重 复领奖;④其他标签号均奖1支铅笔。那么游艺会为该项活动准备的奖 支铅笔 那么游艺会为该项活动准备的奖 品铅笔共有多少支?
小学数学奥数举一反三四年级数学容斥原理35

小学 数学奥数 举一反三
【练习5】 1,科技节那天,学校的科技室里展出了每个年级学生的科技作品,其中有110件 不是一年级的,有100件不是二年级的,一、二年级参展的作品共有32件。其他 年级参展的作品共有多少件?
2,六(1)儿童节那天,学校的画廊里展出了每个年级学生的图画作品,其中有 25幅画不是三年级的,有19幅画不是四年级的,三、四两个年级参展的画共有8 幅。其他年级参展的画共有多少幅?
3,某校选出50名学生参加区作文比赛和数学比赛,结 果3人两项比赛都获奖了,有27人两项比赛都没有获奖。 已知作文比赛获奖的有14人,问数学比赛获奖的有多 少人?
小学 数学奥数 举一反三 【例题3】 某班有56人,参加语文竞赛的有28人,参加数学 竞赛的有27人,如果两科都没有参加的有25人,那么同时参 加语文、数学两科竞赛的有多少人? 【思路导航】 要求两科竞赛同时参加的人数,应先求出至少参加一科竞赛 的人数:56-25=31人,再求两科竞赛同时参加的人数:28 +27-31=24人。
小学 数学奥数 举一反三
【练习1】 1,五年级有122名学生参加语文、数学考试,每人至 少有一门功课取得优秀成绩。其中语文成绩优秀的有 65人,数学优秀的有87人。语文、数学都优秀的有多 少人?
2,四年级一班有54人,订阅《小学生优秀作文》和 《数学大世界》两种读物的有13人,订《小学生优秀 作文》的有45人,每人至少订一种读物,订《数学大 世界》的有多少人?
小学 数学奥数 举一反三
【练习4】
1,在1到200的全部自然数中,既不是5的倍数又不是8的倍数的数有多少 个?
2,在1到130的全部自然数中,既不是6的倍数又不是5的倍数的数有多少 个?
3,五(1)班做广播操,全班排成4行,每行的人数相等。小华排的位置 是:从前面数第5个,从后面数第8个。这个班共有多少个学生?
四年级奥数---容斥原理教案

四年级奥数---容斥原理教案奥数:容斥原理教学目标:1、理解容斥原理,会画图分析其中关系,正确的找出答案。
2、培养学生的逻辑思维和数学思考能力。
3、培养学生良好的书写习惯。
一、教学内容(一)知识介绍容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n 个事物,如果采用不同的分类标准,按性质a 分类与性质b 分类(如图),那么具有性质a 或性质b 的事物的个数=N a +N b -N ab 。
(二)例题精讲例1、一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
【思路导航】完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79人,多于全班人数。
这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以,这个班语文、数作业都完成的有:79-48=31人。
例2、某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有Nab NbNa23人,两题都答对的有15人。
问多少个同学两题都答得不对?【分析与解答】已知答对第一题的有25人,两题都答对的有15人,可以求出只答对第一题的有25-15=10人。
又已知答对第二题的有23人,用只答对第一题的人数,加上答对第二题的人数就得到至少有一题答对的人数:10+23=33人。
所以,两题都答得不对的有36-33=3人。
例3、某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?【分析与解答】要求两科竞赛同时参加的人数,应先求出至少参加一科竞赛的人数:56-25=31人,再求两科竞赛同时参加的人数:28+27-31=24人。
小学四年级奥数竞赛:容斥原理
课题容斥原理年级4授课对象编写人时间学习目标利用抽屉原理1、抽屉原理2解题。
学习重点、难点(1)找出题干中物品对应的量;(2)合理构造抽屉(简单问题中抽屉明显,找出即可);(3)利用抽屉原理1、抽屉原理2解题。
教学过程T (测试)1,五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人,数学优秀的有87人。
语文、数学都优秀的有多少人?2,四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?3,学校文艺组每人至少会演奏一种乐器,已知会拉手风琴的有24人,会弹电子琴的有17人,其中两种乐器都会演奏的有8人。
这个文艺组一共有多少人?S (归纳)容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用不同的分类标准,按性质a分类与性质b分类(如图),那么具有性质a或性质b的事物的个数=Na+Nb-Nab。
Nab NbNaE (典例)例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
分析完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79人,多于全班人数。
这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以,这个班语文、数作业都完成的有:79-48=31人。
例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?分析与解答:已知答对第一题的有25人,两题都答对的有15人,可以求出只答对第一题的有25-15=10人。
四年级奥数专题-容斥原理

四年级奥数专题-容斥原理专题简析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理.即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分.容斥原理:对n 个事物,如果采用不同的分类标准,按性质a 分类与性质b 分类(如图),那么具有性质a 或性质b 的事物的个数=N a +N b -N ab .例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手.又问:“谁做完数学作业?请举手!”有42人举手.最后问:“谁语文、数学作业都没有做完?”没有人举手.求这个班语文、数学作业都完成的人数.分析 完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79人,多于全班人数.这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次.所以,这个班语文、数作业都完成的有:79-48=31人.练 习 一1,五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩.其中语文成绩优秀的有65人,数学优秀的有87人.语文、数学都优秀的有多少人?Nab NbNa2,四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?3,学校文艺组每人至少会演奏一种乐器,已知会拉手风琴的有24人,会弹电子琴的有17人,其中两种乐器都会演奏的有8人.这个文艺组一共有多少人?例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人.问多少个同学两题都答得不对?分析与解答:已知答对第一题的有25人,两题都答对的有15人,可以求出只答对第一题的有25-15=10人.又已知答对第二题的有23人,用只答对第一题的人数,加上答对第二题的人数就得到至少有一题答对的人数:10+23=33人.所以,两题都答得不对的有36-33=3人.练习二1,五(1)班有40个学生,其中25人参加数学小组,23人参加科技小组,有19人两个小组都参加了.那么,有多少人两个小组都没有参加?2,一个班有55名学生,订阅《小学生数学报》的有32人,订阅《中国少年报》的有29人,两种报纸都订阅的有25人.两种报纸都没有订阅的有多少人?3,某校选出50名学生参加区作文比赛和数学比赛,结果3人两项比赛都获奖了,有27人两项比赛都没有获奖.已知作文比赛获奖的有14人,问数学比赛获奖的有多少人?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?分析与解答:要求两科竞赛同时参加的人数,应先求出至少参加一科竞赛的人数:56-25=31人,再求两科竞赛同时参加的人数:28+27-31=24人.练习三1,一个旅行社有36人,其中会英语的有24人,会法语的有18人,两样都不会的有4人.两样都会的有多少人?2,一个俱乐部有103人,其中会下中国象棋的有69人,会下国际象棋的有52人,这两种棋都不会下的有12人.问这两种棋都会下的有多少人?3,三年级一班参加合唱队的有40人,参加舞蹈队的有20人,既参加合唱队又参加舞蹈队的有14人.这两队都没有参加的有10人.请算一算,这个班共有多少人?例4:在1到100的自然数中,既不是5的倍数也不是6的倍数的数有多少个?分析与解答:从1到100的自然数中,减去5或6的倍数的个数.从1到100的自然数中,5的倍数有100÷5=20个,6的倍数有16个(100÷6=16……4),其中既是5的倍数又是6的倍数(即5和6的公倍数)的数有3个(100÷30=3……10).因此,是6或5的倍数的个数是16+20-3=33个,既不是5的倍数又不是6的倍数的数的个数是:100-33=67个.练习四1,在1到200的全部自然数中,既不是5的倍数又不是8的倍数的数有多少个?2,在1到130的全部自然数中,既不是6的倍数又不是5的倍数的数有多少个?3,五(1)班做广播操,全班排成4行,每行的人数相等.小华排的位置是:从前面数第5个,从后面数第8个.这个班共有多少个学生?例5:光明小学举办学生书法展览.学校的橱窗里展出了每个年级学生的书法作品,其中有24幅不是五年级的,有22幅不是六年级的,五、六年级参展的书法作品共有10幅,其他年级参展的书法作品共有多少幅?分析与解答:由题意知,24幅作品是一、二、三、四、六年级参展作品的总数,22幅是一、二、三、四、五年级参展作品的总数.24+22=46幅,这是一个五、六年级和两个一、二、三、四年级参展的作品数,从其中去掉五、六两个年级共参展的10幅作品,即得到两个一、二、三、四年级参展作品的总数,再除以2,即可求出其他年级参展作品的总数.(24+22-10)÷2=18幅.练习五1,科技节那天,学校的科技室里展出了每个年级学生的科技作品,其中有110件不是一年级的,有100件不是二年级的,一、二年级参展的作品共有32件.其他年级参展的作品共有多少件?2,六(1)儿童节那天,学校的画廊里展出了每个年级学生的图画作品,其中有25幅画不是三年级的,有19幅画不是四年级的,三、四两个年级参展的画共有8幅.其他年级参展的画共有多少幅?3,实验小学举办学生书法展,学校的橱窗里展出每个年级学生的书法作品,其中有28幅不是五年级的,有24幅不是六年级的,五、六年级参展的书法作品共有20幅.一、二年级参展的作品总数比三、四年级参展作品的总数少4幅.一、二年级参展的书法作品共有多少幅?。
完整版小学四年级奥数容斥问题

容斥问题涉及到一个重要的原理一一包含与排除原理,也称为容斥原理,即当两个计数部分有重复包含时,为了不重复地计数,应从它们的和中排除重复部分。
这一讲我们先介绍容斥原理1对n个事物,如果采用两种不同的分类标准:按性质a分类与性质b分类(如图1),那么,具有性质a或性质b的事物的个数=Na+Nb-Nad例1•一个班有55名学生,订阅《小学生数学报》的有12人,订阅《今日少年报》的有9人,两种报纸都订阅的有5人。
(1)订阅报纸的总人数有多少?(2)两种报纸都没订阅的有多少人?例2•一个旅行社有36人,其中会英语的有24人,会俄语的有18人,两样都不会的有4人,两样都会的有多少人?例3.在1到100的全部自然数中,既不是6的倍数也不是5的倍数的数有多少个?例4•艺术节那天,学校的画廊里展了了每个年级学生的图画作品,其中有23幅画不是五年级的,有21幅画不是六年级的,五、六年级参展的画共有8幅。
其他年级参展的画共有多少幅?练习与思考1•将边长分别为4厘米和5厘米的正方形纸片部分重叠,盖在桌面上(如图6),已知重叠的部分为9平方厘米,两块正方形纸片盖住桌面的总面积是多少平方厘米?2 . 二(2)班有50名学生,下课后每人都至少做完了一门作业,其中做完语文作业的有35人,做完数学作业的有40人,两种作业都做完的有多少人?3.有62名学生,其中会弹钢琴的有11名,会吹竖笛的有56名,两样都不会的有4名,两样都会的有多少名?4 •某校选出50名学生参加区作文比赛和数学比赛,作文比赛获奖的有14人,数学比赛获奖的有12人,有3人两项比赛都获奖的,两项比赛都没获奖的有多少人?5 •四(1)班有40个学生,其中有25人参加数学小组,23人参加航模水组,有19人两个小组都参加了,那么,有多少人两个小组都没有参加?6 •在一次数学测验中,所有同学都答了第1、2两题,其中答对第1题的有35人,答对第2题的有28人,这两题都答对的有20人,没有人两题都答错。
小学四年级奥数容斥问题

容斥问题容斥问题波及到一个重要原理——包括与清除原理,也叫容斥原理。
即当两个计数部分有重复包括时,为了不重复的计数,应从它们的和中清除重复部分。
容斥原理:对n 个事物,假如采纳两种不一样的分类标准,按性质a 分类与性质b 分类(如图),Na Nab Nb那么拥有性质 a 或性质 b 的事物的个数 =Na+Nb-Nab。
练习 1、1 四( 2)班有人,做完数学作业的有50 名学生,下课后每人都起码做完了一门作业,此中做完语文作业的有40 人。
两种作业都做完的有多少人?35练习 1、2 五( 1)班有 40 名学生,此中 25 人参加数学小组, 23 人参加科技小组,有 19 人两组都参加了。
那么,有多少人两个小组都没有参加?练习 2、1 某班有 36 个同学在一项测试中,答对第一题的有 25 人,答对第二题的有 23 人,两题都答对的有 15 人。
问多少个同学两题都答得不对?练习 2、2 一个旅游社有职工 36 人,此中会英语的有 24 人,会俄语的有 18 人,两样都不会的有 4 人。
两样都会的有多少人?练习 3、1 在 1-200 的所有自然数中,既不是 4 的倍数也不是 5 的倍数的数有多少个?练习 3、2 在 1-1000 的所有自然数中,既不是 5 的倍数也不是 7 的倍数的数有多少个?练习 4、科技节那一天,学校的科技室里展出了每个年级学生的科技作品,此中有 114 件不是一年级的,有 96 件不是二年级的,一、二年级参展的作品共 32 件。
其余年级参展的作品共有多少件?作业题:1、光明小学举办学生书法展览。
学校的橱窗里展出了每个年级学生的书法作品,此中有 24 幅不是五年级的,有 22 幅不是六年级的,五、六年级参展的书法作品共有 10 幅,其余年级参展的书法共有多少幅?2、有 40 名运动员,此中 25 人会摔交,有 20 人会击剑,有 10 人击剑摔交都不会,问既会摔交又会击剑的运动员有多少人?3、一个班有学生 42 人,参加体育代表队的有 30 人,参加文艺代表队的有 25 人,而且每人都起码参加了一个队,这个班两队都参加的有多少人?4、30 名学生中, 8 人学法语, 12 人学西班牙语, 3 人既学法语又学西班牙语,问有多少名学生两种语言都不学?5、五年级有 122 名学生参加语文、数学考试,每人起码有一门功课获得优异成绩,此中语文成绩优异的有 65 人,数学优异的有 87 人。
四年级奥数教材第23讲 容斥问题(一)

第23讲容斥问题(一)容斥问题涉及到一个重要的原理——包含与排除原理,也称为容斥原理,即当两个计数部分有重复包含时,为了不重复地计数,应从它们的和中排除重复部分。
这一讲我们先介绍容斥原理1对n个事物,如果采用两种不同的分类标准:按性质a分类与性质b分类(如图1),那么,具有性质a或性质b的事物的个数=Na+Nb-Nab。
例1.一个班有55名学生,订阅《小学生数学报》的有12人,订阅《今日少年报》的有9人,两种报纸都订阅的有5人。
(1)订阅报纸的总人数有多少?(2)两种报纸都没订阅的有多少人?例2.一个旅行社有36人,其中会英语的有24人,会俄语的有18人,两样都不会的有4人,两样都会的有多少人?例3.在1到100的全部自然数中,既不是6的倍数也不是5的倍数的数有多少个?例4.艺术节那天,学校的画廊里展了了每个年级学生的图画作品,其中有23幅画不是五年级的,有21幅画不是六年级的,五、六年级参展的画共有8幅。
其他年级参展的画共有多少幅?练习与思考1.将边长分别为4厘米和5厘米的正方形纸片部分重叠,盖在桌面上(如图6),已知重叠的部分为9平方厘米,两块正方形纸片盖住桌面的总面积是多少平方厘米?2.二(2)班有50名学生,下课后每人都至少做完了一门作业,其中做完语文作业的有35人,做完数学作业的有40人,两种作业都做完的有多少人?3.有62名学生,其中会弹钢琴的有11名,会吹竖笛的有56名,两样都不会的有4名,两样都会的有多少名?4.某校选出50名学生参加区作文比赛和数学比赛,作文比赛获奖的有14人,数学比赛获奖的有12人,有3人两项比赛都获奖的,两项比赛都没获奖的有多少人?5.四(1)班有40个学生,其中有25人参加数学小组,23人参加航模水组,有19人两个小组都参加了,那么,有多少人两个小组都没有参加?6.在一次数学测验中,所有同学都答了第1、2两题,其中答对第1题的有35人,答对第2题的有28人,这两题都答对的有20人,没有人两题都答错。
四年级奥数 第35讲 容斥问题

第35周容斥问题专题简析:容斥问题涉及一个重要原理一一包含与排除原理,也叫容斥原理。
当两个计数部分有重复包含时,为了不重复地计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用两种不同的分类标准,按性质a分类与性质b分类(如右图所示),那么具有性质a或性质b的事物的个数是Na 十Nb- Nab。
例1:一个班有48人,班主任在班会上问“谁做完语文作业了?请举手!”有37人举手。
又问:“谁做完数学作业了?请举手!”有42人举手。
最后问“谁语文、数学作业都没有做完?“没有人举手。
求这个班语文、数学作业都完成的人数。
练习一:1、五年级有122 名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65 人,数学成绩优秀的有87 人。
语文、数学成绩都优秀的有多少人?2、四(1)班有54 人,订阅<小学生优秀作文》和(数学大世界)两种读物的有13 人,订《小学生优秀作文》的有45 人,每人至少订种读物。
订《数学大世界》》的有多少人?3、学校文艺组每人至少会演奏一种乐器,已知会拉手风琴的有24人,会弹电子琴的有17人,其中两种乐器都会演奏的有8人。
这个文艺组一共有多少人?例2:城中小学选出10名学生参加区作文和数学比赛,结果每人都获奖。
其中有3人两项比赛都获奖,作文比赛获奖的有5 人,求数学比赛获奖的有多少人?练习:1、一个班有55 名学生,他们分别订阅了《小学生数学报》和《中国少年报》。
其中订阅《小学生数学报》的有32 人,两种报纸都订阅的有15 人,求订阅《中国少年报》的有多少人?2、四(1)班有40 个学生,有19 人参加了数学和科技两个兴趣小组。
其中有11人两个小组都没参加,有25人参加数学小组,求有多少人参加了科技小组?3、在四年级96 个学生中调查会下中国象棋和围棋的人数。
调查结果显示:有78人会下中国象棋,有24 人两样都会,还有12人两样都不会。
求会下围棋的有多少人?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?练习:1、一个旅行社有36 人,其中会英语的有24 人,会法语的有18 人,两样都不会的有4 人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲包含与排除——容斥原理
知识要点
以前我们是不是遇到过这样问题:从左边数,小明排在第8个,从右边起小明排在第15个,这一排一共有多少个人?这道题是不是小明被重复计算啦,如果要使得计算的结果既不重复,又无遗漏,就需要把重复的计数排除出去,这样的计数方法就是容斥原理,也称之为重叠问题。
解决这类问题,我们还可以借助韦恩图来分析数量关系。
小明
1人
8人 15人
一般先把包含的所有数量都计算出来,再把重叠的部分排除出去,就可以计算出不重复、不遗漏的数量了:8+15-1=22(人)
精典例题
例1:四(2)班参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加了,这个班有多少人参加了语文或数学兴趣小组?
模仿练习
学校文艺组的每位同学至少会演奏钢琴和手风琴中的一种乐器,已知会演奏钢琴的有24人,会演奏手风琴的有17人,其中两种乐器都会演奏的有8人,那么文艺组一共有多少人?
精典例题
例2:某餐馆有40道招牌菜,牛牛吃过其中的15道,丁丁吃过其中的9道,且有4道菜是两人都吃过的,那么有多少道招牌菜两人都没有吃过?
模仿练习
在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的人有7人,既没有采樱桃又没有采杏的有6人,只采了杏的有多少人?
先画韦恩图分析数量关系,再利用包含与排除的方法来计算。
先算他们吃过的菜,再算没有吃过的。
精典例题
例3:在1到100这100个自然数中,5和6的倍数一共有多少个?
模仿练习
在1到100这100个自然数中,不能被5和8整除的数一共有多少个?
精典例题
例4:50名同学面向老师站成一行,老师先让大家从左往右按1、2、3……一次报数,然后让报数是4的倍数的同学向后转,接着又让报数是6的倍数同学向后转。
现在还面向老师的同学有多少名?
模仿练习
一根长60里面的木棍,每5厘米用红点标记,每6厘米用蓝点标记,延标记的地方把木棍锯断,木棍总共被锯成了多少段?
精典例题
例5:光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个小组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的人数有10人,同时参加了中国象棋和国际象棋比赛的有9人,三种都参加了的有5人,问:参加棋类比赛的共有多少人?
模仿练习
三位经理投资了若干只股票,张经理买了66只,王经理买了40只,李经理买了23只,张经理和王经理都买了有17只,王经理和李经理都买了的有13只,李经理和张经理都买了的有9只,三人都买了的有6只,请问这三位经理一共买了多少只不同的股票?
先弄清楚有多少同学转了,有多少个同学没转,再思考哪些同学转了两次,因为没转
的和转了两次的同学都是面向老师的。
先找5的倍数有多少个?6的倍数有多少个?再利用包含与排除的方法解决。
这是属于三个数量的容斥问题,先计算参加三类棋人数的总和,在把重复计算了两次
的人数减去,但要思考:其中重复计算了3次5人,有没有被减掉?减了几次?
家庭作业
1.四(3)班有45人,参加数学兴趣小组的有30人,参加语文兴趣小组的有22人,并且每人至少参加了一个兴趣小组,那么两样都参加了的有几人?
2.对全班的同学调查发现,会游泳的有20人,会打篮球的有25人,两项都会的有10人,两项都不会的有9人,这个班一共有多少人?
3.1到100这些自然数中,4和5的倍数一共有多少个?
4. 36个学生回答两个问题,答对第一题的有23人,答对第二题的有25人,两题都答对的有14人,两题都没有答对的有多少人?
5.47名同学参加数学和语文考试,其中语文得分95分以上的有14人,数学得分95分以上的有21人,两门都没有在95分以上的有22人,求两门都在95分以上的有多少人。
6.30名同学面向老师站成一排,老师先让大家从左往右按1、2、3……一次报数,然后让报数是2的倍数的同学向后转,再让报数是3的倍数的同学向后转,现在还有多少名同学面向老师?
7.四年级课外活动有体育、音乐和书法,参加的人数分别是54人、46人、36人,其中参加体育和音乐两组有7人,参加音乐和书法两组的有10人,参加体育和书法两组的有10人,三个组都参加了的有2人,五年级参加课外活动的一共有多少人?。
