大学物理学(第三版)课后习题答案
大学物理学(第三版)课后习题答案解析

1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 222s h l +=将上式对时间t 求导,得tss t l ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴ tsv v t l v d d ,d d 0-==-=船绳 即 θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 mv=0,求该质点在t =10s 时的速度和位置. 解:∵ t tva 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+= 积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔 60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R .(提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示.题1-10图 (1)在最高点,o 0160cos v v v x == 21s m 10-⋅==g a n又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1s m -⋅,而 o60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v =30km ·h -1沿直线向东行驶,另一小艇在其前方以速率2v =40km ·h -1沿直线向北行驶,问在船上看小艇的速度为何?在艇上看船的速度又为何?解:(1)大船看小艇,则有1221v v v-=,依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船,则有2112v v v-=,依题意作出速度矢量图如题1-13图(b),同上法,得5012=v 1h km -⋅2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ①Y 方向: y y ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ,得220sin 21x g v y ⋅=α 2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-=分离变量,得mtk v v d d -=即 ⎰⎰-=vv t mt k v v00d d m kte v v -=ln ln 0∴ tm k ev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零,即t →∞,故有 ⎰∞-=='00d kmv t ev x tm k(4)当t=km时,其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1. 2-10 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm,问击第二次时能击入多深,假定铁锤两次打击解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t 时,f 'f -=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y kky y ky A ② 由题意,有2)21(212kmv A A =∆== ③即222122k k ky =- 所以, 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端 一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆ 弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB =BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量,则h BC AC l )12(-=-=∆联立上述两式,得()()212221122mm khgh m m v +-+-=μ题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽,如题2-19图所示.质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度.解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有222121MV mv mgR +=又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有0=-MV mv联立,以上两式,得()M m MgR v +=2习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204r q E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024dq πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p=,场点到偶极子中心O 点的距离为r ,矢量r与l 的夹角为θ,(见题8-5图),且l r >>.试证P点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r平行的分量θsin p 和垂直于r 的分量θsin p .∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向,即θ方向场强分量300π4sin r p E εθ=题8-5图 题8-6图8-6 长l =15.0cmAB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)2220d d π41d +=x xE Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε 22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==ϕϕελϕπd cos π4)cos(d d 0RE E y-=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴ RE E x0π2ελ==,方向沿x 轴正向. 8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E解: 如8-8图示,正方形一条边上电荷4q 在P 点产生物强PEd方向如图,大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴ 24π4d 22220l r l l r E P++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE+++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq 4=λ∴ 2)4(π422220l r l r qrE P++=ε 方向沿8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(xR arctan =α)解: (1)由高斯定理0d εq S E s⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εqe=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则24εq e =Φ,如果它包含q 所在顶点则0=Φe.如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强. 解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=qr E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E )(21210σσε-= 1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+= n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a). (1) ρ+球在O 点产生电场010=E,ρ-球在O 点产生电场d π4π3430320OO r E ερ=∴ O 点电场'd 33030OO r E ερ= ;(2) ρ+在O '产生电场dπ4d 3430301E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='EOO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r ',相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =,3ερr E O P '-=' ,∴ 0003'3)(3ερερερd OO r r E E E O P PO P=='-=+='∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C-1解: ∵ 电偶极子p在外场E 中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=[)2sin(π-2sin π-] R0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===A B200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E 与电势U 的关系U E -∇=,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图)解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势 200π4cos ])cos 21(1)cos 2(1[π4r ql llr qU εθθθε=+--=∴ 30π2cos r p r U E rεθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反; (2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同. 8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =,即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC ACAC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q(1)外球壳上的电荷分(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+RqR q εε 得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力;(2)小球3依次交替接触小球1,2很多次后移去,小球1,2之解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电 2q q =',小球3再与小球2接触后,小球2与小球3均带电 q q 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r q q F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得 Sq 261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意:因为C 片带电,所以2U U C≠,若C 片不带电,显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D ε ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得 11σ=D ,22σ=D 而 101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212 r d r d ⋅+⋅=⎰⎰∞∞rrE E U 外内题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S则 rlD S DS π2d )(=⋅⎰当)(21R r R <<时,Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度.解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力..为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-32 1C 和2C 两电容器分别标明“200 pF 、500 V”和“300 pF 、900 V”,把它们串联起来后等值电容是多少?如果两端加上1000 V?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿. 8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求:(1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r r Q E ε=3R r >时 302π4r r Q E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r r Q E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向? 解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ 外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B的轴向分量为零,而垂直于轴的圆周方向分量rI B πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m-2x轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb(或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB产生 01=B CD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学第三版课后题答案[1]
![大学物理学第三版课后题答案[1]](https://img.taocdn.com/s3/m/ff349a040a4e767f5acfa1c7aa00b52acfc79cdd.png)
大学物理学第三版课后题答案[1]1-4在离水面高h米的岸上,有人用绳子拉船靠岸,船在离岸s处,如题1-4图所示.当人以v0(ms速率收绳时,试求船运动的速度和加速度的大小.1)对图1-4解决方案:假设人与船之间的绳子长度为l,那么绳子与水面成一条直线?角度,L2?h2?s2将上式对时间t求导,得2ldlds?2sdtdt问题的图1-4根据速度的定义,并注意到l,s是随t减少的,3V绳索??DLD?V0,V??Dtdt是v船吗??vdsldll v0?0dtsdtscos?lv0(h2?s2)1/2v0?或v船?ss取V船对T的导数,得到船的加速度1-6已知一质点作直线运动,其加速度为a=4+3tm?s?2,开始运动时,x=5m,v=0,求该质t=10s时点的速度和位置解:∵a?dv?4?3tdt分离变量,得dv?(4?3t)dt积分,3V?4t?t2?c12由题知,t?0,v0?0,∴c1?0那么V3呢?4t?t22又因为v?dx3?4t?t2dt2分离变量,dx3?(4t?t2)dt21? 2t2?t3?c22积分得x由题知t?0,x0?5,∴c2?5那么X1呢?2t2?t3?五2所以t?10s时v10?4.10? 3.102? 1.9亿?s十二1x10?2?102??103?5?705m2?11-10以初速度v0=20m?s抛出一小球,抛出方向与水平面成幔60°的夹角,求出:(1)球面轨道最高点的曲率半径R1;(2)着陆点处的曲率半径R2(提示:利用曲率半径与法向加速度之间的关系)解决方案:让小球形成的抛物线轨道如图1-10所示题1-10图(1)在最高点,v1?vx?V060OAN1?G10米?s二又∵an1?v12?1v12(20?60?)2.1.an110∴10m(2)在落地点,v2?v0?两千万?s1.而an2?g?cos60o∴2v2(20)2?280man210?cos60?-一-11-13一艘船以V1=30公里小时的速度直线向东行驶,另一艘小船以V2=40公里小时的速度直线向北行驶。
大学物理学(第三版上)课后习题3答案详解

习题33.1选择题(1) 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A) (B) 02ωmRJ J +02)(ωR m J J +(C) (D) 02ωmRJ 0ω[答案: (A)](2) 如题3.1(2)图所示,一光滑的内表面半径为10cm 的半球形碗,以匀角速度ω绕其对称轴OC 旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm ,则由此可推知碗旋转的角速度约为(A)13rad/s (B)17rad/s(C)10rad/s (D)18rad/s (a)(b)题3.1(2)图[答案: (A)](3)如3.1(3)图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A )动能不变,动量改变。
(B )动量不变,动能改变。
(C )角动量不变,动量不变。
(D )角动量改变,动量改变。
(E )角动量不变,动能、动量都改变。
[答案: (E)]3.2填空题(1) 半径为30cm 的飞轮,从静止开始以0.5rad·s -2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度a τ= ,法向加速度a n = 。
0.15; 1.256[答案:](2) 如题3.2(2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的 守恒,原因是 。
木球被击中后棒和球升高的过程中,对木球、子弹、细棒、地球系统的 守恒。
题3.2(2)图[答案:对o轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对o轴的合外力矩为零,机械能守恒](3) 两个质量分布均匀的圆盘A和B的密度分别为ρA和ρB (ρA>ρB),且两圆盘的总质量和厚度均相同。
大学物理学(第三版上) 课后习题6答案详解

习题66.1选择题(1)一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:(A)它的动能转化为势能. (B)它的势能转化为动能.(C)它从相邻的一段质元获得能量其能量逐渐增大.(D)它把自己的能量传给相邻的一段质元,其能量逐渐减小.[答案:D ](2) 某时刻驻波波形曲线如图所示,则a,b 两点位相差是(A)π (B)π/2 (C)5π/4 (D)0[答案:A](3) 设声波在媒质中的传播速度为u,声源的频率为v s .若声源S不动,而接收器R相对于媒质以速度V B 沿着S、R连线向着声源S运动,则位于S、R连线中点的质点P的振动频率为 (A)s v (B)s Bv uV u + (C)s B v V u u + (D) s Bv V u u-[答案:A]6.2填空题(1)频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距____m 。
[答案:0.5m ](2)一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是____,波长是____,频率是____,波的传播速度是____。
[答案:0.02;2.5;100;250/m m Hz m s ](3) 设入射波的表达式为])(2cos[1πλνπ++=xt A y ,波在x =0处反射,反射点为一固定端,则反射波的表达式为________________,驻波的表达式为____________________,入射波和反射波合成的驻波的波腹所在处的坐标为____________________。
[答案:)(2cos 2λνπxt A y -= ;2cos(2)cos(2)22x A t ππππνλ++ (21)4x k λ=-]6.3产生机械波的条件是什么?两列波叠加产生干涉现象必须满足什么条件?满足什么条件的两列波才能叠加后形成驻波?在什么情况下会出现半波损失?答:产生机械波必须具备两个条件:有作机械振动的物体即波源;有连续的介质。
大学物理学(第三版上)课后习题6答案详解

习题 66.1 选择题(1) 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移 处的过程中:(A) 它的动能转化为势能 . (B) 它的势能转化为动能 . (C)它从相邻的一段质元获得能量其能量逐渐增大 .(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小 .[ 答案: D](2) 某时刻驻波波形曲线如图所示,则 a,b 两点位相差是(A)π (C)5π/4[ 答案: A](3) 设声波在媒质中的传播速度为u,声源的频率为 v s .若声源S不动,而接收器R相对于媒质以速度 V B 沿着S、R连线向着声源S运动,则位于S、 R连线中点的质点P的振动频率为[ 答案: A]6.2 填空题(1) ______________________ 频率为 100Hz ,传播速度为 300m/s 的平面简谐波,波线上两点振动的相位 差为 π /3,则此两点相距 m 。
[答案: 0.5m ](2)一横波的波动方程是 y 0.02sin2 (100t 0.4x)( SI ) ,则振幅是 ________ ,波长是 ___ ,频率是 __ ,波的传播速度是 __ 。
[ 答案: 0.02m;2.5 m;100 Hz;250 m / s ]x(D)0(A) v s(B)u V B u (C)vsu V B s(D)u u V Bvs(B)π/2(3) 设入射波的表达式为y1 Acos[2 ( t ) ] ,波在x =0处反射,反射点为一固定端,则反射波的表达式为__________________ ,驻波的表达式为____________________ ,入射波和反射波合成的驻波的波腹所在处的坐标为x[ 答案:y2 Acos2 ( t ) ;x2 A cos(2 )cos(2 t )22x (2k 1) ]46.3 产生机械波的条件是什么?两列波叠加产生干涉现象必须满足什么条件?满足什么条件的两列波才能叠加后形成驻波?在什么情况下会出现半波损失?答:产生机械波必须具备两个条件:有作机械振动的物体即波源;有连续的介质。
(完整版)大学物理学(第三版)课后习题答案

1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得tss t l ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴ tsv v t l v d d ,d d 0-==-=船绳 即 θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m ,v=0,求该质点在t =10s 时的速度和位置. 解:∵ t tva 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+= 积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔 60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R .(提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示.题1-10图 (1)在最高点,o 0160cos v v v x == 21s m 10-⋅==g a n又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1s m -⋅,而 o60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v =30km ·h -1沿直线向东行驶,另一小艇在其前方以速率2v =40km ·h -1沿直线向北行驶,问在船上看小艇的速度为何?在艇上看船的速度又为何?解:(1)大船看小艇,则有1221v v v ρϖϖ-=,依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船,则有2112v v v ρϖϖ-=,依题意作出速度矢量图如题1-13图(b),同上法,得5012=v 1h km -⋅2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v ϖ方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ①Y 方向: y y ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ,得220sin 21x g v y ⋅=α 2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-=分离变量,得mtk v v d d -=即 ⎰⎰-=vv t mt k v v00d d m kte v v -=ln ln 0∴ tm k ev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零,即t →∞,故有 ⎰∞-=='00d kmv t ev x tm k(4)当t=km时,其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1. 2-10 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm ,问击第二次时能击入多深,假定铁锤两次打击铁钉时的速度相同.解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t 时,f 'f -=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y kky y ky A ② 由题意,有2)21(212kmv A A =∆== ③即222122k k ky =- 所以, 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端 一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势能之比.解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆ 弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB =BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量,则h BC AC l )12(-=-=∆联立上述两式,得()()212221122m m khgh m m v +-+-=μ题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽,如题2-19图所示.质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度.解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有222121MV mv mgR +=又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有0=-MV mv联立,以上两式,得()M m MgR v +=2习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204r q E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q E ϖϖε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024dq πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力. 8-5一电偶极子的电矩为l q p ϖϖ=,场点到偶极子中心O 点的距离为r ,矢量r ϖ与l ϖ的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p ϖ分解为与r ϖ平行的分量θsin p 和垂直于r ϖ的分量θsin p .∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向,即θ方向场强分量300π4sin r p E εθ=题8-5图 题8-6图8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ,即Q E ϖ只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε 22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==ϕϕελϕπd cos π4)cos(d d 0RE E y-=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴ RE E x0π2ελ==,方向沿x 轴正向. 8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如8-8图示,正方形一条边上电荷4q 在P 点产生物强PE ϖd方向如图,大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴ 24π4d 22220l r l l r E P++=ελP E ϖd 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq 4=λ∴ 2)4(π422220l r l r qrE P++=ε 方向沿8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(xR arctan =α)解: (1)由高斯定理0d εqS E s⎰=⋅ϖϖ立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εqe=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则24εq e =Φ,如果它包含q 所在顶点则0=Φe.如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强. 解: 高斯定理0d ε∑⎰=⋅qS E s ϖϖ,02π4ε∑=qr E当5=r cm 时,0=∑q ,0=E ϖ8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E sϖϖ取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰ϖϖ对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E ϖϖ)(21210σσε-= 1σ面外, n E ϖϖ)(21210σσε+-= 2σ面外, n E ϖϖ)(21210σσε+= n ϖ:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a). (1) ρ+球在O 点产生电场010=E ϖ,ρ-球在O 点产生电场'dπ4π3430320OO r E ερ=ϖ∴ O 点电场'd 33030OO r E ερ=ϖ;(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ϖρ-球在O '产生电场002='E ϖ∴ O ' 点电场 003ερ='E ϖ'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r ϖ',相对O 点位矢为r ϖ (如题8-13(b)图)则 03ερrE PO ϖϖ=,3ερr E O P '-='ϖϖ,∴ 0003'3)(3ερερερdOO r r E E E O P PO P ϖϖϖϖϖϖ=='-=+='∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p ϖ在外场E ϖ中受力矩E p M ϖϖϖ⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εεϖϖ)11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功. 解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点E ϖd 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=[)2sin(π-2sin π-] R0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===A B200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E ϖ与电势U 的关系U E -∇=ϖ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ϖϖϖε=∂∂-= 0r ϖ为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E ϖϖϖ2/3220π4+=∂∂-=ε(3)偶极子l q pϖϖ=在l r >>处的一点电势 200π4cos ])cos 21(1)cos 2(1[π4r ql llr qU εθθθε=+--=∴ 30π2cos r p r U E rεθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有0)(d 32=∆+=⋅⎰S S E sσσϖϖ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反; (2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同. 8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =,即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC ACAC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εεϖϖ (2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+RqR q εε 得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力;(2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电 2q q =',小球3再与小球2接触后,小球2与小球3均带电 q q 43=''∴此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r q q F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得 Sq 261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意:因为C 片带电,所以2U U C≠,若C 片不带电,显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D S ϖϖd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εεϖϖϖϖ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D εϖϖϖ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞ϖϖ外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221ϖϖϖϖ⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E ϖ,真空部分场强为1E ϖ,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D ϖϖ得 11σ=D ,22σ=D 而 101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212 r d r d ϖϖϖϖ⋅+⋅=⎰⎰∞∞rrE E U 外内题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S则 rlD S DS π2d )(=⋅⎰ϖϖ当)(21R r R <<时,Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度.解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力..为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-321C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V的电压,是否会击穿?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿. 8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求:(1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E ϖ在21R r R <<时 301π4r r Q E εϖϖ=3R r >时 302π4r r Q E εϖϖ=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r r Q E εϖϖ=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向? 解: 在同一磁感应线上,各点B ϖ的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B ϖ的方向.9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B ρϖ=∑⎰==-=⋅0d 021I bc B da B l B abcdμϖϖ∴ 21B B ρϖ=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B ϖ方向相反,即21B B ρϖ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L ϖ·d l ϖ=0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L ϖ·d l ϖ=I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μϖϖ外,与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B ϖ的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S B ϖϖΦWb(2)通过befc 面积2S 的磁通量022=⋅=S B ϖϖΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb(或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B )为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B )、CD 三部分电流产生.其中AB产生 01=B ϖ CD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B ϖ方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B ϖ在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学(第三版上) 课后习题3答案详解

习题33.1选择题(1) 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)02ωmRJ J+ (B) 02)(ωR m J J + (C)02ωmRJ(D) 0ω [答案: (A)](2) 如题3.1(2)图所示,一光滑的内表面半径为10cm 的半球形碗,以匀角速度ω绕其对称轴OC 旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm ,则由此可推知碗旋转的角速度约为 (A)13rad/s (B)17rad/s (C)10rad/s (D)18rad/s(a) (b)题3.1(2)图[答案: (A)](3)如3.1(3)图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体 (A )动能不变,动量改变。
(B )动量不变,动能改变。
(C )角动量不变,动量不变。
(D )角动量改变,动量改变。
(E )角动量不变,动能、动量都改变。
[答案: (E)]3.2填空题(1) 半径为30cm 的飞轮,从静止开始以0.5rad·s -2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度a τ= ,法向加速度a n=。
[答案:0.15; 1.256](2) 如题3.2(2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的守恒,原因是。
木球被击中后棒和球升高的过程中,对木球、子弹、细棒、地球系统的守恒。
题3.2(2)图[答案:对o轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对o轴的合外力矩为零,机械能守恒](3) 两个质量分布均匀的圆盘A和B的密度分别为ρA和ρB (ρA>ρB),且两圆盘的总质量和厚度均相同。
(完整版)大学物理学(第三版上)课后习题6答案详解

习题66.1选择题(1)一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:(A)它的动能转化为势能. (B)它的势能转化为动能.(C)它从相邻的一段质元获得能量其能量逐渐增大.(D)它把自己的能量传给相邻的一段质元,其能量逐渐减小.[答案:D ](2) 某时刻驻波波形曲线如图所示,则a,b 两点位相差是(A)π (B)π/2 (C)5π/4 (D)0[答案:A](3) 设声波在媒质中的传播速度为u,声源的频率为v s .若声源S不动,而接收器R相对于媒质以速度V B 沿着S、R连线向着声源S运动,则位于S、R连线中点的质点P的振动频率为 (A)s v (B)s Bv uV u + (C)s B v V u u + (D) s Bv V u u-[答案:A]6.2填空题(1)频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距____m 。
[答案:0.5m ](2)一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是____,波长是____,频率是____,波的传播速度是____。
[答案:0.02;2.5;100;250/m m Hz m s ](3) 设入射波的表达式为])(2cos[1πλνπ++=xt A y ,波在x =0处反射,反射点为一固定端,则反射波的表达式为________________,驻波的表达式为____________________,入射波和反射波合成的驻波的波腹所在处的坐标为____________________。
[答案:)(2cos 2λνπxt A y -= ;2cos(2)cos(2)22x A t ππππνλ++ (21)4x k λ=-]6.3产生机械波的条件是什么?两列波叠加产生干涉现象必须满足什么条件?满足什么条件的两列波才能叠加后形成驻波?在什么情况下会出现半波损失?答:产生机械波必须具备两个条件:有作机械振动的物体即波源;有连续的介质。
大学物理(上册—第三版—修订版)课后习题答案

大学物理(上册)课后习题答案第三版·修订版习题一1-6|r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同?t d d v 和td d v 有无不同?其不同在哪里?试举例说明。
解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v tsd d .trd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rrr +=式中trd d 就是速度径向上的分量,∴trt d d d d 与r 不同如题1-1图所示.题1-6图(3)t d d v 表示加速度的模,即t v a d d=,tv d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以tv t v t v d d d d d d ττ+=式中dt dv就是加速度的切向分量.(tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-7设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t r d d ,及a =22d d tr 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jty i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d tr a t rv ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理上册课后习题答案(第三版_修订版)

因此, A 对地的速度为
v A地
u
v
' A
(u 2gh cos )i ( 2gh sin ) j
题▲图
1-14 一船以速率 v1 = 30km2 h-1沿直线向东行驶,另一小艇在其前方以速率
v2 = 40km2
-1
h
沿直线向北行驶,问在船上看小艇的速度为何 ?在艇上看船的速度又为何 ?
解: (1) 大船看小艇,则有 v21 v2 v1 ,依题意作速度矢量图如题 1-13 图 (a)
R 2 sin t
dvx dt
ay
R 2 cos t
dvy dt
▲
以初速度
v0 = 20 m
s
1
抛出一小球,抛出方向与水平面成幔
60 °的夹角,
求: (1) 球轨道最高点的曲率半径 R1 ; (2) 落地处的曲率半径 R2 .
( 提示:利用曲率半径与法向加速度之间的关系
)
解:设小球所作抛物线轨道如题 1-10 图所示.
习题解答 (注:无选择题,书本已给出)
习题一
1-6 | r |与 r 有无不同 ? dr 和 dr 有无不同 ? d v 和 dv 有无不同 ?其不同在哪里 ?
dt dt
dt d t
试举例说明.
解: ( 1) r 是位移的模, r 是位矢的模的增量,即
r r2 r1 , r r2 r1 ;
(2) dr 是速度的模,即 dr
a
a
2 n
a2
(0.064) 2 (0.08) 2 0.102 m s 2
▲ 如题 1-12 图,物体 A 以相对 B 的速度 v = 2gy 沿斜面滑动, y 为纵坐标,开始时 A
大学物理学第三版下册课后答案
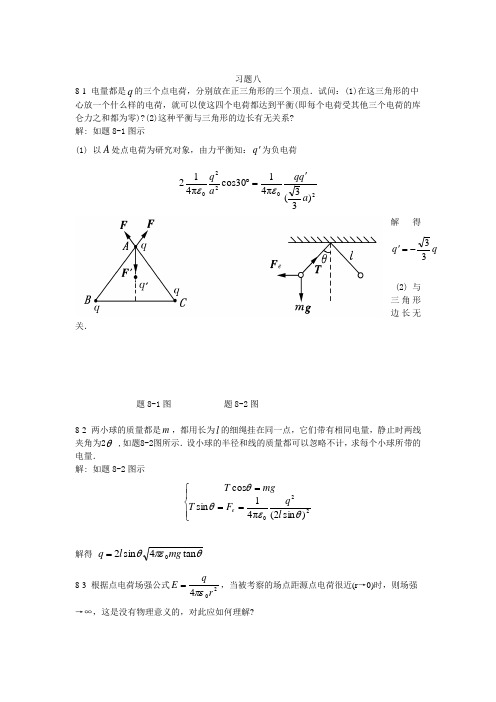
习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得q q 33-='(2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204rq E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强SqE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为S qE 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p =,场点到偶极子中心O 点的距离为r ,矢量r 与l的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin rp πεθ证: 如题8-5所示,将p 分解为与r 平行的分量θsin p 和垂直于r的分量θsin p . ∵ l r >>∴ 场点P 在r 方向场强分量30π2cos rp E r εθ=垂直于r 方向,即θ方向场强分量300π4sin rp E εθ=题8-5图 题8-6图8-6 长l =15.0cm AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε222)(d π4d x a xE E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)2220d d π41d +=x xE Q λε 方向如题8-6图所示由于对称性⎰=l Qx E 0d ,即Q E只有y 分量,∵ 22222220d d d d π41d ++=x x x E Qy λε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d l l x x2220d 4π2+=l lελ 以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强. 解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分R R E x 000π2d sin π4ελϕϕελπ==⎰d cos π400=-=⎰ϕϕελπRE y ∴ RE E x 0π2ελ==,方向沿x 轴正向.8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E解: 如8-8图示,正方形一条边上电荷4q在P 点产生物强P E d 方向如图,大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴ 24π4d 22220l r l l r E P ++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq 4=λ ∴ 2)4(π422220l r l r qrE P ++=ε 方向沿OP8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(xRarctan=α) 解: (1)由高斯定理d εqS E s⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量6εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量6εq e=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则24εqe =Φ,如果它包含q 所在顶点则0=Φe .如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq=[221xR x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外. 8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-= 1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+= n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a). (1) ρ+球在O 点产生电场010=E,ρ- 球在O 点产生电场d π4π3430320OO r E ερ=∴ O 点电场d33030r E ερ= ; (2) ρ+在O '产生电场'd π4d 3430301E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r',相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =,3ερr E O P '-=' ,∴ 0003'3)(3ερερερdr r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C d=0.2cm ,把这电偶极子放在1.0×105N ·C-1解: ∵ 电偶极子p在外场E中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解:⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C点,求移动过程中电场力作的解: 如题8-16图示π41ε=O U 0)(=-RqR q 0π41ε=Uc )3(R q R q -R q 0π6ε-=∴Rqq U U q A o C O00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=[)2sin(π-2sin π-]R0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ 同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O 8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e 0π2ελ== ∴ rv m r e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d=0.5cm 解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E -∇= ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图)解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r rq r r U Eε=∂∂-= 0r为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E2/3220π4+=∂∂-=ε(3)偶极子l q p =在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4rql llr qU εθθθε=+--=∴ 30π2cos r p r U E r εθ=∂∂-= 30π4sin 1rp U r E εθθθ=∂∂-= 8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少? 解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =,即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ 而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计(1) (2) *(3) 解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R Rqr r q r E U εε(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε得 q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+Rq R q εε得 -='q 3q 8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =', 小球3再与小球2接触后,小球2与小球3均带电q q 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力00294π432322F r qq F ==ε*8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A 解得 Sq261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ 所以CB 间电场 S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意:因为C 片带电,所以2U U C ≠,若C 片不带电,显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εε ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外(2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε(3)金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Q r r-+=εεε rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E ,真空部分场强为1E,自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D得11σ=D ,22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε (3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41rq q F ε=但2q 处于金属球壳中心,它受合力..为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q = ∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V ?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U ,而100021=+U U ∴ 6001=U V ,4002=U V 即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112*********U U U C U C q qU C U C q q q q 解得 (1) =1q U C C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r rQ E ε=3R r >时 302π4rrQ E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε ∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r rQ E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R Q W C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管 外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为 ⎰外B L ·d l =I 0μ 这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B 的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m-2x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S BΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 产生 01=BCD 产生RIB 1202μ=,方向垂直向里CD 段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学(第三版)第二章课后答案

习题22.1选择题(1) 一质点作匀速率圆周运动时,(A)它的动量不变,对圆心的角动量也不变。
(B)它的动量不变,对圆心的角动量不断改变。
(C)它的动量不断改变,对圆心的角动量不变。
(D)它的动量不断改变,对圆心的角动量也不断改变。
[答案:C](2) 质点系的内力可以改变(A)系统的总质量。
(B)系统的总动量。
(C)系统的总动能。
(D)系统的总角动量。
[答案:C](3) 对功的概念有以下几种说法:①保守力作正功时,系统内相应的势能增加。
②质点运动经一闭合路径,保守力对质点作的功为零。
③作用力与反作用力大小相等、方向相反,所以两者所作功的代数和必为零。
在上述说法中:(A)①、②是正确的。
(B)②、③是正确的。
(C)只有②是正确的。
(D)只有③是正确的。
[答案:C]2.2填空题(1) 某质点在力(SI)的作用下沿x轴作直线运动。
在从x=0移动到x=10m的过程中,力所做功为。
[答案:290J](2) 质量为m的物体在水平面上作直线运动,当速度为v时仅在摩擦力作用下开始作匀减速运动,经过距离s后速度减为零。
则物体加速度的大小为,物体与水平面间的摩擦系数为。
[答案:](3) 在光滑的水平面内有两个物体A和B,已知m A=2m B。
(a)物体A以一定的动能E k与静止的物体B发生完全弹性碰撞,则碰撞后两物体的总动能为;(b)物体A以一定的动能E k与静止的物体B发生完全非弹性碰撞,则碰撞后两物体的总动能为。
[答案:]2.3 在下列情况下,说明质点所受合力的特点:(1)质点作匀速直线运动;(2)质点作匀减速直线运动;(3)质点作匀速圆周运动;(4)质点作匀加速圆周运动。
解:(1)所受合力为零;(2)所受合力为大小、方向均保持不变的力,其方向与运动方向相反;(3)所受合力为大小保持不变、方向不断改变总是指向圆心的力;(4)所受合力为大小和方向均不断变化的力,其切向力的方向与运动方向相同,大小恒定;法向力方向指向圆心。
大学物理学(第三版)课后习题参考答案

习题11.1选择题(1) 一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为(A)dt dr (B)dt r d(C)dtr d ||(D) 22)()(dt dy dt dx +[答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为(A)t R t R ππ2,2 (B) tRπ2,0 (C) 0,0 (D) 0,2tRπ[答案:B]1.2填空题(1) 一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是 ;经过的路程是 。
[答案: 10m ; 5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m·s -1,则当t 为3s 时,质点的速度v= 。
[答案: 23m·s -1 ](3) 轮船在水上以相对于水的速度1V 航行,水流速度为2V ,一人相对于甲板以速度3V行走。
如人相对于岸静止,则1V 、2V 和3V的关系是 。
[答案: 0321=++V V V]1.3 一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状; (2) 物体的内部结构; (3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1.4 下面几个质点运动学方程,哪个是匀变速直线运动?(1)x=4t-3;(2)x=-4t 3+3t 2+6;(3)x=-2t 2+8t+4;(4)x=2/t 2-4/t 。
给出这个匀变速直线运动在t=3s 时的速度和加速度,并说明该时刻运动是加速的还是减速的。
大学物理学(第三版)课后习题参考答案

习题 11.1选择题(1) 一运动质点在某瞬时位于矢径),(y x r 的端点处,其速度大小为(A)dtdr (B)dtr d (C)dtr d ||(D)22)()(dtdy dt dx [答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2,瞬时加速度2/2s m a ,则一秒钟后质点的速度(A)等于零(B)等于-2m/s (C)等于2m/s(D)不能确定。
[答案:D] (3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为(A)tR t R 2,2(B) t R2,0(C) 0,0(D) 0,2tR[答案:B]1.2填空题(1) 一质点,以1s m 的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是;经过的路程是。
[答案:10m ;5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m ·s -1,则当t 为3s 时,质点的速度v=。
[答案:23m ·s -1](3) 轮船在水上以相对于水的速度1V 航行,水流速度为2V ,一人相对于甲板以速度3V 行走。
如人相对于岸静止,则1V 、2V 和3V 的关系是。
[答案:0321V V V ]1.3一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状;(2) 物体的内部结构;(3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1.4下面几个质点运动学方程,哪个是匀变速直线运动?(1)x=4t-3;(2)x=-4t 3+3t 2+6;(3)x=-2t 2+8t+4;(4)x=2/t 2-4/t 。
给出这个匀变速直线运动在t=3s 时的速度和加速度,并说明该时刻运动是加速的还是减速的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得tss t l ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴ tsv v t l v d d ,d d 0-==-=船绳 即 θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m ,v=0,求该质点在t =10s 时的速度和位置.解:∵ t tva 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+= 积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔 60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R .(提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示.题1-10图 (1)在最高点,o 0160cos v v v x == 21s m 10-⋅==g a n又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1s m -⋅,而 o60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v =30km ·h -1沿直线向东行驶,另一小艇在其前方以速率2v =40km ·h -1沿直线向北行驶,问在船上看小艇的速度为何?在艇上看船的速度又为何?解:(1)大船看小艇,则有1221v v v-=,依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船,则有2112v v v-=,依题意作出速度矢量图如题1-13图(b),同上法,得5012=v 1h km -⋅2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ①Y 方向: y y ma mg F ==αsin ②0=t 时 0=y 0=y v2sin 21t g y α=由①、②式消去t ,得220sin 21x g v y ⋅=α 2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量. 答: (1)∵ tvm kv a d d =-=分离变量,得mtk v v d d -=即 ⎰⎰-=vv t mt k v v00d d m kte v v -=ln ln 0∴ tm k ev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零,即t →∞,故有 ⎰∞-=='00d kmv t ev x tm k(4)当t=km时,其速度为 ev e v ev v km m k 0100===-⋅- 即速度减至0v 的e1. 2-10 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=t bt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm ,问击第二次时能击入多深,假定铁锤两次打击铁钉时的速度相同.解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图ky f -=第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 112d d d ① 式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t 时,f 'f -=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y kky y ky A ② 由题意,有2)21(212kmv A A =∆== ③即222122k k ky =- 所以, 22=y于是钉子第二次能进入的深度为cm 414.01212=-=-=∆y y y2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端 一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势能之比.解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图Mg F F B A ==又 11x k F A ∆=22x k F B ∆=所以静止时两弹簧伸长量之比为1221k k x x =∆∆ 弹性势能之比为12222211121212k kx k x k E E p p =∆∆= 2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB =BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有])(21[)(21212212l k gh m v m m gh m ∆+-+=-μ 式中l ∆为弹簧在A 点时比原长的伸长量,则h BC AC l )12(-=-=∆联立上述两式,得()()212221122m m khgh m m v +-+-=μ题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽,如题2-19图所示.质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度.解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有222121MV mv mgR +=又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有0=-MV mv联立,以上两式,得()M m MgR v +=2习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204r q E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解: 020π4r r q Eε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024dq πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力. 8-5一电偶极子的电矩为l q p=,场点到偶极子中心O 点的距离为r ,矢量r与l 的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r平行的分量θsin p 和垂直于r 的分量θsin p .∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向,即θ方向场强分量300π4sin r p E εθ=题8-5图 题8-6图8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε 22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==ϕϕελϕπd cos π4)cos(d d 0RE E y-=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴ RE E x0π2ελ==,方向沿x 轴正向. 8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如8-8图示,正方形一条边上电荷4q 在P 点产生物强PEd方向如图,大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴ 24π4d 22220l r l l r E P++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ∵ lq4=λ∴ 2)4(π422220lr l r qrE P++=ε 方向沿8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(xR arctan =α)解: (1)由高斯定理0d εqS E s⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εqe=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则24εq e =Φ,如果它包含q 所在顶点则0=Φe.如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强. 解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=qr E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+= n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a). (1) ρ+球在O 点产生电场010=E,ρ-球在O 点产生电场'd π4π3430320OO r E ερ=∴ O 点电场'd 33030OO r E ερ= ;(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r',相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =,3ερr E O P '-=' ,∴ 0003'3)(3ερερερd OO r r E E E O P PO P=='-=+='∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p在外场E 中受力矩E p M⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εε )11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功. 解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=[)2sin(π-2sin π-] R0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===A B200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E 与电势U 的关系U E -∇=,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势 200π4cos ])cos 21(1)cos 2(1[π4r ql llr q U εθθθε=+--=∴ 30π2cos r p r U E rεθ=∂∂-=30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有0)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反; (2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同. 8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =,即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC ACAC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+RqR q εε 得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力;(2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电 2q q =',小球3再与小球2接触后,小球2与小球3均带电 q q 43=''∴此时小球1与小球2间相互作用力00220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r q q F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得 Sq 261==σσSq d U2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E 00422εεσ+==)2d (212d 02Sq U E U U CB C ε+=== 注意:因为C 片带电,所以2UU C≠,若C 片不带电,显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D ε ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞外 介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得 11σ=D ,22σ=D而 101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212 r d r d ⋅+⋅=⎰⎰∞∞rrE E U 外内题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S则 rlD S DS π2d )(=⋅⎰当)(21R r R <<时,Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度.解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力..为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V的电压,是否会击穿?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿. 8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求:(1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r r Q E ε=3R r >时 302π4r r Q E ε=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q r r Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r r Q E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向? 解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ 外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度. 解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB产生 01=BCD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
