第七章属性数据与FREQ过程解析

合集下载

组态王教学-数据词典

数据词典常见问题解答北京亚控科技发展有限公司２００９年７月目录1. 我注意到组态王软件是按软件点数来收费的，请问这个点数是如何计算的？ (1)2. 我想删除一个指定的变量，但数据词典中该变量的删除选项灰色，不允许操作，怎么解决？ (1)3. 我注意到组态王的数据词典里有一个系统自带的“$新报警”变量，请问此变量是如何使用的？ (1)4. 组态王的数据变量的采集频率采用什么规则？有什么注意事项？ (1)5. 在工程比较庞大的情况下，请问我如何能快速的找到某个变量都在那里使用了呢？ (2)6. 我注意到组态王的变量的属性页中有最大值最小值最大原始值最小原始值几个设定项，请问具体怎么来应用？ (2)7. 在定义变量的基本属性时状态栏中的保存数值、保存参数是什么意思？ (2)8. 我需要组态王能记下我运行状态下设定的参数，每次启动时都能按最后一次设定的参数运行，请问如何来做？ (3)9. 我的现场设备的信号采集与变换是非线性的，请问在组态王中我需要如何设置？ (3)10. 请问变量定义时变量的优先级、安全区是如何设置的?如何工作? (3)11. 请问组态王的报警优先级配置是如何设置的? (3)12. 请问变量定义中的生成事件如何使用？ (3)13. 请问什么是内部局部变量？如何使用? (3)14. 组态王在运行系统中如何修改变量的原始值和工程值？ (4)15. 如果设备中有的数据不需要按采集频率读取，按需要读取，在组态王中如何实现？ (4)16. 在组态王运行环境中能够实现控制变量记录的功能？ (4)17. 在组态王文本框中连接变量的时候，单击问号按钮，没有反应，弹不出变量列表框，为什么，应如何解决？ (5)18. 在组态王数据词典中能否成批修改变量的基本属性？ (5)19. 在组态王中能否实现对变量的操作记录下来？ (5)20. 在组态王中如何实现变量的累加计算？ (6)21. 组态王中的内存字符串变量无法保存到组态王历史数据库中，应如何解决？ (6)22. 在组态王运行环境中通过变量域改变报警限值，但是回到开发环境中看到还是原来设置的值，应如何同步修改开发环境中的设定值？ (6)23. 在删除未用变量列表里，我已经选择全部删除，为什么还有些未用变量没有被删除？ (6)1. 我注意到组态王软件是按软件点数来收费的，请问这个点数是如何计算的？组态王软件是按点数收费的，这里讲的点数不是用户在工程设计时设计的采样点的数目，而是组态王数据词典中定义的所有变量（不包括软件本身自带的21个变量），因为在组态王的数据词典中除了要定义采样点外，还需要定义一部分内存变量来实现软件的逻辑控制动画连接等，所以用户在软件选型时要留有一定的点数余量。

freq函数

freq函数在Python中，freq函数用于计算给定列表中每个元素出现的次数。

freq函数采用一个列表作为输入参数，然后返回一个字典，该字典描述了输入列表中每个元素出现的次数。

freq函数是一个非常实用的函数，因为它可以帮助我们快速地分析和描绘一个数据集。

例如，如果我们有一个由学生考试成绩组成的列表，我们可以使用freq函数来计算每个成绩出现的次数，进而获得成绩分布情况。

这可以帮助我们确定每个成绩段的人数，以及评估整体考试成绩的表现。

下面是一个实例：```python。

# 定义列表grades。

grades = [88, 85, 90, 92, 78, 84, 92, 85, 90, 88, 84, 82, 90, 78, 88]。

# 使用freq函数计算每个成绩出现的次数。

freq_dict = {}。

for grade in grades:。

if grade in freq_dict:。

freq_dict[grade] += 1。

else:。

freq_dict[grade] = 1。

#输出结果。

for key, value in freq_dict.items(:。

print(key, ':', value)。

```。

运行上述代码，输出结果如下：```。

88:3。

85:2。

90:3。

92:2。

78:2。

84:2。

82:1。

```。

可以发现，输入的列表中，88分出现了3次，其他的成绩分别出现了1至3次。

实现freq函数的方法有很多，下面介绍两种常见的实现方法：方法一：def freq(lst):。

freq_dict = {}。

for item in lst:。

if item in freq_dict:。

freq_dict[item] += 1。

else:。

freq_dict[item] = 1。

return freq_dict。

```。

方法二：```python。

from collections import Counter。

sas中freq的用法 -回复

sas中freq的用法-回复在SAS中，`FREQ`是一个非常常用的过程，用于生成频率和交叉表。

它可以帮助数据分析师更好地理解数据并发现其中的模式和趋势。

本文将一步一步介绍`FREQ`过程的用法，并提供一个示例来说明其在数据分析中的重要性。

1. 首先，我们需要了解`FREQ`语句的基本结构。

一般而言，`FREQ`语句由以下三部分组成：`TABLES`子句、`/`符号和`OUT`子句。

`TABLES`子句用于指定要生成频率和交叉表的变量，`/`符号用于分隔`TABLES`子句和`OUT`子句，`OUT`子句用于指定输出结果的数据集和变量名。

2. 接下来，我们需要选择要生成频率和交叉表的变量。

在`TABLES`子句中，可以同时指定多个变量，用逗号分隔。

可以选择数值变量或字符变量，甚至可以组合使用两者。

例如，`TABLES var1 var2;`将生成变量`var1`和`var2`的频率和交叉表。

3. 在`TABLES`子句中，还可以使用一些选项来进一步定制输出结果。

例如，`TABLES var1 / NOPRINT MISSING;`将在输出中不显示缺失值。

这对于有效地处理缺失数据非常有用。

4. 当`FREQ`过程运行完毕后，可以使用`OUT`子句来指定输出结果的数据集名称和变量名。

例如，`OUT = outputdata;`将结果存储在名为`outputdata`的数据集中。

这样，我们可以在进一步分析时使用这些结果。

5. 另外，`FREQ`过程还可以生成卡方检验、精确检验和倾向分数。

这些统计指标可以帮助我们判断样本数据是否符合理论分布，并进行统计推断。

现在，让我们通过一个具体的示例来进一步说明`FREQ`过程的用法。

假设我们有一个数据集包含了学生的性别（gender）和考试成绩（score）两个变量。

我们希望通过`FREQ`过程来分析性别和考试成绩之间的关系。

首先，我们需要指定要生成频率和交叉表的变量。

SAS统计分析介绍

proc ttest data=ncd.stat ;
var h; class urd;
urd
N
where gender=1; 1
733
run;
2
840
差 (1-2)
均值标准差标准误最小值最大值差
168.4 6.3642 0.2351 148.0 189.0 164.8 7.5661 0.2611 104.0 193.0 3.6064 7.0317 0.3554
例如： proc print data=score label;
id name; var math english chinese; label name=‘姓名’ math=‘数学’ english=‘英语' chinese=‘语文’; run;
19
FORMAT语句可以为变量输出规定一个输出格式，比如 proc print data=score; format math 5.1 chinese 5.1; 分析
t检验方差分析 logistic回归分析判别分析聚类分析方差分析 logistic回归分析判别分析聚类分析
分类变量
t检验方差分析协方差分析多因素回归分析
c2检验 logistic回归分析
c2检验 logistic回归分析
生存分析
5
有序变量相关分析多因素回归分析
5.304312 标准误差均值
3645 584713.9 72.40189 0.56804 263832.5
0.140937
99% 95% 90% 75% Q3 50% 中位数
25% Q1
179.5 175 172
166.1 160

SAS软件和统计应用教程(1)PPT课件

-
2
SAS软件与统计应用教程
2.1.1 统计学的基本概念
STAT
1. 总体与样本
总体(population)：总体是指所研究对象的全体组成的集合。
样本 (sample) ：样本是指从总体中抽取的部分对象（个体）组成的集合。样本中包含个体的个数称为样本容量。容量为n的样本常用n个随机变量X1，X2，…，Xn 表示，其观测值（样本数据）则表示为x1，...，xn，为简单起见，有时不加区别。
SAS软件与统计应用教程
STAT
第二章 SAS的描述统计功能
2.1 描述性统计的基本概念 2.2 在SAS中计算统计量 2.3 统计图形
-
1
SAS软件与统计应用教程
STAT
2.1 描述性统计的基本概念
2.1.1 统计学的基本概念 2.1.2 表示数据位置的统计量 2.1.3 表示数据分散程度的统计量 2.1.4 表示数据分布形状的统计量 2.1.5 其它统计量
SAS软件与统计应用教程
2.1.3 表示数据分散程度的统计量
STAT
1. 极差（Range）与半极差（Interquartile range）
极差就是数据中的最大值和最小值之间的差：
极差 = max{xi} – min{xi} 上、下四分位数之差Q3 – Q1称为四分位极差或半极差，它描述了中间半数观测值的散布情况。
SAS软件与统计应用教程
STAT
2. 峰度（kurtosis）
峰度描述数据向分布尾端散布的趋势。峰度的计算公
式为： K
n (n 1 )
n(x i x )43 (n 1 )2
(n 1 )n ( 2 )n ( 3 )i 1 s (n 2 )n ( 3 )

SAS培训课白板

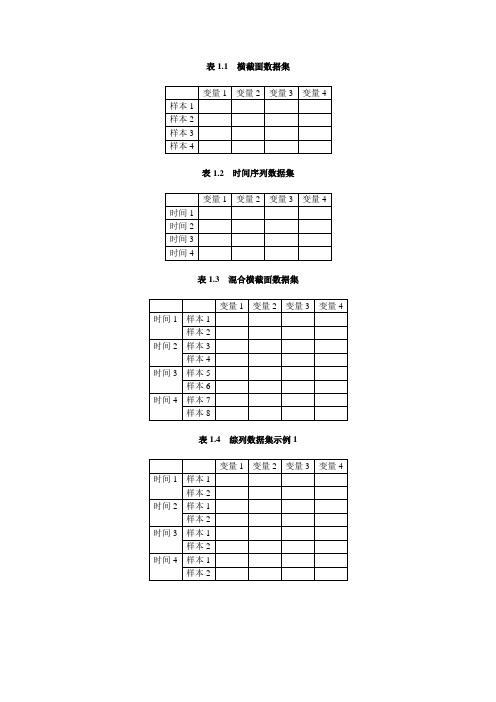
表1.1横截面数据集表1.2时间序列数据集表1.3混合横截面数据集表1.4综列数据集示例1表1.5综列数据集示例2离散数据（discrete data）：也称为定性数据，与定量数据相对应，通常在考察个人、家庭或企业的选择或决策行为时，通过问卷调查获得，如：问题：“您认为未来3个月的物价走势会有什么变化？”选项：①上升②不变③下降被调查者将从以上3个选项中进行选择，得到数据“1”或“2”或“3”即为离散数据或定性数据SAS 是英文Statistical Analysis System的缩写，翻译成汉语是统计分析系统，最初由美国北卡罗来纳州立大学两名研究生研制，1976 年创立SAS公司, 2006年全球员工总数10000人，全球财富500强中的前100家企业有96家使用SAS软件进行“商业智能(Business Intelligence, BI)”上的应用，SAS软件采用按年租用收费制，2005年SAS公司收入16.8亿美元。

在数据处理领域，SAS系统具有十分完备的数据访问、数据管理、数据分析和数据呈现的功能。

国际上, SAS被誉为数据统计分析的标准软件。

SAS软件是一个模块组合式的系统，共有三十多个功能模块，其中最基础的是BASE模块，专门用于统计分析的有STAT模块，专门用于时间序列分析的有ETS模块。

SAS 软件是用汇编语言编写而成的，使用SAS软件通常需要编写程序，因此比较适合专业统计人员使用，非统计专业人员学习SAS比较困难，SAS软件最新版为9.13版，SAS公司的网址是。

FTP主机地址：用户名：pinggu_peixun 密码：回归分析过程REG过程（回归过程）RSREG过程（二次响应面回归过程）ORTHOREG（病态数据回归过程）NLIN过程（非线性回归过程）TRANSREG过程（变换回归过程）CALIS过程（线性结构方程和路径分析过程）方差分析过程ANOV A过程（均衡数据的方差分析过程）TTEST过程（两组比较过程）NPAR1WAY过程（单因子非参数过程）NESTED过程（嵌套过程）LATTICE过程（拉丁方设计过程）PLAN过程（设计方案过程）V ARCOMP过程（方差分量估计过程）GLM过程（一般线性模型过程）MIXED过程（混合线性模型过程）GENMOD过程（广义线性模型过程）属性数据分析过程FREQ过程（频数过程）CATMOD过程（属性数据的建模过程）CORRESP过程（对应分析过程）LOGISTIC过程（Logistic回归过程）多变量过程简介PRINCOMP过程（主分量分析过程）FACTOR过程（因子分析过程）CANCORR过程（典型相关分析过程）MDS过程（多维标度过程）MULTTEST过程（多重检验过程）PRINQUAL过程（定性数据的主分量过程）判别分析过程DISCRIM过程（判别归类过程）CANDISC过程（典型判别过程）STEPDISC过程（逐步判别过程）聚类分析过程CLUSTER过程（系统聚类过程）FASTCLUS过程（快速聚类过程）MODECLUS过程（非参数聚类过程）V ARCLUS过程（变量聚类过程）TREE过程（画树状图过程）ACECLUS过程（数据的预处理过程）实用过程SCORE过程（得分过程）OUTPUT过程（输出传送过程）TEMPLATE过程（模板过程）INBREED过程（近亲繁殖系数过程）GLMMOD过程（构造一般线性模型的设计阵过程）实用新函数及PLOT过程生存分析过程LIFEREG过程（失效数据回归过程）LIFETEST过程（失效数据检验过程）PHREG过程（Cox比例危险模型过程）PROBIT过程（概率单位过程）。

《SAS软件与统计应用教程》第九章属性(分类)数据分析

从变量的测量水平来看分为两类：连续变量和属性 (Categorical)变量，属性变量又可分为有序的(Ordinal) 和无序的变量。
对属性数据进行分析，将达到以下几方面的目的： 1) 产生汇总分类数据——列联表； 2) 检验属性变量间的独立性(无关联性)； 3) 计算属性变量间的关联性统计量； 4) 对高维数据进行分层分析和建模。
这是一张具有r行和c列的一般列联表，称它为rc表。其中，第i行第j列的单元表示为单元ij。交叉表常给出在所有行变量和列变量的组合中的观测个数。表中的总观
测个数用n表示，在单元ij中的观测个数表示为nij，称为单元频数。
9.1.2 属性变量关联性分析
对于不同的属性变量，从列联表中可以得到它们联合
H0：变量之间独立；
H1：变量之间不独立
1. 2检验
在双向表的情形下，如果行变量与列变量无关联性的
原假设H0成立，则列联表中各行的相对分布应近似相等，
即
nij
nij i
（j = 1，2，…，c）
nij
n
或
j
nij
j
nij
i
n
nij
def
mi（j j
=
1，2，…，c）
其中mij称为列联表中单元ij在无关联性假设下的期望频
其中min[(r – 1)(c – 1)]表示取(r – 1)，(c – 1)中较小的一
个。V = 0，表示两个变量相互独立，|V | = 1，表示变量
之间完全相关。
9.1.4 有序变量关联性分析
对于数值变量，可以计算两两的相关系数。属性变量因为没有数值概念所以不能计算相关系数，但对于两个有序变量可以计算类似于相关系数的关联性量度。用来度量有序变量关联程度的统计量有γ统计量、τb统计量和τc统计量等。这几个统计量均由以下定义的观测对一致或不一致的个数（即P和Q）来计算。

sas属性数据分析

run;
(cate21.sas)
21
列联表分析
由原始数据生成列联表的例子
(2) 使用SAS菜单系统“分析员应用”生成列联表.
首先启动“分析员应用”,并打开SAS数据集STATCLAS.
① 在“分析员应用”菜单栏目中选分析(Statistics)=> 表分析(Table Analysis)....
14
列联表分析
属性变量取值的频数表
对属性变量最基本的统计特征就是它可取到的不同数值及取各个不同数值的频数和概率(频率).
(中学生数据的频数表和条形图.)
15
列联表分析
多个属性变量取值的交叉表
19
列联表分析
由原始数据生成列联表的例子
例2.1 对某个“统计入门”课题，记录了该课程中所有学生的性别和专业(′是′为统计专业,′非′ 为其他专业).数据见以下SAS程序的数据行.试用编程方法或菜单系统生成列联表.
27
列联表分析
例2.2 杀人犯的种族是否会影响判处死刑的问题.对1976至1977年美国佛罗里达州20个地区杀人案件中的326个被告进行调查.考虑的种族有白人与黑人;用“是”或“否”表示是否判处死刑.调查后已把数据整理成表格形式(见下表).试用编程方法或菜单系统生成列联表.
白人黑人是 19 17 36 否 141 149 290
26
列联表分析
有些情况下,已经汇总并得出表格中每个单元有多少个观测.在收集数据时,也许是先建立一张表,然后将观测个数记到每个单元中,这样得到的信息.或许是使用以表格形式发表的数据.如:
白人黑人是 19 17 否 141 149
在这种情况下,没有给出样本中每一个个体的观测数据.为了由这种类型的数据生成一张列联表, 首先建立一个包含所有单元观测个数的数据集, 然后使用带有WEIGHT语句的FREQ过程.

proteus教程：属性

proteus教程：属性proteus教程：属性1．简介ISIS中的属性有⾮常⼤的⽤处。

⼀个特定的对象的属性是由⼀些关键字组成，⽐如，在ISIS中，我们使⽤封装的属性与PCB的封装关联。

对象，管脚，电路图都有⾃⼰的属性，如果你想很把这个功能强⼤的软件⽤好你必须很清楚他们之间的联系，这个软件和以前你所⽤过的画电路的软件有些不同。

2．对象属性对象属性有两个类型—系统属性和使⽤属性。

在ISIS中的这些功能是由⼀些保留字所组成，不管是内部的程序⽐如ARES和VSM，或者你⾃⼰所使⽤的软件都是有关联的。

（1）系统属性本proteus教程由/doc/c04a8e4be45c3b3567ec8b23.html 收集整理。

系统属性在ISIS中是由⼀些特殊含义的关键字所够成。

⽐如，⼀个元件中的DEVICE属性是根据元件库在分配时候定义的。

这些属性⼀般是⽂本的—⽐如元件的REF和VALUE属性可以直接从Edit Component 对话框中访问，但是别的⽐如DEVICE属性就是做为图形操作所⽣成的结果。

通常上，如果你关⼼的只是希望去读取它们的数值（values）通过search and tag命令，或者⽤Assignment Tool去修改它们的属性。

⽐如，你可能希望选中在这个设计中的所有的7400元件。

这个需要你知道这个你所要选中的元件的系统属性。

每⼀个对象的系统属性的细节部分都在OBJECT SPECIFICS中给出。

（2）使⽤属性元件，⼦电路和VSM的器件可以加载除了本⾝的标准属性外没有限制的额外的属性，这些使⽤属性是由⼀个⽂本块构成⼀个属性块，它包含很多，⽐如：SUPPLIER=XYZ Electronics你可以直接编辑属性块通过对象的对话框，和⽤Property Assignment Tool⽣成的⼀样好。

为了编辑⼀个对象的属性1．选中这个所要编辑的元件并且点击左键会出现对象的对话框。

2．如果这个对象有它⾃⼰的使⽤属性，这个对话框的将会有⼀个⽂本的编辑框标号为Properties,⿏标移到已经存在的⽂本的下⾯并且按左键。

LS通信指南

目录第一章：变频器IG5 与PC MODBUS通讯例程....................... - 0 -第二章：变频器IG5 与PLC MODBUS通讯例程 . (3)第三章：变频器IGX 与PLC RS-485通讯例程 (5)第四章：变频器IS5 与F-NET通讯例程 (8)第五章：变频器IS5 与PLC D-NET通讯例程........................ - 12 -第六章：变频器IS5 与PLC P-NET通讯例程 (29)第七章：XGB PLC 与XGK PLC 的RS-485 通讯¡¡¡¡¡¡.47 第八章：XGB PLC 与Master-K120S的MODBUS 通讯¡¡..¡.60 第九章：XGB PLC与XGK PLC 的FEnet的通讯¡¡¡¡.¡¡.72 第十章：XGB PLC 与IG5 变频器的MODBUS 通讯¡¡¡..¡.82OK 第一章：变频器IG5 与PC MODBUS 通讯例程一.硬件连接1.PC:安装串口通讯软件CommTester.exe2.变频器:IG5ND-65203.转换器：二.变频器设置1.DRV [控制模式]: 3(RS-485)2.FRQ [频率模式]: 5(RS-485)3.I/O -50 [通讯口]: 7(MODBUS RTU)4.I/O -46 [变频器站号]: 15.I/O -47 [波特率]: 3(出厂值9,600 bps)三.通讯软件参数设置A. 频率设定1.选择通讯方式：Protocol: MODBUS2.变频器站号：INV Number: 13.控制方式设定：Function: 06注：06代表向变频器写数据，04代表从变频器读数据4.目标地址设定：0005注：0005是变频器的频率地址，0006是控制指令地址等，详细见变频器用户手册。

validation_freq参数

validation_freq参数validation_freq参数是指在机器学习模型训练过程中进行验证的频率。

在训练过程中，我们需要使用验证集来评估模型的性能，并及时调整模型的超参数以获得更好的效果。

validation_freq参数决定了模型在训练过程中进行验证的频率，即每经过多少个训练步骤后进行一次验证。

在深度学习中，模型的训练通常需要很长的时间，而验证过程相对较快。

因此，我们可以通过设置较大的validation_freq参数来减少验证的次数，从而加快模型的训练速度。

但是，如果我们设置的validation_freq参数过大，那么模型可能会在训练过程中长时间没有进行验证，无法及时发现模型的问题或调整参数。

因此，我们需要根据具体情况来选择一个合适的validation_freq参数。

在实际应用中，我们可以根据训练数据的规模和模型的复杂程度来选择validation_freq参数。

如果训练数据较大或模型较复杂，那么可能需要设置较大的validation_freq参数，以减少验证的次数。

反之，如果训练数据较小或模型较简单，那么可以设置较小的validation_freq参数，以更频繁地进行验证。

我们还可以根据验证结果来调整validation_freq参数。

如果模型在验证集上的表现较好，那么可以适当增大validation_freq参数，减少验证的次数，从而加快模型的训练速度。

反之，如果模型在验证集上的表现较差，那么可以适当减小validation_freq参数，增加验证的次数，以便及时发现模型的问题并进行调整。

需要注意的是，设置validation_freq参数只是调整模型训练过程中验证的频率，并不会直接影响模型的性能。

模型的性能还取决于其他因素，如模型的结构、损失函数、优化算法等。

因此，在进行模型训练时，我们需要综合考虑这些因素，并进行合理的设置和调整，以获得最佳的模型性能。

总结起来，validation_freq参数是机器学习模型训练过程中进行验证的频率。

82FREQ过程

格频数。 ② NOPERCENT ：禁止打印列联表中
的百分数。 ……
11
8.2.4 举例
DATA A; INPUT A B @@; CARDS; 12 21.2 .. 11 21
PROC FREQ ; TABLES A*B; TITLE '2-WAY CONTINGENCY TABLE';
PROC FREQ ORDER=DATA; TABLES A*B /LIST; TITLE ' 2-WAY FREQUENCY TABLE, ORDER=DATA';
12
13
14
8.2.5 卡方检验
卡方检验为一种用途较广的显著性检验方法，常用于检验两个或两个以上样本率或构成比之间差别的显著性。
对于不同属性的变量，从列联表中可以得到它们联合分布的信息，也可以获得一个变量取不同数值时，另一个变量的分布是否有显著的不同。
15
为了检验：
H0：行列变量无关联； H1：行列变量有关联统计上使用 χ2 统计量。
4
?
PROC FREQ [
选择项列表]；Biblioteka ?DATA=SAS 数据集；
?ORDER=FREQ|DATA|INTERNAL|
FORMATTED
?FORMCHAR （1，2，7）=字符串
规定用来构造列联表单元的轮廓线和分割线的字符。（ 1）垂直线（ 2）水平线（ 3）水平线与垂直交叉线。
缺省， FORMCHAR （1,2,7）=‘-+| '
χ2 =? （（A-T ）2/T），其中A为实际观测到的频数， T为理论频数或期望频数。在 H0成为时A与T值应该比较接近，大的 χ2值是极端情况。

SAS编程：列联表分析

SAS 统计分析与应用从入门到精通一、简单相关分析一、属性数据与列联表 3、FREQ过程
语句说明：（1）PROC语句用于规定运行FREQ过程，并指定要分析的数据集名。（2）TABLES语句用于对规定的变量进行频数统计，并生成列联表。如果不使用TABLES语句，则FREQ过程对数据集中的每个变量都生成一个单项频数表。（3）WEIGHT语句规定的变量用于表示观测的频数，使得FREQ过程在计算频数时将读入的每个观测作为次观测处理，其中为WEIGHT变量的值。（4）BY语句规定了分组变量，它使得FREQ过程对分组内进行处理。在使用BY语句前，应对数据集按照分组变量进行排序。
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
3、相对风险和优势比
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
3、相对风险和优势比
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
4、FREQ过程
FREQ过程除了用来进行频数统计并生成列联表外，还可以用来对列联表进行关联性分析。FREQ过程的语句格式与上一节完全相同，只是通过指定TABLES语句中的选项来实现关联性。
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
1、关联性的检验
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
2、关联性的度量
SAS 统计分析与应用从入门到精通一、列联表的关联性分析
3、相对风险和优势比
在实际问题中，我们最常使用的就是列联表，而且常常用行变量来表示两组样本（例如，吸烟与不吸烟的人群），用列变量来表示某项结果的两种可能性（例如，患有肺癌与没有肺癌）。在这种情况下，我们还可以使用其他一些的统计量来描述变量间的关联性，如相对风险和优势比等。

python freq参数

python freq参数freq是Python中一个常用的函数参数，用于计算某个元素在列表中出现的次数。

在本文中，我们将探讨freq参数在Python中的使用以及相关的应用场景。

在Python中，freq参数常常用于对列表中元素的出现频率进行统计。

通过使用该参数，我们可以轻松地获取元素在列表中出现的次数，从而进行相应的处理和分析。

让我们来看一下freq参数的基本用法。

在Python中，我们可以使用内置的count()函数来实现对元素出现次数的统计。

count()函数接受一个参数，用于指定需要统计的元素，并返回该元素在列表中出现的次数。

下面是一个简单的示例代码：```pythonnumbers = [1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4]print(numbers.count(1)) # 输出：3print(numbers.count(2)) # 输出：3print(numbers.count(3)) # 输出：3print(numbers.count(4)) # 输出：3```在上述代码中，我们定义了一个名为numbers的列表，其中包含了一些整数。

通过调用count()函数，并传入需要统计的元素作为参数，我们可以得到该元素在列表中出现的次数。

除了单个元素的统计，我们还可以使用freq参数来统计多个元素的出现次数。

在这种情况下，我们需要使用for循环来遍历列表，并在每次迭代中调用count()函数来统计元素的出现次数。

以下是一个示例代码：```pythonnumbers = [1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4]freq = {}for num in numbers:freq[num] = numbers.count(num)print(freq) # 输出：{1: 3, 2: 3, 3: 3, 4: 3}```在上述代码中，我们定义了一个空字典freq，用于存储元素的出现次数。

FREQ过程

FREQ过程产生一维到n维频数表和交叉(列联) 表。

对于二维表PROC FREQ 计算检验和属性的度量。

对于n维表PROC FREQ 做分层分析、计算层内统计量, 交叉、分层、频数和统计量同样能输出到SAS数据集。

PROC FREQ能计算一维频数表相等比率、特殊比率或二项式比率统计量检验。

PROC FREQ 能计算任何分层变量列联表在两个分类变量调整之间关系检验的各种统计量。

PROC FREQ 自动显示输出在报告中，并且也能存输出在SAS 数据集中。

某些配对变量，可以检验任何变量之间关系的存在或相关的强度。

如果关系存在的话，决定计算卡方检验、估计相关的强度，等•卡方检验和度量•属性的度量•风险(二项式比率) 和2×2 表的风险差•2×2 表比数比和相对危险•趋势检验•检验和一致性的度量•CMH统计量The following statements are available in PROC FREQ.PROC FREQ < options > ;BY variables ;EXACT statistic-options < / computation-options > ;OUTPUT < OUT=SAS-data-set > options ;TABLES requests < / options > ;TEST options ;WEIGHT variable < / option > ;FISHER Fisher's 精确检验JT Jonckheere-Terpstra 检验KAPPA 简单的kappa系数检验LRCHI 似然比卡方检验MCNEM McNemar's检验MEASURES Pearson 相关和 Spearman相关检验, 和2 ×2表OR置信限MHCHI Mantel-Haenszel卡方检验OR 2 ×2 表OR值的置信限PCHI Pearson卡方检验PCORR Pearson相关系数检验SCORR Spearman相关系数检验TREND Cochran-Armitage趋势检验WTKAP 加权kappa系数检验Computation-Options：ALPHA=指定Monte Carlo p-值估计置信限的水平。

屈曲分析实例解析

屈曲分析屈曲分析- 分析内容屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括：线性屈曲和非线性屈曲分析。

线弹性失稳分析又称特征值屈曲分析；线性屈曲分析可以考虑固定的预载荷，也可使用惯性释放；非线性屈曲分析包括几何非线性失稳分析，弹塑性失稳分析，非线性后屈曲(Snap-through)分析。

欧拉屈曲buckling结构丧失稳定性称作（结构）屈曲或欧拉屈曲。

L.Euler从一端固支另一端自由的受压理想柱出发．给出了压杆的临界载荷。

所谓理想柱，是指起初完全平直而且承受中心压力的受压杆。

设此柱是完全弹性的，且应力不超过比例极限，若轴向外载荷P小于它的临界值，此杆将保持直的状态而只承受轴向压缩。

如果一个扰动(如—横向力)作用于杆，使其有一小的挠曲，在这一扰动除去后。

挠度就消失，杆又恢复到平衡状态，此时杆的直的形式的弹性平衡是稳定的。

若轴向外载荷P大于它的临界值，柱的直的平衡状态变为不稳定，即任意扰动产生的挠曲在扰动除去后不仅不消失，而且还将继续扩大，直至达到远离直立状态的新的平衡位置为止，或者弯折。

此时，称此压杆失稳或屈曲(欧拉屈曲)。

屈曲分析- 分析分类线性屈曲：是以小位移小应变的线弹性理论为基础的，分析中不考虑结构在受载变形过程中结构构形的变化，也就是在外力施加的各个阶段，总是在结构初始构形上建立平衡方程。

当载荷达到某一临界值时，结构构形将突然跳到另一个随遇的平衡状态，称之为屈曲。

临界点之前称为前屈曲,临界点之后称为后屈曲。

侧扭屈曲：梁的截面一般都作成窄而高的形式，对截面两主轴惯性矩相差很大。

如梁跨度中部无侧向支承或侧向支承距离较大，在最大刚度主平面内承受横向荷载或弯矩作用时，荷裁达一定数值，梁截面可能产生侧向位移和扭转，导致丧失承载能力，这种现象叫做梁的侧向弯扭屈曲，简称侧扭屈曲。

理想轴向受压直杆的弹性弯曲屈曲：即假定压杆屈曲时不发生扭转，只是沿主轴弯曲。

但是对开口薄壁截面构件，在压力作用下有可能在扭转变形或弯扭变形的情况下丧失稳定，这种现象称为扭转屈曲或弯扭屈曲。

bifromq 原理解析-概述说明以及解释

bifromq 原理解析-概述说明以及解释1.引言1.1 概述在这一节中，我们将会对bifromq这一概念进行介绍和解释。

Bifromq 是一个新兴的技术，它在计算机科学领域引起了广泛的关注和研究。

其核心原理是基于数据流处理和事件驱动的方式，能够有效地处理大规模数据，提高系统的性能和可扩展性。

在以往的传统架构中，数据的处理往往是集中在一个节点上进行的，这给系统的性能和扩展性带来了一定的限制。

而bifromq的出现，将数据的处理分散到多个节点上，每个节点负责处理特定的数据流，从而提高了系统的并发性和处理速度。

bifromq采用了生产者-消费者的模式，其中生产者负责产生数据流，消费者负责处理数据流。

数据流以事件的形式进行传递，每个事件都包含了一条特定的消息或数据，消费者根据事件的类型和内容进行相应的处理。

为了实现数据的并发处理，bifromq引入了消息队列的概念。

消息队列作为一个中间件，负责接收来自生产者的事件，并将其按照一定的规则存储起来，然后再由消费者进行处理。

消息队列能够有效地缓解生产者和消费者之间的压力差异，实现了生产者和消费者之间的解耦。

此外，bifromq还具有一些其他的特性，例如异步通信、容错处理和高可用性等。

通过使用异步通信，生产者和消费者可以并行地进行数据处理，提高了系统的处理能力。

容错处理能够保证在节点出现故障或网络异常的情况下，数据的可靠传输和处理。

高可用性则能够保证系统的稳定性和可用性，即使某个节点发生故障，系统仍然能够继续运行。

综上所述，bifromq是一种基于数据流处理和事件驱动的新型技术，通过分布式处理和消息队列的方式，提高了系统的性能和可扩展性。

它在大数据处理、实时计算和分布式系统等领域具有广阔的应用前景，为我们解决数据处理难题提供了新的思路和方法。

在接下来的文章中，我们将会详细介绍并分析bifromq的原理和实现细节。

1.2文章结构文章结构部分的内容：文章结构是指文章整体的组织框架，它是为了使读者更容易理解和掌握文章的逻辑关系而进行的规划和安排。

python中的fftfreq函数

python中的fftfreq函数fftfreq函数是Python中用于计算离散傅里叶变换（Discrete Fourier Transform，简称DFT）中的频率（frequency）值的函数。

该函数可以通过numpy 库中的fft模块调用。

首先，我们需要了解一下DFT的基本概念。

DFT是一种将时间域（time domain）信号转换为频率域（frequency domain）信号的方法。

通过傅里叶变换，我们可以将一个连续的信号转换为一系列正弦波的叠加，每个正弦波都有一个特定的频率和振幅。

在数字信号处理中，我们通常处理的是离散信号，因此我们需要使用离散傅里叶变换（DFT）。

在DFT中，输入信号是一个由N个离散值组成的序列，假设为x(n)，其中n为时间或样本的索引。

将输入信号转换为频率域信号后，我们得到了一个包含N 个复数的序列，表示为X(k)，其中k为频率的索引。

这个序列可以表示信号在所有可能频率上的振幅和相位信息。

fftfreq函数的作用是计算在DFT中各个频率分量对应的准确频率值。

该函数的语法如下所示：numpy.fft.fftfreq(n, d=1.0)其中，n为输入信号的长度，d为采样时间（即两个采样点之间的时间间隔），默认值为1.0。

例如，如果我们有一个由100个采样组成的信号，并且采样时间为0.01秒，我们可以使用下面的代码来计算每个频率分量对应的准确频率值：import numpy as npn = 100d = 0.01freq = np.fft.fftfreq(n, d)print(freq)输出结果如下所示：[ 0. 1. 2. 3. 4. -5. -4. -3. -2. -1. …]该结果显示了-0.5到0.5的所有频率值，并且负频率从最后开始往前计数。

这是因为在DFT中，正频率和负频率是对称的，所以我们只需要计算一半的频率分量即可。

值得注意的是，fftfreq函数返回的频率值是以“cycles per unit”的形式给出的。

python freq参数

python freq参数Python是一种广泛使用的编程语言，它具有简单易学、高效、可扩展等特点，因此在数据分析、机器学习等领域得到了广泛应用。

在Python中，freq参数是一个常用的参数，它用于指定数据的频率。

freq参数是Python中pandas库中的一个参数，它用于指定时间序列数据的频率。

在pandas中，时间序列数据是指按照时间顺序排列的数据，例如股票价格、气温等数据。

freq参数可以用来指定时间序列数据的时间间隔，例如每天、每周、每月等。

freq参数的取值可以是一个字符串，也可以是一个pandas中的时间偏移量对象。

字符串的取值可以是以下几种：- D：每日- W：每周- M：每月- Q：每季度- A：每年时间偏移量对象是pandas中的一个类，它表示一个时间间隔。

例如，pandas中的DateOffset类表示一个时间偏移量，可以用来表示一个月、一周、一天等时间间隔。

使用时间偏移量对象时，需要使用pandas中的DateOffset类的实例化对象来表示时间间隔。

在使用freq参数时，需要将时间序列数据转换为pandas中的时间序列对象，例如pandas中的DatetimeIndex对象。

然后，可以使用freq参数来指定时间序列数据的频率。

例如，下面的代码将一个时间序列数据转换为DatetimeIndex对象，并指定其频率为每天：```import pandas as pddata = ['2021-01-01', '2021-01-02', '2021-01-03']index = pd.DatetimeIndex(data, freq='D')```在上面的代码中，使用pd.DatetimeIndex()函数将data转换为DatetimeIndex对象，并使用freq参数指定其频率为每天。

除了使用字符串和时间偏移量对象外，还可以使用pandas中的offset别名来指定时间间隔。

第七章属性数据与FREQ过程解析

组态王教学-数据词典

freq函数

sas中freq的用法 -回复

SAS统计分析介绍

SAS软件和统计应用教程(1)PPT课件

SAS培训课白板

《SAS软件与统计应用教程》第九章 属性(分类)数据分析

sas属性数据分析

proteus教程：属性

LS通信指南

validation_freq参数

82FREQ过程

SAS编程：列联表分析

python freq参数

FREQ过程

屈曲分析实例解析

bifromq 原理解析-概述说明以及解释

python中的fftfreq函数

python freq参数

《SAS软件与统计应用教程》第九章属性(分类)数据分析