《相交线与平行线》单元测试题
平行线与相交线单元测试题

平行线与相交线单元测试题一、选择题(每题2分,共10分)1. 平行线的定义是什么?A. 永远不会相交的直线B. 相交于一点的直线C. 垂直于同一条直线的直线D. 相交于一个点但角度不同的直线2. 如果两条直线相交,它们的角度和是多少度?A. 90度B. 180度C. 360度D. 45度3. 以下哪项不是平行线的性质?A. 平行线在任何地方都不相交B. 平行线之间的距离处处相等C. 平行线可以相交D. 通过平行线之一可以画出无数条平行线4. 两条平行线被第三条直线所截,所形成的内错角的特点是?A. 内错角相等B. 内错角互补C. 内错角和为90度D. 内错角和为180度5. 同位角的定义是什么?A. 两条平行线被第三条直线所截,同侧的角B. 两条直线相交形成的角C. 两条平行线被第三条直线所截,异侧的角D. 两条直线相交形成的同侧角二、填空题(每题2分,共10分)6. 当两条直线相交时,它们形成的角中,____角相等。
7. 如果两条直线相交,且其中一个角是90度,则这两条直线是____。
8. 平行线之间的距离在任何地方都是____。
9. 两条平行线被第三条直线所截,同旁内角的和是____。
10. 如果两条直线相交,且其中一个角是锐角,则这个角的对顶角是____。
三、判断题(每题1分,共5分)11. 平行线永远不会相交。
()12. 垂直线是相交线的一种特殊形式。
()13. 两条平行线之间的夹角总是90度。
()14. 同旁内角互补,即它们的和为180度。
()15. 如果两条直线相交形成的角是钝角,那么这个角的对顶角是锐角。
()四、简答题(每题5分,共10分)16. 解释什么是“对应角”,并给出一个例子。
17. 描述如何使用三角板来测量两条直线是否平行。
五、计算题(每题5分,共10分)18. 如果两条平行线被一条直线所截,形成的内错角分别为40度和140度,请计算同旁内角的度数。
19. 在一个直角三角形中,如果一个锐角是30度,求另一个锐角的度数。
相交线与平行线单元测试题(含答案)

相交线与平行线一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,共24分)1.在下面各图中,∠1与∠2是对顶角的是()A.B.C.D.2.如图,直线a、b相交于点O,若∠1=30°,则∠2等于()A.60°B.30°C.140°D.150°3.如图,直线a,b相交于点O,若∠1=40°,则∠2=()A.40°B.50°C.60°D.140°4.如图,点P在直线l外,点A,B在直线l上,PA=3,PB=7,点P到直线l的距离可能是()A.2 B.4 C.7 D.85.如图,直线a∥b,∠1=50°,则∠2的度数为()A.40°B.50°C.55°D.60°6.如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是()A.连接直线外一点与直线上各点的所有线段中,垂线段最短B.在同一平面内,垂直于同一条直线的两条直线互相平行C.在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D.经过直线外一点,有且只有一条直线与这条直线平行7.如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是()A.两点确定一条直线B.经过一点有且只有一条线段垂直于己知直线C.过一点只能作一条垂线D.垂线段最短8.如图,直线AB∥CD,∠A=70°,∠E=30°,则∠C等于()A.30°B.40°C.60°D.70°二、填空题(本大题共6小题,每小题3分,共18分)9.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:.10.如图,已知O是直线AB上一点,∠1=30°,OD平分∠BOC,则∠2=.11.如图,直线AB、CD相交于点O,EO⊥AB,∠AOC=25°。
(完整版)相交线与平行线单元测试卷(含答案)

12345678(第4题)ab cABCD(第7题)第五章《相交线与平行线》测试卷姓名 _______ 成绩 _______一、选择题(每小题4分,共 40 分) 1、如图所示,∠1和∠2是对顶角的是( )ABC D121212122、如图,在正方体中和AB 垂直的边有( )条.A.1B.2C.3D.4 3、如图AB ∥CD,∠ABE=120°,∠ECD=25°,则∠E=( )A.75°B.80°C.85°D.95°4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件:①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断 是a ∥b 的条件的序号是( )A 、①②B 、①③C 、①④D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相 同,这两次拐弯的角度可能是( ) A 、第一次左拐30°,第二次右拐30° B 、第一次右拐50°,第二次左拐130° C 、第一次右拐50°,第二次右拐130° D 、第一次向左拐50°,第二次向左拐130°6、下列哪个图形是由左图平移得到的( )BDA BCDE(第10题)水面入水点运动员(第14题)ABC D EFG H第13题7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 面积的比是( )A 、3:4B 、5:8C 、9:16D 、1:2 8、下列现象属于平移的是( )① 打气筒活塞的轮复运动,② 电梯的上下运动,③ 钟摆的摆动,④ 转动的门,⑤ 汽车在一条笔直的马路上行走A 、③B 、②③C 、①②④D 、①②⑤ 9、下列说法正确的是( )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
单元测试:相交线与平行线-PDF

13.画立体图形时注意虚线部分.
A1 A
·
14.GM∥HN.理由:因为 GM 平分∠BGF,HN 平分∠CHE,所以∠MGF=
1 1 ∠BGF,∠NHE= ∠CHE,又因为 AB∥CD,所以∠BGF=∠CHE(两直线 2 2
平行,内错角相等) ,所以∠MGF=∠NHE.所以 GM∥HN(内错角相等,两直线 平行). 15.如图,过 E 作 EF∥AB, 则∠1=∠A=30 (……) ; 因为 AB∥CD, 所以 EF∥CD(如果两条直线
A E B
C
0 0
D
16.如图, B处在A处的南偏西45 方向, C处在B处的北偏东80 方向( . 1) 求∠ABC. (2)要使CD∥AB,D处应在C处的什么方向?
北 A
C B 南
能力提升 1.如图,这个图形的周长Biblioteka 多少?6cm ㎝㎝D
4cm
4/9
2.如图,已知∠ABC.请你再画一个∠DEF,使 DE∥AB,EF∥BC,且 DE 交 BC 边 与点 P.探究:∠ABC 与 ∠DEF 有怎样的数量关系?并说明理由.
C.1300
D.1200
①不相交的两条直线平行; ②梯形的两底互相平行; ③同垂直于一条直线的两直线平行; ④同旁内角相等,两直线平行.其中真命题有( A.1 个 4.下列命题: ①两个连续整数的乘积是偶数;②带有负号的数是负数; ③乘积是 1 的两个数互为倒数;④绝对值相等的两个数互为相反数. 其中假命题有( ) A.1 个 B.2 个 C.3 个 D.4 个 ) B.2 个 C.3 个 D.4 个 )
2.图中 OA 表示运动员所跑的路程 y(米)与比赛时间 x(秒)之间的关系,当比 赛进行到第 6 秒时,这名运动员跑了多少米?按此速度计算,这名运动员的 100
人教版初一七年级相交线与平行线单元测试题全套

abM P N123 87654321DCBAB EDA CF相交线与平行线测试题(一)姓名 班级 分数一、选择题(每题3分,共30分)1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )A .50°B .60°C .140°D .160°图1 图2 图3 2、如图2,已知AB ∥CD ,∠A =70°,则∠1的度数是( )A .70°B .100°C .110°D .130°3、已知:如图3,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠ 与2∠的关系一定成立的是( )A .相等 B .互余 C .互补 D .互为对顶角4、如图4,AB DE ∥,65E ∠=,则B C ∠+∠=( )A .135B .115C .36D .65图4 图5 图6 图7 5、如图5,小明从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20方向行走至C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )A .右转80°B .左转80°C .右转100°D .左转100° 6、如图6,如果AB ∥CD ,那么下面说法错误的是( )A .∠3=∠7;B .∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠8 7、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30,那么这两个角是( )DB A C1ab1 2OABCD EF 2 1OB EA B C a b 12 3 A . 42138 、;B . 都是10 ;C . 42138 、或4210、;D . 以上都不对 8、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )A .①、②是正确的命题;B .②、③是正确命题;C .①、③是正确命题 ;D .以上结论皆错9、下列语句错误的是( )A .连接两点的线段的长度叫做两点间的距离;B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等10、如图7,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=( )A .180B .270C .360D .540二、填空题(每题3分,共18分)11、如图8,直线a b ∥,直线c 与a b ,相交.若170∠=,则2_____∠=.图8 图9 图10 12、如图9,已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒.13、如图10,已知AB ∥CD ,BE 平分∠ABC ,∠CDE =150°,则∠C =______ 14、如图11,已知a b ∥,170∠=,240∠=,则3∠ 图11 图12 15、如图12所示,请写出能判定CE ∥AB 的一个条件 .1 2 b ac b ac d1 2 3 4 ABCDE16、如图13,已知AB CD //,∠α=____________ 三、解答题(共52分)17、推理填空:(每空1分,共12分)如图: ① 若∠1=∠2,则 ∥ ( )若∠DAB+∠ABC=1800,则∥ ()②当 ∥ 时,∠ C+∠ABC=1800 ( ) 当 ∥ 时,∠3=∠C ( )18、如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数. (8分)19、已知:如图AB ∥CD ,EF 交AB 于G ,交CD 于F ,FH 平分∠EFD ,交AB 于H ,∠AGE=500,求:∠BHF 的度数.(8分)20、(10分(1321DCBAABCDO123EFHG FEDCBA(3)如图c ,图中共有___对对顶角.(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n 条直线相交于一点,则可形成多少对对顶角?(5)若有2008条直线相交于一点,则可形成 多少对对顶角?21、(6分)如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B =30º,求∠EAD ,∠DAC ,∠C 的度数。
《相交线与平行线》单元测试题

《相交线与平行线》单元测试题一.选择题(共10小题)1.下列图形中,∠1与∠2是对顶角的是()A.B.C.D.2.下列句子中不是命题的是()A.明年是2020年B.延长线段EFC.三角形的内角和是360度D.对顶角相等3.在同一平面内,已知点P在直线l上,过点P画直线l的垂线,可以画出多少条()A.1条B.2条C.3条D.4条4.如图,下列判断正确的是()A.∠3与∠6是同旁内角B.∠2与∠4是同位角C.∠1与∠6是对顶角D.∠5与∠3是内错角5.如图,点P是直线l外一点,从点P向直线l引P A,PB,PC,PD四条线段,其中只有PC与l垂直,这四条线段中长度最短的是()A.P A B.PB C.PC D.PD6.下面推理正确的是()A.∵a∥b,b∥c,∴c∥d B.∵a∥c,b∥d,∴c∥dC.∵a∥b,a∥c,∴b∥c D.∵a∥b,c∥d,∴a∥c7.如图,在下列给出的条件中,不能判定AB∥CD的是()A.∠BAD+∠ADC=180°B.∠ABD=∠BDCC.∠ADB=∠DBC D.∠ABE=∠DCE8.如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=7cm,EC =4cm,那么平移距离为()A.3cm B.5cm C.8cm D.13cm9.如图,AC∥BD,AE∥BF,下列结论错误的是()A.∠A=∠B B.∠A+∠B=180°C.∠B=∠DPE D.∠A=∠APB 10.某同学的作业如下框,其中横线处应填的依据是()如图所示,当∠1=∠2时,∠3=∠4吗?为什么?请完成下面的说理过程.解,∵∠1=∠2(已知).∴直线a∥b(______________).∴∠3=∠4(两直线平行,同位角相等)A.两直线平行,内错角相等B.内错角相等,两直线平行C.两直线平行,同位角相等D.同位角相等,两直线平行二.填空题(共6小题)11.如图所示,△EFG是由△ABC沿水平方向平移得到的,如果∠ABC=90°,AB=3cm,BC=2cm,则EF=,FG=,EG=.12.将命题“互为补角的两个角都是锐角”改写成“如果……,那么……”的形式是.13.如图,在三角形ABC中,∠C=90°,AC=3,BC=4,AB=5,则点A到BC的距离等于.14.如图,在长方体中,与棱AB平行的棱有条.15.如图,一个弯形管道ABCD,若它的两个拐角∠ABC=120°,∠BCD=60°,则管道AB∥CD.这里用到的推理依据是.16.如图,已知∠1=∠2=32°,∠D=78°,则∠BCD=.三.解答题(共8小题)17.如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOD=88°,求∠BOD的度数.18.指出下列命题的题设和结论,并判断其真假,如果是假命题,请举出一个反例.(1)邻补角互补;(2)同旁内角互补.19.如图,△ABC,△A1B1C1的顶点都在边长为1个单位长度的小正方形组成的网格线交点上.(1)将△ABC向右平移4个单位得到△A2B2C2,请画出△A2B2C2.(2)试描述△A1B1C1经过怎样的平移可得到△A2B2C2.20.如图,在直角三角形ABC中,∠C=90°,DE⊥AC交AC于点E,交AB于点D.(1)请分别写出当BC,DE被AB所截时,∠B的同位角、内错角和同旁内角.(2)试说明∠1=∠2=∠B的理由.21.如图,已知AB∥CD,射线AH交BC于点F,交CD于点D,从D点引一条射线DE,若∠B+∠CDE=180°,求证:∠AFC=∠EDH.证明:∵AB∥CD(已知)∴∠B=(两直线平行,内错角相等)∵∠B+∠CDE=180°(已知)∴∠BCD+∠CDE=180°(等量代换)∴BC∥(同旁内角互补,两直线平行)∴=∠EDH()∵=∠BFD(对顶角相等)∴∠AFC=∠EDH(等量代换)22.如图是两个重叠的直角三角形,将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形,求阴影部分的面积(单位:厘米)23.如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连结OF.(1)ED是否平行于AB,请说明理由;(2)若OD平分∠BOF,∠OFD=80°,求∠1的度数.24.如图,图①是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图②和图③,弹弓的两边可看成是平行的,即AB∥CD,各活动小组探索∠APD与∠A,∠C之间数量关系时,有如下发现:(1)在图②所示的图形中,若∠A=30°,∠D=35°,则∠APD=;(2)在图③中,若∠A=150°,∠APD=60°,则∠D=;(3)有同学在图②和图③的基础上,画出了图④所示的图形,其中AB∥CD,请判断∠α,∠β,∠γ之间的关系,并说明理由.。
(完整版)《相交线与平行线》单元测试卷含答案

第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D.对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为()A.40°B.35°C.50°D.45°1 2 33.如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC. ∠B+∠ECB=180°D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为()A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可5.如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D.垂直于同一直线的两直线平行6.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是()A.40°B.70°C.80°D.140°7.同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是()A.a∥dB.a⊥cC.a⊥dD.b⊥d8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120 °B.130°C.140°D.150°9.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为()A.30°B.60°C.80°D.120°10.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()6 8 9 10二、填空题(每题3分,共21分)11.如图所示,某地一条小河的两岸都是直的,小明和小亮分别在河的两岸,他们拉紧了一根细绳,当测出∠1和∠2满足关系________时,河岸的两边才是平行的.12.同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=________.13.在测量跳远成绩时,从落地点到起跳线所拉的皮尺应当与起跳线________.14.如图,在三角形ABC中,BC=5 cm,将三角形ABC沿BC方向平移至三角形A'B'C'的位置时,B'C=3 cm,则三角形ABC平移的距离为cm.11 14 1515.如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是度.16.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=°.17.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是第1个图案经过平移而得,那么第2015个图案中有白色六边形地面砖块.三、解答题(22~24题每题9分,其余每题8分,共59分)18.如图,在一条公路l的两侧有A,B两个村庄.(1)现在镇政府为民服务,沿公路开通公共汽车,同时修建A,B两个村庄到公路的道路,要使两个村庄村民乘车最为方便,请你设计道路路线,在图中画出(标明①),并标出公共汽车停靠点的位置,说出你这样设计的理由;(2)为方便两村物流互通,A,B两村计划合资修建一条由A村到达B村的道路,要使两个村庄物流、通行最为方便,请你设计道路路线,在图中画出(标明②),说出你这样设计的理由.19.如图所示,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.20.如图,CD⊥AB,EF⊥AB,∠E=∠EMC,说明:CD是∠ACB的平分线.21.如图,已知点A,O,B在同一直线上,OC是从点O出发的任意一条射线,OD是∠AOC的平分线,OE是∠COB的平分线,试确定OD和OE的位置关系,并说明理由.22.如图,∠E=∠3,∠1=∠2,试说明:∠4+∠BAP =180°.23.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时,入射光线与平面镜的夹角等于反射光线与平面镜的夹角(∠1=∠2,∠3=∠4).请说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.24.如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(1)当动点P落在第①部分时,如图①,试说明:∠APB=∠PAC+∠PBD;(2)当动点P落在第②部分时,如图②,∠APB=∠PAC+∠PBD是否成立?若不成立,请说明理由.参考答案一、1.【答案】B 2.【答案】C3.【答案】B解:根据两直线平行,同位角相等,得出A正确;根据两直线平行,同旁内角互补,得出C正确;根据两直线平行,内错角相等,得出∠A=∠ACE,而∠ACE+∠B+∠ACB=180°,则∠A+∠B+∠ACB=180°.得出D正确.故选B.4.【答案】C5.【答案】C6.【答案】B7.【答案】C8.【答案】C9.【答案】A10.【答案】B二、11.【答案】∠1=∠212.【答案】4解:a=3,b=1.13.【答案】垂直14.【答案】215.【答案】9016.【答案】14017.【答案】8062三、18.解:(1)画图如图,P,Q即为公共汽车停靠点的位置垂线段最短;(2)画图如图,两点之间,线段最短.19.解:因为AB∥CD,所以∠ECD=∠A=37°,又因为DE⊥AE,所以∠CED=90°,所以∠D=180°-90°-37°=53°.20.解:因为CD⊥AB,EF⊥AB,所以CD∥EF(垂直于同一直线的两直线平行).相等),又因为∠E=∠EMC,所以∠BCD=∠ACD(等量代换).所以CD是∠ACB的平分线(角平分线定义).21.解:OD和OE互相垂直,即OD⊥OE.理由如下:因为点A,O,B在同一直线上,所以∠AOB=180°.又因为OD是∠AOC的平分线,OE是∠COB的平分线,所以∠DOC=∠AOC,∠COE=∠COB.所以∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=×180°=90°,所以OD⊥OE.22.解:因为∠ENM=∠3(对顶角相等),∠E=∠3(已知),所以∠ENM=∠E(等量代换),所以AE∥HM(内错角相等,两直线平行).所以∠EAM=∠AMH(两直线平行,内错角相等).又因为∠1=∠2,所以∠EAM+∠1=∠AMH+∠2(等式性质),即∠BAM=∠AMC.所以AB∥CD(内错角相等,两直线平行).所以∠AMD+∠BAP=180°(两直线平行,同旁内角互补).因为∠4=∠AMD(对顶角相等),所以∠4+∠BAP=180°(等量代换).23.解:根据题意,作出如图所示的几何图形,已知:AB∥CD,∠1=∠2,∠3=∠4.试说明:EF∥GH.说明过程:因为AB∥CD(已知),所以∠2=∠3(两直线平行,内错角相等).又因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4.因为∠5=180°-(∠1+∠2),∠6=180°-(∠3+∠4),所以∠5=∠6,所以EF∥GH(内错角相等,两直线平行).即进入潜望镜的光线和离开潜望镜的光线是平行的.24.解:(1)如图①:过点P作MP∥AC,则MP∥BD,因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,①②(2)不成立.理由如下:如图②,过点P作MP∥AC,则MP∥BD, 因为MP∥AC,所以∠APM=∠PAC,因为MP∥BD,所以∠BPM=∠PBD,所以∠APM+∠BPM =∠PAC+∠PBD,即:360°-∠APB=∠PAC+∠PBD.所以∠APB=∠PAC+∠PBD不成立.。
相交线、平行线单元测试

图 2 A BC图7AO B 《相交线与平行线》单元测试时间:120分钟 满分:120分一、选择题(每题3分,共30分)1. 体育课上,老师测量跳远成绩的依据是( ).A 、平行线间的距离相等B 、两点之间,线段最短C 、垂线段最短D 、两点确定一条直线2. 如图1,给出了过直线外一点作已知直线的平行线的方法,其依据是( ) A 、同位角相等,两直线平行 B 、内错角相等,两直线平行 C 、同旁内角互补,两直线平行 D 、两直线平行,同位角相等3. 如图2所示是“福娃欢欢”的五幅图案,②、③、④、⑤哪一个图案可以通过平移图案①得到 ( ) A 、② B 、③ C 、④ D 、⑤ 4.如图3,若∠1=70°,∠2=110°,∠3=70°,则有( ). A 、a ∥b B 、c ∥d C 、a ⊥d D 、任两条都无法判定是否平行 5.一副三角扳按如图4方式摆放,且∠1的度数比∠2的度数大54°,则∠1=( ) A 、 18° B 、54° C 、72° D 、70° 6.如图5,图中对顶角共有( )对A 、6B 、11C 、12D 、137. 如图6,直线AB ,CD 与EF 相交于G ,H ,下列条件:①∠1=∠2;②∠3=∠6;③∠2=∠8;④∠5+∠8=180º,其中能判定AB ∥CD 的是( ) A 、①③ B 、①②④ C 、①③④ D 、②③④8.如图7,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A 是1200,第二次拐的角∠B 是1500第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 是( ) A 、1200 B 、1300 C 、1400 D 、15009. 下列命题:①两条直线相交,一角的两邻补角相等,则这两条直线垂直;②两条直线相交,一角与其邻补角相等,则这两条直线垂直;③内错角相等,则它们的角平分线互相垂直;④同旁内角互补,则它们的角平分线互相垂直.其中正确的个数为( ). A 、4 B 、3 C 、2 D 、110.如图8探照灯、锅形天线、汽车灯以及其它很多灯具都与抛物线形状 有关,如图所示是一探照灯灯碗的纵剖面,从位于O 点的灯泡发出的两束光线OB OC 、经图 1图3 图4 图 5图6灯碗反射以后平行射出.如果图中ABO DCO αβ∠=∠=,,则BOC ∠的度数为( )A 、180αβ--B 、αβ+C 、1()2αβ+D 、90()βα+-二、填空题(每题3分,共18分) 11.如图9,当剪刀口∠AOB 增大21°时,∠COD 增大 。
七年级数学下册《相交线与平行线》单元测试卷(附答案)

七年级数学下册《相交线与平行线》单元测试卷(附答案)一、选择题(每题3分,共30分)1.如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是()A.垂线段最短B.两点确定一条直线C.两点之间,线段最短D.平行于同一条直线的两条直线平行2.如图,将一个含有30°角的直角三角尺放置在两条平行线a,b上.若∠1=135°,则∠2的度数为()A.95°B.110°C.105°D.115°3.如图,将△ABC沿BC方向平移1个单位得△DEF,若△ABC的周长等于10,则四边形ABFD 的周长为()A.12 B.10 C.9 D.84.下面四个图案中,能由如图经过平移得到的是()A.B. C. D.5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.18cm C.20cm D.22cm6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是()A.垂直B.相等C.平分D.平分且垂直7.如图,下列说法错误的是()A.∠A与∠3是同位角B.∠4与∠B是同旁内角C.∠A与∠C是内错角D.∠1与∠2是同旁内角8.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于()A.4 B.5 C.6 D.以上都不对9.甲、乙、丙3人从图书馆各借了一本书(如下表所示),他们相约在每个星期天相互交换读完的书,经过数次交换后,他们都读完了这3本书.已知甲读的第三本书是乙读的第二本书,则丙读的第二本书是()甲乙丙书A书B书C A.书A B.书B C.书C D.无法确定10.下列各项正确的是()A.直线外一点到已知直线的垂线段叫做这点到直线的距离B.过一点有且只有一条直线与已知直线垂直C.同一平面内,两条直线的位置关系只有相交和平行两种D.有公共顶点且相等的两个角是对顶角二、填空题(每题3分,共24分)11.如图,已知∠1+∠2=180°,则图中与∠1相等的角共有_____个.12.如图,在图中标注的∠1、∠3、∠4、∠5中,当∠2 =∠_______时,AE∥BF.13.如图,已知a∥b,∠1=45°,则∠2=_________.14.“互补的两个角一定是同旁内角”是命题(填“真”或“假”).15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为.16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有个交点.17.如图所示,l1∥l2,点A,E,D在直线l1上,点B,C在直线l2上,满足BD平分∠ABC,BD⊥CD,CE平分∠DCB,若∠BAD=128°,那么∠AEC=.18.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E 交AF于点G,若∠CEF=70°,则∠GFD′=°.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.如图,直线AB与CD相交于点O,OE平分∠BOC,∠AOD=110°,求∠AOE的度数.20.已知,如图a∥b,c∥d,∠1=73°,求∠2和∠3的度数.21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.(1)写出两个不同的条件;(2)从(1)中选择一个来证明.22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.(1)试判断DE与BC的位置关系,并说明理由.(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.23.完成下列画图(1)如图,将△ABC向右平移4个单位,再向上平移2个单位长度,得到△A′B′C′,线段AB 与A′B′位置及数量关系是.(2)如图,一辆汽车在笔直的公路AB上由A向B行驶,M、是位于公路AB一侧的村庄.设汽车行驶到点P时,离村庄M的距离最小,请在图中公路AB上画出点P的位置,并说明数学原理.24.在ABC 中,D 是BC 边上一点,且CDA CAB ∠=∠,MN 是经过点D 的一条直线.(1)若直线MN AC ⊥,垂足为点E . ①依题意补全图1.②若70,CAB ︒∠=20DAB ︒∠=,则CAD ∠=________,CDE ∠=________. (2)如图2,若直线MN 交AC 边于点F ,且CDF CAD ∠=∠,求证:FD AB ∥.参考答案一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案 CCABCDAAAC二、填空题:11.312.413.45°. 解析:∵a∥b,∠1=45°,∴∠2=∠1=45°.14.解:如图,∠1=∠2=90°,∵∠1+∠2=180°,∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,∴“互补的两个角一定是同旁内角”是假命题,故答案为:假.15.解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵GH∥EF,∴∠AEC=∠2=24°,∴∠1=∠ABC﹣∠AEC=36°.故答案为:36°.16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,∴8条直线两两相交,交点的个数最多为=28.故答案为:28.17.【分析】根据平行线的性质和角平分线的性质,可以得到∠AEC的度数,本题得以解决.【解答】解:∵l1∥l2,∴∠BAD+∠ABC=180°,∵∠BAD=128°,∴∠ABC=52°,∵BD平分∠ABC,∴∠DBC=26°,∵BD⊥CD,∴∠BDC=90°,∴∠BCD=64°,∵CE平分∠DCB,∴∠ECB=32°,∵l1∥l2,∴∠AEC+∠ECB=180°,∴∠AEC=148°,故答案为:148°.【点评】本题考查平行线的性质、角平分线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.18.【分析】由AD∥BC可得∠AFE=∠CEF,∠CEF+∠DFE=180°,由翻折可得∠D'FE=∠DFE,进而求解.【解答】解:∵AD∥BC,∴∠AFE=∠CEF=70°,∵∠CEF+∠DFE=180°,∴∠DFE=180°﹣∠CEF=110°,由翻折可得∠D'FE=∠DFE=110°,∴∠GFD'=∠D'FE﹣∠AFE=110°﹣70°=40°,故答案为:40.【点评】本题考查角的相关计算,解题关键是掌握平行线的性质.三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)19.【答案】解:∵∠AOD=110°,∴∠COB=110°,∠AOC=70°,∵OE平分∠BOC,∴∠COE=55°,∴∠AOE=70°+55°=125°.故答案为:∠AOE=125°.20.【答案】解:∵a∥b,∴∠1=∠2=73°,∵c∥d,∴∠3=180°-73°=107°.21.解:此题答案不唯一,合理即可.(1)添加∠FCB=∠CBE或CF∥BE.(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.证明:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠CBE,∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.22.解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC,(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B ,∴∠2+∠5+∠6=3∠B +∠B +∠B =180°, ∴∠B =36°, ∴∠2=108°, ∵∠1+∠2=180°, ∴∠1=72°.23.(1)解:如图,△A ′B ′C ′即为所求作;线段AB 与A ′B ′位置及数量关系分别是平行且相等, 故答案为:平行且相等. (2)解:如图,点P 即为所求.数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短, 24.(1)①如图所示.②70,CAB ︒∠=20DAB ︒∠=,50CAD ︒∴∠=.70CDA CAB ︒∠=∠=,18060C CAD CDA ︒︒∴∠=-∠-∠=.DE AC ⊥,第 11 页 共 11 页 9030CDE C ︒︒∴∠=-∠=. 故答案为50,︒30︒.(2)CDA CAB ∠=∠, 且,CDA CDF ADF ∠=∠+∠CAB CAD BAD ∠=∠+∠, CDF ADF CAD BAD ∴∠+∠=∠+∠. ,CDF CAD ∠=∠,ADF BAD ∴∠=∠FD AB ∴∥.。
相交线与平行线单元测试题含答案

相交线与平行线单元测试题含答案相交线与平行线单元测试题一、选择题1、下列说法正确的是() A. 相交的两条直线一定有一个交点 B. 同位角相等 C. 两直线平行,对角线一定相等 D. 相等的两个角一定是对顶角2、以下不能说明直线AB与CD平行的是() A. AB//CD,A与B在同一方向,C与D在同一方向 B. $\angle 3 = \angle 4$ C. $\angle A = \angle C$ D. $\angle A + \angle B = 180^{\circ}$,$\angleC + \angleD = 180^{\circ}$3、下列说法正确的是() A. 过一点有且只有一条直线与已知直线平行 B. 两直线平行,同位角相等 C. 内错角相等,两直线平行 D. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行4、下列说法正确的是() A. 两条直线被第三条直线所截,同位角相等 B. 相等的两个角是对顶角 C. 两直线平行,同旁内角互补 D. 互补的两个角不一定是邻补角5、下列说法正确的是() A. 同位角相等 B. 互补的角是邻补角 C. 两直线平行,同旁内角相等 D. 两直线平行,内错角相等二、填空题1、同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相________,简述为________.2、两直线平行,同位角________;两直线平行,内错角________;两直线平行,同旁内角________.3、两条直线的位置关系有________、________.4、若三条直线两两相交,则共有________个交点.5、在同一平面内,若两直线都垂直于第三条直线,那么这两条直线________.6、如图所示,若$\angle A + \angle B = 180^{\circ}$,$\angle A = \angle D$,则$\angle B =$________.7、如图所示,若$\angle A = \angle B$,则$\angle C =$________.8、如图所示,若$\angle A + \angle B = 90^{\circ}$,$\angle B + \angle C = 90^{\circ}$,则$\angle A =$________.9、若一个角的两边分别和另一个角的两边分别平行,则这两个角的关系是________.10、如图所示,若AB//CD,则$\angle A + \angle B + \angle C=$________.三、解答题1、已知两条平行线被第三条直线所截,则形成的同位角的数量是多少?这些同位角还具有什么性质?2、利用所给图形探究规律。
人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)
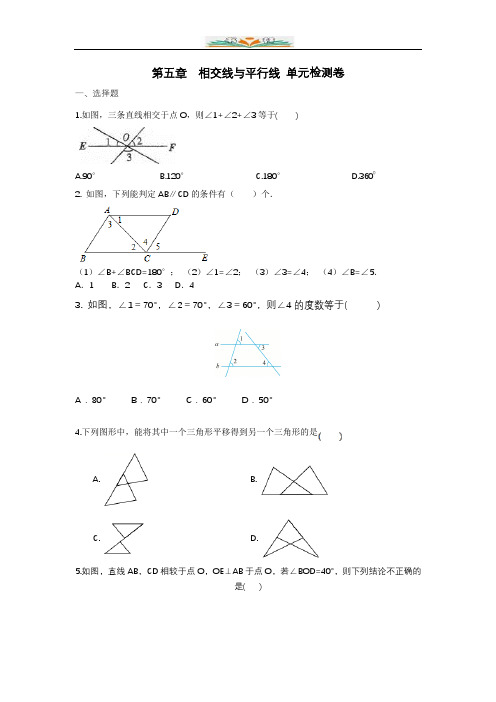
第五章相交线与平行线单元检测卷一、选择题1.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1 B.2 C.3 D.43. 如图,∠1=70°,∠2=70°,∠3=60°,则∠4的度数等于( )A.80°B.70°C.60°D.50°4.下列图形中,能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图,直线AB,CD相较于点O,OE⊥AB于点O,若∠BOD=40°,则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图,点A在直线BG上,AD∥BC,AE平分∠GAD,若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中,∠1与∠2互为邻补角的是( )9.对于图中标记的各角,下列条件能推理得到a∥b的是()A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=18010.下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图,直线AB,CD相交于点O, EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有_____对平行线.13.如图,,则的度数等于14.如图,点0是直线AB上一点平分,图中与互余的角有______ .图中与互补的角有______ .15. 说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=____________.16.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是三、解答题17.如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.(1)求∠BOD的度数;(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.18.已知:如图,AB∥CD,∠1=∠2,∠3=∠4.(1)求证:AD∥BE;(2)若∠B=∠3=2∠2,求∠D的度数.19.如图,D,E,F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G,过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度,你有什么发现?(3)量出线段HD,EG,FM,BC的长度,你又有什么发现?20.请写出命题“两直线平行,同位角相等”的题设和结论:题设:,结论:.21.观察下图,寻找对顶角:(1)如图1,图中共有对对顶角(2)如图2,图中共有对对顶角(3)如图3,图中共有对对顶角(4)若有n条直线相交于一点,则可形成多少对对顶角?22.如图,已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC;(2)若∠AMD=75°,求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
2023-2024学年小学数学西师版四年级上6 相交与平行单元测试(含答案解析)

2023-2024学年西师版小学数学单元测试学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息;2.请将答案正确填写在答题卡上;一、选择题(本大题共计2小题,每题3分,共计6分)1.在两条平行线之间再画几条和平行线垂直的线段,这些线段的长度()A. 都相等B. 不相等C. 无法确定【答案】A【解析】解:由分析可知:在两条平行线之间再画几条和平行线垂直的线段,这些线段的长度都相等;故选:A.2.测量直线外一点到这条直线的距离,要先从这一点到直线画()A. 任意直线B. 任意射线C. 任意线段D. 垂直线段【答案】D【解析】解:从直线外一点到这条直线的距离,是指这一点到这条直线的垂直线段的长度;故选:D.二、填空题(本大题共计13小题,每题3分,共计39分)3.两条直线相交成直角,这两条直线的交点叫________.【答案】垂足【解析】解:由垂足的含义可知:两条直线相交成直角,这两条直线的交点叫垂足;故答案为:垂足。
4.如图中,直线________和直线________互相平行,直线________和直线________互相垂直。
【答案】c, d, a, c(或d)【解析】解:如图中,直线c和直线d互相平行,直线a和直线c或d)互相垂直。
故答案为:c、d、a、c(或d)5.同一平面内,两条直线相交成直角时,这两条直线________.其中一条直线是另一条直线的________,这两条直线的交点叫________.【答案】互相垂直, 垂线, 垂足【解析】解:同一平面内,两条直线相交成直角时,这两条直线互相垂直。
其中一条直线是另一条直线的垂线,这两条直线的交点叫垂足;故答案为:互相垂直,垂线,垂足。
6.观察下面几幅生活中的图片:在同一平面内,两条直线的位置关系有________和________.只有一个公共点的两条直线叫做________,这个公共点叫做________.在同一平面内,不相交的两条直线叫做________.【答案】相交平行相交线交点平行线【解析】略7.两条平行线之间有4条与平行线垂直的线段(如图),这四条线段的长度________,这四条线段互相________.【答案】相等, 平行【解析】解:两条平行线之间有4条与平行线垂直的线段(如图),这四条线段的长度相等,这四条线段互相平行;故答案为:相等,平行。
第2章 相交线与平行线单元测试

第2章 相交线与平行线单元测试一、选择题:1.如果一个角的补角是150°,那么这个角的余角的度数是( )A.30°B.60°C.90°D.120°2.下列语句中,是对顶角的语句为( )A.有公共顶点并且相等的角B.两条直线相交,有公共顶点的角C.顶点相对的角D.两条直线相交,有公共顶点没有公共边的两个角3.如图1,下列说法错误的是( )A.∠1和∠3是同位角;B.∠1和∠5是同位角C.∠1和∠2是同旁内角;D.∠5和∠6是内错角564321G FE D C B A DCB O A(1) (2) (3)4.如图2,已知AB ∥CD ∥EF ,BC ∥AD ,AC 平分∠BAD ,那么图中与∠AGE 相等的角有( )A.5个B.4个C.3个D.2个5.如图3,OB ⊥OD ,OC ⊥OA ,∠BOC=32°,那么∠AOD 等于( )A.148°B.132°C.128°D.90°4.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到直 线m 的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cm二、填空题:1.∠1与∠2互余,∠2与∠3互补,∠1=63°,∠3= .2.∠α和∠β互为补角,又是对顶角,则它们的两边所在的直线 . ∴∠1=∠2( )4.已知,如图,AD ∥BC ,∠BAD=∠BCD ,请说明AB ∥CD 的理由.理由:∵AD ∥BC(已知) ∴∠1=( )( ) 4321D C B A又∵∠BAD=∠BCD(已知)∴∠BAD-∠1=∠BCD-∠2( )即:∠3=∠4∴AB∥CD( )三、解答题2.已知一个角的余角的补角比这个角的补角的一半大90°,则这个角的度数等于多少度?。
相交线与平行线单元测试题及答案

相交线与平行线单元测试题及答案题目 1给定以下图示中的两条线段AB和CD,请判断它们是否相交。
A C\\ /\\ /\\ /X/ \\/ \\/ \\B DA. 相交B. 不相交答案:A. 相交题目 2给定以下图示中的两条线段EF和GH,请判断它们是否相交。
E\\\\\\\\\\\\\\\\FG\\\\\\\\\\\\\\\\\\HA. 相交B. 不相交答案:B. 不相交题目 3给定以下图示中的两条线段IJ和KL,请判断它们是否相交。
I----J| || || |K----LA. 相交B. 不相交答案:B. 不相交题目 4给定以下图示中的两条线段MN和OP,请判断它们是否相交。
M N\\ /\\ /\\ /X/ \\/ \\/ \\O PA. 相交B. 不相交答案:A. 相交题目 5给定以下图示中的两条线段QR和ST,请判断它们是否相交。
Q\\\\\\\\\\\\\\\\\\RS\\\\\\\\\\\\\\\\\\TA. 相交B. 不相交答案:B. 不相交题目 6给定以下图示中的两条线段UV和WX,请判断它们是否平行。
U-------VW-------XA. 平行B. 不平行答案:A. 平行题目 7给定以下图示中的两条线段YZ和AB,请判断它们是否平行。
Y-------ZA---BA. 平行B. 不平行答案:B. 不平行题目 8给定以下图示中的两条线段CD和EF,请判断它们是否平行。
C---DE---------------FA. 平行B. 不平行答案:A. 平行题目 9给定以下图示中的两条线段GH和IJ,请判断它们是否平行。
G--------HI--------JA. 平行B. 不平行答案:A. 平行题目 10给定以下图示中的两条线段KL和MN,请判断它们是否平行。
K--------LM---------------NA. 平行B. 不平行答案:B. 不平行以上为相交线与平行线单元测试题及答案。
相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题(每题2分,共20分)1. 下列说法中,正确的是:A. 经过直线外一点,有且只有一条直线与已知直线平行B. 经过直线外一点,有且只有一条直线与已知直线相交C. 经过直线外一点,可以画无数条直线与已知直线平行D. 经过直线外一点,可以画无数条直线与已知直线相交2. 如果两直线相交,那么它们相交所成的角是:A. 锐角B. 直角C. 钝角D. 任意角3. 两条直线被第三条直线所截,如果同侧的内错角相等,那么这两条直线:A. 平行B. 相交C. 垂直D. 无法判断4. 平行线的性质中,下列说法不正确的是:A. 平行线之间的距离处处相等B. 平行线永不相交C. 两条平行线可以确定一个平面D. 平行线之间的夹角是锐角5. 对于两条平行线,下列说法正确的是:A. 它们之间的距离在任何地方都是相同的B. 它们可以相交C. 它们之间的夹角可以是任意角D. 它们可以确定一个平面二、填空题(每题2分,共10分)6. 如果两条直线相交成直角,则称这两条直线互相______。
7. 两条直线相交,如果其中一个角是锐角,则其他三个角分别是______。
8. 平行线之间的距离是指______。
9. 两条直线相交所成的角中,最大的角是______。
10. 如果两条直线被第三条直线所截,那么内错角相等的条件是这两条直线______。
三、判断题(每题1分,共10分)11. 两条直线相交所成的角都是锐角。
()12. 平行线在任何地方的距离都是相等的。
()13. 两条直线相交,形成的对顶角相等。
()14. 两条平行线之间的夹角是直角。
()15. 如果两条直线被第三条直线所截,同位角相等,则这两条直线平行。
()四、简答题(每题5分,共20分)16. 解释什么是“同位角”、“内错角”和“同旁内角”,并说明它们在判断两条直线是否平行时的作用。
17. 描述如何使用直角三角板来检验两条直线是否平行。
18. 给出两条直线相交的几何图形,并说明如何确定它们相交所成的角的大小。
相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题(每题2分,共10分)1. 两条直线在同一平面内,且不相交,这两条直线叫做平行线。
以下哪项描述不正确?A. 平行线在任何情况下都不会相交B. 平行线之间的距离处处相等C. 平行线可以无限延伸D. 平行线可以相交2. 根据平行线的性质,以下哪个命题是正确的?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 以上都是3. 如果两条直线相交成30度角,那么这两条直线的对顶角是:A. 30度B. 60度C. 90度D. 120度4. 已知直线AB与CD相交于点O,那么OA与OB的关系是:A. OA=OBB. OA垂直于OBC. OA平行于OBD. 无法确定5. 在平面几何中,以下哪个条件不能判定两直线平行?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线没有交点二、填空题(每题2分,共10分)6. 如果两条直线相交所构成的同位角不相等,则这两条直线_________。
7. 平行于同一条直线的两条直线_________。
8. 两条直线相交,如果其中一个角是直角,则这两条直线_________。
9. 如果直线a与直线b相交,且a垂直于直线b,则直线a与直线b所成的角是_________度。
10. 两条平行线被第三条直线所截,同旁内角的度数之和为_________。
三、判断题(每题1分,共5分)11. 两条直线相交所形成的角中,对顶角相等。
()12. 平行线的性质可以推出同位角相等,内错角相等,同旁内角互补。
()13. 如果两条直线相交,那么它们一定在某一点相交。
()14. 两条直线相交所形成的角中,邻角互补。
()15. 平行线之间的距离处处相等,这是平行线的一个性质。
()四、简答题(每题5分,共10分)16. 解释什么是“相交线”,并给出相交线的基本性质。
17. 解释什么是“平行线”,并说明平行线的性质有哪些。
五、解答题(每题15分,共15分)18. 在平面直角坐标系中,已知直线L1: y = 2x + 3 和直线L2: y = -x + 5,请判断这两条直线是否平行或相交,并给出证明。
《相交线与平行线》的单元测试题(含答案)
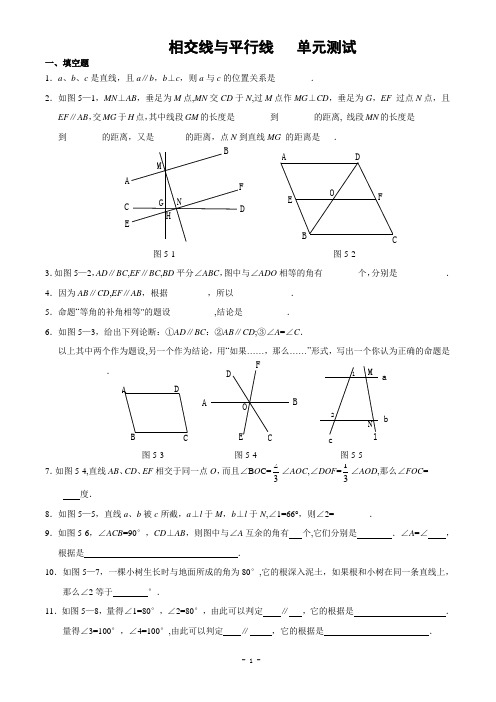
相交线与平行线 单元测试一、填空题1.a 、b 、c 是直线,且a ∥b ,b ⊥c ,则a 与c 的位置关系是________.2.如图5—1,MN ⊥AB ,垂足为M 点,MN 交CD 于N ,过M 点作MG ⊥CD ,垂足为G ,EF 过点N 点,且EF ∥AB ,交MG 于H 点,其中线段GM 的长度是________到________的距离, 线段MN 的长度是________到________的距离,又是_______的距离,点N 到直线MG 的距离是___.3.如图5—2,AD ∥BC ,EF ∥BC ,BD 平分∠ABC ,图中与∠ADO 相等的角有_______ 个,分别是___________. 4.因为AB ∥CD ,EF ∥AB ,根据_________,所以_____________. 5.命题“等角的补角相等"的题设__________,结论是__________. 6.如图5—3,给出下列论断:①AD ∥BC :②AB ∥CD ;③∠A =∠C .以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.7.如图5-4,直线AB 、CD 、EF 相交于同一点O ,而且∠B O C=23∠AOC ,∠DOF =13∠AOD ,那么∠FOC =_____ _ 度.8.如图5—5,直线a 、b 被c 所截,a ⊥l 于M ,b ⊥l 于N ,∠1=66°,则∠2=________.9.如图5-6,∠ACB =90°,CD ⊥AB ,则图中与∠A 互余的角有 个,它们分别是 .∠A =∠ ,根据是 .10.如图5—7,一棵小树生长时与地面所成的角为80°,它的根深入泥土,如果根和小树在同一条直线上,那么∠2等于 °.11.如图5—8,量得∠1=80°,∠2=80°,由此可以判定 ∥ ,它的根据是 .量得∠3=100°,∠4=100°,由此可以判定 ∥ ,它的根据是 .G H NMFEDC BAFEODCBA 图5-1 图5-2DCBAFEO DCBAclNMb a21图5-3 图5-4 图5-512.猜谜语:(打本章两个几何名称)剩下十分钱: ;斗牛 . 13.a 、b 、c 是直线,且a ∥b , b ∥c , 则a ___c ; a 、b 、c 是直线,且a ⊥b , b ⊥c , 则a ___c ;14. 如图5—9,直线AD 、BC 交于O 点,∠+∠=︒AOB COD 110,则∠COD 的度数为 .15. 如图5-10,直线AB 与CD 交于O 点,∠-∠=︒3180,则∠2= .16. 如图5—11,直线AB 、EF 相交于O 点,CD AB ⊥于O 点,∠=︒'EOD 12819,则∠∠BOF AOF,的度数分别为 .二、选择题17.若a ⊥b ,c ⊥d 则a 与c 的关系是( )A .平行B .垂直C .相交D .以上都不对 18.如图5-12,∠ADE 和∠CED 是( )A .同位角B .内错角C .同旁内角D .互为补角 19.如图5—13,l l 1211052140//,,∠=∠=,则∠=α( ) A . 55B . 60C . 65D . 7020.如图5-14,能与∠α构成同旁内角的角有( ) A . 5个 B .4个 C . 3个 D . 2个21.如图5—15,已知AB CD //,∠α等于( ) A .75B . 80C . 85D . 95AB 120°α25°CDBMCA N P D22.如图5—16,AB CD MP AB MN ////,,平分∠∠=∠=AMD A D ,,4030,则∠NMP 等于( ) A . 10B . 15C . 5D . 75.23.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30,那么这两个角是( ) A . 42138、B . 都是10C . 42138、或4210、D . 以上都不对24.如图5—17,a ∥b ,∠1与∠2互余,∠3=1150,则∠4等于( )A .1150B . 1550C . 1350D .125025.如图5—18,∠1=150, ∠AOC =900,点B 、O 、D 在同一直线上,则∠2的度数为( )A .750B .150C .1050D . 1650图5-13 d第(18)题4321cba 第(20)题DCBAO第(19)题DCBA21图5-17 图5-18 图5-19图5-15 图5-1626.如图5—19,能表示点到直线(或线段)距离的线段有( )A . 2条B .3条C .4条D .5条 27.下列语句错误的是( )A .连接两点的线段的长度叫做两点间的距离B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角, 则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等 28.如图5—20,如果AB ∥CD ,那么图中相等的内错角是( )A .∠1与∠5,∠2与∠6;B .∠3与∠7,∠4与∠8;C .∠5与∠1,∠4与∠8;D .∠2与∠6,∠7与∠329.下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )A .①、②是正确的命题B .②、③是正确命题C .①、③是正确命题D .以上结论皆错30.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行;②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )A .3个B .2个C .1个D .0个 三、解答题31.如图5—21,过P 点,画出OA 、OB 的垂线.2.32.如图5-22,过P 点,画出AB 、CD 的垂线.3. B C DBA33.如图5-23,是一条河,C 河边AB 外一点:(1)过点C 要修一条与河平行的绿化带,请作出正确的示意图.(2)现欲用水管从河边AB ,将水引到C 处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)87654321D CB A 图5-20 图5-21图5-22图5-2334.如图5—24,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?NMFE DCBA35.如图5-25,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.36.如图5—26,已知:CE =DF ,AC =BD ,∠1=∠2.求证:∠A =∠B .B37.如图5-27,已知:AB //CD ,AB =CD ,求证:AC 与BD 互相平分.C38.如图5—27,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .图5-24图5-26图5-262 ABECFDHG 139.如图5—28,已知:在∆ABC 中,∠=︒C 90,AC =BC ,BD 平分∠CBA ,DE AB ⊥于E ,求证:AD +DE =BE .40.如图5—29,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)EABCD图5-27 图5-28图5-29参考答案一、填空题 1.互相垂直2.点M ,直线CD 点M,直线EF 平行线AB 、EF 间 线段GN 的长度 3.4个 ∠EOB 、 ∠DOF 、∠ABD 、∠CBD4.两条直线都与第三条直线平行,这两条直线也互相平行 CD ∥EF 5.两个角是相等两角的补角 这两个角相等6.如果一个四边形的两组对边平行,那么它的对角相等;或若一个四边形的一组对边平行,一组对角相等,那么它的另一组对边也互相平行 7.156 8.114°9.两;∠ACD 和∠B;∠BCD ;同角的余角相等 10.10°11.AB ∥CD;同位角相等,两直线平行;EF ∥GH ;内错角相等,两直线平行 12.余角;对顶角 13.∥;∥14.55︒(点拨: ∠=∠∴∠=∠=︒AOB COD AOB COD 55)15.50︒(点拨: ∠+∠=︒∠-∠=︒⎧⎨⎩311803180,∴∠=︒∠=︒⎧⎨⎩1503130,又︒=∠∴∠=∠50221 )16. 3819'︒;14141'︒(点拨:9138909112890'︒=︒-'︒=∠-∠=∠∴︒=∠AOD EOD AOE AOD ,9138'︒=∠=∠∴AOE BOF ,又 ∠+∠=︒BOF AOF 180,141419138180'︒='︒-︒=∠∴AOF )二、选择题 17.C 18.B 19.C 20.A 21.C 22.C 23.D 24.B 25.C 26.D 27.C 28.D 29.A 30.D三、解答题 31.如图5—12.32.如图5—233.略.34.(1)CD∥AB因为CD⊥MN,AB⊥MN,所以CDN=∠ABM=90°所以CD∥AB(2)平行因为∠CDN=∠ABN=90°,∠FDC=EBA所以∠FDN=∠EBN所以FD∥EB35.(1)平行因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义)所以∠1=∠CDB所以AE∥FC(同位角相等两直线平行)(2)平行,因为AE∥CF,所以∠C=∠CBE(两直线平行,内错角相等)又∠A=∠C 所以∠A=∠CBE所以AF∥BC(两直线平行,内错角相等)(3)平分因为DA平分∠BDF,所以∠FDA=∠ADB因为AE∥CF,AD∥BC所以∠FDA=∠A=∠CBE,∠ADB=∠CBD所以∠EBC=∠CBD36.证明:答图5-1∠=∠∴∠=∠=∴+=+==∠=∠=∴≅∴∠=∠⎧⎨⎪⎩⎪12(已知)(等角的补角相等)(已知)即在和中,(已知)(已证)(已证)()(全等三角形的对应角相等)ECB FDA AC BD AC CD BD CDAD BCADF BCE DF CE FDA ECB AD BC ADF BCE SAS A B ∆∆∆∆37. 证明: AB CD //(已知)∴∠=∠∠=∠∠=∠=∠=∠∴≅∴==⎧⎨⎪⎩⎪BAO DCO ABO CDO ABO CDO BAO DCO AB CD ABO CDO ABO CDO ASA AO CO BO DO ,(两直线平行,内错角相等)在和中(已证)(已知)(已证)(),(全等三角形对应边相等)∆∆∆∆即AC 与BD 互相平分. 38. 证明: ∠=∠12(已知)∠=∠∴∠=∠∴∴∠=∠12AHB AHB AF ED D AFC (对顶角相等)(等量代换)(同位角相等,两直线平行)(两直线平行,同位角相等)//又 ∠=∠A D (已知)∴∠=∠∴∴∠=∠A AFC AB CD B C (等量代换)(内错角相等,两直线平行)(两直线平行,内错角相等)//39. 证明: BD CBA 平分(已知)∠∴∠=∠⊥∴∠=︒∠=︒EBD CBD DE AB DEB C (角平分线的定义)(已知)(垂直的定义)(已知)9090∴∠=∠DEB C (等量代换) 在∆∆DEB DCB 和中∠=∠∠=∠=∴≅⎧⎨⎪⎩⎪DEB C EBD CBD DB DB DEB DCB AAS (已证)(已证)(公共边)()∆∆∴==+==∴+=DE DC BE BC AD DC AC BC AD DE BE ,(全等三角形的对应边相等)(已知)(等量代换)40. 证明:(1)连结BD ,如图5—3AB CD ABD CDB BED ABD CDB BED ABE CDE BED //(已知)(两直线平行,同旁内角互补)(三角形内角和为)即∴∠+∠=︒∠+∠+∠=︒︒∴∠+∠+∠+∠+∠=︒∠+∠+∠=︒1801218018012360360(2)延长DE 交AB 延长线于F ,如图5—4AB CD F D ABE FEB F BED FBE F ABE CDE BED//(已知)(两直线平行,同旁内角互补),(三角形一个外角等于和它不相邻的两个内角的和)∴∠+∠=︒∠=∠+∠∠=∠+∠∴∠+∠+∠180=∠+∠+∠+∠+∠FEB F CDE FBE F=︒+︒=︒180180360(3)过点E 作EF//AB ,如图5—5- 11 -AB CD //∴AB EF CD ////(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)∴∠+∠=︒∠+∠=︒∴∠+∠+∠+∠=︒+︒=︒∴∠+∠+∠=︒B BEF D DEF B BEF D DEF B D BED 180180180180360360(两直线平行,同旁内角互补)。
(完整版)《相交线与平行线》单元测试卷含答案
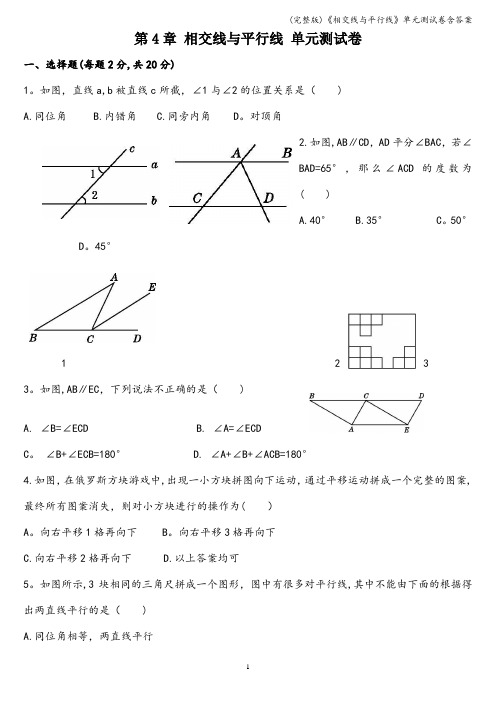
第4章相交线与平行线单元测试卷一、选择题(每题2分,共20分)1。
如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角D。
对顶角2.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD的度数为( )A.40°B.35° C。
50°D。
45°31 2 3。
如图,AB∥EC,下列说法不正确的是()A. ∠B=∠ECDB. ∠A=∠ECDC。
∠B+∠ECB=180° D. ∠A+∠B+∠ACB=180°4.如图,在俄罗斯方块游戏中,出现一小方块拼图向下运动,通过平移运动拼成一个完整的图案,最终所有图案消失,则对小方块进行的操作为( )A。
向右平移1格再向下 B。
向右平移3格再向下C.向右平移2格再向下D.以上答案均可5。
如图所示,3块相同的三角尺拼成一个图形,图中有很多对平行线,其中不能由下面的根据得出两直线平行的是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.平行于同一直线的两直线平行D。
垂直于同一直线的两直线平行6。
如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )A.40°B.70°C.80° D。
140°7。
同一平面内的四条互不重合的直线满足a⊥b,b⊥c,c⊥d,则下列各选项中关系能成立的是( )A。
a∥d B。
a⊥c C。
a⊥d D。
b⊥d8。
如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )A.120 ° B。
130° C.140° D。
150°9。
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )A。
30° B.60° C。
80° D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版七年级数学下册《相交线与平行线》单元测试题班级:姓名:得分:
一、填空题
1.两条直线相交,有_____对对顶角,三条直线两两相交,有_____对对顶角.
2.如图1,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是_____.
3.已知∠AOB=40°,OC平分∠AOB,则∠AOC的补角等于_____.
4.如图2,若l1∥l2,∠1=45°,则∠2=_____.
图1 图2 图3
5.如图3,已知直线a∥b,c∥d,∠1=115°,则∠2=_____,∠3=_____.
6.一个角的余角比这个角的补角小_____.
7.如图4,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=_____.
图4 图5
8.如图5,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_____.
9.如图6,AD∥BC,AC与BD相交于O,则图中相等的角有_____对.
图6 图7
10.如图7,已知AB∥CD,∠1=100°,∠2=120°,则∠α=_____.
11.如图8,DAE是一条直线,DE∥BC,则∠BAC=_____.
12.如图9,AB∥CD,AD∥BC,则图中与∠A相等的角有_____个.
图8 图9 图10
13.如图10,标有角号的7个角中共有_____对内错角,_____对同位角,_____对同旁内角.
14.如图11,(1)∵∠A=_____(已知),
图11
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
二、选择题
15.下列语句错误的是( )
A.锐角的补角一定是钝角
B.一个锐角和一个钝角一定互补
C.互补的两角不能都是钝角
D.互余且相等的两角都是45°
16.下列命题正确的是( )
A.内错角相等
B.相等的角是对顶角
C.三条直线相交,必产生同位角、内错角、同旁内角
D.同位角相等,两直线平行
17.两平行直线被第三条直线所截,同位角的平分线( )
A.互相重合
B.互相平行
C.互相垂直
D.相交
18.如果∠1与∠2互补,∠1与∠3互余,那么 ( )
A.∠2>∠3
B.∠2=∠3
C.∠2<∠3
D.∠2≥∠3
19.如图12,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
图12
A.AD∥BC
B.∠B=∠C
C.∠2+∠B=180°
D.AB∥CD
20.如图13,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于( )
图13
A.40°
B.45°
C.55°
D.65° 21.如图14,若AB ∥CD ,则∠A 、∠E 、∠D 之间的关系是( )
图14
A.∠A +∠E +∠D =180°
B.∠A -∠E +∠D =180°
C.∠A +∠E -∠D =180°
D.∠A +∠E +∠D =270° 三、解答题
22.如图15,CD 平分∠ACB ,DE ∥BC ,∠AED =80°,求∠EDC 的度数.
图15
23.如图16,已知AB ∥CD ,∠B =65°,CM 平分∠BCE ,∠MCN =90°,求∠DCN 的度数.
图16
24.如图17,∠1=
2
1
∠2,∠1+∠2=162°,求∠3与∠4的度数.
图17
25.如图18,CD ∥AB ,∠DCB =70°,∠CBF =20°,∠EFB =130°,问直线EF 与AB 有怎样的位置关系,为什么?
图18
26.如图19,AB ∥CD ,HP 平分∠DHF ,若∠AGH =80°,求∠DHP 的度数.
图19
27.根据下列证明过程填空:
如图20,BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C
图20
证明:∵BD⊥AC,EF⊥AC( )
∴∠2=∠3=90°
∴BD∥EF( )
∴∠4=_____( )
∵∠1=∠4( )
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
28.阅读下面的证明过程,指出其错误.
图21
已知△ABC
求证:∠A+∠B+∠C=180°
证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行,内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
*29.已知:如图22,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,
求证:DA⊥AB.
图22
参考答案
一、1.两六 2.30° 3.160° 4.135 5.115° 115° 6.90° 7.53° 8.80°
9.四 10.40° 11.46° 12.3 13.四二四
14.(1)∠BED同位角相等,两直线平行
(2)∠DFC内错角相等,两直线平行
(3)∠AFD同旁内角互补,两直线平行
(4)DF两直线平行,同旁内角互补
(5)ED两直线平行,同位角相等
二、15.B 16.D 17.B 18.A 19.B 20.A 21.C
三、22.40° 23.32.5° 24.54° 72°
25.平行证明略 26.50° 27.已知同位角相等,两直线平行∠5 两直线平行,同位角相等已知∠5 等量代换内错角相等,两直线平行两直线平行,同位角相等
28.错误:过A作DE∥BC,且使∠1=∠C,应改为:过A作DE∥BC.∵∠1=∠C(画图),理由错,应改为:两直线平行,内错角相等 29.略。
