柯布西耶红蓝尺
柯布西耶模度系统与比例方法的组合应用

74 时代建筑 Time+Architecture 2020/6刘磊LIU Lei柯布西耶模度系统与比例方法的组合应用Combined Application of Le Corbusier's Modulor System and Proportional Methods摘要文章首先回溯历史,阐述了柯布西耶的模度人 与达•芬奇绘制的维特鲁威人的源流关系,然后通过 对柯布西耶的海边小木屋和贾乌尔住宅的分析揭示了 模度应用中涉及的物理尺度、空间尺度和心理尺度,并就从小木屋到贾乌尔住宅模度尺寸应用的差异推测 出柯布西耶在运用模度时的不断修正过程。
最后通过 马赛公寓和昌迪加尔高等法院大楼中模度运用的案例 剖析了柯布西耶在运用模度时采取的两种策略:第一 种通过模度建立以人为本的空间单元,然后运用黄金 分割比的方法确定单元组成后的建筑整体的尺寸;第 二种则先通过整数通约比确定建筑物的轴网等宏观尺 寸,然后再用模度尺寸替代构成整体的轴网尺寸。
最 后得出模度仅仅是一个工具,决定建筑美感的大部分 是建筑师本人。
关键词勒•柯布西耶;模度;红蓝尺;物理尺度;空间尺度;心理尺度;黄金分割;整数通约比 ABSTRACT The paper first explores the relationship between Le Corbusier's modulor system and Leonardo da Vinci's drawing of the Vitruvian Man by retracing the history.Through the analysis of the seaside cabin,"the Cabanon",and the residetial housing Maison Jaoul, it reveals the physical dimension,spatial dimension, and psychological dimension that involved in the application of the modulor system.Then,through the difference in the application of modulor systems from Corbusier's log cabin to residential housing, we can speculate Corbusier's continuous modifying process in the application of modulor st but not least,the case study of the modulor that applied in Unite d'Habitation and the High Court of Chandigarh analyzes two modulor strategies adopted by Le Corbusier: (1)The former one establishes the human-oriented spatial unit through the use of modulors.Then,the overall size of the construction of the building can be determined by the method of the golden section ratio. (2)The latter one first determines the macroscopic dimensions of the axial network in a building through the general ration of integers and then replaces the overall size with the modulor size.Finally,we can conclude that the modulor system is just a tool.It is the architect himself/herself who determines the beauty of the building.KEY WORDS Le Corbusier;Modulor;Red and Blue Series;Physical Dimension;Spatial Dimension; Psychological Dimension;Golden Section;General Ration of Integers中图分类号:TU201.1;TU-098文献标识码:A文章编号:1005-684X(2020)06-0074-06在柯布西耶留给我们的建筑学遗产中,模度无疑 是最为神秘的。
模度

由于“模度”的人体 意义体现在高度上,所以 它在竖向尺寸的确定中.显 得更加生动.“模度”控制了 从层高到栏板厚度的几乎 所有的竖向尺寸.其中每一 居住单元(每单元三层)的一 ( ) 层阳台和二层阳台的桌面 高度.分别为0.7m和0.86m. 如上文提到的.这两个尺寸 分别回应了坐姿和站姿两 种预设.
两个批判“模度”的图解———一幅图解中 “红蓝尺” 边的尺度人被画成正圆中的维特每威人.而中间四肢展开 的人体.被画成1.83m高的高大女人,这一方面是在历史参 照中对“模度”的赞扬,另一方面似乎在问:模度适合女 人吗?在另一幅图解中“比例网格”千脆被倒置了再将人 体刻度一一对应画出的竟是一只猩猩令人不禁生疑—“模 度”中的人,真的是人吗?
“模度”是勒·柯布西耶最 主要的成就之一,爱因斯坦对 此总结道:“此比例系统极易 产生美妙形式,很难产生丑陋 形式。” “模度”就其本身而言并 不复杂,但它却继承和发扬了 西方建筑传统中的一种精神: 数字与人文的结合。简单的数 字和比例背后反映了人的理性 与自然的和谐统一,“模度” 是勒·柯布西耶在这方面最重 要的总结。
在“模度”的 度量控制下,可以 产生无数种矩形板 块.柯布西耶和他 的助手们选择其中 有“建筑潜力“的 板块,在2.26m见 方的边界内做“拼 接练习”
在上述2.26m正方的练习中.由于所有的板块全都出 自“模度”体系具有更大的匹配可能练习的结果都实现了 严密的拼接
当2.05m的“外来”尺度的介入后.在2.26m的边界与 “门板”之间.出现了0.21m宽的空隙.在柯布西耶眼中.这 些干扰构成的空隙非但不是“问题”,反而提供了建筑设 计的“潜力”—这比坚持纯粹的“模度”更为重要.
柯布西耶将“模度”的“身高刻度”定义为6英尺即 1.83m.相应得到以1.13m为起始的‘红尺‘’和以2.26m 为起始的.蓝尺‘’.并将蓝尺的2.26m、1.4m.0.86m.以及 红尺的1.83m.1.13m.0.7m脐高、座椅扶手高、平 坐高.低坐高的人体尺度意义
红尺蓝尺
“模度”是西方传统美学思想的继承和发展
勒· 柯布西耶的“模度”是西方关于几何和比例传统美 学思想的延续, 这种几何和比例并不只是抽象数字和几 何图形的表达, 而常常与人体直接相联系, 是一种人 文主义精神的体现。 埃及金字塔、 希腊的帕提农神庙、 印度寺庙和文艺复 兴教堂等许多伟大建筑, 在建造的过程中都采用了以数 学规律为基础的精确量度体系, 而这些量度体系的工具 是建立在与人体密切相关的: 肘、 腕、 指、 拇指(英 寸)、 脚、 步伐等的基础之上。 量度的工具尺寸是通 过数字——人体数学的一部分——来表达的, 因而它 们是永恒、 和谐和微妙的, 是令我们感动和创 造和谐的源泉。
谢谢观看
姚潇徽
“模度”的意义
“模度” 是与人体尺度相和谐的量度体系, 体系统一在 一起, 因此勒· 柯布西耶认为它将广泛适用于建筑和机械 工程方面。 马赛公寓 是应用“模度” 仅用了 15 种模数 尺寸而设计出来的, 整僮建筑长140 m高70 m, 建筑的 里里外外都体现了人的尺度。 对建筑师而言“模度” 使许多设计工作变得异常的简单, 设计中的许多犹豫和不 确定甚至错误都被提前解决。 即使在勒· 柯布西耶后期的 充满魔幻色彩的朗香教堂中, 墙面的窗洞、 地面分割等 的许多设计中都源于他的“模度”, 同样勒· 柯布西耶把 “模度” 理论应用在更大尺度的规划设计中, 如印度昌 地加尔首府中心的规划设计。
“模度”是西方传统美学思想的继承和发展
黄金分割是几千年来人们基于对自然世界的观察, 以几 何和比例的方式总结的美学规律,勒· 柯布西耶称它为 确定“任何事物的标尺”,是通过“秩序” 与宇宙力相 接触的点, “秩序”通过几何和比例的方式表达, 而 成为神圣的原理。 勒· 柯布西耶的“模度” 是: 建立 在黄金分割与和谐人体的基础上, 用于选择尺寸的精确 量度的工具。 因此通过“模度” 能够利用和理解这些 微妙与和谐的数字。
最新勒柯布西耶LeCorbusier

的空间最大化,并能产生良好的视觉效应。 从他的作品 中我们可以发现他的建筑设计充分发挥了框架结构的特点, 非常具有现代感。不同的时期会有不同的创作特点,而柯 布也在他的后期作品创作中体现出一种浪漫主义与神秘主 义色彩。
柯布西耶的理想城市
柯布西耶认为由钢铁、混凝土和玻璃组成的五光十色的摩 天楼宣告着对大规模工业社会的信仰。他理想的现代城市 模式就是中心区挺立着高耸入云的摩天大楼,外围是高层 楼房,楼房之间有大片绿地,现代化的整齐的道路网布置 在不同标高的平面上。柯布西耶认为人们生活的城市,应 该以设置有各种生活福利设施的“居住单位”为基本要素。 马赛公寓住宅是柯布西耶实现理想的现代化城市居住单位 的第一次尝试。
从模度系统诞生,特别是50年代后,柯布西耶以其作为一 种重要设计工具,在其实践中加以应用,包括马赛公寓、 昌迪加尔、圣迪埃工厂乃至朗香教堂的平面设计,模度系 统都不同程度发挥了其比例控制的效用。
我眼中的勒·柯布西耶
勒·柯布西耶是一名想象力丰富的建筑师,他对理想城市 的诠释、对自然环境的领悟以及对传统的强烈信仰和崇敬 都相当别具一格。是一个极具理性主义色彩的建筑大师。 他用格子、立方体进行设计,还经常用简单的几何图形、 一般的方形、圆形以及三角形等图形建成看似简单的模式。 通过精心的设计,在明暗光线的对比下,他成功地将有限
柯布西耶

勒· 柯布西耶(Le Corbusier)主要建筑作品:
年代不详 佛莱别墅(Villa Fallet) 1927年 国际联盟总部设计方案 1928年 萨伏伊别墅(Villa Savoy 1930-1932年 巴黎瑞士学生宿舍 (Pavillion Suisse A La Cite Universitaire A Paris) 1936年 巴西里约热内卢教育卫生部大楼 1946-1957年 马赛公寓大楼 (L’unite d’Habitation ,Marseille) 1950-1953年 郎香教堂 (La Chapelle de Ronchamp) 50年代初 印度昌迪加尔城市规划
勒· 柯布西耶(Le Corbusier)
简介
勒· 柯布西耶 (Le Corbusier,1887-1965年),是对 当代生活影响最大的建筑师,是20世纪文艺复兴式 的巨人,是毕生充满活力,永无休止进行创造的设 计大师、建筑大师和艺术大师,在现代建筑运动中, 他最有效地充当了前后两大阶级的旗手:20年代的 功能理性主义和后来更广泛的有机建筑阶段。 他是20世纪最多才多艺的大师:建筑师、规划师、 家具设计师、现代派画家、雕塑家、挂毯设计师, 同时他又是多产作家,出版有50多部专著及无数文 章。
萨伏伊别墅(Villa Savoy)
勒· 柯布西耶
萨伏伊别墅宅基为矩形,长约22.5米, 宽为20米,共三层。设计上与以往的欧 洲住宅大异其趣。轮廓简单,像一个白 色的方盒子被细柱支起。水平长窗平阔 舒展,外墙光洁,无任何装饰,但光影 变化丰富。别墅虽然外形简单,但内部 空间复杂,如同一个内部精巧镂空的几 何体,又好像一架复杂的机器。采用了 钢筋混凝土框架结构,平面和空间布局 自由,空间相互穿插,内外彼此贯通, 它外观轻巧,空间通透,装修简洁,与 造型沉重、空间封闭、装修繁琐的古典 豪宅形成了强烈对比。
柯布西耶红蓝尺

“模度”并不 能生成设计,它 只是当设计师遇 到无法精确定义 度量的困境时, 为他们提供确定 度量数据的标准, 而一旦有更为明 确的标准存在, “模度”就会自 动让步。如果只 是专用于赋值 “模度” 工具的应用范围似乎显得过于狭窄,而正因为范围狭窄,它也就特别有 效——在柯布西耶视察马赛公寓施工现场的时候,临时决定在首层架空 的梁底加两个牛腿,以承放纪念建筑工人的雕塑。汽车在等待,这位伟 大的设计者从口袋中拿出红蓝尺,一分钟后,一切尺度细节都被确定下 来,汽车扬长而去……
刘沐奇 10076140015
柯布西耶—度
☼ 模度
☼ 1947 年,勒 · 柯布西耶将一项称为“模度”的发明专利公之于众; 1948年出版了讲述模度的发现历程的专著《模度1》;他提出的模度 是“一个符合人体尺度的和谐的尺寸系列,”是一种“普遍适用于建 筑和机械”等设计的“通用的尺寸系列”。柯布西耶对模度是这样解 释的:“模度(Modulor )是从人体尺寸和数学中产生的一个度量工 具。举起手的人给出了占据空间的关键点:足、肚脐、头,举起的手 的指尖。它们之间的间隔包含了被称为费波纳契的黄金比。另一方面, 数学上也给予它们最简单也是最有力的变化,即单位、倍数、黄金 比。” 柯布西耶把人体尺度、数学、设计等方面有机地结合在一起创 造了模度、模度人及模度理论。
☼ 这样,初始正方形以偏 心的位置嵌套于双正方 的矩形中,在长边产生 两条分割线,再加上双 正方矩形长边的中线, 便形成四种高度,在比 例上恰好分别对应膝高、 脐高、身高和举高。这 一图解被称作“比例网 格”(ProportionGrid), 是“模度”的雏形。
☼ 这是柯布西耶在1943年以前相关“模度”的前期工作,他总结大量法 国传统住宅的室内净高通常为2.2米,认为这刚好是人的举高尺度,于 是将2.2米赋予比例网格的“举高”,相应其它分割点上 1.78米、1.1 米和0.68米的赋值便可直接依“比例网格”折算出来。这套网格在柯 布的“别墅公寓”、“新精神馆”以及“不洁的住宅群 6 号”中都得 到了不同程度的应用。柯布对使用结果的评价是:“比例网格在图解 中决定物体尺度的时候给了我们极端的确定性 ……在这网格中,数学 秩序符合人体尺度,我们使用它,但我们还是不能满意:对我们的发 明,我们始终缺乏定义。”
勒.柯布西耶——模度(比例理论,源自黄金分割和人体)

勒.柯布西耶——模度(比例理论,源自黄金分割和人体)关于《模度》产生的一些背景语言学家们认为不存在真正的哲学问题,或者说,即使存在的话,它们也是关于语言的使用或者语言的意义之类的问题。
然而我们认为至少存在一个哲学问题,所有有思想能力的人都对其感兴趣。
那就是宇宙观的问题:即理解世界——包括作为世界之一部分的我们自己和我们的知识——的问题。
(K.R.Popper.The Logic of scientificDiscovery,huntchinson,1959,p.15)艺术秩序中的数学公式规律一直与视觉美联系在一起,但是,艺术中的美以前并不被看成是一种视觉现象,而是某种更为深奥事物的外在符号:一种与世界之普遍和谐的一致。
正是从这种更为深刻的和谐中,艺术之美获得了它的“善”或“真”与爱因斯坦一样,勒.柯布西耶见多识广,这使得他成为文艺复兴精神的一个传人。
再没有其他现代运动的建筑师给予建筑学中的数学比例如此重要的角色。
对他来说,数学规律不仅仅是对美得一种规定,甚至也不是人类用来理解他们的世界的一种手段,而是宇宙自身的核心或主导性原理,自然的,艺术的统一与和谐之源。
......勒.柯布西耶的态度中有一种根本性的暗示:一种指导性智力或意志控制着宇宙:“这种核心使得我们假定宇宙中行为的统一性,并且承认其背后有一个单一的意志......如果我们认可(并热爱)科学及其作用,这是因为两者迫使我们承认它们是由这种主要的意志所规定的。
如果数学计算在我们看来是令人满意的与和谐的,这是因为它们源自这一核心。
经过计算,如果飞机呈现出一条鱼或者其他某一自然物的特征,这是因为它们已经重新获得了核心。
”(Le Corbusier,The Modulor,pp.29-30.)不可知论者勒.柯布西耶的观点中的具有一种神秘主义色彩:“数学......即绝对,也无限,即可理解,也永远不可捉摸。
他位于围墙之内,人们在其前面徘徊而毫无结果;有时候,存在一扇门:有人打开它——走了进去——他进入另一个王国,诸神的王国,这个房间里放着开启伟大体系的钥匙。
柯布西耶模度与控制线
m人体,窄腰、宽肩、修长四肢和小小的
头部组成了一个符合几何控制线的美学上的理想人体(图3)。人体被限制在三 个重叠且相邻的方形内,三个方形与人的维度建立了联系。人的肚脐正好放 置在中心点上,同时也在轴线上,左手放在正方形的顶边,右手的手指放在 内方形的角点上。 既然人体的高度为确定的黄金分割比的点便产生了:
线,面,体的几何运用和比例,尺度的数 学关系,通过对位,切分等复杂组合关系得 到某些暗示和隐喻,并由此产生情感化的表 现力。
这是我们目前的教学和创作中极度匮乏和需探索研究的。
爱因斯坦对此总结道:“此比例系统极易产生美妙形式,很难 产生丑陋形式。”
数字与人文的结合。简单的数字和比例背后反映了人的 理性与自然的和谐统一,“模度”是勒· 柯布西耶在这方面最重
0.7m—1.13m——1.83m——2.26m。
勒· 柯布西耶的“模度” 产生了两尺寸系列。
第一个序列为“红 尺”——基于1.130 m,
第二序列为“蓝 尺”——基于2.260m。
在红尺和蓝尺的数字级 数中,每两个相邻数字 的级差都是0.618的比率。 大量研究已证明人体的 许多尺寸与黄金分割有 关,因此勒· 柯布西耶的 “模度”为综合数学和 人体尺度的量度体系。
模度并不能赋予人才智和产生天才并不能使愚笨的人变的聪明它只是为那些具有创造力的艺术家和设计师提供精确量度的工具在由模度组合的各种选择中理想的选择完全是由你自己决定的
/bbs / / / /m / /dx/ /sy/ /hlj/ /wj/ /bjdxb /zy/ /zjdx/dx/ /dxb / / / / / / / ? / /m/ / / / / / / /zjdx/ / / / / / / / / / /
柯布西耶

现代建筑大师之勒·柯布西耶(2008-11-29 22:25:16)标签:文化分类:艺术设计 勒·柯布西耶勒·柯布西耶(Le Corbusier1887年10月6日-1965年8月27日),原名Charles Edouard Jeannert-Gris ,是20世纪最重要的建筑师之一,是现代建筑运动的激进分子和主将,被称为“现代建筑的旗手”。
他和瓦尔特·格罗皮乌斯、路德维格·密斯·凡·德·罗以及弗兰克·洛依德·赖特并称为四大现代建筑大师。
柯布西耶出生于瑞士西北靠近法国边界的小镇,父母从事钟表制造,少内时曾在故乡的钟表技术学校学习,对美术感兴趣,1907年先后到布达佩斯和巴黎学习建筑,在巴黎到以运用钢筋混凝土著名的建筑师奥古斯特·贝瑞处学习,后来又到德国贝伦斯事务所工作,彼得·贝伦斯事务所以尝试用新的建筑处理手法设计新颖的工业建筑而闻名,在那里他遇到了同时在那里工作的格罗皮乌斯和密斯·凡·德·罗,他们互相之间都有影响,一起开创了现代建筑的思潮。
他又到希腊和土耳其周游,参观探访古代建筑和民间建筑。
作品简介朗香教堂柯布西耶于1917年定居巴黎,同时从事绘画和雕刻,与新派立体主义的画家和诗人合编杂志《新精神》,按自己外祖父的姓取笔名为勒·柯布西耶,他在第一期就写到:“一个新的时代开始了,它植根于一种新的精神,有明确目标的一种建设性和综合性的新精神。
”后来他把其中发表的一些关于建筑的文章整理汇集出版单行本书《走向新建筑》,激烈否定十九世纪以来的因循守旧的建筑观点、复马赛公寓巴黎瑞士学生宿舍萨伏伊别墅古主义的建筑风格,歌颂现代工业的成就,提出“我们的时代正在每天决定自己的样式”,称颂工程师的工作方法,“工程师受经济法则推动,受数学公式所指导,使我们与自然法则一致,达到了和谐。
柯布西耶说明书
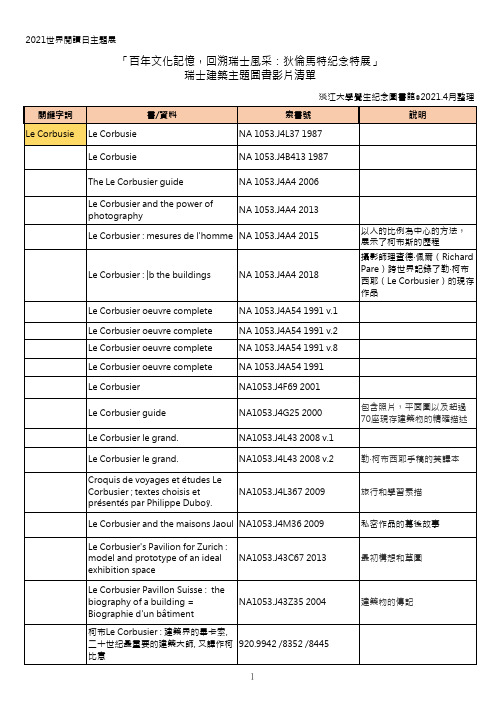
2021世界閱讀日主題展「百年文化記憶,回溯瑞士風采:狄倫馬特紀念特展」瑞士建築主題圖書影片清單淡江大學覺生紀念圖書館◎2021.4月整理Le corbusier = ル.コルビュジエDVD NA 1053.J4C67 2006v.1歐洲電視台於1987年誕辰100週年製作的錄像分為三部分,介紹了勒·柯布西耶(LeCorbusier)隨時間流逝留下的許多著名建築,以及他的採訪音頻。
Le corbusier = ル.コルビュジエDVD NA 1053.J4C67 2006 v.2Le corbusier = ル.コルビュジエDVD NA 1053.J4C67 2006 v.3Le Corbusier, moderne absolumentmoderneDVD NA 1053.J4A4 2014科比意 = Le Corbusier : MorceauxChoisis, 1912-1965923.42 /8352 /8445科比意 : 廿世紀的建築傳奇人物柯布 =Le Corbusier923.42 /8445Mario Botta Mario Botta : architectural poetics NA 1353.B67S35 2000 Multi-use buildings NA 680.C66 n.12Mario Botta architetti : leadingarchitectsNA 1353.B67A4 2017Mario Botta : light and gravity :architecture, 1993-2003NA 1353.B67M375 2004 Mario Botta : public buildings1990-1998NA 1353.B67A4 1998 Mario Botta NA 1353.B67P58 1997Mario Botta NA 1353.B65A4 1979Mario Botta NA 1353.B67P59 1998Mario Botta : Centre DürrenmattNeuchâtelNA 1353.B57A63 2000Herzog & De Meuron Herzog & de Meuron : thecomplete works.NA 1353.H47A4 2009 Herzog & de Meuron NA 1353.H47A4 2002 Herzog & de Meuron : 2013-2017NA1353.H47A4 2017b Herzog & de Meuron : 1978-2002NA1353.H47A4 2019 Herzog & de Meuron : 2003-2019NA1353.H47A4 2019bPeter Zumthor Peter Zumthor, 1985-2013 :buildings and projectsNA 1353.Z86A4 2014 v.1。
勒·柯布西耶

萨伏伊别墅
• 萨伏伊别墅建于1928-1929年间, 为钢筋混凝土构造,位于巴黎旳 近郊,是一种完美旳功能主义作 品。这个建筑表面上看起来平淡 无奇,没有什么太多旳装饰,完 全不同于早期中世纪时期旳建筑 给人旳那种印象。它旳外部装饰 采用白色粉刷,唯一旳能够称为 装饰部件旳是那个长条形排窗, 建筑表面平整,形体也比较简朴; 然而从不同旳方向看过去,都能 够得到完全不同旳印象,这使建 筑外观显得甚为多变。这种不同 不是刻意设计出来旳,而是其实 内部功能空间旳外部体现。
• 该建筑在设计上主要有如下特点: 模数化设计--这是柯布西耶研究数 学、建筑和人体百分比旳成果,目 前这种设计措施广为应用;简朴旳 装饰风格--相对于之前人们经常使 用旳繁琐复杂旳装饰方式而言旳, 其装饰能够说是非常旳简朴;开放 式旳室内空间设计——动态旳、非 老式旳空间组织形式,尤其使用螺 旋形旳楼梯和坡道来组织空间;屋 顶花园旳设计--使用绘画和雕塑旳 体现技巧设计旳屋顶花园;车库旳 设计--特殊旳组织交通流线旳措施, 使得车库和建筑完美旳结合,使汽 车易于停放而又不会使车流和人流 交叉;雕塑化旳设计--是勒·柯布西 耶常用旳设计手法,这使他旳作品 经常体现出一种雕塑感。
• 马赛公寓提升了居民选择旳自由度,从单身 住户到8个孩子旳家庭;室内楼梯将两层空间 连成一体,起居厅两层通高,大块玻璃窗满足 了观景旳开阔视野。马赛公寓在第7、8层布 置了各式商店,满足居民旳多种需求。幼稚 园和托儿所设在顶层,经过坡道可到达屋顶 花园。屋顶上设有小游泳池、小朋友游戏场 地、一种200米长旳跑道,健身房、日光浴室, 还有某些服务设施——被勒·柯布西耶称为 “室外家具”,如混凝土桌子、人造小山、 花架、通风井、室外楼梯、开放旳剧院和电 影院,全部一切与周围景色融为一体,相得 益彰。他把屋顶花园想象成在大海中航行旳 船只旳甲板,供游人欣赏天际线下漂亮旳景
神圣的比例_柯布西耶模数

7
比例网格
柯布在图解的基础上引入了“直角规线”,即连接长边延长端点与初 始正方形中线另一端点成斜线,并以此斜线为一直角边作垂线与该边垂 直,垂线另一端与黄金分割长边延长线相交,得到新延长线的长度恰好 为初始正方形边长的两倍 。这样,初始正方形以偏心的位置嵌套于双正 方的矩形中,在长边产生两条分割线,再加上双正方矩形长边的中线, 便形成四种高度,在比例上恰好分别对应膝高、脐高、身高和举高。
神圣的比例
柯布西耶模度
1
比例被倒置,再将人体刻度一一对应,画出的竟是一只猩猩
2
模数是人类自古以来就建立起的建筑生产方法,其意义存在 于两个方面:
一是模数的技术作用,模数减少了构件种类,无论对工业化 机器大生产还是传统手工生产,都有简化制作的意义,从而有 利于大批量生产预制构件 二是模数的美学作用,在西方古典建筑柱式中,模数以一个 柱径为基本度量单位,其余部分均参照这个基本单位按比例取 值建造,从而获得的柱式整体与细部的比例和谐。
10
模度与美学传统
对于直接将“模度” 视作美学原则的观点, 柯布西耶本人是深恶 痛绝的。柯布还借助 “模度”的比例优势 对文艺复兴的几何不 变性研究展开了批判。 他认为对正多面体、 星形体及正多边形的 研究,背离了基于视 觉判断的建筑学的本 质,因为人眼对不同 距离的事物的认知并 不是均匀、等分的而 是渐变的。
传统建筑形制虽然被打破但是传统建筑创造精神的方法却在延续这个方法就是比例而获得比例的有效方法是利用模数建立秩序从而获得和谐的形象和空间崇高的精神数学的秩序29整个勒氏模度的体系实际上是一种个人工具是柯布对建筑人体和数字相互关系的解虽然由于各种原因导致柯布的模数观念不是十分完美但是他的这个思想方式绝对是正确和先进的对现在所倡导的人体工程学提倡设计要以人为本设计适合人体的最佳尺度具有十分重要的意义
勒·柯布西耶的理念及优秀作品分析

和绿地的城市环境。
对交通和公共空间的关注
03
柯布西耶强调城市交通的重要性,提倡人车分流、设立公共空
间等措施来改善城市交通和居民生活环境。
03 勒·柯布西耶的代表作品
朗香教堂
独特造型
朗香教堂以其独特的几何造型和 曲线结构而著称,体现了勒·柯布 西耶对于建筑形式的创新追求。
光线运用
教堂内部的光线设计巧妙,通过不 同形状和大小的窗户引入自然光, 营造出神圣而神秘的空间氛围。
关注社会问题
勒·柯布西耶的建筑理念不仅关注建筑本身,还关注社会问 题,如城市规划、住房问题等。这种理念提醒建筑师在设 计过程中应综合考虑社会、经济、环境等多方面因素,以 实现建筑与社会的和谐发展。
对当代建筑设计的启示和影响
追求简洁与纯粹
注重空间与光影
强调建筑与环境的融合
勒·柯布西耶的作品以简洁、纯粹著称 ,这种设计风格对当代建筑设计产生 了深远影响。许多建筑师在设计过程 中追求简洁的线条、纯粹的几何形态 ,以营造出具有视觉冲击力的建筑形 象。
柯布西耶认为建筑的首要 任务是满足使用功能,设 计应围绕功能展开。
理性设计
他主张通过理性分析,将 建筑形式简化为基本的几 何形体,以符合功能需求。
反对装饰
柯布西耶反对多余的装饰, 认为装饰会干扰建筑的功 能和纯粹性。
纯粹主义美学
追求简洁和纯粹
对材料和结构的关注
柯布西耶的美学理念强调简洁、纯粹 和几何秩序,追求建筑形式的清晰和 明确。
如何欣赏和理解勒·柯布西耶的建筑艺术
要点一
了解背景与理念
要深入了解勒·柯布西耶的建筑艺术, 首先需要了解他的生平和创作背景, 以及他的建筑理念和设计哲学。
要点二
建筑大师柯布西耶及其主要作品作品简介

的旅程。
朗香教堂是勒·柯布西耶在第二次世界大战后的重要作品,代表了勒·柯布西耶创作风格的转变,在朗香教堂的设计中,勒·柯布西耶脱离朗香教堂的建筑和设计者简介】朗香教堂,又译为洪尚教堂,位于法国东部索恩地区距瑞士边界几英里的浮日山区,坐落于一座小山顶上,1950—1953年由法国建筑大师勒·柯布西耶(Le Corbusier)设计建造,1955年落成。
朗香教堂的设计对现代建筑的发展产生了重要影响,被誉为20世纪最为震撼、最具有表现力的建筑。
朗香教堂的白色幻象盘旋在欧圣母院朗香村之上,从13世纪以来,这里就是朝圣的地方。
教堂规模不大,仅能容纳200余人,教堂前有一可容万人的场地,供宗教节日时来此朝拜的教徒使用。
出生于瑞士的勒·柯布西耶是现代建筑里程碑式的人物,其设计作品显示了同时代的绘画与雕塑到建筑的概念转换,在其努力变革并逃离历史风格束缚的过程中,建筑和其他视觉艺术共享了进入抽象了理性主义,转到了浪漫主义和神秘主义。
【朗香教堂的布局、结构和体系】在朗香教堂的设计中,勒·柯布西耶把重点放在建筑造型上和建筑形体给人的感受上。
他摒弃了传统教堂的模式和现代建筑的一般手法,把它当作一件混凝土雕塑作品加以塑造。
教堂造型奇异,平面不规则;墙体几乎全是弯曲的,有的还倾斜;塔楼式的祁祷室的外形象座粮仓;沉重的屋顶向上翻卷着,它与墙体之间留有一条40厘米高的带形空隙;粗糙的白色墙面上开着大大小小的方形或矩形的窗洞,上面嵌着彩色玻璃;入口在卷曲墙面与塔楼的交接的夹缝处;室内主要空间也不规则,墙面呈弧线形,光线透过屋顶与墙面之间的缝隙和镶着彩色玻璃的大大小小的窗洞投射下来,使室内产生了一种特殊的气氛。
【朗香教堂的构思与设计过程】勒氏生前曾说了不少和写了不少关于朗香教堂的事情,都是很重要的材料,可是还不够。
应该承认,有时候创作者本人也不一定能把自己的创作过程讲得十分清楚。
柯布西耶的作品及特点

柯布西耶的作品及特点
柯布西耶(Paul Cézanne,1839-1906),是法国印象派的重要成员之一,他被誉为后印象派的先驱。
他早期的作品受到印象派的影响,
但他的独特的风格和方法使他成为一个独立的创造者。
柯布西耶一生
作品丰富,主要涉及静物、风景、人物等领域,他的作品风格独特,
被誉为“艺术史上的画笔之父”。
柯布西耶的作品主要特点体现在色彩和构图方面。
色彩方面,柯布西
耶喜欢用大面积的颜色来表现自己的主题,他强调色彩和形状的关系,认为色彩、形状和空间可以互相影响、互相制约。
他的作品呈现出明
快的色彩,用大面积的颜色区分不同的空间,营造出一种独特的艺术
氛围。
柯布西耶的构图特点则表现在他独特的“重心理论”中。
他认为画面
中应该有一个主要的重心,并使画面中的元素向这个重心聚拢,从而
营造出一种稳定、平衡的感觉。
柯布西耶还注重运用形体语言来表现
画面中的物体和空间,他利用各种形状、线条和笔触来烘托画面的氛
围和气氛。
除此之外,柯布西耶还喜欢捕捉自然的特点,并将其融入到自己的作
品中。
他在绘画中注重人的感官体验和直接感受,注重细节,尤其是
光线和色彩的变化,使得他的作品产生一种浓重的现实感。
综上所述,柯布西耶的作品具有独特的艺术风格和深刻的艺术内涵。
他对色彩和构图的处理以及对自然的表现手法,对后世的绘画艺术产生了深刻的影响。
柯布西耶所代表的“后印象派”思潮,也推动了二十世纪艺术的发展和变革。
从勒·柯布西耶的作品中精选出来的17处建筑

1. 勒·柯布西耶简介勒·柯布西耶(Le Corbusier),原名夏尔-埃德华-杰纳雷-居贝德- 西耶(Charles-Édouard Jeanneret-Gris),was born on October 6, 1887, in La Chaux-de-Fonds, Switzerland. He was a prominent Swiss-French architect, designer, and urban planner who is renowned for his contributions to modern architecture. Throughout his career, Le Corbusier revolutionized architectural design with his innovative concepts and functionalist approach.2. 勒·柯布西耶的作品风格As a pioneer of modernist architecture, Le Corbusier's works are characterized by their clean lines, geometric forms, and the use of materials such as concrete and glass. He believed in the marriage of architecture and technology, which he advocated through his famous dictum "A house is a machine for living in." His designs often integrated principles of functionality and efficiency, 本人ming to create spaces that were in harmony with the surrounding environment.3. 勒·柯布西耶作品中的17处建筑Among Le Corbusier's extensive body of work, there are 17 architectural masterpieces that stand out for their significance and influence on the development of modern architecture.These iconic structures showcase his unique vision and lasting impact on the built environment.4. Villa Savoye, Poissy, FranceCompleted in 1931, Villa Savoye is considered one of the most important works of modern architecture. It is a prime example of Le Corbusier's "Five Points of Architecture," which include pilotis (supports), flat roof terrace, open floor plan, horizontal windows, and free facade. The villa's design emphasizes functionality and simplicity, with an emphasis on the integration of interior and exterior spaces.5. Notre Dame du Haut, Ronchamp, FranceDesigned and constructed between 1950 and 1955, Notre Dame du Haut is a modernist pilgrimage chapel that has be a major work of religious architecture. Its sculptural form and innovative use of light and space make it apelling example of Le Corbusier's experimentation with new architectural forms.6. Unité d'Habitation, Marseille, FranceCompleted in 1952, the Unité d'Habitation is a pioneering residential housing project that embodies Le Corbusier's vision of urban living. It features a modular design that allows forflexible floor plans andmunal amenities, showcasing hismitment to improving the quality of urban life.7. Chandigarh, IndiaLe Corbusier was instrumental in the planning and design of Chandigarh, a new city in India that serves as the capital of the states of Punjab and Haryana. His urban master plan for Chandigarh, executed in the 1950s, emphasized the segregation of traffic, the provision of open green spaces, and the rational organization of public buildings.8. Villa La Roche, Paris, FranceBuilt between 1923 and 1925, Villa La Roche is a prime example of Le Corbusier's early experimentation with modernist principles. It is an architectural manifesto that showcases his use of bold geometric forms and innovative spatial configurations, setting the stage for his later groundbreaking designs.9. Cité Radieuse, Marseille, FranceThe Cité Radieuse, also known as La M本人son du Fada, waspleted in 1952 as a revolutionary housingplex that reimagined the concept of urban living. It features modular apartments,munal facilities, and a rooftop garden, all integratedinto a bold, sculptural form that reflects Le Corbusier's vision of a "vertical garden city."10. Villa Stein, Garches, FranceDesigned and constructed between 1927 and 1928, Villa Stein is a modernist residence that exemplifies Le Corbusier's principles of "Purism" and "The Five Points of Architecture." Its sleek, white facade and open plan layout demonstrate hismitment to functional simplicity and spatial efficiency.11. Ronchamp City, FranceIn addition to the Notre Dame du Haut chapel, Le Corbusier's involvement in the planning of Ronchamp extended to the design of the surrounding city, including residential buildings, public facilities, and landscaping elements. His holistic approach 本人med to create an integratedmunity that embodied his ideals of modern urbanism.12. Villa Jeanneret-Perret, La Chaux-de-Fonds, SwitzerlandAs one of Le Corbusier's early works, the Villa Jeanneret-Perret holds special significance as a testament to his formative years as an architect. Completed in 1912, it features elements of Art Nouveau and showcases his evolving design sensibilities beforethe emergence of his modernist style.13. High Court of Chandigarh, IndiaLe Corbusier's design for the High Court of Chandigarh,pletedin 1956, is a striking example of his architectural vision for the new Indian city. The building's sculptural form, iconic brise soleil, and functional layout reflect hismitment to creating monumental structures that respond to their cultural and environmental context.14. Palace of Assembly, Chandigarh, IndiaAs part of hisprehensive plan for Chandigarh, Le Corbusier designed the Palace of Assembly, also known as the Legislative Assembly Building, to serve as the seat of government for the new city. Completed in 1961, the building's monumental scale, symbolic significance, and rational design principles reflect his enduring legacy in urban planning.15. Cabanon de vacances, Roquebrune-Cap-Martin, FranceThe Cabanon de vacances, a small vacation cabin designed by Le Corbusier for himself, exemplifies his ability to create innovative architectural solutions within a modest footprint. Completed in 1952, the cabin's efficient use of space,minimalistic design, and integration with nature reflect his principles of practical, sust本人nable living.16. The Carpenter Center for the Visual Arts, Cambridge, Massachusetts, USALe Corbusier's only building in North America, the Carpenter Center for the Visual Arts at Harvard University, waspleted in 1963. Its bold, sculptural form and use of concrete as a primary material demonstrate his ongoingmitment to pushing the boundaries of architectural expression and spatial experience.17. Firminy-Vert, FranceFirminy-Vert stands as a testament to Le Corbusier's enduring influence on urban planning and architecture. The project, which includes a stadium, cultural center, and residential buildings, was executed based on his original design principles after his death, highlighting the lasting impact of his visionary ideas.18. 总结In conclusion, Le Corbusier's 17 selected architectural works represent a diverse and influential body of work that continuesto inspire architects and urban planners around the world. Hismitment to functionalism, modernity, and the integration of art and architecture has left an indelible mark on the built environment, shaping the way we think about space, form, and the relationship between people and their surroundings. Through his visionary designs, Le Corbusier has left a lasting legacy that transcends time and continues to resonate with contemporary audiences.。
建筑设计理与创作.中南最牛老师课件

4.包豪斯认清了“技术知识”可以传授,而“创作能 力”只能启发的事实,为现代设计教育立下良好的规 范。
►
5.包豪斯发展了现代的设计风格,为现代设计指示出
包豪斯与现代艺术
人物: 1.建筑大师:格罗皮乌斯, 密斯,汉斯·迈耶
2.艺术家:康定斯基—— 抽象艺术 约翰·伊顿,保罗·克利—— 表现主义 纳吉——构成主义 凡·杜思堡——风格派
► 马赛公寓、昌迪加尔、圣迪埃工厂乃至朗香教堂的平面设计,模度系统都不同程 度发挥了其比例控制的效用。且在实际的Biblioteka 用中,这两套系统的数字是混合使用的。
图片链接
马赛公寓的思考: 1.居住理念:房间尺寸及家具组织结合人体尺度;
享受普照大地的阳光和广阔的天空是人与生俱来的 权利
2.技术实现:可装配式居住单元和混凝土预制构
►表皮技术——复合界面空间
推荐书目
►1.《现代建筑语言》(布鲁诺.赛维) ►2.《现代建筑--一部批判的历史》
(肯尼思.弗莱姆普敦)
►3. 《包豪斯 》(英)弗兰克·惠特福德 ► 4. 《建构文化研究》 (肯尼思.弗莱姆普敦) ► 5 .《现代建筑理论》 (刘先觉) ►6. 沃尔特·格罗皮乌斯(华中科技大学出版社)
建筑设计理论及创作
第一讲 课程框架
以设计大师及其作品为课程主线索
结合人物介绍各流派建筑思潮,通过作品了解 设计方法
以现代建筑四位大师为起点,以现代之后及当 代西方活跃的建筑师为重点内容
►介绍部分当今国内实验性先锋建筑师
第二讲 勒.柯布西耶与赖特 读经典是与伟人对话
►一.勒.柯布西耶
参考书目:
蓝尺-红尺
► 蓝尺: 以113X2=226的算法诞生了蓝尺的起点。再 从226X0.618出发开始向下推导出140,86,53,33。 这些数字可以形成一个递减的斐波那契数列
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柯布西耶—模度
☼ 1947 年,勒 · 柯布西耶将一项称为“模度” 的发明专利公之于众;1948年出版了讲述模 度的发现历程的专著《模度 1 》;他提出的 模度是“一个符合人体尺度的和谐的尺寸系 列,”是一种“普遍适用于建筑和机械”等 设计的“通用的尺寸系列”。柯布西耶对模 度是这样解释的:“模度(Modulor )是从 人体尺寸和数学中产生的一个度量工具。举 起手的人给出了占据空间的关键点:足、肚 脐、头,举起的手的指尖。它们之间的间隔 包含了被称为费波纳契的黄金比。另一方面, 数学上也给予它们最简单也是最有力的变化, 即单位、倍数、黄金比。” 柯布西耶把人体 尺度、数学、设计等方面有机地结合在一起 创造了模度、模度人及模度理论。
柯布西耶—模度
☼ 随着结合实践的深入思考,柯布和他的的工作室成员发现,基于相对 矮小的法国人人体尺度赋值的“模度”,不能适应高大人种的需要, 于是,根据一份英国的调查报告,柯布西耶将“模度”的“身高刻度” 定义为6 英尺(报告中英国人的完美高度),即 1.83 米,相应得到以 1.13 米为起始的“ 红尺 ”和以 2.26 为起始的“ 蓝尺 ”,并将蓝尺的 2.26米、1.4米、0.86米、和红尺的1.83米、1.13米、0.7米、0.43米和 0.27米八个刻度,分别赋以单手举高、胸高、垂手高、身高、脐高、 座椅扶手高、平坐高、低坐高的人体尺度意义。
刘沐奇 10076140015
柯布西耶—模度
☼ 模度
☼ 1947 年,勒 · 柯布西耶将一项称为“模度”的发明专利公之于众; 1948年出版了讲述模度的发现历程的专著《模度1》;他提出的模度 是“一个符合人体尺度的和谐的尺寸系列,”是一种“普遍适用于建 筑和机械”等设计的“通用的尺寸系列”。柯布西耶对模度是这样解 释的:“模度(Modulor )是从人体尺寸和数学中产生的一个度量工 具。举起手的人给出了占据空间的关键点:足、肚脐、头,举起的手 的指尖。它们之间的间隔包含了被称为费波纳契的黄金比。另一方面, 数学上也给予它们最简单也是最有力的变化,即单位、倍数、黄金 比。” 柯布西耶把人体尺度、数学、设计等方面有机地结合在一起创 造了模度、模度人及模度理论。
昌迪加尔
设计初期,他 感到困惑,说: “没有丝毫限制, 倒是件极麻烦的 事。”他所得意 的是在充满复杂 条件的世界上, 提出简明的回答, 并且在工作进程 中作出过细思考 的方法。说到底, 这不就是演绎的 手法么?可是在昌 迪加尔他实在难 以抓到头绪。
他的“模度”体 系是从人体尺度出 发从一个步行者的 世界出发的尺度理 论,现在面临着大 规模设计的挑战。 在此我们挑选几个 蓝色系列的数字来 看,跳出来的是 449,727, 1177m等几个数字, 将这些数字加上路 宽就可以得到 800m,1200m等 分划市区的模数了。
在马赛公寓的 2.26米(蓝尺) 高、3.66米(蓝 尺)宽的厨房里, 吊柜的高和宽都 是1.13米(红 尺);0.86米 (蓝尺)高的操 作台面,由三个 0.86米高、0.86 米宽的方形柜并 排拼成,1.13米 高的高橱柜宽度 也是0.86 米,总宽度是0.86×4=3.44米,虽然无法填满3.66米的宽度,但是, 这满足了标准化:制作整组橱柜只需要0.86米和1.13米两种长度的板 材。
柯布西耶模数系统在其设计中的应用
☼ 从模度系统诞生,特别是50年代后,柯布以其作为一种重要设计 工具,在其实践中加以应用,包括马赛公寓、昌迪加尔、圣迪埃工厂 乃至朗香教堂的平面设计,模度系统都不同程度发挥了其比例控制的 效用。
在设计马赛公寓的过程中,勒·柯布西耶运用 文 艺复兴时期达·芬奇的人文主义思想,演变 出一 套“模数”系列,这套“模数”以男子身 体的各部分 尺寸为基础形成一系列接近黄金分 割的定比数 列,他套用“模数”来确定建筑物 的所有尺寸。
☼ 模数是人类自古以来就建立起的建筑生产方法,其意义存在于两个方 面: ☼ 一是模数的技术作用,模数减少了构件种类,无论对工业化机器大 生产还是传统手工生产,都有简化制作的意义,从而有利于大批量生 产预制构件
☼
二是模数的美学作用,在西方古典建筑柱式中,模数以一个柱径为 基本度量单位,其余部分均参照这个基本单位按比例取值建造,从而 获得的柱式整体与细部的比例和谐。
柯布西耶—模度
☼ 在“红蓝尺”下,不但“举高”被纳入了“黄金分割”的“菲波纳济 等比数列”,在两套比例的相互交叠、相互加减下,划分也变得足够 精微。 ☼ 克服了诸多难关,随着1945年“红蓝尺”的问世,柯布西耶终于完成 了一套令他自己满意的度量体系,并于 1946 年将其命名为“模度” (Modulor)。
他首先在脑海 里画了个800m 的正方形。就像 东京银座的各商 业街,由八块街 区组成,每块 100m长。800m 看来是商业街以 及相似街道的最 大长度,多少可 以作为结论了。 有趣的是这个长 度大约相当于英 国和美国的半英里。800m的商业街在住宅区的环境里是适得其所的。
为了解决这个矛 盾,他把两块 400m的正方形的 一边相贴,这与他 早先在创造模度时 的实验是相同的, 他一定期待着会再 次出现奇迹。他把 这两个相贴的正方 形的共同边界,置 于原先想象的 800m正方形一边 的中间,其结果是 个美丽的设计。
柯布西耶—模度
比列网格
☼ 柯布用欧洲美学传统中最为常见的两种工具 ——“黄金分割”和“直 角规线”,创造了一套新的度量比例体系。图解创造的起始是一个正 方形,将其二等分成两个矩形后,以其中一个矩形的对角线长沿中线 与正方形一边交点做弧,交于该边延长线。被延长的边与原边长成 1 : 0.618的黄金比,这是黄金分割的几何图理,并非柯布西耶的创新。柯 布的工作是在以上图解的基础上引入了“直角规线”,即连接长边延 长端点与初始正方形中线另一端点成斜线,并以此斜线为一直角边作 垂线与该边垂直,垂线另一端与黄金分割长边延长线相交,得到新延 长线的长度恰好为初始正方形边长的两倍。
勒氏模度
☼
柯布在《模度》 里所说的:“对问题 根源的调整,将改变 一切,将开启思想的 大门,使想象自由流 淌。” 他正是要追寻 度量问题的根源,从 中寻求突破的可能。
勒氏模数
☼ “模数进行度 量和统一,基准 线进行建造并使 人满意……基准 线可以做出非常 美的东西,它们 是这些东西为什 么美的原因…… 基准线导致探索 精巧的比例和和 谐的比例,他给 作品以协调。”
“菲波纳济等比数列”和“红蓝尺”
☼ “比例网格”基本实现了数学原则与人体尺度的巧合,也能在决定物体尺度时提供足够 的“确定性”,然而,对四种尺度的简单定义,虽然粗略适应人的最基本活动,却不可 能成为一个足以取代强大的“英制”和“公制”体系的新度量标准。要实现这一理想, 必须发展出更为精微的“网格”。要使“网格”精微化,有理的增加分割点是最直接和 有效的办法——既然黄金分割能生成“比例网格”,它也当然能将网格中的比例进行再 分或放大。这样,在同一比例控制下,这套“网格”中的尺度就可以同时趋于无限小和 无限大。在黄金分割的算术表达中,1.618:1与1:0.618是等值的,于是当黄金分割中 的小项依黄金分割再分,自然形成了前两项加和等于第三项的算术“巧合”,这正好在 比例上形成了著名的“菲波纳济等比数列”:0,1,1,2,3,5,……(随项递增逐 渐趋于黄金比)数学的和谐使这种无限分割的方式更具说服力,但是在柯布看来,这样 划分的结果仍不够精微——越大数量级的尺度中就越缺少细致的划分,尤其是在0.68米 “膝高”到1.78 米“身高”之间的重要人体尺度区间,不再可能出现划分。另外,在 “比例网格”中,所有的黄金比都以初始正方形的边长作为“起始单元”,而被赋予重 要的“举高”意义的“二倍单元”出自“直角规线”的再加工,并不在“菲波纳济等比 数列”之中。柯布西耶的解决方式,是将代表“举高”的“二倍单元”作为起始尺度, 通过黄金分割,生成一套和上述网格相同比例关系但不同尺度的新网格,称为“蓝尺”, 而起始于“一倍单元”的“比例网格”称为“红尺”,这就是著名的“红蓝尺”(此时 的赋值以1.75米的法国人平均身高为起始尺寸)。
刘沐奇 10076140015
柯布西耶—模度
☼ 模度人
☼ 柯布西耶提出的“模度人”,是用来制定和绘制模度的一种标准人体 图形,具有理想化的和谐的比例关系。1946年,柯布西耶以法国人的 平均身高1.75米为基本单位画了一幅最初的模度与模度人图示,与最 后为大家所熟知的模度与模度人图示相比较可知,其中的尺寸略有不 同,由身高1.75米、举手高2.16、脐高1.08米调整为身高1.83米(6英 尺=1.829米≈1.83米)、举手高2.26米、脐高1.13米,分别增加了0.08、 0.10、0.05米,使尺寸系列在米制和英制的互换方面得到了改善。
“模度”并不 能生成设计,它 只是当设计师遇 到无法精确定义 度量的困境时, 为他们提供确定 度量数据的标准, 而一旦有更为明 确的标准存在, “模度”就会自 动让步。如果只 是专用于赋值 “模度” 工具的应用范围似乎显得过于狭窄,而正因为范围狭窄,它也就特别有 效——在柯布西耶视察马赛公寓施工现场的时候,临时决定在首层架空 的梁底加两个牛腿,以承放纪念建筑工人的雕塑。汽车在等待,这位伟 大的设计者从口袋中拿出红蓝尺,一分钟后,一切尺度细节都被确定下 来,汽车扬长而去……
柯布西耶—模度
☼ “模度”不但俱备“黄金分割”的完美比例和精确的度量数据,也同 时满足了对人体的适应性。这是柯布西耶对“模度”的最终“定稿”, 在此后以马赛公寓为代表的大量建筑实践中,这一版“模度”都成为 柯布西耶确定物体尺度的有效度量工具。
模度与美学传统
☼ 对于直接将“模度”视 作美学原则的观点,柯 布西耶本人是深恶痛绝 的。柯布还借助“模度” 的比例优势对文艺复兴 的几何不变性研究展开 了批判。他认为对正多 面体、星形体及正多边 形的研究,离的事物的认知并不是 均匀、等分的而是渐变 的。
☼ 这样,初始正方形以偏 心的位置嵌套于双正方 的矩形中,在长边产生 两条分割线,再加上双 正方矩形长边的中线, 便形成四种高度,在比 例上恰好分别对应膝高、 脐高、身高和举高。这 一图解被称作“比例网 格”(ProportionGrid), 是“模度”的雏形。
