Origin分段线性拟合
Origin如何进行单段和多段的线性拟合

Origin如何进行单段和多段的线性拟合在进行数据处理时,如果需要对绘制的散点图进行线性拟合,应该怎么操作呢?针对更为复杂的情况,按照不同需要进行分段线性拟合时,怎么样才能够实现多段拟合呢?一、单段线性拟合1、首先,把数据导入origin中;2、选中需要绘制的两列数据,点击屏幕左下角,绘制散点图;3、拟合散点图:依次点击Analysis (分析)→ Fitting(拟合)→Linear Fit (线性拟合),弹出Linear Fit对话框,对话框里面不作修改,采取默认点击OK(确定)即可。
4、弹出Reminder Message(提示信息)对话框,询问是否需要转出report sheet?选中Yes,点击 OK即可。
5、现在可以看到,表格里面给出了线性拟合方程的具体信息包括斜率和截距,图中给出了线性拟合曲线。
6、如果想要更为详细的拟合数据,可以在原数据表格中点击Fit Linear1寻找。
二、多段线性拟合1、首先,把数据导入origin中,绘制散点图;可以看到的是这个散点图需要分为两段进行线性拟合,那么怎么才能实现呢?2、工具栏中选中Data(数据),点击Mask Data Points(屏蔽数据点),鼠标如图所示发生变化,拖拽鼠标选中需要屏蔽的数据点,被选中的数据点将变为红色,说明已被屏蔽;3、接下来就是对未屏蔽的散点图进行拟合,重复“单段线性拟合”中步骤3-6继续操作;得到黑色散点的线性拟合曲线,那么怎么继续对剩余部分进行线性拟合呢?4、对屏蔽点进行拟合:选中任意屏蔽点,右键弹出工作框,点击Mark,选择Swap (系统将自动交换屏蔽点和未屏蔽点,颜色发生变化);5、接下来就是剩余散点进行拟合,重复“单段线性拟合”的步骤3-6继续操作;可以看到两段拟合的曲线和相关信息都在图中展现出来。
origin拟合函数

origin拟合函数Origin是一款功能强大的数据分析软件,它提供了丰富的数据分析工具来处理实验数据,其中包括曲线拟合功能。
本文将着重介绍Origin中的曲线拟合功能,包括常见的拟合函数及其应用。
一、拟合函数在Origin中,可以通过选择不同的拟合函数来拟合所需的曲线。
常见的拟合函数有线性函数、二次函数、三次函数、指数函数、对数函数、幂函数、指数增长函数、正弦函数、余弦函数等。
下面将对这些函数进行详细介绍。
1. 线性函数一元线性函数的表达式为y=a+bx,其中a和b分别为截距和斜率,x为自变量,y为因变量。
线性函数是最简单的拟合函数之一,适用于线性关系较为明显的数据。
例如,当我们在光电效应实验中测量出光电子的动能和光子的频率时,它们之间就存在着线性关系,此时可以使用线性函数来拟合数据。
2. 二次函数三次函数的表达式为y=a+bx+cx^2+dx^3,其中a、b、c和d分别为常数,x为自变量,y为因变量。
三次函数通常用于描述抛物线,这种函数在物理和工程学中经常被应用。
例如,在材料科学中可以使用三次函数来描述一个材料的弹性行为。
4. 指数函数指数函数的表达式为y=ae^(bx),其中a和b为常数,x为自变量,y为因变量。
指数函数适用于描述随时间或位置而变化的某些现象。
例如,当我们观察放射性衰变时,衰变速率随时间的变化可以使用指数函数来拟合。
8. 正弦函数正弦函数的表达式为y=a sin(bx+c),其中a、b和c为常数,x为自变量,y为因变量。
正弦函数适用于描述像周期性的变化,例如,天文学中的多个现象,如日、月、星星的运动都是可以用正弦函数表示的。
二、常见应用在实际应用中,我们可以使用Origin中的曲线拟合功能来解决各种问题。
下面列举几种常见的应用。
1. 数据分析在实验数据分析中,使用拟合函数可以帮助我们理解和预测实验数据的变化趋势。
例如,在物理实验中,我们可以使用线性函数来分析位移和时间的关系,使用指数函数来分析辐射物质的衰变过程。
Origin 常用小技巧1 分段线性拟合
Origin 常用小技巧 1 分段线性拟合
By D. J. Liu
6 点上图中 From 和 To 后面的框中输入第二部确定的拟合范围,点击 OK,出现如下结果。
4
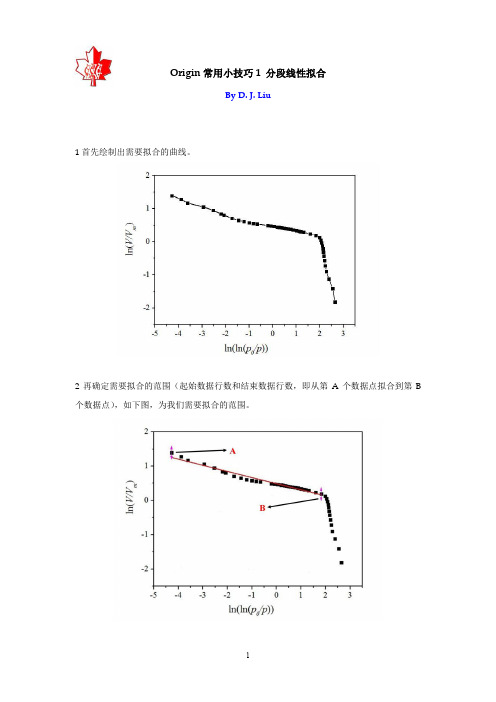
1 首先绘制出需要拟合的曲线。
2 再确定需要拟合的范围(起始数据行数和结束数据行数,即从第 A 个数据点拟合到第 B 个数据点) ,如下图,为我们需要拟合的范围。
1
3 Analysis → Fitting → Fitting Linear → Open Dialog
4 打开对话框后,如下图。
2
5 点击上图中红框的加号,展开对话框。
origin 分段函数拟合

origin 分段函数拟合
分段函数拟合是一种常用的数学方法,用于逼近复杂函数。
它将整个定义域分成多个段落,每个段落内使用简单的函数进行拟合。
这样做的目的是用一组简单的函数来近似整个函数的行为,从而简化计算和分析过程。
在分段函数拟合中,我们首先确定分段点,即将整个定义域划分为不同的段落。
然后,针对每个段落,选择一种适当的函数类型进行拟合。
常用的函数类型包括线性函数、二次函数、指数函数和对数函数等等。
在每个段落内,我们通过调整函数的参数,使得拟合函数与实际函数的取值尽可能接近。
这可以通过最小二乘法等统计方法来实现。
通过不断优化参数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数。
分段函数拟合可以应用于多个领域,如物理学、经济学和工程学等。
它可以用于描述非线性关系、曲线拟合和数据分析等问题。
通过将问题分解为多个简单的段落,分段函数拟合可以简化复杂问题的处理,并提高计算效率。
总的来说,分段函数拟合是一种有效的数学方法,可以将复杂函数近似为一组简单的函数。
通过合理选择分段点和拟合函数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数,从而简化计算和分析过程。
origin分段函数拟合

origin分段函数拟合
拟合的函数形式为:
\[ f(x) =
\begin{cases}
a_1x + b_1 & \text{if } x < x_1 \\
a_2x + b_2 & \text{if } x_1 \leq x < x_2 \\
\vdots \\
a_{n-1}x + b_{n-1} & \text{if } x_{n-2} \leq x < x_{n-1} \\ a_nx + b_n & \text{if } x \geq x_{n-1} \\
\end{cases}
\]
其中,$a_i$和$b_i$为拟合参数,$x_i$为分段点。
拟合的过程可以分为以下几步:
1. 确定分段点$x_i$的个数和位置。
可以根据数据的分布情况和特点来选择合适的分段点。
2. 对每个区间$(x_{i-1}, x_i)$内的数据进行线性拟合,得到参数$a_i$和$b_i$。
3. 将每个区间的拟合结果拼接起来,得到最终的拟合函数。
具体的拟合算法可以使用最小二乘法来求解,最小化真实数据与拟合函数之间的误差。
可以使用数值优化算法,如梯度下降法或牛顿法来求解最优的参数值。
需要注意的是,拟合的结果可能会受到分段点的选择和初始参数值的影响,因此需要进行多次尝试和调整,以找到最优的拟合结果。
origin拟合曲线选取点

在Origin中拟合曲线时,选取合适的数据点非常重要。
以下是几个建议:
1. 代表性:选择具有代表性的数据点进行拟合。
这些点应该能够反映数据整体的变化规律。
2. 分布均匀:尽量选择分布均匀的数据点,避免在某些区域选择过多的点,而其他区域选择过少的点。
3. 考虑噪声和异常值:在选择数据点时,应考虑噪声和异常值的影响。
对于噪声,可以选择滤波或平滑处理来减少其影响。
对于异常值,可以将其去除或进行特殊处理。
4. 交互式拟合:可以在Origin中采用交互式拟合方式,即手动选择需要拟合的数据点,然后进行拟合。
这样可以更灵活地选择数据点,并获得更好的拟合效果。
5. 分段拟合:对于具有不同变化趋势的数据,可以考虑采用分段拟合方法。
这样可以更好地适应数据的局部变化规律,提高拟合精度。
6. 非线性拟合:如果数据呈现出非线性变化趋势,可以选择合适的非线性拟合函数进行拟合。
在Origin中,可以通过Analysis > Fitting > Nonlinear Curve Fit菜单进行非线性拟合。
7. 拟合曲线类型:根据数据的特征和变化规律,选择合适的拟合曲线类型。
例如,线性拟合、多项式拟合、指数拟合、对数拟合等。
总之,在Origin中拟合曲线时,需要仔细考虑数据点的选择,并根
据实际情况灵活调整拟合策略,以获得最佳的拟合效果。
Origin的使用方法汇总

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
R2
n i 1 n i 1
ˆ Y Y i
i
2
Y Y
2
2
1
n i 1 n i 1
ˆ Yi Y i
i
2
Y Y
2
1
2 e i i 1
n
Y Y
i 1 i
n
2
0 R 1
一般情况下,R2的值越大,拟合得越好。
直线拟合的相关系数
平均人口数 (百万人) 48.2 48.9 49.54 50.25 51.02 51.84 52.76 56.39 54.55 55.35 56.16 56.98
若1990年该省国民收入使用额为67十亿元,平均 人口为58百万人,试估计1990年消费基金
二、非线性模型
有n组观测数据: , n 拟合 设因变量Y 和自变量X 满足: Y f X ,
在Result Log中只显示简单的拟合结果,包括截距、斜率、 标准误差、相关系数、编制偏差、拟合图形的点数和P值
在Results Log中显示所有的拟合结果,除了上面介绍的 以外,还显示t-检验值和ANOVA(方差分析)列表
选中,则进行y=Bx回归分析,不选, 则执行标准线性回归分析 选中,则按指定的斜率值进行拟合,不选, 则执行标准线性回归分析 选中,使用误差值作为权重(如果激活的是 Worksheet,必须选中一列Y误差列,如果激 活的是Graph,图中必须有误差线) 只对拟合过程中的误差参数有影响 绘制数据上、下可信范围 绘制数据上、下预期范围 执行拟合 根据拟合公式计算的X值(已知Y值) 根据拟合公式计算的Y值(已知X值)
Origin线性拟合方法

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
最后得到的拟合曲线上点的个数
表示Graph窗口中拟合直线在两端多于曲线 X值范围的百分比
可信度,设置可信范围、预期范围
n Yi Yˆi 2
n
ei2
R2
i 1 n
2
1
i 1 n
1
2
n
i 1
2
Yi Y
Yi Y
Yi Y
i 1
i 1
i 1
0 R 2 1 一般情况下,R2的值越大,拟合得越好。
直线拟合的相关系数
r R2 1 r r
r 与斜率 b1 取相同的符号
r = 1: 完全正相关 r = -1: 完全负相关 r = 0: 无线性关系
分别就k 3和k 4两种情况,
1.9
3.5
2.2
4 在Origin中对表中的数据进行拟合,
2.3
7
2.5 2.6
7.5 9.9
求出b0 ,b1,b2 , , bk。
2.9
10.9
3.1
11.9
3.4
13.5
3.8
13
4.1
11.9
4.4
9
4.7
6.5
4.8
4
4.9
1.5
5
0
5.1
-2.5
5.3
-5
Origin:线性拟合
• 1. 线性回归(basic linear regression ) • 2. 多项式回归(polynomial regression) • 3. 多重回归(multiple linear regression)
Pl Origin 线性拟合

PL教程之Origin 拟合
一、 Origin数据线性拟合的方法
1.根据数据作散点图(plot-symbol-scatter)
2.点击散点图中的任意一个点,然后进入Analysis菜单,点击“Fit Linear-
Open Dialog”
3.设置拟合参数(如无需特殊要求,可以不作任何改变,系统自己会生产参数),
然后点击“OK”。
注意:Input Dat:拟合数据范围
Fit Option:拟合选项(包括是否给出固定的截距或者斜率等)
4.系统会自动给出结果,红色的线即为拟合得到的曲线,并提供了一张数据表。
Equation : 拟合方程
Adjusted R-squared: 调整后的离差平方和 Intercept: 截距
Slope: 斜率
Standard Error: 标准偏差
所以此数据拟合得到的拟合方程为所以此数据拟合得到的拟合方程为:: Y = -0.5536X + 6.2520
5. 拟合的详细情况, 可以通过双击工作表查看。
Origin8.5拟合两条直线

Origin8.5拟合两条直线
Origin 8.5拟合两条直线
1.将数据输入或复制到表格,选择全部数据,点击左下角三点标志,会出现一个散点图。
2.在表格中选择一条直线的几个点,点击Analysis,选择Fitting,点击Linear Fit,选择Open Dialog,点击OK。
3.回到表格,选择另一条直线的几个点,同2操作。
4.双击表格下面的散点图,右击左上角的1,选择Layer Contents,将左边的两个线性添加到右边,点击OK,这时会出现两条线性。
5.右击线性,选择Plot Details,修改Size,点击OK。
6.左击像锁一样的东西,选择Change Parameters,找到Fitted Curves Plot,找到Range,选择Custom,去掉Auto的勾,可以设置X的延伸范围。
利用Origin进行线性拟合

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
线性模型
线性模型,例如: y a bx y a bx cx
2 2
y a bx c sin x y a b1 x1 b2 x2
Origin 中的 Linear Model
basic linear regression model(线性回归)
where β0, β1 are coefficients and ε is the random error
根据样本数据 对β0和β1 进行估计
β0和β1的估计
值为b0和b1 建立一元线性回归方程
ˆ Y b0 b1 X
一般而言,所求的b0和b1应能使每个 样本观测点(Xi,Yi)与回归直线之间的偏 差尽可能小。
一元线性回归方程
Y与X之间 为线性关系
最小 二乘法
选出一条最能反 映Y与X之间关系 规律的直线
在Results Log中显示所有的拟合结果,除了上面介绍的 以外,还显示t-检验值和ANOVA(方差分析)列表
选中,则进行y=Bx回归分析,不选, 则执行标准线性回归分析 选中,则按指定的斜率值进行拟合,不选, 则执行标准线性回归分析 选中,使用误差值作为权重(如果激活的是 Worksheet,必须选中一列Y误差列,如果激 活的是Graph,图中必须有误差线) 只对拟合过程中的误差参数有影响 绘制数据上、下可信范围 绘制数据上、下预期范围 执行拟合 根据拟合公式计算的X值(已知Y值) 根据拟合公式计算的Y值(已知X值)
Origin拟合操作

a) 图 9 非线性拟合 Code 项 a) Function b) Parameter Init
-5-
b)
在 Parameters 页和 Bounds 页中可以对参数作系统的全面地修改和约束, 如图 10~11 所示。
图 10 非线性拟合 Parameters 项
图 11 非线性拟合 Bounds 项
-7-
a)
b)
图 8-
二、 多项式拟合
与线性拟合相比,多项式拟合仅多了一项功能,即选择拟合多项式的次数。如图 3 所示 的“Polynomial Order”选项。
三、 拟合报表
拟合报表是拟合操作完成后,Origin 会默认给出两个表单。可以根据需要在图 1 所示的 扩展选项中勾选相关功能,一般情况下,不需要输出报表的所有拟合相关结果,这样只会增 加寻找目标参数的时间。拟合报表是 Origin 拟合操作中的核心功能。我们不仅可以从中读取 到拟合曲线(曲面)的具体信息,还可以从概率论与数理统计的基础上获得大量拟合结果参 数,用于对各类模型或者试验离散点的拟合效果的对比。 图 4 和图 5 分别是拟合报表 1 和 2。表单名称为“Fit Linear 1”和“Fit Linear Curves 1” 。
a) 图 8 非线性拟合 Setting 项 a) Data Selection b) Function Selection
b)
“Code” , “Parameters”和“bounds”三页都是对已选拟合函数类型具体表达式和参数的 查看与修改。如图 9 所示,函数项(Function)在这里是不可编译的。而参数赋值和参数约束 项可以修改,注意使用 C 语言的格式。
一、 线性拟合
线性拟合(Linear Fitting)是最简单的一种拟合方式。线性回归拟合将选中的数据点拟合 为直线,选择 Analysis-Fit linear,那么 Origin 将曲线拟合为直线,以 X 为自变量,Y 为因变 量,回归拟合的函数形式为: y Ax b ,其中 A,b 为参数,由最小二乘法确定。对话框如 下图 1。
origin数据拟合成曲线

origin数据拟合成曲线
Origin数据拟合成曲线的步骤如下:
1. 打开Origin软件,导入数据。
在菜单栏上选择“File”->“Import Data”->“From File”,然后选择数据文件导入。
2. 将数据添加到表格中。
在菜单栏上选择“File”->“New”->“Worksheet”,将数据添加到新的工作表中。
3. 选择数据列,然后在工具栏上选择“Plot”->“Line”,将数据绘制成散点图。
4. 在散点图上右键单击,选择“Add Trendline”->“Linear”,添加线性拟合线。
5. 在弹出的“Linear Fit”对话框中,设置拟合参数,如截距、斜率等,然后点击“OK”。
6. 拟合线将自动添加到散点图中,可以根据需要调整线条样式和颜色等属性。
需要注意的是,Origin提供了多种拟合函数和参数估计方法,可以根据实际需要选择适合的拟合函数和方法。
同时,在拟合过程中需要注意数据的异常值和缺失值等可能影响拟合结果的因素。
1origin讲解(原创!线性拟合)

制冷与低温
行的插入和删除
插入行
select Edit: Insert right-click and select Insert
删除行
Edit: Delete right-click and select Delete.
制冷与低温
直线拟合讲解(实例)
实例:自变量:风速、进风温度。 因变量:换热系数
制冷与低温
列的插入、 列的插入、删除和重排
1、增加列 1) Column: Add New Columns. 2) Add New Columns button Right3) Right-click , Select Add New Column 2、插入列 1) Edit: Insert 2) Right-click → select Insert Right3、删除列 1) Edit: Delete Right2) Right-click → select Delete (保留列 保留列) 3) Edit: Clear (保留列) 4、移动列 1) Column: Move to First. 2) Column: Move to Last.
最后生成自己需要的坐标图
直接在origin中 生成的图形复 制到visio里面, 即使不经过任 何处理得到的 效果都比从 origin中直接复 制得到的好。
制冷与低温
THE END
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

12.50
1.365
12.75
1.463
13.00
1.548
13.25
1.682
13.50
1.767
13.75
1.836
14.00
1.918
测定 次序
27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
苯甲酸
t /min
T /℃
14.25
2.036
图 1 体系吸热的雷诺温度校正图 Fig.1 Renolds temperature emendatory figure of
system heat- absorption
图 2 体系散热的雷诺温度校正图 Fig.2 Renolds temperature emendatory figure of
system heat- disperse
25.00
2.069
26.00
2.056
萘
t/min
T /℃
14.25
1.978
14.75
2.076
15.00
2.124
15.25
2.151
15.50
2.174
15.75
2.196
16.00
2.209
16.25
2.226
16.50
2.236
16.75
2.258
17.00
2.268
17.25
2.274
&$0.111+0.008 73t,
t∈[1,10],R=0.996 95;
$
$
$
T2=
$$ # $ $
1+exp[-
Origin的使用方法汇总

统计关系
即当X值确定后,Y值不是唯一确定的, 但大量统计资料表明,这些变量之间还 是存在着某种客观的联系。
回归分析(Regression Analysis)
• 应用统计方法,对大量的观测数据进行整 理、分析和研究,从而得出反映事物内部 规律性的一些结论。 • 描述不同变量之间的关系,找出相应函数 的系数,建立经验公式或数学模型。 • 只有一个或二个自变量时,回归分析的目 的就是找到符合数据的曲线或曲面,所以 回归分析也经常被称为 “curve fitting” 或 “surface fitting
最后得到的拟合曲线上点的个数 表示Graph窗口中拟合直线在两端多于曲线 X值范围的百分比 可信度,设置可信范围、预期范围 根据现有的坐标刻度进行拟合 在整个X轴坐标范围绘制拟合曲线,此时上面 设置的Range值无效 在相应的Worksheet窗口中生成两列: Fit(Y)列(拟合数据) Residual(Y)列(剩余误差) 拟合图层中的所有曲线 在Result Log中只显示简单的拟合结果 在Results Log中显示所有的拟合结果
y 0 -2.5 -4 -5.7 -3.5 -2 -1 2 3.5 4 7 7.5 9.9 10.9 11.9 13.5 13 11.9 9 6.5 4 1.5 0 -2.5 -5
某同学实验测得数据如左表所示, 设y和x之间满足: y b0 b1 x b2 x
2
bk x 。
k
分别就k 3和k 4两种情况, 在Origin中对表中的数据进行拟合, 求出b0 , b1 , b2 , , bk。
直线拟合上机练习2
2、Polynomial Fit 模型
yi 0 1 xi x
2 2 i
origin 对数坐标分峰拟合

origin 对数坐标分峰拟合在数据分析的过程中,经常会遇到对数坐标下数据进行拟合的情况。
而当数据中存在多个峰值时,我们需要进行分峰拟合,以准确地描述每个峰的特征。
本文将介绍一种常用的方法——origin对数坐标分峰拟合方法,帮助读者更好地理解和应用该方法。
首先,我们先简要介绍一下对数坐标。
对数坐标是以对数作为坐标轴单位的坐标系,它可以有效地展示数据在不同量级下的变化情况,尤其适用于展示极大或极小的数据。
在对数坐标下,数据的大小由其对应的指数值表示,而非传统线性坐标系下的实际数值。
因此,在进行数据拟合时,我们需要特别注意坐标系的选择和相关的数据变化。
那么,对数坐标分峰拟合的方法是如何实现的呢?我们可以使用Origin软件中的分峰拟合工具来完成这一任务。
首先,我们需要将数据导入到Origin软件中,并切换到对数坐标模式。
接下来,选择分峰拟合工具,并按照下面的步骤进行操作:1. 首先,选择适当的拟合函数。
根据数据的特点和需求,选择合适的函数来拟合数据。
常见的拟合函数包括高斯函数、洛伦兹函数等。
根据数据的分布情况,选择具有合适峰形的函数进行拟合。
2. 其次,设置拟合区域。
在分峰拟合中,我们通常关注特定的峰值,而对于其他部分的数据不感兴趣。
因此,我们需要设置拟合区域,将拟合的范围限定在我们关注的峰附近。
3. 然后,进行初始化参数设置。
根据我们对数据的初步了解,我们可以根据经验设定一些初始参数,以帮助拟合算法更好地收敛。
这包括峰的位置、宽度和幅度等参数。
4. 接下来,进行拟合计算。
在设置好参数后,我们可以开始进行拟合计算。
Origin软件会自动应用拟合算法,并给出拟合曲线和相关参数的结果。
5. 最后,进行结果分析和评估。
通过对拟合结果的分析和评估,我们可以判断拟合的质量和适用性。
特别是在分析多峰数据时,我们需要对每个峰的拟合结果进行评估,并进行比较和进一步的分析。
通过以上步骤,我们可以完成对数坐标下的分峰拟合。
Origin实用教程7.5版__线性拟合篇
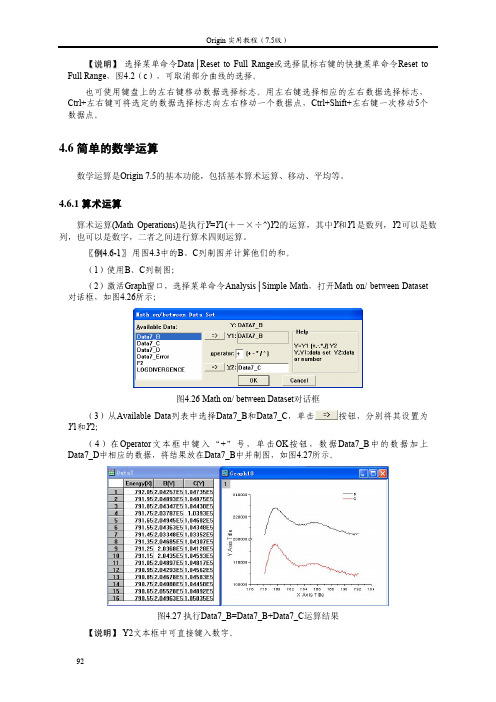
92【说明】 选择菜单命令Data │Reset to Full Range 或选择鼠标右键的快捷菜单命令Reset to Full Range ,图4.2(c ),可取消部分曲线的选择。
也可使用键盘上的左右键移动数据选择标志。
用左右键选择相应的左右数据选择标志,Ctrl+左右键可将选定的数据选择标志向左右移动一个数据点,Ctrl+Shift+左右键一次移动5个数据点。
4.6 简单的数学运算数学运算是Origin 7.5的基本功能,包括基本算术运算、移动、平均等。
4.6.1 算术运算算术运算(Math Operations)是执行Y =Y 1(+-×÷^)Y 2的运算,其中Y 和Y 1是数列,Y 2可以是数列,也可以是数字,二者之间进行算术四则运算。
〖例4.6-1〗 用图4.3中的B 、C 列制图并计算他们的和。
(1)使用B 、C 列制图;(2)激活Graph 窗口,选择菜单命令Analysis │Simple Math ,打开Math on/ between Dataset 对话框,如图4.26所示;图4.26 Math on/ between Dataset 对话框(3)从Available Data 列表中选择Data7_B 和Data7_C ,单击按钮,分别将其设置为Y 1和Y 2; (4)在Operator 文本框中键入“+”号,单击OK 按钮,数据Data7_B 中的数据加上Data7_D中相应的数据,将结果放在Data7_B 中并制图,如图4.27所示。
图4.27 执行Data7_B=Data7_B+Data7_C 运算结果【说明】 Y2文本框中可直接键入数字。
如果Y2和Y1对应的X点不相同的话,采用内插法或外插法来确定Y2值。
选择菜单命令Analysis│Subtract│Reference Data,也会打开同样的对话框,在Operator文本框中直接显示减号,这样就可以减去参考列了。
