人教版八年级下数学一次函数压轴题研究(二)一次函数与几何综合

合集下载

八年级下册----一次函数压轴题解析

八年级下册----一次函数压轴题一．选择题〔共17小题〕1．〔2021•平塘县二模〕如图，是一个下底小而上口大的圆台形容器，将水以恒速〔即单位时间内注入水的体积一样〕注入，设注水时间为t，容器内对应的水高度为h，那么h与t 的函数图象只可能是〔〕A．B．C．D．2．〔2021•XX〕如图，在Rt△ABC中，∠C=90°，AC=1cm，BC=2cm，点P从点A出发，以1cm/s的速度沿折线AC→CB→BA运动，最终回到点A，设点P的运动时间为x〔s〕，线段AP的长度为y〔cm〕，那么能够反映y与x之间函数关系的图象大致是〔〕A．B．C．D．3．〔2021秋•XX期末〕如下图．直线y=x+2与y轴相交于点A，OB1=OA，以OB1为底边作等腰三角形A1OB1，顶点A1在直线y=x+2上，△A1OB1记作第一个等腰三角形；然后过B1作平行于OA1的直线B1A2与直线y=x+2相交于点A2，再以B1A2为腰作等腰三角形A2B1B2，记作第二个等腰三角形；同样过B2作平行于OA1的直线B2A3与直钱y=x+2相交于点A3，再以B2A3为腰作等腰三角形A3B2B3，记作第三个等腰三角形；依此类推，那么等腰三角形A10B9B10的面积为〔〕A．3•48B．3•49C．3•410D．3•4114．〔2021春•海曙区校级期中〕如图，直线y=﹣x+3与x轴，y轴交于A，B两点．点P是线段OB上的一动点〔能与点O，B重合〕，假设能在斜边AB上找到一点C，使∠OCP=90°．设点P的坐标为〔m，0〕，那么m的取值X围是〔〕D．0≤m≤3A．3≤m≤4 B．2≤m≤4 C．0≤m≤5．〔2021•〕如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=2．设弦AP的长为x，△APO的面积为y，那么以下图象中，能表示y与x的函数关系的图象大致是〔〕A．B．C．D．6．〔2021•大城县校级模拟〕如图，M是边长为4的正方形AD边的中点，动点P自A点起，由A⇒B⇒C⇒D匀速运动，直线MP扫过正方形所形成面积为y，点P运动的路程为x，那么表示y与x的函数关系的图象为〔〕A．B．C．D．7．〔2021•XX模拟〕如图，直线l是菱形ABCD和矩形EFGH的对称轴，C点在EF边上，假设菱形ABCD沿直线l从左向右匀速运动，运动到C在GH边上为止，在整个运动的过程中，菱形与矩形重叠局部的面积〔S〕与运动的路程〔x〕之间的函数关系的图象大致是〔〕A．B．C．D．8．〔2021•温岭市校级三模〕如图，在直角坐标系中，等腰直角△ABO的O点是坐标原点，A的坐标是〔﹣4，0〕，直角顶点B在第二象限，等腰直角△BCD的C点在y轴上移动，我们发现直角顶点D点随之在一条直线上移动，这条直线的解析式是〔〕C．y=﹣3x﹣2 D．y=﹣x+2A．y=﹣2x+1 B．y=﹣x+29．〔2021•延庆县一模〕如图：P是线段AB上的动点〔P不与A，B重合〕，分别以AP、PB 为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；点C、D 在线段AB上且AC=BD，当点P从点C运动到点D时，设点G到直线AB的距离为y，那么能表示y与P点移动的时间x之间函数关系的大致图象是〔〕A．B．C．D．10．〔2021•XX二模〕某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开场调出物资〔调进物资与调出物资的速度均保持不变〕．储运部库存物资w〔吨〕与时间t〔小时〕之间的函数关系如下图，这批物资从开场调进到全部调出需要的时间是〔〕A．4.5小时B．4.75小时C．5小时D．5小时11．〔2021•房山区一模〕如图，P是边长为1的正方形ABCD对角线AC上一动点〔P与A、C不重合〕，点E在射线BC上，且PE=PB．设AP=x，△PBE的面积为y．那么能够正确反映y与x之间的函数关系的图象是〔〕A．B．C．D．12．〔2021•XX模拟〕四条直线y=kx﹣3，y=﹣1，y=3和x=1所围成的四边形的面积是12，那么k的值为〔〕A．1或2 B．1或﹣2 C．﹣1或2 D．﹣1或﹣213．〔2021•东城区一模〕如图，在矩形ABCD中，AB=5，BC=4，E、F分别是AB、AD的中点．动点R从点B出发，沿B→C→D→F方向运动至点F处停顿．设点R运动的路程为x，△EFR的面积为y，当y取到最大值时，点R应运动到〔〕A．B C的中点处B．C点处C．C D的中点处D．D点处14．〔2021•XX模拟〕某人匀速上坡一段时间后，由于有急事，又以更快的速度匀速地沿原路返回；这一情境中，速度V与时间t的关系，用图象可大致表示为〔〕A．B．C．D．15．〔2021•江干区模拟〕如图，直线l1：y=x+1与直线l2：相交于点P〔﹣1，0〕．直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，B n，A n，…那么当动点C到达A n处时，运动的总路径的长为〔〕A．n2B．2n﹣1 C．2n﹣1+1 D．2n+1﹣216．〔2021•东阳市〕汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，假设把这一过程中汽车的行驶路程s看作时间t的函数，其图象可能是〔〕A．B．C．D．17．〔2021•新城区校级模拟〕甲、乙两人分别从相距25千米的A、B两地同时相向而行．甲步行，每小时行5千米，乙骑自行车，每小时行15千米，乙到达A地后立即原路返回，追上甲为止，他们所行时间x〔小时〕，与离A地的距离y〔千米〕的函数图象大致是〔〕A ．B．C．D．二．选择题〔共5小题〕18．〔2007•随州〕在四边形ABCD中，AB边的长为4，设动点P沿折线B⇒C⇒D⇒A由点B向点A运动，设点P运动的距离为x，△PAB的面积为y，y与x的函数图象如下图．给出以下四个结论：①四边形ABCD的周长为14；②四边形ABCD是等腰梯形；③四边形ABCD是矩形；④当△PAB面积为4时，点P移动的距离是2．你认为其中正确的结论是．〔只填所有正确结论的序号例如①〕19．〔2007•XX〕一个水池有2个速度一样的进水口，1个出水口，单开一个进水口每小时可进水10立方米，单开一个出水口每小时可出水20立方米．某天0点到6点，该水池的蓄水量与时间的函数关系如下图〔至少翻开一个进水口〕．给出以下三个论断：〔1〕0点到3点只进水不出水；〔2〕3点到4点不进水只出水，〔3〕4点到6点不进水也不出水．那么错误的论断是．〔填序号〕20．〔2007•XX〕函数y=，那么x的取值X围是；假设x是整数，那么此函数的最小值是．21．〔2021•昌平区二模〕当光线射到x轴的点C后进展反射，如果反射的路径经过点A〔0，1〕和点B〔3，4〕，如图，那么入射线所在直线的解析式为．22．〔2021•萧山区模拟〕当k取不同整数时，经过第一、二、四象限的所有直线y=〔2k﹣1〕x+k+2与坐标轴在第一象限围成一个多边形，这个多边形的面积等于．三．解答题〔共8小题〕23．〔2021 •建邺区二模〕小林家、小华家与图书馆依次在一条直线上．小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书，小林到达图书馆花了20分钟．设两人出发x〔分钟〕后，小林离小华家的距离为y〔米〕，y与x的函数关系如下图．〔1〕小林的速度为米/分钟，a=，小林家离图书馆的距离为米；〔2〕小华的步行速度是40米/分钟，设小华步行时与家的距离为y1〔米〕，请在图中画出y1〔米〕与x〔分钟〕的函数图象；〔3〕小华出发几分钟后两人在途中相遇？24．〔2021 •峄城区校级模拟〕甲船从A港出发顺流匀速驶向B港，行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．乙船从B 港出发逆流匀速驶向A港．救生圈漂流的速度和水流速度一样；甲、乙两船在静水中的速度一样．甲、乙两船到A港的距离y1、y2〔km〕与行驶时间x〔h〕之间的函数图象如下图．〔1〕写出乙船在逆流中行驶的速度；〔2〕求甲船在逆流中行驶的路程；〔3〕求甲船到A港的距离y1与行驶时间x之间的函数关系式；〔4〕求救生圈落入水中时，甲船到A港的距离．25．〔2021 •XX模拟〕一条笔直的公路上依次有A、B、C三地，甲、乙两车同时从B地出发，匀速驶往C地．乙车直接驶往C地，甲车先到A地取一物件后立即调转方向追赶乙车〔甲车取物件的时间忽略不计〕．两车间距离y〔km〕与甲车行驶时间x〔h〕的关系图象如图1所示．〔1〕求两车的速度分别是多少？〔2〕填空：A、C两地的距离是：，图中的t=〔3〕在图2中，画出两车离B地距离y〔km〕与各自行驶时间x〔h〕的关系图象，并求两车与B地距离相等时行驶的时间．26．〔2021 春•晋安区期末〕模型建立：如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E．求证：△BEC≌△CDA．模型应用：〔1〕直线l1：y=x+4与y轴交与A点，将直线l1绕着A点顺时针旋转45°至l2，如图2，求l2的函数解析式．〔2〕如图3，矩形ABCO，O为坐标原点，B的坐标为〔8，6〕，A、C分别在坐标轴上，P 是线段BC上动点，设PC=m，点D在第一象限，且是直线y=2x﹣6上的一点，假设△APD 是不以A为直角顶点的等腰Rt△，请直接写出点D的坐标．27．〔2021•XX〕在平面直角坐标系中，O为原点，直线l：x=1，点A〔2，0〕，点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．〔Ⅰ〕假设点M的坐标为〔1，﹣1〕，①当点F的坐标为〔1，1〕时，如图，求点P的坐标；②当点F为直线l上的动点时，记点P〔x，y〕，求y关于x的函数解析式．〔Ⅱ〕假设点M〔1，m〕，点F〔1，t〕，其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．28．〔2021•江阴市二模〕如图，A、B两点分别在x轴和y轴上，且OA=OB=，动点P、Q分别在AB、OB上运动，运动时，始终保持∠OPQ=45°不变，设PA=x，OQ=y．〔1〕求y与x的函数关系式．〔2〕点M在坐标平面内，是否存在以P、Q、O、M为顶点的四边形是菱形？假设存在，求出点M的坐标；假设不存在，说明理由．〔3〕点D在AB上，且AD=，试探究：当点P从点A出发第一次运动到点D时，点Q 运动的路径长为多少？29．〔2021•XX〕为了迎接“十•一〞小长假的购物顶峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：甲乙运动鞋价格进价〔元/双〕m m﹣20售价〔元/双〕240 160：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量一样．〔1〕求m的值；〔2〕要使购进的甲、乙两种运动鞋共200双的总利润〔利润=售价﹣进价〕不少于21700元，且不超过22300元，问该专卖店有几种进货方案？〔3〕在〔2〕的条件下，专卖店准备对甲种运动鞋进展优惠促销活动，决定对甲种运动鞋每双优惠a〔50＜a＜70〕元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？30．〔2021•XX〕某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂方案生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x〔千克〕．〔1〕列出满足题意的关于x的不等式组，并求出x的取值X围；〔2〕该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？八年级下册----一次函数压轴题参考答案与试题解析一．选择题〔共17小题〕1．〔2021•平塘县二模〕如图，是一个下底小而上口大的圆台形容器，将水以恒速〔即单位时间内注入水的体积一样〕注入，设注水时间为t，容器内对应的水高度为h，那么h与t 的函数图象只可能是〔〕A．B．C．D．考点：函数的图象．专题：计算题；压轴题．分析：此题需先根据容器下底小而上口大的特点得出容器内对应的水高度h随时间t的增加而增加，但增加的速度越来越慢即可得出正确答案．解答：解：∵容器下底小而上口大，∴将水以恒速注入，那么容器内对应的水高度h随时间t的增加而增加，但增加的速度越来越慢∴h与t的函数图象只可能是D应选D点评：此题主要考察了函数的图象问题，在解题时要结合题意找出正确的函数图象是此题的关键．2．〔2021•XX〕如图，在Rt△ABC中，∠C=90°，AC=1cm，BC=2cm，点P从点A出发，以1cm/s的速度沿折线AC→CB→BA运动，最终回到点A，设点P的运动时间为x〔s〕，线段AP的长度为y〔cm〕，那么能够反映y与x之间函数关系的图象大致是〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题．分析：这是分段函数：①点P在AC边上时，y=x，它的图象是一次函数图象的一局部；②点P在边BC上时，利用勾股定理求得y与x的函数关系式，根据关系式选择图象；③点P在边AB上时，利用线段间的和差关系求得y与x的函数关系式，由关系式选择图象．解答：解：①当点P在AC边上，即0≤x≤1时，y=x，它的图象是一次函数图象的一局部；②点P在边BC上，即1＜x≤3时，根据勾股定理得AP=，即y=，那么其函数图象是y随x的增大而增大，且不是一次函数．故B、C、D错误；③点P在边AB上，即3＜x≤3+时，y=+3﹣x=﹣x+3+，其函数图象是直线的一局部．综上所述，A选项符合题意．应选：A．点评：此题考察了动点问题的函数图象．此题涉及到了函数y=的图象问题，在初中阶段没有学到该函数图象，所以只要采取排除法进展解题．3．〔2021秋•XX期末〕如下图．直线y=x+2与y轴相交于点A，OB1=OA，以OB1为底边作等腰三角形A1OB1，顶点A1在直线y=x+2上，△A1OB1记作第一个等腰三角形；然后过B1作平行于OA1的直线B1A2与直线y=x+2相交于点A2，再以B1A2为腰作等腰三角形A2B1B2，记作第二个等腰三角形；同样过B2作平行于OA1的直线B2A3与直钱y=x+2相交于点A3，再以B2A3为腰作等腰三角形A3B2B3，记作第三个等腰三角形；依此类推，那么等腰三角形A10B9B10的面积为〔〕A．3•48B．3•49C．3•410D．3•411考点：一次函数综合题．专题：压轴题；规律型．分析：令x=0求解得到点A的坐标，然后求出OA的长，过点A1作A1C1⊥x轴于C1，根据等腰三角形三线合一的性质求出OC1，再根据直线解析式求出A1C1，然后判断出△A2B1B2∽△A1OB1，过点A2作A2C2⊥x轴于C2，根据相似三角形的性质用B1C2表示出A2C2，再根据A2在直线上列式求解得到第二个等腰三角形的底边与高，同理求出第三个等腰三角形的底边与高，然后根据规律判断出△A10B9B10的底边与高，再根据三角形的面积公式列式计算即可得解．解答：解：令x=0，那么y=2，∴点A的坐标为〔0，2〕，∴OA=2，∴OB1=OA=2，过点A1作A1C1⊥x轴于C1，那么OC1=OB1=×2=1，∵A1在直线y=x+2上，∴A1C1=x+2=1+2=3，∴A1C1=3OC1，由题意得，△A2B1B2∽△A1OB1，过点A2作A2C2⊥x轴于C2，那么A2C2=3B1C2，设B1C2=a，那么A2C2=3a，∵A2在直线y=x+2上，∴A2C2=x+2=〔2+a〕+2=3a，解得a=2，∴B1B2=2×2=4，同理可得B2B3=8=23，A2C3=12=3×22，…，△A10B9B10的底边B9B10=210，高为3×29，∴△A10B9B10的面积=×210×3×29，=3•49．应选B．点评：此题是一次函数综合题型，主要考察了等腰三角形的性质，一次函数图象上点的坐标特征，求出等腰三角形底边上的高等于底边一半的3倍是解题的关键，也是此题的难点．4．〔2021春•海曙区校级期中〕如图，直线y=﹣x+3与x轴，y轴交于A，B两点．点P是线段OB上的一动点〔能与点O，B重合〕，假设能在斜边AB上找到一点C，使∠OCP=90°．设点P的坐标为〔m，0〕，那么m的取值X围是〔〕A．3≤m≤4 B．2≤m≤4 C．D．0≤m≤30≤m≤考点：一次函数综合题．专题：压轴题．分析：令y=0求出点B的坐标，过点C作CD⊥x轴于D，设点C的坐标横坐标为a，那么OD=a，PD=m﹣a，求出△OCD和△CPD相似，利用相似三角形对应边成比例列式表示出m，然后求出m的最小值，再根据点P在线段OB上判断出OC⊥AB时，点P、B重合，m最大，然后写出m的取值X围即可．解答：解：令y=0，那么﹣x+3=0，解得x=4，所以，点B的坐标为〔4，0〕，过点C作CD⊥x轴于D，设点C的坐标横坐标为a，那么OD=a，PD=m﹣a，∵∠OCP=90°，∴△OCD∽△CPD，∴=，∴CD2=OD•DP，∴〔﹣a+3〕2=a〔m﹣a〕，整理得，m=a+﹣，所以，m≥2﹣=3，∵点P是线段OB上的一动点〔能与点O，B重合〕，∴OC⊥AB时，点P、B重合，m最大，∴m的取值X围是3≤m≤4．应选A．点评：此题是一次函数综合题型，主要利用了一次函数与坐标轴的交点的求法，相似三角形的判定与性质，难点在于列不等式求出m的最小值．5．〔2021•〕如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=2．设弦AP的长为x，△APO的面积为y，那么以下图象中，能表示y与x的函数关系的图象大致是〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题．分析：作OC⊥AP，根据垂径定理得AC=AP=x，再根据勾股定理可计算出OC=，然后根据三角形面积公式得到y=x•〔0≤x≤2〕，再根据解析式对四个图形进展判断．解答：解：作OC⊥AP，如图，那么AC=AP=x，在Rt△AOC中，OA=1，OC===，所以y=OC•AP=x•〔0≤x≤2〕，所以y与x的函数关系的图象为A选项．应选：A．排除法：很显然，并非二次函数，排除B选项；采用特殊位置法；当P点与A点重合时，此时AP=x=0，S△PAO=0；当P点与B点重合时，此时AP=x=2，S△PAO=0；当AP=x=1时，此时△APO为等边三角形，S△PAO=；排除B、C、D选项，应选：A．点评：此题考察了动点问题的函数图象：先根据几何性质得到与动点有关的两变量之间的函数关系，然后利用函数解析式和函数性质画出其函数图象，注意自变量的取值X围．6．〔2021•大城县校级模拟〕如图，M是边长为4的正方形AD边的中点，动点P自A点起，由A⇒B⇒C⇒D匀速运动，直线MP扫过正方形所形成面积为y，点P运动的路程为x，那么表示y与x的函数关系的图象为〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题；动点型．分析：分别求出P在AB段，BC段，CD段的函数解析式或判断函数的类型，即可判断．解答：解：点P在AB段时，函数解析式是：y=AP•AM=×2x=x，是正比例函数；点P在BC段时：y=2x﹣4；这段的直线的斜率大于AB段的斜率．故A，B选项错误；点P在CD段时，面积是梯形ABCM的面积加上△MCP面积，梯形ABCM的面积不变，而△MCP中CP边上的高一定，因而面积是CP长的一次函数，因而此段的面积是x的一次函数，应是线段．故C错误，正确的选项是D．应选D．点评：此题主要考察了函数的性质，注意分段讨论是解决此题的关键．7．〔2021•XX模拟〕如图，直线l是菱形ABCD和矩形EFGH的对称轴，C点在EF边上，假设菱形ABCD沿直线l从左向右匀速运动，运动到C在GH边上为止，在整个运动的过程中，菱形与矩形重叠局部的面积〔S〕与运动的路程〔x〕之间的函数关系的图象大致是〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题；分段函数．分析：要找出准确反映s与x之间对应关系的图象，需分析在不同阶段中S随x变化的情况，解答：解：当0＜x＜2时，S=x2，当2≤x≤4时，S=×2×4﹣〔4﹣x〕×〔4﹣x〕，=﹣x 2+4x﹣4，由分析可知，应选D．点评：此题以动态的形式考察了分类讨论的思想，函数的知识和等腰三角形，具有很强的综合性．8．〔2021•温岭市校级三模〕如图，在直角坐标系中，等腰直角△ABO的O点是坐标原点，A的坐标是〔﹣4，0〕，直角顶点B在第二象限，等腰直角△BCD的C点在y轴上移动，我们发现直角顶点D点随之在一条直线上移动，这条直线的解析式是〔〕C．y=﹣3x﹣2 D．y=﹣x+2A．y=﹣2x+1 B．y=﹣x+2考点：一次函数综合题．专题：计算题；压轴题．分析：抓住两个特殊位置：当BC与x轴平行时，求出D的坐标；C与原点重合时，D在y 轴上，求出此时D的坐标，设所求直线解析式为y=kx+b，将两位置D坐标代入得到关于k与b的方程组，求出方程组的解得到k与b的值，即可确定出所求直线解析式．解答：解：当BC与x轴平行时，过B作BE⊥x轴，过D作DF⊥x轴，交BC于点G，如图1所示，∵等腰直角△ABO的O点是坐标原点，A的坐标是〔﹣4，0〕，∴AO=4，∴BC=BE=AE=EO=GF=OA=2，OF=DG=BG=CG=BC=1，DF=DG+GF=3，∴D坐标为〔﹣1，3〕；当C与原点O重合时，D在y轴上，此时OD=BE=2，即D〔0，2〕，设所求直线解析式为y=kx+b〔k≠0〕，将两点坐标代入得：，解得：．那么这条直线解析式为y=﹣x+2．应选D9．〔2021•延庆县一模〕如图：P是线段AB上的动点〔P不与A，B重合〕，分别以AP、PB 为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；点C、D 在线段AB上且AC=BD，当点P从点C运动到点D时，设点G到直线AB的距离为y，那么能表示y与P点移动的时间x之间函数关系的大致图象是〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题；数形结合．分析：分别延长AE，BF交于点H，那么可证得四边形EPFH为平行四边形，利用平行四边形的性质：对角线相互平分，可得G为EF的中点，也是PH的中点，所以G的运动轨迹是三角形HCD的中位线，所以点G到直线AB的距离为y是一个定值，问题得解．解答：解：如图，分别延长AE，BF交于点H，∵∠A=∠FPB=60°，∴AH∥PF，∵∠B=∠EPA=60°，∴BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分，∴G为HP的中点，∵EF的中点为G，∴P从点C运动到点D时，G始终为PH的中点，∴G运动的轨迹是三角形HCD的中位线MN，又∵MN∥CD，∴G到直线AB的距离为一定值，∴y与P点移动的时间x之间函数关系的大致图象是一平行于x轴的射线〔x≥0〕．应选D．点评：此题考察了动点问题的函数图象，利用到的是三角形的中位线定理：三角形的中位线平行且等于第三边的一半．对于此类问题来说是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．10．〔2021•XX二模〕某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开场调出物资〔调进物资与调出物资的速度均保持不变〕．储运部库存物资w〔吨〕与时间t〔小时〕之间的函数关系如下图，这批物资从开场调进到全部调出需要的时间是〔〕A．4.5小时B．4.75小时C．5小时D．5小时考点：函数的图象．专题：应用题；压轴题．分析：通过分析题意和图象可求调进物资的速度，调出物资的速度；从而可计算最后调出物资20吨所花的时间．解答：解：调进物资的速度是50÷2=25〔吨/时〕；当在第4小时时，库存物资应该有100吨，从图象上可知库存是20吨，所以调出速度是80÷2=40〔吨/时〕，所以剩余的20吨完全调出需要20÷40=0.5〔小时〕．故这批物资从开场调进到全部调出需要的时间是4+0.5=4.5〔小时〕．应选A．点评：主要考察了函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．11．〔2021•房山区一模〕如图，P是边长为1的正方形ABCD对角线AC上一动点〔P与A、C不重合〕，点E在射线BC上，且PE=PB．设AP=x，△PBE的面积为y．那么能够正确反映y与x之间的函数关系的图象是〔〕A．B．C．D．考点：动点问题的函数图象．专题：压轴题；数形结合．分析：过点P作PF⊥BC于F，假设要求△PBE的面积，那么需要求出BE，PF的值，利用条件和正方形的性质以及勾股定理可求出BE，PF的值．再利用三角形的面积公式得到y与x的关系式，此时还要考虑到自变量x的取值X围和y的取值X围．解答：解：过点P作PF⊥BC于F，∵PE=PB，∴BF=EF，∵正方形ABCD的边长是1，∴AC==，∵AP=x，∴PC=﹣x，∴PF=FC=〔﹣x〕=1﹣x，∴BF=FE=1﹣FC=x，∴S△PBE=BE•PF=x〔1﹣x〕=﹣x2+x，即y=﹣x2+x〔0＜x＜〕，∴y是x的二次函数〔0＜x＜〕，应选A．点评：此题考察了动点问题的函数图象，和正方形的性质；等于直角三角形的性质；三角形的面积公式．对于此类问题来说是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．12．〔2021•XX模拟〕四条直线y=kx﹣3，y=﹣1，y=3和x=1所围成的四边形的面积是12，那么k的值为〔〕A．1或2 B．1或﹣2 C．﹣1或2 D．﹣1或﹣2考点：一次函数的性质．专题：压轴题；探究型．分析：首先根据四条直线的解析式画出示意图，从而发现四边形是梯形，求得梯形的四个顶点的坐标，再进一步根据梯形的面积公式进展计算．解答：解：如下图，根据题意，得A〔1，3〕，B〔1，﹣1〕，C〔，﹣1〕，D〔，3〕．显然ABCD是梯形，且梯形的高是4，根据梯形的面积是12，那么梯形的上下底的和是6，那么有①当k＜0时，1﹣+1﹣=6，∴2﹣=6，∴=﹣4，解得k=﹣2；②当k＞0时，﹣1+﹣1=6，∴=8，解得k=1．综上所述，那么k=﹣2或1．应选B．点评：此题考察了用图象法表示函数、两条直线的交点坐标和梯形的面积公式，注意此题的两种情况．13．〔2021•东城区一模〕如图，在矩形ABCD中，AB=5，BC=4，E、F分别是AB、AD的中点．动点R从点B出发，沿B→C→D→F方向运动至点F处停顿．设点R运动的路程为x，△EFR的面积为y，当y取到最大值时，点R应运动到〔〕A．B C的中点处B．C点处C．C D的中点处D．D点处考点：一次函数的应用．专题：几何动点问题；压轴题．分析：根据题意，△EFR的面积=边EF×其对应的高，当△EFR的面积最大时，边EF对应的高最大，从而转化为求点R运动到何处时，到线段EF的距离最大．解答：解：根据题意，△EFR的面积=边EF×其对应的高，当△EFR的面积最大时，边EF对应的高最大，从而将问题转化为求点R运动到何处时，到线段EF的距离最大．由所给图形可以看出当点R运动到C点时，点R到线段EF的距离最大．应选B．点评：此题考察了一次函数的应用，难度不大，将问题适当的转化是解答该题的关键．14．〔2021•XX模拟〕某人匀速上坡一段时间后，由于有急事，又以更快的速度匀速地沿原路返回；这一情境中，速度V与时间t的关系，用图象可大致表示为〔〕A．B．C．D．考点：函数的图象．专题：压轴题．分析：根据行驶速度是匀速，可知v在两段时间内分别不变，是一条平行于t轴的直线，可知匀速上坡后，又沿原路返回，所以路程是相等的，根据s=vt，由于返回是速度更快了，所以所用时间就短了．解答：解：∵某人匀速上坡一段时间，∴v在这段时间不变，是一条平行于t轴的直线，∵又以更快的速度匀速地沿原路返回，∴此时v增大，仍然是一条平行于t轴的直线，而且所用时间缩短，应选：A，点评：此题主要考察了实际问题与函数图象的结合，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．15．〔2021•江干区模拟〕如图，直线l1：y=x+1与直线l2：相交于点P〔﹣1，0〕．直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，B n，A n，…那么当动点C到达A n处时，运动的总路径的长为〔〕A．n2B．2n﹣1 C．2n﹣1+1 D．2n+1﹣2考点：一次函数综合题．专题：压轴题；规律型．。

人教版八年级下一次函数与几何综合训练(PDF,无答案)

«一次函数»几何综合专题训练卷班级:㊀姓名:㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀１.如图ꎬ直线ｌ１:ｙ１＝－２３ｘ＋ｂ过点Ａ(６ꎬ０)ꎬ交ｙ轴于点Ｂꎬ直线ｌ２:ｙ２＝１３ｘ＋１与ｘ轴交于点Ｃꎬ两直线ｌ１㊁ｌ２相交于点Ｄꎬ连接ＢＣ.㊀(１)求直线ｌ１的解析式及点Ｄ的坐标ꎻ㊀(２)求әＢＣＤ的面积ꎻ㊀(３)根据图象ꎬ直接写出当ｙ１>时ｘ的取值范围.㊀２.在平面直角坐标系中ꎬＯ为原点ꎬ点Ｐ的坐标为(３ꎬ３)ꎬ点Ａ坐标为(２ꎬ０)ꎬ平行于ｙ轴动直线ｌ交ｘ轴于Ｍꎬ交直线ＯＰ于Ｆꎬ交直线ＡＰ于Ｅ.㊀(１)求直线ＯＰꎬ直线ＡＰ的解析式ꎻ㊀(２)若设Ｍ点的横坐标为ｔꎬ试用含ｔ的式子表示ＥＦꎬ并求当ＥＦ＝２时Ｍ点的坐标ꎻ㊀(３)当әＯＥＦ是直角三角形时ꎬ试求Ｍ１３.如图ꎬ直线ｌ１的函数表达式为ｙ１＝－３ｘ＋３ꎬ且ｌ１与ｘ轴交于点Ｄꎬ直线ｌ２:ｙ２＝ｋｘ＋ｂ经过点ＡꎬＢꎬ与直线ｌ１交于点Ｃ.㊀(１)求直线ｌ２的函数表达式ꎬ并利用图象回答ꎬ何时ｙ１>ｙ２ꎻ㊀(２)求әＡＤＣ的面积ꎻ㊀(３)在直角坐标系中有点Ｅꎬ和ＡꎬＣꎬＤ构成平行四边形ꎬ请直接写出Ｅ点的坐标.４.如图ꎬ在平面直角坐标系ｘＯｙ中ꎬ直线ｙ＝－４３ｘ＋８与ｘ轴ꎬｙ轴分别交于点Ａꎬ点Ｂꎬ点Ｄ在ｙ轴的负半轴上ꎬ若将әＤＡＢ沿直线ＡＤ折叠ꎬ点Ｂ恰好落在ｘ轴正半轴上的点Ｃ处.㊀(１)求ＡＢ的长和点Ｃ的坐标ꎻ㊀(２)求直线ＣＤ的解析式.５.已知一次函数ｙ＝ｋｘ＋ｂ的图象与ｘ轴㊁ｙ轴分别交于点Ａ(－２ꎬ０)㊁Ｂ(０ꎬ４)ꎬ直线ｌ经过点Ｂꎬ并且与直线ＡＢ垂直.点Ｐ在直线ｌ上ꎬ且әＡＢＰ是等腰直角三角形.㊀(１)求直线ＡＢ的解析式ꎻ㊀(２)求点Ｐ的坐标ꎻ㊀(３)点Ｑ(ａꎬｂ)在第二象限ꎬ且ＳәＱＡＢ＝ＳәＰＡＢ.㊀①用含ａ的代数式表示ｂꎻ㊀②若ＱＡ＝ＱＢꎬ求点Ｑ的坐标.６.如图ꎬ已知点Ａ(０ꎬａ)ꎬＢ(ｂꎬ０)ꎬＣ(０ꎬｃ)ꎬ且∣ａ＋４∣＋ｂ２－８ｂ＋１６＝０ꎬ(ｃ＋１)２ɤ０ꎬ点Ｄ与点Ｃ关于直线ＡＢ对称.㊀(１)求直线ＡＢ的解析式和点Ｃ㊁Ｄ的坐标ꎻ㊀(２)点Ｅ在直线ＡＢ上ꎬ直接写出∣ＥＯ－ＥＤ∣的最大值和最小值及对应的点Ｅ的坐标..３７.如图ꎬ在平面直角坐标系ｘＯｙ中ꎬ一次函数ｙ＝ｋ１ｘ＋ｂ的图象与ｘ轴交于点Ａ(－３ꎬ０)ꎬ与ｙ轴交于点Ｂꎬ且与正比例函数ｙ＝ｋｘ的图象交点为Ｃ(３ꎬ４).求:㊀(１)求ｋ值与一次函数ｙ＝ｋ１ｘ㊀(２)若点Ｄ在第二象限ꎬәＤＡＢ是以ＡＢ为直角边的等腰直角三角形ꎬ请求出点Ｄ的坐标ꎻ㊀(３)在ｙ轴上求一点Ｐ使әＰＯＣ为等腰三角形ꎬ请求出所有符合条件的点Ｐ的坐标.角әＰＢＣꎬ求点Ｃ的坐标.㊀８.如图ꎬ平面直角坐标系中ꎬ直线ＡＢ:ｙ＝－ｘ＋ｂ交ｙ轴于点Ａ(０ꎬ４)ꎬ交ｘ轴于点Ｂ.㊀(１)求直线ＡＢ的表达式和点Ｂ的坐标ꎻ㊀(２)直线ｌ垂直平分ＯＢ交ＡＢ于点Ｄꎬ交ｘ轴于点Ｅꎬ点Ｐ是直线ｌ上一动点ꎬ且在点Ｄ的上方ꎬ设点Ｐ的纵坐标为ｎ.㊀①用含ｎ的代数式表示әＡＢＰ的面积ꎻ㊀②当ＳәＡＢＰ＝８时ꎬ求点Ｐ的坐标ꎻ㊀③在②的条件下ꎬ以ＰＢ为斜边在第一象限作等腰直９.(１６绍兴)如图ꎬ在矩形ＡＢＣＤ中ꎬ点Ｏ为坐标原点ꎬ点Ｂ的坐标为(４ꎬ３)ꎬ点Ａ㊁Ｃ在坐标轴上ꎬ点Ｐ在ＢＣ边上ꎬ直线ｌ１:ｙ＝２ｘ＋３ꎬ直线ｌ２:ｙ＝２ｘ－３.㊀(１)分别求直线ｌ１与ｘ轴ꎬ直线ｌ２与ＡＢ的交点坐标ꎻ㊀(２)已知点Ｍ在第一象限ꎬ且是直线ｌ２上的点ꎬ若әＡＰＭ是等腰直角三角形ꎬ求点Ｍ的坐标.１０.如图ꎬ长方形ＡＢＣＯ位于直角坐标平面ꎬＯ为原点ꎬＡ㊁Ｃ分别在坐标轴上ꎬＢ的坐标为(８ꎬ６)ꎬ线段ＢＣ上有一动点Ｐꎬ已知点Ｄ在第一象限.(１)Ｄ是直线ｙ＝２ｘ＋６上一点ꎬ若әＡＰＤ是等腰直角三角形ꎬ求点Ｄ的坐标ꎻ(２)Ｄ是直线ｙ＝２ｘ－６上一点ꎬ若әＡＰＤ是等腰直角三角形.求点Ｄ的坐标.５１１.(１７盘锦)如图ꎬ在平面直角坐标系中ꎬ直线ｌ:ｙ＝－３３ｘ＋４与ｘ轴㊁ｙ轴分别交于点ＭꎬＮꎬ高为３的等边三角形ＡＢＣꎬ边ＢＣ在ｘ轴上ꎬ将此三角形沿着ｘ轴的正方向平移ꎬ在平移过程中ꎬ得到әＡ１Ｂ１Ｃ１ꎬ当点Ｂ１与原点重合时ꎬ解答下列问题:(１)求出点Ａ１的坐标ꎬ并判断点Ａ１是否在直线ｌ上ꎻ(２)求出边Ａ１Ｃ１所在直线的解析式ꎻ(３)在坐标平面内找一点Ｐꎬ使得以Ｐ㊁Ａ１㊁Ｃ１㊁Ｍ为顶点的四边形是平行四边形ꎬ请直接写出Ｐ点坐标.１２.(１７无锡)操作: 如图１ꎬＰ是平面直角坐标系中一点(ｘ轴上的点除外)ꎬ过点Ｐ作ＰＣʅｘ轴于点Ｃꎬ点Ｃ绕点Ｐ逆时针旋转６０ʎ得到点Ｑ. 我们将此由点Ｐ得到点Ｑ的操作称为点的Ｔ变换.(１)点Ｑ的坐标为㊀㊀㊀㊀ꎻ若点Ｍ经过Ｔ变换后得到点Ｎ(６ꎬ－３)ꎬ则点Ｍ的坐标为㊀㊀㊀㊀.(２)Ａ是函数ｙ＝３２ｘ图象上异于原点Ｏ的任意一点ꎬ经过Ｔ变换后得到点Ｂ.①求经过点Ｏꎬ点Ｂ的直线的函数表达式ꎻ②如图２ꎬ直线ＡＢ交ｙ轴于点Ｄꎬ求әＯＡＢ的面积与әＯＡＤ的面积之比.６。

人教版-数学-八年级下册一次函数综合题型归纳讲义

一次函数综合题型归纳类型一：一次函数与最值问题例题1.如图，平面直角坐标系中，直线y=2x+my轴交于点A，与直线y=−x+5交于点B(4，n)，P为直线y=−x+5上一点．(1)求m，n的值；(2)求线段AP的最小值，并求此时点P的坐标．例题2.如图，直线l1：y=−x+3与x轴相交于点A，直线l2：y=kx+b经过点(3，−1)，与x轴交于点B(6，0)，与y轴交于点C，与直线l1相交于点D．(1)求直线l2的函数关系式；(2)点P是l2上的一点，若△ABP的面积等于△ABD的面积的2倍，求点P的坐标；(3)设点Q的坐标为(m，3)，是否存在m的值使得QA+QB最小？若存在，请求出点Q的坐标；若不存在，请说明理由．例题3.如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系.已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．(Ⅰ)直接写出点E.F的坐标；(Ⅱ)若M为x轴上的动点，N为y轴上的动点，当四边形MNFE的周长最小时，求出点M、N 的坐标，并求出周长的最小值．变式练习：1.如图，正方形ABOD的边长为2，OB在x轴上，OD在y轴上，且AD//OB，AB//OD，点C为AB的中点，直线CD交x轴于点F．(1)求直线CD的函数关系式；(2)过点C作CE⊥DF且交于点E，求证：∠ADC=∠EDC；(3)求点E坐标；(4)点P是直线CE上的一个动点，求PB+PF的最小值．类型二一次函数与几何问题例题1.如图，平面直角坐标系中，直线l分别交x轴、y轴于A.B两点(OA<OB)且OA.OB的长分别是一元二次方程x2−(√3+1)x+√3=0的两个根，点C在x轴负半轴上，且AB：AC=1：2(1)求A.C两点的坐标；(2)若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；(3)点P是y轴上的点，在坐标平面内是否存在点Q，使以A.B.P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．例题2.如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA.OB的长分别是一元二次方程x2−7x+12=0的两个根(OA>OB)．(1)求点D的坐标．(2)求直线BC的解析式．(3)在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．例题3.如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=kx+b的图象经过点B(0，−1)，与x轴以及y=x+1的图象分别交于点C.D，且点D的坐标为(1，n)，(1)则n=______ ，k=______ ，b=______ ；(2)函数y=kx+b的函数值大于函数y=x+1的函数值，则x的取值范围是______(3)求四边形AOCD的面积；(4)在x轴上是否存在点P，使得以点P，C，D为顶点的三角形是直角三角形？若存在求出点P的坐标；若不存在，请说明理由．变式练习：1.如图，在平面直角坐标系中，直线AB与x轴、y轴的正半轴分别交于点A，B，直线CD与x轴正半轴、y轴负半轴分别交于点D，C，AB与CD相交于点E，点A，B，C，D的坐标分别为(8，0)、(0，6)、(0，−3)、(4，0)，点M是OB的中点，点P在直线AB上，过点P作PQ//y轴，交直线CD于点Q，设点P的横坐标为m．(1)求直线AB，CD对应的函数关系式；(2)用含m的代数式表示PQ的长；(3)若以点M，O，P，Q为顶点的四边形是矩形，请直接写出相应的m的值．2.已知一次函数y=kx+b的图象经过点M(−1，3)、N(1，5).直线MN与坐标轴相交于点A.B两点．(1)求一次函数的解析式．(2)如图1，点C与点B关于x轴对称，点D在线段OA上，连结BD，把线段BD顺时针方向的值．旋转90∘得到线段DE，作直线CE交x轴于点F，求DF−DAEF(3)如图2，点P是直线AB上一动点，以OP为边作正方形OPNM，连接ON、PM交于点Q，连BQ，当点P在直线AB上运动时，BQ的值是否会发生变化？若不变，请求出其值；若变化，OP请说明理由．类型三一次函数与面积问题例题1.如图，在平面直角坐标系中，直线AC：y=−x+2.5与x轴交于C点，与y轴交于A点，直线AB与x轴交于C点，与y轴交于A点，已知B(−3，0)．(1)求直线AB的解析式．(2)直线AD过点A，交线段BC于点D，把s△ABC的面积分为1：2两部分；求出此时的点D的坐标．x+2与x轴、y轴交于A.B两点，在y轴上有一个点C(0，4)，例题2.已知直线L：y=−12动点M从A点出发，以每秒1个单位的速度沿x轴向左移动．(1)求A.B两点的坐标．(2)求△COM的面积S与点M移动的时间t之间的函数关系式．(3)当t=6时，①求直线CM所对应的解析式．②问直线CM与直线L有怎样的位置关系？为什么？变式练习：平面直角坐标系xOy中，点P的坐标为(m+1，m−1)．(1)试判断点P是否在一次函数y=x−2的图象上，并说明理由；(2)如图，一次函数y=−1x+3的图象与x轴、y轴分别相交于点A.B，若点2P在△AOB的内部，求m的取值范围．x+m的图象交于P(n，−2)．如图，函数y=−2x+3与y=−12(1)求出m、n的值；(2)求出△ABP的面积．类型四、一次函数与方程不等式例题1.如图，已知函数y1=2x+b和y2=ax−3的图象交于点P (−2，−5)，这两个函数的图象与x轴分别交于点A.B．(1)分别求出这两个函数的解析式；(2)求△ABP的面积；(3)根据图象直接写出不等式2x+b<ax−3的解集．例题2.如图，函数y=−2x+3与y=−12x+m的图象交于P(n，−2)．(1)求出m、n的值；(2)直接写出不等式−12x+m>−2x+3的解集；(3)求出△ABP的面积．变式练习：1.在同一坐标系中画出了三个一次函数的图象：y=1−x，y=x+1和y=3x−1(1)求y=1−x和y=3x−1的交点A的坐标；(2)根据图象填空：①当x______ 时3x−1>x+1；②当x______ 时1−x>x+1；(3)对于三个实数a，b，c，用max{a，b，c}表示这三个数中最大的数，如max{−1，2，3}=3，max{−1，2，a}={2(当a≤2时)a(当a>2时)，请观察三个函数的图象，直接写出max{1−x，x+1，3x−1}的最小值．。

八下压轴题一次函数与几何动点问题教师版

八年级下数学期末压轴题精选1.等腰三角形存在性（2017广西柳州）23．（10分）如图，在四边形OABC中，OA∥BC，∠OAB=90°，O为原点，点C的坐标为（2，8），点B的坐标为（24，8），点D从点B出发，以每秒1个单位长度的速度沿BC向点C运动，点E同时从点O出发，以每秒3个单位长度的速度沿OA向A运动，当点E达到点A时，点D也停止运动，从运动开始，设D（E）点运动的时间为t秒．（1）连接AD，记△ADE得面积为S，求S与t的函数关系式，写出t的取值范围；（2）当t为何值时，四边形ABDE是矩形；（3）在（2）的条件下，当四边形ABDE是矩形，在x轴上找一点P，使得△ADP 为等腰三角形，直接写出所有满足要求的P点的坐标．【分析】（1）根据三角形面积公式计算即可；（2）当BD=AE时，四边形ABDE是矩形，由此构建方程即可解决问题；（3）分三种情形：①当AD=AP时，②当DA=DP时，③当PD=PA时，分别求解即可；【解答】解：（1）如图1中，S=×（24﹣3t）×8=﹣12t+96（0≤t≤8）．（2）∵OA∥BD，∴当BD=AE时，四边形BDEA是平行四边形，∵∠OAB=90°，∴四边形ABDE是矩形，∴t=24﹣3t，t=6s，∴当t=6s时，四边形ABDE是矩形．（3）分三种情形讨论：由（2）可知D（18，8），A（24，0），∴AD==10，①当AD=AP时，可得P1（14，0），P2（34，0），②当DA=DP时，可得P3（12，0），③当PD=PA时，设PD=PA=x，在Rt△DP4E中，x2=82+（x﹣6）2，解得x=，∴P4（，0），综上所述，满足条件的点P坐标为（14，0）或（34，0）或（12，0）或（，0）；【点评】本题考查四边形的综合题、矩形的判定和性质、等腰三角形的判定和性质、勾股定理等知识，解题的关键是学会用转化的思想思考问题，学会用分类讨论的思想解决问题，属于中考压轴题．2.直角三角形存在性（2017深圳新华）如图，在平面直角坐标系中，O是坐标原点，平行四边形的顶点C的坐标为（8，8），顶点A的坐标为（﹣6，0），边AB在x轴上，点E 为线段AD的中点，点F在线段DC上，且横坐标为3，直线EF与y轴交于点G，有一动点P以每秒1个单位长度的速度，从点A沿折线A﹣B﹣C﹣F运动，当点P到达点F时停止运动，设点P运动时间为t秒．（1）求直线EF的表达式及点G的坐标；（2）点P在运动的过程中，设△EFP的面积为S（P不与F重合），试求S与t 的函数关系式；（3）在运动的过程中，是否存在点P，使得△PGF为直角三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【分析】（1）根据点C的坐标可求出点F的纵坐标，结合题意可得出点F的坐标，过点E作EH⊥x轴于点H，利用△AHE∽△AOD，可求出点E的坐标，从而利用待定系数法可确定直线EF的解析式，令x=0，可得出点G的坐标．（2）延长HE交CD的延长线于点M，讨论点P的位置，①当点P在AB上运动时，②当点P在BC边上运动时，③当点P在CF上运动时，分别利用面积相减法可求出答案．（3）很明显在BC上存在两个点使△PGF为直角三角形，这两点是通过①过点G 作GP⊥EF，②过点F作FP⊥EF得出来的．【解答】解：（1）∵C（8，8），DC∥x轴，点F的横坐标为3，∴OD=CD=8．∴点F的坐标为（3，8），∵A（﹣6，0），∴OA=6，∴AD=10，过点E作EH⊥x轴于点H，则△AHE∽△AOD．又∵E为AD的中点，∴===．∴AH=3，EH=4．∴OH=3．∴点E的坐标为（﹣3，4），设过E、F的直线为y=kx+b，∴∴∴直线EF为y=x+6，令x=0，则y=6，即点G的坐标为（0，6）．（2）延长HE交CD的延长线于点M，则EM=EH=4．∵DF=3，∴S△DEF=×3×4=6，且S平行四边形ABCD=CD•OD=8×8=64．①当点P在AB上运动时，如图3，S=S平行四边形ABCD﹣S△DEF﹣S△APE﹣S四边形PBCF．∵AP=t，EH=4，∴S△APE=×4t=2t，S四边形PBCF=（5+8﹣t）×8=52﹣4t．∴S=64﹣6﹣2t﹣（52﹣4t），即：S=2t+6．②当点P在BC边上运动时，S=S平行四边形ABCD﹣S△DEF﹣S△PCF﹣S四边形ABPE．过点P作PN⊥CD于点N．∵∠C=∠A，sin∠A==，∴sin∠C=．∵PC=18﹣t，∴PN=PC•sin∠C=（18﹣t）．∵CF=5，∴S△PCF=×5×（18﹣t）=36﹣2t．过点B作BK⊥AD于点K．∵AB=CD=8，∴BK=AB•sin∠A=8×=．∵PB=t﹣8，∴S四边形ABPE=（t﹣8+5）×=t﹣．∴S=64﹣6﹣（36﹣2t）﹣（t﹣），即S=﹣t+．（8分）③当点P在CF上运动时，∵PC=t﹣18，∴PF=5﹣（t﹣18）=23﹣t．∵EM=4，∴S△PEF=×4×（23﹣t）=46﹣2t．综上：S=（3）存在．P1（，）．P2（，）．3.一次函数与平行四边形：（2016山西晋中）（1）在直角坐标系中，A（1，2），B（4，0），在图1中，四边形ABCD为平行四边形，请写出图中的顶点C的坐标（ 5 ， 2 ）（2）平面内是否存在不同于图1的点C，使得以O、A、B、C为顶点的四边形为平行四边形，请在图2中画出满足情况的平行四边形，并在图中直接标出点C 的坐标．（3）如图3，在直角坐标系中，A（1，2），P是x轴上一动点，在直线y=x上是否存在点Q，使以O、A、P、Q为顶点的四边形为平行四边形？若存在，画出所有满足情况的平行四边形，并求出对应的Q的坐标；若不存在，请说明理由．【分析】（1）根据平行四边形的性质对边相等，即可解决问题．（2）存在．注意有两种情形．点C坐标根据平行四边形的性质即可解决．（3）存在．如图3中所示，平行四边形AQ1P1O，平行四边形AOQ2P2，平行四边形AQ1OP2．点Q的坐标根据平行四边形的性质即可解决．【解答】解：（1）如图1中，∵四边形ABCD是平行四边形，∴OB=AC，OB∥AC，∵A（1，2），B（4，0），∴AC=4，∴点C坐标（5，2）．故点C坐标为（5，2）．（2）存在．点C坐标如图2中所示，（3）存在．如图3中所示，平行四边形AQ1P1O，平行四边形AOQ2P2，平行四边形AQ1OP2．点Q1（2，2），点Q2（﹣2，﹣2）．【点评】本题考查四边形综合题、点与坐标的关系等知识，解题的关键是学会正确画出图形，学会分类讨论，不能漏解，属于中考常考题型．（2017襄阳）25．（11分）如图，平面直角坐标系中，直线l：y=﹣x+分别交x轴，y轴于A，B两点，点C在x轴负半轴上，且∠ACB=30°．（1）求A，C两点的坐标．（2）若点M从点C出发，以每秒1个单位长度的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，求出S关于t的函数关系式，并写出自变量的取值范围．（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A，B，P，Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．【分析】（1）由直线方程易得点A的坐标．在直角△BOC中，利用30度所对的直角边等于斜边的一半求出BC的长，利用勾股定理求出OC的长，确定出C的坐标即可；（2）先求出∠ABC=90°，分两种情况考虑：当M在线段BC上；当M在线段BC延长线上；表示出BM，利用三角形面积公式分别表示出S与t的函数关系式即可；（3）点P是y轴上的点，在坐标平面内存在点Q，使以A、B、P、Q为顶点的四边形是菱形，分两种情况，如图所示，利用菱形的性质求出AQ的长，根据AQ与y轴平行得到Q与A横坐标相同，求出满足题意Q得坐标即可．【解答】解：（1）当x=0时，y=；当y=0时，x=1．∴点A坐标为（1，0），点B坐标为（0，），在Rt△BOC中，∠OCB=30°，OB=，∴BC=2．∴OC==3．∴点C坐标为（﹣3，0）．（2）如图1所示：∵OA=1，OB=，AB=2，∴∠ABO=30°，同理：BC=2，∠OCB=30°，∴∠OBC=60°，∴∠ABC=90°，分两种情况考虑：若M在线段BC上时，BC=2，CM=t，可得BM=BC﹣CM=2﹣t，此时S△ABM=BM•AB=×（2﹣t）×2=2﹣t（0≤t＜2）；若M在BC延长线上时，BC=2，CM=t，可得BM=CM﹣BC=t﹣2，此时S△ABM=BM•AB=×（t﹣2）×2=t﹣2（t≥2）；综上所述，S=；（3）P是y轴上的点，在坐标平面内存在点Q，使以A、B、P、Q为顶点的四边形是菱形，如2图所示，当P在y轴正半轴上，四边形ABPQ为菱形，①可得AQ=AB=2，且Q与A的横坐标相同，此时Q坐标为（1，2），②AP=AQ=，Q与A的横坐标相同，此时Q坐标为（1，），当P在y轴负半轴上，四边形ABPQ为菱形，①可得AQ=AB=2，且Q与A横坐标相同，此时Q坐标为（1，﹣2），②BP垂直平分AQ，此时Q坐标为（﹣1，0），综上，满足题意Q坐标为（1，2）、（1，﹣2）、（1，）、（﹣1，0）．【点评】此题属于一次函数综合题，涉及的知识有：含30度直角三角形的性质，勾股定理，坐标与图形性质，待定系数法求一次函数解析式，菱形的性质，利用了分类讨论的思想，熟练掌握待定系数法是解本题第二问的关键．4.一次函数与矩形:（2017重庆江津）26．（12分）如图，在平面直角坐标系中，一次函数y=mx+n （m≠0）的图象与x轴交于点A（﹣3，0），与y轴交于点B，且与正比例函数y=2x的图象交于点C（3，6）．（1）求一次函数y=mx+n的解析式；（2）点P在x轴上，当PB+PC最小时，求出点P的坐标；（3）若点E是直线AC上一点，点F是平面内一点，以O、C、E、F四点为顶点的四边形是矩形，请直接写出点F的坐标．【分析】（1）由A、C坐标，可求得答案；（2）由一次函数解析式可求得B点坐标，可求得B点关于x轴的对称点B′的坐标，连接B′C与x轴的交点即为所求的P点，由B′、C坐标可求得直线B′C 的解析式，则可求得P点坐标；（3）分两种情形分别讨论即可①当OC为边时，四边形OCFE是矩形，此时EO ⊥OC，②当OC为对角线时，四边形OE′CF′是矩形，此时OE′⊥AC；【解答】解：（1）∵一次函数y=mx+n（m≠0）的图象经过点A（﹣3，0），点C（3，6），∴，解得，∴一次函数的解析式为y=x+3．（2）如图1中，作点P关于x轴的对称点B′，连接CB′交x轴于P，此时PB+PC 的值最小．∵B（0，3），C（3，6）∴B′（﹣3，0），∴直线CB′的解析式为y=3x﹣3，令y=0，得到x=1，∴P（1，0）．（3）如图，①当OC为边时，四边形OCFE是矩形，此时EO⊥OC，∵直线OC的解析式为y=2x，∴直线OE的解析式为y=﹣x，由，解得，∴E（﹣2，1），∵EO=CF，OE∥CF，∴F（1，7）．②当OC为对角线时，四边形OE′CF′是矩形，此时OE′⊥AC，∴直线OE′的解析式为y=﹣x，由，解得，∴E′（﹣，），∵OE′=CF′，OE′∥CF′，∴F′（，），综上所述，满足条件的点F的坐标为（1.7）或（，）．【点评】本题考查一次函数综合题、轴对称最短问题、矩形的判定和性质等知识，解题的关键是学会利用对称解决最短问题，学会用分类讨论的思想思考问题，属于中考压轴题．5.一次函数与正方形如图（1），四边形AOBC是正方形，点C的坐标是（，0），（1）求点A的坐标点和正方形AOBC的面积；（2）将正方形绕点O顺时针旋转45°，求旋转后的正方形与原正方形的重叠部分的面积；（3）如图（2），动点P从点O出发，沿折线O﹣A﹣C﹣B方向以1个单位/每秒匀速运动；另一动点Q从点C出发，沿折线C﹣B﹣O﹣A方向以2个单位/每秒匀速运动．P、Q两点同时出发，当Q运动到点A 时P、Q同时停止运动．设运动时间为t秒，是否存在这样的t值，使△OPQ成为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．【分析】（1）连接AB，根据△OCA为等腰三角形可得AD=OD的长，从而得出点A的坐标，则得出正方形AOBC的面积；（2）根据旋转的性质可得OA′的长，从而得出A′C，A′E，再求出面积即可；（3）存在，从Q点在不同的线段上运动情况，可分为三种：①当Q点在BC上时，使OQ=QP，则有OP=2BQ，而OP=t，BQ=4﹣2t，列式可得出t；②当Q点在OB上时，使OQ=OP，而OP=t，OQ=8﹣2t，列式可得出t；③当Q点在OA上时，使OQ=PQ，列式可得出t．【解答】解：（1）如图1，连接AB，与OC交于点D，由△OCA为等腰Rt△，得AD=OD=OC=2，故点A的坐标为（2，2），故正方形AOBC的面积为：×4×4=16；（2）如图1，旋转后可得OA′=OB=4，则A′C=4﹣4，而可知∠CA′E=90°，∠OCB=45°，故△A′EC是等腰直角三角形，则A′E=A′C=4﹣4，故S四边形OA’EB=S△OBC﹣S△A’EC=16﹣16．（3）存在，从Q点在不同的线段上运动情况，可分为三种：①如图2，当Q点在BC上时，使OQ=QP，QM为OP的垂直平分线，则有OP=2OM=2BQ，而OP=t，BQ=4﹣2t，则t=2（4﹣2t），解得：t=．②如图3，当Q点在OB上时，使OQ=OP，而OP=t，OQ=8﹣2t，则t=8﹣2t，解得：t=．③当Q点在OA上时，如图4，使OQ=PQ，t2﹣24t+96=0，解得：t=12+4（舍去），t=12﹣4．【点评】此题考查了正方形的性质，等腰三角形的判定以及旋转的性质，是中考压轴题，综合性较强，难度较大．6.四边形综合（1）（2017武汉新洲）如图，正方形ABCD中，P为AB边上任意一点，AE⊥DP于E，点F在DP的延长线上，且EF=DE，连接AF、BF，∠BAF的平分线交DF于G，连接GC．（1）求证：△AEG是等腰直角三角形；（2）求证：AG+CG=DG．【分析】（1）根据线段垂直平分线的定义得到AF=AD，根据等腰三角形的性质、角平分线的定义证明即可；（2）作CH⊥DP，交DP于H点，证明△ADE≌△DCH（AAS），得到CH=DE，DH=AE=EG，证明CG=GH，AG=DH，计算即可．【解答】（1）证明：∵DE=EF，AE⊥DP，∴AF=AD，∴∠AFD=∠ADF，∵∠ADF+∠DAE=∠PAE+∠DAE=90°，∴∠AFD=∠PAE，∵AG平分∠BAF，∴∠FAG=∠GAP．∵∠AFD+∠FAE=90°，∴∠AFD+∠PAE+∠FAP=90°∴2∠GAP+2∠PAE=90°，即∠GAE=45°，∴△AGE为等腰直角三角形；（2）证明：作CH⊥DP，交DP于H点，∴∠DHC=90°．∵AE⊥DP，∴∠AED=90°，∴∠AED=∠DHC．∵∠ADE+∠CDH=90°，∠CDH+∠DCH=90°，∴∠ADE=∠DCH．∵在△ADE和△DCH中，，∴△ADE≌△DCH（AAS），∴CH=DE，DH=AE=EG．∴EH+EG=EH+HD，即GH=ED，∴GH=CH．∴CG=GH．∵AG=EG，∴AG=DH，∴CG+AG=GH+HD，∴CG+AG=（GH+HD），即CG+AG=DG．（2）（2017天津）24．（8分）如图（1），正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，连结EB，过点A作AM⊥BE，垂足为M，AM与BD 相交于点F．（1）求证：OE=OF；（2）如图（2）若点E在AC的延长线上，AM⊥BE于点M，AM交DB的延长线于点F，其他条件不变，结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由．【分析】（1）根据正方形的性质对角线垂直且平分，得到OB=OA，又因为AM ⊥BE，所以∠MEA+∠MAE=90°=∠AFO+∠MAE，从而求证出Rt△BOE≌Rt△AOF，得到OE=OF．（2）根据第一步得到的结果以及正方形的性质得到OB=OA，再根据已知条件求证出Rt△BOE≌Rt△AOF，得到OE=OF．【解答】解：（1）∵四边形ABCD是正方形．∴∠BOE=∠AOF=90°，OB=OA．又∵AM⊥BE，∴∠MEA+∠MAE=90°=∠AFO+∠MAE，∴∠MEA=∠AFO．在△BOE和△AOF中，∵，∴△BOE≌△AOF．∴OE=OF．（2）OE=OF成立．∵四边形ABCD是正方形，∴∠BOE=∠AOF=90°，OB=OA．又∵AM⊥BE，∴∠F+∠MBF=90°，∠E+∠OBE=90°，又∵∠MBF=∠OBE，∴∠F=∠E．在△BOE和△AOF中，∵，∴△BOE≌△AOF．∴OE=OF．【点评】本题主要考查正方形的性质和全等三角形的判定与性质，将待求线段放到两个三角形中，通过证明三角形全等得到对应边相等是解题的关键．7.动点问题：（1）（2017黄石大冶）如图1，正方形ABCD的边长为6cm，点F从点B出发，沿射线AB方向以1cm/秒的速度移动，点E从点D出发，向点A以1cm/秒的速度移动（不到点A）．设点E，F同时出发移动t秒．（1）在点E，F移动过程中，连接CE，CF，EF，则△CEF的形状是，始终保持不变；（2）如图2，连接EF，设EF交BD于点M，当t=2时，求AM的长；（3）如图3，点G，H分别在边AB，CD上，且GH=3cm，连接EF，当EF 与GH的夹角为45°，求t的值．【解答】解：（1）等腰直角三角形．理由如下：如图1，在正方形ABCD中，DC=BC，∠D=∠ABC=90°．依题意得：DE=BF=t．在△CDE与△CBF中，，∴△CDE≌△CBF（SAS），∴CF=CE，∠DCE=∠BCF，∴∠ECF=∠BCF+∠BCE=∠DCE+∠BCE=∠BCD=90°，∴△CEF是等腰直角三角形．故答案是：等腰直角三角形．（2）如图2，过点E作EN∥AB，交BD于点N，则∠NEM=∠BFM．∴∠END=∠ABD=∠EDN=45°，∴EN=ED=BF．在△EMN与△FMB中，，∴△EMN≌△FMB（AAS），。

部编数学八年级下册专题09一次函数与几何图形综合的七种考法(解析版)含答案

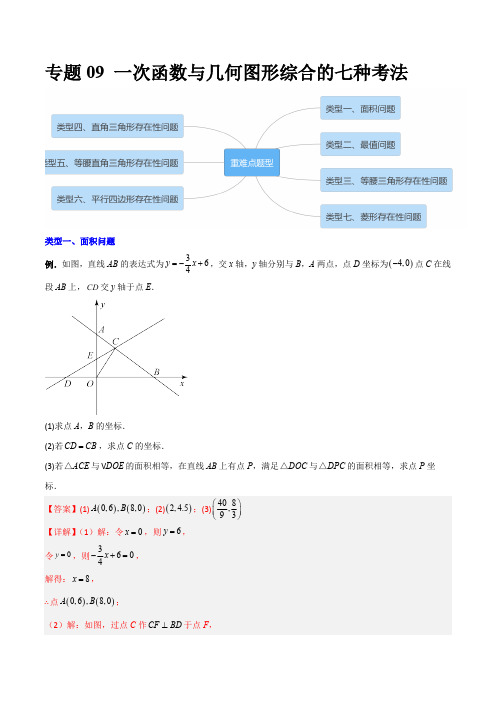
专题09 一次函数与几何图形综合的七种考法类型一、面积问题例．如图，直线AB 的表达式为364y x =-+，交x 轴，y 轴分别与B ，A 两点，点D 坐标为()4,0-点C 在线段AB 上，CD 交y 轴于点E ．(1)求点A ，B 的坐标．(2)若CD CB =，求点C 的坐标．(3)若ACE △与DOE V 的面积相等，在直线AB 上有点P ，满足DOC △与DPC △的面积相等，求点P 坐标．∵CD CB =，∴DF BF =，∵点D 坐标为()4,0-，点B 的坐标为(∴12BD =，8OB =，∴6BF =，∴2OF =，∵DOC △与DPC △的面积相等，∴点O 和点P 到距离相等，此时OP ∥∴直线OP 的解析式为35y x =，联立得：36435y x y xì=-+ïïíï=ïî，解得：x y ì=ïïíï=ïî【变式训练1】如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．(1)填空：k =________；b =________；m =________；(2)在x 轴上是否存在一点E ，使BCE V 的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由；(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动，连接AP ，设点P 的运动时间为t 秒．是否存在t 的值，使ACP △和ADP △的面积比为1:2？若存在，直接写出t 的值；若不存在，请说明理由．（3）∵点P 在射线DC 上从点∴(2,0)D -，∵(2,2)C ，∴22(22)225CD =++=，∵点P 的运动时间为t 秒．②点P 在线段DC 的延长线上，∵ACP △和ADP △的面积比为1:∴12CP DP =，∴22545DP =´=，综上：存在t 的值，使ACP △和【变式训练2】在平面直角坐标系中，O 为原点，点()4,0A ，()2,0B -，()3,2C -，点D 是y 轴正半轴上的动点，连接CD 交x 轴于点E ．(1)如图①，若点D 的坐标为()0,2，求ACD V 的面积；(2)如图②，若12ABD ABC S S =V V ，求点D 的坐标．(3)如图③，若BDE ACE S S =△△，请直接写出点D 的坐标．【变式训练3】如图，平面直角坐标系中，直线AB ：13y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．过点()1,0E 且垂直于x 轴的直线DE 交AB 于点D ，P 是直线DE 上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式和点B 的坐标；(2)求ABP V 的面积（用含n 的代数式表示）；(3)当ABP V 的面积为2时，以PB 为边在第一象限作等腰直角三角形BPC ，求出点C 的坐标．，则90PEB BP CGB Ð=Ð=Ð=°，PB BC =，∴90PBE BPE Ð+Ð=°，90BPE CPG Ð+Ð=°，∴BPE CPG Ð=Ð，∴()AAS BEP PGC ≌V V ，∴2BE PG ==，2PE CG ==，∴点()3,4C ；②以PB 为底时，如图，过点C 作CG PE ^于点G ，作CH x ^轴于点H ，则90PGC CGE CHB PEB PCB Ð=Ð=Ð=°=Ð=Ð，CP CB =，∴90GCH PCB Ð=°=Ð，∴PCG BCH Ð=Ð，∴∴()AAS BCH PCG ≌V V ，∴BH PG =，CH CG =，∴BE BH PE PG +=-，即22BH BH +=-，∴0BH PG ==，∴点()3,2C ；综上，符合题意的点C 坐标为()5,2或()3,4或()3,2．类型二、最值问题例．如图，在平面直角坐标系xOy 中，一次函数()0y kx b k =+¹的图像经过()4,0A 、()0,4B 两点．(1)k =______，b =______．(2)已知()1,0M -、()3,0N ，①在直线AB 上找一点P ，使PM PN =．用无刻度直尺和圆规作出点P （不写画法，保留作图痕迹）；②点P 的坐标为______；③点Q 在y 轴上，那么PQ NQ +的最小值为______．【答案】(1)1-，4；(2)①见解析；②()1,3；③5【详解】（1）解：将()4,0A 、()0,4B 代入()0y kx b k =+¹中，得：044k b b =+ìí=î，解得；14k b =-ìí=î，故答案为：1-，4；（2）①如图，点P 即为所求；【变式训练1】在平面直角坐标系中，已知直线l经过1,32Aæöç÷èø和()3,2B-两点，且与x轴，y轴分别相交于C，D两点．(1)求直线l的表达式；V的面积等于2时，求点E的坐标；(2)若点E在直线AB上，当ODE-的值最小，则点P的坐标为______；(3)①在x轴上找一点P，使得PA PB-的值最大，则点Q的坐标为______．②在x轴上找一点Q，使得QA QB【变式训练2】如图，一次函数2y x =+的图象分别与x 轴和y 轴交于C ，A 两点，且与正比例函数y kx=的图象交于点()1,B m -．(1)求正比例函数的表达式；(2)点D 是一次函数图象上的一点，且OCD V 的面积是4，求点D 的坐标；(3)点P 是y 轴上一点，当BP CP +的值最小时，若存在，点P 的坐标是______．取点C 关于y 轴的对称点C ¢，则PC PC =CP BP C P BP C B ¢¢\+=+³，即点P 位于C B ¢与x 轴的交点时，BP +∵点(2,0)C - ，【变式训练3】如图，在平面直角坐标系内，()3,4A -，()3,2B ，点C 在x 轴上，AD x ^轴，垂足为D ，BE x ⊥轴，垂足为E ，线段AB 交y 轴于点F ．若AC BC =，ACD CBE Ð=Ð．(1)求点C 的坐标；(2)如果经过点C 的直线y kx b =+与线段BF 相交，求k 的取值范围；(3)若点P 是y 轴上的一个动点，当PA PC -取得最大值时，求BP 的长．类型三、等腰三角形存在性问题例．如图，在平面直角坐标系中，一次函数21y x =--的图像分别交x 轴、y 轴于点A 和B ．已知点C 的标为()3,0-，若点P 是x 轴上的一个动点．(1)A 的坐标是______，B 的坐标是______；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的BPC △为等腰三角形时、请求出所有符合条件的P 点坐标．【变式训练1】直线8y kx =-与x 轴、y 轴分别交于B C 、两点，且43OC OB =．(1)求OB 的长和k 的值：(2)若点A 是第一象限内直线8y kx =-上的一个动点，当它运动到什么位置时，AOB V 的面积是12？(3)在（2）成立的情况下，y 轴上是否存在点P ，使POA V 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．（写过程）由题意得，12OB AD ´´=6OB =Q ，\解得，AD当21294OA OP =+==当397OA OP ==时，3P 当22AP OP =时，作2P H ^22AP OP =Q Q 2P 为线段OA 垂直平分线与【变式训练2】在平面直角坐标系中，直线MN 交x 轴正半轴于点M ，交y 轴负半轴于点()0,3N -，30Ð=°ONM ，作线段MN 的垂直平分线交x 轴于点A ，交y 轴于点B ．(1)如图1，求直线MN 的解析式和A 点坐标；(2)如图2，过点M 作y 轴的平行线l ，P 是l 上一点，若ANP S =△P 坐标；(3)如图3，点Q 是y 轴的一个动点，连接QM 、AQ ，将MAQ V 沿AQ 翻折得到1M AQ △，当1M MN △是等腰三角形时，求点Q 的坐标．过T 作TS AM ^于S ，则AT ∴22333322AS æö=-=ç÷èø，同理2315Q P y x =--：，综上：()3,6P ，(3,P -（3）①如图，当MN MM =由轴对称的性质可得：AM ∵()223323AN =+=，∴()0,1Q ．②当1NM NM =时，如图，由23AN NM AM ===，∴ANM V 为等边三角形，此时Q ，N 重合，∴()0,3Q -；③当11M M M N =时，1M 在直线∵30OAB Ð=°，【变式训练3】如图，一次函数()0y kx b k =+¹的图象与x 轴交于点C ，与y 轴交于点()0,5A ，与正比例函数12y x =的图象交于点B ，且点B 的横坐标为2，点P 为y 轴上的一个动点．(1)求B 点的坐标和k 、b 的值；(2)连接CP ，当ACP △与AOB V 的面积相等时，求点P 的坐标；(3)连接BP ，是否存在点P 使得PAB V 为等腰三角形?若存在，请求出点P 的坐标；若不存在，请说明理由．③当PA PB =时，如图2，设(0,P m 22(5)PA m =-，1PH m =-，所以PB 所以222(5)(1)2m m -=-+，解得m类型四、直角三角形存在性问题例．如图1，在平面直角坐标系xOy 中，点O 为坐标原点，直线AB :3y 4x b =+与直线AC ：9y kx =+交于点(2,)A n ，与x 轴分别交于点0()6,B -和点C ．点D 为线段BC 上一动点，将ABD △沿直线AD 翻折得到ADE V ，线段AE 交x 轴于点F ．(1)直线AC 的函数表达式．(2)当点D 在线段BO 上，点E 落在y 轴上时，求点E 的坐标．(3)若DEF V 为直角三角形，求点D 的坐标．【变式训练1】综合与探究：如图，在平面直角坐标系中，直线2y x =+与x 轴，y 轴分别交于点A ，B ，与直线11433y x =-+交于点C ．直线11433y x =-+与x 轴交于点D ，若点P 是线段AD 上的一个动点，点P 从点D 出发沿DA 方向，以每秒2个单位长度匀速运动到点A （到 A 停止运动）．设点P 的运动时间为s t ．(1)求点A 和点B 的坐标；△的面积为12时，求t的值；(2)当ACP△为直角三角形？若存在，请直接写出t的值；(3)试探究，在点P运动过程中，是否存在t的值，使ACP若不存在，请说明理由．【变式训练2】如图，平面直角坐标系中，直线AB 与x 轴交于点()30A -，与y 轴交于点()06B ，，点C 是直线AB 上的一点，它的坐标为()4m ，，经过点C 作直线CD x ∥轴交y 轴于点D ．(1)求点C 的坐标；(2)已知点P 是直线CD 上的动点，①若POC △的面积为4，求点P 的坐标；②若POC △为直角三角形，请求出所有满足条件的点P 的坐标．②Q OCP Ð一定不是直角，当90OPC Ð=°时，点P 恰好在点D ，\()04P ，，当90POC Ð=°时，，由题可得221417OC =+=，2222416OP DP DP =+=+，()221CP DP =+，Q 222CP OC OP =+，\()2211716DP DP +=++，\16DP =，\()164P ，，综上所述，所有满足条件的点P 的坐标为()04，或()164P ，．【变式训练3】如图，已知函数1y x =+的图象与y 轴交于点A ，一次函数y kx b =+的图象经过点()0,1B -，与x 轴以及1y x =+的图象分别交于点C ，D ，且点D 的坐标为()1,n ．(1)则k =______，b =______，n =______；(2)关于x ，y 的二元一次方程组y =x +1,y =kx +b的解为______；(3)求四边形AOCD 的面积；(4)在x 轴上是否存在点P ，使得以点P ，C ，D 为顶点的三角形是直角三角形，请求出点P 的坐标．①当P D DC ¢^时，22P C P D ¢¢=类型五、等腰直角三角形存在性问题例．模型建立：如图1，等腰直角三角形ABC 中，90ACB Ð=°，CB CA =，直线ED 经过点C ，过A 作AD ED ^于D ，过B 作BE ED ^于E ．(1)求证：BEC CDA V V ≌．(2)模型应用：已知直线14:43l y x =+与y 轴交与A 点，将直线1l 绕着A 点顺时针旋转45°至2l ，如图2，求2l 的函数解析式．(3)如图3，矩形ABCO ，O 为坐标原点，B 的坐标为()8,6，A 、C 分别在坐标轴上，P 是线段BC 上动点，设PC m =，已知点D 在第一象限，且是直线26y x =-上的一点，若APD △是不以A 为直角顶点的等腰直角三角形，请直接写出点D 的坐标．∵45BAC Ð=°，∴ABC V 为等腰直角三角形，由（1）得：CBD BAO V V ≌∴BD AO =，CD OB =，∵直线4:4l y x =+，∴()626122AE x =--=-由（1）得：ADE DPF △△≌∴DF AE =，即1228x x -=-，解得：4x =；∴()4,2D ；∴266212BF x x =--=-；同（1）得，APB PDF △≌△∴8AB PF ==，PB DF ==∴()88BF PF PB x =-=--=∴21216x x -=-，解得：283x =；∴2838,33D æöç÷èø；【变式训练1】综合与探究：如图1，平面直角坐标系中，一次函数334y x =-+的图像分别与x 轴、y 轴交于点A ，B ，点C 是线段OA 的中点，点D 与点C 关于y 轴对称，作直线BD ．(1)求A ，B 两点的坐标；(2)求直线BD 的函数表达式；(3)若点P 是直线BD 上的一个动点．请从A ，B 两题中任选一题作答．我选择______题．A ．如图2，连接AP ，CP ．直接写出ACP △为直角三角形时点P 的坐标．B ．如图3，连接CP ，过点P 作PQ x ^轴于点Q ．直接写出CPQ V 为等腰直角三角形时点P 的坐标．【变式训练2】如图，平面直角坐标系中，直线1:3AB y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．直线1x =交AB 于点D ，交x 轴于点E ，P 是直线1x =上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式；(2)当2ABP S =△时，在第一象限内找一点C ，使BCP V 为等腰直角三角形，求点C 的坐标．∵1x =时，12133y x =-+=，P 在点∴23PD n =-，∴12PAB APD BPD S S S PD AM =+=×+V V V ∵2ABP S =△，3∵90,45CPB EPB Ð=°Ð=°，∴45NPC EPB Ð=Ð=°．又∵90,CNP PEB BP PC Ð=Ð=°=，∴CNP BEP ≌V V ，∴2PN =NC =EB =PE =，∴224NE NP+PE ==+=，∴()3,4C ；若90,PBC BP BC Ð=°=，如图，过点C 作CF x ^轴于点F ．∵90,45PBC EBP Ð=°Ð=°，∴45CBF PBE Ð=Ð=°．又∵90,CFB PEB BC BP Ð=Ð=°=，∴CBF PBE ≌V V ．∴2BF CF PE EB ====，∴325OF OB BF =+=+=，∴()5,2C ；若90,PCB CP EB Ð=°=，如图，∴45CPB EBP Ð=Ð=°，∵,,CP EB CPB EBP BP BP =Ð=Ð=，∴PCB PEB ≌V V ，∴2PC CB PE EB ====，∴()3,2C ；∴点C 的坐标是()3,4或()5,2或()3,2．【变式训练3】如图，在平面直角坐标系xOy 中，直线AP 交x 轴于点(),0P p ，与y 轴交于点()0,A a ，且a ，p ()230a +=．(1)求直线AP 的解析式；(2)如图1，直线2x =-与x 轴交于点N ，点M 在x 轴上方且在直线2x =-上，若MAP △的面积等于6，请求出点M 的坐标；(3)如图2，已知点()2,4C -，若点B 为射线AP 上一动点，连接BC ，在坐标轴上是否存在点Q ，使BCQ △是以BC 为底边，点Q 为直角顶点的等腰直角三角形，若存在，请直接写出点Q 坐标；若不存在，请说明理由．∵MD AP P ，MAP △的面积等于∴DAP V 的面积等于6，∴162A DP y ××=，即12DP ×∴4DP =，∴()3,0D -，y∴,33OE t BE t ==-，∵BCQ △是以BC 为底边的等腰直角三角形，∴BQ CQ =，90BQC Ð=∴90BQE NQC Ð=°-Ð=又∵BEQ QNC Ð=Ð，∴()AAS BEQ QNC V V ≌，∴BG t =，33OG t =-，∴BT t =，33OT t =-，同②可证CFQ QTB V V ≌∴QF BT t ==，QT CF =∴OQ OT QT OF =+=+∴52t =，∴513422OQ =+=，类型六、平行四边形存在性问题例．在平面直角坐标系xOy 中，直线36y x =+分别与x 、y 轴相交于A 、B 两点，将线段AB 绕点A 顺时针旋转90°得到线段AC ．连接BC 交x 轴于点D ．(1)求点C 的坐标；(2)P 为x 轴上的动点，连接PB ，PC ，当PB PC -的值最大时，求此时点P 的坐标．(3)点E 在直线AC 上，点F 在x 轴上，若以B 、D 、E 、F 为顶点的四边形是平行四边形，请直接写出点F 的坐标；【答案】(1)点C 的坐标为()4,2-(2)()6,0P (3)点F 的坐标为()17,0-或()13,0或()23,0【详解】（1）解：令0y =，则2x =-，()2,0A \-，令0x =，则6y =，()0,6B \，26OA BO \==，，过点C 作CH x ^轴于H ，9090CAD BAO BAO ABO ÐÐÐÐ+=°+=°Q ，，CAD ABO ÐÐ\=，90AHC BOA ÐÐ\==°，由旋转得AB AC =，()AAS ABO CAH \V V ≌，26CH OA AH BO \====，，4OH AH OA \=-=，\点C 的坐标为()4,2-；（2）作点C 关于x 轴的对称点C ¢，连接BC ¢延长交x 轴于点P ，则点P 就是所求的最大值点，\()4,2C ¢设直线BC ¢的解析式为y kx b =+，\642b k b =ìí+=î，解得16k b =-ìí=î，6y x \=-+，()6,0P \；（3）()()()2,04,20,6A C B --Q ，，，设直线AC 的解析式为y mx n =+，则2042m n m n -+=ìí+=-î【变式训练1】如图1，在平面直角坐标系中，直线AB 与x 轴交于点(),0A m ，与y 轴交于点()0,B n ，且m n ，满足：()260m n n ++-=．(1)求：AOB S V 的值；(2)D 为OA 延长线上一动点，以BD 为直角边作等腰直角BDE V ，连接EA ，求直线EA 与y 轴交点F 的坐标；(3)在（2）的条件下，当2AD =时，在坐标平面内是否存在一点P ，使以B E F Р、、、为顶点的四边形是平行四边形，如果存在，直接写出点Р的坐标，若不存在，说明理由．∵EDB △为等腰直角三角形，∴,90DE DB EDB =Ð=°，∴18090EDG ODB Ð+Ð=°-。

2023-2024人教版八年级下册压轴题型汇总：一次函数(二)(原版)

2023-2024学年人教版八年级下册压轴题型汇总：一次函数（二）（原版）1、如图，直线l1：y＝2x+4与x轴交于点A，与y轴交于点B，将直线l1关于坐标原点中心对称后得到直线l2，l2与x轴交于点C，与y轴交于点D．（1）求直线l2的表达式；（2）求证：四边形ABCD为菱形；（3）除菱形ABCD外，是否在直线l1上还存在点P，在直线l2上还存在点Q，使得以点B、C、P、Q为顶点的四边形为菱形？若存在，求出符合条件的所有点P坐标，若不存在，说明理由．2、已知直线AC经过点（1，5）和（-1，1)与直线BC ：y=-2x-1相交于点C。

（1）求直线AC的解析式.（2）求直AC与y轴交点A的坐标及直线BC与x轴的交点D的坐标.（3）求两直线交点C的坐标.（4）求△ABC的面积.D3、为了响应国家”精准扶贫”政策,甲城有化肥200吨,乙城有化肥300吨,现要把化肥运往C和D两乡进行扶贫，,从甲城运往C和D两乡的运费分别是20元/吨与25元/吨；从乙城运往C和D两乡的运费分别为15元/吨和24元/吨,现已知C乡需要240吨, D乡需要260吨,如果某个个体户承包了这项运输任务,请你帮他算一算,怎样调运运费最少?（1）若甲城运往C乡化肥x吨，请写出将化肥运往C、D两乡的总运费y（元）与x（吨）的函数关系式。

（2）求自变量x的取值范围。

（3）当甲、乙两城各运往C、D两乡多少吨化肥时，总运费最省，最省的总运费是多少？4、甲、乙两家商场以同样价格销售相同的商品，在同一促销期间两家商场都让利酬宾.甲商场所有商品都按原价的八折出售，乙商场只对一次购物中超过100元后的价格部分按原价的七折出售.某顾客打算在促销期问到这两家商场中的一家去购物，如果该顾客在次购物中的购物金额的原价为x元，让利后的购物金额为y元.（1）分别就甲乙两家商场付出y与x的函数解析式；（2）该顾客选择去哪家商场购物会更省钱？并说明理由.t(分钟)y(海里) 4 6 9o5L 1L 265、如图信息，为走私船，为我公安快艇，航行时路程与时间的函数图象，问（1）在刚出发时我公安快艇距走私船多少㎞？（2）计算走私船与公安快艇的速度分别是多少？（3）写出, 的解析式. （4）问6分钟时两艇相距几海里。

人教版八下数学期末难点突破4 一次函数与几何大综合(二)全等、特殊四边形、最值

人教版八下数学期末难点突破4 一次函数与几何大综合（二）全等、特殊四边形、最值x+2与x轴交于点A，与y轴交于点D，以1.如图，在平面直角坐标系中，直线AD:y=−12OA为边向上作正方形OABC，OE⊥AD交BC于点E．(1) 求点E的坐标；(2) 若M是直线AD上的一动点，则在x轴上是否存在点N，使得以点O，E，M，N为顶点的四边形是平行四边形？若存在，求点N的坐标；若不存在，请说明理由；(3) 如图2，点P为AB右侧的一点，且△PAB的面积为4，直接写出：当△POE的周长最小时，直线PE的解析式为．答案1. 【答案】(1) 由y=−12x+2得A(4,0)，D(0,2)，证△AOD≌△OCE，∴OC=OA=4，CE=OD=2，∴E(2,4)．(2) 设点M(m,−12m+2)．①当OE为平行四边形的边时，MN∥OE，且MN=OE，过点M作MH⊥x轴于点H，则△MNH≌△OEC，∴MH=OC，∣∣−12m+2∣∣=4，解得m=−4或12，∴M(−4,4)或(12,−4)，∴易得点N(−6,0)或(14,0)；②当OE为平行四边形的对角线时，EM∥ON，且EM=ON，∴点M的纵坐标为4，∴−12m+2=4，解得m=−4，∴M(−4,4)，∴ON=EM=6，∴N(6,0)．综上所述，x轴上存在点N，使得以O，E，M，N为顶点的四边形为平行四边形，点N的坐标为N(−6,0)或(14,0)或(6,0)．(3) y=−25x+245【解析】(3) 易知点P在直线x=6上，作点E关于直线x=6的对称点F，连接OF交直线x=6于点P，PE=PF，∴PO+PE最小等于OF的长，∵OE长度不变，∴此时△POE的周长最小，可得直线l OF:y=25x，当x=6时，y=125，∴此时P(6,125)，∴直线PE的解析式为y=−25x+245．。

精选八年级数学一次函数与几何综合压轴题练习汇总

精选八年级数学一次函数与几何综合压轴题44题1．如图，在平面直角坐标系中，已知A（7a，0），B（0，﹣7a），点C为x轴负半轴上一点，AD⊥AB，∠1=∠2．（1）求∠ABC+∠D的度数；（2）如图①，若点C的坐标为（﹣3a，0），求点D的坐标（结果用含a的式子表示）；（3）如图②，在（2）的条件下，若a=1，过点D作DE⊥y轴于点E，DF⊥x 轴于点F，点M为线段DF上一点，若第一象限内存在点N（n，2n﹣3），使△EMN 为等腰直角三角形，请直接写出符合条件的N点坐标，并选取一种情况计算说明．2．如图1，点A和点B分别在y轴正半轴和x轴负半轴上，且OA=OB，点C 和点D分别在第四象限和第一象限，且OC⊥OD，OC=OD，点D的坐标为（m，n），且满足（m﹣2n）2+|n﹣2|=0．（1）求点D的坐标；（2）求∠AKO的度数；（3）如图2，点P，Q分别在y轴正半轴和x轴负半轴上，且OP=OQ，直线ON ⊥BP交AB于点N，MN⊥AQ交BP的延长线于点M，判断ON，MN，BM的数量关系并证明．3．如图①，平面直角坐标系XOY中，若A（0，a）、B（b，0）且（a﹣4）2+=0，以AB为直角边作等腰Rt△ABC，∠CAB=90°，AB=AC．（1）求C点坐标；（2）如图②过C点作CD⊥X轴于D，连接AD，求∠ADC的度数；（3）如图③在（1）中，点A在Y轴上运动，以OA为直角边作等腰Rt△OAE，连接EC，交Y轴于F，试问A点在运动过程中S△AOB：S△AEF的值是否会发生变化？如果没有变化，请直接写出它们的比值（不需要解答过程或说明理由）．4．等腰Rt△ACB，∠ACB=90°，AC=BC，点A、C分别在x轴、y轴的正半轴上．（1）如图1，求证：∠BCO=∠CAO（2）如图2，若OA=5，OC=2，求B点的坐标（3）如图3，点C（0，3），Q、A两点均在x轴上，且S△CQA=18．分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，连接MN交y轴于P点，OP的长度是否发生改变？若不变，求出OP的值；若变化，求OP的取值范围．5．如图1，在平面直角坐标系中，点A、B分别在x轴、y轴上．（1）如图1，点A与点C关于y轴对称，点E、F分别是线段AC、AB上的点（点E不与点A、C重合），且∠BEF=∠BAO．若∠BAO=2∠OBE，求证：AF=CE；（2）如图2，若OA=OB，在点A处有一等腰△AMN绕点A旋转，且AM=MN，∠AMN=90°．连接BN，点P为BN的中点，试猜想OP和MP的数量关系和位置关系，说明理由．6．如图，在平面直角坐标系中，已知A（0，a）、B（﹣b，0）且a、b满足+|a﹣2b+2|=0．（1）求证：∠OAB=∠OBA；（2）如图1，若BE⊥AE，求∠AEO的度数；（3）如图2，若D是AO的中点，DE∥BO，F在AB的延长线上，∠EOF=45°，连接EF，试探究OE和EF的数量和位置关系．7．如图，直线AB交x轴于点A（a，0），交y轴于点B（0，b），且a、b满足|a+b|+（a﹣5）2=0（1）点A的坐标为，点B的坐标为；（2）如图，若点C的坐标为（﹣3，﹣2），且BE⊥AC于点E，OD⊥OC交BE 延长线于D，试求点D的坐标；（3）如图，M、N分别为OA、OB边上的点，OM=ON，OP⊥AN交AB于点P，过点P作PG⊥BM交AN的延长线于点G，请写出线段AG、OP与PG之间的数列关系并证明你的结论．8．如图，在平面直角坐标系中，A（0，a）、B（b，0）、C（c，0），且+|b﹣2|+（c+2）2=0．（1）直接写出A、B、C各点的坐标：A、B、C；（2）过B作直线MN⊥AB，P为线段OC上的一动点，AP⊥PH交直线MN于点H，证明：PA=PH；（3）在（1）的条件下，若在点A处有一个等腰Rt△APQ绕点A旋转，且AP=PQ，∠APQ=90°，连接BQ，点G为BQ的中点，试猜想线段OG与线段PG的数量关系与位置关系，并证明你的结论．9．如图，平面直角坐标系中，已知点A（a﹣1，a+b），B（a，0），且+（a﹣2b）2=0，C为x轴上点B右侧的动点，以AC为腰作等腰△ACD，使AD=AC，∠CAD=∠OAB，直线DB交y轴于点P．（1）求证：AO=AB；（2）求证：OC=BD；（3）当点C运动时，点P在y轴上的位置是否发生改变，为什么？10．等腰Rt△ABC中，AC=AB，∠BAC=90°，点A、点B分别是y轴、x轴上的两个动点．（1）如图1，若A（0，2），B（1，0），求C点的坐标；（2）如图2，当等腰Rt△ABC运动，直角边AC交x轴于点D，斜边BC交y 轴于点E，且点D恰为AC中点时，连接DE，求证：∠ADB=∠CDE；（3）如图3，在等腰Rt△ABC不断运动的过程中，直角边AC交x轴于点D，斜边BC交y轴于点E，若BD始终是∠ABC平分线，试探究：线段BD与OA+OD 之间存在的数量关系，并说明理由．11．在△ABC中，∠BAC=90°，AB=AC．（1）如图1，若A、B两点的坐标分别是A（0，4），B（﹣2，0），求C点的坐标；（2）如图2，作∠ABC的角平分线BD，交AC于点D，过C点作CE⊥BD于点E，求证：CE=BD；（3）如图3，点P是射线BA上A点右边一动点，以CP为斜边作等腰直角△CPF，其中∠F=90°，点Q为∠FPC与∠PFC的角平分线的交点，当点P运动时，点Q 是否恒在射线BD上？若在，请证明；若不在，请说明理由．12．已知点A与点C为x轴上关于y轴对称的两点，点B为y轴负半轴上一点．（1）如图1，点E在BA延长线，连接EC交y轴于点D，若BE=8，EC=6，CB=4，求△ADE的周长；（2）如图2，点G为第四象限内一点，BG=BA，连接GC并延长交y轴于F，试探究∠ABG与∠FCA之间有和数量关系？并证明你的结论；（3）如图3，A（﹣3，0），B（0，﹣4），点E（﹣6，4）在射线BA上，以BC 为边向下构成等边△BCM，以EC为边向上构造等腰△CNE，其中CN=EN，∠CNE=120°，连接AN，MN，求证：．13．已知A（0，a）和B（b，0），且a、b满足（a﹣4）2+|b﹣4|=0（1）试通过计算判断△AOB的形状．（2）如图1，若D为OB的中点，过O作AD的垂线交AB于E，连DE，求证：AD=OE+DE．（3）如图2，M、N同时从D点出发，以相同的速度向x轴正方向和负方向运动到如图所示的位置，过O作AM的垂线交AB于E，连NE，求证：∠AMB=∠ONE．14．如图1，在平面直角坐标系中，点B与点C关于x轴对称，点D为x轴上一点，点A为射线CE上一动点，且∠BAC=2∠BDO，过D作DM⊥AB于M．（1）求证：∠ABD=∠ACD；（2）求证：AD平分∠BAE；（3）当A点运动时（如图2），的值是否发生变化？若不变化，请求出其值；若变化，请说明理由．15．如图1，在平面直角坐标系中，∠BAC=90°，AB=AC，已知点A点的坐标是（m，n），且m，n满足等式+|m﹣n+1|=0．（1）求点A的坐标；（2）若B点的坐标为（6，0），求点C的坐标；（3）如图2，在（2）的条件下，连接OA，作AD⊥AO，且AD=AO，连接CD，已知点E（3，0），线段AE与CD有何数量关系与位置关系？写出你的结论并加以证明．16．已知，如图，在平面直角坐标系中，点A、B、C分别在坐标轴上，且OA=OB=OC，S△ABC=25．点P从C点出发沿y轴负方向以1个单位/秒的速度向下运动，连接PA、PB，D为线段AC的中点．（1）求D点的坐标；（2）设点P运动的时间为t秒，求当t为何值时，DP与DB垂直相等；（3）若PA=PB，在第四象限内有一动点Q，连QA、QB、QP，且∠QBA=∠PBQ+∠QAB=30°．当Q在第四象限内运动时，判断△APQ的形状，并说明理由．17．在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（0，﹣1），AB=．（1）如图1，以点A为圆心，线段AB的长为半径画弧，与x轴的负半轴交于点C，过点A作AH⊥BC于H交y轴于D，求点D的坐标；（2）如图2，在线段OA上有一点E满足S△OEB：S△EAB=1：，直线AN平分△OAB的外角交BE于N．求∠BNA的度数；（3）如图3，动点Q为A右侧x轴上一点，另有在第四象限的动点P，动点P、Q，总满足∠PAB=∠PBA和∠PQA=∠PAQ．①请画出满足题意的图形；②若点B在y轴上运动，其他条件不变，∠ABO=α，请直接用含α的式子表示∠BPQ 的值（不需证明）．18．如图所示，在平面直角坐标系中，A点坐标为（﹣2，2）．（1）如图（1），在△ABO为等腰直角三角形，求B点坐标．（2）如图（1），在（1）的条件下，分别以AB和OB为边作等边△ABC和等边△OBD，连结OC，求∠COB的度数．（3）如图（2），过点A作AM⊥y轴于点M，点E为x轴正半轴上一点，K为ME延长线上一点，以MK为直角边作等腰直角三角形MKJ，∠MKJ=90°，过点A作AN⊥x轴交MJ于点N，连结EN．则①的值不变；②的值不变，其中有且只有一个结论正确，请判断出正确的结论，并加以证明和求出其值．19．如图1，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴与G，连OB、OC．（1）判断△AOG的形状，并予以证明；（2）若点B、C关于y轴对称，求证：AO⊥BO；（3）在（2）的条件下，如图2，点M为OA上一点，且∠ACM=45°，BM交y 轴于P，若点B的坐标为（3，1），求点M的坐标．20．如图1，在平面直角坐标系中，已知A（﹣5，0），C（0，﹣4），点B在y 轴正半轴上，满足S△ABC=20，点P（m，0），（﹣4＜m＜0），线段PB绕点P顺时针旋转90°至PD．（1）求证：OB=OC；（2）求点D的坐标；（用含m的式子表示）（3）如图2，连接CD并延长交x轴于点E，求证：∠PDC=45°+∠PBO．21．如图，已知B（﹣1，0），C（1，0），A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC=∠BAC．（1）求证：∠ABD=∠ACD；（2）求证：AD平分∠CDE；（3）若在D点运动的过程中，始终有DC=DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数？22．已知：如图1：点A（5，0）B（0，2），AB=AC，∠BAC=90°．（1）求点C的坐标．（2）以AB为斜边作等腰直角△ABD，请直接写出点D的坐标；（3）如图2，若E、F分别在BC、AB上，∠AEC=75°，FE⊥BC．求证：BF=AE．23．在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足++（2﹣d）2=0，DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．（1）求点A、B、D的坐标；（2）求点E、F的坐标；（3）如图，过P（0，﹣1）作x轴的平行线，在该平行线上有一点Q（点Q在P的右侧）使∠QEM=45°，QE交x轴于N，ME交y轴正半轴于M，求的值．24．如图1，A、B分别为x、y轴上的点，O为坐标原点，设OA=a，OB=b，AB=c，（1）若正数a、b、c满足a2+b2+c2﹣6a﹣8b﹣10c+50=0，且OP⊥AB于P，求OP的长；（2）如图2，若P为线段AB的中点，试探究线段OP与AB间的数量关系，并说明理由．（3）如图3，若P是线段AB上一动点（不与A、B点重合），在射线OP上取一点E，使AE=a，此时∠AOE=∠AEO．在第一象限内，过E作AE的垂线，并截取ED=b，连AD、BD，BD交射线OP于F点．当P点运动时，的值不变，请说明理由，并求这个不变的值．25．如图：平面直角坐标系中，△ABC的三个顶点的坐标为A（a，0），B（b，0），C（0，c），且a，b，c满足．点D为线段OA上一动点，连接CD．（1）判断△ABC的形状并说明理由；（2）如图，过点D作CD的垂线，过点B作BC的垂线，两垂线交于点G，作GH⊥AB于H，求证：；（3）如图，若点D到CA、CO的距离相等，E为AO的中点，且EF∥CD交y 轴于点F，交CA于M．求的值．26．如图，直角坐标系中，点B（a，0），点C（0，b），点A在第一象限．若a，b满足（a﹣t）2+|b﹣t|=0（t＞0）．（1）证明：OB=OC；（2）如图1，连接AB，过A作AD⊥AB交y轴于D，在射线AD上截取AE=AB，连接CE，F是CE的中点，连接AF，OA，当点A在第一象限内运动（AD不过点C）时，证明：∠OAF的大小不变；（3）如图2，B′与B关于y轴对称，M在线段BC上，N在CB′的延长线上，且BM=NB′，连接MN交x轴于点T，过T作TQ⊥MN交y轴于点Q，求点Q的坐标．27．已知，在平面直角坐标系中，A（a，0）、B（0，b），a、b满足．C 为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO=PD，DE⊥AB于E．（1）求∠OAB的度数；（2）设AB=6，当点P运动时，PE的值是否变化？若变化，说明理由；若不变，请求PE的值；（3）设AB=6，若∠OPD=45°，求点D的坐标．28．在平面直角坐标系中，A（a，b）在第一象限内，且a、b满足条件：b﹣a=，AB⊥y轴于B，AC⊥x轴于C．（1）求△AOC的面积；（2）如图，E为线段OB上一点，连AE，过A作AF⊥AE交x轴于F，连EF，ED平分∠OEF交OA于D，过D作DG⊥EF于G，求的值；（3）如图，D为x轴上一点，AC=CD，E为线段OB上一动点，连DA、CE，F 是线段CE的中点，若BF⊥FK交AD于K，请问∠KBF的大小是否变化？若不改变，请求其值；若改变，求出变化的范围．29．如图1，在直角坐标系中，A点的坐标为（a，0），B点的坐标为（0，b），且a、b满足．（1）求证：∠OAB=∠OBA．（2）如图2，△OAB沿直线AB翻折得到△ABM，将OA绕点A旋转到AF处，连接OF，作AN平分∠MAF交OF于N点，连接BN，求∠ANB的度数．（3）如图3，若D（0，4），EB⊥OB于B，且满足∠EAD=45°，试求线段EB 的长度．30．已知：在直角坐标系中，A为x轴负半轴上的点，B为y轴负半轴上的点。

【解答压轴题型一次函数综合题】2022-2023学年八年级数学下学期期末考试练习(人教版)解析版

解答压轴题型：一次函数综合题一．解答题（共33小题）1．（2022春•越秀区期末）如图，点(0,2)A ，(3,3)B ，(7,1)C −，四边形OBCD 是矩形，BD 与x 轴交于点E ．（1）求直线AB 的解析式；（2）求线段OE 的长；（3）若点P 为直线AB 上一动点，设POB ∆的面积为1S ，OBE ∆的面积为2S ，且122S S =，求点P 的坐标．【答案】见解析【详解】解：（1）设直线AB 解析式为y kx b =+，将(0,2)A ，(3,3)B 代入y kx b =+得233b k b =⎧⎨=+⎩，解得132k b ⎧=⎪⎨⎪=⎩，123y x ∴=+．（2）连接OC 交BD 于点F ，四边形OBCD 是矩形，点C 坐标为(7,1)−，点O 坐标为(0,0)，点F 为OC 中点，∴点F 坐标为7(2，1)2−，设直线BD 解析式为y kx b =+，将(3,3)，7(2，1)2−代入y kx b =+得331722k b k b =+⎧⎪⎨−=+⎪⎩，解得724k b =−⎧⎨=⎩，724y x ∴=−+，将0y =代入724y x =−+得0724x =−+，解得247x =，∴点E 坐标为24(7，0)，即247OE =．（3）OBE ∆的面积为211243632277B S OE y =⋅=⨯⨯=， 127227S S ∴==，作BM y ⊥轴于点M ，①当点P 在y 轴左侧时，连接OP ，作PN y ⊥轴于点N ，POB POA AOB S S S ∆∆∆=+，1172151232727POA POB AOB B S S S S OA x ∆∆∆∴=−=−⋅⋅=−⨯⨯=， ∴1151||2()227P P OA x x ⋅=⨯−=，解得517P x =−，将517x =−代入123y x =+得51132737y =−⨯+=−， ∴点P 坐标为51(7−，3)7−．②当点P 在y 轴右侧，连接OP ，作PN y ⊥轴于点N ，727POB POA AOB S S S ∆∆∆=−=， 7219323727POA POB AOB S S S ∆∆∆∴=+=+⨯⨯=， ∴19327P OA x ⋅=，解得937P x =，将937x =代入123y x =+得457y =， ∴点P 坐标为93(7，45)7．综上所述，点P 坐标为51(7−，3)−93(7，45)7．2．（2022春•海珠区期末）直线24y x =−+与x 轴，y 轴分别交于点A 、B ，过点A 作AC AB ⊥于点A ，且AC AB =，点C 在第一象限内．（1）求点A 、B 、C 的坐标；（2）在第一象限内有一点(3,)P t ，使PAB ABC S S ∆∆=，求t 的值．【答案】见解析【详解】解：（1）令0x =代入24y x =−+中，4y ∴=，(0,4)B ∴，令0y =代入24y x =−+中，2x ∴=，(2,0)A ∴，过点C 作CD x ⊥轴于点D ，90BAC ∠=︒，90DAC BAO ABO BAO ∴∠+∠=∠+∠=︒，ABO DAC ∴∠=∠，在ABO ∆与CAD ∆中，ABO DAC BOA CDA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABO CAD AAS ∴∆≅∆2CD OA ∴==，4AD OB ==，6OD ∴=，(6,2)C ∴；（2）在第一象限内有一点(3,)P t ，使PAB ABC S S ∆∆=，//CP AB ∴，设直线CP 为2y x b =−+，代入C 的坐标得，226b =−⨯+，解得14b =，∴直线CP 为214y x =−+，把点(3,)P t 代入得，23148t =−⨯+=，t ∴的值为8．3．（2022春•海珠区期末）当m ，n 为实数，且满足m nm n +=时，就称点(,)m P m n 为“状元点”．已知点(0,7)A 和点M 都在直线y x b =+上，点B ，C 是“状元点”，且B 在直线AM 上，（1）求b 的值及判断点(2,6)F 是否为“状元点”；（2）请求出点B 的坐标；（3）若AC …C 的横坐标的取值范围．【答案】见解析【详解】解：（1）点A 在直线y x b =+上，∴把(0,7)A 代入y x b =+，7b ∴=，∴直线AM 解析式为7y x =+．m nm n +=， ∴1m m n =−，(,1)P m m ∴−，当2m =时，116m −=−≠∴点(2,6)F 不是“状元点”；（2）点B 是“状元点”，∴设点B 的横坐标为p ，则纵坐标为1p −，点B 的坐标为(,1)p p −，点B 在直线:7AM y x =+上，∴把点(,1)B p p −代入7y x =+得，3p =−，14p ∴−=，(3,4)B ∴−；（3）由71y x y x =+⎧⎨=−+⎩，解得34x y =−⎧⎨=⎩，点N 是直线7y x =+与直线1y x =−+的交点，(3,4)N ∴−，直线1y x =−与直线1y x =−+互相垂直．，由勾股定理得，218AN =，当AC =NC ，此时NC ==4CH =，所以点C 的横坐标为1或7−，∴当AC …C 的横坐标的取值范围为71c −……．4．（2022春•天河区期末）已知直线12y x =，记为1l ．（1）填空：直线112y x =+可以看作是由直线1l 向平移个单位得到；（2）将直线1l 沿x 轴向右平移4个单位得到直线2l ，解答下列问题： ①求直线2l 的函数解析式；②若x 取任意实数时，函数||y x m =−的值恒大于直线2l 的函数值，结合图象求出m 的取值范围．【答案】见解析【详解】解：（1）如下图所示，112y x =+是由12y x =向上平移1个单位得到的；故答案为：上，1；（2）①当12y x =沿x 轴向右平移4个单位后经过点(4,0)， ∴平移得到的直线2l 的函数解析式为11(4)222y x x =−=−； ②如下图所示，画出||y x =的图象，||y x m =−的函数图象可以看作是||y x =沿x 轴水平移动m 个单位，当0m >时，||y x =向右平移m 个单位，当0m <时，||y x =向左平移m 个单位，要是函数||y x m =−的值恒大于直线2l 的函数值，则函数||y x m =−的图象位于直线2l 的上方，由函数图象可知当4m <时函数||y x m =−的图象位于直线2l 的上方， m ∴的取值范围为4m <．5．（2022春•荔湾区期末）如图，在平面直角坐标系中，O 为坐标原点，矩形OABC 的顶点(8,0)A ，(0,6)C ，将矩形OABC 的一个角沿直线BD 折叠，使得点A 落在对角线OB 上的点E 处，折痕与x 轴交于点D ．（1）线段OB 的长度；（2）求直线BD 所对应的函数表达式；（3）若点Q 在线段BD 上，在线段BC 上是否存在点P ，使以D ，E ，P ，Q 为顶点的四边形是平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】见解析【详解】解：（1）由题意，得：点B 的坐标为(8,6)，8OA =，6AB OC ==，10OB ∴=，故答案为：10．（2）设AD a =，则DE a =，8OD a =−，1064OE OB BE =−=−= 222OD OE DE =+，即222(8)4a a −=+，3a ∴=，5OD ∴=，∴点D 的坐标为(5,0)．设直线BD 所对应的函数表达式为(0)y kx b k =+≠，将(8,6)B ，(5,0)D 代入y kx b =+，得：8650k b k b +=⎧⎨+=⎩，解得：210k b =⎧⎨=−⎩， ∴直线BD 所对应的函数表达式为210y x =−；（3）存在，理由：过点E 作EF x ⊥轴于点F ，如图所示．90BED BAD ∠=∠=︒，18090OED BED ∴∠=︒−∠=︒1122ODE S OD EF OE DE ∆∴=⋅=⋅， 431255OE DE EF OD ⋅⨯∴===，在Rt OEF ∆中，165OF ==， ∴点E 的坐标为1612(,)55，由//PE BD ，设直线PE 的解析式为：2y x b =+，把1612(,)55E 代入得：1216255b =⨯+，解得：4b =−， ∴直线PE 的解析式为：24y x =−，令6y =，则624x =−，解得：5x =，∴存在，点P 的坐标为：(5,6)．6．（2022春•番禺区期末）如图，直线:l y =+与两坐标轴分别交于A 、B 两点，点M 为线段AB 的中点．（1）求A 、B 、M 的坐标；（2）直线l 关于y 轴对称的直线为l '，写出直线l '的解析式；（3）若直线l '交x 轴于点C ，直线MC 与y 轴的交点为N ，连接OM ，求OM ON．【答案】见解析【详解】解：（1）令0x =，则y =+A ∴，令0y =，则0+=，解得1x =−， (1,0)B ∴−，点M 为线段AB 的中点．1(2M ∴−；（2）(1,0)B −，∴点B 关于y 轴的对称点(1,0)，设直线l '的解析式为y kx =代入点(1,0)得，0k =+k =，∴直线l '的解析式为y =（3）设直线MC 的解析式为y ax b =+，把点C 、M的坐标代入得012a b a b +=⎧⎪⎨−+=⎪⎩，解得a b ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线MC的解析式为y =+ 令0x =，则y =ON ∴， (0,3)A ，(1,0)B −，2AB ∴==，OM 是直角三角形AOB 斜边的中线，112OM AB ∴==，∴OM ON ==． 7．（2022春•番禺区期末）如图，已知一次函数12y x b =−+的图象过点(0,3)A ，点P 是该直线上的一个动点，过点P 分别作PM 垂直x 轴于点M ，PN 垂直y 轴于点N ，在四边形OMPN 的边上分别截取：23OB OM =，23MC MP =，13OE ON =，13ND NP =．（1）求b 的值；（2）求证：四边形BCDE 是平行四边形；（3）在直线12y x b =−+上是否存在这样的点P ，使四边形BCDE 为正方形？若存在，请求出所有符合的点P 的坐标；若不存在，请说明理由．【答案】见解析【详解】解：（1）一次函数12y x b =−+的图象过点(0,3)A ， 1302b =−⨯+，解得：3b =．（2）证明：过点P 分别作PM 垂直x 轴于点M ，PN 垂直y 轴于点N ，90OMP PNO MON ∴∠=∠=∠=︒，∴四边形PMON 是矩形，PM ON ∴=，OM PN =，90MPN ∠=︒． 23OB OM =，23MC MP =，13OE ON =，13NO NP =， PC OE ∴=，CM NE =，ND BM =，PD OB =，在OBE ∆和PDC ∆中，OB PD EOB CPD OE PC =⎧⎪∠=∠⎨⎪=⎩，()OBE PDC SAS ∴∆≅∆，BE DC ∴=．在MBC ∆和NDE ∆中，MB ND BMC END MC NE =⎧⎪∠=⎨⎪=⎩，()MBC NDE SAS ∴∆≅∆，DE BC ∴=．BE DC =，DE BC =，∴四边形BCDE 是平行四边形．（3）存在；理由：设P 点坐标(,)x y ，当OBE MCB ∆≅∆时，四边形BCDE 为正方形，OE BM =，当点P 在第一象限时，即1133y x =，x y =．P 点在直线上，132y x y x⎧=−+⎪⎨⎪=⎩，解得22x y =⎧⎨=⎩，当点P 在第二象限时，x y −=132y x y x⎧=−+⎪⎨⎪=−⎩，解得66x y =−⎧⎨=⎩，在直线12y x b =−+上存在这样的点P ，使四边形BCDE 为正方形，P 点坐标是(2,2)或(6,6)−．8．（2022春•武昌区期末）如图，在平面直角坐标系中，直线46y x =+与x 轴交于点A ，与y 轴交于点B ，点C 是x 轴正半轴上一点，且332ABC S ∆=．（1）直接写出点C 的坐标为，直线BC 的解析式为；（2）设点(1,)D m −在直线AB 上，点E 在y 轴上，连接DE ，以DE 为边向DE 右侧作正方形DEFG ． ①在E 点的运动过程中，当顶点F 落在直线BC 上时，求点E 的坐标；②点E 从B 点运动到O 点的过程中，正方形DEFG 的对角线交点T 运动的路径长为．【答案】见解析【详解】解：（1）在46y x =+中，令0x =得6y =，令0y =得32x =−，3(2A ∴−，0)，(0,6)B ， 332ABC S ∆=， ∴13322AC OB ⋅=，即133622AC ⨯⨯=， 112AC ∴=，点C 是x 轴正半轴上一点，(4,0)C ∴；设BC 解析式为y kx b =+，640b k b =⎧⎨+=⎩，解得326k b ⎧=−⎪⎨⎪=⎩， BC ∴解析式为362y x =−+；故答案为：(4,0)，362y x =−+；（2）①当点E 在D 的下方时，过D 作//DM y 轴，过E 作//EM x 轴交DM 于M ，过F 作FN EM ⊥交直线EM 于N ，如图：(1,)D m −在直线46y x =+上，462m ∴=−+=，(1,2)D ∴−，设(0,)E t ，则2DM t =−，1ME =，四边形DEFG 是正方形，DE FE ∴=，90DEF ∠=︒，90DEM FEN EFN ∴∠=︒−∠=∠，90M N ∠=∠=︒，()DEM EFN AAS ∴∆≅∆，2EN DM t ∴==−，1FN ME ==，(2,1)F t t ∴−+，把(2,1)F t t −+代入362y x =−+得： 31(2)62t t +=−−+，解得4t =−， (0,4)E ∴−，当点E 在D 的上方时，同理可得(2,1)F t t −−，则(0,4)E ，综上：(0,4)E −或(0,4)；②由①知，当点E 在D 的上方时，设(0,)E t ，则(2,1)F t t −−，DF ∴的中点31(,)22t t T −+， ∴点T 在直线2y x =+上运动，当点E 与B 重合时，6t =，37(,)22T ∴，当点E 运动到(0,2)时，2t =，1(2T ∴−，3)2，∴点T 经过的路径长为当点E 在D 的下方时，(2,1)F t t −+，则13(,)22t t T −+， ∴点T 在直线2y x =−+上运动，同理可得，点T 的运动路径为综上：点T 的运动路径为+=故答案为：．9．（2022春•白云区期末）如图，一次函数1y kx =+的图象上A ，B 两点，点A 在第一象限，点B 在x 轴上．点D 在x 轴正半轴上，点C 的坐标为(1,2)−，四边形OADC 为菱形．（1）求k 的值；（2）求ABD ∆的面积；（3）设点P 是直线AB 上一动点，且12AOP OADCS S ∆=菱形，求点P 的坐标．【答案】见解析【详解】解：（1）由菱形的性质可知，点A 的坐标为(1,2)，(2,0)D ，把点(1,2)A 代入1y kx =+得，12k +=，解得1k =；（2）由（1）得一次函数的关系式为1y x =+，当0y =时，1x =−，∴点(1,0)B −，即1OB =，123BD ∴=+=，13232ABD S ∆∴=⨯⨯=；（3）设点(,1)P x x +，1122222AOP OADC S S ∆==⨯⨯=菱形， ①当点P 在BA 的延长线上时，有2AOP BOP AOB S S S ∆∆∆=−=， ∴111|1|12222x ⨯⨯+−⨯⨯=，解得5x =或7x =−（舍去），当5x =时，6y =，∴点P 的坐标为(5,6)；②当点P 在AB 的延长线上时，有2AOP BOP AOB S S S ∆∆∆=+=， ∴111|1|12222x ⨯⨯++⨯⨯=，解得3x =−或1x =（舍去），此时点P 的坐标为(3,2)−−，综上所述，符合条件的点(5,6)P 或(3,2)−−．10．（2022春•广州期末）在平面直角坐标系xOy 中，对于两点A ，B ，给出如下定义：以线段AB 为边的正方形称为点A ，B 的“确定正方形”．如图1为点A ，B 的“确定正方形”的示意图．（1）如果点M 的坐标为(0,1)，点N 的坐标为(3,1)，那么点M ，N 的“确定正方形”的面积为 9 ；（2）已知点O 的坐标为(0,0)，点C 为直线y x b =+上一动点，当点O ，C 的“确定正方形”的面积最小，且最小面积为2时，求b 的值．（3）已知点E 在以边长为2的正方形的边上，且该正方形的边与两坐标轴平行，对角线交点为(,0)P m ，点F 在直线2y x =−−上，若要使所有点E ，F 的“确定正方形”的面积都不小于2，直接写出m 的取值范围．【答案】见解析【详解】解：（1）(0,1)M ，(3,1)N ，3MN ∴=， ∴以MN 为边的正方形的面积239==，故答案为9．（2）点O ，C 的“确定正方形”面积为2，OC ∴=，点O ，C 的“确定正方形”面积最小，OC ∴⊥直线y x b =+于点C ．①当0b >时，如图1中，由题意可知OM ON =，MON ∆为等腰直角三角形，可求OC NC MC ===2b ∴=②当0b <时，同理可求2b =−，2b ∴=±．（3）如图2中，当正方形ABCD 在直线2y x =−−的下方时，延长DB 交直线2y x =−−于H ．易知BH ⊥直线2y x =−−，当BH =点E ，F 的“确定正方形”的面积的最小值为2，此时(6,0)P −．如图3中，当正方形ABCD 在直线2y x =−−的上方时，延长DB 交直线2y x =−−于H ．易知BH ⊥直线2y x =−−，当BH =点E ，F 的“确定正方形”的面积的最小值为2，此时(2,0)P ，观察图象可知：当6m −…或2m …时，所有点E ，F 的“确定正方形”的面积都不小于2．11．（2022春•花都区期末）将一张矩形的纸片放到平面直角坐标系中，使矩形OABC 的两边OA 、OC 分别落在x 轴、y 轴上．如图，将OAB ∆沿对角线OB 翻折到ONB ∆，ON 与CB 交于点M ．（1）重叠部分OBM ∆是什么形状的三角形，请说明你的理由；（2）已知3OC =，BM =M 坐标( ， )．【答案】见解析【详解】解：（1）OBM ∆是等腰三角形，理由如下：由折叠的性质得：BON AOB ∠=∠，四边形OABC 是矩形，//BC OA ∴，AOB CBO ∴∠=∠，BON CBO ∴∠=∠，OM BM ∴=，OBM ∴∆是等腰三角形；（2）由折叠的性质得：3BN AB OC ===，由（1）可知，OM BM ==四边形OABC 是矩形，90OCB ∴∠=︒，在Rt OCM ∆中，根据勾股定理得：1CM ==，∴点M 的坐标为(1,3)，故答案为：1，3．12．（2022春•花都区期末）读一读“数形结合”是一种重要的数学思想，其简而言之就是把数学中“数”和数学中“形”结合起来解决数学问题的一种数学思想．具体地说就是将抽象数学语言与直观图形结合起来，使抽象思维与形象思维结合起来，通过“数”与“形”之间的对应和转换来解决数学问题．在中学数学的解题中，主要有三种类型：以数化形、以形变数、形数互变．研一研【定义】在平面直角坐标系xOy 中，如果点A ，C 为某个菱形的一组对角的顶点，且点A ，C 在直线y x =上，那么称该菱形为点A ，C 的“最佳菱形”，如图是点A ，C 的“最佳菱形”的一个示意图．【运用】已知点M 的坐标为(2,2)，点P 的坐标为(4,4)．（1）下列各组点，能与点M ，P 形成“最佳菱形”的是．①(3,4)E ，(4,3)F②(2,3)G ，(3,2)H③(2,4)I ，(4,2)J（2）如果四边形MNPQ 是点M ，P 的“最佳菱形”．①当点N 的坐标为(6,0)时，求四边形MNPQ 的面积；②当四边形MNPQ 的面积为16，且与直线y x b =+有公共点时，求b 的取值范围．【答案】见解析【详解】解：（1）如图1，观察图象可得：I ，J 能与点M ，P 形成“最佳菱形”，故答案为：③；（2）①如图2，(2,2)M ，(4,4)P ，(6,0)N ，设点Q 的坐标为(,)x y ，则11(24)(6)22x +=+且11(24)(0)22y +=+，解得：06x y =⎧⎨=⎩，故点Q 的坐标为(0,6)，由点P 、M 的坐标得，PM ==同理可得：QN则边形MNPQ 的面积12MN QN =⋅12=⨯12=； ②如图2，“点M 的坐标为(2,2)，点P 的坐标为(4,4)，PM ∴=四边形MNPQ 的面积为16，1162MNPQ S PM QN ∴=⋅=四边形，即1162QN ⨯=，QN ∴=四边形MNPQ 是菱形，QN MP ∴⊥，EM =EN =，作直线QN ，交x 轴于A ，过点N 作x 轴的平行线交于点M '，(2,2)M ，OM ∴=OE ∴= M 和P 在直线y x =上，45MOA M ∴∠=∠'=︒，∴△EM N '是等腰直角三角形，EM EN ∴'==∴8M N '=，OM =则点(1,1)M '−−，故点N 的纵坐标为：1−，点N 的横坐标为：817−=，则点N 的坐标为(7,1)−，将N 的坐标(7,1)−代入y x b =+，得：17b −=+，解得：8b =−，同理可知：Q 的坐标为(1,7)−，此时，8b =，由题意得：四边形MNPQ 与直线y x b =+有公共点时，b 的取值范围是：88b −……．13．（2022春•增城区期末）如图所示，在平面直角坐标系中，直线1y x =+与x 轴交于点B ，直线334y x =−+与x 轴交于点C ，与y 轴交于点D ．（1）直接写出点B 、C 的坐标；（2）点(,)M x y 是直线1y x =+图象上一点，设BCM ∆的面积为S ，请求出S 关于x 的函数关系式；并探究当点M 运动到什么位置时（求出点坐标即可），BCM ∆的面积为10，并说明理由；（3）线段CD 上是否存在点P ，使CBP ∆为等腰三角形，如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】见解析【详解】解：（1）在1y x =+中，令0y =，则1x =−，(1,0)B ∴−，在334y x =−+中，令0y =，则4x =， (4,0)C ∴，（2）点(,)M x y 是直线1y x =+图象上一点，1y x ∴=+，115||5|1||1|222S BC y x x ∴=⨯⨯=⨯⨯+=+；当10S =时，5|1|102x +=，解得3x =或5x =−，(3,4)M ∴或(5,4)−−；（3）存在点P ，使CBP ∆为等腰三角形，理由如下：设3(,3)4P t t −+，(04)t <<，5BC ∴=，CP =，BP ，①当BC CP =5=，解得0t =或8t =，(0,3)P ∴，(8,3)P −（舍)；②当BC BP =5，解得4t =（舍)或125t =−， 12(5P ∴−，24)5（舍)；③当CP BP ==，解得32t =， 3(2P ∴，15)8；综上所述：P 点坐标为(0,3)，3(2，15)8． 14．（2022春•增城区期末）如图1所示，菱形ABCD 的顶点A ，B 在x 轴上，点A 在点B 的左侧，点D 在y 轴的正半轴上．点C 的坐标为(4，，动点P 从点A 出发，以每秒1个单位长度的速度，按照A D C B A →→→→的顺序在菱形的边上匀速运动一周，设运动时间为t 秒．（1）求菱形ABCD 的面积；（2）当3t =时，问线段AC 上是否存在点E ，使得PE DE +最小，如果存在，求出PE DE +最小值；如果不存在，请说明理由；（3）点P 至AC 的距离为1时，直接写出点P 的运动时间t 的值．【答案】见解析【详解】解：（1）(4C ，，90AOD ∠=︒，4DC ∴=，DO =四边形ABCD 为菱形，4AB CD ∴==．∴菱形ABCD 的面积4AB OD =⋅=⨯=（2）存在，如图1所示：在菱形ABCD 中，点P 关于AC 的对称点为P '，3AP '=，连接DP '交AC 于点E ，连接PE ，PE DE P E ED P D ''∴+=+=．四边形ABCD 为菱形，4AD CD ∴==． 2OD =2OA ∴=，1OP '∴=，在Rt DOP '∆中，222DO P O P D ''+=，2221P D '∴+=，P D '∴=PE DE ∴+；（3）如图2所示：①当点P 在AD 上时，过点P 作PE AC ⊥，垂足为．，，，，，由菱形的性质可知：，，，，．．②当点在上时，如图3所示：由菱形的性质可知：，，，，．E 90AOD ∠=︒2OA =4AD =30ADO ∴∠=︒60DAO ∠=︒1302PAE DAB ∠=∠=︒1PE =30PAE ∠=︒90PEA ∠=︒2AP ∴=2t ∴=PDC 1302PCE DCB ∠=∠=︒1PE =30PCE ∠=︒90PEC ∠=︒2CP ∴=．．③如图4所示：当点在上时．由菱形的性质可知：，，，，．．．④如图5所示；点在上时．由菱形的性质可知：，，，，．．．综上所述，当或或或时，点到的距离是1．15．（2022春•武汉期末）如图，平面直角坐标系中，直线分别交、轴于、两点，点为线段的中点．（1）直接写出点的坐标；（2）如图1，点是轴正半轴上的一动点，过点作交轴正半轴于点，连接，点、426AD DP ∴+=+=6t ∴=PBC 1302PCE DCB ∠=∠=︒1PE =30PCE ∠=︒90PEC ∠=︒2CP ∴=44210AD DC CP ∴++=++=10t ∴=PAB 1302PAE DAB ∠=∠=︒1PE =30PAE ∠=︒90PEA ∠=︒2AP ∴=444214AD DC BC BP ∴+++=+++=14t ∴=2t =6t =10t =14t =P AC 4y x =+x y A B P AB P C x P PD PC ⊥y D CD M分别是、的中点，连接，求的度数；（3）如图2，点是轴上的一个动点，连接．把线段绕点逆时针旋转至线段，连接、．当的值最小时，求此时点的坐标．【答案】见解析【详解】解：（1）在中，令，则，，令，则，，点为线段的中点，，故答案为：；（2）过点作轴交于点，过点作交于点，过点作轴交于，，，，，，，，，设，，N CD OB MN MNO ∠Q x PQ PQ Q 90︒QT PT OT PT OT +T 4y x =+0x =4y =(0,4)B ∴0y =4x =−(4,0)A ∴−P AB (2,2)P ∴−(2,2)−P EF x ⊥F D DE EF ⊥E M MG y ⊥G CP PD ⊥90CPD ∴∠=︒90EPD FPC ∴∠+∠=︒90EPD EDP ∠+∠=︒FPC EDP ∴∠=∠2PF ED ==()PED CFP AAS ∴∆≅∆PE FC ∴=(,0)C x 2FC x ∴=+，，是的中点，，，，，是的中点，，，，，；（3）过点作轴，过点作交于点，延长，使，过点作交于，，，，点是的中点，，，，，作点关于的对称点，连接，，当、、三点共线时，的值最小，最小值为，，，，，，，设，，，4EF x ∴=+(0,4)D x ∴+M CD (2x M ∴2)2x +2x GM ∴=22x OG =+N OG (0,2)N ∴2x GN ∴=GN GM ∴=45GNM ∴∠=︒135MNO ∴∠=︒Q RS x ⊥P PR RS ⊥R PQ PQ QK =T TS RS ⊥S PQ TQ =90PQT ∠=︒45PTQ ∴∠=︒Q PK TQ QK ⊥TQ PQ KQ ∴==90PTK ∴∠=︒PT KT =O RS O 'O T 'OT PT O T TK '∴+=+∴O 'T K PT OT +KO '90PQR TQS ∴∠+∠=︒90PQR QPR ∠+∠=︒TQS QPR ∴∠=∠()PQR QTS AAS ∴∆≅∆PR QS ∴=RQ TS =(,0)Q t 2PR t ∴=+2RQ =，，，设直线的解析式为，，解得，，，解得，．16．（2022春•硚口区期末）直线经过，两点，点的坐标为．（1）求和的值；（2）点为线段上一点，点为直线上一点，．(2,2)T t t ∴−−−(24,0)O t '∴−(22,2)K t +−Q K 'y kx b =+∴(24)0(22)2t k b t k b −+=⎧⎨++=−⎩132433k b t ⎧=−⎪⎪⎨⎪=−⎪⎩124333y x t ∴=−+−1242(2)333t t t ∴−−=−−+−1t =−(3,1)T ∴−−y kx b =+(2,0)A −(0,4)B C (0,1)−k b E AB F AC 3EF =①如图1，若，求点坐标；②如图2，若，请直接写出点坐标．【答案】见解析【详解】解：（1）根据题意得，解得；（2）设直线的解析式为，把代入得，解得，直线为， ①若，则，，，把的坐标代入得，解得，，； ②若，则，．，把点的坐标代入得，解得，，． //EF BC E //EF AOE 204k b b −+=⎧⎨=⎩24k b =⎧⎨=⎩AC 1y mx =−(2,0)A −210m −−=12m =−∴AC 112y x =−−//EF BC (,24)E x x +3EF =(,21)F x x ∴+F 112y x =−−12112x x +=−−45x =−4(5E ∴−12)5//EF AO (,24)E x x +3EF =(3,24)F x x ∴−+F 112y x =−−124(3)12x x +=−−−75x =−7(5E ∴−6)517．（2022春•硚口区期末）直线与轴交于点，与轴交于点，点在轴的正半轴上，面积为10．（1）直接写出点的坐标；（2）如图1，为线段的中点，点在轴上，以为边，向右作正方形，点落在直线上，求点的坐标；（3）如图2，在射线上，点在射线上，直线交轴于点，若，求的值．【答案】见解析【详解】解：（1）直线与轴交于点，与轴交于点，令，，令，，，，，，，，，，（2）设直线的解析式为：，把，，代入得：，解得：，直线的解析式为：；由（1）知：，，设，24y x =+x A y B C x ABC ∆C F AB G y FG FGQP Q BC G M BA N BC MN y H HB HM =HMHN24y x =+x A y B 0y =2y =−0x =4x =(2,0)A ∴−(0,4)B 2OA ∴=4OB=1102ABC S AC OB ∆=⋅⋅=5AC ∴=3OC ∴=(3,0)C ∴BC y kx b =+(0,4)B (3,0)C 304k b b +=⎧⎨=⎩434k b ⎧=−⎪⎨⎪=⎩∴BC 443y x =−+(2,0)A −(0,4)B (0,)G n①当时，如图，点落在上时，过作直线平行于轴，过点，作该直线的垂线，垂足分别为，，四边形是正方形，，，，而，，，，，在直线上，，，；①当时，如图，2n>Q BC G MN x F Q M N FGQP 90FGQ ∴∠=︒FG QG =90FGM NGQ GQN ∴∠=︒−∠=∠90FMG GNQ ∠=∠=︒()FMG GNQ AAS ∴∆≅∆1MG NQ ∴==2FM GN n ==−(2,1)Q n n ∴−−Q ∴443y x =−+41(2)43n n ∴−=−−+237n ∴=23(0,)7G ∴2n<点落在上时，过作直线平行于轴，过点，作该直线的垂线，垂足分别为，．四边形是正方形，，，，，，，，，在直线上，，，；综上所述，满足条件的点坐标为或；（3）过点作轴交于点，交轴于，，，，，，，在中，由勾股定理得：，，，轴，Q BC G MN x F Q M N FGQP 90FGQ ∴∠=︒FG QG =90FGM NGQ GQN ∴∠=︒−∠=∠90FMG GNQ ∠=∠=︒()FMG GNQ AAS ∴∆≅∆1MG NQ ∴==2FM GN n ==−(2,1)Q n n ∴−+Q ∴443y x =−+41(2)43n n ∴+=−−+1n ∴=−(0,1)G ∴−G 23(0,)7(0,1)−M //MP x BC P yQ (0,4)B (3,0)C (2,0)A −5AC ∴=4OB =3OC =Rt BOC∆5BC 5AC BC ∴==ABC BAC ∴∠=∠//MP x，，，，，，即轴，，，，，，． 18．（2022春•江汉区期末）已知，直线经过第一象限内的定点．（1）求点的坐标；（2）如图（1），已知点，过点作轴，交直线于点，连接，若平分，求的值；（3）如图（2），点是，以为腰作等腰，，按逆时针顺序排列），，连接的最小值．【答案】见解析【详解】解：（1）当时，，即点的坐标为；BMP BAC ∴∠=∠90AOB MQH ∠=∠=︒BMP ABC ∴∠=∠HM HB=HBM HMB ∴∠=∠ABC HBM BMP HMB ∴∠−∠=∠−∠//MP x ()MHQ BHN ASA ∴∠≅∆90MNB MQH BOC ∴∠=∠=∠=︒OBC OBC ∠=∠BHN BCO ∴∆∆∽∴53BH BC HN OC ==∴53HM HB HN HN ==:l y kx k =−+P P (2,)A t A //AB y l B OB BP OBA ∠k Q x PQ PQ (PQR P ∆Q R 120QPR ∠=︒OR QR +(1)y kx k k x =−−1x =y =P（2）点在直线时，，即点，设直线轴交于点，令，则，即点，如图1，，平分，，，，，则，即，解得：；（3）中，，，过点作，，，，，，当的值就是最小值，如图：轴以点为旋转中心，逆时针旋转，点旋转到点位置，点与点重合，，)B y kx k =−2x =y k =+(2,B k +y kx k =−y H 0x =y k =−(0,H k −BP OBA ∠ABH OBH ∴∠=∠//AB y ABH OHB ∴∠=∠OBH OHB ∴∠=∠OB OH =2222()k k +=k =PQR ∆120QPR ∠=︒PQ PR =P PE QR ⊥30Q ∴∠=︒12PE PQ =QE ER ====2QR QE ==∴)PR OR PR +=+=+∴OR QP +QR +x P 120︒O M Q R OPQ MPR ∆≅∆，设直线的解析式为：，，，，轴，代入，得，直线的解析式为：，点、是定点，点在直线上运动，作点关于直线的对称点，，又，时，即，此时的值最小，，点关于直线的对称点的坐标为，（这里求出直线的解析式，构建方程组求出交点坐标，再利用中点坐标公式，可得结论），，，的最小值为．19．（2022春•东莞市期末）如图，在平面直角坐标系中，一次函数的图象与轴，轴分别交于，两点，与正比例函数的图象交于点，点的纵坐标为4．（1）求，，三点的坐标；（2）若动点在射线上运动，当的面积是的面积的时，求点的坐标；（3）若点在的内部（不包括边界），请直接写出的取值范围．60QCO ∴∠=︒tan tan 60QCO ∴∠=︒∴RM y b =+(1,3)P 2OP PM ∴==60POQ PMR QCO ∠=∠=︒=∠//PM x ∴M y b =+b =∴RM y =+O P ∴R RM P RM P 'PR P R '∴=PQ PR =OR PR OP '∴+=OR QP OP '+=OR QP +(1,3)P ∴P y =+P '(4PP 'OP '∴=∴)QR OR QP +=+==∴QR +y x b =+x y A B 2y x =−C C A B C CA OAP ∆OBC ∆18P (,2)Q m OBC ∆m【答案】见解析【详解】解：（1）当时，，解得，，又过点，，解得，，当时，时，，当时，，；（2）设，，，，解得，又动点在射线上运动，，点的坐标是或；（3）当时，，解得，当时，，解得，．4y =24x −=2x =−(2,4)C ∴−y x b =+(2,4)−24b ∴−+=6b =6y x ∴=+0x =6y =(0,6)A ∴0y =6x =−(6,0)B ∴−(,6)P x x+18OAP OBC S S ∆∆=∴111||||282c AO x BO y ⋅=⨯⨯⋅∴1116||64282x ⨯=⨯⨯⨯12x =±P CA 2x ∴−…∴P 111(,)22−113(,)222y =26x =+4x =−2y =22x =−1x =−41m ∴−<<−20．（2022春•青山区期末）如图1，直线与轴交于点，与轴交于点．（1）求的面积；（2）点为轴上一点，直线交直线于点，若，求点的坐标；（3）如图2，将直线向下平移得到直线，点，点为直线上的两点，直线与直线交于点，求点的横坐标．【答案】见解析【详解】解：（1）当时，，解得：，，当时，，，的面积为：；（2）如图，:26l y x =−+x A y B AOB ∆(0,1)P −y PC l C 45PCA ∠=︒C l :2l y x b '=−+2(,6)M m m m −++2(,6)N n n n −++l 'BM AN QQ 0y =260x −+=3x =(3,0)A ∴0x =266y x =−+=(0,6)B ∴AOB ∴∆13692⨯⨯=以为对角线作正方形，可得，，，以为圆心，为半径作交于点，则，为所求，设，则，，解得：（舍去），，，为半径作交于，为所求，设，则，，解得：（舍去），，综上所述，点的坐标为：或；（3）由题意得，，为线与的两个交点，，整理得：，，如图，AP AMPN (1,1)M (2,2)N −AM =M AM M AB 1C 11452PC A AMP ∠=∠=︒1C ∴1(,26)C m m −+1C M MA =∴222(1)(261)m m −+−+−=13m =273m =1716(,)55C∴N AB 2C 2C ∴2(,26)C n n −+2C N =∴222(2)(262)n n −+−++=1221,35n n ==22112(,)55C ∴−C 716(,)552112(,)55−M N :2l y x b '=−+26y x x =−++226x b x x ∴−+=−++23(6)0x x b −+−=∴x =，，，，，，，，，，，即，，点的横坐标为：． 21．（2022春•中山市期末）如图，直线分别与轴、轴相交于点、，，点从点出发以每秒2个单位长度的速度向点匀速运动，点同时从点出发以每秒1个单位长度的速度向点匀速运动，当其中一个点到达终点时，另一个点也停止运动．设点、运动的时间为秒，过点作轴于点，连接、．（1）是否存在某个时间，使得四边形成为菱形？请说明理由；（2）当为何值时，为直角三角形？请说明理由．【答案】见解析【详解】解：（1）存在时间，使得四边形成为菱形，理由如下：令，则，，， EQ BQ MG BM =FQ AQ HN AN =//AB MN ∴BQ AQ BM AN =∴EQ FQ MQ HN=Q EQ x =3Q FQ x =−MG ∴3HN =−=MG HN =EQ FQ ∴=3Q Q x x =−∴32Q x =∴Q 323y kx =+x y A B 30OAB ∠=︒C A B D B O C D t (0)t >C CE x ⊥E CD DE t BDEC t CDE∆t BDEC 0x =3y =(0,3)B ∴3OB ∴=，，，，轴，，由题意得，，，，在中，，，；（2）当时，轴，此时，即，；当时，过点作交于，，，，，，，，，，，，轴，，30OAB ∠=︒6AB ∴=OA =A ∴0)CE x ⊥//CE OB ∴2AC t =BD t =62BC t ∴=−Rt ACE ∆CE t =62t t ∴−=2t ∴=90ECD ∠=︒//CD x CE OD =3t t =−32t ∴=90CDE ∠=︒C CG BO ⊥G 90CDE ∠=︒90GDC ODE ∴∠+∠=︒90GDE DCG ∠+∠=︒GCD ODE ∴∠=∠CDG DEO ∴∆∆∽∴GC GD DO OE=CE t =2AC t =AE ∴=3OA =OE ∴=CE x ⊥GC OE ∴==，，，，，解得或，解法二：利用，构建方程，可得结论．当时，此时点运动到点处，点与点重合，不满足题意；当时，点与点重合，此时，不满足题意；综上所述：的值为或．22．（2022无论取何值时，都经过定点．（1）点坐标为；（2）如图1，直线与轴交于点，且，点位于直线上，若坐标系内有一点，与点，，可以组成菱形，试求点的坐标；（3）如图2，直线与轴交于点，且，，点位于轴上点右侧，若，求点的坐标．BDt =3OB =3DO t ∴=−OGt =23GD t ∴=−∴3t =125222CD DE EC +=3t =C B E O 90DEC ∠=︒D O 3t =t 321256y kx k =−k A A 6y kx k =−y B 30BAO ∠=︒C AB N O A C N 6y kx k =−y B (0B C x A 30CBA ∠=︒C【答案】见解析【详解】解：（1）直线，时，，定点的坐标为，故答案为：；（2），，，，在中，，，（负值舍去），，，直线为，分三种情况：①四边形为菱形时，如图：连接交于，四边形为菱形，，，，当时，，点的坐标为；②四边形为菱形时，如图：6(6)y kx k k x =−=−6x∴=0y =∴A (6,0)(6,0)30BAO ∠=︒(6,0)A 2AB OB ∴=6OA =Rt AOB ∆222AB OB OA =+222(2)6OB OB ∴=+OB ∴=AB =(0B ∴∴AB y =+OCAN CN OA D OCAN (6,0)A 3OD AD ∴==CD ND =3x =y =+=C ∴∴N (3,OACN四边形为菱形，，，，点位于直线直线为，设，，，点的坐标为，或，；③四边形为菱形时，如图：作轴于，四边形为菱形，，，，，，，，，点的坐标为，；综上，点的坐标为或，或，或，；OACN (6,0)A //ON AC ∴6ONOA ==C:AB y x =+∴ON y =(,)N n 2226()n ∴=+n ∴=±∴N (−3)3)−OANC CE x ⊥E OANC (6,0)A 6OC OA ∴==30OCA BAO ∴∠=∠=︒120AOC ∴∠=︒1209030OCE AOC OEC ∴∠=∠=∠=︒−︒=︒132OE OC ∴==CE =(3C ∴−∴N (3N (3,(−3)3)−(3（3）过点作交的延长线于，直线与轴交于点，且，，定点的坐标为，，设，则，，，，，，，，，，，，，点的坐标为．23．（2022春•武汉期末）（1）如图①，在平面直角坐标系中，已知菱形的顶点，点在轴上，，点在轴上．①求直线的解析式；②已知点在直线的下方，且的值． C CD BA ⊥BA D 6y kx k =−y B (0B OB ∴=A (6,0)6OA ∴=AB (,0)C x 6AC x =−90CDA BOA ∠=∠=︒BAO CAD ∠=∠BAO CAD ∴∆∆∽∴AD CD AC AO BO AB ==∴6AD ==AD ∴=CD 30CBA ∠=︒CD BA ⊥BD ∴=∴=27x ∴=∴C (27,0)ABCD (1,0)A −B y 120ABC ∠=︒D x CD (1,)M m −CD CDM ∆m（2）如图②，已知中，，，，点为内一点，且点到三边的距离之和为，直接写出的最小值是．【答案】见解析【详解】解：（1）①，四边形为菱形，，，，，，，，，，设所在直线的解析式为：，把，代入得：，解得：所在直线的解析式为：②由①得：，所在直线的解析式为：点到直线即点在与的直线上（在下方），Rt OMN ∆5OM =12ON =90MON ∠=︒P Rt OMN ∆P Rt OMN ∆6813PO 120ABC ∠=︒ABCD //BC AD ∴18060BAD ABC ∴∠=︒−∠=︒30ABO ∠=︒(1,0)A −1OA ∴=2AB BC AD ∴===OB =1OD AD OA ∴=−=(1,0)D ∴C CD y kx b =+(1,0)D C 02k b k b =+⎧⎪=+k b ⎧=⎪⎨=⎪⎩CD ∴y =2CD =CD y =CDM S ∆=∴M CD M CD l CD设的解析式为，与轴交于点，过点作于点，即，，，，，，，即，代入，解得直线解析式为：在直线上，代入解得：；（2）如图：，，，，l y b =+l x E EEF CD ⊥F EF =120ABC ∠=︒60C FDE ∴∠=∠=︒30DEF ∠=︒12DF DE ∴=FE ==1DF ∴=2DE =(3,0)E :l y b =+b =−∴l y −(1,)M m −l ∴y =−1)m =−−3m =5OM =12ON =90MON ∠=︒13MN ∴过做、、上的垂线段，对应长度记为、、，利用三角形等面积法可得：，即①，由题目得：②， ②①得：，，，，当时，取最小值为：．故答案为：． 24．（2022春•武汉期末）如图1，在平面直角坐标系中，，，，．（1）求直线的解析式；（2）如图2，已知为直线上一点，且，求点的坐标；（3）若点为第一象限内一动点，且，求的最小值．P ON OMMN 1h 2h 3h 12311112222ON h OM h MN h OM ON ⨯⨯+⨯⨯+⨯⨯=⨯⨯1231251360h h h ++=1236813h h h ++=13⨯−1288h h +=1288h h ∴=−OP h =OP ∴====∴26465h =OP OP ==//BC OA 2BC =6OA =AB =AB P 1:52l y x =−+512ABP ABCO S S ∆=四边形P D 45ODC ∠=︒BD【答案】见解析【详解】解：（1）过点作于点，，，，，，在中，，，，设直线的解析式为：，把，，代入得：，解得：，直线的解析式为：；（2）设，作轴交直线于点，B BD OA ⊥D 90BDA ∴∠=︒//BC OA 2BC =6OA =624AD ∴=−=Rt ABD∆6BD ===(2,6)B ∴(6,0)A AB y kx b =+(2,6)B (6,0)A 6206k b k b =+⎧⎨=+⎩323k b ⎧=−⎪⎨⎪=⎩∴AB 392y x =−+1(,5)2P m m −+//PQ y ABQ则，，，，，或，即或，或9，点的坐标为：或；（3）取，则为等腰三角形，为的外心，，点在上，连接交于点，此时最小，，，，最小．25．（2022春•汉阳区期末）如图，已知直线经过、两点，若．（1）求的值； 3(,9)2Q m m −+31|||95||4|22Q P PQ y y m mm ∴=−=−++−=−624A B x x −=−=∴11()4|4||82|22ABP A B S PQ x x m m ∆=⋅−=⨯⨯−=−()1266242ABCO S =⨯+⨯=四边形5|82|2412m ∴−=⨯|82|10m −=8210m −=2810m −=1m ∴=−∴P 11(1,)2−1(9,)2(3,3)M OM ==DMC ∆M ∴ODC ∆45ODC ∴∠=︒∴D AEC BM AEC D BD DM BM =−DM CM OM ===(2,6)B (3,3)M BM ∴=BD ∴DM BM =−=6y kx k =−A B 9OAB S ∆=k。

人教版八年级下册数学第19章一次函数综合(压轴题)示范

人教版八年级下册数学第19章一次函数综合（压轴题）示范1．如图，直线l 1的解析式为y =12x+1，且l 1与x 轴交于点D ，直线l 2经过定点A 、B ，直线l 1与l 2交于点C ．（1）求直线的解析式；（2）求△ADC 的面积；（3）在x 轴上是否存在一点E ，使△BCE 的周长最短？若存在，请求出点E 的坐标；若不存在，说明理由．【分析】（1）利用待定系数法即可直接求得l 2的函数解析式；（2）首先解两条之间的解析式组成的方程组求得C 的坐标，然后利用三角形的面积公式即可求解；（3）求得C 关于y 轴的对称点，然后求得经过这个点和B 点的直线解析式，直线与x 轴的交点就是E ．【解析】（1）设l 2的解析式是y ＝kx+b ，根据题意得：{4k +b =0−k +b =5，解得{k =−1b =4，则函数的解析式是：y ＝﹣x+4；（2）在y =12x+1中令y ＝0，即y =12x+1＝0，解得：x ＝﹣2，则D 的坐标是（﹣2，0）．解方程组{y =−x +4y =12x +1，解得{x =2y =2，则C 的坐标是（2，2）．则S △ADC =12×AD ×y C =12×6×2＝6；（3）存在，理由：设C （2，2）关于y 轴的对称点C ′（2，﹣2），连接BC ′交x 轴于点E ，则点E 为所求点， △BCE 的周长＝BC+BE+CE ＝BC+BE+C ′E ＝BC+BC ′为最小，设经过（2，﹣2）和B 的函数解析式是y ＝mx+n ，则{2m +n =−2−m +m =5，解得：{m =−73n =83，则直线的解析式是y =−73x +83，令y ＝0，则y =−73x +83=0，解得：x =87．则E 的坐标是（87，0）．【小结】本题考查了待定系数法求一次函数的解析式，以及对称的性质，正确确定E 的位置是本题的关键． 2、矩形ABCD 在如图所示的平面直角坐标系中，点A 的坐标为（0，3），BC ＝2AB ，直线经过点B ，交AD 边于点P 1，此时直线l 的函数表达式是y ＝2x ＋1．（1）求BC ，AP 1的长；（2）沿y 轴负方向平移直线l ，分别交AD ，BC 边于点P ，E ． ①当四边形BEPP 1是菱形时，求平移的距离；②设AP ＝m ，当直线l 把矩形ABCD 分成两部分的面积之比为3:5时，求m 的值．解：（1）∵直线y ＝2x ＋1经过y 轴上的B 点，∴B （0，1），又∵A 的坐标为（0，3）；∴AB=2;BC=2AB=4；P 1（1，3）；AP 1=1；（2）①当四边形BEPP 1是菱形时，BP 1=BE=5；∴E （5，1）；设平移之后的直线解析式为：y ＝2x ＋b ，将点E 代入；b=1-25；与y 轴的交点B ’（0，1-25），∴沿y 轴负方向平移距离为25；②∵AP=m ；AP 1=1；PP 1=BE=m-1；而S 梯形ABEP =83S 矩形ABCD 或S 梯形ABEP =85S 矩形ABCD ； ∴53m 1-m 221或）（=+⨯；m=2或3. 3、如图，一次函数y 1=54x+n 与x 轴交于点B ，一次函数y 2=−34x+m 与y 轴交于点C ，且它们的图象都经过点D （1，−74）．（1）则点B 的坐标为，点C 的坐标为；（2）在x 轴上有一点P （t ，0），且t ＞125，如果△BDP 和△CDP 的面积相等，求t 的值；（3）在（2）的条件下，在y 轴的右侧，以CP 为腰作等腰直角△CPM ，直接写出满足条件的点M 的坐标．【分析】（1）根据待定系数法，可得函数解析式，分别令y ＝0和x ＝0，可得B 、C 点坐标；（2）根据面积的和差，可得关于t 的方程，根据解方程，可得答案；（3）分情况讨论，注意是在y 轴的右侧，有三个符合条件的点M ，作辅助线，构建三角形全等，根据全等三角形的判定与性质，可得M 的坐标．【解析】（1）将D （1，−74）代入y =54x+n ，解得n ＝﹣3，即y =54x ﹣3，当y ＝0时，54x ﹣3＝0．解得x =125，即B 点坐标为（125，0）；将（1，−74）代入y =−34x+m ，解得m ＝﹣1，即y =−34x ﹣1，当x ＝0时，y ＝﹣1．即C 坐标为（0，﹣1）；（2）如图1，S △BDP =12（t −125）×|−74|=78t −2110，当y ＝0时，−34x ﹣1＝0，解得x =−43，即E 点坐标为（−43，0）， S △CDP ＝S △DPE ﹣S △CPE =12（t +43）×74−12×（t +43）×|﹣1|=38t +12，由△BDP 和△CDP 的面积相等，得：78t −2110=38t +12，解得t ＝5.2；（3）以CP 为腰作等腰直角△CPM ，有以下两种情况： ①如图2，当以点C 为直角顶点，CP 为腰时，点M 1在y 轴的左侧，不符合题意，过M 2作M 2A ⊥y 轴于A ， ∵∠PCM 2＝∠PCO+∠ACM 2＝∠PCO+∠OPC ＝90°，∴∠ACM 2＝∠OPC ，∵∠POC ＝∠CAM 2，PC ＝CM 2，∴△POC ≌△CAM 2（AAS ），∴PO ＝AC ＝5.2，OC ＝AM 2＝1， ∴M 2（1，﹣6.2）；②如图3，当以点P 为直角顶点，CP 为腰时，过M 4作M 4E ⊥x 轴于E ，同理得△COP ≌△PEM 4，∴OC ＝EP ＝1，OP ＝M 4E ＝5.2，∴M 4（6.2，﹣5.2），同理得M 3（4.2，5.2）；综上所述，满足条件的点M 的坐标为（1，﹣6.2）或（6.2，﹣5.2）或（4.2，5.2）．【小结】本题考查了一次函数综合题，利用待定系数法求函数解析式；利用面积的和差得出关于t 的方程是解题关键；利用全等三角形的判定与性质得出对应边相等是解题关键．4、如图，已知直线y ＝2x+2与y 轴、x 轴分别交于A 、B 两点，点C 的坐标为（﹣3，1）．（1）直接写出点A 的坐标，点B 的坐标．（2）求证△ABC 是等腰直角三角形．（3）若直线AC 交x 轴于点M ，点P （−52，k ）是线段BC 上一点，在线段BM 上是否存在一点N ，使直线PN 平分△BCM 的面积？若存在，请求出点N 的坐标；若不存在，请说明理由．【分析】（1）利用待定系数法解决问题即可．（2）作CD ⊥x 轴于点D ，证明△CDB ≌△BOA （SAS ）即可解决问题．（3）求出点P 的坐标，利用面积法求出BN 的长即可解决问题．【解答】（1）对于直线y ＝2x+2，令x ＝0，得到y ＝2，令y ＝0，得到x ＝﹣1，∴A （0，2），B （﹣1，0）．（2）证明：作CD ⊥x 轴于点D ，由题意可得CD ＝1，OD ＝3，OB ＝1，OA ＝2，∴CD ＝OB ＝1，BD ＝OA ＝2， ∵∠CDB ＝∠AOB ＝90˚，∴△CDB ≌△BOA （SAS ），∴BC ＝BA ，∠CBD ＝∠BAO ，∵∠ABO+∠BAO ＝90˚，∴∠ABO+∠CBD ＝90˚，即∠ABC ＝90˚，∴△ABC 是等腰直角三角形．（3）∵P （−52，k ）在直线BC ：y =−12x −12上，∴P (−52，34)，∵直线AC ：y =13x +2交x 轴于M ，∴M （﹣6，0），∵S △BCM =12×5×1=52，假设存在点N ，使直线PN 平分△BCM 的面积，则S △BPN =12⋅BN ⋅34=12×52，∴BN =103，∴ON ＝BN+OB =103+1=133，∴N(−133，0)．【小结】本题考查属于一次函数综合题，考查了一次函数的性质，等腰直角三角形的判定，三角形的面积等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．5、如图1，在平面直角坐标系xOy 中，直线y ＝kx+8分别交x 轴，y 轴于A 、B 两点，已知A 点坐标（6，0），点C 在直线AB 上，横坐标为3，点D 是x 轴正半轴上的一个动点，连结CD ，以CD 为直角边在右侧构造一个等腰Rt △CDE ，且∠CDE ＝90°．（1）求直线AB 的解析式以及C 点坐标；（2）设点D 的横坐标为m ，试用含m 的代数式表示点E 的坐标；（3）如图2，连结OC ，OE ，请直接写出使得△OCE 周长最小时，点E 的坐标．【分析】（1）把A （6，0）代入y ＝kx+8中，得6k+8＝0，解得：k =−43，即可求解；（2）证明△CDF ≌△DEG （AAS ），则CF ＝DG ＝4，DF ＝EG ＝3﹣m ，OG ＝4+m ，则E （4+m ，m ﹣3）；（3）过点O 作直线l 的对称点O ′，连接CO ′交直线l 于点E ′，则点E ′为所求点，即可求解．【解析】（1）把A （6，0）代入y ＝kx+8中，得6k+8＝0，解得：k =−43，∴y =−43x +8，把x ＝3代入，得y ＝4，∴C （3，4）；（2）作CF ⊥x 轴于点F ，EG ⊥x 轴于点G ，∵△CDE 是等腰直角三角形，∴CD ＝DE ，∠CDE ＝90°， ∴∠CDF ＝90°﹣∠EDG ＝∠DEG ，且∠CFD ＝∠DGE ＝90°，∴△CDF ≌△DEG （AAS ）∴CF ＝DG ＝4，DF ＝EG ＝3﹣m ，∴OG ＝4+m ，∴E （4+m ，m ﹣3）；（3）点E （4+m ，m ﹣3），则点E 在直线l ：y ＝x ﹣7上，设：直线l 交y 轴于点H （0，﹣7），过点O 作直线l 的对称点O ′， ∵直线l 的倾斜角为45°，则HO ′∥x 轴，则点O ′（7，﹣7），连接CO ′交直线l 于点E ′，则点E ′为所求点，OC 是常数，△OCE 周长＝OC+CE+OE ＝OC+OE ′+CE ′＝OC+CE ′+O ′E ′＝OC+CO ′为最小，由点C 、O ′的坐标得，直线CO ′的表达式为：y =−114x +494联立{y =x −7y =−114x +494，解得：{x =7715y =−2815，故：E(7715，−2815)．【小结】本题考查的是一次函数综合运用，涉及到一次函数的性质、等腰直角三角形的性质、点的对称性等，综合性很强，难度较大．6．如图①，直线y ＝x ＋1交x 轴于点A ，交y 轴于点C ，OB ＝30A ，M 在直线AC 上，AC ＝CM ．（1）求直线BM 的解析式；（2）如图①，点N 在MB 的延长线上，BN ＝AC ，连CN 交x 轴于点P ，求点P 的坐标；（3）如图②，连接OM ，在直线BM 上是否存在点K ，使得∠MOK ＝45°，若存在，求点K 的坐标，若不存在，说明理由．解：（1）利用A(-1,0)；C （0,1）；AC=AM;∴M （1,2）；B （3,0）；∴BM ：y ＝-x ＋3．（2）过C 作CS ∥MN 交x 轴与S 点，可证△PCS ≌△PNB ，可证P 为BS 的中点，可证OA=OS=1; 则BS=2；则P （2,0）。

2020-2021学年人教版八年级数学下册期末复习(一次函数压轴题)

人教版2020-2021年八年级下册期末复习（一次函数压轴题）一．解答题（共15小题）1．在平面直角坐标系中，A （0，8），点B 是直线y ＝x ﹣8与x 轴的交点．（1）写出点B 的坐标（，）；（2）点C 是x 轴正半轴上一动点，且不与点B 重合，∠ACD ＝90°，且CD 交直线y ＝x ﹣8于D 点，求证：AC ＝CD ；（3）在第（2）问的条件下，连接AD ，点E 是AD 的中点，当点C 在x 轴正半轴上运动时，点E 随之而运动，点E 到BD 的距离是否为定值？若为定值，求出这个值，若不是定值，请说明理由．2．已知，如图：在正方形OABC 中，A （0，1），B （1，1），C （1，0），D 为OB 延长线上的一动点，以AD 为一边在直线AD 下方作正方形ADEF ，AF 交OC 于点G ．（1）若S △AOD ＝1，求D 点的坐标；（2）①求证：点E 始终落在x 轴上；②若S 四边形ABCG ＝a •S △ABE ，1＜a ＜2，利用a 表示此时直线AF 的解析式．3．如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A （0，4）、B （﹣2，0）、C （23，0），点D 是边AC 上的一点，DE ⊥BC 于点E ．点F 在边AB 上，且D ，F 两点关于y 轴上的某点成中心对称．连接DF ，EF ．设点D 的横坐标为m ，EF 2为l ，请解决下列问题：（1）若一次函数的图象经过A 、C 两点，则此一次函数的表达式为；（2）若以EF 为边长的正方形面积为S ，请你求出S 关于m 的函数表达式及自变量的取值范围，并求出线段EF 长度的最小值；（3）△BEF 能否成为直角三角形．若能，求出m 的值；若不能，说明理由．4．如图，在平面直角坐标系中，一次函数12x 512-y +=的图象交x 轴、y 轴于A 、B 两点，以AB 为边在直线右侧作正方形ABCD ，连接BD ，过点C 作CF ⊥x 轴于点F ，交BD 于点E ，连接AE ．（1）求线段AB 的长；（2）求点C 的坐标（3）求证：AD 平分∠EAF ；（4）求△AEF 的周长5．如图1，已知直线y ＝kx +1交x 轴于点A 、交y 轴于点B ，且OA ：OB ＝4：3．（1）求直线AB 的解析式（2）如图2，直线y ＝31x +2与x 轴、y 轴分别交于点C 、D ，与直线AB 交于点P ． ①若点E 在线段P A 上且满足S △CDE ＝S △CDO ，求点E 的坐标；②若点M是位于点B上方的y轴上一点，点Q在直线AB上，点N为第一象限内直线CD上一动点，是否存在点N，使得以点B、M、N、Q为顶点的四边形是菱形？若存在，求出点N坐标；若不存在，请说明理由．6．如图，直线y＝﹣x+1与y轴、x轴分别交于A、B两点，点C在线段AB上从A向B运动，另一动点P从B出发，沿直线x＝1运动，记AC的长为t，P的坐标为（1，b），分析此图后，对下列问题作出探究：（1）当t＝且b＝时，△AOC≌△BCP；（2）当OC与CP垂直时，①判断线段OC和CP的数量关系？并证明你得到的结论；②试写出b关于t的函数关系式和变量t的取值范围．③求出当△PBC为等腰三角形时点P的坐标．7．如图，在平面直角坐标系中，点O为坐标原点，直线y＝kx+6分别交x轴，y轴于点A，B，已知点A的坐标为（6，0）．（1）求k的值；（2）点C是线段OA上一点（不与点O，A重合），点D是OB的延长线上一点，连接CD交AB于点E，且CE＝DE，设OC的长为t，BD的长为d，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，过点E 作EF ⊥CD 交y 轴于点F ，点G 在线段DE 上，且EG ＝EF ，连接BG 并延长交FE 的延长线于点H ，若BF ＝d 43-29，求点E 的坐标．8．平面直角坐标系中，O 为坐标原点，直线b x 3y +=交y 轴于A ，x 轴于B ，S △AOB ＝83．（1）求b 的值；（2）点C 为射线BA 上一动点，连接OC ，以C 为边作等边△OCD ，点D 在OC 的右侧，求点D 的纵坐标；（3）在（2）的条件下，连接AD 、BD ，△BOC 的面积是△ACD 的面积的2倍，M 是x 轴上一点，连接DM ，若∠DMB ﹣∠DBM ＝90°，求点M 坐标．9．如图1，在矩形ABCD 中，动点P 沿着边AB 从点A 运动到点B ，同时动点Q 沿着边BC ，CD 从点B 运动到点D ，它们同时到达终点，若点Q 的运动路程x 与线段BP 的长y 满足y ＝8x 74-+，BD 与PQ 交于点E ．（1）求AB ，BC 的长．（2）如图2，当点Q 在CD 上时，求DE BE ．（3）将矩形沿着PQ 折叠，点B 的对应点为点F ，连接EF ，当EF 所在直线与△BCD的一边垂直时，求BP的长．10．平面直角坐标系中，设一次函数y＝（2a﹣1）x+3﹣b的图象是直线l1．（1）如果把l1向下平移2个单位后得到直线y＝3x+1，求a，b的值；（2）当直线l1过点（m，6﹣b）和点（m+3，4a﹣7）时，且﹣3＜b＜12，求a的取值范围；（3）点P（﹣2n+3，3n﹣1）在直线l2上运动，直线l2与直线l1无交点，求a、b所需满足的条件．11．如图，在平面直角坐标系中，直线y＝kx+b与x轴，y轴分别相交于点A（4，0），点B（0，3），点C是线段OB的中点，动点P从点B开始以每秒1个单位长度的速度沿路线B→A向终点A匀速运动，设运动的时间为t秒，连接CP．（1）求直线AB的函数解析式；（2）请直接写出点P的坐标；（用含t的代数式表示）（3）①当S△BCP：S四边形AOCP＝1：4时，求t的值；②将△BCP沿CP翻折，使点B落在点B′处，当PB′平行于坐标轴时，请直接写出t的值．12．如图1，在平面直角坐标系xOy中，直线l：y＝mx+m（m＞1）与x轴、y轴分别交于A、B两点，点Q为x轴上一动点．（1）若OB＝2OA，求直线l的解析式；（2）在（1）的条件下，若∠QBA ＝45°，求满足条件的点Q 的坐标；（3）如图2，在x 轴的负半轴上是否存在点Q ，使得以BQ 为边作正方形BQMN 时，点M 恰好落在直线l 上，且正方形BQMN 的面积被x 轴分成了1：2的两部分？若存在，请求出点Q 的坐标，若不存在，请说明理由．13．如图，在平面直角坐标系xOy 中，一次函数y ＝kx +b （k ≠0）经过点A （6，0）和点B （0，9），其图象与直线y ＝x 43交于点C ．（1）求一次函数y ＝kx +b （k ≠0）的表达式；（2）点P 是线段OA 上的一个动点（点P 不与点O ，A 重合），过点P 作平行于y 轴的直线l ，分别交直线AB ，OC 于点M ，N ，设点P 的横坐标为m ．①线段PM 的长为；（用含m 的代数式表示）②当点P ，M ，N 三点中有一个点是另两个点构成线段的中点时，请直接写出m 的值； ③直线l 上有一点Q ，当∠PQA 与∠AOC 互余，且△PQA 的周长为227时，请直接写出点Q 的坐标．14．如图1，已知直线y ＝﹣2x +2与y 轴、x 轴分别交于A 、B 两点，以B 为直角顶点在第一象限内作等腰Rt △ABC ．（1）A （）；B （）；（2）求BC 所在直线的函数关系式；（3）如图2，直线BC 交y 轴于点D ，在直线BC 上取一点E ，使AE ＝AC ，AE 与x 轴相交于点F ．①求证：BD ＝ED ；②在直线AE 上是否存在一点P ，使△ABP 的面积等于△ABD 的面积？若存在，直接写出点P 的坐标；若不存在，说明理由．15．在平面直角坐标系中，直线y ＝32x ﹣6与x 轴交于点A ，与y 轴交于点B ，点D 在直线AB 上，点D 的横坐标为3，点C （﹣6，0），动点F 从C 出发，沿x 轴正方向运动，速度为每秒1个单位长度，到达终点A 停止运动，设运动时间为t （t ＞0）．（1）如图1①求点A 、B 的坐标；②当t ＝3时，求证DF ＝DA ．（2）过点B 作BE ∥OA ，当BE ＝ED 时，连接ED 并延长交x 轴于点Q①点Q 的坐标为；②当∠FDE ＝3∠QFD 时，t 的值为．。

初二下学期压轴题练习- 一次函数与几何变换(含答案)

专题09一次函数与几何变换一．选择题1．（2021春•大同期末）对于一次函数y＝﹣2x+4，下列结论正确的是（）A．函数的图象与y轴的交点坐标是（4，0）B．函数的图象不经过第三象限C．函数的图象向上平移4个单位长度得y＝﹣2x的图象D．若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＜y22．（2021•扬州）如图，一次函数y＝x+的图象与x轴、y轴分别交于点A，B，把直线AB绕点B顺时针旋转30°交x轴于点C，则线段AC长为（）A．+B．3C．2+D．+3．（2020秋•天桥区期末）如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（）A．5B．4C．3D．24．（2020秋•碑林区校级期中）将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的表达式为（）A．y＝﹣3x+6B．y＝﹣3x﹣6C．y＝﹣3x+2D．y＝﹣3x﹣2 5．（2020•碑林区校级模拟）若直线y＝kx+3与直线y＝2x+b关于直线x＝1对称，则k、b值分别为（）A．k＝2、b＝﹣3B．k＝﹣2、b＝﹣3C．k＝﹣2、b＝1D．k＝﹣2、b＝﹣1 6．（2019•嘉祥县三模）在平面直角坐标系中，将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，则下列平移作法正确的是（）A．将y1向上平移2个单位长度B．将y1向上平移4个单位长度C．将y1向左平移3个单位长度D．将y2向右平移6个单位长度7．（2018春•雨花区校级月考）如图，A（0，1），M（3，2），N（4，4）．点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，当M、N位于直线l的异侧时，t应该满足的条件是（）A．3＜t＜6B．4＜t＜7C．3＜t＜7D．＜t＜7二．填空题8．（2021春•安丘市期末）在平面直角坐标系xOy中，Rt△AOB的直角顶点B在y轴上，点A的坐标为（1，），将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，过A'作A'C垂直于OA′交y轴于点C，则点C 的坐标为．9．（2021春•东台市月考）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么ABCD面积为．10．（2021•广东模拟）如图，已知一条直线经过点A（﹣1，0），B（0，﹣2），将这条直线向右平移与x 轴、y轴分别交于点C、D，若AB＝AD，则直线CD的函数表达式为．11．（2020春•黄陂区期末）将直线y＝2x﹣3沿y轴向上平移2个单位后，所得直线的解析式是．12．（2018秋•福田区校级期中）如图，过点A1（1，0）作x轴的垂线，交直线y＝2x于点B1；点A2与点O关于直线A1B1对称；过点A2（2，0）作x轴的垂线，交直线y＝2x于点B2；点A3与点O关于直线A2B2对称；过点A3（4，0）作x轴的垂线，交直线y＝2x于点B3；…，按此规律作下去，则点B n的坐标为．13．（2017秋•碑林区校级期末）如图，一次函数y＝，的图象向下平移2个单位后得直线l，直线l交x轴于点A、交y轴于点B，在线段AB上有一动点P（不与点A、B重合），过点P分别作PE⊥x 轴点E，PF⊥y轴于点F，当线段EF的长最小时，点P的坐标为．14．（2018春•丰南区期末）如图，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线l将图形分成面积相等的两部分，则将直线l向右平移3个单位长度后所得直线l′的函数解析式为．15．（2019春•西湖区校级期中）在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y＝4x+1以每秒2个单位的速度向下平移，经过秒该直线可将平行四边形OABC的面积平分．16．（2019•天津二模）将函数y＝3x+1的图象平移，使它经过点（1，1），则平移后的函数表达式是．17．（2019春•常州期中）如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点B（6，2），C（4，0），直线y＝2x+1以每秒1个单位长度的速度沿y轴向下平移，经过秒该直线可将平行四边形OABC分成面积相等的两部分．三．解答题18．（2021春•古丈县期末）如图，直线l是一次函数y＝kx+b的图象．（1）求出这个一次函数的解析式；（2）将该函数的图象向下平移5个单位，求出平移后一次函数的解析式，并写出平移后的图象与x轴的交点坐标．19．（2021春•武汉月考）已知，在平面直角坐标系中，函数y1＝2|x﹣a|，（1）若该函数经过点A（1，0），求该函数的解析式，并在图1中画出函数图象；（2）在（1）的条件下，将函数y2＝x向上平移m个单位后与函数y1的图象相交于点B和C点，若BC ＝，求m；（3）如图2，设直线y3＝6n与直线y4＝2n分别与函数y1＝2|x﹣a|相交于点E、F和M、N，点P为直线y3＝6n上一点，连接PM、PN并延长交直线y5＝kn于点G、H，若2EF＝3GH，求k．20．（2021春•河北区期末）如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x 轴，点A的坐标为（5，4）经过点O、点C作直线l，将直线l沿y轴上下平移．（1）当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；（2）当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F，连接BE、BF，求△BEF的面积．21．（2019秋•罗湖区校级期末）如图，在平面直角坐标系中，直线l1：y＝x与直线l2：y＝kx+b相交于点A，点A的横坐标为3，直线l2交y轴于点B，且OA＝OB．（1）试求直线l2的函数表达式；（2）若将直线l1沿着x轴向左平移3个单位，交y轴于点C，交直线l2于点D．试求△BCD的面积．22．（2018秋•宿迁期末）如图，一次函数y＝（m+1）x+4的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB面积为4．（1）则m＝，点A的坐标为（，）．（2）过点B作直线BP与x轴的正半轴相交于点P，且OP＝4OA，求直线BP的解析式；（3）将一次函数y＝（m+1）x+4的图象绕点B顺时针旋转45°，求旋转后的对应的函数表达式．23．（2019•大渡口区模拟）如图，在平面直角坐标系中，边长为2的正方形ABCD在第一象限内，AD∥y轴，点A的坐标为（5，3），已知直线l：y＝x﹣2．（1）将直线l向上平移m个单位，使平移后的直线恰好经过点A，求m的值；（2）在（1）的条件下，平移后的直线与正方形的边长BC交于点E，求△ABE的面积．24．（2018春•沙坪坝区校级期末）如图：一次函数y＝x+2交y轴于A，交y＝3x﹣6于B，y＝3x﹣6交x轴于C，直线BC顺时针旋转45°得到直线CD．（1）求点B的坐标；（2）求四边形ABCO的面积；（3）求直线CD的解析式．25．（2017春•武昌区期末）已知一次函数y＝kx+b的图象过点A（﹣4，﹣2）和点B（2，4）（1）求直线AB的解析式；（2）将直线AB平移，使其经过原点O，则线段AB扫过的面积为．26．（2017春•安岳县期中）已知直线y＝（m+1）x|m|﹣1+（2m﹣1），当x1＞x2时，y1＞y2，求该直线的解析式．并求该直线经过怎么的上下平移就能过点（2，5）？27．（2016春•大兴区期末）阅读材料：通过一次函数的学习，小明知道：当已知直线上两个点的坐标时，可以用待定系数法，求出这个一次函数的表达式．有这样一个问题：直线l1的表达式为y＝﹣2x+4，若直线l2与直线l1关于y轴对称，求直线l2的表达式．下面是小明的解题思路，请补充完整．第一步：求出直线l1与x轴的交点A的坐标，与y轴的交点B的坐标；第二步：在平面直角坐标系中，作出直线l1；第三步：求点A关于y轴的对称点C的坐标；第四步：由点B，点C的坐标，利用待定系数法，即可求出直线l2的表达式．小明求出的直线l2的表达式是．请你参考小明的解题思路，继续解决下面的问题：（1）若直线l3与直线l1关于直线y＝x对称，则直线l3的表达式是；（2）若点M（m，3）在直线l1上，将直线l1绕点M顺时针旋转90°．得到直线l4，求直线l4的表达式．28．（2016•河北模拟）如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B（﹣3，3）也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．（1）求点C的坐标和直线l1的解析式；（2）若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；（3）已知直线l2：y＝x+b经过点B，与y轴交于点E，求△ABE的面积．29．（2015秋•栖霞区期末）课本P152有段文字：把函数y＝2x的图象分别沿y轴向上或向下平移3个单位长度，就得到函数y＝2x+3或y＝2x﹣3的图象．【阅读理解】小尧阅读这段文字后有个疑问：把函数y＝﹣2x的图象沿x轴向右平移3个单位长度，如何求平移后的函数表达式？老师给了以下提示：如图1，在函数y＝﹣2x的图象上任意取两个点A、B，分别向右平移3个单位长度，得到A′、B′，直线A′B′就是函数y＝﹣2x的图象沿x轴向右平移3个单位长度后得到的图象．请你帮助小尧解决他的困难．（1）将函数y＝﹣2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为．A．y＝﹣2x+3；B．y＝﹣2x﹣3；C．y＝﹣2x+6；D．y＝﹣2x﹣6【解决问题】（2）已知一次函数的图象与直线y＝﹣2x关于x轴对称，求此一次函数的表达式．【拓展探究】（3）一次函数y＝﹣2x的图象绕点（2，3）逆时针方向旋转90°后得到的图象对应的函数表达式为．（直接写结果）专题09一次函数与几何变换一．选择题1．（2021春•大同期末）对于一次函数y＝﹣2x+4，下列结论正确的是（）A．函数的图象与y轴的交点坐标是（4，0）B．函数的图象不经过第三象限C．函数的图象向上平移4个单位长度得y＝﹣2x的图象D．若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＜y2【思路引导】代入y＝0求出与之对应的x值，即可得出A不正确；根据一次函数的系数结合一次函数的性质，即可得知B选项正确、D选项不正确，根据平移的规律求得平移后的解析式，即可判断C不正确，此题得解．【完整解答】解：A、令y＝﹣2x+4中y＝0，则x＝2，∴一次函数的图象与x轴的交点坐标是（2，0），故本选项不符合题意；B、∵k＝﹣2＜0，b＝4＞0，∴一次函数的图象经过第一、二、四象限，即函数的图象不经过第三象限，故本选项符合题意；C、根据平移的规律，函数的图象向上平移4个单位长度得到的函数解析式为y＝﹣2x+4+4，即y＝﹣2x+8，故本选项不符合题意；D、∵k＝﹣2＜0，∴一次函数中y随x的增大而减小，∴若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＞y2，故本选项不符合题意．故选：B．【考察注意点】本题考查了一次函数的图象以及一次函数的性质，解题的关键是逐条分析四个选项．本题属于基础题，难度不大，解决该题时，熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键．2．（2021•扬州）如图，一次函数y＝x+的图象与x轴、y轴分别交于点A，B，把直线AB绕点B顺时针旋转30°交x轴于点C，则线段AC长为（）A．+B．3C．2+D．+【思路引导】根据一次函数表达式求出点A和点B坐标，得到△OAB为等腰直角三角形和AB的长，过点C作CD⊥AB，垂足为D，证明△ACD为等腰直角三角形，设CD＝AD＝x，结合旋转的度数，用两种方法表示出BD，得到关于x的方程，解之即可．【完整解答】解：∵一次函数y＝x+的图像与x轴、y轴分别交于点A、B，令x＝0，则y＝，令y＝0，则x＝﹣，则A（﹣，0），B（0，），则△OAB为等腰直角三角形，∠ABO＝45°，∴AB＝＝2，过点C作CD⊥AB，垂足为D，∵∠CAD＝∠OAB＝45°，∴△ACD为等腰直角三角形，设CD＝AD＝x，∴AC＝＝x，由旋转的性质可知∠ABC＝30°，∴BC＝2CD＝2x，∴BD＝＝x，又BD＝AB+AD＝2+x，∴2+x＝x，解得：x＝+1，∴AC＝x＝（+1）＝，故选：A．【考察注意点】本题考查了一次函数与坐标轴的交点问题，等腰直角三角形的判定和性质，直角三角形的性质，勾股定理，二次根式的混合运算，知识点较多，解题的关键是作出辅助线，构造特殊三角形．3．（2020秋•天桥区期末）如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（）A．5B．4C．3D．2【思路引导】先根据△AEF为等腰直角三角形，可得直线l与直线BD平行，即直线l沿x轴的负方向平移时，同时经过B，D两点，再根据BD的长即可得到b的值．【完整解答】解：如图1，连接BD并且两端延长，直线y＝x﹣3中，令y＝0，得x＝3；令x＝0，得y ＝﹣3，即直线y＝x﹣3与坐标轴围成的△OEF为等腰直角三角形，∴直线l与直线BD平行，即直线l沿x轴的负方向平移时，同时经过B，D两点，由图2可得，t＝2时，直线l经过点A，∴AO＝3﹣2×1＝1，∴A（1，0），由图2可得，t＝12时，直线l经过点C，∴当t＝+2＝7时，直线l经过B，D两点，∴AD＝（7﹣2）×1＝5，∴等腰Rt△ABD中，BD＝5，即当a＝7时，b＝5．故选：A．【考察注意点】本题考查了动点问题的函数图象，一次函数图象与几何变换，用图象解决问题时，要理清图象的含义即会识图．解决问题的关键是掌握正方形的性质以及平移的性质．4．（2020秋•碑林区校级期中）将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的表达式为（）A．y＝﹣3x+6B．y＝﹣3x﹣6C．y＝﹣3x+2D．y＝﹣3x﹣2【思路引导】根据平移性质可由已知的解析式写出新的解析式．【完整解答】解：根据题意，得直线向右平移2个单位，即对应点的纵坐标不变，横坐标减2，所以得到的解析式是y＝﹣3（x﹣2）＝﹣3x+6．故选：A．【考察注意点】此题主要考查了一次函数图象与几何变换，解题时注意：y＝kx左右平移|a|个单位长度的时候，即直线解析式是y＝k（x±|a|）；当直线y＝kx上下平移|b|个单位长度的时候，则直线解析式是y ＝kx±|b|．5．（2020•碑林区校级模拟）若直线y＝kx+3与直线y＝2x+b关于直线x＝1对称，则k、b值分别为（）A．k＝2、b＝﹣3B．k＝﹣2、b＝﹣3C．k＝﹣2、b＝1D．k＝﹣2、b＝﹣1【思路引导】先求出一次函数y＝kx+3与y轴交点关于直线x＝1的对称点，得到b的值，再求出一次函数y＝2x+b与y轴交点关于直线x＝1的对称点，代入一次函数y＝kx+3，求出k的值即可．【完整解答】解：∵一次函数y＝kx+3与y轴交点为（0，3），∴点（0，3）关于直线x＝1的对称点为（2，3），代入直线y＝2x+b，可得4+b＝3，解得b＝﹣1，一次函数y＝2x﹣1与y轴交点为（0，﹣1），（0，﹣1）关于直线x＝1的对称点为（2，﹣1），代入直线y＝kx+3，可得2k+3＝﹣1，解得k＝﹣2．故选：D．【考察注意点】本题考查的是一次函数图象与几何变换，待定系数法求函数解析式，先根据题意得出直线与坐标轴的交点是解决问题的关键．6．（2019•嘉祥县三模）在平面直角坐标系中，将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，则下列平移作法正确的是（）A．将y1向上平移2个单位长度B．将y1向上平移4个单位长度C．将y1向左平移3个单位长度D．将y2向右平移6个单位长度【思路引导】利用一次函数图象的平移规律，左加右减，上加下减，得出即可．【完整解答】解：∵将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，∴2（x+a）﹣2＝2x+4，解得：a＝3，故将y1向左平移3个单位长度．故选：C．【考察注意点】此题主要考查了一次函数图象与几何变换，正确把握变换规律是解题关键．7．（2018春•雨花区校级月考）如图，A（0，1），M（3，2），N（4，4）．点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，当M、N位于直线l的异侧时，t应该满足的条件是（）A．3＜t＜6B．4＜t＜7C．3＜t＜7D．＜t＜7【思路引导】分别求出直线l经过点M、点N时的t值，即可得到t的取值范围．【完整解答】解：当直线y＝﹣x+b过点M（3，2）时，2＝﹣3+b，解得：b＝5，5＝1+t，解得t＝4．当直线y＝﹣x+b过点N（4，4）时，4＝﹣4+b，解得：b＝8，8＝1+t，解得t＝7．故若点M，N位于l的异侧，t的取值范围是：4＜t＜7．故选：B．【考察注意点】本题考查了坐标平面内一次函数的图象与性质，关键是利用一次函数图象上点的坐标特征解答．二．填空题8．（2021春•安丘市期末）在平面直角坐标系xOy中，Rt△AOB的直角顶点B在y轴上，点A的坐标为（1，），将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，过A'作A'C垂直于OA′交y轴于点C，则点C 的坐标为（0，﹣4）．【思路引导】依据轴对称的性质可得OB'＝OB＝，A′B′＝AB＝1，OA′＝OA＝2，进而通过证得△A′OB′∽△COA′，求得OC＝4，即可证得C的坐标为（0，﹣4）．【完整解答】解：∵点A的坐标为（1，），∴AB＝1，OB＝，∴OA＝＝＝2，∵将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，∴OB'＝OB＝，A′B′＝AB＝1，OA′＝OA＝2，∴A'（﹣，﹣1），∵过A'作A'C垂直于OA'交y轴于点C，∴∠A′OC+∠A′CO＝90°，∵∠A′OB′+∠A′OC＝90°，∴∠A′CO＝∠A′OB′，∵∠A′B′O＝∠OA′C＝90°，∴△A′OB′∽△OCA′，∴＝，即＝，∴OC＝4，∴C（0，﹣4），故答案是：（0，﹣4）．【考察注意点】本题考查了轴对称的性质，正比例函数的性质，求得对称点的坐标是解题的关键．9．（2021春•东台市月考）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么ABCD面积为8．【思路引导】通过图象中（4，0），（7，2），（8，2）可得直线运动到A，D，B三点时所移动距离，从而求出AB长度，再通过添加辅助线构造直角三角形求出平行四边形的高而求解．【完整解答】解：由图象可知，直线经过A时移动距离为4，经过D时移动距离为7，经过B时移动距离为8，∴AB＝8﹣4＝4．如图，当直线经过点D时，交AB于点E，作DF垂直于AB于点F，由图2可知DE＝2，∵直线与AB夹角为45°，∴DF＝EF＝2，∴ABCD面积为AB•DF＝4×2＝8．故答案为：8．【考察注意点】本题考查一次函数图象与图形结合问题，解题关键是掌握k＝﹣1时直线与x轴所夹锐角为45°．10．（2021•广东模拟）如图，已知一条直线经过点A（﹣1，0），B（0，﹣2），将这条直线向右平移与x 轴、y轴分别交于点C、D，若AB＝AD，则直线CD的函数表达式为y＝﹣2x+2．【思路引导】先求出直线AB的解析式，再根据平移的性质求直线CD的解析式．【完整解答】解：设直线AB的解析式为y＝kx+b（k≠0），∵点A（﹣1，0）点B（0，﹣2）在直线AB上，∴，解得，∴直线AB的解析式为y＝﹣2x﹣2，∵AB＝AD，AO⊥BD，∴OD＝OB，∴D（0，2），∴直线CD的函数解析式为：y＝﹣2x+2，故答案为：y＝﹣2x+2．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．11．（2020春•黄陂区期末）将直线y＝2x﹣3沿y轴向上平移2个单位后，所得直线的解析式是y＝2x﹣1．【思路引导】直接根据“上加下减，左加右减”的原则进行解答即可．【完整解答】解：由“上加下减”的原则可知，直线y＝2x﹣3沿y轴向上平移2个单位，所得直线的函数关系式为y＝2x﹣3+2，即y＝2x﹣1；故答案为y＝2x﹣1．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．12．（2018秋•福田区校级期中）如图，过点A1（1，0）作x轴的垂线，交直线y＝2x于点B1；点A2与点O关于直线A1B1对称；过点A2（2，0）作x轴的垂线，交直线y＝2x于点B2；点A3与点O关于直线A2B2对称；过点A3（4，0）作x轴的垂线，交直线y＝2x于点B3；…，按此规律作下去，则点B n的坐标为（2n﹣1，2n）．【思路引导】先根据题意求出A2点的坐标，再根据A2点的坐标求出B2的坐标，以此类推总结规律便可求出点B n的坐标．【完整解答】解：∵点A1坐标为（1，0），∴OA1＝1，过点A1作x轴的垂线交直线于点B1，可知B1点的坐标为（1，2），∵点A2与点O关于直线A1B1对称，∴OA1＝A1A2＝1，∴OA2＝1+1＝2，∴点A2的坐标为（2，0），B2的坐标为（2，4），∵点A3与点O关于直线A2B2对称．故点A3的坐标为（4，0），B3的坐标为（4，8），依此类推便可求出点A n的坐标为（2n﹣1，0），点B n的坐标为（2n﹣1，2n）．故答案为：（2n﹣1，2n）．【考察注意点】本题考查了一次函数图象上点的坐标特征：一次函数图象上点的坐标满足其解析式．也考查了轴对称的性质．13．（2017秋•碑林区校级期末）如图，一次函数y＝，的图象向下平移2个单位后得直线l，直线l交x轴于点A、交y轴于点B，在线段AB上有一动点P（不与点A、B重合），过点P分别作PE⊥x轴点E，PF⊥y轴于点F，当线段EF的长最小时，点P的坐标为（﹣，）．【思路引导】利用勾股定理和一次函数图象上点的坐标特征，列出二次函数关系式，结合二次函数最值的求法解答．【完整解答】解：由已知条件得到直线l解析式为：y＝﹣2，即y＝，设P（a，），所以EF2＝a2+（）2＝a2+a+．当EF取最小值时，a＝﹣＝﹣，此时，＝，即P（﹣，），故答案是：（﹣，）．【考察注意点】考查了一次函数图象与几何变换，解题时，利用了二次函数最值的求法，熟记二次函数顶点坐标公式是解题的关键．14．（2018春•丰南区期末）如图，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线l将图形分成面积相等的两部分，则将直线l向右平移3个单位长度后所得直线l′的函数解析式为y＝x﹣．【思路引导】设直线l和八个正方形的最上面交点为A，过点A作AB⊥y轴于点B，过点A作AC⊥x 轴于点C，易知OB＝3，利用三角形的面积公式和已知条件求出A的坐标，再利用待定系数法可求出该直线l的解析式，再根据平移规律即可得到直线l′的函数解析式．【完整解答】解：设直线l和八个正方形的最上面交点为A，过A作AB⊥OB于B，过A作AC⊥OC于C，∵正方形的边长为1，∴OB＝3，∵经过原点的一条直线l将这八个正方形分成面积相等的两部分，∴两边分别是4，∴三角形ABO面积是5，∴OB•AB＝5，∴AB＝，∴OC＝，由此可知直线l经过（，3），设直线l为y＝kx，则3＝k，k＝，∴直线l解析式为y＝x，∴直线l向右平移3个单位长度后所得直线l′的函数解析式为y＝（x﹣3），即y＝x﹣，故答案为：y＝x﹣．【考察注意点】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质，解题的关键是作AB⊥y轴，作AC⊥x轴，根据题意即得到：直角三角形ABO，利用三角形的面积公式求出AB的长．15．（2019春•西湖区校级期中）在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y＝4x+1以每秒2个单位的速度向下平移，经过6秒该直线可将平行四边形OABC的面积平分．【思路引导】首先连接AC、BO，交于点D，当y＝4x+1经过D点时，该直线可将▱OABC的面积平分，然后计算出过D且平行直线y＝4x+1的直线解析式，从而可得直线y＝4x+1要向下平移，进而可得答案．【完整解答】解：连接AC、BO，交于点D，当y＝4x+1经过D点时，该直线可将▱OABC的面积平分；∵四边形AOCB是平行四边形，∴BD＝OD，∵B（6，2），点C（4，0），∴D（3，1），设DE的解析式为y＝kx+b，∵平行于y＝4x+1，∴k＝4，∵过D（3，1），∴DE的解析式为y＝4x﹣11，∴直线y＝4x+1要向下平移12个单位，∴时间为6秒，故答案为：6【考察注意点】此题主要考查了平行四边形的性质，以及一次函数，关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积．16．（2019•天津二模）将函数y＝3x+1的图象平移，使它经过点（1，1），则平移后的函数表达式是y＝3x﹣2．【思路引导】根据函数图象平移的性质得出k的值，设出相应的函数解析式，再把经过的点代入即可得出答案．【完整解答】解：新直线是由一次函数y＝3x+1的图象平移得到的，∴新直线的k＝3，可设新直线的解析式为：y＝3x+b．∵经过点（1，1），则1×3+b＝1，解得b＝﹣2，∴平移后图象函数的解析式为y＝3x﹣2；故答案为：y＝3x﹣2．【考察注意点】此题考查了一次函数图形与几何变换，求直线平移后的解析式时要注意平移时k和b的值的变化．17．（2019春•常州期中）如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点B（6，2），C（4，0），直线y＝2x+1以每秒1个单位长度的速度沿y轴向下平移，经过6秒该直线可将平行四边形OABC分成面积相等的两部分．【思路引导】首先连接AC、BO，交于点D，当y＝2x+1经过D点时，该直线可将▱OABC的面积平分，然后计算出过D且平行直线y＝2x+1的直线解析式，从而可得直线y＝2x+1要向下平移6个单位，进而可得答案．【完整解答】解：连接AC、BO，交于点D，当y＝2x+1经过D点时，该直线可将▱OABC的面积平分；∵四边形AOCB是平行四边形，∴BD＝OD，∵B（6，2），点C（4，0），∴D（3，1），设DE的解析式为y＝kx+b，∵平行于y＝2x+1，∴k＝2，∵过D（3，1），∴DE的解析式为y＝2x﹣5，∴直线y＝2x+1要向下平移6个单位，∴时间为6秒，故答案为：6．【考察注意点】此题主要考查了平行四边形的性质，以及一次函数，关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积．三．解答题18．（2021春•古丈县期末）如图，直线l是一次函数y＝kx+b的图象．（1）求出这个一次函数的解析式；（2）将该函数的图象向下平移5个单位，求出平移后一次函数的解析式，并写出平移后的图象与x轴的交点坐标．【思路引导】（1）利用待定系数法确定该一次函数的解析式；（2）根据平移规律“上加下减”写出平移后一次函数解析式，然后根据一次函数图象上点的坐标特征求直线与x轴的交点坐标．【完整解答】解：（1）∵一次函数y＝kx+b的图象经过点（﹣2，0）和点（2，2），∴．解得k＝，b＝1．∴一次函数的解析式为：y＝x+1；（2）∵一次函数y＝x+1向下平移5个单位的解析式为y＝x+1﹣5＝x﹣4，即y＝x﹣4．∴当y＝0时，x＝8，∴平移后的图象与x轴的交点坐标为（8，0）．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的性质是解答此题的关键．19．（2021春•武汉月考）已知，在平面直角坐标系中，函数y1＝2|x﹣a|，（1）若该函数经过点A（1，0），求该函数的解析式，并在图1中画出函数图象；（2）在（1）的条件下，将函数y2＝x向上平移m个单位后与函数y1的图象相交于点B和C点，若BC＝，求m；（3）如图2，设直线y3＝6n与直线y4＝2n分别与函数y1＝2|x﹣a|相交于点E、F和M、N，点P为直线y3＝6n上一点，连接PM、PN并延长交直线y5＝kn于点G、H，若2EF＝3GH，求k．【思路引导】（1）把点A坐标代入函数，求出a，得到函数y1的解析式，画出图象；（2）设出函数y2的解析式，得到B、C的坐标，根据BC＝列出方程，求m的值；（3）由三角形相似得出MN和GH的比例，求出k的值．【完整解答】解：（1）把点A（1，0）代入y1＝2|x﹣a|，得：2|1﹣a|＝0，解得：a＝1，∴y1＝2|x﹣1|，图象如右所示．（2）由题意得y2＝x+m（m＞0），x≤1时，y1＝﹣2x+2，x＞1时，y1＝2x﹣2，由，解得：，∴B（，），由，解得：，∴C（m+2，2m+2），∵BC＝，∴（m+2﹣）2+（2m+2﹣）2＝128，解得：m1＝5，m2＝﹣7（舍），∴m＝5．（3）∵直线y3＝6n与直线y4＝2n间的距离为4n，直线y4＝2n与x轴间的距离为2n，∴EF＝3MN，∵2EF＝3GH，∴MN：GH＝1：2，∴MN是△PGH的中位线，∴y3＝6n与y4＝2n间的距离和y3＝6n与y5＝kn间的距离相等，∴k＝﹣2．【考察注意点】本题考查了分段函数图象和函数图象变换，画图的关键顺序是“列表﹣描点﹣连线”，需要注意的是连线的时候要用平滑的曲线连接．20．（2021春•河北区期末）如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x 轴，点A的坐标为（5，4）经过点O、点C作直线l，将直线l沿y轴上下平移．（1）当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；（2）当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F，连接BE、BF，求△BEF的面积．【思路引导】（1）根据题意求得正方形各顶点的坐标，然后根据待定系数法求得直线l的解析式，直线平移，斜率不变，设平移后的直线方程为y＝x+b；把点B和D的坐标代入进行解答即可；（2）根据正方形是中心对称图形，当直线l经过对角线的交点时，恰好平分正方形ABCD的面积，求得交点坐标，代入y＝x+b，根据待定系数法即可求得直线l此时的解析式，然后求得E、F的坐标，根据待定系数法求得直线BE的解析式，得到与y轴的交点Q的坐标，根据三角形面积公式即可求得．【完整解答】解：（1）∵长为3的正方形ABCD中，点A的坐标为（5，4），∴B（2，4），C（2，1），D（5，1），设直线l的解析式为y＝kx，把C（2，1）代入得，1＝2k，解得k＝，∴直线l为y＝，设平移后的直线方程为y＝x+b，。

中考数学压轴题讲解分析：一次函数与几何综合问题.doc

中考数学压轴题讲解分析：一次函数与几何综合问题下面我们先来看一道典型例题。

中考数学，一次函数与几何相关综合题，典型例题分析1：如图，已知一次函数y=－x+7与正比例函数y=4x/3的图象交于点A，且与x轴交于点B．（1）求点A和点B的坐标；（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O﹣C﹣A 的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA 或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．①当t为何值时，以A、P、R为顶点的三角形的面积为8？②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．考点分析：一次函数综合题.题干分析：（1）根据图象与坐标轴交点求法直接得出即可，再利用直线交点坐标求法将两直线解析式联立即可得出交点坐标；（2）①利用S梯形ACOB－S△ACP－S△POR－S△ARB ＝8，表示出各部分的边长，整理出一元二次方程，求出即可；②根据一次函数与坐标轴的交点得出，∠OBN＝∠ONB ＝45°，进而利用勾股定理以及等腰三角形的性质和直角三角形的判定求出即可。

解题反思：此题主要考查了一次函数与坐标轴交点求法以及三角形面积求法和等腰直角三角形的性质等知识，此题综合性较强，利用函数图象表示出各部分长度，再利用勾股定理求出是解决问题的关键。

动态综合问题一直是中考数学压轴题非常喜欢考查的内容，解决此类问题需要考生根据变量之间的关系，对动态几何中的“变量”进行分类讨论,如运动的点、运动的线等等。

考生要想正确解决此类问题，关键在于要抓住点与线的运动和变化,数量之间的关系也随之发生着变化,再把这些“变化”的几何问题就转化为函数问题。

中考数学，一次函数与几何相关综合题，典型例题分析2：如图，在平面直角坐标系中，以点B（0，8）为端点的射线BG∥x轴，点A是射线BG上的一个动点（点A与点B 不重合）．在射线AG上取AD=OB，作线段AD的垂直平分线，垂足为E，且与x轴交于点F，过点A作AC⊥OA，交射线EF于点C．连接OC、CD，设点A的横坐标为t．（1）用含t的式子表示点E的坐标为_______；（2）当t为何值时，∠OCD=180°？（3）当点C与点F不重合时，设△OCF的面积为S，求S与t之间的函数解析式．考点分析：一次函数综合题；相似三角形的判定与性质．题干分析：（1）由点B坐标为（0，8），可知OB=8，根据线段垂直平分线的定义可知：AE=4，从而求得：BE=t+4，故此点E 的坐标为（t+4，8）；（2）过点D作DH⊥OF，垂足为H．先证明△OBA∽△AEC，由相似三角形的性质可知，EC/AB=AE/OB可求得EC=t/2，从而得到点C的坐标为（t+4，8﹣t/2），因为∠OCD=180°，CF∥DH，可知，OF/OH=FC/DH即从（t+4）/（t+8）=（8﹣t/2）/8而可解得t的值；（3）三角形OCF的面积=OF•FC/2从而可得S与t的函数关系式．解题反思：本题主要考查的是相似三角形的性质和判定，用含字母t 的式子表示点C的坐标是解题的关键。

一次函数与几何综合(k,b的几何意义二)(人教版)(含答案)

一次函数与几何综合（k，b的几何意义二）（人教版）一、单选题(共7道，每道14分)1.如图，将正方形ABCD置于平面直角坐标系的第一象限内，使AB落在x轴正半轴上，直线经过点C，与x轴交于点E，若点A的坐标是(1，0)，则四边形AECD的面积是( )A.4B.6C.10D.16答案：C解题思路：试题难度：三颗星知识点：一次函数与几何综合2.如图，已知直线与直线相交于点F，分别交x轴于点E，G，矩形ABCD顶点C，D分别在直线上，顶点A，B都在x轴上，且点B与点G 重合，则长方形ABCD的面积为( )A.12B.18C.24D.32答案：B解题思路：试题难度：三颗星知识点：一次函数、坐标、几何三角通道互转3.正方形……按照如图所示的方式放置，点……和点……分别在直线l和x轴上，已知点(1，1)，(3，2)，则的坐标是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：一次函数k的几何意义4.已知函数的图象为直线，点P的坐标为(2，1)，则点P到直线的距离为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：一次函数k的几何意义5.如图，点A的坐标为(-1，0)，点B在直线y=x-3上运动，则线段AB最短为( )A. B.4C. D.答案：C解题思路：试题难度：三颗星知识点：k的几何意义6.已知直线PQ的斜率为，将直线PQ绕点P(，0)顺时针旋转60°所得直线的表达式为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：一次函数与几何综合7.如图，直线与x轴相交于点A，与y轴相交于点B，将△ABO沿着AB翻折，得到△ABC，则直线BC的表达式为( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：一次函数与几何综合。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一次函数压轴题研究（二）一次函数与几何综合（讲义及答案）➢课前预习
1.小明认为，在一次函数y=kx+b中，x每增加1，kx+b就增加了k，y也就增
加了k．因此要想求出一次函数表达式中的k，只需要知道x每增加1个单位长度，y增加的单位长度即可．例如：在如图所示的一次函数图象中，x从1变到2时，y的值由3变到5，即x每增加1个单位长度，y就增加2个单位长度，因此k的值就是2．再结合b为函数图象与y轴交点纵坐标，可得b=1．故容易求出一次函数表达式为y=2x+1．请你用待定系数法验证小明的说法．
x
请根据小明的思路，直接写出下图中一次函数的表达式．
➢知识点睛
1.一次函数表达式：y=kx+b（k，b为常数，k≠0）
①k是斜率，表示倾斜程度，可以用几何中的坡度（或坡比）来解释．坡面
的竖直高度与水平宽度的比叫坡度或坡比，如图所示，AM即为____________，
BM即为____________，则=AM
k
BM
．
M
A
B
②b 是截距，表示直线与y 轴交点的纵坐标．
2. 设直线l 1：y 1=k 1x +b 1，直线l 2：y 2=k 2x +b 2，其中k 1，k 2≠0．
①若k 1=k 2，且b 1≠b 2，则直线l 1_____l 2； ②若k 1·k 2=_________，则直线l 1_____l 2． 3. 一次函数与几何综合解题思路
①要求坐标，②要求函数表达式，③要研究几何图形，
➢ 精讲精练
1. 如图，点B ，C 分别在直线y =2x 和y =kx 上，A 形ABCD 是正方形，则k 的值为________．
第1题图第2题图
坐标
几何图形
一次函数
2. 如图，点A ，B 分别在直线y =kx 和y =-4x 上，C ，D 是x 轴上的两点，若四
边形ABCD 是矩形，且AB :AD =3:2，则k 的值为________．
3. 如图，在平面直角坐标系中放入一张矩形纸片OABC ，点D 在AB 边上，将
第3题图第4题图
4. 已知点A 的坐标为(3，0)，直线y =x +b （b >0）与y 轴交于点B ，连接
AB ，
若∠α
=75°，则b 的值为_________．
5. 如图，已知直线l ：y x =+与x 轴交于点A ，与y 轴交于点B ，将△AOB 沿直线l 折叠，点O 落在点C 处，则直线AC 的
表达式为__________________．
第5题图第6题图 6. 如图，△OAB 是边长为2的等边三角形，过点A 的直线y =-x +m 与x 轴交于点C ，则点C 的坐标为__________．
7. 如图，直线l 1与x 轴、y 轴分别交于点A ，B ，直线l 2与x 轴、y 轴分别交于
点C ，D ，OA =OD =m ，OB =OC =n ，直线l 1与直线l 2交于点E ，则l 1____l 2；若直线l 1，l 2的斜率分别为k 1，k 2，则k 1·k 2=_______．
第7题图第8题图
8.如图，已知点A的坐标为(1，0)，点B在直线y=2x+4上运动，当线段AB最
短时，点B的坐标为__________．
9.如图，直线
4
8
3
y x
=-+与x轴、y轴分别交于点A，B，线段AB的垂直平分
线交x轴于点C，交AB于点D，则直线CD的表达式为____________．
第9题图第10题图
10.如图，直线y=x+4与x轴、y轴分别交于点A和点B，点C为线段AB的中
点，点D的坐标为(0，1)，点P为OA上一动点，当PC+PD值最小时，点P 的坐标为____________．
11.如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA，OC分别落在
x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′处，连接AA′，交OB于点D．若OA=1，AB=2，则点D的坐标为______________，点A′的坐标为______________．
【参考答案】
➢课前预习
1.小明的说法正确，验证过程略
32
y x
=-，22
y x
=-+
➢知识点睛
1.竖直高度，水平宽度
2.①∥；②-1，⊥
3.①利用函数表达式或线段长转坐标
②待定系数法或k，b的几何意义
③坐标转线段长或k，b的几何意义➢精讲精练
1.2 3
2.4 5
3.
1
9
3
y x
=-+
4.
5.y=+
6.（0）
7.⊥，-1
8.
76
55（-，）
9.
37
44 y x
=+
10.(
2
3
-，0)
11.(1
5
，
2
5
)；(
3
5
-，
4
5
)。