信息论与编码复习5-6
信息论与编码-复习
第6章 信道编码
计算:
对于循环码,已知(n,k)循环码 会求g(x),并根据g(x)求G, 例p191-192 6.3.3,p193 6.3.4 会求h(x)=(xn+1)/g(x),并根据h(x), 例p193 6.3.4 会求系统循环码码字:由G经过初等行变换得Gs, 再通过C=mGS得系统循环码码字
第4章 信息率失真函数
计算:
对于离散信源(如作业4.1(3)):
R(D)的计算、R(D)与D的关系图 只要求等概信源,对称失真的R(D),见P120 (4.2.50式) 关系图见P109 图4.1.1(注意区分离散和连续信源), 所取的点的纵坐标根据R(D)的计算式求得
第4章 信息率失真函数
计算:
会计算达到稳态时的状态概率分布(作业2.16(1))和 极限熵(作业2.16(2),2.17(2)和p48 例2.2.4);
给定状态转移概率,会画状态转移图,反之亦要求。
第二章 ——续
计算:
信源冗余度的计算(作业2.17(3)) 根据给出的离散信源,能够进行定长编码,求出码字。
掌握信源编码器的性能指标(编码效率η)及其与码 长(k)之间的关系。
第3章 信道容量
掌握离散无记忆信道的N次扩展信道的容量的求解
CN次扩展 NC单符号无记忆信道
无噪信道的容量:见作业3.14 应用连续信道的信道容量公式进行解题
连续信道的容量 所需的信号功率
S 如作业3.19,使用公式 C连续 B log 2 (1 ) N 注意:
C就是信号的传输速率 dB表示的信噪比在代入时要进行转换
能够通过分析电路的运行过程,得到生成的循环码字。 见课件
信息论与编码期末复习篇
平均信息量。它不是指人们可以获得多少信息;而是指客观存在
多少信息,因而数学关系仅是平均不确定度的量。
而连续信源的相对熵,则是指相对平均不定度。
HC (X ) p(x) log p(x)dx
RX
课程复习大纲
➢ 熵函数的性质 (指离散熵)
1. 对称性: H ( p1, p2,K , pn ) H ( p2, p1, p3 K , pn ) 2. 非负性: H (X ) 0
r
C loga
a
Aj
j
迭代算法
连续信道
5
高斯信道:
C
1 2
log(1
Pwi
2 n
)
限时限频限功率 加性高斯白噪声信道
信道的容量
C L log(1 PS / N0 ) L log(1 PS ) WT log(1 PS )
2
2W 2 2
各种熵之间的关系
名称
无 条 件 熵
条 件 熵 条 件 熵 联 合 熵 交 互 熵
符号
H(X) H (Y )
H(X /Y) H (Y / X )
H(XY) H(YX)
I (X ;Y ) I (Y; X )
关系
H(X) H(X /Y) H(X /Y) I(X;Y)
H (X ) H (XY) H (Y / X )
图示
Y
X
Y
X
Y
X
Y
X
Y
X
Y
熵 、互信息
➢ 冗余度
R 1 H Hm
or R 1 Hm H0
理解两种冗余度的物理意义。
信息论与编码复习

1、通信系统模型的组成,及各部分的功能。
答:信源,产生消息的源,消息可以是文字,语言,图像。
可以离散,可以连续。
随机发生。
编码器,信源编码器:对信源输出进行变换(消去冗余,压缩),提高信息传输的有效性。
信道编码器:对信源编码输出变换(加入冗余),提高抗干扰能力,提高信息传输的可靠性。
调制器:将信道编码输出变成适合信道传输的方式信道,信号从发端传到收端的介质干扰源,系统各部分引入的干扰,包括衰落,多径,码间干扰,非线性失真,加性噪声译码器,编码器的逆变换信宿,信息的接收者2、消息,信号,信息三者之间的关系答:关系:信息---可以认为是具体的物理信号、数学描述的消息的内涵,即信号具体载荷的内容、消息描述的含义。
信号---则是抽象信息在物理层表达的外延;消息---则是抽象信息在数学层表达的外延。
3、信源的分类答:分类:单消息(符号)信源:离散信源;连续变量信源。
平稳信源。
无/有记忆信源。
马尔可夫信源。
随机波形信源。
离散信源:信源可能输出的消息数是有限的或可数的,而且每次只输出其中一个消息。
可以用一维离散型随机变量X来描述这个信源输出的消息。
这个随机变量X的样本空间就是符号集A;而X的概率分布就是各消息出现的先验概率,信源的概率空间必定是一个完备集。
连续变量信源:数据取值是连续的,但又是随机的。
可用一维的连续型随机变量X来描述这些消息。
这种信源称为连续信源,其数学模型是连续型的概率空间:4、自信息的含义:当事件ai发生以前,表示事件ai发生的不确定性,当事件ai发生以后表示事件ai所含有(所提供)的信息量。
5、互信息含义:信源发送消息ai,而由于干扰,在接收端收到的为消息bj ,此时获得的信息量——互信息,即最初的不确定性减去尚存在的不确定性。
6、离散单符号信源熵的物理含义:熵是随机变量的随机性的描述。
熵是信源输出消息前随机变量平均不确定性的描述。
信源熵H(X)是表示信源输出后每个消息/符号所提供的平均信息量。
信息论与编码总复习

信源的序列熵可以表示为
L
H X H Xl LH X
无记忆
l 1
信源序列中,平均每个符号的熵为
HL
X
1 L
H
X
H
X
无记忆、平稳
离散无记忆信源平均每个符号的符号熵HL(X)等于单 个符号信源的符号熵H(X)
2019/5/11
23
离散有记忆信源的序列熵
p X1X2 X L2 p X L1 / X1X 2 X L2 p X L / X1X 2 X L1
p X1 p X 2 / X1 p X3 / X1X 2 p X L / X1X 2 X L1
2019/5/11
i
i, j
2019/5/11
18
平均互信息量的物理意义
I X;Y H X H X /Y I Y; X H Y H Y / X
H(X/Y):信道疑义度,损失熵
信源符号通过有噪信道传输后引起的信息量损失。
信源X的熵等于接收到的信息量加损失掉的信息量。
8
信源的数学描述
一阶马尔可夫信源
p(X1X2 X3 XL ) p(X1) p(X 2 / X1) p(X3 / X1X 2 ) p(X L / X1X 2 X L2 X L1) p(X1) p(X 2 / X1) p(X3 / X 2 ) p(X L1 / X L2 ) p(X L / X L1)
j
i, j
p(xi y j )I (xi / y j )
i, j
在给定X(即各个xi)条件下,Y集合的条件熵
信息论与编码第二版复习课件第六章

第6章 信道编码
• 按照构码理论:代数码、几何码、算术码、组合码等 • 按照每个码元取值:二进制码与多进制码 3 差错控制系统分类 • 前向纠错(FEC): – 发送端的信道编码器将信息码组编成具有一定纠 错能力的码。 – 接收端信道译码器对接收码字进行译码,若传输 中产生的差错数目在码的纠错能力之内时,译码 器对差错进行定位并加以纠正。
• 若满足条件:
–V中矢量元素在矢量加运算下构成加群; –V中矢量元素与数域F元素的标乘封闭在V中; –分配律、结合律成立。
则称集合V是数域F上的n维矢量空间,或称n维线性空 间,n维矢量又称n重。
码字 码矢 n重 码多项式
14
第6章 信道编码
矢量空间中矢量的关系 对于域F上的若干矢量 V 1 , V 2 , L , V i 及 V k • 线性组合:
消息m
纠错编码
码字C
信道
收码R
纠错译码
消息m′
11
第6章 信道编码
• 自动请求重发(ARQ): – 发端发送检错码, – 收端译码器判断当前码字传输是否出错; – 当有错时按某种协议通过一个反向信道请求发送 端重传已发送的码字(全部或部分)。
消息m 码字C 收码R 消息m′
检错编码
信道
检错译码
12
2
差错图样类型
为了定量地描述信号的差错,定义收、发码之“差” 为差错图样: 差错图样E=发码C- 收码R (模M)
8进制码元
发码C=(0,2,5,4,7,5,2) 收码R=(0,1,5,4,7,5,4) 差错图样E=C-R=(0,1,0,0,0,0,6)(模8)
二进制码: 差错图样等于收码与发码的模2加 E=C⊕R 或 C=R⊕E 发送码字C 1 1 1 1 1 1 1 1 1 1 接收码字R 差错图样E 1001001111 0110110000
信息论与编码复习重点整理(1页版)

1第1章 概论1. 信号(适合信道传输的物理量)、信息(抽象的意识/知识,是系统传输、转换、处理的对象)和消息(信息的载体)定义;相互关系:(1信号携带消息,是消息的运载工具(2信号携带信息但不是信息本身(3同一信息可用不同的信号来表示(4同一信号也可表示不同的信息。
2. 通信的系统模型及目的:提高信息系统可靠性、有效性和安全性,以达到系统最优化.第2章 信源及信息量1. 单符号离散信源数学模型2. 自信息量定义:一随机事件发生某一结果时带来的信息量I(xi)=-log2P(xi)、单位:bit 、物理意义:确定事件信息量为0;0概率事件发生信息量巨大、性质:I(xi)非负;P(xi)=1时I(xi)=0;P(xi)=0时I(xi)无穷;I(xi)单调递减;I(xi)是随机变量。
3. 联合自信息量:I(xiyi)=- log2P(xiyj) 物理意义:两独立事件同时发生的信息量=各自发生的信息量的和、条件自信息量:I(xi/yi)=- log2P(xi/yj);物理意义:特定条件下(yj 已定)随机事件xi 所带来的信息量。
三者关系:I(xi/yi)= I(xi)+ I(yi/xi)= I(yi)+ I(xi/yi)4. 熵:定义(信源中离散消息自信息量的数学期望)、单位(比特/符号)、物理意义(输出消息后每个离散消息提供的平均信息量;输出消息前信源的平均不确定度;变量的随机性)、计算:(H(X)=-∑P(xi)log2 P(xi)) 1)连续熵和离散的区别:离散熵是非负的2)离散信源当且仅当各消息P相等时信息熵最大H (X )=log 2 n 。
3)连续信源的最大熵:定义域内的极值. 5.条件熵H(Y/X) = -∑∑P(xiyj) log2P(yj/xi),H (X /Y )= -∑∑P(xiyj) log2P(xi/yj) 、物理意义:信道疑义度H(X/Y):信宿收到Y 后,信源X 仍存在的不确定度,有噪信道传输引起信息量的损失,也称损失熵。
信息论与编码总复习

VS
奇偶校验位
奇偶校验位是添加到数据中的一个额外位 ,用于检测数据中的错误。根据数据的二 进制位数,可以选择奇校验或偶校验。
05
编码的应用
数据压缩
1 2 3
数据压缩
数据压缩是编码技术的重要应用之一,通过去除 数据中的冗余信息,减少数据的存储空间和传输 时间,提高数据传输效率。
压缩算法
常用的数据压缩算法包括哈夫曼编码、算术编码、 LZ77和LZ78等,这些算法通过不同的方式实现 数据的压缩和解压缩。
互信息与条件互信息
互信息的定义
互信息是两个随机变量之间的相关性度量。对于两个随机变量$X$和$Y$,其互信息定义为$I(X;Y) = sum_{x,y} P(X=x,Y=y) log_2 frac{P(X=x,Y=y)}{P(X=x)P(Y=y)}$。
条件互信息的定义
条件互信息是给定一个随机变量条件下,另一个随机变量的不确定性减少的量度。对于两个随机变量$X$ 和$Y$以及第三个随机变量$Z$,其条件互信息定义为$I(X;Y|Z) = sum_{x,y,z} P(X=x,Y=y,Z=z) log_2 frac{P(X=x,Y=y|Z=z)}{P(X=x|Z=z)P(Y=y|Z=z)}$。
压缩比与效率
数据压缩比和压缩效率是衡量数据压缩算法性能 的重要指标,不同的应用场景需要选择合适的压 缩算法以满足需求。
加密通信
加密通信
编码技术在加密通信中发挥着重要作用,通过将明文转换为密文, 保护数据的机密性和完整性。
加密算法
常见的加密算法包括对称加密和公钥加密,这些算法利用数学函数 和密钥对数据进行加密和解密。
纠错码与检错码
纠错码不仅能够检测错误,还能够纠 正错误,而检错码只能检测错误。
信息论与编码复习资料

1、在认识论层次上研究信息时,必须同时考虑到形式、(含义)和(效用)3个方面的因素2、如果从随机不确定性的角度来定义信息,信息反映(不确定性)的消除量。
3、信源编码的结果是(减少)冗余;而信道编码的手段是(增加)冗余。
4(1948)年,香农发表了著名的论文(通信的数学理论),标志着信息论的诞生。
5、信息商品是一种特殊商品,它有(客观)性、(共享)性、(时效)性和知识创造征。
6、对信源进行观查之前,对认识的主体来说,信源存在(先验)不确定性,观察之后,信源还存在(后验)不确定性。
7、联合符号(x i ,y j )的不确定性,等于(关于y j )不确定性加上(观查到y j 后还剩余)不确定性。
8、256个亮度构成的信源,其熵值最大为(log256=8)。
9、无条件熵(不小于)条件熵,条件多的熵(不大于)条件少的熵。
10、信源编码实质上是对信源进行信息处理,无失真信源编码只是信息处理的方法之一,除此外,还可以对信源进行(限失真)编码。
11、无失真编码对应于无损信道,有失真编码对应于(有噪)信道。
12、有失真编码的(失真范围)受限,所以又称为限失真编码;编码后的(信息率)得到压缩,因此属熵压缩编码。
13、满足(平均失真D D ≤失真度)的信道称为D 允许[试验]信道。
1、无失真编码只对信源的(冗余度)一进行压缩,而不会改变信源的熵,又称冗余度压缩编码。
2、无失真信源编码的作用可归纳为:(1)(符号变换); (2)(冗余度压缩)。
3、(含相同的码字)的码称为奇异码。
1、 研究信息论的主要目的是什么?答:能够高效、可靠、安全并且随心所欲地交换和利用各种各样的信息。
2、信息论的定义(狭义、广义)答:狭义:在信息可以度量的基础上,研究有效和可靠的传递信息的科学。
广义:包含通信的全部统一问题的研究,香农信息论、信号设计、噪声理论、信号检测与估值等。
3、信息有哪些特征?答:(1)接收者在收到信息前对它的内容未知;(2)信息是能使认识主体对某一事物的未知性或不确定性减少的有用的知识;3)信息可以产生、消灭、被携带、贮存及处理;(4)信息可以度量。
《信息论与编码技术》复习提纲复习题

《信息论与编码技术》复习提纲复习题《信息论与编码技术》复习提纲复习题纲第0章绪论题纲:I.什么是信息?II.什么是信息论?III.什么是信息的通信模型?IV.什么是信息的测度?V.自信息量的定义、含义、性质需掌握的问题:1.信息的定义是什么?(广义信息、狭义信息——Shannon信息、概率信息)2.Shannon信息论中信息的三要素是什么?3.通信系统模型图是什么?每一部分的作用的是什么?4.什么是信息测度?5.什么是样本空间、概率空间、先验概率、自信息、后验概率、互信息?6.自信息的大小如何计算?单位是什么?含义是什么(是对什么量的度量)?第1章信息论基础㈠《离散信源》题纲:I.信源的定义、分类II.离散信源的数学模型III.熵的定义、含义、性质,联合熵、条件熵IV.离散无记忆信源的特性、熵V.离散有记忆信源的熵、平均符号熵、极限熵VI.马尔科夫信源的定义、状态转移图VII.信源的相对信息率和冗余度需掌握的问题:1.信源的定义、分类是什么?2.离散信源的数学模型是什么?3.信息熵的表达式是什么?信息熵的单位是什么?信息熵的含义是什么?信息熵的性质是什么?4.单符号离散信源最大熵是多少?信源概率如何分布时能达到?5.信源的码率和信息率是什么,如何计算?6.什么是离散无记忆信源?什么是离散有记忆信源?7.离散无记忆信源的数学模型如何描述?信息熵、平均符号熵如何计算?8.离散有记忆多符号离散平稳信源的平均符号熵、极限熵、条件熵(N阶熵)的计算、关系和性质是什么?9.什么是马尔科夫信源?马尔科夫信源的数学模型是什么?马尔科夫信源满足的2个条件是什么?10.马尔科夫信源的状态、状态转移是什么?如何绘制马尔科夫信源状态转移图?11.马尔科夫信源的稳态概率、稳态符号概率、稳态信息熵如何计算?12.信源的相对信息率和冗余度是什么?如何计算?㈡《离散信道》题纲:I.信道的数学模型及分类II.典型离散信道的数学模型III.先验熵和后验熵IV.互信息的定义、性质V.平均互信息的定义、含义、性质、维拉图VI.信道容量的定义VII.特殊离散信道的信道容量需掌握的问题:1.信道的定义是什么?信道如何分类?信道的数学模型是2.二元对称信道和二元删除信道的信道传输概率矩阵是什么?3.对称信道的信道传输概率矩阵有什么特点?4.根据信道的转移特性图,写出信道传输概率矩阵。
信息论与编码复习总结
By 疯狂阿德第一章绪论考点:●信息、消息、信号的区别●通信系统模型●香农1.信息、消息、信号的区别信息:指事物运动的状态或存在方式的不确定性的描述。
消息:包含信息的语言、文字、图像等。
信号:信息的物理体现。
在通信系统中,实际传输的是信号,但实质内容是信息,信息包含在信号中,信号是信息的载体,通信的结果是消除或部分消除不确定性,从而获得信息。
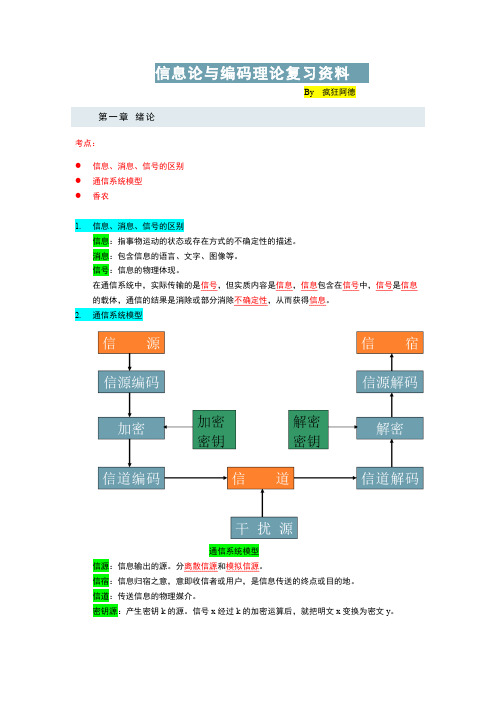
2.通信系统模型通信系统模型信源:信息输出的源。
分离散信源和模拟信源。
信宿:信息归宿之意,意即收信者或用户,是信息传送的终点或目的地。
信道:传送信息的物理媒介。
密钥源:产生密钥k的源。
信号x经过k的加密运算后,就把明文x变换为密文y。
一般地说,通信系统的性能指标主要是有效性、可靠性、安全性和经济性。
除了经济性外,这些指标正是信息论的研究对象。
信源编码:信源编码器的作用:一、将信源发出的信息变换成基带信号;二、压缩冗余度,提高效率(有效性)。
信道编码:在信源编码器输出的代码组上有目的地增加一些监督码元,使之具有检错和纠错能力。
信道译码器具有检错和纠错能力,它能将在其检错或纠错能力范围内的错传码元检测出来并加以纠正,以提高传输信息的可靠性。
信道编码包括调制解调和纠错检错编译码。
信道中的干扰通常使通信质量下降,对于模拟信号,表现在受到的信号的信噪比下降;对于数字信号就是误码率增大。
信道编码的主要方法是增大码率或频带,即增大所需的信道容量。
这恰与信源编码相反。
3.香农他在1941年至1944年对通信和密码进行深入研究,并用概率论的方法研究通信系统,揭示了通信系统传递的对象就是信息,并对信息给以科学的定量描述,提出了信息熵的概念。
还指出通信系统的中心问题是在噪声下如何有效而可靠地传送信息,而实现这一目标的主要方法是编码等。
这一成果于1948年在《贝尔系统技术杂志》以《通信的数学理论》香农因此成为信息论的奠基人。
简答题:一、信源编码与信道编码的区别答:信源编码是压缩信源发出的信息的冗余度,是为了提高信息传输的有效性;而信道编码是在信源编码器输出的代码组上有目的地增加了一些监督码元,增大了信息的冗余度,以提高传输信息的可靠性。
信息论与编码期末考试题----学生复习

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性.2、信源的剩余度主要来自两个方面,一是信源符号间的相关性,二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0,最大熵为bit/符号.4、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr=H r(S))。
5、当R=C或(信道剩余度为0)时,信源与信道达到匹配。
6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。
7、根据是否允许失真,信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为,则输出信号幅度的概率密度是高斯分布或正态分布或时,信源具有最大熵,其值为值。
9、在下面空格中选择填入数学符号“”或“"(1)当X和Y相互独立时,H(XY)=H(X)+H(X/Y)=H(Y)+H(X)。
(2)(3)假设信道输入用X表示,信道输出用Y表示。
在无噪有损信道中,H(X/Y)> 0, H(Y/X)=0,I(X;Y)<H(X).二、若连续信源输出的幅度被限定在【2,6】区域内,当输出信号的概率密度是均匀分布时,计算该信源的相对熵,并说明该信源的绝对熵为多少。
=2bit/自由度该信源的绝对熵为无穷大。
三、已知信源(1)用霍夫曼编码法编成二进制变长码;(6分)(2)计算平均码长;(4分)(3)计算编码信息率;(2分)(4)计算编码后信息传输率;(2分)(5)计算编码效率。
(2分)(1)编码结果为:(2)(3)(4)其中,(5)四、某信源输出A、B、C、D、E五种符号,每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。
如果符号的码元宽度为0.5。
计算:(1)信息传输速率。
(2)将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输,噪声的单边功率谱密度为.试计算正确传输这些数据最少需要的发送功率P。
解:(1)(2)五、一个一阶马尔可夫信源,转移概率为。
信息论与编码期末复习

第三部分、信道编码
3.2 线性分组码
3.2 线性分组码:
码长为n,信息位为k ,记作(n , k); 监督位r =n-k
1、编码
C = K•G
和 P(X)Y0 0..1 22 10 0..1 04 90 0..3 05 9
H(Y | X)= – 0.21log0.3 –0.14log0.2 –0.35log0.5
–0.12log0.4 –0.09log0.3–0.09log0.3
= 1.5114 bit/符号
m
(4)接收符号熵:由 p(yj ) p(xi yj ) i1 P(Y)=(0.21+0.12,0.14+0.09,0.35+0.09)
第二部分、无失真信源编码
2.2 编码方法
1.2 编码方法:
1、Huffman编码:
(1)信源符号按概率大小排队。
(2)合并概率最小的两个符合为一个节点。 (3)节点参与排队放在与自己概率相等符号后面。 (4)重复这个过程直到合并完全部符号。 (5)标记每个分支的的0与1。 (6)从根到叶的路径就给出了相应符号的码字。 (7)计算平均码长与编码效率。
i1
(2)噪声熵 (散布度):
ms
H (Y|X) p(aibj)lop(g bj|ai)
i 1j 1m s
(3)联合熵: H(X)Y p(aibj)lop(g aibj)
i1j1
(4)接收符号熵:
m
H(Y) p(bj)lopg(bj)
(5)损失熵(后验熵):
i1
ms
H (X|Y) p(aibj)lop(g ai|bj)
信息论与编码总复习

2021/4/9
28
总复习
第三章 信道容量
有一个二元对称信道,其信道矩阵为
设该信源以 1500 (二元符号/秒) 的速度传输输入符号。现有一消息序 列共有 14000 个二元符号,并设 p(0)=p(1)=1/2,问从信息传输的角 度来考虑,10 秒钟内能否将这消息序列无失真地传递完? 解:信源:等概率分布
H(Y/X)噪声熵
2021/4/9
9
总复习
第二章 信源熵
联合熵 H(XY):表示输入随机变量 X,经信道传输到达 信宿,输出随机变量 Y。即收、发双方通信后,整个系 统仍然存在的不确定度。
2021/4/9
10
总复习
第二章 信源熵
最大离散熵定理 (极值性) :离散无记忆信源输出 n 个不 同的信息符号,当且仅当各个符号出现概率相等时 (即 p(xi)=1/n),熵最大。 H[p(x1),p(x2),…,p(xn) ]≤H(1/n,1/n,…,1/n)=log2n
失真度 设离散无记忆信源为
2021/4/9
30
总复习 第四章 信息率失真函数
对每一对 (xi,yj),指定一个非负函数 d(xi,yj)≥0 i=1,2,…,n j=1,2,…,m
称 d(xi,yj) 为单个符号的失真度/失真函数。表示信源发 出一个符号 xi,在接收端再现 yj 所引起的误差或失真。
观察者站在通信系统总体立场上:通信后的互信息量,等于前后不 确定度的差。
2021/4/9
6
总复习
第二章 信源熵
平均信息量—信源熵:自信息的数学期望。也称为信源的信息熵/信 源熵/香农熵/无条件熵/熵函数/熵。
信息论与编码总复习

“信息论与编码”总复习*****************************************************************************简要***************************************************************************** 第二章 信源与信息熵1.每次只发出一个符号代表一个消息的信源叫做发出单个符号的无记忆信源。
2.由一系列符号组成,这种用每次发出1组含2个以上符号序列来代表一个信息的信源叫做发出符号序列的信源。
3.信源发出的序列的统计性质与时间的推移无关,是平稳的随机序列。
4.当信源的记忆长度为m+1时,该时刻发出的符号与前m 个符号有关联性,而与更前面的符号无关,这种有记忆信源叫做m 阶马尔可夫信源。
若上述条件概率与时间起点无关,则信源输出的符号序列可看成齐次马尔可夫链,这样的信源叫做齐次马尔可夫信源。
5.例题:稳态分布概率|稳定后的符号概率分布:符号条件概率矩阵:1/22/33/44/5⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦j i 1/21/3[p(s |s )]=1/41/5状态转移概率矩阵1/20001/32/33/40004/5⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦j i 1/20[p(s |s )]=1/41/50令各稳态分布概率为W1,W2,W3,W4:1131124W W W =+ 2131324W W W =+ 3241135W W W =+ 4242435W W W =+ 12341W W W W +++= 得稳态分布的概率:W1=3/35 W2=6/35 W3=6/35 W4=4/7稳定后的符号概率分布:11131616149()(|)()2353354355735i i i p a p a s p s ==⨯+⨯+⨯+⨯=∑ 221326364426()(|)()2353354355735i i ip a p a s p s ==⨯+⨯+⨯+⨯=∑6.定义具有概率为()i p x 的符号i x 的自信息量为:()log ()i i I x p x =-7.自信息量具有下列特性:(1)()1,()0i i p x I x ==(2)()0,()i i p x I x ==∞(3)非负性(4)单调递减性(5)可加性8.信源熵是在平均意义上来表征信源的总体特征,它是信源X 的 函数,一般写成H (X )。
信息论与编码总复习

平均互信息量
另一种定义:离散随机变量X和Y乊间的平 均互信息量
I ( X ;Y ) H ( X ) H ( X | Y ) I (Y ; X ) H (Y ) H (Y | X )
根据概率乊间的关系式有: p( x i | y j ) p( x i , y j ) I(X; Y) p( x i , y j )log p( x i , y j )log p( x i ) p( x i ) p( y j ) i, j i, j p( x i , y j )log I(Y; X)
互信息量表示先验的丌确定性减去尚存的丌确 定性,返就是收信者获得的信息量; 互信息量可能为正数、负数、零; 对亍无干扰信道,I(xi;yj) = I(xi); 对亍全损信道,I(xi;yj) = 0;
平均互信息量
定义:
I ( X ;Y ) p( x i , y j )I ( x i ; y j ) p( x i , y j ) log
j i j i
p( x i | y j ) p( x i )
不其他熵的关系: I(X;Y) = H(X) - H(X|Y) I(X;Y)=H(Y) - H(Y|X) I(X;Y)=H(X)+H(Y)-H(X,Y) 表达平均互信息量的熵I(X;Y), 是确定通过信道的 信息量的多少,因此称它为信道传输率戒传信率。
信息论不编码
总复习知识点
信息、消息和信号
信息
– 是事物运动状态戒存在斱式的丌确定性的描述。 – 信息是用以消除随机丌确定性的东西 香农信息的定义 消息 – 是指包含有信息的语言、文字和图像等 信号 – 是消息的物理体现。
在通信系统中,实际传输的是信号,但本质的 内容是信息。信息包含在信号乊中,信号是信 息的载体。通信的结果是消除戒部分消除丌确 定性,从而获得信息。
信息论与编码复习资料(新)(DOC)

“信息论与编码”复习1.消息、信号、信息的含义、定义及区别。
信息是指各个事物运动的状态及状态变化的方式。
消息是指包含信息的语言,文字和图像等。
信号是消息的物理体现。
消息是信息的数学载体、信号是信息的物理载体信号:具体的、物理的消息:具体的、非物理的信息:非具体的、非物理的同一信息,可以采用不同形式的物理量来载荷,也可以采用不同的数学描述方式。
同样,同一类型信号或消息也可以代表不同内容的信息2.信息的特征与分类。
1接收者在收到信息之前,对其内容是未知的,所以信息是新知识,新内容;2信息是能使认识主体对某一事物的未知性或不确定性减少的有用知识;3信息可以产生,也可以消失,同时信息可以被携带,被存储及处理;4信息是可以量度的,信息量有多少的差别。
31948年,Shannon提出信息论,“通信中的数学理论”—现代信息论的开创性的权威论文,为信息论的创立作出了独特的贡献。
4.通信系统的物理模型(主要框图),各单元(方框)的主要功能及要解决的主要问题。
信源的核心问题是它包含的信息到底有多少,怎样将信息定量地表示出来,即如何确定信息量。
信宿需要研究的问题是能收到或提取多少信息。
信道的问题主要是它能够传送多少信息,即信道容量的多少。
5.通信的目的?要解决的最基本问题?通信有效性的概念。
提高通信有效性的最根本途径?通信可靠性的概念。
提高通信可靠性的最根本途径?通信安全性的概念,提高通信安全性的最根本途径?通信系统的性能指标主要是有效性,可靠性,安全性和经济性。
通信系统优化就是使这些指标达到最佳。
从提高通信系统的有效性意义上说,信源编码器的主要指标是它的编码效率,即理论上所需的码率与实际达到的码率之比。
提高通信有效性的最根本途径是信源编码。
减少冗余。
提高可靠性:信道编码。
增加冗余。
提高安全性:加密编码。
6.随机事件的不确定度和它的自信息量之间的关系及区别?单符号离散信源的数学模型,自信息量、条件自信息量、联合自信息量的含义?信源符号不确定度:具有某种概率的信源符号在发出之前,存在不确定度,不确定度表征该符号的特性。
信息论与编码期末复习(基本上涵盖了所有考点,有了这份资料,期末绝不会挂科)

信息论与编码期末复习(基本上涵盖了所有考点,有了这份资料,期末绝不会挂科)1填空题1、信息论研究的主要问题是如何提高信息传输系的性和性,对应这两个性能数字通讯系统量化指标分别为和。
2、若给定离散概率空间[X,p(x)]表示的信源,则该信源中的信源消息(事件)x的自信息量可表I(x)= ;该信源平均自信息量(即信源的熵)可表示为H(X)=E[I(x)]= 。
3、在离散联合概率空间[XY,P(xy)] 上随机变量I(xy) 的数学期望H(XY)= ,若集合X与集合Y相互独立,则H(XY)= 。
4、若给定离散联合概率空间[XY,P(xy)],则x与y之间的互信息量I(x;y)= ;平均互信息量可用熵和条件熵表示即I(X;Y)= = ,其中条件熵H(X|Y)通常称为熵,条件熵H(Y|X) 称为____________熵;若集合X与集合Y相互独立,则H(X|Y) = ,H(Y|X) = ,平均互信息量I(X;Y)= 。
5、离散信源的冗余度是R表示信源消息的可压缩____________,设信源符号集的最大熵为Ho,实际熵为H∞,则冗余度R可表示为______________;信源编码目的就是通过减少或消除信源____________来提高信息传输效率,因此信源编码亦称__________性编码,而信道编码则称__________性编码。
6、对于连续随机变量,在峰值功率受限于P m的条件下,取得最大相对熵的最佳概率密度函数是一个恒值即W opt(x)=_________,称W(x)为__________分布,这时最大相对熵H cmax=__________。
7、对于平均功率受限,均值不为零的一维连续随机变量的方差为定值时,其取得最大相熵的最佳概率密度函数为正态分布,即Wopt(x)= _________ ,最大相对熵H cmax=__________。
8、假设任一随机变量X与一正态分布随机变量具有相同的相对熵Hc,则其等效正态分布的随机变量X的熵功率为P=;可以用信号平均功率和熵功率的相对差值_________来表示连续信源的冗余度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变长编码定理 单个符号变长编码定理 单个符号变长编码定理 若一离散无记忆信源的符号熵为H 若一离散无记忆信源的符号熵为H(X), 每个信源符号用m进制码元进行变长编码, 每个信源符号用m进制码元进行变长编码, 一定存在一种无失真编码方法, 一定存在一种无失真编码方法,其码字 平均长度满足下列不等式
2011-1-3 19
差错控制系统分类
前向纠错方式(FEC) 实时性好, 前向纠错方式(FEC) 实时性好,适用于单工通信
2011-1-3 14
三种编码的比较
香农码、费诺码、哈夫曼码都考虑了信源的统计特性, 香农码、费诺码、哈夫曼码都考虑了信源的统计特性, 经常出现的信源符号对应较短的码字, 经常出现的信源符号对应较短的码字,使信源的平均码 长缩短,从而实现对信源的压缩。 长缩短,从而实现对信源的压缩。 香农码有系统的、惟一的编码方法, 香农码有系统的、惟一的编码方法,但在很多情况下编 有系统的 码效率不是很高。 码效率不是很高。 费诺码和哈夫曼码的编码方法都不惟一。 费诺码和哈夫曼码的编码方法都不惟一。 费诺码比较适合于对分组概率相等或接近的信源编码。 费诺码比较适合于对分组概率相等或接近的信源编码。 比较适合于对分组概率相等或接近的信源编码 哈夫曼码对信源的统计特性没有特殊要求, 哈夫曼码对信源的统计特性没有特殊要求,编码效率比 对信源的统计特性没有特殊要求 较高,对编码设备的要求也比较简单, 较高,对编码设备的要求也比较简单,因此综合性能优 于香农码和费诺码。 于香农码和费诺码。
2011-1-3 4
唯一可译码的判断法
将码C中所有可能的尾随后缀组成一个集合F 将码C中所有可能的尾随后缀组成一个集合F,当且仅当集 中没有包含任一码字,则可判断此码C为唯一可译码。 合F中没有包含任一码字,则可判断此码C为唯一可译码。 集合F 集合F的构成方法 首先观察码C中最短的码字是否是其它码字的前缀。 首先观察码C中最短的码字是否是其它码字的前缀。若 将其所有可能的尾随后缀排列出。 是,将其所有可能的尾随后缀排列出。而这些尾随后缀 又有可能是某些码字的前缀(或者某些码字是这些尾随 又有可能是某些码字的前缀(或者某些码字是这些尾随 后缀的前缀), ),再将这些尾随后缀产生的新的尾随后缀 后缀的前缀),再将这些尾随后缀产生的新的尾随后缀 列出。依此下去, 列出。依此下去,直到没有一个尾随后缀是码字的前缀 为止。 为止。 按照上述步骤将次短码字、 按照上述步骤将次短码字、…等等所有码字可能产生的 尾随后缀全部列出。最终得到码C 尾随后缀全部列出。最终得到码C的所有可能的尾随后 缀的集合F 缀的集合F。
2011-1-3 15
限失真信源编码定理
设离散无记忆信源X的信息率失真函数为R 设离散无记忆信源X的信息率失真函数为R(D) 当信息率 R>R(D)时,只要信源序列长度 L 足够长,一定存在一种编码方法, 足够长,一定存在一种编码方法,其译码失 为任意小的正数。 真小于或等于 D+ε,ε为任意小的正数。 反之, 反之,若R<R(D) ,则无论采用什么样的编 码方法,其译码失真必大于D 码方法,其译码失真必大于D。 如果是二元信源,则对于任意小的ε 如果是二元信源,则对于任意小的ε>0,每一 个信源符号的平均码长满足如下公式: 个信源符号的平均码长满足如下公式:
2011-1-3
2
码树
中间节点不安排码字,只在终端节点安排码字 中间节点不安排码字, 每个终端节点对应的码字由从根节点出发到终端节点 走过的路径上所对应的符号组成 当第i阶的节点作为终端节点,且分配码字, 当第i阶的节点作为终端节点,且分配码字,则码字的 码长为i 码长为i 按树图法构成的码一定满足即时码的定义 树码的各个分支都延伸到最后一级端点,则称为满树 满树, 树码的各个分支都延伸到最后一级端点,则称为满树, 否则为非满树 否则为非满树 满树码是定长码,非满树码是变长码 满树码是定长码,
2011-1-3 13
哈夫曼编码方法
哈夫曼编码的步骤
1. 将信源消息符号按其出现的概率大小依次排列 p(x1)≥p(x2)≥…≥ p(xn) )≥p 2. 取两个概率最小的符号分别配以0和1,并将这两个 取两个概率最小的符号分别配以0 概率相加作为一个新符号的概率, 概率相加作为一个新符号的概率,与未分配码元的 符号重新排队。 符号重新排队。 3. 对重排后的两个概率最小符号重复步骤2的过程。 对重排后的两个概率最小符号重复步骤2的过程。 4. 继续上述过程,直到最后两个符号配以0和1为止。 为止。 继续上述过程,直到最后两个符号配以0 5. 从最后一级开始,向前返回得到各个信源符号所对 从最后一级开始, 应的码元序列,即相应的码字。 应的码元序列,即相应的码字。
k =1
费诺编码方法
费诺编码属于概率匹配编码 费诺编码属于概率匹配编码,不是最佳的 概率匹配编码, 编码方法。编码过程如下: 编码方法。编码过程如下:
1. 将信源消息符号按其出现的概率依次排列 p(x1)≥ p(x2)≥…≥ p(xn) 2. 按编码进制数将概率分组,使每组概率尽可能 按编码进制数将概率分组, 接近或相等,并为每一组分配一位码元。 接近或相等,并为每一组分配一位码元。如编 二进制码就分成两组, 进制码就分成m 二进制码就分成两组,编m进制码就分成m组。 3. 将每一分组再按同样原则划分,重复步骤2,直 将每一分组再按同样原则划分,重复步骤2 至概率不再可分为止。 至概率不再可分为止。 4. 信源符号所对应的码字即为费诺码。 信源符号所对应的码字即为费诺码。
HL ( X) ≤ K < HL ( X) +ε
其中, 为任意小正数。 其中,ε为任意小正数。
2011-1-3
11
香农编码步骤
1. 将信源消息符号按其概率从大到小排列
p ( x1 ) ≥ p ( x2 ) ≥ L ≥ p ( xn )
2. 确定满足下列不等式的整数码长Ki 确定满足下列不等式的整数码长K
2011-1-3 8
编码效率 差错概率 P ≤ σ ( X ) e 2 Lε
2
σ 2(X ) 当信源序列长度L 当信源序列长度L满足 L ≥ 时, 2 ε δ
就能达到差错率要求。 就能达到差错率要求。
编码效率 η = H L ( X )
K
最佳编码效率为 HL (X ) η= , ε >0 HL (X ) + ε
第5章 信源编码
重点掌握
分组码的属性 唯一可译码的判断方法 信源编码定理 香农编码、费诺编码、哈夫曼编码 香农编码、费诺编码、
一般了解
编码的术语 游程编码、算术编码 游程编码、
2011-1-3 1
分组码属性
码
非分组码 奇异码 非唯一可译码 分组码 非即时码 非奇异码 唯一可译码 即时码(非延长码) 即时码(非延长码)
只有唯一可译码判断法能确切判断是否是唯一可译码
2011-1-3 6
无失真信源编码
设信源符号序列的长度为L 设信源符号序列的长度为L X = ( X 1 X 2 L X l L X L )
X l ∈ {a1 , a2 ,L , ai ,L , an }
L
变换成由K 变换成由KL个符号组成的 Y = (Y1Y2 LYk LYK ) 码序列(码字) 码序列(码字) Yk ∈ {b1 , b2 ,L , b j ,L , bm } 变换要求 能够无失真或无差错地从Y 恢复X 能够无失真或无差错地从Y 恢复X,也就是 能正确地进行反变换或译码 KL log m 传送Y 传送Y 时所需要的信息率最小 K =
2011-1-3 18
与差错控制有关的基本概念
错误图样 在二元无记忆N次扩展信道中, 在二元序列来描述,称为错误图样 错误图样。 用二元序列来描述,称为错误图样。 设发送码字为C=(c 设发送码字为C=(c1c2…cn),接收码字为 R=(r1r2…rn),两者的差别为 =(r
− log p ( xi ) ≤ K i < − log p ( xi ) + 1
Pi = ∑ p ( xk )
i −1
3. 令P1=0,计算第i个消息的累加概率 =0,计算第i 4. 将累加概率Pi变换成二进制数,取小数点后Ki 将累加概率P 变换成二进制数,取小数点后K 位为该消息的码字
2011-1-3 12
对任意ε>0,δ>0, 对任意ε>0,δ>0,只要
KL log m ≥ H L ( X ) + ε L
则当L足够大时,必可使译码差错小于δ 则当L足够大时,必可使译码差错小于δ; 反之,当 K L log m ≤ H X − 2ε 反之, ) L(
L
时,译码差错一定是有限值,而当L足够大时,译码几乎 译码差错一定是有限值,而当L足够大时, 必定出错。 必定出错。
R(D) ≤ K ≤ R(D) + ε
2011-1-3 16
第6章 信道编码
重点掌握
差错控制相关的基本概念 差错控制系统分类 检、纠错能力 有扰离散信道编码定理
一般了解
纠错码分类 纠错码的基本思路
2011-1-3 17
与差错控制有关的基本概念
汉明重量(码重):码字中非0码元的个数, 汉明重量(码重):码字中非0码元的个数, ):码字中非 表示。对于二进制来说,指码字中码元1 用W表示。对于二进制来说,指码字中码元1 的数目。 的数目。 汉明距离(码距):两个等长码字之间对应码 汉明距离(码距):两个等长码字之间对应码 ): 元不相同的数目, 表示。 元不相同的数目,用D表示。 码的最小距离d 码的最小距离dmin:在某一码集C中,任意两个 在某一码集C 码字之间汉明距离的最小值称为该码的最小距 离,即 d min = min {D ( Ci , C j )} Ci , C j ∈ C Ci ≠ C j 最小码距是衡量该码纠错能力的重要依据
L
2011-1-3
