MATLAB汽车仿真技术复习答案
MATLAB与系统仿真期末考试模拟试题3及答案

模拟试题3一、填空题(2’×15=30’)1、在Matlab开发环境是一个集成的工作环境,包括、、、和等。
2、Matlab命令窗口中的“>>”符号表示。
3、clc表示:;more表示:;who表示:。
4、文件编辑器中的赋值语句后面的冒号“;”表示:;“%”表示:。
5、求矩阵行列式的函数:;求矩阵特征值和特征向量的函数。
6、在Matlab命令窗口中运行命令可以打开Simulink模块库浏览器窗口。
二、简答题(6’×4=24’)1、如何实现退出Matlab环境?2、在Matlab中绘制一个图形的步骤有哪些?3、Matlab提供了哪四类程序控制结构方式?4、说明进入到Matlab开发环境的方法?三、程序设计及分析(6’×7+4’=46’)1、在命令窗口中执行“>>x=ones(3,2)”的结果是:2、编程实现连接str1和str2,str1='My name is LI ming',str2='your name'?3、把2行3列矩阵A变成1行6列的矩阵B。
(123456A⎡⎤=⎢⎥⎣⎦)?4、设随机变量X~N(0,1),求概率P{X<=0.4}?5、求3()25f x x x=--在[0,5]内的最小值点?6、对表达式31f a=-进行因式分解?7、分析以下程序执行后的效果?x=-2:0.2:2;y=x;[x,y]=meshgrid(x,y);z=x.*exp(-x.^2-x.^2);mesh(x,y,z);模拟试题3及答案一、填空题(2’×15=30’)7、在Matlab开发环境是一个集成的工作环境,包括Matlab命令窗口、文件编辑调试器、工作空间、数组编辑器和在线帮助文档等。
8、Matlab命令窗口中的“>>”符号表示命令提示符。
9、clc表示:清空命令窗口中的显示内容;more表示:在命令窗口中控制其后每页的显示内容行数;who表示:查阅Matlab内存变量名。
MATLAB仿真技术

MATLAB仿真技术作业合集页脚内容1页脚内容1第1章 习题5.利用直接输入法和矩阵编辑器创建矩阵A=⎥⎦⎤⎢⎣⎡642531。
解:⑴利用直接输入法输入程序A=[1 3 5;2 4 6]按Enter 键后,屏幕显示A = 1 3 52 4 6⑵用矩阵编辑器创建矩阵,如图1.1所示。
图1.1 MATLAB 编辑器7.用矩阵编辑器创建矩阵a,使a 具有如下矩阵形式。
页脚内容2a=⎥⎦⎤⎢⎣⎡642531⇒a=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡654321⇒a=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡987654321⇒a=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡098706540321⇒a=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000098706540321 解:用矩阵编辑器创建矩阵a 的过程如图1.2、1.3、1.4、1.5、1.6所示。
图1.2 图1.3图1.4 图1.5图1.6页脚内容39.已知矩阵B=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡922518113211912102201304161475231501017,试:①提取矩阵B 的第一行和第二行的第2、4、5个元素组成新矩阵1B ;②提取矩阵B 的第三行和第一行的全部元素组成新矩阵2B ;③使矩阵B 的第一行和第三行的第2;4个元素为0;④标出矩阵B 的第一行中小于5的元素。
解:①如上题,用矩阵编辑器生成矩阵B ,再输入程序B1=B([1,2],[2,4,5])按Enter 键后,屏幕显示B1 = 0 0 155 14 16②输入程序B2=B([1,3],:)按Enter 键后,屏幕显示B2 = 17 0 1 0 15 4 0 13 0 22③第一行和第三行的第2;4个元素原本就为0。
④输入程序如下C=B(1,:)<5; %将B矩阵第一行中小于5 的值标记为1D=B(1,C) %去B矩阵第一行中标为1的元素按Enter键后,屏幕显示D= 0 1 011.已知矩阵a为4阶魔方阵,令a+3赋值给b,a+b赋值给c,求b和c。
MATLAB汽车仿真技术复习答案

汽车仿真技术复习题一、术语解释:1.计算机仿真:是利用计算机对一个实际系统的结构和行为进行动态演示,以评价或预测该系统的行为效果。
是解决复杂问题的一条有效途径。
2. 矩阵的秩:矩阵线性无关的行数与列数称为矩阵的秩。
3.传递函数: 在线性定常系统中,当初始条件为零时,系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
4.伯德图:幅频特性曲线图和相频特性曲线图两张图合起来称为伯德图。
5.根轨迹法: 用作图的方法表示特征方程的根与系统某一参数的全部数值关系,当这一参数取特定值时,对应的特征根可在上述关系图中找到。
这种方法叫根轨迹法二、填空题1.58.135.0+=-ea =( 4.29 );程序为: >> format bank;>> a= exp(-0.5)+sqrt(13.58) a =4.292.建立M 文件求取表达式?2009998321=++++++Λ的值。
sum=0;for i=1:1:200 sum=sum+i; end在命令平台上键入sum 后回车(键入Enter 键),记录计算结果。
3. 方程的求解:0312512.5657.1069.3212345=-+-+-x x x x x,>> d=[1 -21 3.69 -10.57 56.12 -3125]; >> roots(d) ans =20.8577 2.4747 + 2.6023i 2.4747 - 2.6023i -2.4035 + 2.4168i -2.4035 - 2.4168i4.一圆柱形金属构件,直径为20cm,长为110cm,质量为362kg,求此金属的密度(3g/cm )。
试补充划线部分的程序。
>> d=20; >> L=110;>> v=pi*(d/2)*(d/2)*L; >> m=362000; >> rou=m/vrou =10.47535.复数绘图,已知复数g 的表达式)6)(5)(2)(1(60++++=ωωωωj j j j g ,ω的范围[]200,200-,增量取0.01。
MATLAB复习题(答案仅供参考)1

MATLAB复习题(答案仅供参考)1⼀、填空题1. MATLAB命令窗⼝中可⽤clear 命令清除⼯作区中的变量;⽤clc 命令清除命令窗⼝中的内容。
2. MATLAB中的运算符包括数学运算符、矩阵运算符、数组运算符。
3 MATLAB的含义为矩阵运算。
4. MATLAB中的函数类型有嵌套函数、主函数、⼦函数、私有函数和匿名函数。
5. MATLAB中⽤系统预定义的特殊变量nargin 表⽰函数输⼊参数个数。
6. size命令的功能确定数组⼤⼩。
7. MATLAB中⽤linspace 符号定义单元数组。
8. MATLAB中⽤hold on 命令打开图形保持功能。
9 MATLAB中如果⼀个变量名为123,该变量名是否合法否(填是或否)。
10. MATLAB中⽤inv 函数完成矩阵的求逆运算,⽤det 函数求矩阵的⾏列式。
11.已知C={2+5i,’Hi’;1:4,[1 2]} 输⼊s=C(3) 即s=__'_Hi__'___.12.先输⼊P=struct(‘name’,’Jack‘,’num’,43) ,再输⼊s= 即s=___Jack___.13.当x=[ 1 2 3; 4 5 6] , y=[ 5 8; 5 8 ] 时,__不能__(能﹨不能)使⽤plot 命令绘图。
14.sym 或syms _能_______(能﹨不能)创建符号矩阵。
15.已知x=3:2:24,则x有__11_个元素。
结构的开始是“if”命令,结束是_end____命令。
17.已知x为⼀个向量,计算ln(x)的MATLAB命令是计算_log(x)___。
18.命令:>>subplot(3,3,x)中有__9_个⼦图。
19.已知s=‘显⽰“hey”’,则s的元素个数是___9__。
y=f()global WW=2y=f1(5)function y=f()global Wy=w+W创建以上函数⽂件,在命令窗⼝中运⾏“y=f”命令则显⽰__出错___。
汽车理论习题答案及MATLAB编程

汽车理论课后习题答案(部分题目)教材:汽车理论(第5版)清华大学余志生主编机械工业出版社出版本文档包含习题答案:第一章:1.1 1.2 1.7 1.8第二章:2.2 2.3 2.4第三章第四章:4.1 4.2 4.3 4.5第五章:5.1 5.8 5.10 5.11 5.12 5.14 5.17第六章:6.1~6.5其中第三章 4.3 5.11 6.2 6.4 6.5所要求的MATLAB编程见本作者另一百度文库文档。
获取方法:点击左上角本作者的昵称,进入本作者的文库,《汽车理论课后习题答案—附MATLAB编程》第三章:解:(完整解题含MATLAB编程见另一文件)根据“货车最高车速为100km/h左右”,为满足五种主减速器与两种变速器匹配后车速均能达到100km/h,参照表中发动机转速,可选3006r/min、3403r/min、3804r/min三种。
结合万有特性图,考虑到动力性与燃油经济性的统一,选择转速3403r/min进行计算。
由于本人能力有限,暂难以完成EPA循环工况下的燃油消耗量计算,故以“货车采用最高档、90%负荷率工况下”的等速百公里油耗代替表示燃油经济性。
取汽油密度为0.7kg/L。
燃油经济性以等速百公里油耗Qs(L/100km)表示;动力性以2挡起步加速行驶至96.6km/h车速所用时间t(s)表示。
下面运用MATLAB编程实现计算和绘图,编程(m文件)列于最后,运行结果(4挡)如下:t=48.4235t=46.3511t=41.5557t=33.3796t=30.556490%负荷Pe=55.5647Qs4=25.103126.365628.307829.958730.7356图1加速度倒数-速度曲线图2燃油经济性-加速时间曲线由此可得出:主减速器传动比越大,动力性越好,燃油经济性越差。
与4挡变速器相比,采用5挡变速器时动力性和燃油经济性有所提高和改善。
(完整解题含MATLAB 编程见另一文件)图1图25.8某种汽车的质心位置、轴距和前后轮胎的型号已定。
(完整版)汽车理论课后作业答案MATLAB
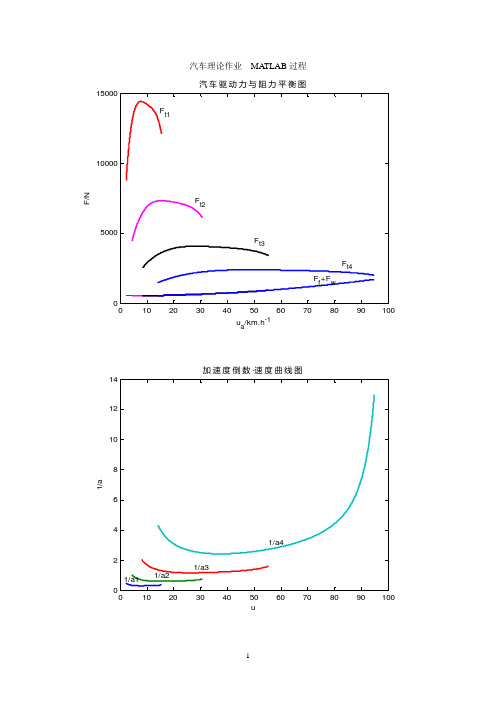
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序:《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知,他们无交点,u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档,较高转速(n取3401 ),最经济负荷(即90%负荷大约 46.9366Kw)行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间:(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间)因与题1.3第三问求法相同,这里不在累述,可直接有计算机求得:figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31)前轴利用附着系数为:gf zh b zL +=βϕ后轴利用附着系数为: ()gr zh a zL --=βϕ1空载时:g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。
Matlab与控制系统仿真部分习题答案

【4.2】程序:num=[5,0];den=conv([1,1],conv([1,2],[1,3])); [numc,denc]=cloop(num,den);[z,p,k]=tf2zp(numc,denc);[A,B,C,D]=tf2ss(numc,denc);g_zp=zpk(z,p,k)g_tf=tf(numc,denc)g_ss=ss(A,B,C,D)运行结果:Zero/pole/gain:5 s----------------------------------(s+0.4432) (s^2 + 5.557s + 13.54)Transfer function:5 s----------------------s^3 + 6 s^2 + 16 s + 6a =x1 x2 x3x1 -6 -16 -6x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 5 0d =u1y1 0【4.3】程序:A=[0 0 0 -1;1 0 0 -2;0 1 0 -3;0 0 1 -4]; B=[0;0;0;1];C=[1 0 0 0];g_ss=ss(A,B,C,D)[num,den]=ss2tf(A,B,C,D);g_tf=tf(num,den)[z,p,k]=ss2zp(A,B,C,D);g_zpk=zpk(z,p,k)运行结果:a =x1 x2 x3 x4x1 0 0 0 -1x2 1 0 0 -2x3 0 1 0 -3x4 0 0 1 -4b =u1x1 0x2 0x3 0x4 1c =x1 x2 x3 x4y1 1 0 0 0d =u1y1 0Continuous-time model.Transfer function:-3.109e-015 s^3 - s^2 - 3.331e-015 s - 4.441e-016 -------------------------------------------------s^4 + 4 s^3 + 3 s^2 + 2 s + 1Zero/pole/gain:- s^2----------------------------------------------(s+0.6724) (s+3.234) (s^2 + 0.0936s + 0.4599)【5.1】(1)程序num=[0,10];den=conv([1,0],[1,7,17]); [numc,denc]=cloop(num,den,-1); G=tf(numc,denc)[y,t]=step(G);plot(t,y,'b-')C=dcgain(G);n=1;while y(n)<0.1*Cn=n+1;endm=1;while y(m)<0.9*Cm=m+1;endrisetime=t(m)-t(n)[Y,k]=max(y); percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettlingtime=t(i)运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10risetime =2.7312percentovershoot =-0.4399settlingtime =5.1372图:0123456700.10.20.30.40.50.60.70.80.91(2)程序k=[10,100,1000];t=linspace(1,20,200);num=1;den=conv([1,0],[1,7,17]);for j=1:3;s1=tf(num*k(j),den);sys=feedback(s1,1)y(:,j)=step(sys,t);endplot(t,y(:,1),'r',t,y(:,2),'b',t,y(:,3),'g')gtext('k=10');gtext('k=100');gtext('k=1000') 运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10Transfer function:100------------------------s^3 + 7 s^2 + 17 s + 100Transfer function:1000-------------------------s^3 + 7 s^2 + 17 s + 1000图:024681012141618200.20.40.60.811.21.41.61.8图:02468101214161820-3-2-1123422【6.1】程序:(1)num1=[1,1];den1=conv([1,0,0],conv([1,2],[1,4]));sys1=tf(num1,den1)rlocus(sys1)运行结果:-12-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(2)num2=[1,1];den2=conv([1,0],conv([1,-1],[1,4,16]));sys2=tf(num2,den2)rlocus(sys2)运行结果:-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(3)num3=[1,8];den3=conv([1,0,0],conv([1,3],conv([1,5],conv([1,7],[1,15])))); sys3=tf(num3,den3)rlocus(sys3)运行结果:-30-25-20-15-10-5051015-20-15-10-505101520Root LocusReal Axis I m a g i n a r y A x i s【6.3】程序:num=[1,2];den=conv([1,0],conv([1,4],conv([1,8],[1,2,5])));sys=tf(num,den)rlocus(sys)[k,poles]=rlocfind(sys)运行结果:Transfer function:s + 2---------------------------------------s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 sSelect a point in the graphics windowselected_point =0.0296 + 2.2826i k =135.8815poles =-7.3248-5.41040.0145 + 2.3021i0.0145 - 2.3021i -1.2939图:-20-15-10-5051015-15-10-551015Root LocusReal Axis I m a g i n a r y A x i s【7.3】程序(1)画波特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)bode(sys)grid图(1)-150-100-50050100M a g n i t u d e (d B)10-210-1100101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)程序(2)画奈奎斯特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)nyquist(sys)grid图(2)-16-14-12-10-8-6-4-20-300-200-100100200300Nyquist DiagramReal Axis I m a g i n a r y A x i s程序(3)画零极点图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)pzmap(sys1)gird图(3)P ole-Zero MapReal Axis I m a g i n a r y A x i s -12-10-8-6-4-20-1.5-1-0.50.511.5程序(4)计算相角裕量和幅值裕量num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)[gm,pm,wcg,wcp]=margin(sys)运行结果Transfer function:50---------------------3 s^3 + 31 s^2 + 10 sTransfer function:50--------------------------3 s^3 + 31 s^2 + 10 s + 50gm =2.0667pm =7.5615wcg =1.8257wcp =1.2645程序(5)绘制阶跃响应曲线num=[50];den=conv([1,0],conv([1,10],[3,1])); sys=tf(num,den)sys1=feedback(sys,1)step(sys1)图(5)00.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d e【7.4】程序如下:num=[300];den=conv([1,0,0],conv([0.2,1],[0.02,1]));sys=tf(num,den)margin(sys)grid波特图如下:-150-100-50050100M a g n i t u d e (d B )10-1100101102103-360-315-270-225-180P h a s e (d e g )Bode DiagramGm = Inf , P m = -78 deg (at 11 rad/sec)Frequency (rad/sec)【9.3】程序:A=[-2 2 -1;0 -2 0;1 -4 0];B=[0;0;1];C=[1,0,0];D=0;M=ctrb(A,B)m=rank(M)if m==3;disp('系统可控')elsedisp('系统不可控')endN=obsv(A,C)n=rank(N)if n==3;disp('系统可观')elsedisp('系统不可观') endsys=ss(A,B,C,D) [num,den]=ss2tf(A,B,C,D) sys1=tf(num,den)[z,p,k]=ss2zp(A,B,C,D)运行结果:M =0 -1 20 0 01 0 -1m =2系统不可控N =1 0 0-2 2 -13 -4 2n =2系统不可观a =x1 x2 x3x1 -2 2 -1x2 0 -2 0x3 1 -4 0b =u1x1 0x2 0x3 1c =x1 x2 x3y1 1 0 0d =u1y1 0 Continuous-time model.0 0 -1 -2den =1 4 5 2Transfer function:-s - 2---------------------s^3 + 4 s^2 + 5 s + 2z =-2p =-1-1-2k = -1【10.1】(1)程序:A=[0,1,0,0;0,5,0,0;0,0,-7,0;0,0,0,-8]; B=[0;1;0;1];C=[1,2,3,4];D=zeros(1,1);G_ss=ss(A,B,C,D)运行结果:a =x1 x2 x3 x4x1 0 1 0 0x2 0 5 0 0x3 0 0 -7 0x4 0 0 0 -8u1x1 0x2 1x3 0x4 1c =x1 x2 x3 x4y1 1 2 3 4d =u1y1 0(2):程序:[num1,den1]=ss2tf(A,B,C,D); p=roots(den1)i=0;for k=1:1:length(p)if real(p(k))>0i=i+1;endendif i>0disp('系统不稳定');elsedisp('系统稳定');end运行结果:p =5.0000-8.0000-7.0000系统不稳定(3)(4)程序:AA=[0,1,0;0,5,0;0,0,-8];BB=[0;1;1];P=[-1,-2,-8];K=acker(AA,BB,P);i=4;K(4)=0;Kpp=eig(A-B*K)sys1=tf(num1,den1);[y1,t]=step(sys1);plot(t,y1)hold onA_feedback=A-B*K;[num2,den2]=ss2tf(A_feedback,B,C,D); sys2=tf(num2,den2);[y2,t]=step(sys2);plot(t,y2,'r')gridgtext('反馈前')gtext('反馈后')运行结果:K =2 8 0 0pp =-8-2-1-7图形:01234560123456【13.1】程序:A=[0,1;0,0];B=[0;1];C=[1,0];D=zeros(1,1);G_ss=ss(A,B,C,D)M=ctrb(A,B);if rank(M)==2disp('系统完全能控'); elsedisp('系统不完全能控'); endS=[1,0];N=obsv(A,S);if rank(N)==2disp('(A,S)可观测'); elsedisp('(A,S)不可观测'); endR=1;Q=[1,0;0,0];[K,P,E]=Lqr(A,B,Q,R)A_new=A-B*K;G_new=ss(A_new,B,C,D);t=linspace(0,5,100)';y1=step(G_ss,t);y2=step(G_new,t);plot(t,y1,'r:',t,y2,'b-')gridgtext('反馈前')gtext('反馈后')运行结果:a =x1 x2x1 0 1x2 0 0b =u1x1 0x2 1c =x1 x2y1 1 0d =u1y1 0Continuous-time model. 系统完全能控(A,S)可观测K =1.0000 1.4142P =1.4142 1.00001.0000 1.4142E =-0.7071 + 0.7071i-0.7071 - 0.7071i图形:00.51 1.52 2.53 3.54 4.5502468101214。
汽车理论课后习题MATLAB编程-武汉理工版

汽车理论课后习题MATLAB编程1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间。
解:(1) 求汽车驱动力与行驶阻力平衡图和汽车最高车速:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;ua=[0:5:120];Ff=G*f;Fw=CDA*ua.^2/21.15;Fz=Ff+Fw;plot(ua1,Ft1,ua2,Ft2,ua3,Ft3,ua4,Ft4,ua5,Ft5,ua,Fz);title('驱动力-行驶阻力平衡图');xlabel('ua(km/s)');ylabel('Ft(N)');gtext('Ft1'),gtext('Ft2'),gtext('Ft3'),gtext('Ft4'),gtext('Ft5'),gtext('Ff+Fw');zoom on;[x,y]=ginput(1);zoom off;disp('汽车最高车速=');disp(x);disp('km/h');汽车最高车速=99.3006km/h(2)求汽车最大爬坡度程序:n=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;Ff=G*f;Fw1=CDA*ua1.^2/21.15;Fz1=Ff+Fw1;Fi1=Ft1-Fz1;Zoom on;imax=100*tan(asin(max(Fi1/G)));disp('汽车最大爬坡度=');disp(imax);disp('%');汽车最大爬坡度=35.2197%(3)求最大爬坡度相应的附着率和求汽车行驶加速度倒数曲线程序:clearn=[600:10:4000];Tq=-19.313+295.27*(n/1000)-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/10 00).^4;m=3880;g=9.8;nmin=600;nmax=4000;G=m*g;ig=[5.56 2.769 1.644 1.00 0.793];nT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;L=3.2;a=1.947;hg=0.9;If=0.218;Iw1=1.798;Iw2=3.598;Ft1=Tq*ig(1)*i0*nT/r;Ft2=Tq*ig(2)*i0*nT/r;Ft3=Tq*ig(3)*i0*nT/r;Ft4=Tq*ig(4)*i0*nT/r;Ft5=Tq*ig(5)*i0*nT/r;ua1=0.377*r*n/ig(1)/i0;ua2=0.377*r*n/ig(2)/i0;ua3=0.377*r*n/ig(3)/i0;ua4=0.377*r*n/ig(4)/i0;ua5=0.377*r*n/ig(5)/i0;Fw1=CDA*ua1.^2/21.15;Fw2=CDA*ua2.^2/21.15;Fw3=CDA*ua3.^2/21.15;Fw4=CDA*ua4.^2/21.15;Fw5=CDA*ua5.^2/21.15;Ff=G*f;deta1=1+(Iw1+Iw2)/(m*r^2)+(If*ig(1)^2*i0^2*nT)/(m*r^2);deta2=1+(Iw1+Iw2)/(m*r^2)+(If*ig(2)^2*i0^2*nT)/(m*r^2);deta3=1+(Iw1+Iw2)/(m*r^2)+(If*ig(3)^2*i0^2*nT)/(m*r^2);deta4=1+(Iw1+Iw2)/(m*r^2)+(If*ig(4)^2*i0^2*nT)/(m*r^2);deta5=1+(Iw1+Iw2)/(m*r^2)+(If*ig(5)^2*i0^2*nT)/(m*r^2);a1=(Ft1-Ff-Fw1)/(deta1*m);ad1=1./a1;a2=(Ft2-Ff-Fw2)/(deta2*m);ad2=1./a2;a3=(Ft3-Ff-Fw3)/(deta3*m);ad3=1./a3;a4=(Ft4-Ff-Fw4)/(deta4*m);ad4=1./a4;a5=(Ft5-Ff-Fw5)/(deta5*m);ad5=1./a5;plot(ua1,ad1,ua2,ad2,ua3,ad3,ua4,ad4,ua5,ad5);axis([0 99 0 10]);title('汽车的加速度倒数曲线');xlabel('ua(km/h)');ylabel('1/a');gtext('1/a1');gtext('1/a2');gtext('1/a3');gtext('1/a4');gtext('1/a5');a=max(a1);af=asin(max(Ft1-Ff-Fw1)/G);C=tan(af)/(a/L+hg*tan(af)/L);disp('假设后轮驱动,最大爬坡度相应的附着率=');disp(C);假设后轮驱动,最大爬坡度相应的附着率=0.4219(4) >>clearnT=0.85;r=0.367;f=0.013;CDA=2.77;i0=5.83;If=0.218;Iw1=1.798;Iw2=3.598;L=3.2;a=1.947;hg=0.9;m=3880;g=9.8;G=m*g; ig=[5.56 2.769 1.644 1.00 0.793];nmin=600;nmax=4000;u1=0.377*r*nmin./ig/i0;u2=0.377*r*nmax./ig/i0;deta=0*ig;for i=1:5deta(i)=1+(Iw1+Iw2)/(m*r^2)+(If*(ig(i))^2*i0^2*nT)/(m*r^2);endua=[6:0.01:99];N=length(ua);n=0;Tq=0;Ft=0;inv_a=0*ua;delta=0*ua;Ff=G*f;Fw=CDA*ua.^2/21.15;for i=1:Nk=i;if ua(i)<=u2(2)n=ua(i)*(ig(2)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(2)*i0*nT/r;inv_a(i)=(deta(2)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(3)n=ua(i)*(ig(3)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(3)*i0*nT/r;inv_a(i)=(deta(3)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elseif ua(i)<=u2(4)n=ua(i)*(ig(4)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(4)*i0*nT/r;inv_a(i)=(deta(4)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;elsen=ua(i)*(ig(5)*i0/r)/0.377;Tq=-19.313+295.27*(n/1000)-165.44*(n/1000)^2+40.874*(n/1000)^3-3.8445*(n/100 0)^4;Ft=Tq*ig(5)*i0*nT/r;inv_a(i)=(deta(5)*m)/(Ft-Ff-Fw(i));delta(i)=0.01*inv_a(i)/3.6;enda=delta(1:k);t(i)=sum(a);endplot(t,ua);axis([0 80 0 100]);title('汽车2档原地起步换挡加速时间曲线');xlabel('时间t(s)');ylabel('速度ua(km/h)');>> ginputans =25.8223 70.073725.7467 70.0737所以汽车2档原地起步换挡加速行驶至70km/h的加速时间约为25.8s2.7已知货车装用汽油发动机的负荷特性与万有特性。
Matlab与系统仿真试题及答案

Matlab 与系统仿真试题及答案一、填空题(每空2分,共30分)1、单位取样序列定义为________________。
2、单位阶跃序列定义为__________________。
3、取样定理中,采样频率和原始信号频率之间至少应该满足公式_______________。
4、实现IIR 滤波器可以采用三种不同的结构:_______________、__________________和_______________。
5、对于理想的滤波特性()jwH e ,相应的()d h n 一般为无限时宽,从而使非因果的。
为此,使显示一般通过如下公式__________实现加窗处理,相应的傅里叶表达形式为_________________。
6、设计IIR 滤波器的基础是设计模拟低通滤波器的原型,这些原型滤波器有:_________、________和______________低通滤波器。
7、实现FIR 滤波器可以采用以下4中结构:________________,_______________,______________和____________。
二、阅读下列Matlab 程序,并回答完成的功能(每题5分,共10分)1、f=[00.60.61];m=[1100];b=fir2(30,f,m);[h ,w]=freqz(b,1,128);Plot(f,m,w/pi,abs)本段程序的功能是:2、[b ,a]=butter(9,300/500,’high’);Freqz(b,a,128,1000)本段程序的功能是:三、用Matlab 语言编程实现下列各小题(每小题15分,共60分)1、产生序列0.3,16p s A dB πΩ==55n -≤≤,并绘出离散图,标注图形标题为“Sequence in Example 3.1a”。
实现程序如下:2、设11()23X z z z-=++,212()2435X z z z z -=+++,求312()()()X z X z X z =+。
汽车理论课后习题答案及MATLAB编程

汽车理论课后习题答案—附MATLAB编程教材:汽车理论(第5版)清华大学余志生主编机械工业出版社出版本文档包含第三章 4.3 5.11 6.2 6.4 6.5所要求的MATLAB编程其它习题答案:第一章:1.1 1.2 1.7 1.8第二章:2.2 2.3 2.4第三章第四章:4.1 4.2 4.3 4.5第五章:5.1 5.8 5.10 5.11 5.12 5.14 5.17第六章:6.1~6.5见本作者另一百度文库文档。
获取方法:点击左上角本作者的昵称,进入本作者的文库,《汽车理论课后习题答案(含MATLAB编程)》第三章:m=3880;%总质量g=9.8;%重力加速度r=0.367;%车轮半径eta_t=0.85;%传动系机械效率f=0.013;%滚动阻力系数CDA=2.77;%空气阻力系数*迎风面积i0=[5.175.435.836.176.33];%主减速器传动比If=0.218;%飞轮转动惯量Iw1=1.798;Iw2=3.598;%两前轮/四后轮转动惯量Iw=Iw1+Iw2;ig4=[6.09 3.091.711];%4挡变速器传动比ig5=[5.56 2.7691.64410.793];%5挡变速器传动比n=600:1:4000;%发动机转速Tq=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;%4挡发动机for i=1:5Ft1=Tq*ig4(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig4(2)*i0(i)/r;Ft3=Tq*ig4(3)*i0(i)/r;Ft4=Tq*ig4(4)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig4(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig4(2));u3=0.377*r*n/(i0(i)*ig4(3));u4=0.377*r*n/(i0(i)*ig4(4));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;delta1=1+(Iw+If.*ig4(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig4(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig4(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig4(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;figure(1)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=96.6;x1=[];x2=[];x3=[];x4=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];elseif u4(k)<=u4maxx3=[k];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=b4(q2:q3);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s=[s2s3s4];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs4(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs4=');disp(Qs4);tt=[48.423546.351141.555733.379630.5564];figure(2)plot(Qs4,tt,'*')hold onxi=25:0.001:31;pp=interp1(Qs4,tt,xi,'cubic');plot(xi,pp)title('燃油经济性-加速时间曲线');xlabel('燃油经济性--等速百公里油耗(L/100km)');ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')%5挡发动机for i=1:5Ft1=Tq*ig5(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig5(2)*i0(i)/r;Ft3=Tq*ig5(3)*i0(i)/r;Ft4=Tq*ig5(4)*i0(i)/r;Ft5=Tq*ig5(5)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig5(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig5(2));u3=0.377*r*n/(i0(i)*ig5(3));u4=0.377*r*n/(i0(i)*ig5(4));u5=0.377*r*n/(i0(i)*ig5(5));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;F5=m*g*f+CDA*u5.^2/21.15;delta1=1+(Iw+If.*ig5(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig5(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig5(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig5(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta5=1+(Iw+If.*ig5(5).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);a5=(Ft5-F5)/(delta5*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;b5=1./a5;figure(3)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4,u5,b5);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext('1/a5')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=max(u4);u5min=u4max;u5max=96.6;x1=[];x2=[];x3=[];x4=[];x5=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];endendq2=max(x2);ua4=u4(q2:y);a4=b4(q2:y);for l=1:3401if u5(l)<=u5minx3=[l];elseif u5(l)<=u5maxx4=[l];endendq2=max(x2);q3=max(x3);q4=max(x4);ua5=u5(q3:q4);a5=b5(q3:q4);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s5=trapz(ua5,a5);%五挡运行时间s=[s2s3s4s5];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;Pe5=Ft5.*u5./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs5(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs5=');disp(Qs5);tt=[93.973058.283444.678445.366744.9793];figure(2)plot(Qs5,tt,'*')hold onxi=30:0.001:100;pp=interp1(Qs5,tt,xi,'cubic');plot(xi,pp)%title('燃油经济性-加速时间曲线');%xlabel('燃油经济性--等速百公里油耗(L/100km)');%ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')运行结果:t=48.4235t=46.3511t=41.5557t=33.3796t=30.556490%负荷Pe=55.5647Qs4=25.103126.365628.307829.958730.7356图1加速度倒数-速度曲线图2燃油经济性-加速时间曲线4.3%空载(no load)—1;满载(full load)—2m1=4080;m2=9290;hg1=0.845;hg2=1.170;L=3.950;a1=2.100;a2=2.950;b1=L-a1;b2=L-a2;beta=0.38;%利用附着系数与制动强度的关系曲线z=0:0.01:1;phi_f1=L*beta.*z./(b1+z*hg1);%前轮利用附着系数(空载)phi_r1=L*(1-beta).*z./(a1-z*hg1);%空载时后轮利用附着系数(空载)phi_f2=L*beta.*z./(b2+z*hg2);%前轮利用附着系数(满载)phi_r2=L*(1-beta).*z./(a2-z*hg2);%后轮利用附着系数(满载)phi=z;%最理想情况figure(1);plot(z,phi_f1,'g--',z,phi_f2,'g-',z,phi_r1,'b--',z,phi_r2,'b-',z,phi,'k-'); axis([0,1,0,1]);grid on;box off;axis square;title('利用附着系数与制动强度的关系曲线');xlabel('制动强度z/g');ylabel('利用附着系数{\phi}');%ECE法规要求界限hold on;z1=0.2:0.01:0.8;z2=0.15:0.01:0.3;z3=0.3:0.01:1;phi1=(z1+0.07)/0.85;phi2=z2-0.08;phi3=z2+0.08;phi4=(z3-0.02)/0.74;plot(z1,phi1,'r-.',z2,phi2,'r-.',z2,phi3,'r-.',z3,phi4,'r-.'); legend('{\phi}_{f}(空载)','{\phi}_{f}(满载)','{\phi}_{r}(空载)',...'{\phi}_{r}(满载)','{\phi}=z','ECE法规要求界限');legend('Location','northwest');%制动效率曲线Ef1=z./phi_f1*100;Er1=z./phi_r1*100;Ef2=z./phi_f2*100;Er2=z./phi_r2*100;figure(2);plot(phi_f1,Ef1,'k',phi_r1,Er1,'k',phi_f2,Ef2,'b',phi_r2,Er2,'b'); axis([0,1,0,100]);grid on;box off;axis square;title('制动效率曲线');xlabel('附着系数{\phi}');ylabel('制动效率(%)');text(0.25,90,'E_f');text(0.6,88,'满载');text(0.8,90,'E_r');text(0.7,65,'空载');text(0.72,72,'E_r');程序运行结果如下:图1图2 5.11L=3.048;K=0.0024;i=20;ua=0:0.01:120;f=1/L.*(1./(3.6./ua+K.*ua./3.6));syms uF(u)=(1/L.*(1./(1./u+K.*u)))./i;plot(ua,f,'b-');xlabel('u_a(km/h)');ylabel('\omega_r/\delta)_s');F(22.35)运行结果:ans=0.1667386094155036.2f=0.1:0.1:100;Gq1=5.12*10^(-5)./f.^2;Gq2=2.02*10^(-3).*f./f;Gq3=7.98*10^(-2).*f.^2;figure(1);loglog(f,Gq1,'b-');box off;axis square;title('位移功率谱密度'); xlabel('f/Hz');ylabel('G_q(f)/(m^2s)');figure(2);loglog(f,Gq2,'b-');box off;axis square;title('速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''(f)/(m^2/s)');figure(3);loglog(f,Gq3,'b-');box off;axis square;title('加速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''_''(f)/(m^2/s^3)');运行结果如下:6.4f1=0.1:0.01:1;f2=1:0.01:10;G1=0.010106.*f1.^2;G2=0.010106.*f2./f2;loglog(f1,G1,'b-');hold onloglog(f2,G2,'b-');title('车身加速度的功率谱密度'); xlabel('f/Hz');ylabel('G_z_''_''(f)/m^-^1'); axis([0.1,10,0.0001,0.1]);运行结果如下:6.51.计算说明1)①幅频特性()122222114z q λζλγ⎡⎤-+⎢=⎢⎥∆⎣⎦,其中0ωλω=,()2222222111141λλγζλγλμμ⎡⎤⎡⎤⎛⎫⎛⎫∆=-+--+-⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦;()12222222211414z z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦;()1222222221414s s s s s p z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦,其中s s ωλω=;②均方根谱()()221~j 2z q H f f ωππ=;()()222~j 2z qH f f ωππ== ;()()2221~1j 2p qz z H f f z qωππ== ;③其他值()0.5360q q G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536110z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536220z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.5360a a G f df σ⎡⎤=⎢⎥⎣⎦⎰()()()()()()13622w 012222412.5362202412.5d 12.5 0.5d d 1d d 4a a a a a a W f G f f f G f f G f f G f f G f f f ⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰⎰其中,()()()()()0.5 0.52 2441 412.512.512.536f f f W f f f f <<⎧⎪⎪<<⎪=⎨<<⎪⎪<<⎪⎩()aw w 020lg L a =2)见1)中计算式3)()()()22004q q q G f G G n n uωπ== ()()()1122363622d ~00d d dd f q q f q f H f G f f G f f q σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122d 12f q f γλπ⎡⎤=⎢⎥∆⎣⎦ ()()()1122363622d //~00d d dd F Gq q F G q F H f G f f G f f Gq σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122222d 1412F f Gq g λζλμπγ⎡⎤⎛⎫-+⎢⎥⎪+⎢⎥⎝⎭=⎢⎥∆⎢⎥⎢⎥⎣⎦其余见1)中计算式2.程序清单1)f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi*fs;lambda=omega./omega0;lambda_s=omega./omega_s;%计算并绘制幅频特性delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;figure(1)loglog(f,z1_q,'b-',0:0.1:100,(0:0.1:100)./(0:0.1:100),'g-');axis([0.1,100,0.1,10]);grid on ;title('z_1~q 的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_1}{q}|$$','Interpreter','latex');gtext('0:1');figure(2)loglog(f,z2_z1,'b-',0:0.1:1,(0:0.1:1)./(0:0.1:1),'g-',1:0.1:100,1./...(1:0.1:100),'g-');axis([0.1,100,0.01,10]);grid on;title('z_2~z_1的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_2}{z_1}|$$','Interpreter','latex'); gtext('0:1');gtext('-1:1');figure(3)loglog(f,p_z2,'b-');axis([0.1,100,0.01,10]);grid on;title('p~z_2的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{p}{z_2}|$$','Interpreter','latex');%计算并绘制均方根谱sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q; figure(4)loglog(f,sqrt_Gz1,'b-');grid on;title('车轮位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''1}(f)}$','Interpreter','latex'); figure(5)loglog(f,sqrt_Gz2,'b-');grid on;title('车身位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''2}(f)}$','Interpreter','latex'); figure(6)loglog(f,sqrt_Ga,'b-');grid on;title('传至人体的位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_a(f)}$','Interpreter','latex');%计算其它值sigma_q=sqrt(trapz(f,sqrt_Gq.^2));%路面不平度加速度均方根值sigma_z1=sqrt(trapz(f,sqrt_Gz1.^2));%车轮加速度均方根值sigma_z2=sqrt(trapz(f,sqrt_Gz2.^2));%车身加速度均方根值sigma_a=sqrt(trapz(f,sqrt_Ga.^2));%传至人体的加速度均方根值for i=1:Nif f(i)<=2W(i)=0.5;elseif f(i)<=4W(i)=f(i)/4;elseif f(i)<=12.5W(i)=1;elseW(i)=12.5/f(i);endendaw=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));%加权加速度均方根值a0=10^(-6);Law=20*log10(aw/a0);%加权振级format shortdisp('路面不平度加速度均方根值=');disp(sigma_q);disp('车轮加速度均方根值=');disp(sigma_z1);disp('车身加速度均方根值=');disp(sigma_z2);disp('传至人体的加速度均方根值=');disp(sigma_a);disp('加权加速度均方根值=');disp(aw);disp('加权振级=');disp(Law);2)%随fs变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=1.5:0.01:6;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;lambda=omega./omega0;for i=1:length(fs)omega_s=2*pi.*fs(i);lambda_s=omega./omega_s;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(fs,aw);grid ontitle('a_w随f_s的变化曲线');xlabel('f_s/Hz');ylabel('a_w/m·s^-^2');figure(2)plot(fs,Law);grid ontitle('L_aw随f_s的变化曲线');xlabel('f_s/Hz');ylabel('L_a_w/dB');%随zeta_s变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_ss=0.125:0.001:0.5;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi.*fs;lambda=omega./omega0;lambda_s=omega./omega_s;for i=1:length(zeta_ss)zeta_s=zeta_ss(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(zeta_ss,aw);grid ontitle('a_w随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('a_w/m·s^-^2');figure(2)plot(zeta_ss,Law);grid ontitle('L_aw随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('L_a_w/dB');3)%随f0变化f0=0.25:0.01:3;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;lambda_s=omega./omega_s;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(f0)omega0=2*pi*f0(i);lambda=omega./omega0;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(f0==1.5);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(f0,sm_z2,f0,sm_fd,f0,sm_FdG);axis([0.25,3,-25,10]);grid on;title('各响应量均方根值随f_0变化的曲线');xlabel('f_0/Hz');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随zeta变化f0=1.5;zeta0=0.125:0.001:0.5;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(zeta0)zeta=zeta0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(zeta0==0.25);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(zeta0,sm_z2,zeta0,sm_fd,zeta0,sm_FdG);axis([0.125,0.5,-4,4]);grid on;title('各响应量均方根值随\zeta变化的曲线');xlabel('\zeta');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');%随gamma变化f0=1.5;zeta=0.25;gamma0=4.5:0.1:18;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(gamma0)gamma=gamma0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(gamma0==9);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(gamma0,sm_z2,gamma0,sm_fd,gamma0,sm_FdG);axis([4.5,18,-6,6]);grid on;title('各响应量均方根值随\gamma变化的曲线');xlabel('\gamma');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随mu变化f0=1.5;zeta=0.25;gamma=9;mu0=5:0.1:20;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(mu0)mu=mu0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(mu0==10);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(mu0,sm_z2,mu0,sm_fd,mu0,sm_FdG);axis([5,20,-2,2]);grid on;title('各响应量均方根值随\mu变化的曲线');xlabel('\mu');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB');legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');3.结果分析1)路面不平度加速度均方根值=0.3523车轮加速度均方根值=0.2391车身加速度均方根值=0.0168传至人体的加速度均方根值=0.0161加权加速度均方根值=0.0100加权振级=80.0287分析:根据课本中表6-2,a w=0.0100<0.315,L aw=80.0287<110,故乘客没有不舒适。
汽车理论 matlab编程 作业答案

4.3(1)利用附着系数空载时前轴的利用附着系数φf1:φf1=βz1L b+zh g=0.38z13.951.85+0.845z空载时后轴的利用附着系数φr1:φr1=(1−β)z1L a−zh g=(1−0.38)z13.952.1−0.845z满载时前轴的利用附着系数φf2:φf2=βz1L b+zh g=0.38z13.951.0+1.17z满载时后轴的利用附着系数φr2:φr2=(1−β)z1L a−zh g=(1−0.38)z13.952.95−1.17zMatlab程序:clcclearsyms z;f1=0.38*z/((1/3.95)*(1.85+0.845*z));r1=(1-0.38)*z/((1/3.95)*(2.1-0.845*z)); f2=0.38*z/((1/3.95)*(1.0+1.17*z));r2=(1-0.38)*z/((1/3.95)*(2.95-1.17*z)); f=z;ezplot(f1);hold on;ezplot(f2);ezplot(r1);ezplot(r2);ezplot(f);axis([0 1.0 0 1.0]);title('利用附着系数曲线');xlabel('制动强度z');ylabel('利用附着系数');text(0.38,0.8,'Ør(空载)');text(0.6,0.9,'Ør(满载)');text(0.8,0.45,'Øf(空载)');text(0.8,0.6,' Øf(满载)');text(0.85,0.9,'Ø=z')制动效率空载时前轴的制动效率E f1:E f1=bLβ−φf gL=1.85/3.95f空载时后轴的制动效率E r1:E r1=aL(1−β)−φr gL=2.1/3.95r满载时前轴的制动效率E f2:E f2=bLβ−φf gL=1.0/3.950.38−φf∙1.17/3.95满载时后轴的制动效率E r2:E r2=aL(1−β)−φr gL=2.95/3.95rMatlab程序:clearsyms x;Er1=2.1/3.95/(1-0.38+x*0.845/3.95); Ef2=1.0/3.95/(0.38-x*1.17/3.95);Er2=2.95/3.95/(1-0.38+x*1.17/3.95); ezplot(Ef2);hold on;ezplot(Er1);ezplot(Er2);axis([0 1.0 0 1.0]);title('前后轴制动效率曲线'); xlabel('附着系数'); ylabel('制动效率(%)'); text(0.35,0.9,'Ef'); text(0.8,0.9,'Er'); text(0.55,0.78,'Er'); text(0.65,0.94,'满载'); text(0.55,0.65,'空载');(2)①由图可得:空载时,在φ=0.8时的制动效率为0.7,则其制动减速度为0.8g*0.7=0.56g 。
MATlab 仿真部分习题答案
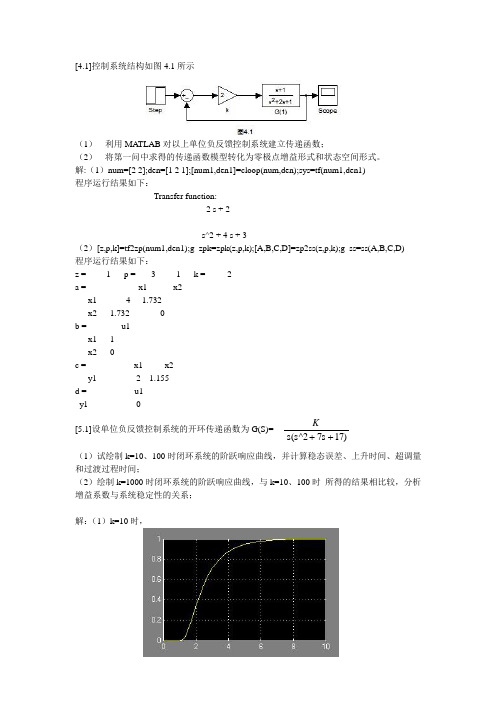
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
MATLAB与系统仿真期末考试模拟试题2及答案

模拟试题B一、填空题(2’×18=36’)1、Matlab系统由、、、和5大部分组成。
2、Matlab的基本运算符包括、、等。
3、在Matlab编辑器中运行程序的快捷键是:。
4、函数rand表示:;randn函数表示:;size函数表示:。
5、实现Fourier变换在Matlab中的对应函数为:;Laplace变换的函数:。
6、函数M文件的有效第一行的执行标识为:。
7、通常程序调试有两种方法:和利用。
8、Matlab提供的图形用户界面开发环境是:。
二、简答题(6’×4=24’)1、在命令行中输入“save Filename1a b”表示?2、分析以下函数执行过程,回答问题:function c=testarg1(a,b)if(nargin==1)c=a.^2;elseif(nargin==2)c=a+b;end如果用户使用一个参数调用函数testarg1,函数执行什么功能?如果使用两个参数调用函数testarg1,函数又执行什么?3、打开和关闭文件的函数是什么?分别说明其作用。
4、新建Simulink仿真模型文件的方法是什么?三、程序设计及分析(6’×6+4’=40’)1、编程实现函数3()25f x x x =--的根?2、将下列字符矩阵S 转换为数字矩阵('1''2''3''4'S ⎡⎤=⎢⎥⎣⎦)?3、把矩阵A ,B 分别在垂直方向,水平方向连接,A=[123],B=[456]?4、求()1020x f x x =-+=在00.5x =附近的根?5、编程实现一元二次方程20ax bx c ++=?6、绘制函数图形:1sin(),2cos()y x y x ==。
要求:(1)[]0,2x π∈;(2)数据采样间隔/50π?(3)设置网格;(4)添加图形标注;(5)两幅图叠加在一张图中。
模拟试题B及答案一、填空题(2’×18=36’)9、Matlab系统由Matlab开发环境、Matlab语言、Matlab数学函数库、Matlab图形处理系统和Matlab应用程序接口5大部分组成。
MATLAB语言及控制系统仿真_参考答案解析_第2章

2.12 MATLAB 语言的数值运算-实训2.12.1实训目的1.学会矩阵的建立方法及其矩阵的转置、相乘、求逆等运算;2.识别了解特殊矩阵;3.学会求解方程与方程组;4.学会通过编程解决一些实际问题; 2.12.2实训内容 1.矩阵建立及其运算]4321012345[1-----=A[]0.19.08.07.06.05.04.03.02.01.02=A ]0.19.08.07.06.05.04.03.02.01.0[3=A][40.19.08.07.06.05.04.03.02.01.0e e e e e e e e e e A = ]2222222222[50.19.08.07.06.05.04.03.02.01.0=A求(1)211A A D += (2)232A A D -= (3)4/.13A D = (4)5*.44A A D = (5)5*35A D = (6))2(.^16A D =>> A1=-5:4;>> A2=0.1:0.1:1.0; >> A3=sqrt(A2); >> A4=exp(A2); >> A5=2.^(A2); >> format bank >> D1=A1+A2 D1 =-4.90 -3.80 -2.70 -1.60 -0.50 0.60 1.70 2.80 3.90 5.00 >> D2=A3-A2 D2 =0.22 0.25 0.25 0.23 0.21 0.17 0.14 0.09 0.05 0 >> D3=1./A4 D3 =0.90 0.82 0.74 0.67 0.61 0.55 0.50 0.45 0.41 0.37 >> D4=A4.*A5D4 =1.18 1.40 1.66 1.972.33 2.763.27 3.874.595.44 >> D5=3*A5 D5 =3.22 3.45 3.69 3.964.24 4.55 4.875.22 5.606.00 >> D6=A1.^2 D6 =25.00 16.00 9.00 4.00 1.00 0 1.00 4.00 9.00 16.002.建立矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=1418712106114231359152345686420B(1)矩阵B 的逆矩阵)(inv B (2)矩阵B 对应的行列式)det(B>> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]B =0 2.00 4.00 6.00 8.00 -6.00 -5.00 -4.00 -3.00 -2.00 15.00 9.00 5.00 13.00 3.00 2.00 4.00 11.00 6.00 10.00 12.00 7.00 8.00 1.00 14.00 >> inv(B) ans =-0.18 0.29 0.11 0.07 0.07 0.31 -0.72 -0.20 -0.23 -0.07 -0.21 0.11 0.03 0.21 -0.02 0.05 0.11 0.08 0.02 -0.04 0.12 0.04 -0.02 -0.06 0.06 >> det(B) ans =-17568.00(3)利用矩阵元素的提取方法建立以下矩阵 ①矩阵b01:矩阵B 的3~4行元素; ②矩阵b02:矩阵B 的2~5列元素;③矩阵b03:由矩阵B 的1~3行2~4列交叉点所对应的元素组成; >> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]; >> b01=B(3:4,:) b01 =15.00 9.00 5.00 13.00 3.002.00 4.00 11.00 6.00 10.00 >> b02=B(:,2:5) b02 =2.00 4.00 6.00 8.00 -5.00 -4.00 -3.00 -2.00 9.00 5.00 13.00 3.004.00 11.00 6.00 10.00 7.00 8.00 1.00 14.00 >> b03=B(1:3,2:4) b03 =2.00 4.00 6.00 -5.00 -4.00 -3.00 9.00 5.00 13.00 3.矩阵的转置与翻转已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=151413121110987654321m ,求取以下矩阵观察并记录。
MATLAB系统仿真试题复习资料,有答案

PART I 教材复习要点第一章 MATLAB 入门测试1.11.MATLAB 的命令窗口的作用是什么?编辑/调试窗口?图象窗口? MATLAB 命令窗口是MATLAB 起动时第一个看到的窗口,用户可以在命令窗口提示符">>"后面输入命令,这些命令会被立即执行。
命令窗口也可以用来执行M 文件。
编辑/调试窗口是用来新建,修改或调试M 文件的。
图像窗口用来显示MATLAB 的图形输出。
2.列出几种不同的得到MATLAB 帮助的方法。
(1)在命令窗口中输入help <command_name>,本命令将会在命令窗口中显示关于些命令的有信息。
(2)在命令窗口中输入lookfor <keyword>,本命令将会在命令窗口中显示所有的在第一注释行中包含该关键字的命令和函数。
(3)通过在命令窗口输入helpwin 或helpdesk 启动帮助浏览器,或者是在启动板中选择"Help"。
帮助浏览器包含了基于超文本的MATLAB 所有特性的描述,HTML 或PDF 格式的在线手册,这是MATLAB 最全面的帮助资源。
3.什么是工作区?在同一工作区内,你如何决定它里面存储了什么?工作区是命令、M 文件或函数执行时被MATLAB 使用的变量或数组的收集器,所有命令都在命令窗口(所有的脚本文件也是从命令窗口执行)共享公共工作区,因此它们也共享所有变量,工作区的内容可以通过whos 命令来查看,或者通过工作区浏览器来图形化地查看。
4.你怎样清空MATLAB 工作区内的内容?要清除工作区的内容,只需在命令窗口中输入clear 或clear variables 即可。
第二章MATLAB 基础测试2.11.数组,矩阵,向量有什么区别?数组是在内存中被组织成行和列的数据集合,只有一个名称,数据要通过在数组名后面圆括号里加上表示数据所在行和列的数字来访问。
汽车理论1.3和2.7matlab编程答案

孙野 200812681.3(1)绘制汽车驱动力与行驶阻力平衡图 选用5挡变速器进行整车性能计算发动机转速与汽车行驶速度之间的关系:0377.0i i rn u g a = 发动机使用外特性的T q -n 曲线拟合公式:432)1000(8445.3)1000(874.40)1000(44.165)1000(27.295313.19n n n n T q -+-+-=汽车驱动力:ri i T F Tg q t η0=行驶阻力:2215.2115.21a D a D j w i f u A C mgf dt du m u A C Gi Gf F F F F +=+++=+++δ用matlab 编写程序如下: m1=2000; m2=1800; mz=3880; g=9.81; r=0.367; CdA=2.77; f=0.013; nT=0.85; ig=[5.56 2.769 1.644 1.00 0.793];i0=5.83; If=0.218; Iw1=1.798; Iw2=3.598; %输入已知参数 Iw=2*Iw1+4*Iw2; fori=1:69n(i)=(i+11)*50;Ttq(i)=-19.313+295.27*(n(i)/1000)-165.44*(n(i)/1000)^2+40.874*(n(i)/1000)^3-3.8445*(n(i)/1000)^4; end %从600~4000rpm 油拟合公式计算发动机转距 for j=1:5 fori=1:69Ft(i,j)=Ttq(i)*ig(j)*i0*nT/r; ua(i,j)=0.377*r*n(i)/(ig(j)*i0);Fz(i,j)=CdA*ua(i,j)^2/21.15+mz*g*f;endend%计算各档位下的驱动力和行驶阻力plot(ua,Ft,ua,Fz)title('汽车驱动力与行驶阻力平衡图'); xlabel('ua(km/h)');ylabel('Ft(N)');%作汽车驱动力与行驶阻力平衡图得到汽车驱动力与行驶阻力平衡图如下:(2)①计算汽车最高车速Matlab程序如下:for k=1:175 n1(k)=3300+k*0.1;Ttq(k)=-19.313+295.27*(n1(k)/1000)-165.44*(n1(k)/1000)^2+40.874*(n1(k)/1000)^33.8445*(n1(k)/1000)^4;Ft(k)=Ttq(k)*ig(5)*i0*nT/r;ua(k)=0.377*r*n1(k)/(ig(5)*i0);Fz(k)=CdA*ua(k)^2/21.15+mz*g*f;E(k)=abs((Ft(k)-Fz(k)));end%从3300rpm开始以0.1rpm为步长搜索直到找到for k=1:175 %驱动力与行驶阻力之差绝对值最小点(Ⅴ档处) if(E(k)==min(E))%通过其他检验程序可估计出该点大致位置(3310rpm附近) disp('汽车最高车速='); disp(ua(k));disp('km/h');end%输出结果end汽车最高车速=98.7627km/h计算得汽车最高车速为98.7627km/h。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^2 2-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^22-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
MATLAB与系统仿真期末考试模拟试题1及答案

模拟试题1一、填空题(2’×16=32’)1、Matlab 的全称为。
2、Matlab 的工作界面主要由、、、、和组成。
3、Matlab 预定义变量ans 表示:;eps 表示:;nargin 表示:。
4、在Matlab 中inf 表示:。
5、建立结构数组或转换结构数组的函数为:;6、Matlab 提供了两种方法进行程序分析和优化,分别为:;。
7、MATLAB 编写的程序文件称为M 文件,M 文件有和两种。
二、简答题(6’×3=18’)1、描述在Matlab 中矩阵运算的含义,如A*B ,A.*B 表示什么运算过程?2、简述脚本M 文件和函数M 文件的区别?3、GUI 窗口中添加控件的两种方法是什么?三、程序设计及分析(7’×7+1’=50’)1、求2[122(74)]3+⨯-÷的算术运算在Command Window 中应该输入什么?2、编程实现323()5327()483b x x x x a x x x +-+=-++的部分分式展开?3、在Matlab 命令窗口中显示“Wellcome to MATLAB Program ”?4、求下列方程的解。
212345202711x y z x y z x y z -+=⎧⎪++=⎨⎪-++=⎩5、用sym 生成符号方程:a*x^2+b*x+c=0?6、编程求解由方程2210,50,240x y z x y z x y z -+=+-=-+=构成的线性方程组?7、用while 循环编程实现!100n <的最大的n 值?模拟试题1及答案一、填空题(2’×16=32’)8、Matlab 的全称为矩阵实验室。
9、Matlab 的工作界面主要由菜单栏、工具栏、当前工作目录窗口、工作空间管理窗口、历史命令窗口和命令窗口组成。
10、Matlab 预定义变量ans 表示:没有指定输出变量名;eps 表示:系统精度;nargin 表示:函数输入参数的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
汽车仿真技术复习题一、术语解释:1.计算机仿真:是利用计算机对一个实际系统的结构和行为进行动态演示,以评价或预测该系统的行为效果。
是解决复杂问题的一条有效途径。
2. 矩阵的秩:矩阵线性无关的行数与列数称为矩阵的秩。
3.传递函数: 在线性定常系统中,当初始条件为零时,系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
4.伯德图:幅频特性曲线图和相频特性曲线图两张图合起来称为伯德图。
5.根轨迹法: 用作图的方法表示特征方程的根与系统某一参数的全部数值关系,当这一参数取特定值时,对应的特征根可在上述关系图中找到。
这种方法叫根轨迹法二、填空题1.58.135.0+=-ea =( 4.29 );程序为: >> format bank;>> a= exp(-0.5)+sqrt(13.58) a =4.292.建立M 文件求取表达式?2009998321=++++++Λ的值。
sum=0;for i=1:1:200 sum=sum+i; end在命令平台上键入sum 后回车(键入Enter 键),记录计算结果。
3. 方程的求解:0312512.5657.1069.3212345=-+-+-x x x x x,>> d=[1 -21 3.69 -10.57 56.12 -3125]; >> roots(d) ans =20.8577 2.4747 + 2.6023i 2.4747 - 2.6023i -2.4035 + 2.4168i -2.4035 - 2.4168i4.一圆柱形金属构件,直径为20cm,长为110cm,质量为362kg,求此金属的密度(3g/cm )。
试补充划线部分的程序。
>> d=20; >> L=110;>> v=pi*(d/2)*(d/2)*L; >> m=362000; >> rou=m/vrou =10.47535.复数绘图,已知复数g 的表达式)6)(5)(2)(1(60++++=ωωωωj j j j g ,ω的范围[]200,200-,增量取0.01。
试补充划线部分的程序。
w=-200:0.01:200;g=60./((1+j*w).* (2+j*w) .* (5+j*w) .* (6+j*w)); plot(g); grid;6.数值计算⎰⎰-+10195.212)3sin(dy y x dx )(>> dblquad(inline('sin(3*x)+y.^2'),1,10,-1,2.95) ans =78.510537211633487.求1)sin(5.0+=-x e y x 在[2,8]内的最小值。
>>f=inline('exp(-0.5*x).*sin(x)+1'); >> [xmin,fval]=fminbnd(f,2,8) xmin =4.24872619592456 fval =0.893108658607248.利用函数绘图命令绘制)8/2sin(5.0π-=-x e y x ,其中]5,0[∈x ;>> fplot( 'exp(-0.5*x).*sin(2*x-pi/8)',[0,5,-1.1,1.1] ) 9.请补充完整以下程序: x=0; n=1; while n<6 x= n+x ; n= n+1 ; end x运行结果x= 15 .三、简答题1.绘制三维曲面图)2.0sin())cos(sin(x y x z -+=,其中 [x,y]=meshgrid(0:0.2:13)。
试写出程序。
(已给出结果图,如图1)[x,y]=meshgrid(0:0.2:13); z=sin(x+cos(y))-sin(0.2*x); mesh(x,y,z);title('三维曲面图');2.写出以下系统的多项式模型,并将其转换为零极点模型2153173261552115.35291)(23452341++++++-+-=s s s s s s s s s s G>> n1=[91,-52,3.5,-11,52]; d1=[1,15,26,73,31,215]; sys1=tf(n1,d1)[z1,p1,k1]=tf2zp(n1,d1) sys1zp=zpk(z1,p1,k1)3..已知单位负反馈系统的开环传递函数为()()()10.5s 10.2s 1s 1.0ks G +++=)(要求编程绘制50=k 时的极坐标图,确定曲线与负实轴的交点坐标及频率值。
(已给出结果图2) n=50;d=conv([0.1,1],conv([0.2,1],[0.5,1])); sys=tf(n,d); nyquist(sys)曲线与负实轴的交点坐标为-3.76; 曲线与负实轴的交点频率值9.2;4.单位反馈系统的开环传递函数为)3)(2()1()(+++=s s s s K s G g试编程绘制闭环系统的根轨迹(根轨迹图已给出,如图3)。
并回答 (1)闭环系统稳定的g K 的取值范围; (2)系统的阶跃响应有超调的g K 的取值范围; (3)分离点的坐标。
编程:%ggj01.m z=[-1];p=[0;-2;-3]; k=[1];sys=zpk(z,p,k); rlocus(sys)(1)系统稳定的g K 的取值范围:0>g K ;(2)系统的阶跃响应有超调的g K 的取值范围:419.0>g K ,(3)分离点的坐标:47.2-=d5.有二个系统如图(a )、(b )所示,编程分别绘制各系统的单位阶跃响应和单位脉冲响应。
(a )(b))(s R⊗(c ) 图5-176.增量与绘图,通过仿真结果回答问题(1)程序1t1=0:4*pi;y1=sin(2*t1);plot(t1,y1);程序1可得到图形正弦曲线A(增量为默认值1)。
(2)程序2t2=0:0.2:4*pi;y2=sin(2*t2);plot(t2,y2);程序2可得到图形正弦曲线B(增量为0.2)。
(3)程序3t3=0:0.01:4*pi;y3=sin(2*t3);plot(t3,y3);程序3可得到图形正弦曲线C(增量为0.01)。
(4)程序4t4=0:0.00001:4*pi;y4=sin(2*t4);plot(t4,y4);程序4可得到图形正弦曲线D(增量为0.00001):回答问题:①通过MATLAB仿真得到的正弦曲线A、B、C有何区别?答:曲线A失真严重,曲线B略有失真,曲线C几乎没有失真。
②通过MATLAB仿真得到的正弦曲线C、D有何区别?答:曲线C和曲线D区别不大。
③你得到的结论是通常情况下增量(步长)取多少为宜?答:通常情况下增量(步长)取0.01即可满足一般的仿真要求和仿真精度。
7. 绘制)3cos(t r =,[]π3,0∈t 的极坐标(polar )图,试写出程序。
t=0:0.01:3*pi; r=cos(3*t); polar(t,r)8.采用图形保持,在同一坐标内绘制曲线)sin(1x y = ,)sin(25.0x e y x -=,)cos(3x y =,]10,0[∈x 。
试写出程序。
(已给出结果图2)x=0:0.01:10; y1=sin(x);y2=exp(-0.5*x).*sin(x); y3=cos(x);plot(x,y1, 'k'); hold on;plot(x,y2, 'r'); plot(x,y3, 'b'); hold off;9. 试编写计算程序画出曲线与曲面图形.22,22,)1((2).);20(cos sin (1).223322≤≤-≤≤-++=≤≤⎪⎩⎪⎨⎧==--y x y x ex z t ty t x y x π%1 %2t=0:0.1: 2*pi; [x,y]=meshgrid(-2:0.1:2);x= sin(t).^3; z=(x.^2+1).* exp(-x.^2- y.^2+)+x.^2.*y;y= cos (t).^3; mesh(x,y,z) plot(x,y)10. 编写程序解决下列问题: (1)试产生1004阶矩阵使其元素在0—100之间的随机整数,可将此矩阵理解为100名同学的四门课程(课程1, 课程2, 课程3, 课程4)的成绩. (2)计算出每门课程和每位同学的平均成绩; (3)统计出总的优秀人次(90分及以上为优秀);(4)统计出四门课程成绩至少有两门课程不及格的人数 (1) a=fix((100-0+1)*rand(100,4)); (2) mean(a) mean(a,2) (3)sum(sum(a>=90,2)==4) (4)sum(sum(a<60,2)>=2) 11.).50,20(]2,0[)2()),(1:(;)1(,sin )1()(11==-=∑=+n n x fun y function kx k x f nk k 分别取内图形用子图画出该函数在程序的第一句为返回该函数并保存试编写函数式文件程序设π(1). function y=fun1(x,n) (2). x=0:0.1:2*pi;y=0; y1= fun1 (x,20); for k=1:n y2= fun1 (x,50);y=y+ ((-1)^(k+1)*sin(k*x))/k; subplot(2,1,1),plot(x,y1) end subplot(2,1,2),plot(x,y2) y。
