数据 模型与决策例题分析
MBA《数据、模拟与决策》案例报告

《数据、模型与决策》案例一《火花塞铁壳的质量抽样检验》第2小组案例分析报告组员:陈迪学号:17920091150628组员:高霄霞学号:17920091150668组员:陆彬彬学号:17920091150764组员:罗志锐学号:17920091150767组员:王晋军学号:17920091150811组员:许冰学号:17920091150856案例《火花塞铁壳的质量抽样检验》第2小组案例分析报告摘要:产品质量检验是生产过程中的一个重要阶段,实际生产中,检查每批产品中的不合格品的件数,一般用计件抽样检验方案。
计件抽样检验的方法包括:百分比抽样检验方案和标准型一次抽样方案等,本文通过火花塞铁壳的质量抽样检验,对以上两种抽样检验方案的合理性进行了理论分析。
关键字:抽样检验百分比抽样法标准型一次性抽样法 OC曲线Abstract:Quality inspection is a very important step in production process. In actual process, we use sample inspection methods by counting to inspect every batch for the reject products. Sample inspection plans include percentage sampling inspection and standard sampling inspection. This thesis takes ‘the spark plug case’ as an example to analyze the rationality of the two Sample inspection plans.Key words: Sample inspection plans, percentage sampling inspection, standard sampling inspection, OC curve一问题的提出企业生产出的产品是否符合规定要求,要通过检验来判定。
数据模型与决策案例-排班问题

排班问题————数据模型与决策案例一、背景描述在21世纪的全球就业环境下,自由职业工作者已成为社会人力资源的不可忽略的一部分。
他们具有较灵活的工作时间和较为工作成本。
在某个行业或某个领域,雇用自由职业工作者的成本更低。
尤其是在电子商务日益流行的今天,使得很多人能够只是用一台电脑就可以在网上进行办公,省去了很多不必要的时间成本及交通成本。
尤其是在一些特殊的工作时间安排上,自由工作者工作的随意性和临时性更适应当今社会的快速发展。
二、问题描述这是一个如何高效使用人力资源的问题。
某公司新建了一个客户中心,雇用了多名线上客服人员,他们每天工作3节,每节3小时,每节开始时间为0点、3点钟、6点钟,9点、12点、15点、18点、21点,为方便上客服人员上下班,管理层安排每位上客服人员每天连续工作3节,根据调查,对于不同的时间,由于业务量不同,需要的话务员的人数也不相同,公司付的薪水也不相同,有关数据见下表。
那如何安排话务员才能保证服务人数,又使总成本最低呢?三、问题分析这个问题实际上是一个成本效益平衡问题。
公司在向客户提供满意服务水平的同时要控制成本,因此必须寻找成本与效益的平衡。
由于每节工作时间为3小时,一天被分为8班,每人连续工作3节,为建立数学模型,对应于一般成本效益平衡问题,我们首先必须明确包含的活动数目,活动一个单位是对应于分派一个话务员到该班次,效益的水平对应于时段。
收益水平就是该时段里上下班的话务员数目,各活动的单位效益贡献就是在该时间内增加的在岗位话务员数目。
成本效益平衡问题参数表如下表:决策变量xi表示分派到第i班的话务员人数(i=1,2,3,4,5,6,7,8),约束条件为:0-3时间段:x1+x7+x8≥8(最低可接受水平)3-6时间段:x1+x2+x8≥66-9时间段:x1+x2+x3≥159-12时间段:x2+x3+x4≥2012-15时间段:x3+x4+x5≥2515-18时间段:x4+x5+x6≥2318-21时间段:x5+x6+x7≥1821-0时间段:x6+x7+x8≥10非负约束:xi≥0i=1,2,3,4,5,6,7,8目标函数为最小化成本:Z=84x1+80x2+70x3+62x4+62x5+66x6+72x7+80四、问题求解如下表所示,将可变单元格列留空,令总费用最小作为目标单元格,令缺少人数为可变单元格减去最低需求人数的值,约束缺少人数大于等于0.求解后系统自动将可变单元格进行填充(上表已经是填充后的结果)。
《数据模型与决策》案例分析报告-劳动力安排

——数学模型与决策分析案例报告
1
分析报告内容
➢案例背景 ➢基本思路 ➢分析过程 ➢报表 ➢Excel运算过程
2
案例背景
戴维斯仪器公司在佐治亚州的亚特兰大有两家制造厂。每月的产品需求变化很
大,使戴维斯公司很难排定劳动力计划表。最近,戴维斯公司开始雇用由劳
工无限公司提供的临时工。该公司专长于为亚特兰大地区的公司提供临时工。
•将工作细分,每个员工培训的内容也按具体工作需求进行, 无需全面培训; •雇用已具备所需工作技能的员工,从而减少培训项目
13
分析过程
若雇用10名全职员工,工资及培训费用运算结果如下:
项目
月份 1月份 2月份 3月份 4月份 5月份 6月份 合计
雇用人数分配表
雇用一个月 雇用二个月 雇用三个月
人数
人数
雇用一个月人数为7人,雇用二个月的人数为3人,雇 用三个月人数为33人。
10
分析过程
当培训降低至700$/人时运算结果如下:
雇用人数分配表
项目 月份
雇用一个月 雇用二个月 雇用三个月 总雇用人
人数
人数
人数
数
1月份
10
0
0
10
2月份
23
0
0
23
3月份
19
0
0
19
4月份
26
0
0
26
5月份
20
0
20
6月份
人数
0
0
0
4
0
9
0
0
0
0
3
4
3
0
0
7
3
13
数据、模型与决策第十讲案例分析

二、农户种植计划的优化问题
设选择种植第一、第二、第三、第四、第五、第六种作物的
份数(1份对应于获得100元收入所需要的亩数)分别为x1、x2、 x3、x4、x5、x6,则可建立该问题的线性规划模型如下: 目标函数 max z =
100x1+100x2+100x3+100x4+100x5+100x6
四、产品结构优化问题
在以上技术状态约束下,经测算,提供给甲客户产品的单 套利润为48万元,提供给乙客户产品的单套利润为46万元 ,提供给丙客户产品的单套利润为36万元。
经生产能力平衡测算,各种部件产品的年生产能力上限分 别为:A1部件年产624个,A2部件年产920个,B1部件年 产412个,B2部件年产770个,B3部件年产350个。
约束条件 0.4x1 +0.2x3+0.18x4
≤10
0.3x1+0.25x2+0.15x3+0.1x4
≤8
0.4x3 +0.15x5+0.1x6≤5
x1,x2,x3,x4,x5,x6≥0
解得:
x1*=0,x2*=9.777778,x3*=0,x4*=55.55556,x5*=0,x6*=50。 全部的5亩水田都用来种植第六种作物;在旱地中拿出2.45
约束条件
x1
≤1
x1 + x2 ≤2.5
x1 + x2 + x3 ≤3.5
x1,x2,x3 ≥0
解得:x1*=1,x2*=1.5,x3*=1,z*=2.25。
显然,最优的选择是自然科学类选修课自修时间与当前自
修时间的比值为1.5,即下午和晚上各增加半个小时。三类
数据模型和决策课程案例分析

数据模型和决策课程案例分析目录一、内容概括 (2)二、数据模型基础知识概述 (2)三、案例研究 (4)3.1 案例选择背景与意义 (5)3.2 数据收集与预处理过程 (7)3.3 数据模型建立与实施步骤 (8)四、案例分析一 (10)4.1 背景介绍及问题定义 (11)4.2 数据集介绍及特点分析 (12)4.3 预测模型选择与构建过程 (14)4.4 模型训练与验证结果展示 (15)4.5 模型应用与决策支持探讨 (16)五、案例分析二 (18)5.1 背景介绍及问题定义 (19)5.2 数据集介绍及特点分析 (20)5.3 优化决策模型构建思路 (21)5.4 模型求解过程与结果展示 (22)5.5 决策优化方案讨论与实施建议 (23)六、案例分析三 (25)6.1 背景介绍及数据挖掘目标设定 (27)6.2 数据集介绍及预处理流程梳理 (29)6.3 数据挖掘算法选择与运用阐述 (30)6.4 挖掘结果分析与可视化展示 (31)6.5 基于数据挖掘的决策支持策略探讨 (33)七、总结与展望 (35)一、内容概括本课程旨在为学员提供一个全面的框架,使其能够理解和应用数据模型在决策过程中的重要性。
通过系统地分析实际案例,学员将学会如何收集、处理和分析数据,以及如何利用这些信息做出明智的商业决策。
课程内容包括但不限于数据模型的基本原理、不同类型数据模型的比较与选择、数据分析技术、机器学习与数据挖掘的方法、多变量分析和预测建模的工具等。
此外,课程还将教授学员如何将数据模型的概念应用到具体业务场景中,如市场分析、财务规划、供应链优化、客户行为预测等。
通过案例分析,学员能够体会到数据驱动决策过程的实际操作,培养批判性思维和问题解决能力,同时也会学到项目管理和团队协作的技巧。
课程鼓励学员进行实战演练,通过模拟真实世界的问题和挑战,运用所学的知识和技能来制定决策方案。
通过这个过程,学员将能够深化对理论知识的理解,并且提升将数据模型应用于实际业务中的能力。
《数据模型与决策》案例分析报告生产策略.ppt

贝贝加100
85%
贝贝加200
15%
16
数据模型与决策分析—生产战略
案例问题解答
• 定义约束条件—有贝贝加200的产量占25%的约束
约束
制型和焊接 喷漆和成型 装配、调试和包装 产量约束(贝贝加200占 25%)
耗用时间
≤ ≤ ≤
可用时间
600 450 140
S-0.75*S-0.75*D
≤
0
17
8
数据模型与决策分析—生产战略
线性规划解决问题步骤
步骤
1 描述目标 2 描述约束条件 3 定义决策变量
主要内容
本题的目标就是使产品的利润贡献最大
对于生产时间来说,一共有3个约束条件,它们制约着贝贝 加100和贝贝加200的生产数量 贝贝加100的产量S,贝贝加200的产量D
4
用决策变 量写出目标
总利润函数 Max
Contents
1. 案例背景资料
2. 案例分析思路
3. 案例问题解答
4. Excel运算过程
2
数据模型与决策分析—生产战略
案例背景资料
3
数据模型与决策分析—生产战略
案例背景资料
比特健身公司在长岛自由港设有生产厂。最近公司设计了两种适合种种体形 的家庭健身器材。这两种器材都使用了BETTER塑形专利技术,大大增加了健 身者的活动范围,可以满足各种运动动作的需要。现在这种功能只有昂贵笨重 的物理理疗器才有。 在最近的贸易展览会上。由于这种机器的参与,使得公司的收效显著。事实 上,订单要求的生产数量已经大大超过了公司现阶段的生产能力。于是,公司 的管理层决定生产这两种器材。这两种器材分别叫作贝贝加100和贝贝加200, 是由不同的原材料生产出来的。 贝贝加100由一个柜架单元、压力源和PEC源组成。制造每个柜架需要用4 个小时进行制型和焊接,2个小时进行喷漆和成型。每个压力源都需要用2个小 时进行制型和焊接,1个小时进行喷漆和成型。每个PEC源都需要用2个小时进 行制型和焊接,2个小时进行喷漆和成型。此外对于每个贝贝加100型的器材还 需要用2个小时进行装配、调试和包装。柜架单元的原材料的价格是450美元, 压力源的材料价格是300美元,PEC源的材料价格是250美元,包装的成本预计 是每台50美元。
数据分析与决策案例

数据分析与决策案例某轴承公司生产两种不同的电子组件,即322A和802B,公司在接下来的3个月里都会通知该公司的销售人员每个星期的需求量,下图是刚刚接到的未来3个月的订单:接到订单后需求报告将会送到生产布,该部门必须制定未来3个月的组件生产计划,需要考虑生产总成本、库存持有成本和改变生产负荷导致的费用。
根据以往数据,生产一个322A组件的成本为20,生产一个802B 组件的成本为10.每月的基本库存持有成本占据总成本的1.5%。
成本与生产负荷的水平有关系,生产负荷增加一个单位时新增的成本为0.5;生产负荷减少一个单位时成本减少0.2.假定3月份322A的生产量为1500,802B的生产量为1000。
322A组件的初期库存为500,6月最小安全库存为400;802B的初期库存为200,6月最小安全库存为200。
同时员工的工作时长、机器的最大生产能力和库容等因素均是限制生产的约束条件。
生产部门需要在以上条件下制定出满足客户需要的最佳生产计划方案。
(1)将信息抽象成数学模型在满足客户需求的基础上生产计划的安排会直接影响总成本的变化,成本最优是公式的目标,因此设置总成本为目标变量。
需要做的决策是如何来安排生产计划,因此决策变量是每月322A 和802B两种产品在未来3个月的生产计划,共6个决策变量。
该模型中共有4个约束条件,即6月末最小安全库存限制、每月总库容限制、机器和人工能力限制。
由于有些约束条件涉及每个月,因此每项约束条件展开可能有多项,如机器能力限制3个月就应是3个约束条件由于案例中未来几个月的订单数量已知,因此模型暂时不需要假设变量。
(2)建立Excel模型总成本由3个方面组成:一是生产成本,即生产所产生的成本;二是库存成本,即存放在仓库里的成本;三是生产负荷变化成本,即每个月与上月的负荷变量导致的成本的变化。
因此总成本与生产计划息息相关,逻辑关系如下:总成本=生产成本+库存成本+变化成本。
生产成本=每月322A组件生产件数*单位成本+每月802B组件生产件数*单位成本。
数据模型和决策习题和案例讨论题

习题和案例讨论题第二章数据的整理和描述1.某镇50个企业的固定资产原值(单位:万元)数据如下表:48 67 89 120 125 156 168 176 189 192205 233 246 248 267 285 290 298 312 320325 329 339 340 367 386 392 395 398 414450 465 470 485 492 515 562 580 599 620659 694 760 785 793 795 856 880 980 1538⑴对该镇的企业按固定资产规模进行分组统计(以100为组距作等距分组,最后一组为>1000),用Excel制作频数分布表;⑵按频数分布表绘制该镇企业固定资产规模分布的直方图,说明其分布特征。
2.根据习题1的分组频数数据,计算该镇企业固定资产原值的平均值、中位数、众数。
3.用Excel计算第二章习题1中企业固定资产未分组数据的均值、总体方差、总体标准差、偏度系数等统计指标。
5.某地区私营企业注册资金分组资料如下,求该地区私营企业注册资金的平均数、中位数和众数。
本章习题答案2. x=412,M e=363.64,M0=337.5,S=241.57,SK=0.3083.x=433.94,σ2=77558.02,σ=278.49,偏度系数=1.4714. x=123.6,M e=119.64,M0=115.22第三章时间数列分析1.某企业一季度职工人数变动情况如下,求该企业第一季度的平均职工人数。
2. 某商店第一季度商品销售和月末库存情况如下,求:(1)该商店第一季度各月的商品流转次数;(2)该商店第一季度的月平均商品流转次数;其中:商品流转次数= 商品销售额/同期平均商品库存额3. 某企业部分资料如下:(1)求上半年月平均销售产值和平均职工人数; (2)求上半年月平均全员劳动生产率 (3)求上半年的全员劳动生产率。
其中:平均职工人数产值劳动生产率4.用Excel 求解该地区1998~2003年薪增绿地面的年平均增长速度。
数据模型与决策案例分析

数据模型与决策案例分析数据模型是指对一些特定领域的数据进行抽象和建模的过程,用于描述数据之间的逻辑关系和操作。
在决策案例分析中,数据模型的作用是帮助分析人员更好地理解和分析决策案例中的数据,并通过对数据模型的建立和使用,提供决策支持和优化方案。
决策案例分析是指通过对已知的决策案例进行分析,并提取出其中的决策模式和经验,以供后续决策参考和借鉴。
数据模型在决策案例分析中的应用可以帮助分析人员更好地理解和把握决策案例中的数据特征和关系,为决策提供更准确和有效的依据。
一个典型的数据模型与决策案例分析的例子是在线销售平台的用户行为数据分析。
以电商平台为例,用户的行为数据包括浏览商品、加入购物车、下单购买等行为。
在分析这些数据时,可以建立一个用户行为数据模型,来描述用户行为数据之间的关系。
在用户行为数据模型中,可以包括用户属性、商品属性和行为属性等。
用户属性包括用户的地区、性别、年龄等基本信息,商品属性包括商品的价格、品牌、类别等信息,行为属性包括用户的浏览时间、购买时间、购买数量等信息。
通过对这些属性的建模和分析,可以得出一些有用的决策模式和经验,如哪些商品更受用户喜欢,哪些用户更容易购买等。
基于用户行为数据模型的分析结果,可以为决策提供一些有效的决策支持和优化方案。
比如可以通过分析用户行为模式,确定哪些商品可以进行重点推荐,提高用户购买率;可以通过分析用户购买模式,优化供应链管理,提高商品库存管理效率;还可以通过分析用户流失模式,制定用户留存策略,提高用户忠诚度。
总之,数据模型与决策案例分析的应用可以帮助分析人员更好地理解和分析决策案例中的数据,提供决策支持和优化方案。
在不同的领域和情境下,数据模型与决策案例分析的应用也有很大的差异,需要根据具体情况进行定制和优化。
但无论如何,数据模型与决策案例分析的应用都是提高决策质量和效率的重要手段之一,值得我们深入研究和应用。
大数据、模型与决策例题分析报告
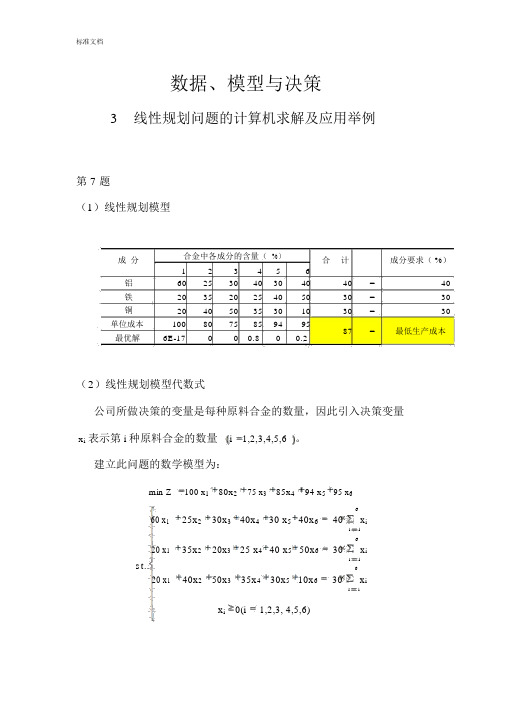
数据、模型与决策3线性规划问题的计算机求解及应用举例第 7 题(1)线性规划模型成分合金中各成分的含量(%)合计成分要求( %)123456铝60253040304040=40铁20352025405030=30铜20405035301030=30单位成本100807585949587=最低生产成本最优解6E-17000.800.2(2)线性规划模型代数式公司所做决策的变量是每种原料合金的数量,因此引入决策变量x i表示第i种原料合金的数量i1,2,3,4,5,6。
建立此问题的数学模型为:min Z100 x180x275 x385x494 x595 x6660 x125x230x340x430 x540x640x ii1620 x135x220x325 x440 x550x630x ist..i1620 x140x250x335x430x510x630x ii1x i0(i1,2,3, 4,5,6)第 8 题(1)线性规划模型营养成分每千克每千克每千克每千克合计每日最小需求玉米槽料红薯麸皮碳水化合物852********.000≥250蛋白质35853565280.509≥190维生素152********.000≥160脂肪1089840.000≥40单位成本0.80.40.60.42.259=最低成本最优解0.000 1.063 1.725 1.997(2)线性规划模型代数式公司所做决策的变量是每种原料数,因此引入决策变量x i表示第i 种原料数i1,2,3,4。
建立此问题的数学模型为:min Z0.8x10.4x20.6 x30.4 x485x120 x240x380x4250st..35x185x235x365x419015 x125 x260x315 x416010 x18x29 x38x440第 9 题线性规划模型代数式车间所做决策的变量是A i( i1,2,3)机床生产B j( j1,2)零件数,因此引入决策变量xij表示加工B j( j1,2) 零件使用的A i( i1,2, 3)机床台数。
数据模型与决策案例分析

数据模型与决策案例分析数据模型是指对数据进行描述、组织和存储的一种结构化方法。
在现代企业管理中,数据模型的构建和分析对于决策制定和业务发展具有重要意义。
本文将从数据模型的概念入手,结合实际案例进行分析,探讨数据模型在决策案例中的应用。
首先,我们来介绍一下数据模型的基本概念。
数据模型是对现实世界中某一特定方面的抽象,它描述了数据的结构、特性、约束和操作。
数据模型可以分为概念模型、逻辑模型和物理模型三个层次。
概念模型描述了数据在业务领域中的含义和关系,逻辑模型描述了数据的逻辑结构和特性,物理模型描述了数据的存储方式和组织形式。
通过构建数据模型,我们可以更好地理解数据之间的关系,为决策提供支持。
接下来,我们将通过一个实际案例来说明数据模型在决策中的应用。
假设某电商企业需要对其销售数据进行分析,以制定下一阶段的营销策略。
首先,我们可以构建一个销售数据模型,包括产品信息、销售额、销售时间、客户信息等要素。
通过对这些数据进行建模分析,我们可以发现不同产品的销售额与销售时间之间存在一定的关联,某些客户的购买行为具有一定的规律性。
基于这些发现,企业可以针对不同产品的销售情况和客户的购买行为制定相应的营销策略,从而提高销售业绩。
在实际应用中,数据模型的构建和分析需要结合业务场景和具体问题,以达到更好地支持决策的目的。
同时,数据模型的建立也需要不断地进行优化和更新,以适应业务发展的需求。
通过数据模型的构建和分析,企业可以更好地理解数据,发现数据之间的关联和规律,从而为决策提供更有力的支持。
综上所述,数据模型在决策案例中具有重要的应用意义。
通过构建和分析数据模型,企业可以更好地理解数据,发现数据之间的关联和规律,为决策提供更有力的支持。
希望本文的内容能够对读者有所启发,促进数据模型在实际应用中的进一步发展和应用。
数据,模型与决策案例分析

数据,模型与决策案例分析案例1XXX这事发生在不久前。
马萨诸塞州坎布里奇市Kendall广场的XXX(KCL)夜间货运主管XXX在他的办公室里焦虑地看着电视中的天气频道。
一场暴风雪迅速地沿大西洋海岸从北方直逼波士顿。
天气预报指出,有50%的可能暴风雪将在下午5:00左右到达波士顿地区,有50%的可能入海不会再来波士顿及北大西洋沿岸各地。
XXX并不是Kendall广场唯一一个紧张地看天气频道的人。
因为波士顿的XXX在暴风雪来临时也许不得不关闭。
许多商业运输也只得焦急地等待未来的天气信息。
从历史上看,这样巨大的暴风雪抵达波士顿的话,每五个中有一个会迫使Logan航空港在暴风雪期间关闭。
XXXXXX(XXX)1962年建于马萨诸塞州坎布里奇,是波士顿地区一家XXX。
到1985年,XXX大幅度消减了蟹的业务,扩大了虾的经营,包括对美国东北部的餐馆、华盛顿特区的顾客、缅因州Presque岛的夜间送货。
1995年,XXX年销售额达到2200万美元,雇员数超过100.KCL认为它的成功在于为广大顾客服务,它致力于产品的快递市场化和广告化,希望普及到在一些特殊场合的菜单上都能有龙虾这一项。
XXX知道食品服务领域中任何行业成功的关键是为顾客服务,保持为顾客服务的出色声誉应是最优先考虑的事。
XXX是MIT斯隆办理学院的学生时在XXX工作过,毕业后他成了XXX的员工。
他在公司里很快升到现在这个夜间货运主管职位,夜间货运在公司里是最重要的部门。
他知道有些最高层办理者正关注着他,他希望不久能得到进一步提升。
龙虾龙虾是一道极大众的菜。
这是因为它有极美的滋味,同时它引人注目的外形也十分漂亮地装点了每张餐桌。
人们总是以吃龙虾来庆祝一个特殊的时刻,吃过word文档可自由复制编辑龙虾是幸运的和值得兴奋的。
此外,龙虾的烹调也极简单,只要将活的龙虾置于沸水中煮15分钟即可食用。
但是,龙虾极易腐烂,以至于必须用活虾烧煮。
死虾和未煮透的龙虾会迅速变质。
数据模型与决策分析案例

数据模型与决策分析案例一、问题提出美国R银行最近赢得了一份合同,为宾夕法尼亚的众多公司修建一个服务区,使得他们可以开启网上交易,便捷各自的生活。
R银行负责区域银行卡的网上注册,数据维护与测试。
为了完成这项工作,美国R银行的负责人兼总经理Bob xx估计,区域内所有员工银行卡的注册与网上注册所需要的总工期大约需要4个月,并且完成这项庞大的任务需要许多的云服务器支持,从各项数据,可以得知,从第1个月到第4个月需要的云服务器分别为10、12、14、8台云服务器。
虽然说到目前为止美国R银行已经有20台云服务器,但大部分的台云服务器都有任务,都要支持运行维护已经注册的人员的银行数据,因此,必须从从P xx云服务器租赁公司租借部分的云服务器。
并且Bob估计,虽然说本公司这些云服务器有其他的任务,但每个月任然有部分可以抽调出来供这一份项目使用,第1个月有1台云服务器可以用于服务区的网上注册,数据维护与测试任务,第2个月有2台云服务器可以用于服务区任务,第3个月有3台云服务器可以用于服务区任务,第4个月有1台云服务器可以用于服务区任务。
因此为了完成任务,美国R银行还需要租借更多的云服务器来完成这一份合同。
从P xx云服务器公司长期租用云服务器的费用是每台云服务器每月600美元。
云服务器的坐守监视工作人员的工资是每小时20美元,每台云服务器每天消耗流量电量等数据网络方面花费为100美元。
所有的云服务器维修费用由Pxx云服务器公司承担。
根据美国R银行工作计划,美国R银行每天工作8小时,每周5天,每月工作4周。
Bob认为现在的情况下,美国R银行如果长期租赁云服务器是不明智的。
在与P xx云服务器公司对短期租赁合同进行讨论后,Bob了解到他可以获得1-4个月的短期租赁。
短期云服务器租赁和坐守监视技术人员的工资的价格水平都与长期租赁不同。
P xx云服务器公司司同意支付短期租赁的成本。
以下是一台云服务器一个坐守监视技术人员的短期租赁费用。
数据、模型与决策第十讲案例分析共33页文档

三、王五管理的科研课题经费使用规划问题
获得净收入1万元,这样就可以保证每月正常的人员经费开 支,所节余的1万元可向课题组上缴,同时该子课题的试验 与器材经费开支需求是每月8万元。
根据经验,在坡地种植第一种获得100元收入所需要 的面积是0.4亩,在旱地种植第一种作物获得100元收入 所需要的面积是0.3亩;在旱地种植第二种作物获得100 元收入所需要的面积是0.25亩;在坡地种植第三种作物 获得100元收入所需要的面积是0.2亩,在旱地种植第三 种作物获得100元收入所需要的面积是0.15亩,在水田种 植第三种作物获得100元收入所需要的面积是0.4亩;在 坡地种植第四种作物获得100元收入所需要的面积是0.18
数据、模型与决策
第十讲 案例分析 主讲:邓旭东教授
教学内容
1
李四企业的生产经营规划问题
2
农户种植计划的优化问题
3
王五管理的科研课题经费使用规划问题
4
产品结构优化问题
5
张三同学的自习时间分配方案规划问题
教学内容
6
连续投资的优化问题
7
人员需求规划问题
8
问题
现在仓库里还存有A原料40000千克,后续货源供应难以 得到保证;库存B原料20000千克,如果需要,后续容易从市
一、李四企业的生产经营规划问题
场采购得到;库存C原料30000千克,如果需要,后续容易从 市场采购得到。
李四想转行经营其他业务,但苦于仓库里还积压着90000 千克原料,如果直接出售原料,则比生产后出售成品赔得更多 。没有办法,李四只好向运筹学专家咨询,看看如何组织生产 才能将损失降到最低。
2.45亩地种植第二种作物,其余的5.55亩旱地全部种植第四种
《数据模型与决策》案例分析报告-比尔_桑普拉斯暑期工作的寻找

一、比尔·桑普拉斯暑期工作的寻找比尔正处于其在斯隆管理学院第一个学期的第三周。
在准备课程外,他开始认真考虑下一个夏天的工作问题。
1.在比尔8月份飞往波士顿的途中,他和邻座的温妮沙进行了一次有趣的谈话。
她是一家投资银行负责证券的副总监。
文妮沙被比尔的行为举止及其在短期投资方面的工作经验所吸引(比尔曽在一家列入财富500强公司的财务部工作了四年),她告诉比尔她很乐意与比尔在11月中讨论夏季雇佣他的问题。
当在11月中旬之前她的公司不可能与比尔讨论夏季工作问题。
(1)比尔到斯隆的就业服务中心了解到,文妮沙的公司付给第一年的MBA的暑期工资估计为$14,000(12周)。
(2)我们再估计一下文妮沙的公司录取比尔的可能性。
在没有过多的考虑下假定为50%。
考虑到比尔曽给文妮沙留下深刻的印象,可能性应增加一些,但此类工作的申请竞争是非常激烈的,而比尔的同学们都非常由天份,最后我们假定为0.60。
2.在比尔离开原来公司之前,其原先的老板约翰告诉他,他可以在下一个夏天回来工作,工资是$12,000(12周)。
但是比尔必须在10月底前给予答复,否则,约翰的许诺就无效了。
3.除上面的两个机会外,比尔还有一个机会,他可以参加斯隆学院举办的一个夏季工作征召计划,从中还可能找到工作。
当然,前提是他在前两个机会中没有被接受(或他自己拒绝了它们)。
这个计划举办时间为明年1月和2月。
斯隆学院的学生暑假工作的收入资料假定被收集到了,去年的情况是这样的(指第一年的MBA 学生的收入):周工资总的工资(12周)获得此类工资的学生所占的百分比$1,800$21,6005%$1,400$16,80025%$1,000$12,00040%$500$6,00025%$0$05%(其中5%的学生没有得到他们的收入资料,假定他们的收入为0。
)并且假定上表中所列各项目百分比为比尔在这个计划中所得到的不同收入的可能性的近似值。
即我们假定比尔能找到收入为$21.600的可能性近似为5%,…。
MBA《数据、模型与决策》作业(案例)

《数据、模型与决策》案例1 企业背景SGT特殊钢铁公司是我国西部地区最大、西北地区唯一的百万吨资源型特殊钢生产基地,是国家级创新型企业、国家军工产品配套企业。
经过多年的发展,通过传统产业升级改造和优势产业发展壮大,已形成年产焦炭75万吨、普通钢400万吨、特殊钢400万吨的综合生产能力,成为集“特钢制造、煤炭焦化”为一体的资源综合开发钢铁联合企业。
SGT公司钢铁制造始终坚持以“打造西部重要的特种钢生产基地”为己任,牢固树立品牌意识,顺应新型特殊钢材料发展趋势,努力提升工艺技术及装备水平,拥有“高炉—转炉—精炼—连铸—连轧”五位一体的长流程生产线和“电炉(兑铁水)冶炼—精炼—连铸(模铸)—连轧(半连轧)”的短流程生产线。
建成了极具特色的“功勋牌”特钢产品体系,产品涵盖轴承钢、模合结钢、碳工钢、工具钢等钢种,产品广泛应用于汽车、工程制造、机械制造、石油、军工、航空、铁路运输、新能源、新基建等多种行业。
公司整体生产工艺及技术在行业中处于领先水平,特别是“十二五”期间,公司对工艺装备进行了全面升级改造,先后建成110吨Consteel电炉、410* 530mm三机三流大方坯连铸机、精品特钢大棒材生产线、精品特钢小棒材生产线。
尤其是精品特钢大、小棒材生产线采用了当今世界顶尖工艺技术及装备,达到国际钢铁工业的先进水平。
公司目前已拥有五十余项特殊钢生产的专有技术,其中主要有钢包、连铸耐材材质控制技术,分钢种脱氧工艺与技术,分钢种渣系控制技术,残余元素与有害元素的控制技术,非金属夹杂物形态控制技术,硫化物夹杂弥散细化技术,含硫钢纯净化技术,含S,Al,B钢连铸技术,炉前化学成分精确控制技术,炉前淬透性(DI值)动态控制技术,模铸、连铸碳偏析及凝固组织控制技术,在线正火轧制技术,在线超快冷技术,在线控轧控冷一热机轧制(TMCP)技术,大规格热轧材高精度轧制技术,小规格热轧材高精度轧制技术,热轧材非标规格轧制技术,银亮材剥、碾光表面光洁度控制技术,低中碳钢低硬度球化退火技术,钢材零缺陷无损探伤检测技术,电炉、转炉全铁冶炼技术,电炉、转炉底吹搅拌,高品质特殊钢精品生产技术集成,富氮合金、高氮中间合金及氮化硅锰冶炼螺纹钢技术,小粒度石灰石在电炉、转炉直接炼钢技术,高品质系列钢锭缺陷控制技术,马氏体不锈钢大方坯连铸技术,电弧炉炼钢复合吹炼技术等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据、模型与决策
3 线性规划问题的计算机求解及应用举例
第7题
(1)线性规划模型
(2)线性规划模型代数式
公司所做决策的变量是每种原料合金的数量,因此引入决策变量
i x 表示第i 种原料合金的数量()1,2,3,4,5,6i =。
建立此问题的数学模型为:
123456min 1008075859495Z x x x x x x =+++++
6
1234561
6
12345616
12345616025304030404020352025405030..204050353010300(1,2,3,4,5,6)i
i i i i
i i x x x x x x x x x x x x x x s t x x x x x x x
x i ===⎧
+++++=⨯⎪⎪
⎪
+++++=⨯⎪⎪⎨⎪+++++=⨯⎪⎪⎪≥=⎪⎩
∑∑∑
第8题
(1)线性规划模型
(2)线性规划模型代数式
公司所做决策的变量是每种原料数,因此引入决策变量i x 表示第i
种原料数()1,2,3,4i =。
建立此问题的数学模型为:
1234min 0.80.40.60.4Z x x x x =+++
12341234
1234123485204080250
35853565190..152560151601089840
x x x x x x x x s t x x x x x x x x +++≥⎧⎪+++≥⎪⎨
+++≥⎪⎪+++≥⎩
第9题
线性规划模型代数式
车间所做决策的变量是(1,2,3)i A i =机床生产(1,2)j B j =零件数,因此
引入决策变量ij x 表示加工(1,2)j B j =零件使用的(1,2,3)i A i =机床台数。
建立此问题的数学模型为:
111221223132max 304565403542Z x x x x x x =+++++
1112212231328060..300(1,2,3,1,2)
ij x x x x s t x x x i j +≤⎧
⎪+≤⎪
⎨
+≤⎪⎪≥==⎩ (1)线性规划模型
(2)使用sumproduct 函数
第10题
(1)线性规划模型
(2)线性规划模型代数式
公司所做决策可用网络配送图表示(如下图),图中节点123,,v v v 表
示1、2、3三个工厂,节点4v 表示配送中心,节点567,,v v v 表示1、2、
3三个仓库。
每一条有向弧表示一条可能的运输路线,并给出了相应的单位运输成本,对运输量有限制的路线的最大运输能力也同时给出。
网络配送模型
引入变量ij f 表示由i v 经过路线(),i j v v 运输到j v 的产品属。
问题的目
标是总运输成本最小化:
1516142524273436min 9080307035804075Z f f f f f f f f =+++++++
37454647
85303530f f f f ++++
15161425272436
3734
14243445464715254516
3646
273747142434454647ij 100
90100
..110
80
8060,60,60,60,60,60,0
f f f f f f f f f f f f f f f s t f f f f f f f f f f f f f f f f ⎧++=⎪
++=⎪⎪++=⎪++=++⎪⎪
++=⎨⎪++=⎪⎪++=⎪
≤≤≤≤≤≤⎪⎪≥⎩
所有
第12题
(1)线性规划模型
(2)线性规划模型代数式
医院所做决策的变量是每时段开始上班的人数,因此引入决策变
量i x 表示第i 个时段上班的人数()1,2,3,4,5,6i =。
建立此问题的数学模型为:
123456
min (3028)(2830)(3032)(3238)(3840)(4030)Z x x x x x x =+++++++++++
61122334455680100110..7540550(1,2,3,4,5,6)i
x x x x x x s t x x x x x x x i +≥⎧⎪+≥⎪⎪+≥⎪+≥⎨⎪+≥⎪
+≥⎪
⎪≥=⎩
第13题
(1)线性规划模型
工时需求
(2)线性规划模型代数式
公司所做决策的变量是不同工人生产不同手套的数量,因此引入决策变量如下表:
手 套 全 职
兼 职
男 式 11x 12x 女 式 21x
22x 儿 童
31x
32x
建立此问题的数学模型为:
111221223132max 9()10()6()40151020
Z x x x x x x =+++++-⨯-⨯
112131112131122232
1112
21223132
(0.50.60.55)/4020(0.50.60.55)/402(0.50.60.55)/20..2() 1.6()0.9()5000
0(,1,2,3)ij x x x x x x x x x s t x x x x x x x i j ++≥⎧
⎪++⎪≥⎪++⎨⎪+++++=⎪≥=⎪⎩。
