(完整版)2018年华东师大版初中数学一~三年级所有知识点总结,推荐文档
华师版初中数学全部知识点大全
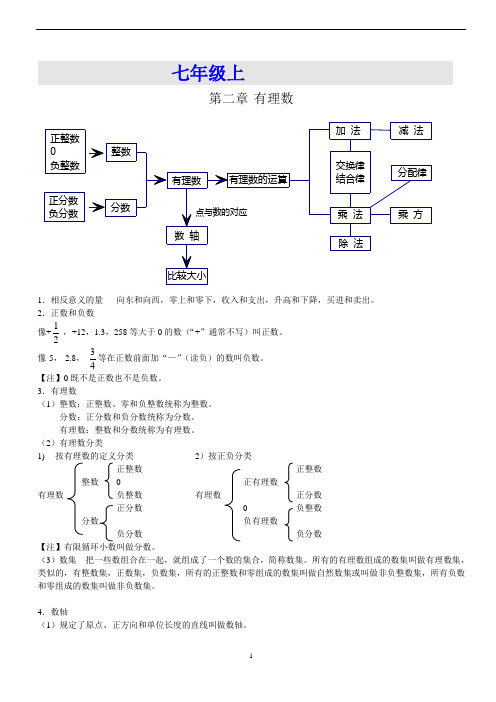
七年级上第二章 有理数正分数负分数正整数0负整数1.相反意义的量 向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+21,+12,1.3,258等大于0的数(“+”通常不写)叫正数。
像-5,-2.8,-43等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1) 按有理数的定义分类 2)按正负分类正整数 正整数 整数 0 正有理数有理数 负整数 有理数 正分数 正分数 0 负整数分数 负有理数负分数 负分数【注】有限循环小数叫做分数。
(3)数集 把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴(1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数.(2)在数轴上比较有理数的大小1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数(1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义) (3)0的相反数是0。
也只有0的相反数是它的本身。
(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a 的相反数是—a 。
(6)多重符号化简多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负; 如果是偶数个,则结果为正。
最新华师版初中数学全部知识点大全(最新整理)

2.代数式 (1)由数和字母用运算符号连接起所成的式子叫做代数式,单独的一个数或一个字母也叫代数式。
【注】运算符号指加、减、乘、除、乘方、开方。代数式中不可含有“>”、“<”、“=”、“ ”、“ ”、“ ”等表
示相等或不等关系的符号。 (2)代数式书写要求
1)代数式中出现的乘号,通常写作“ ”或省略不写。但数字与数字相乘时,要用“ ”。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数. (2)在数轴上比较有理数的大小
1)在数轴上表示的两个数,右边的数总比左边的数大。 2)由正、负数在数轴上的位置可知:正数都有大于 0,负数都小于 0,正数大于一切负数。 5.相反数 (1)只有符号不同的两个数称互为相反数,如-5 与 5 互为相反数。 (2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。(几何意义) (3)0 的相反数是 0。也只有 0 的相反数是它的本身。 (4)相反数是表示两个数的相互关系,不能单独存在。 (5)数 a 的相反数是—a。 (6)多重符号化简 多重符号化简的结果是由“-”号的个数决定的。如果“-”号是奇数个,则结果为负; 如果是偶数个,则结果为正。 可简写为“奇负偶正”。 6.绝对值 (1)在数轴上表示数 a 的点离开原点的距离,叫做数 a 的绝对值。 (2)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零.
3.由视图到立体图形
7
吉大教育辅导学校 初中数学知识点总结(华师)
主视图:可分清物体的长与高。 俯视图:可分清物体的长与宽。 左视图:可分清物体的宽与高。 口诀:主俯长对正,主左高齐平,俯左宽相等。 4.立体图形的表面展开图
多面体是由平面图形围成的的立体图形,沿着多面体的一些棱将它剪开,可以把多面体的表面展开成一个平 面图形,这个平面图形叫做多面体的表面展开图。
华师大版初中数学知识点总结doc资料

华师大版初中数学知识点总结华师大版初中数学知识点总结七年级上第二章有理数1.相反意义的量向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+,+12,1.3,258等大于0的数(“+”通常不写)叫正数。
像-5,-2.8,-等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1)按有理数的定义分类2)按正负分类正整数正整数整数0 正有理数有理数负整数有理数正分数正分数0 负整数分数负有理数负分数负分数【注】有限循环小数叫做分数。
(3)数集把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴(1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数.(2)在数轴上比较有理数的大小1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数(1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义)(3)0的相反数是0。
也只有0的相反数是它的本身。
(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a的相反数是—a。
(6)多重符号化简多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负;如果是偶数个,则结果为正。
可简写为“奇负偶正”。
华师大版初中数学知识点总结材料

数学知识点总结七年级上第二章有理数1.相反意义的量向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+12,1.3,258等大于0的数(“+”通常不写)叫正数。
像-5,-2.8,等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1)按有理数的定义分类2)按正负分类正整数正整数整数0 正有理数有理数负整数有理数正分数正分数0 负整数分数负有理数负分数负分数【注】有限循环小数叫做分数。
(3)数集把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴(1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数.(2)在数轴上比较有理数的大小1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数(1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义)(3)0的相反数是0。
也只有0的相反数是它的本身。
(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a的相反数是—a。
(6)多重符号化简多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负;如果是偶数个,则结果为正。
可简写为“奇负偶正”。
6.绝对值(1)在数轴上表示数a的点离开原点的距离,叫做数a的绝对值。
最新华师版初中数学全部知识点大全

第二章 有理数正分数负分数正整数0负整数1.相反意义的量 向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+21,+12,1.3,258等大于0的数(“+”通常不写)叫正数。
像-5,-2.8,-43等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1) 按有理数的定义分类 2)按正负分类正整数 正整数 整数 0 正有理数有理数 负整数 有理数 正分数 正分数 0 负整数分数 负有理数负分数 负分数【注】有限循环小数叫做分数。
(3)数集 把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴(1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数.(2)在数轴上比较有理数的大小1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数(1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义) (3)0的相反数是0。
也只有0的相反数是它的本身。
(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a 的相反数是—a 。
(6)多重符号化简多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负; 如果是偶数个,则结果为正。
华师版初中数学全部知识点大全

七年级上第二章 有理数正分数负分数正整数0负整数1.相反意义的量 向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+21,+12,,258等大于0的数(“+”通常不写)叫正数。
像-5,,-43等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
;3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1) 按有理数的定义分类 2)按正负分类正整数 正整数 整数 0 正有理数 …有理数 负整数 有理数 正分数 正分数 0 负整数分数 负有理数负分数 负分数【注】有限循环小数叫做分数。
(3)数集 把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴 ,(1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数.(2)在数轴上比较有理数的大小1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数(1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义) (3)0的相反数是0。
也只有0的相反数是它的本身。
>(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a 的相反数是—a 。
(6)多重符号化简多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负; 如果是偶数个,则结果为正。
华师大版初中数学知识点总结

华师大版初中数学知识点总结
初中数学(华师大版)知识点总结:
一、代数:
1、定义:代数是学习数的一个重要分支,通过讨论各种各样的数量
的静态变化,记号法,定义,性质,运算,解决实际问题的技术,来把数
学研究的内容概括为一个整体。
2、术语:代数术语包括:变量、常数、基本运算、表达式、方程和
不等式、根、函数、因式和因子、和、积、分式、幂和指数、比率、比值、百分数、数列和级数、立体几何体等。
3、类型:代数中常见的几种题型有:简单方程组、一元二次方程、
分式、幂指数与根式、比值等。
4、思想:代数是通过思维推理,综合运用符号表达式、数学公式和
算法,来解决问题和实践领域中的应用问题。
二、几何:
1、定义:几何是以形体的几何特性,以及相关的空间几何关系来研
究实物形状、大小和位置的数学学科。
2、类型:几何问题可以分为:图形结构类、运动类、测量类和计算
类问题。
3、概念:常见的几何性质和概念有:
(1)图形的属性:角、平行线、平行四边形、锐角三角形等;
(2)图形大小关系:直角和锐角三角形、正方形等;
(3)空间图形关系:棱和面、相交、相切等;。
华师大版初中数学知识点总结材料

###数学知识点总结七年级上第二章 有理数1.相反意义的量 向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
2.正数和负数像+12,1.3,258等大于0的数(“+”通常不写)叫正数。
像-5,-2.8,等在正数前面加“—”(读负)的数叫负数。
【注】0既不是正数也不是负数。
3.有理数(1)整数:正整数、零和负整数统称为整数。
分数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
(2)有理数分类1) 按有理数的定义分类 2)按正负分类正整数 正整数 整数 0 正有理数有理数 负整数 有理数 正分数 正分数 0 负整数分数 负有理数负分数 负分数【注】有限循环小数叫做分数。
(3)数集 把一些数组合在一起,就组成了一个数的集合,简称数集。
所有的有理数组成的数集叫做有理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负整数集,所有负数和零组成的数集叫做非负数集。
4.数轴 (1)规定了原点、正方向和单位长度的直线叫做数轴。
【注】1)数轴的三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都是有理数. (2)在数轴上比较有理数的大小 1)在数轴上表示的两个数,右边的数总比左边的数大。
2)由正、负数在数轴上的位置可知:正数都有大于0,负数都小于0,正数大于一切负数。
5.相反数 (1)只有符号不同的两个数称互为相反数,如-5与5互为相反数。
(2)从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。
(几何意义) (3)0的相反数是0。
也只有0的相反数是它的本身。
(4)相反数是表示两个数的相互关系,不能单独存在。
(5)数a 的相反数是—a 。
(6)多重符号化简 多重符号化简的结果是由“-”号的个数决定的。
如果“-”号是奇数个,则结果为负; 如果是偶数个,则结果为正。
华师大版初中数学考点总结

华师大版初中数学考点总结一、数的四则运算1.整数四则运算:包括加减乘除的运算。
2.分数的四则运算:包括分数的加减乘除的运算。
3.小数的四则运算:包括小数的加减乘除的运算。
4.保留小数计算:要求学生掌握小数精确到一定位数的计算方法。
二、代数与方程1.提取公因式:学生需要学会提取公因式的方法,简化计算。
2.合并同类项:学生需要学会合并同类项的方法,简化计算。
3.方程的解:学生需要学会解一元一次方程、一元一次方程组、一元二次方程等。
4.代数式与方程式的计算:包括根据给定的条件计算代数式和方程式的值,以及根据代数式和方程式的值计算未知数的值。
三、几何1.角的概念:学生需要理解角的概念,包括角的度量和角的种类。
2.图形的性质:学生需要了解各种图形的性质,包括线段、角、三角形、四边形等。
3.面积与体积的计算:学生需要学会计算平行四边形、三角形、矩形等图形的面积,以及长方体、正方体等立体图形的体积。
4.相似与全等:学生需要了解相似与全等的概念,以及相似与全等的判定方法。
四、数据与概率1.统计量与频率分布表:学生需要学会计算统计量,包括众数、中位数、均值等。
2.折线图与条形图:学生需要学会制作折线图和条形图,并能够从图中读取信息。
3.概率计算:学生需要学会计算概率,包括事件的概率和多个事件的概率。
五、函数与图像1.函数的表示与性质:学生需要了解函数的概念,包括函数的表示方法和函数的性质。
2.函数的图像:学生需要学会根据函数的表达式绘制函数的图像。
3.函数的应用:学生需要学会应用函数解决实际问题,包括线性函数和比例函数的应用。
六、解决实际问题1.解决实际问题:学生需要学会将数学知识应用到实际问题中,进行问题分析和解决。
2.数学建模:学生需要学会利用数学方法对实际问题进行建模,并给出解决方案。
通过对华师大版初中数学教材考点的总结,我们可以看出,该教材注重基础知识的学习和应用,涵盖了数学的各个方面。
学生需要通过对这些考点的学习和掌握,培养自己的数学思维和解决问题的能力,为更高层次的学习打下坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理数集,类似的,有整数集,正数集,负数集,所有的正整数和零组成的数集叫做自然数集或叫做非负
整数集,所有负数和零组成的数集叫做非负数集。
三要素:原点、正方向、单位长度缺一不可。
2)数轴能形象地表示数,所有的有理数都可用数轴上的点表示,但数轴上的点所表示的数并不都
七年级上 第二章 有理数 1. 相反意义的量 2. 正数和负数
华东师大版初中数学所有知识点总结
向东和向西,零上和零下,收入和支出,升高和下降,买进和卖出。
1
像+ 2 ,+12,1.3,258 等大于 0 的数(“+”通常不写)叫正数。
3
像-5,-2.8,- 4 等在正数前面加“—”(读负)的数叫负数。
1
华东师大版初中数学所有知识点总结
a, a 0
a
0,aa,
a
0
0
(3) 绝对值的主要性质 一个数的绝对值是一个非负数,即 a≥0,因此,在实数范围内,绝对值最小的数是零. (4)两个相反数的绝对值相等. (5)运用绝对值比较有理数的大小 两个负数,绝对值大的反而小.
(6)比较两个负数的方法步骤是: 1 先分别求出两个负数的绝对值; 2 比较这两个绝对值的大小; 3 根据“两个负数,绝对值大的反而小”作出正确的判断. 7. 有理数的加法(1)有 理数加法法则
2一个大于 0 的数就记成 a 10n 的形式。其中1 a 10, n 是正整数。像这样的记数法叫做科学记 数
法。 3 用科学记数法表示一个数时,10 的指数等于原数的整数位数减 1。(或等于小数点向右移动的位数。
14. 有理数的混合运算 1 先算乘方,再算乘除,最后算加减。 2 同级运算,按照从左至右的顺序进行。 3 如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的。 15. 近似数和有效数字 1 准确数:完全符合实际的数。 2 近似数:和准确数非常接近的数。近似数和准确数接近的程度叫做精确度。 3一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位,这时,从左边第一个不是 0 的数 字 起到精确到的位数止,所有的数字都叫做这个数的有效数字。 4 近似数的精确度有两种形式:1)精确到哪一位,2)保留几个有效数字。
第三章 整式的加减 1. 用字母表示数 2. 代数式 1 由数和字母用运算符号连接起所成的式子叫做代数式,单独的一个数或一个字母也叫代数式。
【注】运算符号指加、减、乘、除、乘方、开方。代数式中不可含有“>”、“<”、“=”、“ ”、“”、 “ ”等表示相等或不等关系的符号。
2 适当的应用加法运算律。 10.有理数的乘法 1 有理数的乘法法则 两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘都得零。 2几个不等于零的数相乘,积的正负号由负因数的个数决定,当负号的个数为奇数时,积为负;当负 号 的个数为偶数时,积为正。
几个数相乘,有一个因数为零,积就为零。 3乘法运算律 乘法交 换律: ab=ba
乘法结合律:(ab)c=a(bc) 乘法对加法的分配律:a(b+c)=ab+ac
11.有理数的除法
1 倒数:乘积为 1 的两个数互为倒数。 【注】0 没有倒数。 2 有理数除法法则 1:除以一个数等于乘以这个数的倒数。 【注】0 不能做除数。
a b a 1 (b 0) b
3 有理数的除法法则 2:两数相除,同号得正,异号得负,并把绝对值相除。 零除以任何一个不等于的数,都得零。
(3)0 的相反数是 0。也只有 0 的相反数是它的本身。
4 相反数是表示两个数的相互关系,不能单独存在。 5 数 a 的相反数是—a。 6 多重符号化简 多重符号化简的结果是由“-”号的个数决定的。如果“-”号是奇数个,则结果为负; 如果是偶数个, 则结果为正。可简写为“奇负偶正”。
6. 绝对值 1 在数轴上表示数 a 的点离开原点的距离,叫做数 a 的绝对值。 2 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;零的绝对值是零.
1 同号两数相加,取相同的符号,并把绝对值相加。 2 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 3 互为相反数的两个数相加得零。 4 一个数与 0 相加,仍得这个数。 (2)有理数加法的运算律 加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c) 8. 有理数的减法 减去一个数等于加上这个数的相反数。
【注】0 既不是正数也不是负数。
3. 有理数 1整数:正整数、零和负整数统称为整数。 分
数:正分数和负分数统称为分数。
有理数:整数和分数统称为有理数。
2 有理数分类 按有理数的定义分类
2)按正负分类
正整数
正整数
有理数
整数
0 负整数
正分数
有理数
正有理数 0
正分数 负整数
分数
负分数
负有理数
负分数
【注】有限循环小数叫做分数。 (3) 数集 把一些数组合在一起,就组成了一个数的集合,简称数集。所有的有理数组成的数集叫做有
2
华东师大版初中数学所有知识点总结
12.有理数的乘方 1 求几个相同因数积的运算,叫做乘方。
aaaaan
n个
2 乘方的结果叫做幂,a 叫做底数,n 叫做指数。 3 有理数乘方法则: 正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数,0 的任何非 0 次幂都是零。 13.科学记数法 1 一般的,10 的 n 次幂,在 1 的后面有 n 的 0。
a-b=a+(-b) 9. 有理数的加减混合运算 1省略加号和的形式:在一个和式里,通常把各个加数的括号和它前面的加号省略不写。例如:把- 8+
(+10)+(-6)+(-4)写成省略加号和的形式为-8+10-6-4。读作“负 8,正 10,负 6,负 4 的和”也
可读作“负 8 加 10 减 6 减 4。
是有理数.
2 在数轴上比较有理数的大小 1 在数轴上表示的两个数,右边的数总比左边的数大。 2 由正、负数在数轴上的位置可知:正数都有大于 0,负数都小于 0,正数大于一切负数。 5. 相反数 1 只有符号不同的两个数称互为相反数,如-5 与 5 互为相反数。 2从数轴上看,位于原点两旁,且与原点距离相等的两点所表示的两个数叫做互为相反数。(几何意 义 )
