无约束最优化的直接法
无约束优化的直接搜索法

针对具体问题的特性,可以构造出更加有效的钩子函数,如利用问 题的对称性、稀疏性等。
参数调整
钩子函数中的参数对优化过程有很大影响,需要通过实验和调整来 确定最佳参数值。
求解过程及收敛性证明
求解过程
利用钩子函数引导搜索方向,结合一定的线 搜索或信赖域策略来求解无约束优化问题。
收敛性证明
在适当的条件下,可以证明利用钩子函数法 进行无约束优化问题的求解具有全局收敛性 和局部超线性收敛速度。这需要概念及性质介绍
单纯形定义
在n维空间中,选取n+1个线性无关的点作为顶点,这些顶点构成的凸多面体称为n维 单纯形。
单纯形性质
单纯形的顶点数、边数、面数等具有固定的数学关系;单纯形内部任意一点都可以由其 顶点线性表示。
替换规则与策略选择
反射规则
扩展规则
当搜索陷入局部最优时,通过反射操作将 搜索方向转向单纯形外部,以期找到更优 解。
粒子群优化算法
粒子群优化算法通过模拟鸟群觅食行为来寻找最优解,与直接搜索法 结合后,可以加快搜索速度并提高搜索精度。
挑战和未来发展方向
高维复杂问题
随着问题维度的增加,搜索空间急剧扩大,如何设计高效的直接搜索 法以应对高维复杂问题是一个重要挑战。
约束处理问题
实际优化问题中往往存在各种约束条件,如何在直接搜索法中有效处 理这些约束条件是一个需要研究的问题。
02 坐标轮换法
基本原理及步骤
坐标轮换法的基本原理
通过依次沿坐标轴方向进行一维搜索来寻求目标函数的极小值点。在每次迭代 中,选择一个坐标方向进行搜索,然后更新该坐标方向上的变量值。
坐标轮换法的步骤
首先给定初始点,然后按照一定顺序(如依次沿各坐标轴方向)进行一维搜索, 得到新的点并更新目标函数值。不断重复此过程,直到满足收敛条件或达到最 大迭代次数。
无约束最优化方法直接搜索法课件

x2
S(1)
S2(1
)
(1)
X3 X2 (1)
X* X2 (2) X1 (2)
S(2)
X0 (1)
X 1 (1)
S1(1) x1
• 鲍威尔基本算法的缺点
鲍威尔基本算法仅具有理论意义,不要说对于一般的 函数,就是对于二次函数,它也可能失效。因为在迭代过程 中的n个搜索方向有时会变成线性相关,而不能形成共轭方向, 从而张不成n维空间,导致随后的迭代搜索在降维(“退化”) 的空间中进行,可能求不到极小点,故需进行改进。
x 2 XL X2
Xn+3 Xn+2
Xn+1
Xห้องสมุดไป่ตู้ XH
X1 XG x1
6)扩张:当 fn+2 < f L 时,取扩张点Xn+3 ,即
Xn+3 = Xn+1 + (Xn+2 – Xn+1)
( =1.2~2.0 )
并计算 fn+3 = f (Xn+3 ) 。 若 fn+3 < fn+2 ,则以Xn+3 代替 X H , fn+3 代替 fH ,构造一个新的单纯形;否则,以 X n+2 代 替XH , fn+2 代替fH ,构造新的单纯形;然后返回到 3)。
鲍威尔条件:
若 f 3 < f 1, ( f1 - 且2f2 + f3) (f1 - f2 - △m(k))2 < 0.5 △m(k) (f1 - f3 )2 同时成立,则用 S ( k ) 替代 S m ( k ) ;否则,仍用 就是鲍威尔修正算法,通常所说的鲍威尔算法就是指这一修正算法。
• 鲍威尔算法的计算步骤及算法框图
第三讲 多维无约束最优化共轭方向法

在每一步的过程中,搜索方向线性独立是 非常重要的,否则可能不收敛。 例2: Rosenbrock函数的极小值 例3:
f ( x1 , x2 , x3 ) ( x1 x2 x3 ) 2 ( x1 x2 x3 ) 2 ( x1 x2 x3 ) 2
(d ) Az i z d i T i z , j 1, 2,...m i 1 ( z ) Az
j j
j 1
j T
i
则 z1, z2,… zm 关于A 共轭。
二次终结性
一个算法用于解正定二次函数的无约束极小时, 若有限步迭代可达最优解,则称该算法具有二 次终结性。 共轭方向 + 精确一维搜索 = 二次终结 设 z1, z2,… zm 关于正定阵A 共轭。则从任意初 始点出发,二次型目标函数
共轭方向
当A=I(单位矩阵)时, d(1)TAd(2)= d(1)Td(2)=0,即正交关系。
共轭方向 正交方向 当d(1),d(2), …,d(m) 关于正定矩阵A两两共 轭时, d(1),d(2), …,d(m) 线性无关。
构造共轭方向的Schmidt过程
设d(1),d(2), …,d(m) 线性无关。令
一些改进方法
Rosenbrock算法(旋转方向法) Hooke-Jeeves算法(步长加速法)
多维无约束最优化:共轭方向法
1.
2.
基本思想:沿着某些方向依次进行精确 的一维搜索,确定最佳的步长。 共轭方向 定义:设 An×n 对称正定,d (1),d (2) ∈Rn , d (1) ≠0,d(2) ≠0,满足 d(1)TAd(2)=0, 称d(1),d(2) 关于矩阵A共轭。 共轭向量组:d(1),d(2), …,d(m) ∈Rn 均 非零,满足d(i)TAd(j)=0,(i≠j) .
第三章 无约束最优化方法

f x f x
*
所以函数f(x)在 x * 处取得局部极小值,称x *为
局部极小点。 而优化问题一般是要求目标函数在某一区域内 的全局极小点。 函数的局部极小点是不是一定是全局极小点呢?
5
第三章 无约束最优化方法
下凸的一元函数
可以证明凸规划问题的局部最小点就是其全局最小点。
6
第三章 无约束最优化方法
f x 0
x Rn
的问题。一般地,这是一个非线性方程组, 17 可对其采用迭代法求解之。
第三章 无约束最优化方法
下降迭代算法
算法:给定目标函数 f x 的极小点的一个初始估计点 x0 , 然后按一定的规则产生一个序列 xk ,这种规则通常称 为算法。如果这个序列的极限恰好是问题(3-1)的极 小点 x* ,即
正定矩阵 设 Q是n×n 阶对称矩阵。
若 x Rn 且 x 0 都有 x T Q x 0 ,则称矩阵Q 是正定的 若 x R
n n
T x 都有 Q x 0 ,则称矩阵Q 是半正定的
若 x R 且 x 0 都有 xT Q x 0 ,则称矩阵Q 是负定的 若 x Rn 都有 x T Q x 0 ,则称矩阵Q 是半负定的
为正定的定义是:若对任何向量d (d!=0),有
d T 2 f x* d 0
对称正定方阵 2 f x* 的检验方法是所有主子式均大于零。 二、迭代方法 求解 无约束最优化问题 T f x min x x1, x2 , , xn 的问题可以转变为求解n 元方程组
26
3-2
一维搜索(0.618法)
设给定一个较小的步长δ,从α=0开始,先计算φ(0),然 后计算在 (1.618)0 的函数值φ(δ);如果φ(δ)<φ(0), 则讲步长δ增大1.618倍,得到一个新点 1.618 2.618 , 计算φ(2.618δ);如果φ(2.618δ)仍小于φ(δ),再继续增加 步长为原步长的1.618倍,如下图所示,从而得到一系列 j 点的αj的值为 '
第8章 无约束问题最优化方法

8 . 1 . 3 计算举例
例 8-1 用变量轮换法求解
2 2 min f ( x) 3x12 2x2 x3 ,
( n 1) (1) T x (1) 0.01 时停止 已知初始点 x (1, 2, 3) ,当 x
迭代.
8.2
模式搜索方法
模式搜索方法 ( Pattern Search Method ) 是 R.Hooke 和 T.A.Jeeves 于 1961 年提出的 , 因此也称为 Hook-Jeeves 方法 , 此方法有明显的几何意义 , 为介绍这种方法 , 从求一个二元函 数的极小点谈起.这相当于寻找某个曲面的最低点 , 或者形象 地说 , 相当于从一座山岭的某处出发 , 设法走到附近某一盆地 的最低点 , 怎样才能尽快达到这一目标呢 ? 很显然 , 如果能找 到一条山谷 , 沿山谷行进是最好的方法. 模式搜索方法就是根据上述思想设计的.它由两部分组成 , 包括探测移动和模式移动. 利用这种算法建立的迭代点移动 不需要使用一维搜索技巧.
(1) (1) (1) (1) (1) (1) e2 ) f (t 2 ) , 则 置 t3 t3 t2 e2 ; 否 则 若 f (t 2 t2 e2 ; 否 则
置 t 3 (1) = t 2 (1) .
(1) 重复以上过程, 最后得到 t n 1 .
8 . 2 . 2 模式移动
8.3 可变单纯形法
可变单纯形法的基本思想是, 给定 R n 中的一个单纯 形, 求出 n +1 个顶点的函数值 , 并确定这些函数值中的 最大值、 次大 值和最小 值, 然后通过 反射 、扩张、 内 缩、缩边 等方 法(几种 方法 不一定同 时使 用)求出 一 个较好点,用它取代最大值的点,以构成新的单纯形, 通过多次 迭代 逼近极小 点, 迭代过程 中逐 渐地把单 纯 形向最优点移动.
工程优化设计-无约束直接法

X1
X2 S
无约束直接搜索方法
四.共轭方向法及其改进后的Powell法 (2) 共轭方向法 第一轮: S1(1), S2(1) 不一定 共轭, 产生S(1). 第二轮: 取S1(2)= S2(1) S2(2) =S(1), 产生S(2). 第三轮: 取S1(3)= S(1) S2(3) =S(2), 所以,由性质(3)知, 对于 二次函数, S(1), S(2)共轭. 第二轮 第一轮
Powell算法
2.依次一维搜索: X(k)i= X(k)i-1+aS(k)i : min f(X(k)i-1+aS(k)i), i=1,2,…,n
转步6. 转步7.
转步7.
7.如果 否则. k=k+1, 转步2. 结束.
无约束直接搜索方法
Powell法另一形式(保证线性无关) 引理: 设k =det(S1/|S1|, S2/|S2|,…, Sn/|Sn|), k+1=det(S1/|S1|, S2/|S2|,…, Sm-1/|Sm-1|, Sn+1/|Sn+1|, Sm+1/|Sm+1|,…,Sn/|Sn|), 则 k+1= k *am/|Xn(k)-X0(k)|, 这里 Xm(k)=Xm-1(k)+amSm
工程优化设计
黄正东
二0一0年九月
内容提要
• • • • • • • • • • 工程优化问题建模 优化数学理论 一维搜索方法 无约束问题直接搜索方法 无约束问题间接接搜索方法 约束问题直接搜索方法 线性规划与二次规划问题求解 约束问题间接搜索方法 启发式算法 优化软件系统
无约束优化方法

第四章无拘束优化方法——最速降落法,牛顿型方法概括在求解目标函数的极小值的过程中,若对设计变量的取值范围不加限制,则称这种最优化问题为无拘束优化问题。
只管对于机械的优化设计问题,多半是有拘束的,无拘束最优化方法仍然是最优化设计的基本构成部分。
因为拘束最优化问题能够经过对拘束条件的办理,转变为无拘束最优化问题来求解。
为何要研究无拘束优化问题(1)有些实质问题,其数学模型自己就是一个无拘束优化问题。
(2)经过熟习它的解法能够为研究拘束优化问题打下优秀的基础。
(3)拘束优化问题的求解能够经过一系列无拘束优化方法来达到。
所以无拘束优化问题的解法是优化设计方法的基本构成部分,也是优化方法的基础。
依据构成搜寻方向所使用的信息性质的不一样,无拘束优化方法能够分为两类。
一:间接法——要使用导数的无拘束优化方法,如梯度法、(阻尼)牛顿法、变尺度法、共轭梯度法等。
二:直接法——只利用目标函数值的无拘束优化问题,如坐标轮换法、鲍威尔法纯真形法等。
无拘束优化问题的一般形式可描绘为:求 n 维设计变量X x1x2L x n T R n使目标函数 f ( X )min当前已研究出好多种无拘束优化方法,它们的主要不一样点在于结构搜寻方向上的差异。
无拘束优化问题的求解:1、分析法能够利用无拘束优化问题的极值条件求得。
马上求目标函数的极值问题变为求方程min f ( X * )0的解。
也就是*使其知足求Xf ( X *)0x1f ( X*)x2f ( X*)x n解上述方程组,求得驻点后,再依据极值点所需知足的充足条件来判断能否为极小值点。
但上式是一个含有n个未知量,n个方程的方程组,在实质问题中一般是非线性的,很难用分析法求解,要用数值计算的方法。
由第二章的叙述我们知道,优化问题的一般解法是数值迭代的方法。
所以,与其用数值方法求解非线性方程组,还不如用数值迭代的方法直接求解无拘束极值问题。
2、数值方法数值迭代法的基本思想是从一个初始点 X (0)出发,依据一个可行的搜寻方向 d ( 0)搜寻,确立最正确的步长0使函数值沿 d (0 )方向降落最大,获得 X (1)点。
无约束最优化直接方法和间接方法的异同

无约束最优化直接方法和间接方法的异同一、什么是无约束最优化最优化方法(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。
其的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。
最优化问题分为无约束最优化和约束最优化问题,约束最优化问题是具有辅助函数和形态约束条件的优化问题,而无约束优化问题则没有任何限制条件。
无约束最优化问题实际上是一个多元函数无条件极值问题。
虽然在工程实践中,大多数问题都是具有约束的优化问题,但是优化问题的处理上可以将有约束的优化问题转化为无约束最优化问题,然后按无约束方法进行处理。
或者是将约束优化问题部分转化为无约束优化问题,在远离极值点和约束边界处按无优化约束来处理,在接近极值点或者约束边界时按照约束最优化问题处理。
所以无约束优化问题的解法不仅是优化设计方法的基本组成部分,也是优化方法的基础。
无约束最优化方法大致分为两类:一类是使用导数的间接方法,即在计算过程中要用到目标函数的导数;另一类是直接方法,即只要用到目标函数值,不需要计算导数。
这里我们比较这两类方法的异同。
二、无约束最优化方法1.使用导数的间接方法1.1 最速下降法函数的负梯度方向是函数值在该点下降最快的方向。
将 n 维问题转化为一系列沿负梯度方向用一维搜索方法寻优的问题,利用负梯度作为搜索方向,故称最速下降法或梯度法。
无约束优化问题的数学模型可以表示为:min f x x R n,我们假设函数xf x 具有一阶连续偏导数。
最优化方法:第三章无约束问题的最优化方法

f1 f 2 ,则新区间= [a, 2 ]
f1 f 2
[a1 , b]
a 1 , 1 2 , f1 f 2
,记N0=1;
4)检查区间是否缩短到足够小和函数值收敛到足够精度,
如果收敛条件满足,则取最后两试验点的平均值作为极小 点的数值近似解。如果条件不满足则转向步骤5)。
(3)产生新的探测点a3=a1+h,y3=f(a3); (4) 比较函数值 y2与y3: (a) 如y2>y3, 加大步长 h=2 h ,a1=a2, a2=a3,转(3) 继续探测。 (b)如y2<y3, 则初始区间得到: a=min[a1,a3], b=max[a3,a1],函数最小值所在的区间 为 [a , b] 。
解得: b
c
p 3 a b 3 c 3 f 3
2 2 2 2
2 3 f1 3 1 f 2 1 2 f 3 1 2 2 3 3 1
3 f1 3 1 f 2 1 2 f 3 1 2 2 3 3 1
确定的搜索区间必定
f (x) f (x)
α
是一个含有最优点α*的 单峰区间。
0Leabharlann α1α3α
0
α1
α3
α
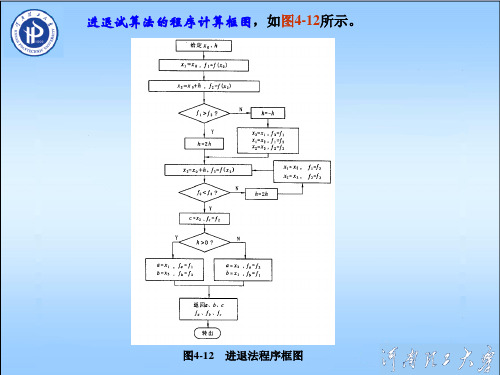
2、确定初始单谷区间的进退法 基本思想: 对f(x)任选一个初始点a1及初始步长h, 通过比较这两点函数 值的大小,确定第三点位置,比较这三点的函数值大小,确定是 否为 “高—低—高” 形态。 步骤: (1)选定初始点a, 初始步长h=h0,计算 y1=f(a1),y2=f(a1+h)。 (2)比较y1和y2。 (a)如y1>y2, 向右前进;加大步长 h=2 h ,转(3)向前; (b)如y1<y2, 向左后退;h=- h0, 将a1与a2,y1与y2的 值互换。转(3)向后探测; (c)如y1=y2,极小点在a1和a1+h之间。
运筹学第16讲 无约束最优化方法 (2)

k=k+1 d(k)=-H(k) ▽ f(x(k)) 一维搜索得λk x(k+1)=x(k)+ λk d(k)
修正H(k)产生H(k+1)
N
||x(k+1)-x(k)||<
ε?
y
Stop. x(k+1)----解
第五章4 变尺度法
下面构造H(k) ,要求H(k) 是▽2f(x(k))的近似且能逐次迭
第五章 2 Newton法
二、 Newton法的改进: (1)为减小工作量,取m(正整数),使每m次迭代使用同一个 Hesse阵,迭代公式变为: x(km+j+1)=x(km+j)-[▽2f(x(km))]-1 ▽f(x(km+j)) j=0,1,2, …,m-1 , k=0,1,2, … 特点:收敛速度随m的增大而下降 m=1时即Newton法, m→∞ 即线性收敛。 (2)带线性搜索的Newton法: 在Newton迭代中,取d(k)= -[▽2f(x(k)) ]-1 ▽f(x(k)) , 加入线性搜索:min f(x(k)+λk d(k)) 求得λk , x(k+1)=x(k)+λkd(k) 特点:可改善局部收敛性,当d(k)为函数上升方向时,可向负方 向搜索,但可能出现± d(k)均非下降方向的情况。
第五章4 变尺度法
二、DFP法: (续)
令修正公式为 ( 秩 2 公式 )。满足拟 则 H = H + α UU Newton 条件
T
+ β VV
T
u,v ∈ R n
S = H y.
S = Hy + α ( u T y ) u + β ( v T y ) v v = Hy 1 ST y ,
04 无约束优化方法

F 1A C
向上的极小点,而非原函数的 -2 -1
0
1
2
3
x1
极小点。
解决办法:阻尼牛顿法。
7
二.阻尼牛顿法
1.迭代公式
沿牛顿方向-[H(X(k))]-1f(X(k))作一维搜索,迭代公式:
X (k1) X (k ) k [H ( X (k ) )]1f ( X (k ) )
其中λ k使
f ( X (k ) k s(k ) ) min f ( X (k ) k s(k ) )
S1
1 0 ,S2
0 1
正交不共轭
19
2.正定二次函数的特点
(1)正定二次二元函数的等值线是椭圆线簇,椭圆线簇的中心
即目标函数的极值点。
(2)过同心椭圆线簇中心作任意直线,此直线与诸椭圆交点处
的切线相互平行。
反之过两平行线与椭圆切点X(a)和
x2
X(b)的连线必通过椭圆的中心。因此
只要沿方向X(a)—X(b)进行一维搜索,
1、坐标轮换法具有程序简单,易于掌握的优点,但它的计
算效率较低,因此它虽然步步在登高,但相当于沿两个垂直方
向在爬山,路途迂迴曲折,收敛很慢,因此它适用于维数较低
(一般n<10)的目标函数求优。
2、有“脊线”的目标函数等值线的情形,沿坐标轴方向函数值
不一定下降。
脊线
x2
A
p
0
x1
13
五、练习 用最优步长法求解 f (X)=(x1-2)4+(x1-2x2)2的极小点。 初始点X(0)=[0,3]T,要求迭代一轮。 请注意沿坐标轴移动的方向。
22
二、迭代过程
以二维问题为例: ① X(0)
无约束最优化直接方法和间接方法的异同

无约束最优化直接方法和间接方法的异同一、什么是无约束最优化最优化方法(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。
其的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。
最优化问题分为无约束最优化和约束最优化问题,约束最优化问题是具有辅助函数和形态约束条件的优化问题,而无约束优化问题则没有任何限制条件。
无约束最优化问题实际上是一个多元函数无条件极值问题。
虽然在工程实践中,大多数问题都是具有约束的优化问题,但是优化问题的处理上可以将有约束的优化问题转化为无约束最优化问题,然后按无约束方法进行处理。
或者是将约束优化问题部分转化为无约束优化问题,在远离极值点和约束边界处按无优化约束来处理,在接近极值点或者约束边界时按照约束最优化问题处理。
所以无约束优化问题的解法不仅是优化设计方法的基本组成部分,也是优化方法的基础。
无约束最优化方法大致分为两类:一类是使用导数的间接方法,即在计算过程中要用到目标函数的导数;另一类是直接方法,即只要用到目标函数值,不需要计算导数。
这里我们比较这两类方法的异同。
二、无约束最优化方法1. 使用导数的间接方法1.1 最速下降法函数的负梯度方向是函数值在该点下降最快的方向。
将n维问题转化为一系列沿负梯度方向用一维搜索方法寻优的问题,利用负梯度作为搜索方向,故称最速下降法或梯度法。
无约束优化问题的数学模型可以表示为:()n R f ∈x x xmin ,我们假设函数()x f 具有一阶连续偏导数。
第4章 优化设计(无约束优化-直接法)
(k ) 2 m
(4-43)
同时成立,则表明方向S 与原方向组线性无关,因此可将新方向 (k ) S ( k )作为下一轮的迭代方向,并去掉方向 S m 而构成第k+1轮迭代的 搜索方向组; 否则,仍用原来的方向组进行第k+1轮迭代。 (k ) F1 f ( X 0 ) —— 为第 k 轮起始点函数值; 上式中: (k ) F2 f ( X n ) —— 为第 k 轮方向组一维搜索终点函数值; (k ) (k ) (k ) (k ) X —— 为 对 Xn 的映射点函数值; 0 F3 f (2 X n X 0 ) k ) —— 为第 k 轮方向组中沿诸方向一维搜索所得的各函 (m (k )。 数值下降量中之最大者,其相对应的方向记为 S m
•
若共轭方向不好,则不用它作为下一 轮的迭代方向,而仍采用原来的一组迭 代方向; • 若共轭方向好,则可用它替换前轮迭 代中使目标函数值下降最多的一个方向, 而不一定是替换第一个迭代方向。 这样得到的方向组,其收敛性更好。
修正鲍威尔法对于是否用新的方向来替换原方向组的某一方向 的判别条件为: 在第 k 轮搜索中,若
进行第二轮迭代时, 去掉第一个方向 S1(1) e1 ,将方向 S (1) 作为最 末一个迭代方向, 即从 X (1) X 0(2) 出发,依次沿着方向 S S e 及 S (2) S (1) X (1) X (1)
(2) 1 (1) 2 2
2
2
0
进行一维搜索,得到极小点: X1(2) 、X 2(2) ; ( 2) X2 然后利用 X 0(2) 、 构成另一个迭代方向 (2) (2) S (2) X 2 X0 即 S ( 2) 并沿此方向搜索得到 X (2) 。
无约束最优化的直接方法 最优化理论与算法 教学PPT课件

y( j1) y( j)
j:= j
3. 若j<n,则置j:=j+1,转步2,否则,进行步4.
22
2. Rosenbrock算法
4.若f ( y(n1) ) f (x(k) ),则令 y(1)= y(n+1)
置j=1,转步2.若 f ( y(n1) ) f ( y(1) ),则进行步5.
24
24
12
1 模式搜索法
j x(k )
y( j) f (y( j))
x(2) 0 (1,1) 0 1 (1,1) 0
2 (1,1)
y( j) + ej f ( y( j) + ej) y( j) - ej f ( y( j) - e j)
(5 ,1) 1165 1.64 4 256
( 3 ,1) 1 5 1.02 4 256
给定初始点x(1),放大因子 1,缩减因子 (1,0)
给定初始搜索方向和步长.
14
2. Rosenbrock算法
设第k次迭代的初始点为x(k) ,搜索方向
d (1) , d (2) ,..., d (n)
它们是单位正交方向,沿各方向的步长为
1, 2 ,..., n
每轮探测的起点和终点用y(1) 和y(n+1) 表示. 令y(1) = x(k) ,开始第1轮探测移动
y(2) y(1) e1
并从y(2)出发,沿e2进行探测.
(1.2)
5
1.模式搜索法
若f ( y(1) e1) f ( y(1) ),则沿 - e1方向的探测失败,令
y(2) y(1)
(1.3)
无约束最优化直接方法之单纯形法

无约束最优化直接方法之单纯形法数学与计算科学学院实验报告实验项目名称所属课程名称实验类型实验日期班学姓成级号名绩1n +1v 0=∑v ii =1, i ≠h2)反射。
按如下公式通过v 0反射v h :v r =v 0+α(v 0-v h ) α>0为反射系数,常取α=1, v r称为v h 的反射点。
因v h 是坏点,则一般有f(v r )3)延伸。
经过反射,若不仅有f(v r )1是延伸系数,常取r=2,也可用直线搜索技术确定r.此时若有f(v e )4)收缩。
(如在R 中,由图a 知以v e 、v i 、v l 为顶点的新单纯形已向极小点靠近了一步。
)否则,以反射点替换构成单纯形,转6步(如R 中,由图19.1.1b 可知以v r 、v i 、v l 为顶点的新单纯形向极小点靠近了一步)图19.1.1a 图19.1.1b若f(v r )4.2若对i=1,2,3--n+1(但i ≠h ) 均有f(v r )>=f(v i ), 则要进行收缩。
收缩分以下两种情况4.2.1若f(v r ) >=f(v h ), 即反射点比原来单纯形的坏点还坏,则舍弃v r ,对方向v h -v0进行收缩。
如图d计算公式为v c =v 0+β(v h -v 0) ;其中v c 是v h β=1若f(v c )>f(v h ) ,即收缩点比原单纯形最坏点还坏,因此放弃v c 点,转5步进行棱长减半工作。
否则以v c 替换v h 构成新单纯形,转6。
4.2.2若f(v r )v c =v o +β(v r -v o )若f(v c )>f(v h ), 即收缩点v c 比反射点v r 还坏,则放弃收缩点v c ,转5进行棱长减半工作,否则以v c 替换v h 构成新单纯形,转6。
图19.1.1c 图19.1.1b 图19.1.1e5)减小棱长。
将原单纯形的最好点保持不动,各棱长减半,计算公式为1v i =v i +v l , i ≠1, 2, 3 n +122n +11n +11n +! *6)终止原则。
第三章无约束最优化方法技巧

2 在每次迭代中需要计算 。
3 每次迭代需要求解线性方程组,程
,该方
组有可能是奇异或病态的(有时 非正定),
可能不是下降方向。 (4)收敛于鞍点或极大点的可能性并不小。
§3.3.3 Newton法的改进
为了克服Newton法的缺点,人们保留选取Newton方向作为搜索方
向,采用一维搜索确定最优步长,由此产生的算法称为修正Newton法
1 给定初点 ,允许误差 >0,令k=0。
2 计算搜索方向
(3)若
,则
,停止;否则令
,
由一维搜索步长 ,使得
(4)令
,k=k+1,转步骤(2)。
§3.2.1 最速下降法
例 3.2.1 用最速下降法求解 解:
,设初始点为 。
显然,目标函数是正定二次函数,有唯一的极小点
。
可以证明,如果 是正定二次函数,则由精确一维搜索确定步长
§3.4.1 共轭方向法
定义3.4.1 共轭向量 设G为n阶正定矩阵,
为n维向量组,如果
=0,i,j=1,2,……k,i≠j 则称向量组
关于G共轭。
如果G=I,则化为
=0,即
是正交的,所以共
轭概念是正交概念的推广。
定理3.4.1 设G为n阶正定矩阵,非零向量组
关于G共轭,则此向
量组线性无关。
推论1
(或阻力Newton法)。其迭代步骤如下:
(1)选取初始点 ,令k=0。
(2)计算 ,若
停止迭代,输出 ,否则转(3)。
(3)构造Newton方向。计算 ,取
。
(4)进行一维搜索。求 ,使得
。
令
,k=k+1,转(2)。
常用无约束最优化方法

最速下降法算法流程图
6
满足终 止准则 N X0= X , f0= f , g0= g
上页 返回
输 出 X, Y f
结 束
下页
目标函数为正定二次函数的最速下降法
1 T 设正定二次函数 f ( X ) X AX bT X c 2
求 Xk+1的表达式. gk= g(Xk+1)= AXk+1+b f(X)关于X 求梯度: g(X)=AX+b 现在从Xk出发沿-gk作直线搜索以确定Xk+1: X k 1 X k t k g k 其中tk是最优步长因子.有 g ( X k 1 )T g k 0 得: [ A( X k tk gk ) b]T gk 0 或 [ g k t k Qgk ]T g k 0 T 由此解出: t k g k g k2 200
由此说明相邻两个搜索方向 P g1, P0 g0 ; P2 g2 , P g1 是正交的. 1 1
上页 返回 下页
8
三、最速下降法有关说明
最速下降法的优点是算法简单,每次迭代计算量小,占用内 存量小,即使从一个不好的初始点出发,往往也能收敛到局 部极小点.但它有一个严重缺点就是收敛速度慢. 沿负梯度方向函数下降很快的说法,容易使人们产生一种 错觉,认为这一定是最理想的搜索方向,沿该方向搜索时收 敛速度应该很快,然而事实证明,梯度法的收敛速度并不快. 特别对等值线(面)有狭长深谷形状的函数,收敛速度更慢. 其原因是由于每次迭代后下一次搜索方向总是与前一次搜 索方向相互垂直, 如此继续下去就产生所谓的锯齿现象. 即从直观上看,在远离极小点的地方每次迭代 可能使目标函数有较大的下降, 但是在接近极小点的地方,由于锯齿现象, 从而导致每次迭代行进距离缩短, 因而收敛速度不快 如图所示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 无约束最优化的直接法本章主要内容:坐标轮换法及其收敛性 模式搜索法及其收敛性 旋转方向法、Powell 法。
教学目的及要求:掌握坐标轮换法并理解其收敛性,掌握模式搜索法并理解其收敛性;了解旋转方向法、Powell 法。
教学重点:Powell 法. 教学难点:Powell 法. 教学方法:启发式.教学手段:多媒体演示、演讲与板书相结合. 教学时间:6学时. 教学内容:§8.1 坐标轮换法考虑无约束最优化问题min ()f x , (8.1.1) 其中,:n n x R f R R ∈→.算法8-1(坐标轮换法)Step1 选取初始数据.选取初始点0x ,给定允许误差0ε>,令1k =.Step2 进行一维搜索.从1k x -出发,沿坐标轴方向010k e ⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭进行一维搜索,求1k λ-和k x ,使得111()min ()k k k k k f x e f x e λλλ---+=+,11k k k k x x e λ--=+.Step3 检查迭代次数.若k n =,转Step4;否则,令:1k k =+,返回Step2. Step4 检查是否满足终止准则.若0n x x ε-<,迭代终止,得n x 为问题(8.1.1)的近似最优解;否则,令0:,:1n x x k ==,返回Step2.定理8.1.2 设:n f R R →具有一阶连续偏导数,0n x R ∈,记0()f x α=,且水平集(,)S f α有界.若{}k x 是用坐标轮换法求解问题(8.1.1)产生的点列,且在每次一维搜索中所得到的最优解都是唯一的,则(1)当{}k x 为有穷点列时,其最后一个点是f 的平稳点;(2)当{}k x 为无穷点列时,它必有极限点,并且其任一极限点都是f 的平稳点.例1 用坐标轮换法求解问题2212112min ()3f x x x x x x =+--, (8.1.3) 其中12(,)T x x x =.取初始点(0)(0,0)T x =,允许误差0.1ε=.解 从点(0)x 出发沿1e 进行一维搜索:(0)101000x e λλλ⎛⎫⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,将12,0x x λ==代入2212112()3f x x x x x x =+--中,易得(1)(0)00133,(,0)22T x x e λλ==+=;从点(1)x 出发沿2e 进行一维搜索,得(2)(1)112333,(,)424T x x e λλ==+=;(2)(0)x x ε->.再从点(2)x 出发沿1e 进行一维搜索,得(3)(2)2213153,(,)884Tx x e λλ==+=; 从点(3)x 出发沿2e 进行一维搜索,得(4)(3)33231515,(,)4816Tx x e λλ==+=; (4)(2)x x ε->.再从点(4)x 出发沿1e 进行一维搜索,得(5)(4)44136315,(,)323216T x x e λλ==+=;从点(5)x 出发沿2e 进行一维搜索,得(6)(5)55236363,(,)643264T x x e λλ==+=; (6)(4)x x ε->.再从点(6)x 出发沿1e 进行一维搜索,得(7)(6)661325563,(,)12812864Tx x e λλ==+=; 从点(7)x 出发沿2e 进行一维搜索,得(8)(7)7723255255,(,)256128256Tx x e λλ==+=; (8)(6)x x ε-<.迭代终止,得问题(8.1.3)的近似最优解为(8)255255(,)128256Tx =. 其实问题(8.1.3)的最优解为(2,1)T .§8.2 模式搜索法算法8-2(模式搜索法)Step1 选取初始数据.选取初始点0x ,初始步长00δ>,给定收缩因子(0,1)α∈,给定允许误差0ε>,令0k =.Step2 确定参考点.令,1k y x j ==.Step3 进行正轴向探测.从点y 出发,沿j e 作正轴向探测:若()()k j f y e f y δ+<,令:k j y y e δ=+,转Step5;否则,转Step4.Step4 进行负轴向探测.从点y 出发,沿j e 作负轴向探测:若()()k j f y e f y δ-<,令:k j y y e δ=-,转Step5;否则,转Step5.Step5 检验探测次数.若j n <,令:1j j =+,返回Step3;否则,令1k x y +=,转Step6.Step6 进行模式移动.若1()()k k f x f x +<,从点1k x +出发沿加速方向1k kx x +-作模式移动,令112,,:1,1k k k k y x x k k j δδ++=-==+=,返回Step3;否则,转Step7.Step7 检查是否满足终止准则.若k δε<,迭代终止,得问题(8.1.1)的近似最优解为k x ;否则,转Step8.Step8 缩短步长.若1k k x x +=,令1,:1k k k k δαδ+==+,返回Step2;否则,令11,,:1k k k k x x k k δδ++===+,返回Step2.定理8.2.1 设:n f R R →是具有一阶连续偏导数的凸函数,0n x R ∈,记0()f x α=,并且水平集(,)S f α有界.若{}k x 为由模式搜索法求解问题(8.1.1)产生的点列,则{}k x 必存在极限,且其任一极限点都是问题(8.1.1)的最优解.§8.3 旋转方向法算法8-3(旋转方向法)Step1 选取初始数据.选取初始点0x ,初始单位正交方向组12,,,n d d d (可取12,,,n d d d 为坐标轴方向12,,,n e e e ).给定初始步长(0)(0)(0)(0)12(,,,)T n δδδδ=,收缩因子(0,1)α∈,放大因子1β>,允许误差0ε>,令0k =.Step2 确定参考点.取参考点k y x =,并令,1k z x j ==.Step3 进行轴向探测.若()()()k j j f y d f y δ+<,令()()():,:k k k j j j j y y d δδβδ=+=,转Step4;否则,令()():k k j j δαδ=-,转Step4.Step4 检验探测次数.若j n <,令:1j j =+,返回Step3;否则,转Step5. Step5 判断探测是否结束.若()()f y f z <,令,1z y j ==,返回Step3;若()(),()()k f y f z f y f x =<,令1k x y +=,转Step6;若()()()k f y f z f x ==,转Step7.Step6 检查是否满足终止准则.若1k k x x ε+-<,迭代终止,1k x +为问题(8.1.1)的近似最优解;否则,转Step8.Step7 检验步长大小.若对一切()1,2,,,k j j n δε=<,迭代终止,k x 为问题(8.1.1)的近似最优解;否则,令,1z y j ==,返回Step3.Step8 进行轴向旋转.计算各轴向移动的步长的代数和:12,,,n λλλ,利用,0,,0.j j n j i i j i jd p d λλλ==⎧⎪=⎨≠⎪⎩∑ (8.3.1)11,1,, 2.j T j j i j j j jT i i i p j q q p p d j q p λ-==⎧⎪=⎨-≥⎪⎩∑ (8.3.2) ,1,2,,j j jq d j n q ==. (8.3.1)构造新的单位正交方向12,,,n d d d ,并令(1)(),,1,2,,,:1k k j j j j d d j n k k δδ+====+,返回Step2.§8.4 Powell 法算法8-4(Powell 法)Step1 选取初始数据.选取初始点0x ,n 个线性无关的初始搜索方向011,,,n d d d -,给定允许误差0ε>,令0k =.Step2 进行基本搜索.令0k y x =,依次沿011,,,n d d d -进行一维搜索.对一切1,2,,j n =,记11111()min ()j j j j j f y d f y d λλλ-----+=+,111j j j j y y d λ---=+.Step3 检查是否满足终止准则.取加速方向0n n d y y =-,若n d ε<,迭代终止,得n y 为问题的近似最优解;否则,转Step4.Step4 确定搜索方向.按1101()()max {()()}m m j j j n f y f y f y f y ++≤≤--=- (8.4.17)确定m ,若001()2()(2)2[()()]n n m m f y f y f y y f y f y +-+-<- (8.4.18)成立,转Step5;否则,转Step6.Step5 调整搜索方向.从点n y 出发沿方向n d 作一维搜索.求出n λ,使得()min ()n n n n n f y d f y d λλλ+=+.令1k n n n x y d λ+=+,再令1:,,1,,1j j d d j m m n +==+-,:1k k =+,返回Step2.Step6 不调整搜索方向.令1k n x y +=,:1k k =+,返回Step2.例2 用Powell 法求解问题(8.1.3):2212112min ()3f x x x x x x =+--,仍取初始点(0)(0,0)T x =,初始搜索方向组01(0,1),(1,0)T T d d ==,给定允许误差0.1ε=.解 第一次迭代:令(0)(0)(0,0)T y x ==,从点(0)y 出发沿0d 进行一维搜索,易得(1)(0)0000,(0,0)T y y d λλ==+=;接着从点(1)y 出发沿1d 进行一维搜索,得(2)(1)11133,(,0)22T y y d λλ==+=由此有加速方向(2)(0)23(,0)2T d y y =-=.因为23/2d ε=>,所以要确定调整方向.由于 (0)(1)(2)9()0,()0,()4f y f y f y ===-,按(8.4.17)式有(1)(2)()(1)()()max{()()|0,1}j j f y f y f y f y j +-=-=,因此1m =,并且()(1)(1)(2)9()()()()4m m f y f y f y f y +-=-=.又因(2)(0)(2)0f y y -=,故(8.4.18)式不成立.于是,不调整搜索方向组,并令(1)(2)3(,0)2T x y ==.第二次迭代:取(0)(1)3(,0)2T y x ==,从点(0)y 出发沿0d 作一维搜索,得(1)(0)000333,(,)424T y y d λλ==+=.接着从点(1)y 出发沿方向1d 作一维搜索,得(2)(1)1113153,(,)884Ty y d λλ==+=. 由此有加速方向(2)(0)233(,)84T d y y =-=.因为2d ε=>,所以要确定调整方向.因(0)(1)(2)945189(),(),()41664f y f y f y =-=-=-, 故按(8.4.17)式易知0m =,并且()(1)(0)(1)9()()()()16m m f y f y f y f y +-=-=. 由于(2)(0)45(2)16f y y -=-, 因此(8.4.18)式成立。
