合肥工业大学第一学期《高等数学》试卷A试题
合肥工业大学试卷参考答案(A卷)

又因 N 必须为 2 的整数幂 所以一个记录中的最少点数为 N=210=1024。 二. 简答题(共 40 分,10 分/题) 1. 采用 FFT 算法,可用快速卷积实现线性卷积。现欲计算两个长度分别为 N1 和 N2 的有限 长序列 x(n)、 h(n)的线性卷积 x(n)*h(n), 试写出该快速卷积算法的计算步骤 (注意说明点数) 。 M 1 将序列 x(n)、h(n) 补零至长度 N,其中:N≥N1+N2−1 且 N=2 (M 为整数) 答:○ ; 2 利用 FFT 算法分别计算序列 x(n)、h(n)的 N 点离散傅里叶变换 X(k)、H(k); ○ 3 计算频谱 X(k)、H(k)的乘积,即 ○
Y (k ) = X (k ) H (k )
4 计算 Y(k)的 IFFT 变换,则求得序列 x(n)、h(n)的 N 点线性卷积 x(n)*h(n),即 ○
x(n) ∗ h(n) = y (n) = IFFT [ X (k ) H (k )]
此快速卷积过程如图所示,图中,N≥N1+N2-1,且 N=2M(M 为整数) 。
−π
π
3. 试画出图示的两个有限长序列的六点循环卷积。
第 1 页 共 4 页
解:由循环卷积的定义,可知
6 x ( n) = [ x (( n)) ○ * x ((n )) ]R ( n) y (n) = x1 (n) ○ 2 1 6 2 6 6 * 3δ ((n − 3)) ]R ( n) = [ x1 ((n)) 6 ○ 6 6
第 3 页 共 4 页
∑
n =0
N −1
x (n) =
2
1 N
∑ X (k )
k =0
N −1
2
证:由 DFT 的定义,可知
合肥工业大学大一上学期高数期末考试题

咼数期末考试一、填空题(本大题有4小题,每小题4分,共16分)2.lim (1 + 3x)sinx =1. x -0_______________________________________.已知cosx是f(x)的一个原函数, 则2.xx兀2兀22兀 2 n — 1lim — (cos 2— + cos 2 ——+||| + cos 2兀)= 3. “世 n n n n ______________ .1 2 2x arcsin x 1 , dx 二2—1书1 一 X4. _ 运______________________ .二、单项选择题(本大题有4小题,每小题4分,共16分)设口(x) = —x, P (x)=3-3%'x ,则当 X T 1 时()5.1 x.(A)〉(x)与-(x)是同阶无穷小,但不是等价无穷小; (B )〉(x)与](x)是等价无穷小;(C (X)是比-(x)高阶的无穷小; (D ) -(x)是比〉(X)高阶的无穷小.6 设 f (x) = cos x( x + sin x ),则在 x = 0处有(A C) ■ (D ) f(x)不可导. x7.若F (x )二0( 2—x ) f( t ) dt ,其中f (x)在区间上(-1,1)二阶可导且f (x),则().(A) 函数F(x)必在x=0处取得极大值; (B) 函数F (x)必在x = 0处取得极小值; (C) 函数F(x)在x=0处没有极值,但点(0, F(0))为曲线y = F(x)的拐点;(D) 函数F(x)在x=0处没有极值,点(0,F(0))也不是曲线y 二F(x)的拐点。
1设f (x)是连续函数,且 f (x) = x + 2 j° f (t)dt ,贝U f (x)=((A ) 2解答题(本大题有5小题,每小题8分,共40分)10. 设函数厂y (x)由方程e x y-sin(xy)二1确定,求y (x)以及y (°).1 - x 78. 2—+2(B ) 2(C ) x 1 (D ) x 2.9.三求—dx.11.x(1 x )y(1) =14.求微分方程xy 2^xlnx满足9的解.四、解答题(本大题10分)15. 已知上半平面内一曲线 y 二y(x)(x 一0),过点(0,1),且曲线上任一点M&o ’y 。
安徽大学20-21第一学期高数A(一)期末考试A卷

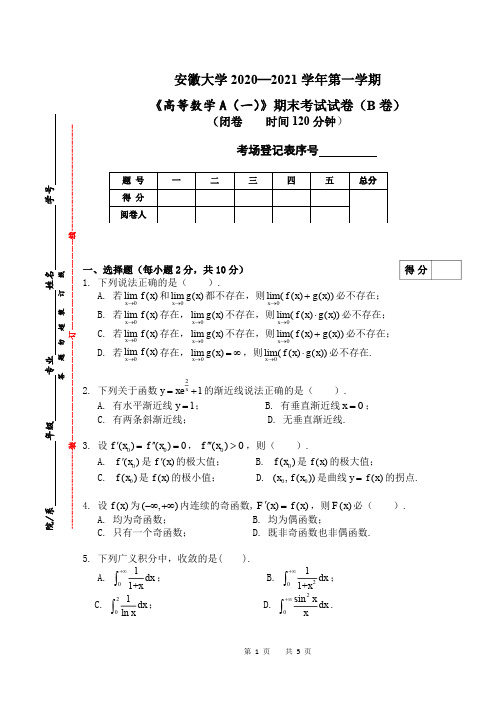
安徽大学2020—2021学年第一学期《高等数学A (一)》期末考试试卷(A 卷)(闭卷 时间120分钟)考场登记表序号一、选择题(每小题2分,共10分) 1. 下列说法正确的是( ).A. 若数列2{}nx 收敛,则数列{}n x 必收敛; B. 若数列{}n x 收敛,()f x 是(,)-∞+∞上单调有界函数,则{()}n f x 必收敛;C. 若数列{}n x 收敛于a ,数列{}n y 发散,则数列{}n n x y 必发散;D. 若数列{}n x 收敛于a ,则数列3{}n x 与数列31{}n x +均收敛于a .2. 下列关于函数2e 1xy x =-的渐近线说法正确的是( ).A. 有水平渐近线1y =;B. 有垂直渐近线1x =±;C. 有两条斜渐近线;D. 无垂直渐近线.3. 已知方程330x x k -+=有3个不同的实根,则k 的取值范围是( ). A. (,2)-∞-; B. (2,)+∞; C. (2,2)-; D. [2,2]-.4. 设函数()f x ,()g x 均在[0,1]上可导,且()()f x g x <,则必有( ). A. 11lim ()lim ()x x f x g x →→<; B. ()()f x g x ''<;C. 110()d ()d f x x g x x <⎰⎰; D.()d ()d f x x g x x <⎰⎰.5. 若()f x 为(,)-∞+∞上可导的偶函数,则()()d f x f x x '-=⎰( ).A . 21()2f x C -+; B .21()2f x C +; C .21()2f x C -+; D .21()2f x C +.院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分二、填空题(每小题2分,共10分)6. 极限sin lim sin n n nn n→∞+=- .7. 设22()||(1)x xf x x x +=-,则x = 是其可去间断点.8. 已知2()y f x =,2()arctan f x x '=,则1d d x yx == .9.函数 1()(2 (0)xf x t x =>⎰的单调增加区间为 .10. 星形线33cos ,(0)sin ,x a t a y a t ⎧=>⎨=⎩在t 从0到2π上的全长为 .三、计算题(每小题9分,共54分)11.求极限 (e1)lim xx x +-→.12.已知极限201xx →=,求a 和b .得分得分13.设()y y x =是由方程 y x y =确定的隐函数,求微分d y .14.计算.15. 计算 120ln(1+)d (2)x x x -⎰.答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------16. 计算 2 11d (1)x x x +∞+⎰.四、应用题(每小题8分,共16分)17. 求曲线2y x =上任一点处的曲率,并问哪一点处曲率最大?得分18. 设曲线xy a =,直线x a =,2 (0)x a a =>及0y =所围成的平面图形分别绕x 轴与y 轴旋转得到的旋转体体积分别记作x V 和y V ,问a 为何值时,x y V V =.五、证明题(每小题10分,共10分)19. 证明ln ln ()ln 2x yx x y y x y ++>+ (0,0,)x y x y >>≠.得分答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------。
合肥工业大学2014-2015第一学期《高等数学》试卷A试题

一、填空题(每小题3分,共15分) 1、极限2sin 0lim(13)x x x →+= .2、设2arctan()y x x =,则y ' . 3、设()f x 的一个原函数为2x e-,则()________xf x dx '=⎰.4、曲线xe y =过原点的切线方程为____________. 5、曲线2r eθ=从0=θ至2πθ=的一段弧长=l ____________.二、选择题(每小题3分,共15分) 1、当1x →-时,31x +与3(1)x +为()(A) 高阶无穷小 (B) 低阶无穷小(C) 等价无穷小 (D) 同阶但不等价无穷小2、若()f x 的导函数为sin ,x 则()f x 的一个原函数是( )(A) 1sin x + (B) 1sin x - (C) 1cos x + (D) 1cos x -3、设()f x 在0x =处连续,且0()lim 11cos x f x x→=-,则在点0x =处( ). (A) (0)f '不存在 (B) (0)0f '=,且(0)f 为()f x 的极小值 (C) (0)f '存在,且(0)0f '≠ (D) (0)0f '=,且(0)f 为()f x 的极大值4、下列广义积分发散的是( )(A)1+∞⎰(B)111sin dx x -⎰ (C)221ln dx x x+∞⎰(D) 2x xe dx +∞--∞⎰5、曲线2211x x e y e--+=-()(A) 没有渐近线 (B) 仅有水平渐近线 (C) 仅有铅直渐近线 (D) 既有水平渐近线又有铅直渐近线三、计算下列各题(每小题6分,共36分)1、222111lim ()2n n n n n n πππ→∞++++++L . 2、)cos 1)(1(1cossin 3lim 20x e x x x xx +---→. 3、求sin (0)xy xx =>的导数()y x '. 4、已知()2ln 1,arctan ,x t y t ⎧=+⎪⎨=⎪⎩求22d d ,d d y yx x . 5、2arctan x dx x ⎰. 6、设2ln(1)0()101x x f x x x +≥⎧⎪=⎨<⎪+⎩,求20(1)f x dx -⎰. 四、(本题满分10分)设 ()()22021cos , 0, 1, 0,1cos d , 0,xx x x f x x t t x x ⎧-<⎪⎪==⎨⎪⎪>⎩⎰ 讨论()f x 在0x =处的连续性和可导性.五、(本题满分10分)设曲线2xe y =,切线2ey x =及y 轴围成的平面图形为D ,求D 绕y 轴旋转一周所得旋转体体积V .六、(本题满分8分)证明不等式:0>x 时,有11ln ≥+xx . 七、(本题满分6分)设函数)(x f 在]1,0[上连续,在)1,0(内可导,0)(≠x f (01x <<),且0)1()0(==f f ,证明:在)1,0(内至少存在一点ξ,使()2015()f f ξξ'=.。
合肥工业大学第二学期《高等数学》试卷A试题

一、填空题(每小题3分,共15分)1、椭球面∑:222216x y z ++=在点0(2,2,2)P 处的切平面方程是___________. 2、设曲线L 的方程为221x y +=,则2[()]Lx y y ds +-=⎰.3、设()21,0,1,0,x f x x x ππ--<≤⎧=⎨+<≤⎩ 则其以2π为周期的傅里叶级数在点x π=处收敛于 .4、微分方程220y y y '''++=的通解为 .5、设23(,,)2f x y z x y z =++,则(1,1,1)grad f =u u u u u r.二、选择题(每小题3分,共15分) 1、设222zx y ze ++=,则11x y dz===( ))(A 2(dx dy)-+ )(B 22(z 1)e (z 1)e z zdx dy --+++)(C 22dx dy + )(D 22dx dy -+2、二次积分2(,)dx f x y dy ⎰化为极坐标下累次积分为( )drr F d D drr F d C drr F d B dr r F d A ),(2)(),()(),()(),()(cos 202cos 2022cos 20cos 200θθθθθθθθθπθππθππθπ⎰⎰⎰⎰⎰⎰⎰⎰--3、微分方程sin y y x x '''+=+的特解形式可设为( ).(A )*()sin cos y x ax b A x B x =+++ (B )*(sin cos )y ax b x A x B x =+++ (C )*(sin cos )y x ax b A x B x =+++ (D )*sin cos y ax b A x B x =+++ 4、直线1121410214x y z x y z -+-==-++=-与平面2的位置关系是( ) )(A l ∥π但l 不在π上 )(B l 在平面π上 )(C l ⊥π )(D l 与π斜交5、设曲面∑的方程为222,x y z z ++=,1∑为∑在第一卦限的部分,则下列结论不正确...的是( ).(A )0xdS ∑=⎰⎰ (B )0zdS ∑=⎰⎰(C )1224zdS z dS ∑∑=⎰⎰⎰⎰ (D )22x dS y dS ∑∑=⎰⎰⎰⎰三、(本题满分10分)设(,)sin xz f xy y y=+,其中f 具有二阶连续偏导数,求2,z z x x y ∂∂∂∂∂. 四、(本题满分12分)求22(,)2f x y x y =-+在椭圆域D :2214y x +≤上的最大值和最小值.五、(本题满分10分)计算二重积分:2D I y xd σ=-⎰⎰,其中:11,02D x y -≤≤≤≤.六、(本题满分12分)已知积分22(5())()xx Ly yef x dx e f x dy ---+⎰与路径无关,且6(0)5f =.求()f x ,并计算(2,3)22(1,0)(5())()x x I y ye f x dx e f x dy --=-+⎰.七、(本题满分12分)计算积分2232222()(2)xz dydz x y z dzdx xy y z dxdyI x y z ∑+-++=++⎰⎰,其中∑是上半球面z =,取上侧.八、(本题满分10分).求幂级数∑∞=---12112)1(n n n x n 的收敛域及和函数,并求数项级数∑∞=---1112)1(n n n 的和.九、(本题满分4分)设0(1,2,3,...)n u n ≠=,且lim1n nnu →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑是否收敛?如果是收敛的,是绝对收敛还是条件收敛?。
合肥工业大学第二学期《高等数学》试卷A试题

一、填空题(每小题3分,共15分) 1、椭球面∑:222216x y z ++=在点0(2,2,2)P 处的切平面方程是___________.2、设曲线L 的方程为221x y +=,则2[()]Lx y y ds +-=⎰ .3、设()21,0,1,0,x f x x x ππ--<≤⎧=⎨+<≤⎩则其以2π为周期的傅里叶级数在点x π=处收敛于 . 4、微分方程220y y y '''++=的通解为 . 5、设23(,,)2f x y z x y z =++,则(1,1,1)grad f = .二、选择题(每小题3分,共15分) 1、设222z x y ze ++=,则11x y dz ===( )2、二次积分20(,)dx f x y dy ⎰ 化为极坐标下累次积分为( )3、微分方程sin y y x x '''+=+的特解形式可设为( ).(A )*()sin cos y x ax b A x B x =+++ (B )*(sin cos )y ax b x A x B x =+++ (C )*(sin cos )y x ax b A x B x =+++ (D )*sin cos y ax b A x B x =+++ 4、直线1121410214x y z x y z -+-==-++=-与平面2的位置关系是( ))(A l ∥π但l 不在π上 )(B l 在平面π上 )(C l ⊥π )(D l 与π斜交5、设曲面∑的方程为222,x y z z ++=,1∑为∑在第一卦限的部分,则下列结论不正确...的是( ).(A )0xdS ∑=⎰⎰ (B )0zdS ∑=⎰⎰(C )1224z dS z dS ∑∑=⎰⎰⎰⎰ (D )22x dS y dS ∑∑=⎰⎰⎰⎰三、(本题满分10分)设(,)sin xz f xy y y =+,其中f 具有二阶连续偏导数,求2,z zx x y∂∂∂∂∂.四、(本题满分12分)求22(,)2f x y x y =-+在椭圆域D :2214y x +≤上的最大值和最小值.五、(本题满分10分)计算二重积分:2DI y x d σ=-⎰⎰,其中:11,02D x y -≤≤≤≤.六、(本题满分12分)已知积分22(5())(x xLy ye f x dx e f x ---+⎰与路径无关,且6(0)5f = .求()f x ,并计算(2,3)22(1,0)(5())()x x I y ye f x dx e f x dy--=-+⎰.七、(本题满分12分)计算积分2232222()(2)xz dydz x y z dzdx xy y z dxdy I x y z ∑+-++=++⎰⎰,其中∑是上半球面z =,取上侧.八、(本题满分10分).求幂级数∑∞=---12112)1(n nn x n 的收敛域及和函数,并求数项级数∑∞=---1112)1(n n n 的和.九、(本题满分4分)设0(1,2,3,...)n u n ≠=,且lim 1n nnu →∞=,则级数11111(1)()n n n n u u ∞+=+-+∑是否收敛如果是收敛的,是绝对收敛还是条件收敛。
合肥工业大学第一学期高等数学试卷A试题

合肥工业大学第一学期高等数学试卷A试题Happy childhood is the best, June 12, 2023一、填空题每小题3分,共15分 1、极限2sin 0lim(13)xx x →+= .2、设2arctan()y x x =,则y ' .3、设()f x 的一个原函数为2x e -,则()________xf x dx '=⎰. 4、曲线x e y =过原点的切线方程为____________. 5、曲线2r e θ=从0=θ至2πθ=的一段弧长=l ____________.二、选择题每小题3分,共15分 1、当1x →-时,31x +与3(1)x +为A 高阶无穷小B 低阶无穷小C 等价无穷小D 同阶但不等价无穷小2、若()f x 的导函数为sin ,x 则()f x 的一个原函数是 A 1sin x + B 1sin x - C 1cos x + D 1cos x -3、设()f x 在0x =处连续,且0()lim 11cos x f x x→=-,则在点0x =处 .A (0)f '不存在B (0)0f '=,且(0)f 为()f x 的极小值C (0)f '存在,且(0)0f '≠D (0)0f '=,且(0)f 为()f x 的极大值4、下列广义积分发散的是A 1+∞⎰111sin dx x -⎰ C 221ln dx x x +∞⎰ D 2x xe dx +∞--∞⎰ 5、曲线2211x x e y e--+=-A 没有渐近线B 仅有水平渐近线C 仅有铅直渐近线D 既有水平渐近线又有铅直渐近线三、计算下列各题每小题6分,共36分1、222111lim ()2n n n n n n πππ→∞++++++. 2、)cos 1)(1(1cossin 3lim 20x e x x x xx +---→. 3、求sin (0)xy xx =>的导数()y x '. 4、已知()2ln 1,arctan ,x t y t ⎧=+⎪⎨=⎪⎩求22d d ,d d y yx x .5、2arctan x dx x ⎰. 6、设2ln(1)0()101x x f x x x +≥⎧⎪=⎨<⎪+⎩,求2(1)f x dx -⎰.四、本题满分10分设 ()()22021cos , 0, 1, 0,1cos d , 0,xx x x f x x t t x x ⎧-<⎪⎪==⎨⎪⎪>⎩⎰ 讨论()f x 在0x =处的连续性和可导性.五、本题满分10分设曲线2x e y =,切线2ey x =及y 轴围成的平面图形为D ,求D 绕y 轴旋转一周所得旋转体体积V .六、本题满分8分证明不等式:0>x 时,有11ln ≥+xx . 七、本题满分6分设函数)(x f 在]1,0[上连续,在)1,0(内可导,0)(≠x f 01x <<,且0)1()0(==f f ,证明:在)1,0(内至少存在一点ξ,使()2015()f f ξξ'=.。
高等数学第一学期试题(附参考答案)

《高 等 数 学》课程试题一、填空题 .(每小题3分,共24分) 1. 设=+=)]([,1)(2x f f xx x f 则2. =→xx x 5sin 3sin lim 03. 设⎩⎨⎧≥+<=0,0,)(x x a x e x f x 在0=x 连续,则常数=a4. 曲线x y ln 2=上点(1, 0)处的切线方程为5.设参数方程⎩⎨⎧==ty t x sin 2,则=dxdy 6. 函数x x f 2arctan )(=,则=dy7. ⎰=)(cos x xd 8. ⎰-201dx x =二、选择题 .(每小题3分,共24分)1.设函数⎩⎨⎧<<-≥-+=10,11,42)(22x x x x x x f ,则)(lim 1x f x →等于( )A .-3B .-1C . 0D .不存在 2. 当)1ln(0x ,,x +→两个无穷小比较时是比x ( )A. 高阶的无穷小量B. 等价的无穷小量C. 非等价的同阶无穷小量D. 低阶的无穷小量3.设)(x f 的一个原函数为)1ln(+x x ,则下列等式成立的是( ) A .C x x dx x f ++=⎰)1ln()( B.C x x dx x f +'+=⎰]1ln([)(班级:姓名:学号:试题共页加白纸张密封线C.⎰+=+C x f dxx x )()1ln( D.C x f dx x x +='+⎰)(])1ln([ 4. 设函数)(x f y =在0x x =处可导,则必有( )A .0=∆y B. 0lim=∆→y xx C. dy y =∆ D. 0=dy 5.设)12)(1()(+-='x x x f ,则在)1,21(内,曲线)(x f 是( )A .单调增加且是凹的B .单调增加且是凸的C .单调减少且是凹的D .单调减少且是凸的 6.设)0(),1ln(≠+=a ax y ,则二阶导数y ''=( ) A .22)1(ax a+ B.2)1(ax a + C. 22)1(ax a+-D. 2)1(ax a+-7.积分=⎰-dx x1121( )A .是发散的 B. 2 C. -2 D . 0 8.设函数⎰-=Φ2)(xtdttex ,则其导数=Φ')(x ( )A .x xe - B. xxe--;C.232xex -D.232xex --三、求极限.(每小题5分,共10分) (1)3)21(lim +∞→+x x x(2)xx x x sin cos 1lim+-→四、求下列导数或微分. (每小题6分,共12分) (1)求由方程1ln =+y ye x确定的隐函数)(x f y =的导数dxdy ;(2)求函数xe y sin =在01.0,0=∆=x x 处的微分dy五、求下列积分.(每小题6分,共18分) (1) ⎰+dxeexx 21(2)⎰212ln exdx x(3)⎰20sin πdx x六、设x:,0求证(5分)>1>ex x+七、欲做一个长方体的带盖箱子,其体积为723m,而底面的长与宽成2:1的关系。
合工大高等数学A(上)习题册.

合⼯⼤⾼等数学A(上)习题册.习题1 函数的概念具有某种特性的函数1? 初等函数两个常⽤不等式1.设函数2,0(2,0,x x x f x x ,+≤?=?>?,求(1(1f ?,(0f ,(1f ;(2((0f x f x Δ?Δ,((0f xf x ?Δ?Δ(0x Δ>.2.已知1(f x x =(f x .3.证明:(2sin f x x =+x 在(,?∞+∞内是严格递增函数.4.设(f x 在[,上是奇函数,证明:若]a a ?(f x 在[0上递增,则,]a (f x 在[,上也递增. 0a ?]5.利⽤均值不等式证明:111(1(11n n n n ++<++(1,2,n = .6.求证:1(13n n +<(1,2,n = .习题数列的极限函数的极限极限的性质21?1. 求下列极限:1(23(1lim (23n nn n n ++→∞?+?+1;22111(2lim(1(1(123n n →∞2; 22(3lim[(1(1(1]nn r r r →∞+++ (1r <;(4lim x ;3131(5lim(11x x x →??++.2.求常数a和b,使得2lim1→=.3.若111 (1xxef x e+ = ?,求lim( xf x→,lim(xf x+→,lim(xf x→.习题⽆穷⼩、⽆穷⼤22?1.利⽤等价⽆穷⼩的代换求下列极限:0tan(2ln(1(1lim sin(3arctan(2x x x x x →?+?; 20(2lim sin x x →?;201cos(sin(3lim x x x →?..设ln(12,0(,10x x x f x x x +?>??=?≤23?1.计算下列极限:30tan sin (1lim x x x x →?;22sin(2(2lim 4x x x →??;2(3lim(x x x x →∞?;2221(4lim(1x xx x →∞+?.2.设110,x =1n x +=(1,2,3,n =,试证数列{}n x 的极限存在,并求此数列极限.习题连续函数及其性质24?1.求函数11(1x xf x e ?=?的间断点,并说明其类型.2.设221(lim 1nn n x f x x x →∞=+,试求函数(f x 的表达式,若有间断点,并说明其类型.3.设21cos ,0,(,0x x f x x a x x ?>?=??+≤?,要使(f x 在(,?∞+∞内连续,确定常数. a4.讨论sin ,0(1,0,1,0xx x f x x x x ,的连续性.5.求下列极限:0ln(1(1limx x xα→+(α为常数;sin sin (2limx a x a x a→??;0(3lim x xx e e xαβ→?(,αβ为常数.6.设函数(f x 在[]0,2π上连续,且(0(2f f π=,证明在[]0,π上⾄少存在⼀点ξ,使得((ff ξξπ=+.习题导数的概念31?1.求曲线1y x x =?在点13,22??处的切线⽅程与法线⽅程.2.若函数(f x 可导,求lim [((n abn f x f x n n →∞+?? (,0a b ≠.3.讨论函数(sin f x x =在点0x =处的连续性与可导性. 习题求导的运算法则32?1.求下列函数的导数:2(1ln 2lg 3log y x x =?+x ; (22(sin cos x y x x x =+; 21(31x y x ?=+;sec (41tan xy x =+;(5y =;21sin (6x y e =;2(7ln(2a y x =?+;(8arctan y =.2.设(f x 可导,求下列函数的导数:2(1(x y f x =;(2y =.3.设(f x 满⾜13(2(f x f x x +=,求(f x ′.4.已知2sin(y x =,求23,,dydy dydx dx dx .习题⾼阶导数33?1.设,求ln sec y x =y ′′′.2.设(f x g =,其中是⼆阶可导函数,试求g (f x ′′.3.设1y y xe =+,求220x d ydx =.4.求下列函数的阶导数n (n y :(1ax y e = (α为常数;21(232y x x =?+;2(3sin y x =.习题隐函数与参变量函数的求导⽅法34?1.求下列函数的导数dy dx :(1x y xy e += ;(2y xx y =.2.证明:双曲线2xy a =上任⼀点处的切线与两坐标轴围成的三⾓形的⾯积都等于. 22a3.设(,((,x f t y tf t f t ′=??′=??其中(f t ⼆阶可导,求22d ydx .4.设tan ,x y arc t ??=?=??求22d ydx .5.求曲线在对应于(10,10y x t t te y +?=??++=?0t =的点处的切线⽅程.习题微分中值定理41?1.证明:arctan arccot 2x x π+=.2.设函数(f x 在[],a b 上连续,在(内可导.证明:⾄少存在⼀点,使得,a b (,a bξ∈((((bf b af a f f b aξξξ?′=+?.3.若(f x 在[上⼆阶可导,且]3,a b 12(((f x f x f x ==,其中123a x x x b <<<<,证明:在(,内⾄少存在⼀点,使得a b c (0f c ′′=.习题洛必达(L′Hospital法则42?1.求下列极限:30sin (1lim x x xx →?;2ln (2lim ln x x xx x →+∞+;2011(3lim(tan x x x x →?;0ln(tan(4lim ln(tan x ax bx +→ ;(0,0a b >>11(5lim (x xx x a b →∞? ;(0,0a b >>20(6lim(2x x xx a b →+(0,0a b >>.2.若,(00f =(f x ′在点0x =的某邻域内连续,且(00f ′≠,试求(0lim f x x x +→.习题 Taylor 中值定理43?1.写出2(ln f x x =x 在处的四阶泰勒展开式.01x =2.写出(x f x xe ?=的阶麦克劳林公式.n习题函数的单调性与极值44?1.求函数(1((1x x x x x ??=?在内的极值.0x <<12.求函数((5f x x =?在[1上的最⼤值和最⼩值.,4]?3.过点引⼀条直线,使其在两坐标轴上的截距均为正,且它们之和为最⼩,求此直线⽅程. (1,4M4.在半径为R 的球内作⼀内接圆锥体,要使锥体体积最⼤,问其⾼、底半径应是多少?习题曲线的凹凸性及曲线的拐点45?1.讨论曲线21xy x x =+?的凹凸性及拐点.2.求过x y xe ?=上的极⼤值点和拐点的连线的中点,并垂直于0x =的直线⽅程.习题曲线整体形状的研究46?1.求曲线2211x x e y e ??+=?的⽔平与铅直渐近线.2.描绘函数222(1x y x =?的图形.习题导数在不等式证明中的应⽤47?1.证明:当02x π<<时,有sin tan 2x x x +>.2.设,,证明:.0a b >>1n >11((n n n n nb a b a b na a b3.设函数(f x 在[],a b 上连续,在(内⼆阶可导,若,a b ((0f a f b ′′==,则在内⾄少存在⼀点( ,a b ξ,使得2((((4b a f b f a f ξ?′′?≤.4.证明:当时,(正整数.0x ≥1(1n nx n x ≤1n 1n >习题定积分的概念与性质51?1.利⽤定积分的⼏何意义计算下列定积分:20(1xdx ∫;(2∫.2.⽐较下列积分的⼤⼩:21(1ln xdx ∫与221(ln x dx ∫;与.312(2x e dx ∫312x e dx ??∫3.设(f x 为连续函数,且20(2(f x x f x d =+∫x ,求(f x .习题微积分学基本公式52?1.求函数0(x x x xe dx ?Φ=∫的极值.2. 求下列极限:200cos (1lim x x t dt x →∫;21cos 20(2lim t x x e dt x ?→∫.3.设cos ,0,2(1,0,2x x f x x orx ππ?≤≤??=??<>??求函数0((x x f t dt Φ=∫在(,?∞+∞内的表达式.4.计算下列定积分:1(1∫x ;0(2π∫;(3设231(1x f x x ?=+,计算220(1(fx dx f x ′+∫.习题不定积分的概念与性质53?求下列不定积分:21.tan xdx ∫.4222.1x dx x +∫.2213.sin cos dx x x ?∫.1cos 4.1cos 2xdx x ??∫.习题换元积分法54?1. 求下列不定积分: (12x xe dx ?∫;(2;(3;(43;(5;(61(8x x dxe e ?+∫;(9(10;(11x;(12.2.计算下列定积分: 41(1∫;1 (2∫41(3(2f x d ?∫x ,其中2,0(1,101cos x xe x f x x x ??≥?=?,. ?< 3.证明:200sin 2sin n n xdx xdx ππ=∫∫.4.若(f x 为连续的偶函数,证明0(xf t dt ∫为奇函数.习题分部积分法55?1.求下列不定积分:(1;(2(xf x dx ′′∫(其中(f x ⼆阶可导; (3arctan x xdx ?∫;2.计算下列定积分:2130(1x x e dx ∫;10(2arctan xdx ∫;120(3∫.3.设sin xx 是(f x 的⼀个原函数,计算2 (xf x dx ππ′∫.习题有理函数的积分及应⽤。
合肥工业大学高数习题册上册答案详解

合肥工业大学 2011-2012学年第一学期高等数学习题册参考解答何先枝2011 .10――――――――――――――――――――――――――――――――――――――――――――― 习题11- 函数1.设函数2,0,()2,0,x x x f x x +≤⎧=⎨>⎩,求(1)(1)f -,(0)f ,(1)f ; (2)()(0)f x f x ∆-∆,()(0)f x f x-∆-∆(0x ∆>).【解】(1)2|2)1(,2|)2()0(,1|)2()1(101===+==+=-==-=x x x x f x f x f ;(2)()(0)f x f x ∆-∆⎪⎩⎪⎨⎧<∆>∆∆-=⎪⎩⎪⎨⎧<∆∆-∆+>∆∆-=∆∆.0,1,0,220,2)2(,0,22x x x x x x x x xx()(0)f x f x-∆-∆)0(12)2(>∆-=∆-∆-=x x x 。
■2.已知1()f x x=()f x .【解】令x t 1=,则2111)(t t t f ++=,故2111)(xx x f ++=。
■ 3.证明:()2sin f x x x =+在(,)-∞+∞内是严格递增函数. 【证】方法1(定义法)∵对任意2121),,(,x x x x <+∞-∞∈,有)s i n 2()s i n 2()()(112212x x x x x f x f +-+=-2sin 2cos2)(2sin sin )(21221121212xx x x x x x x x x -++-=-+-= 2)1(2)(22sin )1(2)(212121212xx x x x x x x -⋅-⋅+->-⋅-⋅+-≥012>-=x x ,其中用到)0(sin ,cos 1>≤≤-x x x x ,∴()2s i n f x x x =+在(,)-∞+∞内是严格递增函数。
合肥工业大学大一上学期高数期末考试题

高数期末考试一、填空题(本大题有4小题,每小题4分,共16分) 1. =+→xx x sin 20)31(lim .2.,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.3.lim(cos cos cos )→∞-+++=22221L n n nnn n ππππ .4. =-+⎰21212211arcsin -dx xx x .二、单项选择题 (本大题有4小题, 每小题4分, 共16分)5. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.6. )(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.7. 若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
(A )22x (B )222x +(C )1x - (D )2x +.三、解答题(本大题有5小题,每小题8分,共40分)8. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y . 9. 设函数)(xf 连续,=⎰10()()g x f xt dt,且→=0()lim x f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.10. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)11. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程. 五、解答题(本大题10分)12. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题(本大题有2小题,每小题4分,共8分)13. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.14. 设函数)(x f 在[]π,0上连续,且0)(0=⎰πx d x f ,0cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5. 6e . 6.c x x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 11.解:1033()x f x dx xe dx ---=+⎰⎰⎰12. 解:由(0)0f =,知(0)0g =。
《高等数学》2019-2020学年第一学期期末考试A卷

河海大学2019-2020学年第一学期期末考试《高等数学》试题(A)卷姓名:学号:班级:成绩:一、选择题(每题3分,共12分)1.若2,0,(),0x e x f x a x x ⎧<=⎨+>⎩为连续函数,则a 的值为().(A)1(B)2(C)3(D)-12.已知(3)2,f '=则0(3)(3)lim 2h f h f h→--的值为().(A)1(B)3(C)-1(D)123.定积分22ππ-⎰的值为().(A)0(B)-2(C)1(D)24.若()f x 在0x x =处不连续,则()f x 在该点处().(A)必不可导(B)一定可导(C)可能可导(D)必无极限二、填空题(每题3分,共12分)1.平面上过点(0,1),且在任意一点(,)x y 处的切线斜率为23x 的曲线方程为.2.1241(sin )x x x dx -+=⎰.3.201lim sinx x x→=.4.3223y x x =-的极大值为.三、计算题(每题6分,共42分)1.求2ln(15)lim.sin 3x x x x→+2.设2,1y x =+求.y '3.求不定积分2ln(1).x x dx +⎰4.求3(1),f x dx -⎰其中,1,()1cos 1, 1.x xx f x xe x ⎧≤⎪=+⎨⎪+>⎩5.设函数()y f x =由方程0cos 0yxte dt tdt +=⎰⎰所确定,求.dy 6.设2()sin ,f x dx x C =+⎰求(23).f x dx +⎰7.求极限3lim 1.2nn n →∞⎛⎫+ ⎪⎝⎭四、解答题(每题6分,共24分)1.设(ln )1,f x x '=+且(0)1,f =求().f x 2.求由曲线cos 22y x x ππ⎛⎫=-≤≤ ⎪⎝⎭与x 轴所围成图形绕着x 轴旋转一周所得旋转体的体积.3.求曲线3232419y x x x =-+-在拐点处的切线方程.4.求函数y x =+在[5,1]-上的最小值和最大值.五、证明题(10分)设()f x ''在区间[,]a b 上连续,证明:1()[()()]()()().22bbaab a f x dx f a f b x a x b f x dx -''=++--⎰⎰标准答案一、1B;2C;3D;4 A.二、131;y x =+22;330;40.三、1解原式25lim3x x x x →⋅=5分53=1分2解22ln ln ln(1),12xy x x ==-++ 2分2212[121xy x x '∴=-++4分3解原式221ln(1)(1)2x d x =++⎰3分222212[(1)ln(1)(1)]21x x x x dx x =++-+⋅+⎰2分2221[(1)ln(1)]2x x x C =++-+1分4解令1,x t -=则2分321()()f x dx f t dt-=⎰⎰1分1211(1)1cos t tdt e dtt -=+++⎰⎰1分210[]t e t =++1分21e e =-+1分5两边求导得cos 0,yey x '⋅+=2分cos yx y e '=- 1分cos sin 1x x =-1分cos sin 1xdy dxx ∴=-2分6解1(23)(23)(22)2f x dx f x d x +=++⎰⎰2分21sin(23)2x C =++4分7解原式=23323lim 12n n n ⋅→∞⎛⎫+ ⎪⎝⎭4分=32e2分四、1解令ln ,xt =则,()1,t t x e f t e '==+3分()(1)t f t e dt =+⎰=.t t e C ++2分(0)1,0,f C =∴= 2分().x f x x e ∴=+1分2解222cos x V xdx πππ-=⎰3分2202cos xdxππ=⎰2分2.2π=2分3解23624,66,y x x y x '''=-+=-1分令0,y ''=得 1.x =1分当1x -∞<<时,0;y ''<当1x <<+∞时,0,y ''>2分(1,3)∴为拐点,1分该点处的切线为321(1).y x =+-2分4解1y '=-=2分令0,y '=得3.4x=1分35(5)5 2.55,,(1)1,44y y y ⎛⎫-=-+≈-== ⎪⎝⎭2分∴最小值为(5)5y -=-+最大值为35.44y ⎛⎫= ⎪⎝⎭2分五、证明()()()()()()bbaax a x b f x x a x b df x '''--=--⎰⎰1分[()()()]()[2()bb a a x a x b f x f x x a b dx ''=----+⎰1分[2()()ba x ab df x =--+⎰1分{}[2()]()2()bba a x ab f x f x dx =--++⎰1分()[()()]2(),ba b a f a f b f x dx =--++⎰1分移项即得所证.1分。
大学第一学期高等数学期末考试A(含答案)打印

第一学期期末考试机电一体化专业《 高等数学 》 试卷( A )1.函数()314ln 2-+-=x x y 的定义域是(),2[]2,(∞+--∞Y )。
2.若函数52)1(2-+=+x x x f ,则=)1(f ( -5 )。
3.=→xx x 20lim ( 0 ) 4.函数xxx f -=)(的间断点是x =( 0 )。
5. 设735223-+-=x x x y 则y '=( 31062+-x x )。
1、设()00=f , 且()00='f 存在, 则()=→xx f x 0lim ( C );A. ()x f ' B. ()0f ' C. ()0f D. ()021f 2、17下列变量中是无穷小量的有 ( C ); A. )1ln(1lim0+→x x B. )1)((2()1)(1(lim 1-++-→x x x x x C. x x x 1cos 1lim ∞→ D. xx x 1sin cos lim 0→3、下列各组函数为同一函数的原函数的是 ( C );A. 31)(x x F =与324)(x x F -= B. 31)(x x F =与32214)(x x F -=C. C x x F +=21sin 21)(与x C x F 2cos 41)(2-=D.x x F ln )(1=与22ln )(x x F =4、在函数()x f 连续的条件下, 下列各式中正确的是 ( C );A. ()()x f dx x f dx d b a =⎰ B. ()()x f dx x f dx d ab =⎰C. ()()x f dt t f dx d x a =⎰ D. ()()x f dt t f dxd ax =⎰ 5、下列说法正确的是 ( D ); A. 导数不存在的点一定不是极值点 B. 驻点肯定是极值点 C. 导数不存在的点处切线一定不存在D. ()00='x f 是可微函数()x f 在0x 点处取得极值的必要条件1、函数的三要素为: 定义域, 对应法则与值域. (√ )2、函数)(x f 在区间[]b a ,上连续是)(x f 在区间[]b a ,上可积的充分条件。
合肥工业大学近两年高数上试卷

2014-2015试卷 一、填空题1、极限2sin 0lim(13)x x x →+=. 2、设2arctan()y x x =,则y ′ . 3、设()f x 的一个原函数为2x e−,则()________xf x dx ′=∫.4、曲线xe y =过原点的切线方程为____________. 5、曲线2r e θ=从0=θ至2πθ=的一段弧长=l ____________.二、选择题 1、当1x →−时,31x+与3(1)x +为()(A) 高阶无穷小 (B) 低阶无穷小(C) 等价无穷小 (D) 同阶但不等价无穷小2、若()f x 的导函数为sin ,x 则()f x 的一个原函数是( )(A) 1sin x + (B) 1sin x − (C) 1cos x + (D) 1cos x −3、设()f x 在0x =处连续,且0()lim11cos x f x x→=−,则在点0x =处( ). (A) (0)f ′不存在 (B) (0)0f ′=,且(0)f 为()f x 的极小值 (C) (0)f ′存在,且(0)0f ′≠ (D) (0)0f ′=,且(0)f 为()f x 的极大值4、下列广义积分发散的是( )(A)1∫(B)111sin dx x −∫ (C)221ln dx x x+∞∫(D) 2x xe dx +∞−−∞∫5、曲线2211x x e y e−−+=−()(A) 没有渐近线 (B) 仅有水平渐近线 (C) 仅有铅直渐近线 (D) 既有水平渐近线又有铅直渐近线三、计算下列各题(每小题6分,共36分)1、222111lim ()2n n n n n n πππ→∞++++++ . 2、)cos 1)(1(1cossin 3lim 20x e x x x xx +−−−→.3、求sin (0)xy xx =>的导数()y x ′.4、已知()2ln 1,arctan ,x t y t =+ = 求22d d ,d d y y x x .5、2arctan x dx x∫. 6、设2ln(1)0()101x x f x x x+≥= < + ,求20(1)f x dx −∫. 四、(本题满分10分)设 ()()22021cos , 0, 1, 0,1cos d , 0,xx x x f x x t t x x −<== > ∫ 讨论()f x 在0x =处的连续性和可导性.五、(本题满分10分)设曲线2xe y =,切线2ey x =及y 轴围成的平面图形为D ,求D 绕y 轴旋转一周所得旋转体体积V .六、(本题满分8分)证明不等式:0>x 时,有11ln ≥+xx . 七、(本题满分6分)设函数)(x f 在]1,0[上连续,在)1,0(内可导,0)(≠x f (01x <<),且0)1()0(==f f ,证明:在)1,0(内至少存在一点ξ,使()2015()f f ξξ′=2013-2014高数试卷一、填空题 1、极限0_________x →=.2、曲线221x xy y −+=在点(1,1)处的切线方程为 .3、设曲线()y f x =过点(0,0),且当x 在0x =处取得增量x ∆时相应的函数值增量3()(0)y x o x x ∆=∆+∆∆→,则2lim ()________n nf n→∞=.4、设连续函数()f x 满足1()2()d f x x f x x =,则1()d __________f x x =∫.5、积分121[ln(]_________x x −+=∫.二、选择题1、设lim n n x →∞与lim n n y →∞均不存在,那么下列命题正确的是( ).(A )若lim()n n n x y →∞+不存在,则lim()n n n x y →∞−必也不存在(B )若lim()n n n x y →∞+存在,则lim()n n n x y →∞−必也存在(C )lim()n n n x y →∞+与lim()n n n x y →∞−均不存在(D )lim()n n n x y →∞+与lim()n n n x y →∞−中只要有一个存在,另一个必定不存在2、已知0x =是函数ln()()sin a x f x x bx+=−的可去间断点,则常数,a b 的取值情况为( ).(A )1,a b =为任意实数 (B )1,b a =为任意实数 (C )1,a b ≠为任意实数 (D )=1,1a b ≠3、设21sin ,0()0,0,x x f x xx ≠= = 那么()f x 在0x =处( ). (A) 不连续 (B) 连续但不可导 (C) 可导但()f x ′不连续 (D) 可导且()f x ′也连续 4、极限22212lim()12n nn n n n→∞++⋅⋅⋅+=+++( ). (A) 14 (B) 13 (C) 12(D) 15、设2sin 1x +为)(x f 的一个原函数,则()d x f x x ′=∫( ).(A) 22cos x x C + (B) 2222cos sin x x x C −+ (C) 2222sin cos x x x C −+ (D) 222cos sin x x x C ++三、计算下列各题(每小题5分,共30分)1、011lim()ln(1)x x x →−+.2、设,0,(),0,x e x f x x x ≤= >求()21sin 0lim()d xxx f t t+−∞→∫.3、设y =d y 及y ′′.4、设()y y x =由220ln(1),d 1,1u t x te y u u =+ −= +∫确定,求1d d t y x =.5、x .6、设20sin ()d 1cos xt f x t t=+∫,求220()d 1()f x x f x π′+∫. 四、(本题满分8分)已知0x →时,22cos sin ()x x A Bx Cx o x +=+++,其中2()o x 是2x 的高阶无穷小,求常数,,A B C 的值.五、(本题满分10分)设2()1xf x x x =+−,(1)求函数()f x 的单调区间,(2)求函数()f x 的极值.六、(本题满分10分)如图所示1D 是由抛物线22y x x =−与直线(0)y kx k =>围成的图形,2D 是由曲线22y x x =−与直线y kx =及x 轴围成的图形,设1D 的面积为1S ,2D 的面积为2S ,若12:1:7S S =. (1)求常数k 的值;(2)求1D 绕x 轴旋转一周所得到的旋转体的体积x V 及2D 绕y 轴旋转一周所得到的旋转体的体积y V . 七、(本题满分6分)证明:0x ≠时,2cos 12x x >−.八、(本题满分6分)设()f x 在[]0,1上连续,在()0,1内可导,且1(0)(1)0,(0)()02f f f f ><.证明:(1)在()0,1内存在两个不同的点,ξη,使得()()0f f ξη==成立;(2)(0,1)ζ∃∈使得()()0f f ζζζ′−=成立。
安徽大学20-21第一学期高数A(一)期中试卷答案详解

安徽大学2020—2021学年第一学期《高等数学A (一)》期中考试试卷答案详解一、填空题(每小题2分,共10分)1.C2.B3.C4.A5.D 二、选择题(每小题2分,共10分)6.127.2y x e π=-+8.32-9.231t t +-10.2(21)t t e dt+三、计算题(每小题9分,共63分)11、(1)【证明】因为00>a ,由递推公式可知:0>n a而1191322n n n a a a +⎛⎫=+≥⋅= ⎪⎝⎭,所以n a 有下界为3;又1121911(11)122n n n n n a a a a a ++⎛⎫=+≤+=⇒≤ ⎪⎝⎭,所以n a 单调递减;由单调有界必有极限可知n n a ∞→lim 存在.5分(2)【解】令A a n n =∞→lim ,对1192n n n a a a +⎛⎫=+ ⎪⎝⎭两边取∞→n 的极限,即得:1932A A A A ⎛⎫=+⇒=± ⎪⎝⎭所以lim 3n n a →∞=9分12.【解】sin sin sin 00022(1)sin lim lim 11sin 22x x x x x x x x e e x x x x x x -→→→--==⋅⋅302116lim 132x x x x →==⋅9分13.【解】001(1)1lim lim 1(1)x x x x x x x x e xe xe x e e x x e →→⎛⎫+++--= ⎪--⎝⎭2200(1)13lim lim 2x x x xx x xe x e xe x e x x→→++-+==20353lim 22x x x x e xe x e →++==9分14.224424424400111111()1()cos 22!42!4!lim lim x x x x x o x x x o x e x x x -→→⎡⎤⎡⎤-+⋅+--++⎢⎥⎢⎥-⎣⎦⎣⎦=44401()112lim 12x x o x x →+==9分15.【解】在方程中令0x =可得(0)0y =;将方程两边对x 求导,得6620y e y y xy x ''+++=,(*)将0x =和(0)0y =代入,有(0)0y '=;4分将(*)式两边再对x 求导,得()212620y y e y e y y xy '''''++++=,将0x =,(0)0y =和(0)0y '=代入,有(0)2y ''=-9分16.【解】11arctan arctan dy d x x ϕ⎛⎫⎛⎫'=⋅ ⎪ ⎝⎭⎝⎭2111arctan 11d x x x ϕ⎛⎫⎛⎫'=⋅ ⎪ ⎪⎝⎭⎝⎭⎛⎫+ ⎪⎝⎭22111arctan 11dx x x x ϕ⎛⎫⎛⎫'=⋅⋅- ⎪ ⎪⎝⎭⎝⎭⎛⎫+ ⎪⎝⎭211arctan 1dx x x ϕ⎛⎫'=-⋅⋅ ⎪+⎝⎭9分17.【解】(1)0(1)11(2)1111()()()()()(1)2()()n n n n n n n n n f x C x a g x C n x a g x C n n x a g x --------=-+-++-- (1)11(2)1()()()()!()()n n n n n x a g x C n x a g x n x a g x ----=-+-++- (1)()0n f a -=11()()()()lim lim !()!()n n n x a x a f x f a f a n g x n g a x a --→→-===-9分四、综合分析题(每小题10分,共10分)18.120,0,1()arctan 1,0,x x f x e x x x >⎧⎪⎪=⎨⋅+⎪<⎪⎩4分1112220001arctan 1lim ()lim lim lim 044x t x x t t x x x e e t x f x x x eππ----=→+∞→→→⋅+====,0lim ()0x f x +→=,则0x =为第一类的可去间断点;12101arctan 1lim ()lim 2x x x e x f x x e π--→-→⋅+==,12101arctan 1lim ()lim 2x x x e x f x x eπ+-→-→⋅+==-,则1x =-为第二类的跳跃间断点.10分五、证明题(每小题7分,共7分)19.【证明】〖证明〗(1)(零点定理)构造辅助函数()()a F x f x a b =-+,因为()F x 在[0,1]上连续,(0)(0)0a a F f a b a b =-=-<++,而(1)(1)0a b F f a b a b =-=>++,由零点定理可得至少存在一点(0,1)c ∈,使得()0F c =,即()a f c a b=+3分(2)拉格朗日中值定理()f x 分别在[0,]c 和[,1]c 上应用拉格朗日中值定理,得()(0)()()f c f a f c a b c ξ-'==+,1(1)()()11()(1)a f f cb a b fc c a b c η--+'===--+-其中01c ξη<<<<于是有()()a b a b f f ξη+=+''.7分。
合肥工业大学高数习题册上册答案详解

ln(1 + 2 x) , x > 0, x 2.设 f ( x) = 确定正数 a 的值,使得 lim f ( x) 存在. x →0 a + x − a − x , −1 ≤ x < 0, x
= x2 − x1 > 0 ,其中用到 − 1 ≤ cos x, sin x ≤ x( x > 0) ,
∴ f ( x) = 2 x + sin x 在 (−∞, +∞) 内是严格递增函数。 方法 2(导数法) ∵ f ′( x) = 2 − cos x > 0(−∞ < x < +∞) ∴ f ( x) ∈↑ (−∞,+∞) 。■ 4.设 f ( x) 在 [− a, a ] 上是奇函数,证明:若 f ( x) 在 [0, a ] 上递增,则 f ( x) 在 [− a, 0] 上也递增.
(1) f (−1) , f (0) , f (1) ; (2 )
f (∆x) − f (0) f (−∆x) − f (0) , ( ∆x > 0 ) . ∆x ∆x
【解】 (1) f (−1) = (2 + x) | x = −1 = 1, f (0) = (2 + x) | x = 0 = 2, f (1) = 2 x | x =1 = 2 ;
n
2
2n
(1 − r 2 )(1 + r 2 )L(1 + r 2 ) 1− r2 = =L= , 1− r 1− r
合肥工业大学《高等数学》2018-2019学年第二学期试卷

合肥工业大学2018-2019学年第二学期《高等数学》期末试卷(A卷)答题时限:120 分钟考试形式:闭卷、笔试一、填空题(每小题3 分,共15 分)1. 直线⎩⎨⎧==+1zyx绕x轴旋转形成的旋转曲面方程为.2. 函数22z x y xy=+在点(1,1)处的最大方向导数为.3.设空间区域Ω为球体2221x y z++≤,则三重积分222()dx y z VΩ++=⎰⎰⎰.4. 设曲面∑的方程为z=d z S∑=⎰⎰.5. 2()dx tf x e t=⎰在区间(,)-∞+∞内关于x的幂级数展开式为.二、选择题(每小题3 分,共15 分)1.设(0,0)1,(0,0)2,(0,0)3x yf f f''===,l对x轴正向的逆时针方向转角为4π,则下列说法一定正确的是( ).(A)(,)f x y在(0,0)点连续,且lim(,)1xyf x y→→=(B)(,)f x y在(0,0)点可微,且(0,0)d(,)2d3df x y x y=+(C)(,)f x y在(0,0)点沿l方向的方向导数存在,且(0,0)52fl∂=∂(D)(,)f x y在(0,0)点不取极值2.设(,)f x y为连续函数,则121cos sind(cos,sin)df r r r rπθθθθθ+=⎰⎰( ).(A)100d(,)dx f x y y⎰(B)10d(,)dyy f x y x⎰(C)1d (,)d xx f x y y ⎰(D)11d (,)d xx f x y y -⎰3. 设:,[0,1]L y x x =∈,第一类曲线积分1=()d LI k y x s -⎰,22=()d LI y x s -⎰,其中k为常数,则12,I I 的大小关系为( ).(A)12I I <(B) 12I I > (C) 12I I =(D) 无法比较4. 设常数0λ>,则级数21sin (1)n n n n λ∞=+-∑是( ). (A)条件收敛 (B) 绝对收敛 (C) 发散 (D) 敛散性与常数λ有关5.设()f x 是周期2π的函数,且21,0,(),0,x x f x x x ππ+-≤<⎧=⎨≤<⎩()s x 为()f x 的傅里叶级数展开,则(5)s =( ).(A)2(52)π-(B)62π- (C)6 (D)25三、计算题( 本大题共6小题,共64分)1.设函数22u x y z =++,其中(),()y y x z z x ==由隐函数方程组20,ln 1y x x ye xz z ⎧+-=⎨+=⎩确定,求0d x u =。
安徽大学《高等数学》2020-2021第一学期期末试卷
安徽大学2020—2021学年第一学期《高等数学A (一)》期末考试试卷(B 卷)(闭卷 时间120分钟)考场登记表序号一、选择题(每小题2分,共10分) 1. 下列说法正确的是( ).A. 若0lim ()x f x →和0lim ()x g x →都不存在,则0lim(()())x f x g x →+必不存在;B. 若0lim ()x f x →存在,0lim ()x g x →不存在,则0lim(()())x f x g x →⋅必不存在;C. 若0lim ()x f x →存在,0lim ()x g x →不存在,则0lim(()())x f x g x →+必不存在;D. 若0lim ()x f x →存在,0lim ()x g x →=∞,则0lim(()())x f x g x →⋅必不存在.2. 下列关于函数2e 1xy x =+的渐近线说法正确的是( ).A. 有水平渐近线1y =;B. 有垂直渐近线0x =;C. 有两条斜渐近线;D. 无垂直渐近线.3. 设00()()0f x f x '''==,0()0f x '''>,则( ).A. 0()f x '是()f x '的极大值;B. 0()f x 是()f x 的极大值;C. 0()f x 是()f x 的极小值;D. 00(,())x f x 是曲线()y f x =的拐点.4. 设()f x 为(,)-∞+∞内连续的奇函数,()()F x f x '=,则()F x 必( ). A. 均为奇函数; B. 均为偶函数;C. 只有一个奇函数;D. 既非奇函数也非偶函数.5. 下列广义积分中,收敛的是( ).A. 0l d 1+x x +∞⎰;B. 201d 1+x x +∞⎰; C. 201d ln x x ⎰; D. 20sin d xx x+∞⎰.院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分二、填空题(每小题2分,共10分)6.极限n →∞= .7.=y 是x 的函数,则d y = .8. e sin x y x =的10阶导数为 .9. 已知3 ()e x f x x '=且(1)0f =,则()f x = .10. 光滑曲线由极坐标()r r θ= ([,])θαβ∈表示,其弧长计算公式s = .三、计算题(每小题9分,共54分)11.求极限 1lim 2nn n n →∞+⎛⎫⎪+⎝⎭.12.求极限3limx x →.得分得分13.设11xy x ⎛⎫=+ ⎪⎝⎭,求导数y '.14. 计算 4d 1xx -⎰.15. 计算 12 0ln d x x ⎰.答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------16. 计算4422(sin 4cos )d x x x x ππ-+⎰.四、应用题(每小题8分,共16分)17. 求曲线 2e ,e ,t tx y -⎧=⎨=⎩在0t =相应的点处的切线方程和法线方程.得分18. 求由曲线36y x x =-与直线2y x =所围成的平面图形的面积.五、证明题(每小题10分,共10分)19. 设()f x 在(,)-∞+∞内连续,且()0f x >.证明00()d ()()d xx tf t tF x f t t=⎰⎰在(0,)+∞内单调增加.得分答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------。
安徽大学11-12第一学期高数A(一)B(一)A卷答案(修)

安徽大学2011—2012学年第一学期 《高等数学A (一)、B(一)》(A 卷)考试试题参考答案及评分标准一、填空题(每小题2分,共10分)1.;2.62()xf x ;3. 2−;4. ;5.。
321x +二、单项选择题(每小题2分,共10分)6.D ; 7.C ; 8.D ; 9.C ; 10.B 。
三、计算题(每小题7分,共56分)11.≤≤,又1x x ==,故利用夹逼准则得到1x =。
12.解:01)arcsin limcos 1x x x →−−=0sin arcsin lim cos 1x x xx →−=220lim 22x x x →=−−。
13. 解:2ln sin sin xdx x∫=ln sin (cot )xd x −∫ =2 cotln sin cot x x x −+dx ∫ =2 cotln sin (csc 1)x x x −+dx −∫ = cotln sin cot x x x x −−−C +。
14. 解:由题意2222sin (sin )12sin 1sin x f x x x ′=−+−,故1()21f u u u′=−−。
于是1()(2)1f u u du c +u=−−∫=2ln 1u u C ,−−−+这样,当01x ≤<时,2()ln 1f x x x C =−−−+。
15.解:0,1x x ==均为瑕点,故1∫=12 0∫+ 1∫=12 0lim a a +→∫+ c 1lim c −→=0lim 2arcsin a +→1lim 2arcsin c −→=2arcsin1π=。
16.解: 0π∫=20cos π∫2cos ππ−∫x=2(sin )(sin )x x ππ−∫sin t x==1−∫∫t=21+∫==ln(1+。
17. 解:方程对应的齐次微分方程为32y y y 0′′′−+=,其特征方程为:232λλ−+=0,解得特征根为121, 2λλ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题(每小题3分,共15分) 1、极限2sin 0
lim(13)
x x x →+= .
2、设2
arctan()y x x =,则y ' . 3、设()f x 的一个原函数为2
x e
-,则()________xf x dx '=⎰
.
4、曲线x
e y =过原点的切线方程为____________. 5、曲线2r e
θ
=从0=θ至2
π
θ=
的一段弧长=l ____________.
二、选择题(每小题3分,共15分) 1、当1x →-时,3
1x +与3(1)x +为()
(A) 高阶无穷小 (B) 低阶无穷小
(C) 等价无穷小 (D) 同阶但不等价无穷小
2、若()f x 的导函数为sin ,x 则()f x 的一个原函数是( )
(A) 1sin x + (B) 1sin x - (C) 1cos x + (D) 1cos x -
3、设()f x 在0x =处连续,且0()
lim 11cos x f x x
→=-,则在点0x =处( )
. (A) (0)f '不存在 (B) (0)0f '=,且(0)f 为()f x 的极小值 (C) (0)f '存在,且(0)0f '≠ (D) (0)0f '=,且(0)f 为()f x 的极大值
4、下列广义积分发散的是( )
(A)
1
+∞
⎰
111sin dx x -⎰ (C) 221ln dx x x +∞⎰ (D) 2
x xe dx +∞--∞⎰ 5、曲线2
2
11x x e y e
--+=
-()
(A) 没有渐近线 (B) 仅有水平渐近线
(C) 仅有铅直渐近线 (D) 既有水平渐近线又有铅直渐近线
三、计算下列各题(每小题6分,共36分)
1、22
211
1lim (
)2n n n n n n ππ
π
→∞
++++++. 2、)cos 1)(1(1
cos
sin 3lim 20x e x x x x
x +---→. 3、求sin (0)x
y x
x =>的导数()y x '. 4、已知()2
ln 1,arctan ,
x t y t ⎧=+⎪⎨=⎪⎩求
22d d ,d d y y
x x . 5、2arctan x dx x ⎰. 6、设2ln(1)0()101x x f x x x +≥⎧⎪
=⎨<⎪+⎩,求20
(1)f x dx -⎰. 四、(本题满分10分)设 ()()220
2
1cos , 0, 1, 0,1cos d , 0,x
x x x f x x t t x x ⎧-<⎪⎪
==⎨⎪⎪>⎩⎰ 讨论()f x 在0x =处的连续性和可导性.
五、(本题满分10分)设曲线2
x
e y =,切线2
e
y x =及y 轴围成的平面图形为D ,求D 绕y 轴旋转一周所得旋转体体积V .
六、(本题满分8分)证明不等式:0>x 时,有11
ln ≥+
x
x . 七、(本题满分6分)设函数)(x f 在]1,0[上连续,在)1,0(内可导,0)(≠x f (01x <<),
且0)1()0(==f f ,
证明:在)1,0(内至少存在一点ξ,使()2015()f f ξξ'=.。
