SPSS探索性因子分析的过程
用SPSS做探索性因子分析
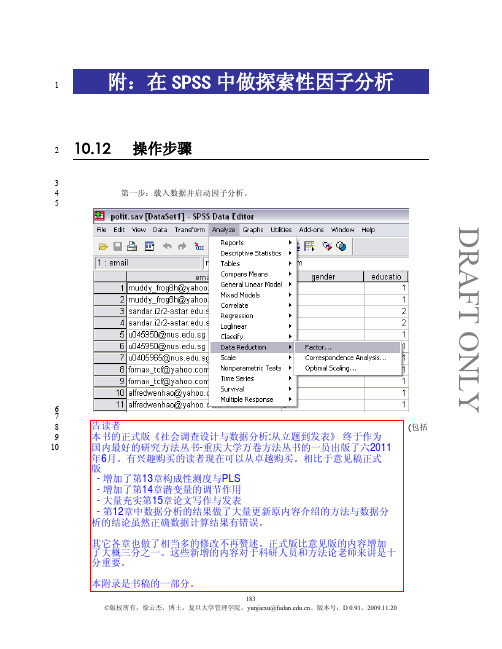
DRAFT ONLY附:在SPSS 中做探索性因子分析110.12操作步骤23 第一步:载入数据并启动因子分析。
4567 第二步:选择因子所对应的测度项。
在这个研究中,我们选择对应于七个变量(包括8 自变量、因变量、与控制变量) 的测度项。
910告读者丗本书的正式版丆《社会调查设计与数据分析:从立题到发表》丆 终于作为国内最好的研究方法丛书-重庆大学万卷方法丛书的一员出版了乮六2011年6月乯。
有兴趣购买的读者现在可以从卓越购买。
相比于意见稿丆正式版丗- 增加了第13章丆构成性测度与PLS•C - 增加了第14章丆潜变量的调节作用 - 大量充实第15章丆论文写作与发表- 第12章中数据分析的结果做了大量更新丆原内容介绍的方法与数据分析的结论虽然正确丆数据计算结果有错误。
其它各章也做了相当多的修改丆不再赘述。
正式版比意见版的内容增加了大概三分之一。
这些新增的内容对于科研人员和方法论老师来讲是十分重要。
本附录是书稿的一部分。
DRAFT ONLY12第三步:设定因子求解办法为主成分分析法。
使用相关系数矩阵,并设定主要因子的34特征根大于1。
5678第四步:设计因子旋转方法为“Varimax”。
然后在“Factor Analysis”窗口中按“ok”开始计算。
910DRAFT ONLY1210.13主成分分析的结果34 对应于27个测度项,主成分分析法一共产生了27个因子。
这是可以产生的因子个数5 的上限。
“Total ”列报告了每一个因子所对应的特征值。
“% of Variance ”表示这个特征6 值在所有特征值和中的比例。
“Extraction Sums of Squared Loadings ”这一列反映了特征根7 大于1的因子。
在这个例子中,我们顺利地得到了7个因子。
相应地,在用碎石坡法对因8 子进行目测时,我们得到的结果是一致的。
请读者参看本章中的相应图例。
值得一提的9 是,第八个因子的特征根为0.967,十分接近1。
SPSS探索性因子分析报告地过程

现要对远程学习者对教育技术资源和使用情况进行了解,设计一个李克特量表,如下图所示:问题题项从未使用很少使用有时使用经常使用总是使用1 2 3 4 5a1 电脑a2 录音磁带a3 录像带a4 网上资料a5 校园网或因特网a6 电子邮件a7 电子讨论网a8 CAI课件a9 视频会议a10 视听会议一.因子分析的定义在现实研究过程中,往往需要对所反映事物、现象从多个角度进行观测。
因此研究者往往设计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。
多变量大样本虽然会为我们的科学研究提供丰富的信息,但却增加了数据采集和处理的难度。
更重要的是许多变量之间存在一定的相关关系,导致了信息的重叠现象,从而增加了问题分析的复杂性。
因子分析是将现实生活中众多相关、重叠的信息进行合并和综合,将原始的多个变量和指标变成较少的几个综合变量和综合指标,以利于分析判定。
用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间彼此是不相关的,代表各类信息的综合指标成为因子。
因子分析就是用少数几个因子来描述许多指标之间的联系,以较少几个因子反应原资料的大部分信息的统计方法。
二.数学模型im im i i i i U F F F F Z +++++=αααα · · · 332211i Z 为第i 个变量的标准化分数;(标准分是一种由原始分推导出来的相对地位量数,它是用来说明原始分在所属的那批分数中的相对位置的。
)m F 为共同因子;m 为所有变量共同因子的数目;i U 为变量i Z 的唯一因素;im α为因子负荷。
(也叫因子载荷,统计意义就是第i 个变量与第m 个公共因子的相关系数,它反映了第i 个变量在第m 个公共因子上的相对重要性也就是第m 个共同因子对第i 个变量的解释程度。
)因子分析的理想情况,在于个别因子负荷im α不是很大就是很小,这样每个变量才能与较少的共同因子产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则i U 彼此间不能有关联存在。
使用SPSS进行探索式因素分析的教程

使用SPSS进行探索式因素分析的教程探索性因素分析是一种统计方法,用于确定一组变量之间的潜在结构。
SPSS是一种常用于数据分析的软件工具,它提供了强大的因素分析功能。
以下是一个使用SPSS进行探索性因素分析的简单教程,该教程可以帮助您了解如何使用SPSS来执行因素分析并对结果进行解释。
步骤1:导入数据步骤2:准备数据确保您的数据符合因素分析的前提条件。
确定您要进行因素分析的变量是否具有线性关系,并进行必要的数据转换(例如,对数转换)以满足这个条件。
步骤3:执行因素分析在SPSS的“分析”菜单下,选择“数据准备”和“因子”。
在弹出的对话框中,选择您要进行因素分析的变量并将其移动到“因子”框中。
选择“萃取方法”(如主成分分析或最大似然估计)并指定要提取的因素的数量。
您还可以选择执行因子旋转以获得更简单和解释性更强的因子结构。
步骤4:解读结果SPSS将生成一个因素分析的输出报告,其中包含多个表格和图形。
以下是一些常见的解读步骤:-总体解释:观察“总体解释”表,了解因子数量和提取方法的解释力度。
查看“因素”的特征值,了解提取的因子解释的总方差比例。
-因子负荷:查看“因子负荷”表,该表显示了原始变量与提取的因子之间的相关性。
较高的因子负荷表示原始变量与特定因子之间的较强关联。
-因子旋转:如果您选择了因子旋转,则查看“旋转因子载荷矩阵”表,该表显示了旋转后的因子负荷。
查看这些旋转后的因子负荷以确定是否存在更简单的因子结构。
-因子得分:根据选定的因子分析方法,可以生成每个观测值的因子得分。
这些得分表示了每个观测值在每个因子上的得分情况,可以用于后续的分析和解释。
步骤5:解释因子根据因子负荷和因子名称,解释每个因子代表的潜在结构。
结合领域知识和因子负荷,您可以确定每个因子是否与特定概念或潜在维度相关联。
步骤6:结果报告根据您的研究目的和需要,将因子分析的结果写入报告中。
确保清楚地描述因子数量、命名以及每个因子代表的结构或概念。
如何利用SPSS做因子分析等分析

如何利用SPSS做因子分析等分析SPSS是一款强大的统计分析软件,可以用于各种数据分析任务,包括因子分析。
因子分析是一种用于探究观测变量之间关系的统计方法,它可以帮助我们理解数据集中不同变量之间的相关性和结构。
下面是一个简要的关于如何利用SPSS进行因子分析的步骤:1.准备数据首先,需要确保将数据整理成适合因子分析的格式。
确保数据集中的变量是连续型变量,并且不存在缺失值。
如果存在缺失值,需要进行数据处理或进行数据填充。
2.导入数据打开SPSS软件,然后依次选择“File”、“Open”来导入数据文件。
选择正确的文件路径和文件名,然后点击“打开”按钮。
3.创建因子分析模型选择“Analyze”菜单下的“Dimension Reduction”子菜单,然后选择“Factor”。
将需要进行因子分析的变量移至右侧的“Variables”框中,然后点击“OK”按钮。
4.选择因子提取方法5.设置因子提取参数出现因子提取对话框后,可以选择提取的因子数目和提取标准。
默认情况下,SPSS会提取所有可能的因子。
也可以根据实际需要进行调整。
完成设置后,点击“Continue”按钮。
6.选择因子旋转方法因子旋转可帮助我们更好地理解因子结构。
在因子分析向导的旋转选项中,可以选择旋转方法,如正交旋转和斜交旋转等。
选择一个适合你的需求的旋转方法,然后点击“Rotation”按钮。
7.设置旋转参数出现旋转参数对话框后,可以选择旋转的方法和旋转的标准。
默认情况下,SPSS会选择最大方差法和标准负荷量,但你可以根据需要进行调整。
完成设置后,点击“Continue”按钮。
8.检查结果在因子分析向导的“Descriptives”选项中,可以查看因子提取和旋转后的结果。
这些结果包括因子载荷矩阵、公因子方差和解释方差等信息。
仔细检查结果,确保它们符合你的预期。
9.解释结果在进行因子分析后,需要解释因子载荷矩阵以及其他统计结果。
因子载荷矩阵可以告诉你每个变量与每个因子之间的关系。
如何利用SPSS进行因子分析(七)

因子分析是一种用于探索变量之间关系的统计方法。
在研究中,我们常常需要对大量的变量进行分析,以了解它们之间的关联性。
因子分析可以帮助我们发现变量之间的潜在结构,同时也可以帮助我们减少数据集中的复杂性。
在本文中,我们将探讨如何利用SPSS软件进行因子分析。
1. 数据准备在进行因子分析之前,首先需要准备好数据。
数据可以是定量的,也可以是定性的。
在SPSS中,我们可以通过导入Excel表格或者直接输入数据进行分析。
在导入数据之后,我们需要对数据进行清洗和筛选,确保数据的完整性和准确性。
2. 变量选择在因子分析中,我们需要选择适当的变量进行分析。
通常情况下,我们会选择相关性较高的变量进行分析,以便发现它们之间的潜在结构。
同时,我们也可以通过相关性分析或者变量筛选的方法来确定需要进行因子分析的变量。
3. 因子分析模型在SPSS中进行因子分析的时候,我们需要选择合适的因子分析模型。
通常情况下,我们可以选择主成分分析或者最大似然法进行因子分析。
在选择模型的时候,我们需要考虑数据的性质和研究的目的,以确保选择合适的模型进行分析。
4. 因子提取在进行因子分析的过程中,我们需要对因子进行提取。
在SPSS中,我们可以选择合适的提取方法,比如主成分法或者最大似然法。
在进行因子提取的时候,我们需要考虑提取的因子数目和因子的解释性,以便选择最合适的因子进行分析。
5. 因子旋转在因子分析中,我们通常会对因子进行旋转,以便更好地解释因子的结构。
在SPSS中,我们可以选择方差最大旋转或者极大似然旋转等方法进行因子旋转。
在进行因子旋转的时候,我们需要考虑因子的解释性和简单性,以便选择最合适的旋转方法。
6. 因子负荷在因子分析的结果中,我们通常会关注因子负荷。
因子负荷可以帮助我们理解变量和因子之间的关系,以及变量在因子上的权重。
在SPSS中,我们可以通过因子负荷矩阵和因子旋转后的因子负荷矩阵来进行观察和分析。
7. 结果解释在完成因子分析之后,我们需要对结果进行解释。
SPSS探索性因子分析的过程

SPSS探索性因子分析的过程探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,旨在帮助研究者理解和解释大量变量之间的关系。
它可以用于数据降维、信度分析和测量模型构建等多种研究目的。
以下是SPSS中进行探索性因子分析的详细步骤:1.数据准备:-打开SPSS软件,并导入数据文件。
-确保数据变量符合连续性或有序性测量标准。
如果存在分类变量,需要进行变量转换,如使用哑变量编码。
2.确定分析目的和因变量:-确定研究目的,明确是否要进行因子分析以及预期得到的结果。
-选择用于分析的变量,这些变量应当在理论上与研究目的相关,并且在实践中已经得到应用。
3.进行初始的探索性因子分析:-在「分析」菜单中选择「数据降维」,然后选择「因子」。
-从左侧的变量列表中选择需要进行因子分析的变量,将其添加到右侧的「因子分析」框中。
-在「提取」选项卡中,选择提取的因子数量。
通常,可以通过解释方差方法选择大于1的特征根值,或者根据理论确定因子数量。
-点击「列表」按钮,查看提取出的因子信息,包括特征根值、解释方差和因子载荷。
根据因子载荷大小判断变量与因子之间的关系。
4.进行旋转:-在「提取」选项卡中,点击「旋转」按钮。
- 在旋转选项卡中,选择旋转方法。
常用的旋转方法包括方差最大化(Varimax)、直角旋转(Orthogonal rotation)和斜交旋转(Oblique rotation)。
-点击「列表」按钮,查看旋转后的因子载荷。
选择合适的旋转结果,以使因子载荷更加清晰和解释性更好。
5.进行因子得分估计:-在主对话框中,点击「因子得分」选项卡。
-选择要估计的因子得分的方法。
可选择「最大似然估计」或「预测指标法」。
-点击「存储因子得分」复选框,以将因子得分保存到数据文件中。
-点击「OK」按钮进行分析。
6.结果解读:-分析结果包括提取的因子信息、旋转后的因子载荷、因子得分和信度分析等。
-根据因子载荷和理论知识,解释每个因子代表的潜在构念。
SPSS探索性因素分析之具体步骤探讨

SPSS探索性因素分析之具体步骤探讨探索性因素分析之具体步骤探讨文/哈工程大学应用心理学系曹国兴这主要针对的是预试问卷而言,也就是说在初试问卷经过了语义分析,专家讨论论证之后最终得出的问卷。
以下的经验是根据我编制职业承诺问卷的基础上总结而来,错误之处希望同行指教。
首先要说的是关于样本数量的问题。
按照统计学标准而言,一般样本数应为题目数的5-10倍。
由于我的题目为50,故样本至少为250个。
前期我计划发放样本数为6倍也就是300份,由于样本流失及废卷的原因,最终回收到有效问卷为256份,有效率为85.33%。
当然这是无法避免的。
下面我主要谈一下进行探索性分析的具体步骤:第一:比较明确的一步就是做一下关于各个项目的鉴别度(区分度)的分析。
在这个条件下会删除一部分不适合的题目。
删除程序为SPSS下的Analyze→Scale→ReliabilityAnalysis。
比较保险的的是从比较小的鉴别度一步一步删除,每次删一些较低的题目就看一下科隆巴赫系数的大小,直到满意为止。
当然也可以直接将低于0.3的题目删除。
注意的是删除的应为那些删除后科隆巴赫系数值提高的题目,如果删除后科隆巴赫系数值降低,这就需要重新考虑了。
结合语义分析取舍。
第二:在这种情况下一般而言,进行问卷设计之前所有的题目究竟是属于哪一个维度或者有几个维度应该有一定的假设,此时应该如下操作:(1)首先是反向题目的更改。
这方面需要注意的就是每次关闭文件的时候注意不要保存或者你将反向题目更改后的文件保存下来,一定要注明,因为如果你忘记了,就会混淆到底反向题目有没有修改过。
(2)也就是重点阶段。
顾名思义探索性因子分析就好比你是一个探险家在探索一块未知的领域,你不知道去哪一个方向才是正确的,也许你走了很长的路却与你所期望的目的地相反。
为避免在进行探索性因子分析的时候做无用功,我采用了如下的方法:在最大变异法和极大相等法两种正交旋转下分别对题目进行讨论。
SPSS探索性因子分析的过程

一.因子分析的定义在现实研究过程中,往往需要对所反映事物、现象从多个角度进行观测。
因此研究者往往设计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。
多变量大样本虽然会为我们的科学研究提供丰富的信息,但却增加了数据采集和处理的难度。
更重要的是许多变量之间存在一定的相关关系,导致了信息的重叠现象,从而增加了问题分析的复杂性。
因子分析是将现实生活中众多相关、重叠的信息进行合并和综合,将原始的多个变量和指标变成较少的几个综合变量和综合指标,以利于分析判定。
用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间彼此是不相关的,代表各类信息的综合指标成为因子。
因子分析就是用少数几个因子来描述许多指标之间的联系,以较少几个因子反应原资料的大部分信息的统计方法。
二.数学模型im im i i i i U F F F F Z +++++=αααα · · · 332211i Z 为第i 个变量的标准化分数;(标准分是一种由原始分推导出来的相对地位量数,它是用来说明原始分在所属的那批分数中的相对位置的。
)m F 为共同因子;m 为所有变量共同因子的数目;i U 为变量i Z 的唯一因素;im α为因子负荷。
(也叫因子载荷,统计意义就是第i 个变量与第m 个公共因子的相关系数,它反映了第i 个变量在第m 个公共因子上的相对重要性也就是第m 个共同因子对第i 个变量的解释程度。
)因子分析的理想情况,在于个别因子负荷im α不是很大就是很小,这样每个变量才能与较少的共同因子产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则i U 彼此间不能有关联存在。
所谓的因子负荷就是因子结构中原始变量与因子分析时抽取出共同因子的相关,即在各个因子变量不相关的情况下,因子负荷im α就是第i 个原有变量和第m 个因子变量间的相关系数,也就是i Z 在第m 个共同因子变量上的相对重要性,因此,im α绝对值越大则公共因子和原有变量关系越强。
spss因子分析的步骤 (精华!)

spss因子分析的步骤(精华!)spss因子分析可以帮助研究者揭示数据中潜在的结构或内在模式,因而它是一种有用的统计分析工具。
本文首先给出因子分析的定义以及它的目的,然后解释运用spss进行因子分析的步骤。
当一个研究者想要探索数据中潜在的结构时,他们可能会使用因子分析。
因子分析是一种运用统计方法来测量隐藏在数据集中的复杂关系的方法,它已被广泛应用在心理学、营销学、经济学等因素测量领域。
因子分析的主要目的是从测量变量中将相关性分解为潜在因素,潜在因子是隐藏在这些变量中的抽象概念,它们是一组高度相关的测量变量的等价表示,而这些变量反映着更大的概念。
第一步:准备数据首先,必须准备要使用的数据,数据必须是一组有关联的变量,其中每个变量的值都来自同一个样本。
数据必须被仔细检查以确保它们正确和完整。
第二步:查找因子使用SPSS查找因子,主要包括以下步骤:(1)打开SPSS,并选择需要处理的数据文件。
(2)在SPSS控制台上选择“分析”,然后选择“对实变量进行因子分析”。
(3)在新弹出的窗口中,选择要分析的变量,然后点击“继续”按钮。
(4)点击“计算”,SPSS将根据选定的变量计算因子。
第三步:确定因子在计算结果中,SPSS给出了一个变量贡献表,可以在这个表中确定哪些变量贡献最大的能量,选择最显著的变量作为因子。
然后点击“因子变量”,保存变量以及贡献最大的能量变量,最后点击“完成”来完成分析。
第四步:解释结果解释SPSS给出了一系列统计量来说明因子分析的结果,其中可以用来解释结果的主要统计量有:变量可被因子解释的比例(在标准因子分析中,这通常认为是75%-90%以上)、因子本身的贡献(因子得分解释的比例),因子分析综合评分(KMO综合得分)等。
如果希望加深对结果的理解,可以使用另一个特征以及其载荷来标记变量,以便更清楚地描述数据中潜在结构。
最后,研究者必须思考结果是否合理,以及这些结果是否意义重大,以便为因子分开获得有价值的结论。
SPSS探索性因子分析的过程

SPSS探索性因子分析的过程SPSS探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,旨在通过将大量的观测变量分解为较小的、相互关联的潜在因子,来帮助研究者理解潜在的数据结构和模式。
本文将介绍SPSS中进行探索性因子分析的过程,包括数据准备、模型设定、因子提取和解释因子。
一、数据准备在进行探索性因子分析之前,需要确保数据准备工作已经完成。
这包括了数据的清洗、缺失值的处理和变量的选择等。
清洗数据:删除不适用的或异常的数据,确保数据的一致性和可靠性。
处理缺失值:根据缺失数据的性质和缺失的模式,选择适当的处理方法,如删除带有缺失值的观测、替换缺失值(如均值填充)等。
选择变量:根据研究目的和理论基础,选择合适的变量进行因子分析。
二、模型设定在SPSS中,打开要进行因子分析的数据集,选择"数据"菜单下的"概要统计",然后选择"因子"。
选择因子旋转方法:因子旋转是为了使提取出的因子更易解释和理解。
常用的旋转方法有正交旋转(如Varimax旋转)和斜交旋转(如Oblimin旋转)等。
在进行因子旋转时,可以根据理论和实际情况选择适当的旋转方法。
三、因子提取在SPSS的因子分析过程中,需要进行因子提取来确定潜在因子的数量。
选择因子数:在进行因子提取时,需要预设潜在因子的数量。
根据Kaiser准则和Scree图等指标,确定因子的个数。
Kaiser准则建议保留特征值大于1的因子,Scree图则可通过图形分析法确定因子数。
执行因子分析:根据前面设定的方法和参数,执行因子分析。
根据提取出的因子载荷矩阵进行因子解释。
因子载荷矩阵反映了每个观测变量与每个因子之间的关系。
载荷值表示观测变量与因子之间的相关性,值越大表示相关性越大。
四、解释因子根据因子载荷矩阵来解释因子。
通过观察载荷矩阵,找出与每个因子高相关的观测变量(载荷值绝对值大于0.4),根据这些观测变量来解释因子的含义。
spssau因子分析全流程总结

spssau因子分析全流程总结下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!SPSSAU因子分析全流程深度解析SPSSAU,全称为“SPSS Assistance for University”,是一款基于SPSS的统计分析插件,它简化了复杂的统计过程,使得因子分析变得更加易操作。
SPSS探索性因子分析的过程

现要对长途进修者对教导技巧资本和应用情形进行懂得,设计一个李克特量表,如下图所示:一.因子剖析的界说在实际研讨进程中,往往须要对所反应事物.现象从多个角度进行不雅测.是以研讨者往往设计出多个不雅测变量,从多个变量收集大量数据以便进行剖析查找纪律.多变量大样本固然会为我们的科学研讨供给丰硕的信息,但却增长了数据收集和处理的难度.更重要的是很多变量之间消失必定的相干关系,导致了信息的重叠现象,从而增长了问题剖析的庞杂性.因子剖析是将实际生涯中浩瀚相干.重叠的信息进行归并和分解,将原始的多个变量和指标变成较少的几个分解变量和分解指标,以利于剖析剖断.用较少的分解指标剖析消失于各变量中的各类信息,而各分解指标之间彼此是不相干的,代表各类信息的分解指标成为因子.因子剖析就是用少数几个因子来描写很多指标之间的接洽,以较少几个因子反响原材料的大部分信息的统计办法.二.数学模子iZ 为第i 个变量的尺度化分数;(尺度分是一种由原始分推导出来的相对地位量数,它是用来解释原始分在所属的那批分数中的相对地位的.)mF 为配合因子;m 为所有变量配合因子的数量;iU 为变量i Z 的独一身分;α为因子负荷.(也叫因子载荷,统计意义就是第i个变量与第m个公共因子的相im干系数,它反应了第i个变量在第m个公共因子上的相对重要性也就是第m个配合因子对第i个变量的解释程度.)α不是很大就是很小,如许每个变量因子剖析的幻想情形,在于个体因子负荷im才干与较少的配合因子产生亲密接洽关系,假如想要以起码的配合身分数来解释变量间的关系程度,则i U彼此间不克不及有接洽关系消失.所谓的因子负荷就是因子构造华夏始变量与因子剖析时抽掏出配合因子的相干,α就是第i个原有变量和第m个因子即在各个因子变量不相干的情形下,因子负荷imα绝对变量间的相干系数,也就是i Z在第m个配合因子变量上的相对重要性,是以,im值越大则公共因子和原有变量关系越强.在因子剖析中有两个重要指针:一为“配合性”,二为“特点值”.所为配合性,也称变量配合度或者公共方差,就是每个变量在每个配合因子的负荷量的平方总和(一横列中所有因子负荷的的平方和),也就是个体变量可以被配合因子解释的变异量百分比,这个值是个体变量与配合因子间多元相干的平方.从配合性的大小可以断定这个原始变量与配合因子间的关系程度.假如大部分变量的配合度都高于0.8,则解释提掏出的配合因子已经根本反应了各原始变量80%以上的信息,仅有较少的信息丧掉,因子剖析后果较好.而各变量的独一身分就是1减掉落该变量配合性的值,就是原有变量不克不及被因子变量所能解释的部分.所谓特点值,是每个变量在某一配合因子的因子负荷的平方总和(一向行所有因子负荷的平方和),在因子剖析的的配合因子抽取中,特点值最大的配合因子会最先被抽取,其次是次大者,最后抽取的配合因子的特点值会最小,平日会接近于0.将每个配合因子的特点值除以总题数,为此配合因子可以解释的变异量,因子剖析的目标之一,即在身分构造的简略化,愿望以起码的配合因子能对总变异量做最大的解释,因而抽取的身分越少越好,但抽取的因子的累积变异量越大越好.三.SPSS中实现进程(一)录入数据(二)因子剖析“剖析”|“降维”|“因子剖析”选项卡,打开如图所示“因子剖析”对话框.从原变量量表中选择须要进行因子剖析的变量,然后单击箭头按钮将选中的变量选入“变量”列表中.“变量列表”的变量为要进行因子剖析的的目标变量,变量在区间或比率级别应当是定量变量.分类数据(如:性别等)不合适因子剖析.2.“描写按钮”:重要设定对原始变量的根本描写并对原始变量进行相干性剖析.选中“原始剖析成果”复选框,暗示因子剖析未转轴前之配合性.特点值.变异数百分等到累积百分比,这是一个中央成果,对主成分剖析来说,这些值是要进行剖析变量的相干或协方差矩阵的对角元素.KMO与Bartlett球形度磨练用来磨练适不合适用来做因子剖析.KMO磨练,磨练变量间的偏相干是否很小;巴特利特球形磨练,磨练相干阵是否是单位阵.KMO值越接近1越合适做因子剖析,巴特利特磨练的原假设设为相干矩阵为单位阵,假如Sig值谢绝原假设暗示变量间消失相干关系,是以合适做因子剖析.“抽取”按钮:重要设定提取公共因子的办法和公共因子的个数.办法:主成分剖析法.SPSS默认办法.该办法假定原变量是因子变量的线性组合,第一主成分有最大的方差,后续成分可解释的方差越来越少.这是应用最多的因子提取办法.剖析:相干性矩阵.暗示以相干性矩阵作为提取公共因子的根据,当剖析中应用不合的尺度测量变量时比较合适.输出:未扭转的因子解.显示未扭转时因子负荷量.特点值及配合性.碎石图.暗示输出与每个因子相接洽关系的特点值的图,该图用于肯定应保持的因子个数,平日该图显示大因子的峻峭斜率和残剩因子平缓的尾部之间明显的中止.按特点值大小分列,有助于肯定保存若干个因子.抽取:基于特点值.暗示抽取特点值超出指定值的所有因子,在“特点值大于”输入框中指定值,一般为1.4.扭转:用于设定因子扭转的办法.扭转的目标是为了简化构造,以帮忙解释因子SPSS默认不扭转.办法:最大方差法:是一种正交扭转办法,他使得对每个因子有高负载的变量的数量达到最小,并简化了因子的解释.输出:扭转解.该复选框只有在选择里扭转办法之后才干选择,对于正交扭转会显示已扭转的模式矩阵和因子变换矩阵.5.得分:用于对因子得分进行设置,即盘算因子得分.取默认值,单击持续按钮.6.选项:用于设定对变量缺掉值的处理和系数显示的格局.缺掉值:按列表消除个案.去除所有含缺掉值的个案后再进行剖析.系数显示格局:按大小分列.载荷系数按照数值的大小分列,并组成矩阵,使得在统一因子上具有较高载荷的变量的分列在一路,便于得到结论.(三)成果剖析1.KMO及Bartlett’磨练当KMO值愈大时,暗示变量间的配合因子愈多,愈合适进行因子剖析,根据专家不雅点,假如KMO的值小于0.5时,较不宜进行因子剖析,此处的KMO值为0.695,暗示合适因子剖析.此外Bartkett’s球形磨练的原假设为相干系数矩阵为单位阵,Sig值为0.000小于明显程度0.05,是以谢绝虚无假设,解释变量之间消失相干关系,合适做因子剖析.(Bartkett’s球形磨练的2 为234.438,自由度为45,达到明显,代表母群体的相干矩阵间有配合因子消失,合适进行因子剖析.)2.配合性,显示因子间的配合性成果.在主成分剖析中,有若干个原始变量便有若干个成分,所以配合性会等于1,没有独一身分.所以本成果中央一栏显示初试配合性都为1,则暗示抽取办法为主成分剖析法,最右一栏为题项的配合性.从该表可以得到,因子剖析的变量配合度都异常高,标明变量中的大部分信息均可以或许被因子所提取,解释因子剖析的成果是有用的. 3.整体解释的变异数--------扭转之前的数据.该表给出了因子进献率的成果,表中左侧部分为初始特点值,中央为提取主因子成果,右侧为扭转后的主因子成果.“合计”指因子的特点值,“方差的%”暗示该因子的特点值占总特点值百分比,“累积%”÷10=63.579%.个中自有前三个因子的特点值大于1,并且前三个因子的特点值之和占总特点值的89.366%,是以提取前三个因子作为主因子列于右边,这也是因子剖析时所抽出的公共因子数.因为特点值是由大到小分列,所以第一个公同因子的解释变异量平日是最大者,其次是第二个1.547,再是第三个1.032.扭转后的特点值为 4.389,3.137,1,411,解释变异量为43.885%,31.372%,14.108%,累积的解释变异量为43.885%,75.257%,89.366%.扭转后的特点值不合于转轴前的特点值.4.碎石图.特点值的碎石图.平日该图显示大因子的峻峭斜率和残剩因子平缓的尾部,之间有明显的中止.一般取主因子在异常峻峭的斜率上,而处在平缓斜率上的因子对变异的解释异常小.可以从此碎石图中看出,从第三个身分今后,坡线甚为平展,因而可以保存3个身分较为合适.5.成分矩阵:给出了未扭转的因子载荷.从该表中可以得到应用主成分剖析办法提取的三个因子的载荷量,个中因子负荷量小于0.1的未被显示,因子为了便利解释因子寄义,须要进行因子扭转.6.扭转成份矩阵:给出了扭转后的因子载荷值,个中扭转办法采取的是Kaiser尺度化的正交扭转法.经由过程因子扭转,各个因子有了比较明白的寄义.从图中可以看出:a1,a8,a6,a5,a4位因子1,a10,a9,a7为因子2,a3,a2为因子3.题项在其所属的因子层面次序是按照因子负荷量的高下分列的.7.成份转换矩阵:六.成果解释根据因子的特点值和扭转后的因子矩阵,采取了主成分剖析法抽掏出3个因子作为配合因子,并应用因子扭转办法中的最大方差法,按照从大到小的次序进行分列,使得变量与因子的关系豁然清楚明了,对其做如下表所示的因子剖析摘要表.。
使用SPSS软件进行因子分析和聚类分析的方法

使用SPSS软件进行因子分析和聚类分析的方法随着统计分析软件的进步,SPSS(Statistical Package for the Social Sciences)软件作为一款功能强大、易于使用的统计分析工具受到广泛欢迎。
它能援助探究人员进行各种统计分析,其中包括因子分析和聚类分析。
本文将介绍如何使用SPSS软件进行因子分析和聚类分析,并针对每个分析方法提供详尽步骤和操作示例。
一、因子分析因子分析是一种常用的统计方法,在数据维度缩减和相关变量结构分析方面具有广泛的应用。
以下是使用SPSS软件进行因子分析的步骤:1. 数据筹办起首,需要将原始数据导入SPSS软件中。
可以通过选择“文件”>“打开”>“数据”,然后选择合适的数据文件进行导入。
确保数据是以矩阵的形式存储,每个变量占据一列,每个观察单位占据一行。
2. 因子分析设置在SPSS软件中,选择“分析”>“数据筹办”>“特殊分析”>“因子”。
在弹出的对话框中,选择需要进行因子分析的变量,将它们挪动到“因子”框中。
然后,选择所需的因子提取方法(如主成分分析或因子分析),并指定所需的因子个数。
可以选择默认值,也可以依据实际需求进行调整。
3. 统计输出完成因子分析设置后,点击“确定”按钮开始分析。
SPSS软件将生成一个因子分析结果报告。
报告中将包含因子载荷矩阵、特征值、诠释的方差比例等统计指标。
通过这些指标,可以对变量和因子之间的干系、每个因子的诠释能力进行分析。
4. 结果解读对于因子载荷矩阵,可以依据因子载荷的大小来裁定变量与因子之间的干系。
一般来说,载荷肯定值大于0.3的变量与因子之间具有显著关联。
诠释的方差比例表示每个因子能够诠释变量总方差的比例,一般来说,越大越好。
在解读结果时,需要综合思量因子载荷和诠释的方差比例。
二、聚类分析聚类分析是一种用于数据分类的统计方法。
它依据观测值之间的相似性将数据对象分组到不同的类别中。
SPSS因子分析实验报告

SPSS因子分析实验报告一、实验目的本次实验旨在运用 SPSS 软件进行因子分析,以探索和简化数据结构,发现潜在的因子,并对变量之间的关系进行深入理解。
通过因子分析,我们希望能够提取主要的公共因子,解释数据中的大部分变异,为进一步的数据分析和决策提供有价值的信息。
二、实验数据来源本次实验所使用的数据来源于具体数据来源。
该数据集包含了具体变量描述等多个变量,共样本数量个观测值。
这些数据反映了数据所涉及的研究对象或领域的相关情况。
三、实验步骤1、数据预处理首先,对原始数据进行了初步的检查和清理。
检查了数据中是否存在缺失值,并对缺失值进行了适当的处理(如删除含缺失值的观测、用均值或中位数插补等)。
同时,对数据进行了标准化处理,以消除量纲的影响,使不同变量在相同的尺度上进行比较。
2、适用性检验在进行因子分析之前,需要对数据进行适用性检验,以确定数据是否适合进行因子分析。
常用的检验方法包括巴特利特球形检验(Bartlett's Test of Sphericity)和 KMO 检验(KaiserMeyerOlkin Measure of Sampling Adequacy)。
巴特利特球形检验的原假设是相关系数矩阵为单位矩阵,即变量之间相互独立。
如果检验结果显著(p 值小于 005),则拒绝原假设,表明变量之间存在相关性,适合进行因子分析。
KMO 检验用于评估变量之间的偏相关性。
KMO 值越接近 1,表明数据越适合进行因子分析;一般认为,KMO 值大于 06 时适合进行因子分析。
3、提取因子根据适用性检验的结果,确定可以进行因子分析后,使用主成分法(Principal Component Analysis)或主轴因子法(Principal Axis Factoring)等方法提取因子。
在提取因子时,需要确定提取因子的个数。
常用的确定因子个数的方法有特征值准则(Eigenvalue Criterion)和碎石图(Scree Plot)。
SPSS探索性因子分析过程

一.因子分析的定义在现实研究过程中,往往需要对所反映事物、现象从多个角度进行观测。
因此研究者往往设计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。
多变量大样本虽然会为我们的科学研究提供丰富的信息,但却增加了数据采集和处理的难度。
更重要的是许多变量之间存在一定的相关关系,导致了信息的重叠现象,从而增加了问题分析的复杂性。
因子分析是将现实生活中众多相关、重叠的信息进行合并和综合,将原始的多个变量和指标变成较少的几个综合变量和综合指标,以利于分析判定。
用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间彼此是不相关的,代表各类信息的综合指标成为因子。
因子分析就是用少数几个因子来描述许多指标之间的联系,以较少几个因子反应原资料的大部分信息的统计方法。
二.数学模型im im i i i i U F F F F Z +++++=αααα · · · 332211i Z 为第i 个变量的标准化分数;(标准分是一种由原始分推导出来的相对地位量数,它是用来说明原始分在所属的那批分数中的相对位置的。
)m F 为共同因子;m 为所有变量共同因子的数目;i U 为变量i Z 的唯一因素;im α为因子负荷。
(也叫因子载荷,统计意义就是第i 个变量与第m 个公共因子的相关系数,它反映了第i 个变量在第m 个公共因子上的相对重要性也就是第m 个共同因子对第i 个变量的解释程度。
)因子分析的理想情况,在于个别因子负荷im α不是很大就是很小,这样每个变量才能与较少的共同因子产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则i U 彼此间不能有关联存在。
所谓的因子负荷就是因子结构中原始变量与因子分析时抽取出共同因子的相关,即在各个因子变量不相关的情况下,因子负荷im α就是第i 个原有变量和第m 个因子变量间的相关系数,也就是i Z 在第m 个共同因子变量上的相绝对值越大则公共因子和原有变量关系越强。
如何利用SPSS进行因子分析(Ⅰ)

进行因子分析是一种常用的统计方法,用于探索变量之间的关系和潜在的结构。
SPSS(Statistical Package for the Social Sciences)是一款广泛使用的统计软件,能够帮助研究人员进行因子分析。
本文将介绍如何利用SPSS进行因子分析,包括数据准备、因子提取和旋转、解释因子结果等内容。
一、数据准备在进行因子分析之前,首先需要准备好数据。
在SPSS中,可以通过导入Excel文件或手动输入数据来创建数据集。
数据集应包含需要进行因子分析的变量,确保数据的完整性和准确性。
另外,需要对数据进行缺失值处理和异常值处理,以保证因子分析的结果准确性。
二、因子提取和旋转在SPSS中,进行因子分析的步骤包括因子提取和因子旋转。
因子提取是指从一组变量中提取出共同的因子,用于解释变量之间的共变性。
SPSS提供了常用的因子提取方法,如主成分分析和最大似然法。
用户可以根据自己的研究目的和数据特点选择合适的因子提取方法。
在进行因子提取后,通常需要对提取出的因子进行旋转,以便更好地解释因子结果。
SPSS提供了多种因子旋转方法,如方差最大旋转和极大似然估计旋转。
用户可以根据自己的需要选择合适的因子旋转方法,并对结果进行比较和解释。
三、解释因子结果在完成因子提取和旋转后,需要对因子结果进行解释。
SPSS可以输出因子载荷矩阵、因子旋转后的载荷矩阵和因子得分系数矩阵等结果,帮助用户进行因子结果的解释和分析。
用户可以根据因子载荷的大小和模式来解释提取出的因子,识别出潜在的结构和关系。
此外,用户还可以通过绘制因子图和因子得分图来更直观地展现因子结果。
SPSS提供了丰富的图表功能,可以帮助用户进行数据可视化和结果呈现。
用户可以根据需要选择合适的图表类型,并对图表进行美化和修改,使其更符合研究需求。
四、结果验证和应用在完成因子分析后,需要对结果进行验证和应用。
用户可以通过内部一致性检验、因子得分的解释和实际情境中的应用等方法,对因子分析结果进行验证和评估。
因子分析SPSS操作

因子分析SPSS操作因子分析是一种常用的统计方法,用于探索多个变量之间的潜在关系。
它能够帮助研究人员识别出变量之间的关联,从而提取出共同的因素。
SPSS软件是一种广泛使用的统计分析工具,提供了强大的因子分析功能。
下面将详细介绍如何在SPSS中进行因子分析。
首先,在SPSS中打开要进行因子分析的数据集。
确保数据集包含需要进行因子分析的变量。
接下来,选择"分析"菜单,然后选择"尺度",再选择"因子"。
这会打开"因子分析"对话框。
在"因子分析"对话框中,将需要进行因子分析的变量移动到右侧的框中,通过单击变量名称,再单击右侧的"箭头"按钮,将其添加到因子分析的变量列表中。
在"因子分析"对话框中,有几个选项需要设置。
首先是"提取方法",它决定了如何提取因子。
常用的方法有主成分分析和最大似然估计。
主成分分析通常用于连续变量,最大似然估计用于分类变量。
选择一个适当的方法。
其次,是选择"旋转方法",它决定了如何旋转因子。
常用的方法有方差最大化和直角旋转。
方差最大化旋转使得每个因子解释的变异最大化,直角旋转使得因子之间不相关。
根据研究目的选择一个合适的旋转方法。
最后,设置"因子的数目",它决定了最终提取几个因子。
通常,根据因子的方差解释度和解释的变量数目来决定提取几个因子。
可以尝试提取不同数目的因子,然后根据结果进行选择。
点击"确定"按钮后,SPSS会进行因子分析,并在输出窗口中显示结果。
输出结果包括因子的提取度、因子载荷矩阵、解释的方差比例等。
根据因子载荷矩阵可以判断变量与因子之间的关系。
载荷大于0.3或0.4的变量与因子有较强的关联。
可以根据载荷大小对因子进行命名,进一步解释因子所代表的潜在构念。
根据调查问卷,进行因子分析SPSS操作步骤

根据调查问卷,进行因子分析SPSS操作步骤1. 调查问卷数据准备首先,将所有参与者的调查问卷数据收集并整理成电子表格格式(如Excel)。
确保每个问题都有相应的变量标签,并且每个参与者的回答都在正确的列中。
2. 导入数据到SPSS打开SPSS软件,并选择导入数据选项。
选择你准备好的电子表格文件,并按照提示进行导入操作。
3. 数据清洗和预处理3.1 缺失数据处理检查数据中是否有缺失数据。
如果有缺失数据,可以选择删除或使用合适的填充方式(如平均值填充)进行处理。
3.2 数据标准化如果你的问卷包含了不同量表的问题(如1-5分和1-10分),需要对数据进行标准化,以便在因子分析中进行比较。
你可以使用SPSS的计算功能来进行标准化。
4. 进行因子分析4.1 选择因子分析方法根据你的研究目的和数据特点,选择合适的因子分析方法。
常用的因子分析方法包括主成分分析和最大似然估计。
4.2 设置因子提取的条件在进行因子提取之前,需要设置一些条件,如提取的因子数量和旋转方法。
根据你的研究目的和数据分布情况,选择适当的条件。
4.3 进行因子提取点击SPSS的因子分析功能,并根据之前设置的条件进行因子提取。
SPSS会生成提取后的因子载荷和共享方差解释比等结果。
4.4 因子旋转因子旋转可以帮助我们解释因子结构更清晰和简单。
根据需要选择合适的旋转方法,如方差最大旋转或直角旋转。
4.5 解释因子分析结果根据因子载荷和共享方差解释比等结果,解释因子分析的结果。
查看每个因子的载荷表,并根据载荷大小判断每个因子代表的含义。
5. 结果解读和报告根据因子分析的结果,进行结果解读和报告。
将主要结果和结论整理成文档,并添加合适的图表和表格来支持你的发现。
以上是根据调查问卷进行因子分析SPSS操作的步骤。
根据你的研究目的和数据特点,可以适当调整和修改这些步骤。
记得保存和备份你的数据和结果,以便日后参考。
SPSS探索性因子分析过程

SPSS探索性因子分析过程探索性因子分析是一种数据降维技术,用于发现潜在的结构和模式。
在SPSS中,进行探索性因子分析的过程可以分为以下几个步骤:数据准备、模型选择、变量解释、因子旋转和解释因子。
第一步:数据准备在进行因子分析之前,需要确保所使用的数据符合一些基本的前提条件,包括样本量的要求和变量的合理性。
通常来说,样本量应该可以支持因子分析的进行,一般要求至少有200个样本。
此外,变量之间应该具有一定的相关性,因为因子分析是通过变量之间的相关性来发现潜在的结构和模式。
因此,在进行因子分析之前,可以先进行相关性分析,衡量变量之间的相关性。
第二步:模型选择在SPSS中进行探索性因子分析时,有两种选择可供选择:主成分分析和最大似然法。
主成分分析假设观测数据是通过一组未知的线性组合来表达的,最大似然法假设观测数据是由多个潜在变量引起的。
对于主成分分析,变量之间的相关性是主要的判断因素,而对于最大似然法,变量之间的共变性是主要的判断因素。
根据数据的特点和研究目标,选择适合的模型。
第三步:变量解释在进行因子分析之前,可以先查看变量之间的相关矩阵,了解变量之间的关系。
对于相关系数大于0.3的变量,考虑将其纳入因子分析。
通常,相关系数较高的变量在因子分析中有更高的可解释性。
第四步:因子旋转在进行因子分析之后,需要进行因子旋转来使得提取的因子更易于解释。
旋转方法有很多种,包括方差最大旋转、极大似然法旋转和最小相关旋转等。
在SPSS中,可以选择适合的旋转方法,并查看旋转后的因子载荷矩阵和因子组合矩阵。
第五步:解释因子在进行因子分析之后,需要对提取的因子进行解释。
根据因子载荷矩阵和因子组合矩阵,可以确定每个因子所代表的特定视角或概念。
通常,因子载荷大于0.4的变量可以被视为该因子的组成部分。
根据解释的因子,可以为后续的研究和分析提供指导。
除了以上的基本步骤,还有一些其他的注意事项和技巧需要考虑。
例如,可以根据初始抽样方差解释率确定因子的数量,一般选择解释率大于等于50%的因子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S P S S探索性因子分析的
过程
Company Document number:WUUT-WUUY-WBBGB-BWYTT-1982GT
现要对远程学习者对教育技术资源和使用情况进行了解,设计一个李克特量表,如下图所示:
一.因子分析的定义
在现实研究过程中,往往需要对所反映事物、现象从多个角度进行观测。
因此研究者往往设计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。
多变量大样本虽然会为我们的科学研究提供丰富的信息,但却增加了数据采集和处理的难度。
更重要的是许多变量之间存在一定的相关关系,导致了信息的重叠现象,从而增加了问题分析的复杂性。
因子分析是将现实生活中众多相关、重叠的信息进行合并和综合,将原始的多个变量和指标变成较少的几个综合变量和综合指标,以利于分析判定。
用较少的综合指标分析存在于各变量中的各类信息,而各综合指标之间彼此是不相关的,代表各类信息的综合指标成为因子。
因子分析就是用少数几个因子来描述许多指标之间的联系,以较少几个因子反应原资料的大部分信息的统计方法。
二.数学模型
Z为第i个变量的标准化分数;(标准分是一种由原始分出来的,它是用来说明原始分i
在所属的那批分数中的相对位置的。
)
m F 为共同因子;
m 为所有变量共同因子的数目;
i U 为变量i Z 的唯一因素;
im α为因子负荷。
(也叫因子载荷,统计意义就是第i 个变量与第m 个公共因子的相关
系数,它反映了第i 个变量在第m 个公共因子上的相对重要性也就是第m 个共同因子对第i 个变量的解释程度。
)
因子分析的理想情况,在于个别因子负荷im α不是很大就是很小,这样每个变量才能与较少的共同因子产生密切关联,如果想要以最少的共同因素数来解释变量间的关系程度,则i U 彼此间不能有关联存在。
所谓的因子负荷就是因子结构中原始变量与因子分析时抽取出共同因子的相关,即在各个因子变量不相关的情况下,因子负荷im α就是第i 个原有变量和第m 个因子变量间的相关系数,也就是i Z 在第m 个共同因子变量上的相对重要性,因此,im α绝对值越大则公共因子和原有变量关系越强。
在因子分析中有两个重要指针:一为“共同性”,二为“特征值”。
所为共同性,也称变量共同度或者公共方差,就是每个变量在每个共同因子的负荷量的平方总和(一横列中所有因子负荷的的平方和),也就是个别变量可以被共同因子解释的变异量百分比,这个值是个别变量与共同因子间多元相关的平方。
从共同性的大小可以判断这个原始变量与共同因子间的关系程度。
如果大部分变量的共同度都高于,则说明提取出的共同因子已经基本反映了各原始变量80%以上的信息,仅有较少的信息丢失,因子分析效果较好。
而各变量的唯一因素就是1减掉该变量共同性的值,就是原有变量不能被因子变量所能解释的部分。
所谓特征值,是每个变量在某一共同因子的因子负荷的平方总和(一直行所有因子
负荷的平方和),在因子分析的的共同因子抽取中,特征值最大的共同因子会最先被抽取,其次是次大者,最后抽取的共同因子的特征值会最小,通常会接近于0。
将每个共同因子的特征值除以总题数,为此共同因子可以解释的变异量,因子分析的目的之一,即在因素结构的简单化,希望以最少的共同因子能对总变异量做最大的解释,因而抽取的因素越少越好,但抽取的因子的累积变异量越大越好。
三.SPSS中实现过程
(一)录入数据
(二)因子分析
1.在菜单栏中依次单击“分析”|“降维”|“因子分析”选项卡,打开如图所示“因子分析”对话框。
从原变量量表中选择需要进行因子分析的变量,然后单击箭头按钮将选中的变量选入“变量”列表中。
“变量列表”的变量为要进行因子分析的的目标变量,变量在区间或比率级别应该是定量变量。
分类数据(如:性别等)不适合因子分析。
2.“描述按钮”:主要设定对原始变量的基本描述并对原始变量进行相关性分析。
选中“原始分析结果”复选框,表示因子分析未转轴前之共同性、特征值、变异数百分比及累积百分比,这是一个中间结果,对主成分分析来说,这些值是要进行分析变量的相关或协方差矩阵的对角元素。
KMO与Bartlett球形度检验用来检验适不适合用来做因子分析。
KMO检验,检验变量间的偏相关是否很小;巴特利特球形检验,检验相关阵是否是单位阵。
KMO值越接近1越适合做因子分析,巴特利特检验的原假设设为相关矩阵为单位阵,如果Sig值拒绝原假设表示变量间存在相关关系,因此适合做因子分析。
3.单击“抽取”按钮:
主要设定提取公共因子的方法和公共因子的个数。
方法:主成分分析法。
SPSS默认方法。
该方法假定原变量是因子变量的线性组合,第一主成分有最大的方差,后续成分可解释的方差越来越少。
这是使用最多的因子提取方法。
分析:相关性矩阵。
表示以相关性矩阵作为提取公共因子的依据,当分析中使用不同的尺度测量变量时比较适合。
输出:未旋转的因子解。
显示未旋转时因子负荷量、特征值及共同性。
碎石图。
表示输出与每个因子相关联的特征值的图,该图用于确定应保持的因子个数,通常该图显示大因子的陡峭斜率和剩余因子平缓的尾部之间明显的中断。
按特征值大小排列,有助于确定保留多少个因子。
抽取:基于特征值。
表示抽取特征值超过指定值的所有因子,在“特征值大于”输入框中指定值,一般为1。
4.旋转:用于设定因子旋转的方法。
旋转的目的是为了简化结构,以帮助解释因子SPSS 默认不旋转。
方法:最大方差法:是一种正交旋转方法,他使得对每个因子有高负载的变量的数目达到最小,并简化了因子的解释。
输出:旋转解。
该复选框只有在选择里旋转方法之后才能选择,对于正交旋转会显示已旋转的模式矩阵和因子变换矩阵。
5.得分:用于对因子得分进行设置,即计算因子得分。
取默认值,单击继续按钮。
6.选项:用于设定对变量缺失值的处理和系数显示的格式。
缺失值:按列表排除个案。
去除所有含缺失值的个案后再进行分析。
系数显示格式:按大小排列。
载荷系数按照数值的大小排列,并构成矩阵,使得在同一
因子上具有较高载荷的变量的排列在一起,便于得到结论。
(三)结果分析
1.KMO及Bartlett’检验
当KMO值愈大时,表示变量间的共同因子愈多,愈适合进行因子分析,根据专家观点,如果KMO的值小于时,较不宜进行因子分析,此处的KMO值为,表示适合因子分析。
此外Bartkett’s球形检验的原假设为相关系数矩阵为单位阵,Sig值为小于显着水平,因此拒绝虚无假设,说明变量之间存在相关关系,适合做因子分析。
(Bartkett’s球形检验的2 为,自由度为45,达到显着,代表母群体的相关矩阵间有共同因子存在,适合进行因子分析。
)
2. 共同性,显示因子间的共同性结果。
在主成分分析中,有多少个原始变量便有多少个成分,所以共同性会等于1,没有唯一因素。
所以本结果中间一栏显示初试共同性都为1,则表示抽取方法为主成分分析法,最右一栏为题项的共同性。
从该表可以得到,因子分析的变量共同度都非常高,表明变量中的大部分信息均能够被因子所提取,说明因子分析的结果是有效的。
3.整体解释的变异数--------旋转之前的数据。
该表给出了因子贡献率的结果,表中左侧部分为初始特征值,中间为提取主因子结果,右侧为旋转后的主因子结果。
“合计”指因子的特征值,“方差的%”表示该因子的特征值占总特征值百分比,“累积%”表示累积的百分比。
左边10个成分因子的特征值总和等于10。
解释变异量为特征值除以题项数,如第一个特征值的解释变异量为÷10=%。
其中自有前三个因子的特征值大于1,并且前三个因子的特征值之和占总特征值的%,因此提取前三个因子作为主因子列于右边,这也是因子分析时所抽出的公共因子数。
由于特征值是由大到小排列,所以第一个公同因子的解释变异量通常是最大者,其次是第
二个,再是第三个。
旋转后的特征值为,,1,411,解释变异量为%,%,%,累积的解释变异量为%,%,%。
旋转后的特征值不同于转轴前的特征值。
4.碎石图。
特征值的碎石图。
通常该图显示大因子的陡峭斜率和剩余因子平缓的尾部,之间有明显的中断。
一般取主因子在非常陡峭的斜率上,而处在平缓斜率上的因子对变异的解释非常小。
可以从此碎石图中看出,从第三个因素以后,坡线甚为平坦,因而可以保留3个因素较为适宜。
5.成分矩阵:给出了未旋转的因子载荷。
从该表中可以得到利用主成分分析方法提取的三个因子的载荷量,其中因子负荷量小于的未被显示,因子为了方便解释因子含义,需要进行因子旋转。
6.旋转成份矩阵:给出了旋转后的因子载荷值,其中旋转方法采用的是Kaiser标准化的正交旋转法。
通过因子旋转,各个因子有了比较明确的含义。
从图中可以看出:a1,a8,a6,a5,a4位因子1,a10,a9,a7为因子2,a3,a2为因子3。
题项在其所属的因子层面顺序是按照因子负荷量的高低排列的。
7.成份转换矩阵:
六.结果说明
根据因子的特征值和旋转后的因子矩阵,采用了主成分分析法抽取出3个因子作为共同因子,并使用因子旋转方法中的最大方差法,按照从大到小的顺序进行排列,使得变量与因子的关系豁然明了,对其做如下表所示的因子分析摘要表。
