在数控车床上实现椭圆的粗、精加工
数控车床加工椭圆类零件的初步探讨

数控车床加工椭圆类零件的初步探讨摘要:本文以SIEMENS802S/C 数控系统为例,介绍在数控车床上加工椭圆类零件的多种方法。
采用圆弧逼近法—四心法,可以采用一般G指令加工出精度要求不高的椭圆形状;采用直线逼近法—参数编程,可以加工出精度要求高的椭圆形状。
关键词:数控车床车削椭圆类零件圆弧逼近法直线逼近法R参数在技工学校高级数控的培训课题中,椭圆类零件的加工是不可或缺的内容.椭圆的加工属于非圆曲线的特殊零件加工,相对比较复杂。
在数控车床上加工该类零件,我们一般采用逼近法:圆弧逼近法和直线逼近法.1、圆弧逼近法圆弧逼近法是采用多段圆弧逼近椭圆的加工方法,利用机械制图中绘制椭圆的近似画法(四心法),求得多段圆弧的切点和半径来加工椭圆。
在加工精度要求比较低的情况下可以考虑用此方法.(1)加工原理通过机械制图近似绘制椭圆的方法,画出椭圆。
椭圆是由四段圆弧组成的。
如图1所示。
①画出长轴AB与短轴CD,连接AC并在AC上截取AF,使其等于AO与CO之差CE。
②作AF的垂直平分线,使其分别交于AB和CD于O1点和O2点。
③分别以O1点和O2点为圆心,O1A和O2C为半径作出圆弧AG和CG,,该圆弧即为四分之一的椭圆。
④用同样的方法画出整个椭圆。
(2)计算组成椭圆的四段圆弧半径、切点坐标等数据.(3)编写加工程序只要计算出如O1、O2、G点坐标,O1A和O2C的半径数值等就很容易编写加工这四段圆弧的程序。
2、直线逼近法直线逼近法是采用多段直线逼近椭圆的加工方法,应用这种方法加工非圆曲线时,只要步距足够小,在工件上所形成的最大误差,就会小于所要求的最小误差,从而加工出标准的椭圆。
常用的直线逼近法,加工精度高.直线逼近法加工椭圆是通过参数编程来加工的,用数控车床的普通G代码指令是难以加工的。
参数编程指令适合抛物线、椭圆、双曲线等非圆曲线编程,还适合于图形相同,只是尺寸不同的系列零件编程,同样适用于工艺路径一样,只是位置数据不同的系列零件的编程。
在数控车床上实现椭圆的粗、精加工
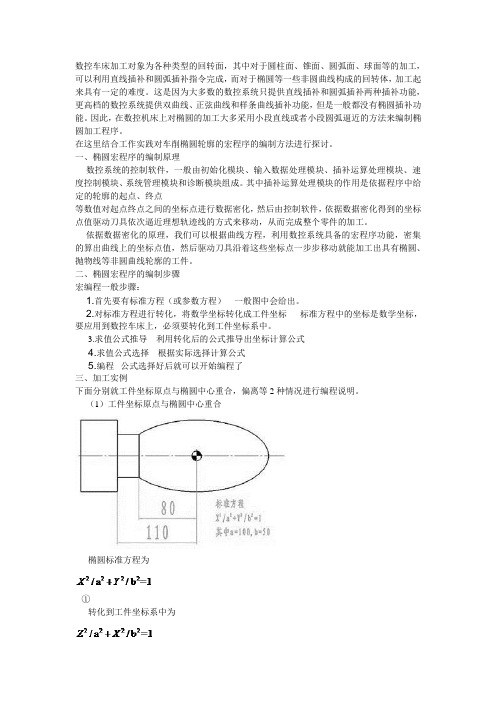
数控车床加工对象为各种类型的回转面,其中对于圆柱面、锥面、圆弧面、球面等的加工,可以利用直线插补和圆弧插补指令完成,而对于椭圆等一些非圆曲线构成的回转体,加工起来具有一定的难度。
这是因为大多数的数控系统只提供直线插补和圆弧插补两种插补功能,更高档的数控系统提供双曲线、正弦曲线和样条曲线插补功能,但是一般都没有椭圆插补功能。
因此,在数控机床上对椭圆的加工大多采用小段直线或者小段圆弧逼近的方法来编制椭圆加工程序。
在这里结合工作实践对车削椭圆轮廓的宏程序的编制方法进行探讨。
一、椭圆宏程序的编制原理数控系统的控制软件,一般由初始化模块、输入数据处理模块、插补运算处理模块、速度控制模块、系统管理模块和诊断模块组成。
其中插补运算处理模块的作用是依据程序中给定的轮廓的起点、终点等数值对起点终点之间的坐标点进行数据密化,然后由控制软件,依据数据密化得到的坐标点值驱动刀具依次逼近理想轨迹线的方式来移动,从而完成整个零件的加工。
依据数据密化的原理,我们可以根据曲线方程,利用数控系统具备的宏程序功能,密集的算出曲线上的坐标点值,然后驱动刀具沿着这些坐标点一步步移动就能加工出具有椭圆、抛物线等非圆曲线轮廓的工件。
二、椭圆宏程序的编制步骤宏编程一般步骤:1.首先要有标准方程(或参数方程)一般图中会给出。
2.对标准方程进行转化,将数学坐标转化成工件坐标标准方程中的坐标是数学坐标,要应用到数控车床上,必须要转化到工件坐标系中。
3.求值公式推导利用转化后的公式推导出坐标计算公式4.求值公式选择根据实际选择计算公式5.编程公式选择好后就可以开始编程了三、加工实例下面分别就工件坐标原点与椭圆中心重合,偏离等2种情况进行编程说明。
(1)工件坐标原点与椭圆中心重合椭圆标准方程为①转化到工件坐标系中为②根据以上公式我们可以推导出以下计算公式③④在这里我们取公式③。
凸椭圆取+号,凹椭圆取-号。
即X值根据Z值的变化而变化,公式④不能加工过象限椭圆,所以舍弃。
椭圆的数学模型建立及数控车削手工编程

CAD/CAM与制造业信息化60椭圆的数学模型建立及数控车削手工编程撰文/江苏省盐城市教育科学研究院 解太林椭圆属于非圆曲线,在数控车床加工中,非圆曲线工件的手工编程是比较复杂的,对编程者的数学基础要求较高。
文中主要以椭圆为例来介绍非圆曲线数学模型的建立与编程加工。
一、前言在数控车床加工中,非圆曲线工件的手工编程,要求编程者对数控原理非常熟悉,且要有一定的数学功底。
二、编程方法非圆曲线工件的手工编程,有两种方法,一是用圆弧逼近法或直线逼近法编程;二是用用户宏程序编程。
三、用圆弧逼近法或直线逼近法编程1.工件装夹如图1所示,在数控车床上直接用三爪卡盘装夹,为了方便对刀和编制程序,将程序原点设定在工件的右侧中心线上。
图1 椭圆2.数学模型工件右边部分为标准椭圆,长轴半径为20,短轴半径为14,所以标准方程为:Z 2/202+X 2/162=1在Z 轴上负向取点,通过椭圆方程计算出各点坐标如表所示。
3.参考程序(椭圆的精车程序)用车锥法粗车椭圆(程序略),用直线逼近法精车椭圆,程序如下。
O0001;N5 G90G97T0101;设定刀具号及刀具补偿号N10 M03 S1200; 设定转速及转向N15 G00X30Z5; 设定加工起点N20 X0;N25 G01X0Z0F0.1;精加工椭圆N30 X0.88Z-0.01;N35 X1.25Z-0.02;N40 X1.979Z-0.05;N45 X2.796Z-0.1;N50 X3.423Z-0.15;N55 X3.950Z-0.2;N60 X4.832Z-0.3;N65 X5.572Z-0.4;N70 X6.222Z-0.5;N75 X6.807Z-0.6;N80 X7.343Z-0.7;表 各点坐标N85 X7.84Z-0.8;N90 X8.305Z-0.9;N95 X8.743Z-1;N100 X9.55Z-1.2;N105 X10.29Z-1.4;N110 X10.974Z-1.6;N115 X11.610Z-1.8;N120 X12.205Z-2;N125 X13.805Z-2.6;N130 X14.750Z-3;N135 X15.617Z-3.4;N140 X16.225Z-3.7;N145 X16.8Z-4;N150 X17.695Z-4.5;N155 X18.520Z-5;N160 X19.285Z-5.5;N165 X19.996Z-6;N170 X20.659Z-6.5;N175 X21.278Z-7;N180 X21.857Z-7.5;N185 X22.4Z-8;N190 X22.908Z-8.5;N195 X23.385Z-9;N200 X23.831Z-9.5;N205 X24.249Z-10;N210 X24.640Z-10.5;N215 X25.005Z-11;N220 X25.662Z-12;N225 X26.229Z-13;N230 X26.710Z-14;N235 X27.111Z-15;N240 X27.434Z-16;N245 X27.683Z-17;N250 X27.860Z-18;N255 X27.965Z-19N260 X28Z-20;N265 X27.860Z-22;N270 X27.683Z-23;N275 X27.434Z-24;N280 X27.111Z-25;N285 X26.710Z-26;N290 X26.229Z-27;N295 X25.662Z-28;N300 X25.005Z29;N305 X24.640Z-29.5;N310 X24.249Z-30;N315 Z-31;N320 G00X30;N325 X100Z100; 快速回到换刀点N330 M05; 转速停止N335 M30; 程序结束返回程序号四、用用户宏程序编程1.以Z坐标作为变量(1)工件装夹。
数控车削加工椭圆的粗车方法

( 山学 院 , 唐 唐山 0 3 2 ) 6 0 0
Ro g u nn t o n n me ia t e u e lp e ma hn n u h t r ig me h d o u r la h s d i el s c i ig c l n i
+ c ) () 1
R- 2
( ) 算半 径 R = C 2计 0,
三 角形 M AO 中
图 1椭圆的近似画法 图2 C D作图 A
。 , A = c- , A 争 争A c x A cF O ±
=
() 中心线 A 1画 B和 C D分 别 等 于椭 圆 长轴 尺 寸 和短 轴 尺 寸
2 和 2 ;2连接 A 在 A 0 b() C, C线上取点 F, C = 0 C ;3作 使 FA 一 O () ,垂直平分线交 O A于 0 点 ,其延长交 C 。 D延长线与 0 点 ; : () 0 为圆点 0 1 4以  ̄ 为半径画弧 , 以 0 为圆点 以 0C为半径 再 。 。
3 圆弧代 替 椭 圆 的坐标 值得 确定 用
3 1 绘 图 法 .用
利用 C D软件 按 照 1 1 比例 ,. 1 的精 度 绘 图 , A :的 0 0 mm 0 然
★来稿 日期:0 0 0 - 0 2 1- 6 2
() 3 计算 G点 Z坐 标 , v一 E Z= G
c = c [ E =
机 械 设 计 与 制 造
1 68
文章 编 号 :0 13 9 ( 0 )4 0 6 - 2 10 — 9 7 2 1 0 — 180 1
M a h n r De in c iey sg
&
M a u a t r n fcue
数控车椭圆加工

以是一个常数; #k—被操作的第二变量,也可以
是一个常数。
B类宏程序格式为:
• (1) 非模态调用(或单一调用G65)
• G65 P(程序号)L(自变量赋值);
• 式中:P——指定宏程序号;
•
L——重复调用次数(1~9999,调用1次时L可
#2=13;椭圆的短半轴’#2=b
#3=15;椭圆的起点距椭圆中心的Z向距离---#3=z
N10#4= #2*SQRT[#1*#1 -#3*#3]/#1
;椭圆X半径变量#4=x
坐标系变换
x2 a2
y2 b2
1
z2 a2
x2 b2
1
x2
1
z2 a2
*b2
xb* 1a z2 2 b* a2z2/a
代入变量:#1=a,#2=b,#3=z,#4=x,
#3=#3-0.5
;z向变量递减(逐段)
IF [#3GE-10.34]GOTO10 ;Z向变量的判断, 椭圆轨迹的 终点 与椭圆的坐标系的距离
G02X26Z-36R12 G01Z-50
椭圆中心距编 程原点z向距离
…..
椭圆终点距离椭圆
坐标系z向距离,
左+右—
方程的推导:
#1=20 ;椭圆的长半轴;#1=a
Z-12.144 #1=20 #2=15 #3=12.86 N15#4=#2*SQRT[#1*#1-#3*#3]/#1 G01X[2*#4]Z[#3-25] #3=#3-0.5 IF[#3GE=0]GOTO15 N20G01G40X42
#1=40 #2=21 #3=31.41 N15#4=#2*SQRT[# 1*#1-#3*#3]/#1 G01X[2*#4]Z[#3-54] #3=#3-0.5 IF[#3GE4.68]GOTO 15
数控车床加工椭圆的宏程序

数控车床加工椭圆的宏程序随着数控技术不断进步,数控车床加工中各种复杂形面也日渐增多,如椭圆、抛物线、正弦曲线、余弦曲线、双曲线等各种非圆曲面。
对于上述各种复杂成形面,利用CAM软件进行自动编程相对简单,但由于种种原因,在绝大多数情况下数控车床主要还是依靠手工编程。
椭圆轴线与数控车床Z轴重合的情形相对比较简单,其解决方案也多见于各类文献,但在本例中椭圆轴线与数控车床Z轴呈一定夹角,编程和加工难度陡增,主要原因如下:①机床数控系统本身既不存在加工椭圆等非圆曲线的G指令,更没有类似G68这样的旋转指令,使编程难度大大增加。
②加工中变量的参数直接影响着加工的效率以及质量,很容易产生过切报警,即使程序正确无误,实际加工时的参数调整也非常困难,直接影响着加工能否顺利进行,以及加工精度能否保证。
总而言之,目前尚未见有表述类似实例的文章。
本实例进行了有益的尝试和探索,给出了切实可行的解决方案,为类似问题提供了难得的参考及借鉴。
椭圆宏程序的编制如下。
1.椭圆方程宏程序主要利用各种数学公式进行运算加工,因此编制旋转椭圆程序操作者必须要掌握椭圆方程和旋转公式等各种数学公式的计算方法并加以灵活运用。
椭圆方程有两种形式,分别是椭圆的标准方程和参数方程。
椭圆标准方程:椭圆参数方程:其中a、b分别为X、Z所对应的椭圆半轴。
2.旋转公式由于数控车床并不像加工中心那样存在着旋转指令,所以要利用旋转公式来进行椭圆的旋转。
旋转公式的定义:如图1所示,平面上绕点O旋转,使平面上任意一对对应点P和P′与一个定点O连接的线段都相等,即OP=OP′,且角∠POP′等于角θ,点O称为旋转中心,角θ称为旋转角。
旋转公式:如图1所示,取直角坐标系,以原点O为旋转中心,旋转角为θ,平面上任意一点P(x,z)旋转到P′(x′,z′),令∠XOP=α,则∠XOP′=α+θ,且OP=OP′。
于是X′=OPx′=|OP′|cos(α+θ)=|OP′|(cosα×cosθ-sinα×sinθ)=|OP|cosα×cosθ-|OP|sinα×sinθ=OPxcosθ-PxPsinθ=xcosθ-zsinθ同理Z′=xsinθ+zcosθ车床旋转公式为其中,X′、Z′为旋转后的坐标,X、Z为旋转之前的坐标值,θ为旋转角度。
椭圆宏程序在数控车床加工的方法

椭圆宏程序在数控车床加工的方法椭圆宏程序的基本原理是利用圆的特性来实现椭圆形的加工。
椭圆是一种圆的特殊形式,其变形是通过改变加工过程中的切削刀具的移动轨迹来实现的。
椭圆宏程序通过数学计算和编程实现刀具的移动轨迹变化,从而实现椭圆形的加工。
1.定义椭圆的参数:椭圆的形状可以通过两个半径参数来定义,分别为长半径和短半径。
这些参数可以根据零件的要求进行调整。
2.计算椭圆的切削路径:通过数学计算,可以确定刀具在加工过程中的移动轨迹。
这个轨迹是一个连续而光滑的曲线,可以通过数学公式或计算机模拟来得到。
3.编写椭圆宏程序:根据计算所得的切削路径,编写相应的宏程序。
宏程序是一种特殊的程序,可以在数控机床上执行。
它包含了一系列指令,用于控制刀具的移动、切削深度等参数。
4.设定加工参数:在执行宏程序之前,需要将一些重要的加工参数进行设定。
这些参数包括切削速度、进给速度、切削深度等。
它们的选择需要根据材料的性质和要求进行调整。
5.执行宏程序:当所有参数设置完成后,就可以执行宏程序了。
数控机床会按照宏程序中定义的指令和轨迹来进行切削,从而实现椭圆形的加工。
椭圆宏程序的优点是可以高效地制造复杂形状的椭圆零件。
相比于传统的手工加工或其他编程方法,椭圆宏程序的精度更高,生产效率更高。
此外,它还具有良好的可编程性和易于调整的特点,可以适应不同类型的椭圆加工需求。
总结起来,椭圆宏程序是一种用于数控车床加工的方法,通过定义椭圆参数、计算切削路径、编写宏程序以及设定加工参数等步骤来实现椭圆形的加工。
它能够提高零件的精度和质量,提高生产效率,适用于制造复杂形状的椭圆零件。
数控车床上椭圆的编程加工

国家职业资格全省统一鉴定数控车工技师论文(国家职业资格二级)论文题目:数控车床上椭圆的编程加工姓名:身份证号:所在省市:数控车床上椭圆的编程加工摘 要:要掌握椭圆的编程方法必须先理解椭圆的数学模型即方程式,在此基础上理解数控车床加工曲线的实质,然后利用宏程序来找到椭圆上各点的坐标值,依次加工出连续的各点,若椭圆的中心发生了平移则只需视具体情况对各点的坐标值进行统一的调整,就解决了椭圆的编程问题。
关键词:数控加工 椭圆 方程 宏程序椭圆曲线是一种复杂的二次曲线,一般只适合在数控机床上加工,而且椭圆曲线的编程也是比较复杂的。
然而,无论是何种曲线,都是坐标点按照曲线方程连续移动形成的,也就是点动成线。
而构成曲线的点有无数,不可能将每个点都找到,只能根据精度要求选择适合的间隔找出一些点,把它们连接起来,近似地表达曲线了。
这也是数控加工中编程计算复杂曲线坐标点的一个基本思路。
对于椭圆这类二次曲线的编程现在主要使用手工编程和自动编程。
在手工编程时椭圆上各点坐标值计算非常麻烦,编程也复杂。
我们就会用到宏程序来简化编程。
一、椭圆的基本方程图1所示椭圆长半轴a 、短半轴b 。
则椭圆方程为:12222=+by a x在数控车床上根据工件坐标系的建立方法,我们将X 轴转变为Z 轴,将Y 轴转变为X 轴,就将数学模型和编程的工件坐标系建立了联系。
如图2所示椭圆方程改变为:12222=+bx a z 。
若在上述方程中已知椭圆上某点P 的X 坐标值为1X ,则通过上述方程可计算出该点的Z 坐标值,即2211bXa a Z -⨯=。
因此对椭圆上的任意点只要知道X 或Z 坐标中的一个值就可以通过方程计算出另一个值,所以椭圆上各点的坐标都可以要求出来。
二、数控车床加工曲线轮廓的机理在数控车床加工时,刀具的运动轨迹是折线,而不是光滑的曲线,只能沿折线轨迹逼近所要加工的曲线运动。
实际上是以脉冲当量为最小位移单位通过X 、Z 轴交替插补进行的,由于脉冲当量很小,所以加工表面仍有较好的质量及表面光洁度,所以我们将椭圆分为足够多的小段直线来加工,关键只要找出椭圆上各点的坐标值,问题就解决了。
GSK980TD数控系统宏程序粗精车加工椭圆实例

宏程序粗精车椭圆以上是车削好的实物图加工图加工椭圆的宏程序如下(椭圆长半轴为40mm, 短半轴为24mm.)O0143 (O0143)G99 G96 M3 S150 T0101G50 S850G0 X52.0 Z41.0 (定位到工件端面1mm处)#1=38.496 (变量设定)N1 #3=0 (角度变量设定为0.)N2 #5=2*(24*SIN#3) (短半轴计算坐标尺寸)#5=#5+#1 (把X0.0偏移到38.496处)#6=40*COS#3 (长半轴计算坐标尺寸)#7=#6G1 X#5 Z#7 F0.32 (椭圆切削)#3=#3+5 (角度变量每次加5度)IF(#3LE120)GOTO2(如果条件达不到120度重头开始,达到120度执行下面程序)G2 U8.44 W-3.11 R3.26 F0.2 (切削R3.26)G0 X55.0 Z45.0X#1G1 Z40.0 F0.2#1=#1-3.8 (38.496每次减3.8mm)IF(#1GE0.496)GOTO1 (如果条件达不到0.496mm重头开始,达到0.496mm执行下面程序)G0 X200.0 Z100.0 (以上是粗车椭圆)T0101 (以下是精车椭圆)G0 X0.0 Z42.0G1 Z40.0 F0.2#8=0N4 #10=2*(24*SIN#8)#12=40*COS#8G1 X#10 Z#12 F0.32#8=#8+0.215IF(#8LE120)GOTO4G2 U8.44 W-3.11 R3.26 F0.2G0 X200 Z100M30(注:对刀零点是以椭圆中心为零点)此程序适用于GSK980TDa, GSK980TDb系统版本。
如想用于GSK980TD系统版本的,只要把变量(例如#1等)改成G65 H_ P_Q_R_就可以了。
简析数控车床上椭圆加工的编程方法

A PPLICATION技术与应用168OCCUPATION2014 06摘 要:目前,在机械加工中,非圆曲线越来越被广泛地应用,依靠传统的靠模加工已经不能满足现实的精度要求,取而代之的是在数控机床上进行加工。
本文对常见的椭圆加工的几种常用方法进行编程示例。
关键词:数控编程 椭圆 方法简析数控车床上椭圆加工的编程方法文/史先伟目前,随着数控机床的广泛应用,机械生产加工技术不断进步,对各种各样工件加工精度要求进一步提高,非圆曲线的加工情况也越来越多,精度要求也越来越高。
但依靠传统的普通机床上进行靠模加工,已经不能满足现实的加工精度要求。
笔者以下图所示椭圆加工为例,采用FANUC数控系统,总结以下编程方法,供大家参考。
图一、G73仿形法1.利用直角坐标方程进行加工这个方法需要首先设定某一个坐标为自变量,然后用该坐标把另外一个坐标表示出来。
在此,把Z 轴方向的坐标设为变量#1,则X 轴方向的坐标#2可以用#1表示为:/3(即:#2=1/3*SQRT[900-#1*#1])。
加工程序如下:O 1; N 2 #2=1/3*SQRT[900-#1*#1];G 99 T 0101; G 01 X[2*#2] Z[#1-30.];M 03 S 500; #1=#1-0.1;G 00 X 21.Z 5.; IF[#1GT 0] GOTO 2;G 73 U 11. W 0 R 5; N 3 X 21.;G 73 P 1 Q 3 U 1. W 0 F 0.2; G 70 P 1 Q 3;N 1 G 00 X 0; G 00 X 100. Z 100.;G 1 Z 0 F 0.06; M 05;#1=30.; M 30;2.利用参数方程进行加工该椭圆参数方程为:,设自变量为#1;则可得Z 为#2=30*COS[#1],X 为#3=10*SIN[#1]。
加工程序 如下:O 2; #3=10.*SIN[#1];G 99 T 0101; G 01 X[2*#3] Z[#2-30.];M 03 S 500; #1=#1+1.;G 00 X 21.Z 5.; IF[#1LT 90] GOTO 2;G 73 U 11. W 0 R 5; N 3 X 21.;G 73 P 1 Q 3 U 1. W 0 F 0.2; G 70 P 1 Q 3;N 1 G 00 X 0; G 00 X 100. Z 100.;G 1 Z 0 F 0.06; M 05;#1=0; M 30;N 2 #2=30.*COS[#1];二、G90车削椭圆采用G 90车削椭圆时,我们一般只是利用直角坐标方程来进行,这样在车削时的切削深度比较容易控制,而参数方程就不太容易控制。
数控车床加工椭圆的方法

数控车床加工椭圆的方法摘要本文讲述在数控车床上利用椭圆直角坐标和极坐标方程,通过对宏程序进行编程来加工椭圆,同时总结了针对不同尺寸规格椭圆的编程方法。
关键词数控车床;加工椭圆;方法1概述二维轮廓的椭圆形零件在日常生活中使用得非常多,尤其是在机械制造业中更是应用广泛,但是,该零件加工起来的难度是非常大的。
椭圆形零件的加工方法有很多种,比较常见的有以下几种:在普通车床上进行近似加工[1];根据椭圆的形成原理,设计专用的加工装置进行加工[2];在数控车床上利用“虚拟轴”原理实现椭圆曲线的数控加工[3];利用圆弧逼近法[4]、直线逼近法加工等。
本文仅讨论利用直线逼近法(宏程序)加工椭圆。
2直线逼近法现今,计算机和自动化技术发展迅速,数控车床相关技术也随之不断进步,给椭圆形截面零件的加工创造了很好的条件。
从目前的技术来说,各种数控车床进行椭圆加工的插补原理基本相同,不同的是实现插补运算的方法。
圆弧插补与直线插补是两种常用的实现插补运算的方法,但是目前还没有椭圆插补。
因为受到各方面的限制,尤其在设备和条件方面,通常我们无法手工来编制程序,必须借助于电脑来实现。
一般来说,通过拟合运算及直线逼近法编写宏程序来加工椭圆。
宏程序指令适用于抛物线、双曲线、椭圆等没有插补指令的非圆曲线编程;还适用于图形相同,只是尺寸不同的一系列零件编程,同样还适用于工艺路线一样,只是位置数据不同的系列零件的编程。
相比于其他编程方法,宏程序实现椭圆形截面零件的加工的优点在于,其能有效的简化程序,提高程序的运行速度,并且能扩展数控机床的使用范围。
3用户宏程序法数控车床通过程序来实现某项功能,将编写的程序存储在数控车床中,并将这些实现某项功能的程序用某个简单命令代表,利用数控车床进行加工时,只需要写入代表命令就可以执行相应的功能,极大的减少了操作流程,提高了工作效率。
其中,把存入数控机床的一组程序称作用户宏程序主体,简称为宏程序;把代表命令称作用户宏程序命令,简称为宏命令。
数控车床椭圆加工功能扩展

C 案例ASESOCCUPATION912013 06摘 要:本文以数控车床上加工椭圆曲线为例,重点介绍了加工非圆曲线的宏程序的编制原理,并对通过编写通用宏程序以扩展数控系统功能的方法进行了深入的研究。
关键词:宏程序 椭圆加工 功能扩展数控车床椭圆加工功能扩展文/岳少剑 石晓红逻辑代数法是以逻辑代数为工具的一种编程方法,编程元件的输出(通电、断电)状态被当成是以控制元件触点的闭合、断开(或控制条件的满足和不满足)为逻辑变量的逻辑函数。
通过化简求解逻辑函数,可以编制出较为简捷的梯形图程序。
这是一种较为可靠实用的编程方法,其编程步骤为:根据设计任务书确定的程序流程图画出相应部分程序输出元件和控制元件的状态波形图;分析波形图,列出对应输出元件的逻辑函数表达式;对表达式进行逻辑化简;用PLC的编程语言写出对应的程序。
三、PLC控制系统的调试PLC系统的调试可分为基本调试、程序调试和系统整体调试三部分。
基本调试主要是对硬件进行的,是为了检查设计安装的效果。
其主要内容有:检验基本环境的条件,调试各个单元的电源,系统的外部接线等。
程序调试通常分为单元调试、总体实验室联合调试和现场调试三部分。
现场调试应结合系统整体调试进行。
单元调试是对组成系统的各个单元进行单独的调试,当各个单元调试通过后,再在实验室的条件下(不与实际设备相连接)进行总体实验室联调。
对于简单的系统,实验室联调也可在生产现场进行。
联调所需的输入信号可通过模拟方法解决,但一定注意不能与实际设备连接。
系统整体调试包括准备阶段、空载调试阶段和负载调试阶段。
准备阶段需做好调试的各项准备工作。
空载调试开始时,首先是主回路不通电的调试,然后进行主回路单机空载调试,最后是空载联合调试。
负载调试阶段还可分为半载调试和满载调试等。
调试是一项重要的工作,其基本原则是:先简单后复杂,先软件后硬件,先单机后整体,先空载后负载。
调试期间注意随时拷贝程序、随时修改图样、随时完善系统。
浅谈数控车床椭圆加工方法

浅谈数控车床椭圆加工方法摘要:在教学和工作实践中常面对着如何加工椭圆零件的问题,但不同的数控系统实现椭圆加工的方法有所不同,尝试对各种常用数控车椭圆加工方法进行总结探讨,论述了宏程序法、椭圆指令法、参数修改法和自动编程加工法等数控车常用椭圆加工方法。
关键词:数控车床;椭圆轮廓;加工方法;CAD /CAM在近几年的职业资格考试、各级数控技能大赛中,用宏指令编程已经成为一个重要的考核点之一。
用宏程序来加工非圆曲线轮廓,不仅能提高学生学习数控编程的兴趣和积极性,而且对整体提高各职业院校数控操作人员的技能水平起到重要推动作用。
在实际应用中,常会遇到各种各样的曲线形加工零件,其中椭圆形零件就是常见的一种二维轮廓工件,也是比较难以加工的工件。
目前椭圆形零件的加工方法主要有:在普通车床上进行近似加工、设计专用加工装置进行加工、数控车床加工、特种加工等。
对于在数控车床上加工椭圆,需要针对不同系统数控车床采用适当的加工方法。
有的系统可以用宏程序加工(如华中数控系统、法兰克数控系统),有的系统可以直接用椭圆指令加工(如广数TDA),有的系统可通过修改相关参数来配合椭圆加工(如广数 980T),多数系统都可以用比较方便的自动编程法加工。
从实用角度还是从美观角度来讲,表面轮廓要求为非圆曲线生成的新产品也越来越多。
像椭圆、双曲线、抛物线以及三角函数等非线性轮廓,用一般的直线和圆弧指令无法编程。
而用 CAD/CAM 自动编程软件,还需要三维绘图、自动编程,相对来说,比较繁琐;对于单件小批量的生产加工任务,更是不经济。
如果利用数控系统的宏指令编程,则可以较为方便快捷地实现非圆曲线轮廓零件的粗精加工。
下面以图所示椭圆手柄为例,分别针对不同系统介绍宏程序法、椭圆指令法、参数修改法和自动编程法等数控车床的椭圆加工方法。
该宏程序的原理是利用微直线插补轨迹逐渐逼近椭圆轮廓,每段直线插补的终点以 z 为自变量,根据椭圆数学公式求出 x 的值确定,自变量 z 每次自减量要根据情况设置适当,如果设置太大则走刀轨迹不够光滑逼真,如果设置太小则插补运算时间过长使加工太慢。
椭圆零件在数控车床上的加工方法

椭圆零件在数控车床上的加工方法【摘要】轴类零件上一些高精度的曲面如椭圆、正弦曲线等,用普车难以加工,必须采用数控车床才可以加工。
本文根据平时加工中总结出的一些经验,简单谈下在广州数控系统数控车床上车削椭圆的一些看法,就编制步骤、宏程序组成、编程实例等几方面进行了探讨。
【关键字】数控加工椭圆宏程序编程椭圆加工,普通机床很难完成,而数控机床确实能够轻松的加工出来,主要是因为椭圆加工的时候X、Z两坐标是同时变化的,数控机床是通过程序控制的方式来驱动两轴,实现两轴的共同运动。
但数控车床只具有直线插补和圆弧插补两种基本插补功能,不具备椭圆插补功能,所以加工椭圆时可以采用直线逼近法的方式进行加工,即把曲线用许多小段的直线来代替,无限接近椭圆轮廓的加工方法。
下面选用广州数控980TB数控车削系统,结合教学工作实践谈谈如何巧用宏程序解决椭圆编程问题。
一、椭圆宏程序的编制步骤1.标准方程。
2.对标准方程进行转化成车床椭圆方程。
3.求值公式推导有些零件的椭圆中心不在工件原点处,就要根据实际椭圆写出正确的方程。
为编程方便,一般用Z作为变量。
二、宏程序组成1.变量的类型变量号#0,空变量;变量号#1~#33,局部变量;变量号#100~#109、#500~#999,公共变量;变量号#1000以上,系统变量。
2.变量的运算定义#1=#2;加法#1=#2+#3、减法#1=#2-#3、乘法#1=#2*#3、除法#1=#2/#3;正弦#1=SIN[#2]、余弦#1=COS[#2]、正切#1=TAN[#2];平方根#1=SQRT[#2]、绝对值#1=ABS[#2]。
3.运算符EQ(=)、GE(≥)、NE(≠)、LT()、LE(≤)。
按照优先的先后顺序依次是函数→乘和除运算→加和减运算。
4.条件转移(IF)功能语句IF[表达式]GOTO n。
指定的条件不满足时,转移到标有顺序号n的程序段。
三、980TB系统宏指令加工椭圆曲线编程实例1.凸椭圆中心不在零件轴线上例:毛坯直径为Ф40,总长为40,用变量进行编程,经计算椭圆起点的X 轴坐标值为10.141。
在FANUC数控车床上使用宏程序编制椭圆加工程序-精选文档

在FANU数控车床上使用宏程序编制椭圆加工程序i=rCAD/CAM勺普及计算机自动编程虽然有取代手工编程的趋势。
但是巧用宏程序开发加工程序,可以提高编程效率, 达到事半功倍的效果。
1 宏程序概述1.1 宏程序定义所谓宏程序, 即用户宏程序的简称。
该功能的含义是把一组采用变量和演算式的命令所构成的某一功能, 如同子程序那样,记录在数控装置的存储器中, 其记录的这组命令(又称为用户宏程序体)就是宏程序。
它可以用一个特定的指令代码(如P XXXX )来代表,通过呼出用户程序指令(如G65X XXX )即可调用这一功能。
1.2 宏程序编程随着数控系统的不断更新, 宏指令应用越来越广泛。
以日本FANUC-O系统为例Q 系统使用B类宏指令,在0系列的早期版本中,曾使用A类宏指令,主要特征为使用G65代码为宏指令专用代码,包括宏变量的赋值、运算、条件调用等。
B类宏指令功能相对A类而言,其功能更强大,编程更直观。
在FANUC-Oi系统的固定循环指令中,毛坯切削循环G71指令内,平行轮廓削循环G73指令内部都可以使用宏程序进行编程。
宏指令编程像高级语言一样, 可以使用变量进行算术运算逻辑运算和函数混合运算进行编程。
在宏程序形式中, 一般都提供循环判断分支和子程序调用的方法。
可编制各种复杂的零件加工程序。
熟练应用宏程序指令进行编程, 可大大精简程序量, 还可以增强机床的加工适应能力。
比如可以将抛物线、椭圆等非圆曲线的算法标准化后做成内部宏程序, 以后就可以像圆弧插补一样按标准格式编程调用, 相当于增加了系统的插补功能。
2 椭圆形加工宏程序的编程在数控系统中,G02/G03圆弧插补指令只能加工标准圆弧,对于非标准圆弧所构成的特殊曲线或曲面除采用专业软件自动生成加工程序外, 还可利用宏程序编程方法进行加工。
设Z坐标为自变量#2,X坐标为因变量#1,自变量步长为△ W, 则公式曲线段的精加工程序宏指令编程模板如下#2=Z1(给自变量#2赋值Z1:Z1是公式曲线自身坐标系下起始点的坐标值)WHILE #2 GE Z2(自变量#2的终止值Z2:Z2是公式曲线自身坐标系下终止点的坐标值)#1=b*SQRT(1-#2*#2/a2)函数变换:确定因变量#1(X)相对于自变量#2(Z) 的宏表达式)#11=±#1 + △ X(计算工件坐标系下的X坐标值#11:编程中使用的是正轮廓,#1前冠以正,反之冠以负;△ X为公式曲线自身坐标原点相对于编程原点的X轴偏移量。
数控车床宏程序案例

由浅入深宏程序数控车床旋转正弦函数宏程序正弦函数曲线旋转宏程序坐标点旋转1s = x cos(b) – y sin(b)t = x sin(b) + y cos(b)根据下图,原来的点(#1,#2),旋转后的点(#4,#5),则公式:#4=#1*COS[b]- #2*SIN[b]#5=#1*SIN[b]+ #2*COS[b]公式中角度b,逆时针为正,顺时针为负。
下图中正弦曲线如果以其左边的端点为参考原点,则此条正弦曲线顺时针旋转了16度,即b=-16正弦函数旋转图纸1此正弦曲线周期为24,对应直角坐标系的360对应关系【0,360】 y=sin(x)【0,24】 y=sin(360*x/24)可理解为:360/24是单位数值对应的角度360*x/24是当变量在【0,24】范围取值为x时对应的角度sin(360*x/24)是当角度为360*x/24时的正弦函数值旋转正弦函数曲线粗精加工程序如下:M3S800G0X52Z5#6=26 工件毛坯假设为50mm,#6为每层切削时向+X的偏移量。
N5 G0X[#6+18.539]G1Z0F0.1#1=48N10 #2=sin【360*#1/24】#4=#1*COS[-16]- #2*SIN[-16] 旋转30度之后对应的坐标值#5=#1*SIN[-16]+ #2*COS[-16]#7=#4-【50-3.875】坐标平移后的坐标。
#8=45+2*#5+#6G1X[#8]Z[#7]F0.1 沿小段直线插补加工#1=#1-0.5 递减0.5,此值越小,工件表面越光滑。
IF [#1 GE 0] GOTO 10 条件判断是否到达终点。
G1X52 直线插补切到工件外圆之外G0Z5#6=#6-2IF [#6 GE 0] GOTO 5G0X150Z150M5M30镂空立方体宏程序范例镂空立方体图纸及宏程序范例此零件六个面加工内容相同,在加工时,调面装夹时要注意考虑夹紧力。
椭圆零件在数控车床上的加工

椭圆零件在数控车床上的加工摘要:随着当前数控车床技术不断进步, 数控车床加工的各种复杂形面也日渐增多,而椭圆等非圆曲线则是出现频率比较广泛的复杂型面。
本文通过对椭圆在车床上车削所需要的工艺分析、编程方法、注意事项、等方面及椭圆编程实例,简述了椭圆零件在数控车床上的加工。
关键词:椭圆编程方法注意事项因为并不是所有曲线都可以在数控系统中通过插补指令来完成,比如绝大多数数控系统仅仅提供了直线和圆弧插补。
如果加工对象是其它曲线例如椭圆,则需要根据曲线拟合的数学模型,使用数控系统提供的计算参数和程序跳转指令编制出各种曲线的数控加工程序。
椭圆在车床的车削需要宏程序来实现。
宏程序与普通程序相比较,普通程序的程序字为常量,一个程序只能描述一个几何形状,缺乏灵活性和适用性。
而在用户宏程序的本体中,可以使用变量进行编程,还可以用宏指令对这些变量进行赋值、运算等处理。
以下以FANUC 0I MATE TD数控系统为例简述椭圆零件在数控车床上的加工。
一、椭圆的编程椭圆在数控车床上应用较为广泛的宏程序编制方法为椭圆方程的编程方法。
而椭圆方程有椭圆参数方程及椭圆标准方程两种。
1.椭圆参数方程编程椭圆参数方程:其中a 、b 分别为X、Z 所对应的椭圆半轴。
以下图为例,对其进行参数编程:#1=0 椭圆开始角度N10#1=#1+0.1 Z向每次进给量#2=36*SIN[#1] X向角度变量#3=30*COS[#1] Z向角度变量G64G1 X#2 Z#3 XZ判定IF [#1GT#2] GOTO10 条件判断及跳转2.椭圆标准方程:由上式可得:X=a*√1-Z*Z/b*b其中a 、b 分别为X、Z 所对应的椭圆半轴。
以下图为例,对其进行标准方程编程#1=30 椭圆中心相对于椭圆起点的距离(自变量)N10#2=18*SQRT[1-#1*#1/900] X在椭圆中心的半径坐标值(应变量)#3=2*#2 X直径值#1=#1-0.1 Z向每次进给量#4=#1-30 Z在工件坐标系中的位置G64G1X#3 Z#4 XZ判定IF [#4GT-30]GOTO10 条件判断及跳转在FANUC系统中采用#作为变量,一般应用#1--#100作为赋值。
宏程序数控车椭圆粗精加工设计方法

宏程序数控车椭圆粗精加工设计方法
宏程序数控车椭圆粗精加工设计方法是应用于数控车床的一种加工方式,通过对工件进行椭圆形的切削加工来达到精准的加工效果。
为了
确保加工质量,我们需要遵循以下步骤。
1. 定义工件形状和加工要求
首先,我们需要对工件的形状和加工要求进行定义,包括工件的长度、宽度、高度、椭圆形状的参数、加工精度等。
这些参数的定义将直接
影响后续的宏程序设计和加工过程,因此需要尽可能详细地确定。
2. 设计宏程序
在确定了工件形状和加工要求之后,我们需要设计宏程序,即加工过
程中的控制程序。
宏程序主要包括数控车床的操作指令和参数设置,
以确保加工过程的准确性和稳定性。
3. 调试和优化宏程序
设计好宏程序后,需要进行调试和优化。
通过对宏程序进行反复调试
和测试,发现问题并逐一解决,以确保程序运行的稳定性和加工质量。
4. 加工工件
完成了宏程序的设计和调试后,就可以进行机床加工了。
在加工过程中,需要注意机床的运转时刻以及切削工具的选择,以确保工件能够
按照预定要求进行加工,同时也要注意操作安全。
5. 检测加工结果
完成了工件的加工后,需要进行加工结果的检测。
通过测量和对比加
工结果和设计要求,确认加工精度是否符合要求,并进行记录和分析。
综上所述,宏程序数控车椭圆粗精加工设计方法是一种精准而复杂的
加工方式,需要依照以上步骤进行设计和加工。
只有这样,才能保证
工件加工的准确性和稳定性,最终实现加工质量的提高。
在GSK980TD数控机床中如何加工椭圆形工件

在GSK980TD数控机床中如何加工椭圆形工件摘要:在实际应用中会遇到各种各样的曲线形加工特征。
而在现今的数控系统中,没有椭圆、双曲线、抛物线等插补指令。
文章介绍了在GSK980TD车床中如何用宏程序手工编程来实现椭圆形工件的加工。
关键词:GSK980TD数控机床;椭圆形工件;A类宏程序;宏指令;参数方程在实际应用中,我们会遇到各种各样的曲线形加工特征。
而在现今的数控系统中,无论硬件数控系统,还是软件数控系统,其插补的基本原理是相同的,只是实现插补运算的方法有所区别。
常见的是直线插补和圆弧插补,没有椭圆、双曲线、抛物线等插补。
椭圆的加工,运用宏程序来解决就非常简单了。
用户宏程序是提高数控机床性能的一种特殊功能。
使用中,通常把能完成某一功能的一系列指令像子程序一样存入存储器,然后用一个总指令代表它们,使用时只需给出这个总指令指令就能执行其功能。
用户宏程序的最大特点是可以对变量进行运算,使程序应用更加灵活、方便。
虽然子程序对编制相同加工操作的程序非常有用,但用户宏程序由于允许使用变量算术和逻辑运算及条件转移,使得编制相同加工操作的程序更方便、更容易。
用户宏程序有A、B两类,GSK980TD数控车床中,使用的是A类宏程序。
下面我就以我校GSK980TD数控车床为例,介绍如何用宏程序对椭圆形工件进行编程加工。
一、熟悉宏指令用户宏程序本体的一般形式:G65 Hm P#i Q#j R#km:01~99表示运算命令或转移命令功能;#i:存入运算结果的变量名;#j:进行运算的变量名1,也可以是常数。
常数直接表示,不带#;#k:进行运算的变量名2;也可以是常数。
指令意义:#i=#j?誕#k(注:?誕为运算符号,由Hm决定)。
二、掌握椭圆的参数方程的含义在实际的图形中,一般给出椭圆的长半轴a和短半轴b。
当椭圆的长轴在X轴上,短轴在Y轴上,这时椭圆的参数方程如下:x=a cos?兹y=b sin?兹(1)当椭圆的长轴在Y轴上,短轴在X轴上,这时椭圆的参数方程如下:x=b cos?兹y=a sin?兹(2)椭圆参数方程中的离心角在第一象限(0°~90°),第二象限(90°~180°),第三象限(180°~270°)及第四象限(270°~360°)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数控车床加工对象为各种类型的回转面,其中对于圆柱面、锥面、圆弧面、球面等的加工,可以利用直线插补和圆弧插补指令完成,而对于椭圆等一些非圆曲线构成的回转体,加工起来具有一定的难度。
这是因为大多数的数控系统只提供直线插补和圆弧插补两种插补功能,更高档的数控系统提供双曲线、正弦曲线和样条曲线插补功能,但是一般都没有椭圆插补功能。
因此,在数控机床上对椭圆的加工大多采用小段直线或者小段圆弧逼近的方法来编制椭圆加工程序。
在这里结合工作实践对车削椭圆轮廓的宏程序的编制方法进行探讨。
一、椭圆宏程序的编制原理
数控系统的控制软件,一般由初始化模块、输入数据处理模块、插补运算处理模块、速度控制模块、系统管理模块和诊断模块组成。
其中插补运算处理模块的作用是依据程序中给定的轮廓的起点、终点
等数值对起点终点之间的坐标点进行数据密化,然后由控制软件,依据数据密化得到的坐标点值驱动刀具依次逼近理想轨迹线的方式来移动,从而完成整个零件的加工。
依据数据密化的原理,我们可以根据曲线方程,利用数控系统具备的宏程序功能,密集的算出曲线上的坐标点值,然后驱动刀具沿着这些坐标点一步步移动就能加工出具有椭圆、抛物线等非圆曲线轮廓的工件。
二、椭圆宏程序的编制步骤
宏编程一般步骤:
1.首先要有标准方程(或参数方程)一般图中会给出。
2.对标准方程进行转化,将数学坐标转化成工件坐标标准方程中的坐标是数学坐标,要应用到数控车床上,必须要转化到工件坐标系中。
3.求值公式推导利用转化后的公式推导出坐标计算公式
4.求值公式选择根据实际选择计算公式
5.编程公式选择好后就可以开始编程了
三、加工实例
下面分别就工件坐标原点与椭圆中心重合,偏离等2种情况进行编程说明。
(1)工件坐标原点与椭圆中心重合
椭圆标准方程为
①
转化到工件坐标系中为
②
根据以上公式我们可以推导出以下计算公式
③
④
在这里我们取公式③。
凸椭圆取+号,凹椭圆取-号。
即X值根据Z值的变化而变化,公式④不能加工过象限椭圆,所以舍弃。
下面就是FANUC系统0i椭圆精加工程序:
O0001; 程序名
#1=100; 用#1指定Z向起点值
#2=100; 用#2指定长半轴
#3=50; 用#3指定短半轴
G99 T0101 S500 M03; 机床准备相关指令
G00 X150. Z150. M08; 程序起点定位,切削液开
X0 Z101.;快速定位到靠近椭圆加工起点的位置
WHILE[#1GE-80]DO1;当Z值大于等于-80时执行DO1到END1 之间的程序
#4=#3*SQRT[1-#1*#1/[#2*#2]]; 计算X值,就是把公式
里面的各值用变量代替
G01 X[#4*2] Z#1 F0.15; 直线插补,这里#4×2是因为公
式里面的X值是半径值
#1=#1-0.1; 步距0.1,即Z值递减量为0.1,此值过大
影响形状精度,过小加重系统运算负担,
应在满足形状精度的前提下尽可能取大值。
END1; 语句结束,这里的END1与上面的DO1对应
G01 Z-110 ; 加工圆柱面
X102.; 退刀
G00 X150. Z150.;回程序起点
M09; 切削液关
M05; 主轴停止
M30; 程序结束
(2)工件坐标原点与椭圆中心偏离
数控车床编程原点与椭圆中心不重合,这时需要将椭圆Z(X)轴负向移动长半轴的距离,使起点为0,原公式
转变为:
⑤
Z1----编程原点与椭圆中心的Z向偏距;此例中为-100
X1----编程原点与椭圆中心的X向偏距;此例中为0
可推导出计算公式:
⑥
(精加工程序)
O0001; 程序名
#1=0; 用#1指定Z向起点值
#2=100; 用#2指定长半轴
#3=50; 用#3指定短半轴
#5=-100; Z向偏距
G99 T0101 S500 M03;
G00 X150. Z150. M08;
X0 Z1.;
WHILE[[#1-#5]GE-80]DO1;
#4=#3*SQRT[1-[#1-#5]*[#1-#5]/[#2*#2]];
G01 X[#4*2] Z[#1-#5] F0.15;
#1=#1-0.1;
END1;
G01 Z-110 ;
X102.;
G00 X150. Z150. M09;
M05;
M30;
三、完整粗、精加工程序
以上两个实例均只编写了精加工程序,另外可以利用宏调用子程序进行粗加工,下面以第一个图(工件坐标原点与椭圆中心重合的零件)为例说明。
O0001; 程序名
#6=95;定义总的加工余量
G99 T0101 S500 M03;
G00 X150. Z150. M08;
G00 X#6 Z101.;
N10 #6=#6-5;
M99 P0002;
IF [#6GE0]GOTO10;
G00 X150.Z150.;
M05;
M30 ;
O0002 ;子程序
#1=100; 用#1指定椭圆加工Z向起点值
#2=100; 用#2指定长半轴
#3=50; 用#3指定短半轴
WHILE[#1GE-80]DO1;
#4=#3*SQRT[1-#1*#1/[#2*#2]];
G01 X[#4*2+#6] Z#1 F0.15;
#1=#1-0.1;
END1;
G01Z-110 ;
X102.;
G00 Z101.;
X#6;
M99;
除了用标准方程加工椭圆外,还可以用参数方程加工椭圆曲线。
在这里就不一一阐述了。
加工椭圆的注意事项
利用数控车床加工椭圆曲线,应注意以下几点:
(1)车削后工件的精度与编程时所选择的步距有关。
步距值越小,加工精度越高;但是减小步距会造成数控系统工作量加大,运算繁忙,影响进给速度的提高,从而降低加工效率。
因此,必须根据加工要求合理选择步距,一般在满足加工要求前提下,尽可能选取较大的步距。
(2)对于椭圆轴中心与Z轴不重合的零件,需要将工件坐标系进行偏置后,然后按文中所述的方法进行加工。
结论
使用宏程序编程,大部分零件尺寸和工艺参数可以传递到宏程序中,程序的修改比较方便。
图样改变时,仅需修改几个参数,因此,柔性好,极易实现系列化生产。
另外,使用宏程序除了能加工椭圆面外,还可以加工抛物线、双曲线等非圆曲线,有效的扩展数控机床的加工范围,提高加工效率和品质,充分发挥机床的使用价值。
