matlab首次试验
MATLAB第一次实验报告

MATLAB第一次实验报告1. 编程实现以下数列的图像,用户能输入不同的初始值以及系数。
并以x,y为坐标显示图像x(n+1) = a*x(n)-b*(y(n)-x(n)^2);y(n+1) = b*x(n)+a*(y(n)-x(n)^2)程序:function [y1,y2]=draw(a,b,c,x1,y1)x=[];y=[];x(1)=x1;y(1)=y1;n=c;for i=1:nx(i+1)=a*x(i)-b*(y(i)-x(i)^2);y(i+1)=b*x(i)+a*(y(i)-x(i)^2);endy1=x;y2=y;plot(y1,y2)输入:draw(5,1,1,1,2)2. 编程实现奥运5环图,允许用户输入环的直径。
程序:clcclearr=input('input a mnmber:')color1=['b','k','r'];color2=['y','g'];t=linspace(0,2*pi);a1=r+0.2*r;a2=3*r+0.4*r;a3=5*r+0.6*r;a=[a1,a2,a3];b1=2*r+0.3*r;b2=4*r+0.5*r;b=[b1,b2];for i=1:3x=r*cos(t)+a(i);y=r*sin(t);plot(x,y,color1(i),'linewidth',5) axis([0,7*r,-2*r,1.5*r]);hold onaxis equalendfor n=1:2x=r*cos(t)+b(n);y=r*sin(t)-r;plot(x,y,color2(n),'linewidth',5) hold onendaxis off输入:6(圆的半径)3. 实现对输入任意长度向量元素的冒泡排序的升序排列。
不允许使用sort函数。
第一次MatlAB实验报告

实验一 数学模型的MatlAB 描述一、MatlAB 中数学模型的表示MatlAB 中数学模型的表示主要有三种基本形式:传递函数分子/分母多项式模型、传递函数零极点增益模型和状态空间模型。
它们各有特点,有时需在各种模型之间进行转换。
1. 传递函数分子/分母多项式模型当传递函数为nn n nm m m m a s a sa s ab s b sb sb s G ++++++++=----11101110)(时,在MatlAB 中,直接用分子、分母的系数表示,即],,,[10m b b b num = ],,,[10n a a a d e n = ),()(d e n num tf s G =例1:已知一系统的传递函数2432328()3842ss G s s s s s ++=++++,提取其分子和分母多项式,并绘制零极点图*。
>> num=[3 2 8]; den=[1 3 8 4 2]; G=tf(num,den) [tt,ff]=tfdata(G ,'v') pzmap(G)grid on 结果如下:2. 传递函数的零极点增益模型当传递函数为)())(()())(()(1010n m p s p s p s z s z s z s Ks G ------=时,在MatlAB 中,用[z,p,k]矢量组表示,即[][][]),,()(,,,,,1010k p z zpk s G K k p p p p z z z z n m ====例2:求一传递函数222328()(61)(24)s s G s s s s s ++=++++的零极点及其增益,并绘制零极点图。
>> num=[3 2 8];den=conv([1 6 12],[1 2 4]); G=tf(num,den) GG=zpk(G)[z,p,k]=zpkdata(G ,'v') pzmap(G) grid结果如下:3.状态空间模型当系统的数学模型为状态空间表达式{BuAXX+='+=DuCXY时,在MatlAB中,用[A、B、C、D]矩阵组表示,即系统表示为()DCBAss、、、实验3:已知两系统串联,其中2132265452s sGs s s++=+++,222712432s sGs s++=++,求此串联系统的总的传递函数。
matlab第一次实验

fc=10000;fs=80000;N=4096;ts=1/fs;tp=10/fm;t=ts*tp;fHz=[0:4095]/4096*fs;wc=1,5*2*pi*fm/fs;B=firl(16,wc/pi);[h,w]=freqz(B,1,N); %低通滤波器mt=cos(2*pi*fm*t);mxt=sin(2*pi*fm*t); %m(t)的希尔伯特变换ct=cos(2*pi*fc*t);cqt=sin(2*pi*fc*t); %Cq(t)c1t=cos(2*pi*fc*t+pi/8); %相移pi/8的载波c2t=cos(2*pi*fc*t+pi/4); %相移pi/4的载波c3t=cos(2*pi*fc*t+pi/3); %相移pi/3的载波c4t=cos(2*pi*fc*t+pi/2); %相移pi/2的载波d0t=mt.*ct; %DSB已调信号a0t=[1+m(t)].*ct; %AM的已调信号s0t=0.5*mt*ct-0.5*mxt*cqt; %SSB已调信号上边带s1t=0.5*mt*ct+0.5*mxt*cqt; %SSB已调信号下边带Cw=fft(ct,N);Mw=fft(mt,N);D0w=fft(d0t,N);A0w=fft(a0t,N);S0w=fft(s0t,N);S1w=fft(s1t,N);figure(1);subplot(2,1,1);plot(t,mt);title(‘调制信号的时域波形’);xlabel(‘t’);ylabel(‘m(t)’);subplot(2,1,2);plot(t,ct);title(‘载波的时域波形’);xlabel(‘t’);ylabel(‘c(t)’);figure(2);subplot4,1,1);title(‘DSB已调信号的时域波形’);xlabel(‘t’);ylabel(‘d0(t)’);subplot(4,1,2);plot(t,a0t);title(‘AM已调信号的时域波形’);xlabel(‘t’);ylabel(‘a0(t)’);subplot4,1,3);plot(t,s0t);title(‘SSB已调信号上边带的时域波形’);xlabel(‘t’);ylabel(‘s0 (t)’);subplot4,1,4);plot(t,s1t);title(‘SSB已调信号下边带的时域波形’);xlabel(‘t’);ylabel(‘s1(t)’);figure(3);subplot(6,1,1);plot([0:N-1]/N*fs,abs(Cw));title(‘载波信号频谱图’);xlabel(‘w’);ylabel(‘C(w)’);subplot(6,1,2);plot([0:N-1]/N*fs,abs(Mw));title(‘调制信号频谱图’);xlabel(‘w’);ylabel(‘M(w)’);subplot(6,1,3);plot([0:N-1]/N*fs,abs(D0w));title(‘DSB已调信号频谱图’);xlabel(‘w’);ylabel(‘D0(w)’);subplot(6,1,4);plot([0:N-1]/N*fs,abs(A0w));title(‘AM调制信号频谱图’);xlabel(‘w’);ylabel(‘A0(w)’);subplot(6,1,5);plot([0:N-1]/N*fs,abs(S0w));title(‘SSB已调信号上边带频谱图’);ylabel(‘S0(w)’);subplot(6,1,6);plot([0:N-1]/N*fs,abs(S1w));title(‘SSB已调信号下边带频谱图’);xlabel(‘w’);ylabel(‘S1(w)’);figure(4)subplot(1,1,1);plot(w*fs/(2*pi),20*log10(abs(h))); title(‘低通滤波器的频谱图’);xlabel(‘w’);ylabel(‘H (w)’);。
matlab入门实验报告

matlab入门实验报告Matlab入门实验报告引言:Matlab是一种功能强大的数值计算和科学计算软件,广泛应用于工程、科学和金融等领域。
本实验报告旨在分享我在学习和使用Matlab过程中的一些经验和心得,希望对初学者有所帮助。
一、Matlab的基本操作Matlab的基本操作包括变量定义、运算符使用、矩阵操作等。
通过简单的例子,我们可以快速上手Matlab。
首先,我们可以定义一个变量并进行简单的运算。
例如,我们定义一个变量a,并赋值为5,然后进行加法运算。
a = 5;b = a + 3;disp(b);接下来,我们可以进行矩阵的操作。
例如,我们定义一个3x3的矩阵A,并对其进行转置操作。
A = [1 2 3; 4 5 6; 7 8 9];B = A';disp(B);二、Matlab的图形绘制功能Matlab具有强大的图形绘制功能,可以绘制各种类型的图形,如曲线图、散点图、柱状图等。
下面是一个简单的例子,展示了如何使用Matlab绘制曲线图。
首先,我们定义一个自变量x和一个因变量y,并生成一组数据。
x = linspace(0, 2*pi, 100);y = sin(x);然后,我们使用plot函数将数据绘制成曲线图。
plot(x, y);通过设置不同的参数,我们可以对图形进行进一步的美化和定制。
例如,我们可以设置x轴和y轴的标签,并添加图例。
xlabel('x');ylabel('y');legend('sin(x)');三、Matlab的数据分析功能Matlab提供了丰富的数据分析功能,可以进行数据的统计、拟合、回归等操作。
下面是一个简单的例子,展示了如何使用Matlab进行线性回归分析。
首先,我们生成一组随机数据,并假设其满足线性关系。
x = linspace(0, 10, 100);y = 2*x + 3 + randn(size(x));然后,我们使用polyfit函数进行线性回归分析,并得到拟合的系数。
MATLAB试验报告
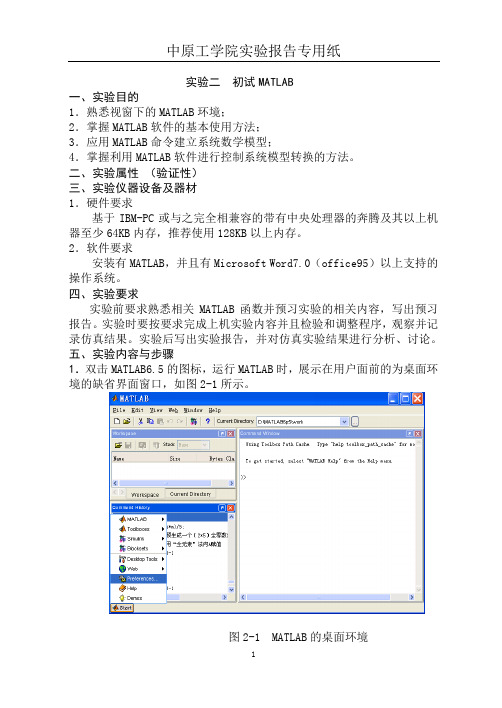
实验二初试MATLAB一、实验目的1.熟悉视窗下的MATLAB环境;2.掌握MATLAB软件的基本使用方法;3.应用MATLAB命令建立系统数学模型;4.掌握利用MATLAB软件进行控制系统模型转换的方法。
二、实验属性(验证性)三、实验仪器设备及器材1.硬件要求基于IBM-PC或与之完全相兼容的带有中央处理器的奔腾及其以上机器至少64KB内存,推荐使用128KB以上内存。
2.软件要求安装有MATLAB,并且有Microsoft Word7.0(office95)以上支持的操作系统。
四、实验要求实验前要求熟悉相关MATLAB函数并预习实验的相关内容,写出预习报告。
实验时要按要求完成上机实验内容并且检验和调整程序,观察并记录仿真结果。
实验后写出实验报告,并对仿真实验结果进行分析、讨论。
五、实验内容与步骤1.双击MATLAB6.5的图标,运行MATLAB时,展示在用户面前的为桌面环境的缺省界面窗口,如图2-1所示。
图2-1 MATLAB的桌面环境要求熟悉视窗下的MATLAB环境,分别观察和熟悉菜单项、工具栏、历史命令窗口、命令窗口、当前目录浏览器、工作空间浏览器、目录分类窗口、M文件编辑器/调试器、超文本帮助浏览器。
2.单击工具栏中帮助按钮(或者单击Help菜单中的MATLAB Help),打开MATLAB6.5的帮助系统,练习和熟悉MATLAB6.5的帮助系统的使用。
3.应用MATLAB命令编写相应M文件,建立图2-2系统的数学模型——闭环传递函数。
图2-2 调速系统g1=tf(1,[0.01,1]);g2=tf([0.17,1],[0.085,0]);g3=g1;g4=tf([0.15,1],[0.05,0]);g5=tf(70,[0.0067,1]);g6=tf(0.21,[0.15,1]);g7=tf(130,[1,0]);g11=feedback(g6,0.01*g4*g5*g1);g22=feedback(g1*g7,0.212);g33=feedback(g2*g3*g4*g5*g22,0.0044*g1);g=g1*g33Transfer function:2.321 s^3 + 261.2 s^2 + 3003 s + 9100--------------------------------------------------------------- 2.848e-013 s^8 + 1.564e-010 s^7 + 3.487e-008 s^6 + 4.042e-006 s^5 + 0.0002572 s^4 + 0.01876 s^3 + 1.266 s^2+ 13.21 s + 40.04实验三 基于MATLAB 的系统时域分析一、实验目的1.熟悉MATLAB 的各种绘图命令;2.掌握基于MATLAB 的控制系统时域分析方法。
初识MATLAB的实验报告

初识MATLAB的实验报告1. 引言MATLAB(Matrix Laboratory)是一种高级的技术计算环境和编程语言。
它具有强大的矩阵计算能力和丰富的科学和工程绘图功能,被广泛应用于各个领域的科研与工程实践中。
本实验旨在初步了解MATLAB的基本语法和功能,通过实际操作加深对MATLAB编程的理解。
2. 实验目的1. 掌握MATLAB的安装和基本使用方法;2. 学习MATLAB中的常用数学函数和操作;3. 了解MATLAB绘图功能并能够绘制简单的图形。
3. 实验步骤3.1 MATLAB安装首先,在官方网站(3.2 MATLAB入门3.2.1 MATLAB语法MATLAB的语法类似于其他常见的编程语言,每个语句以分号结尾。
在MATLAB 中,可以直接进行基本的数学运算,例如加减乘除、指数、对数等。
通过以下代码可以计算两个变量的和并将结果打印出来:matlaba = 10;b = 20;sum = a + b;disp(sum);3.2.2 MATLAB变量在MATLAB中,可以创建和操作各种类型的变量,例如数值、字符串、矩阵等。
以下代码演示了如何创建一个矩阵:matlabmatrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];disp(matrix);3.2.3 MATLAB函数MATLAB提供了许多内置的数学函数,可以直接调用。
以下代码演示了如何计算正弦函数值并打印结果:matlabx = pi/4;y = sin(x);disp(y);3.3 MATLAB绘图MATLAB具有强大的绘图功能,可以绘制各种图形,如曲线、散点图、柱状图等。
以下代码演示了如何绘制一个简单的正弦曲线:matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);xlabel('x');ylabel('y');title('Sine Curve');4. 实验结果与分析在完成上述实验步骤后,我们成功安装了MATLAB,并学习了基本的语法、变量和函数的使用方法。
MATLAB数学实验报告

MATLAB数学实验报告姓名:李帆班级:机械(硕)21学号:2120104008第一次数学实验报告——线性规划问题一,实验问题1,某饲养场饲养动物出售,设每头动物每天至少需要700g蛋白质,30g矿物质,100mg 维生素。
现有五种饲料可供选择,各种饲料的每千克营养成分含量和单价如下表。
是确定既能满足动物生长的营养需要,游客是费用最省的选用饲料方案。
2,某工厂生产甲、乙、丙三种产品,单位产品所需工时分别为2、3、1个;单位产品所需原料分别为3、1、5公斤;单位产品利润分别为2、3、5元。
工厂每天可利用的工时为12个,可供应的原料为15公斤。
为使总利润为最大,试确定日生产计划和最大利润。
二,问题分析1,1)该题属于采用线性规划的方式求出最优解的数学问题。
该题有以下特点,1.目标函数有线性,是求目标函数的最小值;2.约束条件为线性方程组;3.未知变量都有非负限制。
1,2)求解该类问题的方法有图解法,理论解法和软件解法。
图解法常用于解变量较少的线性规划问题。
理论解法要构建完整的理论体系。
目前用于解线性规划的理论解法有:单纯形法,椭球算法等。
在此,我们采用单纯形法的MATLAB软件解法来求解该问题。
1,3)此题中,要求既要满足动物生长的营养需要,又要使费用最省,则使每种饲料的选用量为变量,以总费用的最小值为所求量,同时每种饲料的使用量要符合营养成分的要求。
1,4)在此,首先确定建立线性规划模型。
设饲料i选用量为xi公斤,i=1,2,3,4,5.则有模型:Minz=0.2x1+0.7x2+0.4x3+0.3x4+0.8x5s.t. {3x1+2x2+6x4+18x5>=700;x1+0.5x2+0.2x3+2x4+0.5x5>=300.5x1+x2+0.2x3+2x4+0.8x5>=100Xj>=0,j=1,2,3,4,5解之得:x1=x2=x3=0X4=39.74359X5=25.14603Zmin=32.435902, 1)该问题与第一题分析步骤相似,故只在此写出其线性规划模型Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15三,程序设计流程图第一题:c=[0.2,0.7,0.4,0.3,0.8]A=[3,2,1,6,18;1,0.5,0.2,2,0.5;0.5,1,0.2,2,0.8;1,0,0,0,0;0,1 ,0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]b=[700,30,100,0,0,0,0,0][x,fval]=linprog(c,-A,-b)c =0.2000 0.7000 0.4000 0.3000 0.8000A =3.0000 2.0000 1.0000 6.0000 18.00001.0000 0.5000 0.20002.0000 0.50000.5000 1.0000 0.2000 2.0000 0.80001.0000 0 0 0 00 1.0000 0 0 00 0 1.0000 0 00 0 0 1.0000 00 0 0 0 1.0000b =700 30 100 0 0 0 0 0Optimization terminated.x =0.0000-0.00000.000039.743625.6410fval =32.4359第二题c=[-2 -3 -5]A=[2 3 1;3 1 5]b=[12;15]lb=[0 0 0][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
安徽大学matlab第一次试验

Matlab 第一次实验作业----------2015年11月3日星期二班级:软件工程学号:E21314003 姓名:李世 2.编写命令计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
>> clear>> A=[5 3 5;3 7 4;7 9 8]A =5 3 53 7 47 9 8>> B=[2 4 2;6 7 9;8 3 6]B =2 4 26 7 98 3 6>> F=A+BF =7 7 79 14 1315 12 143.请产生一个100*5的矩阵,矩阵的每一行都是[1 2 3 4 5]>> clear>> repmat(1:5,100,1)ans =1 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 54对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,编写命令求解X 。
>> A=[4 9 2;7 6 2;3 5 7]A =4 9 27 6 23 5 7>> B=[37;26;28]B =372628>> F=B\AF =0.1463 0.22230.11385求2010201000,sinex dx x xdxπ⎰⎰定积分>> clear>> syms x>> Q1=(x^2010,0,pi)??? Q1=(x^2010,0,pi)|Error: Incomplete or misformed expression or statement. >> Q1=int(x^2010,0,pi)Q1 =1/2011*pi^2011>> clear>> syms x>> Q2=int((x^2)*sin(x),0,esp)??? Undefined function or variable 'esp'.>> Q2=int((x^2)*sin(x),0,exp)??? Error using ==> expNot enough input arguments.Error in ==> exp at 15[varargout{1:nargout}] = builtin('exp', varargin{:}); >> Q2=int((x^2)*sin(x),0,2.72)Q2 =-3374/625*cos(68/25)+136/25*sin(68/25)-26根据1252222=-+ay a x 绘制平面曲线,并分析 参数a 对其形状的影响。
【原创】MATLAB实验报告-第一次-MATLAB语言程序设计基础-北京交通大学

输入what<目录名>,表示将分类显示所选择目录下的所有相关文件;
输入ver singal,表示列出singal工具箱的版本信息。
2、在命令窗口中输入 命令,执行后用方向 或 键(历史命令)将该命令调出,在行内编辑,将其改为6阶魔术矩阵命令。
输入magic(4),显示4阶魔术矩阵,按上方向键调出magic(4)命令,并将4改为6,便显示出6阶魔术矩阵。
3、用Matlab语言绘制函数 在 内的曲线。
输入>> t=0:0.1:2*pi;y=t.*cos(t);plot(t,y),显示出图像。
4、选择适当的坐标范围,用Matlab语言绘制函数: 的三维曲线。
输入
>> [x,y]=meshgrid(-3:0.1:3);
>> z=(x.^2+y).*exp(-x.^2-y.^2/2);
输入addpath E:\qinmin,将E:\qinmin目录添加到Matlab包含的路径下:
>> addpath E:\qinmin
(3)显示格式
输入format long,表示输出双精度数时小数点后保留14位有效数字,输出单精度数是小数点后保留7位有效数字;
输入format short e,表示输出数字用5位科学技术表示;
>> surf(x,y,z),colorbar
显示三维图像:
三、实验感想
本次Matlab上机实验是我第一次亲自操作Matlab软件并实现一些简单的功能。虽然只是实验了一些基本的命令,显示了魔术矩阵和绘制了简单的函数图像,但是这次实验也使我意识到了Matlab软件的强大。Matlab是著名的数学工具,在各科研领域都具有不可忽视的影响力。作为通信工程的本科生,我们也不可避免地需要使用Matlab来处理一些实验数据,所以熟练使用Matlab也是我们必备的技能之一。
Matlab实验第一次实验答案

实验一Matlab使用方法和程序设计一、实验目的1、掌握Matlab软件使用的基本方法;2、熟悉Matlab的数据表示、基本运算和程序控制语句3、熟悉Matlab绘图命令及基本绘图控制4、熟悉Matlab程序设计的基本方法二、实验内容:1、帮助命令使用help命令,查找 sqrt(开方)函数的使用方法;解:sqrtSquare rootSyntaxB = sqrt(X)DescriptionB = sqrt(X) returns the square root of each element of the array X. For the elements of X that are negative or complex, sqrt(X) produces complex results.RemarksSee sqrtm for the matrix square root.Examplessqrt((-2:2)')ans =0 +0 +2、矩阵运算(1)矩阵的乘法已知A=[1 2;3 4]; B=[5 5;7 8];求A^2*B解:A=[1 2;3 4 ];B=[5 5;7 8 ];A^2*B(2)矩阵除法已知 A=[1 2 3;4 5 6;7 8 9]; B=[1 0 0;0 2 0;0 0 3];A\B,A/B解:A=[1 2 3;4 5 6;7 8 9 ];B=[1 0 0;0 2 0;0 0 3 ];A\B,A/B(3)矩阵的转置及共轭转置已知A=[5+i,2-i,1;6*i,4,9-i];求A.', A'解:A=[5+1i,2-1i,1;6*1i,4,9-1i ];A1=A.',A2=A'(4)使用冒号表达式选出指定元素已知: A=[1 2 3;4 5 6;7 8 9];求A中第3列前2个元素;A中所有列第2,3行的元素;方括号[]解:A=[1 2 3;4 5 6;7 8 9 ];B=A([1,2],[3]),C=A(2:end, : )用magic 函数生成一个4阶魔术矩阵,删除该矩阵的第四列3、多项式(1)求多项式 42)(3--=x x x p 的根解:A=[1 0 -2 -4];B=roots(A)(2)已知A=[ 3 5 ;5 5 6;3 9 0 1;1 2 3 4] ,求矩阵A 的特征多项式;解:A=[ 3 5 .9 ; 5 5 6 ;3 9 0 1 ;1 2 3 4];A=poly(A);A=poly2sym(A)把矩阵A作为未知数代入到多项式中;4、基本绘图命令(1)绘制余弦曲线 y=cos(t),t∈[0,2π]解:t=0:.1:2*pi;y=cos(t);plot(t,y),grid(2)在同一坐标系中绘制余弦曲线y=cos和正弦曲线y=sin,t∈[0,2π] t=0:.1:2*pi; y1=cos;y2=sin;plot(t,y1,t,y2)grid5、基本绘图控制绘制[0,4π]区间上的x1=10sint曲线,并要求:(1)线形为点划线、颜色为红色、数据点标记为加号;(2)坐标轴控制:显示范围、刻度线、比例、网络线(3)标注控制:坐标轴名称、标题、相应文本;t=0:.01:4*pi;y=10*sin(t);plot(t,y,'-.',t,y,'r')grid6、基本程序设计(1)编写命令文件:计算1+2+…+n<2000 时的最大n值;解法1:s=0;i=0;while(s<2000) i=i+1;s=s+i; ends=s-i,i=i-1解法2:s=0;for i=1:1000; s=s+i;if(s>2000) ,break;endends=s-i,i=i-1(2)编写函数文件:分别用for和while循环结构编写程序,求2的0到n次幂的和。
MATLAB - 第一次试验结果

>> Ex01_02
3. 画出衰减振荡曲线 y = e
−
t 3
sin 3t 及其包络线 y 0 = e 3 ,y0 = e 3 。t 值的范围是 [0,4π ] 。
%Ex01_03 function y=Ex01_03
−
t
t
t=0:0.1:4*pi; y=sin(3*t).*exp(-t/3); y00=-exp(-t/3); y01=exp(-t/3); plot(t,y,'-',t,y00,'--',t,y01,'-.'); title('衰减震荡曲线及其包络线'); xlabel('t'); ylabel('y');
实 验 报 告
班级 机械 2 班 学号 081704 姓名 刘鑫 实 验 名 称 Matlab 第一次试验 1.掌握 Matlab 绘制曲线; 实 验 目 的 2.掌握 Matlab 绘制曲面; 3、掌握构造分段函数的方法; 参加实验时间 实 验 地 点 实验结果 − 4 − 2 0 2 4 1.找出数组 A = 中所有绝对值大于 3 的元素。 − 3 − 1 1 3 5
%Ex01_02 function Ex01_02 %画出所表示的三维曲面,用暖色调。 x=[-8:0.1:8]; y=[-8:0.1:8]; [xx,yy]=meshgrid(x,y);%设置栅格坐标矩阵 zz=sin(sqrt(xx.^2+yy.^2))./sqrt(xx.^2+yy.^2); surf(xx,yy,zz);%画三维曲面图 shading interp; colormap(hot);%暖色
-3-
matlab实验一实验报告

matlab实验一实验报告实验一:Matlab实验报告引言:Matlab是一种强大的数学软件工具,广泛应用于科学计算、数据分析和工程设计等领域。
本实验旨在通过使用Matlab解决实际问题,探索其功能和应用。
一、实验目的本次实验的主要目的是熟悉Matlab的基本操作和常用函数,了解其在科学计算中的应用。
二、实验内容1. 数值计算在Matlab中,我们可以进行各种数值计算,包括基本的加减乘除运算,以及更复杂的矩阵运算和方程求解。
通过编写相应的代码,我们可以实现这些功能。
例如,我们可以使用Matlab计算两个矩阵的乘积,并输出结果。
代码如下:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 数据可视化Matlab还提供了强大的数据可视化功能,可以将数据以图表的形式展示出来,更直观地观察数据的规律和趋势。
例如,我们可以使用Matlab绘制一个简单的折线图,来展示某个物体在不同时间下的位置变化。
代码如下:```matlabt = 0:0.1:10;x = sin(t);plot(t, x);xlabel('Time');ylabel('Position');title('Position vs. Time');```3. 图像处理Matlab还可以进行图像处理,包括图像的读取、处理和保存等操作。
我们可以通过Matlab对图像进行增强、滤波、分割等处理,以及进行图像的压缩和重建。
例如,我们可以使用Matlab读取一张图片,并对其进行灰度化处理。
代码如下:```matlabimg = imread('image.jpg');gray_img = rgb2gray(img);imshow(gray_img);```三、实验结果与分析在本次实验中,我们成功完成了数值计算、数据可视化和图像处理等任务。
MATLAB第一次实验

、实验报告填写说明
(实验项目名称、实验项目类型必须与实验教学大纲保持一致)
1.实验环境:
实验用的软、硬件环境。
2.实验目的:
根据实验教学大纲,写出实验的要求和目的。
3.实验原理:
简要说明本实验项目所涉及的理论知识。
4.实验方案:
这是实验报告极其重要的容。
对于验证性验,要写清楚操作方法,需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验,还应写出设计思路和设计方法。
对于创新性实验,还应注明其创新点。
5.实验过程:
写明执行实验方案的实验过程。
6.实验结论:
根据实验过程中得到的结果,做出结论。
7.实验小结:
本次实验的体会和建议。
8.指导教师评语及成绩:
指导教师依据学生的实际报告内容,给出本次实验报告的评价和成绩。
附录1:源程序。
MALAB第一次实验

实验一MATLAB 语言概述一、实验环境计算机MATLAB软件二、实验目的1.熟悉MATLAB的命令窗口。
2.掌握MATLAB一些基本操作,能进行一般的数值计算。
3.实现语句的重调和修改。
三、实验内容1.MATLAB 概述MATLAB是集数值计算、符号运算及图形处理等强大功能于一体的科学计算语言,是一种交互式的以矩阵为基础的系统计算平台,它用于科学和工程的计算与可视化。
它的优点在于快速开发计算方法,而不在于计算速度。
MATLAB已成为一门高校必修的课程,也是最为普遍的计算工具之一。
2.Matlab的发展MATLAB名字由MATrix和LABoratory 两词的前三个字母组合而成。
那是20世纪七十年代,时任美国新墨西哥大学计算机科学系主任的Cleve Moler出于减轻学生编程负担的动机,为学生设计了一组调用LINPACK和EISPACK矩阵软件工具包库程序的的“通俗易用”的接口,此即用FORTRAN编写的萌芽状态的MATLAB。
1984年由Little、Moler、Steve Bangert合作成立MathWorks 公司,并把MATLAB正式推向市场。
从这时起,MATLAB的内核采用C语言编写,而且除原有的数值计算能力外,还新增了数据图视功能。
1997年春,MATLAB5.0版问世,紧接着是5.1、5.2,以及和1999年春的5.3版。
现今的MATLAB拥有更丰富的数据类型和结构、更友善的面向对象、更加快速精良的图形可视、更广博的数学和数据分析资源、更多的应用开发工具。
2000年末又推出6.0版本。
无论在界面的设计上还是在内容上较以前版本都有很大的进展。
2004年又推出了7.0版本。
3.MATLAB语言的特点1)友好的工作平台和编程环境2)简单易用的程序语言3)强大的科学计算及数据处理能力4)出色的图形处理功能5)应用广泛的模块集和工具箱6)实用的程序接口和发布平台7)模块化的设计和系统级的仿真4.MATLAB的工作环境单行命令执行方式执行结果直接显示图形窗(Figure Window) 用图形方式表示计算结果文本编辑窗(File Editor) 多行命令组成语言组,可以文件方式存盘MATLAB 的主界面MATLAB 的工具栏MATLAB 的窗口——命令窗口MATLAB 的窗口——历史命令窗口四、实验步骤1.启动MATLAB2.观察MATLAB窗口的各个组成部分1)了解菜单栏各菜单功能,用鼠标打开MATLAB各个菜单,在状态栏里显示当前鼠标所指的菜单项的含义。
matlab实验一实验报告

matlab实验一实验报告一、实验目的本次实验的主要目的是熟悉 MATLAB 软件的基本操作环境和编程语法,通过实际编写和运行简单的程序,初步掌握 MATLAB 在数值计算、图形绘制和数据处理方面的基本功能。
二、实验环境本次实验使用的是 MATLAB R2020a 版本,运行在 Windows 10 操作系统上。
计算机配置为:Intel Core i5 处理器,8GB 内存。
三、实验内容及步骤1、矩阵运算创建一个 3×3 的矩阵 A,元素分别为 1 到 9。
创建一个 3×3 的零矩阵 B。
计算 A+B 和 A×B 的结果。
在 MATLAB 中,我们可以使用以下代码实现:```matlabA = 1 2 3; 4 5 6; 7 8 9;B = zeros(3);C = A + B;D = A B;disp(C);disp(D);```2、数据类型转换定义一个整数变量 x 为 5。
将 x 转换为双精度浮点数。
将 x 转换为字符串类型。
代码如下:```matlabx = 5;y = double(x);z = num2str(x);disp(y);disp(z);```3、函数调用定义一个函数 fun,输入参数为 x,返回值为 x 的平方。
调用函数 fun,计算 3 的平方。
函数定义及调用代码:```matlabfunction y = fun(x)y = x^2;endresult = fun(3);disp(result);```4、图形绘制绘制函数 y = sin(x)在区间0, 2π上的图像。
使用以下代码实现:```matlabx = 0:001:2pi;y = sin(x);plot(x, y);```四、实验结果1、矩阵运算A+B 的结果为:```matlab1 2 34 5 67 8 9```A×B 的结果为:```matlab0 0 00 0 00 0 0```2、数据类型转换将整数 5 转换为双精度浮点数,结果为 50000。
试验一MATLAB语言基础实验

试验一MATLAB 语言基础实验(软件仿真)一、MATLAB的基本操作1、实验目的(1)学习了解MATLAB语言环境(2)练习MATLAB命令的基本操作(3)练习m文件的基本操作2、实验内容(练习MATLAB命令的基本操作中的内容)1)常规矩阵输入>> a=[1 2 3]a =1 2 3>> a=[1;2;3]a =123>> b=[1 2 5]b =1 2 5>> b=[1 2 5];>> aa =123>> a'ans =1 2 3>> bb =1 2 5>> b'ans =125>> c=a*bc =1 2 52 4 103 6 15>> c=a*b'??? Error using ==> *Inner matrix dimensions must agree.>> a=[1 2 3;4 5 6;7 8 0]a =1 2 34 5 67 8 0>> a^2ans =30 36 1566 81 4239 54 69>> a^0.5ans =0.5977 + 0.7678i 0.7519 + 0.0979i 0.5200 - 0.4680i1.4102 + 0.1013i 1.7741 + 0.6326i 1.2271 - 0.7467i1.2757 - 1.0289i 1.6049 - 1.0272i 1.1100 + 1.6175i 2)作循环命令程序>> makesum=0;for i=1:1:100makesum=makesum+i;end>> makesummakesum =50503)分别执行下列命令>> a=[1 2 3;4 5 6;7 8 0]a =1 2 34 5 67 8 0>> poly(a)ans =1.0000 -6.0000 -72.0000 -27.0000>> rank(a)ans =3>> det(a)ans =27>> trace(a)ans =6>> inv(a)ans =-1.7778 0.8889 -0.11111.5556 -0.7778 0.2222-0.1111 0.2222 -0.1111 >> eig(a)ans =12.1229-0.3884-5.73454)练习m文件的基本操作>> penddemo倒立摆控制系统:二、MATLAB的数值运算1、实验目的(1)学习MATLAB语言的基本矩阵运算(2)学习MATLAB语言的点运算(3)学习复杂运算2、实验内容(1)基本矩阵运算1)创建数值矩阵>>a=[1 2 3;4 5 6;7 8 9];>> aa =1 2 34 5 67 8 9>> a(3,2)ans =8>> a(:,1)ans =147>>t=0:10t =Columns 1 through 100 1 2 3 4 5 6 7 8 9 Column 1110>> u=0:0.1:10u =Columns 1 through 60 0.1000 0.2000 0.3000 0.4000 0.5000 Columns 7 through 120.6000 0.7000 0.8000 0.9000 1.0000 1.1000 Columns 13 through 181.2000 1.3000 1.4000 1.5000 1.6000 1.7000 Columns 19 through 241.8000 1.90002.0000 2.1000 2.2000 2.3000 Columns 25 through 302.4000 2.5000 2.6000 2.7000 2.8000 2.9000 Columns 31 through 363.0000 3.1000 3.2000 3.3000 3.4000 3.5000 Columns 37 through 423.6000 3.7000 3.8000 3.90004.0000 4.1000Columns 43 through 484.2000 4.3000 4.4000 4.5000 4.6000 4.7000 Columns 49 through 544.8000 4.90005.0000 5.1000 5.2000 5.3000 Columns 55 through 605.4000 5.5000 5.6000 5.7000 5.8000 5.9000 Columns 61 through 666.0000 6.1000 6.2000 6.3000 6.4000 6.5000 Columns 67 through 726.6000 6.7000 6.8000 6.90007.0000 7.1000 Columns 73 through 787.2000 7.3000 7.4000 7.5000 7.6000 7.7000 Columns 79 through 847.8000 7.9000 8.0000 8.1000 8.2000 8.3000 Columns 85 through 908.4000 8.5000 8.6000 8.7000 8.8000 8.9000 Columns 91 through 969.0000 9.1000 9.2000 9.3000 9.4000 9.5000 Columns 97 through 1019.6000 9.7000 9.8000 9.9000 10.0000>>a(:,3)=[2;3;4]a =1 2 24 5 37 8 4>>b=[1 1+2i;3+4i 3]b =1.0000 1.0000 +2.0000i3.0000 +4.0000i 3.00002)创建特殊矩阵>> a=ones(3,3)a =1 1 11 1 11 1 1>> b=zeros(2,2)b =0 00 0>> c=eye(4)c =1 0 0 00 1 0 00 0 1 00 0 0 1>> magic(4)ans =16 2 3 135 11 10 89 7 6 124 14 15 13)练习矩阵运算>>a=[0 1 0;0 0 1;-6 -11 -6];>> b=[1 2;3 4;5 6];>> c=[1 1 0;0 1 1];>> v1=c*av1 =0 1 1-6 -11 -5>> v2=a*bv2 =3 45 6-69 -92>> v3=c*a*bv3 =8 10-64 -86>> v4=b*cv4 =1 3 23 7 45 11 6>> v5=c*bv5 =4 68 10>> a^2ans =0 0 1-6 -11 -636 60 25>> a^(1/2)ans =0.0000 + 0.4894i -0.0000 - 0.5588i -0.0000 - 0.0482i0.0000 + 0.2891i 0.0000 + 1.0195i -0.0000 - 0.2696i0.0000 + 1.6179i 0.0000 + 3.2553i 0.0000 + 2.6374i >> a1=a+b*ca1 =1 4 23 7 5-1 0 0>> a2=c*b-a(1:2,1:2)a2 =4 58 10>> a3=a(1:2,2:3)+c*ba3 =5 68 11>> ar=c/aar =-0.8333 -1.0000 -0.16671.0000 1.0000 0 >> al=a\bal =-5.6667 -8.66671.00002.00003.00004.00004)练习矩阵特征运算>> a'ans =0 0 -61 0 -110 1 -6>> inv(a)ans =-1.8333 -1.0000 -0.16671.0000 0 00 1.0000 0 >> diag(a)ans =-6>> tril(a)ans =0 0 00 0 0-6 -11 -6>> inv(a)ans =-1.8333 -1.0000 -0.16671.0000 0 00 1.0000 0>> poly(a)ans =1.0000 6.0000 11.0000 6.0000>> rank(a)ans =3>> det(a)ans =-6>> trace(a)ans =-6>> eig(a)ans =-1.0000-2.0000-3.0000(2)MATLAB语言点的运算1)练习点乘与点除>>a1=[1 2;3 4];>> a2=0.2*a1;>> [a1 a2]ans =1.00002.0000 0.2000 0.40003.00004.0000 0.6000 0.8000>> [a1.*a2 a1./a2]ans =0.2000 0.8000 5.0000 5.00001.8000 3.2000 5.0000 5.00002)由点运算完成标量函数运算与作图>>t=0:2*pi/180:2*pit =Columns 1 through 60 0.0349 0.0698 0.1047 0.1396 0.1745Columns 7 through 120.2094 0.2443 0.2793 0.3142 0.3491 0.3840Columns 13 through 180.4189 0.4538 0.4887 0.5236 0.5585 0.5934Columns 19 through 240.6283 0.6632 0.6981 0.7330 0.7679 0.8029Columns 25 through 300.8378 0.8727 0.9076 0.9425 0.9774 1.0123 Columns 31 through 361.0472 1.0821 1.1170 1.1519 1.1868 1.2217 Columns 37 through 421.2566 1.2915 1.3265 1.3614 1.3963 1.4312 Columns 43 through 481.4661 1.5010 1.5359 1.5708 1.6057 1.6406 Columns 49 through 541.6755 1.7104 1.7453 1.7802 1.8151 1.8500 Columns 55 through 601.8850 1.9199 1.9548 1.98972.0246 2.0595 Columns 61 through 662.0944 2.1293 2.1642 2.1991 2.2340 2.2689 Columns 67 through 722.3038 2.3387 2.3736 2.4086 2.4435 2.4784 Columns 73 through 782.5133 2.5482 2.5831 2.6180 2.6529 2.6878 Columns 79 through 842.7227 2.7576 2.7925 2.8274 2.8623 2.8972 Columns 85 through 902.9322 2.96713.0020 3.0369 3.0718 3.1067 Columns 91 through 963.1416 3.1765 3.2114 3.2463 3.2812 3.3161 Columns 97 through 1023.3510 3.3859 3.4208 3.4558 3.4907 3.5256 Columns 103 through 1083.5605 3.5954 3.6303 3.6652 3.7001 3.7350 Columns 109 through 1143.7699 3.8048 3.8397 3.8746 3.9095 3.9444 Columns 115 through 1203.97944.0143 4.0492 4.0841 4.1190 4.1539 Columns 121 through 1264.1888 4.2237 4.2586 4.2935 4.3284 4.3633 Columns 127 through 1324.3982 4.4331 4.4680 4.5029 4.5379 4.5728 Columns 133 through 1384.6077 4.6426 4.6775 4.7124 4.7473 4.7822 Columns 139 through 1444.8171 4.8520 4.8869 4.9218 4.9567 4.9916 Columns 145 through 1505.0265 5.0615 5.0964 5.1313 5.1662 5.2011 Columns 151 through 1565.2360 5.2709 5.3058 5.3407 5.3756 5.4105 Columns 157 through 1625.4454 5.4803 5.5152 5.5501 5.5851 5.6200Columns 163 through 1685.6549 5.6898 5.7247 5.7596 5.7945 5.8294Columns 169 through 1745.8643 5.8992 5.9341 5.96906.0039 6.0388Columns 175 through 1806.0737 6.1087 6.1436 6.1785 6.2134 6.2483Column 1816.2832>>y1=sin(t)y1 =Columns 1 through 60 0.0349 0.0698 0.1045 0.1392 0.1736Columns 7 through 120.2079 0.2419 0.2756 0.3090 0.3420 0.3746Columns 13 through 180.4067 0.4384 0.4695 0.5000 0.5299 0.5592Columns 19 through 240.5878 0.6157 0.6428 0.6691 0.6947 0.7193Columns 25 through 300.7431 0.7660 0.7880 0.8090 0.8290 0.8480Columns 31 through 360.8660 0.8829 0.8988 0.9135 0.9272 0.9397Columns 37 through 420.9511 0.9613 0.9703 0.9781 0.9848 0.9903Columns 43 through 480.9945 0.9976 0.9994 1.0000 0.9994 0.9976Columns 49 through 540.9945 0.9903 0.9848 0.9781 0.9703 0.9613Columns 55 through 600.9511 0.9397 0.9272 0.9135 0.8988 0.8829Columns 61 through 660.8660 0.8480 0.8290 0.8090 0.7880 0.7660Columns 67 through 720.7431 0.7193 0.6947 0.6691 0.6428 0.6157Columns 73 through 780.5878 0.5592 0.5299 0.5000 0.4695 0.4384Columns 79 through 840.4067 0.3746 0.3420 0.3090 0.2756 0.2419Columns 85 through 900.2079 0.1736 0.1392 0.1045 0.0698 0.0349Columns 91 through 960.0000 -0.0349 -0.0698 -0.1045 -0.1392 -0.1736Columns 97 through 102-0.2079 -0.2419 -0.2756 -0.3090 -0.3420 -0.3746 Columns 103 through 108-0.4067 -0.4384 -0.4695 -0.5000 -0.5299 -0.5592 Columns 109 through 114-0.5878 -0.6157 -0.6428 -0.6691 -0.6947 -0.7193 Columns 115 through 120-0.7431 -0.7660 -0.7880 -0.8090 -0.8290 -0.8480 Columns 121 through 126-0.8660 -0.8829 -0.8988 -0.9135 -0.9272 -0.9397 Columns 127 through 132-0.9511 -0.9613 -0.9703 -0.9781 -0.9848 -0.9903 Columns 133 through 138-0.9945 -0.9976 -0.9994 -1.0000 -0.9994 -0.9976 Columns 139 through 144-0.9945 -0.9903 -0.9848 -0.9781 -0.9703 -0.9613 Columns 145 through 150-0.9511 -0.9397 -0.9272 -0.9135 -0.8988 -0.8829 Columns 151 through 156-0.8660 -0.8480 -0.8290 -0.8090 -0.7880 -0.7660 Columns 157 through 162-0.7431 -0.7193 -0.6947 -0.6691 -0.6428 -0.6157 Columns 163 through 168-0.5878 -0.5592 -0.5299 -0.5000 -0.4695 -0.4384 Columns 169 through 174-0.4067 -0.3746 -0.3420 -0.3090 -0.2756 -0.2419 Columns 175 through 180-0.2079 -0.1736 -0.1392 -0.1045 -0.0698 -0.0349 Column 181-0.0000>> y2=cos(t)y2 =Columns 1 through 61.0000 0.9994 0.9976 0.9945 0.9903 0.9848 Columns 7 through 120.9781 0.9703 0.9613 0.9511 0.9397 0.9272 Columns 13 through 180.9135 0.8988 0.8829 0.8660 0.8480 0.8290 Columns 19 through 240.8090 0.7880 0.7660 0.7431 0.7193 0.6947 Columns 25 through 300.6691 0.6428 0.6157 0.5878 0.5592 0.5299 Columns 31 through 360.5000 0.4695 0.4384 0.4067 0.3746 0.3420 Columns 37 through 420.3090 0.2756 0.2419 0.2079 0.1736 0.1392 Columns 43 through 480.1045 0.0698 0.0349 0.0000 -0.0349 -0.0698 Columns 49 through 54-0.1045 -0.1392 -0.1736 -0.2079 -0.2419 -0.2756 Columns 55 through 60-0.3090 -0.3420 -0.3746 -0.4067 -0.4384 -0.4695 Columns 61 through 66-0.5000 -0.5299 -0.5592 -0.5878 -0.6157 -0.6428 Columns 67 through 72-0.6691 -0.6947 -0.7193 -0.7431 -0.7660 -0.7880 Columns 73 through 78-0.8090 -0.8290 -0.8480 -0.8660 -0.8829 -0.8988 Columns 79 through 84-0.9135 -0.9272 -0.9397 -0.9511 -0.9613 -0.9703 Columns 85 through 90-0.9781 -0.9848 -0.9903 -0.9945 -0.9976 -0.9994 Columns 91 through 96-1.0000 -0.9994 -0.9976 -0.9945 -0.9903 -0.9848 Columns 97 through 102-0.9781 -0.9703 -0.9613 -0.9511 -0.9397 -0.9272 Columns 103 through 108-0.9135 -0.8988 -0.8829 -0.8660 -0.8480 -0.8290 Columns 109 through 114-0.8090 -0.7880 -0.7660 -0.7431 -0.7193 -0.6947 Columns 115 through 120-0.6691 -0.6428 -0.6157 -0.5878 -0.5592 -0.5299 Columns 121 through 126-0.5000 -0.4695 -0.4384 -0.4067 -0.3746 -0.3420 Columns 127 through 132-0.3090 -0.2756 -0.2419 -0.2079 -0.1736 -0.1392 Columns 133 through 138-0.1045 -0.0698 -0.0349 -0.0000 0.0349 0.0698 Columns 139 through 1440.1045 0.1392 0.1736 0.2079 0.2419 0.2756 Columns 145 through 1500.3090 0.3420 0.3746 0.4067 0.4384 0.4695 Columns 151 through 1560.5000 0.5299 0.5592 0.5878 0.6157 0.6428 Columns 157 through 1620.6691 0.6947 0.7193 0.7431 0.7660 0.7880 Columns 163 through 1680.8090 0.8290 0.8480 0.8660 0.8829 0.8988 Columns 169 through 1740.9135 0.9272 0.9397 0.9511 0.9613 0.9703 Columns 175 through 1800.9781 0.9848 0.9903 0.9945 0.9976 0.9994 Column 1811.0000>>y=y1.*y2y =Columns 1 through 60 0.0349 0.0696 0.1040 0.1378 0.1710 Columns 7 through 120.2034 0.2347 0.2650 0.2939 0.3214 0.3473 Columns 13 through 180.3716 0.3940 0.4145 0.4330 0.4494 0.4636 Columns 19 through 240.4755 0.4851 0.4924 0.4973 0.4997 0.4997 Columns 25 through 300.4973 0.4924 0.4851 0.4755 0.4636 0.4494 Columns 31 through 360.4330 0.4145 0.3940 0.3716 0.3473 0.3214 Columns 37 through 420.2939 0.2650 0.2347 0.2034 0.1710 0.1378 Columns 43 through 480.1040 0.0696 0.0349 0.0000 -0.0349 -0.0696 Columns 49 through 54-0.1040 -0.1378 -0.1710 -0.2034 -0.2347 -0.2650 Columns 55 through 60-0.2939 -0.3214 -0.3473 -0.3716 -0.3940 -0.4145 Columns 61 through 66-0.4330 -0.4494 -0.4636 -0.4755 -0.4851 -0.4924 Columns 67 through 72-0.4973 -0.4997 -0.4997 -0.4973 -0.4924 -0.4851 Columns 73 through 78-0.4755 -0.4636 -0.4494 -0.4330 -0.4145 -0.3940 Columns 79 through 84-0.3716 -0.3473 -0.3214 -0.2939 -0.2650 -0.2347 Columns 85 through 90-0.2034 -0.1710 -0.1378 -0.1040 -0.0696 -0.0349 Columns 91 through 96-0.0000 0.0349 0.0696 0.1040 0.1378 0.1710 Columns 97 through 1020.2034 0.2347 0.2650 0.2939 0.3214 0.3473 Columns 103 through 1080.3716 0.3940 0.4145 0.4330 0.4494 0.4636 Columns 109 through 1140.4755 0.4851 0.4924 0.4973 0.4997 0.4997 Columns 115 through 1200.4973 0.4924 0.4851 0.4755 0.4636 0.4494 Columns 121 through 1260.4330 0.4145 0.3940 0.3716 0.3473 0.3214 Columns 127 through 1320.2939 0.2650 0.2347 0.2034 0.1710 0.1378 Columns 133 through 1380.1040 0.0696 0.0349 0.0000 -0.0349 -0.0696 Columns 139 through 144-0.1040 -0.1378 -0.1710 -0.2034 -0.2347 -0.2650 Columns 145 through 150-0.2939 -0.3214 -0.3473 -0.3716 -0.3940 -0.4145 Columns 151 through 156-0.4330 -0.4494 -0.4636 -0.4755 -0.4851 -0.4924 Columns 157 through 162-0.4973 -0.4997 -0.4997 -0.4973 -0.4924 -0.4851 Columns 163 through 168-0.4755 -0.4636 -0.4494 -0.4330 -0.4145 -0.3940 Columns 169 through 174-0.3716 -0.3473 -0.3214 -0.2939 -0.2650 -0.2347 Columns 175 through 180-0.2034 -0.1710 -0.1378 -0.1040 -0.0696 -0.0349 Column 181-0.0000>> plot(t,[y' y1' y2']);>> w=0.1:0.1:2w =Columns 1 through 60.1000 0.2000 0.3000 0.4000 0.5000 0.6000 Columns 7 through 120.7000 0.8000 0.9000 1.0000 1.1000 1.2000 Columns 13 through 181.3000 1.4000 1.5000 1.6000 1.7000 1.8000 Columns 19 through 201.90002.0000>> g1=(1+0.5*w*i)/(1-0.5*w*i)g1 =-1.0296>>g2=(1+0.5*w*i)./(1-0.5*w*i)g2 =Columns 1 through 6-1.5000 -1.2222 -1.1429 -1.1053 -1.0833 -1.0690 Columns 7 through 12-1.0588 -1.0513 -1.0455 -1.0408 -1.0370 -1.0339 Columns 13 through 18-1.0313 -1.0290 -1.0270 -1.0253 -1.0238 -1.0225 Columns 19 through 20-1.0213 -1.0202>>plot(g2)>>xlabel('real g2(w)')>>ylabel('imag g2(w)')>>axis('square')(3)多项式运算1)建立多项式向量>>ap=[1 3 3 1]a p=1 3 3 1>> b=[-1 -2 -3]b =-1 -2 -3>>bp=poly(b)bp =1 6 11 62)练习多项式乘与求根>>p=conv(ap,bp)p =1 9 32 58 57 29 6 >> roots(p)ans =-3.0000-2.0000-1.0003-1.0000 + 0.0003i-1.0000 - 0.0003i-0.99973)练习多项式运算>>a=[1 2 3 4]a =1 2 3 4>> b=[1 -1]b =1-1>>c=a+[zeros(1,length(a)-length(b)) b]c =1 2 4 3>>poly2str(c,'x')ans =x^3 + 2 x^2 + 4 x + 3>> polyvalm(a,3)ans =58三、MATLAB的符号运算1、实验目的(1)学习MATLAB语言的基本符号运算(2)学习MATLAB语言的矩阵符号运算2、实验内容(1)基本符号运算1)符号微分、积分>>syms t>> f1=sin(2*t)f1 =sin(2*t)>> df1=diff(f1)df1 =2*cos(2*t)>> if1=int(f1)if1 =-1/2*cos(2*t)2)泰勒级数展开>>tf1=taylor(f1,8)tf1 =2*t-4/3*t^3+4/15*t^5-8/315*t^73)符号代数方程求解>>syms a b c x>> f=a*x^2+b*x+cf =a*x^2+b*x+c>> ef=solve(f)ef =[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))][ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]4)符号微分方程求解>>f='D2x+2*Dx+10*x=0'f =D2x+2*Dx+10*x=0>> g='Dx(0)=1,x(0)=0'g =Dx(0)=1,x(0)=0>> dfg=dsolve(f,g)dfg =1/3*exp(-t)*sin(3*t)5)积分变换>>syms t>>f1=exp(-2*t)*sin(5*t)>>F1=laplace(f1)F1=5/((s+2)^2+25)>>syms s>>F2=1/(s+2)^2>>f2=ilaplace(F2)>>f2=t*exp(-2*t)>>syms t>>f1=sin(t)>>Fz1=ztrans(f1)Fz1=-z*sin(1)/(2*z*cos(1)-z^2-1)>>syms z>>Fz2=z/(z-2)+z/(z-3)>>fz2=iztrans(Fz2)fz2=2^n+3^n6)计算精度>>g=sym('[pi/2 2;3 exp(1)]')g=[pi/2, 2][ 3,exp(1)]>>g1=vpa(g)g1=[1.570796326794897...,2. ][ 3.,2.718281828459045...] >>digitsDigits=32>>g1=vpa(g,5)g1=[1.5708, 2.][ 3.,2.7183](2)符号矩阵运算1)创建与修改符号矩阵>>G1=sym('[1/(s+1),s/(s+1)/(s+2);1/(s+1)/(s+2),s/(s+2)]') G1 =[ 1/(s+1), s/(s+1)/(s+2)][ 1/(s+1)/(s+2), s/(s+2)]>> G2=subs(G1,G1(2,2),'0')G2 =[ 1/(s+1), s/(s+1)/(s+2)][ 1/(s+1)/(s+2), 0]>> G3=G1(1,1)G3 =1/(s+1)2)符号线性代数>> a=[1 2 3 4];>> inv aans =0.0103>> det aans =97>> eig aans =97>> transpose aans =a3)常规符号运算>>syms s>> d1=1/(s+1);d2=1/(s+2);d=d1*d2d =1/(s+1)/(s+2)>> ad=sym('[s+1 s;0 s+2]');G=d*adG =[ 1/(s+2), s/(s+1)/(s+2)][ 0, 1/(s+1)]>> n1=[1 2 3 4 5];n2=[1 2 3];>> p1=poly2sym(n1);p2=poly2sym(n2);>> p=p1+p2p =x^4+2*x^3+4*x^2+6*x+8>> pn=sym2poly(p)pn =1 2 4 6 8>> a=[0 1;-2 -3];>> gcha=poly2sym(poly(eig(a)))gcha =x^2+3*x+2>> sym sans =s>> mg=s*eye(2)-amg =[ s, -1][ 2, s+3]>> geig=transpose(eig(mg))geig =[ s+1, s+2]>> gdet=det(mg)gdet =s^2+3*s+2>> groot=transpose(solve(gdet))groot =[ -2, -1]>> G=inv(mg)G =[ (s+3)/(s^2+3*s+2), 1/(s^2+3*s+2)][ -2/(s^2+3*s+2), s/(s^2+3*s+2)]>> g11=ilaplace(G(1,1));>> g12=ilaplace(G(1,2));>> g21=ilaplace(G(2,1));>> g22=ilaplace(G(2,2));>> g=[g11 g12;g21 g22]g =[ -exp(-2*t)+2*exp(-t), exp(-t)-exp(-2*t)] [ -2*exp(-t)+2*exp(-2*t), 2*exp(-2*t)-exp(-t)]。
MATLAB第一次实验

华北水利水电大学信息工程学院Matlab实验报告学号:201215828姓名:谭秋教师:陈黎霞实验1.基本操作命令练习一、实验目的1.熟悉matlab软件及基本操作命令;2.通过实验掌握矩阵的建立方法;二、实验环境1.计算机2.matlab软件三、实验说明1.熟悉matlab运行环境,正确操作,认真观察;2.实验学时:2学时;3.整理实验结果,提交实验报告。
四、实验内容1.熟悉(1)命令窗口的使用;(2)工作空间窗口的使用;(3)工作目录、搜索路径的设置;(4)命令历史记录窗口的使用;(5)各菜单及帮助系统的使用。
2.练习常用的键盘操作和快捷键4. (1)输入 A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2; 3 3 3],在MATLAB中可以得到A,B两个矩阵。
如下图所示:在命令窗口中执行下列表达式,掌握其含义:A(2, 3) , A(:,2) ,A(3,:) , A(:,1:2:3) , A(:,3).*B(:,2),A(:,3)*B(2,:),A(2, 3)表示A矩阵里边第二行第三列的元素;A(:,2)表示A矩阵里边第二列的元素;A(3,:)表示A矩阵里边第三行的元素;A(:,1:2:3)表示A矩阵里边按列取,取第一列和第三列的元素;A(:,3).*B(:,2)表示A矩阵里边的第三列元素和B矩阵里边第二列元素的点运算。
A(:,3)*B(2,:)表示A矩阵里边的第三列元素和B矩阵里边的第二列元素的矩阵运算。
(2)输入 C=1:2:20,则C(i)表示什么?其中 i=1,2,3, (10)答:输入 C=1:2:20,则C(i)表示在1到20之间从1开始取数,且每个数相差2,到20截止。
如下图所示。
(3)保存变量 C 到指定路径下;删除workspace中的C,重新加载C。
答:点击save workspace,将变量C保存到本地磁盘D:\ matlab\ bin 里边,并且命名为matlab变量C.m。
matlab第一次实验题目(任选一题)及实验报告模板

To 各位同学:本次实验请在以下三题中选择一题。
另外附录中还有实验报告模板两份。
请同学完成报告后将其打印出来上交。
上交的截止时间是本学期结束之前。
如果您觉得此次试验完成不了任务,可以留待平时解决。
在12月19日我们还有一次实验,到时我会把题目再发给你们。
本学期一共两次实验,要求大家提交两份实验报告。
----------------------------------------------------------------------------------------------------- 实验题1:平衡结构的梁受力计算(线性方程组的应用)有一个平面结构如下所示,有13条梁(图中标号的线段)和8个铰接点(图中标号的圈)联结在一起。
其中1号铰接点完全固定,8号铰接点竖直方向固定,并在2号、5号和6号铰接点上,分别有图示的10吨、15吨和20吨的负载。
在静平衡的条件下,任何一个铰接点上水平和竖直方向受力都是平衡的;已知每条斜梁的角度都是45º。
(1)请列出由各铰接点处受力平衡方程构成的线性方程组;(2)用MATLAB软件求解该线性方程组,确定每条梁受力情况。
目的: 1. 了解MA TLAB软件, 学会MATLAB软件的一些基本操作.2. 练习编写简单的MATLAB程序.3. 利用线性方程组的知识并借助MATLAB软件解决问题。
要求: 1. 实验报告用A4纸打印, 参考附录的格式. 报告上交的截止时间是本学期结束之前。
实验题2:平板的稳态温度分布问题(线性方程组应用)在热传导的研究中,一个重要的问题是确定一块平板的稳态温度分布。
假定下图中的平板代表一条金属梁的截面,并忽略垂直于该截面方向上的热传导。
已知平板内部有30个节点,每个节点的温度近似等于与它相邻的四个节点温度的平均值,例如4292530rd T T T T T +++=;设4条边界上的温度分别等于每位同学学号的后四位的5倍,例如学号为16308209的同学计算时,选择40=l T 、10=u T 、0=r T 、45=d T 。
MATLAB第一次实验

第一次实验1. 求f(x) = 4x 6-x+x 3-95在(0,100)上最大值、最小值,根。
(使用函数fminbnd 、roots ) >>[x,y]=fminbnd('4*x.^6-x+x.^3-95',0,100)x = 0.4432y = -95.3258>> [x,y]=fminbnd('-4*x.^6+x-x.^3+95',0,100)x = 99.9999y = 4.0000e+012>> a=[4 0 0 1 0 -1 -95];roots(a)ans = 1.68600.8525 + 1.4852i0.8525 - 1.4852i-1.7050-0.8431 + 1.4514i-0.8431 - 1.4514i2. 已知t,n 测得对应数据如下:(多项式插值interp1)t = [0,20,40,60,80,100,120,140];n = [0,15,25,-8,12,17,24,19];采用不同的插值方式(line,nearest,spline,cubic )进行插值计算,并在一个figure 中绘制不同的插值方式得到的曲线图(subplot ),标明横坐标、纵坐标,添加相应的注释。
t0=[0,20,40,60,80,100,120,140,160,183.5];n0=[0,1153,2045,2800,3466,4068,4621,5135,5619,6152];n=0:0.001:6152;t=interp1(n0,t0,n,'spline');p=polyfit(n,t,2)p = 0.0000 0.0144 0.0631试求a 和b 的值。
3. 计算积分值: 1).⎰++102dx 1x x (trapz 、quad 两种方法)f=inline('sqrt(x.^2+x+1)','x');>> quad(f,0,1)ans = 1.3369>> x=0:0.01:1;y=sqrt(x.^2+x+1);trapz(x,y)ans = 1.33692).⎰⎰+++++102022)12(dxdy y x xy y x (使用函数dblquad )dblquad('x.^2+y.^2+x*y+2*x+y+1', 0, 1, 0, 2)ans = 10.33334. 编写函数求解 y=⎪⎪⎩⎪⎪⎨⎧>-≤<-≤≤--<2x 7x 22x 11x 1x 21x -2x 1-x 2-22(if ,else, elseif),并绘制x 在[-3,3]之间的曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、实验内容
解:(1)
f1=sym('(2-exp(-2*t))*heaviside(t)');
ezplot(f1,[-10,10]) %符号法
t=-10:0.01:10;
u=stepfun(t,0);
g=(2-exp(-2*t)).*u;
plot(t,g) %向量表示法
运行结果见右图。
(2)
f=sym('cos(pi*t/2)*(heaviside(t)-heaviside(t-4))'); ezplot(f,[-10,10]) %符号法
t=-10:0.01:10;
u1=stepfun(t,0);
u2=stepfun(t,4);
g=cos(pi*t/2).*((u1)-(u2));
plot(t,g) %向量表示法
运行结果见右图。
(3)
f=sym('exp(t)*cos(t)*heaviside(t)'); ezplot(f,[20,40]) %符号法
t=20:0.001:40;
u1=stepfun(t,0);
g=(exp(t)).*cos(t).*u1;
plot(t,g) %向量表示法运行结果见右图。
(4)
f=sym('(2/3)*t*heaviside(t+2)'); ezplot(f,[-10,10]) %符号法
t=-10:0.01:10;
u1=stepfun(t,-2);
g=((2/3)*t).*(u1);
plot(t,g) %向量表示法
运行结果见右图。
解:信号可以表示成以下函数:
f=sym('2*heaviside(t)-heaviside(t-1)-heaviside(t-2)');
那么,根据f可以写出:(选择符号法绘波形,区间适当取值便于展示)
(1)f=sym('2*heaviside(-t)-heaviside(-t-1)-heaviside(-t-2)');
ezplot(f,[-4,1])
图1 第一小题结果图2 第二小题结果
(2)f=sym('2*heaviside(t-2)-heaviside(t-2-1)-heaviside(t-2-2)');
ezplot(f,[0,5])
(3)f=sym('2*heaviside(0.5*t)-heaviside(0.5*t-1)-heaviside(0.5*t-2)');
subplot(2,1,1),ezplot(f,[-1,5]) %a=0.5的时候
f=sym('2*heaviside(2*t)-heaviside(2*t-1)-heaviside(2*t-2)');
subplot(2,1,2),ezplot(f,[-0.5,1.5]) %a=2的时候,图在下页
图3 上图a=0.5;下图a=2。
第三小题
(4)f=sym('2*heaviside(0.5*t+1)-heaviside((0.5*t+1)-1)-heaviside((0.5*t+1)-2)');
ezplot(f,[-5,5]) %下图是第四小题图
解:由题意可以看出,f1是-1~1上的门函数,f2是0~1上的门函数,故仿照例题:t1=-1:0.01:0;
t2=0:0.01:1;
t3=-1:0.01:1; %定义卷积结果范围,易知-1~1
f1=ones(size(t1)); %f1门函数定义
f2=ones(size(t2)); %f2门函数定义
g=conv(f1,f2); %f1*f2卷积
subplot(3,1,1),plot(t1,f1);
subplot(3,1,2),plot(t2,f2);
subplot(3,1,3),plot(t3,g);
运行结果图
解:t=-10:0.01:10;
t1=-5:0.01:5;
u1=stepfun(t1,0);
f1=t1.*u1;
f2=t1.*exp(-t1).*u1.*(t1>=0)+exp(t1).*(t1<0);
g=conv(f1,f2);
subplot(3,1,1);plot(t1,f1);
subplot(3,1,2);plot(t1,f2);
subplot(3,1,3);plot(t,g)
运行结果图。
