2015年广西高考文科数学试题与答案(word版)

合集下载

2015年全国新课标2卷高考文科数学及答案详解

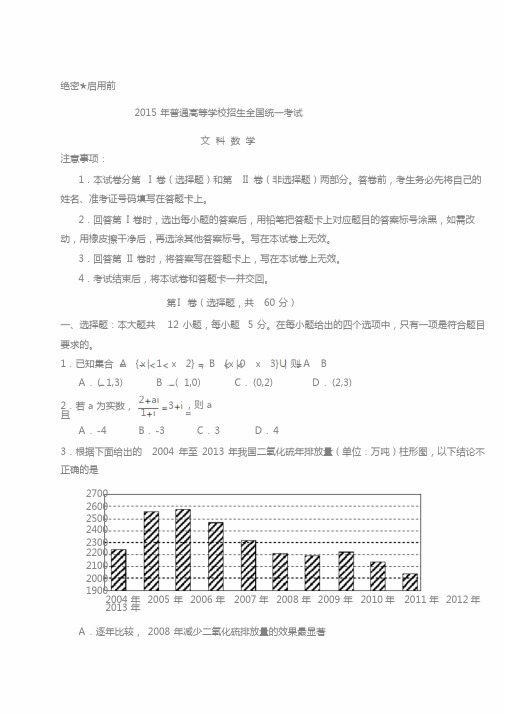
2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟．第Ⅰ卷一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合{}{}30|,21|<<=<<-=x x B x x A ，则=⋃B A ( )A ．(－1,3)B ．(－1,0)C ．(0,2)D ．(2,3)2．若a 为实数，且i iai +=++312，则=a ( ) A ．－4 B ．－3 C ．3 D ．43．根据下面给出的2004年至2013年我国二氧化硫年排放量(单位：万吨)柱形图，以下结论中不正确的是( )A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现成效C ．2006年以来我国二氧化硫年排放量呈减少趋势D ．2006年以来我国二氧化硫年排放量与年份正相关4．向量()1,1-=a ，()2,1-=b ，则()=⋅+a b a 2 ( )A ．－1B ．0C ．1D ．25．设n S 是等差数列{}n a 的前n 项和，若3531=++a a a ，则=5S ( )A ．5B ．7C ．9D ．11 6.第6题图一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为( ) A.18 B.17 C.16 D.157．已知三点()01，A ()30，B ，()32，C ，则ABC ∆外接圆的圆心到原点的距离为( )A.53B.213C.253D.438.第8题图右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的=a ( )A ．0B ．2C ．4D ．149．已知等比数列{}n a 满足411=a ，()14453-=a a a ，则=2a ( ) A ．2 B ．1 C.12 D.1810．已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B ．64π C．144π D．256π11.如图，长方形ABCD 的边AB ＝2，BC ＝1，O 是AB 的中点．点P 沿着边BC ，CD 与DA 运动，记∠BOP ＝x ，将动点P 到A ，B 两点距离之和表示为x 的函数f (x )，则y ＝f (x )的图象大致为( )12.设函数()()2111ln x x x f +-+=，则使得()()12->x f x f 成立的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，1B.()∞+⋃⎪⎭⎫ ⎝⎛∞，，131- C.⎝ ⎛⎭⎪⎫－13，13 D.⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛∞，，3131-- 第Ⅱ卷二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知函数()x ax x f 23-=的图象过点()4,1-，则=a ________.14．若x ，y 满足约束条件⎩⎨⎧ x ＋y －5≤0，2x －y －1≥0，x －2y ＋1≤0，则y x z +=2的最大值为________． 15．已知双曲线过点()34，，且渐近线方程为x y 21±=，则该双曲线的标准方程为________．16．已知曲线x x y ln +=在点()1,1处的切线与曲线()122+++=x a ax y 相切，则=a ________. 三、解答题(解答应写出文字说明，证明过程或演算步骤)17．(本小题满分12分) ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，DC BD 2=(1)求CB sin sin (2)若︒=∠60BAC ，求B ∠18.(本小题满分12分)某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表．图①B地区用户满意度评分的频数分布表满意度评分[50,60)[60,70)[70,80)[80,90)[90,100] 分组频数281410 6 2015·新课标Ⅱ卷第4页(1)在图②中作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)．图②(2)根据用户满意度评分，将用户的满意度分为三个等级：满意度评分低于70分 70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大？说明理由．19.(本小题满分12分)如图，长方体1111D C B A ABCD -中，16=AB ，10=BC ,81=AA ，点E ,F 分别在11B A ,11C D 上，411==F D E A .过点E ,F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值．20.(本小题满分12分)已知椭圆C ：12222=+by a x ()0.>>b a 的离心率为22，点()22，在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ,B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．21.(本小题满分12分)已知函数()()x a x x f -+=1ln ．(1)讨论()x f 的单调性；(2)当()x f 有最大值，且最大值大于22-a 时，求a 的取值范围．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号．22. （本小题满分10分）选修4-1：几何证明选讲如图O 是等腰三角形AB C 内一点, ⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点.（I ）证明EF ∥BC .（II ）若AG 等于⊙O 的半径,且23AE MN == ,求四边形EDCF 的面积23.（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值24.(本小题满分10分)选修4－5：不等式选讲设a ，b ，c ，d 均为正数，且a ＋b ＝c ＋d .证明：(1)若ab >cd ，则a ＋b >c ＋d ；N M G OFE D C B A(2)a＋b>c＋d是|a－b|<|c－d|的充要条件．2015·新课标Ⅱ卷第8页1、选A2、故选D3、选D4、选B5、解：在等差数列中，因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++6、解：如图所示，选D.7、选B.8、故选B.9、解：因为{}),1(4,414531-==a a a a a n 满足所以， .21241,2,2),1(4123144424=⨯=====-=q a a q q a a a a a 所以，所以又解得故选C.10、解：因为A,B 都在球面上，又为该球面上动点，C AOB ,90︒=∠所以三棱锥的体积的最大值为3661213132==⨯⨯R R R ，所以R=6，所以球的表面积为 S=14442=R ππ，故选C.11、解：如图，当点P 在BC 上时， ,tan 4tan ,tan 4,tan ,22x x PB PA x PA x PB x BOP ++=+∴+===∠ 当4π=x 时取得最大值51+，以A,B 为焦点C,D 为椭圆上两定点作椭圆，显然，当点P 在C,D 之间移动时PA+PB<51+. 又函数)(x f 不是一次函数，故选B.xP O DC B A12、解：因为函数时函数是增函数是偶函数，),0[,11)1ln()(2+∞∈+-+=x x x x f .131,)12(,12)12()(22<<->∴->∴->x x x x x x f x f 解得故选A.第二卷一、填空题：本大题共4个小题，每小题5分 13、答：a=-214、解：当x=3,y=2时，z=2x+y 取得最大值8.15、解：设双曲线的方程为.43,4),0(422=≠=-k k k y x ）代入方程，解得，点（1422=-∴y x 双曲线的标准方程为16、解：.122,11'-=∴+=x y xy ，切线方程为切线的斜率为 .8120.08,08,021)2(12222=+=====-=∆=+++++=-=a x y a a a a a ax ax x a ax y x y 所以与切线平行，不符。

2015年高考真题——文科数学(新课标Ⅰ卷)Word版含答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n∈N},B={6,8,12,14},则集合A⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|=（A）3 （B）6 （C）9 （D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛（7）已知是公差为1的等差数列，则=4，=（A）（B）（C）10 （D）12（8）函数f(x)=的部分图像如图所示，则f(x)的单调递减区间为（A）（k-, k-）,k（A）（2k-, 2k-）,k（A）（k-, k-）,k（A）（2k-, 2k-）,k（9）执行右面的程序框图，如果输入的t=0.01，则输出的n=（A）5 （B）6 （C）7 （D）8（10）已知函数，且f（a）=-3，则f（6-a）=（A）-74（B）-54（C）-34（D）-14（11）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r=（A）1(B) 2(C) 4(D) 8（12）设函数y=f（x）的图像关于直线y=-x对称，且f（-2）+f（-4）=1，则a=（A）-1 （B）1 （C）2 （D）42015年普通高等学校招生全国统一考试文科数学第Ⅱ卷注意事项：第Ⅱ卷共3页，须用黑色墨水签字笔在答题卡上作答。

广西2015高考真题试卷(语文+数学+英语+文综+理综和答案)

2015年普通高等学校招生全国统一考试语文本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至4页，第Ⅱ卷5至8页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。

3．第Ⅰ卷共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项符合题目要求。

一、（12分，每小题3分）1．下列词语中加点的字，读音全都正确的一组是A．逾越（yú）鸟瞰（kàn）一丘之貉（lùo）栩栩如生（xǚ）B．溃败（kuì）凹陷（wā）贻笑大方（yí）兢兢业业（jīng）C．咀嚼（zǔ）桧柏（guì）罄竹难书（qìng）饕餮大餐（tiè）D．觊觎（jì）攻讦（jié）光阴荏苒（rǎn）心怀叵测（pǒ）2.下列各句中，加点的成语使用恰当的一项是A．我读过弗莱的著作，很喜欢他那高屋建瓴的气势和包罗万象的体系，更欣赏他努力摆脱主观印象式品评的文学批评方法。

B．奚羽先生指导弟子写论文时强调，学术论文要有的放矢，论证严密，语言准确而简洁，不能模棱两可，也不能繁文缛节。

C．这是一家国家级出版社，近几年来，出版了很多深受读者尤其是在校大学生喜爱的精品图书，不少作家都对它趋之若鹜。

D．虽然已经是晚上了，但候车大厅里依然人来人往，热闹非凡，大喇叭的广播声、商贩的叫卖声、孩子的哭泣声不绝如缕。

3．下列各句中，没有语病的一句是A．不同的生活习俗、自然条件以及地理环境，使各地的民居在平面布局、结构方法、造型等方面呈现出淳朴自然，而又有着各自的特色。

B．历时三年的第六次全国人口普查是一次成功的国情大盘点，其数据将为我国社会经济发展规划的制定和政府的相关决策提供重要参考。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试(全国卷1)文科数学本试卷分第I卷(选择题)和第n卷(非选择题)两部分。

第I卷1至3页，第n卷4至6页。

注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第n卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3. 考试结束，监考员将试题卷、答题卡一并收回。

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)已知集合A={x|x=3n+2,n - N},B={6,8,12,14}, 则集合A - B中元素的个数为(A) 5 (B) 4 ( C) 3 (D) 2T T(2)已知点 A ( 0,1 ), B (3,2 ),向量AC= (-4 , -3 ),则向量BC =(A) (-7 , -4 ) ( B) (7,4 ) ( C) (-1,4 ) (D) (1 , 4)(3)已知复数z满足(z-1 ) i=i+1，则z=(A) -2-I ( B) -2+I (C) 2-I ( D) 2+i(4)如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1, 2, 3,4, 5中任取3个不同的数，则3个数构成一组勾股数的概率为10 1 1 1(A) (B) (C) (D)3 5 10 201(5)已知椭圆E的中心在坐标原点，离心率为，E的右焦点与抛物线C: y2=8x的焦点重合，A,2 B是C的准线与E的两个焦点，贝U |AB|=(A) 3 (B) 6 (C) 9 (D) 12(6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。

数学_2015年广西某校高考数学模拟试卷(文科)(二)(含答案)

2015年广西某校高考数学模拟试卷（文科）（二）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知全集U ＝{1, 2, 3, 4, 5}，集合M ＝{3, 4, 5}，N ＝{1, 2, 5}，则集合{1, 2}可以表示为（）A M ∩NB (∁U M)∩NC M ∩(∁U N)D (∁U M)∩(∁U N)2. 若复数a+3i1+2i （α∈R ，i 为虚数单位）是纯虚数，则实数α的值为（）A −6B −4C 4D 63. 若等比数列{a n }的前n 项和S n =a ⋅3n −2，则a 2=( ) A 4 B 12 C 24 D 364. 已知命题p:∃x ∈R ，x −2>0，命题q:∀x ∈R ，2x >x 2，则下列说法中正确的是（）A 命题p ∨q 是假命题B 命题p ∧q 是真命题C 命题p ∧(￢q)是真命题D 命题p ∨(￢q)是假命题5. 设a =0.36，b =log 36，c =log 510，则（）A c >b >aB b >c >aC a >c >bD a >b >c 6. 某几何体的三视图如图所示，则该几何体的体积为（）A 43 B 52 C 73 D 537. 已知{x ≥1x −y +1≥02x −y −2≤0若ax +y 的最小值是2，则a =( )A 1B 2C 3D 48. 若f(x)=2cos(ωx +φ)+m ，对任意实数t 都有f(t +π4)=f(−t)，且f(π8)=−1则实数m 的值等于（）A ±1B −3或1C ±3D −1或39. 执行如图所示的程序框图，则输出的结果是（）A 14B 15C 16D 1710. △ABC 中，∠BAC ＝120∘，AB ＝2，AC ＝1，D 是边BC 上的一点（包括端点），则AD →⋅BC →的取值范围是（）A [1, 2]B [0, 1]C [0, 2]D [−5, 2]11.如图过拋物线y 2=2px(p >0)的焦点F 的直线依次交拋物线及准线于点A ，B ，C ，若|BC|=2|BF|，且|AF|=3，则拋物线的方程为（） A y 2=32x B y 2=3x C y 2=92x D y 2=9x12. 已知f(x)是定义在R 上的奇函数，f(−1)=−1，且当x >0时，有xf′(x)>f(x)，则不等式f(x)>x 的解集是（）A (−1, 0)B (1, +∞)C (−1, 0)∪(1, +∞)D (−∞, −1)∪(1, +∞)二、填空题：本大题共4小题，每小题5分． 13. 已知sin α2=23，则cos(π−α)=________．14. 甲、乙、丙三名同学中只有一人考了满分，当他们被问到谁考了满分时，甲说：丙没有考满分；乙说：是我考的；丙说：甲说真话．事实证明：在这三名同学中，只有一人说的是假话，那么得满分的同学是________． 15. 在边长为4的正方形ABCD 内部任取一点M ，则满足∠AMB 为锐角的概率为________． 16. A ，B ，C ，D 是同一球面上的四个点，其中△ABC 是正三角形，AD ⊥平面ABC ，AD =4，AB =2√3，则该球的表面积为________．三、解答题：解答应写出文字说明．证明过程或演算步骤17. 已知数列{a n}的前n项和为S n=n2，n∈N∗．（1）证明：数列{a n}是等差数列；（2）设b n=2a n+(−1)n a n，求数列{b n}的前2n项和．18. 在中学生综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评．某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：表1：男生（1）从表二的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率；（2）从表二中统计数据填写下边2×2列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”．参考数据与公式：K2=n(ad−bc)2，其中n=a+b+c+d．(a+b)(c+d)(a+c)(b+d)临界值表：k0 2.706 3.841 6.63519. 如图，已知AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB= 90∘，AB // CD，AD=AF=CD=2，AB=4．(1)求证：AC⊥平面BCE；(2)求三棱锥E−BCF的体积．20. 已知抛物线Γ：y2＝2px(p>0)的焦点到准线的距离为2．(Ⅰ)求p的值；(Ⅱ)如图所示，直线l1与抛物线Γ相交于A、B两点，C为抛物线Γ上异于A、B的一点，且AC⊥x轴，过B作AC的垂线，垂足为M，过C作直线l2交直线BM于点N，设l1，l2的斜率分别为k1，k2，且k1k2＝1．(i)线段|MN|的长是否为定值？若是定值，请求出定值；若不是定值，请说明理由；(ii)求证：A，B，C，N四点共圆．21. 已知函数f(x)=(x2−2x)⋅lnx+ax2+2（1）当a=−1时，求f(x)在（1, f(1)）处的切线方程；（2）设函数g(x)=f(x)−x−2；(I)若函数g(x)有且仅有一个零点时，求a的值；(II)在(I)的条件下，若e−2<x<e，g(x)≤m，求m的取值范围．三.请考生在A，B，C三题中任选一题作答，如果多做，则按所做的第一题记分．作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．（本小题满分10分）A:[选修4-1：几何证明选讲]22. 如图所示，AB为圆O的直径，BC，CD为圆O的切线，B，D为切点．(Ⅰ)求证：AD // OC；(Ⅱ)若圆O的半径为2，求AD⋅OC的值．B:[选修4-4：坐标系与参数方程]23. 在直角坐标系xOy中，圆C的参数方程为{x=3+2cosθy=−4+2sinθ（θ为参数）．（1）以原点为极点、x轴正半轴为极轴建立极坐标系，求圆C的极坐标方程；（2）已知A(−2, 0)，B(0, 2)，圆C上任意一点M(x, y)，求△ABM面积的最大值．C:[选修4-5：不等式选讲]24. 已知函数f(x)＝k−|x−3|，k∈R，且f(x+3)≥0的解集为[−1, 1]．(Ⅰ)求k的值；(Ⅱ)若a、b、c是正实数，且1ka +12kb+13kc=1，求证：19a+29b+39c≥1．2015年广西某校高考数学模拟试卷（文科）（二）答案1. B2. A3. B4. C5. B6. A7. B8. B9. C10. D11. B12. C13. −1914. 甲15. 1−π816. 32π17. （1）证明：当n=1时，a1=S1=1，当n≥2时，a n=S n−S n−1=n2−(n−1)2= 2n−1．当n=1时，上式也成立，∴ a n=2n−1．∴ 当n≥2时，a n−a n−1=(2n−1)−(2(n−1)−1)=2，∴ 数列{a n}是等差数列，以1为首项，2为公差．（2）解：b n=2a n+(−1)n a n=22n−1+(−1)n(2n−1)，∴ 数列{b n}的前2n项和=(21+23+...+22n−1)+[(−1+3)+(−5+7)+...+(−(4n−3)+ (4n−1))]=2(42n−1)4−1+2n=2×42n3+2n−23．18. 解：（1）设从高一年级男生中抽出m人，则m500=45500+400，m=25∴ x=25−15−5=5，y=20−18=2表2中非优秀学生共5人，记测评等级为合格的3人为a，b，c，尚待改进的2人为A，B，则从这5人中任选2人的所有可能结果为(a, b)，(a, c)，(a, A)，(a, B)，(b, c)，(b, A)，(b, B)，(c, A)，(c, B)，(A, B)共10种，记事件C表示“从表二的非优秀学生5人中随机选取2人，恰有1人测评等级为合格”则C的结果为：(a, A)，(a, B)，(b, A)，(b, B)，(c, A)，(c, B)，共6种，∴ P(C)=610=35，故所求概率为35；（2）∵ 1−0.9=0.1，P(K 2≥2.706)=45(15×5−15×10)230×15×25×20=98=1.125<2.706∴ 没有90%的把握认为“测评结果优秀与性别有关”． 19. (1)证明：过C 作CM ⊥AB ，垂足为M ，∵ AD ⊥DC ，∴ 四边形ADCM 为矩形， ∴ AM =MB =2. ∵ AD =2，AB =4，∴ AC =2√2，CM =2，BC =2√2， ∴ AB 2=AC 2+BC 2，即AC ⊥BC . ∵ AF ⊥平面ABCD ，AF // BE ， ∴ EB ⊥平面ABCD .∵ AC ⊂平面ABCD ，∴ AC ⊥EB . ∵ EB ∩BC =B ， ∴ AC ⊥平面BCE .(2)解：∵ AF ⊥平面ABCD ，CM ⊂平面ABCD ， ∴ AF ⊥CM .∵ CM ⊥AB ，AB ∩AF =A ， ∴ CM ⊥平面ABEF ，∴ V E−BCF =V C−BEF =13×12×BE ×EF ×CM =16×2×4×2=83．20. （1）由题意得，p ＝2；(2)(i)设A(x 1, y 1)，B(x 2, y 2)，则C(x 1, −y 1)，M(x 1, y 2)；直线l 1的方程为y ＝k 1x +b ，由{y =k 1x +b y 2=4x消元整理可得：k 12x 2+(2bk 1−4)x +b 2＝0，所以x 1+x 2=4−2bk 1k 12，x 1x 2=b 2k 12；可得y 1+y 2=4k 1；y 1y 2=4bk 1；直线l 2的方程为：y +y 1＝k 2(x −x 1)，所以可求得N(y 1+y 2k 2+x 1, y 2)；所以|MN|=y 1+y 2k 2=4k 1k 2=4；(ii)证明：AB 的中点E(2−bk 1k 12, 2k 1)；则AB 的中垂线方程为：y −2k 1=−1k 1(x −2−bk 1k 12)；与AC 的中垂线x 轴的交点为：O′(2k 12−bk 1+2k 12, 0)；所以△ABC 的外接圆的方程为： (x −2k 12−bk 1+2k 12)2+y 2＝(2k 12−bk 1+2k 12−x 2)2+y 22；由上可知，N(x 1+4, y 2)； ∵ x 1+4−2k 12−bk 1+2k 12+x 2−2k 12−bk 1+2k 12=x 1+x 2+4−22k 12−bk 1+2k 12=0，∴ (x 1+4−2k 12−bk 1+2k 12)2+y 22＝(2k 12−bk 1+2k12−x 2)2+y 22；所以A ，B ，C ，N 四点共圆．21. 解：（1）当a =−1时，f(x)=(x 2−2x)⋅lnx −x 2+2，定义域(0, +∞) ∴ f′(x)=(2x −2)⋅lnx +(x −2)−2x ． ∴ f′(1)=−3，又f(1)=1，∴ f(x)在（1, f(1)）处的切线方程3x +y −4=0． (2)(I)令g(x)=f(x)−x −2=0则(x 2−2x)⋅lnx +ax 2+2=x +2，即a =1−(x−2)lnxx令ℎ(x)=1−(x−2)lnxx ，则ℎ′(x)=1−x−2lnxx 2令t(x)=1−x −2lnx ，则t′(x)=−x−22∵ x >0，∴ t′(x)<0，∴ t(x)在(0, +∞)上是减函数，又∵ t(1)=ℎ′(1)=0，∴ 当0<x <1时，ℎ′(x)>0，当x >1时，ℎ′(x)<0， ∴ ℎ(x)在(0, 1)上单调递增，在(1, +∞)上单调递减， ∴ ℎ(x)max =ℎ(1)=1，∴ 当函数g(x)有且仅有一个零点时a =1，(II)当a =1时，g(x)=(x 2−2x)⋅lnx +x 2−x ，若e −2<x <e ，g(x)≤m ，只需证明g(x)max ≤m ， ∴ g′(x)=(x −1)(3+2lnx)，令g′(x)=0得x =1或x =e −32 又∵ e −2<x <e ，∴ 函数g(x)在（e−2, e−32）上单调递增，在(e−32, 1)上单调递减，在(1, e)上单调递增又g（e−32）=−12e−3+2e−32，g(e)=2e2−3e∵ g（e−32）=−12e−3+2e−32<2e−32<2e<2e(e−32)=g(e)，∴ g（e−32）<g(e)，∴ m≥2e2−3e22. （1）证明：如图，连接BD、OD．∵ CB、CD是⊙O的两条切线，∴ BD⊥OC，∴ ∠2+∠3＝90∘又AB为⊙O直径，∴ AD⊥DB，∠1+∠2＝90∘，∴ ∠1＝∠3，∴ AD // OC；（2）AO＝OD，则∠1＝∠A＝∠3，∴ Rt△BAD∽Rt△ODC，∵ 圆O的半径为2，∴ AD⋅OC＝AB⋅OD＝8．23. 圆C的参数方程为{x=3+2cosθy=−4+2sinθ（θ为参数）所以普通方程为(x−3)2+(y+4)2＝4．，x＝ρcosθ，y＝ρsinθ，可得(ρcosθ−3)2+(ρsinθ+4)2＝4，化简可得圆C的极坐标方程：ρ2−6ρcosθ+8ρsinθ+21＝0．点M(x, y)到直线AB:x−y+2＝0的距离为d=√2△ABM的面积S=12×|AB|×d=|2cosθ−2sinθ+9|=|2√2sin(π4−θ)+9|所以△ABM面积的最大值为9+2√224. （1）f(x+3)≥0的解集为[−1, 1]，即为|x|≤k的解集为[−1, 1]，(k>0)，即有[−k, k]＝[−1, 1]，解得k＝1；（2）证明：将k＝1代入可得，1 a +12b+13c=1(a, b, c>0)，则a+2b+3c＝(a+2b+3c)(1a +12b+13c)＝3+(2ba+a2b)+(3ca+a3c)+(3c2b+2b3c)≥3+2√2ba ⋅a2b+2√3ca⋅a3c+2√3c2b⋅2b3c=3+2+2+2＝9，当且仅当a＝2b＝3c，上式取得等号．则有19a+29b+39c≥1．。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试（全国卷1）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3. 考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n ∈N},B={6,8,12,14},则集合A ⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|= （A）3 （B）6 （C）9 （D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛（7）已知是公差为1的等差数列，则=4，= （A）（B）（C）10 （D）12（8）函数f(x)=的部分图像如图所示，则f(x)的单调递减区间为（A）（k-, k-）,k（A）（2k-, 2k-）,k（A）（k-, k-）,k（A）（2k-, 2k-）,k（9）执行右面的程序框图，如果输入的t=0.01，则输出的n=（A）5 （B）6 （C）7 （D）8（10）已知函数，且f（a）=-3，则f（6-a）=（A）-74（B）-54（C）-34（D）-14（11）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r=（A ）1 (B) 2 (C) 4 (D) 8（12）设函数y=f （x ）的图像关于直线y=-x 对称，且f （-2）+f （-4）=1，则a= （A ）-1 （B ）1 （C ）2 （D ）4第Ⅱ卷注意事项：第Ⅱ卷共3页，须用黑色墨水签字笔在答题卡上作答。

2015年普通高等学校招生全国统一考试文科数学试题及答案.

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

页。

注意事项：1. 1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 2. 第Ⅰ卷每小题选出答案后，用第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答毫米黑色签字笔书写作答..若在试题卷上作答，答案无效。

答，答案无效。

3. 3. 考试结束，监考员将试题卷、答题卡一并收回。

考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n ÎN},B={6,8,12,14},N},B={6,8,12,14},则集合则集合A ÇB 中元素的个数为中元素的个数为（A ）5（B ）4（C ）3（D ）2（2）已知点A （0,10,1）），B （3,23,2）），向量AC =（-4-4，，-3-3）），则向量BC = （A ）（-7-7，，-4-4））（（B ）（7,47,4））（（C ）（-1,4-1,4））（（D ）（1，4）（3）已知复数z 满足（满足（z-1z-1z-1））i=i+1i=i+1，则，则z=（（A ）-2-I -2-I （（B ）-2+I -2+I （（C ）2-I 2-I （（D ）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，个整数可作为一个直角三角形三条边的边长，则称这则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为个数构成一组勾股数的概率为（（A ）103（（B ）15（（C ）110（（D ）120（5）已知椭圆E 的中心在坐标原点，离心率为12，E 的右焦点与抛物线C ：y ²=8x 的焦点重合，的焦点重合，A A ，B 是C 的准线与E 的两个焦点，则的两个焦点，则|AB|= |AB|=（（A ）3 3 （（B ）6 6 （（C ）9 9 （（D ）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题::“今有委米依垣内角，下周八尺，高五尺。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试(全国卷1）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1。

答题前,考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动,用橡皮擦干净后,在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答。

若在试题卷上作答,答案无效。

3。

考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分,在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合A=｛x|x=3n+2,n ∈N｝，B=｛6,8,12，14｝,则集合A ⋂B中元素的个数为(A）5 (B）4 （C）3 （D）2(2）已知点A（0，1）,B(3,2），向量AC=(-4，—3），则向量BC=（A）（—7，—4） (B）（7,4）（C）（—1,4）（D）（1，4）（3）已知复数z满足（z—1)i=i+1，则z=（A）—2-I （B)—2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数，从1，2，3,4,5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103(B）15(C）110(D）120(5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则｜AB｜= （A）3 (B）6 （C)9 （D)12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问：积及为米几何?”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3,估算出堆放斛的米约有A.14斛 B。

2015年全国高考文科数学试题及答案-新课标1汇编

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3. 考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n ∈N},B={6,8,12,14},则集合A ⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|= （A）3 （B）6 （C）9 （D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛（7）已知{a n }是公差为1的等差数列，S n 为{a n }的前n 项和。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试（全国卷1）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n∈N},B={6,8,12,14},则集合A⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|= （A）3 （B）6 （C）9 （D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛（7）已知是公差为1的等差数列，则=4，=（A）（B）（C）10 （D）12（8）函数f(x)=的部分图像如图所示，则f(x)的单调递减区间为（A）（k-, k-）,k（A）（2k-, 2k-）,k（A）（k-, k-）,k（A）（2k-, 2k-）,k（9）执行右面的程序框图，如果输入的t=0.01，则输出的n=（A）5 （B）6 （C）7 （D）8（10）已知函数，且f（a）=-3，则f（6-a）=（A）-74（B）-54（C）-34（D）-14（11）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r=（A ）1 (B) 2 (C) 4 (D) 8（12）设函数y=f （x ）的图像关于直线y=-x 对称，且f （-2）+f （-4）=1，则a= （A ）-1 （B ）1 （C ）2 （D ）4第Ⅱ卷注意事项：第Ⅱ卷共3页，须用黑色墨水签字笔在答题卡上作答。

2015年全国高考文科数学试题及答案-新课标2

绝密★启用前2015 年普通高等学校招生全国统一考试文科数学注意事项：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

答卷前，考生务必先将自己的姓名、准考证号码填写在答题卡上。

2．回答第I 卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第II 卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第I 卷（选择题，共60 分）一、选择题：本大题共12 小题，每小题 5 分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合 A { x| 1 x 2} ，B {x |0x 3} ，则 A BA．( 1,3) B．( 1,0) C．(0,2) D．(2,3)2．若 a 为实数，且21aii3i，则 a=A．-4 B．-3 C．3 D．43．根据下面给出的2004 年至2013 年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论不正确的是2700260025002400230022002100200019002004 年2005 年2006 年2007 年2008 年2009 年2010 年2011 年2012 年2013 年A．逐年比较，2008 年减少二氧化硫排放量的效果最显著B．2007 年我国治理二氧化硫排放显现成效C．2006 年以来我国二氧化硫年排放量呈减少趋势D．2006 年以来我国二氧化硫年排放量与年份正相关4．向量 a (1, 1) ，b ( 1,2) ，则 (2a b) aA．-1 B．0 C．1 D．35．设 S n 等差数列 { a n } 的前 n 项和。

若a1 + a3 + a5 = 3，则 S5 = A．5 B．7 C．9 D．116．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为A ．18B．17C．16D．157．已知三点A(1,0) ，B(0, 3) ，C (2, 3) ，则ΔABC 外接圆的圆心到原点的距离为A ．53B．213C．2 53D．438．右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试（全国卷1）文科数学本试卷分第Ⅰ卷（选择题)和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1. 答题前,考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2。

第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答。

若在试题卷上作答，答案无效。

3。

考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的.(1）已知集合A={x｜x=3n+2,n ∈N｝，B={6，8,12，14｝，则集合A ⋂B中元素的个数为(A）5 （B）4 （C）3 (D）2（2）已知点A（0，1）,B(3,2），向量AC=（-4，-3），则向量BC=（A）（—7，—4) (B)（7,4）（C）(-1,4） (D)（1，4)（3）已知复数z满足(z-1）i=i+1,则z=（A）—2—I （B）—2+I (C）2—I （D)2+i(4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2,3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A)103(B）15（C）110(D）120（5）已知椭圆E的中心在坐标原点，离心率为12,E的右焦点与抛物线C:y²=8x的焦点重合,A，B是C的准线与E的两个焦点，则|AB｜= （A）3 （B）6 （C）9 (D）12（6）《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。

问：积及为米几何？"其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?"已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A。

[实用参考]2015年全国高考文科数学试题及答案-新课标

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3.考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={G|G=3n+2,n∈N},B={6,8,12,14},则集合A⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC= （A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I（B）-2+I（C）2-I（D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8G的焦点重合，A，B是C的准线与E的两个焦点，则|AB|=（A）3（B）6（C）9（D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有A.14斛B.22斛C.36斛D.66斛（7）已知是公差为1的等差数列，则=4，= （A）（B）（C）10（D）12（8）函数f(G)=的部分图像如图所示，则f(G)的单调递减区间为（A）（k-,k-）,k（A）（2k-,2k-）,k（A）（k-,k-）,k（A）（2k-,2k-）,k（9）执行右面的程序框图，如果输入的t=0.01，则输出的n=（A）5（B）6（C）7（D）8（10）已知函数，且f（a）=-3，则f（6-a）=（A）-74（B）-54（C）-34（D）-14（11）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示，若该几何体的表面积为16+20π，则r=（A）1(B)2(C)4(D)8（12）设函数y=f（G）的图像关于直线y=-G对称，且f（-2）+f（-4）=1，则a=（A）-1（B）1（C）2（D）4第Ⅱ卷注意事项：第Ⅱ卷共3页，须用黑色墨水签字笔在答题卡上作答。

2015年广西高考文科数学试题与答案（word版）

2015年广西高考文科数学试题与答案（word版）2015年广西高考文科数学试题与答案（word 版）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A=｛x|-1<x<x< p="">（A ）(-1,3) （B ）(-1,0) （C ）(0,2) （D ）(2,3)（2）若a 为实数且231ai i i+=++,则a= （A ）-4 （B ）-3 （C ）3 （D ）4（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是（A ）逐年比较，2008年减少二氧化硫排放量的效果最显著(B)2007年我国治理二氧化硫排放显现(C)2006年以来我国二氧化硫年排放量呈减少趋势(D)2006年以来我国二氧化硫年排放量与年份正相关（4）=?+-=-=→→→→→a b a b a )2(),2,1(),1,1(则（A ）-1 （B ）0 （C ）1 （D ）2（5）n S 是等差数列｛a n ｝的前n 项和，若a 1+ a 3+ a 5=3，则=5S（A ）5 （B ）7 （C ）9 （D ）11（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的与剩余部分体积的比值为（A ）81 （B ）71 （C ）61 （D ）51 （7）过三点A （0,0），B （0,3），C （2,3）则ABC ?外接圆的圆心到原点的距离为（A ）35（B ）321（C ）352 （D ）34 （8）右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b 分别为14,18，则输出的a=A.0B.2C.4D.14（9）已知等比数列{}n a 满足114a =，()35441a a a =-，则2a = （A ）2 （B ）1 （C ）21 （D ）81 （10）已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC 体积的最大值为36，则球O 的表面积为A ．36π B.64π C.144πD.256π（11）.如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x 。

2015年全国高考文科数学试题及标准答案

绝密★启封并使用完毕前2０１５年普通高等学校招生全国统一考试(全国卷1）文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项:1. 答题前,考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

２. 第Ⅰ卷每小题选出答案后，用２B铅笔把答题卡上对应题目的答案标号涂黑;如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用０．５毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3．考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题,每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(１）已知集合A={x｜x=３n+2,ｎ∈N}，Ｂ＝{6,8,12,１４｝，则集合A ⋂Ｂ中元素的个数为ﻩ（A)5ﻩ(B）4ﻩﻩ（C）3 （D)2(2）已知点Ａ（0，1）,Ｂ（3,2)，向量AC＝（-4，－3），则向量BC＝（Ａ）（-7，-4）(B）(7,4）（C)(－１,4) (D）(1，4）(3)已知复数z满足(z－1)i=i+１，则z=（A)-2-I （B）-2+I （C)2-Ｉ (D）２+i（4)如果３个整数可作为一个直角三角形三条边的边长，则称这３个数为一组勾股数,从１,2,3，４，5中任取３个不同的数,则3个数构成一组勾股数的概率为(A）103（B)15(Ｃ）110(Ｄ)120（５）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²＝8x的焦点重合,A,Ｂ是C的准线与E的两个焦点，则|AB｜＝（A）3 (B)6 （Ｃ)9 (Ｄ)12(６)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问：积及为米几何?”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一),米堆底部的弧度为８尺,米堆的高为５尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为１.６2立方尺,圆周率约为3，估算出堆放斛的米约有ﻩ A.１4斛 B.22斛Ｃ.36斛 D.66斛（7）已知是公差为1的等差数列，则＝4，=(A)（B）（Ｃ）１0 (D）12(８）函数ｆ(x)＝的部分图像如图所示,则f(x)的单调递减区间为(A)(k－， k-),ｋ(A）(2k-, ２ｋ-),k。

2015年全国高考文科数学试题及答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试(全国卷1）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0。

5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效.3。

考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x｜x=3n+2,n ∈N},B=｛6，8,12,14},则集合A ⋂B中元素的个数为（A）5 （B）4 （C)3 （D）2(2）已知点A（0，1),B（3,2)，向量AC=（—4,—3），则向量BC=(A）（—7，—4）（B）（7，4）（C）（—1，4) （D）(1，4)（3）已知复数z满足(z—1)i=i+1,则z=（A）-2—I （B)-2+I （C）2-I （D)2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1,2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D)120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点,则|AB｜= （A）3 （B）6 （C）9 （D）12(6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何？”其意思为:“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？"已知1斛米的体积约为1。

2015年全国高考文科数学试题与答案

绝密★启封并使用完毕前2015年普通高等学校招生全国统一考试（全国卷1）文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

注意事项：1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上。

考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。

2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。

第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。

3. 考试结束，监考员将试题卷、答题卡一并收回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x=3n+2,n ∈N},B={6,8,12,14},则集合A ⋂B中元素的个数为（A）5 （B）4 （C）3 （D）2（2）已知点A（0,1），B（3,2），向量AC=（-4，-3），则向量BC=（A）（-7，-4）（B）（7,4）（C）（-1,4）（D）（1，4）（3）已知复数z满足（z-1）i=i+1，则z=（A）-2-I （B）-2+I （C）2-I （D）2+i（4）如果3个整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则3个数构成一组勾股数的概率为（A）103（B）15（C）110（D）120（5）已知椭圆E的中心在坐标原点，离心率为12，E的右焦点与抛物线C：y²=8x的焦点重合，A，B是C的准线与E的两个焦点，则|AB|= （A）3 （B）6 （C）9 （D）12（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2015年广西高考文科数学试题与答案
（word 版）
一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合A=｛x|-1<x<2｝，B=｛x|0<x<3｝,则AUB=
（A ）(-1,3) （B ）(-1,0) （C ）(0,2) （D ）(2,3) （2）若a 为实数且
231ai
i i
+=++,则a= （A ）-4 （B ）-3 （C ）3 （D ）4
（3）根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。

以下结论不正确的是
（A ）逐年比较，2008年减少二氧化硫排放量的效果最显著 (B)2007年我国治理二氧化硫排放显现
(C)2006年以来我国二氧化硫年排放量呈减少趋势 (D)2006年以来我国二氧化硫年排放量与年份正相关（4）=⋅+-=-=→
→
→
→
→
a b a b a )2(),2,1(),1,1(则
（A ）-1 （B ）0 （C ）1 （D ）2
（5）n S 是等差数列｛a n ｝的前n 项和，若a 1+ a 3+ a 5=3，则=5S
（A ）5 （B ）7 （C ）9 （D ）11
（6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的与剩余部分体积的比值为
（A ）
81 （B ）71 （C ）61 （D ）5
1 （7）过三点A （0,0），B （0,
3），C （2,3）
则ABC ∆外接圆的圆心到原点的距离为（A ）35 （B ）
321（C ）352 （D ）3
4 （8）右边程序抗土的算法思路源于我国古
代数学名著《九章算术》中的“更相减损术”。

执行该程序框图，若输入a,b 分别为14,18，则输出的a=
A.0
B.2
C.4
D.14 （9）已知等比数列{}n a 满足11
4a =
，()35441a a a =-，则2a = （A ）2 （B ）1 （C ）21 （D ）8
1
（10）已知A,B 是球O 的球面上两点，∠AOB=90,C 为该球面上的动点，若三棱锥O-ABC
体积的最大值为36，则球O 的表面积为 A ．36π B.64π C.144π D.256π
（11）.如图，长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x 。

将动点P 到AB 两点距离之和表示为x 的函数f （x ），则f （x ）的图像大致为
（12）的取值范围是成立的则使得设函数x x f x f x x x f )12()(,11
)1ln()(2
->+-+= （A ）)1,31( （B ）),1()31,(+∞-∞ （C ）)3131(，-（D ）)3
1
()31(∞+--∞，，
二、填空题
（13）=--=a x ax x f ）则的图象过点（已知函数4,12)(3
（14）若x ，y 满足约束条件⎪⎩
⎪⎨
⎧≤+-≥--≤-+0120120
5y x y x y x ，则y x z
+=2的最大值为____________.
（15）已知双曲线过点)3,4(且渐近线方程为x y 2
1
±
=，则该双曲线的标准方程是（16）已知曲线y=x+lnx 在点（1,1）处的切线与曲线1)2(3
+++=x a ax y 相切，则a= 三．解答题
（17）∆ABC 中，D 是BC 上的点，AD 平分∠BAC ，BD=2DC (Ⅰ) C
B ∠∠sin sin 求
(Ⅱ) B BAC ∠=∠求若,600
(18)某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表
（1）做出B 地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评
分的平均值及分散程度（不要求计算出具体值，给出结论即可）（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：
满意度评分低于70分 70分到89分
不低于90分满意度等级
不满意
满意
非常满意
估计哪个地区用户的满意度等级为不满意的概率大
19．（12分）如图，长方体ABCD-A 1B 1C 1D 1中AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4。

过E ，F 的平面与此长方体的面相交，交线围成一个正方形（Ⅰ）在图中画出这个正方形（不必说出画法和理由）（Ⅱ）求平面a 把该长方体分成的两部分体积的比值。

20. 椭圆C ：0)b (a 1,b y a x 22
22>>=+的离心率）2，2，点（2
2
在C 上（1）求椭圆C 的方程
（2）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M.
证明：直线OM 的斜率与l 的斜率的乘积为定值； 21.设函数
(Ⅰ)讨论：f(x)的单调性；
（Ⅱ）当f(x)有最大值，且最大值大于2a-2时，求a 的取值范围
请考生在22、23、24题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清题号。

（22）（本小题满分10分）选修4—1：几何证明选讲如图，O 为等腰三角形ABC 内一点，圆O 与ABC 的底边BC 交于M 、N 两点与底边上的高AD 交于点G ，且与AB 、AC 分别相切于E 、F 两点.
（1）证明：EF 平行于BC
（2）若AG 等于圆O 的半径，且AE=MN=
,求四边形
EBCF 的面积。

（23）（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线
在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线：
，曲线：
.
（1）.求与交点的直角坐标（2）.若与
相交于点A ，与
相交于点B ，求
的最大值
（24）（本小题满分10分）选修4-5不等式选讲设a 、b 、c 、d 均为正数，且a+b=c+d,证明：
d c b a cd ab +>+>则若,)1(
)
1(ln )(x a x x f -+=⎩
⎨⎧<≤≠==)0,0t (sin cos :1πααα
为参数，t t y t x C
的充要条件是d c b a d c b a -<-+>+)2(。

2015年广西高考文科数学试题与答案(word版)

2015年全国新课标2卷高考文科数学及答案详解

2015年高考真题——文科数学(新课标Ⅰ卷)Word版含答案

广西2015高考真题试卷(语文+数学+英语+文综+理综和答案)

2015年全国高考文科数学试题及答案

数学_2015年广西某校高考数学模拟试卷(文科)(二)(含答案)

2015年全国高考文科数学试题及答案

最新2015年全国高考文科数学试题及答案

2015年普通高等学校招生全国统一考试文科数学试题及答案.

2015年全国高考文科数学试题及答案

2015年全国高考文科数学试题及答案-新课标1汇编

2015年全国高考文科数学试题及答案

2015年全国高考文科数学试题及答案-新课标2

2015年全国高考文科数学试题及答案

[实用参考]2015年全国高考文科数学试题及答案-新课标

2015年广西高考文科数学试题与答案（word版）

2015年全国高考文科数学试题及标准答案

2015年全国高考文科数学试题及答案

2015年全国高考文科数学试题与答案