振动位移速度加速度
何谓振幅振动速度振速振动加速度

何谓振幅振动速度振速振动加速度振动一般可以用以下三个单位表示:mm、mm/s、mm/s2。
振幅、振动速度(振速)、振动加速度。
振幅是表象,速度和加速度是转子激振力的程度。
mm振动位移:一般用于低转速机械的振动评定; mm/s振动速度:一般用于中速转动机械的振动评定;mm/s2 振动加速度:一般用于高速转动机械的振动评定。
工程实用的振动速度是速度的有效值,表征的是振动的能量;加速度是用的峰值,表征振动中冲击力的大小。
振幅理解成路程,单位是mm;把振速理解成速度,单位是mm/s;振动加速度理解成运动加速度,单位mm/s2。
速度描述的是运动快慢;振速就是振动快慢,一秒内能产生的振幅。
振幅相同的设备,它的振动状态可能不同,所以引入了振速。
位移、速度、加速度都是振动测量的度量参数。
就概念而言,位移的测量能够直接反映轴承固定螺栓和其它固定件上的应力状况。
例如:通过分析透平机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。
速度反映轴承及其它相关结构所承受的疲劳应力。
而这正是导致旋转设备故障的重要原因。
加速度则反映设备内部各种力的综合作用。
表达上三者均为正弦曲线,分别有90度,180度的相位差。
现场应用上,对于低速设备(转速小于1000RPM)来说,位移是最好的测量方法。
而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。
另外还需要了解传感器的工作原理及应用选择,提及一点,例如采用涡流传感器测量的位移和应用加速度传感器通过两次积分输出的位移所得到的东西是完全不一样的。
涡流传感器测量轴承与轴杆之间的相对运动,加速度传感器测量轴承顶部的振动,然后转换成位移。
如整个轴承振动的很厉害,轴与轴承的相对运动很小,涡流传感器就不能反应出这样的状态,而加速度传感器则可以。
两种传感器测量两种不同的现象。
振动单位换算表
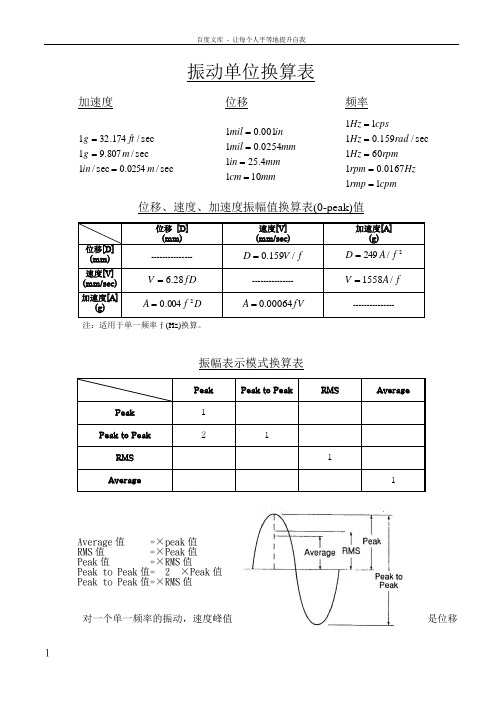
振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注:适用于单一频率f (Hz)换算。
振幅表示模式换算表Peak Peak to PeakRMS AveragePeak 1 Peak to Peak2 1 RMS 1 Average1Average 值 =×peak 值 RMS 值 =×Peak 值 Peak 值 =×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动,速度峰值是位移峰值的2πf倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
振动加速度计算公式

振动加速度计算公式
振动是物体在固定点或轴线周围做有规律地往复运动。
振动加速度是描述物体振动情况的一个物理量,表示单位时间内物体所获得的速度变化量。
首先,简谐振动的运动方程可以表示为:
x = Acos(ωt + φ)
其中,x为物体的位移,A为振幅,ω为角频率,t为时间,φ为相位常数。
其次,速度是位移对时间的导数,即
v = dx/dt = -Aωsin(ωt + φ)
再次,加速度是速度对时间的导数,即
a = dv/dt = -Aω^2cos(ωt + φ)
根据上述推导,振动加速度计算公式为:
a = -Aω^2cos(ωt + φ)
在上述公式中,A表示振幅,ω表示角频率,t表示时间,φ表示相位常数。
振幅决定了振动的幅度大小,角频率则影响振动的周期,相位常数则决定了振动的起始位置。
此外,还有一种计算振动加速度的方法是使用泰勒级数。
泰勒级数是一种将函数在其中一点展开成无穷级数的方法,通过求取一定阶数的导数来逼近其中一函数的值。
对于振动加速度,可以使用泰勒级数展开cos函数来计算。
根据泰勒
级数展开可得到:
cos(x) = 1 - (x^2/2!) + (x^4/4!) - (x^6/6!) + ...
通过对cos(x)函数进行泰勒级数展开,并截取一定阶数的项,可以
计算出振动加速度的近似值。
综上所述,振动加速度的计算公式可以根据物体振动特性得出,根据
简谐振动的运动方程和泰勒级数展开可以求得振动加速度的精确或近似值。
这些计算方法能够帮助我们更好地理解和描述振动现象。
第二章 旋转机械振动分析基础汇总
第二章 旋转机械振动分析基础振动在设备故障诊断中占了很大的比重,是影响设备安全、稳定运行的重要因素。
振动又是设备的“体温计”,直接反映了设备的健康情况,是设备安全评估的重要指标。
一台机组正常运行时,其振动值和振动变化值都应该比较小。
一旦机组振动值变大,或振动变的不稳定,都说明设备出现了一定程度的故障。
第一节 振动分析的基本概念振动是一个动态量。
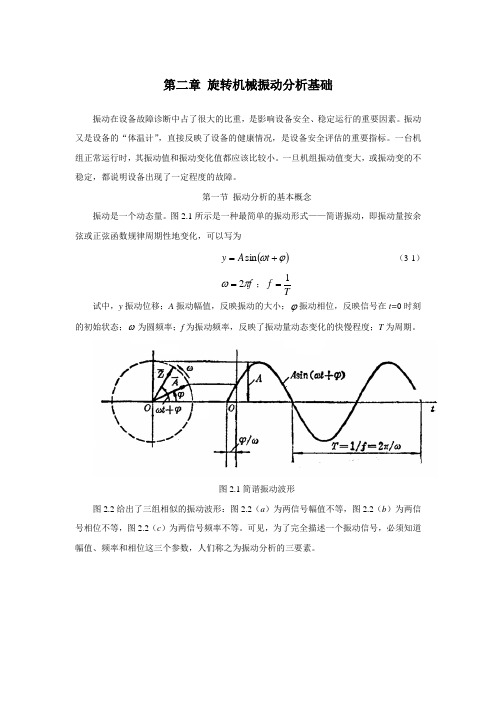
图2.1所示是一种最简单的振动形式——简谐振动,即振动量按余弦或正弦函数规律周期性地变化,可以写为()ϕω+=t A y sin (3-1)f πω2=;Tf 1= 试中,y 振动位移;A 振动幅值,反映振动的大小;ϕ振动相位,反映信号在t=0时刻的初始状态;ω为圆频率;f 为振动频率,反映了振动量动态变化的快慢程度;T 为周期。
图2.1简谐振动波形图2.2给出了三组相似的振动波形:图2.2(a )为两信号幅值不等,图2.2(b )为两信号相位不等,图2.2(c )为两信号频率不等。
可见,为了完全描述一个振动信号,必须知道幅值、频率和相位这三个参数,人们称之为振动分析的三要素。
(a)幅值不等;(b)相位不等;(c)频率不等图2.2 三组相似的振动波型简谐振动时最简单的振动形式,实际发生的振动要比简谐振动复杂的多。
但是根据付立叶变换理论知道,不管振动信号多复杂,都可以将其分解为若干具有不同频率的简谐振动。
图2.3 付立叶变换图解旋转机械振动分析离不开转速,为了方便和直观起见,常以1x表示与转动频率相等的频率,又称为工(基)频,分别以0.5x、2x、3x等表示转动频率的0.5倍、2倍、3倍等相等的频率,又称为半频、二倍频、三倍频。
采用信号分析理论中的快速傅立叶变换可以很方便地求出复杂振动信号所含频率分量的幅值和相位。
目前频谱分析已成为振动故障诊断领域最基本的工具。
频谱分析所起的作用可以概括为以下两点:1)特定故障的频率特征具有必然性。
例如,转子不平衡的频率为工频,气流基振和油膜振荡等故障的频率为低频,电磁激振等故障为高频。
《振动测试》实验讲义
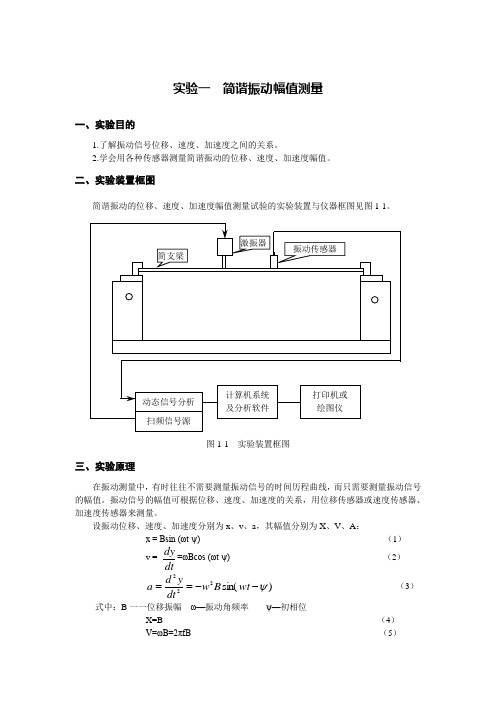
实验一 简谐振动幅值测量一、实验目的1.了解振动信号位移、速度、加速度之间的关系。
2.学会用各种传感器测量简谐振动的位移、速度、加速度幅值。
二、实验装置框图简谐振动的位移、速度、加速度幅值测量试验的实验装置与仪器框图见图1-1。
图1-1 实验装置框图三、实验原理在振动测量中,有时往往不需要测量振动信号的时间历程曲线,而只需要测量振动信号的幅值。
振动信号的幅值可根据位移、速度、加速度的关系,用位移传感器或速度传感器、加速度传感器来测量。
设振动位移、速度、加速度分别为x 、v 、a ,其幅值分别为X 、V 、A :x = Bsin (ωt -ψ) (1)v =dtdy =ωBcos (ωt -ψ) (2) )sin(222ψ--==wt B w dtyd a (3)式中:B 一一位移振幅 ω—振动角频率 ψ—初相位X=B (4) V=ωB=2πfB (5)A=ω2B=(2πf)2B (6)振动信号的幅值可根据式(6)中位移、速度、加速度的关系,分别用位移传感器、速度传感器或加速度传感器来测量。
也可利用动态分析仪中的微分、积分功能来测量。
四、实验方法1、安装激振器把激振器安装在支架上,将激振器和支架固定在实验台基座上,并保证激振器顶杆对简支梁有一定的预压力(不要超过激振杆上的标识),用专用连接线连接激振器和DH1301扫频信号源输出接口。
2、连接仪器和传感器把加速度传感器安装在简支梁的中部,输出信号接到电荷放大器的输入端,并将电荷放大器的输出接到数采分析仪的1通道。
3、仪器参数设置打开数采仪器的电源开关,开机进入DAS2003数采分析软件的主界面,设置采样率(2kHz)、量程范围,输入加速度传感器的灵敏度。
打开一个窗口,分别显示三个通道的信号。
4、采集并显示数据调节扫频信号源的输出频率,使梁产生振动。
分别调整电荷放大器为加速度、速度、位移状态,同时在窗口中读取当前振动的最大值(位移、速度、加速度)。
5、计算数据与实验数据比较按公式计算位移、速度或加速度值,并与实验数据比较。
振动计算力学公式

振动计算力学公式一、简谐振动(Simple Harmonic Motion)简谐振动指的是一个物体在一个平衡位置附近做低幅度的周期性振动。
简谐振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * cos(ωt + φ)其中,x表示位移,A表示振幅,ω表示角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * ω * sin(ωt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = -A * ω^2 * cos(ωt + φ)其中,a表示加速度。
4. 动能(Kinetic Energy):K = 0.5 * m * v^2其中,K表示动能,m表示质量。
5. 势能(Potential Energy):P = 0.5 * k * x^2其中,P表示势能,k表示弹性系数。
6. 总机械能(Total Mechanical Energy):E = K + P其中,E表示总机械能。
7. 振动周期(Vibration Period):T = 2π/ω其中,T表示振动周期。
二、阻尼振动(Damped Vibration)阻尼振动指的是振动过程中受到了阻尼力的影响,导致振幅逐渐减小。
阻尼振动的一些重要的力学公式如下:1. 位移(Displacement):x = A * e^(-βt) * cos(ωdt + φ)其中,x表示位移,A表示振幅,β表示阻尼系数,ωd表示阻尼角频率,t表示时间,φ表示相位。
2. 速度(Velocity):v = -A * β * e^(-βt) * cos(ωdt + φ) - A * ωd * e^(-βt) * sin(ωdt + φ)其中,v表示速度。
3. 加速度(Acceleration):a = A * (β^2 * e^(-βt) *cos(ωdt + φ) + 2β * ωd * e^(-βt) * sin(ωdt + φ)) - A *ωd^2 * e^(-βt) * cos(ωdt + φ)其中,a表示加速度。
振动监测参数及标准

振动监测参数及标准
振动监测参数主要包括振动的振幅、频率、相位、振动速度、振动加速度、振动位移等。
1. 振幅:振幅是指振动的最大偏离量,通常用峰值或峰-峰值
表示。
2. 频率:频率是指振动的周期性重复次数,通常以赫兹(Hz)表示。
3. 相位:相位是指振动波形相对于特定参考点的时间偏移角度或时间延迟量。
4. 振动速度:振动速度是指振动物体通过空气、液体或固体传导的振动能量的速度。
5. 振动加速度:振动加速度是指振动物体加速度的大小,通常以米每秒平方(m/s^2)表示。
6. 振动位移:振动位移是指物体振动时从平衡位置到最大偏移的距离。
振动监测的标准通常采用国家或行业制定的振动监测标准,例如ISO10816标准。
该标准将振动级别划分为四个等级:I级
表示良好状态,II级表示可接受状态,III级表示存在问题或
需要进行进一步检查,IV级表示严重故障。
除ISO10816标准外,还有许多其他振动监测标准,如API 670、VDI 2056和ASME PTC 19.3等。
这些标准通常根据不
同的应用领域和设备类型提供了不同的振动限制值和评估方法。
正弦振动加速度与速度与振幅与频率关系

正弦振动加速度与速度与振幅与频率关系Prepared on 24 November 2020正弦振动一共有四个参数来描述,即:加速度(用a表示)m/s^2速度(用v表示) m/s位移(用D表示)行程(2倍振幅)m频率(用f表示)Hz公式:a=2πfvv=2πfd(其中d=D/2)a=(2πf)2d (2为平方)说明:以上公式中物理量的单位均为国际单位制例如频率为10HZ,振幅为10mmV=2**10*10/1000=0.628m/sa=(2**10)^2*10/1000=m/s^2正弦运动振幅5mm 频率200HZ我想你是在做一个弹簧振子,加速度是变化的,我想你需要的应该是弹簧的弹性系数k首先写出振动方程Y=5sin(x/200)根据设计要求,弹簧要使振子在1/200s的时候运动距离达到5mm,速度由最大的V0变为0,在这个过程中属于变力做功,(不知道你会积分不)如果不会也没有关系,我们知道弹簧的弹性势能为^2(式中H是弹簧的伸长量),在达到振幅时,H=5mm=5×10^(-3)m应用动能定理:^2=1/2mV0^2同时,应满足时间频率要求,应用动量定理,就必须用积分了,弹力在1/800(完成1/4周期需要的时间)时间内的冲量为I,I是以函数kHt为被积函数,对H由0到5,t由0到1/800的定积分,即I=×10^(-5)k由动量定理I=mV1-mV0,得,mV0=×10^(-5)k联立两式解得:k=256m(式中m不是单位,是振子得质量)而且初速度为400米每秒振动台上放置一个质量m=10kg的物体,它们一起上下作简谐振动,其频率ν=10Hz、振幅A=2×10-3m,求:(1)物体最大加速度的大小;(2)在振动的最高位置、最低位置,物体分别对台面的压力。
解:取x轴竖直向下,以振动的平衡位置为坐标原点,列运动方程x=Acos(2πνt+φ)于是,加速度a=-4π2ν2Acos(2πνt+φ)(1)加速度的最大值|a m|=4π2ν2A=m·s-2(2)由于物体在振动过程中仅受重力mg及竖直向上的托力f,按牛顿第二定律在最高位置mg-f=m|a m|f=m(g-|a|)=m这时物体对台面的压力最小,其值即在最低位置mg-f=m(-|a m|)f=m(g+|a|)=177Nm这时物体对台面的压力最大,其值即177N频率为60HZ,振幅为0.15mm的正弦振动,换算成加速度是多少只要了解一下其物理方法就不难得到结果了。
振幅、加速度、振动频率三者的关系式

振幅、加速度、振动频率三者的关系式振动加速度、振幅、频率三者关系在低频范围内,振动强度与位移成正比;在中频范围内,振动强度与速度成正比;在高频范围内,振动强度与加速度成正比。
因为频率低意味着振动体在单位时间内振动的次数少、过程时间长,速度、加速度的数值相对较小且变化量更小,因此振动位移能够更清晰地反映出振动强度的大小;而频率高,意味着振动次数多、过程短,速度、尤其是加速度的数值及变化量大,因此振动强度与振动加速度成正比。
也可以认为,振动位移具体地反映了间隙的大小,振动速度反映了能量的大小,振动加速度反映了冲击力的大小。
振动加速度的量值是单峰值,单位是重力加速度[g]或米/秒平方[m/s2],1[g]=9.81[m/s2]。
最大加速度20g(单位为g)。
最大加速度=0.002×f2(频率Hz的平方)×D(振幅p-pmm)f2:频率的平方值举例:10Hz最大加速率=0.002×10*10×5=1g在任何頻率下最加速率不可大于20g 最大振幅5mm最大振幅=20/(0.002×f2)举例:100Hz最大振幅=20/(0.002×100*100)=1mm在任何频率下振幅不可大于5mm加速度与振幅换算1g=9.8m/s2A =0.002*F2*DA:加速率(g)F:頻率(Hz) 2是F的平方D:位移量(mm)2-13.2Hz振幅为1mm13.2-100Hz加速率为7m/s2A=0,002X(2X2)X1A=0.002X4X1A=0.008g单位转换1g=9.81m/s2A=0. m/s2,也就是2Hz频率时。
它的加速度是0.m/s2.以上公式按到对应的参数输入计算套出你想要的结果。
振动计算力学公式

振动计算力学公式公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]振动台力学公式1、求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )m 2—试件(包括夹具、安装螺钉)质量(kg )A — 试验加速度(m/s 2)2、加速度(A )、速度(V )、位移(D )三个振动参数的互换运算公式 A=ωv ……………………………………………………公式(2) 式中:A —试验加速度(m/s 2)V —试验速度(m/s ) ω=2πf (角速度) 其中f 为试验频率(Hz )V=ωD ×10-3 ………………………………………………公式(3) 式中:V 和ω与“”中同义D —位移(mm 0-p )单峰值A=ω2D ×10-3 ………………………………………………公式(4) 式中:A 、D 和ω与“”,“”中同义 公式(4)亦可简化为:A=D f ⨯2502式中:A 和D 与“”中同义,但A 的单位为g1g=s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5) 式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
加速度与位移平滑交越点频率的计算公式f A-D =DA ⨯⨯23)2(10π ……………………………………公式(7) 式中:f A-D — 加速度与位移平滑交越点频率(Hz ),(A 和D 与前面同义)。
振动加速度计算公式

振动加速度计算公式在一维简谐振动中,振动加速度与位移和时间的关系可以由如下公式描述:a(t)=-ω²x(t)其中,a(t)表示物体在时刻t的振动加速度,x(t)表示物体在时刻t 的位移,ω表示振动的角频率。
这个公式的推导基于牛顿第二定律以及简谐振动的基本假设。
根据牛顿第二定律,物体受到的合力F与物体的质量m和加速度a的关系为:F = ma在简谐振动中,振动物体只受到恢复力F = -kx的作用,其中k是物体的弹性系数。
将恢复力代入牛顿第二定律中,得到:-mω²x = ma两边除以m,得到:ω²x=-a移项后得到振动加速度的计算公式:a=-ω²x其中,负号表示振动加速度的方向与位移方向相反。
由于振动加速度的数值与物体的位移成正比,所以振动加速度的大小与位移大小呈非线性关系。
当物体位移达到最大值时,振动加速度为零;当物体位移为零时,振动加速度达到最大值。
对于其他类型的振动,如二维和三维振动,振动加速度的计算公式也可以根据具体情况进行推导。
在这些情况下,振动加速度的计算公式通常包含物体的质量、位移、速度以及加速度的各个分量。
振动加速度计算公式的应用非常广泛。
例如,在工程领域中,振动加速度常用于分析和设计各种振动系统,如机械结构、传动系统和软件系统等。
通过计算和测量振动加速度,我们可以评估系统的稳定性、响应特性以及可能的故障和损坏情况。
此外,在物理学和材料科学中,振动加速度的计算公式也被用于研究材料的弹性特性、声学特性和磁学特性等。
总结起来,振动加速度计算公式是描述物体振动过程中加速度变化的数学公式。
它在物理学和工程领域中有着广泛的应用,对于分析振动系统并评估系统的性能和稳定性非常重要。
振动位移,速度,加速度公式

振动位移,速度,加速度公式
速度公式:vt=v0+at①
位移公式:s=v0t+at2②
速度位移关系式:-=2as③
平均速度公式:=④
=(v0+vt)⑤
=⑥
位移差公式:△s=aT2⑦
公式说明:(1)以上公式除④式之外,其它公式只适用于匀变速直线运动。
(2)公式⑥指的是在匀变速直线运动中,某一段时间的平均速度之值恰好等于这段时间中间时刻的速度,这样就在平均速度与速度之间建立了一个联系。
6.对于初速度为零的匀加速直线运动有下列规律成立:
(1).1T秒末、2T秒末、3T秒末…nT秒末的速度之比
为:1:2:3:…:n。
(2).1T秒内、2T秒内、3T秒内…nT秒内的位移之比
为:12:22:32:…:n2。
(3).第1T秒内、第2T秒内、第3T秒内…第nT秒内的位移之比为:1:3:5:…:(2n-1)。
(4).第1T秒内、第2T秒内、第3T秒内…第nT秒内的平均速度之比为:1:3:5:…:(2n-1)。
振动试验常用公式

欢迎共阅振动台在使用中经常运用的公式1、求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )21g=9.8m/s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 3.1 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5)式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
3.2 速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
3.3 加速度与位移平滑交越点频率的计算公式4式中:n —倍频程(oct )f H —上限频率(Hz ) f L —下限频率(Hz ) 4.2.2 扫描速率计算公式R=TLg f f LgLH2/ ……………………………公式(10)式中:R —扫描速率(oct/min 或)f H —上限频率(Hz ) f L —下限频率(Hz ) T —扫描时间T=n/R ……………………………………………公式(11)式中:T —扫描时间(min 或s )n —倍频程(oct )5A 1=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+=+⎰111)(m b a b f f f f m f w df f w b ba……………………升谱计算公式 A 1=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=-⎰121112111)(m f f f f m f w df f w ……………………降谱计算公式式中:m=N/3 N 为谱线的斜率(dB/octive ) 若N=3则n=1时,必须采用以下降谱计算公式A3=2.3w 1f 1 lg12f f 加速度总均方根值:g mis=321A A A ++ (g )…………………………公式(13-1)设:w=w b =w 1=0.2g 2/Hz f a =10Hz f b =20Hz f 1=1000Hz f 2=2000Hz若干矩形和三角形,并利用上升斜率(如3dB/oct )和下降斜率(如-6dB/oct )分别算出w a 和w 2,然后求各个几何形状的面积与面积和,再开方求出加速度总均方根值g rms =53241A A A A A ++++ (g)……公式(13-2)注意:第二种计算方法的结果往往比用升降谱计算结果要大,作为大概估算可用,但要精确计算就不能用。
振动试验中 加速度 频率 位移 关系

振动试验中加速度频率位移关系振动试验是工程中常用的一种测试手段,通过对结构体进行加速度、频率和位移的测试,可以得到结构体在振动条件下的响应特性。
加速度、频率和位移之间存在着一定的关系,下面将从加速度、频率和位移三个方面进行讨论。
我们来看加速度与频率的关系。
加速度是描述物体在单位时间内速度变化率的物理量,其单位为m/s²。
在振动试验中,加速度可以用来衡量结构体受到的振动力的大小。
频率是描述物体振动的快慢程度的物理量,其单位为Hz。
在振动试验中,频率可以用来表示结构体振动的周期性。
实验中发现,加速度与频率之间存在着一定的关系,即在一定频率范围内,加速度随着频率的增加而增加,且呈现出一定的规律性。
这是因为在振动试验中,结构体受到的振动力与频率有关,当频率变化时,结构体对振动力的响应也会发生变化,从而导致加速度的变化。
因此,通过加速度与频率之间的关系,可以更好地了解结构体在不同频率下的振动特性。
我们来看加速度与位移的关系。
位移是描述物体位置变化的物理量,其单位为m。
在振动试验中,位移可以用来表示结构体振动的幅度大小。
实验中发现,加速度与位移之间存在着一定的关系,即在一定加速度范围内,加速度随着位移的增加而增加,且呈现出一定的规律性。
这是因为在振动试验中,结构体受到的振动力与位移有关,当位移变化时,结构体对振动力的响应也会发生变化,从而导致加速度的变化。
因此,通过加速度与位移之间的关系,可以更好地了解结构体在不同位移下的振动特性。
加速度、频率和位移之间存在着一定的关系。
在振动试验中,通过对加速度、频率和位移的测试,可以综合考虑这三个因素对结构体的影响,从而得到结构体在振动条件下的响应特性。
通过研究加速度、频率和位移之间的关系,可以更好地了解结构体的振动特性,为工程设计和结构优化提供有力的依据。
同时,对加速度、频率和位移之间的关系进行深入研究,也有助于进一步提高振动试验的精度和可靠性,为工程实践提供更好的支持。
请根据振动过程图说明振动物体的位移、回复力、回复加速度、势能、速度、动能 的大小变化特点,方向特点

请根据振动过程图说明振动物体的位移、回复力、回复加速度、势能、速度、动能的大小变化特点,方向特点理解振动过程中各物理量的变化特点和方向特点是理解振动现象的关键。
下面我将根据振动过程图说明各物理量的变化特点和方向特点:1. 位移:•位移是振动物体从平衡位置偏离的距离。
•在振动过程中,位移随时间周期性地变化,呈正弦曲线。
•方向特点:位移的方向沿着振动方向,可以是正向(朝向平衡位置的方向)或负向(远离平衡位置的方向)。
2. 回复力:•回复力是振动物体受到的恢复原来平衡位置的力。
•在振动过程中,回复力与位移成正比,且方向与位移方向相反。
•当位移为正时,回复力方向与位移方向相反;当位移为负时,回复力方向与位移方向相同。
3. 回复加速度:•回复加速度是振动物体在回复力作用下加速度的大小。
•在振动过程中,回复加速度与位移成反比,且方向与位移方向相反。
•当位移为正时,回复加速度方向与位移方向相反;当位移为负时,回复加速度方向与位移方向相同。
4. 势能:•势能是振动物体由于位置而具有的能量。
•在振动过程中,势能随着位移的变化而变化,呈正弦曲线。
•方向特点:势能的方向沿着振动方向,可以是正向或负向。
5. 速度:•速度是振动物体运动的快慢程度。
•在振动过程中,速度随时间周期性地变化,呈正弦曲线。
•方向特点:速度的方向沿着振动方向,可以是正向或负向。
6. 动能:•动能是振动物体由于速度而具有的能量。
•在振动过程中,动能随着速度的变化而变化,呈正弦曲线。
•方向特点:动能的方向沿着振动方向,可以是正向或负向。
总的来说,振动过程中各物理量的变化特点是周期性的,并且它们之间存在一定的相位关系。
回复力和回复加速度的方向与位移方向相反,而速度和动能的方向与位移方向一致。
势能的方向与位移方向一致,但与速度方向相反。
振动加速度和振动位移的关系

振动加速度和振动位移的关系稿子一嘿,朋友!今天咱们来聊聊振动加速度和振动位移这对小伙伴的关系。
你知道吗?振动位移就像是一个物体在振动过程中走过的路程,它能告诉我们物体到底移动了多远。
而振动加速度呢,就像是在后面推或者拉着物体的一股神秘力量,让物体的速度发生变化。
比如说,当振动加速度很大的时候,物体的速度变化就会特别快,那振动位移也会跟着有比较大的改变。
反过来,如果振动加速度比较小,物体速度变化慢,振动位移的变化也就相对小一些啦。
想象一下,一个小球在弹簧上跳动。
如果弹簧拉得特别紧,给小球的加速度很大,小球就会跳得又高又远,位移也就大得很。
要是弹簧松松的,加速度小,小球就只能轻轻蹦跶一下,位移也就小咯。
有时候振动加速度和振动位移就像两个调皮的孩子,一个跑得快,一个走得远,相互影响又相互制约。
怎么样,是不是觉得还挺有趣的?稿子二亲爱的小伙伴,咱们来唠唠振动加速度和振动位移的那些事儿!你想啊,振动位移就是物体在振动时位置的变化量。
比如说荡秋千,从这边荡到那边的距离就是振动位移。
那振动加速度呢?它就像是个急性子,决定着振动速度变化的快慢。
如果振动加速度大,就好像有人在后面猛推一把,物体的速度一下子就变快了,位移也会跟着变得明显。
打个比方,就像蹦床,你跳得越高,加速度越大,落下时的位移也就越大。
但要是振动加速度小,就像轻轻推了你一下,速度变化不大,位移也就不那么突出啦。
它们俩的关系啊,有点像跳舞的搭档。
位移是那个优美的舞姿,而加速度就是带动节奏的动力。
有时候振动加速度突然变大,振动位移也会跟着来个大跳跃。
反过来,加速度减小,位移的变化也会变得温柔起来。
振动加速度和振动位移相互关联,共同演绎着物体振动的精彩故事!是不是很有意思呀?。
振动中的位移、速度和加速度之间的转换关系

振动中的位移、速度和加速度之间的转换关系嘿,朋友们!今天咱来聊聊振动中的位移、速度和加速度这三个家伙的转换关系。
咱先说说位移吧,这就好比是一个人在旅途中走过的路程。
它能告诉我们物体从一个地方到另一个地方移动了多远。
就像你从家走到学校,这中间的距离就是位移啦。
那速度呢,就像是这个人走路的快慢呀!速度快,就好比是一阵风似的“嗖”一下就过去了;速度慢呢,就像蜗牛在慢悠悠地爬。
加速度可就有意思了,它就像是给速度加了一把劲或者踩了一脚刹车。
如果加速度是正的,那速度就会越来越快;要是负的呢,速度就会变慢。
咱打个比方哈,一辆汽车在路上跑,位移就是它从这里开到了那里有多远;速度就是它开得多快;加速度呢,就是它突然加速或者减速的那个劲儿。
你想想看,要是没有位移,那我们怎么知道物体到底移动到哪儿了呢?没有速度,我们怎么知道它移动得快还是慢呢?没有加速度,那物体的运动状态不就一成不变了,多没意思呀!它们三个之间的关系可紧密着呢!位移的变化会引起速度的变化,速度的变化又会带来加速度的改变。
这就好像是一环扣一环的链条呀!比如说,一个球从高处落下,刚开始位移不大,速度也不快,但是随着它往下落,位移越来越大,速度也越来越快,加速度也在起作用呢。
这是不是很神奇呀?就像生活中的很多事情一样,看似不相关,其实内在有着千丝万缕的联系。
我们在理解这些的时候,可不能死记硬背呀,得结合实际去感受。
就像你骑自行车,你加速的时候,不就是有加速度了嘛,速度也变快了,骑过的距离就是位移呀。
所以呀,大家一定要好好理解振动中的位移、速度和加速度的转换关系,这对我们理解很多自然现象和物理问题都有很大的帮助呢!它们就像是隐藏在振动世界里的小秘密,等着我们去发现和探索。
总之,位移、速度和加速度,它们相互关联,相互影响,共同构成了振动世界的奇妙景象。
大家要多多体会,多多思考,才能真正掌握它们之间的奥秘哟!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
