《时间序列分析》案例04
时间序列分析ppt课件

目录
• 时间序列分析简介 • 时间序列的基本概念 • 时间序列分析方法 • 时间序列分析案例 • 时间序列分析的未来发展
01 时间序列分析简介
时间序列的定义与特点
定义
时间序列是指按照时间顺序排列的一 系列观测值。
特点
时间序列具有动态性、趋势性和周期 性等特点,这些特点对时间序列分析 具有重要的影响。
时间序列的季节性
总结词
时间序列的季节性是指时间序列在固定周期内重复出现的模式,这种模式可能是由于季节性因素、周 期性事件或数据采集的频率所引起的。
详细描述
季节性是时间序列中的一个重要特征,许多时间序列都表现出季节性。例如,一个表示月度销售的序 列可能会在每个月份都出现类似的销售模式。在进行时间序列分析时,需要考虑季节性对模型的影响 ,以便更准确地预测未来的趋势和模式。
时间序列分析在金融领域的应用广泛,如股票价格预测 、风险评估等。未来将进一步探索时间序列分析时间序列分析可用于医学影像分析、疾病 预测等方面。未来将进一步拓展其在健康领域的应用范 围,为医疗保健提供有力支持。
谢谢聆听
时间序列分析的意义
01
预测未来趋势
通过对时间序列进行分析,可以了解数据的变化趋势, 从而预测未来的走势,为决策提供依据。
02
揭示内在规律
时间序列分析可以帮助我们揭示数据背后的内在规律和 机制,进一步理解事物的本质。
03
优化资源配置
通过对时间序列的预测和分析,可以更好地优化资源配 置,提高资源利用效率。
03 时间序列分析方法
图表分析法
总结词
通过图表直观展示时间序列数据,便 于观察数据变化趋势和异常点。
详细描述
《时间序列分析法》课件

目录
• 时间序列分析法概述 • 时间序列数据的预处理 • 时间序列的模型选择 • 时间序列的预测与分析 • 时间序列分析法的实际应用案例 • 时间序列分析法的未来发展与挑战
01
时间序列分析法概述
时间序列分析法的定义
时间序列分析法是一种统计方法,通 过对某一指标在不同时间点的观测值 进行统计分析,以揭示其内在的规律 和趋势。
处理速度要求高
大数据时代要求快速处理和分析时间序列数据 ,以满足实时性和高效率的需求。
数据质量与噪声处理
大数据中存在大量噪声和异常值,需要有效的方法进行清洗和预处理。
时间序列分析法与其他方法的融合
统计学方法
时间序列分析法可以与统计学方 法相结合,利用统计原理对数据 进行建模和推断。
深度学习方法
深度学习在处理复杂模式和抽象 特征方面具有优势,可以与时间 序列分析法相互补充。
ARIMA模型
适用于平稳时间序列的预测, 通过差分和整合方式处理非平
稳数据。
指数平滑法
适用于具有趋势和季节性变化 的时间序列,通过不同权重调 整预测值。
神经网络
适用于复杂非线性时间序列, 通过训练数据建立预测模型。
支持向量机
适用于小样本数据和分类问题 ,通过核函数处理非线性问题
。
预测精度评估
均方误差(MSE)
它通常用于预测未来趋势、分析周期 波动、研究长期变化等方面。
时间序列分析法的应用领域
金融市场分析
用于股票、债券、商品等市场的价格预测和 风险评估。
气象预报
通过对历史气象数据的分析,预测未来的天 气变化。
经济周期研究
分析经济周期波动,预测经济走势。
【精品】121第四章时间序列分析

-0.36
1989
2
15.04
-0.69
1998
11
9.14
-0.92
1990
3
14.39
-0.65
1999
12
8.18
-0.96
1991
4
12.98
-1.41
2000
13
7.58
-0.6
1992
5
11.6
-1.38
2001
14
6.95
-0.63
1993
6
11.45
-0.15
2002
15
6.45
STAT
简捷计算法:
奇数项: a=17.43,b=1.72 yc=17.43+1.72t
STAT
偶数项: a=16.55,b=0.85 yc=16.55+0.85t b:半年平均增长量注:A、变量y与变量t之间并不存在因果(相关)关系; B、预测时需假定现象的变动不大,故长期预测效果不佳。
STAT
三、增长量与平均增长量(一)增长量1、定义:报告期水平—基期水平
STAT
2、数量关系(1)逐期增长量=累计增长量。
(2)相邻的两个累计增长量的差等于相应的逐期增长量。
STAT
(二)平均增长量1、定义:逐期增长量的平均水平
STAT
三、发展速度与增长速度(一)发展速度1、定义:报告期水平/基期水平
首尾折半法n指标值个数n1时间长度
STAT
(4)间隔不等的间断的时点数列
STAT
[计算公式]
STAT
(三)相对数、平均数时间数列求序时平均数[例]某厂第二季度有关资料如下。试据此求该厂第二季度平均的计划完成程度。
时间序列分析案例

时间序列分析案例时间序列分析是指对一系列按时间顺序排列的数据进行分析和预测的方法。
它在许多领域都有着广泛的应用,比如经济学、金融学、气象学等。
通过对时间序列数据的分析,我们可以揭示数据中的趋势、周期性和随机性,从而进行有效的预测和决策。
下面,我们以一个销售数据的时间序列分析案例来说明时间序列分析的基本方法和步骤。
首先,我们收集了某公司过去几年的销售数据,包括每个月的销售额。
接下来,我们需要对这些数据进行可视化,以便更好地理解数据的特点和规律。
我们可以绘制销售额随时间变化的折线图,观察销售额的趋势和周期性变化。
通过观察折线图,我们发现销售额在整体上呈现出逐渐增长的趋势,同时还存在着明显的季节性波动。
接下来,我们可以利用时间序列分析的方法来对销售数据进行进一步的分析。
首先,我们可以对销售数据进行平稳性检验,以确保数据符合时间序列分析的基本假设。
平稳性是指数据的均值和方差在不同时间段上保持不变。
如果数据不平稳,我们可以对其进行差分操作,将其转化为平稳序列。
接着,我们可以对平稳序列进行自相关和偏自相关的分析,以确定时间序列模型的阶数。
自相关函数(ACF)和偏自相关函数(PACF)可以帮助我们找到合适的ARIMA模型的阶数,从而进行有效的建模和预测。
在确定了时间序列模型的阶数之后,我们可以利用历史数据来估计模型的参数,并进行模型诊断。
模型诊断可以帮助我们检验模型的拟合效果和预测能力,确保模型的有效性和可靠性。
最后,我们可以利用已建立的时间序列模型对未来的销售额进行预测。
通过对销售额的预测,我们可以为公司的经营决策提供有力的支持,比如制定合理的生产计划和销售策略,以应对未来的市场变化。
通过以上案例,我们可以看到时间序列分析在实际中的重要性和应用价值。
它不仅可以帮助我们更好地理解和把握数据的规律,还可以为我们提供有效的预测和决策支持。
因此,掌握时间序列分析的方法和技巧对于数据分析人员和决策者来说是非常重要的。
利用时间序列模型进行网络流行度预测的案例分析(四)

利用时间序列模型进行网络流行度预测的案例分析随着互联网的迅猛发展,人们对于网络流行度的预测需求越来越高。
预测网络内容的流行度能够帮助企业制定有效的营销策略、提前安排资源,对于社会热点话题的分析也能帮助政府做出更有针对性的决策。
本文将通过一个实际的案例分析,介绍利用时间序列模型进行网络内容流行度预测的过程和方法。
首先,我们需要定义流行度的计量指标。
一般而言,流行度可以通过观测网络内容的阅读量、分享量或讨论数量来进行衡量。
在本案例中,我们选择了微博平台上的某一条话题作为研究对象,将转发量作为流行度指标。
接下来,我们需要收集数据。
我们可以通过网络爬虫技术,收集该话题在微博平台上的转发量数据。
获取到的数据需要具备一定的时间跨度,以覆盖不同时间段内的转发情况。
且数据的频率应尽量高,以便更全面地观察流行度的变化。
对于时间序列模型来说,数据的平稳性是非常重要的。
平稳性是指时间序列的均值和方差在时间上是稳定的,不呈现明显的趋势、季节性和周期性。
为了确保数据的平稳性,我们可以对原始数据进行平滑处理,如使用移动平均法或指数平滑法。
接下来,我们需要对平稳化后的时间序列进行建模。
常用的时间序列模型包括自回归移动平均模型(ARMA)、季节自回归移动平均模型(SARMA)、自回归积分移动平均模型(ARIMA)等。
在本案例中,我们选择了ARIMA模型来进行预测。
ARIMA模型被广泛用于时间序列预测,并且有很好的预测性能。
该模型有三个参数,分别是p、d、q。
其中,p表示自回归过程的阶数,d表示差分操作的次数,q表示移动平均过程的阶数。
通过对数据进行自相关性和偏自相关性分析,可以确定ARIMA模型的参数。
在确定好ARIMA模型的参数后,我们可以进行模型的拟合,并对模型进行评估。
常用的评估方法包括计算残差平均值、确定残差的白噪声特性、计算均方根误差等。
通过评估模型的性能,我们可以判断模型是否合适,是否需要调整参数。
最后,我们可以利用已训练好的ARIMA模型进行网络流行度的预测。
时间序列分析案例

时间序列分析案例时间序列分析是指对一系列按照时间顺序排列的数据进行分析和预测的统计方法。
在实际生活中,时间序列分析可以应用于经济预测、股票价格预测、气象预测等多个领域。
本文将以一个实际案例来介绍时间序列分析的基本步骤和方法。
首先,我们选取了某公司过去五年的月销售额数据作为研究对象。
我们首先对数据进行可视化分析,绘制出销售额随时间变化的折线图。
通过观察折线图,我们可以初步判断销售额是否存在趋势、季节性和周期性等特点。
接下来,我们对销售额数据进行平稳性检验。
平稳性是时间序列分析的基本假设之一,如果数据不是平稳的,就需要对数据进行差分处理。
我们使用单位根检验(ADF检验)来判断销售额数据是否平稳。
如果数据不是平稳的,我们将对数据进行一阶差分处理,直到数据变得平稳为止。
在确认数据平稳后,我们将对销售额数据进行自相关性和偏自相关性分析。
自相关性分析可以帮助我们确定时间序列的阶数,偏自相关性分析可以帮助我们确定ARIMA模型的参数。
通过自相关性和偏自相关性图,我们可以初步确定ARIMA 模型的参数p和q的取值。
接下来,我们将建立ARIMA模型并进行参数估计。
ARIMA模型是一种常用的时间序列预测模型,它可以很好地捕捉时间序列的趋势、季节性和周期性。
我们使用最大似然估计方法对ARIMA模型的参数进行估计,并对模型的拟合效果进行检验。
最后,我们将使用建立好的ARIMA模型对未来几个月的销售额进行预测。
我们将绘制出销售额的预测图,并计算出预测误差的均方根误差(RMSE)。
通过对预测结果的分析,我们可以评估ARIMA模型的预测效果,并对未来的销售额进行合理的预测。
通过以上案例,我们可以看到时间序列分析在实际中的应用。
通过对销售额数据的分析和预测,我们可以为公司的经营决策提供重要的参考依据。
同时,时间序列分析也可以应用于其他领域,帮助我们更好地理解数据的规律和特点,为未来的预测和决策提供支持。
时间序列模型案例分析

时间序列模型案例分析时间序列模型案例分析: 新冠疫情趋势预测背景:新冠疫情自2020年开始全球流行,给世界各国的医疗体系和经济造成了巨大冲击。
为了有效应对疫情,政府和医疗机构需要准确预测疫情未来的趋势,并做出相应的决策和应对措施。
数据:本案例使用了每天的新增确诊病例数作为时间序列数据。
数据包括了从疫情开始到某一时间点的每天新增病例数,以及历史病例数、疫情防控政策等其他相关因素。
目标:利用时间序列模型预测未来疫情的趋势,帮助政府和医疗机构制定合理的防控策略。
方法:我们采用了ARIMA模型(自回归移动平均模型)进行疫情趋势预测。
ARIMA模型是一种广泛应用于时间序列分析的经典模型,可对时间序列数据进行模拟和预测。
步骤:1. 数据预处理: 首先,我们进行了数据清洗和转换,确保数据的准确性和一致性。
我们还对数据进行了平稳性检验,如果数据不平稳,则需要进行差分操作。
2. 模型选择: 然后,我们选择了合适的ARIMA模型。
模型选择的关键是要找到合适的参数p、d和q,它们分别代表了自回归阶数、差分阶数和移动平均阶数。
3. 参数估计和模型拟合: 我们使用最大似然估计方法来估计模型的参数,并对模型进行拟合。
拟合后,我们对模型进行残差分析,以检验模型的拟合效果。
4. 模型评估和预测: 接下来,我们使用已有的数据来评估模型的预测效果。
我们将模型的预测结果与实际数据进行比较,并计算误差指标,如均方根误差(RMSE)和平均绝对误差(MAE)。
最后,我们使用拟合好的模型来进行未来疫情的趋势预测。
结果与讨论:经过模型拟合和评估,我们得到了一个较为准确的ARIMA模型来预测未来疫情的趋势。
根据模型的预测结果,政府和医疗机构可以制定对应的防控策略,以应对疫情的发展。
结论:时间序列模型在新冠疫情趋势预测中发挥了重要作用。
通过对历史疫情数据的分析和建模,我们可以预测未来疫情的走势,并相应地采取措施。
然而,需要注意的是,时间序列模型是一种基于过去数据的预测方法,其预测精度可能受到多种因素的影响。
时间序列分析的应用与案例

交通流量分析
交通流量数据的收集与整理 时间序列分析在交通流量中的应用 交通流量预测模型的建立与评估 实际案例分析:交通拥堵预测与缓解策略
Hale Waihona Puke 销售预测与库存管理● 销售预测:利用时间序列分析方法,对未来销售趋势进行预测,为生产计划和库存管理提供依据。 ● 库存管理:通过时间序列分析,实时监控库存水平,避免库存积压和缺货现象,提高库存周转率
金融市场波动性预测: 利用时间序列分析方 法,预测金融市场的 波动性,帮助投资者 了解市场风险。
金融市场趋势预测: 通过对历史数据进行 分析,预测金融市场 的整体趋势,为投资 者提供投资方向。
气候变化研究
时间序列分析在气候变化研究中的应用 气候变化数据的收集与整理 气候变化趋势的预测与模拟 气候变化对环境和人类活动的影响评估
时间序列分析的应用 与案例
,a click to unlimited possibilities
汇报人:
目录 /目录
01
时间序列分析 概述
02
时间序列分析 的应用领域
03
时间序列分析 案例展示
04
时间序列分析 的优缺点及未 来发展趋势
01 时间序列分析概述
定义与特点
时间序列分析的 定义
时间序列分析的 特点
运行。
03 时间序列分析案例展示
股票价格预测案例
背景介绍:股票价格预测的意义和挑战
数据准备:选取合适的股票数据,进行预处理和特征提取
模型选择:选择适合的时间序列分析模型,如ARIMA、LSTM等
模型训练与评估:对选定的模型进行训练,并使用适当的评估指标对 预测结果进行评估
结果展示:展示预测结果,并分析模型的优缺点和改进方向
《统计学》案例——时间序列趋势分析

《统计学》案例——时间序列趋势分析囤积粮食可以创高价吗1、问题的提出某贸易公司是经营粮油副食品的批发公司,基于前4年当地的消费物价指数的变化,该公司认为今后两年内消费物价指数将有大幅度上涨,为此该公司计划囤积粮食至下一年(第6年)以创高价。
这个计划是否可行?2、方法的选择根据下表的数据,可采用时间序列的趋势分析方法和季节变动分析方法,进行相应的分析预测,以了解消费物价指数的发展趋势。
表23 122.434 139.373、消费物价指数的预测根据题意需预测出第6年各季的物价指数,若指数升幅较大,那么粮食价格将会提高,否则囤积货物只会增加保管成本而不可能得到高价。
在物价指数预测中,循环变动和不规则变动难以准确预测,故仅考虑长期趋势与季节变动的影响。
本案例分析应用EXCEL软件。
(1)计算移动平均数。
输出结果见下表和图:表3.(2)分离长期趋势T。
对于T×C,按照表8.14中时间顺序,用最小平方法建立长期趋势模型yc=111.498+1.173t ,据以计算各期趋势值T(见上表)。
(3)分离季节变动S。
首先剔除长期趋势的影响y/T×C,即T×C×S×I/T×C=S×I;然后根据S×I序列计算各期季节比率S。
计算结果为:1季度季节比率=0.9773,2季度季节比率=0.9874,3季度季节比率=1.0076,4季度季节比率=1.0277。
(4)预测第6年各季消费物价指数。
首先需要根据时间序列模型计算第6年各季的趋势值,即将t=19、20、21、22分别代入yc=111.498+1.173t计算得第6年各季度趋势值:1季的趋势值为133.792季趋势值为134.963季趋势值为136.144季趋势值为137.31然后分别乘以各自季节比率得到各季预测值,1季物价指数=133.79×0.9773=130.75%2季物价指数=134.96×0.9874=133.26%3季物价指数=136.14×1.0076=137.17%4季物价指数=137.31×1.0277=141.11%。
时间序列分析法(ppt42页)

3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。08:305.26.202108:305.26.202108:3008:30:575.26.202108:305.26.2021
第七章 时间序列分析
➢ 第一节 时间序列的概念和表示方法 ➢ 第二节 时间序列分析的基本原理 ➢ 第三节 趋势拟合方法 ➢ 第四节 季节变动预测
第一节 时间序列概念和表示方法
时间序列分析方法由 Box-Jenkins (1976) 年 提出。它适用于各种领 域的时间序列分析。
第一节 时间序列的概念和表示
型为
▪ 乘法模型
Y=T+S+C+I
(3.3.1)
假定时间序列是基于4种成份相乘而成的。假定季 节变动与循环变动为长期趋势的函数。该模型的方程 式为
Y T SCI
(3.3.2)
二、趋势拟合方法
(一)平滑法
时间序列分析的平滑法主要有三类 :
移动平均法
设某一时间序列为 y1,y2,…,yt,则t+1 时刻的预测值为
1.自相关性判断
①时间序列的自相关,是指序列前后期 数值之间的相关关系,对这种相关关系程度 的测定便是自相关系数。
② 测度:设y1,y2,…,yt,…,yn,共有 n个观察值。把前后相邻两期的观察值一一成 对,便有(n-1)对数据,即(y1,y2),(y2, y3),…,(yt,yt+1),…,(yn-1,yn)。
15、一年之计,莫如树谷;十年之计 ,莫如 树木; 终身之 计,莫 如树人 。2021年6月上 午9时57分21.6.2609:57June 26, 2021
时间序列分析课件_理论与案例介绍
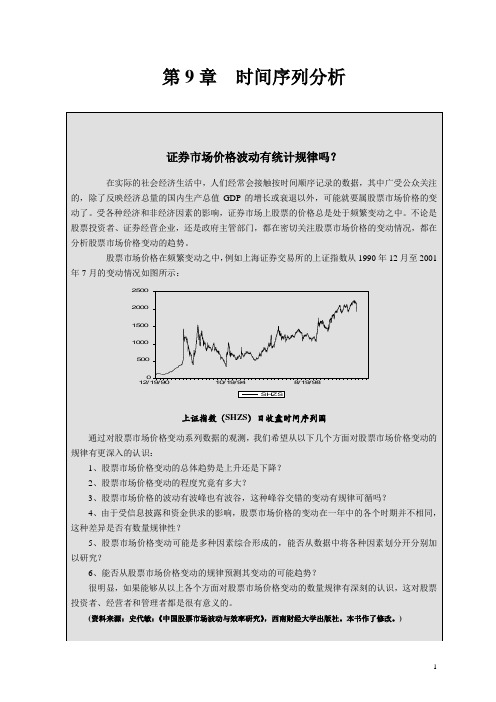
第9章时间序列分析根据社会经济现象在不同时间下的数量表现来研究它的发展变化过程,认识它的发展规律并预测其发展变化趋势,为科学的预测和决策提供依据。
本章将重点介绍编制时间数列的方法和进行时间数列的分析。
9.1 时间序列的对比分析一、时间序列的概念时间数列是将社会经济现象的某一指标在不同时期或时点上的指标数值按时间的先后顺序加以排列而形成的数列,又称为动态数列。
例如,为了说明改革开放以来中国的经济发展状况,总是把香港地区从1988年-2003年经济发展的数据按年度顺序排列起来。
象这样形成的随时间记录的数据序列称为时间序列,有时也称为动态数列。
任何一个时间序列都具有两个基本要素:一是被研究现象所属的时间范围;二是反映该现象一定时间条件下数量特征的数值,即在不同时间上的统计数据。
时间序列中每一项数据反映了现象在各个时间上达到的规模或水平,也称为相应时间上的发展水平。
【例9.1】表9.1所列出的是中国1990年至2002年国内生产总值、人口、消费等数据:表9.1 香港1988-2003年生产总值年份本地生产总值(按当年价格计算)本地生产总值与上年人均本地生产总值(按当年价格计算) (亿港元)(亿美元)比较的实际增长(%)(港元)(美元)19884572 586 8.0 81251 10409 19895271 676 2.6 92695 11884 19905876 754 3.7 103010 13225 19916772 872 5.6 117741 15151 19927913 1022 6.6 136423 17623 19939128 1180 6.3 154687 19996 199410298 1333 5.5 170622 22078 199510963 1417 3.9 178078 23019 199612109 1566 4.3 188163 24329 199713445 1737 5.1 207194 26762 199812799 1652 -5.0 195585 25253 199912461 1606 3.4 188622 24313 200012883 1654 10.2 193299 24811 200112699 1628 0.5 188835 24213 200212474 1599 1.9 183790 23566 200312198 1567 3.2 179308 23027对时间序列进行分析的目的,一是,它可以描述社会经济现象的发展变化过程和结果;二是,它可以研究社会经济现象的发展趋势和发展速度;三是,对时间数列进行长期趋势测定,对以揭示社会经济现象发展变化的规律性;四是,利用时间数列资料可预测社会经济现象。
《时间序列分析》案例04

《时间序列分析》案例案例名称:时间序列分析在经济预测中的应用内容要求:确定性与随机性时间序列之比较设计作者:许启发,王艳明设计时间:2003年8月案例四:时间序列分析在经济预测中的应用一、案例简介为了配合《统计学》课程时间序列分析部分的课堂教学,提高学生运用统计分析方法解决实际问题的能力,我们组织了一次案例教学,其内容是:对XX市的未来经济发展状况作一预测分析,数据取XX市1949—1998年国内生产总值(GDP)的年度数据,并以此为依据建立预测模型,对1999年和2000年的国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动的最终成果,是反映国民经济活动最重要的经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套的方针政策具有重要的理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例的教学目的与要求,明确案例所涉及的教学内容;然后给学生一段时间,由学生根据资料,运用不同的方法进行预测分析,并确定具体的讨论日期;在课堂讨论时让学生自由发言,阐述自己的观点;最后,由主持教师作点评发言,取得了良好的教学效果。
经济预测是研究客观经济过程未来一定时期的发展变化趋势,其目的在于通过对客观经济现象历史规律的探讨和现状的研究,求得对未来经济活动的了解,以确定社会经济活动的发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标的历史数据按照时间的先后顺序排列,然后分析它随时间的变化趋势及自身的统计规律,外推得到预测目标的未来取值。
它与回归分析预测法的最大区别在于:该方法可以根据单个变量的取值对其自身的变动进行预测,无须添加任何的辅助信息。
本案例的最大特色在于:它汇集了统计学原理中的时间序列分析这一章节的所有知识点,通过本案例的教学,可以把不同的时间序列分析方法进行综合的比较,便于学生更好地掌握本章的内容。
二、案例的目的与要求(一)教学目的1.通过本案例的教学,使学生认识到时间序列分析方法在实际工作中应用的必要性和可能性;2.本案例将时间序列分析中的水平指标、速度指标、长期趋势的测定等内容有机的结合在一起,以巩固学生所学的课本知识,深化学生对课本知识的理解;3.本案例是对XX市的国内生产总值数据进行预测,通过对实证结果的比较和分析,使学生认识到对同一问题的解决,可以采取不同的方法,根据约束条件,从中选择一种合适的预测方法;4.通过本案例的教学,让学生掌握EXCEL软件在时间序列分析中的应用,对统计、计量分析软件SPSS或Eviews等有一个初步的了解;5.通过本案例的教学,有助于提高学生运用所学知识和方法分析解决问题的能力、合作共事的能力和沟通交流的能力。
统计学课件动态相对数时间序列分析

时间序列中无法预测的随机波 动。
时间序列分析的方法与步骤
收集数据
收集具有时间顺序的数据,确保数据的准确 性和完整性。
数据预处理
对数据进行清洗、整理和转换,使其满足分析 要求。
描述性分析
对数据进行描述性统计,如均值、方差、中位数 等,以初步了解数据分布和变化规律。
趋势分析
通过图表或数学方法分析数据随时间变化的趋势, 如线性回归、指数平滑等。
优点
能够直观地反映现象在不同时间点上的变化情况,便于比较和评估。能够消除不同时间点上规模大小的影响,突 出变化趋势。计算方法简单易懂,易于操作。
缺点
容易受到数据波动的影响,导致结果不稳定。无法反映现象的绝对水平,只能反映相对变化情况。计算过程中可 能存在数据失真和误差问题。
02 时间序列分析基础
时间序列的定义与分类
根据预测结果和实际需求,制定相应的决策方案,如投资决策、市场预测、政策制定等,以提高决策 的科学性和准确性。
04 动态相对数时间序列分析案例
案例一
总结词
销售额的波动性
详细描述
通过分析某公司销售额的动态相对数时间序列,可以观 察到销售额随时间的变化趋势,了解其波动性。例如, 是否存在季节性波动、周期性变化等。
通过机器学习算法的应用,可以进一 步提高动态相对数时间序列分析的自 动化和智能化水平,减少人工干预和 误差。
可视化与交互性
通过可视化技术和交互性设计,可以 更加直观地展示动态相对数时间序列 分析的结果,便于用户理解和使用。
THANKS 感谢观看
通过时间序列分析,可以对市场情绪进行评估。例如, 当市场情绪高涨时,股价通常会上涨;当市场情绪低迷 时,股价则可能下跌。
管理统计学4 第四章 时间序列

星蓝海学习网
4.2序时平均数和平均发展速度
4.2.2相对数的序时平均数和平均数的序时平均数
库存周转速度属于相对数,该相对数的分母为时点数。从年度上看,年周转速度应等 于年销售量与年平均库存量的比值。因此,先平均后对比是计算相对数序时平均的基 本方法。 平均数序时平均数的计算与相对数的序时平均数的计算方法相同,也是先平均后对比。
管理统计学 [第四版]
星蓝海学习网
第四章 时间序列分析
星蓝海学习网
案例导入
近年来,中国房地产发展繁荣,房价更是水涨船高。下表是国家统计局对十 年来广东省商品房年销售价格的统计数。
年份 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 售价 4443 4853 5914 5953 6513 7486 7879 8112 9090 9083
4.1 发展水平和发展速度分析
4.1.2 发展水平和增长量
发展水平 发展水平是指时间数列上指标的具体数值。 发展水平的指标形式可以是绝对数,也可以是相对数或平均数。 增长量 为了分析上方便,就把作为研究对象的发展水平称为报告期水平,把要对比的基础水 平则称为基期水平。 用报告期水平减去基期水平,就等于增长量。其中,当基期水平为上期水平时,就称 为逐期增长量;当基期水平为某个时期的固定发展水平(X0)时,就称为累计增长量。 逐期增长量:X1-X0、X2-X1、X3-X2、…Xn-Xn-1 。 累计增长量:X1-X0、X2-X0、X3-X0、…Xn-X0。 二者的关系:(Xn-X0)= (X1 -X0)+(X2-X1)+(X3-X2)+…(Xn-Xn-1)。
《时间序列分析》案例04

《时间序列分析》案例案例名称:时间序列分析在经济预测中的应用内容要求: 确定性与随机性时间序列之比较设计作者: 许启发,王艳明设计时间: 2003年8月ﻬ案例四:时间序列分析在经济预测中的应用一、案例简介为了配合《统计学》课程时间序列分析部分的课堂教学,提高学生运用统计分析方法解决实际问题的能力,我们组织了一次案例教学,其内容是:对烟台市的未来经济发展状况作一预测分析,数据取烟台市1949—1998年国内生产总值(GDP)的年度数据,并以此为依据建立预测模型,对1999年和2000年的国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动的最终成果,是反映国民经济活动最重要的经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套的方针政策具有重要的理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例的教学目的与要求,明确案例所涉及的教学内容;然后给学生一段时间,由学生根据资料,运用不同的方法进行预测分析,并确定具体的讨论日期;在课堂讨论时让学生自由发言,阐述自己的观点;最后,由主持教师作点评发言,取得了良好的教学效果。
经济预测是研究客观经济过程未来一定时期的发展变化趋势,其目的在于通过对客观经济现象历史规律的探讨和现状的研究,求得对未来经济活动的了解,以确定社会经济活动的发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标的历史数据按照时间的先后顺序排列,然后分析它随时间的变化趋势及自身的统计规律,外推得到预测目标的未来取值。
它与回归分析预测法的最大区别在于:该方法可以根据单个变量的取值对其自身的变动进行预测,无须添加任何的辅助信息。
本案例的最大特色在于:它汇集了统计学原理中的时间序列分析这一章节的所有知识点,通过本案例的教学,可以把不同的时间序列分析方法进行综合的比较,便于学生更好地掌握本章的内容。
二、案例的目的与要求(一)教学目的1.通过本案例的教学,使学生认识到时间序列分析方法在实际工作中应用的必要性和可能性;2.本案例将时间序列分析中的水平指标、速度指标、长期趋势的测定等内容有机的结合在一起,以巩固学生所学的课本知识,深化学生对课本知识的理解;3.本案例是对烟台市的国内生产总值数据进行预测,通过对实证结果的比较和分析,使学生认识到对同一问题的解决,可以采取不同的方法,根据约束条件,从中选择一种合适的预测方法;4.通过本案例的教学,让学生掌握EXCEL软件在时间序列分析中的应用,对统计、计量分析软件SPSS或Eviews等有一个初步的了解;5.通过本案例的教学,有助于提高学生运用所学知识和方法分析解决问题的能力、合作共事的能力和沟通交流的能力。
时间序列分析应用实例(使用Eviews软件实现)

时间序列分析应⽤实例(使⽤Eviews软件实现)引⾔某公司的苹果来货量数据是以时间先后为顺序记录的⼀组数据,从计量经济学的⾓度来分类就是⼀组时间序列数据。
为了提⾼苹果来货量预测的准确度以及预测结果的可信度,下⾯运⽤Eviews软件包(即Econometrics Views 计量经济学软件包)并结合计量经济学的理论知识,选取2017年1⽉⾄2019年4⽉的苹果来货量⽉度数据(事前对原始数据进⾏处理,把数值单位从吨转换为万吨)为样本数据,⽤⼀个时间序列模型来拟合上述样本数据,然后利⽤建⽴好的模型预测苹果未来⼏个⽉的来货量情况,并对预测结果进⾏分析。
1 平稳性检验1.1 初步检验设来货量时间序列为Qt,⾸先观察Qt的折线图,如图1所⽰:图1 Qt的折线图从图1可知,苹果来货量的⽉度数据总体呈下降趋势,并存在季节性因素,进⽽通过序列原⽔平的⾃相关系数图进⼀步探讨序列的平稳性,结果如图2所⽰:图2 Qt的⾃相关系数图从图2可以看到,所有的⾃相关系数(Autocorrelation)均落在2倍标准差之内(垂⽴的两道虚线表⽰2倍标准差),初步判定序列Qt是平稳的。
下⾯运⽤ADF单位根检验法证明序列的平稳性。
1.2 ADF单位根检验假设序列Qt的特征⽅程存在多个特征根,那么序列平稳的条件为所有特征根λi的绝对值均⼩于1,即所有特征根都在单位圆内。
构造该ADF 检验的原假设H0:存在i,使得λi>1,备择假设H1:λ1, λ2, … , λp<1,运⽤Eviews软件对序列Qt的原⽔平进⾏带常数项(Intercept)的ADF检验,采⽤SC准则⾃动选择滞后阶数,检验结果如图3所⽰:图3 ADF检验根据图3的检验结果可知,t统计量(t-Statistic)的伴随概率p为0.00,在显著性⽔平α=0.05下,因此我们有理由拒绝原假设(p<α),说明序列Qt是平稳的。
2 模型识别从图2可知,序列Qt的⾃相关系数(Autocorrelation)和偏⾃相关系数(Partial correlation)均在阶数1处突然衰减为在零附近⼩值波动,因此我们初步选择AR(1)、ARMA(1,1)这两个模型拟合样本数据3 模型参数估计3.1 AR(1)模型的拟合与参数估计设AR(1)模型为:Qt=C + Φ*Qt-1 +εt,其中C为常数项,Φ为待估计的Qt滞后⼀阶的系数,εt为服从均值为零、⽅差为常数正态分布的正态分布(即⽩噪声序列),下⾯运⽤Eviews软件对AR(1)模型的参数采⽤最⼩⼆乘估计法(⽆偏估计)进⾏参数估计,模型估计结果如图4所⽰:图4 AR(1)模型拟合结果根据图4的参数估计结果来看,在显著性⽔平α=0.05下,常数项显著不为零,⽽参数Φ的显著性估计结果并不是太好,另外AR(1)模型的特征⽅程的根(Inverted AR Roots)为-0.16,印证了序列Qt是平稳的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《时间序列分析》案例案例名称:时间序列分析在经济预测中应用内容要求:确定性与随机性时间序列之比较设计作者:许启发,王艳明设计时间:2003年8月案例四:时间序列分析在经济预测中应用一、案例简介为了配合《统计学》课程时间序列分析部分课堂教学,提高学生运用统计分析方法解决实际问题能力,我们组织了一次案例教学,其内容是:对烟台市未来经济发展状况作一预测分析,数据取烟台市1949—1998年国内生产总值(GDP)年度数据,并以此为依据建立预测模型,对1999年和2000年国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动最终成果,是反映国民经济活动最重要经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套方针政策具有重要理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例教学目与要求,明确案例所涉及教学内容;然后给学生一段时间,由学生根据资料,运用不同方法进行预测分析,并确定具体讨论日期;在课堂讨论时让学生自由发言,阐述自己观点;最后,由主持教师作点评发言,取得了良好教学效果。
经济预测是研究客观经济过程未来一定时期发展变化趋势,其目在于通过对客观经济现象历史规律探讨和现状研究,求得对未来经济活动了解,以确定社会经济活动发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标历史数据按照时间先后顺序排列,然后分析它随时间变化趋势及自身统计规律,外推得到预测目标未来取值。
它与回归分析预测法最大区别在于:该方法可以根据单个变量取值对其自身变动进行预测,无须添加任何辅助信息。
本案例最大特色在于:它汇集了统计学原理中时间序列分析这一章节所有知识点,通过本案例教学,可以把不同时间序列分析方法进行综合比较,便于学生更好地掌握本章内容。
二、案例目与要求(一)教学目1.通过本案例教学,使学生认识到时间序列分析方法在实际工作中应用必要性和可能性;2.本案例将时间序列分析中水平指标、速度指标、长期趋势测定等内容有机结合在一起,以巩固学生所学课本知识,深化学生对课本知识理解;3.本案例是对烟台市国内生产总值数据进行预测,通过对实证结果比较和分析,使学生认识到对同一问题解决,可以采取不同方法,根据约束条件,从中选择一种合适预测方法;4.通过本案例教学,让学生掌握EXCEL软件在时间序列分析中应用,对统计、计量分析软件SPSS或Eviews等有一个初步了解;5.通过本案例教学,有助于提高学生运用所学知识和方法分析解决问题能力、合作共事能力和沟通交流能力。
(二)教学要求1.学生必须具备相应时间序列分析基本理论知识;2.学生必须熟悉相应预测方法和具备一定数据处理能力;3.学生以主角身份积极地参与到案例分析中来,主动地分析和解决案例中问题;4.在提出解决问题方案之前,学生可以根据提供样本数据,自己选择不同统计分析方法,对这一案例进行预测,比较不同预测方法异同,提出若干可供选择方案;5.学生必须提交完整分析报告。
分析报告内容应包括:选题目及意义、使用数据特征及其说明、采用预测方法及其优劣、预测结果及其评价、有待于进一步改进思路或需要进一步研究问题。
三、数据搜集与处理时间序列数据按照不同分类标准可以划分为不同类型,最常见有:年度数据、季度数据、月度数据。
本案例主要讨论对年度数据如何进行预测分析。
考虑到案例设计时侧重点,本案例只是对烟台市国内生产总值进行预测,故数据搜集与处理过程相对简单。
我们通过查阅《烟台统计年鉴》、《烟台五十年》等有关资料获得烟台市1949—2000年共52年国内生产总值资料数据(原始数据详见表3)。
该指标是反映国民经济发展情况最重要指标之一,我们选择该指标进行预测具有较强实用价值。
此外,预测方法具有普遍适用性,使用者也可以将其应用于其它研究领域。
资料数据是预测依据和基础,一般是根据确定预测目标及影响因素搜集有关资料和数据,并结合初步拟定预测模型,对所搜集数据进行分析和处理,然后再选取适当预测模型。
我们可以将整个数据处理过程概括如下,见图1。
图1 经济预测流程图四、建议使用预测分析方法(一)确定性时间序列分析法1.指标法:平均增长量法、平均发展速度法;2.趋势预测法:移动平均法、指数平滑法、曲线拟合法。
(二)随机性时间序列分析法1.ARIMA 模型预测; 2.组合模型预测。
五、案例分析过程(一)确定性时间序列分析法1.平均增长量法该方法是利用历史资料计算出它平均增长量,然后再假定在以后各期当中,它仍按这样一个平均增长量去增长,从而得出在未来一段时期内预测值。
根据烟台市国内生产总值1949年—1998年观察值,我们计算出GDP 平均增长量为150647.69万元(水平法)和38437.81万元(总和法),利用其对烟台市1999年和2000年GDP 值进行预测并与实际GDP 值[1]比较,结果见表1。
表1 平均增长量法预测结果教师点评:①平均增长量法不仅得到了烟台市1999年、2000年GDP 数据预测值,而且还让学生认识到平均增长量预测法中水平法与总和法区别所在,图1较明显地反映出平均增长量水平法与累计法计算区别,即水平法仅考虑首尾年份数值,而不考虑中间年份数值变化,因而有n a n a =∆-+)1(0;②而总和法则考虑了整个样本区间上总体变化情况,有∑=∆+++∆++∆+ni a n a a a 000)()2()(Λ,图2中A 面积和B 面积应该相等。
2.平均发展速度法该方法就是利用时间序列资料计算出它平均发展速度,然后再假定在以后各期当中,它仍按这样一个平均发展速度去变化,从而得出时间序列预测值。
我们计算出GDP 在1949年—1998年间平均发展速度为113.036%(几何法)和112.248%(方程法)[2],利用其对烟台市1999年和2000年GDP 进行预测得到结果见表2。
[1] 1999年为8006600万元,2000年为8795900万元。
[2] 在该问题中几何法与方程法计算出平均发展速度差别不大。
图2 由平均增长量推算出时间序列变化图表2 平均发展速度法预测结果教师点评:①同平均增长量计算方法一样,平均发展速度计算方法也有两种,其中几何法也只是考虑起始年份取值,有n n X a a 0=,而方程式法则要考虑到整个年份取值变化,有∑==+++ni i na X a X a X a 10200Λ,方程式法内插预测曲线与原始曲线所夹面积A 和面积B 也相等;②在方程式法计算中,计算平均增长速度可以采取试错法(让学生尝试着编写小循环程序求解)或插值法;③同平均增长量计算一样,平均发展速度计算方法也有两种,其中几何法也只是考虑起始年份取值,而方程法则要考虑到整个年份取值变化;④由预测结果可以看出,无论是平均增长量法还是平均发展速度法只适于作短期预测,否则预测相对误差会显著提高。
3.移动平均法移动平均法是根据时间序列资料,采取逐项移动平均办法,计算一定项数序时平均数,以反映长期趋势方法。
移动平均法主要有简单移动平均法、加权移动平均法、趋势移动平均法等。
这里主要介绍简单移动平均法。
记11,t t t N t y y y M t N N--++++=≥L为t 期移动平均数;N 为移动平均项数。
由于移动平均可以平滑数据,消除周期变动和不规则变动影响,使长期趋势显示出来,可以利用其进行外推预测。
预测公式为:1ˆt t yM +=,即以第t 期移动平均数作为第t +1期预测值。
表3 移动平均预测结果图3 由平均发展速度推算出时间序列变化图由图4,我们可以得出这样结论:移动平均法对原始序列产生了一个修匀作用,并且移动平均所使用间隔期越长,即N 越大,修匀程度也越大,但对原始数据反应越不灵敏;反之,则反是。
为此,我们需要依据误差分析选择间隔时期N ,结果见表4。
表4 烟台市GDP 移动平均预测法误差分析 由表4中分析可知,在N=3时产生误差较小,因此,选定N=3进行预测,得到1999年烟台市GDP 预测值为6767466.7万元。
教师点评:①简单移动平均法只适合作近期预测,且如果目标发展影响因素发生较大变化,采用简单移动平均法就会产生较大预测偏差和滞后;②移动平均法会损失一部分数据,因而需要数据量较大;③移动平均法对所平均N 个数据等权看待,而对t N 期以前数据则完全不考虑,这往往不符合实际。
4.指数平滑法指数平滑法是移动平均法改进和发展,它既不需要存储很多历史数据,又考虑了各期数据重要图4 烟台市GDP 移动平均预测曲线性,且使用了全部历史资料。
指数平滑计算公式为:)1(1)1()1(--+=t t t S a ay S ,其中:a 为权数,)1(t S 为一阶指数平滑值。
二阶指数平滑就是在一阶指数平滑基础上再进行一次指数平滑,高阶依此类推。
由于指数平滑存在着滞后现象,因此,无论一次指数平滑或二次、三次指数平滑值[3](数据略),都不宜直接作为预测值。
但可以利用它来修匀时间序列,以获得时间序列变化趋势,从而建立预测模型。
由相应指数平滑数值,可以建立如下指数平滑二次曲线趋势预测模型。
2ˆl c l b a P D G tt t l t ++=+ 其中(1)(2)(3)(1)(2)(3)22(1)(2)(3)233[(65)2(54)(43)]2(1)[2]2(1)t t t t t t t t t t t t a S S S a b a S a S a S a a c S S S a ⎧⎪=-+⎪⎪⎪=---+-⎨-⎪⎪⎪=-+-⎪⎩, )1(t S 、)2(t S 、)3(t S 为当前时间点处一次、二次、三次指数平滑值,l 为预测时段长。
为了预测烟台市1999年和2000年国内生产总值,可以取t=49,l 分别取1和2。
由指数平滑数值可计算出:49a =7583559.18,21b =936865.62,21c =294704.17,故得二次曲线指数平滑预测模型为:24917.29470462.93686518.7583559ˆl l P D G l⨯+⨯+=+ (1)分别令l =1、l =2得预测结果见表5。
表5 指数平滑预测结果教师点评:①在作指数平滑时,涉及到初始值和权数a 选取问题,不同取值导致结果各不相同;②由于指数平滑法也存在着严重滞后现象,所以直接用平滑值去预测未来值会带来较大误差,当建立指数平滑模型进行预测时,就会大大地减少预测误差。
5.曲线拟合法多项式曲线拟合法亦称趋势拟合法或时间回归法,该方法根据时间序列随时间变化趋势,运用LS 拟合一条曲线,而后利用该曲线随时间变化规律对时间序列未来取值进行预测。
我们根据烟台市GDP (1949—1998)资料拟合出如下曲线:GDP=29669.339+12267.158×T -4330.927×T 2+473.564×T 3-18.571×T 4+0.244×T 5 R 2=0.9905。
