第七章 习题答案
《统计学》-第7章-习题答案

第七章思考与练习参考答案1.答:函数关系是两变量之间的确定性关系,即当一个变量取一定数值时,另一个变量有确定值与之相对应;而相关关系表示的是两变量之间的一种不确定性关系,具体表示为当一个变量取一定数值时,与之相对应的另一变量的数值虽然不确定,但它仍按某种规律在一定的范围内变化。
2.答:相关和回归都是研究现象及变量之间相互关系的方法。
相关分析研究变量之间相关的方向和相关的程度,但不能确定变量间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况;回归分析则可以找到研究变量之间相互关系的具体形式,并可变量之间的数量联系进行测定,确定一个回归方程,并根据这个回归方程从已知量推测未知量。
3.答:单相关系数是度量两个变量之间线性相关程度的指标,其计算公式为:总体相关系数,样本相关系数。
复相关系数是多元线性回归分析中度量因变量与其它多个自变量之间的线性相关程度的指标,它是方程的判定系数2R 的正的平方根。
偏相关系数是多元线性回归分析中度量在其它变量不变的情况下两个变量之间真实相关程度的指标,它反映了在消除其他变量影响的条件下两个变量之间的线性相关程度。
4.答:回归模型假定总体上因变量Y 与自变量X 之间存在着近似的线性函数关系,可表示为t t t u X Y ++=10ββ,这就是总体回归函数,其中u t 是随机误差项,可以反映未考虑的其他各种因素对Y 的影响。
根据样本数据拟合的方程,就是样本回归函数,以一元线性回归模型的样本回归函数为例可表示为:tt X Y 10ˆˆˆββ+=。
总体回归函数事实上是未知的,需要利用样本的信息对其进行估计,样本回归函数是对总体回归函数的近似反映。
两者的区别主要包括:第一,总体回归直线是未知的,它只有一条;而样本回归直线则是根据样本数据拟合的,每抽取一组样本,便可以拟合一条样本回归直线。
第二,总体回归函数中的0β和1β是未知的参数,表现为常数;而样本回归直线中的0ˆβ和1ˆβ是随机变量,其具体数值随所抽取的样本观测值不同而变动。
数据结构课后习题答案第七章
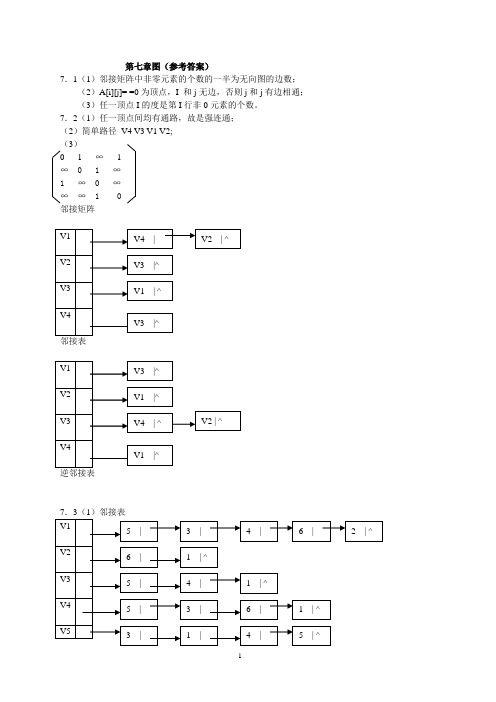
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第七章图 习题答案

第七章图习题答案基础知识:7.1 在图7.23所示的各无向图中:(1)找出所有的简单环。
(2)哪些图是连通图?对非连通图给出其连通分量。
(3)哪些图是自由树(或森林)?答:(1)所有的简单环:(同一个环可以任一顶点作为起点)(a)1231(b)无(c)1231、2342、12341(d)无(2)连通图:(a)、(c)、(d)是连通图,(b)不是连通图,因为从1到2没有路径。
具体连通分量为:(3)自由树(森林):自由树是指没有确定根的树,无回路的连通图称为自由树:(a)不是自由树,因为有回路。
(b)是自由森林,其两个连通分量为两棵自由树。
(c)不是自由树。
(d)是自由树。
7.2 在图7.24(下图)所示的有向图中:(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
(3) 请给出每个顶点的度,入度和出度。
(4) 请给出其邻接表、邻接矩阵及逆邻接表。
答:(1)该图是强连通的,所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径。
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4、另包括所有有向环,有向环如下:v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)(3)每个顶点的度、入度和出度:D(v1)=3ID(v1)=1OD(v1)=2D(v2)=2 ID(v2)=1OD(v2)=1D(v3)=3 ID(v3)=2OD(v3)=1D(v4)=2 ID(v4)=1OD(v4)=1(4)邻接表:(注意边表中邻接点域的值是顶点的序号,这里顶点的序号是顶点的下标值-1) vertex firstedge next┌─┬─┐┌─┬─┐┌─┬─┐0│v1│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘1│v2│─→│ 2│∧│├─┼─┤├─┼─┤2│v3│─→│ 0│∧│├─┼─┤├─┼─┤3│v4│─→│ 2│∧│└─┴─┘└─┴─┘逆邻接表:┌─┬─┐┌─┬─┐0│v1│─→│ 2│∧│├─┼─┤├─┼─┤1│v2│─→│ 0│∧│├─┼─┤├─┼─┤┌─┬─┐2│v3│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘3│v4│─→│ 0│∧│└─┴─┘└─┴─┘邻接矩阵:0 1 0 10 0 1 01 0 0 00 0 1 07.3 假设图的顶点是A,B...,请根据下述的邻接矩阵画出相应的无向图或有向图。
基础会计学 第七章习题及答案

第七章习题复习思考题1.什么是账务处理程序?其意义如何?2.账务处理程序的种类有哪些?企业中普遍采用的有哪几种?3.各种账务处理程序的特点是什么?它们有哪些优缺点?其适用范围如何?4.简述各种账务处理程序的基本步骤。
5.区别不同账务处理程序的主要标志是什么?6.记账凭证账务处理程序需要采用哪些凭证和账簿?他们有哪些格式要求?名词解释账务处理程序科目汇总表一、判断题1.汇总记账凭证账务处理程序下,总分类账帐页格式一般采用三栏式()2.记账凭证账务处理程序登记总账的依据是原始凭证()3.汇总记账凭证账务处理程序的适用范围是规模较大、业务量较少的单位。
()4.账务处理程序中最基本的处理程序是科目汇总表账务处理程序。
()5.为了便于汇总转账凭证,在编制转账凭证时,其账户的对应关系应是一借一贷或多借一贷。
()6.采用科目汇总表账务处理程序,不仅可简化登记总账的工作,而且便于检查和分析经济业务。
()7.账务处理程序不同,现金日记账、银行存款日记账登记的依据也不同。
()8.各种账务处理程序的区别主要在于编制会计报表的依据和方法不同。
()9.企业总分类账采用何种格式取决于账务处理程序。
()10.各种账簿都是直接根据记账凭证进行登记的。
()二、单项选择题1.各种会计核算程序的主要区别是()A.填制会计凭证的依据和方法不同B.登记总账的依据和方法不同C.编制会计报表的依据和方法不同D.登记明细账的依据和方法不同2.汇总记账凭证核算程序下,总分类账账页格式一般采用()A.三栏式B.多栏式C.设有“对应科目”栏的三栏式D.数量金额式3.编制科目汇总表的直接依据是()A.原始凭证B.原始凭证汇总表C.记账凭证D.汇总记账凭证4.各种账务处理程序中最基本的是()A. 记账凭证账务处理程序B. 汇总记账凭证账务处理程序C. 科目汇总表账务处理程序D. 多栏式日记账账务处理程序5.特定的会计凭证账簿组织和特定的记账程序相结合的方式称为()A. 会计核算前提B. 会计核算原则C. 会计核算方法D. 会计核算形式6. 直接根据记账凭证,逐笔登记总分类账的形式是()A. 日记总账账务处理程序B. 汇总记账凭证账务处理程序C. 记账凭证账务处理程序D. 科目汇总表账务处理程序7. 科目汇总表账务处理程序的主要缺点是()A. 加大了登记总账的工作量B. 据此登帐易产生错误C. 不具有试算平衡作用D. 不便于查对账目8. 科目汇总表账务处理程序和汇总记账凭证账务处理程序的主要相同点是()A. 登记总账的依据相同B. 记账凭证都需要汇总并且记账步骤相同C. 汇总凭证格式相同D. 记账凭证汇总的方向相同9. 记账凭证账务处理程序的适用范围是()A. 规模较大、业务较多的单位B. 规模较小、业务较少的单位C. 规模较大、业务较少的单位D. 规模较小、业务较多的单位10. 汇总记账凭证账务处理程序的主要缺点是()A. 登记总账的工作量大B. 不利于会计人员分工C. 体现不了账户的对应关系D. 明细账与总账无法核对三、多项选择题1. 汇总记账凭证核算程序的优点是()A.总账能反映账户对应关系,便于对经济业务进行分析和检查B.减少登记总账的工作量C.同一贷方科目的转账凭证不多时,可减少核算工作量D.有利于对全部账户的发生额进行试算平衡E.有利于会计人员分工2. 在采用汇总记账凭证核算程序时,编制记账凭证的要求是()A.收款、付款、转账凭证均可一借一贷B.转账凭证可一借多贷C.转账凭证可一贷多借D.收款凭证可一借多贷E.付款凭证可一贷多借3. 科目汇总表的作用有()A.减少总分类账的记账工作量B.进行登记总账前的试算平衡C.反映账户的对应关系D.汇总有关账户的本期借、贷方发生额E.汇总有关账户的余额4. 会计核算程序的内容包括()A.账簿组织B.报表体系C.记账程序及方法D.编制报表的方法5. 登记总分类账的根据可以是()A.记账凭证B.汇总记账凭证C.科目汇总表D.多栏式现金、银行存款日记账E.日记总账6.在下列会计凭证中,可以作为登记总分类账簿的直接依据的有()A. 记账凭证B. 原始凭证C. 汇总记账凭证D. 原始凭证汇总表E. 科目汇总表7.科目汇总表的缺点有()A. 不能反映账户之间的对应关系B. 编制科目汇总表的工作量较大C. 加大登记总账的工作量D. 不便于查对账目E. 不便于了解经济业务的来龙去脉四、业务题自力公司本月发生经济业务如下:(1) 6月2日,通过银行缴纳上月应交的税金67600元。
高等数学第七章习题详细解答

第七章习题答案习题7.01.下列各种情形中,P 为E 的什么点?(1)如果存在点P 的某一邻域()U P ,使得()⊂c U P E (c E 为E 的余集); (2)如果对点P 的任意邻域()U P ,都有, ()(),C U P E U P E φφ≠≠; (3)如果对点P 的任意邻域()U P ,都有. 解 (1)P 为E 的外点;(2)P 为E 的边界点;(3)P 为E 的聚点。
2.判定下列平面点集的特征(说明是开集、闭集、区域、还是有界集、无界集等?)并分别求出它们的导集和边界.(1) (){},0≠x y y ;(2) (){}22,620≤+≤x y x y ; (3) (){}2,≤x y y x ;(4) ()(){}()(){}2222,11,24+-≥⋂+-≤x y x y x y x y .解 (1) 是开集,是半开半闭区域,是无界集,导集为2R ,边界集为(){},0=x y y ;(2)既不是开集也不是闭集,是半开半闭区域,是有界集,导集为(){}22,620≤+≤x y x y ,边界集为(){}2222,=6=20++,x y x y x y ;(3) 是闭集,是半开半闭区域,是无界集,导集为集合本身,边界集为(){}2,=x y y x ;是闭集,是闭区域,是有界集,导集为集合本身,边界集为()()(){}2222,11,24+-=+-=x y x y x y习题7.11. 设求1. 解 令,=-=yu x y v x,解得,11==--u uv x y v v,故()22,11⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭u uv f u v v v ,即()()21+,1=-u v f u v v ,所以,()()21+y ,1=-x f x y y φ≠-}){()(P E P U 22,,y f x y x y x ⎛⎫-=- ⎪⎝⎭(,).f x y2.已知函数()22,cot =+-x f x y x y xy y,试求(),f tx ty .2. 解 因为()22,cot =+-y f x y x y xy x,所以,()2222,cot ,=+-t y f tx ty tx ty txty t x即()()222,cot =+-y f tx ty t x y t xy x.3.求下列各函数的定义域 (1) 25)1(=-+z ln y xy ;(2) =z ;(3) =z(4) )0;=>>u R r(5) =u3. 解 (1)(){}2,510-+>x y yxy ;(2)(){},0->x y x y ;(3)(){}2,≥x y x y ;(4)(){}22222,<++≤x y r x y z R ;(5)(){}222,≤+x y z x y4. 求下列各极限:(1) ()()233,0,31lim →-+x y x yx y ;(2)()(,1,1ln lim→+x x y y e(3)()(,0,0lim→x y(4)()(,0,0lim→x y ;(5)()()(),0,2sin lim→x y xy x ;(6)()()()()222222,0,01cos lim→-++x y x y x y xy e.4. 解 (1)()()2333,0,31101lim 0327→--==++x y x y x y ;(2)()(()1,1,1ln ln 11lim2→+++===x x y y e e e (3)()()()(,0,0,0,0limlim→→=x y x y ()(,0,01lim4→==x y (4)()(()()),0,0,0,01limlim→→=x y x y xy xy()()),0,0=lim1=2→+x y(5)()()()()()(),0,2,0,2sin sin limlim 122→→=⋅=⋅=x y x y xy xy y x xy(6)()()()()()()()()()222222222222222,0,0,0,01cos 1cos limlim→→-+-++=⋅++x y x y x y x y x y x y xy xy eex y()()()()()()()2222222022,0,0,0,01cos 10limlim=02→→-++=⋅⋅=+x y x y x y x y xy e exy5.证明下列极限不存在: (1)()(),0,0lim→-+x y x yx y ;(2)()(),0,0lim→+-x y xyxy x y .5. (1) 解 令=y kx ,有()(),0,001limlim 1→→---==+++x y x x y x kx kx y x kx k ,k 取不同值,极限不同,故()(),0,0lim→-+x y x yx y 不存在.(2) 解令=x y()()22,0,00lim lim 1→→==+-x y x xy x xy x yx ;令2=x y()()()()22,0,02,0,0022lim lim lim 0221→→→===+-++x y y y y xy y y xy x y y y y ;01≠,故()(),0,0lim→+-x y xyxy x y不存在.6.函数=y z a 为常数)在何处间断?6. 解 因为=y z 是二元初等函数,且函数只在点集(){,x y y 上无定义,故函数在点集(){,x y y 上间断.7.用 εδ- 语言证明()(,0,0lim0→=x y .7. 证明 对0∀>ε,要使220-=≤=<ε2<ε,取=2δε<δ0-<ε,所以()(,0,0lim 0→=x y习题7.21. 设()(),sin 1arctan ,π==+-xy xz f x y e y x y 试求()1,1x f 及()1,1y f1. 解()221,sin arctan 1=+++xy x x yf x y ye y xx yyπ22=sin arctan+++xy x xy ye y y x y π.()()222,sin cos 11-=++-+xy xyy x y f x y xe y e y x x yπππ 222sin cos -=+++xyxyx x xe y e y x y πππ()()1,1,1,1∴=-=-x y f e f e2.设(),ln 2⎛⎫=+ ⎪⎝⎭y f x y x x ,求()1,0'x f ,()1,0'y f .2. 解()()222122,22--==++x yx y x f x y y x x y x x()2112,22==++y x f x y yx y x x()()11,011,02∴==,x y f f . 3.求下列函数的偏导数(1) 332=++z x y xy ,(2) ()1=+xz xy , (3) ()222ln =+z y x y ,(4) ln tan=y z x, (5) ()222ln =+z x x y ;(6)=z (7) ()sec =z xy ;(8) ()1=+yz xy ;(9) ()arctan =-zy x y ;(10) .⎛⎫=⎪⎝⎭zx u y 3. 解 (1)2232,32z z x y y x x y ∂∂=+=+∂∂(2)因为 ()ln 1,x xy z e+=所以()()()()ln 1ln 11ln 111x x xy z xy xy e xy xy xy x xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭()()22ln 1111x x xy z x x e xy y xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭(3)()2322222222,2ln z xy z y y x y x x y y x y ∂∂==++∂+∂+(4)222222sec sec 111sec ,sec tan tan tantan y yy z y y z y x x y y y y x x x y x x x x x x x x∂∂⎛⎫⎛⎫=-=-== ⎪ ⎪∂∂⎝⎭⎝⎭ (5)()32222222222ln ,z x z x y x x y x x y y x y ∂∂=++=∂+∂+(6)z z x y ∂∂====∂∂(7)()()()()sec tan ,sec tan z z y xy xy x xy xy x y ∂∂==∂∂(8)()()22ln 1111y y xy z y y e xy x xy xy +⎛⎫⎛⎫∂==+ ⎪ ⎪∂++⎝⎭⎝⎭()()()()ln 1ln 11ln 111y y xy z xy xy e xy xy xy y xy xy +⎛⎫⎛⎫∂=++=+++ ⎪ ⎪∂++⎝⎭⎝⎭ (9)()()()()()()()11222ln ,,111z z zz z z z x y z x y x y x y u u u x y z x y x y x y ------∂∂∂==-=∂∂∂+-+-+-(10)因为 ln,x z yu e=所以ln ln ln 21,,ln zzx x x z z z y y y u z x z u z x x z u x e e e x x xy y x y y y y z y y y⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂=⋅==⋅-=-= ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭4.设ln=z ,求证: 12∂∂+=∂∂z z xy x y . 4.证明 因为ln,z =所以z zx y∂∂====∂∂从而有12 z zx yx y∂∂+=+=+=∂∂5.求下列函数的二阶偏函数:(1)已知33sin sin=+z x y y x,求2∂∂∂zx y;(2)已知ln=xz y,求2∂∂∂zx y;(3)已知(ln=z x,求22∂∂z x和2∂∂∂z x y;(4)arctan=yzx求22222,,∂∂∂∂∂∂∂z z zx y x y和2∂∂∂zy x.5. 解(1)3323sin sin,3sin coszz x y y x x y y xx∂=+∴=+∂从而有223cos3coszx y y xx y∂=+∂∂(2)ln ln1,lnx xzz y y yx x∂⎛⎫=∴= ⎪∂⎝⎭从而有()()()ln1ln1ln11ln ln ln ln1xx xz yxy y y x yx y x y x--⎛⎫∂=+⋅=+⎪∂∂⎝⎭(3)(()1222 ln,zz x x yx-∂=∴===+∂从而有()()3322222222122zx y x x x yx--∂=-+=-+∂()()332222222122z x y y y x y x y --∂=-+=-+∂∂ (4)22221arctan,1y z y y z x xx x y y x ∂⎛⎫=∴=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭ 222111z x yx x y y x ∂⎛⎫=⋅= ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭从而有()()()()2222222222222222222,x y y z xy z y x x x y x y x y x y -++∂∂-===∂∂∂+++ ()()2222222222222222,z xy z x y xy x y y y x x y x y x y ⎛⎫∂-∂+--=== ⎪∂∂∂+⎝⎭++ 6. 设()ln =z y xy ,求2∂∂∂z x y 及22∂∂zy .6. 解 因为()ln ,z y xy =所以()(),ln ln 1z y y z x y xy y xy x xy x y xy∂∂===+=+∂∂从而有22211,.z z x y x y y∂∂==∂∂∂ 习题7.31. 求下列函数的全微分.(1) 2222+=-s t u s t ;(2) ()2222+=+x y xyz x y e;(3) ()arcsin0=>xz y y;(4) ⎛⎫-+ ⎪⎝⎭=y x x y z e ;1.解 (1)()()222232322222222()()22222∂--+⋅---==∂--u s s t s t s s st s t s s s t s t()()222223232222222()()22222u t s t s t t ts t ts s t s t s t ∂--+---==∂-- ()()2322222244u u st t dz ds dt ds dt s t s t s t ∂∂-∴=+=-∂∂--(2)()()()222222222222++++∂=++⋅∂x y x y xyxyx y x y yzxe x y exxy()2222222244222222+++⎛⎫--=++⋅=+ ⎪⎝⎭x y x y x y xyxyxyx y x y xe x y e x e x y x y()()()22222222222-2+++∂=++⋅∂x y x y xy xyy x x y xzye x y eyxy()()2222222222442222+++-+⎛⎫-=+⋅=+ ⎪⎝⎭x y x y x y xyxyxyy x x y y x yeey e xy xy2244442222x y xyz z x y y x dz dx dy x edx y dy x y x y xy +⎛⎫⎛⎫∂∂--∴=+=+++ ⎪ ⎪∂∂⎝⎭⎝⎭ (3)2222211∂=⋅==∂--⎛⎫yzxyyy x y x x22⎛⎫⎛⎫∂=-=-= ⎪ ⎪∂⎝⎭⎝⎭z x x yy y z zdz dx dy x y∂∂∴=+=∂∂(4)22221y x y x x y x y z y y x e e x x y x y ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-= ⎪∂⎝⎭ 22221y x y x x y x y z x x y e e y x y xy ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫∂-=-+= ⎪∂⎝⎭222222y x y x x y x y z z z y x x y dz dx dy e dx e dy x y y x y xy⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭∂∂∂--∴=+==+∂∂∂ 2. 求函数2arctan1=+xz y 在1,1==x y 处的全微分.2.解()()()()()()()22222222222222222211111111111++∂++=⋅=⋅=∂++++++++y y z y y x xy y x y y xy()()()()()()22222222222222211222111111+∂-⋅--=⋅=⋅=∂++++++++y z x y xy xyx yy y x y y xy()()21,11125111z x ∂+∴==∂++ , ()()21,12125111∂-⋅==-∂++z y ()1,12255dz dx dy ∴=- 3. 求函数22=-xyz x y 当2,1,0.02,0.01==∆=∆=x y x y 时的全微分和全增量,并求两者之差.3.解 ()()()(),, 2.02,1.011,1z z x x y y z x y z z ∆=+∆+∆-=-()()22222.02 1.0121 2.0420.6670.667021 4.08 1.0232.02 1.01⨯⨯=-=-=-=--- ()()()2223222222222--⋅∂--===-∂---y x y xy x z x y y y x x y x y x y ()()()()22322222222--⋅-∂+==∂--x x y xy y z x xy y x y x y ()2,111413z x ∂∴=-=-∂- ,()()22,182110941z y ∂+⨯==∂- ()2,11100.020.010.070.0110.00439dz ∴=-⨯+⨯=-+=00.0040.004z dz ∴∆-=-=-.*4讨论函数()()()()(),0,0,0,,0,0⎧≠⎪=⎨⎪=⎩xy x y f x y x y 在()0,0点的连续性、可导性、可微性以及其偏导函数在()0,0的连续性.4.解()()()()()(),0,0,0,0lim,lim 00,0x y x y f x y xy f →→===(),f x y ∴在()0,0点连续 又()()()00,00,0000,0limlim 0x x x f x f f x x∆→∆→∆--===∆∆ ()()()000,0,0000,0limlim 0y y y f y f f y y∆→∆→∆--===∆∆ ()()0,00,0,00x y f f ∴==.()(()(,0,0,0,0,0,00limlim limx y x y f x yf z dzρρ→∆∆→∆∆→∆∆--∆-==()()()0,0,0x y<∆∆→∆lim0z dzρρ→∆-∴=故函数(),f x y 在()0,0点可微. 由()(),0,0x y ≠时(),=-x f x yy xy()23222sinx yy xy=-+(),=-y f x y x xy ()23222xy x xy=-+()(),0,0lim 0x y y →= ,()()()()23,0,0222lim→=+x y x yy kx xy()()()33323222=lim11→==+⋅+x kx ky kx k xk ,k 不同值不同()()()23,0,0222lim→∴+x y xy xy 不存在,故()()(),0,0lim ,xx y f x y →不存在.(),x f x y ∴在()0,0点不连续,同理可证(),y f x y 在点()0,0不连续.*5.计算()2.050.99的近似值.5.解 令00,1,2,0.01,0.05yz x x y x y ===∆=∆= 则1,ln y y z z yx x x x y-∂∂==∂∂ ()()1,21,22,0z zx y ∂∂∴==∂∂ ()()()2.0521,21,20.991120.0100.0510.02 1.02∂∂∴≈+∆+∆=+⨯+⨯=+=∂∂z zx y x y*6.设有厚度为,内高为,内半径为的无盖圆柱形容器,求容器外壳体积的近似值(设容器的壁和底的厚度相同).6.解 设容器底面积半径为r ,高为h则容器体积2V r h π=22,V Vrh r r hππ∂∂==∂∂ 22∴=+dV rhdr r dh ππ002,10,0.1,0.1r cm h cm r cm h cm ==∆=∆=()()22,102,1020.10.1400.140.1 4.4∴∆≈=⋅+⋅=⨯+⨯=V dV rh r πππππ*7. 测得直角三角形两直角边的长分别为7±0.1cm 和24±0.1cm ,试求利用上述二值来计算斜边长度时的绝对误差和相对误差.0.1cm 10cm 2cm7.解 设直角三角形的直角边长分别为,x y ,则斜边z =,zz xy∂∂==∂∂由题意007,24,0.1,0.1x y x y δδ====z ∴的绝对误差为()()7,247,247240.10.10.242525∂∂=+=⨯+⨯=∂∂z x y z z x y δδδz 的相对误差()7,240.240.009625=≈zz δ 习题7.41.设,,,求. 1.解 ()3222sin 22cos 23cos 6---∂∂=⋅+⋅=⋅-⋅=-∂∂x y x y t t du z dx z dy e t e t e t t dt x dt y dt2.设,而,,求. 2.解2123∂∂=⋅+⋅=+∂∂dz z dy z dV x dx u dx V dx2341-=x3.设,,,求,. 3.解 ()()222cos 2sin ∂∂∂∂∂=⋅+⋅=-+-∂∂∂∂∂z z u z v uv v y u uv y x u x v x()()2222222cos sin sin cos cos 2cos sin sin x y y x y y x y x y y y =-+-()23sin cos cos sin x y y y y =-()()()222sin 2cos z z u z v uv v x y u uv x y y u y v y∂∂∂∂∂=+=--+-∂∂∂∂∂ ()()()2222222cos sin sin sin cos 2cos sin cos x y y x y x y x y x y y x y =--+-()()3333cos sin 2cos sin sin cos x y y x y y y y =+-+2e x y u -=sin x t =3y t =d d u tarccos()z u v =-34u x =3v x =d d zx22z u v uv =-cos u x y =sin v x y =zx ∂∂z y∂∂4.设,而,,求,. 4.解 222ln 3∂∂∂∂∂⎛⎫=⋅+⋅=⋅+- ⎪∂∂∂∂∂⎝⎭z z u z v u y u v x u x v x v x()()()2322632ln 326ln 3x y y y y x y x y x x x x +⎛⎫=+-=+-- ⎪⎝⎭5.设求5.解 ()()1wf x xy xyz y yz x ∂'=++++∂()()()()1wf x xy xyz x xz x z f x xy xyz y∂''=+++=+++∂ ()()wf x xy xyz xy xyf x xy xyz z ∂''=++=++∂6.求下列函数的一阶偏导数(其中具有一阶连续偏导数):(1);(2);(3);(4).6.解 (1)()()222222∂''=-⋅=-∂z f x y x xf x y x()()()222222∂''=-⋅-=--∂zf x y y yf x y y(2)121110∂'''=+⋅=∂u f f f x y y12122211u x x f f f f y y z y z ⎛⎫∂⎛⎫''''=-+=-+ ⎪ ⎪∂⎝⎭⎝⎭122220∂⎛⎫'''=⋅+-=- ⎪∂⎝⎭u y y f f f z z z (3)1231231∂''''''=⋅+⋅+⋅=++∂uf f y f yz f yf yzf x123230∂'''''=⋅+⋅+⋅=+∂uf f x f xz xf xzf y2ln z u v =32u x y =+y v x =zx ∂∂z y∂∂(),w f x xy xyz =++,,.w w wx y z∂∂∂∂∂∂f 22()z f x y =-,x y u f y z ⎛⎫= ⎪⎝⎭(,,)u f x xy xyz =22(,e ,ln )xy u f x y x =-123300∂''''=⋅+⋅+⋅=∂uf f f xy xyf z (4)1231231122∂''''''=⋅+⋅⋅+⋅=++∂xy xyu f x f e y f xf ye f f x x x()12312202∂'''''=⋅-+⋅+⋅=-+∂xy xy uf y f e x f yf xe f y7.求下列函数的二阶偏导数,,(其中具有二阶连续偏导数):(1),(2). 7.解(1)22121222∂''''=⋅+⋅=+∂zf xy f y xyf y f x22121222∂''''=⋅+⋅=+∂zf x f xy x f xyf y()()222211112212222222∂'''''''''∴=+⋅+⋅+⋅+⋅∂zyf xy f xy f y y f xy f y x233341111221222422yf x y f xy f xy f y f '''''''''=++++ 23341111222244yf x y f xy f y f '''''''=+++()()2222111122212222222∂''''''''''=+⋅+⋅++⋅+⋅∂∂zxf xy f x f xy yf y f x f xy x y322223111122212222422xf x yf x y f yf x y f xy f ''''''''''=+++++ 32231111222222522xf x yf x y f yf xy f ''''''''=++++()2222211122212222222∂'''''''''=+++⋅+⋅∂zx f x x f xy xf xy f x f xy y43221112222424x f x yf xf x y f '''''''=+++(2)()()222222∂''=+⋅=+∂zf x y x xf x y x()()222222∂''=+⋅=+∂zf x y y yf x y y22zx∂∂2z x y ∂∂∂22z y ∂∂f 22(,)z f x y xy =22()z f x y =+()()()()2222222222222224∂''''''∴=+++⋅=+++∂zf x y xf x y x f x y x f x y x()()22222224∂'''=+⋅=+∂∂z xf x y y xyf x y x y()()()()2222222222222224∂''''''=+++⋅=+++∂zf x y yf x y y f x y y f x y y8.设其中F 是可微函数,证明8.解()()()cos sin sin cos cos cos sin sin ux F y x x x xF y x x∂''=+--=--∂ ()sin sin cos uF y x y y∂'=-∂ ()()cos cos cos cos sin sin cos cos sin sin cos u uy x x xF y x y yF y x x x y∂∂''∴+=--+-⎡⎤⎣⎦∂∂ ()()cos cos cos cos sin sin cos cos sin sin cos cos x y x yF y x x yF y x x y ''=--+-=.习题7.51.设,φ⎛⎫= ⎪⎝⎭x y z z 其中为可微函数,求∂∂+∂∂z z x y x y . 1.解 z是,x y函数由方程xx z y φ⎛⎫= ⎪⎝⎭确定。
微生物的遗传变异与育种答案解析

第七章习题答案一.名词解释1.转座因子:具有转座作用的一段DNA序列.2.普遍转导:通过极少数完全缺陷噬菌体对供体菌基因组上任何小片段DNA进行“误包”,而将其遗传性状传递给受体菌的现象称为普遍转导。
3.准性生殖:是一种类似于有性生殖,但比它更为原始的两性生殖方式,这是一种在同种而不同菌株的体细胞间发生的融合,它可不借减数分裂而导致低频率基因重组并产生重组子.4.艾姆氏试验:是一种利用细菌营养缺陷型的回复突变来检测环境或食品中是否存在化学致癌剂的简便有效方法5.局限转导:通过部分缺陷的温和噬菌体把供体的少数特定基因携带到受体菌中,并与后者的基因整合,重合,形成转导子的现象.6.移码突变:诱变剂使DNA序列中的一个或几个核苷酸发生增添或缺失,从而使该处后面的全部遗传密码的阅读框架发生改变.7.感受态:受体细胞最易接受外源DNA片段并能实现转化的一种生理状态.8. 高频重组菌株:该细胞的F质粒已从游离态转变为整合态,当与F- 菌株相接合时,发生基因重组的频率非常高.9.基因工程:通过人工方法将目的基因与载体DNA分子连接起来,然后导入受体细胞,从而使受体细胞获得新的遗传性状的一种育种措施称基因工程。
10.限制性内切酶:是一类能够识别双链DNA分子的特定序列,并能在识别位点内部或附近进行切割的内切酶。
11.基因治疗:是指向靶细胞中引入具有正常功能的基因,以纠正或补偿基因的缺陷,从而达到治疗的目的。
12.克隆:作为名词,也称为克隆子,它是指带有相同DNA序列的一个群体可以是质粒,也可以是基因组相同的细菌细胞群体。
作为动词,克隆是指利用DNA体外重组技术,将一个特定的基因或DNA序列插入一个载体DNA分子上,进行扩增。
二. 填空1.微生物修复因UV而受损DNA的作用有光复活作用和切除修复.2.基因组是指一种生物的全套基因。
3.基因工程中取得目的基因的途径有 _____3_____条。
4.基因突变可分为点突变和染色体突变两种类型。
电力系统分析第7章习题答案

第七章 思考题及习题答案7-1 电力系统短路的分类、危害及短路计算的目的是什么?答:短路的类型有三相短路、两相短路、单相接地短路和两相接地短路。
短路对电力系统的危害有:短路电流很大,并会电气设备使发热急剧增加,导致设备因过热而损坏;导体产生很大的电动力,有可能引起设备机械变形、扭曲甚至损坏;短路时系统电压大幅度下降,会影响电气设备的正常工作;发生不对称短路时,不平衡电流所产生的不平衡磁通会对邻近的通信系统造成干扰;短路情况严重时,会导致并列运行的发电厂失去同步,破坏系统的稳定性。
短路计算目的有:设计和选择合理的发电厂、变电所及电力系统的电气主接线;选择有足够动稳定度和热稳定度的电气设备及载流导体;合理配置各种继电保护和自动装置并正确地整定其参数;分析和计算在短路情况下电力系统的稳定问题。
7-2 无限大功率电源的含义是什么?由无限大电源供电的系统三相短路时,短路电流包括几种分量?有什么特点?答:无限大功率电源是指其容量为无限大、内阻抗为零的电源。
由无限大功率电源供电的系统三相短路时,短路电流包括周期分量和非周期分量。
其特点是在外电路发生短路时,电源电压基本上保持恒定,因此周期分量不随时间而变化。
7-3 什么叫短路冲击电流?它出现在短路后的哪一时刻?冲击系数的大小与什么有关? 答:短路冲击电流是指在最严重短路情况下三相短路电流的最大瞬时值。
它出现在短路发生半个周期(0.01s )时。
冲击系数与短路回路中电抗与电阻的相对大小有关。
7-4 什么是短路功率?在三相短路计算中,对某一短路点,短路功率的标幺值与短路电流的标幺值有何关系?答:短路功率等于短路电流有效值乘以短路处的正常工作电压(一般用平均额定电压)。
短路功率的标幺值与短路电流的标幺值相等。
7-5 什么是短路电流的最大有效值?与冲击系数有什么关系?答:短路电流的最大有效值是指短路后第一周的电流有效值。
它与冲击系数的关系为2)1(21−+=imp p imp K I I7-6 什么是电力系统三相短路的实用计算?分为几个方面的内容?答:电力系统三相短路的实用计算,主要是计算系统中含多台发电机、电源并非无限大功率电源供电时,三相短路电流周期分量的有效值。
西方经济学(微观经济学)课后练习答案第七章

西⽅经济学(微观经济学)课后练习答案第七章微观第七章习题⼀、名词解释完全垄断市场垄断竞争市场寡头市场价格歧视博弈纳什均衡占优策略均衡⼆、选择题1、对于垄断⼚商来说,()。
A、提⾼价格⼀定能够增加收益;B、降低价格⼀定会减少收益;C、提⾼价格未必会增加收益,降低价格未必会减少收益;D、以上都不对。
2、完全垄断的⼚商实现长期均衡的条件是()。
A、MR=MC;B、MR=SMC=LMC;C、MR=SMC=LMC=SAC;D、MR=SMC=LMC=SAC=LAC。
3、完全垄断⼚商的总收益与价格同时下降的前提条件是()。
A、Ed>1;B、Ed<1;C、Ed=1;D、Ed=0。
4、完全垄断⼚商的产品需求弹性Ed=1时()。
A、总收益最⼩;B、总收益最⼤;C、总收益递增;D、总收益递减。
5、完全垄断市场中如果A市场的价格⾼于B市场的价格,则()A、A市场的需求弹性⼤于B市场的需求弹性;B、A市场的需求弹性⼩于B市场的需求弹性;C、A市场的需求弹性等于B市场的需求弹性;D、以上都对。
6、以下关于价格歧视的说法不正确的是()。
A、价格歧视要求垄断者能根据消费者的⽀付意愿对其进⾏划分;B、⼀级价格歧视引起⽆谓损失;C、价格歧视增加了垄断者的利润;D、垄断者进⾏价格歧视,消费者就必定不能进⾏套利活动。
7、垄断竞争的⼚商短期均衡时,()。
A、⼀定能获得差额利润;B、⼀定不能获得经济利润;C、只能得到正常利润;D、取得经济利润、发⽣亏损和获得正常利润都有可能。
8、垄断竞争⼚商长期均衡点上,长期平均成本曲线处于( B )A、上升阶段B、下降阶段C、⽔平阶段D、以上三种情况都有可能9、垄断竞争⼚商实现最⼤利润的途径有:( D )A、调整价格从⽽确定相应产量B、品质竞争C、⼴告竞争D、以上途径都可能⽤10、按照古诺模型下列哪⼀说法不正确,()。
A、双头垄断者没有认识到他们的相互依耐性;B、每⼀个寡头都认定对⽅的产量保持不变;C、每⼀个寡头垄断者都假定对⽅价格保持不变;D、均衡的结果是稳定的。
国际金融习题答案第七章

国际金融习题答案第七章习题答案第七章国际资本流动与国际金融危机本章重要概念国际资本流动:是指资本从一个国家或地区转移到另一个国家和地区。
直接投资:是指一国居民以一定生产要素投入到另一国并相应获得经营管理权的跨国投资活动。
证券投资:是指投资者通过在国际证券市场上购买中长期债券,或购买外国企业发行的股票所进行的投资。
出口信贷:出口信贷属于中长期贸易信贷,是一国为支持和扩大本国大型设备的出口和加强国际竞争能力,鼓励本国的银行对本国的出口商或外国进口商(或银行)提供优惠利率贷款,以解决本国出口商资金周转的困难,或满足国外进口商对本国出口商支付货款需要的一种融资方式。
债务危机:指债务国不再具备还本付息的能力。
偿债率:即一国当年还本付息额占当年贸易和非贸易外汇收入的比率,是衡量一国还款能力的主要参考指标。
负债率:即一国当年外债余额占当年GNP的比率,这是衡量一国对外债的依赖程度,或一国总体的债务风险的参考指标。
国际游资:是指那些没有固定的投资领域,以追逐高额短期利润而在各市场之间频繁移动的短期资本。
投机性冲击:投机资金利用和制造各种资产(如外汇)价格的波动,而获取利润,并给所在国的金融体系乃至整体经济运行造成严重的后果,称之为投机性冲击。
复习思考题1.如何理解国际资本流动的含义?答:国际资本流动是指资本从一个国家或地区转移到另一个国家和地区,它包括资本流出和资本流入两个方面。
资本流出是指本国资本流向外国,它意味着外国在本国的资产减少、外国对本国的负债增加、本国对外国的负债减少、本国在外国的资产增加。
资本流入是指外国资本流入本国,它意味着外国对本国的负债减少、本国对外国的负债增加、外国在本国的资产增加和本国在外国的资产减少。
2.试述国际资本流动发展的特点。
答:1)20世纪90年代以前国际资本流动的特点:(1)截至二战前,大体上讲,世界长期资本输出的规模不大,地区流向、部门结构和资金流动方式等均较单一。
(2)二战后至20世纪90年代,从量上看,国际资本流动的规模空前膨胀,国际直接投资规模急剧扩大,国际直接投资的增长速度不仅超过了国民生产总值和工业生产的增长速度,也超过了国际贸易的增长速度,取代国际贸易成为推动世界经济发展的主要力量;从质上看,资本流向、资本输出方式、资本结构等方面也发生了深刻的变化。
投资学第7章习题及答案

课后习题1.简述债券的定义及种类。
2.影响债券定价的因素有哪些?这些因素如何影响债券价值的?3.简述债券定价原理。
4.简述常见的债券收益率。
5.什么是债券的时间价值?6.假定A公司发行了两种具有相同息票率和到期日的债券,一种是可赎回的,而另一种是不可赎回的,哪一种售价更高?7.有一30年期、息票率为8%的债券,计算其在市场半年利率为3%时的价格。
比较利率下降所造成的资本利得和当利率上升到5%时的资本损失。
8.两种10年期债券的到期收益率目前均为7%,各自的赎回价格皆为1100美元。
其中之一的息票率为6%,另一种为8%。
为简单起见,假定在债券的预期支付现值超过赎回价格时立即赎回。
如果市场利率突然降至6%,每种债券的资本利得分别是多少?第七章本章习题答案1. 债券(bond)是以借贷协议形式发行的证券。
借者为获取一定量的现金而向贷者发行(如出售)债券,债券是借者的“借据”。
这张借据使发行者有法律责任,需在指定日期向债券持有人支付特定款额。
典型的息票债券使发行者有义务在债券有效期内向持有人每半年付息一次,这叫做息票支付,因为在计算机发明之前,大多数债券带有息票,投资者将其剪下并寄给发行者索求利息。
债券到期时,发行者再付清面值(par value, face value)。
债券的息票率(coupon rate)决定了所需支付的利息:每年的支付按息票率乘以债券面值计算。
息票率、到期日和面值是债券契约(bond indenture)的各个组成部分,债券契约是债券发行者与持有者之间的合约。
政府债券的发行主体是政府。
政府债券是政府主体为筹措财政资金,以政府信用为基础向社会发行,承诺到期还本付息的一种债券凭证。
政府债券又分为中央政府债券和地方政府债券。
中央政府债券又称为国债。
公司债券,是公司按照法定程序发行,约定在一定期限内还本付息的债权债务凭证。
公司债券代表着发债的公司和投资者之间的一种债权债务关系。
债券持有人是公司的债权人, 不是所有者,无权参与或干涉公司经营管理,但债券持有人有权按期收回本息。
第七章相关与回归分析习题答案.doc

334229.09425053.730.7863334229.0922.0889V425053.73=0.003204 245.4120第七章相关与回归分析习题答案一、填空题1.完全相关、不完全相关、不相关2. —iWrWl3.函数、|r| = l4.无线性相关、完全正相关、完全负相关5.密切程度6.正相关、负相关7.直线相关、曲线相关8.回归系数9.随机的、给定的10.最小二乘法,残差平方和二、 单项选择题I. B 2. B 3. A 4. A 5. B 6. C 7. D 8. B9. A 10. CII. C 12. B 13. D 14. B 15. C三、 多项选择题1. BCD2. ACD3. ABD4. ABCD5. ACE四、 计算题1解:B\=V - p 2x = 549.8 - 0.7863 * 647.88 = 40.37202 _ [£ (匕顼(X,侦)]2 '"£(x,-x )2£(y,-y )20.999834425053.73*262855.25 ;2=(1-产切 _y )2 =43.6340= 2.0889 n — 2(3) H°:”2=0,H I :”2 邳腐 _ 0.7863~S~ ~ 0.003204〃2券(〃-2)=诲(10) = 2.228t 值远大于临界值2.228,故拒绝零假设,说明月在5%的显著性水平下通过了显著性 检验。
(4) Y f =40.3720 + 0.7863*800 = 669.41 (万元)0.0273 S' =S l + 厂 Xf =2.0089」1 + 土 +华°「647・88)2 = 2 1429 所以,Yf 的置信度为 7V n Z (X,-X )2 V 12 425053.73 95 %的预测区间为:Y f ±t a/2(n-2)S ef = 669.41 ±2.228* 1.0667 = 669.41 ±2.3767 所以,区间预测为: 664.64 < Y f <674.182解:A _ £(匕一双%一灭)—N £X ,E —£x,£匕) 乃一 Z (x,一文尸一 (£x )9*803.02-13.54*472 八= ------------------------------------ =0.02739*28158-472*472& = Y-$2X =13.54/9-0.0273 * 472/9 = 0.0727(2)决定系数: , [y (y-F )(x-%)]2 r 2 =¥,_ 盘——;=0.9723Z (x,-x )Na-V )-残差平方和^<=(l-r 2)^(y-y )2 =0.0722 (3)身高与体重的相关系数: r =序=J0.9723 = 0.9861H O :A = A = O ,H 1:A W 2不同时为零厂。
毛概第七章试题库答案

第七章社会主义改革开放理论习题答案一、单项选择题1 D2 A3 D4 B5 D6 A7 D8 A9 D 10 C 11 C 12 C 13 D 14 A二、多项选择题1 ABC2 ABC3 ACD4 ABC5 AB6 ABC7 ABD8 BCD三、辨析题1.答:这种说法是正确的。
这个说法在理论上和实践上解决了社会主义发展的直接动力问题。
相对于推翻“三座大山”、建立社会主义制度的第一次革命而言,改革之所以是中国的第二次革命,是因为:第一,改革同革命一样,其性质都是为了解放生产力。
第二,改革同革命一样,都是特定社会历史阶段发展的直接动力。
第三,改革同革命一样,其特点都具有根本性、广泛性和深刻性。
2.答:这种说法是正确的。
改革是社会主义制度的自我完善,改革要达到的总的目的是要有利于巩固社会主义制度,有利于巩固党的纲领,有利于在党的领导和社会主义制度下发展生产力。
无论从解放生产力、扫除发展生产力的障碍这个意义上来说,还是从政策的重新选择、体制的重新建构这个转变的深刻性和广泛性,以及由此引起的社会生活和人们观念变化的深刻性和广泛性来说,改革都是一场新的革命,是推动社会主义社会发展的直接动力。
而且,改革是社会主义制度的自我完善和发展,解决社会主义社会矛盾的主要方式就是通过改革,不断解放和发展生产力使之与先进的生产关系相适应。
四、简答题1.答:第一,是对中国长期停滞落后的历史教训深刻总结的结果;第二,是对当代世界经济、科技发展和国际形势敏锐观察的结果;第三,为了适应社会主义现代化建设的需要;第四,为了借鉴和吸收人类文明的一切优秀成果。
2.答:(1)稳定是前提,改革是动力,发展是目的;(2)保持改革、发展、稳定在动态中的相互协调和相互促进;(3)把改革的力度、发展的速度和社会可以承受的程度统一起来;(4)把不断改善人民生活水平作为处理改革、发展和稳定关系的重要结合点。
五、论述题答:改革开放是一场新的伟大革命。
中国共产党在20世纪70年代末做出实行改革开放的重大决策,是有其深刻的国内和国际两方面的背景。
基础会计学 第七章习题及答案

第七章习题复习思考题1.什么是账务处理程序?其意义如何?2.账务处理程序的种类有哪些?企业中普遍采用的有哪几种?3.各种账务处理程序的特点是什么?它们有哪些优缺点?其适用范围如何?4.简述各种账务处理程序的基本步骤。
5.区别不同账务处理程序的主要标志是什么?6.记账凭证账务处理程序需要采用哪些凭证和账簿?他们有哪些格式要求?名词解释账务处理程序科目汇总表一、判断题1.汇总记账凭证账务处理程序下,总分类账帐页格式一般采用三栏式()2.记账凭证账务处理程序登记总账的依据是原始凭证()3.汇总记账凭证账务处理程序的适用范围是规模较大、业务量较少的单位。
()4.账务处理程序中最基本的处理程序是科目汇总表账务处理程序。
()5.为了便于汇总转账凭证,在编制转账凭证时,其账户的对应关系应是一借一贷或多借一贷。
()6.采用科目汇总表账务处理程序,不仅可简化登记总账的工作,而且便于检查和分析经济业务。
()7.账务处理程序不同,现金日记账、银行存款日记账登记的依据也不同。
()8.各种账务处理程序的区别主要在于编制会计报表的依据和方法不同。
()9.企业总分类账采用何种格式取决于账务处理程序。
()10.各种账簿都是直接根据记账凭证进行登记的。
()二、单项选择题1.各种会计核算程序的主要区别是()A.填制会计凭证的依据和方法不同B.登记总账的依据和方法不同C.编制会计报表的依据和方法不同D.登记明细账的依据和方法不同2.汇总记账凭证核算程序下,总分类账账页格式一般采用()A.三栏式B.多栏式C.设有“对应科目”栏的三栏式D.数量金额式3.编制科目汇总表的直接依据是()A.原始凭证B.原始凭证汇总表C.记账凭证D.汇总记账凭证4.各种账务处理程序中最基本的是()A. 记账凭证账务处理程序B. 汇总记账凭证账务处理程序C. 科目汇总表账务处理程序D. 多栏式日记账账务处理程序5.特定的会计凭证账簿组织和特定的记账程序相结合的方式称为()A. 会计核算前提B. 会计核算原则C. 会计核算方法D. 会计核算形式6. 直接根据记账凭证,逐笔登记总分类账的形式是()A. 日记总账账务处理程序B. 汇总记账凭证账务处理程序C. 记账凭证账务处理程序D. 科目汇总表账务处理程序7. 科目汇总表账务处理程序的主要缺点是()A. 加大了登记总账的工作量B. 据此登帐易产生错误C. 不具有试算平衡作用D. 不便于查对账目8. 科目汇总表账务处理程序和汇总记账凭证账务处理程序的主要相同点是()A. 登记总账的依据相同B. 记账凭证都需要汇总并且记账步骤相同C. 汇总凭证格式相同D. 记账凭证汇总的方向相同9. 记账凭证账务处理程序的适用范围是()A. 规模较大、业务较多的单位B. 规模较小、业务较少的单位C. 规模较大、业务较少的单位D. 规模较小、业务较多的单位10. 汇总记账凭证账务处理程序的主要缺点是()A. 登记总账的工作量大B. 不利于会计人员分工C. 体现不了账户的对应关系D. 明细账与总账无法核对三、多项选择题1. 汇总记账凭证核算程序的优点是()A.总账能反映账户对应关系,便于对经济业务进行分析和检查B.减少登记总账的工作量C.同一贷方科目的转账凭证不多时,可减少核算工作量D.有利于对全部账户的发生额进行试算平衡E.有利于会计人员分工2. 在采用汇总记账凭证核算程序时,编制记账凭证的要求是()A.收款、付款、转账凭证均可一借一贷B.转账凭证可一借多贷C.转账凭证可一贷多借D.收款凭证可一借多贷E.付款凭证可一贷多借3. 科目汇总表的作用有()A.减少总分类账的记账工作量B.进行登记总账前的试算平衡C.反映账户的对应关系D.汇总有关账户的本期借、贷方发生额E.汇总有关账户的余额4. 会计核算程序的内容包括()A.账簿组织B.报表体系C.记账程序及方法D.编制报表的方法5. 登记总分类账的根据可以是()A.记账凭证B.汇总记账凭证C.科目汇总表D.多栏式现金、银行存款日记账E.日记总账6.在下列会计凭证中,可以作为登记总分类账簿的直接依据的有()A. 记账凭证B. 原始凭证C. 汇总记账凭证D. 原始凭证汇总表E. 科目汇总表7.科目汇总表的缺点有()A. 不能反映账户之间的对应关系B. 编制科目汇总表的工作量较大C. 加大登记总账的工作量D. 不便于查对账目E. 不便于了解经济业务的来龙去脉四、业务题自力公司本月发生经济业务如下:(1) 6月2日,通过银行缴纳上月应交的税金67600元。
(完整版)高等数学-习题答案-方明亮-第七章

高等数学方明亮版第七章习题7-11.判定下列平面点集中哪些是开集、闭集、区域、有界集、无界集?并指出集合的边界.(1){}(,)0,0x y x y ≠≠; (2){}22(,)14x y x y <+≤; (3){}2(,)x y y x >;(4){}2222(,)(1)1(2)4x y x y x y +-≥+-≤且.解 (1)集合是开集,无界集;边界为{(,)0x y x =或0}y =. (2)集合既非开集,又非闭集,是有界集;边界为2222{(,)1}{(,)4}x y x y x y x y +=+=.(3)集合是开集,区域,无界集;边界为2{(,)}x y y x =. (4)集合是闭集,有界集;边界为2222{(,)(1)1}{(,)(2)4}x y x y x y x y +-=+-=2.已知函数(,)v f u v u =,试求(,)f xy x y +. 解 ()()(,)x y f xy x y xy ++=.3.设(,)2f x y xy =,证明:2(,)(,)f tx ty t f x y =.解)222(,)222f tx ty t xy t t xy t xy ===2(,)t f x y =.4.设y f x ⎛⎫=⎪⎝⎭(0)x >,求()f x . 解由于y f x ⎛⎫== ⎪⎝⎭,则()f x =. 5.求下列各函数的定义域:(1)2222x y z x y +=-; (2)ln()arcsinyz y x x=-+; (3)ln()z xy =; (4)z =(5)z = (6)u =.解 (1)定义域为{}(,)x y y x ≠±; (2)定义域为{}(,)x y x y x <≤-;(3)定义域为{}(,)0x y xy >,即第一、三象限(不含坐标轴);(4)定义域为2222(,)1x y x y a b ⎧⎫+≤⎨⎬⎩⎭;(5)定义域为{}2(,)0,0,x y x y x y ≥≥≥; (6)定义域为{}22222(,,)0,0x y z x y z x y +-≥+≠. 6.求下列各极限:(1)22(,)(2,0)lim x y x xy y x y →+++; (2)(,)(0,0)lim x y →;(3)22(,)(0,0)1lim ()sinx y x y xy →+; (4)(,)(2,0)sin()lim x y xy y→;(5)1(,)(0,1)lim (1)xx y xy →+; (6)22(,)(,)lim()x y x y x y e --→+∞+∞+.解:(1)22(,)(2,0)4lim(2,0)22x y x xy y f x y →++===+; (2)(,)(0,0)00112limlim 2x y u u u u →→→===; (3)因为22(,)(0,0)lim ()0x y x y →+=,且1sin1xy≤有界,故22(,)(0,0)1lim ()sin0x y x y xy→+=;(4)(,)(2,0)(,)(2,0)sin()sin()limlim 212x y x y xy xy x y xy →→==⋅=;(5)111(,)(0,1)(,)(0,1)lim (1)lim (1)y xyxx y x y xy xy e e ⋅→→+=+==;(6)当0x N >>,0y N >>时,有222()()0x y x yx y x y e e++++<<, 而()22(,)(,)22limlim lim lim 0x yu u u x y u u u x y u u e e e e+→+∞+∞→+∞→+∞→+∞+==== 按夹逼定理得22(,)(,)lim()0.x y x y x y e --→+∞+∞+=7.证明下列极限不存在: (1)(,)(0,0)limx y x yx y →+-;(2)设2224222,0,(,)0,0,x yx y x yf x y x y ⎧+≠⎪+=⎨⎪+=⎩(,)(0,0)lim (,)x y f x y →.证明 (1)当(,)x y 沿直线y kx =趋于(0,0)时极限(,)(0,0)01limlim 1x y x y kxx y x kx kx y x kx k →→=+++==--- 与k 有关,上述极限不存在.(2)当(,)x y 沿直线y x =和曲线2y x =趋于(0,0)有2242422(,)(0,0)00lim lim lim 01x y x x y x y x x y x x x x y x x x →→→=====+++, 2222442444(,)(0,0)001lim lim lim 22x y x x y xy xx y x x x x y x x x →→→=====++, 故函数(,)f x y 在点(0,0)处二重极限不存在.8.指出下列函数在何处间断:(1)22ln()z x y =+; (2)212z y x=-. 解(1)函数在(0,0)处无定义,故该点为函数22ln()z x y =+的间断点;(2)函数在抛物线22y x =上无定义,故22y x =上的点均为函数212z y x=-的间断点.9.用二重极限定义证明:(,)lim0x y →=.证22102ρ-=≤=(,)P x y ,其中||OP ρ==,于是,0ε∀>,20δε∃=>;当0ρδ<<0ε<成立,由二重极限定义知(,)lim0x y →=.10.设(,)sin f x y x =,证明(,)f x y 是2R 上的连续函数.证 设2000(,)P x y ∈R .0ε∀>,由于sin x 在0x 处连续,故0δ∃>,当0||x x δ-<时,有0|sin sin |x x ε-<.以上述δ作0P 的δ邻域0(,)U P δ,则当0(,)(,)P x y U P δ∈时,显然00||(,)x x P P ρδ-<<,从而000|(,)(,)||sin sin |f x y f x y x x ε-=-<,即(,)sin f x y x =在点000(,)P x y 连续.由0P 的任意性知,sin x 作为x 、y 的二元函数在2R 上连续.习题7-21.设(,)z f x y =在00(,)x y 处的偏导数分别为00(,)x f x y A =,00(,)y f x y B =,问下列极限是什么?(1)00000(,)(,)lim h f x h y f x y h →+-; (2)00000(,)(,)lim h f x y f x y h h→--;(3)00000(,2)(,)lim h f x y h f x y h →+-; (4)00000(,)(,)lim h f x h y f x h y h→+--.解 (1)0000000(,)(,)lim (,)x h f x h y f x y z x y A h→+-==;(2)000000000000(,)(,)(,)(,)lim lim (,)y h h f x y f x y h f x y h f x y z x y B h h→→----===-;(3)0000000000(,2)(,)(,2)(,)lim lim 222h h f x y h f x y f x y h f x y B h h →→+-+-=⋅=;(4)00000(,)(,)limh f x h y f x h y h→+--[][]0000000000000000000000000000(,)(,)(,)(,)lim(,)(,)(,)(,)lim (,)(,)(,)(,)lim lim 2.h h h h f x h y f x y f x y f x h y hf x h y f x y f x h y f x y h f x h y f x y f x h y f x y h h A A A →→→→+-+--=+----=+---=+-=+= 2.求下列函数的一阶偏导数: (1)x z xy y=+; (2)ln tan x z y =;(3)e xyz =; (4)22x y z xy+=;(5)222ln()z x x y =+; (6)z = (7)sec()z xy =; (8)(1)y z xy =+;(9)arctan()z u x y =- (10)zx u y ⎛⎫= ⎪⎝⎭.解(1)1z y x y ∂=+∂,2z xx y y∂=-∂; (2)12211tan sec cot sec z x x x x x y y y y y y -⎛⎫⎛⎫∂=⋅⋅= ⎪ ⎪∂⎝⎭⎝⎭, 12222tan sec cot sec z x x x x x x y y y y y y y-⎛⎫⎛⎫⎛⎫∂=⋅⋅-=- ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭; (3)xy xy ze y ye x∂=⋅=∂,xy xy z e x xe y ∂=⋅=∂;(4)()2222222222()2()1z x xy x y y x y x y y y x x y y x xy ∂⋅-+⋅-+⋅===-∂, ()2222222222()2()1z y xy x y x xy x y x x y x y x y xy ∂⋅-+⋅-+⋅===-∂; (5)232222222222ln()22ln()z x x x x y x x x y x x y x y ∂=++⋅=++∂++,22222222z x x y y y x y x y∂=⋅=∂++; (6)1z y x xy ∂=⋅=∂,1z x y xy ∂=⋅=∂; (7)tan()sec()tan()sec()zxy xy y y xy xy x∂=⋅=∂, tan()sec()tan()sec()zxy xy x x xy xy y∂=⋅=∂; (8)121(1)(1)y y zy xy y y xy x--∂=+⋅=+∂, ln(1)(1)ln(1)1y xy z xy e y xy xy y y xy +⎡⎤∂∂⎡⎤==+⋅++⎢⎥⎣⎦∂∂+⎣⎦; (9)11221()()1()1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+-, 11221()()(1)1()1()z z z z u z x y z x y y x y x y --∂-=⋅-⋅-=-∂+-+-, 221()ln()()ln()1()1()z zz zu x y x y x y x y z x y x y ∂--=⋅-⋅-=∂+-+-; (10)111z z ux z x z x y y y y --⎛⎫⎛⎫∂=⋅= ⎪ ⎪∂⎝⎭⎝⎭,12z zux x z x z y y y y y -⎛⎫⎛⎫⎛⎫∂=⋅-=- ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭, ln zu x x y y y⎛⎫∂=⋅ ⎪∂⎝⎭. 3.设(,)ln 2y f x y x x ⎛⎫=+ ⎪⎝⎭,求(1,0)x f ,(1,0)y f .解法一 由于(,0)ln f x x =,所以1(,0)x f x x=,(1,0)1x f =; 由于(1,)ln 12y f y ⎛⎫=+ ⎪⎝⎭,所以11(1,)212y f y y =⋅+,1(1,0)2y f =.解法二 21(,)122x y f x y y x x x ⎛⎫=⋅- ⎪⎝⎭+,11(,)22y f x y y x x x=⋅+, 10(1,0)110212x f ⎛⎫=⋅-= ⎪⎝⎭+,111(1,0)02212y f =⋅=+. 4.设(,)(f x y x y =+-(,1)x f x . 解法一由于(,1)(11)f x x x =+-=,(,1)()1x f x x '==. 解法二1(,)1x f x y y =,(,1)1x f x =. 5.设2(,)xt yf x y e dt -=⎰,求(,)x f x y ,(,)y f x y .解 2(,)x x f x y e -=,2(,)y f x y e -=-. 6.设yxz xy xe =+,证明z zxy xy z x y∂∂+=+∂∂. 解 由于21y y yx x x z y y y e xe y e x x x ⎛⎫∂⎛⎫=+-⋅=+-⎪ ⎪∂⎝⎭⎝⎭, 1y yx x z x xe x e y x∂=+⋅=+∂, 所以1()yy y yx x x xz z y x y x y e y x e xy e x y xy ye x y x ⎡⎤⎛⎫∂∂⎛⎫+=+-++=+-++ ⎪⎢⎥ ⎪∂∂⎝⎭⎣⎦⎝⎭yxxy xe xy xy z =++=+.7.(1)22,44x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与x 轴正向所成的倾角是多少? (2)1z x ⎧=⎪⎨=⎪⎩在点处的切线与y 轴正向所成的倾角是多少?解 (1)按偏导数的几何意义,(2,4)x z 就是曲线在点(2,4,5)处的切线对于x 轴正向所成倾角的斜率,而21(2,4)12x x z x ===,即tan 1k α==,于是倾角4πα=.(2)按偏导数的几何意义,(1,1)y z就是曲线在点处的切线对于y 轴正向所成倾角的斜率,而11(1,1)3y z ===,即1tan 3k α==,于是倾角6πα=.8.求下列函数的二阶偏函数:(1)已知33sin sin z x y y x =+,求2z x y ∂∂∂; (2)已知ln xz y =,求2z x y∂∂∂;(3)已知ln(z x =,求22zx∂∂和2z x y ∂∂∂;(4)arctan y z x =求22zx∂∂、22z y ∂∂、2z x y ∂∂∂和2z y x ∂∂∂.解(1)233sin cos z x y y x x∂=+∂,2223cos 3cos z x y y x x y ∂=+∂∂; (2)ln ln 1ln ln x xz y y y y x x x∂=⋅=∂, 2ln ln 1ln 1111ln ln (1ln ln )xx x z y y x y y x y x y x y x--⎛⎫∂=+⋅⋅=+ ⎪∂∂⎝⎭; (3)1z x ⎛⎫∂=+=∂==()232222zxx xy∂-==∂+,()23222zyx y xy∂-==∂∂+;(4)222211zy y xx x y y x ∂⎛⎫=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,222111z x y x x yy x ∂=⋅=∂+⎛⎫+ ⎪⎝⎭, ()222222z xy x x y ∂=∂+,()222222z xy y x y ∂-=∂+, ()()2222222222222z x y y y x x y x y x y ∂+--=-=∂∂++,()()2222222222222z x y x y x y x x y x y ∂+--==∂∂++. 9.设222(,,)f x y z xy yz zx =++,求(0,0,1)xx f ,(1,0,2)xz f ,(0,1,0)yz f -及(2,0,1)zzx f .解 因为22x f y xz =+,2xx f z =,2xz f x =, 22y f xy z =+,2yz f z =,22z f yz x =+,2zz f y =,0zzx f =,所以(0,0,1)2xx f =,(1,0,2)2xz f =,(0,1,0)0yz f -=,(2,0,1)0zzx f =.10.验证: (1)2esin kn ty nx -=满足22y yk t x∂∂=∂∂;(2)r =2222222r r r x y z r∂∂∂++=∂∂∂.证 (1)因为22esin kn t y kn nx t -∂=-∂,2e cos kn t y n nx x-∂=∂,2222e sin kn t y n nx x -∂=-∂ 所以()2222esin kn ty y k n nx k t x-∂∂=-=∂∂; (2)因为r x xr ∂==∂,2222231r x x x r x x x r r r r r ∂∂-⎛⎫==-⋅= ⎪∂∂⎝⎭,由函数关于自变量的对称性,得22223r r y y r ∂-=∂,22223r r z z r∂-=∂, 所以 2222222222223332r r r r x r y r z x y z r r r r∂∂∂---++=++=∂∂∂. 习题7-31.求下列函数的全微分:(1)2222s t u s t+=-; (2)2222()e x y xyz x y +=+;(3)arcsin (0)x z y y=>; (4)ey x x y z ⎛⎫-+ ⎪⎝⎭=;(5)222ln()u x y z =++; (6)yz u x =.解 (1)()()222222222222()2()4u s s t s s t st s s t s t ∂--+==-∂--,()()222222222222()2()4u t s t t s t s tt s t s t ∂-++==∂--, ()()()22222222222444d d d (d d )st s tstu s t t s s t ststst=-+=-----;(2)22222222244222222()2()2x y x y x y xyxyxyzx y x y yx y xex y eex xx y x y +++⎛⎫∂-+-=++=+ ⎪∂⎝⎭,由函数关于自变量的对称性可得224422x y xyzy x ey y xy +⎛⎫∂-=+ ⎪∂⎝⎭, 22444422d 2d 2d x y xyx y y x z ex x y y x y xy +⎡⎤⎛⎫⎛⎫--=+++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦; (3)21d d arcsin d d x x x z x y y yy y ⎛⎫⎫===- ⎪⎪⎝⎭⎭)d d y x x y =-;(4)d d d y x y x x yx y y x z e e x y ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭⎡⎤⎛⎫⎢⎥==-⋅+ ⎪⎢⎥⎝⎭⎣⎦2211d d y x x y y x ex y y x x y ⎛⎫-+ ⎪⎝⎭⎡⎤⎛⎫⎛⎫=--+-⎢⎥ ⎪⎪⎝⎭⎝⎭⎣⎦; (5)()2222222221d d ln()d u x y z x y z x y z⎡⎤=++=++⎣⎦++ 2222222d 2d 2d 2(d d d )x x y y z z x x y y z z x y z x y z ++==++++++;(6)()1d d d ln d ln d yz yz yz yz u x yzx x x z x y x y x z -==++()1d ln d ln d yz x yz x xz x y xy x z -=++.2.求下列函数的全微分:(1)22ln(1)z x y =++在1x =,2y =处的全微分; (2)2arctan 1xz y=+在1x =,1y =处的全微分. 解 (1)因为2222222211d d ln(1)d(1)(2d 2d )11z x y x y x x y y x yx y ⎡⎤=++=++=+⎣⎦++++所以12112d (2d 4d )d d 633x y z x y x y ===+=+;(2)因为22221d d arctan d 1111x x z y y x y ⎛⎫⎛⎫== ⎪ ⎪++⎛⎫⎝⎭⎝⎭+ ⎪+⎝⎭()22222222211212d d d d 11111y xy xy x y x y y x y y x y y ⎡⎤⎛⎫+⎢⎥=-=- ⎪⎢⎥++++++⎝⎭+⎣⎦所以()1222111121d d d d d 113x y x y xy z x y x y y x y ====⎛⎫=-=- ⎪+++⎝⎭. 3. 求函数23z x y =当2x =,1y =-,0.02x ∆=,0.01y ∆=-时的全微分. 解 因为()23322322d d 2d 3d 23z x y xy x x y y xy x x y y ==+=∆+∆所以当2x =,1y =-,0.02x ∆=,0.01y ∆=-时全微分为d 4120.080.120.2z x y =-∆+∆=--=-.4.求函数22xyz x y =-当2x =,1y =,0.01x ∆=,0.03y ∆=时的全微分和全增量,并求两者之差.解 因为()()222222222d()d()d d x y xy xy x y xy z x y x y ---⎛⎫== ⎪-⎝⎭- ()()()()()222332222222(d d )(2d 2d )d d x y y x+x y xy x x y y x y y x+x +xy yxyx y -----==--所以当2x =,1y =,0.01x ∆=,0.03y ∆=时全微分的值为()()()2332222(,)(2,1)0.01,0.030.25d 0.0277779x y x y x y y x+x +xy yz x y =∆=∆=--∆∆==≈-, 而当2x =,1y =,0.01x ∆=,0.03y ∆=时的全增量为()()()()2222(,)(2,1)0.010.030.028252x y x y x x y y xy z x y x x y y =∆=∆=⎡⎤+∆+∆∆=-≈⎢⎥-+∆-+∆⎢⎥⎣⎦, 全增量与全微分之差为d 0.0282520.0277770.000475z z ∆-≈-=.习题7-4 1.设2e x y u -=,sin x t =,3y t =,求d d ut.解3222sin 22d d d cos 23(cos 6)d d d x y x y t t u u x u ye t e t e t t t x t y t---∂∂=+=-⋅=-∂∂. 2.设arccos()z u v =-,而34u x =,3v x =,求d d z x. 解2d d d 123d d d z z u z v x x u x v x ∂∂=+=+∂∂2314x -=.3.设22z u v uv =-,cos u x y =,sin v x y =,求zx∂∂,z y ∂∂.解()()222cos 2sin z z u z vuv v y u uv y x u x v x∂∂∂∂∂=⋅+⋅=-⋅+-⋅∂∂∂∂∂ 23sin cos (cos sin )x y y y y =-,()()()222sin 2cos z z u z v uv v x y u uv x y y u y v y∂∂∂∂∂=⋅+⋅=-⋅-+-⋅∂∂∂∂∂ 33232(sin 2sin cos cos 2cos sin )x y y y y y y =-+-.4.设2ln z u v =,而32u x y =+,y v x =,求zx ∂∂,z y ∂∂.解 222ln 3z z u z v u y u v x u x v x vx ∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅- ⎪∂∂∂∂∂⎝⎭216(32)ln(32)y x y x y x x=+-+, 22112ln 24(32)ln (32)z z u z v u y u v x y x y y u y v y v x x y∂∂∂∂∂=⋅+⋅=⋅+⋅=+++∂∂∂∂∂. 5. 设2(,,)ln(sin )z f u x y u y x ==+,e x y u +=,求zx∂∂,z y ∂∂. 解22112cos sin sin x y z z u f u e y x x u x x u y x u y x+∂∂∂∂=⋅+=⋅⋅+⋅∂∂∂∂++ ()()222cos sin x yx y e y xe y x+++=+, 22112sin sin sin x y z z u f u e x y u y y u y x u y x+∂∂∂∂=⋅+=⋅⋅+⋅∂∂∂∂++ ()()222sin sin x yx y e xe y x+++=+. 6.设222sin()u x y z =++,x r s t =++,y rs st tr =++,z rst =,求u r ∂∂,us∂∂,ut∂∂. 解[]22222()2cos()u u x u y u z x y s t zst x y z r x r y r z r∂∂∂∂∂∂∂=⋅+⋅+⋅=+++++∂∂∂∂∂∂∂ 222222()()cos ()()()r s t rs st tr s t rs t r s t rs st tr rst ⎡⎤⎡⎤=+++++++++++++⎣⎦⎣⎦,[]22222()2cos()u u x u y u z x y r t zrt x y z s x s y s z s∂∂∂∂∂∂∂=⋅+⋅+⋅=+++++∂∂∂∂∂∂∂ 222222()()cos ()()()r s t rs st tr r t r st r s t rs st tr rst ⎡⎤⎡⎤=+++++++++++++⎣⎦⎣⎦,[]22222()2cos()u u x u y u zx y s r zrs x y z t x t y t z t∂∂∂∂∂∂∂=⋅+⋅+⋅=+++++∂∂∂∂∂∂∂ 222222()()cos ()()()r s t rs st tr r s r s t r s t rs st tr rst ⎡⎤⎡⎤=+++++++++++++⎣⎦⎣⎦.7.设arctanx z y =,x u v =+,y u v =-,求z u ∂∂,zv∂∂,并验证: 22z z u vu v u v∂∂-+=∂∂+. 解222221111111z z x z y x y xu x u y uy y x y x x y y ⎛⎫∂∂∂∂∂-=⋅+⋅=⋅⋅+⋅-⋅= ⎪∂∂∂∂∂+⎛⎫⎛⎫⎝⎭++ ⎪ ⎪⎝⎭⎝⎭, ()222221111111z z x z yx y xv x v y vy y x y x x y y ⎛⎫∂∂∂∂∂+=⋅+⋅=⋅⋅+⋅-⋅-= ⎪∂∂∂∂∂+⎛⎫⎛⎫⎝⎭++ ⎪ ⎪⎝⎭⎝⎭, 则222222222()()()z z y x y x u v u v u v x y x y u v u v u v∂∂-+--+=+==∂∂++++-+. 8.设22(,,)z f x y t x y t ==-+,sin x t =,cos y t =,求d d zt. 解d d d 2cos 2(sin )12sin 21d d d z z x z y f x t y t t t x t y t t∂∂∂=⋅+⋅+=--+=+∂∂∂. 9.求下列函数的一阶偏导数(其中f 具有一阶连续偏导数):(1)22()z f x y =-; (2),x y u f y z ⎛⎫= ⎪⎝⎭;(3)(,,)u f x xy xyz =; (4)22(,,ln )xy u f x y e x =-. 解(1)222()zxf x y x∂'=-∂,222()z yf x y y ∂'=--∂;(2)111f u f x y y '∂'=⋅=∂,12122211u x x f f f f y y z y z ⎛⎫∂''''=⋅-+⋅=-+ ⎪∂⎝⎭,2222u y y f f z z z ∂⎛⎫''=⋅-=- ⎪∂⎝⎭; (3)123u f yf yzf x ∂'''=++∂,23u xf xzf y ∂''=+∂,3uxyf z ∂'=∂; (4)12312xy u xf ye f f x x∂'''=++∂,122xy u yf xe f y ∂''=-+∂. 10.设()z xy xF u =+,而yu x=,()F u 为可导函数,证明: z zxy z xy x y∂∂+=+∂∂. 证 ()()()z z u u xy x y F u xF u y x xF u x y x y ⎡⎤∂∂∂∂⎡⎤''+=++++⎢⎥⎢⎥∂∂∂∂⎣⎦⎣⎦ []()()()y x y F u F u y x F u x ⎡⎤''=+-++⎢⎥⎣⎦()xy xF u xy z xy =++=+. 11.设[cos()]z y x y ϕ=-,试证:z z zx y y∂∂+=∂∂. 证sin()[cos()]sin()z z y x y x y y x y x yϕϕϕ∂∂''+=--+-+-∂∂ [cos()]z x y yϕ=-=. 12.设,k z y u x F x x ⎛⎫= ⎪⎝⎭,且函数,z y F x x ⎛⎫⎪⎝⎭具有一阶连续偏导数,试证:u u uxy z ku x y z∂∂∂++=∂∂∂. 证11222k k u z y kx F x F F x x x -∂⎡⎤⎛⎫⎛⎫''=+-+- ⎪ ⎪⎢⎥∂⎝⎭⎝⎭⎣⎦,1221k k ux F x F y x -∂''=⋅=∂,1111k k u x F x F z x-∂''=⋅=∂, 11111111k k k k k u u u xy z kx F x zF x yF x yF x zF ku x y z----∂∂∂''''++=--++=∂∂∂. 13.设sin (sin sin )z y f x y =+-,试证:sec sec 1z zxy x y∂∂+=∂∂. 证cos zf x x ∂'=∂,cos (cos )z y y f y ∂'=+-∂,sec sec sec cos sec cos sec (cos )1z zxy x xf y y y y f x y∂∂''+=++-=∂∂. 14.求下列函数的二阶偏导数22zx∂∂,2z x y ∂∂∂,22z y ∂∂(其中f 具有二阶连续偏导数):(1)(,)z f xy y =; (2)22()z f x y =+; (3)22(,)z f x y xy =; (4)(sin ,cos ,)x y z f x y e +=. 解 (1)令s xy =,t y =,则(,)z f xy y =,s 和t 是中间变量.11z sf yf x x∂∂''=⋅=∂∂,1212d d z s t f f xf f y y y ∂∂''''=⋅+⋅=+∂∂.因为(,)f s t 是s 和t 的函数,所以1f '和2f '也是s 和t 的函数,从而1f '和2f '是以s 和t 为中间变量的x 和y 的函数.故()22111112z z s yf yf y f x x x x x∂∂∂∂∂⎛⎫'''''===⋅= ⎪∂∂∂∂∂⎝⎭, ()211111211112d d z z s t yf f y f f f xyf yf x y y x y y y ⎛⎫∂∂∂∂∂⎛⎫'''''''''''===+⋅+⋅=++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭,()212111221222d d d d z z s t s t xf f x f f f f y y y y y y y y ⎛⎫⎛⎫∂∂∂∂∂∂''''''''''==+=+++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭21112222x f xf f ''''''=++. (2)令22s x y =+,则22()z f x y =+是以s 为中间变量的x 和y 的函数.2z sf xf x x∂∂''=⋅=∂∂,2z s f yf y y ∂∂''=⋅=∂∂.因为()f s 是s 的函数,所以f '也是s 的函数,从而f '是以s 中间变量的x 和y 的函数.故()()222222224z z xf f xf x f x f x x x x∂∂∂∂⎛⎫'''''''===+⋅=+ ⎪∂∂∂∂⎝⎭, ()()22224z z xf xf y xyf x y y x y∂∂∂∂⎛⎫'''''===⋅= ⎪∂∂∂∂∂⎝⎭, ()()222222224z z yf f yf y f y f y y y y⎛⎫∂∂∂∂'''''''===+⋅=+ ⎪∂∂∂∂⎝⎭. (3)令2s xy =2t x y =,则212122z s tf f y f xyf x x x ∂∂∂''''=⋅+⋅=+∂∂∂,212122z s t f f xyf x f y y y ∂∂∂''''=⋅+⋅=+∂∂∂.()221222z z y f xyf x x x x∂∂∂∂⎛⎫''==+ ⎪∂∂∂∂⎝⎭ 211122212222s t s t y f f yf xy f f x x x x ∂∂∂∂⎛⎫⎛⎫'''''''''=⋅+⋅++⋅+⋅ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭()()2221112221222222y y f xyf yf xy y f xyf '''''''''=++++ 43222111222244yf y f xy f x y f '''''''=+++, ()22122z z y f xyf x y y x y∂∂∂∂⎛⎫''==+ ⎪∂∂∂∂∂⎝⎭ 21111222122222s t s t yf y f f xf xy f f y y y y ⎛⎫⎛⎫∂∂∂∂''''''''''=+⋅+⋅++⋅+⋅ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭ ()()222111122212222222yf y xyf x f xf xy xyf x f ''''''''''=+++++ 32231211122222252yf xf xy f x y f x yf ''''''''=++++, ()221222z z xyf x f y y y y⎛⎫∂∂∂∂''==+ ⎪∂∂∂∂⎝⎭211112212222s t s t xf xy f f x f f y y y y ⎛⎫⎛⎫∂∂∂∂'''''''''=+⋅+⋅+⋅+⋅ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭ ()()2221111221222222xf xy xyf x f x xyf x f '''''''''=++++ 22341111222244xf x y f x yf x f '''''''=+++. (4)令sin u x =,cos v y =,x y w e +=,则1313d cos d x y z u wf f xf e f x x x +∂∂''''=+=+∂∂,2323d sin d x y z v w f f yf e f y y y +∂∂''''=+=-+∂∂. ()2132cos x y z z xf e f x x x x+∂∂∂∂⎛⎫''==+ ⎪∂∂∂∂⎝⎭ 1111333133d d sin cos d d x y x y u w u w xf x f f e f e f f x x x x ++∂∂⎛⎫⎛⎫''''''''''=-+++++ ⎪ ⎪∂∂⎝⎭⎝⎭()()1111333133sin cos cos cos x y x y x y x y xf x xf e f e f e xf e f ++++''''''''''=-+++++ ()2231111333sin cos 2cos x y x y x y e f xf xf e xf e f +++''''''''=-+++, ()213cos x y z z xf e f x y y x y+∂∂∂∂⎛⎫''==+ ⎪∂∂∂∂∂⎝⎭ 121333233d d cos d d x y x y v w v w x f f e f e f f y y y y ++⎛⎫⎛⎫∂∂'''''''''=++++ ⎪ ⎪∂∂⎝⎭⎝⎭()()121333233cos sin sin x y x y x y x y x yf e f e f e yf e f ++++'''''''''=-+++-+ ()2312133233cos sin cos sin x y x y x y x y e f x yf e xf e yf e f ++++'''''''''=-+-+, ()2232sin x y z z yf e f y y y y+⎛⎫∂∂∂∂''==-+ ⎪∂∂∂∂⎝⎭ 2222333233d d cos sin d d x y x y v w v w yf y f f e f e f f y y yy ++⎛⎫⎛⎫∂∂''''''''''=--++++ ⎪ ⎪∂∂⎝⎭⎝⎭ ()()2222333233cos sin sin sin x y x y x y x y yf y yf e f e f e yf e f ++++''''''''''=---+++-+ ()2232222333cos sin 2sin x y x y x y e f yf yf e yf e f +++''''''''=-+-+.习题7-51.设2cos e 0x y x y +-=,求d d y x. 解 设2(,)cos e x F x y y x y =+-,则22d e 2e 2d sin sin x x x y F y xy xyx F y x y x --=-=-=--+. 2.设ln ln 1xy y x ++=,求1d d x yx=.解 设(,)ln ln 1F x y xy y x =++-,则221d 1d x y y F y xy y x x F x y x x y++=-=-=-++. 当1x =时,由ln ln 1xy y x ++=知1y =,所以1d 1d x y x==-.3.设ln arctany x =,求d d y x. 解设(,)arctan yF x y x =,则2222222222211d 111d 1x yy x x y y F yx y x y x y x y y x x F x y xx y x y y x ⎛⎫-⋅- ⎪⎝⎭⎛⎫++ ⎪+++⎝⎭=-=-=-=--⋅-++⎛⎫+ ⎪⎝⎭.4.设222cos cos cos 1x y z ++=,求zx∂∂,z y ∂∂. 解 设222(,,)cos cos cos 1F x y z x y z =++-,则2cos sin sin 22cos sin sin 2x z F z x x x x F z z z ∂-=-=-=-∂-,2cos sin sin 22cos sin sin 2y z F z y y yy F z z z ∂-=-=-=-∂-. 5.设方程(,)0F x y z xy yz zx ++++=确定了函数(,)z z x y =,其中F 存在偏导函数,求zx∂∂,z y ∂∂. 解 1212()()x z F F y z F z x F F y x F ''++∂=-=-∂''++,1212()()y z F F x z F zy F F y x F ''++∂=-=-∂''++.6.设由方程(,,)0F x y z =分别可确定具有连续偏导数的函数(,)x x y z =,(,)y y x z =,(,)z z x y =,证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证 因为y xF xy F ∂=-∂,z y F y z F ∂=-∂,x z F z x F ∂=-∂,所以 1y xzx yz F F F x y z y z x F F F⎛⎫⎛⎫⎛⎫∂∂∂⋅⋅=-⋅-⋅-=- ⎪ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭. 7.设(,)u v ϕ具有连续偏导数,证明由方程(,)0cx az cy bz ϕ--=所确定的函数(,)z f x y =满足z zab c x y∂∂+=∂∂. 证 令u cx az =-,v cy bz =-,则x u u u c x ϕϕϕ∂=⋅=∂,y v v v c y ϕϕϕ∂=⋅=∂,z u v u v u va b z zϕϕϕϕϕ∂∂=⋅+⋅=--∂∂.x u z u v c z x a b ϕϕϕϕϕ∂=-=∂+,y v z u vc zy a b ϕϕϕϕϕ∂=-=∂+. 于是 u v u v u vc c z zab a bc x y a b a b ϕϕϕϕϕϕ∂∂+=⋅+⋅=∂∂++. 8.设0ze xyz -=,求22zx∂∂.解 设(,,)z F x y z e xyz =-,则x F yz =-,z z F e xy =-. 于是x z z F z yz x F e xy∂=-=∂-, ()222()z z zz z ye xy yz e y z z x x x x x e xy ∂∂⎛⎫--- ⎪∂∂∂∂∂⎛⎫⎝⎭== ⎪∂∂∂⎝⎭-()22z z zyzy z yz e y e xy e xy ⎛⎫-⋅- ⎪-⎝⎭=- ()2322322z zzy ze xy z y z e exy --=-.9.设(,)z z x y =是由方程2e 0zxz y --=所确定的隐函数,求2(0,1)zx y∂∂∂.解 设2(,,)e z F x y z xz y =--,则x F z =-,e z z F x =-,2y F y =-.于是 x z z F z z x F e x ∂=-=∂-,2y zz F z yy F e x∂=-=∂-, ()()22z z zz ze x z e z z y yx y y x ex ∂∂--⋅⋅∂∂∂∂∂⎛⎫== ⎪∂∂∂∂⎝⎭-()()222z zz zz y y e x ze e x e x e x ----=- ()()322z zzy e x yze ex --=-.由20ze xz y --=,知(0,1)0z =,得2(0,1)2zx y ∂=∂∂. 10.求由方程xyz =(,)z z x y =在点(1,0,1)-处的全微分d z .解设(,,)F x y z xyz =x z F zx F xy ∂=-==∂y z F zy F xy ∂=-==∂+,d d d z zz x y x y x y ∂∂=+=∂∂,(1,0,1)d d z x y -=.11.求由下列方程组所确定的函数的导数或偏导数:(1)设22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩求d d y x ,d d z x ; (2)设0,1,xu yv yu xv -=⎧⎨+=⎩求u x ∂∂,u y ∂∂,vx ∂∂,v y ∂∂;(3)设sin ,cos ,uux e u v y e u v ⎧=+⎪⎨=-⎪⎩求u x ∂∂,u y ∂∂,v x ∂∂,v y ∂∂. 解 (1)分别在两个方程两端对x 求导,得d d 22,d d d d 2460.d d z y x y x xy z x y z x x ⎧=+⎪⎪⎨⎪++=⎪⎩称项,得d d 22,d d d d 23.d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪+=-⎪⎩ 在 2162023y D yz y y z-==+≠的条件下,解方程组得213d 6(61)d 622(31)x x z yxz x x z x D yz y y z ------+===++. 222d 2d 6231y x y x z xy xx D yz y z --===++. (2)此方程组确定两个二元隐函数(,)u u x y =,(,)v v x y =,将所给方程的两边对x 求导并移项,得,.uv x y u x xu v y x v xx ∂∂⎧-=-⎪⎪∂∂⎨∂∂⎪+=-⎪∂∂⎩ 在220x y J x y yx-==+≠的条件下,22u yv x u xu yv x y x x y y x---∂+==--∂+, 22x uy v v yu xv x y x x y y x--∂-==-∂+. 将所给方程的两边对y 求导,用同样方法在220J x y =+≠的条件下可得22u xv yu y x y∂-=∂+,22v xu yvy x y ∂+=-∂+. (3)此方程组确定两个二元隐函数(,)u u x y =,(,)v v x y =是已知函数的反函数,令(,,,)sin u F x y u v x e u v =--,(,,,)cos u G x y u v y e u v =-+.则 1x F =,0y F =,sin u u F e v =--,cos v F u v =-, 0x G =,1y G =,cos u u G e v =-+,sin v G u v =-.在sin cos (,)(sin cos )0(,)cos sin u u u e v u vF G J ue v v u u v e v u v ---∂===-+≠∂-+-的条件下,解方程组得1cos 1(,)1sin 0sin (,)(sin cos )1uu v u F G vu v x J x v J e v v -∂∂=-=-=-∂∂-+, 0cos 1(,)1cos 1sin (,)(sin cos )1uu v u F G vu v y J y v J e v v -∂∂-=-=-=-∂∂-+, sin 11(,)1cos (,)[(sin cos )1]cos 0u uu u e v v F G v e x J u x J u e v v e v --∂∂-=-=-=∂∂-+-+,sin 01(,)1sin (,)[(sin cos )1]cos 1u uu ue v v F G v e x J u x J u e v v e v --∂∂+=-=-=∂∂-+-+.习题7-61.求下列曲线在指定点处的切线方程和法平面方程: (1)2x t =,1y t =-,3z t =在(1,0,1)处; (2)1t x t =+,1t y t+=,2z t =在1t =的对应点处; (3)sin x t t =-,1cos y t =-,4sin2t z =在点1,1,2π⎛- ⎝处; (4)2222100,100,x y y z ⎧+-=⎪⎨+-=⎪⎩在点(1,1,3)处. 解 (1)因为2t x t '=,1t y '=-,23t z t '=,而点(1,0,1)所对应的参数1t =,所以(2,1,3)=-T .于是,切线方程为11213x y z --==-. 法平面方程为2(1)3(1)0x y z --+-=,即 2350x y z -+-=.(2)因为2211(1)(1)t t t x t t +-'==++,22(1)1t t t y t t-+'==-,2t z t '=,1t =对应着点1,2,12⎛⎫⎪⎝⎭,所以 1,1,24⎛⎫=- ⎪⎝⎭T .于是,切线方程为 1212148x y z ---==-. 法平面方程为 281610x y z -+-=.(3)因为1cos t x t '=-,sin t y t '=,2cos 2t t z '=,点1,1,2π⎛- ⎝对应在的参数为2t π=,所以(=T .于是,切线方程为112x y π-+=-=. 法平面方程为402x y π+--=. (4)将2222100,100,x y y z ⎧+-=⎪⎨+-=⎪⎩的两边对x 求导并移项,得 d 22,d d d 220,d d yy x xy z y z xx ⎧=-⎪⎪⎨⎪+=⎪⎩ 由此得2002d 420d 422x z y xz x y x yz y y z --===-,2220d 420d 422y xy z xy xy x yz z y z-===. (1,1,3)d 1d y x =-,(1,1,3)d 1d 3z x =.从而 11,1,3⎛⎫=- ⎪⎝⎭T .故所求切线方程为113331x y z ---==-. 法平面方程为 3330x y z -+-=.2.在曲线x t =,2y t =,3z t =上求一点,使此点的切线平行于平面24x y z ++=.解 因为1t x '=,2t y t '=,23t z t '=,设所求点对应的参数为0t ,于是曲线在该点处的切向量可取为200(1,2,3)t t =T .已知平面的法向量为(1,2,1)=n ,由切线与平面平行,得0⋅=T n ,即2001430t t ++=,解得01t =-和13-.于是所求点为(1,1,1)--或111,,3927⎛⎫-- ⎪⎝⎭.3.求下列曲面在指定点处的切平面和法线方程: (1)222327x y z +-=在点(3,1,1)处; (2)22ln(12)z x y =++在点(1,1,ln 4)处; (3)arctany z x =在点1,1,4π⎛⎫ ⎪⎝⎭处.解(1)222(,,)327F x y z x y z =+--,(,,)(6,2,2)x y z F F F x y z ==-n ,(3,1,1)(18,2,2)=-n .所以在点(3,1,1)处的切平面方程为9(3)(1)(1)0x y z -+---=,即 9270x y z +--=. 法线方程为311911x y z ---==-. (2)22(,,)ln(12)F x y z x y z =++-,222224(,,),,11212x y z x yF F F x y x y ⎛⎫==- ⎪++++⎝⎭n , (1,1,ln 4)1,1,12⎛⎫=- ⎪⎝⎭n .所以在点(1,1,ln 4)处的切平面方程为2234ln 20x y z +--+=.法线方程为 12ln 2122y z x ---==-. (3)(,,)arctanyF x y z z x=-,2222(,,),,1x y z y xF F F x y x y ⎛⎫-==- ⎪++⎝⎭n , 1,1,411,,122π⎛⎫ ⎪⎝⎭⎛⎫=-- ⎪⎝⎭n . 所以在点1,1,4π⎛⎫ ⎪⎝⎭处的切平面方程为202x y z π-+-=. 法线方程为 114112z x y π---==-. 4.求曲面2222321x y z ++=上平行于平面460x y z ++=的切平面方程. 解 设222(,,)2321F x y z x y z =++-,则曲面在点(,,)x y z 处的一个法向量(,,)(2,4,6)x y z n F F F x y z ==.已知平面的法向量为(1,4,6),由已知平面与所求切平面平行,得246146x y z ==,即12x z =,y z =. 代入曲面方程得 22223214z z z ++=.解得 1z =±,则12x =±,1y =±.所以切点为 1,1,12⎛⎫±±± ⎪⎝⎭.所求切平面方程为 21462x y z ++=±5.证明:曲面(,)0F x az y bz --=上任意点处的切平面与直线x yz a b==平行(a ,b 为常数,函数(,)F u v 可微).证 曲面(,)0F x az y bz --=的法向量为1212(,,)F F aF bF ''''=--n ,而直线的方向向量(,,1)a b =s ,由0⋅=n s 知⊥n s ,即曲面0F =上任意点的切平面与已知直线x yz a b==平行. 6.求旋转椭球面222316x y z ++=上点(1,2,3)--处的切平面与xOy 面的夹角的余弦.解 令222(,,)316F x y z x y z =++-,曲面的法向量为(,,)(6,2,2)x y z F F F x y z ==n ,曲面在点(1,2,3)--处的法向量为1(1,2,3)(6,4,6)--==--n n ,xOy 面的法向量2(0,0,1)=n ,记1n 与2n 的夹角为θ,则所求的余弦值为1212cos θ⋅===n n n n .7.证明曲面3xyz a =(0a >,为常数)的任一切平面与三个坐标面所围成的四面体的体积为常数.证 设3(,,)F x y z xyz a =-,曲面上任一点(,,)x y z 的法向量为(,,)n yz xz xy =,该点的切平面方程为()()()0yz X x xz Y y xy Z z -+-+-=,即 33yzX xzY xyZ a ++=.这样,切平面与三个坐标面所围成的四面体体积为33331333962a a a V a yz xz xy =⋅⋅⋅=.习题7-71.求函数22z x y =+在点(1,2)处沿从点(1,2)到点(2,2+的方向的方向导数.解按题意,方向l =,12l ⎛= ⎝⎭e .又2zx x∂=∂,2z y y ∂=∂,(1,2)2z x ∂=∂,(1,2)4zy ∂=∂,。
微观第七章习题及答案

微观第七章习题及答案微观第七章习题一、名词解释完全垄断市场垄断竞争市场寡头市场价格歧视博弈纳什均衡占优策略均衡二、选择题1、对于垄断厂商来说,()。
A、提高价格一定能够增加收益;B、降低价格一定会减少收益;C、提高价格未必会增加收益,降低价格未必会减少收益;D、以上都不对。
2、完全垄断的厂商实现长期均衡的条件是()。
A、MR=MC;B、MR=SMC=LMC;C、MR=SMC=LMC=SAC;D、MR=SMC=LMC=SAC=LAC。
3、完全垄断厂商的总收益与价格同时下降的前提条件是()。
A、Ed>1;B、Ed<1;C、Ed=1;D、Ed=0。
4、完全垄断厂商的产品需求弹性Ed=1时()。
A、总收益最小;B、总收益最大;C、总收益递增;D、总收益递减。
5、完全垄断市场中如果A市场的价格高于B市场的价格,则()A、A市场的需求弹性大于B市场的需求弹性;B、A市场的需求弹性小于B市场的需求弹性;C、A市场的需求弹性等于B市场的需求弹性;D、以上都对。
6、以下关于价格歧视的说法不正确的是()。
A、价格歧视要求垄断者能根据消费者的支付意愿对其进行划分;B、一级价格歧视引起无谓损失;C、价格歧视增加了垄断者的利润;D、垄断者进行价格歧视,消费者就必定不能进行套利活动。
7、垄断竞争的厂商短期均衡时,()。
A、一定能获得差额利润;B、一定不能获得经济利润;C、只能得到正常利润;D、取得经济利润、发生亏损和获得正常利润都有可能。
8、垄断竞争厂商长期均衡点上,长期平均成本曲线处于( B )A、上升阶段B、下降阶段C、水平阶段D、以上三种情况都有可能9、垄断竞争厂商实现最大利润的途径有:( D )A、调整价格从而确定相应产量B、品质竞争C、广告竞争D、以上途径都可能用10、按照古诺模型下列哪一说法不正确,()。
A、双头垄断者没有认识到他们的相互依耐性;B、每一个寡头都认定对方的产量保持不变;C、每一个寡头垄断者都假定对方价格保持不变;D、均衡的结果是稳定的。
《统计学》-第7章-习题答案

第七章思考与练习参考答案1 •答:函数关系是两变量之间的确定性关系,即当一个变量取一定数值时,另一个变量有确定值与之相对应;而相关关系表示的是两变量之间的一种不确定性关系,具体表示为当一个变量取一定数值时,与之相对应的另一变量的数值虽然不确定,但它仍按某种规律在定的范围内变化。
2•答:相关和回归都是研究现象及变量之间相互关系的方法。
相关分析研究变量之间相关的方向和相关的程度,但不能确定变量间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况;回归分析则可以找到研究变量之间相互关系的具体形式,并可变量之间的数量联系进行测定,确定一个回归方程,并根据这个回归方程从已知量推测未知量。
3•答:单相关系数是度量两个变量之间线性相关程度的指标,其计算公式为:总体相关系数二样本相关系数,「一】。
复相关系数是多元线性回归分析中度量因变量与其它多个自变量之间的线性相关程度的指标,它是方程的判定系数R2的正的平方根。
偏相关系数是多元线性回归分析中度量在其它变量不变的情况下两个变量之间真实相关程度的指标,它反映了在消除其他变量影响的条件下两个变量之间的线性相关程度。
4.答:回归模型假定总体上因变量Y与自变量X之间存在着近似的线性函数关系,可表示为Y^ 11X t u t,这就是总体回归函数,其中u t是随机误差项,可以反映未考虑的其他各种因素对Y的影响。
根据样本数据拟合的方程,就是样本回归函数,以一元线性回归模型的样本回归函数为例可表示为:Y?=耳+弭x t。
总体回归函数事实上是未知的,需要利用样本的信息对其进行估计,样本回归函数是对总体回归函数的近似反映。
两者的区别主要包括:第一,总体回归直线是未知的,它只有一条;而样本回归直线则是根据样本数据拟合的,每抽取一组样本,便可以拟合一条样本回归直线。
第二,总体回归函数中的-0和-1是未知的参数,表现为常数;而样本回归直线中的'?Q和?i是随机变量,其具体数值随所抽取的样本观测值不同而变动。
第07章_存储器习题答案

第七章习题答案7.1.1 指出下列存储系统各具有多少个存储单元,至少需要几根地址线和数据线。
(1)64K×1 (2)256K×4 (3)lM×1 (4)128K×8解:求解本题时,只要弄清以下几个关系就能很容易得到结果:存储单元数=字数×位数地址线根数(地址码的位数)n与字数N的关系为:N=2n数据线根数=位数(1)存储单元〓64K×1〓64K(注:lK=1024);因为,64K〓2’。
,即亢〓16,所以地址线为16根;数据线根数等于位数,此处为1根。
同理得:(2)1M个存储单元,18根地址线,4根数据线。
(3)1M个存储单元,18根地址线,1根数据线。
!_(4)lM个存储单元,17根地址线,8根数据线。
7.1.2 设存储器的起始地址为全0,试指出下列存储系统的最高地址为多少?(1)2K×1 (2)16K×4 (3)256K×32解:因为存储系统的最高地址=字数十起始地址一1,所以它们的十六进制地址是:(1)7FFH (2)3FFFH (3)3FFFFH '7,2.4 一个有1M×1位的DRAM,采用地址分时送人的方法,芯片应具有几条地址线?解:由于1M=210×210,即行和列共需20根地址线。
所以,采用地址分时送人的方法,芯片应具有10根地址线。
7.2.5 试用一个具有片选使能CE、输出使能OE、读写控制WE、容量为8 K×8位的sRAM 芯片,设计一个16K×16位的存储器系统,试画出其逻辑图。
解:采用8K×8位的sRAM构成16K×16位的存储器系统,必须同时进行字扩展和位扩展。
用2片8K×8位的芯片,通过位扩展构成8K×16位系统,此时需要增加8根数据线。
要将8K×16位扩展成16K×16位的存储器系统,还必须进行字扩展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 习题解答7-1已知下列时间函数()c t ,设采样周期为T 秒,求它们的z 变换。
(a )2()1()c t t t = (b )()()1()c t t T t =- (c )()()1()c t t T t T =-- (d )()1()at c t t te -= (e )()1()sin at c t t e t ω-= (f )()1()cos at c t t te t ω-= 解:(a )根据z 域微分定理有[][]222222431()111()1(1)(1)(1)2(1)(1)1()(1)(1)(1)z Z t z d z z z TzZ t t TzTz dz z z z d Tz T z Tz z T z z Z t t Tz Tz dz z z z =---⎡⎤=-=-=⎢⎥---⎣⎦⎡⎤---+⎡⎤=-=-=⎢⎥⎣⎦---⎣⎦(b )因为()1()1()1()t T t t t T t -=-所以[][][]22(2)()1()1()1()(1)1(1)Tz Tz Tz z Z t T t Z t t Z T t z z z --=-=-=--- (c )根据时域位移定理有[][]1122()1()()1()(1)(1)Tz TZ t T t T z Z t t z z z ----===--(d )根据复域位移定理有221()(1)()aT aTataT aT Tze Tze Z t teze z e ---⎡⎤==⎣⎦-- (e )根据复域位移定理有22sin 1()sin 2cos aT ataT aTze T Z t et z z Te e ωωω----⎡⎤=⎣⎦-+(f )根据复域位移定理有22(cos )1()cos 2cos aT ataT aTz z e T Z t et z z Te e ωωω-----⎡⎤=⎣⎦-+7-2已知()c t 的拉氏变换为下列函数,设采样周期为T 秒,求它们的z 变换。
(a )21()C s s =(b )()()aC s s s a =+ (c )2()()a C s s s a =+(d )1()()()()C s s a s b s c =+++(e )2221()()C s s s a =+(f )()1()1sT C s e s-=-解:(a )[]221(1)TzZ z t s z ⎡⎤==⎢⎥-⎣⎦(b )11(1)1()1()()1(1)()T at T T a z z z e Z Z Z t e t s s a s s a z z e z z e ααα----⎡⎤-⎡⎤⎡⎤=-=-=-=⎢⎥⎣⎦⎢⎥++----⎣⎦⎣⎦(c )2222111111()1()()()(1)(1)(1)()(1)(1)()at TT T a Z Z Z t t e t s s a s as a s a a a Tz z z Tz z e z a z a z e z a z z e ααα----⎡⎤⎡⎤⎡⎤=-+=-+⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦-=-+=------- (d )1()()()111()()()()()()()()()()()()()()()()()()aT bT cT Z s a s b s c Z b a c a s a c b a b s b a c b c s c z z z b a c a z e c b a b z e a c b c z e ---⎡⎤⎢⎥+++⎣⎦⎡⎤=++⎢⎥--+--+--+⎣⎦=++---------(e )22222222223211111sin ()()(1)2cos 1Tz z aTZ Z s s a a s a s a a z a z z aT ⎡⎤⎡⎤=-=-⎢⎥⎢⎥++--+⎣⎦⎣⎦(f )111111sT sT e e z Z Z s s s z z --⎡⎤⎡⎤-=-=-=⎢⎥⎢⎥--⎣⎦⎣⎦7-3求下列函数的z 反变换。
(a )0.5(1)(0.4)zz z --(b )2()()T T zz e z e ----(c )22(1)(2)z z z ++解: (a)1100.555521()(1)(0.4)6160.465nn z z z Z Z t nt z z z z δ∞--=⎛⎫⎡⎤⎡⎤⎛⎫=-=-- ⎪ ⎪⎢⎥⎢⎥ ⎪----⎣⎦⎝⎭⎣⎦⎝⎭∑ (b )()11222222011()()1()T T T T T T T T nT nTT Tn z z z Z Z z e z e e e z e e e z e e e t nT ee δ----------∞----=⎡⎤⎡⎤=-⎢⎥⎢⎥------⎣⎦⎣⎦=---∑ (c)21122102(1)(2)(2)21(1)(2)(12)()n nn z z z z Z Z z z z z z n t nT δ--∞+=⎡⎤⎡⎤-=++⎢⎥⎢⎥+++++⎣⎦⎣⎦⎡⎤=-+---⎣⎦∑7-4已知0k <时,()0c k =,()C z 为如下所示的有理分式120121212()1nn nn b b z b z b z C z a z a z a z ------++++=++++L L则有0(0)c b =以及[]1()()nk i i c kT b a c k i T ==--∑式中k n >时,0k b =。
(a )试证明上面的结果。
(b )设23220.5()0.5 1.5z z C z z z z +-=-+-应用(a )的结论求(0)c 、()c T 、(2)c T 、(3)c T 、(4)c T 、(5)c T 。
解: (a )设121234012012341212()1n n nn b b z b z b z C z c c z c z c z c z a z a z a z----------++++==+++++++++L L L显然有00c b =以及1011020211200011kkkk k i i k k i i k k i ii i i b c a c a b c a c a c a b c a c a c a c c a ---====+=++==+=+∑∑∑M式中k n >时,0k b =。
上式即[]1()()nk i i c kT b a c k i T ==--∑k n >时,0k b =。
证毕。
(b )设23220.5()0.5 1.5z z C z z z z +-=-+-应用关系式1kk k k i ii c b c a -==-∑有(0)0()2(1)02(2)1(1)()0.503(3)0.5(1)30.52(1.5)0 1.5(4)0(1) 1.5(0.5)3( 1.5)2003(5)0(1)30.5 1.5( 1.5)30200 6.75c c T c T c T c T c T c T ==--⨯==--⨯-⨯==---⨯-⨯-⨯==--⨯-⨯--⨯-⨯==--⨯-⨯--⨯-⨯-⨯=7-5试用部分分式法、幂级数法和留数法,求下列函数的z 反变换。
(a )10()(1)(2)zE z z z =--(b )1123()12z E z z z ----+=-+(c )2()(1)(31)zE z z z =++ (d )2()(1)(0.5)zE z z z =-+解: (a )部分分式法1110101010102(1)(2)12n z z z Z Z z z z z --⎡⎤-⎡⎤=+=-+⨯⎢⎥⎢⎥----⎣⎦⎣⎦幂级数法11234121010103070150(1)(2)132z z z z z z z z z z-------==++++---+L留数法121010()Res Res 10102(1)(2)(1)(2)n nn z z z z e nT z z z z ==⎡⎤⎡⎤=+=-+⨯⎢⎥⎢⎥----⎣⎦⎣⎦ (b )1221222333()1221(1)z z z z zE z z z z z z ----+-+-+===-+-+-部分分式法2112232332(1)(1)1z z z z Z Z n z z z --⎡⎤⎡⎤-+--=+=--⎢⎥⎢⎥---⎣⎦⎣⎦幂级数法210123212333579(1)12z z z z z z z z z-------+-+==----+--+L留数法212122112113()Res (1)3(1)3(1)32(1)n z n n n z z z z e nT z z d z z z z n z nz n dz z -=--==⎡⎤-+=⎢⎥-⎣⎦⎡⎤-+⎡⎤=-=-++=--⎢⎥⎣⎦-⎣⎦(c )部分分式法()()2211122213113(1)(31)4143141431111cos sin 44242111sin 30422n nn nn z z z z z z Z Z Z z z z z z z n n n πππ---⎡⎡⎤⎡⎤-=-=-⎢⎢⎥⎢⎥++++++⎣⎦⎣⎦⎣⎦⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭o幂级数法22345621230.3330.3330.2220.2220.259(1)(31)33z z z z z z z z z z z z---------==-+-++++++L 留数法()()222121()Res Res Res (1)(31)(1)(31)(1)(31)(31)11413144n nnz z z n nn z z z nnk k z z z e nT z z z z z z z z =-==-=-=-=⎡⎤⎡⎤⎡⎤=++⎢⎥⎢⎥⎢⎥++++++⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤=++⎢⎥+⎣⎦-=-+=--()()()()()()6111cos sin 44242111sin 30422n n n n nnnn n n j j j j n n n πππ⎧⎫⎡⎤⎡⎤+---⎪⎣⎦⎨⎪⎩⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭o (d )部分分式法11221442(1)(0.5)9190.53(0.5)4412199232nn z z z z Z Z z z z z z n ---⎡⎤⎡⎤=--⎢⎥⎢⎥-+-++⎣⎦⎣⎦⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭幂级数法22452230.750.25(1)(0.5)10.750.25z z z z z z z z z------==+++-+--L留数法2210.51212210.5120.5()Res Res (1)(0.5)(1)(0.5)(1)(0.5)(1)(0.5)(1)(0.5)491(1)4412199232z z n n z z n nz nn z ze nT z z z z z d z z z z z z z dz z z nz zz z n ==---==--=-⎡⎤⎡⎤=+⎢⎥⎢⎥-+-+⎣⎦⎣⎦⎡⎤⎡⎤=-++⎢⎥⎢⎥-+-+⎣⎦⎣⎦⎡⎤=+-⎢⎥--⎣⎦⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭1-7-6用z 变换法求下面的差分方程(2)3(1)2()0,(0)0,(1)1x k x k x k x x ++++===并与用迭代法得到的结果(0)x 、(1)x 、(2)x 、(3)x 、(4)x 相比较。
