十大数学公式
世界著名的十大公式
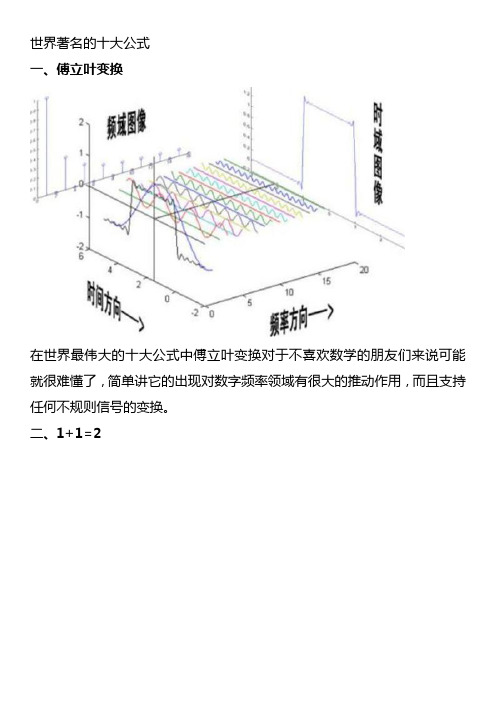
世界著名的十大公式一、傅立叶变换在世界最伟大的十大公式中傅立叶变换对于不喜欢数学的朋友们来说可能就很难懂了,简单讲它的出现对数字频率领域有很大的推动作用,而且支持任何不规则信号的变换。
二、1+1=21+1=2这个公式和上一个相比较应该就是无人不知了吧,从幼儿园开始它就伴随着我们,简单好理解,它的出现在整个数学领域可以说是引起轰动了的呢!三、毕达哥拉斯定理毕达哥拉斯定理也就是我们数学学习生涯中常见勾股定理,如今有四百多种图形被毕达哥拉斯定理给证明了,是非常伟大又典型的解决图形问题的公式。
四、麦克斯韦方程组人们评价说,如果没有麦克斯韦方程组就没有现代社会的文明,整个方程也是完美到无可挑剔,可以说宇宙间的任何电磁用这个方程组都能很好的被解释。
五、欧拉公式这个欧拉公式从形式上看非常的巧妙,没有任何多余的“杂质”,数学家们评论说凡是第一眼爱上这个公式的人必定会成为数学家,可见该公式的伟大之处。
六、质能方程在世界最伟大的十大公式中质能方程著名的物理学家爱因斯坦提出来的,该公式很好的揭示了质量和能量之间的关系,也正是质能方程的出现才有了当今的原子弹,氢弹等。
七、德布罗意方程组德布罗意方程组揭示出了任何物质都是有粒子性和波动性的,让波长和能量等之间有了一个很好的关系解释,提出者也在1929年获得了诺贝尔奖。
八、圆的周长公式圆的周长公式,这个伴随着整个数学学习生涯,如果用圆的周长公式来说计算太阳系包起来的周长,误差的直径不到百万分之一。
九、牛顿第二定律牛顿第二定律可以说是当下物理学的核心公式,它的出现可以是标志着真正物理学研究的开始,学习上好多的方程也都要依靠牛顿第二定律导出来。
十、薛定谔方程在世界最伟大的十大公式中薛定谔方程可谓是经典中的经典,它的出现很好的揭示了力学中位移和速度的关系,如今该公式在物理学的应用极为广泛,影响力也很大。
十大数学公式

1. 欧拉恒等式这是一个非常著名的恒等式。
它给出了3个看似随机的量之间的联系:π、e和-1的平方根。
许多人认为这是数学中最漂亮的公式。
一个更一般的公式是e^(ix) =cosx+isinx (a^b表示a的b次方,下同)。
当x=π,cosx取值为-1,而isinx取值为0。
由-1+1=0,我们得到了欧拉恒等式。
2. 欧拉乘积公式等式左边的符号是无穷求和,而右边的符号则是无穷乘积。
这个公式也是欧拉首先发现的。
它联系了出现在等式左边的自然数(如n=1,2,3,4,5等等)与出现在等式右边的素数(如p=2,3,5,7,11等等)。
而且我们可以选取s为任意大于1的数,并保证等式成立。
欧拉乘积公式的左边是黎曼ζ函数最常见的一种表示形式。
3. 高斯积分函数e^(-x²)本身在积分中是很难对付的。
可是当我们对它在整个实数轴上积分,也就是说从负无穷到正无穷时,我们却得到了一个十分干净的答案。
至于为什么曲线下面的面积是π的平方根,这可不是一眼就能看出来的。
由于这个公式代表了正态分布,它在统计中也十分重要。
4. 连续统的基数上面的公式说明了实数集的基数与自然数全体子集的基数相同。
这首先是被集合论的建立者康托尔证明的。
值得注意的是,这也说明了连续统是不可数,因为2^N > N。
一个相关的假设是连续统假设。
这个假设是说,在N和R之间不存在其它的基数。
有趣的是,这个假设有一个奇怪的性质:它既不能被证明也不能被证伪。
5. 阶乘函数的解析延拓阶乘函数通常被定义为n!=n(n-1)(n-2)……1。
但是这个定义只对n是正整数时有效,而上面积分方程则对分数和小数也有效,而且还可以用于负数、复数等等……同样的积分式中我们把n换成n-1就定义了伽马函数。
6. 勾股定理勾股定理恐怕是这个清单中最熟悉的公式了。
它给出了直角三角形三边的联系,其中a和b是直角边长,而c 是斜边长。
这个公式还将三角形和正方形联系了起来。
7. 斐波那契数列的通项这里,注意到φ这个数字是黄金分割比例。
最伟大的十个公式

最伟大的十个公式
最伟大的十个公式包括但不限于:
1. 1+1=2,它表明了最基本的算术基础,是数学中最基本的公理之一。
2. E=mc^2,它揭示了质量和能量之间的关系,是物理学中最重要的公式之一。
3. 圆周公式,即圆的周长与直径的比值等于π,它展示了圆的曲线美,是几何学中最重要的公式之一。
4. 欧拉公式,它将三角函数、指数和对数函数等基本数学概念联系在一起,是数学中最重要的公式之一。
5. 牛顿第二定律,即F=ma,它揭示了力与加速度之间的关系,是经典力学中最重要的公式之一。
6. 薛定谔方程,它是量子力学中的基本方程之一,揭示了微观世界中粒子的运动规律。
7. 麦克斯韦方程组,它描述了电磁场的运动规律,是电磁学中最重要的公式之一。
8. 爱因斯坦的相对论公式,它揭示了时间和空间的关系,是现代物理学中最重要的公式之一。
9. 德布罗意公式,即λ=h/p,它揭示了微观粒子波粒二象性的关系,是量子力学中重要的公式之一。
10. 狄拉克方程,它是描述电子运动的方程,是量子力学中重要的公式之一。
以上排名不分先后,仅供参考。
这些公式在科学、技术和工程领域都有着广泛的应用和重要的意义。
改变世界的十大数学公式

改变世界的十大数学公式
1. 费马大定理:对于n>2的情况下,找不到整数解的x,y,z使
得x^n+y^n=z^n成立。
2. 美第奇定理:任意复数只要不是无理数,都可以用一个乘法单位和加法单位构成一个有限个单位之和。
3. 黎曼猜想:所有非平凡零论函数的零点都在直线s = 1/2 + it 上。
4. 欧拉公式:e^(iπ) + 1 = 0,将数学中的五个最重要的常数(0、1、e、i、π)联系在一起。
5. 泰勒级数:将一个函数表示为无限个项相加的形式,可以用来近似计算函数的值。
6. 极限定义:用极限来描述函数的变化趋势,为微积分提供了基础。
7. 平方根算法:用于计算平方根的算法,如牛顿迭代法和二分法。
8. 黑色-斯科尔定理:描述了在物体运动中系统熵的增加程度。
9. 贝叶斯定理:用于计算在已知一些先验概率和观察到的证据之后的后验概率。
10. 矩阵理论:用于描述线性方程组和线性变换的数学工具,广泛应用于计算机图形学、工程和经济学等领域。
世界上十大著名公式

世界上十大著名公式
1. 欧拉公式:eπi + 1 = 0
2. 欧几里得定理:a² + b² = c²
3. 黎曼假设:没有一个数字可以同时被两个不同素数整除
4. 勒贝格定理:任何一个正整数都可以表示成若干个素数的乘积
5. 兰开斯特定理:每一个整数都可以写成四个整数的平方和
6. 马尔可夫定理:任何一个图都可以用四条边分割成四个面
7. 拉格朗日定理:任何一个多项式都可以用一系列的积分表示
8. 默尔定理:任何一个正整数都可以写成若干个素数的和
9. 哥德巴赫猜想:任何一个大于2的偶数都可以表示成两个质数的和
10. 布尔定理:任何一个自然数都可以表示成若干个素数的乘积。
高等数学十大定理公式

高等数学十大定理公式高等数学十大定理公式有有界性、最值定理、零点定理、费马定理、罗尔定理、拉格朗日中值定理、柯西中值定理、泰勒定理(泰勒公式)、积分中值定理(平均值定理)。
1、有界性|f(x)|≤K2、最值定理m≤f(x)≤M3、介值定理若m≤μ≤M,∃ξ∈[a,b],使f(ξ)=μ4、零点定理若f(a)⋅f(b)<0∃ξ∈(a,b) ,使f(ξ)=05、费马定理设f(x)在x0处:1,可导2,取极值,则f′(x0)=06、罗尔定理若f(x)在[a,b] 连续,在(a,b) 可导,且f(a)=f(b) ,则∃ξ∈(a,b) ,使得f′(ξ)=07、拉格朗日中值定理若f(x)在[a,b] 连续,在(a,b) 可导,则∃ξ∈(a,b) ,使得f(b)−f(a)=f′(ξ)(b−a)8、柯西中值定理若f(x)、g(x)在[a,b] 连续,在(a,b) 可导,且g′(x)≠0 ,则∃ξ∈(a,b) ,使得f(b)−f(a)g(b)−g(a)=f′(ξ)g′(ξ)9、泰勒定理(泰勒公式)n阶带皮亚诺余项:条件为在$x_0$处n阶可导$f(x)=f(x_0)f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+...+\dfra c{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n)\ ,x\xrightarrow{} x_0$ n阶带拉格朗日余项:条件为n+1阶可导$f(x)=f(x_0)f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+...+\dfra c{f^{(n)}(x_0)}{n!}(x-x_0)^n+\dfrac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0 )^{n+1}\ ,x\xrightarrow{} x_0$10、积分中值定理(平均值定理)若f(x)在[a,b] 连续,则∃ξ∈(a,b),使得∫baf(x)dx=f(ξ)(b−a)。
十大著名数学公式

十大著名的数学公式
以下是十大著名的数学公式:
1 欧拉公式:e^(iπ) + 1 = 0。
这个公式将五个重要的数学常数联系在一起:自然对数的底e、虚数单位i、圆周率π、单位元素1 和零0。
2 皮亚诺公理:这是数学基础理论的公理系统,用于推导整数的性质和运算规则。
3 傅里叶变换:这个公式将一个函数在频域和时域之间进行转换,可以将一个信号分解成一系列不同频率的正弦和余弦分量。
4 黎曼猜想:由黎曼提出的一个关于素数分布的猜想,尚未被证明或者推翻。
5 二项式定理:(a + b)^n = C(n,0)a^nb^0 + C(n,1)*a^(n-1)*b^1 + ... + C(n,n)a^0b^n。
这个公式展示了如何展开一个二项式的幂。
6费马大定理:由费马提出的一个关于整数解存在性的问题,直到近几年才被安德鲁·怀尔斯证明。
7斯特林公式:这个公式给出了n 的阶乘的近似值,以及对数函数在正实数范围内的近似值。
8黑-斯科尔定理:这个公式用于计算曲线围成的面积,推广了基本的微积分概念。
9导数定义:f'(x) = lim(h->0) [f(x+h)-f(x)]/h。
这个公式给出了函数的导数定义,描述了函数在某一点的变化率。
10 矩阵乘法规则:矩阵乘法的公式,使得矩阵代数成为现代数学和应用中至关重要的工具。
这些公式在数学领域有着广泛的应用,对于数学研究和实际问题的解决起到了重要的作用。
十个最伟大的公式

十个最伟大的公式1. 帕斯卡定理:组合数规律,表达式为C(n,m)=C(n-1,m)+C(n-1,m-1),其中C为组合数。
2. 欧拉公式:描述了立体图形中的面数、顶点数及边数之间的关系,即V-E+F=2。
3. 高斯定理:描述了向量场和曲面的关系,表达式为∬S rotF·dS=∮L F·dr,其中rot为旋度,∬S和∮L分别为曲面S和曲线L 上的积分。
4. 能量守恒定律:能量在一定条件下不会减少或增加,表达式为E=mc²,其中E为能量,m为质量,c为光速。
5. 万有引力定律:任意两个物体之间的万有引力与它们的质量成正比,与它们之间的距离的平方成反比,表达式为F=G·m1m2/r²,其中G为引力常数,m1、m2为物体的质量,r为它们之间的距离。
6. 热力学第一定律:能量不会被创造或毁灭,只会从一个物体传递到另一个物体,表达式为ΔU=Q-W,其中ΔU为内能变化,Q为吸收的热量,W为做功。
7. 热力学第二定律:热量不可能自发地从低温物体传递到高温物体,表达式为ΔS≥0,其中ΔS为熵变化。
8. 卢瑟福散射公式:描述了荷电粒子在靶核上碰撞后散射的角度分布,表达式为dσ/dΩ=(kZ/z)²cos²(θ/2),其中dσ/dΩ为散射截面,k为波数,Z为靶核的原子序数,z为入射粒子电荷数,θ为散射角度。
9. 波动方程:描述了波动传播的规律,表达式为∂²u/∂t²=c²∇²u,其中u为波函数,t为时间,c为波速,∇²为拉普拉斯算子。
10. 黎曼猜想:描述素数分布的规律,还未被证明或证伪,是数学领域中的一个重要难题。
影响人类文明 的十大数学公式

影响人类文明的十大数学公式以影响人类文明的十大数学公式为标题,下面将介绍这些数学公式以及它们对人类文明的重大影响。
第一,皮亚诺公理。
这是数学中的基本公理系统,它提供了数学推理的基础。
皮亚诺公理确保了数学的逻辑一致性,为其它公式的推导提供了保障,为人类文明提供了数学基础。
第二,欧拉公式。
这是数学中最具美感和深度的公式之一。
欧拉公式将三个基本常数e、i和π联系在一起,具有许多重要的数学和物理应用。
欧拉公式的发现和研究推动了复数和指数函数的发展,对数学、物理和工程科学产生了深远的影响。
第三,牛顿-莱布尼茨公式。
这是微积分的基本公式,描述了函数的导数和积分之间的关系。
牛顿-莱布尼茨公式使微积分成为现代科学和工程的基础,对人类文明的发展做出了巨大贡献。
第四,费马定理。
这是数论中的一个著名问题,它提出了一个简洁而深刻的数学断言。
费马定理的证明历经数学家们几百年的努力,最终由英国数学家安德鲁·怀尔斯在1994年给出。
费马定理的证明不仅展示了数学的美丽和深奥,也推动了数论的研究和发展。
第五,高斯定理。
这是数学中的一个重要公式,描述了向量场通过一个封闭曲面的流量与该曲面内源项之间的关系。
高斯定理在物理学中有广泛的应用,如电磁学、流体力学和热力学等领域。
它的发现和应用推动了人类对物质和能量的理解和探索。
第六,傅里叶变换。
这是一种数学工具,用于将一个函数表示为一组正弦和余弦函数的和。
傅里叶变换在信号处理、图像处理、量子力学和概率论等领域有广泛的应用。
它的发展和应用极大地改进了人类对信息的处理和传输能力。
第七,矩阵理论。
矩阵是一种数学结构,用于表示线性方程组和线性变换。
矩阵理论在计算机科学、物理学、经济学和社会科学等领域有广泛的应用。
它的发展和应用推动了人类对复杂系统和大规模数据的分析和建模能力。
第八,黎曼猜想。
这是数论中的一个重要问题,涉及素数的分布规律。
黎曼猜想被认为是数论中最重要的未解问题之一,解决它将对数论和密码学等领域产生重大影响。
世界最美的十大数学公式

世界最美的十大数学公式数学对很多人来说或许都是“大魔鬼”,但对喜欢的朋友,数学绝对是“天使”,尤其是那一个个公式,下面整理了世界最美的十大数学公式,一起来看看吧!一、微积分基本定理在世界最美的十大数学公式中微积分基本定理是数学中微分和积分的总称,它的诞生可以说是人类史上最大的创举,如今在化学、生物学、地理学等领域都离不开这个公式。
二、麦克斯韦方程组麦克斯韦方程组被评价为是数学中最伟大的方程组之一,它很好的揭示了电场和磁场之间的关系,当时在牛顿发现相对论的时候该方程组可是给了他很大的启发。
三、圆的周长公式圆的周长公式,这个不论是喜欢还是不喜欢数学的朋友应该都是相当了解的,从初中到如今圆的周长公式好像有点如影随形一般,当下人们计算圆周率完全就是为了检验计算机的能力。
四、傅立叶变换傅立叶变换虽然很美,但相对来说是很难被理解通透的一个数学公式,它的出现对当代电子计算机的发展可以说是起到了重要在的推动作用。
五、薛定谔方程薛定谔方程是一位奥地利的物理学家提出来的,当时直到至今在物理学和数学界中都占有着极高的地位,1933年的时候创造者也凭借此公式获得了诺贝尔奖。
六、勾股定理在世界最美的十大数学公式中勾股定理又是一个几乎伴随着所有数学学习生涯的公式,简单的讲好多数学题都需要用此公式来解答,不是最美数学公式那是什么呢?七、欧拉公式不少是数学家都说如果第一次看到欧拉公式没有被它的美震撼到,那他便很难成为一位优秀的数学家,该公式将数学最常见的三个常数运用到了一起,就好像没有任何杂质一般。
八、德布罗意方程组德布罗意方程组在数学和物理中的应用非常广,光从公式的形式上来看就能感受到它的不同,很好的证明波长、能量等之间的关系。
九、牛顿第二定律牛顿第二定律的提出对当时和当下数学及物理学发展都有着极大的推动作用,公式很好的展现了物体运动状态下的相对变化,很美,很经典。
十、1+1=2在世界最美的十大数学公式中这个1+1=2的公式真的可以说是相当美啊,而且这个公式几乎可以说是伴随着我们的一生,即便是不喜欢数学的朋友应该都能感受到它的美吧!。
全球十大公式

全球十大公式全球十大公式是指在全球范围内被广泛应用的十个数学公式。
这些公式不仅在学术领域有着重要的应用,而且在工程、科技、金融等领域也有着广泛的应用。
下面我们来一一介绍这十大公式。
1.欧拉公式:e^(iπ)+1=0欧拉公式是数学中最美丽的公式之一,它将三个最基本的数学常数e、i和π联系在了一起。
欧拉公式在物理、工程、金融等领域都有着广泛的应用。
2.贝叶斯公式:P(A|B)=P(B|A)P(A)/P(B)贝叶斯公式是概率论中的重要公式,它可以用来计算在已知某些条件下,某个事件发生的概率。
贝叶斯公式在人工智能、机器学习等领域有着广泛的应用。
3.高斯公式:∫e^(-x^2)dx=√π高斯公式是数学中的重要积分公式,它在统计学、物理学、工程学等领域有着广泛的应用。
4.牛顿-莱布尼茨公式:∫f(x)dx=F(x)+C牛顿-莱布尼茨公式是微积分中的基本公式,它可以用来计算函数的积分。
牛顿-莱布尼茨公式在物理学、工程学等领域有着广泛的应用。
5.费马小定理:a^(p-1)≡1(mod p)费马小定理是数论中的重要定理,它可以用来判断一个数是否为质数。
费马小定理在密码学、计算机科学等领域有着广泛的应用。
6.傅里叶变换:F(ω)=∫f(t)e^(-iωt)dt傅里叶变换是数学中的重要变换,它可以将一个函数在时域中的表达式转换为在频域中的表达式。
傅里叶变换在信号处理、图像处理等领域有着广泛的应用。
7.熵公式:H(X)=-∑p(x)logp(x)熵公式是信息论中的重要公式,它可以用来衡量信息的不确定性。
熵公式在通信、数据压缩等领域有着广泛的应用。
8.斯特林公式:n!=√(2πn)(n/e)^n斯特林公式是数学中的重要公式,它可以用来估算阶乘的值。
斯特林公式在概率论、统计学等领域有着广泛的应用。
9.泊松分布公式:P(X=k)=λ^ke^(-λ)/k!泊松分布公式是概率论中的重要公式,它可以用来描述稀有事件的发生概率。
泊松分布公式在统计学、物理学等领域有着广泛的应用。
初中数学十大公式

初中数学十大公式初中数学十大公式包括:1. 周长公式:长方形周长=(长+宽)×2,C=2(a+b);正方形周长=边长×4,C=4a。
2. 面积公式:长方形面积=长×宽,S=ab;正方形面积=边长×边长,S=a²;三角形面积=底×高÷2,S=ah/2;平行四边形面积=底×高,S=ah;梯形面积=(上底+下底)×高÷2,S=1/2(a+b)h;圆形面积=半径×半径×圆周率,S=πr²;扇形面积=半径×半径×圆周率×圆心角度数(n)÷360,S=nπr²/360。
3. 判别式:b²-4ac=0,注:方程有两个相等的实根;b²-4ac>0,注:方程有两个不等的实根;b²-4ac<0,注:方程没有实根,有共轭复数根。
4. 两角和公式:sin(A+B)=sinAcosB+cosAsinB。
5. 圆的有关公式:弧长L=nπR/180;扇形面积S扇形=nπR²/360=LR/2;内公切线长d-(R-r)=外公切线长d-(R+r)。
6. 正n边形的每个内角都等于(n-2)×180°/n。
7. 圆的切线判定定理:经过半径的外端点并且垂直于半径的直线是圆的切线。
8. 圆的切线性质定理:圆的切线垂直于过切点的半径。
9. 相交两圆的连心线垂直平分两圆的公共弦。
10. 圆和圆的位置关系:两圆外离d>R+r;两圆外切d=R+r;两圆相交R-r<d<R+r(R>r);两圆内切d=R-r(R>r);两圆内含d<R-r(R>r)。
以上是初中数学中的部分公式,初中数学还有许多其他重要的公式和定理,建议查看初中数学教材或咨询数学老师进行学习。
世界上最伟大的十个数学公式

世界上最伟大的十个数学公式以下是世界上被认为最伟大的十个数学公式(排序不分先后):1. 欧拉公式(Euler's formula):e^ix = cos(x) + i*sin(x),将三个基本数学常数e、i和π联系在一起,涵盖了实数、虚数、三角函数以及指数函数。
2. 二项式定理(Binomial theorem):(a+b)^n = C(n,0)*a^n*b^0 + C(n,1)*a^(n-1)*b^1 + ... + C(n,n-1)*a^1*b^(n-1) +C(n,n)*a^0*b^n,展开了一个二项式的幂。
3. 黎曼猜想(Riemann hypothesis):数学家黎曼提出的假设,关于素数分布的一种描述,至今未被证明或者证伪。
4. 费马大定理(Fermat's Last Theorem):Pierre de Fermat于1637年提出的定理,指出当n大于2时,方程x^n + y^n = z^n没有正整数解。
5. 导数的定义(Derivative definition):f'(x) = lim(h->0) [f(x+h) - f(x)]/h,定义了函数在某一点的瞬时变化率。
6. 泰勒展开(Taylor series):将某个函数在某点附近展开成无穷级数的表达式,使得在该点附近的近似计算变得更加精确。
7. 傅里叶变换(Fourier transform):将一个函数表示为一系列正弦和余弦函数的和,用来分析信号的频谱和频域特性。
8. 十进制无理数的表示(Decimal representation of irrational numbers):证明了有些无理数能够以无限循环的小数形式表示,例如圆周率π=3.14159...9. 黄金分割比(Golden ratio):φ = (1 + √5) / 2,一种特殊的数学比例,在建筑、美学和自然界中有广泛的应用。
10. 矩阵乘法(Matrix multiplication):将两个矩阵相乘的操作,是线性代数中的基础运算,在图像处理、机器学习等领域具有重要作用。
世界上最伟大的十大公式

世界上最伟大的十大公式
1. 欧拉公式:e^(iπ) + 1 = 0。
它将数学中的五个基本常数(e、
i、π、1和0)结合在一起,以一种简洁而优雅的方式。
2. 直角三角形的勾股定理:a² + b² = c²。
这个公式描述了直角三角形中三条边之间的关系,是几何学中最重要的定理之一。
3. 爱因斯坦的质能方程:E = mc²。
这个公式描述了质量和能量之间的等价关系,揭示了相对论的基本原理。
4. 麦克斯韦方程组:这是一组描述电磁场的四个基本方程,包括高斯定律、法拉第电磁感应定律、安培环路定律和法拉第电磁感应定律。
它们统一了电磁学的基本原理。
5. 黎曼猜想:尚未被证明的数学猜想,涉及到复数域上的素数分布规律。
如果该猜想成立,将对数论产生深远的影响。
6. 波尔兹曼熵公式:S = k ln W。
它描述了统计物理学中系统的熵和系统的微观状态数之间的关系,是热力学第二定律的基础。
7. 黑-施陶尔兹迈尔方程:描述流体运动的偏微分方程,是流体力学的基本方程之一。
8. 熵增定律:描述了自然界中系统总是趋向于熵增加的趋势,是热力学和统计物理学中基本的原理之一。
9. 维里定律:描述了电阻产生的焦耳热与电流、电阻和时间的关系,是电学中的基本定律之一。
10. 斯特雷克公式:描述了光谱线的位移与外加电场的关系,揭示了原子和分子的结构与性质之间的关联。
数学中最具影响力的十大公式

数学中最具影响力的十大公式1971年5月15日,尼加拉瓜发行了十张一套题为“改变世界面貌的十个数学公式”邮票,由一些著名数学家选出十个以世界发展极有影响的公式来表彰。
这十个公式不但造福人类,而且具有典型的数学美,即:简明性、和谐性、奇异性。
(一)手指计数基本法则邮票“1+1=2”是这套邮票的第一枚,这是人类一开始对数量认识的基础公式。
人类的祖先就是以这一公式开始,堆石子,数贝壳、树枝、竹片,而后刻痕计数,结绳计数等,直至再后来创造文字、数字及计数用具如算盘、筹算、计算器等。
一切都是从手指计数基本法则开始,因为人有十个手指,计算时以手指辅助。
毫无疑问,正是这一事实自然地孕育形成了现在我们熟悉的十进制系统。
记数法与十进制的诞生是文明史上的一次飞跃。
(二)勾股定理(毕达哥拉斯定理)若一直角三角形的直角边为A、B,斜边为C,则有A2+B2=C2,这就是欧氏几何中最为著名的勾股定理。
它在数学与人类的实践活动中有着极其广泛的应用。
在国外最早给出这一定理证明的是古希腊著名哲学家和数学家毕达哥拉斯,因而国外一般称之为“毕达哥拉斯定理”。
中国在商高时代就已经知道“勾三股四弦五”的关系,远早于毕达哥拉斯,不过,中国对于勾股定理的证明却是比较迟的事情,一直到三国时期的赵爽才用面积割补法给出它的第一种证明。
勾股定理的一大影响是无理数的发现。
边长为1的正方形对角线长度为,不能用整数或整数之比即分数来表示,这一发现否定了毕氏学派“万物皆数”的信条,当时的人觉得整数与分数是容易理解的,称之为有理数,而新发现的这个数不好理解但却存在就取名为“无理数”。
(三)阿基米德杠杆原理第三枚邮票表彰的数学公式F1X1=F2X2,其中F为作用力,X 为力臂,FX即为力矩,从原则上说,只要动力臂足够长,而阻力臂足够短,就可以用足够小的力撬动足够重的物体。
为此,阿基米德说了一句古名言:“给我一个支点,我就能撬动地球”。
呵呵,看看物理学家多自信!!!除杠杆原理外,阿基米德还发现了著名的浮力定律和大量的几何学定理,他也是微积分的先驱之一。
数学总结—公式大全

数学总结—公式大全1.代数方面的公式1.1 一次方程:ax + b = 0,其中a≠0。
1.2 二次方程:ax² + bx + c = 0,其中a≠0。
1.3 一元二次不等式:ax² + bx + c > 0或ax² + bx + c < 0。
1.4勾股定理:a²+b²=c²,其中a、b为直角三角形的两条直角边,c 为斜边。
1.5 二项式定理:(a + b)ⁿ = C(n,0)aⁿ + C(n,1)aⁿ⁻¹b + ... +C(n,n-1)abⁿ⁻¹ + C(n,n)bⁿ,其中C(n,k)表示组合数。
1.6四则运算规则:加法:a+b=b+a,乘法:a×b=b×a。
2.几何方面的公式2.1 三角形面积公式:S = 1/2bh,其中S表示三角形的面积,b表示底边的长度,h表示高。
2.2直角三角形三边关系:a²+b²=c²,其中a、b为直角三角形的两条直角边,c为斜边。
2.3 正弦定理:a/sinA = b/sinB = c/sinC = 2R,其中a、b、c为三角形的边长,A、B、C为对应的内角,R为三角形外接圆的半径。
2.4 余弦定理:c² = a² + b² - 2abcosC,其中a、b、c为三角形的边长,C为对应的内角。
2.5 面积公式:三角形面积S = 1/2absinC,其中a、b为三角形的两条边,C为对应的夹角。
2.6弧长公式:L=rθ,其中L表示弧长,r表示弧的半径,θ表示圆心角的度数。
3.微积分方面的公式3.1 导数定义:f'(x) = lim (f(x + h) - f(x))/h,其中f'(x)表示函数f(x)在x处的导数。
3.2导数的基本运算法则:常数法则、乘法法则、除法法则、链式法则等。
3.3反函数导数:(f⁻¹)'(y)=1/f'(x),其中f⁻¹表示f的反函数。
史上十大数学公式及鲜为人知的故事

史上十大数学公式及鲜为人知的故事一、欧拉公式欧拉公式是数学中最重要的公式之一,它表达了自然对数、三角函数和复数之间的关系:e^ix = cos(x) + i*sin(x)其中,e是自然对数的底数,i是虚数单位,x是任意实数。
二、费马大定理费马大定理是数论中一条闻名世界的定理,它最早由法国数学家费马于17世纪提出,直到358年后才由英国数学家安德鲁·怀尔斯证明。
费马大定理表示:“当n大于2时,方程x^n+y^n=z^n没有正整数解。
”即使对于最简单的情况n=3,也没有找到满足这个条件的整数解。
这个定理的证明过程非常复杂,需要运用到了现代代数学和数论中的许多深刻理论。
费马大定理的证明直到1994年才得到解决,当时怀尔斯使用了一种全新的数学方法,创建了一种被称为“椭圆曲线方法”的技术,解决了这个长期以来困扰数学界的难题。
这个证明被认为是数学史上最伟大的成就之一三、无穷级数和在数学中,无穷级数是由无限多项相加而成的数列。
其中一些无穷级数有着令人惊讶的求和结果。
最著名的例子就是1+1/2+1/4+1/8+…这个级数,它可以用数学方法证明收敛并求出其和为2、这个结果对于绝大多数人来说都很令人意外,因为看起来似乎无法有一个有限的和。
然而,数学家通过使用极限的概念,证明了这个无穷级数的和等于2四、黄金分割比黄金分割比是一个重要的数学比例,它的近似值约为1.618、这个比例在美学、建筑、艺术和自然界中广泛存在。
黄金分割比的特点是将一条线段分成两部分,使整体与较大部分的比例等于较大部分与较小部分的比例。
这个比例被认为是最美、最和谐的比例之一,被广泛运用在建筑设计、艺术创作和品味选择等方面。
五、复数的麦克劳林级数展开麦克劳林级数展开是一种用多项式逼近复杂函数的方法。
这个方法由苏格兰数学家麦克劳林于18世纪提出,并被广泛应用于数学和物理领域。
麦克劳林级数展开的思想是将一个复杂的函数在其中一点附近进行多项式逼近,从而可以用简单的多项式函数来近似复杂函数的性质。
十大必学公式

十大必学公式在学习数学的过程中,公式是不可或缺的一部分。
公式的掌握不仅可以帮助我们更好地理解数学知识,还可以在解题时提高效率。
下面是十大必学公式,希望对大家的学习有所帮助。
1.勾股定理:a²+b²=c²,其中a、b、c分别为直角三角形的两条直角边和斜边。
2.二次方程求根公式:对于ax²+bx+c=0,其根为x1=(-b+√(b²-4ac))/2a,x2=(-b-√(b²-4ac))/2a。
3.三角函数公式:sin²θ+cos²θ=1,tanθ=sinθ/cosθ,cotθ=cosθ/sinθ。
4.圆的面积公式:S=πr²,其中S为圆的面积,r为圆的半径。
5.立方体的体积公式:V=a³,其中V为立方体的体积,a为立方体的边长。
6.平行四边形的面积公式:S=bh,其中S为平行四边形的面积,b 为底边长,h为高。
7.三角形的面积公式:S=1/2bh,其中S为三角形的面积,b为底边长,h为高。
8.等差数列求和公式:Sn=n(a1+an)/2,其中Sn为等差数列的前n项和,a1为首项,an为末项。
9.等比数列求和公式:Sn=a1(1-qⁿ)/(1-q),其中Sn为等比数列的前n项和,a1为首项,q为公比。
10.导数公式:f'(x)=lim(h→0)(f(x+h)-f(x))/h,其中f'(x)为函数f(x)在x处的导数。
以上是十大必学公式,掌握这些公式可以帮助我们更好地理解数学知识,提高解题效率。
当然,公式的掌握并不是学习数学的全部,还需要不断地练习和思考,才能真正掌握数学的精髓。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十大美丽的数学公式,快来选出你的最爱!
广州虎妈猫爸2015-06-05 21:05
Top 10
无名公式(好吧发现者似乎倾向于将其命名为姐妹公式):这组公式是原贴作者发现的,具有惊人的镜像般的高度对称感,但作者表示考虑到之后九个的大神般存在,还是默默放到第十了。
TOP 9
圆周率与自然对数底的近似关系式:能把圆周率和e联系起来的初等公式在数学界是少之又少,是数学王国中的国宝级公式。
除了大名鼎鼎的欧拉公式,恐怕就是这个式子比较出名了。
这个公式的形式异常的漂亮,只可惜它只是个近似公式。
所以排名第九。
虽然是个近似公式,但是近似程度相当的高,有七位有效数字是相同的,也就是说二者的差别在千万分之一以内。
可以用电脑上的计算器一试。
钦公式:熟悉圆周率计算方法的人应该对这个公式不陌生。
这个公式的神奇之处在于它将圆周率表示为了两个分数的反正切之和。
利用复数的指数表达式可以直接证明这个式子。
它是历史上第一个用于快速计算圆周率的公式,因为上式中的反正切函数值可以被泰勒级数所逼近。
真不知道如果祖冲之知道了这个计算圆周率的方法会埋头算到小数点后几百位……
TOP 7
约翰-伯努利公式之一(只是传说是他发现的):这个神奇的公式传说是约翰-伯努利发现的。
式子的神奇之处就不用我说了吧,连续与离散的关系被表现得淋漓尽致。
如果你自认为你的微积分水平还不错,可以挑战一下这个已经具有300多年历史的公式,看你能否证明它。
我的成绩是十分钟得到了证明(这是原贴作者)。
TOP 6
又是无名式:话说世人皆知勾三股四弦五,而鲜有知道这个简单等式的。
这个简单的式子可以在英国分析学大师G·H·哈代(就是拉马努金在英国的合作者)所著的《数论导引》中找到,它是一类三次不定方程最简单的特解。
还是无名式:这个公式来自于印度数学奇才拉马努金。
他曾经深入的研究了形如上式的无穷根式并得到了这个神奇的结果。
传说拉马努金曾经把这个结果放在《印度数学会刊》上征集证明,结果数月内无人能应。
各位看官有没有蠢蠢欲动的?
TOP 4
高斯公式之一:不消说,这个余弦特殊值足以说明:正十七边形是可以尺规作图的。
在发现此式之前人们找到的、能用根式表达余弦值的角度大部分还停留在欧几里得时期的水平。
高斯也因为他在19岁就做出的这项了不起的成果而开始从事数学研究。
古典文学从此永远的失去了高斯。
在作出这项告慰古希腊先贤们的贡献之后,小高斯就建立了一个自己的科学笔记,专门介绍自己最新的数学发现。
TOP 3
扯淡忽悠人公式:这个貌似神奇的式子来自50多年前的《Scientific American》(其神奇之处在于它似乎把无理的e表达为有理了)。
当时著名的趣味数学大师马丁·加德纳所主持的一个专栏上出现了这个公式,只可惜出版的当天日期是4月1号。
这个式子或许可以蒙普通读者,但是绝对蒙不了数学家,因为根据著名的林德曼定理容易判定等式左边的e指数一定是一个超越数,绝对不可能是一个整数。
然而如果你用mathematica去计算的话会惊奇的发现:这个超越数的值是:262537412640768743.9999999999992500725972……
竟然有12个9!!即使如此它仍然是一个超越数,一种比无理数还“无理”的数……
TOP 2
那就是受到我们万世敬仰的欧拉公式(music起):上面欧拉公式的漂
亮之处就不用我解释了吧。
人们经常把它与老爱同志的E=mc^2并列
为数学和物理学公式中的双子星。
历史上的欧拉是一位全才数学家,
同时也是一名虔诚的教徒,笃信上帝的存在。
据说有一次俄国的叶卡
捷琳娜二世邀请狄德罗来访问她的宫廷,而狄德罗是一名不折不扣的
无神论者。
不久叶卡捷琳娜二世就厌倦了狄德罗那喋喋不休的无神论
说教之词,让欧拉来好好教训他一顿。
欧拉开门见山的质问道:
“e^i*pi+1=0(就是欧拉公式),所以上帝存在,请回答!”结果不懂数
学的狄德罗被弄得一头雾水,无言以对。
TOP 1
拉马努金连分数公式:这个绝美的公式不仅像欧拉公式一样联系起了
圆周率和e,同时它还将黄金分割数也包含在内!在1913年,来自南
印度的小职员拉马努金,给当时32岁就已经执掌英国数学界牛耳的哈
代去了一封长达9页的信,信中附带了120条拉马努金自己发现的公式,上面这个公式就是其中的一条。
这条公式令哈代完全摸不到头脑,他这辈子都没见过这样的公式,连稍微接近点的都没有!但是哈代确
信这个公式是对的,因为没有人能有这样的想象力去编造这样漂亮的
公式。
虽然不久之后,数学家们就严格的证明了这个式子,但是它和
谐而又气势磅礴的形式令每一个初次见到它的人都会为之悸动!所以,拉马努金的这个公式绝对无愧于我们的最美数学公式榜首位置!(鼓掌……)。
