编译原理与实践作业答案
编译原理试题参考答案

编译原理试题参考答案编译原理试题参考答案编译原理是计算机科学中的一门重要课程,它研究的是将高级语言源代码转换成机器语言的过程。
在学习编译原理的过程中,试题是一种常见的考核方式。
下面是一些编译原理试题的参考答案,希望对大家的学习有所帮助。
1. 什么是编译器?编译器是一种将高级语言源代码转换成机器语言的程序。
它包括了词法分析、语法分析、语义分析、中间代码生成、代码优化和目标代码生成等多个阶段。
编译器的主要作用是将高级语言源代码转换成可执行的机器语言程序。
2. 什么是词法分析?词法分析是编译器的第一个阶段,它将源代码分解成一个个的词法单元,比如关键字、标识符、常量和运算符等。
词法分析器通常使用有限自动机来实现,它可以根据事先定义好的词法规则来识别源代码中的词法单元。
3. 什么是语法分析?语法分析是编译器的第二个阶段,它将词法分析得到的词法单元组织成一个语法树。
语法分析器通常使用上下文无关文法来描述语法规则,并通过递归下降、LL(1)分析或LR分析等算法来进行语法分析。
4. 什么是语义分析?语义分析是编译器的第三个阶段,它对语法树进行语义检查和语义规则的处理。
语义分析器通常会进行类型检查、符号表管理和语义规则的处理,以确保源代码的语义正确性。
5. 什么是中间代码生成?中间代码生成是编译器的第四个阶段,它将语法树转换成一种中间表示形式,比如三地址码、虚拟机代码或抽象语法树。
中间代码是一种与具体机器无关的表示形式,它方便后续的代码优化和目标代码生成。
6. 什么是代码优化?代码优化是编译器的第五个阶段,它通过对中间代码的分析和变换,来改进程序的执行效率和资源利用率。
代码优化的目标是在保持程序语义不变的前提下,尽可能地减少程序的执行时间和资源消耗。
7. 什么是目标代码生成?目标代码生成是编译器的最后一个阶段,它将中间代码转换成目标机器的机器语言程序。
目标代码生成器通常会进行寄存器分配、指令选择和指令调度等操作,以生成高效的目标代码。
《编译原理》作业参考答案

《编译原理》作业参考答案一、填空1.图二图一。
2.文法是无ε产生式,且任意两个终结符之间至多有一种优先关系的算符文法。
3.最右推导最右推导。
4.对于循环中的有些代码,如果它产生的结果在循环中是不变的,就把它提到循环外来。
把程序中执行时间较长的运算替换为执行时间较短的运算。
5.对于文法中的每个非终结符A的各个产生式的候选首符集两两不相交;对文法中的每个非终结符A,若它存在某个候选首符集包含ε,则FIRST(A)∩FOLLOW(A)= ø6.控制。
7.语义分析和中间代码产生8.自上而下自下而上自上而下9.自下而上表达式10.自下而上11.源程序单词符号12. DFA初态唯一,NFA初态不唯一;DFA弧标记为Σ上的元素,NFA弧标记为Σ*上的元素;DFA的函数为单射,NFA函数不是单射13.词法,词法分析器,子程序,语法14.ε,a,ab,ab15.终结符号,非终结符号,产生式16.L(G)={a n | n≥1}17.1型,2型,3型18.二义的19.快20.终态,输入字21.单词符号,终结符22.归约23.必须24.直接25.终结符,更快26.E→E+∙T, E→E∙+T, E→∙E+T, E→E+T∙27.归约—归约28.类型检查,一致性检查29.词法分析、词法30.语法分析程序、语法31。
终结符号、产生式、开始符号、非终结符32.2、2、333.不需要避开34.符合、不符合35.推导36.包括37.Ass38.一定没有、一定没有、至多只有一个39.SLR(1)40.移进——归约41.a.控制流检查、b.一致性检查、c.相关名字检查二、判断下面语法是否正确1 ×2 ×3 √4 ×5 √6 ×三、简答题1.词法分析的任务是对输入的源程序进行单词及其属性的识别,为下一步的语法分析进行铺垫;有两种方法可以实现词法分析器:一,手工编写词法分析程序。
二,由词法分析器自动生成程序生成。
编译原理作业与答案

编译原理独立作业2010.5一、简答题1、 构造一个文法使其生成的语言是不允许0打头的偶正整数集合。
2、文法][E G :T T E T E E -+→,F F T F T T /*→,i E F )(→,构造句型i T T T *+-的语法树,并指出该句型的短语、直接短语、句柄、素短语和最左素短语。
3、 某LL(1)文法的预测分析表如下,请在下述分析过程表中填入输入串( a , a )$ 的分析过程。
4、 文法][S G :R L S =→,R S →,R L *→,i L →,L R →,求增广文法中LR(1)项目集的初态项目集I 0。
5、文法][S G :G G S S ;→,()G G t H →,)(S a H →,求出各非终结符的FISTVT 和LASTVT 集合。
二、分析题:1、构造自动机,使得它能识别字母表{0,1}上以00结尾的符号串,将构造的自动机确定化,并写出相应的正规文法。
2、文法][S G :RT eT S → εDR T → εdR R → bd a D →,写出每个非终结符的FIRST 集和FOLLOW 集,并判断该文法是否为LL(1)文法。
3、若有文法][S G :AB S → εaBa A → εb A b B → (1)试证明该文法是SLR(1) 文法,并构造SLR(1)分析表。
(2)给出输入串aa # 的分析过程。
参考答案一、简答题1、构造一个文法使其生成的语言是不允许0打头的偶正整数集合。
8|6|4|2|ABC Z → 9|8|7|6|5|4|3|2|1→A ε|0|B AB B → |8|6|4|2|0→C2、文法][E G :T T E T E E -+→,F F T F T T /*→,i E F )(→,构造句型i T T T *+-的语法树,并指出该句型的短语、直接短语、句柄、素短语和最左素短语。
短语:T ,T-T ,i ,T*i ,T-T+T*i直接短语:T , i 句柄: T素短语(P72):T-T,i 最左素短语:T-T3 某LL(1)文法的预测分析表如下,请在下述分析过程表中填入输入串( a , a )$ 的分析过程。
编译原理作业答案

《编译原理》习题解答:第一次作业:P14 2、何谓源程序、目标程序、翻译程序、汇编程序、编译程序和解释程序?它们之间可能有何种关系?答:被翻译的程序称为源程序;翻译出来的程序称为目标程序或目标代码;将汇编语言和高级语言编写的程序翻译成等价的机器语言,实现此功能的程序称为翻译程序;把汇编语言写的源程序翻译成机器语言的目标程序称为汇编程序;解释程序不是直接将高级语言的源程序翻译成目标程序后再执行,而是一个个语句读入源程序,即边解释边执行;编译程序是将高级语言写的源程序翻译成目标语言的程序。
关系:汇编程序、解释程序和编译程序都是翻译程序,具体见P4 图 1.3。
P14 3、编译程序是由哪些部分组成?试述各部分的功能?答:编译程序主要由8个部分组成:(1)词法分析程序;(2)语法分析程序;(3)语义分析程序;(4)中间代码生成;(5)代码优化程序;(6)目标代码生成程序;(7)错误检查和处理程序;(8)信息表管理程序。
具体功能见P7-9。
P14 4、语法分析和语义分析有什么不同?试举例说明。
答:语法分析是将单词流分析如何组成句子而句子又如何组成程序,看句子乃至程序是否符合语法规则,例如:对变量x:= y 符合语法规则就通过。
语义分析是对语句意义进行检查,如赋值语句中x与y类型要一致,否则语法分析正确,语义分析则错误。
补充:为什么要对单词进行内部编码?其原则是什么?对标识符是如何进行内部编码的?答:内部编码从“源字符串”中识别单词并确定单词的类型和值;原则:长度统一,即刻画了单词本身,也刻画了它所具有的属性,以供其它部分分析使用。
对于标识符编码,先判断出该单词是标识符,然后在类别编码中写入相关信息,以表示为标识符,再根据具体标识符的含义编码该单词的值。
P38 1、设T1={11,010},T2={0,01,1001},计算:T2T1,T1*,T2+。
T2T1={011,0010,0111,01010,100111,1001010}T1*={ε,11,010,1111,11010,01011,010010……}T2+={0,01,1001,00,001,01001,010,0101……}P38-39 8、设有文法G[S]:S∷=aAbA∷=BcA | BB∷=idt |ε试问下列符号串(1)aidtcBcAb (2)aidtccb(4)abidt是否为该文法的句型或句子。
编译原理作业参考答案

最左推导:NNDDD3D34
NNDNDDDDD5DD56D568
最右推导:NNDN4D434
NNDN8ND8N68D68568
2*.写出一个文法,使其语言是奇数集,且每个奇数是不以0开头。
答:
SCAB|B(考虑了正负号)
A1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | AA | A0 |
低级语言:机器语言和汇编语言。
高级语言:是人们根据描述实际问题的需要而设计的一个记号系统。如同自然语言(接近数学语言和工程语言)一样,语言的基本单位是语句,由符号组和一组用来组织它们成为有确定意义的组合规则。
翻译程序:能够把某一种语言程序(源语言程序)改变成另一种语言程序(目
标语言程序),后者与前者在逻辑上是等价的。其中包括:编译程序,解释程序,汇编程序。
{2,4}a = {1,0},{2,4}b = {3,5},无需划分
{3,5}a = {3,5},{3,5}b = {2,4},无需划分
{0,1}a = {1},{0,1}b = {2,4},无需划分
因此,最终的划分为:{0,1}、{2,4}和{3,5},化简后的结果:
5.(P65,14)构造一个DFA M,它接受={0,1}上所有满足如下条件的字符串:每个1都有0直接跟在右边。
T*(i+i)F*(i+i)i*(i+i)
⑵构造语法树
E最左推导构造语法树
E + T
E + T i
T i
i
3.(P36, 9)证明下面的文法是二义的:
SiSeS | iSi
答:对于句子iiiei有两棵不同的语法树。因此该文法是二义的。
SiSeSiiSeSiiieSiiiei
编译原理及实践冯博琴冯岚教程中文版课后答案

编译原理及实践冯博琴冯岚教程中文版课后答案解释术语:1.翻译程序:是一种系统程序,它将计算机编程语言编写的程序翻译成另外一种计算机语言的一般来说等价的程序,主要包括编译程序和解释程序,汇编程序也被认为是翻译程序。
编译程序:也称为编译器,是指把用高级程序设计语言书写的源程序,翻译成等价的机器语言格式目标程序的翻译程序。
编译程序属于采用生成性实现途径实现的翻译程序。
它以高级程序设计语言书写的源程序作为输入,而以汇编语言或机器语言表示的目标程序作为输出。
编译出的目标程序通常还要经历运行阶段,以便在运行程序的支持下运行,加工初始数据,算出所需的计算结果。
2.解释程序:是一种语言处理程序,在词法、语法和语义分析方面与编译程序的工作原理基本相同,但在运行用户程序时,它直接执行源程序或源程序的内部形式(中间代码)。
因此,解释程序并不产生目标程序,这是它和编译程序的主要区别。
源程序:也称源代码,是指未编译的按照一定的程序设计语言规范书写的文本文件,是一系列人类可读的计算机语言指令。
在现代程序语言中,源代码可以是以书籍或者磁带的形式出现,但最为常用的格式是文本文件,这种典型格式的目的是为了编译出计算机程序。
计算机源代码的最终目的是将人类可读的文本翻译成为计算机可以执行的二进制指令,这种过程叫做编译,通过编译器完成。
3.目标程序:又称为“目的程序”,是源程序经编译可直接被计算机运行的机器码集合,在计算机文件上以.obj作扩展名----由语言处理程序(汇编程序,编译程序,解释程序)将源程序处理(汇编,编译,解释)成与之等价的由机器码构成的,计算机能够直接运行的程序,该程序叫目标程序。
目标代码尽管已经是机器指令,但是还不能运行,因为目标程序还没有解决函数调用问题,需要将各个目标程序与库函数连接,才能形成完整的可执行程序。
遍:把对源程序或其等价的中间表示形式从头到尾扫描并完成规定任务的过程。
4.前端:编译前端包括词法分析,语法分析,语义分析和中间代码生成,以及部分代码优化工作,是对源程序进行分析的过程,它主要与源语言有关,与目标机无关,主要根据源语言的定义静态分析源程序的结构,以检查是否符合语言的规定,确定原源程序所表示的对象和规定的操作,并以某种中间形式表示出来。
编译原理与实践第四章答案

The exercises of Chapter Four4.2Grammar: A → ( A ) A | εAssume we have lookahead of one token as in the example on p. 144 in the text book. Procedure A()if (LookAhead() ∈{‘(‘}) thenCall Expect(‘(‘)Call A()Call Expect (‘)’)Call A()elseif (LookAhead()∈{‘)‘, $}) thenreturn()else/* error */fifiend4.3 Given the grammarstatement→assign-stmt|call-stmt|otherassign-stmt→identifier:=expcall-stmt→identifier(exp-list)[Solution]First, convert the grammar into following forms:statement→identifier:=exp | identifier(exp-list)|otherThen, the pseudocode to parse this grammar:Procedure statementBeginCase token of( identifer : match(identifer);case token of( := : match(:=);exp;( (: match(();exp-list;match());else error;endcase(other: match(other);else error;endcase;end statement4.7 aGrammar: A → ( A ) A | εFirst(A)={(,ε } Follow(A)={$,)}4.7 bSee theorem on P.178 in the text book1.First{(}∩First{ε}=Φ2.ε∈Fist(A), First(A) ∩Follow(A)= Φboth conditions of the theorem are satisfied, hence grammar is LL(1)4.9 Consider the following grammar:lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp, lexp-seq|lexpa. Left factor this grammar.b. Construct First and Follow sets for the nonterminals of the resulting grammar.c. Show that the resulting grammar is LL(1).d. Construct the LL(1) parsing table for the resulting grammar.e. Show the actions of the corresponding LL(1) parser, given the input string (a,(b,(2)),(c)). [Solution]a.lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp lexp-seq’lexp-seq’→, lexp-seq|εb.First(lexp)={number, identifier, ( }First(atom)={number, identifier}First(list)={( }First(lexp-seq)={ number, identifier, ( }First(lexp-seq’)={, , ε}Follow(lexp)={, $, } }Follow(atom)= {, $, } }Follow(list)= {, $, } }Follow(lexp-seq)={$, } }Follow(lexp-seq’)={$,} }c. According to the defination of LL(1) grammar (Page 155), the resulting grammar is LL(1) as each table entry has at most one production as shown in (d).4.10 aLeft factored grammar:1. decl → type var-list2. type → int3. type → float4. var-list → identifier B5. B → , var-list6. B→ ε4.10 b4.10 c4.10 e4.12 a. Can an LL(1) grammar be ambigous? Why or Why not?b. Can an ambigous grammar be LL(1)? Why or Why not?c. Must an unambigous grammar be LL(1)? Why or Why not?[Solution]Defination of an ambiguous grammar: A grammar that generates a string with two distinct parse trees. (Page 116)Defination of an LL(1) grammar: A grammar is an LL(1) grammar if the associatied LL(1) parsing table has at most one priduction in each table entry.a.An LL(1) grammar can not be ambiguous, since the defination implies that an unambiguous parse canbe constructed using the LL(1) parsing tableb.An ambiguous grammar can not be LL(1) grammar, but can be convert to be ambiguous by usingdisambiguating rule.c.An unambiguous grammar may be not an LL(1) grammar, since some ambiuous grammar can beparsed using LL(K) table, where K>1.4.13Left recursive grammars can not be LL(1):Consider a grammar with a production A →A βwith symbol t in its first set. IF A is on the top of the stack and the current look-ahead token is t, A will be popped off the stack and then βwill be pushed onto the stack followed by A. A will again be the top of the stack and the look-ahead token will still be t, so it will repeat again, and again, infinitely, or until you get a stack overflow.Note: The first set for the recursive production will have a non-empty intersection with the first set for the terminating production, which will lead to a conflict when creating the LL(1) table.。
编译原理与实践作业答案
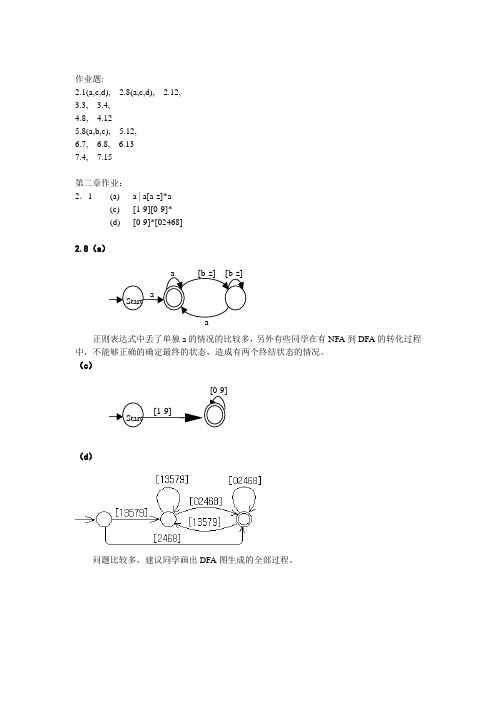
作业题:2.1(a,c,d), 2.8(a,c,d), 2.12,3.3, 3.4,4.8, 4.125.8(a,b,c), 5.12,6.7, 6.8, 6.137.4, 7.15第二章作业: 2.1 (a) a | a[a-z]*a(c) [1-9][0-9]* (d) [0-9]*[02468]2.8(a )正则表达式中丢了单独a 的情况的比较多,另外有些同学在有NFA 到DFA 的转化过程中,不能够正确的确定最终的状态,造成有两个终结状态的情况。
(c )(d )问题比较多,建议同学画出DFA 图生成的全部过程。
Start[1-9]Startaa [b-z] a [b-z]2.123.4(c ).rewrite this grammar to establish the correct precedences for the operator.rexp -> rexp “|” rexp1 | rexp1 rexp1 -> rexp1 rexp2 | rexp2 rexp2 -> rexp3 * | rexp3 rexp3 -> (rexp) | letter 左结合 4.8(a ) 消除左递归lexp -> atom | list atom -> number | identifier list -> (lexp-seq) lexp-seq -> lexp lexp-seq’ lexp-seq’ -> lexp lexp-seq’ | εfirst (lexp)= { number ,identifier,( } first (atom)= { number, identifier } first (list) = { ( }first (lexp-seq)= { number ,identifier,( } first (lexp-seq’)= { number ,identifier,( , ε}follow(lexp)= { $,),number,identifier,(}follow (atom)= { $,), number,identifier,( }follow (list) = {$,), number,identifier,(}follow (lexp-seq)= { )}follow (lexp-seq’)= { )}4.12(a)LL(1)文法不会是二义的,因为它的分析表的每个入口是唯一的。
编译原理作业参考答案

编译原理作业参考答案作业一一、是非题1.(×)2.(×)3.(×)4.(×)5.(×)6.(√)7. (√)8.(√)9.(√) 10.(×) 11.(√) 12.(√) 13.(√)二、填空题1.(词法分析),(语法分析),(中间代码生成),(代码优化),(目标代码生成)2.(单词符号),(语法单位)。
3.(源程序),(单词符号)4.(语法),(语义)5. (词法分析)、(语法分析)、(语义分析),(中间代码产生),(代码优化),(目标代码生成)6.(解释方式)7. (语法规则)8. (上下文无关文法)9. (自上而下分析法),(自下而上分析法)10. (规范推导)11. (最左归约)三、名词解释题:1.词法分析器-----执行词法分析的程序。
2. 自编译方式------先对语言的核心部分构造一个小小的编译程序,再以它为工具构造一个能够编译更多语言成分的较大编译程序。
如此扩展下去,就像滚雪球一样,越滚越大,最后形成人们所期待的整个编译程序。
3. 遍-----所谓“遍”就是对源程序或中间结果长头到尾扫描一次,并作有关的加工处理,生成新的中间结果或目标程序。
4. 编译程序-----一种翻译程序: 能够把某一种语言程序(称为源语言程序)转换成另一种语言(成为目标程序),而后着与前者在逻辑上是等价的。
5. 超前搜索-----所谓超前搜索是在词法分析过程中,有时为了确定词性,需超前扫描若干个字符。
6. 短语------令G是一个文法,S划文法的开始符号,假定αβδ是文法G的一个句型,如果有SαAδ且Aβ,则称β是句型αβδ相对非终结符A的短语。
7. 规范句型------由规范推导所得到的句型。
8. 句柄------一个句型的最左直接短语。
9. -规范推导-----最右推导又称为规范推导。
四、简答题:1. 正规式a ( a | b )*。
2.(a*b|b*a)={a,b,ab,ba,aab,bba……}3.状态转换图是一张有限方向图。
编译原理作业题答案编译原理课后题答案

第二章高级语言的语法描述6、令文法G 6为:N →D|ND D → 0|1|2|3|4|5|6|7|8|9(1)G 6 的语言L (G 6)是什么?(2)给出句子01270127、、34和568的最左推导和最右推导。
解答:思路:由N N →→ D|ND 可得出如下推导N =>=>ND ND ND=>=>=>NDD NDD NDD=>…=>=>…=>=>…=>D D n(n >=1=1))可以看出,N 最终可以推导出1个或多个(也可以是无穷)D ,而D D →→ 0|1|2|3|4|5|6|7|8|9可知,每个D 为0~9中的任一个数字,所以,中的任一个数字,所以,N N N 最终推导出的就是由最终推导出的就是由0~9这10个数字组成的字符串。
(1)G 6 的语言L (G 6)是由0~9这10个数字组成的字符串个数字组成的字符串,,或{0{0,,1,1,……,9}+。
(2)(2)句子句子01270127、、34和568的最左推导分别为的最左推导分别为: : N =>=>ND ND ND=>=>=>NDD NDD NDD=>=>=>NDDD NDDD NDDD=>=>=>DDDD DDDD DDDD=>=>=>0DDD 0DDD 0DDD=>=>=>01DD 01DD 01DD=>=>=>012D 012D 012D=>=>=>0127 0127 N =>=>ND ND ND=>=>=>DD DD DD=>=>=>3D 3D 3D=>=>=>34 34N =>=>ND ND ND=>=>=>NDD NDD NDD=>=>=>DDD DDD DDD=>=>=>5DD 5DD 5DD=>=>=>56D 56D 56D=>=>=>568 568 句子01270127、、34和568的最右推导分别为的最右推导分别为: :N =>=>ND ND ND=>=>=>N7N7N7=>=>=>ND7ND7ND7=>=>=>N27N27N27=>=>=>ND27ND27ND27=>=>=>N127N127N127=>=>=>D127D127D127=>=>=>0127 0127 N =>=>ND ND ND=>=>=>N4N4N4=>=>=>D4D4D4=>=>=>34 34N =>=>ND ND ND=>=>=>N8N8N8=>=>=>ND8ND8ND8=>=>=>N68N68N68=>=>=>D68D68D68=>=>=>568 5687、写一个文法,使其语言是奇数集,且每个基数不以0开头。
(完整版)编译原理习题及答案(整理后)

2、对无二义性文法来说,一棵语法树往往代表了 。
a. 多种推导过程
b. 多种最左推导过程
c.一种最左推导过程
d.仅一种推导过程 e.一种最左推导过程
3、如果文法 G 存在一个句子,满足下列条件 之一时,则称该文法是二义文法。
a. 该句子的最左推导与最右推导相同
b. 该句子有两个不同的最左推导
c. 该句子有两棵不同的最右推导
T→T*P|P
P→(E)|I
则句型 P+T+i 的句柄和最左素短语为 。
a.P+T 和 i b. P 和 P+T c. i 和 P+T+i d.P 和 T
8、设文法为:S→SA|A
A→a|b
则对句子 aba,下面 是规范推导。
a. SSASAAAAAaAAabAaba
b. SSASAAAAAAAaAbaaba
标语言
第二章
一、单项选择题
1、文法 G:S→xSx|y 所识别的语言是 。
a. xyx
b. (xyx)* c. xnyxn(n≥0) d. x*yx*
2、文法 G 描述的语言 L(G)是指 。
a. L(G)={α|S⇒+ α , α∈VT*}
b. L(G)={α|S⇒* α, α∈VT*}
c. L(G)={α|S⇒* α,α∈(VT∪VN*)} d. L(G)={α|S⇒+ α, α∈(VT∪VN*)}
第一章
1、将编译程序分成若干个“遍”是为了
。
a.提高程序的执行效率
b.使程序的结构更加清晰
c.利用有限的机器内存并提高机器的执行效率
d.利用有限的机器内存但降低了机器的执行效率
编译原理课后习题答案+清华大学出版社第二版

注意:如果问编译程序有哪些主要构成成分,只要回答六部分就可以。如果搞不清楚, 就回答八部分。
第 2题
若 PL/0 编译程序运行时的存储分配策略采用栈式动态分配,并用动态链和静态链的方
式分别解决递归调用和非局部变量的引用问题,试写出下列程序执行到赋值语句 b∶=10
时运行栈的布局示意图。 var x,y; procedure p; var a; procedure q; var b;
begin (q)
答案:
PL/0 编译程序所产生的目标代码中有 3 条非常重要的特殊指令,这 3 条指令在 code 中的位置和功能以及所完成的操作说明如下:
INT 0 A 在过程目标程序的入口处,开辟 A 个单元的数据段。A 为局部变量的个数+3。 OPR 0 0
3
《编译原理》课后习题答案第二章
在过程目标程序的出口处,释放数据段(退栈),恢复调用该过程前正在运行的过程的数 据段基址寄存器 B 和栈顶寄存器 T 的值,并将返回地址送到指令地址寄存器 P 中,以使调 用前的程序从断点开始继续执行。
3
《编译原理》课后习题答案第一章
第6题
计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?
答案:计算机执行用高级语言编写的程序主要途径有两种,即解释与编译。 像 Basic 之类的语言,属于解释型的高级语言。它们的特点是计算机并不事先对高级语
言进行全盘翻译,将其变为机器代码,而是每读入一条高级语句,就用解释器将其翻译为一 条机器代码,予以执行,然后再读入下一条高级语句,翻译为机器代码,再执行,如此反 复。
编译原理习题参考答案

编译原理习题参考答案第⼆章2.构造产⽣下列语⾔的⽂法(2){a n b m c p|n,m,p≥0}解: G(S) :S→aS|X,X→bX|Y,Y→cY|ε(3){a n # b n|n≥0}∪{cn # dn|n≥0}解: G(S):S→X,S→Y,X→aXb|#, Y→cYd|# }(5)任何不是以0 打头的所有奇整数所组成的集合解:G(S):S→J|IBJ,B→0B|IB|ε,I→J|2|4|6|8, J→1|3|5|7|9}(6)(思考题)所有偶数个0 和偶数个1 所组成的符号串集合解:对应⽂法为 S→0A|1B|ε,A→0S|1C B→0C|1S C→1A|0B3.描述语⾔特点(2)S→SS S→1A0 A→1A0 A→ε解:L(G)={1n10n11n20n2… 1nm0nm |n1,n2,…,nm≥0;且n1,n2,…nm 不全为零}该语⾔特点是:产⽣的句⼦中,0、1 个数相同,并且若⼲相接的1 后必然紧接数量相同连续的0。
(5)S→aSS S→a解:L(G)={a(2n-1)|n≥1}可知:奇数个a5. (1) 解:由于此⽂法包含以下规则:AA→ε,所以此⽂法是0 型⽂法。
7.解:(1)aacb 是⽂法G[S]中的句⼦,相应语法树是:最右推导:S=>aAcB=>aAcb=>aacb最左推导:S=>aAcB=>aacB=>aacb(3)aacbccb 不是⽂法G[S]中的句⼦aacbccb 不能从S推导得到时,它仅是⽂法G[S]的⼀个句型的⼀部分,⽽不是⼀个句⼦。
11.解:最右推导:(1) S=>AB=>AaSb=>Aacb=>bAacb=>bbAacb=>bbaacb上⾯推导中,下划线部分为当前句型的句柄。
对应的语法树为:3 假设M:⼈ W:载狐狸过河,G:载⼭⽺过河,C:载⽩菜过河6 根据⽂法知其产⽣的语⾔是L={a m b n c i| m,n,i≧1}可以构造如下的⽂法VN={S,A,B,C}, VT={a,b,c}P={ S →aA, A→aA, A→bB, B→bB, B→cC, C→cC, C→c} 其状态转换图如下:7 (1) 其对应的右线性⽂法是:A →0D, B→0A,B→1C,C→1|1F,C→1|0A,F→0|0E|1A,D→0B|1C,E→1C|0B(2) 最短输⼊串011(3) 任意接受的四个串: 011,0110,0011,000011(4) 任意以1 打头的串.9.对于矩阵(iii)(1) 状态转换图:(2) 3型⽂法(正规⽂法)S→aA|a|bB A→bA|b|aC|a B→aB|bC|b C→aC|a|bC|b(3)⽤⾃然语⾔描述输⼊串的特征以a 打头,中间有任意个(包括0个)b,再跟a,最后由⼀个a,b 所组成的任意串结尾或者以b 打头,中间有任意个(包括0个)a,再跟b,最后由⼀个a,b 所组成的任意串结尾。
编译原理与实践 第三章 答案

The exercises of Chapter Three3.2 Given the grammar A →AA|(A)|εa. Describe the language it generates;b. Show that it is ambiguous.[Solution]:a. Generates a string of balanced parenthesis, including the empty string.b. parse trees of ():3.3 Given the grammar exp → exp addop term | termaddop → + | -term → term mulop factor| factormulop → *factor → ( exp ) | numberWrite down leftmost derivations, parse trees, and abstract syntax trees for the following expression:a. 3+4*5-6b. 3*(4-5+6)c. 3-(4+5*6)[Solution]:a. The leftmost derivations for the expression3+4*5-6:Exp => exp addop term =>exp addop term addop term=>term addop term addop term=> factor addop term addop term=>3 addop term addop term => 3 + term addop term=>3+term mulop factor addop term =>3+factor mulop factor addop term=>3+4 mulop factor addop term => 3+4* factor addop termA ( ) ε A AA AA ( ) ε ε=>3+4*5 addop term => 3+4*5-term=> 3+4*5-factor=>3+4*5-63.5 Write a grammar for Boolean expressions that includes the constants true and false, the operators and, or and not, and parentheses. Be sure to give or a lower precedence than and and and a lower precedence that not and to allow repeated not’s, as in the Boolean expression not not true. Also be sre your grammar is not ambiguous.[solution]bex p→bexp or A | AA→ A and B | BB→ not B | CC→ (bexp) | true | falseEx: not not trueboolExp → A→ B→ not B→ not not B→ not not C→ not not true3.8 Given the following grammarstatement→if-stmt | other | εif-stmt→ if ( exp ) statement else-partelse-part→ else statement | εexp→ 0 | 1a. Draw a parse tree for the stringif(0) if (1) other else else otherb. what is the purpose of the two else’s?The two else’s allow the programmer to associate an else clause with the outmost else, when two if statements are nested and the first does not have an else clause.c. Is similar code permissible in C? Explain.The grammar in C looks like:if-stmt→if ( exp ) statement | if (exp) statement else statement the way to override “dangling else”problem is to enclose the inner if statement in {}s. e.g. if (0) { if(1) other } else other.3.10 a. Translate the grammar of exercise 3.6 into EBNF.b. Draw syntax diagramms for the EBNF of part (a).[Solution]a. The original grammarlexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp-seq lexp| lexpThe EBNF of the above grammar:lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp {lexp}b. The syntax diagramms for the above EBNF:3.12. Unary minuses can be added in several ways to the simple arithmetic expression grammar of Exercise 3.3. Revise the BNF for each of the cases that follow so that it satisfies the stated rule.a. At most one unary minus is allowed in each expression, and it must come at the beginning of an expression, so -2-3 is legal ( and evaluates to -5 ) and -2-(-3) is legal, but -2--3 is not.exp →exp addop term | termaddop →+ | -term → term mulop factor| factormulop →*factor →( exp) | (-exp) | number |b. At most one unary minus are allowed before a number or left parenthesis, so -2--3 is legal but --2 and -2---3 are not.exp →exp addop term | termaddop →+ | -term → term mulop factor| factormulop →*factor →( exp) | -(exp) | number | -numberc. Arbitrarily many unary minuses are allowed before numbers and left parentheses, so everything above is legal.3.19 In some languages ( Modula-2 and Ada are examples), a procedure declaration is expected to be terminated by syntax that includes the name of the procedure. For example, in Modular-2 a procedure is declared as follows:PROCEDURE P;BEGIN……END P;Note the use of the procedure name P alter the closing END. Can such a requirement be checked by a parser? Explain.[Answer]This requirement can not be handled as part of the grammar without making a new rule for each legal variable name, which makes it intractable for all practical purposes, even if variable names are restricted to a very short length. The parser will just check the structure, that an identifier follows the keyword PROCEDURE and an identifier also follows the keyword END, however checking that it is the same identifier is left for semantic analysis. See the discussion on pages 131-132 of your text.3.20 a. Write a regular expression that generate the same language as the following grammar:A→aA|B|εB→bB|Ab. Write a grammar that generates the same language as the following regularexpression:(a|c|ba|bc)*(b|ε)[Solution]a. The regular expression:(a|b)*b. The grammar:Step 1:A→BCB→aB|cB|baB|bcB|εC→b|εStep 2:A→Bb|BB→aB|cB|baB|bcB|ε。
习题参考答案-编译原理及实践教程(第3版)-黄贤英-清华大学出版社

附录部分习题参考答案第1章习题1. 解释下列术语。
翻译程序,编译程序,解释程序,源程序,目标程序,遍,前端,后端解答:略!2. 高级语言程序有哪两种执行方式?阐述其主要异同点。
描述编译方式执行程序的过程。
解答:略!3. 在你所使用的C语言编译器中,观察程序1.1经过预处理、编译、汇编、链接四个过程生成的中间结果。
解答:略!4. 编译程序有哪些主要构成成分?各自的主要功能是什么?解答:略!5. 编译程序的构造需要掌握哪些原理和技术?编译程序构造工具的作用是什么?解答:略!6. 复习C语言,其字母表中有哪些符号?有哪些关键字、运算符和界符?标识符、整数和实数的构成规则是怎样的?各种语句和表达式的结构是什么样的?解答:略!7.编译技术可应用在哪些领域?解答:略!8. 你能解释在Java编译器中,输入某个符号后会提示一些单词、某些单词会变为不同的颜色是如何实现的吗?你能解释在Code Blocks中在输入{后,会自动添加},输入do 会自动添加while()是为什么吗?解答:略!第2章习题1. 判断题,对下面的陈述,正确的在陈述后的括号内画√,否则画×。
(1) 有穷自动机识别的语言是正规语言。
()(2) 若r1和r2是Σ上的正则表达式,则r1|r2也是。
()(3) 设M是一个NFA,并且L(M)={x,y,z},则M的状态数至少为4个。
()(4) 令Σ={a,b},则所有以b开头的字构成的正规集的正则表达式为b*(a|b)*。
()(5) 对任何一个NFA M,都存在一个DFA M',使得L(M')=L(M)。
()1解答:略!2.从供选择的答案中,选出应填入下面叙述中?内的最确切的解答。
有穷自动机可用五元组(Q,V T,δ,q0,Q f)来描述,设有一有穷自动机M定义如下:V T={0,1},Q={q0,q1,q2},Q f={q2},δ的定义为:δ (q0,0)=q1δ (q1,0)=q2δ (q2,1)=q2δ (q2,0)=q2M是一个 A 有穷状态自动机,它所对应的状态转换图为 B ,它所能接受的语言可以用正则表达式表示为 C 。
编译原理教程课后习题答案

编译原理教程课后习题答案【篇一:编译原理教程课后习题答案——第一章】完成下列选择题:(1) 构造编译程序应掌握a. 源程序b. 目标语言c. 编译方法d. 以上三项都是(2) 编译程序绝大多数时间花在上。
a. 出错处理b. 词法分析c. 目标代码生成d. 表格管理(3) 编译程序是对。
a. 汇编程序的翻译b. 高级语言程序的解释执行c. 机器语言的执行d. 高级语言的翻译【解答】(1) d (2) d(3) d1.2 计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?【解答】计算机执行用高级语言编写的程序主要有两种途径:解释和编译。
在解释方式下,翻译程序事先并不采用将高级语言程序全部翻译成机器代码程序,然后执行这个机器代码程序的方法,而是每读入一条源程序的语句,就将其解释(翻译)成对应其功能的机器代码语句串并执行,而所翻译的机器代码语句串在该语句执行后并不保留,最后再读入下一条源程序语句,并解释执行。
这种方法是按源程序中语句的动态执行顺序逐句解释(翻译)执行的,如果一语句处于一循环体中,则每次循环执行到该语句时,都要将其翻译成机器代码后再执行。
在编译方式下,高级语言程序的执行是分两步进行的:第一步首先将高级语言程序全部翻译成机器代码程序,第二步才是执行这个机器代码程序。
因此,编译对源程序的处理是先翻译,后执行。
从执行速度上看,编译型的高级语言比解释型的高级语言要快,但解释方式下的人机界面比编译型好,便于程序调试。
这两种途径的主要区别在于:解释方式下不生成目标代码程序,而编译方式下生成目标代码程序。
1.3 请画出编译程序的总框图。
如果你是一个编译程序的总设计师,设计编译程序时应当考虑哪些问题?【解答】编译程序总框图如图1-1所示。
作为一个编译程序的总设计师,首先要深刻理解被编译的源语言其语法及语义;其次,要充分掌握目标指令的功能及特点,如果目标语言是机器指令,还要搞清楚机器的硬件结构以及操作系统的功能;第三,对编译的方法及使用的软件工具也必须准确化。
编译原理习题与答案共61页

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
Thank you
பைடு நூலகம்
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
编译原理课后作业参考答案

作业参考答案第二章 高级语言及其语法描述6、(1)L (G 6)={0,1,2,......,9}+(2)最左推导:N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127 N=>ND=>DD=>3D=>34N=>ND=>NDD=>DDD=>5DD=>56D=>568 最右推导:N=>ND =>N7=>ND7=>N27=>ND27=>N127=>D127=>0127 N=>ND=>N4=>D4=>34N=>ND=>N8=>ND8=>N68=>D68=>568 7、G:S →ABC | AC | CA →1|2|3|4|5|6|7|8|9B →BB|0|1|2|3|4|5|6|7|8|9C →1|3|5|7|98、(1)最左推导:E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*iE=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F)=>i*(i+i) 最右推导:E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*iE=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i)=>F*(i+i)=>i*(i+i) (2)9、证明:该文法存在一个句子iiiei 有两棵不同语法分析树,如下所示,因此该文法是二义的。
编译原理与实践 第二章 答案

The exercises of Chapter Two2.1 Write regular expression for the following character sets, or give reasons why no regular expression can be written:a. All strings of lowercase letters that begin and end in a. [Solution]a[a-z]*a | ab. All strings of lowercase letters that either begin or end in a ( or both)both: a(a|b|c|…|z)* ac. All strings of digits that contain no leading zeros[Solution][1-9][0-9]*d. All strings of digits that represent even numbers(0|1|2|…|9)*(0|2|4|6|8)e. All strings of digits such that all the 2’s occur before all the 9’s [Solution]a=(0|1|3|4|5|6|7|8)r=(2|a)*(9|a)or[^9]*[^2]*or[^9]*2(1|[3-8])*9[^2]*g. All strings of a’s and b’s that contain an odd number of a’s or an odd number of b’s(or both)[Solution]r1=b*a(b|ab*a)*--------odd number of a’sr2= a*b(a|ba*b)*-------odd number of b’sr1|r2|r1r2|r2r1orb*a(b*ab*a)*b*|a*b(a*ba*b)*a*i. All strings of a’s and b’s that contain exactly as many a’s as b’s [Solution]No regular expression can be written, as regular expression can not count.2.2 Write English descriptions for the languages generated by the following regular expressions:a. (a|b)*a(a|b|ε)[Solution]All the strings of a’s and b’s that end with a, ab or aa.OrAll the strings of a’s and b’s th at do not end with bb.b. All words in the English alphabet of one or more letters, which start with one capital letter and don’t contain any other capital letters.c. (aa|b)*(a|bb)*[Solution]All the strings of a’s and b’s that can be divided into two s ub-stings, where in the left substring, the even number of consecutive a’s are separated by b’s while in the right substring, the even number of consecutive b’ are separated by a’s.d. All hexadecimal numbers of length one or more, using the numbers zero through nine and capital letters A through F, and they are denoted with a lower or uppercase “x” at the end of the number string.2.12 a. Use Thompson’s construction to convert the regular expression (a|b)*a(a|b|ε) into an NFA.b. Convert the NFA of part (a) into a DFA using the subset construction.[Solution]a.b. The subsets constructed as follows:{ 7 } = { 7, 5,1,3,8,9}{ 7 }a = {2, 10}{ 7 }b= {4}{2,10} = {2,6,5,1,3,8,9, 10,17,11,13,15,16,18}{2,10}a = {2, 10, 12} {2,10}b ={4, 14}{2,10,12} = {2,6,5,1,3,8,9,12,18,10,17,11,13,15,16} {2,10,12}a = {2,10,12} {2,10,12}b = {4, 14}{4,14} = {4,6,5,1,3,8,9,14,18} {4,14}a = {2,10} {4,14}b = {4}{4} = {4,6,5,1,3,8,9} {4}a ={2,10} {4}b={4}2.15Assume we have r* and s* according to figure 1 and 2:Consider r*s* as followThis accepts, for example, rsrs which is not in r*s*. I. e., in this case we cannot eliminatethe concatenating ε transition.2.16 Apply the state minimization algorithm of section 2.4.4 to the following DFAs: a.aFigure 2 s*Figure 2 r*s*[Solution]a.Step 1: Divide the state set into two subsets:{1, 2, 3}{4, 5}Step 2: Further divide the subset {1,2,3} into two new subsets:{1}{2, 3}Step 3: Can not divide the subsets any more, finally obtains three subsets: {1}{2, 3}{4, 5}Therefore, the minimized DFA is:[Solution]b. Step 1: Divide the state set into two subsets:{1, 2}{3, 4, 5}Step 2: Further divide the subset {1,2} into two new subsets:{1}{2}Step 2: Further divide the subset {3,4,5} into two new subsets:{3}{4, 5}Step 4: Can not divide the subsets any more, finally obtains three subsets: {1}{2}{ 3}{4, 5}Therefore, the minimized DFA is:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业题:
2.1(a,c,d), 2.8(a,c,d), 2.12,
3.3, 3.4,
4.8, 4.12
5.8(a,b,c), 5.12,
6.7, 6.8, 6.13
7.4, 7.15
第二章作业: 2.1 (a) a | a[a-z]*a
(c) [1-9][0-9]* (d) [0-9]*[02468]
2.8(a )
正则表达式中丢了单独a 的情况的比较多,另外有些同学在有NFA 到DFA 的转化过程
中,不能够正确的确定最终的状态,造成有两个终结状态的情况。
(c )
(d )
问题比较多,建议同学画出DFA 图生成的全部过程。
Start
[1-9]
Start
a
a [b-z] a [b-z]
2.12
3.4
(c ).rewrite this grammar to establish the correct precedences for the operator.
rexp -> rexp “|” rexp1 | rexp1 rexp1 -> rexp1 rexp2 | rexp2 rexp2 -> rexp3 * | rexp3 rexp3 -> (rexp) | letter 左结合 4.8
(a ) 消除左递归
lexp -> atom | list atom -> number | identifier list -> (lexp-seq) lexp-seq -> lexp lexp-seq’ lexp-seq’ -> lexp lexp-seq’ | ε
first (lexp)= { number ,identifier,( } first (atom)= { number, identifier } first (list) = { ( }
first (lexp-seq)= { number ,identifier,( } first (lexp-seq’)= { number ,identifier,( , ε}
follow(lexp)= { $,),number,identifier,(}
follow (atom)= { $,), number,identifier,( }
follow (list) = {$,), number,identifier,(}
follow (lexp-seq)= { )}
follow (lexp-seq’)= { )}
4.12
(a)LL(1)文法不会是二义的,因为它的分析表的每个入口是唯一的。
就不会是二义文法
了。
(b)二义文法也不可能是LL(1)的,否则在LL(1)的parsing table 中会产生各种冲突。
非二义的文法不一定是LL(1)的,因为二义文法是非LL(1)文法的一个因素,但不是唯一的因素。
如一些带有左递归的文法也不是LL(1)文法。
第五章作业
5.12
s’ →s
s→a A d | b B d | a B e | b A e
5.8 Consider the following grammar
declaration -> type var-list
type -> int | float
var-list -> identifier, var-list | identifier
(a) declaration -> type var-list
type -> int | float
var-list -> var-list, identifier | identifier
(b) decl -> type vlist
type -> int
type ->float
vlist -> vlist, id vlist -> id
1
3
5 follow(decl)= { $ }, follow(type)= { id } follow(vlist)= { $, , }
(c ) construct the SLR(1) parsing table for the rewritten grammar 6.7
decl → var-list: type var-list.dtype = type.dtype
vsr-list11 → var-list2, id var-list2.dtype = var-list1.dtype
id.dtype = var-list1.dtype
type → integer type.dtype = int
type → real type.dtype = float
6.8
decl → id var-list id.dtype = var-list.dtype
var-list1 → , id var-list2 var-list1.dtype = var-list2.dtype
id.dtype = var-list2.dtype
var-list → : type var-list.dtype = type.dtype
type →integer type.dtype = int
type → real type.dtype = float
6.13 Solution:
a.
One correct order can be:
C.v = 1
B.u = S.u
B.v = B.u
A.u =
B.v +
C.v
A.v = 2 * A.u
S.v = A.v
b.
8.
c.
The value is not calculable due to the circularity of the dependency graph. The value of C.u depends on that of A.v, which in turn depends on that of A.u, which in its own turn depends on C.v, which finally depends on that of C.u, which is to be decided by the calculation.
6.13s.v = -2, 存在环,不是一个拓扑排序。
7.4 main procedure
a
b procedure
7.15
A、1,1
B、3,1
C、2,1
D、2,2。
