LZW编码算法matlab实现
数据压缩算法LZLZ和LZW的原理与实现

数据压缩算法LZLZ和LZW的原理与实现在计算机科学领域,数据压缩算法是一种用于减小数据文件大小的方法。
其中,LZLZ和LZW是两种常见的数据压缩算法。
本文将详细介绍这两种算法的原理和实现。
一、LZLZ算法LZLZ算法是一种基于字典的数据压缩算法。
该算法的原理是将连续出现的重复字符序列替换为较短的标记。
具体实现过程如下:1. 初始化字典,将所有可能的字符序列添加到字典中。
2. 从输入数据中读取字符序列,并查找字典中是否存在相同的序列。
3. 如果找到匹配的序列,则将其替换为字典中对应的标记,并将序列长度增加1。
4. 如果未找到匹配的序列,则将当前字符添加到字典中,并输出该字符。
5. 重复步骤2至4,直到处理完所有输入数据。
通过将重复的序列替换为较短的标记,LZLZ算法可以有效地减小数据文件的大小。
二、LZW算法LZW算法也是一种基于字典的数据压缩算法,与LZLZ算法类似,但存在一些差异。
下面是LZW算法的原理和实现过程:1. 初始化字典,将所有可能的单字符添加到字典中。
2. 从输入数据中读取字符序列,并根据当前已读的序列来搜索字典。
3. 如果找到匹配的序列,则将已读的序列继续扩展一个字符,并重复步骤2。
4. 如果未找到匹配的序列,则将字典中最长的已读序列对应的标记输出,并将已读的序列和下一个字符添加到字典中。
5. 重复步骤2至4,直到处理完所有输入数据。
LZW算法通过动态扩展字典,可以更好地利用数据的重复性。
相比于LZLZ算法,LZW算法通常能够达到更高的压缩率。
三、LZLZ和LZW的比较LZLZ算法和LZW算法在原理上有相似之处,都是通过字典来实现数据压缩。
然而,两者之间存在一些差异。
首先,LZLZ算法使用固定长度的标记,这使得算法相对简单,但可能导致压缩率较低。
与之相反,LZW算法可以根据需要动态扩展字典,以适应不同类型的数据,从而获得更高的压缩率。
其次,LZLZ算法的字典只包含单个字符和字串,而LZW算法的字典可以包含任意长度的序列。
霍夫曼编码的MATLAB实现(完整版)说课材料

霍夫曼编码的M A T L A B 实现(完整版)%哈夫曼编码的MATLAB实现(基于0、1编码):clc;clear;A=[0.3,0.2,0.1,0.2,0.2];信源消息的概率序列A=fliplr(sort(A));%按降序排列T=A;[m,n]=size(A);B=zeros(n,n-1);%空的编码表(矩阵)for i=1:nB(i,1)=T(i);%生成编码表的第一列endr=B(i,1)+B(i-1,1);%最后两个元素相加T(n-1)=r;T(n)=0;T=fliplr(sort(T));t=n-1;for j=2:n-1%生成编码表的其他各列for i=1:tB(i,j)=T(i);endK=find(T==r);B(n,j)=K(end);%从第二列开始,每列的最后一个元素记录特征元素在%该列的位置r=(B(t-1,j)+B(t,j));%最后两个元素相加T(t-1)=r;T(t)=0;T=fliplr(sort(T));t=t-1;endB;%输出编码表END1=sym('[0,1]');%给最后一列的元素编码END=END1;t=3;d=1;for j=n-2:-1:1%从倒数第二列开始依次对各列元素编码for i=1:t-2if i>1 & B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));END(i)=END1(x(d));endy=B(n,j+1);END(t-1)=[char(END1(y)),'0']; END(t)=[char(END1(y)),'1']; t=t+1;END1=END;endA%排序后的原概率序列END%编码结果for i=1:n[a,b]=size(char(END(i)));L(i)=b;endavlen=sum(L.*A)%平均码长H1=log2(A);H=-A*(H1')%熵P=H/avlen%编码效率。
利用Matlab进行数据压缩与加密技术详解

利用Matlab进行数据压缩与加密技术详解在当今科技快速发展的时代,数据压缩与加密技术日趋重要。
随着数字化时代的到来,数据的产生与传输量不断增加,如何高效地存储和传输数据成为了一个亟待解决的问题。
同时,随着信息安全威胁的不断增加,数据加密也成为了保护信息安全的重要手段之一。
在这样的背景下,Matlab作为一个强大的数学计算工具,提供了丰富的数据压缩与加密函数,成为了研究和实践者们的首选。
1. 数据压缩技术数据压缩技术是将大容量的数据通过一定的算法和方法进行转换和编码,以减少所占用的存储空间或传输带宽。
Matlab提供了多种数据压缩的方法和函数。
1.1 无损压缩无损压缩是一种将原始数据转化为压缩文件,但在解压缩时恢复得到与原始数据完全一样的数据的压缩技术。
Matlab中常用的无损压缩方法有哈夫曼编码和Lempel-Ziv-Welch(LZW)算法。
哈夫曼编码是一种用于数据压缩的算法,通过构建霍夫曼树将较高频率的字符用较短的二进制编码表示,而将较低频率的字符用较长的二进制编码表示,从而实现对数据的压缩。
在Matlab中,可以使用`huffmandict`函数生成霍夫曼编码字典,并使用`huffmanenco`和`huffmandeco`函数进行编码和解码。
LZW算法是一种以词典为基础的无损压缩算法,利用词典来对数据进行压缩和解压缩。
在Matlab中,可以使用`lzwenco`和`lzwdeco`函数实现LZW算法的编码和解码。
1.2 有损压缩有损压缩是指在压缩数据的过程中,丢弃部分数据的精确信息,从而得到一个对原始数据的近似表示。
有损压缩可以显著减小数据的存储空间和传输带宽,但也会引入一定的失真。
Matlab提供了多种有损压缩方法和函数,如离散余弦变换(DCT)、小波变换(Wavelet Transform)等。
DCT技术是一种常用的图像压缩方法,它通过将图像划分为非重叠的小块,然后对每个小块进行变换来减少冗余信息。
LZW编码算法matlab实现

LZW编码算法,尝试使用matlab计算%encoder LZW for matlab%yu 20170503clc;clear;close all;%初始字典dic = cell(512,1);for i = 1:256dic{i} = {num2str(i)};end%输入字符串a,按空格拆分成A,注意加1对应范围1~256 a = input('input:','s');a = deblank(a);A = regexp(a,'\s+','split');L = length(A);for j=1:LA{j} = num2str(str2num(A{j})+1);endA_t = A{1};%可识别序列B_t = 'test';%待验证词条d = 256;%字典指针b = 1;%输出指针B = cell(L,1);%输出初始output = ' ';%输出初始j=1;for j = 2:Lm=1;B_t =deblank([A_t,' ',A{j}]);%合成待验证词条while(m <= d)if strcmp(dic{m},B_t)A_t = B_t;breakelsem=m+1;endendwhile(m == d+1)d = d+1;dic{d} = B_t;q=1;for q=1:dif strcmp(dic{q},A_t)B{b} = num2str(q);b = b+1;endendA_t = A{j};endendfor q=1:d%处理最后一个序列输出if strcmp(dic{q},A_t)B{b} = num2str(q);b = b+1;endendfor n = 1:(b-1)B{n} =num2str(str2num(B{n})-1);output=deblank([output,' ',B{n}]);endoutput运算结果计算结果为39 39 126 126 256 258 260 259 257 126LZW解码算法,使用matlab计算%decoder LZW for matlab%yu 20170503clc;clear;close all;%初始字典dic = cell(512,1);for i = 1:256dic{i} = {num2str(i)};end%输入字符串a,按空格拆分成A,注意加1对应范围1~256 a = input('input:','s');a = deblank(a);A = regexp(a,'\s+','split');L = length(A);for j=1:LA{j} = num2str(str2num(A{j})+1);endB_t = A{1};%待验证词条d = 256;%字典指针b = 1;%输出指针B = cell(L,1);%输出初始output = ' ';%输出初始j=1;B{b} = char(dic{str2num(A{j})});b = b+1;for j = 2:LBB = char(dic{str2num(A{j})});B_d = regexp(BB,'\s+','split');%按空格拆分L_B = length(B_d);p=1;for p=1:L_BB{(b+p-1)} = B_d{p};m=1;B_t =deblank([char(B_t),' ',char(B_d{p})]);%合成待验证词条while(m <= d)if strcmp(dic{m},B_t)B_t = B_t;breakelsem=m+1;endendwhile(m == d+1)d = d+1;dic{d} = B_t;B_t = B_d{p};endendb = b+L_B;endfor n = 1:(b-L_B)B{n} = num2str(str2num(B{n})-1);output=deblank([output,' ',B{n}]); endoutput运算结果运算结果为39 39 126 126 39 39 126 126 39 39 126 126 39 39 126 126。
LZW编码与译码编程实现
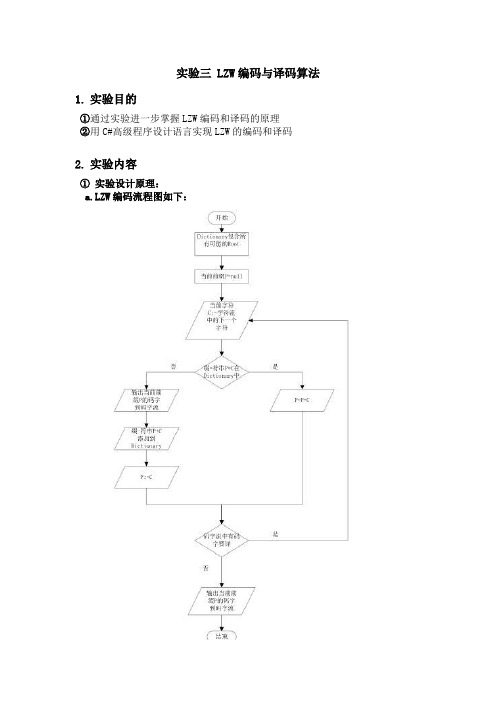
实验三 LZW编码与译码算法1.实验目的①通过实验进一步掌握LZW编码和译码的原理②用C#高级程序设计语言实现LZW的编码和译码2.实验内容①实验设计原理:a.LZW编码流程图如下:b.LZW译码流程图如下:②实验源代码:using System;using System.Collections.Generic; using System.Linq;using System.Text;using System.Threading.Tasks;namespace LZW{class Program{static void Main(string[] args){Encode();//编码Decode();//译码}public static void Encode()//编码函数{string Input = "ABBABABAC";//需要编码的字符流Console.WriteLine("编码前字符流:{0}",Input);Console.WriteLine();string P = null;//当前前缀P为空string X = null;int i = 0, j = 0, m = 3, n = 4, h = 0;string C = null;//当前字符Cstring[,] Dictionary=new string [9,2];//定义词典//词典初始化Dictionary[0,0]="1";Dictionary[0,1]="A";Dictionary[1,0]="2";Dictionary[1,1]="B";Dictionary[2,0]="3";Dictionary[2,1]="C";//LZW算法编码Console.Write("编码后码字流:");while (h<9){C = Input.ToCharArray()[h].ToString();X = P + C;for (i = 0; i < 9; i++){if (X.Equals(Dictionary[i, 1]))//缀-符串P+C在词典中{P = P + C;//P:=P+Cbreak;}}j = i;if (j >= 9)//缀-符串P+C不在词典中{for (i = 0; i < 9; i++){if (P.Equals(Dictionary[i, 1])){Console.Write(Dictionary[i, 0]);//把代表当前前缀P的码字输出到码字流Console.Write(" ");}}Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//把缀-符串P+C添加到词典P = C;//P:=Cm++;n++;}i = 0;j = 0;h++;}for (i = 0; i < 9; i++)//码字流中无码字要译{if (P.Equals(Dictionary[i, 1])){Console.Write(Dictionary[i, 0]);//把代表当前前缀P的码字输出到码字流Console.Write(" ");}}//输出DictionaryConsole.WriteLine();Console.WriteLine();Console.WriteLine("Dictionary如下:");for (i = 0; i < 9; i++, Console.WriteLine()){for (j = 0; j < 2; j++){Console.Write(Dictionary[i, j]);Console.Write(" ");}}}public static void Decode()//译码函数{string Output = "122473";//码字流string cW = null;//当前码字string pW = null;//先前码字string P = null;//当前前缀string C = null;//当前字符int i = 0, j = 0, h = 1, m = 3, n = 4;string[,] Dictionary = new string[20, 2];//定义词典//词典初始化Dictionary[0, 0] = "1";Dictionary[0, 1] = "A";Dictionary[1, 0] = "2";Dictionary[1, 1] = "B";Dictionary[2, 0] = "3";Dictionary[2, 1] = "C";Console.Write("解码后字符流:");cW = Output.ToCharArray()[0].ToString();//当前码字cW=码字流中的第一个码字Console.Write(Dictionary[int.Parse(cW) - 1, 1]);//输出当前缀-符串string.cW到字符流Console.Write(" ");while (h < 6){pW = cW;//先前码字=当前码字cW = Output.ToCharArray()[h].ToString();//当前码字递增for (i = 0; i < 9; i++){try{if (Dictionary[int.Parse(cW) - 1, 1].Equals(Dictionary[i, 1]))//当前缀-符串string.cW在词典中{Console.Write(Dictionary[int.Parse(cW) - 1, 1]);//当前缀-符串string.cW 输出到字符流Console.Write(" ");P = Dictionary[int.Parse(pW) - 1, 1];//当前前缀P:=先前缀-符串string.pWC = Dictionary[int.Parse(cW) - 1, 1].ToCharArray()[0].ToString();//当前字符C:=当前缀-符串string.cW的第一个字符Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//把缀-符串P+C添加到词典m++;n++;break;}}catch{continue;}}j = i;if (j >= 9)//当前缀-符串string.cW不在词典中{P = Dictionary[int.Parse(pW) - 1, 1];//当前前缀P:=先前缀-符串string.pWC = Dictionary[int.Parse(pW) - 1, 1].ToCharArray()[0].ToString();//当前字符C:=先前缀-符串string.pW的第一个字符Console.Write(P + C);//输出缀-符串P+C到字符流Console.Write(" ");Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//将缀-符串P+C添加到词典中m++;n++;}h++;i = 0;j = 0;}Console.WriteLine();Console.WriteLine();Console.WriteLine("Dictionary如下:");//输出词典for (i = 0; i < 9; i++,Console.WriteLine()){for (j = 0; j < 2; j++){Console.Write(Dictionary[i,j]);Console.Write(" ");}}}}}3.实验结果(截图)及分析①实验结果:②结果分析:由①中的实验结果可以看出,此次实验成功地对字符流ABBABABAC进行了编码和译码,并且在编码和译码过程中分别生成的Dictionary完全一致。
matlab 霍夫曼编码解析

matlab 霍夫曼编码解析【知乎文章】1. 概述霍夫曼编码是一种广泛应用于数据压缩领域的编码算法,由大卫·霍夫曼于1952年提出。
该编码方法通过对出现频率较高的字符赋予较短的编码,提高了数据的压缩率。
在本文中,我将详细介绍霍夫曼编码的原理和实现过程,并探讨其在Matlab中的应用。
2. 霍夫曼编码原理2.1 符号频率统计在进行霍夫曼编码之前,首先需要统计待编码字符的出现频率。
这可以通过计算每个字符在信源中的出现次数来实现。
2.2 构建霍夫曼树在统计得到每个字符的频率后,接下来需要构建一棵霍夫曼树。
霍夫曼树是一种特殊的二叉树,它的每个叶子节点都对应一个字符,并且每个节点的权重等于其左右子树权重之和。
构建霍夫曼树的方法通常采用贪心算法,即每次选择权重最小的两个节点合并。
2.3 生成霍夫曼编码在得到霍夫曼树后,可以通过从根节点遍历到叶子节点的路径上的每一次分支决策,赋予相应的编码。
这样,每个字符就对应一个唯一的霍夫曼编码。
3. Matlab实现在Matlab中,可以通过以下步骤实现霍夫曼编码的解析:3.1 构建霍夫曼树利用Matlab中的数据结构——二叉树,可以方便地构建霍夫曼树。
根据字符频率的统计结果,创建叶子节点。
每次选择频率最小的两个节点合并为一个新节点,并将其作为新的叶子节点插入树中。
重复这个过程直到只剩下一个节点,即为根节点。
3.2 生成霍夫曼编码在构建好霍夫曼树后,可以通过从根节点遍历到叶子节点的路径上的每一次分支决策,生成霍夫曼编码。
这可以通过递归遍历二叉树实现,每次遍历左子树时添加'0',每次遍历右子树时添加'1'。
4. 观点和理解霍夫曼编码作为一种高效的数据压缩算法,在实际应用中有着广泛的应用。
通过赋予频率较高的字符较短的编码,可以在保证信息完整性的前提下大幅减小数据的存储空间。
Matlab作为一种功能强大的数据分析和处理工具,在霍夫曼编码的实现上也提供了便捷的方法。
Matlab中的数据压缩与图像编码方法

Matlab中的数据压缩与图像编码方法引言在当今数码时代,数据的传输和存储已经成为人们生活中不可或缺的一部分。
然而,随着数据量的不断增长,传输和存储的需要也变得越来越庞大。
为了解决这一问题,数据压缩和图像编码方法被广泛应用于各种领域。
本文将介绍一些在Matlab中实现数据压缩和图像编码的常用方法。
一、数据压缩1. 频谱压缩频谱压缩是一种将信号的频谱范围压缩到较小范围的方法。
在Matlab中,可以使用FFT(快速傅里叶变换)和IFFT(逆快速傅里叶变换)函数来实现频谱压缩。
首先,通过FFT将信号转换成频域表示,然后对频域信号进行一定的处理,例如减小高频分量的权重,最后通过IFFT将信号转换回时域表示。
这样就可以实现信号的频谱压缩,减小信号的数据量。
2. 基于哈夫曼编码的数据压缩哈夫曼编码是一种基于变长编码的压缩方法,它通过使用较短的编码表示出现频率较高的符号,而使用较长的编码表示出现频率较低的符号。
在Matlab中,可以使用`huffmandict`函数创建哈夫曼字典,然后使用`huffmanenco`函数对数据进行编码,使用`huffmandeco`函数对数据进行解码。
这样就可以实现基于哈夫曼编码的数据压缩。
3. 无损压缩与有损压缩无损压缩是一种保持数据完整性的压缩方法,它通过使用编码和解码技术来减小数据的存储和传输需求,同时保持数据的完整性。
在Matlab中,可以使用无损压缩算法,如Lempel-Ziv-Welch(LZW)算法和Run Length Encoding(RLE)算法,来实现无损压缩。
有损压缩是一种通过牺牲数据的一部分信息来实现更高压缩比的压缩方法。
在Matlab中,可以使用一些常见的有损压缩算法,如JPEG压缩算法和GIF压缩算法。
这些算法通常将图像划分为多个块,并对每个块应用离散余弦变换(Discrete Cosine Transform,DCT)或离散小波变换(Discrete Wavelet Transform,DWT)。
MATLAB中的图像压缩和编码方法

MATLAB中的图像压缩和编码方法图像压缩和编码是数字图像处理的重要领域,在各种图像应用中起着至关重要的作用。
在本文中,我们将探讨MATLAB中的图像压缩和编码方法,包括无损压缩和有损压缩,并介绍其中的一些经典算法和技术。
一、图像压缩和编码概述图像压缩是指通过一定的算法和技术来减少图像数据的存储量或传输带宽,以达到节约存储空间和提高传输效率的目的。
而图像编码则是将原始图像数据转换为一系列二进制编码的过程,以便存储或传输。
图像压缩和编码通常可以分为无损压缩和有损压缩两种方法。
无损压缩是指压缩后的数据可以完全还原为原始图像数据,不会引入任何失真或变化。
常见的无损压缩算法有Run-Length Encoding (RLE)、Lempel-Ziv-Welch (LZW)、Huffman编码等。
这些算法通常针对图像中的冗余数据进行编码,如重复的像素值或相似的图像区域。
有损压缩则是在保证一定程度的视觉质量下,通过舍弃或近似原始图像数据来减小存储或传输的数据量。
常见的有损压缩算法有JPEG、JPEG2000、GIF等。
这些算法通过离散余弦变换(DCT)、小波变换或颜色量化等方法,将图像数据转换为频域或颜色空间的系数,并通过量化、编码和压缩等步骤来减小数据量。
二、无损压缩方法1. Run-Length Encoding (RLE)RLE是一种简单高效的无损压缩算法,通过计算连续重复像素值的数量来减小数据量。
在MATLAB中,可以使用`rle`函数实现RLE编码和解码。
例如,对于一幅图像,可以将连续的像素值(如白色)编码为重复的个数,然后在解码时根据重复的个数恢复原始像素值。
2. Lempel-Ziv-Welch (LZW)LZW是一种字典压缩算法,通过将图像中连续的像素序列映射为一个短代码来减小数据量。
在MATLAB中,可以使用`lzwencode`和`lzwdecode`函数实现LZW 编码和解码。
例如,对于一段连续的像素序列,可以将其映射为一个短代码,然后在解码时根据代码恢复原始像素序列。
Matlab函数实现哈夫曼编码算法

编写Matlab函数实现哈夫曼编码的算法一、设计目的和意义在当今信息化时代,数字信号充斥着各个角落。
在数字信号的处理和传输中,信源编码是首先遇到的问题,一个信源编码的好坏优劣直接影响到了后面的处理和传输。
如何无失真地编码,如何使编码的效率最高,成为了大家研究的对象。
哈夫曼编码就是其中的一种,哈夫曼编码是一种变长的编码方案。
它由最优二叉树既哈夫曼树得到编码,码元内容为到根结点的路径中与父结点的左右子树的标识。
所以哈夫曼在编码在数字通信中有着重要的意义。
可以根据信源符号的使用概率的高低来确定码元的长度。
既实现了信源的无失真地编码,又使得编码的效率最高。
二、设计原理哈夫曼编码(Huffman Coding)是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。
uffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫作Huffman编码。
而哈夫曼编码的第一步工作就是构造哈夫曼树。
哈夫曼二叉树的构造方法原则如下,假设有n个权值,则构造出的哈夫曼树有n个叶子结点。
n 个权值分别设为w1、w2、…、wn,则哈夫曼树的构造规则为:(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加入森林;(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
具体过程如下图1产所示:(例)图1 哈夫曼树构建过程哈夫曼树构造成功后,就可以根据哈夫曼树对信源符号进行哈夫曼编码。
具体过程为先找到要编码符号在哈夫曼树中的位置,然后求该叶子节点到根节点的路径,其中节点的左孩子路径标识为0,右孩子路径标识为1,最后的表示路径的01编码既为该符号的哈夫曼编码。
利用Matlab进行数据压缩与解压缩

利用Matlab进行数据压缩与解压缩数据压缩与解压缩是信息技术领域中一项重要的工作,它可以帮助我们减少数据的存储空间和传输带宽,提高数据的传输速度和存储效率。
而Matlab作为一种功能强大的数学软件,也提供了多种方法和工具来进行数据压缩与解压缩的操作。
本文将介绍如何利用Matlab进行数据压缩与解压缩的过程,并探讨一些常用的压缩算法与技术。
一、数据压缩的概念与重要性数据压缩是将原始数据通过一定的算法和技术,使得压缩后的数据在占用存储空间或者传输带宽上减少,但保持原始数据的一些重要特征。
数据压缩有着广泛的应用场景,比如在图像和视频处理中,我们经常需要对大量的图像和视频数据进行传输和存储,若能将这些数据压缩后再传输和存储,就能大大提高传输效率和节省存储空间。
二、Matlab的数据压缩与解压缩函数Matlab提供了多种数据压缩与解压缩的函数和工具箱,其中最常见的有gzip、zlib、zip等函数。
gzip函数可以将一个或多个文件压缩成一个gzip格式的文件,zlib函数可以将一个或多个文件压缩成一个zlib格式的文件,zip函数则可以将一个或多个文件压缩成一个zip格式的文件。
这些函数的使用方法非常简单,只需传入待压缩文件的路径和压缩文件的路径即可进行压缩和解压缩。
三、常用的数据压缩算法1. 哈夫曼编码哈夫曼编码是一种可变字长编码技术,它根据每个符号(或字符)出现的概率来赋予该符号的编码,出现概率高的符号会被赋予较短的编码,出现概率低的符号会被赋予较长的编码。
在Matlab中,可以使用huffmandict函数生成哈夫曼编码的字典,使用huffmanenco函数对数据进行编码,使用huffmandeco函数对数据进行解码。
2. Lempel-Ziv-Welch(LZW)算法LZW算法是一种基于词典的无损压缩算法,它的主要思想是将连续出现的字符序列映射为一个索引,并将该索引存储起来,从而达到压缩数据的目的。
matlab decode的 实现原理

matlab decode的实现原理摘要:MATLAB解码是一种在MATLAB环境中实现解码功能的方法。
本文将介绍MATLAB解码的实现原理,包括编码和解码过程的关键步骤和原理。
一、引言MATLAB是一种广泛应用于科学计算和数据可视化的编程语言。
通过使用MATLAB解码功能,用户可以将经过编码的数据还原为原始形式。
本文将详细介绍MATLAB解码的实现原理,包括编码和解码过程的关键步骤和原理。
二、编码过程1. 数据压缩在编码过程中,数据首先需要进行压缩。
压缩可以通过不同的算法实现,如LZW、Huffman等。
这些算法可以将原始数据压缩为较小的数据流,以便于存储和传输。
2. 数据编码压缩后的数据需要通过特定的编码方法转换为可以由MATLAB解码的格式。
这种编码方法通常包括将压缩数据分割为特定长度的数据块,并为每个数据块分配一个标识符。
这些标识符可以作为解码过程的输入。
三、解码过程1. 数据解压缩在解码过程中,首先需要对编码后的数据进行解压缩。
解压缩是通过使用与编码过程中相同的压缩算法来实现的。
解压缩后的数据将接近原始数据的形式。
2. 数据解码解压缩后的数据需要通过特定的解码方法还原为原始数据。
这种解码方法通常包括将编码后的数据块与对应的标识符进行匹配,从而恢复原始数据的结构。
四、MATLAB解码实现在MATLAB中,可以使用内置的函数来实现解码功能。
这些函数通常提供了一种简单的方法来处理编码后的数据,并返回原始数据的结构。
以下是一个简单的示例:```matlab```% 假设我们有一个经过编码的数据文件data.enc```% 使用decompress函数进行解压缩decompressed_data = decompress('data.enc');```然后,可以使用`decode`函数对解压缩后的数据进行解码:```matlab```% 使用decode函数进行解码original_data = decode(decompressed_data);```五、编码和解码的选择在MATLAB解码中,我们需要选择适当的编码和解码算法。
使用MATLAB进行图像压缩与图像编码方法

使用MATLAB进行图像压缩与图像编码方法图像压缩是一种将图像数据进行无损或有损压缩以减小文件大小的过程。
在计算机视觉和图像处理中,图像压缩扮演着重要的角色。
它不仅可以节省存储空间,还可以加快图像传输的速度。
在这篇文章中,我们将探讨MATLAB中常用的图像压缩和编码方法以及它们的实现。
在图像压缩中,有两种主要的压缩方法,分别是无损压缩和有损压缩。
无损压缩是指压缩过程中不会丢失任何图像信息,压缩后的文件可以100%恢复为原始图像。
而有损压缩是指在压缩过程中丢失一些图像信息,导致压缩后的文件无法完全恢复为原始图像。
有损压缩方法通常用于对图像质量要求不高的场景,以减小文件的大小。
MATLAB提供了许多用于图像压缩和编码的函数和工具箱。
下面我们将介绍一些常用的图像压缩和编码方法,并给出它们在MATLAB中的实现。
1. Huffman编码Huffman编码是一种常用的无损压缩方法,它根据字符出现的频率来构建一个可变长度的编码表。
出现频率较高的字符使用较短的编码,出现频率较低的字符使用较长的编码。
MATLAB中的函数`huffmandict`可以用来生成Huffman编码的字典,函数`huffmanenco`可以用来对图像数据进行编码,函数`huffmandeco`可以用来对编码后的数据进行解码。
2. 离散余弦变换(DCT)离散余弦变换是一种常用的有损压缩方法,它将图像转换为由一系列基函数组成的频域信号。
在DCT域中,高频分量较低,可以被丢弃或使用较少的比特进行表示。
MATLAB提供了函数`dct2`和`idct2`,可以对图像进行DCT变换和逆DCT 变换。
3. 小波变换小波变换是另一种常用的有损压缩方法,它将图像转化为频域和空域的基函数,可以对不同的频率和分辨率进行调整。
MATLAB中的函数`wavedec2`和`waverec2`可以用来进行小波变换和逆变换。
小波变换在图像压缩和图像增强等应用中有广泛的应用。
matlab霍夫曼编码函数 -回复

matlab霍夫曼编码函数-回复Matlab霍夫曼编码函数是一种用于数据压缩的算法,通过将频率较高的字符用较短的编码表示,而用较长的编码表示频率较低的字符,从而实现数据的高效压缩。
在本文中,我们将逐步讨论Matlab霍夫曼编码函数的实现细节和关键步骤。
首先,让我们简要介绍一下霍夫曼编码的原理。
霍夫曼编码是一种前缀编码方法,即没有一个编码是另一个编码的前缀。
其基本思想是根据字符出现的频率构建一颗哈夫曼树,然后通过树的路径来得到每个字符的编码。
频率较高的字符拥有较短的编码,而频率较低的字符拥有较长的编码。
接下来,我们将详细介绍实现Matlab霍夫曼编码函数的步骤。
第一步是计算每个字符的频率。
我们可以通过遍历输入数据,统计每个字符出现的次数来得到频率列表。
在Matlab中,我们可以使用函数`histcounts`或`tabulate`来快速计算字符频率。
第二步是构建霍夫曼树。
我们可以使用一个优先队列(通常使用最小堆)来构建霍夫曼树。
初始时,我们将每个字符和其对应的频率作为一个节点,然后将这些节点插入优先队列中。
接下来,我们不断弹出两个频率最低的节点,将它们作为子节点构建一个新节点,并将该新节点的频率设为子节点频率之和。
最后,我们得到的堆顶节点即为霍夫曼树的根节点。
第三步是根据霍夫曼树构建每个字符的编码。
我们可以使用递归方式遍历霍夫曼树,找到每个字符的路径并将其路径上的方向(0或1)作为编码的一部分。
在Matlab中,我们可以使用一个结构体数组来保存字符和其对应的编码。
第四步是将输入数据编码为霍夫曼编码。
我们可以将输入数据中的每个字符作为索引,在之前构建的结构体数组中查找对应的编码,并将这些编码连接起来即可得到数据的霍夫曼编码。
最后,我们还可以根据霍夫曼编码解码数据。
解码的过程是从根节点开始,根据编码的每一位(0或1)选择左子节点或右子节点,直到叶子节点为止。
在Matlab中,我们可以使用一个循环来实现解码过程,直到找到对应的字符。
实验二 LZW编码算法的实现

实验二LZW编码算法的实现一、实验目的1、学习Matlab软件的使用和编程2、进一步深入理解LZW编码算法的原理二、实验内容阅读Matlab代码,画原理图。
三、实验原理LZW算法中,首先建立一个字符串表,把每一个第一次出现的字符串放入串表中,并用一个数字来表示,这个数字与此字符串在串表中的位置有关,并将这个数字存入压缩文件中,如果这个字符串再次出现时,即可用表示它的数字来代替,并将这个数字存入文件中。
压缩完成后将串表丢弃。
如"print"字符串,如果在压缩时用266表示,只要再次出现,均用266表示,并将"print"字符串存入串表中,在图象解码时遇到数字266,即可从串表中查出266所代表的字符串"print",在解压缩时,串表可以根据压缩数据重新生成。
四、LZW编码的Matlab源程序及运行结果function lzw_test(binput)if(nargin<1)binput=false;elsebinput=true;end;if binputn=0;while(n==0)P=input('please input a string:','s')%提示输入界面n=length(P);end;else%Tests the special decoder caseP='Another problem on long files is that frequently the compression ratio begins...';end;lzwInput=uint8(P);[lzwOutput,lzwTable]=norm2lzw(lzwInput);[lzwOutput_decode,lzwTable_decode]=lzw2norm(lzwOutput);fprintf('\n');fprintf('Input:');%disp(P);%fprintf('%02x',lzwInput);fprintf('%s',num2str(lzwInput));fprintf('\n');fprintf('Output:');%fprintf('%02x',lzwOutput);fprintf('%s',num2str(lzwOutput));fprintf('\n');fprintf('Output_decode:');%fprintf('%02x',lzwOutput);fprintf('%s',num2str(lzwOutput_decode));fprintf('\n');fprintf('\n');for ii=257:length(lzwTable.codes)fprintf('Output_encode---Code:%s,LastCode%s+%s Length%3d\n',num2str(ii), num2str(lzwTable.codes(ii).lastCode),...num2str(lzwTable.codes(ii).c),lzwTable.codes(ii).codeLength)fprintf('Output_decode---Code:%s,LastCode%s+%s Length%3d\n',num2str(ii), num2str(lzwTable_decode.codes(ii).lastCode),...num2str(lzwTable_decode.codes(ii).c),lzwTable_decode.codes(ii).codeLength) end;function[output,table]=lzw2norm(vector,maxTableSize,restartTable)%LZW2NORM LZW Data Compression(decoder)%For vectors,LZW2NORM(X)is the uncompressed vector of X using the LZW algorithm. %[...,T]=LZW2NORM(X)returns also the table that the algorithm produces.%%For matrices,X(:)is used as input.%%maxTableSize can be used to set a maximum length of the table.Default%is4096entries,use Inf for ual sizes are12,14and16%bits.%%If restartTable is specified,then the table is flushed when it reaches%its maximum size and a new table is built.%%Input must be of uint16type,while the output is a uint8.%Table is a cell array,each element containig the corresponding code.%%This is an implementation of the algorithm presented in the article%%See also NORM2LZW%$Author:Giuseppe Ridino'$%$Revision:1.0$$Date:10-May-200414:16:08$%How it decodes:%%Read OLD_CODE%output OLD_CODE%CHARACTER=OLD_CODE%WHILE there are still input characters DO%Read NEW_CODE%IF NEW_CODE is not in the translation table THEN%STRING=get translation of OLD_CODE%STRING=STRING+CHARACTER%ELSE%STRING=get translation of NEW_CODE%END of IF%output STRING%CHARACTER=first character in STRING%add translation of OLD_CODE+CHARACTER to the translation table%OLD_CODE=NEW_CODE%END of WHILE%Ensure to handle uint8input vector and convert%to a rowif~isa(vector,'uint16'),error('input argument must be a uint16vector')Endvector=vector(:)';if(nargin<2)maxTableSize=4096;restartTable=0;end;if(nargin<3)restartTable=0;end;function code=findCode(lastCode,c)%Look up code value%if(isempty(lastCode))%fprintf('findCode:----+%02x=',c);%else%fprintf('findCode:%04x+%02x=',lastCode,c);%end;if(isempty(lastCode))code=c+1;%fprintf('%04x\n',code);return;Elseii=table.codes(lastCode).prefix;jj=find([table.codes(ii).c]==c);code=ii(jj);%if(isempty(code))%fprintf('----\n');%else%fprintf('%04x\n',code);%end;return;end;Endfunction[]=addCode(lastCode,c)%Add a new code to the tablee.c=c;%NB using variable in parent to avoid allocation coststCode=lastCode;e.prefix=[];e.codeLength=table.codes(lastCode).codeLength+1;table.codes(table.nextCode)=e;table.codes(lastCode).prefix=[table.codes(lastCode).prefix table.nextCode];table.nextCode=table.nextCode+1;%if(isempty(lastCode))%fprintf('addCode:----+%02x=%04x\n',c,table.nextCode-1);%else%fprintf('addCode:%04x+%02x=%04x\n',lastCode,c,table.nextCode-1);%end;Endfunction str=getCode(code)%Output the string for a codel=table.codes(code).codeLength;str=zeros(1,l);for ii=l:-1:1str(ii)=table.codes(code).c;code=table.codes(code).lastCode;end;Endfunction[]=newTable%Build the initial table consisting of all codes of length1.The strings%are stored as prefixCode+character,so that testing is very quick.To%speed up searching,we store a list of codes that each code is the prefix%for.e.c=0;stCode=-1;e.prefix=[];e.codeLength=1;table.nextCode=2;if(~isinf(maxTableSize))table.codes(1:maxTableSize)=e;%Pre-allocate for speedElsetable.codes(1:65536)=e;%Pre-allocate for speedend;for c=1:255e.c=c;stCode=-1;e.prefix=[];e.codeLength=1;table.codes(table.nextCode)=e;table.nextCode=table.nextCode+1;end;End%%Main loop%e.c=0;stCode=-1;e.prefix=[];e.codeLength=1;newTable;output=zeros(1,3*length(vector),'uint8');%assume compression of33%outputIndex=1;lastCode=vector(1);output(outputIndex)=table.codes(vector(1)).c;outputIndex=outputIndex+1;character= table.codes(vector(1)).c;、、tic;for vectorIndex=2:length(vector),%if mod(vectorIndex,1000)==0%fprintf('Index:%5d,Time%.1fs,Table Length%4d,Complete%.1f%%\n', outputIndex,toc,table.nextCode-1,vectorIndex/length(vector)*100);%*ceil(log2(size(table, 2)))/8);%tic;%end;element=vector(vectorIndex);if(element>=table.nextCode)%add codes not in table,a special case.str=[getCode(lastCode)character];else,str=getCode(element);Endoutput(outputIndex+(0:length(str)-1))=str;outputIndex=outputIndex+length(str);if((length(output)-outputIndex)<1.5*(length(vector)-vectorIndex))output=[output zeros(1,3*(length(vector)-vectorIndex),'uint8')];end;if(length(str)<1)keyboard;end;character=str(1);if(table.nextCode<=maxTableSize)addCode(lastCode,character);if(restartTable&&table.nextCode==maxTableSize+1)%fprintf('New table\n');newTable;end;end;lastCode=element;end;output=output(1:outputIndex-1);table.codes=table.codes(1:table.nextCode-1);Endfunction[output,table]=norm2lzw(vector,maxTableSize,restartTable)%NORM2LZW LZW Data Compression Encoder%For vectors,NORM2LZW(X)is the compressed vector of X using the LZW algorithm. %[...,T]=NORM2LZW(X)returns also the table that the algorithm produces.%For matrices,X(:)is used as input.%maxTableSize can be used to set a maximum length of the table.Default%is4096entries,use Inf for ual sizes are12,14and16%bits.%If restartTable is specified,then the table is flushed when it reaches%its maximum size and a new table is built.%Input must be of uint8type,while the output is a uint16.%Table is a cell array,each element containing the corresponding code.%This is an implementation of the algorithm presented in the article%See also LZW2NORM%$Author:Giuseppe Ridino'$%$Revision:1.0$$Date:10-May-200414:16:08$%Revision:%Change the code table structure to improve the performance.%date:22-Apr-2007%by:Haiyong Xu%Rework the code table completely to get reasonable performance.%date:24-Jun-2007%by:Duncan Barclay%How it encodes:%STRING=get input character%WHILE there are still input characters DO%CHARACTER=get input character%IF STRING+CHARACTER is in the string table then%STRING=STRING+character%ELSE%output the code for STRING%add STRING+CHARACTER to the string table%STRING=CHARACTER%END of IF%END of WHILE%output the code for STRING%Ensure to handle uint8input vector and convert%to a double row to make maths workif~isa(vector,'uint8'),error('input argument must be a uint8vector')Endvector=double(vector(:)');if(nargin<2)maxTableSize=4096;restartTable=0;end;if(nargin<3)restartTable=0;end;function code=findCode(lastCode,c)%Look up code value%if(isempty(lastCode))%fprintf('findCode:----+%02x=',c);%else%fprintf('findCode:%04x+%02x=',lastCode,c);%end;if(isempty(lastCode))code=c+1;%fprintf('%04x\n',code);return;Elseii=table.codes(lastCode).prefix;jj=find([table.codes(ii).c]==c);code=ii(jj);%if(isempty(code))%fprintf('----\n');%else%fprintf('%04x\n',code);%end;return;end;code=[];return;Endfunction[]=addCode(lastCode,c)%Add a new code to the tablee.c=c;%NB using variable in parent to avoid allocation coststCode=lastCode;e.prefix=[];e.codeLength=table.codes(lastCode).codeLength+1;table.codes(table.nextCode)=e;table.codes(lastCode).prefix=[table.codes(lastCode).prefix table.nextCode];table.nextCode=table.nextCode+1;%if(isempty(lastCode))%fprintf('addCode:----+%02x=%04x\n',c,table.nextCode-1);%else%fprintf('addCode:%04x+%02x=%04x\n',lastCode,c,table.nextCode-1);%end;Endfunction[]=newTable%Build the initial table consisting of all codes of length1.The strings%are stored as prefixCode+character,so that testing is very quick.To%speed up searching,we store a list of codes that each code is the prefix%for.e.c=0;stCode=-1;e.prefix=[];e.codeLength=1;table.nextCode=2;if(~isinf(maxTableSize))table.codes(1:maxTableSize)=e;%Pre-allocate for speedElsetable.codes(1:65536)=e;%Pre-allocate for speedend;for c=1:255e.c=c;stCode=-1;e.prefix=[];e.codeLength=1;table.codes(table.nextCode)=e;table.nextCode=table.nextCode+1;end;End%%Main loop%e.c=0;stCode=-1;e.prefix=[];e.codeLength=1;newTable;output=vector;outputIndex=1;lastCode=[];tic;for index=1:length(vector),%if mod(index,1000)==0%fprintf('Index:%5d,Time%.1fs,Table Length%4d,Ratio%.1f%%\n',index,toc, table.nextCode-1,outputIndex/index*100);%*ceil(log2(size(table,2)))/8);%tic;%end;code=findCode(lastCode,vector(index));if~isempty(code)lastCode=code;Elseoutput(outputIndex)=lastCode;outputIndex=outputIndex+1;%fprintf('output****:%04x\n',lastCode);if(table.nextCode<=maxTableSize)addCode(lastCode,vector(index));if(restartTable&&table.nextCode==maxTableSize+1)%fprintf('New table\n');newTable;end;end;lastCode=findCode([],vector(index));end;end;output(outputIndex)=lastCode;output((outputIndex+1):end)=[];output=uint16(output);table.codes=table.codes(1:table.nextCode-1);End五、运行结果1、请写下实验结果Input:111111111111111111111111111111111111111111111111111111111111111111111111111111 Output:?????????????????????????????Input:123123123123123123123123123123123123123123123123123123123123123123123 Output:?????????????????????????????2、请在实验代码中加入计算压缩比例的代码,并显示上述两种输入的不同压缩比。
使用Matlab进行图像压缩与编码的方法

使用Matlab进行图像压缩与编码的方法一、引言随着数字化时代的快速发展,图像的处理和传输已经成为了人们日常生活中不可或缺的一部分。
然而,图像的处理和传输过程中,数据量庞大往往是一个十分严重的问题。
为了解决这个问题,图像压缩与编码技术应运而生。
本文将介绍如何利用Matlab进行图像压缩与编码的方法,以实现高效的图像传输与存储。
二、图像压缩的原理与方法图像压缩是通过减少图像数据的冗余性,以达到减少数据量的目的。
常用的图像压缩方法包括无损压缩和有损压缩。
1. 无损压缩无损压缩技术可以完全恢复原始图像,但是压缩比较低。
其中,最常见的无损压缩方法是Huffman编码和LZW编码。
Huffman编码根据字符频率构建一颗Huffman树,使得频率高的字符编码短,频率低的字符编码长,从而实现编码的高效性。
而LZW编码则是利用字典来存储和恢复图像的编码信息。
2. 有损压缩有损压缩技术通过牺牲部分图像质量来获得更高的压缩比。
常见的有损压缩方法包括离散余弦变换(DCT)、小波变换(Wavelet Transform)以及预测编码等。
离散余弦变换是JPEG图像压缩标准所采用的一种技术,其将图像从空间域变换到频域,然后对频域信号进行量化和编码。
这种方法在保留图像主要特征的同时,实现了较高的压缩比。
小波变换是一种多尺度的信号分析方法,其能够将图像按照不同的频率组成进行分离,并对各个频率成分进行独立的处理。
小波变换不仅可以应用于图像压缩,还可以应用于图像增强和去噪等领域。
三、Matlab实现图像压缩与编码Matlab是一种强大的数学计算及可视化软件,其提供了丰富的函数和工具箱,便于进行图像处理和压缩编码。
1. 图像读取与显示首先,我们需要读取原始图像,并使用imshow函数来显示原始图像。
```matlabimg = imread('image.jpg');imshow(img);```2. 无损压缩对于无损压缩,在Matlab中可以使用imwrite函数来保存图像。
Matlab中的数据压缩与图像加密方法

Matlab中的数据压缩与图像加密方法引言:数据压缩和图像加密是当今计算机科学领域中的重要研究方向。
数据压缩技术能够有效地减小数据的尺寸并提高存储和传输效率,而图像加密技术则可以有效保护敏感信息的安全性。
在本文中,我们将探讨Matlab中常用的数据压缩和图像加密方法,介绍它们的原理和应用领域。
一、数据压缩1. Huffman编码Huffman编码是一种常用的数据压缩算法。
其基本原理是根据待压缩数据中字符的出现频率来构建一个最优二叉树。
通过对每个字符赋予对应的编码,可以实现对数据的高效压缩。
Huffman编码在Matlab中可以通过构建Huffman树并对数据进行编码实现。
2. Lempel-Ziv-Welch(LZW)算法LZW算法是一种无损的数据压缩算法,常用于文本和图像压缩。
该算法通过建立一个字典来存储已经出现的字符组合,并将其替换为对应的索引值。
这样可以实现对数据的高效压缩。
在Matlab中,可以使用LZW算法对文本和图像进行压缩和解压缩。
3. 小波变换压缩小波变换是一种非常有效的数据压缩方法。
其基本思想是通过对数据进行一系列尺度和平移变换,将数据从时域转换到频域。
通过选择适当的小波基函数,可以实现对数据的高效压缩。
Matlab提供了丰富的小波变换函数,可以方便地进行数据压缩。
二、图像加密1. 基于置乱和扩散的加密算法基于置乱和扩散的加密算法是一种常用的图像加密方法。
其基本思想是通过对图像进行像素置乱和扩散等操作,使得原始图像的信息变得不可分辨。
这样可以有效保护图像的安全性。
在Matlab中,可以使用随机数生成器和像素重排等函数实现基于置乱和扩散的图像加密。
2. RSA算法RSA算法是一种常用的公钥加密算法。
其基本原理是通过对数据进行加密和解密,实现对敏感信息的安全传输。
在RSA算法中,每个用户都有一对密钥,包括公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
在Matlab中,可以使用RSA算法对图像进行加密和解密。
在Matlab中进行数据压缩的技术实现

在Matlab中进行数据压缩的技术实现数据压缩是一种常见的数据处理技术,用于减少数据占用的存储空间和传输带宽。
在大数据时代,数据压缩成为了非常重要的技术之一。
Matlab作为一种强大的数学计算软件,也提供了丰富的数据压缩工具和算法。
本文将介绍在Matlab中进行数据压缩的技术实现。
1. 概述数据压缩可以分为有损压缩和无损压缩两种类型。
有损压缩是指在压缩过程中会丢失部分数据变化的细节,但可以大幅减少数据的存储空间。
无损压缩则是保证经压缩和解压缩后数据的完全一致性。
2. 无损压缩在Matlab中,无损压缩常常使用的是一些经典的算法,如Huffman编码、Lempel-Ziv-Welch (LZW)编码和自适应算术编码等。
Huffman编码是一种基于字符频率统计的压缩算法。
在Matlab中,可以使用`huffmandict`函数生成Huffman编码所需的编码字典,然后使用`huffmanenco`函数对数据进行编码,使用`huffmandeco`函数进行解码。
LZW编码是一种无损的字典压缩算法。
在Matlab中,可以使用`lzwenc`函数对数据进行编码,使用`lzwdec`函数进行解码。
自适应算术编码是一种根据数据概率动态更新编码表的压缩算法。
在Matlab 中,可以使用`arithenco`函数对数据进行编码,使用`arithdeco`函数进行解码。
这些无损压缩算法在Matlab中的实现简单而高效,能够有效地减少数据的存储空间。
3. 有损压缩有损压缩常用于图像、音频和视频等需要高压缩比的数据。
在Matlab中,有损压缩常常使用的是一些经典的算法,如JPEG和MP3等。
JPEG(Joint Photographic Experts Group)是一种广泛应用于图像压缩的有损压缩算法。
在Matlab中,可以使用`imresize`函数将图像进行降采样,使用`dct2`函数对图像进行离散余弦变换,然后使用量化矩阵将高频分量进行量化,再使用`huffmanenco`函数对量化后的数据进行哈夫曼编码。
Matlab中的数据压缩与编码算法

Matlab中的数据压缩与编码算法数据压缩和编码是计算机科学领域中的重要课题,而Matlab作为一种强大的数学计算软件,也提供了丰富的工具来实现数据压缩和编码算法。
在本文中,将介绍Matlab中的数据压缩和编码算法,并探讨其在实际应用中的优势和挑战。
一、基础知识概述数据压缩和编码是指将原始数据通过某种算法转化为更紧凑的表示形式,从而减少数据的存储空间或传输带宽。
数据压缩算法可以分为无损压缩和有损压缩两类。
无损压缩算法能够完全还原原始数据,而有损压缩算法则在一定程度上丢失了原始数据的精确信息。
二、无损压缩算法无损压缩算法是指在压缩数据的同时能够完全还原原始数据的算法。
常用的无损压缩算法包括哈夫曼编码、LZW编码、算术编码等。
在Matlab中,提供了相应的函数和工具箱来实现这些算法。
1. 哈夫曼编码哈夫曼编码是一种基于频率统计的变长编码方法。
在Matlab中,可以使用`huffmanenco`和`huffmandeco`函数来实现对数据的哈夫曼编码和解码。
该编码算法适用于具有较大重复性的数据,可以实现较高的压缩比。
2. LZW编码LZW编码是一种字典编码方法,广泛应用于文本和图像等数据的压缩中。
在Matlab中,可以使用`lzwenco`和`lzwdeco`函数来实现对数据的LZW编码和解码。
该编码算法通过将连续出现的字符序列映射为固定长度的码字,有效地减少了数据的存储空间。
3. 算术编码算术编码是一种根据数据出现概率分布进行编码的方法,具有较高的压缩比。
在Matlab中,可以使用`arithenco`和`arithdeco`函数来实现数据的算术编码和解码。
该编码算法可以对数据进行精确的表示,但计算复杂度较高。
三、有损压缩算法有损压缩算法是指在压缩数据的过程中,为了减小数据的存储空间或传输带宽,牺牲了一定的数据精度。
常见的有损压缩算法包括JPEG图像压缩、MP3音频压缩等。
1. JPEG图像压缩JPEG图像压缩是一种广泛应用于静态图像的有损压缩算法。
如何在MATLAB中进行数据压缩与降维

如何在MATLAB中进行数据压缩与降维数据压缩和降维是现代数据处理和分析中的重要技术,它们可以帮助我们有效地处理大规模数据,减少存储空间和计算复杂度。
在MATLAB中,有许多强大的工具和算法可供我们使用,本文将介绍如何利用MATLAB进行数据压缩和降维。
一、数据压缩的基本概念和方法数据压缩是指通过一系列算法和技术,将原始数据转换为更紧凑和可表示的形式,以减少存储空间或传输带宽。
常用的数据压缩方法包括有损和无损压缩。
无损压缩是指压缩后的数据可以完全还原为原始数据,而有损压缩则会有一定的信息损失。
在MATLAB中,我们可以使用许多压缩算法来处理数据。
其中一个常用的压缩算法是gzip,它采用DEFLATE算法将数据压缩成一个单一的gz文件。
使用gzip压缩数据非常简单,只需使用MATLAB的zlib库即可实现。
另一个常用的压缩算法是Lempel-Ziv-Welch(LZW)算法,它是一种无损压缩算法,常用于文本和图像数据的压缩。
这个算法的核心思想是利用字典来存储已经出现的字符序列,然后将新的字符序列转换为字典中的索引。
在MATLAB中,我们可以使用`lwcompress`函数来实现LZW压缩。
二、数据降维的基本概念和方法数据降维是指通过选择一组最重要的特征或主成分,将高维的数据映射到低维空间中,从而降低数据的维度。
降维可以帮助我们减少数据的存储空间和分析复杂度,同时保持数据的主要结构和特征。
在MATLAB中,有许多经典的降维算法可供使用。
其中最常见的算法是主成分分析(PCA)算法。
PCA可以将原始数据转换为一组无关的主成分,其中每个主成分都是原始数据的线性组合。
在MATLAB中,我们可以使用`pca`函数来进行PCA降维分析。
另一个常用的降维算法是线性判别分析(LDA)。
LDA通过选择最佳投影方向,将多类别数据映射到低维空间中,从而使不同类别之间具有最大的差异性。
在MATLAB中,我们可以使用`classificationlda`函数来进行LDA降维分析。
Matlab在数据压缩与编码中的应用

Matlab在数据压缩与编码中的应用引言:数据压缩与编码是现代信息技术领域中的重要研究方向之一。
随着大数据时代的到来,对数据的存储和传输效率要求越来越高。
在这个背景下,Matlab作为一款强大的数据处理和分析工具,扮演着重要的角色。
本文将探讨Matlab在数据压缩与编码中的应用,并介绍一些相关的算法和方法。
一、数据压缩1、无损压缩无损压缩是指在压缩数据的同时不丢失任何信息。
Matlab提供了许多常用的无损压缩算法,如Lempel-Ziv-Welch(LZW)、Run-Length Encoding(RLE)以及Huffman编码等。
我们可以通过调用Matlab中的相应函数来实现这些算法。
例如,使用"Huffman"函数可以对数据进行Huffman编码。
同时,在实际应用中,我们还可以根据具体需求进行改进和优化。
2、有损压缩有损压缩是指在压缩数据的过程中,对数据进行一定的信息丢失,以达到更高的压缩比。
在图像和音频等领域,有损压缩得到了广泛应用。
Matlab提供了很多常用的有损压缩算法,如JPEG、JPEG2000等。
这些算法通常涉及到信号处理和频域变换等技术。
我们可以根据具体的需求,在Matlab中编写相应的代码来实现这些算法。
二、数据编码数据编码是指将给定的数据序列转换为另一种表示形式的过程。
编码的目的是为了提高数据的存储和传输效率。
在数据编码中,Matlab可以发挥其强大的计算和分析能力。
1、熵编码熵编码是一种常见的数据压缩技术,其基本原理是将出现频率较高的符号用较短的编码表示,从而实现压缩效果。
在熵编码中,常用的算法有Shannon-Fano编码和算术编码。
Matlab提供了相关的函数可以直接调用,例如"arithenco"函数用于进行算术编码。
2、码本设计码本设计是指在给定的码字集合中,设计出一种编码方式,以最小的平均码字长度来表示给定的输入符号。
Matlab在码本设计方面也提供了许多函数和工具箱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%encoder LZW for matlab
%yu 20170503
clc;
clear;
close all;
%初始字典
dic = cell(512,1);
for i = 1:256
dic{i} = {num2str(i)};
end
%输入字符串a,按空格拆分成A,注意加1对应范围1~256
d = 256;%字典指针
b = 1;%输Βιβλιοθήκη 指针B = cell(L,1);%输出初始
output = ' ';%输出初始
j=1;
for j = 2:L
m=1;
B_t =deblank([A_t,' ',A{j}]);%合成待验证词条
while(m <= d)
if strcmp(dic{m},B_t)
for q=1:d%处理最后一个序列输出
if strcmp(dic{q},A_t)
B{b} = num2str(q);
b = b+1;
end
end
for n = 1:(b-1)
B{n} =num2str(str2num(B{n})-1);
output=deblank([output,' ',B{n}]);
if strcmp(dic{m},B_t)
B_t = B_t;
break
else
m=m+1;
end
end
while(m == d+1)
d = d+1;
dic{d} = B_t;
B_t = B_d{p};
end
end
b = b+L_B;
end
for n = 1:(b-L_B)
B{n} = num2str(str2num(B{n})-1);
output=deblank([output,' ',B{n}]);
end
output
运算结果
运算结果为 3939126126393912612639391261263939126126
end
output
运算结果
计算结果为3939126126256258 260 259 257 126
LZW解码算法,使用matlab计算
%decoder LZW for matlab
%yu 20170503
clc;
clear;
close all;
%初始字典
dic = cell(512,1);
for i = 1:256
end
B_t = A{1};%待验证词条
d = 256;%字典指针
b = 1;%输出指针
B = cell(L,1);%输出初始
output = ' ';%输出初始
j=1;
B{b} = char(dic{str2num(A{j})});
b = b+1;
for j = 2:L
BB = char(dic{str2num(A{j})});
a = input('input:','s');
a = deblank(a);
A = regexp(a,'\s+','split');
L = length(A);
for j=1:L
A{j} = num2str(str2num(A{j})+1);
end
A_t = A{1};%可识别序列
B_t = 'test';%待验证词条
B_d = regexp(BB,'\s+','split');%按空格拆分
L_B = length(B_d);
p=1;
for p=1:L_B
B{(b+p-1)} = B_d{p};
m=1;
B_t =deblank([char(B_t),' ',char(B_d{p})]);%合成待验证词条
while(m <= d)
A_t = B_t;
break
else
m=m+1;
end
end
while(m == d+1)
d = d+1;
dic{d} = B_t;
q=1;
for q=1:d
if strcmp(dic{q},A_t)
B{b} = num2str(q);
b = b+1;
end
end
A_t = A{j};
end
end
dic{i} = {num2str(i)};
end
%输入字符串a,按空格拆分成A,注意加1对应范围1~256
a = input('input:','s');
a = deblank(a);
A = regexp(a,'\s+','split');
L = length(A);
for j=1:L
A{j} = num2str(str2num(A{j})+1);
