蚁群算法程序(matlab)
《蚁群算法实验室》流程图

《蚁群算法实验室》流程图蚁群算法计算主流程(该流程在用户控制下可在没达到指定循环次数时停止或暂停):开始I目前蚁群算法主要用在组合优化方面,基本蚁群算法的思路是这样的:1. 在初始状态下,一群蚂蚁外出,此时没有信息素,那么各自会随机的选择一条路径。
2. 在下一个状态,每只蚂蚁到达了不同的点,从初始点到这些点之间留下了信息素,蚂蚁继续走,已经到达目标的蚂蚁开始返回,与此同时,下一批蚂蚁出动,它们都会按照各条路径上信息素的多少选择路线(selection),更倾向于选择信息素多的路径走(当然也有随机性)。
3. 又到了再下一个状态,刚刚没有蚂蚁经过的路线上的信息素不同程度的挥发掉了(evaporation) ,而刚刚经过了蚂蚁的路线信息素增强(reinforcement) 。
然后又出动一批蚂蚁,重复第 2 个步骤。
每个状态到下一个状态的变化称为一次迭代,在迭代多次过后,就会有某一条路径上的信息素明显多于其它路径,这通常就是一条最优路径。
关键的部分在于步骤 2 和3:步骤 2 中,每只蚂蚁都要作出选择,怎样选择呢?selection 过程用一个简单的函数实现:蚂蚁选择某条路线的概率=该路线上的信息素辆有可选择路线的信息素之和假设蚂蚁在i点,p(i,j)表示下一次到达j点的概率,而T (i,j表示ij两点间的信息素,则:P(i,j) = T (i,j)/ 刀T (i)(如果所有可选路线的信息素之和刀T伸0,即前面还没有蚂蚁来过,概率就是一个[0,1]上的随机值,即随机选择一条路线)步骤 3 中,挥发和增强是算法的关键所在(也就是如何数学定义信息素的)evaporation 过程和reinforcement 过程定义了一个挥发因子,是迭代次数k 的一个函数p (k=1 —lnk/ln(k+1)最初设定每条路径的信息素T (i,j,0为相同的值然后,第k+1 次迭代时,信息素的多少对于没有蚂蚁经过的路线:T (i,j,k+1)= (1—p (k)) T (i,j,k显然信息素减少了有蚂蚁经过的路线:T (i,j,k+1)= (1 —p (k)) T (i,j*) p (k)/|W| W为所有点的集合为什么各个函数要如此定义,这个问题很难解释清楚,这也是算法的精妙所在。
蚁群算法matlab程序

D(i,j)=eps;
end
D(j,i)=D(i,j);
end
end
Eta=1./D; %% Eta为启发因子,这里设为距离的倒数
Tau=ones(n,n); %% Tau为信息素矩阵
Tabu=zeros(m,n); %% 存储并记录路径的生成
%% 蚁群算法MATLAB程序第六
end
NC
%% 蚁群算法MATLAB程序第七步:输出结果
Pos=find(L_best==min(L_best));
Shortest_Route=R_best(Pos(1),:)
Shortest_Length=L_best(Pos(1))
subplot(1,2,1)
DrawRoute(C,Shortest_Route) %% 画路线图
subplot(1,2,2)
plot(L_best)
hold on
plot(L_ave,'r')
title('平均距离和最短距离')
P=J; %% 待访问城市的选择概率分布
Jc=1;
for k=1:n
if length(find(visited==k))==0
J(Jc)=k;
%% 蚁群算法MATLAB程序第二步:将m只蚂蚁放到n个城市上
Randpos=[]; %% 随机存取
for i=1:ceil(m/n)
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=Randpos(1,1:m)';
%% m 蚂蚁个数
%% Alpha 表征信息素重要程度的参数
蚁群算法
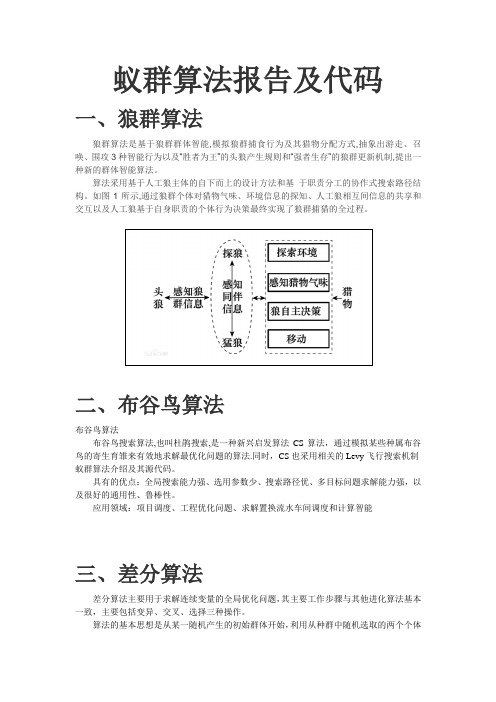
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
Matlab蚁群算法

实现蚂蚁移动和信息素挥发机制
蚂蚁移动
根据蚂蚁的移动规则和信息素值,让蚂 蚁在解空间中移动,并记录其路径。
VS
信息素挥发
模拟信息素的挥发过程,降低信息素值, 以反映信息的衰减。
迭代优化和结果
迭代优化
通过多次迭代,让蚂蚁不断寻找更好的解, 并逐渐逼近最优解。
结果输出
输出最终找到的最优解,以及算法的性能指 标,如收敛速度、最优解质量等。
05 Matlab蚁群算法的优缺点分析
优点分析
并行性
鲁棒性
全局搜索能力
易于实现
蚁群算法是一种自然启发的优 化算法,具有高度的并行性。 在Matlab中实现时,可以利用 多核处理器或GPU加速技术进 一步提高并行计算能力,从而
加快算法的收敛速度。
蚁群算法对初始参数设置不 敏感,具有较强的鲁棒性。 这意味着在Matlab实现时, 即使初始参数设置不当,算
法仍能找到较优解。
蚁群算法采用正反馈机制, 能够发现多条优质路径,具 有较强的全局搜索能力。这 有助于在Matlab中解决多峰、 离散、非线性等复杂优化问
题。
蚁群算法原理相对简单,实 现起来较为容易。在Matlab 中,可以利用现有的工具箱 或自行编写代码来实现该算
法。
缺点分析
01
计算量大
蚁群算法在解决大规模优化问题时,计算量较大,可能 导致算法运行时间较长。在Matlab实现中,可以通过优 化代码、采用并行计算等技术来降低计算量。
Matlab蚁群算法目录来自• 蚁群算法简介 • Matlab实现蚁群算法的步骤 • 蚁群算法的参数调整与优化 • Matlab蚁群算法的案例分析 • Matlab蚁群算法的优缺点分析
01 蚁群算法简介
蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码标题:蚁群算法路径优化 MATLAB 代码正文:蚁群算法是一种基于模拟蚂蚁搜索食物路径的优化算法,常用于求解复杂问题。
在路径优化问题中,蚂蚁需要从起点移动到终点,通过探索周围区域来寻找最短路径。
MATLAB 是一个常用的数值计算软件,可以用来实现蚁群算法的路径优化。
下面是一个基本的 MATLAB 代码示例,用于实现蚁群算法的路径优化:```matlab% 定义参数num_ants = 100; % 蚂蚁数量num_steps = 100; % 路径优化步数search_radius = 2; % 搜索半径max_iterations = 1000; % 最大迭代次数% 随机生成起点和终点的位置坐标start_pos = [randi(100), randi(100)];end_pos = [75, 75];% 初始化蚂蚁群体的位置和方向ants_pos = zeros(num_ants, 2);ants_dir = zeros(num_ants, 2);for i = 1:num_antsants_pos(i, :) = start_pos + randn(2) * search_radius; ants_dir(i, :) = randomvec(2);end% 初始化蚂蚁群体的速度ants_vel = zeros(num_ants, 2);for i = 1:num_antsants_vel(i, :) = -0.1 * ants_pos(i, :) + 0.5 *ants_dir(i, :);end% 初始时蚂蚁群体向终点移动for i = 1:num_antsans_pos = end_pos;ans_vel = ants_vel;for j = 1:num_steps% 更新位置和速度ans_pos(i) = ans_pos(i) + ans_vel(i);ants_vel(i, :) = ones(1, num_steps) * (-0.1 * ans_pos(i) + 0.5 * ans_dir(i, :));end% 更新方向ants_dir(i, :) = ans_dir(i, :) - ans_vel(i) * 3;end% 迭代优化路径max_iter = 0;for i = 1:max_iterations% 计算当前路径的最短距离dist = zeros(num_ants, 1);for j = 1:num_antsdist(j) = norm(ants_pos(j) - end_pos);end% 更新蚂蚁群体的位置和方向for j = 1:num_antsants_pos(j, :) = ants_pos(j, :) - 0.05 * dist(j) * ants_dir(j, :);ants_dir(j, :) = -ants_dir(j, :);end% 更新蚂蚁群体的速度for j = 1:num_antsants_vel(j, :) = ants_vel(j, :) - 0.001 * dist(j) * ants_dir(j, :);end% 检查是否达到最大迭代次数if i > max_iterationsbreak;endend% 输出最优路径[ans_pos, ans_vel] = ants_pos;path_dist = norm(ans_pos - end_pos);disp(["最优路径长度为:" num2str(path_dist)]);```拓展:上述代码仅仅是一个简单的示例,实际上要实现蚁群算法的路径优化,需要更加复杂的代码实现。
基于MATLAB的自适应蚁群聚类算法研究与仿真

关键 词 : 蚁群算法 ; 聚类分析 ; 自适应 ; T A MA L B
中图分类号 :P 8 T 1
文献标 识码 : A
DO : 03 6  ̄i n10 .902 1.7 3 I 1. 9 .s.0 36 7 . 20 . 5 9 s 0 0
Z HOU T n eg
(o t— e t l nv ri f r ain l i , ol eo c m ue i c, h n 3 0 4 C ia S uhC nr i s y o t a ie C l g o p tr c n e Wu a 0 7 , h ) aU e t N o ts e f se 4 n
MATL AB smu a in a d e p r e t l e u t h w h t h s f h l o t m a e etrcu t r g r s l , i h d m o sr t a i lt n x e m n a s l s o t a eu e o e ag r h c n g t t l se n e u t wh c e n t et t o i r s t t i b e i s a h t ea g rt m e sb e h l o h i f a i l. i s
[ ywod ] n oo y loi m; ls r nls ; d pieMA L B Ke r s AБайду номын сангаасt ln g rh Cut ayi A at ; T A c a t ea s v
0 引 言
蚁群 算法 …最早 是由 M. r o V. ni z Doi , Ma l z o等人 首先 g e 提 出来的 , 它是 一种描述 基于蚁 群群体行 为的算法 , 智能群 是 体 算法 的一个分支 。该算法在 旅行商 问题和其 它优化 问题 中 获得 了一 系列理想的实验结果, 充分体现了该 算法 的可行性 。
蚁群算法matlab代码讲解

蚁群算法matlab代码讲解蚁群算法(Ant Colony Algorithm)是模拟蚁群觅食行为而提出的一种优化算法。
它以蚁群觅食的方式来解决优化问题,比如旅行商问题、图着色问题等。
该算法模拟了蚂蚁在寻找食物时的行为,通过信息素的正反馈和启发式搜索来实现问题的最优解。
在蚁群算法中,首先需要初始化一组蚂蚁和问题的解空间。
每只蚂蚁沿着路径移动,通过信息素和启发式规则来选择下一步的移动方向。
当蚂蚁到达目标位置后,会根据路径的长度来更新信息素。
下面是一个用MATLAB实现蚁群算法的示例代码:```matlab% 参数设置num_ants = 50; % 蚂蚁数量num_iterations = 100; % 迭代次数alpha = 1; % 信息素重要程度因子beta = 5; % 启发式因子rho = 0.1; % 信息素蒸发率Q = 1; % 信息素增加强度因子pheromone = ones(num_cities, num_cities); % 初始化信息素矩阵% 初始化蚂蚁位置和路径ants = zeros(num_ants, num_cities);for i = 1:num_antsants(i, 1) = randi([1, num_cities]);end% 迭代计算for iter = 1:num_iterations% 更新每只蚂蚁的路径for i = 1:num_antsfor j = 2:num_cities% 根据信息素和启发式规则选择下一步移动方向next_city = choose_next_city(pheromone, ants(i, j-1), beta);ants(i, j) = next_city;endend% 计算每只蚂蚁的路径长度path_lengths = zeros(num_ants, 1);for i = 1:num_antspath_lengths(i) = calculate_path_length(ants(i, :), distances);end% 更新信息素矩阵pheromone = (1 - rho) * pheromone;for i = 1:num_antsfor j = 2:num_citiespheromone(ants(i, j-1), ants(i, j)) = pheromone(ants(i, j-1), ants(i, j)) + Q / path_lengths(i); endendend```上述代码中的参数可以根据具体问题进行调整。
matlab-蚁群算法-机器人路径优化问题

matlab-蚁群算法-机器人路径优化问题4.1问题描述移动机器人路径规划是机器人学的一个重要研究领域。
它要求机器人依据某个或某些优化原则(如最小能量消耗,最短行走路线,最短行走时间等),在其工作空间中找到一条从起始状态到目标状态的能避开障碍物的最优路径。
机器人路径规划问题可以建模为一个有约束的优化问题,都要完成路径规划、定位和避障等任务。
4.2算法理论蚁群算法(AntColonyAlgorithm,ACA),最初是由意大利学者DorigoM.博士于1991年首次提出,其本质是一个复杂的智能系统,且具有较强的鲁棒性,优良的分布式计算机制等优点。
该算法经过十多年的发展,已被广大的科学研究人员应用于各种问题的研究,如旅行商问题,二次规划问题,生产调度问题等。
但是算法本身性能的评价等算法理论研究方面进展较慢。
Dorigo提出了精英蚁群模型(EAS),在这一模型中信息素更新按照得到当前最优解的蚂蚁所构造的解来进行,但这样的策略往往使进化变得缓慢,并不能取得较好的效果。
次年Dorigo博士在文献[30]中给出改进模型(ACS),文中改进了转移概率模型,并且应用了全局搜索与局部搜索策略,来得进行深度搜索。
Stützle与Hoo给出了最大-最小蚂蚁系统(MA某-MINAS),所谓最大-最小即是为信息素设定上限与下限,设定上限避免搜索陷入局部最优,设定下限鼓励深度搜索。
蚂蚁作为一个生物个体其自身的能力是十分有限的,比如蚂蚁个体是没有视觉的,蚂蚁自身体积又是那么渺小,但是由这些能力有限的蚂蚁组成的蚁群却可以做出超越个体蚂蚁能力的超常行为。
蚂蚁没有视觉却可以寻觅食物,蚂蚁体积渺小而蚁群却可以搬运比它们个体大十倍甚至百倍的昆虫。
这些都说明蚂蚁群体内部的某种机制使得它们具有了群体智能,可以做到蚂蚁个体无法实现的事情。
经过生物学家的长时间观察发现,蚂蚁是通过分泌于空间中的信息素进行信息交流,进而实现群体行为的。
蚁群算法MATLAB代码

蚁群算法MATLAB代码function [y,val]=QACSticload att48 att48;MAXIT=300; % 最大循环次数NC=48; % 城市个数tao=ones(48,48);% 初始时刻各边上的信息最为1rho=0.2; % 挥发系数alpha=1;beta=2;Q=100;mant=20; % 蚂蚁数量iter=0; % 记录迭代次数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((att48(i,2)-att48(j,2))^2+(att48(i,3)-att48(j,3))^2);endendbestroute=zeros(1,48); % 用来记录最优路径routelength=inf; % 用来记录当前找到的最优路径长度% for i=1:mant % 确定各蚂蚁初始的位置% endfor ite=1:MAXITfor ka=1:mant %考查第K只蚂蚁deltatao=zeros(48,48); % 第K只蚂蚁移动前各边上的信息增量为零[routek,lengthk]=travel(distance,tao,alpha,beta);if lengthk<="">routelength=lengthk;bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatao(routek(i),routek(i+1))=deltatao(routek(i),routek(i+1 ))+Q/lengthk;enddeltatao(routek(48),1)=deltatao(routek(48),1)+Q/lengthk;endfor i=1:NC-1for j=i+1:NCif deltatao(i,j)==0deltatao(i,j)=deltatao(j,i);endendendtao=(1-rho).*tao+deltatao;endy=bestroute;val=routelength;function [y,val]=travel(distance,tao,alpha,beta) % 某只蚂蚁找到的某条路径[m,n]=size(distance);p=fix(m*rand)+1;val=0; % 初始路径长度设为0tabuk=[p]; % 假设该蚂蚁都是从第p 个城市出发的for i=1:m-1np=tabuk(length(tabuk)); % 蚂蚁当前所在的城市号p_sum=0;for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);p_sum=p_sum+tao(np,j)^alpha*ada^beta;endendcp=zeros(1,m); % 转移概率for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);cp(j)=tao(np,j)^alpha*ada^beta/p_sum;endendNextCity=pchoice(cp);tabuk=[tabuk,NextCity];val=val+distance(np,NextCity);endy=tabuk;function y=isin(x,A) % 判断数x 是否在向量A 中,如在返回1 ,否则返回0 y=0;for i=1:length(A)if A(i)==xy=1;break;endendfunction y=pchoice(A)a=rand;tempA=zeros(1,length(A)+1); for i=1:length(A) tempA(i+1)=tempA(i)+A(i); endfor i=2:length(tempA)if a<=tempA(i)y=i-1;break;endend。
13基于蚁群算法的连续函数优化通用MATLAB源代码

基于蚁群算法的连续函数优化通用MATLAB源代码此源码是对人工蚁群算法的一种实现,用于无约束连续函数的优化求解,对于含有约束的情况,可以先使用罚函数等方法,把问题处理成无约束的模型,再使用本源码进行求解.function [BESTX,BESTY,ALLX,ALLY]=ACOUCP(K,N,Rho,Q,Lambda,LB,UB)%% Ant Colony Optimization for Unconstrained Continuous Problem%% ACOUCP。
m%% 无约束连续函数的蚁群优化算法%% 此函数实现蚁群算法,用于求解无约束连续函数最小化问题%% 对于最大化问题,请先将其加负号转化为最小化问题% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→http://blog。
/greensim%% 输入参数列表% K 迭代次数% N 蚁群规模% Rho 信息素蒸发系数,取值0~1之间,推荐取值0.7~0。
95% Q 信息素增加强度,大于0,推荐取值1左右% Lambda 蚂蚁爬行速度,取值0~1之间,推荐取值0.1~0.5% LB 决策变量的下界,M×1的向量% UB 决策变量的上界,M×1的向量%%输出参数列表% BESTX K×1细胞结构,每一个元素是M×1向量,记录每一代的最优蚂蚁% BESTY K×1矩阵,记录每一代的最优蚂蚁的评价函数值% ALLX K×1细胞结构,每一个元素是M×N矩阵,记录每一代蚂蚁的位置% ALLY K×N矩阵,记录每一代蚂蚁的评价函数值%% 测试函数设置% 测试函数用单独的子函数编写好,在子函数FIT。
m中修改要调用的测试函数名即可%注意:决策变量的下界LB和上界UB,要与测试函数保持一致%% 参考设置% [BESTX,BESTY,ALLX,ALLY]=ACOUCP(50,30,0.95,1,0.5,LB,UB)%% 第一步:初始化M=length(LB);%决策变量的个数%蚁群位置初始化X=zeros(M,N);for i=1:Mx=unifrnd(LB(i),UB(i),1,N);X(i,:)=x;end%输出变量初始化ALLX=cell(K,1);%细胞结构,每一个元素是M×N矩阵,记录每一代的个体ALLY=zeros(K,N);%K×N矩阵,记录每一代评价函数值BESTX=cell(K,1);%细胞结构,每一个元素是M×1向量,记录每一代的最优个体BESTY=zeros(K,1);%K×1矩阵,记录每一代的最优个体的评价函数值k=1;%迭代计数器初始化Tau=ones(1,N);%信息素初始化Y=zeros(1,N);%适应值初始化%% 第二步:迭代过程while k<=KYY=zeros(1,N);for n=1:Nx=X(:,n);YY(n)=FIT(x);endmaxYY=max(YY);temppos=find(YY==maxYY);POS=temppos(1);%蚂蚁随机探路for n=1:Nif n~=POSx=X(:,n);Fx=FIT(x);mx=GaussMutation(x,LB,UB);if Fmx<FxX(:,n)=mx;Y(n)=Fmx;elseif rand〉1-(1/(sqrt(k)))X(:,n)=mx;Y(n)=Fmx;elseX(:,n)=x;Y(n)=Fx;endendendfor n=1:Nif n~=POSx=X(:,n);Fx=FIT(x);mx=GaussMutation(x,LB,UB);Fmx=FIT(mx);if Fmx〈FxY(n)=Fmx;elseif rand〉1-(1/(sqrt(k)))X(:,n)=mx;Y(n)=Fmx;elseX(:,n)=x;Y(n)=Fx;endendend%朝信息素最大的地方移动for n=1:Nif n~=POSx=X(:,n);r=(K+k)/(K+K);p=randperm(N);t=ceil(r*N);pos=p(1:t);TempTau=Tau(pos);maxTempTau=max(TempTau);pos3=pos(pos2(1));x2=X(:,pos3(1));x3=(1—Lambda)*x+Lambda*x2;Fx=FIT(x);Fx3=FIT(mx);if Fx3〈FxX(:,n)=x3;Y(n)=Fx3;elseif rand〉1—(1/(sqrt(k))) X(:,n)=x3;Y(n)=Fx3;elseX(:,n)=x;Y(n)=Fx;endendend%更新信息素并记录Tau=Tau*(1-Rho);maxY=max(Y);minY=min(Y);DeltaTau=(maxY—Y)/(maxY—minY);Tau=Tau+Q*DeltaTau;ALLX{k}=X;ALLY(k,:)=Y;minY=min(Y);pos4=find(Y==minY);BESTX{k}=X(:,pos4(1));BESTY(k)=minY;disp(k);k=k+1;end%% 绘图BESTY2=BESTY;BESTX2=BESTX;for k=1:KTempY=BESTY(1:k);minTempY=min(TempY);posY=find(TempY==minTempY);BESTY2(k)=minTempY;BESTX2{k}=BESTX{posY(1)};endBESTY=BESTY2;BESTX=BESTX2;plot(BESTY,’—ko','MarkerEdgeColor’,’k’,’MarkerFaceColor','k’,'MarkerSize’,2) ylabel('函数值')xlabel(’迭代次数’)grid on。
蚁群算法matlab代码

蚁群算法matlab代码蚁群算法,英文名为Ant Colony Algorithm,缩写为ACO,是一种启发式算法,是一种模拟蚂蚁寻找食物路径的算法。
在实际生活中,蚂蚁找到食物并返回巢穴后,将其找到食物的路径上的信息素留下,其他蚂蚁通过检测信息素来指导寻路,成为了一种集体智慧行为。
ACO也是通过模拟蚂蚁寻找食物路径的方式来寻找优化问题的最优解。
在ACO算法中,信息素是一个重要的概念,代表了走过某一路径的“好概率”,用这个“好概率”更新一些路径上的信息素,使得其他蚂蚁更可能选择经过这条路径,从而实现路径优化的目的。
在本文中,我们将讨论如何使用Matlab实现蚁群算法来优化问题。
1. 设定问题首先,我们要选取一个优化问题,并将其转换为需要在优化过程中进行选择的决策变量。
例如,我们想要优化旅行商问题(TSP)。
在TSP中,我们需要让旅行商以最短的距离经过所有城市,每个城市仅经过一次,最终回到出发的城市。
我们可以将每个城市编号,然后将TSP转化为一个最短路径选择的问题,即最短路径从编号为1的城市开始,经过所有城市,最终回到编号为1的城市。
2. 设定ACO参数在使用ACO优化问题时,需要设定一些参数,这些参数会影响算法的表现。
ACO算法需要设定的参数有:1.信息素含量:初始信息素的大小,即每个路径上的信息素浓度。
2.信息素挥发速度:信息素的随时间“减弱”程度。
3.信息素加成强度:蚂蚁经过路径后增加的信息素量。
4.启发式权重:用于计算启发式因子,即节点距离的贡献值。
5.蚂蚁数量:模拟蚂蚁数量,即同时寻找路径的蚂蚁个数。
6.迭代次数:模拟的迭代次数,即ACO算法运行的次数。
7.初始节点:ACO算法开始的节点。
3. 创建ACO优化函数我们可以使用Matlab来创建一个函数来实现ACO算法。
我们称其为“ACOoptimization.m”。
function best_path =ACOoptimization(city_location,iter_num,ant_num,init ial_path,alpha,beta,rho,update_flag) %ACO优化函数 %输入: %city_location: 城市坐标矩阵,格式为[x1,y1;x2,y2;...;xn,yn] %iter_num: 迭代次数 %ant_num: 蚂蚁数量 %initial_path: 起始路径,即初始解 %alpha,beta,rho: 超参数,用于调节蚂蚁选择路径的概率 %update_flag: 是否更新信息素的标志(1表示更新,0表示否) %输出: %best_path: 最优解,即最短路径%初始化信息素 pheromone = 0.01 *ones(length(city_location),length(city_location)); %初始化路径权重 path_weight =zeros(ant_num,1); %城市数量 n_cities =length(city_location);%主循环 for iter = 1:iter_num %一个迭代里所有蚂蚁都寻找一遍路径 for ant =1:ant_num %初始化蚂蚁位置current_city = initial_path; %标记是否经过了某个城市 visit_flag =zeros(1,n_cities);visit_flag(current_city) = 1; %用来存储当前路径 current_path = [current_city];%蚂蚁找东西 for i =1:n_cities-1 %计算路径概率p =calculate_probability(current_city,visit_flag,phero mone,city_location,alpha,beta); %蚂蚁选择路径 [next_city,next_index] = select_path(p);%路径更新current_path = [current_path;next_city];visit_flag(next_city) = 1;current_city = next_city;%更新路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end-1),:),city_location(current_path(end),:));end%加入回到起点的路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end),:),city_location(current_path(1),:));%判断是否为最优解 ifant == 1 best_path = current_path; else if path_weight(ant) <path_weight(ant-1) best_path =current_path; end end%更新信息素 ifupdate_flag == 1 pheromone =update_pheromone(pheromone,path_weight,initial_path,current_path,rho); end end end end在函数中,我们首先定义了ACOalg函数的参数,包括城市坐标矩阵,迭代次数,蚂蚁数量,初始路径,超参数alpha,beta,rho,以及是否需要更新信息素。
蚁群算法步骤

蚁群算法(Ant Colony Optimization, ACO)是一种基于蚁群的群体智能算法,用于求解组合优化问题。
下面是蚁群算法的基本步骤:
1.初始化
在算法开始前,需对相关参数进行初始化,例如:蚂蚁群大小、信息素参数等。
此外,需要定义问题空间中每个解的初始状态,以及预设的目标函数。
2.蚁群搜索
在搜索阶段,蚂蚁会基于启发式信息(包括距离信息和信息素信息)进行路径选择,从而寻找到一组解来尽可能地优化目标函数。
对于每个蚂蚁,它将从初始位置出发,经过一系列的决策,最终到达目标位置,同时产生一条路径。
3.更新信息素
当所有的蚂蚁完成搜索后,将根据每个蚂蚁的路径更新信息素表。
结合各蚂蚁的贡献,信息素的浓度将被不断变化以反映出对当前问题具有的经验。
通过信息素的积累,越来越多的蚂蚁会选择这些较优的路径,从而找到更优的解。
4.重复搜索
重复执行步骤2和3,直到满足预设的停止条件。
通常停止条件是指已经经过了预设的搜索迭代次数或运行时间已过期等等。
在整个搜索过程中,各个蚂蚁将会逐渐集中于最优路径周围,以最小化目标函数。
5.解码和输出
最后,需要通过对最优路径进行解码来获得最佳解,并输出到相应的应用中。
总之,蚁群算法是一种有效的算法,在组合优化问题中具有优异的性能,例如旅行商问题、网络路径优化、调度安排等。
掌握蚁群算法的基本步骤和优化策略,可以为相关问题的求解提供有力的支持。
蚁群算法在MATLAB中的实现

速率 挥发 , 过一段 时间 的搜 索 , 短路径 上 的信 息 经 最
素将 会越来越 浓 , 照 最短 路 径移 动 的蚂蚁 将 会 越 按
短路 径 , 然后进行 信息 素 的更 新 , 息素 的更新采用 信
公式 ( )一( ) 3 4 进行 。
来越 多 , 而形成一个 正反馈 , 进 使得 它们 可 以找 到最 短路 径 。所 以在蚁 群算 法 的实现 过 程 中 , 键 的步 关
摘
要 :蚁群 算法是 近年 来兴起 的一种 新型 仿 生优 化 算 法 ,具 有 其他进 化 算 法 不可 比拟 的优 势 。
以旅 行 商问题 为例 ,首先描 述 了蚁群 算 法 的 工作 原理 ,然 后 给 出 了该 算法在 MA L B 中实现 的 TA
详 细步骤 ,最后 分别 以 1 ,2 ,2 7 1 4,4 ,5 ,7 8 1 0为城 市规 模 进 行 了算 法验 证 ,给 出 了算 法运 行 的 最优 结 果、最差 结果 、平 均结果 及 运行 时 间与 结 果 图。 算 法的 实现 为 在 其他 领 域 中的应 用 和 进一 步的 改进提 供 了基础 ,同时也 弥补 了其 他 资料 中很 少涉及 实现 应 用的不足 。
在原 地 打转 。每个 蚂 蚁 在 向新 节点 移 动前 , 用 公 使 式( ) 1 计算 到达 N — itd 中每个 节点 的概率 P oVse 表 i 。
eae能够记 录算法运行 结束 时 的最优路径 Soet rg, h ̄ s —
R ue ot 及最 优路 径长 度 S ot t L n t 算法 的运 hrs e g e— h和
【 蚂蚁 k 经过结 点 , 0, 不
市节 点 , …… 等 , 市 之 间 的 距 离 使 用 欧 式 距 离 表 城 示 。现将 m个蚂 蚁随机放 到 个 城 市节 点 , 每个 蚂 蚁访 问过 的城市节 点放 人到 Vse 中 , 为禁 忌 itd表 i 作
蚁群优化算法原理及Matlab编程实现

蚁群优化算法原理及Matlab编程实现
蚁群算法的提出:
人工蚂蚁与真实蚂蚁的异同比较
相同点比较
不同点比较
蚁群算法的流程图
基本蚁群算法的实现步骤
(i,j)的初始化信息量τij(t) = const,其中const表示常数,且初始时刻Δτij(0) = 0。
(2)循环次数。
(3)蚂蚁的禁忌表索引号k=1。
(4)蚂蚁数目。
(5)蚂蚁个体根据状态转移概率公式计算的概率选择元素(城市)j并前进,。
其中,表示在t时刻蚂蚁k由元素(城市)i转移到元素(城市)j的状态转
重要性,反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重
视程度,其值越大,则该状态转移概率越接近于贪心规则;ηij(t)为启发函数,
表达式为。
式中,d ij表示相邻两个城市之间的距离。
(6)修改禁忌表指针,即选择好之后将蚂蚁移动到新的元素(城市),并把该τij(t + n) = (1 − ρ) * τij(t) + Δτij(t)
(9)若满足结束条件,即如果循环次数,则循环结束并输出程序计算结果,
]蚁群算法的matlab源程序1.蚁群算法主程序:main.m
2.蚁群算法寻找路径程序:path.m
[编辑]蚁群算法仿真结果。
蚁群算法最短路径matlab程序 - 副本

蚁群算法最短路径matlab程序 - 副本蚁群算法最短路径通用Matlab程序下面的程序是蚁群算法在最短路中的应用,稍加扩展即可应用于机器人路径规划function [ROUTES,PL,Tau]=ACASP(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q) D=G2D(G);N=size(D,1);%N表示问题的规模(象素个数) MM=size(G,1);a=1;%小方格象素的边长Ex=a*(mod(E,MM)-0.5);%终止点横坐标if Ex==-0.5Ex=MM-0.5;endEy=a*(MM+0.5-ceil(E/MM)); Eta=zeros(1,N); for i=1:N if ix==-0.5 ix=MM-0.5;endiy=a*(MM+0.5-ceil(i/MM)); if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);PL=zeros(K,M);%% -----------启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁--------------------for k=1:Kdisp(k);for m=1:MW=S;Path=S;PLkm=0;TABUkm=ones(1,N);TABUkm(S)=0;DD=D;DW=DD(W,:);DW1=find(DW)for j=1:length(DW1)if TABUkm(DW1(j))==0 DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD); while W~=E&&Len_LJD>=1 PP=zeros(1,Len_LJD); for i=1:Len_LJDPP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);endPP=PP/(sum(PP)); Pcum=cumsum(PP);Select=find(Pcum>=rand);Path=[Path,to_visit]; PLkm=PLkm+DD(W,to_visit); W=to_visit;for kk=1:Nif TABUkm(kk)==0 DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;for j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数 end ROUTES{k,m}=Path; if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endendDelta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m) ROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分 end %% ---------------------------绘图-------------------------------- plotif=1;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLKPLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)'); xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); hold onendendendhold onROUT=ROUTES{K,M};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=1;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)hold onendend将上述算法应用于机器人路径规划,优化效果如下图所示。
蚁群算法 蚁狮算法

蚁群算法蚁狮算法
蚁群算法(Ant Colony Algorithm)是一种模拟蚂蚁觅食行为的启发式优化算法。
它通过模拟蚂蚁在寻找食物过程中释放信息素的行为,来解决组合优化问题。
蚂蚁在寻找食物时会在路径上释放一种化学物质,称为信息素,其他蚂蚁通过感知到信息素的浓度来选择路径,从而实现最优路径的搜索。
蚁群算法的基本思想是:在解空间中随机生成一群蚂蚁,每只蚂蚁根据当前位置和信息素浓度选择下一个移动位置,移动后释放信息素。
信息素浓度会随着时间的推移逐渐蒸发。
蚂蚁根据信息素浓度和启发函数来选择下一个位置,启发函数一般根据问题的特性来设计。
最终,通过迭代更新信息素浓度和蒸发,蚂蚁群体会逐渐收敛到最优解。
蚁狮算法(Ant Lion Optimizer)是一种基于蚁狮捕食行为的启发式优化算法。
蚁狮是一种昆虫,它会在沙地上挖掘坑穴,然后隐藏在坑穴中等待猎物。
当猎物掉进坑穴时,蚁狮会迅速捕捉并吃掉它。
蚁狮算法模拟了蚁狮捕食行为,通过追踪猎物的行为来寻找最优解。
蚁狮算法的基本思想是:在解空间中随机生成一群蚂蚁,每只蚂蚁根据当前位置和信息素浓度选择下一个移动位置。
与蚁群算法不同的是,蚁狮算法引入了一个蚁狮,它代表了当前最优解,蚂蚁会追踪蚁狮的位置。
当蚂蚁接近蚁狮时,它会增加信息素浓度,从而吸引其他蚂蚁朝着蚁狮方向移动。
蚁狮会不断更新自身位置,以寻找
更优解。
最终,通过迭代更新信息素浓度和蚁狮位置,蚂蚁群体会逐渐收敛到最优解。
matlab智能算法代码

matlab智能算法代码MATLAB是一种功能强大的数值计算和科学编程软件,它提供了许多智能算法的实现。
下面是一些常见的智能算法及其在MATLAB中的代码示例:1. 遗传算法(Genetic Algorithm):MATLAB中有一个专门的工具箱,称为Global Optimization Toolbox,其中包含了遗传算法的实现。
以下是一个简单的遗传算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置遗传算法参数。
options = gaoptimset('Display', 'iter','PopulationSize', 50);% 运行遗传算法。
[x, fval] = ga(fitness, 1, options);2. 粒子群优化算法(Particle Swarm Optimization):MATLAB中也有一个工具箱,称为Global Optimization Toolbox,其中包含了粒子群优化算法的实现。
以下是一个简单的粒子群优化算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置粒子群优化算法参数。
options = optimoptions('particleswarm', 'Display','iter', 'SwarmSize', 50);% 运行粒子群优化算法。
[x, fval] = particleswarm(fitness, 1, [], [], options);3. 支持向量机(Support Vector Machine):MATLAB中有一个机器学习工具箱,称为Statistics and Machine Learning Toolbox,其中包含了支持向量机的实现。
蚁群算法MATLAB解VRP问题
蚁群算法MATLAB解VRP问题Excel exp12_3_2.xls内容:ANT_VRP函数:function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q) %% R_best 各代最佳路线%% L_best 各代最佳路线的长度%% L_ave 各代平均距离%% Shortest_Route 最短路径%% Shortest_Length 最短路径长度%% D 城市间之间的距离矩阵,为对称矩阵%% Demand 客户需求量%% Cap 车辆最⼤载重%% iter_max 最⼤迭代次数%% m 蚂蚁个数%% Alpha 表征信息素重要程度的参数%% Beta 表征启发式因⼦重要程度的参数%% Rho 信息素蒸发系数%% Q 信息素增加强度系数n=size(D,1);T=zeros(m,2*n); %装载距离Eta=ones(m,2*n); %启发因⼦Tau=ones(n,n); %信息素Tabu=zeros(m,n); %禁忌表Route=zeros(m,2*n); %路径L=zeros(m,1); %总路程L_best=zeros(iter_max,1); %各代最佳路线长度R_best=zeros(iter_max,2*n); %各代最佳路线nC=1;while nC<=iter_max %停⽌条件Eta=zeros(m,2*n);T=zeros(m,2*n);Tabu=zeros(m,n);Route=zeros(m,2*n);L=zeros(m,1);%%%%%%==============初始化起点城市(禁忌表)====================for i=1:mCap_1=Cap; %最⼤装载量j=1;j_r=1;while Tabu(i,n)==0T=zeros(m,2*n); %装载量加载矩阵Tabu(i,1)=1; %禁忌表起点位置为1Route(i,1)=1; %路径起点位置为1visited=find(Tabu(i,:)>0); %已访问城市num_v=length(visited); %已访问城市个数J=zeros(1,(n-num_v)); %待访问城市加载表P=J; %待访问城市选择概率分布Jc=1; %待访问城市选择指针for k=1:n %城市if length(find(Tabu(i,:)==k))==0 %如果k不是已访问城市代号,就将k加⼊矩阵J中J(Jc)=k;Jc=Jc+1;endend%%%%%%%=============每只蚂蚁按照选择概率遍历所有城市==================for k=1:n-num_v %待访问城市if Cap_1-Demand(J(1,k),1)>=0 %如果车辆装载量⼤于待访问城市需求量if Route(i,j_r)==1 %如果每只蚂蚁在起点城市T(i,k)=D(1,J(1,k));P(k)=(Tau(1,J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率计算公式中的分⼦else %如果每只蚂蚁在不在起点城市T(i,k)=D(Tabu(i,j),J(1,k));P(k)=(Tau(Tabu(i,visited(end)),J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率计算公式中的分⼦endelse %如果车辆装载量⼩于待访问城市需求量T(i,k)=0;P(k)=0;endendif length(find(T(i,:)>0))==0 %%%当车辆装载量⼩于待访问城市时,选择起点为1Cap_1=Cap;j_r=j_r+1;Route(i,j_r)=1;L(i)=L(i)+D(1,Tabu(i,visited(end)));elseP=P/(sum(P)); %按照概率原则选取下⼀个城市Pcum=cumsum(P); %求累积概率和:cumsum([1 2 3])=1 3 6,⽬的在于使得Pcum的值总有⼤于rand的数Select=find(Pcum>rand); %按概率选取下⼀个城市:当累积概率和⼤于给定的随机数,则选择求和被加上的最后⼀个城市作为即将访问的城市 o_visit=J(1,Select(1)); %待访问城市j=j+1;j_r=j_r+1;Tabu(i,j)=o_visit; %待访问城市Route(i,j_r)=o_visit;Cap_1=Cap_1-Demand(o_visit,1); %车辆装载剩余量L(i)=L(i)+T(i,Select(1)); %路径长度endendL(i)=L(i)+D(Tabu(i,n),1); %%路径长度endL_best(nC)=min(L); %最优路径为距离最短的路径pos=find(L==min(L)); %找出最优路径对应的位置:即为哪只蚂蚁R_best(nC,:)=Route(pos(1),:); %确定最优路径对应的城市顺序L_ave(nC)=mean(L)'; %求第k次迭代的平均距离Delta_Tau=zeros(n,n); %Delta_Tau(i,j)表⽰所有蚂蚁留在第i个城市到第j个城市路径上的信息素增量L_zan=L_best(1:nC,1);post=find(L_zan==min(L_zan));Cities=find(R_best(nC,:)>0);num_R=length(Cities);for k=1:num_R-1 %建⽴了完整路径后在释放信息素Delta_Tau(R_best(nC,k),R_best(nC,k+1))=Delta_Tau(R_best(nC,k),R_best(nC,k+1))+Q/L_best(nC);endDelta_Tau(R_best(nC,num_R),1)=Delta_Tau(R_best(nC,num_R),1)+Q/L_best(nC);Tau=Rho*Tau+Delta_Tau;nC=nC+1;endShortest_Route=zeros(1,2*n); %提取最短路径Shortest_Route(1,:)=R_best(iter_max,:);Shortest_Route=Shortest_Route(Shortest_Route>0);Shortest_Route=[Shortest_Route Shortest_Route(1,1)];Shortest_Length=min(L_best); %提取最短路径长度%L_ave=mean(L_best); 求解程序:clc;clear all%% ==============提取数据==============[xdata,textdata]=xlsread('exp12_3_2.xls'); %加载20个城市的数据,数据按照表格中位置保存在Excel⽂件exp12_3_1.xls中x_label=xdata(:,2); %第⼆列为横坐标y_label=xdata(:,3); %第三列为纵坐标Demand=xdata(:,4); %第四列为需求量C=[x_label y_label]; %坐标矩阵n=size(C,1); %n表⽰节点(客户)个数%% ==============计算距离矩阵==============D=zeros(n,n); %D表⽰完全图的赋权邻接矩阵,即距离矩阵D初始化for i=1:nfor j=1:nif i~=jD(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算两城市之间的距离elseD(i,j)=0; %i=j, 则距离为0;endD(j,i)=D(i,j); %距离矩阵为对称矩阵endendAlpha=1;Beta=5;Rho=0.75;iter_max=100;Q=10;Cap=1;m=20; %Cap为车辆最⼤载重[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q); %蚁群算法求解VRP问题通⽤函数,详见配套光盘Shortest_Route_1=Shortest_Route-1 %提取最优路线Shortest_Length %提取最短路径长度%% ==============作图==============figure(1) %作迭代收敛曲线图x=linspace(0,iter_max,iter_max);y=L_best(:,1);plot(x,y);xlabel('迭代次数'); ylabel('最短路径长度');figure(2) %作最短路径图plot([C(Shortest_Route,1)],[C(Shortest_Route,2)],'o-');grid onfor i =1:size(C,1)text(C(i,1),C(i,2),[' ' num2str(i-1)]);endxlabel('客户所在横坐标'); ylabel('客户所在纵坐标');。
蚁群算法在Matlab中的程序设计

f r ( t +1 )=( 1一P ) ( t )+△
k ㈤ :
2 . 1 . 1 数据的初始化 这个步骤主要完成 以下数据 的初始化 : ①通过 已知 的 n个城市 坐标 , 求 得 每 两个 城 市 间 的距 离并 保存在距离矩阵中; ②初始化信息素矩阵; ③初始化 算法参数 ; ④初始化记录数据的变量及矩阵。 2 . 1 . 2 通过算法寻找最优路径 运行算法 , 通过迭代来计算最优路径 , 直到满足
否则
S t e p 2, 否 则输 出结果 。 整 个步 骤的算 法框 图如 图 2所示 。
2 . 3 运 行结 果及分 析 式( 3 ) 中, Q为 常数 , 表 示蚂 蚁循 环 一次 所 释放 的信
息素的总量 ; 为蚂蚁 k 经过的路径长度 。
2 用M a t l a b实现蚁群 算法
Ma t l a b是一个 功 能强大 的科学 计算 和工 程计 算
结果 数 据 以 图表 的形 式 展示 出来 , 如 图 3和图 4所 示 分 别 为 蚁 群 算 法 最 短 路 径 和 各 代 的 收 敛 情况。 从 图 中可 以看 出 , 本 算 法 得 到 的最 短距 离 为 1 5 6 0 1 . 9 1 9 5 k m, 而最 短距 离 在 迭代 了 1 0 0次 以后 基 本上 就 接近最短 路 径 了 , 平 均 距 离也 在 迭代 次 数 达 到1 0 0次后趋 于平 缓 。程序运行 的输 出结果 为 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%%=========================================================================
%% 主要符号说明
%% C n个城市的坐标,n×2的矩阵
%% NC_max 蚁群算法MATLAB程序最大迭代次数
%% m 蚂蚁个数
NC=1; %迭代计数器,记录迭代次数
R_best=zeros(NC_max,n); %各代最佳路线
L_best=inf.*ones(NC_max,1); %各代最佳路线的长度
%% 蚁群算法MATLAB程序第三步:m只蚂蚁按概率函数选择下一座城市,完成各自的周游
for j=2:n %所在城市不计算
for i=1:m
visited=Tabu(i,1:(j-1)); %记录已访问的城市,避免重复访问
Randpos=[]; %随即存取
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))'; %此句不太理解?
end
L_best(NC)=min(L); %最佳距离取最小
pos=find(L==L_best(NC));
R_best(NC,:)=Tabu(pos(1),:); %此轮迭代后的最佳路线
DrawRoute(C,Shortest_Route) %画路线图的子函数
subplot(1,2,2) %绘制第二个子图形
plot(L_best)
else
D(i,j)=eps; % i = j 时不计算,应该为0,但后面的启发因子要取倒数,用eps(浮点相对精度)表示
end
D(j,i)=D(i,j); %对称矩阵
L_ave=zeros(NC_max,1); %各代路线的平均长度
while NC<=NC_max %停止条件之一:达到最大迭代次数,停止
%% 蚁群算法MATLAB程序第二步:将m只蚂蚁放到n个城市上
%% DrawRoute.m
%% 画路线图的子函数
%%-------------------------------------------------------------------------
%% C Coordinate 节点坐标,由一个N×2的矩阵存储
%% R Route 路线
L(i)=L(i)+D(R(j),R(j+1)); %原距离加上第j个城市到第j+1个城市的距离
end
L(i)=L(i)+D(R(1),R(n)); %一轮下来后走过的距离
J=zeros(1,(n-j+1)); %待访问的城市
P=J; %待访问城市的选择概率分布
Jc=1;
for k=1:n
%% 蚁群算法MATLAB程序第六步:禁忌表清零
Tabu=zeros(m,n); %%直到最大迭代次数
end
%% 蚁群算法MATLAB程序第七步:输出结果
Pos=find(L_best==min(L_best)); %找到最佳路径(非0为真)
for k=1:length(J)
P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
end
P=P/(sum(P));
%% 按概率原则选取下一个城市
Pcum=cumsum(P); %cumsum,元素累加即求和
Delta_Tau=zeros(n,n); %开始时信息素为n*n的0矩阵
for i=1:m
for j=1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
% 以下是蚁群算法MATLAB程序,请尊重原作者劳动,引用时请注明出处。
% 已经运行过,无误。
% 蚁群算法MATLAB程序
function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ACATSP(C,NC_max,m,Alpha,Beta,Rho,Q)
end
end
Eta=1./D; %Eta为启发因子,这里设为距离的倒数
Tau=ones(n,n); %Tau为信息素矩阵
Tabu=zeros(m,n); %存储并记录路径的生成
hold on %保持图形
plot(L_ave,'r')
title('平均距离和最短距离') %标题
% 蚁群算法MATLAB程序子函数
function DrawRoute(C,R)
%%=========================================================================
%% Alpha 表征信息素重要程度的参数
%% Beta 表征启发式因子重要程度的参数
%% Rho 信息素蒸发系数
%% Q 表示蚁群算法MATLAB程序信息素增加强度系数
%% R_best 各代最佳路线
%% L_best 各代最佳路线的长度
%%=========================================================================
if length(find(visited==k))==0 %开始时置0
J(Jc)=k;
Jc=Jc+1; %访问的城市个数自加1
end
end
%% 下面计算蚁群算法MATLAB程序待选城市的概率分布
hold on
for ii=2:N Fra bibliotekplot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
hold on
end
title('旅行商问题优化结果 ')
end
%% 蚁群算法MATLAB程序第四步:记录本次迭代最佳路线
L=zeros(m,1); %开始距离为0,m*1的列向量
for i=1:m
R=Tabu(i,:);
for j=1:(n-1)
Shortest_Route=R_best(Pos(1),:) %最大迭代次数后最佳路径
Shortest_Length=L_best(Pos(1)) %最大迭代次数后最短距离
subplot(1,2,1) %绘制第一个子图形
Select=find(Pcum>=rand); %若计算的概率大于原来的就选择这条路线
to_visit=J(Select(1));
Tabu(i,j)=to_visit;
end
end
if NC>=2
Tabu(1,:)=R_best(NC-1,:);
%%=========================================================================
N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
L_ave(NC)=mean(L); %此轮迭代后的平均距离
NC=NC+1 %迭代继续
%% 蚁群算法MATLAB程序第五步:更新信息素
%% 蚁群算法MATLAB程序第一步:变量初始化
n=size(C,1);%n表示问题的规模(城市个数)
D=zeros(n,n);%D表示完全图的赋权邻接矩阵
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
%此次循环在路径(i,j)上的信息素增量
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
%此次循环在整个路径上的信息素增量
end
Tau=(1-Rho).*Tau+Delta_Tau; %考虑信息素挥发,更新后的信息素
