蚁群算法MATLAB代码

合集下载

蚁群算法

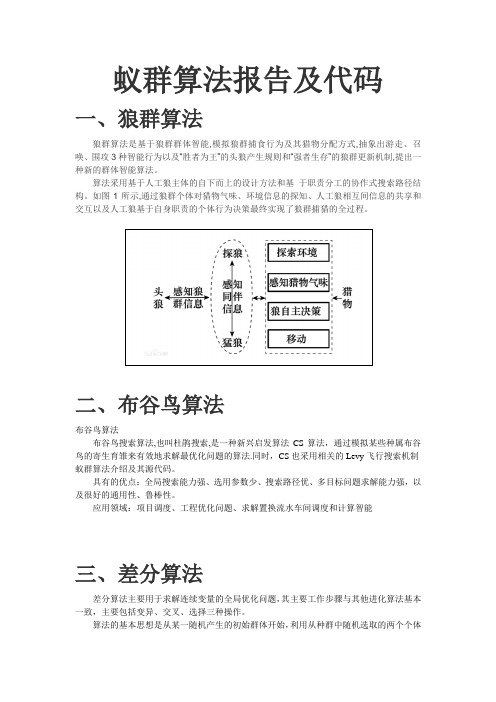
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。

算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。

如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。

二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法，通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时，CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。

具有的优点：全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强，以及很好的通用性、鲁棒性。

应用领域：项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异、交叉、选择三种操作。

算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。

然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。

如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。

在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。

四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。

从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。

五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度。

30个智能算法matlab代码

30个智能算法matlab代码以下是30个使用MATLAB编写的智能算法的示例代码： 1. 线性回归算法：matlab.x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];coefficients = polyfit(x, y, 1);predicted_y = polyval(coefficients, x);2. 逻辑回归算法：matlab.x = [1, 2, 3, 4, 5];y = [0, 0, 1, 1, 1];model = fitglm(x, y, 'Distribution', 'binomial'); predicted_y = predict(model, x);3. 支持向量机算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3];y = [1, 1, -1, -1, -1];model = fitcsvm(x', y');predicted_y = predict(model, x');4. 决策树算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitctree(x', y');predicted_y = predict(model, x');5. 随机森林算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = TreeBagger(50, x', y');predicted_y = predict(model, x');6. K均值聚类算法：matlab.x = [1, 2, 3, 10, 11, 12]; y = [1, 2, 3, 10, 11, 12]; data = [x', y'];idx = kmeans(data, 2);7. DBSCAN聚类算法：matlab.x = [1, 2, 3, 10, 11, 12]; y = [1, 2, 3, 10, 11, 12]; data = [x', y'];epsilon = 2;minPts = 2;[idx, corePoints] = dbscan(data, epsilon, minPts);8. 神经网络算法：matlab.x = [1, 2, 3, 4, 5];y = [0, 0, 1, 1, 1];net = feedforwardnet(10);net = train(net, x', y');predicted_y = net(x');9. 遗传算法：matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;options = gaoptimset('PlotFcns', @gaplotbestf);[x, fval] = ga(fitnessFunction, nvars, [], [], [], [], lb, ub, [], options);10. 粒子群优化算法：matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;options = optimoptions('particleswarm', 'PlotFcn',@pswplotbestf);[x, fval] = particleswarm(fitnessFunction, nvars, lb, ub, options);11. 蚁群算法：matlab.distanceMatrix = [0, 2, 3; 2, 0, 4; 3, 4, 0];pheromoneMatrix = ones(3, 3);alpha = 1;beta = 1;iterations = 10;bestPath = antColonyOptimization(distanceMatrix, pheromoneMatrix, alpha, beta, iterations);12. 粒子群-蚁群混合算法：matlab.distanceMatrix = [0, 2, 3; 2, 0, 4; 3, 4, 0];pheromoneMatrix = ones(3, 3);alpha = 1;beta = 1;iterations = 10;bestPath = particleAntHybrid(distanceMatrix, pheromoneMatrix, alpha, beta, iterations);13. 遗传算法-粒子群混合算法：matlab.fitnessFunction = @(x) x^2 4x + 4;nvars = 1;lb = 0;ub = 5;gaOptions = gaoptimset('PlotFcns', @gaplotbestf);psOptions = optimoptions('particleswarm', 'PlotFcn',@pswplotbestf);[x, fval] = gaParticleHybrid(fitnessFunction, nvars, lb, ub, gaOptions, psOptions);14. K近邻算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitcknn(x', y');predicted_y = predict(model, x');15. 朴素贝叶斯算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; y = [0, 0, 1, 1, 1];model = fitcnb(x', y');predicted_y = predict(model, x');16. AdaBoost算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3];y = [0, 0, 1, 1, 1];model = fitensemble(x', y', 'AdaBoostM1', 100, 'Tree'); predicted_y = predict(model, x');17. 高斯混合模型算法：matlab.x = [1, 2, 3, 4, 5]';y = [0, 0, 1, 1, 1]';data = [x, y];model = fitgmdist(data, 2);idx = cluster(model, data);18. 主成分分析算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; coefficients = pca(x');transformed_x = x' coefficients;19. 独立成分分析算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; coefficients = fastica(x');transformed_x = x' coefficients;20. 模糊C均值聚类算法：matlab.x = [1, 2, 3, 4, 5; 1, 2, 2, 3, 3]; options = [2, 100, 1e-5, 0];[centers, U] = fcm(x', 2, options);21. 遗传规划算法：matlab.fitnessFunction = @(x) x^2 4x + 4; nvars = 1;lb = 0;ub = 5;options = optimoptions('ga', 'PlotFcn', @gaplotbestf);[x, fval] = ga(fitnessFunction, nvars, [], [], [], [], lb, ub, [], options);22. 线性规划算法：matlab.f = [-5; -4];A = [1, 2; 3, 1];b = [8; 6];lb = [0; 0];ub = [];[x, fval] = linprog(f, A, b, [], [], lb, ub);23. 整数规划算法：matlab.f = [-5; -4];A = [1, 2; 3, 1];b = [8; 6];intcon = [1, 2];[x, fval] = intlinprog(f, intcon, A, b);24. 图像分割算法：matlab.image = imread('image.jpg');grayImage = rgb2gray(image);binaryImage = imbinarize(grayImage);segmented = medfilt2(binaryImage);25. 文本分类算法：matlab.documents = ["This is a document.", "Another document.", "Yet another document."];labels = categorical(["Class 1", "Class 2", "Class 1"]);model = trainTextClassifier(documents, labels);newDocuments = ["A new document.", "Another new document."];predictedLabels = classifyText(model, newDocuments);26. 图像识别算法：matlab.image = imread('image.jpg');features = extractFeatures(image);model = trainImageClassifier(features, labels);newImage = imread('new_image.jpg');newFeatures = extractFeatures(newImage);predictedLabel = classifyImage(model, newFeatures);27. 时间序列预测算法：matlab.data = [1, 2, 3, 4, 5];model = arima(2, 1, 1);model = estimate(model, data);forecastedData = forecast(model, 5);28. 关联规则挖掘算法：matlab.data = readtable('data.csv');rules = associationRules(data, 'Support', 0.1);29. 增强学习算法：matlab.environment = rlPredefinedEnv('Pendulum');agent = rlDDPGAgent(environment);train(agent);30. 马尔可夫决策过程算法：matlab.states = [1, 2, 3];actions = [1, 2];transitionMatrix = [0.8, 0.1, 0.1; 0.2, 0.6, 0.2; 0.3, 0.3, 0.4];rewardMatrix = [1, 0, -1; -1, 1, 0; 0, -1, 1];policy = mdpPolicyIteration(transitionMatrix, rewardMatrix);以上是30个使用MATLAB编写的智能算法的示例代码，每个算法都可以根据具体的问题和数据进行相应的调整和优化。

蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码标题：蚁群算法路径优化 MATLAB 代码正文:蚁群算法是一种基于模拟蚂蚁搜索食物路径的优化算法，常用于求解复杂问题。

在路径优化问题中，蚂蚁需要从起点移动到终点，通过探索周围区域来寻找最短路径。

MATLAB 是一个常用的数值计算软件，可以用来实现蚁群算法的路径优化。

下面是一个基本的 MATLAB 代码示例，用于实现蚁群算法的路径优化:```matlab% 定义参数num_ants = 100; % 蚂蚁数量num_steps = 100; % 路径优化步数search_radius = 2; % 搜索半径max_iterations = 1000; % 最大迭代次数% 随机生成起点和终点的位置坐标start_pos = [randi(100), randi(100)];end_pos = [75, 75];% 初始化蚂蚁群体的位置和方向ants_pos = zeros(num_ants, 2);ants_dir = zeros(num_ants, 2);for i = 1:num_antsants_pos(i, :) = start_pos + randn(2) * search_radius; ants_dir(i, :) = randomvec(2);end% 初始化蚂蚁群体的速度ants_vel = zeros(num_ants, 2);for i = 1:num_antsants_vel(i, :) = -0.1 * ants_pos(i, :) + 0.5 *ants_dir(i, :);end% 初始时蚂蚁群体向终点移动for i = 1:num_antsans_pos = end_pos;ans_vel = ants_vel;for j = 1:num_steps% 更新位置和速度ans_pos(i) = ans_pos(i) + ans_vel(i);ants_vel(i, :) = ones(1, num_steps) * (-0.1 * ans_pos(i) + 0.5 * ans_dir(i, :));end% 更新方向ants_dir(i, :) = ans_dir(i, :) - ans_vel(i) * 3;end% 迭代优化路径max_iter = 0;for i = 1:max_iterations% 计算当前路径的最短距离dist = zeros(num_ants, 1);for j = 1:num_antsdist(j) = norm(ants_pos(j) - end_pos);end% 更新蚂蚁群体的位置和方向for j = 1:num_antsants_pos(j, :) = ants_pos(j, :) - 0.05 * dist(j) * ants_dir(j, :);ants_dir(j, :) = -ants_dir(j, :);end% 更新蚂蚁群体的速度for j = 1:num_antsants_vel(j, :) = ants_vel(j, :) - 0.001 * dist(j) * ants_dir(j, :);end% 检查是否达到最大迭代次数if i > max_iterationsbreak;endend% 输出最优路径[ans_pos, ans_vel] = ants_pos;path_dist = norm(ans_pos - end_pos);disp(["最优路径长度为:" num2str(path_dist)]);```拓展:上述代码仅仅是一个简单的示例，实际上要实现蚁群算法的路径优化，需要更加复杂的代码实现。

蚁群算法的Python代码及其效果演示(含注释)

蚁群算法的Python代码及其效果演示（含注释）以下为基本蚁群算法的Python代码（含注释）。

随时可以运行：from turtle import*from random import*from json import loadk=load(open("stats.json"))city_num,ant_num=30,30 #规定城市和蚂蚁总数x_data=k[0] #城市的x坐标之集合y_data=k[1] #城市的y坐标之集合best_length=float("inf")best_path=[]alpha=1beta=7rho=0.5potency_list=[1 for xx in range(city_num**2)]Q=1##城市的index从0开始#下面列表存储城市间距离def get_i_index(n):if n%city_num==0:return n//city_num-1else:return n//city_numdef get_j_index(n):if n%city_num==0:return city_num-1else:return n%city_num-1distance_list=[((x_data[get_i_index(z)]-x_data[get_j_index(z)])**2+(y_data[get_i_index(z)]-y_data[get_j_index(z)])**2)**0.5 for z in range(1,city_num**2+1)]class ant(object):def __init__(self,ant_index):self.ant_index=ant_indexself.cities=list(range(city_num))self.current_length=0self.current_city=randint(0,city_num-1)self.initial_city=self.current_cityself.cities.remove(self.current_city)self.path=[self.current_city]self.length=0#根据城市的index求出两城市间距离def get_distance(self,index_1,index_2):return distance_list[index_1*city_num+index_2]def get_potency(self,index_1,index_2):return potency_list[index_1*city_num+index_2]def get_prob_list(self):res=[self.get_potency(self.current_city,x)**alpha*(1/self.get_distance(self.current_city,x))**bet a for x in self.cities]sum_=sum(res)final_res=[y/sum_ for y in res]return final_res##轮盘赌选择城市def __choose_next_city(self):city_list=self.citiesprob_list=self.get_prob_list()tmp=random()sum_=0for city,prob in zip(city_list,prob_list):sum_+=probif sum_>=tmp:self.length+=self.get_distance(self.current_city,city)self.current_city=cityself.path.append(self.current_city)self.cities.remove(self.current_city)returndef running(self):global best_length,best_pathfor x in range(city_num-1):self.__choose_next_city()self.length+=self.get_distance(self.current_city,self.initial_city)self.path.append(self.initial_city)if self.length<best_length:best_length=self.lengthbest_path=self.pathreturn (self.path,self.length)def go():operation=[]for x in potency_list:x*=(1-rho)for x in range(ant_num):operation.append(ant(x).running())for x in operation:for y in range(city_num-1):potency_list[x[0][y]*city_num+x[0][y+1]]+=Q/x[1]#print(f"potency_list:{potency_list}")#print(f"best_path:{best_path}")#print(f"best_length:{best_length}")for yy in range(1000):go()print(f"best_length:{best_length}")pu()setpos(x_data[best_path[0]],y_data[best_path[0]])pd()for x in range(1,city_num+1):setpos(x_data[best_path[x]],y_data[best_path[x]]) 运行效果：。

蚁群算法路径优化算法

其中，表示在t时刻蚂蚁k由元素（城市）i转移到元素（城市）j的状态转移概率。

allowedk = C − tabuk表示蚂蚁k下一步允许选择的城市。

α为启发式因子，表示轨迹的相对重要性，反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用，其值越大，则该蚂蚁越倾向于选择其他蚂蚁经过的路径，蚂蚁之间的协作性越强。

β为期望启发式因子，表示能见度的相对重要性，反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度，其值越大，则该状态转移概率越接近于贪心规则；ηij(t) 为启发函数，表达式为。

式中，dij表示相邻两个城市之间的距离。

（6）修改禁忌表指针，即选择好之后将蚂蚁移动到新的元素（城市），并把该元素（城市）移动到该蚂蚁个体的禁忌表中。

（7）若集合C中元素（城市）未遍历完，即k<m，则跳转到第（4）步，否则执行第（8）步。

（8）根据公式更新每条路径上的信息量：τij(t + n) = (1 − ρ) * τij(t) + Δτij(t),（9）若满足结束条件，即如果循环次数，则循环结束并输出程序计算结果，否则清空禁忌表并跳转到第（2）步。

蚁群算法的matlab源程序1.蚁群算法主程序：main.m%function [bestroute,routelength]=AntClccleartic% 读入城市间距离矩阵数据文件CooCity = load( 'CooCity.txt' ) ;% 城市网络图坐标数据文件，txt形式给出NC=length(CooCity); % 城市个数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((CooCity(i,2)-CooCity(j,2))^2+(CooCity(i,3)-CooCity(j,3))^2);endendMAXIT=10;%最大循环次数Citystart=[]; % 起点城市编号tau=ones(NC,NC); % 初始时刻各边上的信息痕迹为1rho=0.5; % 挥发系数alpha=1; % 残留信息相对重要度beta=5; % 预见值的相对重要度Q=10; % 蚁环常数NumAnt=20; % 蚂蚁数量routelength=inf; % 用来记录当前找到的最优路径长度for n=1:MAXITfor k=1:NumAnt %考查第K只蚂蚁deltatau=zeros(NC,NC); % 第K只蚂蚁移动前各边上的信息增量为零%[routek,lengthk]=path(distance,tau,alpha,beta,[]); % 不靠率起始点[routek,lengthk]=path(distance,tau,alpha,beta,Citystart); % 指定起始点if lengthk<routelength %找到一条更好的路径:::routelength=lengthk;:::bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatau(routek(i),routek(i+1))=deltatau(routek(i),routek(i+1))+Q/lengthk; % 信息素更新end%deltatau(routek(NC),1)=deltatau(routek(NC),1)+Q/lengthk; %endlength_n(n)=routelength; % 记录路径收敛tau=(1-rho).*tau; % 信息素挥发end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%costtime=toc;subplot(1,2,1),plot([CooCity(bestroute,2)],[CooCity(bestroute,3)],'-*')subplot(1,2,2),plot([1:MAXIT],length_n,'-*')[routelength,costtime]2.蚁群算法寻找路径程序：path.m% 某只蚂蚁找到的某条路径routek,lengthkfunction [routek,lengthk]=path(distance,tau,alpha,beta,Citystart)[m,n]=size(distance);if isempty(Citystart) % 如果不确定起点p=fix(m*rand)+1; % 随机方式初始化起点，均匀概率elsep=Citystart; % 外部给定确定起点 endlengthk=0; % 初始路径长度设为 0routek=[p]; % 蚂蚁路径点序列，即该蚂蚁已经过的城市集合，路径初始起点for i=1:m-1np=routek(end); % 蚂蚁路径城市序号，依次经过的城市编号np_sum=0; % 路由长度初始为 0for j=1:mif inroute(j,routek) % 判断城市节点j是否属于tabuk，即是否已经过continue;else % j为还未经过的点ada=1/distance(np,j); % 预见度np_sum=np_sum+tau(np,j)^alpha*ada^beta; % 路由表：信息痕迹、预见度 endendcp=zeros(1,m); % 转移概率，基于路径长度及路由表for j=1:mifinroute(j,routek)continue;elseada=1/distance(np,j); % 预见度cp(j)=tau(np,j)^alpha*ada^beta/np_sum; % np到j的转移概率endendNextCity=nextcitychoose2(cp); % 根据转移概率确定下一个城市,% 直观地，取转移概率最大值方向方法，决策结果稳定且收敛快routek=[routek,NextCity]; % 更新路径lengthk=lengthk+distance(np,NextCity); % 更新路径长度end蚁群算法仿真结果:其中左边是蚂蚁行走的最短路径，右边是最短路径的值的收敛情况。

(整理)蚂蚁算法源代码如下

源代码如下：/*ant.c*/#define SPACE 0x20#define ESC 0x1b#define ANT_CHAR_EMPTY '+' #define ANT_CHAR_FOOD 153#define HOME_CHAR 'H'#define FOOD_CHAR 'F'#define FOOD_CHAR2 'f'#define FOOD_HOME_COLOR 12 #define BLOCK_CHAR 177#define MAX_ANT 50#define INI_SPEED 3#define MAXX 80#define MAXY 23#define MAX_FOOD 10000#define TARGET_FOOD 200#define MAX_SMELL 5000#define SMELL_DROP_RATE 0.05 #define ANT_ERROR_RATE 0.02 #define ANT_EYESHOT 3#define SMELL_GONE_SPEED 50 #define SMELL_GONE_RATE 0.05 #define TRACE_REMEMBER 50#define MAX_BLOCK 100#define NULL 0#define UP 1#define DOWN 2#define LEFT 3#define RIGHT 4#define SMELL_TYPE_FOOD 0#define SMELL_TYPE_HOME 1#include "stdio.h"#include "conio.h"#include "dos.h"#include "stdlib.h"#include "dos.h"#include "process.h"#include "ctype.h"#include "math.h"void WorldInitial(void);void BlockInitial(void);void CreatBlock(void);void SaveBlock(void);void LoadBlock(void);void HomeFoodInitial(void);void AntInitial(void);void WorldChange(void);void AntMove(void);void AntOneStep(void);void DealKey(char key);void ClearSmellDisp(void);void DispSmell(int type);int AntNextDir(int xxx,int yyy,int ddir);int GetMaxSmell(int type,int xxx,int yyy,int ddir); int IsTrace(int xxx,int yyy);int MaxLocation(int num1,int num2,int num3);int CanGo(int xxx,int yyy,int ddir);int JudgeCanGo(int xxx,int yyy);int TurnLeft(int ddir);int TurnRight(int ddir);int TurnBack(int ddir);int MainTimer(void);char WaitForKey(int secnum);void DispPlayTime(void);int TimeUse(void);void HideCur(void);void ResetCur(void);/* --------------- */struct HomeStruct{int xxx,yyy;int amount;int TargetFood;}home;struct FoodStruct{int xxx,yyy;int amount;}food;struct AntStruct{int xxx,yyy;int dir;int speed;int SpeedTimer;int food;int SmellAmount[2];int tracex[TRACE_REMEMBER];int tracey[TRACE_REMEMBER];int TracePtr;int IQ;}ant[MAX_ANT];int AntNow;int timer10ms;struct time starttime,endtime;int Smell[2][MAXX+1][MAXY+1];int block[MAXX+1][MAXY+1];int SmellGoneTimer;int SmellDispFlag;int CanFindFood;int HardtoFindPath;/* ----- Main -------- */void main(void){char KeyPress;int tu;clrscr();HideCur();WorldInitial();do{timer10ms = MainTimer();if(timer10ms) AntMove();if(timer10ms) WorldChange();tu = TimeUse();if(tu>=60&&!CanFindFood){gotoxy(1,MAXY+1);printf("Can not find food, maybe a block world.");WaitForKey(10);WorldInitial();}if(tu>=180&&home.amount<100&&!HardtoFindPath){gotoxy(1,MAXY+1);printf("God! it is so difficult to find a path.");if(WaitForKey(10)==0x0d) WorldInitial();else{HardtoFindPath = 1;gotoxy(1,MAXY+1);printf(" ");}}if(home.amount>=home.TargetFood){gettime(&endtime);KeyPress = WaitForKey(60);DispPlayTime();WaitForKey(10);WorldInitial();}else if(kbhit()){KeyPress = getch();DealKey(KeyPress);}else KeyPress = NULL;}while(KeyPress!=ESC);gettime(&endtime);DispPlayTime();WaitForKey(10);clrscr();ResetCur();}/* ------ general sub process ----------- */int MainTimer(void)/* output: how much 10ms have pass from last time call this process */ {static int oldhund,oldsec;struct time t;int timeuse;gettime(&t);timeuse = 0;if(t.ti_hund!=oldhund){if(t.ti_sec!=oldsec){timeuse+=100;oldsec = t.ti_sec;}timeuse+=t.ti_hund-oldhund;oldhund = t.ti_hund;}else timeuse = 0;return (timeuse);}char WaitForKey(int secnum)/* funtion: if have key in, exit immediately, else wait 'secnum' senconds then exitinput: secnum -- wait this senconds, must < 3600 (1 hour)output: key char, if no key in(exit when timeout), return NULL */ {int secin,secnow;int minin,minnow;int hourin,hournow;int secuse;struct time t;gettime(&t);secin = t.ti_sec;minin = t.ti_min;hourin = t.ti_hour;do{if(kbhit()) return(getch());gettime(&t);secnow = t.ti_sec;minnow = t.ti_min;hournow = t.ti_hour;if(hournow!=hourin) minnow+=60;if(minnow>minin) secuse = (minnow-1-minin) + (secnow+60-secin); else secuse = secnow - secin;/* counting error check */if(secuse<0){gotoxy(1,MAXY+1);printf("Time conuting error, any keyto exit...");getch();exit(3);}}while(secuse<=secnum);return (NULL);}void DispPlayTime(void){int ph,pm,ps;ph = endtime.ti_hour - starttime.ti_hour;pm = endtime.ti_min - starttime.ti_min;ps = endtime.ti_sec - starttime.ti_sec;if(ph<0) ph+=24;if(pm<0) { ph--; pm+=60; }if(ps<0) { pm--; ps+=60; }gotoxy(1,MAXY+1);printf("Time use: %d hour- %d min- %d sec ",ph,pm,ps);}int TimeUse(void){int ph,pm,ps;gettime(&endtime);ph = endtime.ti_hour - starttime.ti_hour;pm = endtime.ti_min - starttime.ti_min;ps = endtime.ti_sec - starttime.ti_sec;if(ph<0) ph+=24;if(pm<0) { ph--; pm+=60; }if(ps<0) { pm--; ps+=60; }return(ps+(60*(pm+60*ph)));}void HideCur(void){union REGS regs0;regs0.h.ah=1;regs0.h.ch=0x30;regs0.h.cl=0x31;int86(0x10,&regs0,&regs0);}void ResetCur(void){union REGS regs0;regs0.h.ah=1;regs0.h.ch=0x06;regs0.h.cl=0x07;int86(0x10,&regs0,&regs0);}/* ------------ main ANT programe ------------- */ void WorldInitial(void){int k,i,j;randomize();clrscr();HomeFoodInitial();for(AntNow=0;AntNow<MAX_ANT;AntNow++){AntInitial();} /* of for AntNow */;BlockInitial();for(k=0;k<=1;k++)/* SMELL TYPE FOOD and HOME */for(i=0;i<=MAXX;i++)for(j=0;j<=MAXY;j++)Smell[k][i][j] = 0;SmellGoneTimer = 0;gettime(&starttime);SmellDispFlag = 0;CanFindFood = 0;HardtoFindPath = 0;}void BlockInitial(void){int i,j;int bn;for(i=0;i<=MAXX;i++)for(j=0;j<=MAXY;j++)block[i][j] = 0;bn = 1+ MAX_BLOCK/2 + random(MAX_BLOCK/2);for(i=0;i<=bn;i++) CreatBlock();}void CreatBlock(void){int x1,y1,x2,y2;int dx,dy;int i,j;x1 = random(MAXX)+1;y1 = random(MAXY)+1;dx = random(MAXX/10)+1;dy = random(MAXY/10)+1;x2 = x1+dx;y2 = y1+dy;if(x2>MAXX) x2 = MAXX;if(y2>MAXY) y2 = MAXY;if(food.xxx>=x1&&food.xxx<=x2&&food.yyy>=y1&&food.yyy<=y2) return; if(home.xxx>=x1&&home.xxx<=x2&&home.yyy>=y1&&home.yyy<=y2) return;for(i=x1;i<=x2;i++)for(j=y1;j<=y2;j++){block[i][j] = 1;gotoxy(i,j);putch(BLOCK_CHAR);}}void SaveBlock(void){FILE *fp_block;char FileNameBlock[20];int i,j;gotoxy(1,MAXY+1);printf(" ");gotoxy(1,MAXY+1);printf("Save to file...",FileNameBlock);gets(FileNameBlock);if(FileNameBlock[0]==0) strcpy(FileNameBlock,"Ant.ant"); else strcat(FileNameBlock,".ant");if ((fp_block = fopen(FileNameBlock, "wb")) == NULL){ gotoxy(1,MAXY+1);printf("Creat file %s fail...",FileNameBlock);getch();exit(2);}gotoxy(1,MAXY+1);printf(" ");fputc(home.xxx,fp_block);fputc(home.yyy,fp_block);fputc(food.xxx,fp_block);fputc(food.yyy,fp_block);for(i=0;i<=MAXX;i++)for(j=0;j<=MAXY;j++)fputc(block[i][j],fp_block);fclose(fp_block);}void LoadBlock(void){FILE *fp_block;char FileNameBlock[20];int i,j,k;gotoxy(1,MAXY+1);printf(" ");gotoxy(1,MAXY+1);printf("Load file...",FileNameBlock);gets(FileNameBlock);if(FileNameBlock[0]==0) strcpy(FileNameBlock,"Ant.ant"); else strcat(FileNameBlock,".ant");if ((fp_block = fopen(FileNameBlock, "rb")) == NULL){ gotoxy(1,MAXY+1);printf("Open file %s fail...",FileNameBlock);getch();exit(2);}clrscr();home.xxx = fgetc(fp_block);home.yyy = fgetc(fp_block);food.xxx = fgetc(fp_block);food.yyy = fgetc(fp_block);gotoxy(home.xxx,home.yyy); putch(HOME_CHAR);gotoxy(food.xxx,food.yyy); putch(FOOD_CHAR);food.amount = random(MAX_FOOD/3)+2*MAX_FOOD/3+1;/* food.amount = MAX_FOOD; */home.amount = 0;home.TargetFood =(food.amount<TARGET_FOOD)?food.amount:TARGET_FOOD;for(AntNow=0;AntNow<MAX_ANT;AntNow++){AntInitial();} /* of for AntNow */;for(i=0;i<=MAXX;i++)for(j=0;j<=MAXY;j++){block[i][j] = fgetc(fp_block);if(block[i][j]){gotoxy(i,j);putch(BLOCK_CHAR);}}for(k=0;k<=1;k++)/* SMELL TYPE FOOD and HOME */for(i=0;i<=MAXX;i++)for(j=0;j<=MAXY;j++)Smell[k][i][j] = 0;SmellGoneTimer = 0;gettime(&starttime);SmellDispFlag = 0;CanFindFood = 0;HardtoFindPath = 0;fclose(fp_block);}void HomeFoodInitial(void){int randnum;int homeplace;/* 1 -- home at left-up, food at right-down2 -- home at left-down, food at right-up3 -- home at right-up, food at left-down4 -- home at right-down, food at left-up */randnum = random(100);if(randnum<25) homeplace = 1;else if (randnum>=25&&randnum<50) homeplace = 2; else if (randnum>=50&&randnum<75) homeplace = 3; else homeplace = 4;switch(homeplace){case 1: home.xxx = random(MAXX/3)+1;home.yyy = random(MAXY/3)+1;food.xxx = random(MAXX/3)+2*MAXX/3+1;food.yyy = random(MAXY/3)+2*MAXY/3+1;break;case 2: home.xxx = random(MAXX/3)+1;home.yyy = random(MAXY/3)+2*MAXY/3+1;food.xxx = random(MAXX/3)+2*MAXX/3+1;food.yyy = random(MAXY/3)+1;break;case 3: home.xxx = random(MAXX/3)+2*MAXX/3+1; home.yyy = random(MAXY/3)+1;food.xxx = random(MAXX/3)+1;food.yyy = random(MAXY/3)+2*MAXY/3+1;break;case 4: home.xxx = random(MAXX/3)+2*MAXX/3+1;home.yyy = random(MAXY/3)+2*MAXY/3+1;food.xxx = random(MAXX/3)+1;food.yyy = random(MAXY/3)+1;break;}food.amount = random(MAX_FOOD/3)+2*MAX_FOOD/3+1;/* food.amount = MAX_FOOD; */home.amount = 0;home.TargetFood = (food.amount<TARGET_FOOD)?food.amount:TARGET_FOOD;/* data correctness check */if(home.xxx<=0||home.xxx>MAXX||home.yyy<=0||home.yyy>MAXY||food.xxx<=0||food.xxx>MAXX||food.yyy<=0||food.yyy>MAXY||food.amount<=0){gotoxy(1,MAXY+1);printf("World initial fail, any key to exit...");getch();exit(2);}gotoxy(home.xxx,home.yyy); putch(HOME_CHAR);gotoxy(food.xxx,food.yyy); putch(FOOD_CHAR);}void AntInitial(void)/* initial ant[AntNow] */{int randnum;int i;ant[AntNow].xxx = home.xxx;ant[AntNow].yyy = home.yyy;randnum = random(100);if(randnum<25) ant[AntNow].dir = UP;else if (randnum>=25&&randnum<50) ant[AntNow].dir = DOWN;else if (randnum>=50&&randnum<75) ant[AntNow].dir = LEFT;else ant[AntNow].dir = RIGHT;ant[AntNow].speed = 2*(random(INI_SPEED/2)+1);ant[AntNow].SpeedTimer = 0;ant[AntNow].food = 0;ant[AntNow].SmellAmount[SMELL_TYPE_FOOD] = 0;ant[AntNow].SmellAmount[SMELL_TYPE_HOME] = MAX_SMELL;ant[AntNow].IQ = 1;for(i=0;i<TRACE_REMEMBER;i++){ant[AntNow].tracex[i] = 0;ant[AntNow].tracey[i] = 0;}ant[AntNow].TracePtr = 0;/* a sepecail ant */if(AntNow==0) ant[AntNow].speed = INI_SPEED;}void WorldChange(void){int k,i,j;int smelldisp;SmellGoneTimer+=timer10ms;if(SmellGoneTimer>=SMELL_GONE_SPEED){SmellGoneTimer = 0;for(k=0;k<=1;k++)/* SMELL TYPE FOOD and HOME */for(i=1;i<=MAXX;i++)for(j=1;j<=MAXY;j++){if(Smell[k][i][j]){smelldisp =1+((10*Smell[k][i][j])/(MAX_SMELL*SMELL_DROP_RATE));if(smelldisp>=30000||smelldisp<0) smelldisp = 30000; if(SmellDispFlag){gotoxy(i,j);if((i==food.xxx&&j==food.yyy)||(i==home.xxx&&j==home.yyy))/* don't over write Food and Home */;else{if(smelldisp>9) putch('#');else putch(smelldisp+'0');}}Smell[k][i][j]-= 1+(Smell[k][i][j]*SMELL_GONE_RATE); if(Smell[k][i][j]<0) Smell[k][i][j] = 0;if(SmellDispFlag){if(Smell[k][i][j]<=2){gotoxy(i,j);putch(SPACE);}}}} /* of one location */} /* of time to change the world */} /* of world change */void AntMove(void){int antx,anty;int smelltodrop,smellnow;for(AntNow=0;AntNow<MAX_ANT;AntNow++){ant[AntNow].SpeedTimer+=timer10ms;if(ant[AntNow].SpeedTimer>=ant[AntNow].speed){ant[AntNow].SpeedTimer = 0;gotoxy(ant[AntNow].xxx,ant[AntNow].yyy);putch(SPACE);AntOneStep();gotoxy(ant[AntNow].xxx,ant[AntNow].yyy);/* ant0 is a sepecail ant, use different color */if(AntNow==0) textcolor(0xd);if(ant[AntNow].food) putch(ANT_CHAR_FOOD);else putch(ANT_CHAR_EMPTY);if(AntNow==0) textcolor(0x7);/* remember trace */ant[AntNow].tracex[ant[AntNow].TracePtr] = ant[AntNow].xxx; ant[AntNow].tracey[ant[AntNow].TracePtr] = ant[AntNow].yyy; if(++(ant[AntNow].TracePtr)>=TRACE_REMEMBER)ant[AntNow].TracePtr = 0;/* drop smell */antx = ant[AntNow].xxx;anty = ant[AntNow].yyy;if(ant[AntNow].food)/* have food, looking for home */{if(ant[AntNow].SmellAmount[SMELL_TYPE_FOOD]){smellnow = Smell[SMELL_TYPE_FOOD][antx][anty];smelltodrop =ant[AntNow].SmellAmount[SMELL_TYPE_FOOD]*SMELL_DROP_RATE;if(smelltodrop>smellnow) Smell[SMELL_TYPE_FOOD][antx][anty] = smelltodrop;/* else Smell[...] = smellnow */ant[AntNow].SmellAmount[SMELL_TYPE_FOOD]-= smelltodrop;if(ant[AntNow].SmellAmount[SMELL_TYPE_FOOD]<0)ant[AntNow].SmellAmount[SMELL_TYPE_FOOD] = 0;} /* of have smell to drop */} /* of have food */else/* no food, looking for food */{if(ant[AntNow].SmellAmount[SMELL_TYPE_HOME]){smellnow = Smell[SMELL_TYPE_HOME][antx][anty];smelltodrop =ant[AntNow].SmellAmount[SMELL_TYPE_HOME]*SMELL_DROP_RATE;if(smelltodrop>smellnow) Smell[SMELL_TYPE_HOME][antx][anty] = smelltodrop;/* else Smell[...] = smellnow */ant[AntNow].SmellAmount[SMELL_TYPE_HOME]-= smelltodrop;if(ant[AntNow].SmellAmount[SMELL_TYPE_HOME]<0)ant[AntNow].SmellAmount[SMELL_TYPE_HOME] = 0;} /* of have smell to drop */}} /* of time to go *//* else not go */} /* of for AntNow */textcolor(FOOD_HOME_COLOR);gotoxy(home.xxx,home.yyy); putch(HOME_CHAR);gotoxy(food.xxx,food.yyy);if(food.amount>0) putch(FOOD_CHAR);else putch(FOOD_CHAR2);textcolor(7);gotoxy(1,MAXY+1);printf("Food %d, Home %d ",food.amount,home.amount); }void AntOneStep(void){int ddir,tttx,ttty;int i;ddir = ant[AntNow].dir;tttx = ant[AntNow].xxx;ttty = ant[AntNow].yyy;ddir = AntNextDir(tttx,ttty,ddir);switch(ddir){case UP: ttty--;break;case DOWN: ttty++;break;case LEFT: tttx--;break;case RIGHT: tttx++;break;default: break;} /* of switch dir */ant[AntNow].dir = ddir;ant[AntNow].xxx = tttx;ant[AntNow].yyy = ttty;if(ant[AntNow].food)/* this ant carry with food, search for home */{if(tttx==home.xxx&&ttty==home.yyy){home.amount++;AntInitial();}if(tttx==food.xxx&&ttty==food.yyy)ant[AntNow].SmellAmount[SMELL_TYPE_FOOD] = MAX_SMELL; } /* of search for home */else/* this ant is empty, search for food */{if(tttx==food.xxx&&ttty==food.yyy){if(food.amount>0){ant[AntNow].food = 1;food.amount--;ant[AntNow].SmellAmount[SMELL_TYPE_FOOD] = MAX_SMELL; ant[AntNow].SmellAmount[SMELL_TYPE_HOME] = 0;ant[AntNow].dir = TurnBack(ant[AntNow].dir);for(i=0;i<TRACE_REMEMBER;i++){ant[AntNow].tracex[i] = 0;ant[AntNow].tracey[i] = 0;}ant[AntNow].TracePtr = 0;CanFindFood = 1;} /* of still have food */}if(tttx==home.xxx&&ttty==home.yyy)ant[AntNow].SmellAmount[SMELL_TYPE_HOME] = MAX_SMELL; } /* of search for food */}void DealKey(char key){int i;switch(key){case 'p': gettime(&endtime);DispPlayTime();getch();gotoxy(1,MAXY+1);for(i=1;i<=MAXX-1;i++) putch(SPACE);break;case 't': if(SmellDispFlag){SmellDispFlag=0;ClearSmellDisp();}else SmellDispFlag = 1;break;case '1': DispSmell(SMELL_TYPE_FOOD);getch();ClearSmellDisp();break;case '2': DispSmell(SMELL_TYPE_HOME);getch();ClearSmellDisp();break;case '3': DispSmell(2);getch();ClearSmellDisp();break;case 's': SaveBlock();break;case 'l': LoadBlock();break;default: gotoxy(1,MAXY+1);for(i=1;i<=MAXX-1;i++) putch(SPACE); } /* of switch */}void ClearSmellDisp(void){int k,i,j;for(k=0;k<=1;k++)/* SMELL TYPE FOOD and HOME */for(i=1;i<=MAXX;i++)for(j=1;j<=MAXY;j++){if(Smell[k][i][j]){gotoxy(i,j);putch(SPACE);}} /* of one location */}void DispSmell(int type)/* input: 0 -- Only display food smell1 -- Only display home smell2 -- Display both food and home smell*/{int k,i,j;int fromk,tok;int smelldisp;switch(type){case 0: fromk = 0;tok = 0;break;case 1: fromk = 1;tok = 1;break;case 2: fromk = 0;tok = 1;break;default:fromk = 0;tok = 1;break;}SmellGoneTimer = 0;for(k=fromk;k<=tok;k++)/* SMELL TYPE FOOD and HOME */for(i=1;i<=MAXX;i++)for(j=1;j<=MAXY;j++){if(Smell[k][i][j]){smelldisp =1+((10*Smell[k][i][j])/(MAX_SMELL*SMELL_DROP_RATE));if(smelldisp>=30000||smelldisp<0) smelldisp = 30000; gotoxy(i,j);if(i!=food.xxx||j!=food.yyy){if((i==food.xxx&&j==food.yyy)||(i==home.xxx&&j==home.yyy))/* don't over write Food and Home */;else{if(smelldisp>9) putch('#');else putch(smelldisp+'0');}}}} /* of one location */}int AntNextDir(int xxx,int yyy,int ddir){int randnum;int testdir;int CanGoState;int cangof,cangol,cangor;int msf,msl,msr,maxms;int type;CanGoState = CanGo(xxx,yyy,ddir);if(CanGoState==0||CanGoState==2||CanGoState==3||CanGoState==6) cangof = 1;else cangof = 0;if(CanGoState==0||CanGoState==1||CanGoState==3||CanGoState==5) cangol = 1;else cangol = 0;if(CanGoState==0||CanGoState==1||CanGoState==2||CanGoState==4) cangor = 1;else cangor = 0;if(ant[AntNow].food) type = SMELL_TYPE_HOME;else type = SMELL_TYPE_FOOD;msf = GetMaxSmell(type,xxx,yyy,ddir);msl = GetMaxSmell(type,xxx,yyy,TurnLeft(ddir));msr= GetMaxSmell(type,xxx,yyy,TurnRight(ddir));maxms = MaxLocation(msf,msl,msr);/* maxms - 1 - msf is MAX2 - msl is MAX3 - msr is MAX0 - all 3 number is 0 */testdir = NULL;switch(maxms){case 0: /* all is 0, keep testdir = NULL, random select dir */ break;case 1: if(cangof)testdir = ddir;elseif(msl>msr) if(cangol) testdir = TurnLeft(ddir);else if(cangor) testdir = TurnRight(ddir);break;case 2: if(cangol)testdir = TurnLeft(ddir);elseif(msf>msr) if(cangof) testdir = ddir;else if(cangor) testdir = TurnRight(ddir);break;case 3: if(cangor)testdir = TurnRight(ddir);elseif(msf>msl) if(cangof) testdir =ddir;else if(cangol) testdir = TurnLeft(ddir);break;default:break;} /* of maxms */randnum = random(1000);if(randnum<SMELL_DROP_RATE*1000||testdir==NULL)/* 1. if testdir = NULL, means can not find the max smell or the dir to max smell can not gothen random select dir2. if ant error, don't follow the smell, random select dir*/{randnum = random(100);switch(CanGoState){case 0: if(randnum<90) testdir = ddir;else if (randnum>=90&&randnum<95) testdir = TurnLeft(ddir); else testdir = TurnRight(ddir);break;case 1: if(randnum<50) testdir = TurnLeft(ddir);else testdir = TurnRight(ddir);break;case 2: if(randnum<90) testdir = ddir;else testdir = TurnRight(ddir);break;case 3: if(randnum<90) testdir = ddir;else testdir = TurnLeft(ddir);break;case 4: testdir = TurnRight(ddir);case 5: testdir = TurnLeft(ddir);break;case 6: testdir = ddir;break;case 7: testdir = TurnBack(ddir);break;default:testdir = TurnBack(ddir);} /* of can go state */}return(testdir);}int GetMaxSmell(int type,int xxx,int yyy,int ddir){int i,j;int ms; /* MAX smell */ms = 0;switch(ddir){case UP: for(i=xxx-ANT_EYESHOT;i<=xxx+ANT_EYESHOT;i++) for(j=yyy-ANT_EYESHOT;j<yyy;j++){if(!JudgeCanGo(i,j)) continue;if((i==food.xxx&&j==food.yyy&&type==SMELL_TYPE_FOOD)||(i==home.xxx&&j==home.yyy&&type==SMELL_TYPE_HOME)){ms = MAX_SMELL;break;}if(IsTrace(i,j)) continue;if(Smell[type][i][j]>ms) ms =Smell[type][i][j];}break;case DOWN:for(i=xxx-ANT_EYESHOT;i<=xxx+ANT_EYESHOT;i++)for(j=yyy+1;j<=yyy+ANT_EYESHOT;j++){if(!JudgeCanGo(i,j)) continue;if((i==food.xxx&&j==food.yyy&&type==SMELL_TYPE_FOOD)||(i==home.xxx&&j==home.yyy&&type==SMELL_TYPE_HOME)){ms = MAX_SMELL;break;}if(IsTrace(i,j)) continue;if(Smell[type][i][j]>ms) ms =Smell[type][i][j];}break;case LEFT: for(i=xxx-ANT_EYESHOT;i<xxx;i++)for(j=yyy-ANT_EYESHOT;j<=yyy+ANT_EYESHOT;j++) {if(!JudgeCanGo(i,j)) continue;if((i==food.xxx&&j==food.yyy&&type==SMELL_TYPE_FOOD)||(i==home.xxx&&j==home.yyy&&type==SMELL_TYPE_HOME)){ms = MAX_SMELL;break;}if(IsTrace(i,j)) continue;if(Smell[type][i][j]>ms) ms =Smell[type][i][j];}break;case RIGHT: for(i=xxx+1;i<=xxx+ANT_EYESHOT;i++)for(j=yyy-ANT_EYESHOT;j<=yyy+ANT_EYESHOT;j++) {if(!JudgeCanGo(i,j)) continue;if((i==food.xxx&&j==food.yyy&&type==SMELL_TYPE_FOOD)||(i==home.xxx&&j==home.yyy&&type==SMELL_TYPE_HOME)){ms = MAX_SMELL;break;}if(IsTrace(i,j)) continue;if(Smell[type][i][j]>ms) ms =Smell[type][i][j];}default: break;}return(ms);}int IsTrace(int xxx,int yyy){int i;for(i=0;i<TRACE_REMEMBER;i++)if(ant[AntNow].tracex[i]==xxx&&ant[AntNow].tracey[i]==yyy) return(1);return(0);}int MaxLocation(int num1,int num2,int num3){int maxnum;if(num1==0&&num2==0&&num3==0) return(0);maxnum = num1;if(num2>maxnum) maxnum = num2;if(num3>maxnum) maxnum = num3;if(maxnum==num1) return(1);if(maxnum==num2) return(2);if(maxnum==num3) return(3);}int CanGo(int xxx,int yyy,int ddir)/* input: xxx,yyy - location of antddir - now diroutput: 0 - forward and left and right can go1 - forward can not go2 - left can not go3 - right can not go4 - forward and left can not go5 - forward and right can not go6 - left and right can not go7 - forward and left and right all can not go*/{int tx,ty,tdir;int okf,okl,okr;/* forward can go ? */tdir = ddir;tx = xxx;ty = yyy;switch(tdir){case UP: ty--;break;case DOWN: ty++;break;case LEFT: tx--;break;case RIGHT: tx++;break;default: break;} /* of switch dir */if(JudgeCanGo(tx,ty)) okf = 1; else okf = 0;/* turn left can go ? */tdir = TurnLeft(ddir);tx = xxx;ty = yyy;switch(tdir){case UP: ty--;break;case DOWN: ty++;break;case LEFT: tx--;break;case RIGHT: tx++;break;default: break;} /* of switch dir */if(JudgeCanGo(tx,ty)) okl = 1; else okl = 0;/* turn right can go ? */tdir = TurnRight(ddir);tx = xxx;ty = yyy;switch(tdir){case UP: ty--;break;case DOWN: ty++;break;case LEFT: tx--;break;case RIGHT: tx++;break;default: break;} /* of switch dir */if(JudgeCanGo(tx,ty)) okr = 1; else okr = 0;if(okf&&okl&&okr) return(0);if(!okf&&okl&&okr) return(1);if(okf&&!okl&&okr) return(2);if(okf&&okl&&!okr) return(3);if(!okf&&!okl&&okr) return(4); if(!okf&&okl&&!okr) return(5); if(okf&&!okl&&!okr) return(6); if(!okf&&!okl&&!okr) return(7); return(7);}int JudgeCanGo(int xxx,int yyy) /* input: location to judegoutput: 0 -- can not go1 -- can go*/{int i,j;if(xxx<=0||xxx>MAXX) return(0); if(yyy<=0||yyy>MAXY) return(0); if(block[xxx][yyy]) return(0); return(1);}int TurnLeft(int ddir){switch(ddir){case UP: return(LEFT);case DOWN: return(RIGHT);case LEFT: return(DOWN);case RIGHT: return(UP);default: break;} /* of switch dir */}int TurnRight(int ddir){switch(ddir){case UP: return(RIGHT);case DOWN: return(LEFT);case LEFT: return(UP);case RIGHT: return(DOWN);default: break;} /* of switch dir */}int TurnBack(int ddir){switch(ddir){case UP: return(DOWN);case DOWN: return(UP);case LEFT: return(RIGHT);case RIGHT: return(LEFT);default: break;} /* of switch dir */}小小的蚂蚁总是能够找到食物，他们具有什么样的智能呢？设想，如果我们要为蚂蚁设计一个人工智能的程序，那么这个程序要多么复杂呢？首先，你要让蚂蚁能够避开障碍物，就必须根据适当的地形给它编进指令让他们能够巧妙的避开障碍物，其次，要让蚂蚁找到食物，就需要让他们遍历空间上的所有点；再次，如果要让蚂蚁找到最短的路径，那么需要计算所有可能的路径并且比较它们的大小，而且更重要的是，你要小心翼翼的编程，因为程序的错误也许会让你前功尽弃。

matlab-蚁群算法-机器人路径优化问题

matlab-蚁群算法-机器人路径优化问题4.1问题描述移动机器人路径规划是机器人学的一个重要研究领域。

它要求机器人依据某个或某些优化原则(如最小能量消耗，最短行走路线，最短行走时间等)，在其工作空间中找到一条从起始状态到目标状态的能避开障碍物的最优路径。

机器人路径规划问题可以建模为一个有约束的优化问题，都要完成路径规划、定位和避障等任务。

4.2算法理论蚁群算法（AntColonyAlgorithm，ACA），最初是由意大利学者DorigoM.博士于1991年首次提出，其本质是一个复杂的智能系统，且具有较强的鲁棒性，优良的分布式计算机制等优点。

该算法经过十多年的发展，已被广大的科学研究人员应用于各种问题的研究，如旅行商问题，二次规划问题，生产调度问题等。

但是算法本身性能的评价等算法理论研究方面进展较慢。

Dorigo提出了精英蚁群模型（EAS），在这一模型中信息素更新按照得到当前最优解的蚂蚁所构造的解来进行，但这样的策略往往使进化变得缓慢，并不能取得较好的效果。

次年Dorigo博士在文献[30]中给出改进模型（ACS），文中改进了转移概率模型，并且应用了全局搜索与局部搜索策略，来得进行深度搜索。

Stützle与Hoo给出了最大-最小蚂蚁系统（MA某-MINAS），所谓最大-最小即是为信息素设定上限与下限，设定上限避免搜索陷入局部最优，设定下限鼓励深度搜索。

蚂蚁作为一个生物个体其自身的能力是十分有限的，比如蚂蚁个体是没有视觉的，蚂蚁自身体积又是那么渺小，但是由这些能力有限的蚂蚁组成的蚁群却可以做出超越个体蚂蚁能力的超常行为。

蚂蚁没有视觉却可以寻觅食物，蚂蚁体积渺小而蚁群却可以搬运比它们个体大十倍甚至百倍的昆虫。

这些都说明蚂蚁群体内部的某种机制使得它们具有了群体智能，可以做到蚂蚁个体无法实现的事情。

经过生物学家的长时间观察发现，蚂蚁是通过分泌于空间中的信息素进行信息交流，进而实现群体行为的。

蚁群算法matlab代码

蚁群算法matlab代码蚁群算法，英文名为Ant Colony Algorithm，缩写为ACO，是一种启发式算法，是一种模拟蚂蚁寻找食物路径的算法。

在实际生活中，蚂蚁找到食物并返回巢穴后，将其找到食物的路径上的信息素留下，其他蚂蚁通过检测信息素来指导寻路，成为了一种集体智慧行为。

ACO也是通过模拟蚂蚁寻找食物路径的方式来寻找优化问题的最优解。

在ACO算法中，信息素是一个重要的概念，代表了走过某一路径的“好概率”，用这个“好概率”更新一些路径上的信息素，使得其他蚂蚁更可能选择经过这条路径，从而实现路径优化的目的。

在本文中，我们将讨论如何使用Matlab实现蚁群算法来优化问题。

1. 设定问题首先，我们要选取一个优化问题，并将其转换为需要在优化过程中进行选择的决策变量。

例如，我们想要优化旅行商问题（TSP）。

在TSP中，我们需要让旅行商以最短的距离经过所有城市，每个城市仅经过一次，最终回到出发的城市。

我们可以将每个城市编号，然后将TSP转化为一个最短路径选择的问题，即最短路径从编号为1的城市开始，经过所有城市，最终回到编号为1的城市。

2. 设定ACO参数在使用ACO优化问题时，需要设定一些参数，这些参数会影响算法的表现。

ACO算法需要设定的参数有：1.信息素含量：初始信息素的大小，即每个路径上的信息素浓度。

2.信息素挥发速度：信息素的随时间“减弱”程度。

3.信息素加成强度：蚂蚁经过路径后增加的信息素量。

4.启发式权重：用于计算启发式因子，即节点距离的贡献值。

5.蚂蚁数量：模拟蚂蚁数量，即同时寻找路径的蚂蚁个数。

6.迭代次数：模拟的迭代次数，即ACO算法运行的次数。

7.初始节点：ACO算法开始的节点。

3. 创建ACO优化函数我们可以使用Matlab来创建一个函数来实现ACO算法。

我们称其为“ACOoptimization.m”。

function best_path =ACOoptimization(city_location,iter_num,ant_num,init ial_path,alpha,beta,rho,update_flag) %ACO优化函数 %输入： %city_location: 城市坐标矩阵，格式为[x1,y1;x2,y2;...;xn,yn] %iter_num: 迭代次数 %ant_num: 蚂蚁数量 %initial_path: 起始路径，即初始解 %alpha,beta,rho: 超参数，用于调节蚂蚁选择路径的概率 %update_flag: 是否更新信息素的标志（1表示更新，0表示否） %输出： %best_path: 最优解，即最短路径%初始化信息素 pheromone = 0.01 *ones(length(city_location),length(city_location)); %初始化路径权重 path_weight =zeros(ant_num,1); %城市数量 n_cities =length(city_location);%主循环 for iter = 1:iter_num %一个迭代里所有蚂蚁都寻找一遍路径 for ant =1:ant_num %初始化蚂蚁位置current_city = initial_path; %标记是否经过了某个城市 visit_flag =zeros(1,n_cities);visit_flag(current_city) = 1; %用来存储当前路径 current_path = [current_city];%蚂蚁找东西 for i =1:n_cities-1 %计算路径概率p =calculate_probability(current_city,visit_flag,phero mone,city_location,alpha,beta); %蚂蚁选择路径 [next_city,next_index] = select_path(p);%路径更新current_path = [current_path;next_city];visit_flag(next_city) = 1;current_city = next_city;%更新路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end-1),:),city_location(current_path(end),:));end%加入回到起点的路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end),:),city_location(current_path(1),:));%判断是否为最优解 ifant == 1 best_path = current_path; else if path_weight(ant) <path_weight(ant-1) best_path =current_path; end end%更新信息素 ifupdate_flag == 1 pheromone =update_pheromone(pheromone,path_weight,initial_path,current_path,rho); end end end end在函数中，我们首先定义了ACOalg函数的参数，包括城市坐标矩阵，迭代次数，蚂蚁数量，初始路径，超参数alpha，beta，rho，以及是否需要更新信息素。

蚁群算法的Matlab程序

#include<iostream.h>#include<stdlib.h>#include<time.h>#include<math.h>#define citynumber 5#define Q 100#define p 0.5#define NM2 1000#define A 1#define B 5int ccdi=-1;//全局变量,用在myrand()中float myrand()//产生0-1随机数,100个,每调用一次,结果不同{srand(time(0));float my[100];ccdi++;if (ccdi==100)ccdi=0;for(int mi=0;mi<100;mi++){float fav=rand()%10000;my[mi]=fav/10000;}return my[ccdi];}double fpkij(double T[citynumber][citynumber],double n[citynumber][citynumber],int tabu[citynumber][citynumber],int k,int s,int i,int j )//定义函数用于计算Pij{//double A=0.5,B=0.5;double sumup,pkij,sumdown;sumdown=0;for(int aTi=0;aTi<citynumber;aTi++){for(int aTj=0;aTj<citynumber;aTj++)aT[aTi][aTj]=pow(T[aTi][aTj],A);}for(int bni=0;bni<citynumber;bni++){for(int bnj=0;bnj<citynumber;bnj++)bn[bni][bnj]=pow(n[bni][bnj],B);}for (int can=0;can<citynumber;can++)//判断,除掉已经走过的城市{if(can==tabu[k][ci]){aT[i][can]=0;bn[i][can]=0;}}sumup=aT[i][j]*bn[i][j];for(int tj=0;tj<citynumber;tj++)sumdown=aT[i][tj]*bn[i][tj]+sumdown;pkij=sumup/sumdown;return pkij;}void main(){ doublecity[citynumber][2]={{0,1},{0,2},{2,2},{2,4},{1,3}/*,{3,4},{4,7},{2,8},{3,9},{1,10},{1,0},{2,1},{3,0},{4,9},{5,2},{6,2},{7,1},{8,6},{9,0},{10,3}*/}; /*城市坐标*/ double d[citynumber][citynumber]; //L[j][k]是城市j to k距离for(int j=0;j<citynumber;j++){d[j][k]=sqrt((city[j][0]-city[k][0])*(city[j][0]-city[k][0])+(city[j][1]-city[k][1])*(city[j][1]-city[k] [1]));// cout<<d[j][k]<<" ";}//cout<<"\n";} /*计算距离,从j城市到k城市*//* for (int cj=0;cj<10;cj++){float c=myrand();cout<<c<<" "<<"\n";}*///输出随机数double n[citynumber][citynumber];for(int ni=0;ni<citynumber;ni++){for(int j=0;j<citynumber;j++)}//cout<<"\n";} /*初始化visibility nij*/double L[citynumber];int shortest[citynumber];double T[citynumber][citynumber];for(int ti=0;ti<citynumber;ti++){for (int j=0;j<citynumber;j++){//cout<<T[ti][j]<<" ";}//cout<<"\n";}/*初始化t*/double changT[citynumber][citynumber];//step2:for(int NC=0;NC<NM2;NC++){ for(int cti=0;cti<citynumber;cti++){for (int j=0;j<citynumber;j++){changT[cti][j]=0;//cout<<changT[cti][j]<<" ";}//cout<<"\n";} /*初始化changT*/int tabu[citynumber][citynumber];//tabu[k][s]表示第k只蚂蚁,第s次循环所在的城市for (int i=0;i<citynumber;i++)tabu[tai][i]=0;}for (int tabui1=0;tabui1<citynumber;tabui1++)tabu[tabui1][0]=tabui1;/*for (tai=0;tai<citynumber;tai++){for (int i=0;i<citynumber;i++)cout<<tabu[tai][i]<<" ";cout<<"\n";}*///初始化tabufor(int kk=0;kk<citynumber;kk++)L[kk]=0;//第三步开始for(int s=0;s<citynumber-1;s++){for(int k=0;k<citynumber;){int ci,can;float sumpk=0;float pkij;hq2: can++;if (can==citynumber) can=0;for (ci=0;ci<=s;ci++){if(can==tabu[k][ci]) goto hq2;}pkij=fpkij(T,n,tabu,k,s,tabu[k][s],can);sumpk=sumpk+pkij;else goto hq2;tabu[k][s+1]=can;k++;}} //第三步完成/*for (tai=0;tai<citynumber;tai++){for (int i=0;i<citynumber;i++) }*///输出一个循环后的tabu[][]//第四步开始for(int k4=0;k4<citynumber;k4++){s44=s4+1;if (s44==citynumber) s44=0;L[k4]+=d[tabu[k4][s4]][tabu[k4][s44]]; }//cout<<L[k4]<<" ";}//计算L[k]float shortest1=0; int short2=0;//最短距离for(ii=1;shorti<citber;shi++ ){shortest1=L[0];if(L[shorti]<=shortest1){shortest1=L[shorti];short2=shorti;}}//cout<<L[sort2]<<"\n";cout<<short2<<"\n";for(int shoi=0;shoi<ctynumber;shoi++){shortest[shoi]=tabu[short2][shoi];//cout<<shest[shoi]<<" ";}//cout<<"\n";for(int k41=0;k41<citynumber;k41++){for(int s41=0,ss=0;s41<citynumber;s41++){ss=s41+1;if (ss==citynumber) ss=0;changT[tabu[k41][s41]][tabu[k41][ss]]+=Q/L[k41];changT[tabu[k41][ss]][tabu[k41][s41]]=changT[tabu[k41][s41]][tabu[k41][ss]]; }}/* for(int cti4=0;cti4<citynumber;cti4++){for (int j=0;j<citynumber;j++){cout<<changT[cti4][j]<<" ";}cout<<"\n";}*///第四步完// 第五步开始for(int i5=0;i5<citynumber;i5++){for(int j5=0;j5<citynumber;j5++){// cout<<T[i5][j5]<<" ";}//cout<<"\n";}}for(int shoi1=0;shoi1<citynumber;shoi1++){cout<<city[shortest[shoi1]][0]<<" "<<city[shortest[shoi1]][1]<<" ";}}。

蚁群算法在MATLAB中的实现

速率挥发，过一段时间的搜索，短路径上的信息经最
素将会越来越浓，照最短路径移动的蚂蚁将会越按
短路径，然后进行信息素的更新，息素的更新采用信
公式（）一（）３４进行。
来越多，而形成一个正反馈，进使得它们可以找到最短路径。所以在蚁群算法的实现过程中，键的步关
摘
要：蚁群算法是近年来兴起的一种新型仿生优化算法，具有其他进化算法不可比拟的优势。
以旅行商问题为例，首先描述了蚁群算法的工作原理，然后给出了该算法在ＭＡＬＢ中实现的ＴＡ
详细步骤，最后分别以１，２，２７１４，４，５，７８１０为城市规模进行了算法验证，给出了算法运行的最优结果、最差结果、平均结果及运行时间与结果图。算法的实现为在其他领域中的应用和进一步的改进提供了基础，同时也弥补了其他资料中很少涉及实现应用的不足。
在原地打转。每个蚂蚁在向新节点移动前，用公使式（）１计算到达Ｎ — ｉｔｄ中每个节点的概率ＰｏＶｓｅ表ｉ。
ｅａｅ能够记录算法运行结束时的最优路径Ｓｏｅｔｒｇ，ｈ￣ｓ —
Ｒｕｅｏｔ及最优路径长度ＳｏｔｔＬｎｔ算法的运ｈｒｓｅｇｅ— ｈ和
【蚂蚁ｋ经过结点，０，不
市节点， …… 等，市之间的距离使用欧式距离表城示。现将ｍ个蚂蚁随机放到个城市节点，每个蚂蚁访问过的城市节点放人到Ｖｓｅ中，为禁忌ｉｔｄ表ｉ作

基于蚁群算法的PID控制参数优化Matlab源码

基于蚁群算法的PID控制参数优化Matlab源码(2009-07-26 12:31:02)除了蚁群算法，可用于PID参数优化的智能算法还有很多，比如遗传算法、模拟退火算法、粒子群算法、人工鱼群算法，等等。

function [BESTX,BESTY,ALLX,ALLY]=ACOUCP(K,N,Rho,Q,Lambda,LB,UB,Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB)%% 此函数实现蚁群算法，用于PID控制参数优化% GreenSim团队原创作品，转载请注明%Email:****************% GreenSim团队主页：/greensim% [color=red]欢迎访问GreenSim——算法仿真团队→[url=/greensim]/greensim[/url][/color]%% 输入参数列表% K 迭代次数% N 蚁群规模% Rho 信息素蒸发系数，取值0～1之间，推荐取值0.7～0.95% Q 信息素增加强度，大于0，推荐取值1左右% Lambda 蚂蚁爬行速度，取值0～1之间，推荐取值0.1～0.5% LB 决策变量的下界，M×1的向量% UB 决策变量的上界，M×1的向量% Num 被控制对象传递函数的分子系数向量% Den 被控制对象传递函数的分母系数向量% Delay 时间延迟% ts 仿真时间步长% StepNum 仿真总步数% SigType 信号类型，1为阶跃信号，2为方波信号，3为正弦波信号% PIDLB PID控制输出信号限幅的下限% PIDUB PID控制输出信号限幅的上限%% 输出参数列表% BESTX K×1细胞结构，每一个元素是M×1向量，记录每一代的最优蚂蚁% BESTY K×1矩阵，记录每一代的最优蚂蚁的评价函数值% ALLX K×1细胞结构，每一个元素是M×N矩阵，记录每一代蚂蚁的位置% ALLY K×N矩阵，记录每一代蚂蚁的评价函数值%% 第一步：初始化M=length(LB);%决策变量的个数%蚁群位置初始化X=zeros(M,N);for i=1:Mx=unifrnd(LB(i),UB(i),1,N);X(i,:)=x;end%输出变量初始化ALLX=cell(K,1);%细胞结构，每一个元素是M×N矩阵，记录每一代的个体ALLY=zeros(K,N);%K×N矩阵，记录每一代评价函数值BESTX=cell(K,1);%细胞结构，每一个元素是M×1向量，记录每一代的最优个体BESTY=zeros(K,1);%K×1矩阵，记录每一代的最优个体的评价函数值k=1;%迭代计数器初始化Tau=ones(1,N);%信息素初始化Y=zeros(1,N);%适应值初始化%% 第二步：迭代过程while k<=KYY=zeros(1,N);for n=1:Nx=X(:,n);[J,u,yout,error]=PIDOBJ(x(1),x(2),x(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);YY(n)=J;endmaxYY=max(YY);temppos=find(YY==maxYY);POS=temppos(1);%蚂蚁随机探路for n=1:Nif n~=POSx=X(:,n);[J,u,yout,error]=PIDOBJ(x(1),x(2),x(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fx=J;mx=GaussMutation(x,LB,UB);[J,u,yout,error]=PIDOBJ(mx(1),mx(2),mx(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fmx=J;if Fmx<FxX(:,n)=mx;Y(n)=Fmx;elseif rand>1-(1/(sqrt(k)))Y(n)=Fmx;elseX(:,n)=x;Y(n)=Fx;endendendfor n=1:Nif n~=POSx=X(:,n);[J,u,yout,error]=PIDOBJ(x(1),x(2),x(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fx=J;mx=GaussMutation(x,LB,UB);[J,u,yout,error]=PIDOBJ(mx(1),mx(2),mx(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fmx=J;if Fmx<FxY(n)=Fmx;elseif rand>1-(1/(sqrt(k)))X(:,n)=mx;Y(n)=Fmx;elseX(:,n)=x;Y(n)=Fx;endendend%朝信息素最大的地方移动for n=1:Nif n~=POSx=X(:,n);r=(K+k)/(K+K);p=randperm(N);t=ceil(r*N);pos=p(1:t);TempTau=Tau(pos);maxTempTau=max(TempTau);pos2=find(TempTau==maxTempTau);pos3=pos(pos2(1));x2=X(:,pos3(1));x3=(1-Lambda)*x+Lambda*x2;[J,u,yout,error]=PIDOBJ(x(1),x(2),x(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fx=J;[J,u,yout,error]=PIDOBJ(x(1),x(2),x(3),Num,Den,Delay,ts,StepNum,SigType,PIDLB,PIDUB);Fx3=J;if Fx3<FxX(:,n)=x3;Y(n)=Fx3;elseif rand>1-(1/(sqrt(k)))X(:,n)=x3;Y(n)=Fx3;elseX(:,n)=x;Y(n)=Fx;endendend%更新信息素并记录Tau=Tau*(1-Rho);maxY=max(Y);minY=min(Y);DeltaTau=(maxY-Y)/(maxY-minY);Tau=Tau+Q*DeltaTau;ALLX{k}=X;ALLY(k,:)=Y;minY=min(Y);pos4=find(Y==minY);BESTX{k}=X(:,pos4(1));BESTY(k)=minY;disp(k);k=k+1;end。

蚁群优化算法原理及Matlab编程实现

蚁群优化算法原理及Matlab编程实现
蚁群算法的提出：
人工蚂蚁与真实蚂蚁的异同比较
相同点比较
不同点比较
蚁群算法的流程图
基本蚁群算法的实现步骤
（i，j）的初始化信息量τij(t) = const，其中const表示常数，且初始时刻Δτij(0) = 0。

（2）循环次数。

（3）蚂蚁的禁忌表索引号k=1。

（4）蚂蚁数目。

（5）蚂蚁个体根据状态转移概率公式计算的概率选择元素（城市）j并前进，。

其中，表示在t时刻蚂蚁k由元素（城市）i转移到元素（城市）j的状态转
重要性，反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重
视程度，其值越大，则该状态转移概率越接近于贪心规则；ηij(t)为启发函数，
表达式为。

式中，d ij表示相邻两个城市之间的距离。

（6）修改禁忌表指针，即选择好之后将蚂蚁移动到新的元素（城市），并把该τij(t + n) = (1 − ρ) * τij(t) + Δτij(t)
（9）若满足结束条件，即如果循环次数，则循环结束并输出程序计算结果，
]蚁群算法的matlab源程序1.蚁群算法主程序：main.m
2.蚁群算法寻找路径程序：path.m
[编辑]蚁群算法仿真结果。

蚁群算法求解函数最小值

蚁群算法求解函数最小值蚁群算法是一种群体智能算法，它模拟蚂蚁在寻找食物时留下信息、跟随信息和更新信息的行为。

其主要思想是让一群智能体（蚂蚁）在问题空间中随机游走，通过留下信息来指导其他蚂蚁的搜索，最终找到问题的最优解。

本文将介绍如何使用蚁群算法求解函数最小值问题。

1. 问题描述我们要求解函数f(x)的最小值，其中x是一个d维向量，f(x) = ∑(x_i^2)，i=1,2,...,d。

因为所有维度上的值都是正的，所以函数的最小值为0。

但在搜索过程中，优化器需要在向量空间中寻找最小值。

2. 蚁群算法基本思想3. 蚁群算法具体实现1）初始化初始化迭代次数、蚁群大小、信息素浓度以及每只蚂蚁的位置和速度。

对于每个蚂蚁的初始位置和速度，可以使用随机值来生成。

同时，需要记录当前所有蚂蚁中最优的位置和最优的适应度值。

2）信息素选取蚂蚁在搜索过程中留下信息，用于指导其他蚂蚁的行动。

信息素的选择需要权衡两个因素，即蚂蚁个体的局部搜索策略和群体策略。

在局部策略方面，蚂蚁会在已经访问的路径上留下信息素，吸引其他蚂蚁走向已经访问过的区域。

在群体策略方面，信息素可以加速全局搜索，吸引更多的蚂蚁在全局范围内搜索。

3）更新信息素蚂蚁在搜索过程中留下信息，导致当前路径上信息素的浓度增加。

信息素的浓度会随着时间的推移而逐渐降低。

信息素的更新根据当前路径的质量，决定增加或者减少信息素的浓度。

4）更新速度和位置根据留下的信息素和当前位置，更新蚂蚁的速度和位置。

5）计算适应度根据当前位置计算适应度。

这里的适应度即函数的值。

6）更新最优值如果当前的适应度比已记录的最优适应度更优，则更新记录的最优适应度值和位置。

7）终止条件循环运行以上步骤，直到达到指定的迭代次数或满足特定的终止条件。

4. 代码实现示例以Python语言为例，下面给出了求解函数最小值的蚁群算法实现示例：```pythonimport numpy as npclass Ant(object):def __init__(self, dim, max_pos, min_pos):self.dim = dimself.max_pos = max_posself.min_pos = min_posself.pos = np.random.uniform(min_pos, max_pos, size=dim)self.velocity = np.random.uniform(min_pos, max_pos, size=dim)self.pbest = self.posself.pbest_fitness = float('inf')self.fitness = float('inf')def evaluate(self, f):self.fitness = f(self.pos)if self.fitness < self.pbest_fitness:self.pbest = self.posself.pbest_fitness = self.fitnessdef update_velocity(self, other_ant_pos, w, c1, c2, max_velocity):r1 = np.random.rand(self.dim)r2 = np.random.rand(self.dim)self.velocity = w * self.velocity + c1 * r1 * (self.pbest - self.pos) + c2 * r2 * (other_ant_pos - self.pos)self.velocity = np.clip(self.velocity, -max_velocity, max_velocity)def update_pos(self):self.pos = self.pos + self.velocityself.pos = np.clip(self.pos, self.min_pos, self.max_pos)class ACO(object):def __init__(self, f, dim=2, max_iter=100, n_ant=10, max_velocity=1, w=0.5, c1=1, c2=1, max_pos=10, min_pos=-10):self.f = fself.dim = dimself.max_iter = max_iterself.n_ant = n_antself.max_velocity = max_velocityself.w = wself.c1 = c1self.c2 = c2self.max_pos = max_posself.min_pos = min_posself.global_best_fitness = float('inf')self.global_best_pos = np.zeros(dim)self.ants = [Ant(dim, max_pos, min_pos) for i in range(n_ant)]self.init_random_ant()def init_random_ant(self):for ant in self.ants:ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef search(self):for i in range(self.max_iter):for ant in self.ants:for other_ant in self.ants:if ant != other_ant:ant.update_velocity(other_ant.pos, self.w, self.c1, self.c2, self.max_velocity)ant.update_pos()ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef run(self):self.search()print("best fitness: {:.6f}, best position:{}".format(self.global_best_fitness, self.global_best_pos))def f(x):return np.sum(x**2)aco = ACO(f)aco.run()```在这个实现中，我们用Ant表示每个蚂蚁，包含了位置、速度、适应度等信息。

蚁群算法代码（求函数最值）

蚁群算法代码（求函数最值）function [F]=F(x1,x2) %⽬标函数F=-(x1.^2+2*x2.^*cos(3*pi*x1)*cos(4*pi*x2)+;Endfunction [maxx,maxy,maxvalue]=antcolony% 蚁群算法求函数最⼤值的程序ant=200; % 蚂蚁数量times=50; % 蚂蚁移动次数rou=; % 信息素挥发系数p0=; % 转移概率常数lower_1=-1; % 设置搜索范围upper_1=1; %lower_2=-1; %upper_2=1; %for i=1 : antX(i,1)=(lower_1+(upper_1-lower_1)*rand);%随机设置蚂蚁的初值位置X(i,2)=(lower_2+(upper_2-lower_2)*rand);tau(i)=F(X(i,1),X(i,2)); %第i只蚂蚁的信息量end %随机初始每只蚂蚁的位置step=; %⽹格划分单位f='-(x.^2+2*y.^*cos(3*pi*x)*cos(4*pi*y)+';[x,y]=meshgrid(lower_1:step:upper_1,lower_2:step:upper_2); z=eval(f); %eval函数，将字符串内的内容执⾏再赋给对象figure(1);mesh(x,y,z); %⽹格图hold on;plot3(X(:,1),X(:,2),tau,'k*') %蚂蚁初始位置hold on;text,,,'蚂蚁的初始分部位置')xlabel('x');ylabel('y');zlabel('f(x,y)');for t=1:times % 第t次移动lamda=1/t; %步长系数，随移动次数增⼤⽽减少[tau_best(t),bestindex]=max(tau); %第t次移动的最优值及其位置for i=1:ant %第i只蚂蚁p(t,i)=(tau(bestindex)-tau(i))/tau(bestindex); %最优值与第i只蚂蚁的值的差⽐% 计算状态转移概率endfor i=1:antif p(t,i)temp1=X(i,1)+(2*rand-1)*lamda; %移动距离temp2=X(i,2)+(2*rand-1)*lamda;else %全局搜索temp1=X(i,1)+(upper_1-lower_1)*;temp2=X(i,2)+(upper_2-lower_2)*;end %%%%%%%%%%%%%%%%%%%%%% 越界处理if temp1temp1=lower_1;endif temp1>upper_1temp1=upper_1;endif temp2temp2=lower_2;endif temp2>upper_2temp2=upper_2;end %%%%%%%%%%%%%%%%%%%%%%%if F(temp1,temp2)>F(X(i,1),X(i,2))% 判断蚂蚁是否移动X(i,1)=temp1;X(i,2)=temp2;endendfor i=1:anttau(i)=(1-rou)*tau(i)+F(X(i,1),X(i,2)); % 更新信息量end endfigure(2);mesh(x,y,z);hold on;x=X(:,1);y=X(:,2);plot3(x,y,eval(f),'k*')hold on;text,,,'蚂蚁的最终分布位置')xlabel('x');ylabel('y'),zlabel('f(x,y)');[max_value,max_index]=max(tau);maxx=X(max_index,1);maxy=X(max_index,2);maxvalue=F(X(max_index,1),X(max_index,2)); end function [F1]=F1(x) %⽬标函数F1=x.^2-2*x+1;End%蚁群算法求解⼀元函数F1=x^2-2*x+1 close clearclcant=10;times=40;rou=;p0=;lb=-2;ub=2;step=;x=lb::ub;for i=1:antX(i)=lb+(ub-lb)*rand;tau(i)=F1(X(i));endfigure(1);plot(x,F1(x));hold onplot(X,tau,'r*');for kk=1:10for t=1:timeslamda=1/t;%转移次数的倒数[tau_best(t),bestindex]=min(tau);for i=1:antp(t,i)=(tau(bestindex)-tau(i))/tau(bestindex);%转移概率（最优-蚂蚁i）/最优%此种概率选择易陷⼊局部最优解endfor i=1:antif p(t,i)temp=X(i)+(2*rand-1)*lamda;%蚂蚁移动elsetemp=X(i)+(ub-lb)*;endif temptemp=lb;endif temp>ubtemp=ub;endif F1(temp)X(i)=temp;endendfor i=1:anttau(i)=(1-rou)*tau(i)+F1(X(i));endendendfigure(2);plot(x,F1(x));hold onx=X(i);y=tau(i);plot(x,y,'g*');x1=X(length(X))y1=tau(length(tau))。

蚁群算法最短路径matlab程序 - 副本

蚁群算法最短路径matlab程序 - 副本蚁群算法最短路径通用Matlab程序下面的程序是蚁群算法在最短路中的应用，稍加扩展即可应用于机器人路径规划function [ROUTES,PL,Tau]=ACASP(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q) D=G2D(G);N=size(D,1);%N表示问题的规模(象素个数) MM=size(G,1);a=1;%小方格象素的边长Ex=a*(mod(E,MM)-0.5);%终止点横坐标if Ex==-0.5Ex=MM-0.5;endEy=a*(MM+0.5-ceil(E/MM)); Eta=zeros(1,N); for i=1:N if ix==-0.5 ix=MM-0.5;endiy=a*(MM+0.5-ceil(i/MM)); if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);PL=zeros(K,M);%% -----------启动K轮蚂蚁觅食活动，每轮派出M只蚂蚁--------------------for k=1:Kdisp(k);for m=1:MW=S;Path=S;PLkm=0;TABUkm=ones(1,N);TABUkm(S)=0;DD=D;DW=DD(W,:);DW1=find(DW)for j=1:length(DW1)if TABUkm(DW1(j))==0 DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD); while W~=E&&Len_LJD>=1 PP=zeros(1,Len_LJD); for i=1:Len_LJDPP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);endPP=PP/(sum(PP)); Pcum=cumsum(PP);Select=find(Pcum>=rand);Path=[Path,to_visit]; PLkm=PLkm+DD(W,to_visit); W=to_visit;for kk=1:Nif TABUkm(kk)==0 DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;for j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数 end ROUTES{k,m}=Path; if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endendDelta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m) ROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分，新增加一部分 end %% ---------------------------绘图-------------------------------- plotif=1;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLKPLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)'); xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); hold onendendendhold onROUT=ROUTES{K,M};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=1;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)hold onendend将上述算法应用于机器人路径规划，优化效果如下图所示。

蚁群算法TSP问题matlab源代码

function[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ACATSP(C,NC_max,m,Alpha,Beta ,Rho,Q)%%===================================================== ====================%% ACATSP.m%% Ant Colony Algorithm for Traveling Salesman Problem%% ChengAihua,PLA Information Engineering University,ZhengZhou,China%% Email:aihuacheng@%% All rights reserved%%-------------------------------------------------------------------------%% 主要符号说明%% C n个城市的坐标，n×2的矩阵%% NC_max 最大迭代次数%% m 蚂蚁个数%% Alpha 表征信息素重要程度的参数%% Beta 表征启发式因子重要程度的参数%% Rho 信息素蒸发系数%% Q 信息素增加强度系数%% R_best 各代最佳路线%% L_best 各代最佳路线的长度%%===================================================== ====================%%第一步：变量初始化n=size(C,1);%n表示问题的规模（城市个数）D=zeros(n,n);%D表示完全图的赋权邻接矩阵for i=1:nfor j=1:nif i~=jD(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;elseD(i,j)=eps;endD(j,i)=D(i,j);endendEta=1./D;%Eta为启发因子，这里设为距离的倒数Tau=ones(n,n);%Tau为信息素矩阵Tabu=zeros(m,n);%存储并记录路径的生成NC=1;%迭代计数器R_best=zeros(NC_max,n);%各代最佳路线L_best=inf.*ones(NC_m ax,1);%各代最佳路线的长度L_ave=zeros(NC_max,1);%各代路线的平均长度while NC<=NC_max%停止条件之一：达到最大迭代次数%%第二步：将m只蚂蚁放到n个城市上Randpos=[];for i=1:(ceil(m/n))Randpos=[Randpos,randperm(n)];endTabu(:,1)=(Randpos(1,1:m))';%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游for j=2:nfor i=1:mvisited=Tabu(i,1:(j-1));%已访问的城市J=zeros(1,(n-j+1));%待访问的城市P=J;%待访问城市的选择概率分布Jc=1;for k=1:nif length(find(visited==k))==0J(Jc)=k;Jc=Jc+1;endend%下面计算待选城市的概率分布for k=1:length(J)P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta); endP=P/(sum(P));%按概率原则选取下一个城市Pcum=cumsum(P);Select=find(Pcum>=rand);to_visit=J(Select(1));Tabu(i,j)=to_visit;endendif NC>=2Tabu(1,:)=R_best(NC-1,:);end%%第四步：记录本次迭代最佳路线L=zeros(m,1);for i=1:mR=Tabu(i,:);for j=1:(n-1)L(i)=L(i)+D(R(j),R(j+1));endL(i)=L(i)+D(R(1),R(n));endL_best(NC)=min(L);pos=find(L==L_best(NC));R_best(NC,:)=Tabu(pos(1),:);L_ave(NC)=mean(L);NC=NC+1%%第五步：更新信息素Delta_Tau=zeros(n,n);for i=1:mfor j=1:(n-1)Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);endDelta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);endTau=(1-Rho).*Tau+Delta_Tau;%%第六步：禁忌表清零Tabu=zeros(m,n);end%%第七步：输出结果Pos=find(L_best==min(L_best));Shortest_Route=R_best(Pos(1),:)Shortest_Length=L_best(Pos(1))subplot(1,2,1)DrawRoute(C,Shortest_Route)subplot(1,2,2)plot(L_best)hold onplot(L_ave)function DrawRoute(C,R)%%===================================================== ====================%% DrawRoute.m%% 画路线图的子函数%%-------------------------------------------------------------------------%% C Coordinate 节点坐标，由一个N×2的矩阵存储%% R Route 路线%%===================================================== ====================N=length(R);scatter(C(:,1),C(:,2));plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])hold onfor ii=2:Nplot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)]) hold onend设置初始参数如下：m=31;Alpha=1;Beta=5;Rho=0.1;NC_max=200;Q=100; 31城市坐标为：1304 23123639 13154177 22443712 13993488 15353326 15563238 12294196 10044312 7904386 5703007 19702562 17562788 14912381 16761332 6953715 16783918 21794061 23703780 22123676 25784029 28384263 29313429 19083507 23673394 26433439 32012935 32403140 35502545 23572778 28262370 2975运行后得到15602的巡游路径，路线图和收敛曲线如下：。

蚁群算法MATLAB解VRP问题

蚁群算法MATLAB解VRP问题Excel exp12_3_2.xls内容：ANT_VRP函数：function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q) %% R_best 各代最佳路线%% L_best 各代最佳路线的长度%% L_ave 各代平均距离%% Shortest_Route 最短路径%% Shortest_Length 最短路径长度%% D 城市间之间的距离矩阵，为对称矩阵%% Demand 客户需求量%% Cap 车辆最⼤载重%% iter_max 最⼤迭代次数%% m 蚂蚁个数%% Alpha 表征信息素重要程度的参数%% Beta 表征启发式因⼦重要程度的参数%% Rho 信息素蒸发系数%% Q 信息素增加强度系数n=size(D,1);T=zeros(m,2*n); %装载距离Eta=ones(m,2*n); %启发因⼦Tau=ones(n,n); %信息素Tabu=zeros(m,n); %禁忌表Route=zeros(m,2*n); %路径L=zeros(m,1); %总路程L_best=zeros(iter_max,1); %各代最佳路线长度R_best=zeros(iter_max,2*n); %各代最佳路线nC=1;while nC<=iter_max %停⽌条件Eta=zeros(m,2*n);T=zeros(m,2*n);Tabu=zeros(m,n);Route=zeros(m,2*n);L=zeros(m,1);%%%%%%==============初始化起点城市（禁忌表）====================for i=1:mCap_1=Cap; %最⼤装载量j=1;j_r=1;while Tabu(i,n)==0T=zeros(m,2*n); %装载量加载矩阵Tabu(i,1)=1; %禁忌表起点位置为1Route(i,1)=1; %路径起点位置为1visited=find(Tabu(i,:)>0); %已访问城市num_v=length(visited); %已访问城市个数J=zeros(1,(n-num_v)); %待访问城市加载表P=J; %待访问城市选择概率分布Jc=1; %待访问城市选择指针for k=1:n %城市if length(find(Tabu(i,:)==k))==0 %如果k不是已访问城市代号，就将k加⼊矩阵J中J(Jc)=k;Jc=Jc+1;endend%%%%%%%=============每只蚂蚁按照选择概率遍历所有城市==================for k=1:n-num_v %待访问城市if Cap_1-Demand(J(1,k),1)>=0 %如果车辆装载量⼤于待访问城市需求量if Route(i,j_r)==1 %如果每只蚂蚁在起点城市T(i,k)=D(1,J(1,k));P(k)=(Tau(1,J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率计算公式中的分⼦else %如果每只蚂蚁在不在起点城市T(i,k)=D(Tabu(i,j),J(1,k));P(k)=(Tau(Tabu(i,visited(end)),J(1,k))^Alpha)*((1/T(i,k))^Beta); %概率计算公式中的分⼦endelse %如果车辆装载量⼩于待访问城市需求量T(i,k)=0;P(k)=0;endendif length(find(T(i,:)>0))==0 %%%当车辆装载量⼩于待访问城市时，选择起点为1Cap_1=Cap;j_r=j_r+1;Route(i,j_r)=1;L(i)=L(i)+D(1,Tabu(i,visited(end)));elseP=P/(sum(P)); %按照概率原则选取下⼀个城市Pcum=cumsum(P); %求累积概率和：cumsum（[1 2 3])=1 3 6,⽬的在于使得Pcum的值总有⼤于rand的数Select=find(Pcum>rand); %按概率选取下⼀个城市：当累积概率和⼤于给定的随机数，则选择求和被加上的最后⼀个城市作为即将访问的城市 o_visit=J(1,Select(1)); %待访问城市j=j+1;j_r=j_r+1;Tabu(i,j)=o_visit; %待访问城市Route(i,j_r)=o_visit;Cap_1=Cap_1-Demand(o_visit,1); %车辆装载剩余量L(i)=L(i)+T(i,Select(1)); %路径长度endendL(i)=L(i)+D(Tabu(i,n),1); %%路径长度endL_best(nC)=min(L); %最优路径为距离最短的路径pos=find(L==min(L)); %找出最优路径对应的位置：即为哪只蚂蚁R_best(nC,:)=Route(pos(1),:); %确定最优路径对应的城市顺序L_ave(nC)=mean(L)'; %求第k次迭代的平均距离Delta_Tau=zeros(n,n); %Delta_Tau(i,j)表⽰所有蚂蚁留在第i个城市到第j个城市路径上的信息素增量L_zan=L_best(1:nC,1);post=find(L_zan==min(L_zan));Cities=find(R_best(nC,:)>0);num_R=length(Cities);for k=1:num_R-1 %建⽴了完整路径后在释放信息素Delta_Tau(R_best(nC,k),R_best(nC,k+1))=Delta_Tau(R_best(nC,k),R_best(nC,k+1))+Q/L_best(nC);endDelta_Tau(R_best(nC,num_R),1)=Delta_Tau(R_best(nC,num_R),1)+Q/L_best(nC);Tau=Rho*Tau+Delta_Tau;nC=nC+1;endShortest_Route=zeros(1,2*n); %提取最短路径Shortest_Route(1,:)=R_best(iter_max,:);Shortest_Route=Shortest_Route(Shortest_Route>0);Shortest_Route=[Shortest_Route Shortest_Route(1,1)];Shortest_Length=min(L_best); %提取最短路径长度%L_ave=mean(L_best); 求解程序：clc;clear all%% ==============提取数据==============[xdata,textdata]=xlsread('exp12_3_2.xls'); %加载20个城市的数据，数据按照表格中位置保存在Excel⽂件exp12_3_1.xls中x_label=xdata(:,2); %第⼆列为横坐标y_label=xdata(:,3); %第三列为纵坐标Demand=xdata(:,4); %第四列为需求量C=[x_label y_label]; %坐标矩阵n=size(C,1); %n表⽰节点（客户）个数%% ==============计算距离矩阵==============D=zeros(n,n); %D表⽰完全图的赋权邻接矩阵，即距离矩阵D初始化for i=1:nfor j=1:nif i~=jD(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算两城市之间的距离elseD(i,j)=0; %i=j, 则距离为0；endD(j,i)=D(i,j); %距离矩阵为对称矩阵endendAlpha=1;Beta=5;Rho=0.75;iter_max=100;Q=10;Cap=1;m=20; %Cap为车辆最⼤载重[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT_VRP(D,Demand,Cap,iter_max,m,Alpha,Beta,Rho,Q); %蚁群算法求解VRP问题通⽤函数，详见配套光盘Shortest_Route_1=Shortest_Route-1 %提取最优路线Shortest_Length %提取最短路径长度%% ==============作图==============figure(1) %作迭代收敛曲线图x=linspace(0,iter_max,iter_max);y=L_best(:,1);plot(x,y);xlabel('迭代次数'); ylabel('最短路径长度');figure(2) %作最短路径图plot([C(Shortest_Route,1)],[C(Shortest_Route,2)],'o-');grid onfor i =1:size(C,1)text(C(i,1),C(i,2),[' ' num2str(i-1)]);endxlabel('客户所在横坐标'); ylabel('客户所在纵坐标');。

蚁群算法在Matlab中的程序设计

启发函数在转移中起的作用越大；ａｌｌｏｗ（ｋ＝１，２， …，ｍ）表示蚂蚁ｋ下一步允许访问的城市集合。设Ｐ为信息素的挥发系数，则可通过下式来进行信息素的更新：
ｆｒ（ｔ＋１）＝（１一Ｐ）（ｔ）＋△
ｋ㈤：
２．１．１数据的初始化这个步骤主要完成以下数据的初始化： ①通过已知的ｎ个城市坐标，求得每两个城市间的距离并保存在距离矩阵中； ②初始化信息素矩阵； ③初始化算法参数； ④初始化记录数据的变量及矩阵。２．１．２通过算法寻找最优路径运行算法，通过迭代来计算最优路径，直到满足
否则
Ｓｔｅｐ２，否则输出结果。整个步骤的算法框图如图２所示。
２．３运行结果及分析式（３）中，Ｑ为常数，表示蚂蚁循环一次所释放的信
息素的总量；为蚂蚁ｋ经过的路径长度。
２用Ｍａｔｌａｂ实现蚁群算法
Ｍａｔｌａｂ是一个功能强大的科学计算和工程计算
结果数据以图表的形式展示出来，如图３和图４所示分别为蚁群算法最短路径和各代的收敛情况。从图中可以看出，本算法得到的最短距离为１５６０１．９１９５ｋｍ，而最短距离在迭代了１００次以后基本上就接近最短路径了，平均距离也在迭代次数达到１００次后趋于平缓。程序运行的输出结果为：