求阴影部分图形面积测试题
小学数学西师大版第十一册二 圆圆的面积-章节测试习题

章节测试题1.【题文】求阴影部分的面积和周长.【答案】面积:60cm2;周长:38.84cm【分析】用割补法把左边半圆形移到右边拼成一个长方形,阴影部分面积就等于长方形面积.周长是圆的周长加2个10cm.【解答】10×6=60(cm2)3.14×6+10×2=38.84(cm)答:阴影部分的面积是60cm2;周长是38.84cm.2.【题文】一只挂钟的时针长7厘米,这根时针走一圈扫过的面积是多少?【答案】153.86平方厘米【分析】转一圈所扫过的面积是以时针的长度为半径的圆的面积,利用圆的面积即可求解.【解答】3.14×72=153.86(平方厘米)答:这根时针走一圈扫过的面积是153.86平方厘米.3.【题文】一块圆形水稻试验田,周长是125.6米.这块试验田共收水稻2512千克,每平方米产水稻多少千克?【答案】2千克【分析】由圆的周长得,求出圆的半径,再根据圆的面积公式计算出水稻试验田的面积,再依据“总产量÷数量=单产量”用水稻的总产量除以水稻试验田的面积,即可得解.【解答】125.6÷3.14÷2=20(米)2512÷(3.14×202)=2(千克)答:每平方米产水稻2千克.4.【题文】下图池塘的周长251.2米,池塘周围(阴影)是一条5米宽的水泥路,在路的外侧围一圈栏杆.水泥路的面积是多少?栏杆长多少米?【答案】1334.5平方米;282.6米【分析】圆环的面积,求水泥路的面积,实际是求圆环的面积;求栏杆长,实际是求外圆的周长;根据题中给出的条件:池塘的周长251.2米,可求出内圆的半径,水泥路宽5米,据此可求出外圆的半径,由此可知答案.【解答】251.2÷3.14÷2=40(米)40+5=45(米)3.14×(452-402)=1334.5(平方米)3.14×45×2=282.6(米)答:水泥路的面积是1334.5平方米,栏杆长282.6米.5.【题文】将一根长100米的绳子,绕一棵大树20圈少48厘米,这棵大树横截面面积是多少平方厘米?【答案】20096平方厘米【分析】先求出树一圈的长度,即周长,再求横截面面积.据此解答.【解答】100米=10000厘米(10000+48)÷20=502.4(厘米)502.4÷3.14÷2=80(厘米)3.14×802=3.14×6400=20096(平方厘米)答:这棵大树横截面面积是20096平方厘米.6.【题文】已知图中圆的面积是28.26平方厘米,那么正方形的面积是多少平方厘米?【答案】36平方厘米【分析】因为正方形的边长等于圆的半径的2倍,正方形的面积等于;圆的面积.可先求出,再求正方形的面积.【解答】28.26÷3.14=9(平方厘米)9×4=36(平方厘米)答:正方形的面积是36平方厘米.7.【答题】大圆的半径是小圆半径的3倍,大圆的周长是小圆周长的______倍,大圆的面积是小圆面积的______倍.【答案】3 9【分析】此题考查的是圆的周长和面积公式的应用.设小圆的半径为,则大圆的半径为,分别代入圆的周长和面积公式,表示出各自的周长和面积,即可求解.【解答】设小圆的半径为,则大圆的半径为,小圆的周长为,大圆的周长为,,所以大圆的周长是小圆周长的3倍;小圆的面积为,大圆的面积为,,所以大圆的面积是小圆面积的9倍.故此题的答案是3,9.8.【答题】边长是10m的正方形中放置一个最大的圆,这个圆的面积是______m2.【答案】78.5【分析】在边长是10m的正方形中放置一个最大的圆,圆的半径是正方形边长的一半,根据圆的面积公式计算即可求解.【解答】3.14×(10÷2)2=78.5(m2),所以这个圆的面积是78.5m2.故此题的答案是78.5.9.【答题】一个圆形花坛,直径是5米,这个花坛的面积是______平方米.【答案】19.625【分析】此题考查的是圆的面积公式的应用.用直径除以2求出圆形花坛的半径,再利用圆的面积公式,列式解答即可.【解答】半径为5÷2=2.5(米),面积是3.14×2.52=19.625(平方米),所以这个花坛的面积是19.625平方米.故此题的答案是19.625.10.【答题】当正方形、长方形、圆的周长都相等时,面积最大的是()A. 正方形B. 长方形C. 圆【答案】C【分析】此题考查的是长方形、正方形、圆形的面积公式及灵活运用,解答此题可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.【解答】为了便于理解,假设正方形、长方形和圆形的周长都是16,则圆的面积为3.14×(16÷3.14÷2)2≈20.38;正方形的边长为16÷4=4,面积为4×4=16;长方形长宽越接近面积越大,就取长为5,宽为3,面积为5×3=15. 20.38>16>15,所以周长相等的正方形、长方形和圆形,圆面积最大.选C.11.【答题】一个圆的半径是2m,那么它的周长和面积相比,().A. 面积大B. 周长大C. 同样大D. 无法比较【答案】D【分析】此题考查的是圆的周长和面积.【解答】圆的周长和面积不是同类量,它们无法进行比较.选D.12.【答题】在草地中心栓着一头牛,绳长4米,这头牛最多吃到草的面积是多少?正确的列式是()A. 3.14×42B. 3.14×4C. 2×3.14×4D. 2×3.14×42【答案】A【分析】此题考查的是圆的面积公式的应用.将圆的面积公式代入数据求解即可.【解答】这头牛最多吃到草的面积是3.14×42平方米.选A.13.【答题】一个圆的半径扩大2倍,那么面积和周长()A. 面积和周长扩大2倍B. 面积扩大4倍,周长扩大2倍C. 周长扩大4倍,面积扩大2倍【答案】B【分析】此题考查的是圆的周长公式、面积公式的应用.【解答】设圆的半径为,则周长,面积,π是一个定值,圆的半径扩大2倍时,周长也是扩大2倍;扩大2×2=4倍,所以圆的面积就扩大4倍.所以一个圆的半径扩大2倍,则周长扩大2倍,面积扩大4倍.选B.14.【题文】求如图中阴影部分的周长和面积.(单位:厘米)【答案】33.12厘米,25.12平方厘米【分析】观察图形可知,阴影部分的周长等于半径是8厘米的圆的周长的与直径是8厘米的半圆的周长的和;阴影部分的面积等于半径是8厘米的圆的面积的与直径是8的半圆的面积的差;据此即可解答问题.【解答】3.14×8×2×+3.14×8÷2+8=12.56+12.56+8=33.12(厘米)3.14×82×﹣3.14×(8÷2)2÷2=50.24﹣25.12=25.12(平方厘米)答:阴影部分的周长是33.12厘米,面积是25.12平方厘米.15.【题文】在一个半径为2米的圆形花坛外围修一条宽1米的环形小路,这条小路的面积是多少?【答案】15.7平方米【分析】这条小路的面积是圆环的面积等于外圆面积减去内圆面积,已知内圆半径,可求内圆面积,内圆半径加路宽为外圆半径,可求外圆面积,进而求出圆环面积.【解答】内圆面积:3.14×22=12.56(平方厘米),外圆面积:3.14×(2+1)2=28.26(平方厘米),小路面积:28.26﹣12.56=15.7(平方厘米).答:这条小路的面积是15.7平方米.16.【题文】某钟表时针的长度为6cm,从3时到6时,时针扫过的面积是多少平方厘米?【答案】28.26平方厘米【分析】时针所走过的轨迹是以时针的长度为半径,扫过的面积是圆的面积,据此解答即可.【解答】答:时针扫过的面积是28.26平方厘米.17.【题文】计算下图中阴影部分的面积.(单位:厘米)【答案】77平方厘米【分析】阴影部分的面积应该等于半圆的面积减三角形的面积,因此先求半圆的面积和三角形的面积.【解答】半圆的面积:3.14×(20÷2)2÷2=157(平方厘米),三角形的面积:20×8÷2=80(平方厘米),阴影部分的面积:157-80=77(平方厘米).18.【题文】一个运动场的两端都是半圆形,中间是一个边长是40米的正方形(如图).(1)小明每天要沿着这个运动场周围跑5圈,他每天跑多少米?(2)这个运动场占地面积是多少平方米?【答案】(1)1028米;(2)2856平方米【分析】(1)首先求出运动场的周长,运动场的周长等于直径40米的圆的周长加上(40×2)米,然后用运动场的周长乘5即可.(2)运动场的面积=正方形的面积+圆的面积,根据正方形的面积公式、圆的面积公式,把数据代入公式解答.【解答】(1)答:他每天跑1028米.(2)答:这个运动场占地面积是2856平方米.19.【题文】光盘银色部分是一个圆环,内圆半径是2厘米,外圆半径是6厘米.银色部分的面积是多少?【答案】100.48平方厘米【分析】求银色部分的面积就是求圆环的面积.已知内圆和外圆的半径,根据圆环面积等于外圆的面积减内圆的面积可以计算出来.【解答】答:银色部分的面积是100.48平方厘米.20.【题文】求下图中阴影部分的周长和面积.(单位:厘米)【答案】周长:33.12厘米;面积:25.12平方厘米【分析】观察图形可知,阴影部分的周长等于半径是8厘米的圆的周长的与直径是8厘米的半圆的周长的和;阴影部分的面积等于半径是8厘米的圆的面积的与直径是8厘米的半圆的面积的差.据此即可解答问题.【解答】答:阴影部分的周长是33.12厘米,面积是25.12平方厘米.。
《组合图形的面积》练习题(含答案)
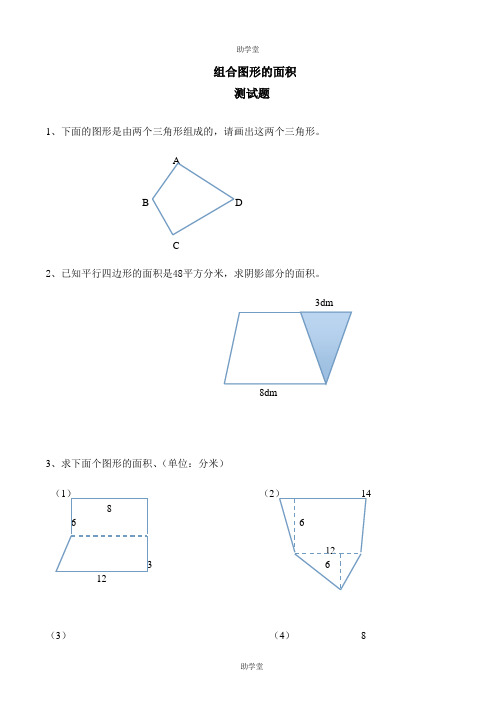
组合图形的面积
测试题
1、下面的图形是由两个三角形组成的,请画出这两个三角形。
A
B D
C
2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm
8dm
3、求下面个图形的面积、(单位:分米)
(1)(2)14 8
6 6
12
3 6
12
(3)(4)8
2.5
5.4 4 1.5
4.2 6
3
4、如图所示,梯形的周长是52厘米,求阴影部分的面积。
16
5、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)
6 2
2
5
6、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)
15
7、有一块土地如图所示,你能用几种方法求出它的面积?(单位:米)
12
15
8
22
7、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?
B
A
8米
【参考答案】。
小学数学人教版(2014秋)五年级上册第六单元 多边形的面积不规则图形的面积-章节测试习题

章节测试题1.【答题】如图所示,它是由18个边长为1厘米的小正方形组成的长方形,图中阴影部分的面积是()平方厘米.A.12B.18C.5D.20【答案】C【分析】如图所示,阴影部分由①、②、③三个三角形组成,分别求出三个三角形的面积,即可得解.【解答】三角形①的面积=1×2÷2=1(平方厘米);三角形②的面积=3×2÷2=3(平方厘米);三角形③的面积=2×1÷2=1(平方厘米).阴影部分的面积=1+3+1=5(平方厘米),选C.2.【答题】下面两个图形的面积相比,()。
A.①>②B.①<②C.①=②【答案】B【分析】因为两图形都在45的网格中,哪个图形所占的格数多,哪个的面积就大,由此得出结论。
【解答】图形①在45的网格中占据9格,图形②在45的网格中占据12格;所以面积大小①<②。
3.【答题】图中整格的有______个,半格的有______个,面积约是______平方厘米.【答案】24,20,34【分析】本题考查估计不规则图形的面积.用方格纸估算不规则图形的面积,先数整格的,再数不满整格的,不满整格的按半格计算.【解答】由图可知,图中整格的有24个,半格的有20个,1个整格的面积是:1×1=1(平方厘米),24+20÷2=34(格),所以不规则图形的面积约是:34×1=34(平方厘米).故本题答案为24,20,34.4.【答题】写出下面图形的面积。
(1)______平方厘米(2)______平方厘米【答案】16,21【分析】本题考查不规则图形面积的计算。
【解答】(1)由图可知,每个小正方形的边长是1cm,则一个小正方形的面积是:1×1=1(cm²);如下图所示:将这个不规则图形分成上、下两部分,每一部分是形状相同的梯形,梯形的上底是2cm,下底是6cm,高是2cm,则梯形的面积是:(2+6)×2÷2=8×2÷2=16÷2=8(cm²);不规则图形的面积是:8×2=16(cm²);(2)图中不规则图形共占了21个小正方形,所以面积是21cm²。
小学数学北京版六年级上册第五单元 圆圆的面积-章节测试习题

章节测试题1.【题文】求如图中阴影部分的周长和面积.(单位:厘米)【答案】33.12厘米,25.12平方厘米【分析】观察图形可知,阴影部分的周长等于半径是8厘米的圆的周长的与直径是8厘米的半圆的周长的和;阴影部分的面积等于半径是8厘米的圆的面积的与直径是8的半圆的面积的差;据此即可解答问题.【解答】3.14×8×2×+3.14×8÷2+8=12.56+12.56+8=33.12(厘米)3.14×82×﹣3.14×(8÷2)2÷2=50.24﹣25.12=25.12(平方厘米)答:阴影部分的周长是33.12厘米,面积是25.12平方厘米.2.【题文】—个圆与一个长方形的面积相等.圆的周长是37. 68厘米.长方形的宽是9厘米,长是多少厘米?【答案】12.56厘米【分析】本题要求长方形的长,要先求出长方形的面积,已知圆的面积等于长方形的面积,所以要先求出圆形的面积.【解答】先求圆的半径,半径:37.68÷3.14÷2=6(厘米),面积:3.14×6×6=113.04(平方厘米),长方形的面积也是113.04平方厘米,宽是9厘米,长是113.04÷9=12.56(厘米).3.【答题】在推导圆的面积公式时,把一个圆分成若干等份后,拼成一个近似长方形,这个长方形的长是()A.圆的半径B.圆的直径C.圆的周长D.圆周长的一半【答案】D【分析】把一个圆分成若干等份后,拼成一个近似长方形,这个长方形的长正好是圆周长的一半,宽是圆的半径.【解答】在推导圆的面积公式时,把一个圆分成若干等份后,拼成一个近似的长方形,这个长方形的长是圆周长的一半.4.【答题】一个圆形花坛,要在花坛内种草皮,求需种多少草皮是求花坛的()A.半径B.直径C.周长D.面积【答案】D【分析】本题考察的知识点是圆的面积的意义.【解答】圆的面积的意义可以知道,铺草皮指的是面积.5.【答题】一个圆,半径是r,它的面积是()A.(π+2)rB.πrC.πr²D.πr+r【答案】C【分析】本题考察的知识点是圆的面积.【解答】S=πr².6.【答题】如图,一个三角形的三个顶点分别为三个半径为3厘米的圆的圆心,则图中阴影部分的面积是()A.π平方厘米B.9π平方厘米C.4.5π平方厘米D.3π平方厘米【答案】C【分析】这道题一定要仔细看图,可以发现阴影部分的圆心角的和正好是180度,而且圆的半径相等,所以阴影部分的面积正好等于半圆的面积.【解答】仔细观察发现阴影部分的面积正好等于半圆的面积,阴影面积是π×3×3÷2=4.5π.7.【答题】小明在计算一道求圆的面积的题时,错把半径当成直径的长度计算,这时只要把计算的结果乘以()就能求出正确答案.A.圆周率B.2C.4【答案】C【分析】设原来的半径为r,则圆面积为πr2;小明把半径当成直径,则圆的半径就被小明错误的认为是r,则圆面积为π×= πr2,可见面积缩小为原来的,因此只要乘上4就能求出正确答案.据此解答.【解答】设原来的半径为r,则圆面积为πr2.因为小明认为r为直径,则半径为r,面积为π× = πr2,所以面积缩小为原来的,因此只要乘上4就能求出正确答案.8.【答题】用三根同样长的钢丝分别围成下面的三种图形,其中面积最大的是()A.长方形B.正方形C.圆【答案】C【分析】此题要明确绳长即周长,然后用假设法进行分析,计算得出;假设这根绳长为6.28米;然后根据长方形,正方形和圆的知识进行分析,并以此算出其面积进行比较即可得出结论.【解答】假设这根绳长为6.28米;圆:6.28÷3.14÷2=1(米),面积为:3.14×12=3.14(平方米);正方形:6.28÷4=1.57(米),面积为:1.57×1.57≈2.46(平方米);长方形:假设长是2,宽则为:1.14米,面积为:2×1.14=2.28(平方米);通过计算可知,同周长的圆、正方形和长方形,所围成的面积圆最大,正方形次之,长方形面积最小.9.【答题】如果圆的周长等于正方形的周长,那么圆的面积()正方形的面积.A.大于B.等于C.小于【答案】A【分析】可设圆及正方形的周长为a,则由圆周长公式C=2πr,可求得圆的半径r= ,从而圆的面积可表示为π()2;另外,正方形的周长为a,则边长为,所以面积为()2,再比较出π()2和()2的大小即可得出答案.【解答】设圆及正方形的周长为a,由圆周长公式C=2πr得,圆的半径r= ,所以圆的面积为:S圆=πr2=π()2= ;因为正方形的周长为a,所以边长为,面积为:S正方形=()2= ,又因为4π<4×4,即4π<16,所以>,即S圆>S正方形.10.【答题】用40厘米长铁丝分别围成三角形、长方形和圆.面积最大的是()A.三角形B.长方形C.圆【答案】C【分析】首先根据题意,可得所围成的图形的周长相等;然后根据若周长一定,所围成的图形越接近圆形,其面积就越大,据此解答即可.【解答】根据题意,可得所围成的图形的周长相等,都是40厘米.若周长一定,所围成的图形越接近圆形,其面积就越大,用同样长的四根铁丝分别围成三角形、长方形、圆形,其中所围成的图形面积最大的是圆.11.【答题】圆的面积与它的()无关.A.圆心B.半径C.周长【答案】A【分析】根据圆的面积公式S=π,圆的面积与圆的半径有关,又因为d=2r、C =2πr所以圆的面积与它的直径和周长也有关系,圆心只能确定圆的位置,而不能确定圆的大小.【解答】圆的面积公式:S=π,π是一个固定值,圆的面积大小与它的半径有关,与它的圆心无关.选A.12.【答题】一个长方形和一个圆的周长相等,它们的面积相比,().A.长方形=圆B.圆<长方形C.圆>长方形【答案】C【分析】本题考点:面积及面积的大小比较.周长相等的情况下利用假设的方法分别求出它们的面积相比较,这是一种常用的方法.假设它们的周长都是6.28厘米,分别依据各自的周长公式求出长方形的长和宽,圆的半径,进而依据各自的面积公式即可求出它们的面积,进而比较出它们的面积的大小.【解答】假设它们的周长是6.28厘米,则长+宽:6.28÷2=3.14(厘米),长方形的长和宽越接近,它的面积越大所以长方形的长可以为1.56厘米,1.58厘米,长方形的面积:1.56×1.58=2.4648(平方厘米)圆的面积:6.28÷3.14÷2=1(厘米),3.14×12=3.14(平方厘米),2.4648<3.14,所以周长相等时圆的面积大于长方形的面积.13.【答题】在一个边长是8厘米的正方形内画一个最大的圆,圆的面积占正方形面积的()A.B.C.D.【答案】D【分析】根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用圆的面积除以正方形的面积即可解答问题.【解答】π×(8÷2)2=π×16=16π(平方厘米),正方形的面积是:8×8=64(平方厘米),所以16π÷64= .所以圆面积占正方形面积的.14.【答题】如果一个大圆的周长是一个小圆周长的4倍,那么大圆的面积是小圆面积的()倍.A.2B.4C.8D.16【答案】D【分析】根据题意,大圆的周长是小圆周长的4倍,则大圆的半径就是小圆的半径的4倍,由此可设小圆的半径是r,则大圆的半径是4r,根据圆的面积公式即可解答.【解答】大圆的周长是小圆周长的4倍,则大圆的半径就是小圆的半径的4倍,由此可设小圆的半径是r,则大圆的半径是4r,则大圆的面积为π(4r)2=16πr2;小圆的面积为πr2,16πr2÷πr2=16倍.15.【答题】把一个圆平均分成32份,然后剪开,拼成一个近似的长方形,这个转化过程中()A.周长、面积都没变B.周长没变,面积边了C.周长变了,面积没变【答案】C【分析】把一个圆形平均分成32份,剪开拼成一个近似的长方形,这个长方形的宽就等于圆的半径,长就等于圆的周长的一半,所以这个转化过程中圆的面积不变,周长增加了两个半径的长度;此解答即可.【解答】把一个圆形平均分成32份,剪开拼成一个近似的长方形,这个转化过程圆的面积不变,周长发生变化,周长增加了两个半径的长度,所以本题选项C正确.16.【答题】一个圆的半径增加1厘米,它的周长就增加()A.1厘米B.2厘米C.6.28厘米D.3.14厘米【答案】C【分析】圆的半径变化引起圆的周长变化的规律.【解答】圆的周长公式为C=2πr,圆的半径增加1厘米,则,它的周长会增加2π厘米,即6.28厘米.17.【答题】光盘是一个圆环,内圆直径是2cm,外圆直径是12cm,这个光盘的面积是______cm2.【答案】109.9【分析】环形面积公式:,依次代入数据计算即可求解.【解答】3.14×(12÷2)2-3.14×(2÷2)2=109.9(cm2).18.【答题】如果大圆和小圆的半径比是5:1,面积比就是25:1.( )【答案】√【分析】根据题意,可设小圆的半径为r,则大圆的半径为5r,可根据圆的面积公式计算出大圆、小圆的面积,然后用大圆的面积比小圆的面积即可.【解答】设小圆的半径为r,则大圆的半径为5r,所以大圆的面积与小圆的面积的比为,所以原题的说法是正确的.19.【答题】圆的半径扩大到原来的3倍,它的周长扩大到原来的3倍,它的面积扩大到原来的6倍.( )【答案】×【分析】根据和以及积的变化规律可得:一个圆的半径扩大到原来的n倍,这个圆的周长就扩大到原来的n倍,面积就扩大到原来的n2倍,据此解答.【解答】根据分析可知,圆的半径扩大到原来的3倍,它的周长扩大到原来的3倍,它的面积扩大到原来的9倍.所以原题的说法是错误的.20.【答题】半径是2厘米的圆,它的周长和面积相等.( )【答案】×【分析】圆的周长是长度单位厘米,圆的面积是面积单位平方厘米,两者之间不能互换,因此无法比较大小.【解答】圆的周长是长度单位,圆的面积是面积单位,不能比较大小,所以原题说法是错误的.。
初一求阴影题5题

初一求阴影题5题
以下是5道适合初一学生练习的求阴影部分的面积题目:
1.正方形中的阴影:
在一个边长为8cm的正方形中,有一个边长为4cm的小正方形。
求大正方形中小正方形之外的阴影部分的面积。
2.矩形中的三角形:
在一个长为10cm、宽为6cm的矩形中,有一个底为6cm、高为4cm的直角三角形。
求矩形中直角三角形之外的阴影部分的面积。
3.圆形中的扇形:
在一个半径为5cm的圆中,有一个圆心角为90°的扇形。
求圆中扇形之外的阴影部分的面积。
4.组合图形的阴影:
有一个边长为6cm的正方形和一个半径为3cm的半圆,它们有一部分重叠。
求不重叠部分的阴影面积。
5.多边形与三角形的组合:
有一个边长为6cm的正六边形和一个底为6cm、高为3cm的三角形。
它们有一部分重叠。
求不重叠部分的阴影面积。
这些题目旨在帮助学生运用几何知识,如正方形、矩形、圆形、扇形、三角形等的基本性质和面积计算公式,来求解阴影部分的面积。
通过练习这些题目,学生可以加深对几何图形面积计算的理解和应用能力。
希望这些题目对初一学生的几何练习有所帮助!。
北师大版五年级数学上册期末复习专题组合图形的面积练习(含答案)

北师大版五年级数学上册期末复习专题组合图形的面积【知识点归纳】 方法:①“割法”:观察图形,把图形进行分割成容易求得的图形,再进行相加减.②“补法”:观察图形,给图形补上一部分,形成一个容易求得的图形,再进行相加减. ③“割补结合”:观察图形,把图形分割,再进行移补,形成一个容易求得的图形. 【典例分析】例1:求图中阴影部分的面积.(单位:厘米)分析:根据图所示,可把组合图形分成一个直角梯形和一个41圆,阴影部分的面积等于梯形的面积减去41圆的面积再加上41圆的面积减去三角形面积的差,列式解答即可得到答案. 解:[(5+8+5)×5÷2-41×3.14×52]+(41×3.14×52-5×5÷2), =[18×5÷2-0.785×25]+(0.785×25-25÷2), =[90÷2-19.625]+(19.625-12.5), =[45-19.625]+7.125, =25.375+7.125,=32.5(平方厘米);答:阴影部分的面积为32.5平方厘米.点评:此题主要考查的是梯形的面积公式(上底+下底)×高÷2、三角形的面积公式底×高÷2和圆的面积公式S=πr 2的应用.同步测试一.选择题(共10小题)1.已知长方形和正方形的面积相等,阴影部分A和B的面积不相等是()A.B.C.D.2.如图是一个直角梯形,图中阴影部分面积是100平方厘米,空白部分面积是()平方厘米.A.140 B.120 C.100 D.703.如图中阴影部分的面积是60平方厘米,空白部分的面积是()平方厘米.A.12 B.30 C.60 D.无法判断4.下面三个完全一样的直角梯形中,阴影部分的面积()A.甲最大B.乙最大C.丙最大D.一样大5.在图的平行四边形中,E、F把AB边分成了相等的三段,平行四边形的面积是48平方厘米,阴影三角形的面积是()A.8平方厘米B.12平方厘米C.16平方厘米D.24平方厘米6.如图,平行四边形的面积是24cm2,则阴影部分的面积是()A.2cm2B.4cm2C.10cm2D.12cm27.两个完全一样的正方形,如果①号图形阴影部分的面积是10平方厘米,那么②号图形阴影部分的面积是()平方厘米.A.30 B.25 C.20 D.108.下面两个是完全一样的平行四边形,涂色部分的面积()A.甲大B.乙大C.一样大9.如图中,阴影部分面积与三角形()的面积相等.A.BCD B.BFC C.BCE10.比较下面两个图形,说法正确的是()A.甲、乙的面积相等,周长也相等B.甲、乙的面积相等,但甲的周长长C.甲、乙的周长相等,但乙的面积大D.甲、乙的面积相等,它们周长不一定相等二.填空题(共8小题)11.如图(单位:dm),半圆是长方形内最大的半圆,则这个长方形的面积是dm2.12.如图的面积是平方厘米.13.如果用1厘米表示如图小方格的边长,那么阴影部分的面积是平方厘米.14.如图,平行四边形的面积是20cm2,那么三角形的高是cm,面积是cm2.15.图中四边形的面积是平方厘米.16.如图,阴影部分是面积是平方厘米.(π取3.14)17.某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是.18.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为.(A)5050m2(B)4900m2(C)5000m2(D)4998m2三.判断题(共5小题)19.图中阴影部分的面积比半圆大..(判断对错)20.如图所示,梯形的上底长等于下底长的一半,空白面积也等于阴影部分面积的一半.(判断对错)21.图中阴影部分的面积为24cm2.(判断对错)22.如图中阴影部分的面积是14平方厘米.(判断对错)23.计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再进行计算..(判断对错)四.计算题(共2小题)24.求阴影部分的面积.(单位:cm)25.计算下面图形的面积.五.解答题(共3小题)26.下面是一个菜园的平面图,算一算这个菜园的面积是多少平方米.27.如图,在平行四边形ABCD中,BC长10厘米,直角三角形BCE的直角边EC长8厘米,已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米,求CF的长.28.李大爷家有一块菜地.(形状如图,单位米)长方形地里种的是圆白菜,右边的梯形地里种的是茄子.(1)每棵圆白菜占地0.15平方米,一共可以种几棵?(2)茄子地一共有多少平方米?参考答案与试题解析一.选择题(共10小题)1.【分析】我们通过对每个选项给出的图形计算可知,A选项中阴影部分A的面积等于正方形的面积的,B的面积等于长方形面积的,而长方形和正方形的面积相等;所以阴影部分A和B的面积;选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积,所以相等;选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积,B的面积得出正方形减去空白部分小长方形的面积,所以不相等.选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积,所以相等;据此解答.解:A选项中阴影部分A的面积等于正方形的面积的,B的面积等于长方形面积的,而长方形和正方形的面积相等;所以阴影部分A和B的面积;选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积,所以相等;选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积,B的面积得出正方形减去空白部分小长方形的面积,所以不相等.选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积,所以相等;故选:C.【点评】本题考查了学生的观察能力,考查了学生灵活解决问题的能力.2.【分析】空白三角形、阴影三角形,以及梯形的高相等,根据三角形的面积=底×高÷2可知,先用阴影三角形的面积乘上2,再除以它的底20厘米,即可求出它的高,再用空白三角形的底乘上高,再除以2,即可求出空白部分的面积.解:100÷20×2=5×2=10(厘米)14×10÷2=140÷2=70(平方厘米)答:空白部分的面积是70平方厘米.故选:D.【点评】本题考查了三角形的面积公式,三角形的面积=底×高÷2,关键是得出两个三角形的高相等.3.【分析】先利用三角形的面积公式S=ah÷2计算出三角形的高,也就等于知道了空白部分的高,从而利用三角形的面积公式进行解答即可.解:60×2÷20=120÷20=6(厘米)10×6÷2=30(平方厘米)答:空白部分的面积是30平方厘米.故选:B.【点评】此题主要考查三角形的面积公式的灵活应用.4.【分析】这几个直角梯形中,阴影部分总面积都是以梯形的下底为底,以梯形的高为高的三角形的面积,由此即可判断它们面积的大小.解:三图中,阴影部分总面积都是以梯形的下底为底,以梯形的高为高的三角形的面积,因为三个梯形完全相同,由此可得:阴影部分的面积都相等.故选:D.【点评】此题主要考查等底等高的三角形面积都相等,据图即可以作出判断.5.【分析】根据图得出阴影部分的三角形,与平行四边形的等高,底是平行四边形底的,又三角形的面积是与它底等高平行四边形面积的一半,所以三角形的面积是平行四边形面积的×=,然后解答即可.解:因为E、F把AB边分成了相等的三段,所以阴影部分三角形的底是平行四边形底的,所以三角形的面积是平行四边形面积的×=,阴影三角形的面积是48×=8(平方厘米).答:阴影三角形的面积是8平方厘米.故选:A.【点评】本题关键理解以三角形的面积是与它底等高平行四边形面积的一半.6.【分析】首先根据平行四边形的面积公式:s=ah,那么a=s÷h,已知平行四边形的面积和高求出平行四边形的底,然后用平行四边形的底减去5就是阴影部分三角形的底,然后根据三角形的面积公式:s=ah÷2,把数据代入公式解答.解:24÷4=6(厘米),(6﹣5)×4÷2=1×4÷2=2(平方厘米),答:阴影部分的面积是2平方厘米.故选:A.【点评】此题主要考查平行四边形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式.7.【分析】由正方形的特征可知,①号图中阴影部分的面积等于正方形面积的,因此正方形的面积就等于图①中阴影部分面积的4倍,已知①号图形阴影部分的面积是10平方厘米,用10乘上4即可得到正方形的面积;而②号图中阴影部分的面积是正方形面积的,因此再用正方形的面积乘上即可得到②号图形阴影部分的面积,据此解答.解:由分析知②号图形阴影部分的面积是:10×4×=40×=20(平方厘米);答:②号图形阴影部分的面积是20平方厘米.故选:C.【点评】解决本题的关键是明确各个图中阴影部分的面积和正方形的面积之间的数量关系.8.【分析】甲图中阴影部分的面积可以看作与平行四边形等底等高的三角形,三角形的面积是平行四边形的面积的一半,乙图中的阴影部分面积也可以看作与平行四边形等底等高的三角形,三角形的面积是平行四边形的面积的一半,平行四边形又是完全一样,所以阴影部分的三角形的面积也是一样据此判断.解:甲图中阴影部分的面积和乙图中的阴影部分面积都可以看作与平行四边形等底等高的三角形,平行四边形的面积一样,它们的面积也一样大.故选:C.【点评】此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.9.【分析】三角形的面积S=ah,只要是三角形的底和高相等,则它们的面积相等,据此即可得解.解:由图意可知:图中3个三角形的底是相等的,要想面积与阴影部分的三角形面积相等,那么如果高与阴影部分的三角形的高相等即可;再根据平行线间的距离相等,所以△BCE的面积与阴影部分的面积相等.故选:C.【点评】解答此题的主要依据是:等底等高的三角形的面积相等.10.【分析】由图形可知,甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以乙的面积大于甲的面积;因为甲的周长=长方形的两条邻边的和+中间的曲线的长,乙的周长=长方形的两条邻边和+中间的曲线的长,进行解答继而得出结论.解:因为甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以甲的面积小于乙的面积;甲的周长=长方形的两条邻边的和+中间的曲线的长,乙的周长=长方形的两条邻边的和+中间的曲线的长,所以甲的周长等于乙的周长;故选:C.【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.二.填空题(共8小题)11.【分析】观察图形可知,长方形的长等于圆的直径是8分米,宽是半圆的半径是8÷2=4分米,据此利用长方形的面积=长×宽计算即可解答问题.解:8÷2=4(分米)8×4=32(平方分米)答:这个长方形的面积是32平方分米.故答案为:32.【点评】掌握长方形内的半圆的特征得出长方形的长与宽的值,是解决本题的关键.12.【分析】根据图示,这个组合图形可以看作由一个梯形和一个长方形拼成的图形,利用长方形和梯形面积公式求解即可.解:如图:该图形可看作一个梯形和一个长方形拼成的图形,其面积为:(12+16)×(10﹣5)÷2+16×5=28×5÷2+80=70+80=150(平方厘米)答:这个图形的面积为150平方厘米.故答案为:150平方厘米.【点评】此题主要考查的是梯形的面积公式:(上底+下底)×高÷2、长方形面积公式:长×宽的应用.13.【分析】右边图形中阴影部分的面积=最上面一行中的2个方格的面积+下面图形中的长方形的面积﹣1个方格的面积,据此即可求解.解:2+4×5﹣1=2+20﹣1=21(平方厘米)答:阴影部分的面积是21平方厘米.故答案为:21.【点评】解答此题的关键是:看利用小方格的边长计算简单还是利用小正方形的面积计算简单,要灵活应对.14.【分析】根据平行四边形的面积变形公式h=S÷a,可求平行四边形的高,根据三角形面积公式S=ah可求三角形的面积;依此即可求解.解:高:20÷5=4(厘米)三角形的面积:3×4÷2=12÷2=6(平方厘米)故答案为:4,6.【点评】本题考查了学生求平行四边形、三角形面积的知识,关键是求出平行四边形的高.15.【分析】根据图意可把这个不规则的四边形,看作是2个直角三角形面积的和来进行解答,然后再根据三角形的面积公式进行计算.解:11×6÷2=66÷2=33(平方厘米)答:这个四边形的面积是33平方厘米.故答案为:33.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.16.【分析】观察图示可知,阴影部分的面积=梯形面积﹣圆面积的,代入数据,解答即可.解:(4+10)×4÷2﹣3.14×42×=28﹣12.56=15.44(平方厘米)答:阴影部分是面积是15.44平方厘米.故答案为:15.44.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.17.【分析】运用面积公式、割补法求阴影部分面积,再与题目的要求比较.解:花坛面积为4m2,一半为2m2,A、阴影部分面积为2×2÷2=2(m2)B、阴影部分面积为1×1+1×1÷2+1×2÷2=2.5(m2)不符合要求;C、阴影部分面积为1×1÷2×4=2(m2)D、把图中上面两个扇形移下来,刚回拼成两个小正方形,面积为2m2;故答案为:B.【点评】本题考查了阴影部分图形面积的计算方法,即规则图形用面积公式求,不规则图形用割补法求解.18.【分析】本题要看图解答.从图中可以看出剩余部分的草坪正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.所以草坪的面积=长×宽=(102﹣2)×(51﹣1)=100×50=5000(米2).故答案为:C.【点评】此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.三.判断题(共5小题)19.【分析】分别计算出阴影部分和半圆的面积,再判断.解:设正方形的边长为a,则:阴影部分面积=πa2﹣=a2;半圆的面积为:π×═a2;所以阴影部分面积等于半圆的面积,原说法错误.故答案为:错误.【点评】解决本题的关键是计算出组合图形中相关部分的面积,再比较.20.【分析】分别运用梯形的面积公式和三角形的面积公式进行列式比较就可做出判断.解:设梯形的上底为a,高为h,则下底为2a;梯形的面积=(a+2a)×h÷2=3ah÷2=ah;空白三角形的面积=a×h÷2=ah;则阴影部分的面积=梯形的面积﹣空白三角形的面积=ah﹣ah=ah;由此可以看出:空白面积等于阴影部分面积的一半.故此题是正确的.故答案为:√.【点评】此题主要考查三角形和梯形的面积公式.21.【分析】观察图形可知,可把右侧阴影部分割补到左侧对称的位置,如下图所示:会发现阴影部分是一个上底为4cm、下底为8cm,高为4cm的梯形,利用梯形的面积公式代入数据计算即可.解:由分析知,阴影部分的面积等于上图所示梯形的面积,梯形的上底为:8﹣8÷2=8﹣4=4(cm),高为:8÷2=4(cm),所以面积为:(4+8)×4÷2=12×4÷2=48÷2=24(cm2);答:图中阴影部分的面积为24cm2.所以题干说法正确.故答案为:√.【点评】本题考查了求组合图形的面积,组合图形的面积一般都是转化为规则图形的面积的和或差,再利用规则图形的面积公式进行计算.22.【分析】把这个图形分成三部分计算,上面是底4厘米、高2厘米的三角形,中间是上底2厘米、下底4厘米、高1厘米的梯形,下面是长与宽分别是3厘米、2厘米的长方形,据此计算出它们的面积,再加起来即可判断.解:4×2÷2+(2+4)×1÷2+2×3=4+3+6=13(平方厘米)答:阴影部分的面积是13平方厘米.故答案为:×.【点评】此题考查了不规则图形的周长与面积的计算方法,一般都是转化到规则图形中利用面积公式计算解答.23.【分析】根据组合图形的面积的计算方法可知:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再利用规则图形的面积公式进行计算,据此即可判断.解:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再根据简单图形的计算公式进行计算.故答案为:√.【点评】此题考查组合图形的面积的计算方法:关键是把组合图形的面积转化为我们学过的图形的面积,再利用相应的面积公式与基本的数量关系解决问题.四.计算题(共2小题)24.【分析】(1)通过旋转平移把阴影部分转化为一个半圆,根据圆的面积公式:S=πr2,把数据代入公式解答.(2)阴影部分的面积等于圆的面积减去正方形的面积,根据圆的面积公式:S=πr2,三角形的面积公式:S=ah÷2,把数据代入公式解答.解:(1)3.14×42÷2=3.14×16÷2=50.24÷2=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.(2)3.14×(10÷2)2﹣10×(10÷2)÷2×2=3.14×25﹣10×5÷2×2=78.5﹣50=28.5(平方厘米);答:阴影部分的面积是28.5平方厘米.【点评】解答求阴影部分的面积关键是观察分析图形是由哪几部分组成的,是各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答.25.【分析】组合图形的面积等于底为35米,高为12米的三角形面积加上底为50米,高为33米的平行四边形的面积;根据三角形和梯形面积公式解答即可.解:33×50+35×12÷2=1650+210=1860(平方米)答:图形的面积是1860平方米.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.五.解答题(共3小题)26.【分析】本题可用长80米、宽40米的长方形面积减去边长10米的正方形面积求出菜园的面积,长方形面积=长×宽,正方形面积=边长×边长.解:80×40﹣10×10=3200﹣100=3100(平方米)答:这个菜园的面积是3100平方米.【点评】本题主要考查了学生利用长方形的面积公式解题的能力,找出正确的计算组合图形的面积的方法是解题关键.27.【分析】根据题意:如图,已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米,则三角形EFG的面积+10平方厘米+梯形BCFG的面积=平行四边形ABCD的面积,又因为三角形EFG的面积+梯形BCFG的面积=三角形BCF的面积,所以三角形BCF的面积+10平方厘米=平行四边形ABCD的面积;CF是平行四边形的高,根据平行四边形的面积=底×高,则高CF=平行四边形的面积÷底即可.解:(10×8÷2+10)÷10=(40+10)÷10=50÷10=5(厘米)答:CF长5厘米.【点评】解决此题的关键用直角三角形的面积+10平方厘米代替平行四边形的面积,根据面积公式求出CF.28.【分析】(1)先利用长方形的面积公式S=ab计算出圆白菜地的面积,再用它的面积除以每棵圆白菜的占地面积,即可得解;(2)依据梯形的面积公式S=(a+b)×h÷2,代入数据即可求解.解:(1)8×4.5÷0.15=36÷0.15=240(棵)答:一共可以种240棵.(2)(4.8+10.5﹣4.5)×(8﹣2)÷2=10.8×6÷2=32.4(平方米)答:茄子地一共有32.4平方米.【点评】此题主要考查长方形和梯形的面积公式的灵活应用.。
面积问题-奥数精讲与测试7年级
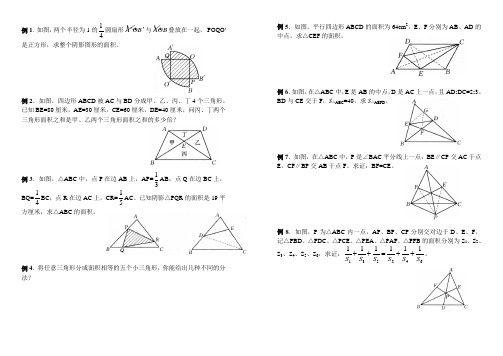
例1.如图,两个半径为1的14圆扇形¼''A OB 与¼AOB叠放在一起,POQO'是正方形,求整个阴影图形的面积。
例2.如图,四边形ABCD被AC与BD分成甲、乙、丙、丁4个三角形。
已知BE=80厘米,AE=30厘米,CE=60厘米,DE=40厘米,问丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?例3.如图,△ABC中,点P在边AB上,AP=13AB;点Q在边BC上,BQ=14BC;点R在边AC上,CR=15AC。
已知阴影△PQR的面积是19平方厘米,求△ABC的面积。
例4.将任意三角形分成面积相等的五个小三角形,你能给出几种不同的分法?例5.如图,平行四边形ABCD的面积为64cm2,E、F分别为AB、AD的中点,求△CEF的面积。
例6.如图,在△ABC中,E是AB的中点,D是AC上一点,且AD:DC=2:3。
BD与CE交于F,S△ABC=40,求S△AEFD。
例7.如图,在△ABC中,P是∠BAC平分线上一点,BE∥CP交AC于点E,CF∥BP交AB于点F。
求证:BF=CE。
例8.如图,P为△ABC内一点,AP、BP、CP分别交对边于D、E、F。
记△PBD、△PDC、△PCE、△PEA、△PAF、△PFB的面积分别为S1、S2、S3、S4、S5、S6,求证:135246111111S S S S S S++=++。
A卷一、填空题01.若长方形的长增加了a%以后,为了使长方形的面积保持不变,则这个长方形的宽应该减少________。
02.已知凸四边形ABC D的面积是a,E、F、G、H分别是AB、BC、CD、DA的中点,且EG,HF交于点O,四边形AEOH与OFCG面积和是________。
03.如图1,一个矩形被分成A、B、C、D四个矩形。
已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,原来矩形的面积是________平方厘米。
小学数学奥数测试题复杂直线型面积8_人教版

⑴ 求三角形ABC的面积是三角形ABD面积的多少倍?
⑵ 求三角形ABD的面积是三角形ADC面积的多少倍?
9.如右图, 和 都是矩形, 的长是 厘米, 的长是 厘米,那么图中阴影部分的面积是多少平方厘米?
10.如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是多少平方厘米?
(法2)连接 、 .由于 与 的面积之和等于正方形 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形 面积的 ,同理可知左、右两个阴影三角形的面积之和等于正方形 面积的 ,所以阴影部分的面积为 平方厘米.
17.4
【解析】因为AD垂直于BC,所以当BC为三角形ABC和三角形EBC的底时,AD是三角形ABC的高,ED是三角形EBC的高,
连接 ,设 份,则其他部分的面积如图所示,所以 份,所以四部分按从小到大各占 面积的
4.3.5
【解析】∵在 和 中, 与 互补,
又 ,所以 .
同理可得 , .
所以
5.5:2
【解析】
根据燕尾定理有 , ,所以
6.
【解析】
连接BG,设 1份,根据燕尾定理 , ,得 (份), (份),则 (份),因此 ,同理连接AI、CH得 , ,
于是:三角形ABC的面积
三角形EBC的面积
所以三角形ABC的面积是三角形EBC的面积的4倍.
18.4
【解析】
连接 ,∵ ,∴ ,
又∵ ,∴ .
19.30平方厘米
【解析】
连接 .根据题意可知, 的面积为 面积的 , 的面积为 面积的 ,所以 的面积为 面积的 .而 的面积为5平方厘米,所以 的面积为 (平方厘米).
小学数学冀教版第十一册圆的周长和面积圆环的面积-章节测试习题(1)

章节测试题1.【题文】求阴影部分的面积.【答案】14.13平方厘米【分析】阴影部分的面积=(大圆的面积﹣小圆的面积)÷2,小圆的半径为:8÷2=4(厘米),大圆的半径为:10÷2=5(厘米),根据公式计算即可.【解答】小圆的半径为:8÷2=4(厘米),大圆的半径为:10÷2=5(厘米),(3.14×52-3.14×42)÷2=14.13(平方厘米).答:阴影部分的面积为14.13平方厘米.2.【答题】如图所示,圆环的面积是()平方分米.(单位:分米)A.3.14B.6.28C.9.42【答案】C【分析】此题考查的是圆环的面积.【解答】圆环的面积=外圆的面积-内圆的面积.由图可知,内圆的半径为:(4-1-1)÷2=(3-1)÷2=2÷2=1(分米);外圆的半径为:4÷2=2(分米).所以圆环的面积为:故此题选C.3.【答题】如图,阴影部分的面积是50平方米,那么图中圆环的面积是()平方米.(π取3.14)A. 50B. 78.5C. 157D. 314【答案】C【分析】此题考查的是圆环的面积.【解答】图中大圆的半径与大正方形的边长相等,设为米;小圆的半径与小正方形的边长相等,设为米.阴影部分的面积是大正方形面积减去小正方形的面积,列式计算为:.圆环的面积是大圆面积减去小圆的面积,列式计算为:选C.4.【答题】一个圆环,内圆半径是5dm,外圆半径是8dm,计算这个圆环面积的算式是()A. 3.14×(8²-5²)B. 3.14×(8-5)²C. 3.14×(8²+5²)【答案】A【分析】此题考查的是圆环的面积.圆环的面积=π×(外圆半径²-内圆半径²).【解答】一个圆环,内圆半径是5dm,外圆半径是8dm,计算这个圆环面积的算式是3.14×(8²-5²).选A.5.【答题】公园里有一个直径是8米的圆形花坛,沿花坛周围修一条2米宽的小路,这条小路的面积是()平方米.A. 10πB. 20πC. 40π【答案】B【分析】此题考查的是圆环的面积.【解答】由题意知,圆形花坛为內圆,它的直径是8米,求它的半径,列式计算为:8÷2=4(米),沿花坛周围修一条2米宽的小路,即小路的形状为一个圆环,则外圆半径为花坛半径与环形小路的宽度之和,求外圆半径,列式计算为4+2=6(米),求圆环的面积,列式计算为:π(62-42)=20π(平方米),即小路的面积为20π平方米.选B.6.【答题】一座圆环形土楼,外圆半径是17米,内圆半径是7米,求这座土楼的占地面积,下面列式错误的是().(π取3.14)A. 3.14×(17²-7²)B. 3.14×(17-7)²C. 3.14×17²-3.14×7²【答案】B【分析】此题考查的是圆环的面积.圆环的面积=外圆面积-内圆面积=π×(外圆半径的平方-内圆半径的平方).【解答】外圆半径是17米,外圆的面积是(3.14×17²)平方米,内圆半径是7米,则内圆的面积是(3.14×7²)平方米,则这座土楼的占地面积为3.14×17²-3.14×7²=3.14×(17²-7²)(平方米).选B.7.【答题】一个圆环,内圆直径是18cm,环宽2cm,它的面积是().(π取3.14)A. 53.38cm²B. 59.66cm²C. 125.6cm²【答案】C【分析】此题考查的是圆环的面积.圆环的面积=外圆的面积-内圆的面积.【解答】一个圆环,内圆直径是18cm,则内圆半径是9cm,所以内圆的面积是3.14×9²=254.34(cm²);环宽2cm,则外圆的半径是9+2=11(cm),所以外圆的面积是3.14×11²=379.94(cm²),则它的面积是379.94-254.34=125.6(cm²).选C.8.【答题】一个圆环,内圆半径为5cm,外圆直径为18cm,计算这个圆环面积的正确算式是()A. 3.14×(18²-5²)B. 3.14×[(18÷2)²-5²]C. 3.14×(18÷2-5²)【答案】B【分析】此题考查的是圆环的面积.圆环的面积=外圆的面积-内圆的面积.【解答】已知一个圆环,内圆半径为5cm,外圆直径为18cm,这个圆环面积为3.14×[(18÷2)²-5²].选B.9.【答题】图中涂色部分的面积是______cm².(π取3.14)【答案】14.13【分析】此题考查的是圆环的面积.由图可知,涂色部分的面积=×(直径是10cm 的大圆的面积-直径是8cm的小圆的面积)【解答】大圆的面积:3.14×(10÷2)2=78.5(cm²);小圆的面积:3.14×(8÷2)2=50.24(cm²);所以涂色部分的面积为×(78.5-50.24)=14.13(cm²).故此题的答案是14.13.10.【答题】图中阴影部分的面积是______cm².(π取3.14)【答案】50.24【分析】此题考查的是圆环的面积.【解答】由图可知,大圆的半径是5cm,它的面积是:S=πr²=3.14×5²=3.14×25=78.5(cm²),小圆的半径是3cm,它的面积是:S=πr²=3.14×3²=3.14×9=28.26(cm²),所以阴影部分的面积是:78.5-28.26=50.24(cm²).故此题答案为50.24.11.【答题】下图中阴影部分的面积是______cm².(π取3.14)【答案】42.39【分析】此题考查的是圆环的面积.阴影部分的面积=×(外面的面积-内圆的面积).【解答】由图可知,外圆的直径是12cm,则外圆的半径是12÷2=6(cm),外圆的面积是:3.14×6²=113.04(cm²);内圆的半径是3cm,则内圆的面积是3.14×3²=28.26(cm²);阴影部分面积是×(113.04-28.26)=42.39(cm²).故此题的答案是42.39.12.【答题】下图中的圆环的面积是______cm².(π取3.14)【答案】37.68【分析】此题考查的是圆环的面积计算公式.【解答】用R表示外圆半径,用r表示内圆半径,圆环的面积=π(R²-r²).由图可知,大圆半径是4cm,小圆半径是2cm,则圆环的面积是:故此题答案为37.68.13.【答题】下图中阴影部分的面积是______dm².(π取3.14)【答案】31.4【分析】此题考查的是圆环的面积.观察图形,阴影部分的面积=×(半径是6dm 的大圆的面积-半径是4dm的小圆的面积).【解答】由图可知,小圆的半径是6-2=4(dm),半径是6dm的大圆的面积为3.14×6²=113.04(dm²);半径是4dm的小圆的面积为3.14×4²=50.24(dm²);阴影部分的面积为×(113.04-50.24)=31.4(dm²).故此题的答案是31.4.14.【答题】下图中涂色部分的面积是______cm².(π取3.14)【答案】75.36【分析】此题考查的是圆环的面积.由图可知,涂色部分为一个圆环,外圆半径为7cm,内圆半径为5cm,求涂色部分的面积是多少,根据圆环的面积=外圆的面积-内圆的面积即可解答.【解答】故此题的答案是75.36.15.【答题】下图中涂色部分的面积是______cm².(π取3.14)【答案】40.82【分析】此题考查的是圆环的面积.涂色部分的面积=×圆环的面积.【解答】大圆的半径是:12+2=14(cm),小圆的半径是12cm,则涂色部分的面积为:故此题的答案是40.82cm².16.【答题】下图中阴影部分的面积是______cm².(π取3.14)【答案】31.4【分析】阴影部分的面积=×圆环的面积+×小圆的面积.【解答】由图可知,大圆的直径为8cm,所以半径为8÷2=4(cm),大圆的面积:3.14×42=50.24(cm2);小圆的直径为4cm,所以半径为4÷2=2(cm),小圆的面积:3.14×22=12.56(cm2).圆环面积为50.24-12.56=37.68(cm2);因为阴影部分的面积=×圆环的面积+×小圆的面积,所以阴影部分的面积为:17.【答题】学校修建一个圆形喷水池,周长是12.56米,在水池周围要修一条1米宽的环形小路,这条小路的面积是______平方米.(π的取值为3.14)【答案】15.7【分析】此题考查的是圆环的面积.【解答】学校修建一个圆形喷水池,周长是12.56米,半径为:12.56÷3.14÷2=4÷2=2(米);在水池周围要修一条1米宽的环形小路,大圆的半径为:2+1=3(米);这条小路的面积是:3×3×3.14-2×2×3.14=9×3.14-4×3.14=28.26-12.56=15.7(平方米).答:这条小路的面积是15.7平方米.18.【答题】一个圆形的喷水池,周长为62.8米,绕着它的周围在外沿修一条宽为1米的小路,则这条小路的面积是______平方米.【答案】65.94【分析】此题考查的是圆的周长和面积.【解答】圆的周长=πd.已知一个圆形的喷水池,周长为62.8米,求这个圆形喷水池的直径是多少,用除法,列式计算为:62.8÷3.14=20(米);圆的面积=πr².求这个圆形喷水池的面积是多少,列式计算为:绕着它的周围在外沿修一条宽为1米的小路,求小路和喷水池的总面积是多少平方米,列式计算为:小路的面积=小路和喷水池的总面积-圆形喷水池的面积,求这条小路的面积是多少平方米,用减法,列式计算为:379.94-314=65.94(平方米).答:这条小路的面积是65.94平方米.19.【答题】一个圆形花坛的周长是12.56m,在它的周围铺上1m宽的甬路(如下图),甬路的面积是______m².(π的取值为3.14)【答案】15.7【分析】此题考查的是求环形的面积.【解答】一个圆形花坛的周长是12.56m,根据圆的周长求圆形花坛的半径:12.56÷3.14÷2=2(m);在圆形花坛的周围铺上1m宽的甬路,求甬路外沿的半径,用加法:2+1=3(m);甬路的面积:故此题的答案是15.7m².20.【答题】一个环形的铁片,外圆半径是7厘米,内圆半径是0.5分米.这个环形的面积是______平方分米.(π取3.14)【答案】0.7536【分析】此题考查的是圆环的面积.环形的面积=外圆的面积-内圆的面积,根据求出外圆和内圆的面积,代入数据即可.【解答】7厘米=0.7分米,求外圆的面积是多少平方分米:3.14×0.72=1.5386(平方分米);内圆半径是0.5分米,求内圆的面积是多少平方分米:3.14×0.52=0.785(平方分米);所以这个环形的面积是:1.5386-0.785=0.7536(平方分米).所以这个环形的面积是0.7536平方分米.故此题的答案是0.7536.。
小升初阴影面积测试题及答案

小升初阴影面积测试题及答案一、选择题1. 下列哪个图形的阴影部分面积可以通过计算其总面积减去非阴影部分面积得到?A. 圆形B. 正方形B. 三角形D. 长方形答案:B2. 如果一个正方形的边长为10厘米,那么它的阴影部分面积(边长为5厘米的内接正方形)是多少平方厘米?A. 25B. 50C. 75D. 100答案:A二、填空题3. 一个长方形的长是15厘米,宽是10厘米,如果在内部有一个边长为5厘米的正方形阴影部分,那么阴影部分的面积是_________平方厘米。
答案:254. 一个圆的直径是20厘米,那么半径为10厘米的内圆阴影部分的面积是_________平方厘米(圆周率取3.14)。
答案:314三、计算题5. 如图所示,一个三角形的底边长为12厘米,高为8厘米,其内有一个边长为6厘米的正方形阴影部分。
求三角形阴影部分的面积。
答案:36平方厘米解析:首先计算三角形的总面积,公式为 \( \frac{1}{2} \times 底 \times 高 = \frac{1}{2} \times 12 \times 8 = 48\) 平方厘米。
然后计算正方形的面积,公式为 \( 边长^2 = 6^2 = 36\) 平方厘米。
最后,三角形阴影部分的面积等于三角形总面积减去正方形面积,即\( 48 - 36 = 12\) 平方厘米。
6. 如图所示,一个圆形的半径为15厘米,其内部有一个半径为10厘米的圆形阴影部分。
求圆形阴影部分的面积。
答案:565平方厘米解析:首先计算大圆的面积,公式为 \( 圆周率 \times 半径^2 = 3.14 \times 15^2 = 706.5\) 平方厘米。
然后计算小圆的面积,公式为 \( 3.14 \times 10^2 = 314\) 平方厘米。
最后,圆形阴影部分的面积等于大圆面积减去小圆面积,即 \( 706.5 - 314 = 392.5\) 平方厘米。
四、解答题7. 如图所示,一个长方形的长为20厘米,宽为8厘米,其内部有一个边长为6厘米的正方形阴影部分。
小学奥数几何专题--复杂直线型面积-3(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-3(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.【答案】8【解析】.【题文】如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】评卷人得分对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.【题文】图是由大、小两个正方形组成的,小正方形的边长是厘米,求三角形的面积.【答案】8【解析】这道题似乎缺少大正方形的边长这个条件,实际上本题的结果与大正方形的边长没关系.连接(见右上图),可以看出,三角形与三角形的底都等于小正方形的边长,高都等于大正方形的边长,所以面积相等.因为三角形是三角形与三角形的公共部分,所以去掉这个公共部分,根据差不变性质,剩下的两个部分,即三角形与三角形面积仍然相等.根据等量代换,求三角形的面积等于求三角形的面积,等于.【题文】如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.【题文】正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?【答案】50【解析】方法一:三角形BEF的面积,梯形EFDC的面积三角形BEF的面积,而四边形CEFH是它们的公共部分,所以,三角形DHF的面积三角形BCH的面积,进而可得,阴影面积三角形BDF的面积三角形BCD的面积(平方厘米).方法二:连接CF,那么CF平行BD ,所以,阴影面积三角形BDF的面积三角形BCD的面积(平方厘米).【题文】已知正方形边长为10,正方形边长为6,求阴影部分的面积.【答案】20【解析】如果注意到为一个正方形的对角线(或者说一个等腰直角三角形的斜边),那么容易想到与是平行的.所以可以连接、,如上图.由于与平行,所以的面积与的面积相等.而的面积为,所以的面积也为20.【题文】图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).【题文】如下图,、分别是梯形的下底和腰上的点,,并且甲、乙、丙个三角形面积相等.已知梯形的面积是平方厘米.求图中阴影部分的面积.【答案】12.8【解析】因为乙、丙两个三角形面积相等,底.所以到的距离与到的距离相等,即与平行,四边形是平行四边形,阴影部分的面积平行四边形的面积的,所以阴影部分的面积乙的面积.设甲、乙、丙的面积分别为份,则阴影面积为份,梯形的面积为份,从而阴影部分的面积(平方厘米).【题文】如图,已知长方形的面积,三角形的面积是,三角形的面积是,那么三角形的面积是多少?【答案】6.5【解析】方法一:连接对角线.∵是长方形∴∴,∴,∴∴.方法二:连接,由图知,所以,又由,恰好是面积的一半,所以是的中点,因此,所以【题文】如图,在平行四边形中,,.求阴影面积与空白面积的比.【答案】1:2【解析】方法一:因为,,所以,.因为,所以,所以,.同理可得,,.因为,所以空白部分的面积,所以阴影部分的面积是.,所以阴影面积与空白面积的比是.【题文】如图所示,三角形中,是边的中点,是边上的一点,且,为与的交点.若的面积为平方厘米,的面积为平方厘米.且是平方厘米,那么三角形的面积是多少平方厘米.【答案】10【解析】,,所以(平方厘米).所以(平方厘米).【题文】如图,在梯形中,,,且的面积比的面积小10平方厘米.梯形的面积是多少平方厘米?【答案】115【解析】根据题意可知,则,,而平方厘米,所以,则平方厘米.又,所以平方厘米.所以(平方厘米).【题文】如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).【题文】如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是,,.那么图中阴影部分的面积是多少?【答案】97【解析】三角形的面积三角形的面积长方形面积阴影部分面积;又因为三角形的面积三角形的面积长方形面积,所以可得:阴影部分面积.【题文】图中是一个各条边分别为5厘米、12厘米、13厘米的直角三角形.将它的短直角边对折到斜边上去与斜边相重合,那么图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米?【答案】【解析】如下图,为了方便说明,将某些点标上字母.有为直角,而,所以也为直角.而.与同高,所以面积比为底的比,及===,设的面积为“8”,则的面积为“5”.是由折叠而成,所以有、面积相等,是由、、组成,所以=“8”+“5”+“5”=“18”对应为,所以“1”份对应为,那么△ADE的面积为=平方厘米.即阴影部分的面积为平方厘米.【题文】如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】平方厘米【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.【题文】如图,三角形田地中有两条小路和,交叉处为,张大伯常走这两条小路,他知道,且.则两块地和的面积比是多少【答案】1:2【解析】方法一:连接.设的面积为1,的面积,则根据题上说给出的条件,由得,即的面积为、;又有,、,而;得,所以.方法二:连接,设(份),则,设则有,解得,所以方法三:过点作∥交于点,由相似得,又因为,所以,所以两块田地ACF和CFB的面积比【题文】如图,,,被分成个面积相等的小三角形,那么|【答案】24【解析】由题意可知,,所以,;又,所以,同样分析可得,所以.【题文】如图,在角的两边上分别有、、及、、六个点,并且、、、、的面积都等于1,则的面积等于.【答案】【解析】根据题意可知,,所以,.【题文】、分别为直角梯形两边上的点,且、、彼此平行,若,,,.求阴影部分的面积.【答案】25【解析】连接、.由于、、彼此平行,所以四边形是梯形,且与该梯形的两个底平行,那么三角形与、三角形与的面积分别相等,所以三角形的面积与三角形的面积相等.而三角形的面积根据已知条件很容易求出来.由于为直角梯形,且,,,,所以三角形的面积的面积为:.所以三角形的面积为25.【题文】已知为等边三角形,面积为400,、、分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形)【答案】43【解析】因为、、分别为三边的中点,所以、、是三角形的中位线,也就与对应的边平行,根据面积比例模型,三角形和三角形的面积都等于三角形的一半,即为200.根据图形的容斥关系,有,即,所以.又,所以.【题文】如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.【题文】如图,点、、在线段上,已知厘米,厘米,厘米,厘米,将整个图形分成上下两部分,下边部分面积是平方厘米,上边部分面积是平方厘米,则三角形的面积是多少平方厘米?【答案】128【解析】连接设的面积是,由于所以的面积是、的面积是由于上半部分的面积是平方厘米所以的面积是()平方厘米,因为下半部分的面积是平方厘米所以的面积是()平方厘米,因为是的2倍所以可以列方程为:()解得,的面积为平方厘米.【题文】如图,正方形的边长为10,四边形的面积为5,那么阴影部分的面积是多少【答案】40【解析】如图所示,设上的两个点分别为、.连接.根据面积比例模型,与的面积是相等的,那么与的面积之和,等于与的面积之和,即等于的面积.而的面积为正方形面积的一半,为.又与的面积之和与阴影部分的面积相比较,多了2个四边形的面积,所以阴影部分的面积为:.【题文】如图,正方形的边长为12,阴影部分的面积为60,那么四边形的面积是多少【答案】6【解析】如图所示,设上的两个点分别为、.连接.根据面积比例模型,与的面积是相等的,那么与的面积之和,等于与的面积之和,即等于的面积.而的面积为正方形面积的一半,为.又与的面积之和与阴影部分的面积相比较,多了2个四边形的面积,所以四边形的面积为:.【题文】如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.【题文】如图所示,矩形的面积为24平方厘米.三角形与三角形的面积之和为平方厘米,则四边形的面积是多少平方厘米?【答案】1.8【解析】因为三角形与三角形的面积之和是矩形的面积的一半,即12平方厘米,又三角形与三角形的面积之和为平方厘米,则三角形与三角形的面积之和是平方厘米,则四边形的面积三角形面积三角形与三角形的面积之和三角形面积(平方厘米).【题文】如图所示,矩形的面积为36平方厘米,四边形的面积是3平方厘米,则阴影部分的面积是多少平方厘米?【答案】12【解析】因为三角形面积为矩形的面积的一半,即18平方厘米,三角形面积为矩形的面积的,即9平方厘米,又四边形的面积为3平方厘米,所以三角形与三角形的面积之和是平方厘米.又三角形与三角形的面积之和是矩形的面积的一半,即18平方厘米,所以阴影部分面积为(平方厘米).【题文】如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.【题文】如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).【题文】如图,阴影部分四边形的外接图形是边长为的正方形,则阴影部分四边形的面积是().【答案】48【解析】如图所示,分别过阴影四边形的四个顶点作正方形各边的平行线,相交得长方形,易知长方形的面积为平方厘米.从图中可以看出,原图中四个空白三角形的面积之和的2倍,等于、、、四个长方形的面积之和,等于正方形的面积加上长方形的面积,为平方厘米,所以四个空白三角形的面积之和为平方厘米,那么阴影四边形的面积为平方厘米.【题文】如图,阴影部分四边形的外接图形是边长为厘米的正方形,则阴影部分四边形的面积是多少平方厘米?【答案】68【解析】如图所示,分别过阴影四边形的四个顶点作正方形各边的平行线,相交得长方形,易知长方形的面积为平方厘米.从图中可以看出,原图中四个空白三角形的面积之和的2倍,等于、、、四个长方形的面积之和,等于正方形的面积加上长方形的面积,为平方厘米,所以四个空白三角形的面积之和为平方厘米,那么阴影四边形的面积为平方厘米.【题文】已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.【题文】如图,三角形的面积是,、的长度分别为11、3.求长方形的面积.【答案】67【解析】如图,过作∥,过作∥,、交于,连接.则另解:设三角形、、的面积之和为,则正方形的面积为.从图中可以看出,三角形、、的面积之和的2倍,等于正方形的面积与长方形的面积之和,即,得,所以正方形的面积为.【题文】如图,长方形中,,.、分别是边上的两点,.那么,三角形面积的最小值是多少?【答案】717【解析】由于长方形的面积是一定的,要使三角形面积最小,就必须使、、的面积之和最大.由于、、都是直角三角形,可以分别过、作、的平行线,可构成三个矩形、和,如图所示.容易知道这三个矩形的面积之和等于、、的面积之和的2倍,而这三个矩形的面积之和又等于长方形的面积加上长方形的面积.所以为使、、的面积之和最大,只需使长方形的面积最大.长方形的面积等于其长与宽的积,而其长,宽,由题知,根据”两个数的和一定,差越小,积越大”,所以当与的差为0,即与相等时它们的积最大,此时长方形的面积也最大,所以此时三角形面积最小.当与相等时,,此时三角形的面积为:.(也可根据得到三角形的面积)【题文】是边长为12的正方形,如图所示,是内部任意一点,、,那么阴影部分的面积是().【答案】34【解析】(法1)特殊点法.由于是内部任意一点,不妨设点与点重合(如上中图),那么阴影部分就是和.而的面积为,的面积为,所以阴影部分的面积为.(法2)寻找可以利用的条件,连接、、、可得右图所示:则有:同理可得:;而,即;同理:,,;所以:而;;所以阴影部分的面积是:即为:.【题文】如图所示,在四边形中,,,,分别是各边的中点,求阴影部分与四边形的面积之比.【答案】1【解析】(法1)设,,,.连接知,,,;所以;同理.于是;注意到这四个三角形重合的部分是四块阴影小三角形,没算的部分是四边形;因此四块阴影的面积和就等于四边形的面积.(法2)特殊值法(只用于填空题、选择题),将四边形画成正方形,很容易得到结果.【题文】如图,、、、分别是四边形各边的中点,与交于点,、、及分别表示四个小四边形的面积.试比较与的大小.【答案】【解析】如图,连接、、、,则可判断出,每条边与点所构成的三角形都被分为面积相等的两部分,且每个三角形中的两部分都分属于、这两个不同的组合,所以可知.【题文】如图,四边形中,,,,已知四边形的面积等于4,则四边形的面积是多少?【答案】【解析】运用三角形面积与底和高的关系解题.连接、、、,因为,,所以,在中,,在中,,在中,,在中,.因为,所以.又因为,所以.【题文】如图,对于任意四边形,通过各边三等分点的相应连线,得到中间四边形,求四边形的面积是四边形的几分之几?【答案】【解析】分层次来考虑:⑴如下左图,,,所以.又因为,,所以;.⑵如右上图,已知,;所以;所以,即是三等分点;同理,可知、、都是三等分点;所以再次应用⑴的结论,可知,.【题文】有正三角形,在边、、的正中间分别取点、、,在边、、上分别取点、、,使,当和、和、和的相交点分别是、、时,使.这时,三角形的面积是三角形的面积的几分之几?请写出思考过程.【答案】【解析】连接、、,显然,是正三角形将放大至如图⑵.连,由对称性知,.因此,.同理,.所以,.【题文】如图:已知在梯形中,上底是下底的,其中是边上任意一点,三角形、三角形、三角形的面积分别为、、.求三角形的面积.【答案】21【解析】如图,设上底为,下底为,三角形与三角形的高相差为.由于,所以.即.又,所以.【题文】如图,已知是梯形,∥,,,,求的面积.【答案】6【解析】本题是09年六年级试题,初看之下,是梯形这个条件似乎可以用到梯形蝴蝶定理,四边形内似乎也可以用到蝴蝶定理,然而经过试验可以发现这几个模型在这里都用不上,因为、这两个点的位置不明确.再看题目中的条件,,,这两个条件中的前一个可以根据差不变原理转化成与的面积差,则是与的面积差,两者都涉及到、以及有同一条底边的两个三角形,于是想到过、分别作梯形底边的平行线.如右图,分别过、作梯形底边的平行线,假设这两条直线之间的距离为.再过作的垂线.由于,所以,故.根据差不变原理,这个差等于与的面积之差.而与有一条公共的底边,两个三角形边上的高相差为,所以它们的面积差为,故.再看,它的面积等于是与的面积之差,这两个三角形也有一条公共的底边,边上的高也相差,所以这两个三角形的面积之差为,故.由于,所以,则,所以.【题文】如图,是一个四边形,、分别是、的中点.如果、与的面积分别是6、7和8,且图中所有三角形的面积均为整数,则四边形的面积为多少.【解析】连接、、.由于是的中点,所以与的面积相等,而比的面积大1,所以比的面积大1;又由于是的中点,所以的面积与的面积相等,那么的面积比的面积大1,所以的面积为9.假设的面积为,则的面积为.根据几何五大模型中的蝴蝶定理,可知的面积为,的面积为.要使这两个三角形的面积为整数,可以为1,3或7.由于的面积为面积的一半,的面积为面积的一半,所以与的面积之和为四边形面积的一半,所以与的面积之和等于四边形的面积,即:,得.将、3、7分别代入检验,只有时等式成立,所以{{10l连接,,,所以,设份,则份,平方厘米,所以份是平方厘米,份就是平方厘米,的面积是平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.【题文】如图,三角形中,是的5倍,是的3倍,如果三角形的面积等于1,那么三角形的面积是多少?【答案】15连接.∵∴又∵∴,∴.。
【多套试卷】人教版小学数学五年级第一学期第二单元 多边形的面积测试试卷1

人教版小学数学五年级第一学期第二单元多边形的面积测试试卷1、计算下面图形面积..(1) (2) (3)2、星光小学建造一个花坛(见下图),这个花坛的面积有多少平方米?3、计算下列阴影部分的面积(单位:米)4、求下面各图形的面积。
(单位:厘米)5、求下列阴影部分的面积。
②已知S平=48dm2,求S阴。
6、已知:阴影部分的面积为24 ④求S阴。
平方厘米,求梯形的面积。
16cm8dm12cm8dm8、如图,ABCD 是一个长12厘米,宽5厘米的长方形,求阴影部分三角形ACE 的面积。
9、已知一个平行四边形的底1是20厘米,底2是12厘米,高2是10厘米,求这个平行四边形的面积?16cm7、.求下面图形中阴影部分的面积。
10已知三角形的底是10厘米,高是5厘米,求三角形的面积?11、平行四边形底是9厘米,高是6厘米,求这个平行四边形的面积?12、若一个平行四边形的底增加8米,面积则增加24平方米;若高增加3米,面积则增加36平方米。
求原来这个平行四边形的面积是多少平方米?13、市政府开展“开荒造林”活动,打算在一块长18千米,宽6千米的长方形荒地上种树,按平均每公顷种树3500棵计算,能种多少棵树?14、一个三角形的底是9厘米,如果底增加3厘米,面积则增加12平方厘米。
求原来这个三角形的面积是多少平方厘米?15、已知梯形面积是60平方厘米,上底是10厘米,下底是20厘米,求梯形的高?16、已知梯形面积是40平方厘米,高是10厘米,上底是2厘米,求梯形的下底?17、已知梯形面积是35平方厘米,高是7厘米,下底是6厘米,求梯形的上底?18、一个平行四边形的停车场,底是90米,高是40米,平均每辆汽车占20平方米,求这个停车场可停车多少辆?19、有一块三角形花坛,底是30米,高是12米,平均每平方米可以栽鲜花50枝,问这块花坛一共可以栽鲜花多少枝?20、一块白菜地的形状是梯形,它的上底是3米,下底是4米,高是9米。
小学数学青岛版(五四)五年级下册第一单元 完美的图形——圆圆的面积-章节测试习题(7)

章节测试题1.【答题】求图中阴影部分的面积.(单位:厘米)【答案】36.48平方厘米【分析】图中阴影部分的面积:用四个半圆即两个圆的面积减去正方形的面积即可.【解答】(平方厘米),答:图中阴影部分的面积是36.48平方厘米.2.【答题】一个圆形游乐场的周长是62.8米,扩建时,半径增加了1米,面积增加了多少平方米?【答案】65.94平方米【分析】根据题意可知,扩建时,半径增加了1米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆周长,首先求出内圆半径,根据环形面积=外圆面积-内圆面积,由此列式解答.【解答】62.8÷3.14÷2=10(米),10+1=11(米),(平方米),答:面积增加了65.94平方米.3.【答题】已知圆的面积为31.4平方厘米,求大小正方形的面积是多少平方厘米?【答案】大正方形的面积是40平方厘米;小正方形的面积是20平方厘米.【分析】由图形可知,圆的面积为31.4平方厘米,则半径的平方为:31.4÷3.14=10,大正方形的边长等于圆的直径,根据正方形的面积公式:,即可求出大正方形的面积,小正方形的对角线的长度等于圆的直径,把小正方形沿对角线分成两个完全相同的三角形,根据三角形的面积公式:,三角形的高等于圆的半径,据此解答.【解答】解:设圆的半径为r厘米,,则(平方厘米);大正方形的面积:(平方厘米);小正方形的面积:(平方厘米);答:大正方形的面积是40平方厘米,小正方形的面积是20平方厘米.4.【答题】一块边长是10米的正方形草地,在相邻的两边的中点各有一棵树,树旁各栓一只羊,羊绳子5米,两只羊都不能吃到的草地面积为多少平方米?【答案】35.75平方米【分析】根据题意,两只羊都不能吃到的草地面积为阴影部分面积,如图所示,图1、2、3的面积相等,先用半圆面积减去三角形OAB的面积即得图1与图2的面积之和,再用两个半圆面积之和(即圆面积)减去图1和2的面积,就是正方形内的空白部分面积,最后用正方形的面积减去空白部分面积,就是阴影部分面积.【解答】解:如图,(平方厘米);(平方厘米);(平方厘米);答:两只羊都不能吃到的草地面积为35.75平方米.5.【答题】图形计算.(单位:厘米)(1)计算图形①中涂色部分的面积.(2)如图②中圆的周长是20厘米,如果圆的面积和长方形的面积相等,计算涂色部分的周长.【答案】(1)面积为6.88平方厘米;(2)周长25厘米【分析】(1)涂色部分的面积=长方形的面积-半圆的面积,根据题意可知:长方形的长=半圆的直径=8,宽=半圆的半径,分别计算出长方形的面积与半圆的面积,即能求出半圆的面积;(2)方法一:先根据圆的周长公式:,计算出圆的半径;再根据圆的面积公式:计算出圆的面积,即长方形的面积;根据长方形的宽=圆的半径,计算出长方形的长;根据圆的周长计算出阴影部分中圆弧的长度;用圆弧的长度+长方形的周长-2个半径的长度=阴影部分的周长.这种做法因为都是四舍五入,与最精确答案有偏差,可以运用方法二比较精确:设圆的半径为r,则分别表示出圆的周长和面积,再根据圆的面积和长方形的面积相等,用r表示出阴影部分的周长,然后根据圆的周长已知,去掉r,得出阴影部分的周长.【解答】(1)8÷2=4(厘米),(平方厘米);(2)设圆的半径为r,则圆的周长:厘米,圆的面积:,长方形的面积:=长×宽;根据題意:,即:=长×宽,因为长方形的宽就是圆的半径,所以可以推出,长等于;所以涂色部分的周长是:答:图形①中涂色部分的面积是6.88平方厘米,涂色部分的周长是25厘米.6.【答题】公园里有一个直径为16米的圆形花圃,在它的周围环绕着一条2米宽的走道.现将走道也改成花圃,现在花圃的面积是多少?【答案】314平方米【分析】由题意可知:现在的花圃也是一个圆形的,其半径为16÷2+2=10米,从而利用圆的面积即可求出现在花圃的面积.【解答】(平方米),答:现在花圃的面积是314平方米.7.【答题】求图中阴影部分的周长和面积.【答案】阴影部分周长为18.84厘米;阴影部分的面积为2.28平方厘米.【分析】(1)阴影部分的周长可看作由下面几部分组成:大圆周长的一半、中间小圆的周长、下面两个小半圆周长的一半,并且小圆直径和两个小半圆直径都相等,根据圆的周长公式解答即可;(2)求阴影部分的面积可作几条辅助线,如图:将阴影1、2、3、4分别移到空白1、2、3、4,处,那么用大半圆的面积减去大三角形的面积即阴影部分的面积,据此解答.【解答】阴影部分周长:3.14×4÷2+3.14×(4÷2)×2=18.84(厘米),阴影部分的面积:3.14×(4÷2)2÷2-4×(4÷2)÷2=2.28(平方厘米),答:阴影部分周长为18.84厘米,面积为2.28平方厘米.8.【答题】求下面阴影部分的面积.【答案】86平方厘米【分析】用正方形的面积减去一个半径是10厘米的圆的面积,就等于阴影部分的面积.【解答】(平方厘米),答:下面阴影部分的面积是86平方厘米.9.【答题】—个花坛(如下图),两端是半径为l0m的半圆,中间是长为30m的长方形.这个花坛的周长是多少米?面积是多少平方米?【答案】这个花坛的周长是122.8米,面积是914平方米.【分析】花坛的周长相当于半径为10m的圆的周长与长为30m的两条线段的长度的和;花坛的面积是一个半径为10m的圆的面积加上一个长是30m,宽是20m的长方形的面积.【解答】30×2+3.14×2×10=122.8(米);30×10×2+3.14×10×10=914(平方米),答:这个花坛的周长是122.8米,面积是914平方米.10.【答题】求阴影部分的面积.(单位:厘米)【答案】75.36平方厘米【分析】根据环形面积公式:,把数据代入公式进行解答.【解答】(平方厘米),答:阴影部分的面积是75.36平方厘米.11.【答题】求下图中阴影部分的面积.【答案】200平方厘米【分析】认真观察图形,阴影部分和空白部分的面积相等,因此只要求出整个图形的面积再除以2就是阴影部分的面积.【解答】解:20×20÷2=200(平方厘米),答:图中阴影部分的面积是200平方厘米.12.【答题】①画一个周长是6.28厘米的圆;②计算这个圆的面积.【答案】①如下图,②3.14平方厘米【分析】根据题意周长为6.28厘米,先计算出圆的半径,然后利用圆规画圆.再计算面积.【解答】6.28÷2÷3.14=1(厘米);3.14×1×1=3.14(平方厘米),答:画图如下,这个圆的面积是3.14平方厘米.13.【答题】求下图中阴影部分的面积.(单位:厘米)【答案】2平方厘米.【分析】仔细观察图,本题不能直接计算阴影部分的面积,因此要采取减法计算.用第一个长方形与和它相邻的圆面积的和减掉空白圆的面积,剩下的就是阴影部分的面积.【解答】解:2×1+3.14×2×2÷4-3.14×2×2÷4=2(平方厘米),图中阴影部分的面积是2平方厘米.14.【答题】求下图阴影部分的面积.(单位:米)【答案】21.5平方米【分析】观察发现四个小扇形的面积能拼成一个圆,所以阴影部分的面积等于正方形的面积减去半径是5厘米的圆的面积.【解答】(平方米),答:图中阴影部分的面积是21.5平方米.15.【答题】计算如图中圆环(阴影部分)的面积.(R=10厘米,r=6厘米)【答案】200.96平方厘米【分析】根据环形面积公式,把数据代入公式进行解答.【解答】(平方厘米),答:圆环的面积是200.96平方厘米.16.【答题】一个钟表的分针长10厘米,它转一圈指针扫过的面积是多大?【答案】314平方厘米【分析】分针要走过1圈,分针走过的路程也就是一个以分针的长度10厘米为半径的圆,求分针针尖所扫过的面积就是求半径是10厘米的圆面积,由此利用圆的面积公式即可解答.【解答】(平方厘米),答:它转一圈指针扫过的积是314平方厘米.17.【答题】计算如图阴影部分的面积,已知d=6厘米.【答案】3.87平方厘米【分析】阴影部分的面积是长6厘米,宽为6÷2=3厘米的长方形的面积减去半径为6÷2=3厘米的圆面积的一半,据此根据长方形的面积公式:和圆的面积公式:代入数据进行解答即可.【解答】解:(平方厘米),答:图中阴影部分的面积是3.87平方厘米.18.【答题】明明有一根长60厘米的铁丝围了一个最大的圆.亮亮说:“如果我画一个半径为10厘米的圆,肯定比你围的圆的面积大”.哪个圆的面积大呢?请你帮忙做出判断,并说明理由.【答案】亮亮画的圆的面积大.【分析】根据圆的周长公式:,求出半径为10厘米的圆的周长,与60厘米比较大小即可求解.【解答】解:3.14×10×2=62.8(厘米),因为62.8厘米>60厘米,所以亮亮画的圆的面积大.19.【答题】求出下列阴影部分的面积(单位:厘米).【答案】第一个图形阴影部分的面积是(平方厘米),答:第一个图形阴影部分的面积是37.68平方厘米;第二个图形阴影部分的面积是(平方厘米),答:第二个图形阴影部分的面积是13.76平方厘米.【分析】图形一根据求圆环的面积公式求出阴影部分的面积,图形二根据用边长8厘米的正方形面积减去直径为8厘米的圆形的面积,依此进一步得解.【解答】(平方厘米),答:第一个图形阴影部分的面积是37.68平方厘米;(平方厘米),答:第二个图形阴影部分的面积是13.76平方厘米.20.【答题】计算如图阴影部分的面积,已知d=6厘米.【答案】阴影部分的面积是3.87平方厘米【分析】阴影部分的面积是长6厘米,宽为6÷2=3厘米的长方形的面积减去半径为6÷2=3厘米的圆面积的一半,据此根据长方形的面积公式和圆的面积公式代入数据进行解答即可.【解答】(平方厘米),答:阴影部分的面积是3.87平方厘米.。
(压轴题)小学数学三年级下册第五单元《面积》 单元测试(有答案解析)

(压轴题)小学数学三年级下册第五单元《面积》单元测试(有答案解析)一、选择题1.如图,每个小方格的面积为4m2.图中阴影部分的面积大约是()m2.A. 100B. 25C. 882.张爷爷家的樱桃园占地面积大约是7()。
A. 公顷B. 平方千米C. 平方米3.一块黑板的面积大约是4()A. 米B. 平方厘米C. 平方分米D. 平方米4.一根长方体木料长4m,宽2dm,厚2dm,沿长锯成4段,表面积增加()A. 12dm2B. 16dm2C. 24dm2D. 32dm25.面积是1平方米的正方形可以剪成()个边长是1分米的小正方形.A. 10个B. 100个C. 1000个6.一张课桌的面积是45()。
A. 平方厘米B. 平方分米C. 平方米D. 公顷7.请估一估,你所在教室地面的面积大约是60()A. 平方米B. 平方厘米C. 平方分米D. 立方厘米8.从下面的长方形纸上剪下一个最大的正方形,正方形的面积是()平方厘米。
A. 144B. 80C. 649.用一根长20厘米的铁丝围成一个正方形,这个正方形的面积是()A. 16B. 25C. 40010.用一根长30厘米的铁丝,围成一个长为10厘米的长方形。
这个长方形的面积为()平方厘米。
A. 50B. 200C. 30011.用三个长都是4分米,宽都是3分米的长方形拼成一个长方形,它的面积是()平方分米.A. 12B. 24C. 42D. 36 12.把正方形的边长扩大3倍,面积就扩大()倍.A. 3B. 6C. 9D. 12二、填空题13.把一个棱长1m的正方体切成棱长1cm的小正方体,可以切成________块,如果把这些小正方体排成一行,一共长________m.14.一个长方形的长是16厘米,宽是11厘米,它的周长是________厘米,面积是________平方厘米。
15.帮助警察叔叔估测一下,嫌疑犯在现场留下脚印的面积大约是________平方厘米。
小学数学人教版(2014秋)六年级上册第五单元 圆扇形-章节测试习题(4)

章节测试题1.【题文】求阴影部分的面积.【答案】阴影部分的面积为28.26平方厘米.【分析】两个扇形的圆心角都是90度,那么每个扇形的面积就占所在圆面积的,用大扇形面积减去小扇形面积就是阴影部分的面积.【解答】3.14×8×8×=3.14×64×=50.24(平方厘米)3.14×10×10×=314×=78.5(平方厘米)78.5-50.24=28.26(平方厘米)答:阴影部分的面积为28.26平方厘米.2.【题文】如图,OABC是正方形,扇形的半径是6厘米,求图中阴影部分的面积.【答案】图中阴影部分的面积是10.26平方厘米.【分析】阴影部分的面积是扇形面积减去空白部分正方形的面积,正方形的边长无法计算,可以把正方形分成两个等腰直角三角形来计算面积.【解答】答:图中阴影部分的面积是10.26平方厘米.3.【题文】图中小正方形的面积是20平方厘米,求阴影部分的面积.【答案】阴影部分的面积是15.7平方厘米.【分析】观察图形可以知道:圆的半径=正方形的边长,正方形的面积=边长×边长,正好就是圆的半径的平方,而圆的面积是π×r2,可以求出整个圆的面积,阴影部分的面积占整个圆面积的.【解答】设圆的半径为r,则正方形边长也为r,所以r²=20πr²=62.8(平方厘米)62.8÷4=15.7(平方厘米)答:阴影部分的面积是15.7平方厘米.4.【答题】下面图形中哪些角是圆心角?()A. B.C. D.【答案】A【分析】判断是不是圆心角的方法:角的顶点是圆心,角的两条边是圆的两条半径.【解答】第一个图是圆心角.选A.5.【答题】下列说法错误的有()句.①圆的面积也可以用“C×r”来计算.②一张圆形纸片,至少对折3次,才能找到圆心.③用4个圆心角都是90°的扇形,一定可以拼成一个圆.A. 1B. 2C. 3【答案】B【分析】①圆的周长公式:C=2πr,圆的面积公式:S=πr2,据此分析解答;②一张圆形纸片,至少对折2次,才能找到圆心,据此判断;③用4个半径相等且圆心角都是90°的扇形,才能拼成一个圆,据此判断.【解答】①因为C×r=×2πr×r=πr2,所以圆的面积也可以用“C×r”来计算,此说法正确;②一张圆形纸片,至少对折2次,才能找到圆心,原题说法错误;③用4个半径相等且圆心角都是90°的扇形,才能拼成一个圆,原题说法错误.选B.6.【答题】以下()选项是圆心角的定义.A. 顶点在圆外的角B. 顶点在圆内的角C. 顶点在圆心的角D. 顶点在圆上的角【答案】C【分析】此题考查的是圆心角的定义.【解答】顶点在圆心的角叫做圆心角.选C.7.【答题】扇形圆心角的度数是().A. 大于0°B. 大于360°C. 大于0°,小于360°D. 任意度【答案】C【分析】弧和经过弧两端的半径所围成的图形叫做扇形.圆心角的度数大于0°,小于360°.【解答】扇形圆心角的度数在0°和360°之间.选C.8.【答题】圆心角大的扇形比圆心角小的扇形大.()【答案】×【分析】扇形的大小与圆心角的大小和半径的长短有关,所以不能只根据圆心角的大小来确定扇形的大小.【解答】圆心角大的扇形不一定比圆心角小的扇形大.故此题是错误的.9.【答题】圆的一部分就是扇形.()【答案】×【分析】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形.【解答】圆的一部分不一定是扇形.故此题是错误的.10.【答题】圆心角越大,扇形的面积就越大.()【答案】×【分析】扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定越大,所以面积无法确定;进而判断即可.【解答】由分析知:扇形的面积大小与圆心角、半径有关系,圆心角越大,半径不一定越大,所以面积无法确定.故此题是错误的.11.【答题】在同一个圆中,圆心角越小,扇形也越小.()【答案】✓【分析】扇形的大小与圆心角大小和半径的长短有关,同一个圆内半径的长度相等,所以圆心角大小决定了扇形的大小.【解答】同一个圆中,圆心角越小,扇形也越小.故此题是正确的.12.【答题】圆形有______条对称轴,扇形有______条对称轴.(填汉字)【答案】无数一【分析】根据对圆的认识可知,圆是轴对称图形,每条直径所在的直线都是它的对称轴,圆有无数条对称轴;扇形是圆的一部分,扇形也是轴对称图形,扇形只有一条轴对称,据此解答.【解答】圆形有无数条对称轴,扇形有一条对称轴.故此题的答案是无数,一.13.【答题】在同一个圆中,扇形的大小与______有关.【答案】圆心角【分析】同一个圆中,扇形的大小与这个扇形的圆心角大小有关,圆心角越大,扇形越大,反之亦然.【解答】在同一个圆中,扇形的大小与圆心角有关.故此题的答案是圆心角.14.【答题】在一个圆上,任意画出三条半径,可以在此图中找出______个扇形.【答案】6【分析】单独的扇形有3个,两个扇形组成的也是扇形,也有3个,共有6个扇形.【解答】如图,可以在图中找出6个扇形.故此题的答案是6.15.【答题】顶点在______的角叫圆心角.【答案】圆心【分析】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形,两条半径组成的角就是圆心角.【解答】顶点在圆心的角叫做圆心角.故此题的答案是圆心.16.【题文】一块正方形的草地,边长为4m,两个对角各有一棵树,树上各栓了一只羊.栓羊的绳子长都是4m.两只羊都能吃到青草的面积是多少平方米?【答案】两只羊都能吃到青草的面积是9.12平方米.【分析】从图中可以看出,两只羊都能吃到青草的面积=圆的面积×2-正方形的面积,其中圆的面积=πr2,正方形的面积=边长×边长.【解答】(3.14×42×)×2-4×4=9.12(m2)答:两只羊都能吃到青草的面积是9.12平方米.17.【题文】圆的面积与长方形的面积相等.求空白部分的面积?(图中单位:厘米)【答案】空白部分的面积是37.68平方厘米.【分析】因为圆面积与长方形面积相等,所以空白部分的面积就是所在圆面积的,由此根据圆面积公式计算即可.【解答】3.14×4²×=37.68(平方厘米)答:空白部分的面积是37.68平方厘米.18.【题文】画一个直径是6cm的圆,再在圆中画一个圆心角是150°的扇形.【答案】【分析】先用圆规画出直径是6cm的圆,然后将圆的顶点与量角器的中心对齐,然后画出圆心角是150°的扇形.【解答】见答案.19.【答题】下列图形中,是扇形的有().A. 1个B. 2个C. 3个D. 4个【答案】B【分析】【解答】20.【答题】扇形的大小与()有关,还与()有关.【答案】半径长短,圆心角大小【分析】【解答】。
五年级下册数学试题 第六单元圆的周长与面积测试卷 苏教版(2014秋)含答案

第六单元综合测试卷整合提高与梯级创新一、计算题。
(共18分)1.求阴影部分的面积。
(12分)(1)2.求阴影部分的周长。
(6分)二、填空题。
(每空1分,共17分)1.公园里有一个半圆形的花坛,直径是6米,周长是()米,面积是()平方米。
2.将一张周长是12.56厘米的圆形纸片剪成两个半圆,每个半圆的周长是()厘米,每个半圆的面积是()平方厘米。
3.一根铁丝刚好围成一个半径是2厘米的圆,现改围成一个正方形,这个正方形的边长是()厘米,面积是()平分厘米。
4.把一个圆沿着半径平均分成若干份,拼成一个近似的长方形,长方形的长是9.42厘米,则长方形的宽是()厘米,面积是()平方厘米。
5.小刚骑自行车行了125.6米,车轮正好转了50圈,这辆自行车的车轮的直径是()米。
6.如右图,在一张长8厘米,宽4厘米的长方形纸上画了两个圆,每个圆的直径是()厘米,周长是()厘米,面积是()平方厘米。
7.一个时钟的时钟长8厘米,分针长10厘米。
从中午12时到下午3时,分针的尖端走了()厘米,时针扫过的面积是()平分厘米。
8.从一张正方形纸片中剪下一个最大的圆,圆的周长是18.84厘米,这张纸剩下的面积是()平方厘米。
9.电脑光盘的半径是7厘米。
如果把它装在一个正方形的包装袋里,这个包装袋一面的面积至少是()平方厘米。
10.在一个长7厘米,宽3厘米的长方形内画一个最大的半圆,这个半圆的面积是()平方厘米。
三、判断题。
(每题1分,共5分)1.如果一个圆的周长是12.56厘米,它的面积是12.56平方厘米。
()2.直径和半径的长度都能决定圆的大小。
()3.半圆和扇形都有无数条对称轴。
()4.当圆的直径与一个正方形的边长相等时,这个正方形的面积一定大于这个圆的面积。
()5.圆心角越大,扇形的面积就越大。
()四、选择题。
(每题2分,共12分)1.如果大圆的面积是小圆面积的9倍,那么大圆的直径是小圆直径的().A. 9B. 18C. 3D.4.52.小红想从下列纸中剪下一个面积比较大的圆,她应该选择().A.长12厘米,宽3厘米的长方形B.边长4厘米的正方形C.长8厘米,宽5厘米的正方形3.右面图形有()条对称轴。
小学数学冀教版第九册多边形的面积组合图形的面积-章节测试习题

章节测试题1.【题文】如图,大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积.【答案】阴影部分的面积是12.5平方厘米【分析】要求阴影部分的面积,只要求出梯形CDFE和三角形BCD面积和,然后减去三角形BEF的面积,即可求得阴影部分的面积.【解答】(5+3)×3÷2+5×5÷2-3×(3+5)÷2=12.5(平方厘米)答:阴影部分的面积是12.5平方厘米.2.【答题】如图,三角形ABC的底边BC长3厘米,BC边上的高是1厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时三角形扫过的面积是()平方厘米。
A.21B.19.5C.17D.15【答案】B【分析】平移时图形的每个点都在移动及整个图形沿同一方向移动同样的距离,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,就是沿高的方向移动了3×2=6cm,三角形扫过的面积应该是一个长方形的面积加上一个三角形的面积。
【解答】扫过的面积应该是矩形BCDF的面积加上上面三角形的面积,3×2=6(厘米),3×6+×3×1=19.5(平方厘米)。
3.【答题】甲和乙的面积比较,结果()。
A.甲大B.乙大C.一样大D.无法确定【答案】D【分析】根据三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定,再根据等量关系可知甲和乙的面积之间的关系。
【解答】由三角形面积公式S=ah÷2和长方形面积公式S=ah可知高和长相等的三角形面积与长方形面积无法确定,甲的面积=三角形面积﹣①的面积乙的面积=长方形面积﹣①的面积则甲的面积和乙的面积无法确定大小。
4.【答题】下面四边形ABCF和CDEG都是正方形,它们的边长分别是8厘米和6厘米,图中阴影部分三角形的面积等于24平方厘米的有()。
小学数学奥数测试题复杂直线型面积10_人教版

【解析】
如图,连接 ,比拟 与 ,由于 , ,即 与 的底与高分别相等,所以 与 的面积相等,那么阴影局部面积与 的面积相等,为6平方厘米.
4.50
【解析】
方法一:三角形BEF的面积 ,梯形EFDC的面积 三角形BEF的面积,而四边形CEFH是它们的公共局部,所以,三角形DHF的面积 三角形BCH的面积,进而可得,阴影面积 三角形BDF的面积 三角形BCD的面积 (平方厘米).
2.8
【解析】
这道题似乎缺少大正方形的边长这个条件,实际上此题的结果与大正方形的边长没关系.连接 (见右上图),可以看出,三角形 与三角形 的底都等于小正方形的边长,高都等于大正方形的边长,所以面积相等.因为三角形 是三角形 与三角形 的公共局部,所以去掉这个公共局部,根据差不变性质,剩下的两个局部,即三角形 与三角形 面积仍然相等.根据等量代换,求三角形 的面积等于求三角形 的面积,等于 .
7.12.8
【解析】因为乙、丙两个三角形面积相等,底 .所以 到 的间隔与 到 的间隔相等,即 与 平行,四边形 是平行四边形,阴影局部的面积 平行四边形 的面积的 ,所以阴影局部的面积 乙的面积 .设甲、乙、丙的面积分别为 份,那么阴影面积为 份,梯形的面积为 份,从而阴影局部的面积 (平方厘米).
方法二:连接CF,那么CF平行BD,
所以,阴影面积 三角形BDF的面积 三角形BCD的面积 (平方厘米).
5.20
【解析】
假如注意到 为一个正方形的对角线(或者说一个等腰直角三角形的斜边),那么容易想到 与 是平行的.所以可以连接 、 ,如上图.
由于 与 平行,所以 的面积与 的面积相等.而 的面积为 ,所以 的面积也为20.
18.
【解析】根据题意可知, ,所以 , .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求阴影部分图形面积近年来的中考数学试卷中,围绕图形面积的知识,出现了一批考查应用与创新能力的新题型,归纳起来主要有:一、规律探究型例1宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r).(1)如图1,分别以线段O1O2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积.(2)如图2,分别以等边△O1O2O3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时,这三个圆相交部分的面积又是多少呢?(3)如图3,分别以正方形O1O2O3O4的四个顶点为圆心,以其边长为半径作四个相同的圆,则这四个圆的相交部分的面积又是多少呢?(2005年黄冈市中考题)分析(1)利用“S阴=S菱形AO1BO2=4S弓形”即可;(2)利用“S阴=S△O1O2O3+3S弓”即可;(3)•直接求解比较困难,可利用求补法,即“S阴=S正方形O1O2O3O4-S空白”,考虑到四个圆半径相同,若延长O2O1交⊙O1•于A,则S空白=4S O1AB,由(1)根据对称性可求S O1BO4,再由“S O1AB=S扇形AO1O4-S O1BO4”,这样S空白可求.解答(1)设两圆交于A、B两点,连结O1A,O2A,O1B,O2B.则S阴=S菱形AO1BO2+4S弓.∵S菱形=2S△AO1O2,△O1O2A为正△,其边长为r.∴S△AO1O232,S弓=260360rπ32=26rπ32.∴S阴=2×34r2+4(6πr2-34r2)=23πr2-32r2.(2)图2阴影部分的面积为S阴=S△O1O2O3+3S弓.∵△O1O2O3为正△,边长为r.∴S△O1O2O3=34r2,S弓=260360rπ-34r2.∴S阴=34r2+3(26rπ-34r2)=2πr2-32r2.(3)延长O2O1与⊙O1交于点A,设⊙O1与⊙O4交于点B,由(1)知,S O1BO4=12(23πr2-32r2).∵S O1AB=S扇形AO1O4-S O1BO4=290360rπ-12(23πr2=32r2)=24rπ-13πr2+34r2.则S阴=S正方形O1O2O3O4-4S O1AB=r2-4(24rπ-13πr2+34r2)=r2+13πr2-3r2=(13π+1-3)r2.二、方案设计型例2 在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半.下面分别是小明和小颖的设计方案.小明的设计方案:如图1,其中花园四周小路的宽度相等,经过解方程,•我得到路的宽为2m或12m.小颖的设计方案:如图2,其中花园中每个角上的扇形都相同.(1)你认为小明的结果对吗?请说明理由.(2)请你帮助小颖求出图中的x(精确到0.1m)(3)你还有其它的设计方案吗?请在右边的矩形中画出你的设计草图,•并加以说明.(2004年新疆建设兵团中考题)分析(1)由小明的设计知,小路的宽应小于矩形荒地宽的一半,由此判断即可;(2)可由“花园面积为矩形面积一半”列方程求x;(3)可由图形对称性来设计.解(1)小明的结果不对.设小路宽xm,则得方程(16-2x)(12-2x)=12×16×12解得:x1=2,x2=12.而荒地的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m 不合题意.(2)由题意,4×24xπ=12×16×12x2=96π,x≈5.5m.(3)方案有多种,下面提供5种供参考:三、网格求值型例3 图中的虚线网格我们称之为正三角形网格,它的每个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.(1)直接写出单位正三角形的高与面积;(2)图1中的ABCD含有多少个单位正三角形?ABCD的面积是多少?(3)求出图1中线段AC的长(可作辅助线);(4)求出图2中四边形EFGH的面积.(2005年吉林省中考题)分析(1)由正三角形边角关系来求;(2)仔细观察图1便可找到答案;(3)考虑到图1中AB=3,BC=4,∠B=60°,可作△ABC 的高AK ,构造直角三角形,•再利用解直角三角形知识即可求得;(4)可利用网格构造特殊格点图形,再由求补法计算四边形EFGH•面积. 解:(1)单位正三角形的角为32,面积为34, (2)ABCD 含有24个单位正三角形,故其面积为24×34=63. (3)如图1,过A 作AK ⊥BC 于K ,在Rt △ACK 中,AK=323,KC=52. ∴AC=22AK KC +=2235(3)()22+=13. (4)如图3,构造EQSR ,过F 作FT ⊥QG 于T ,则S △FQG =12FT ·QG=12×332×4=33.同理可求S △GSH =3,S △EHR =63,S EQSR=183.∴S 四边形EFGH = SEQSR-S △FQG -S △GSH -S △EHR =183 -33-3-63=83.四、图形对称型例4 如图,半圆A 和半圆B 均与y 轴相切于点O ,其直径CD 、EF 均和x 轴垂直,以O 为顶点的两条抛物线分别经过C 、E 和D•、•F ,•则图中阴影部分的面积是_________.•(2005年河南省中考题)分析 由题意知,图中两半圆和两抛物线组成的图形关于y 轴对称,故y 轴左侧阴影部分面积等于半圆B 中的空白面积,所以所求阴影部分面积为半圆B 的面积,即S阴=12π·12=12π. 解答:2π.五、图形变换型例5 如图,矩形ABCD 的长与宽分别是2cm 和1cm ,AB 在直线L 上,依次为B 、C ′、•D ″,依次为B 、C ′、D ″为中心将矩形ABCD 按顺时针方向旋转90°.这样点A•走过的曲线依次为'AA 、'''A A 、'''''A A ,其中'AA 交CD 于点P .(1)求矩形A ′BC ′D ′的对角线A ′C ′的长; (2)求'AA 的长;(3)求图中 部分的面积S ;(4)求图中 部分的面积T .(2005年吉林省中考题)分析 (1)要求A ′C ′,因长宽分别为2和1,利用勾股定理即可;(2)要求'AA ,因'AA 所对圆心角为∠ABA ′=90°,半径AB=2,利用弧长公式即可;(3)因△A ′C ′D•′≌△A ″C ′D ″,故S=S 扇形A`C``A``;(4)连PB ,则PB=AB=2,又BC=1,故∠PBC=60°,∠ABP=30°,•欲求T ,由“T=S 扇形ABP +S △BCP ”即可.解答 (1)A ′C ′2221+5cm ).(2)'AA =90180π×2=π(cm ). (3)S=S 扇形A`CA``=290(5)360π=54π(cm )(4)连结BP ,在Rt △BCP 中,BC=1,BP=2, ∴∠BPC=30°,3ABP=30°,∴T=S 扇形ABP +S △PBC =30360π×22+32=(3π+32)cm 2.六、实际应用型例6 在栽植农作物时,一个很重要的问题是“合理密植”.如图是栽植一种蔬菜时的两种方法,A 、B 、C 、D 四珠顺次连结成为一个菱形,且AB=BD ;A ′、B ′、•C ′、D ′四株连结成一个正方形,这两种图形的面积为四株作物所占的面积,•两行作物间的距离为行距;一行中相邻两株作物的距离为株距;设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积.在株距都为a ,其他客观因素也相同的条件下,•请从栽植的行距,蔬菜所占的面积,充分生长后空隙地面积三个方面比较两种栽植方法.哪种方法能更充分地利用土地.分析:本题立意很新,要合理密植,充分利用土地,只需分别计算并比较两种方案的行距、阴影面积以及S 和S .对应值小的即为合理密植.解 连结AC 交BD 于点O .在菱形ABCD 中,有AB=AD ,AC ⊥BD ,BO=12BD . ∵AB=BD=a ,∴BO=OD=12a . 在Rt △AOD 中,22AD OD -3. ∴S 菱形ABCD =2×12BD ·32,S 正方形A`B`C`D`=a 2.设方法(1)中空隙地面积为S 1,方法(2)中空隙地面积为S 2. 则S 1=S 菱形ABCD -S ☉A =32a 2-4πa 2, S 2=S 正方形A`B`C`D`-S ☉A`=a 2-4πa 2. ∵32<1, ∴AO<A ′B ′,S 菱形ABCD <S 正方形A`B`C`D`,S 1<S 2.∴栽植方法(1)比栽植方法(2)能更充分地利用土地.。
