09 第9章 非正弦交流电路 学习指导及习题解答
非正弦

非正弦周期电路实验目的:(1)验证非正弦周期性电压有效值与其各次谐波电压有效值之间的关系。
例:对称三相非正弦电压A 相电压为t t u A ωω3cos 270cos 2218-=V ,对基波频率的负载复阻抗Ω+=80201j Z ,中线复阻抗Ω=21j Z N ,试计算:(1) 负载相电流及中线电流的有效值。
(2) 如果中线断开,试求负载相电流和中性点间的电压。
解: (1)对于具有正序对称性质的基波分量来说,可归结为一相的计算,等效电路如图所示。
()A j Z U I A A 1.105.21218820218111==+== 在三次谐波作用下,由KVL 可得3.33.3.3.33.333.33A N C B A N N N A A I Z I I I Z I Z I Z U =⎪⎭⎫ ⎝⎛++==- 故 333.3.3N A A Z Z U I +=由上式可作出计算3.A I 的等效电路如图(c )所示,其中()()()()A ==+=Ω=++=+Ω=⨯==96.11.367.7031.363324833333323323333N A A N N Z Z U I X X R Z Z X X 因此负载相电流的有效值为 ()A =+=+=3.1096.11.10222221I I I PH中线电流为()A =⨯==88.596.1333I I N(2)如果中线断开,负载相电流中五三次谐波电流,故()A ==1.101I I PH中性点间的电压为()V U U A N N 7.703'==电路仿真实验:由仿真实验图可知相电流几乎相同,中线电流在数值是相差了1.3A 这应该是在计算过程中对于数值的取了近似值多造成的,每取一次,就会相差一点。
当中线断开时仿真图如下:断开中线后的中性点电压和相电流与理论计算值几乎相同无差异。
实验小结本次实验我们验证了非正弦周期电压(电流)有效值与各次谐波电压(电流)有效值之间的关系。
电子技术(电工学Ⅱ)(第3版)课件:非正弦周期电流电路

5 非正弦周期电流电路
二、教学要求: 1. 通过学习,理解用傅里叶级数将非正弦周 期信号分解为谐波的方法 ; 2. 理解和掌握非正弦周期电流电路中的有效 值、平均值和平均功率的计算 ; 3.了解线性电路在非正弦激励下的计算方法。
返回主目录
5.1非正弦周期量的分解
非正弦周期信号
u
Um
u
u
2 2
5.2.2 平均值 非正弦周期电流、电压的平均值分别为
I av
1 T
T
idt
0
U av
1 T
T
udt
0
返回主目录
5.2效非值正、弦平周均期值电和流平电均路功中率的有 5.2.3 非正弦周期电流电路的平均功率 设某无源二端网络端口处的电压、电流取关联的参 考方向,并设其电压、电流为:
u U0 Ukm sinkt ku k 1
例5-2设二端网络的端口电压、电流为关联的参考方 向,已知:
u 10 141.4sint 50 sin3t 60V
i sin t 700 0.3sin 3t 600 A
求二端网络的平均功率P。
解: P U 0 I 0 U1I1 cos1 U 3 I3 cos3
U0I0
返回主目录
5.3线性电路在非正弦激 励下的计算
例5-3如图所示电路,已知R=100Ω,C=1μF。激励源
uS为矩形波。已知Um=11V,T=1mS,求输出电压 uO 。
11
0
0.5
1
t ms
返回主目录
5.3线性电路在非正弦激 励下的计算
解:由已知条件可得基波角频率
1
2
T
1
2
10
3
非正弦交流电路45页PPT

非正弦交流电路
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
最全第九章(正弦稳态电路分析)习题解答打印版.doc
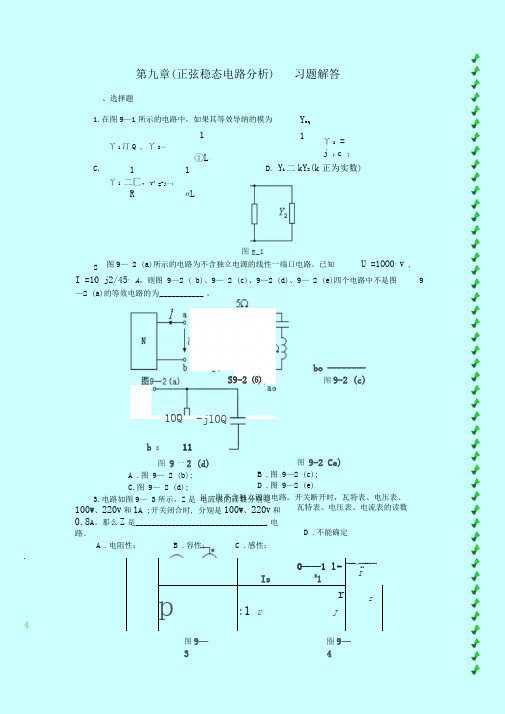
、选择题第九章(正弦稳态电路分析)习题解答1.在图9—1所示的电路中,如果其等效导纳的模为C .1丫1汀Q , 丫2…①L11 丫1 二匚,Y^ =-j —;R«LY eq1丫2 =j ,c ;D . Y i 二kY 2(k 正为实数)图g_i图9— 2 (a )所示的电路为不含独立电源的线性一端口电路。
已知U =1OO0°V ,I =10 j2/45° A ,则图 9—2 ( b )、9— 2 (c )、9—2 (d )、9— 2 (e )四个电路中不是图 9—2 (a )的等效电路的为 ___________ 。
2. S9-2 ⑹10Q -jlOQbo --------图9-2 (c)b D11图 9一2 (d)A .图 9— 2 (b );C .图 9— 2 (d );3.电路如图9— 3所示,Z 是 电流表的读数分别是100W 、220V 和1A ;开关闭合时, 分别是100W 、220V 和0.8A 。
那么Z 是 _________________________________ 电路。
A .电阻性;B .容性;C .感性;图 9-2 Ce)B .图 9—2 (c ); D .图 9—2 (e ) 旦一段不含独立源的电路。
开关断开时,瓦特表、电压表、 瓦特表、电压表、电流表的读数 D .不能确定%O ——1 l -IsZ1---------- ► -----------------■■I 4pr:1 UJTz图9—圏9—入阻抗为(3 - j4)门。
09-52 .线性一端口电路如图 9—6所示, 吸收的复功率,有功功率、无功功率分别为U - -50 /300V, I =2/0^A 。
则此一端口电路100/30°VA 、50 .. 3W 、50Var 。
4.在图9 — 8所示电路中,已知电流表 表V 2的读数为20 V ,则电压表V 的读数为A 的读数为2A ,电压表V 的读数10V ,电压V 。
电路分析第九章习题解答

10.正弦电流电路如图题 9-10 所示,已知图中各电压表读数分别为:第一只 15V,第二只 80V,第三 只 100V。求电路的端电压有效值,并作出相量图。
V1 + R
& U
V2 L C V3
图题 9-10 解:电路的相量模型及电压相量图如下图所示
9.正弦电流电路如图题 9-9 所示,已知图中第一只电压表读数为 30V,第二只电压表读数为 60V; 求电路的端电压有效值,并作出相量图。
V1 + R
& U
L
V2
解: 图题 9-9 电路的相量模型及电压相量图如下图所示
+
& U
−
& − + U 1
R
& L U 2
−
+
& U
& U 2
& U 1
由电压三角形可求得电路的端电压有效值
+
& U L
RL
−
& I
j ωL
& U S
R
−
+
ω = 2π f = 2π × 5 × 10 3 = π × 10 4
Z L = RL + jωL = 700 + j 64 × 10 −3 × π × 10 4 = 700 + j 2010.62 = 2128.99∠70.80 o
Z = Z L + R = 700 + j 2010.62 + 3300 = 4000 + j 2010.62
+ us -
非正弦

一、选择题1.周期电流i(t)=1+cos(ωt +60°)+cos(3ωt -30°)A 的有效值为( B )。
A .1A B .2A C .3A D .3A2.某10Ω电阻上的电压u=[80sin ωt+60sin(3ωt+60°)]V ,则此电阻上消耗的平均功率为( B )。
A .1400WB .500WC .220WD .400W3.已知某元件两端的电压为u(t)=2+2V)10t sin(2︒+ω,则该电压的有效值U =( C )。
A .2V B .V5 C .2V2D .2V34.周期电压u(t)=[1+22sin ωt+22sin(3ωt+30°)]V 的有效值为(B )。
A .1VB .3VC .17V D .(1+42)V5.已知某二端网络的端口电压为u(t)=[1+52sin(ωt-30°)]V ,流入该网络的电流为i(t)=[0.5+22sin ωt]A ,则该二端网络所消耗的平均功率P=( B )。
A .(1+W)321B .(0.5+5W)3 C .(1+5W)3D .(0.5+W)3216. 对非正弦周期电流电路进行分析时,不同谐波的阻抗( A )。
A . 不同 B . 相同 C . 模相同 D . 上述说法都错7.非正弦周期电路的电流有效值为( D )。
A .∑∞=0K KIB .dt |)t (i |T⎰C .)t k sin(I I 1K k m 0∑∞=ϕ+ω+D .∑∞=+1K 2K2I I8.设非正弦周期电路中的电压和电流分别为:U(t)=U 0+∑2U K sin(k ωt+ϕK ),i(t)=I 0+∑2I K sin(k ωt),则对应的平均功率为( A )。
A .U 0I 0+∑U K I K cos ϕKB .U 0I 0+∑U K I K sin ϕKC .U 0I 0+2∑U K I K cos ϕKD .U 0I 0+2∑U K I K sin ϕK9.Ω=ω2L 的电感元件两端电压+ω+︒+ω=t 3sin(6)30t sin(10)t (u )60︒V,其通过的电流)t (i 为( D )。
电工技术复习资料-电路基础 第9章 习题及答案

电路(第九章)9—7、附图中已知 us 200 2 cos(314t / 3)V ,电流表 A 的读数为 2A,电压表 V1、V2的读数均为 200V。
求参数 R、L、C。
并作出该电路的相量图(提示:先作相量图辅助计算)。
+ V1 -解:由于 Us、V1、V2 读数相等,三个电压的相量图为等边△。
ARjωL+1jωC -+ V2-•US 20060V•则:U 1200120V•U22000V•I290A题 9—7 图XC U2 I200 2 100C 1 1 31.8F X C 100 314Z1• U1 • I200120 290 10030 86.6 j50则:R 86.6X L 50L X L 50 0.16H 314•9—8、附图中 iS 14 2 cos(t )mA ,调节电容,使电压U U ,电流表 A1 的读数为50mA。
求电流表 A2 的读数。
A1+ A2R jωL•解:设U U0V画相量图为:••••从相量图可以看出:U I 2 ,且U 与 I S 同相相量图- 题 9—8 图••• ••所以: I S I 2 ,I S 、I 1 、I 2 构成直角三角形。
I2 I12I2 S502 142 48mA9—9、附图中 Z1(10j50), Z2(400•j1000 ), 如果要使 I 2•和US的相位差为90(正交),β应等于多少?如果把图中 CCCS 换为可变电容 C,求ωC。
Z1 1 +Z2 -题 9—9 图 0••••••解:U S Z1 I Z2 I 2 Z1 I 2 Z1 I 2 Z2 I 2 则:•US• Z1 Z1 Z2I2••若要使 I 2 和U S 正交应有:ReZ1 Z1 Z2 0 即:10+10β+400=0β=-41•••••••若把图中 CCCS 换为可变电容 C 时:U S Z1 (I 2 I C ) Z2 I 2 Z1 I 2 jCZ1Z2 I 2 Z2 I 2ReZ1 jCZ1Z2 Z2 0 即:10-30000ωC+400=0 C 1.37 10219—10、已知附图电路中 Z2=j60Ω,各交流电表的读数分别为 V:100V;V1:171V;V2:240V。
电工学-第9章-课后习题答案--PPT课件

(3) 输出电阻 ro :
rO
U OC I SC
对于正弦交流信号 : 放大器输出端开路电压:
rr oo
U•
U o occ
I•
Io
c
sc
•
I Ii i
•
IIoo
U U• OoCc AAooUU• (ii 受控电压源) R S
+
当输出端接有负载时:
U•
Us-s
UO
RL rO RL
UOC
信号源
+
+
UU•i i
Uii
UUi i UUi•i
U•
iUi
RRBB11 RRB2B2 rberbe(1(1)RE)RE
RB1//RB2 //rbe (1)RE 14.2k
•
r o ro UIUI•soccsocc Rc 3.3k -
返回
ii
ib
+
ui RB1 RB2 rbe
_
ic
+
ib
RC RL
uo
_
ii
ib
+
ui RB1 RB2 rbe
+UCC
RB2 180k
RC3.3k
20V
+
+
+ IB IC
+
RB1
ui 20k _
IE
RE 1.3k
+CE
uo _
RL 3.3k
O
若要消除失真必须 改变RB1与RB2的比例, 适当抬高放大器的静态 工作点,如:调节RB2 使其变小则适当抬高了 UB或者增大RB1。
返回
上一节 下一节
上一页
27 下一页
高考物理大一轮复习专题提升十非正弦交流电有效值的计算课件

解析:由有效值的定义式得31R212×T2×2=UR2T,解得 U= 220 V.
答案:220 V
突破三 矩形脉动电流的有效值
如图 Z10-5 所示,电流实质是一种脉冲直流电,当它通入
电阻后一个周期内产生的热量相当于直流电产生热量的Tt ,这里
t 是一个周期内脉动时间.由 I2矩RT=Tt I2mRT 或UR2矩T=Tt UR2mT,得
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的,若把自己预习时所理解过的知识 逻辑结构与老师的讲解过程进行比较,便可以抓住老师的思路。
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等,这些 用语往往体现了老师的思路。来自:学习方法网
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、语 文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候,最好是做个记号,姑且先把这个问题放在一边,继续听老师讲后面的 内容,以免顾此失彼。来自:学习方法网
图 Z10-1
例 1:家用电子调光灯的调光功能是用电子线路将输入的 正弦交流电压的波形截去一部分来实现的,由截去部分的多少 来调节电压,从而实现灯光的可调,比过去用变压器调压方便 且体积小.某电子调光灯经调整后电压波形如图 Z10-2 所示,求 灯泡两端的电压的有效值.
图 Z10-2 解:由UR2T=UR2m2·T2,解得 U=U2m.
非正弦周期交流电路(ppt 53页)

根据数学中傅立叶级数理论,任何满足狄里赫利条 件的周期函数都可以展开成三角级数。如函数 f (t) 可展开分解为
f(t)A 0 [B km s ik n tC km c k o t]s
k 1
式中
A0Akm s ink(tk) k1
BkmAk CkmAk
m mscionskk
310 1.593
式中P是非正弦周期电流电路的平均功率,U和I是非
正弦周期电压和电流的有效值。 32
例题 铁心线圈是一种非线性元件,因此加上正弦电压
u31s1 i3n1tV 4后,其中电流 i0.8s in 31 (t485 )
0.25 s in 94 (t2_105 )A
不是正弦量。试求等效正弦电流。
P1
T pdt 1
T
uidt
T0
T0
设非正弦周期电压和电流如下:
uU0 Ukm s in ktk k1
iI0 Ikm s ikn tkk
k1
28
则可得下列五项:
1T
(1) T 0 U0I0dt
(2)
1T T0U 0k 1Ik
流用等效正弦电压和电流来代替。等效的条件是:等
效正弦量的有效值应等于已知非正弦周期量的有效值,
等效正弦量的频率应等于非正弦周期量的基波的频率,
用等效正弦量代替非正弦周期电压和电流后,其功率
必须等于电路的实际功率。这样等效代替之后,就可
以用相量表示。等效正弦电压与电流之间的相位差应
由下式确定:
cos P UI
24
即:
i I0 i1 i2 I0 I 1 m s it n 1 ( 1 ) I2 m s2 i t n 2 ( 2 )
非线性电路习题解答提示

非线性电路习题习题解答提示第2章2-1以下给出二端元件的赋定关系,试判断该元件属于哪类元件。
(写出判断过程)(1)i e πiu 2+sin =;电阻元件,非线性时不变(2)t u u q sin 2+=2; 电容元件,非线性时变 (3)3+cos =q q ψ忆阻元件,非线性时不变(4)+=+=3i i u biaT dt dT;电阻型动态元件,非线性(5)332=+dt id E u u高阶非线性代数元件,)()()(i u 302-2已知某二端元件的赋定关系为22dt ud i(t)=K ,其中K 为常数,试讨论其类型、性质,并写出其交流阻抗的表达式。
二阶线性代数元件,设221sin 1sin K ωωt,Z(jω)=ωK ωt,i=u=--,频变反比负电阻2-3一个二端电阻元件和二端电容元件串联后所形成的动态二段元件是代数元件还是动态元件? 动态元件2-4试仅用二端线性电阻元件和线性受控源实现下列矩阵描述的二端网络。
(1)3125Z ⎡⎤=⎢⎥⎣⎦; 31001510Z ⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦,第一项可用无源T 型二端口等效,第二项为受1I 控制的受控源,在输出端口看进去串联叠加。
(2)3215Y -⎡⎤=⎢⎥-⎣⎦;31011500Y --⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,第一项可用无源∏型二端口等效,第二项为受2U 控制的受控电流源,在输入端口看进去并联叠加。
(3)25122H ⎡⎤⎢⎥=⎢⎥-⎣⎦; 112225122U I I U ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,输入端为电阻串联2U 控制的电压源,输出端为电导并联由1I 控制的电流源。
(4)0011A ⎡⎤=⎢⎥-⎣⎦12120011U U I I ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,输入端为两个受控电流源并联,仅可求得电流,电压与输出端无关,与输入端外接电路相关。
因此,此等效电路仅能看出输出对输入端的影响,无法给出输入对输出影响的等效电路。
电路分析习题(第九章)答案

实用文档第九章 正弦稳态电路的分析9.1 计算下列各题,并说明电路的性质。
(1)??,55,30100==Ω+=∠=••P I j Z V U (2)???,1653,153000===-∠-=∠=••P X R A I V U (3)???,5,301000300====∠-=-••P X R A e I V U j9.2在如图所示的各电路图中,除A 0和V 0外,其余电流表和电压表的读数在图上都已标出(都是正弦量的有效值),试求电流表A 0或电压表V 0的读数。
实用文档实用文档9.3在RLC 串联电路中,已知,Ω=50R ,mH L 60=,F C μ100=s rad /1000=ω,V U C︒∠=010 ,试求:(1)电路的阻抗Z ;(2)电流•I 和电压•U 、•L U 及有功功率P 、Q 、S ;(3)绘电压、电流相量图。
实用文档实用文档9.4 在图示电路中,V )30314sin(23600+=t u ,R 1=32,R 2=60,X 1=48,X 2=80。
求总电流i ,总有功功率P 及总功率因数。
I.I .I .U .R R j j 1212XX 12+-9.5在如图所示的电路中,,51A I =,252A I =,110V U =,5Ω=R ,2L X R =试求,I ,C X L X 2R 及。
实用文档实用文档9.6 在如图所示的电路中,i u V U A I I 与,100,1021===同相,试求L C X X R I 及,,。
实用文档实用文档9.7单相交流电路如图所示,已知 60401∠=U V ,Ω=5C X ,Ω==4L X R 。
求:(1)电流I 及电压2U 、U ;(2)电路的P 、Q 、S 。
9.8 图示电路中,并联负载Z 1、Z 2的电流分别为I 1=10 A ,I 2=20 A ,其功率因数分别为)0(6.0cos ),0(8.0cos 222111>==<==ϕϕλϕϕλ,端电压U =100 V ,ω=1000 rad/s 。
电路分析基础习题第九章答案(史健芳).doc

第9章9.1 选择题1. 处于谐振状态的RLC 串联电路,当电源频率升高时,电路将呈( B )。
A. 电阻性B. 电感性C. 电容性D. 视电路元件参数而定 2. RLC 串联电路中,发生谐振时测得电阻两端电压为6V ,电感两端电压为8V ,则电路总电压是( C )。
A. 8VB. 10VC. 6VD. 14V3. Ω=5R 、mH L 50=,与电容C 串联,接到频率为1KHz 的正弦电压源上,为使电阻两端电压达到最大,电容应该为( B )。
066.5.A F μ B.F μ5066.0 C.F μ20 D.F μ24. 下列关于谐振说法中不正确的是( D )。
A. RLC 串联电路由感性变为容性的过程中,必然经过谐振点B. 串联谐振时阻抗最小,并联谐振时导纳最小C. 串联谐振又称为电压谐振,并联谐振又称为电流谐振D. 串联谐振电路不仅广泛应用于电子技术中,也广泛应用于电力系统中 5. 如图x9.1所示RLC 并联电路,sI •保持不变,发生并联谐振的条件为( A )。
A.CL ωω1=B.Cj L j ωω1=C.CL 1=D.Cj L j R ωω1=+图x9.1 选择题5图6. 若i i i 21+=,且A sin 101t i ω=,A )902sin(102ο+=t iω,则i 的有效值为( C )。
A. 20A B. A 220 C. 10A D. A 2/109.2 填空题1. 在含有L 、C 的电路中,出现总电压、电流同相位的现象,这种现象称为 谐振 。
Cj ω12. RLC 串联电路发生谐振时,电路中的角频率=0ωLC /1,=0f LC π2/1。
3. Ω=10R ,H 1=L ,F 100μ=C ,串联谐振时,电路的特性阻抗=ρ 100 ,品质因数Q= 10 。
4. 对某RLC 并联电路端口外加电流源供电,改变ω使该端口处于谐振状态时,电压 最大, 导纳 最小,功率因数=λ 1 。
非正弦周期交流电路PPT

非正弦周期交流电路
§5-1. 非正弦周期量的分解 §5-2. 非正弦周期量的有效值 §5-3. 非正弦周期电流的线性电路 §5-4. 非正弦周期电流的平均功率
非正弦周期电路
一、概述
非正弦电流的普遍性和特殊性
工程中常有一些非正弦信号。如计算机中的脉冲 信号;测量技术中将非电电量转换成的电信号; 由语言、音乐、图象转换成的电信号;许多电子 仪器在工作时所需的控制信号等等。 既然是非正弦的电学量,就不能用正弦交流电的 相量分析方法进行讨论分析,这里讨论对非正弦 电流量的分析方法。它是非正弦量的一种特例。
在0 区间,sin sin k d
1 [cos( k 1) cos( k 1) ]d 2
积分后为零。故可知
o
2
t
u U m sin t
Bkm 0
U m 2 系数 C km 0 sin t cos kt d(t ) Um 2 [ 0 sin t cos kt d(t ) sin t cos kt d(t )] Um 2 0 sin t cos kt d(t ) 1 0 sin cos k d [sin( k 1) sin( k 1) ]d 20 1 1 2 1 cos( k 1) cos( k 1) 0 2 [ ] k 1 k 1 k 1 2 k 1 k 1 4U m ( k为偶数) 2 即 (k 1) C km 0 ( k为奇数)
电路中的电流是非正弦周期量。
e1
t
例
周期性方波 的分解
直流分量
t
t
三次谐波 五次谐波
基波
(学习指导)第九章电路核心素养专项提升含答案

核心素养专项提升一、典型物理模型指导突破科学思维之模型建构——等效电源模型模型概述电路中电源与某一电阻串联(如图甲)或并联(如图乙)时,可把图中虚线框内的整体看为一个电源,我们称为“等效电源”。
这个等效电源的正极为A ,负极为B ,则A 、B 断开时,A 、B 两点间的电压即为等效电源的电动势,A 、B 两点间的电阻即为等效电源的内阻。
甲图中等效电源内部没有电流,其等效电动势和内阻分别为E 等效=U AB =Rr+RE<E 、r 等效=R AB =Rrr+R<r ;乙图中等效电源内部为回路、有电流,其等效电动势和内阻分别为E 等效=U AB =E 、r 等效=R AB =r+R>r 。
按照这种思路可求任意等效电源的电动势和内阻。
案例探究1(2020内蒙古高三一模)如图甲所示电路中,电源电动势E=6 V,内阻r=1 Ω,外电路接有三个定值电阻R 1=2 Ω、R 2=3 Ω、R 3=6 Ω,虚线框内的电路可等效为一个电源,如图乙所示,其等效电动势E'等于CD 间未接入用电器时CD 间的电压,若用导线直接将C 和D 两点连接起来,通过该导线的电流等于等效电源的短路电流。
下列说法正确的是( )A.等效电源的电动势E'=5 VB.等效电源的短路电流为1.2 AC.等效电源的内阻r'=7.5 ΩD.等效电源的最大输出功率为0.3 W【拓展】(1)本题不求等效电源的短路电流,能直接求出等效电源的内阻吗?(2)根据本题的情境,如果在C 、D 间接入一个滑动变阻器,则滑动变阻器接入电路的阻值多大时变阻器消耗的功率最大?最大值为多少?应用总结纯电阻电路中电源的输出功率P 出随外电路总电阻R 的增大先增大后减小,当R=r时达到最大P m =E 24r ,所以在纯电阻电路中求可变电阻R x 消耗的功率最大值时,可把该电阻之外的所有电路看成是一个等效电源,当R x =r 等效时,等效电源有最大输出功率,即R x 消耗的功率最大,也可以再求出等效电源的电动势,利用P m =E等效24r等效直接求出。
--非正弦交流电路

第9章非正弦交流电路学习指导与题解一、基本要求1.建立几个频率为整数倍的正弦波可以合成为一非正弦周期的概念。
明确一个非正弦周期波可以分解为一系列频率为整数倍正弦波之和的概念(即谐波分析)、谐波中的基波与高次谐波的含义。
了解谐波分析中傅里叶级数的应用.2.掌握波形对称性与所含谐波分量的关系。
能根据波形的特点判断所含谐波的情况。
了解波形原点选择对所含谐波的影响.3.掌握非正弦周期电压和电流的平均值(即直流分量)和有效值的计算。
能根据给定波形计算出直流分量。
能根据非正弦周期波的直流分量和各次谐波分量,计算出它的有效值。
4.掌握运用叠加定理和谐波分析计算非正弦交流电路中的电压和电流的方法。
5.建立同频率的正弦电压和电流才能形成平均功率的概念。
掌握运用叠加定理和谐波分量计算非正弦交流电路中和平均功率。
二、学习指导在电工技术中,电路除了激励和响应是直流和正弦交流电和情况外,也还遇到有非正弦周期函数电量的情况。
如当电路中有几个不同频率的正弦量激励时,响应是非正弦周期函数;含有非线性元件的电路中,正弦激励下的响应也是非线性的;在电子、计算机等电路中应用的脉冲信号波形,都是非正弦周期函数。
因此,研究非正弦交流电路的分析,具有重要和理论和实际意义。
本章的教学内容可分为如下三部分:1.非正弦周期波由谐波合成的概念;2.非正弦周期波的谐波分析;3.非正弦交流电路的计算。
着重讨论非正弦周期波谐波分析的概念,非正弦周期量的有效值和运用叠加定理计算非正弦交流电路的方法。
现就教学内容中的几个问题分述如下.(一)关于非正弦周期波的谐波的概念非正弦周期波是随时间作周期性变化的非正弦函数。
如周期性变化的方波、三角波等.这类波形,与正弦波相比,都有变化的周期T和频率f,不同的是波形而已。
f t,可以几个频率为整数倍的正弦波,合成是一个非正弦波。
反之,一个非正弦周期波()分解为含直流分量(或不含直流分量)和一系列频率为整数倍的正弦波。
这些一系列频率为整数倍的正弦波,就称为非正弦周期波的谐波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
k
cos kt 项的偶次谐波。即
u e (t )
0
Um
2U m
1 1 1 [ cos 2t cos 4t cos 6t L ] 3 15 35
奇部 u (t ) 如图 9-9( c )所示,它是一正弦函数,即
1 u 0 (t ) U m sin t 2
故非对称性非正弦周期波 u (t ) 的傅里叶级数展开式为
f (t ) 波形对称于纵坐标,满足 f (t )
= f ( t ) 条件,如图 9-1 所示。则 Bk 0 ,傅里叶级数
Ak cos kt 项, k =1,2,3,…。亦即 中只含 A0 和 这类对称性非正弦周期波,只含直流分量和一系列余弦
函数的谐波分量。 (2)奇函数
f (t ) 波形对称于坐标原点,满足
T 与原波形对横轴成镜 2
像对称,又是奇半波对称函数。则傅里叶系数中 A0 0 , Ak 0 , Bk 中 k 为奇数,即 k =1, 3,5…。傅里叶级数中只含 只含正弦函数的奇次谐波。 (6) 偶函数且奇半波对称 = f (t ) 和 f (t ) f (t
B
k
sin kt 项的奇次谐波。所以,这类奇函数且半波对称波,
f (t ) 波形满足 f (t )
T ) 两个条件。如图 9-6 所示, 2 T f (t ) 波形对称于纵坐标,是偶函数,且移动 与原波形 2
对横轴成镜像对称,又是奇半波对称函数。则傅里叶系
A0 0 Bk 0 , Ak 中 k 为奇数,即 k =1,3,5…。傅
里叶级数中只含
A
k
cos kt 项的奇次谐波。 所以,
k 为偶数时,称为偶次谐波。
非正弦周期波的傅里叶级数展开,关键是计算傅里叶系数的问题。 在电工技术中,遇到的非正弦周期波,都满足狄里赫利条件的,均可展开为傅里叶级 数。常见的非正弦周期波的傅里叶级数展开式,已在手册及教材中列出,如下表所示,以供 查用。 常见非正弦周期波的傅里叶级数展开式
f (t ) 波 形 图
A
k
cos kt 项的偶次谐波。所以,这类偶函数且半波重叠波,只含余弦函
数的偶次谐波,包含直流分量。
T f (t ) 波形满足 f (t ) f (t ) 和 f (t ) f (t ) 两个条件, 2 T 如图 9-8 所示。 f (t ) 波形对称于原点,是奇函数,且移动 与原波形重叠,又是半波重 2
·1·
称为基波或一次谐波;频率是基波频率 2 倍的正弦,就称为二次谐波;频率是基波频率 3 倍的正弦波,称为三次谐波;频率是基波频率 k 倍的正弦波,称为 k 次谐波, k 为正整数。 人们通常将二次及二次以上的谐波,统称为高次谐波。 (二)关于谐波分析的方法 在电路分析中,将非正弦周期波的分解,应用傅里叶级数展开的方法,分解为直流分 量(或不含有)和频率为整数倍的一系列正弦波之和,称为傅里叶分析,又称为谐波分析。 一人周期为 T 的函数 f (t ) ,如果满足狄里赫利条件﹡,则 f (t ) 可以展开为如下三角 级数:
图 9-1
偶函数波形举例
f (t ) f (t ) 条件,如图 9-2 所示。则 A0 0 , Ak
=0,傅里叶级数中,只含
B
k
sin kt 项, k =1,2,3,…。亦即这类对称性非正弦周期
波,只含一系列正弦函数的谐波分量。
T )与 2 T 原波形成镜像,即对横轴对称,满足 f (t ) f (t ) 条 2
f ( x) 傅里叶级数展开式
f (t )
Am
(1
2 2 sin t cos 2t cos 4t L ) 2 3 15
﹡ 狄利赫利条件:
f (t ) 在〔
T T , 〕 2 2
或〔0, T 〕区间, (1)除有限个第一类间断点外,其余各点
连续; (2)只有有限个极点。
二、学 习 指 导
在电工技术中,电路除了激励和响应是直流和正弦交流电和情况外,也还遇到有非正 弦周期函数电量的情况。 如当电路中有几个不同频率的正弦量激励时, 响应是非正弦周期函 数;含有非线性元件的电路中,正弦激励下的响应也是非线性的;在电子、计算机等电路中 应用的脉冲信号波形,都是非正弦周期函数。因此,研究非正弦交流电路的分析,具有重要 和理论和实际意义。 本章的教学内容可分为如下三部分: 1.非正弦周期波由谐波合成的概念; 2.非正弦周期波的谐波分析; 3.非正弦交流电路的计算。 着重讨论非正弦周期波谐波分析的概念,非正弦周期量的有效值和运用叠加定理计算 非正弦交流电路的方法。 现就教学内容中的几个问题分述如下。 (一)关于非正弦周期波的谐波的概念 非正弦周期波是随时间作周期性变化的非正弦函数。如周期性变化的方波、三角波等。 这类波形,与正弦波相比,都有变化的周期 T 和频率 f ,不同的是波形而已。 几个频率为整数倍的正弦波,合成是一个非正弦波。反之,一个非正弦周期波 f (t ) ,可 以分解为含直流分量(或不含直流分量)和一系列频率为整数倍的正弦波。这些一系列频率 为整数倍的正弦波,就称为非正弦周期波的谐波。其中频率与非正弦周期波相同的正弦波,
第9章
非正弦交流电路
学习指导与题解
一、基 本 要 求
1.建立几个频率为整数倍的正弦波可以合成为一非正弦周期的概念。明确一个非正弦 周期波可以分解为一系列频率为整数倍正弦波之和的概念(即谐波分析) 、谐波中的基波与 高次谐波的含义。了解谐波分析中傅里叶级数的应用。 2.掌握波形对称性与所含谐波分量的关系。能根据波形的特点判断所含谐波的情况。 了解波形原点选择对所含谐波的影响。 3.掌握非正弦周期电压和电流的平均值(即直流分量)和有效值的计算。能根据给定 波形计算出直流分量。 能根据非正弦周期波的直流分量和各次谐波分量, 计算出它的有效值。 4.掌握运用叠加定理和谐波分析计算非正弦交流电路中的电压和电流的方法。 5.建立同频率的正弦电压和电流才能形成平均功率的概念。掌握运用叠加定理和谐波 分量计算非正弦交流电路中和平均功率。
(8)奇函数且半波重叠
·5·
叠函数。则傅里叶系数中, A0 0 , Ak 0 , Bk 中的 k 为偶数,即 k =2,4,6,…。傅里 叶级数中只含
B
k
sin kt 项的偶次谐波。所以,这类奇函数且半波重叠波,只含正弦函
数的偶次谐波。
图 9-7 偶函数且半波重叠波形举例
图 9-8
奇函数且半波重叠波形举例
·2·
f (t ) 波 形 图
f ( x) 傅里叶级数展开式f (t ) 2 2 2 Am (1 cos 2t cos 4t cos 6t L ) 3 15 35
2
f (t )
1 1 Am (sin t sin 3t sin 5t L ) 3 5
这
类偶函数且奇半波对称对称波,只含余弦函数的奇次谐波。
T f (t ) 波形满足 f (t ) f (t ) 和 f (t ) f (t ) 两个条件。 2 T 如图 9-7 所示, f (t ) 波形对称于纵轴,是偶函数,且移动 与原波形重叠,又是半波重 2
(7)偶函数且半波重叠 叠函数。则傅里叶系数中, Bk 0 , Ak 中 k 为偶函数,即 k =0,2,4,6,…。傅里叶级 数中只含 A0 和
类半波重叠函数,称为偶偕波函数。
·4·
图 9-4
半波重叠函数波形举例
图 9-5
奇函数且半波对称波形举例
(5)奇函数且奇半波对称
若 f (t ) 波形满足 f (t ) f (t ) 和 f (t ) f (t
T ) 两个 2
条件。如图 9-5 所示, f (t ) 波形对称于原点,是奇函数,且移动
(3)奇半波对称函数 若 f (t ) 波形移动半周 ( 件。如图 9-3 所示, f (t ) 波形不对称于纵轴和原点,故它
图 9-2 奇函数举例
不是偶函数和奇函数,只是移动 (
T ) 与原波形对称于 横 2
轴,则傅里叶系数中, A0 0 , Ak 和 Bk 中 k 为奇数,即 k =1,3,5,…。这类非正弦周 期波只含奇次谐波。所以,这类奇半波对称函数 f (t ) ,称为奇谐波函数。 以上是三种对称波形及其谐波分量情况,下面 再介绍半波重叠波和四种双重对称性波形及其谐波 分量情况。 (4)半波重叠函数 若 f (t ) 波形移动半波 (
﹡2。非对称性非正弦周期波谐波分析的简化计算 (1)非对称性非正弦周期波 f (t ) ,可以分解为偶部 f (t ) 和奇部 f (t ) 之和。偶部 f (t ) 是对称于纵轴的偶函数,奇部 f (t ) 是对称于原点的奇函数。即
0
e
0
e
f (t ) f e (t ) f 0 (t ) 1 f e (t ) [ f (t ) f (t )] 2 1 f 0 (t ) [ f (t ) f (t )] 2
(三)关于波形对称性与所含谐波分量的关系 在电工技术中遇到的非正弦周期波,许多具有某种对称性。在对称波形中,傅里叶级 数中,有些谐波分量(包括直流分量。因直流分量是 k 0 的零次谐波分量)不存在。因此,
·3·
利用波形对称性与谐波分量的关系,可以简化傅里叶系数的计算。 1.波形对称性与谐波分量的关系 有如下几个对称性与谐波分量的关系 有如下几个对称性波形及其傅里叶系数情况。 (1)偶函数
T ) 2
与原波形重叠,满足 f (t ) f (t
T ) 条件。如图 9-4 2
所示, f (t ) 不对称于纵轴和原点,故它不是偶函数和 奇函数,只是移动
T 与原波形重叠。则傅里叶系数 2
图 9-3
奇半波对称波形举例
Ak 和 Bk 中 k 为偶数,即 k =0,2,4,6,…。这类非正弦周期波只含偶次谐波。所以,这
