《方差分析多重比较》PPT课件
合集下载
方差分析(ANOVA)PPT参考课件

三、多个样本均数的两两比较
34
2020/1/15
方差分析能说明什么问题?
不拒绝H0,表示拒绝总体均数相等的证据不
足 分析终止
拒绝H0,接受H1, 表示总体均数不全相等
哪两两均数之间相等?哪两 两均数之间不等?
需要进一步作多重比较
35
2020/1/15
能否用T检验呢 当有k个均数需作两两比较时,比较的次数共 有c= = k!/(2!(k-2)!)=k(k-1)/2
18~岁 21.65 20.66
… … 18.82 16 22.07 8.97
30~岁 27.15 28.58
… … 23.93 16 25.94 8.11
45~60岁 20.28 22.88 … … 26.49 16 25.49 27 7.19
2020/1/15
基本步骤
(1)建立假设,确定检验水准
2020/1/15
单因素方差分析 (1) 方差齐性检验
结果分析
2020/1/15
Test of Homogeneity of Variances
no
Levene Statistic 3.216
df1 2
df2 33
Sig. .053
Levene方法检验统计量为3.216,其P值为0.053,可 认为样本所来自的总体满足方差齐性的要求。
方差分析(ANOVA)
1
2020/1/15
n4
n3 n2 n1
Y4
Y3 Y2
Y1
2
2020/1/15
例子:某研究者在某单位工作人员中进行了体重指 数(BMI)抽样调查,随机抽取不同年龄组男性受试 者各16名,测量了被调查者的身高和体重值,由此按 照BMI=体重/身高2公式计算了体重指数,请问,不 同年龄组的体重指数有无差异。
第九章 方差分析ppt课件

SSW/dW f MW S 14.71/5 1 9410 .4111
(3)计算F值。
精选PPT课件
18
(4) 确定显著性水平和F临界值 取α=0.05,查F分布表得 F0.05(3,14) 3.34。由于计
算的F=3.52> F0.05(3,14) 3.34,P<0.05,所以拒绝原假
设,接受备择假设,认为各组平均数中至少有一对不
精选PPT课件
25
计算自由度: dBfk 14 13;
dW fk n k4 5 4 1;6
df T df B df W =16+3=19
求均方:
MS B
SS B df B
370122.3 3
,
MSW
SSW dfW
35622.25 16
(3)计算F值:
FMBS12.325.50 MW S 22.25
1、提出假设 2、计算平方和与自由度 3、计算F值 4、确定显著性水平并查F临界值表 5、列方差分析总表
精选PPT课件
3
一、方差分析的逻辑思想
1、方差分析是一种综合的检验方法
方差分析是对引起方差变化的各种因 素进行统计分析,检验引起各样本差异 的主要原因(或因素),并与理论值比 较,以判断其显著性。
首先将总体变异分解成样本组间变异 和由抽样误差等其它原因产生的组内变 异,然后分析变异各组成部分的关系。
如果样本组间变异比抽样误差等其它 原因产生的变异显著地大,则认为样本 组间有本质性的差异,否则,认为样本 组间无本质差异。
精选PPT课件
6
在方差分析中,观测值之间的差异情 况用离差平方和表示,符号为SS。方差分析首先 是把总体平方和分解为组间平方和和组内平方和, 即:
(3)计算F值。
精选PPT课件
18
(4) 确定显著性水平和F临界值 取α=0.05,查F分布表得 F0.05(3,14) 3.34。由于计
算的F=3.52> F0.05(3,14) 3.34,P<0.05,所以拒绝原假
设,接受备择假设,认为各组平均数中至少有一对不
精选PPT课件
25
计算自由度: dBfk 14 13;
dW fk n k4 5 4 1;6
df T df B df W =16+3=19
求均方:
MS B
SS B df B
370122.3 3
,
MSW
SSW dfW
35622.25 16
(3)计算F值:
FMBS12.325.50 MW S 22.25
1、提出假设 2、计算平方和与自由度 3、计算F值 4、确定显著性水平并查F临界值表 5、列方差分析总表
精选PPT课件
3
一、方差分析的逻辑思想
1、方差分析是一种综合的检验方法
方差分析是对引起方差变化的各种因 素进行统计分析,检验引起各样本差异 的主要原因(或因素),并与理论值比 较,以判断其显著性。
首先将总体变异分解成样本组间变异 和由抽样误差等其它原因产生的组内变 异,然后分析变异各组成部分的关系。
如果样本组间变异比抽样误差等其它 原因产生的变异显著地大,则认为样本 组间有本质性的差异,否则,认为样本 组间无本质差异。
精选PPT课件
6
在方差分析中,观测值之间的差异情 况用离差平方和表示,符号为SS。方差分析首先 是把总体平方和分解为组间平方和和组内平方和, 即:
第三讲-方差分析与多重比较-

比值越小,两者越接近,即处理间的差异
与处理内的差异差不多,说明处理间差异不
显著。反之,差异显著。
F 通过查F表判断: dft(1) dfe(2)
F> F0.05=? F0.01=?
F> > F0.01 p<< 0.01
例1:将4个不同药厂生产的阿司匹林片用崩解仪 法进行片剂释放度的测定,每个样品进行5次实验, 以释放63%所需时间的对数值作为指标问4个药 厂生产的片剂释放度是否有差异?
方差分析可以帮助我们掌握客观 规律的主要矛盾或技术关键,是科学 研究工作的一个十分重要的工具。
二、方差分析的基本原理
• 重复数相等的几个均数的比较
符号:
nn knk knn k k
xxiijj xxijij x为ij 表中所有观测数据之和
ii11 jij111 jii111j1j1
作用:检验多个总体均值是否相等
• 在前面讲了两个样本平均数差异 显著性检验,所用的一般为t检验。 • t检验可判断两组数据平均数的差 异显著性。
• 而方差分析可以同时判断多组数 据平均数(样本≥3)之间的差异显著性。
当然,在多组数据的平均数之间做比较 时,可以在平均数的所有对之间做t检验。但 这样做会提高工作量和显著水平的概率,因 而是不可取的。
1.10 0.57 0.77 0.88 0.83 6.178 1.787 2.971 3.914 14.85
解: dfT=kn-1=4×5-1=19
dft=k-1=4-1=3 dfe=dfT-dft=19-3=16
n nnk kn1 i
nk kn
( x(
ij11 ji11
xjikj 1ij(xixj))2i 2nxi1n)12jjikkn11 ((ijxknk1x11ij(jikxj 1iijj(xx)i2xjxx )ii ))2x22 )i2ni1nnkk1 iijnjnkkk1111(((x(xxixiijij xxx))2)222x)2
单因素方差分析与多重比较课件

通过比较组间方差和组内方差,可以 判断各组平均值是否存在显著差异。
方差分析的步骤
1. 收集数据
收集每个组的观测值,并确保数据满足独立性、正态性和 同方差性。
2. 数据整理
整理数据,将观测值按照组别进行分类和汇总。
3. 计算离差平方和
计算每个组的离差平方和,即每个组内观测值与组平均值 的差的平方和。
详细描述
Duncan法是一种非参数检验方法,它不需要假设数据服从正态分布,因此适用范围更广。该方法通 过多级分类的方式,将各组均值进行排序和比较,能够更全面地了解各组之间的差异情况。Duncan 法的优点在于简单易行,但缺点是对于极端值的敏感度较高。
S-N-K法
总结词
基于秩和的方法
详细描述
S-N-K法(Studentized Range Distribution)是一种基于秩和的方法,它通过对各组秩次进行统计分析,判 断各组均值是否存在显著差异。该方法能够避免极端值对结果的影响,并且对于非正态分布的数据也有较好的 适用性。S-N-K法的优点在于稳健性和可靠性较高,但缺点是计算较为复杂。
否存在显著差异。
随着数据量的增长,单因素方 差分析与多重比较在数据分析 和科学研究中具有越来越重要
的地位。
课程目标
1
掌握单因素方差分析的基本原理和计算方法。
2
理解多重比较的意义和作用,掌握常用的多重比 较方法。
3
学会在实际问题中应用单因素方差分析与多重比 较,提高数据分析能力。
02
单因素方差分析基本概念
单因素方差分析与多重比 较课件
目录
• 引言 • 单因素方差分析基本概念 • 单因素方差分析的数学模型 • 多重比较方法 • 单因素方差分析的应用实例 • 课程总结与展望
方差分析的步骤
1. 收集数据
收集每个组的观测值,并确保数据满足独立性、正态性和 同方差性。
2. 数据整理
整理数据,将观测值按照组别进行分类和汇总。
3. 计算离差平方和
计算每个组的离差平方和,即每个组内观测值与组平均值 的差的平方和。
详细描述
Duncan法是一种非参数检验方法,它不需要假设数据服从正态分布,因此适用范围更广。该方法通 过多级分类的方式,将各组均值进行排序和比较,能够更全面地了解各组之间的差异情况。Duncan 法的优点在于简单易行,但缺点是对于极端值的敏感度较高。
S-N-K法
总结词
基于秩和的方法
详细描述
S-N-K法(Studentized Range Distribution)是一种基于秩和的方法,它通过对各组秩次进行统计分析,判 断各组均值是否存在显著差异。该方法能够避免极端值对结果的影响,并且对于非正态分布的数据也有较好的 适用性。S-N-K法的优点在于稳健性和可靠性较高,但缺点是计算较为复杂。
否存在显著差异。
随着数据量的增长,单因素方 差分析与多重比较在数据分析 和科学研究中具有越来越重要
的地位。
课程目标
1
掌握单因素方差分析的基本原理和计算方法。
2
理解多重比较的意义和作用,掌握常用的多重比 较方法。
3
学会在实际问题中应用单因素方差分析与多重比 较,提高数据分析能力。
02
单因素方差分析基本概念
单因素方差分析与多重比 较课件
目录
• 引言 • 单因素方差分析基本概念 • 单因素方差分析的数学模型 • 多重比较方法 • 单因素方差分析的应用实例 • 课程总结与展望
生物统计学各处理重复数不等的方差分析课件PPT
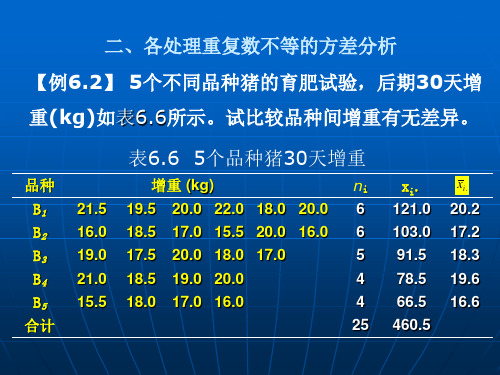
表6.16 表6.15资料各处理组合平均数的LSR值(新复极差测验)
表6.16 表6.14资料各处理组合平均数的新复极差测验
② 各肥类平均数的比较:肥类间的F测验极显著。求得肥类 平均数的标准误:
故有各肥类平均数的LSR 值表6.17,显著性测验结果表6.18 。
表6.17 表6.14资料肥类平均数的LSR值
二、各处理重复肥试验,后期30天增
重(kg)如表6.6所示。试比较品种间增重有无差异。 表6.6 5个品种猪30天增重
品种 增重 (kg) ni 6 6 5
B1
B2 B3
21.5
16.0 19.0
19.5
18.5 17.5
20.0 22.0 18.0 20.0
ix表665个品种猪30天增重1计算各项平方和与自由度2列出方差分析表进行f检验变异来源平方和自由度均方f值值f临界值显著性品种间465041163599f005420287f001420443品种内388420194总变异8534表675个品种育肥猪增重方差分析表3多重比较因为各处理重复数不等应先计算出平均重复次数n0根据dfe20秩次距k2345从附表6中查出005与001的临界ssr值乘以063即得各最小显著极差所得结果列于表68xs表68ssr值及lsr值表将各平均数差数与表68中相应的最小显著极差比较作出推断
(1) 自由度和平方和的分解 根据上表,将各项变异来源的自由度填于表6.15。以下 分解平方和,求得:
(2) F 测验
将上述结果录于表6.15, 求得肥类×土类间的F=4.81/0.928 =5.18>F0.01; 求得肥类间的F=89.69/0.928=96.65>F 0.01; 求得土类间的F=1.98/0.928=2.13<F0.05。 所以该试验肥类×土类的互作和肥类的效应间差异都是 极显著的,而土类间无显著差异。
表6.16 表6.14资料各处理组合平均数的新复极差测验
② 各肥类平均数的比较:肥类间的F测验极显著。求得肥类 平均数的标准误:
故有各肥类平均数的LSR 值表6.17,显著性测验结果表6.18 。
表6.17 表6.14资料肥类平均数的LSR值
二、各处理重复肥试验,后期30天增
重(kg)如表6.6所示。试比较品种间增重有无差异。 表6.6 5个品种猪30天增重
品种 增重 (kg) ni 6 6 5
B1
B2 B3
21.5
16.0 19.0
19.5
18.5 17.5
20.0 22.0 18.0 20.0
ix表665个品种猪30天增重1计算各项平方和与自由度2列出方差分析表进行f检验变异来源平方和自由度均方f值值f临界值显著性品种间465041163599f005420287f001420443品种内388420194总变异8534表675个品种育肥猪增重方差分析表3多重比较因为各处理重复数不等应先计算出平均重复次数n0根据dfe20秩次距k2345从附表6中查出005与001的临界ssr值乘以063即得各最小显著极差所得结果列于表68xs表68ssr值及lsr值表将各平均数差数与表68中相应的最小显著极差比较作出推断
(1) 自由度和平方和的分解 根据上表,将各项变异来源的自由度填于表6.15。以下 分解平方和,求得:
(2) F 测验
将上述结果录于表6.15, 求得肥类×土类间的F=4.81/0.928 =5.18>F0.01; 求得肥类间的F=89.69/0.928=96.65>F 0.01; 求得土类间的F=1.98/0.928=2.13<F0.05。 所以该试验肥类×土类的互作和肥类的效应间差异都是 极显著的,而土类间无显著差异。
chapter6方差分析PPT课件

总均方一般不等于处理间均方加处理内均方。
.
24
某B水iosta产tisti研cs 究所为了比较四种不同配合饲料 对鱼的饲喂效果,选取了条件基本相同的鱼 20尾,随机分成四组,投喂不同饲料,经一 个月试验以后,各组鱼的增重结果列于下表。
.
25
Biostatistics
这是一个单因素试验,处理数k=4,重复数 n=5。各项平方和及自由度计算如下:
(xij xi.)分别eij是μ、(μi-.
14
Biostatistics
告诉我们:
( 每个观或x测ij 值 都i),包故含k处nx理i个j 效观xi.应测(值μ的i-总μ或变异可)x分i.,解与为x.误处. 差理
间的变异和处理内的变异两部分。
.
在单因素试验结果的方差分析中,无效假设
为H0:μ1=μ2=…=μk,备择假设为HA:各μi不 全相等,或H0 :2 =0,H A2 : ≠0;
F=MSt/MSe,也就是要判断处理间均方是否
显著大于处理内(误差)均方。
如果结论是肯定的,我们将否定H0;反之,不 否定H0。
.
33
Biostatistics
次的处理间变异,称为处理间平方和,记为SSt,
即
k
SSt n (xi.x..)2
i1
.
18
式B中ios,tatisticsk n (为xij 各 xi处.)2 理内离均差平方和之和,
i1 j1
反映了各处理内的变异即误差,称为处理内平方
和或误差平方和,记为SSe,即
于是有
kn
SSe
(xij xi.)2
Biostatistics
第六章 方差分析 analysis of variance(ANOVA)
第三章_单因素方差分析与多重比较

SSA
ni
k
xi x 2 ni xi x 2
i1 j1
i 1
前例的计算结果:SSA = 1456.608696
3 - 29
统计分析 软件应用
构造检验的统计量
(计算误项平方和 SSE)
1. 每个水平或组的各样本数据与其组平均值的离差
平方和
2. 反映每个样本各观察值的离散状况,又称组内平
统计分析 软件应用
构造检验的统计量
(计算全部观察值的总均值)
1. 全部观察值的总和除以观察值的总个数 2. 计算公式为
k ni
k
xij
ni xi
x i1 j1 i1
n
n
式中:n n1 n2 nk
3 - 26
统计分析 软件应用
构造检验的统计量
(例题分析)
统计分析 软件应用
方差分析中基本假定
如果原假设成立,即H0: m1 = m2 = m3 = m4
四个行业被投诉次数的均值都相等 意味着每个样本都来自均值为、方差为2的同一
正态总体
f(X)
3 - 17
X
1 2 3 4
统计分析 软件应用
方差分析中基本假定
若备择假设成立,即H1: mi (i=1,2,3,4)不全相
3. 组间方差(between groups) 因素的不同水平(不同总体)下各样本之间的方差 比如,四个行业被投诉次数之间的方差 组间方差既包括随机误差,也包括系统误差
3 - 13
统计分析 方差分析的基本思想和原理
软件应用
(方差的比较)
1. 若不同不同行业对投诉次数没有影响,则组间误差中只包
ni
k
xi x 2 ni xi x 2
i1 j1
i 1
前例的计算结果:SSA = 1456.608696
3 - 29
统计分析 软件应用
构造检验的统计量
(计算误项平方和 SSE)
1. 每个水平或组的各样本数据与其组平均值的离差
平方和
2. 反映每个样本各观察值的离散状况,又称组内平
统计分析 软件应用
构造检验的统计量
(计算全部观察值的总均值)
1. 全部观察值的总和除以观察值的总个数 2. 计算公式为
k ni
k
xij
ni xi
x i1 j1 i1
n
n
式中:n n1 n2 nk
3 - 26
统计分析 软件应用
构造检验的统计量
(例题分析)
统计分析 软件应用
方差分析中基本假定
如果原假设成立,即H0: m1 = m2 = m3 = m4
四个行业被投诉次数的均值都相等 意味着每个样本都来自均值为、方差为2的同一
正态总体
f(X)
3 - 17
X
1 2 3 4
统计分析 软件应用
方差分析中基本假定
若备择假设成立,即H1: mi (i=1,2,3,4)不全相
3. 组间方差(between groups) 因素的不同水平(不同总体)下各样本之间的方差 比如,四个行业被投诉次数之间的方差 组间方差既包括随机误差,也包括系统误差
3 - 13
统计分析 方差分析的基本思想和原理
软件应用
(方差的比较)
1. 若不同不同行业对投诉次数没有影响,则组间误差中只包
第五章方差分析144页PPT

较同需时估没计有一充个分利S用xi 资xj 料,所故提使供得的各信次息比而较使误误差差的估估计计的不精统确一,
性降低,从而降低检验的灵敏性。
上一张 下一张 主 页 退 出
例如,试验有5个处理 ,每个处理 重复 6次,共有30个 观测值。进行t检验时,每次只能利用两个处理共12个观 测值估计试验误差 ,误差自由度为 2(6-1)=10 ;若利 用整个试验的30个观测值估计试验误差 ,显然估计的精 确性高,且误差自由度为5(6-1)=25。可见,在用t检 法进行检验时 ,由 于估计误差的精确性低,误差自由度
方差分析实质上是关于观测值变异原因的数量分析。
上一张 下一张 主 页 退 出
1 方差分析的基本原理与步骤
1.1 线性模型与基本假定
假设某单因素试验有k个处理,每个处理有n 次重复,共有nk个观测值。试验资料的数据模式 如表5-1所示。
上一张 下一张 主 页 退 出
表5-1 k个处理每个处理有n个观测值的数据模式
用 t 检验,须采用方差分析法。
上一张 下一张 主 f variance) 是由英国统计学家
R.A.Fisher于1923年提出的。
方差分析是将k个处理的观测值作为一个整体 看待,把观测值总变异的偏差平方和及自由度分解 为相应于不同变异来源的偏差平方和及自由度,进 而获得不同变异来源的总体方差估计值;由总体方 差估计值构造F统计量,计算F值,检验各样本所属 总体平均数是否相等。
束,即
n
(xi
j
xi.
)
0(i=1,2,…,k。故处理内自
j1
由度为资料中观测值的总个数减k,即kn-k 。
处理内自由度记为dfe,
dfe=kn-k=k(n-1)
性降低,从而降低检验的灵敏性。
上一张 下一张 主 页 退 出
例如,试验有5个处理 ,每个处理 重复 6次,共有30个 观测值。进行t检验时,每次只能利用两个处理共12个观 测值估计试验误差 ,误差自由度为 2(6-1)=10 ;若利 用整个试验的30个观测值估计试验误差 ,显然估计的精 确性高,且误差自由度为5(6-1)=25。可见,在用t检 法进行检验时 ,由 于估计误差的精确性低,误差自由度
方差分析实质上是关于观测值变异原因的数量分析。
上一张 下一张 主 页 退 出
1 方差分析的基本原理与步骤
1.1 线性模型与基本假定
假设某单因素试验有k个处理,每个处理有n 次重复,共有nk个观测值。试验资料的数据模式 如表5-1所示。
上一张 下一张 主 页 退 出
表5-1 k个处理每个处理有n个观测值的数据模式
用 t 检验,须采用方差分析法。
上一张 下一张 主 f variance) 是由英国统计学家
R.A.Fisher于1923年提出的。
方差分析是将k个处理的观测值作为一个整体 看待,把观测值总变异的偏差平方和及自由度分解 为相应于不同变异来源的偏差平方和及自由度,进 而获得不同变异来源的总体方差估计值;由总体方 差估计值构造F统计量,计算F值,检验各样本所属 总体平均数是否相等。
束,即
n
(xi
j
xi.
)
0(i=1,2,…,k。故处理内自
j1
由度为资料中观测值的总个数减k,即kn-k 。
处理内自由度记为dfe,
dfe=kn-k=k(n-1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 方差分析
第一节 单因素方差分析 第二节 两两间多重比较的检验方法 第三节 两因素试验的方差分析
1
第二节 单因素方差分析
例7.1 为研究中药三棱、莪木对肿瘤重 量的影响,以便选定最佳抑癌作用剂量。 今先将一批小白鼠致癌,然后再随机分 成四组(每组10只)分别实施三种剂量 的药物注射及适量的生理盐水注射,经 过相同的实验期之后,测定四组鼠的肿 瘤重量。
2
第二节 单因素方差分析
H0 : 1 2 3 4 ;
H1
:
不全相等
j
方差分析:单因素方差分析
SUMMARY
组
计数
生理盐水A1 10.00
剂量A2 10.00
剂量A3 10.00
剂量A4 10.00
求和 46.60 25.00 24.60 18.70
平均 4.66 2.50 2.46 1.87
8
一、Tukey方法(Student-NewmanKeuls,SNK)
各个水平下进行的试验次数相同:m
1.提出假设
H0 : i j (i, j 1, 2,
,k,i j)
H1
:
H
不成立
0
2.根据检验水平α及因素水平个数k和n-k, 查附表18(P296),得临界值qα( k,n-k),计算:
23
生理盐水A1 2.79 3.11 1.77 2.83 2.69 3.47 2.44 2.52
24
例7.6
水层RNA组A2 3.15 3.97 2.87 4.70 2.03 5.09
酚层RNA组A3 4.92 3.47 3.77 4.26
SAS -建立数据集,求各组均值、标准差
25
SAS -正态性检验+方差齐性检验+方差分析
1与3没有显著性差异 | t1,3 | 2.0715=3
6
第三节 两两间多重比较的检验方法
多重比较从功能上分为两类: a.任何两个均数之间都要进行比较。 b.多个试验组均数之间不比较,但需要将
各试验组分别与同一对照组均数比较。
7
第三节 两两间多重比较的检验方法
具体的方法有很多,各方法的区别就在于控制的误差类型不同。被控制的误差可分 为几种类型: (1)仅控制每作一次比较犯I类错误的概率,简称为控制“比较误差率” (comparison-wise error rate,CER) 。如:T法,LSD法,DUNCAN法; (2)控制分析本资料所作的全部比较的总误差,即犯I类错误的总概率,简称为 “实验误差率” (experiment-wise error rate,EER) 。如:SNK法(即q检 验); (3)控制类似研究条件下分析各批实验结果所作的全部比较或在全部无效假设和 部分无效假设之下得出的最大实验误差率,简称为控制“最大实验误差率”。如: BON法,SIDAK法,CHEFFE法,TUKEY法,GT2法或称SUM法,GABRIEL法, REGWQ法,REGWF法,DUNNETT法。
32
SAS -(2)对秩进行方差分析和多重比较
33
SS 45.09 41.65
df 3.00 36.00
12 总计 86.74 39.00
MS 15.03 1.16
F P-value F crit 12.99 0.00 2.87
例7.5-多重比较
H012 : 1 2
H
23 0
:
2
3
H013 : 1 3
H
24 0
: 2
4
k 4 m 10
H014 : 1 4
剂量A2 10 2.5 0.9
剂量A3 10 2.5 1.4
剂量A4 10 1.9 1.3
H0 : i j (i, j 1, 2, , k, i j)
4
第三节 两两间多重比较的检验方法
n 平均值
方差
生理盐水A1 10 4.7 1.0
剂量A2 10 2.5 0.9
剂量A3 10 2.5 1.4
皮质醇增多症 2.70 4.08 2.81 4.30 2.92 4.30 3.59 5.96 3.86 6.62
29
SAS -秩和检验
30
SAS -两两比较的秩和检验
(1)将数据转换成秩; (2)对秩进行方差分析,等价于秩和检验; (3)对秩进行多重比较,等价于两两比较的 秩和检验。
31
SAS -(1)求秩
H
34 0
: 3
4
3.79 3.84 q (4, 40 4) 3.84 40 30 (36 30) 3.810
q0.05 (4, 30) 3.84 q0.05 (4, 40) 3.79
30
36
40
13
例7.5-多重比较
T0.05 q0.05 (4, 36)
MSE 3.810 m
11 Tij S (k 1, n k) MSE ( ni nj ) 若 | xi x j,|认Tij为μi与μj的差异有统计学意义,反之, 认为差异无统计学意义。
15
SAS
1.建立数据集- 增加分组变量 2.求各组均值等统计量 3.正态性检验 4.方差齐性检验 5.方差分析
16
SAS -建立数据集,求各组均值、标准差
17
SAS -正态性检验+方差齐性检验+方差分析
18
SAS-方差分析结果
19
SAS -多重比较
20
SAS-多重比较SNK法
21
SAS-多重比较SNK法
22
例7.6
用小鼠研究正常肝核糖核酸(RNA)对 癌细胞的生物学作用。试验分为对照组 (生理盐水)、水层RNA组和酚层 RNA组。分别用此三种处理方式诱导肝 癌细胞的果糖二磷酸脂酶(FDP酶)活 力。试比较3组均数两两间是否有显著 差异。
j1 k
(nj 1)
j1
10
例7.5
例7.1 为研究中药三棱、莪木对肿瘤重 量的影响,以便选定最佳抑癌作用剂量。 今先将一批小白鼠致癌,然后再随机分 成四组(每组10只)分别实施三种剂量 的药物注射及适量的生理盐水注射,经 过相同的实验期之后,测定四组鼠的肿 瘤重量。
11
例7.5-方差分析
H0 : 1 2 3 4 ;
剂量A4 10 1.9 1.3
P(一次检验犯一类错误)=0.05
P(6次检验中至少犯1次一类错误)
=1-P(6次检验中没有犯1次一类错误)
1 (1)C42 1 0.956 0.2649
5
第三节 两两间多重比较的检验方法
x1 1.0 x2 2.0 x3 2.2
n1 9 n2 9 n3 9
26
SAS-方差分析结果
27
SAS -多重比较
28
§6.6 非参数检验-秩和检验
例6.24 判断三种不同人群的血浆总皮质醇测 定有无差别?
正常人 0.11 0.86 0.52 1.02 0.61 1.08 0.69 1.27 0.77 1.92
单纯性肥胖 0.17 1.13 0.33 1.38 0.55 1.63 0.66 2.04 0.86 3.75
1.16 1.298 10
4.70 4.80 q0.01(4, 36) 4.80 40 30 (36 30) 4.76
1.16
T0.01 4.76
1.621 10
n 平均值
生理盐水A1 剂量A2 剂量A3
10
10
10
4.7
2.5
2.5
剂量A4 10 1.9
14
二、S方法
各个水平下进行的试验次数不相同 根据检验水平α及k-1和N-k, 查附表19(P299),得临界值Sα,计算Tij值:
s12 0.7 s22 0.63 s32 2.31
t
xi x j
( xi x j )
(ni 1)si2 (nj 1)s2j 1 1
si2
s
2 j
ni nj 2
ni nj
n
成组t检验结果: 1与2有显著性差异 | t1,2 | 2.160<1233 2与3没有显著性差异 | t2,3 | 0.324=583
H1
:
不SUMMARY
组
计数
生理盐水A1 10.00
剂量A2 10.00
剂量A3 10.00
剂量A4 10.00
求和 46.60 25.00 24.60 18.70
平均 4.66 2.50 2.46 1.87
方差 1.02 0.87 1.40 1.34
方差分析 差异源 组间 组内
方差 1.02 0.87 1.40 1.34
方差分析 差异源 组间 组内
SS 45.09 41.65
df 3.00 36.00
3 总计 86.74 39.00
MS 15.03 1.16
F P-value F crit 12.99 0.00 2.87
第三节 两两间多重比较的检验方法
n 平均值
方差
生理盐水A1 10 4.7 1.0
T q (k, n k)
MSE m
3.若 | xi x ,j |认T为μi与μj的差异有统计学意义,反之, 认为差异无统计学意义。
9
一、Tukey方法(Student-NewmanKeuls,SNK)
T q (k, n k)
MSE m
| xi x j | T
k
(nj
1)
S
2 j
MSE
第一节 单因素方差分析 第二节 两两间多重比较的检验方法 第三节 两因素试验的方差分析
1
第二节 单因素方差分析
例7.1 为研究中药三棱、莪木对肿瘤重 量的影响,以便选定最佳抑癌作用剂量。 今先将一批小白鼠致癌,然后再随机分 成四组(每组10只)分别实施三种剂量 的药物注射及适量的生理盐水注射,经 过相同的实验期之后,测定四组鼠的肿 瘤重量。
2
第二节 单因素方差分析
H0 : 1 2 3 4 ;
H1
:
不全相等
j
方差分析:单因素方差分析
SUMMARY
组
计数
生理盐水A1 10.00
剂量A2 10.00
剂量A3 10.00
剂量A4 10.00
求和 46.60 25.00 24.60 18.70
平均 4.66 2.50 2.46 1.87
8
一、Tukey方法(Student-NewmanKeuls,SNK)
各个水平下进行的试验次数相同:m
1.提出假设
H0 : i j (i, j 1, 2,
,k,i j)
H1
:
H
不成立
0
2.根据检验水平α及因素水平个数k和n-k, 查附表18(P296),得临界值qα( k,n-k),计算:
23
生理盐水A1 2.79 3.11 1.77 2.83 2.69 3.47 2.44 2.52
24
例7.6
水层RNA组A2 3.15 3.97 2.87 4.70 2.03 5.09
酚层RNA组A3 4.92 3.47 3.77 4.26
SAS -建立数据集,求各组均值、标准差
25
SAS -正态性检验+方差齐性检验+方差分析
1与3没有显著性差异 | t1,3 | 2.0715=3
6
第三节 两两间多重比较的检验方法
多重比较从功能上分为两类: a.任何两个均数之间都要进行比较。 b.多个试验组均数之间不比较,但需要将
各试验组分别与同一对照组均数比较。
7
第三节 两两间多重比较的检验方法
具体的方法有很多,各方法的区别就在于控制的误差类型不同。被控制的误差可分 为几种类型: (1)仅控制每作一次比较犯I类错误的概率,简称为控制“比较误差率” (comparison-wise error rate,CER) 。如:T法,LSD法,DUNCAN法; (2)控制分析本资料所作的全部比较的总误差,即犯I类错误的总概率,简称为 “实验误差率” (experiment-wise error rate,EER) 。如:SNK法(即q检 验); (3)控制类似研究条件下分析各批实验结果所作的全部比较或在全部无效假设和 部分无效假设之下得出的最大实验误差率,简称为控制“最大实验误差率”。如: BON法,SIDAK法,CHEFFE法,TUKEY法,GT2法或称SUM法,GABRIEL法, REGWQ法,REGWF法,DUNNETT法。
32
SAS -(2)对秩进行方差分析和多重比较
33
SS 45.09 41.65
df 3.00 36.00
12 总计 86.74 39.00
MS 15.03 1.16
F P-value F crit 12.99 0.00 2.87
例7.5-多重比较
H012 : 1 2
H
23 0
:
2
3
H013 : 1 3
H
24 0
: 2
4
k 4 m 10
H014 : 1 4
剂量A2 10 2.5 0.9
剂量A3 10 2.5 1.4
剂量A4 10 1.9 1.3
H0 : i j (i, j 1, 2, , k, i j)
4
第三节 两两间多重比较的检验方法
n 平均值
方差
生理盐水A1 10 4.7 1.0
剂量A2 10 2.5 0.9
剂量A3 10 2.5 1.4
皮质醇增多症 2.70 4.08 2.81 4.30 2.92 4.30 3.59 5.96 3.86 6.62
29
SAS -秩和检验
30
SAS -两两比较的秩和检验
(1)将数据转换成秩; (2)对秩进行方差分析,等价于秩和检验; (3)对秩进行多重比较,等价于两两比较的 秩和检验。
31
SAS -(1)求秩
H
34 0
: 3
4
3.79 3.84 q (4, 40 4) 3.84 40 30 (36 30) 3.810
q0.05 (4, 30) 3.84 q0.05 (4, 40) 3.79
30
36
40
13
例7.5-多重比较
T0.05 q0.05 (4, 36)
MSE 3.810 m
11 Tij S (k 1, n k) MSE ( ni nj ) 若 | xi x j,|认Tij为μi与μj的差异有统计学意义,反之, 认为差异无统计学意义。
15
SAS
1.建立数据集- 增加分组变量 2.求各组均值等统计量 3.正态性检验 4.方差齐性检验 5.方差分析
16
SAS -建立数据集,求各组均值、标准差
17
SAS -正态性检验+方差齐性检验+方差分析
18
SAS-方差分析结果
19
SAS -多重比较
20
SAS-多重比较SNK法
21
SAS-多重比较SNK法
22
例7.6
用小鼠研究正常肝核糖核酸(RNA)对 癌细胞的生物学作用。试验分为对照组 (生理盐水)、水层RNA组和酚层 RNA组。分别用此三种处理方式诱导肝 癌细胞的果糖二磷酸脂酶(FDP酶)活 力。试比较3组均数两两间是否有显著 差异。
j1 k
(nj 1)
j1
10
例7.5
例7.1 为研究中药三棱、莪木对肿瘤重 量的影响,以便选定最佳抑癌作用剂量。 今先将一批小白鼠致癌,然后再随机分 成四组(每组10只)分别实施三种剂量 的药物注射及适量的生理盐水注射,经 过相同的实验期之后,测定四组鼠的肿 瘤重量。
11
例7.5-方差分析
H0 : 1 2 3 4 ;
剂量A4 10 1.9 1.3
P(一次检验犯一类错误)=0.05
P(6次检验中至少犯1次一类错误)
=1-P(6次检验中没有犯1次一类错误)
1 (1)C42 1 0.956 0.2649
5
第三节 两两间多重比较的检验方法
x1 1.0 x2 2.0 x3 2.2
n1 9 n2 9 n3 9
26
SAS-方差分析结果
27
SAS -多重比较
28
§6.6 非参数检验-秩和检验
例6.24 判断三种不同人群的血浆总皮质醇测 定有无差别?
正常人 0.11 0.86 0.52 1.02 0.61 1.08 0.69 1.27 0.77 1.92
单纯性肥胖 0.17 1.13 0.33 1.38 0.55 1.63 0.66 2.04 0.86 3.75
1.16 1.298 10
4.70 4.80 q0.01(4, 36) 4.80 40 30 (36 30) 4.76
1.16
T0.01 4.76
1.621 10
n 平均值
生理盐水A1 剂量A2 剂量A3
10
10
10
4.7
2.5
2.5
剂量A4 10 1.9
14
二、S方法
各个水平下进行的试验次数不相同 根据检验水平α及k-1和N-k, 查附表19(P299),得临界值Sα,计算Tij值:
s12 0.7 s22 0.63 s32 2.31
t
xi x j
( xi x j )
(ni 1)si2 (nj 1)s2j 1 1
si2
s
2 j
ni nj 2
ni nj
n
成组t检验结果: 1与2有显著性差异 | t1,2 | 2.160<1233 2与3没有显著性差异 | t2,3 | 0.324=583
H1
:
不SUMMARY
组
计数
生理盐水A1 10.00
剂量A2 10.00
剂量A3 10.00
剂量A4 10.00
求和 46.60 25.00 24.60 18.70
平均 4.66 2.50 2.46 1.87
方差 1.02 0.87 1.40 1.34
方差分析 差异源 组间 组内
方差 1.02 0.87 1.40 1.34
方差分析 差异源 组间 组内
SS 45.09 41.65
df 3.00 36.00
3 总计 86.74 39.00
MS 15.03 1.16
F P-value F crit 12.99 0.00 2.87
第三节 两两间多重比较的检验方法
n 平均值
方差
生理盐水A1 10 4.7 1.0
T q (k, n k)
MSE m
3.若 | xi x ,j |认T为μi与μj的差异有统计学意义,反之, 认为差异无统计学意义。
9
一、Tukey方法(Student-NewmanKeuls,SNK)
T q (k, n k)
MSE m
| xi x j | T
k
(nj
1)
S
2 j
MSE
