上海大学2011-2012第二学期数值方法试卷(A含答案)
2011-2012学年第二学期高等数学试题 (A)含答案

2011-2012学年第二学期高等数学试题 (A)一、填空题(共4小题,每题4分,共16分)1. 积分222y x dx e dy -⎰⎰的值等于 。
2. 若级数1n n u ∞=∑的部分和序列为21n nS n =+,则1n n u ∞=∑= 。
3. 设向量x 与向量23a i j k =-+ 平行,且满足方程7a x ⋅= ,则x= 。
4.2z ds Γ⎰= ,其中Γ是球面2222x y z R ++=与平面0x y z ++=的交线。
二、选择题(共4小题,每题4分,共16分)1. 设()()()(),x yx yu x y x y x y t dt ϕϕψ+-=++-+⎰,其中函数ϕ具有二阶连续导数,ψ具有一阶导数,则必有 。
(A) 2222u u x y ∂∂=∂∂; (B) 2222u ux y ∂∂=-∂∂; (C) 222u u x y y ∂∂=∂∂∂; (D)222u u x y x ∂∂=∂∂∂2. 曲面222x z y =+平行于平面220x y z +-=的切平面方程为 。
(A) 2230x y z +--=; (B) 30x y z +--=; (C)330x y z +--=; (D) 23230x y z +--=3. 设D 是由曲线sin y x =与x 轴上自0x =至2x π=的线段所围成的有界闭区域,(),f x y 在D 上连续,积分(),Df x y d σ⎰⎰与()()2sin 001,,xdx f x y dy π⎰⎰()()()sin 2sin 002,,,xx dx f x y dy dx f x y dy πππ-⎰⎰⎰⎰()()()1arcsin 02arcsin 0arcsin 1arcsin 3,,,yyyy dy f x y dx dy f x y dx πππ-+--+⎰⎰⎰⎰()()()1arcsin 02arcsin 0arcsin 1arcsin 4,,yyyydy f x y dx dy f x y dx πππ---++⎰⎰⎰⎰相等的是 。
11学年第二学期大学数学2试卷(A卷)-参考答案
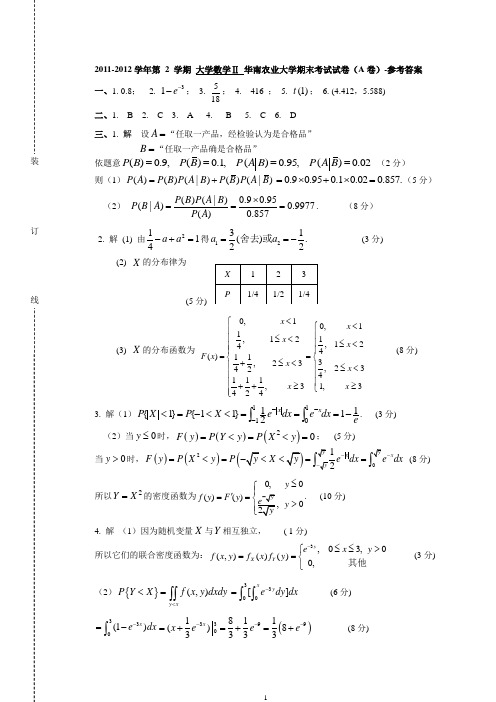
2011-2012学年第 2 学期 大学数学Ⅱ 华南农业大学期末考试试卷(A 卷)-参考答案 一、1. 0.8; 2. 31e --; 3. 518; 4. 416 ; 5. )1(t ; 6. (4.412,5.588) 二、1. B 2. C 3. A 4. B 5. C 6. D 三、1. 解 设A =“任取一产品,经检验认为是合格品” B =“任取一产品确是合格品” 依题意()0.9,()0.1,()0.95,()0.02P B P B P A B P A B ==== (2分) 则(1)()()(|)()(|)P A P B P A B P B P A B =+0.90.950.10.020.857.=⨯+⨯=(5分)(2) ()(|)0.90.95(|)0.9977()0.857P B P A B P B A P A ⨯===. (8分) 2. 解 (1) 由2114a a -+=得1231().22舍去或a a ==- (3分) (2) X 的分布律为 (5分) (3) X 的分布函数为 0,10,111,12,1244()113,23,234241111,3,3424x x x x F x x x x x <⎧<⎧⎪⎪⎪≤<⎪≤<⎪⎪⎪==⎨⎨+≤<⎪⎪≤<⎪⎪⎪⎪≥++≥⎩⎪⎩ (8分)3. 解(1)111011{1}{11}12x x P X P X e dx e dx e ---<=-<<===-⎰⎰. (3分)(2)当0y ≤时,()()()20F y P Y y P X y =<=<=; (5分) 当0y >时,()()(20x x F y P X y P X dx dx --=<=<== (8分)所以2Y X =的密度函数为0,0()()0y f y F y y ≤⎧⎪'==>. (10分)4. 解 (1)因为随机变量X 与Y 相互独立, ( 1分)所以它们的联合密度函数为:3,03,0(,)()()0,y X Y e x y f x y f x f y -⎧≤≤>==⎨⎩其他(3分)(2){}(,)y x P Y X f x y dxdy <<=⎰⎰3300[]x y edy dx -=⎰⎰ (6分) 330(1)x e dx -=-⎰3390181()333xx e e --=+=+()9183e -=+ (8分)(3)解:由密度函数可知~(0,3),~(3)X U Y E (10分) 所以,22(30)311(),(),12439D X D Y -==== (12分) 由X 与Y 相互独立,得3131()()()4936D X Y D X D Y -=+=+= (14分) 四、1. 解 检验假设 20:0.0004H σ=,21:0.0004H σ≠. (1分) 依题意,取统计量:222(1)~(1)n S n χχσ-=-,15n =. (3分) 查表得临界值:220.0252(1)(14)26.1n αχχ-==,220.97512(1)(14) 5.63n αχχ--==, (5分) 计算统计量的观测值得: 22140.02521.8750.0004χ⨯==. (6分) 因2220.9750.025(14)(14)χχχ<<,故接受原假设0H ,即认为总体方差与规定的方差无显著差异. (8分) 2. 解 (1)(2) 解 因为F =5.6681>0.01(3,16) 5.29F =,所以拒绝0H ,即认为不同的贮藏方法对粮食含水率的影响在检验水平0.01α=下有统计意义. (8分)3. 解 2.10=x ,239=y (2分)6.252.10101066221012=⨯-=-=∑=x n x l i i xx (3分)6622392.101025040101=⨯⨯-=-=∑=y x n y x l i i i xy (4分)故1662ˆ25.8625.6xy xx l l β==≈;01ˆˆ23925.8610.224.77y x ββ=-=-⨯=- (6分) 因此所求回归直线方程为 ˆ24.7725.86y x =-+ (8分)。
上海大学数学试题及答案

上海大学数学试题及答案一、选择题(每题4分,共20分)1. 下列哪个选项是正确的?A. \( \sqrt{2} \)是有理数B. \( \sqrt{2} \)是无理数C. \( \sqrt{2} \)是整数D. \( \sqrt{2} \)是复数答案:B2. 函数 \( f(x) = x^2 \) 在区间 \( (0, +\infty) \) 上是:A. 增函数B. 减函数C. 常函数D. 非单调函数答案:A3. 以下哪个数列是等差数列?A. \( 1, 2, 4, 8, \ldots \)B. \( 2, 4, 6, 8, \ldots \)C. \( 1, 1, 1, 1, \ldots \)D. \( 3, 5, 7, 9, \ldots \)答案:D4. 圆的面积公式是:A. \( \pi r^2 \)B. \( \frac{1}{2} \pi r^2 \)C. \( \pi r \)D. \( 2\pi r \)答案:A5. 以下哪个选项是矩阵?A. 一个二维数组B. 一个一维数组C. 一个三维数组D. 一个四维数组答案:A二、填空题(每题4分,共20分)1. 圆周率 \( \pi \) 的近似值是 ________。
答案:3.141592. 函数 \( y = \sin(x) \) 的周期是 ________。
答案:\( 2\pi \)3. 矩阵 \( A \) 和 \( B \) 的乘积记作 ________。
答案:\( AB \)4. 欧拉公式 \( e^{ix} = \cos(x) + i\sin(x) \) 中的 \( i \) 代表 ________。
答案:虚数单位5. 勾股定理表明在一个直角三角形中,斜边的平方等于两直角边的平方和,即 \( a^2 + b^2 = ________ \)。
答案:\( c^2 \)三、解答题(每题30分,共60分)1. 证明函数 \( f(x) = x^3 - 3x \) 在 \( x = 1 \) 处取得极值,并求出该极值。
2011-2012(2)期末考试试卷(A)(高等数学)

u(x,
y)
,
f
,
可导,且
(u)
1,
g
连续,
y
证明: g( y)
z x
g(x)
z y
0
第 1 页(共 1 页)
1. xoy 平面上的曲线 x y 2 1 绕 x 轴旋转一周所得旋转曲面方程为____ 。
2.
若
1
dx
1
xf
(
y)dy
1,
则
1 f (1 x)dx
0
0
0
。
3. 曲面 z e z 2xy 3 在点(1,2,0) 处的一个法线向量与oy 轴正向的夹角成钝角,则它与ox 轴正 向夹角的余弦cos ______。
。 。
二、解答下列各题(每小题 8 分,,总计 80 分)
1.
求过两直线 பைடு நூலகம்1
:
x2
y 2
z 1 1
与
l
2
:
x 1 2
y 0
z
2 1
的平面方程,并求两直线的夹角。
2.
设u
f (x 2 , xy, x
y) ,
f
具有连续的二阶偏导,求
u x
,
2u xy
。
3.
求曲线
2
x2 3x 2
3y2 y
z 2
9. 求 y 2 y 3y (2x 1)e x 的通解。
10. 设 f (x) 可导,且 f ( ) 1 ,又 y(sin x f (x)) dx f (x)dy 在右半平面与路径无关,求 f (x) 。
L
x
三 证明题(本题 8 分)
设 z f (u),由u (u)
11-12-2高等数学下(通信、电子本科)A卷及标准答案

2011 - 2012学年第二学期期末考试《高等数学(下)》试卷(A)答卷说明:1、本试卷共6页,四个大题,满分 100分,120分钟完卷。
2、闭卷考试。
3、适用班级:11级通信系、电子系本科各班题号-一--二二三四总分分数评阅人: ____________ 总分人: __________________________、单项选择题(共 10小题,每小题3分,共30分)。
【A 】设有直线L : 口 =丄二二2及平面二:2x y =1,则直线L1 -2 1(A)平行于二 (B) 在二内 (C)垂直于二 (D) 与二斜交【D 】2.锥面z立体在xoy 面的投影为[A l 4.函数z = f (x, y)在点(x 0, y 0)处可微分,则函数在该点1 1【C 】5.将二次积分pdx. f(x,y)dy 转化成先对x ,后对y 的二次积分为(A)必连续 (C)必有极值(D)(B)偏导数必存在且连续偏导数不一定存在(A) (x -1)2 y 2=1 (B) (x-1)2 y 2 乞 1(C)z= 0,(x -1)2y 2 -1(D)z =0,(x_1)2y 2 _1【C 3.设函数z 二z(x, y)由方程e z = e + xyz 确定,则一z的值为(1,0,1)(A) d(B)e (C)(D)11 1 x( A )°dy y f(x, y)dx(B)°dy 0f(x,y)dx( C )1 y0dy 0f(x,y)dx(D) 1 10dy 0f(x,y)dx【D] 6.设L为圆周x22y =1(逆时针方向),则口L(x y)dx (3y -2x)dy( A 3 二(B) 2 二(C) 4 二(D) -3':【D】7.下列级数中,收敛的级数是001(A) ----------- (B)n4 . 2n 1f (3n4 2n(C)1 nn4 1 * n2(D)nm n ■ 1°°(x _1)n 【B] 8.幕级数a(x n丿■的收敛域为心n3n(A) ( -2, 4) (B)[-2,4)(C)[-2,4](D)(-2, 4]【C】9.微分方程y - y = 0满足初始条件y l x出=2的特解为(A) y =e x1( B)xy = e 2x x(C) y = 2e (D) y = e【B] 10.具有特解y1.x .x二e , y2 二xe的二阶常系数齐次线性微分方程是(A) y -2y y = 0(B)y 2y y = 0(C) y y - 2y = 0(D)y - y 2y = 0得分|二、填空题(共5小题,每小题3分,共15分)1. 设两点A(1,2,1)及B (2,1,3),则| AB | = | AB | = •、6 _;向量AB与z轴的夹角为,r则方向余弦COS ;* = ____ . COS f = ----32. 设z = y x,则dz=_dz = y x In yd^xy x^dy.3. 函数f(x, y) =x2y — y2在点P(1,1)处方向导数的最大值为_T5 _____________ .4. 设L是连接(1,0)及(0,1)两点的直线段,则[(x + y)ds=_J2 _______________ .15.函数 展开成X 的幕级数为3 x1.已知曲面Z =x 2 ・y 2-2上一点M (2,1,3),⑴ 求曲面在M 点处的一个法向量;(2) 求曲面在M 点处的切平面及法线方程•2.求函数 f (x, y) = 2(x 「y)「x 2「y 2 的极值.2 2 2 23.平面薄片的面密度为」(x,y)=x y 1,所占的闭区域 D 为圆周x y =1及坐标轴所围成的第一象限部分,求该平面薄片的质量.4.利用高斯公式计算曲面积分(3z 2x)dydz - (y 3 -2xz)dxdz - (3x 2z)dxdy ,其中Z为上半球面z = a 2 -x 2 - y 2及平面z = 0所围立体的整个边界曲面的外侧5.设曲线通过原点,且曲线上任一点 M (x, y)处的切线斜率等于 x - y ,求该曲线的方程.6. 求微分方程y -3y ,2y =e x 的通解.3n7. 判断级数v (-1)n °半是否收敛?如果收敛,是绝对收敛还是条件收敛?心 4四、综合应用题(共2小题,共13分,其中第1题6分,第2题7分).1. (6分)要用钢板造一个体积为4( m 3)长方体无盖容器,应如何选择容器的尺寸,使n 1n z03nx , -3 ::三、计算题(共7小题,每小题6分,共42分)得用料最省?》 2 * 》2. (7分)设在xoy平面有一变力F(x, y) =(x • y2) i (2x^8) j构成力场,(1)证明质点在此力场中移动时,场力所作的功与路径无关 ;(2)计算质点从点 A(1,0)移动到点《高等数学(下)》试卷(A) 第5页 共6页B(2,1)时场力所作的功(1)|ABH<6; COS 63x(2) dz = y Inydx xy x_l dy、2「¥x n ,—3»3n £3三.计算题(每小题6分,共42分).1.(6 分)(1)由 z = x 2y 2 -2 得,Z x =2x,Z y =2y ,曲面在点M (2,1,3)处的一个法n=(-4, -2,1))2分)⑵ 在点M (2,1,3)的切平面方程为4(x-2),2(y-1)-(z-3) =04x 2y-z -7 -0选择题每小题3分共30分)..填空题(每小题3分,共15分).... (2 分) 法x y 42分)线z -3 -1A 二 f xx (1,—1) = —2,B 二 f xy (1,—1) = °,C 二 f yy (1, — 1) = -2,则2AC - B=4 ° , A :: ° , .................................................................................. (2 分)所 以 (-1 为 极 大 值 点 , 极 大 值f (1,—1) =2 ............................................................. (2 分) 3.(6分)平 面 薄 片的 质M 二 J(x, y )dxdy 二(x 2 y 2 1)dxdy .......................... ( 2 分)DD1 o2dr C 1)Z ° - °v/【丄加丄詩彳二3二 ................................ (2分)2 4 2 84.(6 分)所围空间区域 门={( x, y, z ) |0 _ z _ a 2-X 2 - y 2} 由高斯公式,有原式r "耳◎迅)dv0 ex oy cz!!! (3z 2 3y 2 3x 2)dv ............................. ( 2 分)Q2 a=3茁 2sin 「d 「r 2 r 2dr ................................. ( 2 分)0 - 0 02.(6 分)f x =2_2x, f y =-2—2yf x 二 0,占八(2 分)y=°,(2 分)(-1 xy丑1 6=3 2二[-cos J: [ r5]0 a5......................... ( 2 分)5 55.(6分)设所求曲线为y = y(x),由题意得,y = x- y , y(0) = 0,该方程为一阶线性微分方程y・y=x, 其中P( x) 1 Q, x ........................... x .......................... ( 2 分)_p(x)dx |P(x)dx _|dx f dx故通解为y = e [ e Q(x)dx C] =e [ xe dx C] [xe x dx C]二e ▲ (xe x _ e x C)二Ce」x -1(2 分)2分)从而Q(x)二-x,特解y - -xe x, (2 分)y(0)=0 从而所求曲线为6.(6 分)对应的齐次方程y”-3y、2y=0的特征方程为r2-3r•2=0,得特征根则对应的齐次方程的y =C1e x C2e2x2分)对于非齐次方程y ” -3y: 2y二e x, ' =1为r2-3r *2=0的单根,P(x) =1,设其* y特解为y -Q(x)e x,其中Q(x)=ax, a为待定系数,Q(x)满足Q (x) (2' p)Q(x)二P(x)0 (2 1 _3)(a) =17.(6分)由于》(一1)n 4 3n4ny 二C^x C2e2x_xe x.而|im 加=lim匸匕=丄 , 贝U (—2卑1 )收y u n F 4n 4 心4n 敛,................................... ( 3 分)3n从而'•(_ ni i3n )也收敛,且为绝对收心4n敛. ....................................... (3分)四、综合应用题(共2小题,共13分,其中第1题6分,第2题7分).41.(6分)设该容器的长,宽,高为x, y,z,由题意知xyz=4,则z ,容器的表面积xy4 8 8A = xy 2yz 2xz = xy 2(x y) xy , x 0, y 0xy x y分)( 2 分)因实际问题存在最小值,且驻点唯一,所以当x二y = 2( m), z = 1( m)时,容器的表面积最小,从而用料最省. .....................................................................(1分)2.(7 分)证明:(1)P(x, y)=x y2, Q(x, y) = 2xy-8,由于在xoy面内,—=2y Q恒成立,且P连续,® ex cy ex2分)故质点在该力场中移动时场力所作的功与路径无关. ................................... (4分)⑵质点从点A(1,0)移动到点B(2,1)时场力所作的功(与路径无关),路径L可取折线段A > C,C > B,其中点C(2,0),从而(2,1) * (2,1)W F dr Pdx Qdy%,。
11-12数值分析报告材料试A卷答案详解

上海海事大学2011---2012学年第 2 学期 研究生 数值分析 课程考试试卷A (答案)学生姓名: 学号: 专业:一.填空题(每小格2分共30分)1. 利用Jacobi 迭代法求解Ax=b 时,其迭代矩阵是)(1U L D B J +=-;当系数矩阵A 满足 严格对角占优 时,Jacobi 迭代法收敛 。
x 0 1 2 42. 已知函数)(x f 有数据f 1 9 23 3 则其3次Lagrange插值多式的基函数)(0x l 为147878123+-+-x x x 插值余项为 )4)(2)(1(!4)()4(---x x x x f ξ3. 求解常微分方程初值问题⎩⎨⎧=≤≤=η)(),,('a y bx a y x f y的Euler 公式为),(1i i i i y x hf y y +=+, 它是1 阶方法。
4. 设,1457)(348++-=x x x x f 则差商=]5,...,5,5[810f 7 =]2,...2,2[910f 05. 对于求解Ax=b ,如果右端有b δ的扰动存在而引起解的误差为x δ,则相对误差≤xxδ bbA C o n d δ)(6. Gauss 型数值求积公式)()(0i bani ix f Adx x f ⎰∑=≈的代数精度具有2n+1___次,求积系数的表达式为i A =⎰bai dx x l )(2,且=∑=ni iAb-a7. 幂法是求矩阵 按模最大 特征值和特征向量的计算方法.Jacobi 法是计算 实对称矩阵的所有 特征值和特征向量的计算方法8. 对于给定的正数k ,Newton 法解二次方程02=-k x 的迭代公式为)(21)()(1nn n n n n x kx x f x f x x +='-=+ 二.设函数42)(x x f =,已知188)(244+-=x x x T ,试利用切比雪夫多项式最小零偏差的性质,求函数)(x f 在区间[-1,1]上的次数低于4的最佳一致逼近。
数学_2011-2012学年上海市某校高三(下)联考数学试卷(文科)_(含答案)

2011-2012学年上海市某校高三(下)联考数学试卷(文科)一、填空题(本大题每题4分,满分56分)1. 平面直角坐标系xOy 中,O 为坐标原点,A(1, 2),B(−1, 3),则OA →⋅AB →=________. 2. 复数2+i 1−i的虚部为________.3. 函数y =√3cos2x −sin2x 的最小正周期为________.4. 直线x −2y +1=0关于y 轴对称的直线方程为________.5. 定义集合运算:A ∗B ={z|z =xy, x ∈A, y ∈B}.设A ={1, 2},B ={4, 6},则集合A ∗B 的所有元素之和为________.6. 从集合{1, 2, 3, 4, 5}中任取两数,其乘积大于10的概率为________.7. 若实数a 、b 、m 满足2a =5b =m ,且2a +1b =2,则m 的值为________.8. 若对于任意实数x ,都有x 4=a 0+a 1(x +2)+a 2(x +2)2+a 3(x +2)3+a 4(x +2)4,则a 3的值为________.9. 设等差数列{a n }的公差d 为−2,前n 项和为S n ,则lim n →∞a n2−n 2S n=________.10. 函数y =arcsin 12(x 2+1)的值域为________.11. 与直线x +y −2=0和圆x 2+y 2−12x −12y +70=0都相切的半径最小的圆的标准方程为________.12. 已知S 、A 、B 、C 是球O 表面上的点,SA ⊥平面ABC ,AB ⊥BC ,SA =1,AB =BC =2,则球O 的表面积为________.13. 如果一个正四位数的千位数a 、百位数b 、十位数c 和个位数d 满足关系(a −b)(c −d)<0,则称其为“彩虹四位数”,例如2012就是一个“彩虹四位数”.那么,正四位数中“彩虹四位数”的个数为________.(直接用数字作答)14. 某校数学课外小组在坐标纸上,为一块空地设计植树方案如下:第k 棵树种植在点P k (x k , y k )处,其中x 1=1,y 1=1,当k ≥2时,{x k =x k−1+1−4[T(k−14)−T(k−24)]y k =y k−1+T(k−14)−T(k−24),T(a)表示非负实数a 的整数部分,例如T(3.7)=3,T(0.4)=0.按此方案,在第2012棵树的种植点坐标应为________.二、选择题(本大题每题5分,满分20分)15. “|x|>3成立”是“x(x −3)>0成立”的( )A 充分非必要条件B 必要非充分条件C 充要条件D 非充分非必要条件 16. 已知向量a →、b →满足|a →|=1,|b →|=2,a →与b →的夹角为120∘,则|a →−2b →|等于( ) A 3 B √15 C √21 D 517. 函数y =f(x +1)为定义在R 上的偶函数,且当x ≥1时,f(x)=2x −1,则下列写法正确的是( )A f(13)<f(32)<f(23) B f(23)<f(13)<f(32) C f(23)<f(32)<f(13) D f(32)<f(23)<f(13)18. 椭圆x 24+y 23=1上有n 个不同的点:P 1,P 2,P n ,椭圆的右焦点为F ,数列{|P n F|}是公差大于1100的等差数列,则n 的最大值为( ) A 199 B 200 C 198 D 201三、解答题(本大题74分)19. 在△ABC 中,tanA =23,tanB =15.(1)求角C 的大小;(2)如果△ABC 的最大边长为√13,求最小的边长.20.如图所示,在长方体ABCD −A 1B 1C 1D 1中,AB =1,BC =2,CC 1=5,M 为棱CC 1上一点.(1)若C 1M =32,求异面直线A 1M 和C 1D 1所成角的正切值; (2)若C 1M =1,试证明:BM ⊥平面A 1B 1M .21. 设数列{a n }的前n 项和为S n ,已知a 1=a ,a n+1=2S n +4n ,n ∈N ∗. (1)设b n =S n −4n ,求数列{b n }的通项公式;(2)若对于一切n ∈N ∗,都有a n+1≥a n 恒成立,求a 的取值范围.22. 若函数f(x)定义域为R ,满足对任意x 1,x 2∈R ,有f(x 1+x 2)≤f(x 1)+f(x 2),则称f(x)为“V 形函数”.(1)当f(x)=x 2时,判断f(x)是否为V 形函数,并说明理由; (2)当f(x)=lg(x 2+2)时,证明:f(x)是V 形函数;(3)当f(x)=lg(2x +a)时,若f(x)为V 形函数,求实数a 的取值范围.23. 设C 1是以F 为焦点的抛物线y 2=2px(p >0),C 2是以直线2x −√3y =0与2x +√3y =0为渐近线,以(0,√7)为一个焦点的双曲线.(1)求双曲线C 2的标准方程;(2)若C 1与C 2在第一象限内有两个公共点A 和B ,求p 的取值范围,并求FA →⋅FB →的最大值;(3)是否存在正数p,使得此时△FAB的重心G恰好在双曲线C2的渐近线上?如果存在,求出p的值;如果不存在,说明理由.2011-2012学年上海市某校高三(下)联考数学试卷(文科)答案1. 02. 323. π4. x+2y−1=05. 306. 7157. 2√5.8. −89. −310. [π6, π2 ]11. (x−3)2+(y−3)2=812. 9π13. 364514. (4, 503)15. A16. C17. C18. B19. 解:(1)∵ tanA=23,tanB=15,∴ tan(A+B)=tanA+tanB1−tanAtanB=23+151−23×15=1,∵ C=π−(A+B),∴ tanC=−tan(A+B)=−1.' 又∵ 0<C<π,∴ C=3π4.(2)∵ C=3π4>π2,∴ AB边最大,即AB=√13,又∵ tanA>tanB,A,B∈(0, π2),所以B为最小角,AC边为最小边.∵ {tanB=sinBcosB=15cos2B+sin2B=1且B∈(0, π2),∴ sinB=√2626(舍负).由ABsinC =ACsinB,得AC=ABsinBsinC=√22˙=1.因此,最小的边AC=1.20. 解:(1)连接A1M、B1M∵ 长方体ABCD−A1B1C1D1中,A1B1 // C1D1,∴ ∠B1A1M或其补角即为异面直线A1M和C1D1所成角∵ A1B1⊥平面BB1C1C,B1M⊆平面BB1C1C,∴ A1B1⊥B1M Rt△B1C1M中,B1M=√B1C12+B1M2=52∴ Rt△A1B1M中,tan∠B1A1M=B1MA1B1=52即异面直线A1M和C1D1所成角的正切值等于52;(2)∵ Rt△B1C1M中,C1M=1,B1C1=2且Rt△BCM中,CM=4,BC=2∴ BCC1M =CMB1C1=2,结合∠MC1B1=∠BCM=90∘∴ Rt△B1C1M∽Rt△MCB,可得∠BMC=∠MB1C1=90∘−∠B1MC1.∴ ∠BMC+∠B1MC1=90∘,得BM⊥B1M又∵ A1B1⊥平面BB1C1C,BM⊆平面BB1C1C,∴ A1B1⊥BM∵ A1B1、B1M是平面A1B1M内的相交直线∴ BM⊥平面A1B1M.21. 解:(1)依题意,S n+1−S n=a n+1=2S n+4n,即S n+1=3S n+4n,设b n=S n−4n,则b n+1=S n+1−4n+1∴ b n+1=3b n,∵ b1=S1−4=a−4∴数列{b n}的通项公式为b n=(a−4)×3n−1,n∈N∗.①(2)由①知S n=4n+(a−4)×3n−1,于是,当n≥2时,a n=S n−S n−1=4n+(a−4)×3n−1−[4n−1+(a−4)×3n−2]=3×4n−1+2(a−4)3n−2,a n+1−a n=9×4n−1+4(a−4)×3n−2,当n≥2时,a n+1≥a n等价于9×4n−1+4(a−4)×3n−2≥0∴ 36×(43)n−2+4(a−4)≥0∴ a≥−5.由S n+1=3S n+4n,得S2=3S1+4=3a+4,即a2=2a+4故当n=1时,a2−a1=a+4≥0即a≥−4综上,所求的a的取值范围是[−4, +∞).22. 解:(1)当f(x)=x2时,f(x1+x2)=x12+x22+2x1x2,f(x1)+f(x2)=x12+x22,当x 1,x 2同号时,f(x 1+x 2)≥f(x 1)+f(x 2),不满足V 形函数的定义, 故当f(x)=x 2时,f(x)不是V 形函数;(2)当f(x)=lg(x 2+2)时f(x 1+x 2)=lg[(x 1+x 2)2+2]=lg(x 12+x 22+2x 1x 2+2),f(x 1)+f(x 2)=lg(x 12+2)+lg(x 22+2)=lg[2(x 12+x 22)+x 12x 22+4]∴ 满足对任意x 1,x 2∈R ,有f(x 1+x 2)≤f(x 1)+f(x 2),则f(x)=lg(x 2+2)为“V 形函数”.(3)当f(x)=lg(2x +a)时,若f(x)为V 形函数 则f(x 1+x 2)≤f(x 1)+f(x 2),即lg(2x 1+x 2+a)≤lg(2x 1+a)+lg(2x 2+a)=lg[2x 1+x 2+a(2x 1+x 2)+a 2] ∴ a(2x 1+x 2)+a 2−a ≥0对任意x 1,x 2∈R 恒成立当a =0时,成立,当a <0时不成立,当a >0时,a ≥(1−2x 1+x 2)max ∴ a ≥1或a =023. 因为一个焦点是(0,√7),故焦点在y 轴上,于是可设双曲线C 2的方程为y 2a 2−x 2b 2=1(a >0, b >0)∵ C 2是以直线2x −√3y =0与2x +√3y =0为渐近线, ∴ ab =√3∵ a 2+b 2=7 ∴ a =2,b =√3 ∴ 双曲线方程为y 24−x 23=1;抛物线y 2=2px(p >0)的焦点F(p2, 0),与双曲线方程联立消y 得:4x 2−6px +12=0 ∵ C 1与C 2在第一象限内有两个公共点A 和B ,∴ △>0,∴ p >4√33设A(m, n)、B(e, f),则FA →⋅FB →=(m −p 2, n)⋅(e −p 2, f)=me −(m +e)×p 2+p 24+nf =me −(m +e)×p2+p 24+2p √me由方程知me =3,m +e =3p2代入得FA →⋅FB →=−p 22+2√3p +3=−12(p −2√3)2+9,函数的对称轴为p =2√3 ∵ p >4√33,∴ p =2√3时,FA →⋅FB →的最大值为9;由(2)知△FAB 的重心G(2p 3, n+f 3)∵ n +f =√2pm +√2pe =√3p 2+4√3p ∴ G(2p3, √3p 2+4√3p3)假设G 恰好在双曲线C 2的渐近线上,则2×2p 3−√3×√3p 2+4√3p3=0,∴ 7p 2=12√3p∴ p =0或p =12√37∵ p >4√33,∴ p =12√37∴ 存在正数p =12√37,使得此时△FAB 的重心G 恰好在双曲线C 2的渐近线上.。
2011-2012学年冬季学期《概率论与数理统计A》试卷-A参考答案

2) P( −1 < X < 2) = ∫ 2e
1
2
−2( x −1)
dx = F (2) − F ( −1) = 1 − e 。
( 2 分)
x − 1500 = 1.875 ∈ W , 200 / 25
(2 分)
结论:拒绝原假设,接受备选假设,即认为新工艺确实提高了产品的寿命。 (2 分)
⎧0, 3) FY ( y ) = ⎨ ⎩ P(ln X < y ),
上海大学 2011~2012 学年冬季学期试卷(A 卷) 绩 课程名: 概率论与数理统计 A 课程号: 学分: 5
6、已知随机事件 A 和 B 的概率分别为 P( A) = 0.7 和 P( B ) = 0.5 ,且这两个事件独立,那
么, P( B − A) = P( B ) − P( AB ) = 0.5 − 0.35 = 0.15 。 应试人声明: 我保证遵守《上海大学学生手册》中的《上海大学考场规则》 ,如有考试违纪、作 弊行为,愿意接受《上海大学学生考试违纪、作弊行为界定及处分规定》的纪律处分。 7、设随机变量 X 服从区间 [0,1] 上的均匀分布,则随机变量 Y = e X 的数学期望 应试人 应试人学号 应试人所在院系 1 1 1 1 EY = ∫ e x dx = e − 1 ;方差 DY = ∫ e 2 x dx − ( EY ) 2 = (e 2 − 1) − (e − 1) 2 = (e − 1)(3 − e) 。 2 2 0 0 题号 一 二 三 四 五 得分 5 8、把 5 只球随机放入三个盒中,则每个盒子中至少有一球的概率为 1 − 得分 评卷人 一.是非题(每小题 2 分,5 题共 10 分) 9 、设 X 1 ,K, X 10 是来自总体 X ~ N ( μ , σ 2 ) 的简单样本,当常数 c = 1、 事件 A 与 B 互不相容, 若 A 不发生, 那么 B 一定发生。 2、 事件 A U B 表示事件 “ A 与 B 都没有发生” 。 ( 错)
上海大学数值分析历届考题

数值分析历届考题03-04学年秋季学期一.简答题(每小题5分)1. 数值计算中要注意哪些问题。
答:第一、两个相近的数应避免相减。
第二、绝对值很小的数应避免作除数。
第三、注意选取适当的算法减少运算次数。
第四、两个绝对值相差很大的数运算时,注意“机器零”的问题。
第五、注意算法的收敛性和稳定性。
2. 用迭代法求解非线性方程0)(=x f 时,迭代收敛的条件是什么,可以用什么方法来确定初值0x 。
答:对于非线性方程0)(=x f (其迭代格式为)(x g x =),如果满足: (1) 当],[b a x ∈时,],[)(b a x g ∈;(2) )(x g '在],[b a 上连续,且对任意的],[b a x ∈都有1)(<≤L x g 。
则有结论:对任意给定的],[0b a x ∈,由迭代格式)(1k k x g x =+,k=0,1,2,…产生的序列{}k x 收敛于*x ,即迭代收敛。
可以用二分法来确定初值0x 。
3. 用消元法求解线性方程组时,为什么要选主元。
答: 因为用简单高斯消元法求得的近似解与精确解相差甚远,其主要原因是绝对值很小的数作除数,导致了误差的快速增长。
为了避免这种情况的发生,我们可以通过行交换,在需要消元的列中,取绝对值最大者作为主对角线元素(即主元),计算效果将得到改善。
4. 矩阵的条件数是什么,它对求解线性方程组有什么影响。
答:对于n 阶可逆方阵A ,正实数||A ||||1-A ||称为A 的条件数,记为cond(A)。
条件数对于线性方程组Ax=b 的影响如下:bb A cond xx∆≤∆)(,其中b ∆为A 精确时b 产生的误差;AAA cond x x ∆≤∆)( ,其中A ∆为b 精确时A 产生的误差。
5. 把下列二阶常微分方程的初值问题⎪⎩⎪⎨⎧='=-=-+'--''2)0(,1)0(1111y y x y x y x x y 化为一阶常微分方程组,并写出求解该方程的改进Euler 方法。
2011-2012_2_期末试卷A

2011 —2012 学年第二学期考试统一用答题册考试课程复变函数与积分变换A 班级学号姓名成绩2012 年 6 月 7 日(试题共5页)一、选择题(每题3分,共27分) 1.当ii z -+=11时,5075100z z z ++的值等于( ) (A )i (B )i - (C )1 (D )1- 2.00)Re()Re(lim0z z z z z z --→( )(A )等于i (B )等于i - (C )等于0 (D )不存在 3.设C 为椭圆19422=+y x 正向,则积分⎰C z z d 1= ( )(A )i π2 (B )π (C )0 (D )i π2-4. 设c 为正向圆周21=z ,则=--⎰z z z z cd )1(21cos3 ( )(A )12-ie π (B )0 (C )ie π2 (D )ie π2- 5.设0=z 为函数zz zz sin sin -的m 级极点,那么=m ( )(A )4 (B )3 (C)2 (D )1 6.设c 为正向圆周1=z ,则⎰Czdz=( ) (A )2i π (B )2π (C )-2i π (D )-2π 7.若幂级数∑∞=0n n nz c在i z 21+=处收敛,该级数在i z +=2处的敛散性为( )(A )绝对收敛 (B )条件收敛 (C )发散 (D )不能确定 8.在下列函数中,0]0),([Re =z f s 的是( )(A ) 21)(ze zf z -= (B )z z z z f 1sin )(-= (C )z z z z f cos sin )(+=(D) ze zf z111)(--= 9. 设,)(2itet f -= 则)(t f 的傅立叶变换为(A ))(2ωπδ (B ))2(2-ωπδ (C ))2(2+ωπδ (D )1 二、 填空题(每题3分,共27分)1.1Re ||<+z z 表示的点集是 区域(说明有界还是无界,单连通还是多连通).2. 函数ix y i x z f 3)1()(33--+=在i z +=1处的导数为 .3. 复数=)3ln cos(i .4. 设c 为从0到i 的直线段,积分=⎰cz z z d sin .5. 已知,32)(23xy x x x,y u +-= 则由u 及其共轭调和函数构成的解析函数f (z ) = u + iv = . 6.级数42sin 2++z z z在0=z 处的泰勒展开式的收敛域是 . 7.函数11sin-z 在1=z 处的留数为 . 8. 函数241)(ωω+=F 的傅立叶逆变换为 .9.函数1)(22+=s s s F 的拉普拉斯逆变换为 .三、(12分)计算积分.d )(|3⎰-c zz z πz e四、(10分)将)1(1)(2+=z z f 在适当的圆环域内展成以i 为心的幂级数。
上海大学2011-2012学年 《高等数学》试题

上海大学2011-2012学年 《高等数学Ⅰ(1)》试题一、填空题(本题共5小题,每小题3分,满分15分). 1、极限10lim(1)xx x →-=1e.2、设ln(y x =(a 为常数),则dy =.3、设10()2()f x x f t dt =+⎰,则()f x =1x -.4、1+∞=⎰2π.5、曲线2323x t t y t t ⎧=-⎨=-⎩在对应于2t =处的切线方程为922y x =-.二、选择题(本题共5小题,每小题3分,满分15分). 1、设函数21()lim1nn xf x x →∞+=+,讨论函数()f x 的间断点,其结论为( B )(A )不存在间断点. (B )存在间断点1x =. (C )存在间断点0x =. (D )存在间断点1x =-. 2、当0x →时,20sin x tdt ⎰是3x 的( B )(A )低阶无穷小. (B )高阶无穷小. (C )等价无穷小. (D )同阶但非等价无穷小. 3、设()f x 在x a =的某个邻域内有定义,则0()()limh f a f a h h→--存在是()f x 在x a =可导的( C )(A )充分条件而非必要条件. (B )必要条件而非充分条件. (C )充分条件且必要条件. (D )既非充分条件又非必要条件.4、设()F x 为()f x 在某一区间I 内的一个原函数,则下列命题不成立的是( B ) (A )(())()df x dx f x dx=⎰. (B )()()F x dx F x C ''=+⎰.(C )()()F x dx F x C '=+⎰. (D )(())()d f x dx f x dx =⎰.5、已知2,01()1,12x x f x x ⎧≤<=⎨≤≤⎩,设1()()(02)x F x f t dt x =≤≤⎰,则()F x 为( D )(A )31,(01)3,(12)x x x x ⎧≤<⎪⎨⎪≤≤⎩. (B )311,(01)33,(12)x x x x ⎧-≤<⎪⎨⎪≤≤⎩. (C )31,(01)31,(12)x x x x ⎧≤<⎪⎨⎪-≤≤⎩. (D )311,(01)331,(12)x x x x ⎧-≤<⎪⎨⎪-≤≤⎩.三、(满分9分)设02ln(1),(0)()1sin ,(0)x t dt x f x x x x ⎧+≥⎪=⎨⎪<⎩⎰,求()f x '.解:当0x ≠时,ln(1),0()112sin cos ,0x x f x x x x x +>⎧⎪'=⎨-<⎪⎩. 当0x =时,0000ln(1)()(0)ln(1)(0)limlim lim 001xx x x t dt f x f x f x x++++→→→+-+'====-⎰, 20001sin()(0)1(0)lim lim lim(sin )00x x x x f x f x f x x x x----→→→-'===⋅=-.即(0)0f '=.综上,有 ln(1),0()112sin cos ,0x x f x x x x x +≥⎧⎪'=⎨-<⎪⎩.四、(满分7分)求011lim 1x x x e →⎛⎫- ⎪-⎝⎭.解:原式200001111limlim lim lim (1)222x x x x x x x x e x e x e x x e x x x →→→→-----=====-五、(满分10分)设()y y x =是由方程1cos 12x y y -+=确定的隐函数,求22d y dx .解:将1cos 12x y y -+=两边同时对x 求导,得11sin 02y y y ''--⋅=,解得:22sin y y '=+,则 2324cos cos (2sin )(2sin )yy y y y y '''=-⋅⋅=-++六、(满分10分)对函数21x y x +=填写下表: 解:定义域为(,0)(0,)-∞+∞,且3422(3),x x y y ++'''=-=.七、(本题共2小题,每小题7分,满分14分)求积分:(1)2arctan xdx x ⎰; (2)22ππ-⎰. 解:(1)22arctan 1arctan 11arctan 1x x dx xd dx x x x x x ⎛⎫=-=-+⋅ ⎪+⎝⎭⎰⎰⎰ 2arctan 11x x dx x x x ⎛⎫=-+- ⎪+⎝⎭⎰ 2arctan 1ln ln(1)2x x x C x =-+-++(2)2202sin xdx xdx πππ-===⎰八、(满分7分)求过点(3,0,1)-且平行于直线240350x z y z +-=⎧⎨+-=⎩的直线方程.解:已知直线的方向向量为:10223013i j ks i j k ==--+.则所求直线方程为:31231x y z -+==--.九、(满分10分)考虑抛物线2y x =(01)x ≤≤,问(1)t 为何值时,图中阴影部分的面积1S 与2S 之和12S S S =+最小? (2)求当S 为最小值时,1S 绕y 轴旋转一周所成的旋转体的体积. 解:(1)设抛物线上点P 坐标为2(,)t t (01)t ≤≤,则3321023tt S t x dx =-=⎰;31222221(1)33tt S x dx t t t =--=-+⎰,332322214133333S t t t t t =+-+=-+.2()42S t t t '=-⇒驻点0,1/2t t ==,()82(0)20,(1/2)20S t t S S ''''''=-⇒=-<=>.即1/2t =为12S SS =+的唯一极小值点,从而也为12S S S =+的最小值点. (2)如图,124032y V dy ππ-==⎰十、(满分5分)设函数()f x 在闭区间[]0,1上可微,对于[]0,1上每一个x ,函数()f x 的值在开区间(0,1)内,且()1f x '≠.证明:在开区间(0,1)内有且仅有一个ξ,使()f ξξ=. 证:令()()F x f x x =-,即证:有且仅有一点(0,1),()0F ξξ∈∍=.(1)先证存在性显然[]()0,1F x C ∈,且(0)(0)00;(1)(1)10F f F f =->=-<. 由零点定理知:至少存在一点(0,1),()0F ξξ∈∍=. (2)再证唯一性(反证法)若不然,设1212(0,1),()()0x x F x F x ∃<∈∍==.由Lagrange 中值定理:至少存在一点12(,)(0,1),()0x x F ηη'∈⊂∍=. 又()1,(0,1)()0,(0,1)f x x F x x ''≠∈⇒≠∈.矛盾! 综上所述,即证!。
2010-2011学年第二学期高等数学试题 (A)含答案

2010-2011学年第二学期高等数学试题 (A)一、填空题(每小题4 分,共20分)1. 设区域D 为1x y +≤,则()22Dxyf xy dxdy +⎰⎰= 。
2. 过点0M (2,4,0)且与直线210:320x z L y z +-=⎧⎨--=⎩平行的直线方程是 。
3. 设有一力22F i j k =-+ ,则F 在a i j k =++方向上的分力为 。
4. 设S 为球面2229x y z ++=的外侧面,则曲面积分Szdxdy ⎰⎰的值是 。
5. 敛域14n n n∞=∑的和为 。
二、选择题(每小题4 分,共20分)1. 设数列{}n a 单调减少,lim 0n n a →∞=,()11,2,nn k k S a n ===∑ 无界,则幂级数()11nn n a x ∞=-∑的收敛域为 。
(A) (1,1]-; (B) [1,1)-; (C) [0,2); (D) (0,2]2. 设()101,2,n a n n≤<= ,则下列级数中肯定收敛的是 。
(A)1n n a ∞=∑; (B)()11nn n a ∞=-∑;(C)1n ∞=; (D)()211nn n a ∞=-∑3. 已知()(),f x f y 在区域(){},1D x y x y =+≤上连续,且()()0,0f x f y >>,则()()()()()Daf y bf x dxdy f x f y +=+⎰⎰(A) a b -; (B)a b +; (C) ()2a b +; (D) ()2a b -;4. 设S 是平面4x y z ++=被圆柱面221x y +=截出的有限部分,则曲面积分Syds⎰⎰的值是 。
(A) 0; (B)(C)(D) ;5. 设Ω是由椭球面2222221x y z a b c ++=围成的区域,则2z dxdydz Ω⎰⎰⎰的值为 。
(A )0; (B)3415abc π; (C)(D) π;三、解答题(1~6题每题8分,第7题12分,共60分)1. 设(),f u v 具有二姐连续偏导数,且满足22221u f fv∂∂+=∂∂, 又()()221,,2g x y f xy x y ⎡⎤=-⎢⎥⎣⎦,求2222g g x y ∂∂+∂∂。
数值分析(2011年12月)A卷

湖南大学研究生课程考试命题专用纸考试科目: 数值分析 (A 卷) 专业年级: 2011级各专业 考试形式: 闭 卷(可用计算器) 考试时间:120分钟……………………………………………………………………………………………………………………… 注:答题(包括填空题、选择题)必须答在专用答卷纸上,否则无效。
一、填空题(每空3分,共30分)(1)利用4位浮点数计算,31.97+(2.457+0135。
2)=( )。
(2) 设1||<<x ,为了使计算更准确,应将计算公式xx y 21111---=等价转化为( )。
(3)用二分法求1)(3-+=x x x f 在区间[0,1]内的唯一根,迭代二步后根所在的区间为( )。
(4)求1)(23--=x x x f 在区间(1,2)内的根,用迭代格式111-=+k k x x ,该迭代格式是收敛还是发散? ( )。
(5)用高斯消元法求解n 阶线性方程组,乘除的运算量为( )。
(6)T x )0,1,2,8(-=,则向量x 的1-范数2||||x =( )。
(7)设⎪⎪⎪⎭⎫ ⎝⎛----=8100212322A ,则矩阵A 的无穷范数1||||A =( )。
(8)设x 为n 维列向量,G 为n 阶矩阵,则迭代格式f Gx xk k +=+)()1(收敛的充分必要条件为( )。
(9)已知2)1(1)(x x f +=在 1.2 1.1, ,0.1 三点的函数值分别为0.2066 0.2268, ,25.0,利用三点数值微分公式近似计算f(x) 在1.1处的导数值)1.1('f ≈( )。
(10) 设5228)(257+++=x x x x f ,则差商=]2,,,2,2[821 f ( )。
二、(10分) 当2,1,0,1-=x时,函数值分别为17,4,3,2)(=x f 求f(x)的三次插值多项式。
三、((10分) 求函数x x f ln )(=在区间[1, 3]的最佳平方逼近一次多项式。
《数值计算方法》试题集及答案资料

《数值计算方法》复习试题一、填空题:1、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=410141014A ,则A 的LU 分解为A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦。
答案:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=15561415014115401411A 3、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L4、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;5、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+6、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );7、计算方法主要研究( 截断 )误差和( 舍入 )误差;8、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );10、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 解线性方程组A x =b 的高斯顺序消元法满足的充要条件为(A 的各阶顺序主子式均不为零)。
12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
数值分析A卷(2011年秋)

三、 (10 分)设 f ( x) 在 [ x0 , x3 ] 上有 5 阶连续导数,且 x0 x1 x2 x3 , (1)试作一个次数不高于 4 次的多项式 H 4 ( x) ,满足条件
H 4 ( x j ) f ( x j ) , j 0,1, 2,3, ' ' H 4 ( x1 ) f ( x1 ) ;
(D)、它不是插值型求积公式。
y f x, y 1、求解常微分方程初值问题 的改进的欧拉法是 y x0 y0
阶方法。 ,其 收 敛 阶
2 、 解 非 线性方程 f x 0 的单根 的牛顿法 格 式为 为 。
4 1 2 2 , x 1 , 则 Ax 3 2 1 1 3 3、设矩阵 A 1 2
(2)写出 E( x) f ( x) H 4 ( x) 的表达式。
四、 (10 分)求 f ( x) e x 在 [0,1] 上的二次最佳平方逼近,权为 1。
3
五、 (10 分)用 n 2, 3 的高斯-勒让德公式计算积分 e x sin xdx
1
六、 (10 分)已知
0 1 2 1 , b , 2 5 8 1 请用 Doolittle 三角分解法求解线性方程组 Ax b 。 1 3 7 7 1 3 9 9
,对于其产生的数列 k 0 , 1, 2 , xk ,下列说法正确的是
(A)、若数列 xk 收敛,则迭代函数 x 唯一; (B)、若对于 x a, b , x 1 ,则 xk 收敛; (C)、若对于 x a, b , x 1 ,则 xk 收敛; (D)、若对于 x a, b , x L 1 ,则 xk 收敛。 3、对矩阵 A 采用幂法迭代,如果该方法收敛,则其收敛速度取决于( (A)、模最大特征值和模次最大特征值的比值; (B)、模最大特征值和模次最大特征值的模的比值; (C)、模次最大特征值和模最大特征值的比值; (D)、模次最大特征值和模最大特征值的模的比值。 ) 。
2011年下学期数值分析考试试卷答案(A)

2011年下学期数值分析考试试卷答案(A)D222223221()()(1)(2)(1)21(45)2P x H x Ax x x x x x x x x =+-=-+-=-+余项为 R(x)=(5)22()(1)(2)5!f x x x ξ-- ……………………………12分解法2:构造带重节点的Newton 差商表 0 0 0 0 0 1 1 1 1 1 1 1 0 -1 2211/2 ………………………8分2222221()00(0)1(0)1(0)(1)(0)(1)21(45)2N x x x x x x x x x x =+-+----+--=-+…………………12分三、 (12分) 求()xf x e -= 在区间[-1,1]上的最佳平方逼近2次多项式. (用勒让德正交多项式2121{(),(),()}{1,,(31)}2P x P x P x x x =-) 解:用勒让德多项式20121{(),(),()}{1,,(31)}2P x P x P x x x =-,2(,)21iiP P i =+ …………………………………………………………………………………..3分计算:11101(,)( 2.3504)x f P e dx e e ---==-≈⎰,1111(,)20.7358x f P xe dx e---==-≈-⎰121211(,)(31)70.143132x f P x e dx e e ---=-=-≈⎰…………………………………………………………………………………..8分111101010011(,)(,)2* 1.1752,*3 1.1036(,)2(,)2/3 f P f P e e e a a e P P P P ----==≈==-=-≈-12222(,)7*0.3578(,)2/5f P e e a P P --==≈故最优平方逼近函数为:11112225351()3(31)22211.1752 1.10360.3758(31)20.5367 1.10360.9963e e e e p x e x x x x x x -----=-+⋅-≈-+⋅-=-+。
复旦大学2011~2012学年《高等数学A下》第二学期期末考试试卷及答案

复旦大学数学科学学院2011~2012学年第二学期期末考试试卷A 卷数学科学学院1.(本题满分42分,每小题7分)计算下列各题: (1)设4yx yx z -+=,求dz 。
(2)求曲线1)32()12(22=+++++y x y x 所围有界区域的面积。
(装 订 线 内 不 要 答 题 )(3)计算三重积分⎰⎰⎰Ω+dxdydz y x )(22,其中Ω为抛物面22y x z +=与平面hz =(0>h )所围的有界闭区域。
(4)计算第一类曲面积分⎰⎰∑dS y 2,其中∑是球面2222a z y x =++(0>a )。
(5)求幂级数∑∞=+1!1n nx n n 的和函数。
(6)求微分方程y x y xdx dy =-4(0>x ,0>y )的通解。
2.(本题满分8分)求函数222),,(z y x z y x f ++=在条件1=++cz by ax 下的最小值,其中a ,b ,c 为常数。
3.(本题满分10分)确定常数λ,使得右半平面}0|),({>x y x 上的向量值函数i r λ)(2),(24y x xy y x +=j λ)(242y x x +-为某二元函数),(y x u 的梯度,并求),(y x u 。
4.(本题满分10分)计算第二类曲面积分⎰⎰∑-+-zxdxdy xydzdx dydz x 48)1(22,其中∑是由Oxy 平面上的曲线2y e x =(10≤≤y )绕x 轴旋转一周而成的旋转曲面,且该曲面的法向量与x 轴正向的夹角不小于2π。
5.(本题满分10分)设)(x y n 是定解问题⎪⎩⎪⎨⎧='==--0)1(,0)1(,122y y x dxdyndx y d x n 的解( ,3,2=n )。
(1)求)(x y n ( ,3,2=n );(2)问级数∑∞=2ln )0(n n n y 是否收敛?请说明理由。
6.(本题满分12分)设πϕ<<0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六、名词解释(共 9 分) (答案仅供参考,允许表述形式不一致) 1. (3 分)迭代法:
答:一般采用迭代法求解方程组,因为迭代法则能保持矩阵的稀疏性,具有计算简单, 编制程序容易的优点,并在许多情况下收敛较快。故能有效地解一些高阶方程组
是一种逐次逼近法,从一个假设解开始,通过一系列的迭代求解,最后产生满足精度要 求的近似解 的方法。如 Jacobi 迭代法,GaussSeidel 迭代法 4. (5 分)写出雅可比迭代法和高斯-赛德尔迭代法的迭代公式,并比较它们的优缺点。(10 2. (3 分)绝对误差 分) 一个准确值与其在运算中的近似值的差,称为绝对误差。 雅可比迭代法: (4 分) n 1 x ( k 1) D 1 (b ( L U ) x ( k ) ) ; 3. (3 分)绝对误差限 xi( k 1) (bi aij x (jk ) ) , 或 aii j 1 绝对误差的绝对值小于等于某个常数 ,该常数称为绝对误差限 j i 高斯-赛德尔迭代法: (4 分)
计算得
命題紙使用說明:1、字迹必須端正,以黑色碳素墨水書寫在框線內,文字與圖均不得剪貼,以保證“掃描”質量; 2、命題紙只作考試(測驗)命題所用,不得移作他用。
第 3 页 (共 3 页)
sin(0.34) L2 (0.34) 0.333336
(注至少保留到小数点四位) 3. (5 分)对于线性方程组 Ax b , 已知 A 是高维稀疏矩阵, 则一般采用什么方法求解?为什 么?
n n 1 (bi aij x (jk 1) aij x (jk ) ) aii j i j i , 或
xi( k 1)
七、简答题(共 23 分): 1. (8 分)试写出数值积分中的梯形公式、辛普森公式、辛普森 3/8 公式和布尔公式,且给出 它们各自的精度值。 设 xk=x0+kh 为等距节点,且 fk=f(xk), 则四个数值积分公式分别为: x1 h 梯形公式精度为 1, 具体公式为: f ( x)dx ( f 0 f1 ) x0 2 x2 h 辛普森公式精度为 3,具体公式为: f ( x)dx ( f 0 4 f1 f 2 ) x0 3 辛普森 3/8 公式精度为 3,具体公式为: f ( x)dx
. .
6. 交换 A 矩阵中第 100 列与第 300 列的内容:A=A(:,[1:99,300,101,299,100,301:end])
(评分标准:程序包含多种变化因素,以下答案仅作参考)
第 2 页 (共 3 页) 1. (7 分)编写 Matlab 程序,用回代法求解上三角线性方程组 AX=B,其中 A 是一个上三角矩 1 1 1 1 ( 2 ) 阵。函数名为 backsub U = 0 1 1 , b 1 function X=backsub(A,B) 0 0 2 6 %Input - A is an n x n upper-triangular nosingular matrix 1 0 0 % - B is an n x 1 matrix %Output - X is the solution to the linear system AX=B L = 1 1 0 %Find the dimension of B and initialize X 2 3 1 n=length(B); 2 X=zeros(n,1); X(n)=B(n)/A(n,n); x= 2 for k=n-1:-1: 1 3 X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k) end 2. (10 分)利用偏序选主元策略的高斯消去法求解下列线性方程组: 2. (5 分)请用 Matlab 语言编写算法,以绘制二维曲线 y x 4 3x 2 2x 6 (如下图所示), 其中 x, y [0,1] ,x 的分辨率为 20 点。 axis([0 1 0 1]); x=linspace(0,1,20); y=inline(‘x.^4+3*x.^2-2*x +6'); plot(x,y(x));
x0 x3
x ( k 1) ( D L) 1 (b Ux( k ) ) ;
其中,D 为 A 的对角线,L 为下三角部分,U 下三角部分为上。 优缺点: (2 分) 雅可比迭代法:公式简单,但收敛速度慢; 高斯-赛德尔迭代法:公式稍繁,但收敛速度快;
3h ( f 0 3 f1 3 f 2 f 3 ) 8
(0,0) , (0.30,0.2955 ) , (0.40,0.3894 )。
请用 Gauss 消元法求线性方程组解 x , 并写出分解过程中的 L (下三角矩阵)和 U (上三角矩 阵,f1), (x2,f2)的二次插值多项式为
L2
( x x0 )( x x1 ) ( x x0 )( x x1 ) ( x x1 )( x x 2 ) f0 f1 f2 ( x0 x1 )( x0 x 2 ) ( x1 x0 )( x1 x 2 ) ( x 2 x0 )( x 2 x1 )
课程名: 数值代数与计算方法 课程号: 08305114 学分: 3
应试人声明: 我保证遵守《上海大学学生手册》中的《上海大学考场规则》 ,如有考试违纪、作弊 行为,愿意接受《上海大学学生考试违纪、作弊行为界定及处分规定》的纪律处分。 应试人 题号 得分 一、是非题(本大题共 10 小题,每小题 1 分,共 10 分) 判断下列各题正误,正确者在括号内打“√” ,错误者在括号内打“×” 。 一 二 应试人学号 三 四 五 六 应试人所在院系 卷面分 理论成绩 实践成绩
5. 若线性方程组 Ax b 系数矩阵 A 是严格对角占优矩阵, 则方程组的雅克比迭代法与高斯赛德尔迭代法敛散性为( D )
A) 雅克比迭代法收敛,高斯-赛德尔迭代法发散。 1. 分类搜索算法只能求解在给定区间上的单峰函数的极小值。 (√) 2. 当|x|远远大于 1 或远远小于 1 时, 绝对误差比相对误差能更好地表示近似值的精确程度。 B) 雅克比迭代法发散,高斯-赛德尔迭代法收敛。 C) 两者都发散; D) 两者都收敛。 (×) 3. 在用黄金分割搜索法在区间[a,b]上求函数 f(x) 极值时,对 f(x)在区间[a,b]上没任何要 三、填空题(本大题共 11 空,每空 1 分,共 11 分) 求和限制。 (×) 4. 如果 A 是上三角矩阵, 线性方程组 AX=B 中, 存在某个 k, 使得 A 中的对角元素 akk=0, 则 请在每小题的空格中填上正确答案,填错、不填均无分。 方程组 AX=B 一定是无解。 (×) 1. 设某量的精确值为 x * ,近似值为 x ,则该量的绝对误差为 |x-x*| ,相对误差 n 5. 设 f(x)和 g(x)都是 n 次多项式如果 n+1 个不同节点 {xi }0 上都有 f(xi)和 g(xi),则有 f(x) |x-x*|/|x*| 。 ≡g(x)。 (√) 2. 在求解 n 元线性方程组时,在不考虑计算误差的情况下,直接法可以获得 精确解 , 6. 二分法不能用于求函数方程的复数根。 (√) 迭代法只能获得 近似解 。 7. 如果矩阵 A 是非奇异的,则可以对 A 进行直接的三角分解。 (√) 3. 在超松弛迭代法中,松弛因子 ω = 1 时,就是 高斯-赛德尔迭代 法,ω > 1 时,称为 8. 函数 g(x)的一个不动点(fixed point)是指一个实数 P,满足 P=g(P)。 (√) 超松弛迭代 法,ω<1 时,称为 低松弛迭代 法。 9. 现代科技的三大支柱是:理论研究、科学实验、科学计算。 (√) 4. Matlab 指令,删除向量 V 中的第 3 位到第 50 位上的内容: V(3:50)=[] . 10.求近似解称作为舍入误差。 (×) 5. A 是一个 10 行 4 列的矩阵,在 A 中的第 3 行插入 5,6,7,8 四个数,则指令为: 二、单项选择题(本大题共 5 小题,每题 2 分,共 10 分) 1. 计算机表示的实数由于受到尾数的固定精度,因此有时并不能确切的表示真实值,这一 类型的误差称为:( B )。 A) 截断误差; B) 舍入误差; C) 精度损失; D) 相对误差; 2. 当计算机中表示的两个数 p 和 q 有很好的近似值 Ap 和 Aq 时,其乘积 p*q 的相对误差大
第 1 页 (共 3 页) 致等于:( B )。
上海大学 2011~2012 学年冬季学期试卷(A 卷)
成 绩
A) Ap 和 Aq 的相对误差的积; C) Ap 和 Aq 的绝对误差的积;
B) Ap 和 Aq 的相对误差的和; D) Ap 和 Aq 的绝对误差的和;
3. 误差根据来源可以分为四类,分别是( A ) A) 型误差、观测误差、方法误差、舍入误差; B) 模型误差、测量误差、方法误差、截断误差; C) 模型误差、实验误差、方法误差、截断误差; D) 模型误差、建模误差、截断误差、舍入误差。 4. 设 A 是 N N 方阵,命题“给定任意 N 1 矩阵 B ,线性方程组 AX B 有唯一解。”与( A ) 等价。 A) 矩阵 A 是非奇异的; C) 方程组 AX 0 有多个解; B) 矩阵 A 是奇异的; D) det(A) 0 ;(即 A 的行列式等于 0)
2 x1 3 x 2 100 x3 1 x1 10 x 2 0.001x3 0 3 x 100 x 0.01x 0 2 3 1
解:用偏序选主元策略求解步骤如下: 系数增广矩阵为:
2 3 100 1 [ A | B] 1 10 0.001 0 (注:linspace 的第三个参数定义插值个数,学生定义不同,但只要是大于等于 2 的,都是 0.01 0 3 100 正确的。注意:学生思路不同,个人风格不同,可能给出不同的实现方式。 对第一行选主元,并进行交换并消去系数得: [ A | B](1) 3 100 0.01 0 0 130 / 3 0.013 / 3 0 0 191 / 3 299.98 / 3 1
