2014年科学营参营资格测试试题及答案评分标准

合集下载

浙江省杭州2014年中考科学模拟命题比赛试题26

某某省某某2014年中考科学模拟命题比赛试题26考生须知：1．本试卷分试题卷和答题卷两部分。

考试时间为120分钟，满分为180分。

2．本卷的g均取10N/kg3．本卷可能用到的原子量：C：12，H：1，O：16 K：39，Ca：40, Na：23, Mg：一、选择题（每小题4分，共24分，每小题只有一个选项符合题意）1．2014年3月15日晚，央视曝光的激光笔功率达到800毫瓦，属于国家标准GB 7247.1-2012规定的功率大于500毫瓦的4类激光器。

这类激光器主要用于焊接、切割、打标和机械加工。

由于功率过高，小孩子用此激光笔玩耍，危险度极高，极易导致眼睛失明。

关于该激光笔的相关说法正确的是（）A．功率达到800毫瓦表示激光在单位时间内做功的多少B．激光射到小孩子的眼睛引发眨眼的反射是由脊髓控制的C．用激光进行切割是把光能转化为机械能D．该种激光笔会对视网膜造成永久性伤害，应禁止销售这类激光笔2．某某华大基因研究中心和某某大学生物信息学研究中心为主体的中国科学家几年前成功破译了水稻基因组信息。

下列有关水稻遗传物质的叙述正确的是A．水稻是由DNA分子构成的B．水稻抗病、抗倒伏、高产优质等一系列可遗传的性状均由蛋白质决定C．水稻、人类等生物体内的基因、DNA、染色体不可能发生变化D．水稻基因实质上是水稻DNA分子上起遗传作用的一些片段3．下列各物质按照混合物、单质、氧化物的顺序排列的是( )A．盐水、冰、酒精 B．溴、熟石灰、盐酸C．氮气、石灰石、醋酸 D．洁净的空气、液溴、二氧化碳4．下图中表示的是小车向右加速时，车内悬挂的小球和杯中水面的变化情况，其中与实际情况相符合的是（）【改编自2013年中考模拟卷】5．如右图，电路电流消耗的电能E、做的功W和产生热量Q之间正确的关系是( ) A．E＝W＝Q B．E＝W＞QC．E＞W＞Q D．E＞W＝Q6．下列有关光的现象中，正确的说法是（）A．阳光下，微风吹拂的河面，波光粼粼，这里蕴含着光的反射B．光与镜面成30°角射在平面镜上，则其反射角也是30°C．人在照镜子时，总是靠近镜子去看，其原因是靠近时像会变大D．老年人通过放大镜看书，看到的字的实像二、选择题(每小题3分，共48分，每小题只有一个选项符合题意)7．初中科学知识中有很多的“相等”。

新疆2014年继续教育《科学方法与论文写作》考试题（真题）

新疆2014年继续教育《科学方法与论文写作》考试题（真题）第一篇：新疆2014年继续教育《科学方法与论文写作》考试题(真题) 新疆2014年继续教育《科学方法与论文写作》考试题（真题）一、单选1、标准统一、资料真实、广泛经济且便于处理是哪种研究方法的优点（）访谈调查法实验法测量法问卷调查法2.属于科学认识的“硬件”，即在科学认识活动中进行观察、测量、计算、存储信息的各种物质手段。

科学方法科学器材科学探索科学计量3.学术文献检索时，我们通常用到的最重要的中文综合性网络数据库之一是（）(A)中国知网(B)搜狐(C)百度(D)新浪4.在测量研究中，万用表、电表、水表等是（）(A)测量客体(B)测量内容(C)测量规则(D)测量工具5.下列关于文献检索中，（）具有便于继承和借鉴前人的成果，避免重复研究或走弯路的功能。

资源开发协助性决策继承和借鉴便捷及高效6.科学研究的基本阶段是（）(A)发现问题和解决问题(B)选题、立项和结题(C)研究结题、研究实施、研究立项(D)研究立项、研究实施、研究结题7按某种属性排序，如成绩名次，属于（）类别量表等距量表顺序量表等比量表8.“A组得分将显著高于B组”或“B组得分将显著高于A组”是（）(A)非定向实验假设(B)定向实验假设(C)零假设(D)备择假设9.在统计学的实际运用中，常常需要强调一类假设为应当或期望实现的假设，它是（C）(A)零假设(B)虚无假设(C)备择假设(D)对立假设10.()是科研意义中最基本得意义。

创造学术价值推动技术进步传承科研技术促进社会发展11()是通过对学术期刊整体水平的评价，来界定刊载在该期刊上的学术论文水平和质量的评价方法。

指标评价法期刊评价法专家评价法综合评价法12.前苏联学者巴甫洛夫用一条狗作为研究对象，通过可控的灯光、声音等无关刺激引起了狗分泌唾液，从而发现了条件反射现象，这个研究是（）(A)测验性个案研究(B)实验性个案研究(C)调查性个案研究(D)观察性个案研究13.不能控制无关变量的方法有（）(A)随机抽样(B)等组分配被试(C)增加样本(D)消除物理因素14下列选项中，不属于特种文献的有()科技报告学位论文专利文献专著15.下列不属于统计方法特点的是()数量型技术性模糊性条件性16.科研规划中，()是科研规划的中层，是指规模较大、时间较长的科研计划。

2014学年第二学期八年级科学竞赛卷及答案

2014学年第二学期科学竞赛试题卷分值：120分测试时间：120分钟本次开始可能用到的元素相对原子质量:H:1 O:16 N:14 S:32 P:31 Mg:24 Cl:35.5 一、填空题（每题2分，共60分）1．秋高气爽的夜里，当我们仰望天空时会觉得星光闪烁不定，这主要是因为（）A、星星在运动B、地球在绕太阳公转C、地球在自转D、大气密度分布不稳定，星光经大气后折射后方向随大气密度变化而变化2．植物矮小，根系发达，叶小而厚，叶表皮细胞壁厚，气孔深陷，栅栏组织层次多，此类植物最可能为（）A、水生植物B、旱生植物C、阴生植物D、以上都不对3．奥斯特实验说明了电流周围存在着磁场。

在奥斯特实验中需要一根长直导线水平地放置在小磁针的上方，实验中该直导线的放置方向应是（）A、东西方向B、南北方向C、与南北方向成45°角D、可以是任意方向4．对于育种来说，有性生殖的主要优点是能产生（）A、更多的后代B、差异更大的后代C、健康的后代D、发育更快的后代5．老奶奶用放大镜看报纸时，为了看到更大的清晰的像，应怎么做?（）A、报纸与眼睛不动，放大镜离报纸远些B、报纸与眼睛不动，放大镜离报纸近些C、报纸与放大镜不动，眼睛离报纸近些D、报纸与放大镜不动，眼睛离报纸远些6以上实验最能证明种子发芽需要（）A、阳光B、空气C、温度D、水7．一石块和一玩具气球（在气球内充满空气）捆在一起，浸没在水中下沉，它们在水中下沉的过程中，受到的浮力将（）A、逐渐增大B、逐渐减小C、不变D、先减小，后增大8．从显像管尾部灯丝发射出来的电子，高速撞击在电视机荧光屏上，使荧光屏发光，则在显像管内部（）A、电流从灯丝到荧光屏B、电流从荧光屏到灯丝C、显像管内是真空的，无法通过电流D、电流方向在不断变化9、用排水法收集某种难溶于水的气体，当试管中的水被降排出到如图所示的位置时，则试管中的气体压强 ( )A、等于大气压B、小于大气压C、比大气压大D、难以确定10、光束AB射到一玻璃球表面，经折射而穿过玻璃球，则其中可能正确的光路图是（）A、aB、bC、cD、d11、正常人的眼睛在水中看物体会一片模糊，因为光从空气射人眼睛折射程度大，而光从水中射入眼睛折射程度就明显减小。

2014年中国数学奥林匹克希望联盟夏令营讲义(教师版含答案)

2014年中国数学奥林匹克希望联盟夏令营讲义（一）平面解析几何讲义一、平面几何背景下的解析几何问题（一）解法思想：充分利用平面几何中的几何性质,合理而恰当地把几何特征表示为代数形式,以几何直观为导向,运用代数工具和相应的方法进行推理或论证,达到解题目的．（二）例题选讲：例1．在周长为定值的△ABC 中,已知|AB|=6,且当顶点C 位于定点P 时,cos C 有最小值为257. （I ）建立适当的坐标系,求顶点C 的轨迹方程.（II ）过点A 作直线与(1)中的曲线交于M 、N 两点,求||||BN BM ⋅的最小值.解析（I ）设||,||CA m CB n ==,则222236()236()36cos 1222m n m n mn m n C mn mn mn+-+--+-===-．设定值m n d +=,则222222363627272cos 111122()2d d d C m n mn d d ---=-≥-=-=-+,所以2727125d -=,解得10d =．把,A B 两点放在x 轴上（点A 在左）,线段AB 的垂直平分线为y 轴,建立平面直角坐标系．则据椭圆定义可得顶点C 的轨迹方程为2212516x y +=．（II ）设点,M N 的坐标分别为11(,)x y 和22(,)x y ,则22121212||||()()()BM BN a ex a ex a c x x e x x ⋅=--=-++．当直线MN 的斜率不存在时,12x x c ==-,此时22221156||||225BM BN a c c e ⋅=++=；当直线MN 的斜率存在时,设其方程为()y k x c =+,代入椭圆方程中得 22222222222()20b a k x ca k x a k c a b +++-=可得222222212122222222,ca k a k c a b x x x x b a k b a k-+=-=++,所以 22224222222422222222222()||||c a k k c c b k a c b BM BN a b a k b a k b a k -++⋅=++=+++令222b a k t +=,则2222222242()()||||a c t b a c a b BM BN a t+-++⋅= 222222222222()()34167562525a c b a b a c a a t t+-+=+⋅=-⋅．因为2222162516t b a k k =+=+≥,所以2341675640016252525t -⋅≥=,即得||||BN BM ⋅的最小值为16,此时0k =．例2．设F 是椭圆2212516x y +=的一个焦点,A 是椭圆上距离点F 最远的一个顶点,在椭圆的短轴BC 上取互异的2013个点(1,2,,2013)i P i =,设直线i FP 交线段或于点M ,直线AP 交线段或于点i N ．试问：直线(1,2,,2013)i i M N i =解析：如图示,设点m P 的坐标为(0,)m y ,||||||1||||||m m m m BP AM OF P O FA M B ⋅⋅=,可得||8||3(4)m mm m AM y M B y =-,坐标为15(4)32(,)512512m mm m y y y y -++．同理可得点m N 的坐标为15(4)32(,)320320m m m m y y y y --++,所以直线m M m N 的斜率为815(4)mm y y -+,可得其直线方程为32815(4)()32015(4)320m m m m m m y y y y x y y y ---=++++．令0y =,则4530015(320)15320320m m m m y y x y y ++===++,这说明直线m M m N 经过定点(15,0),而定点(15,0)在椭圆外部,可见任意两条直线(1,2,,2013)i i M N i =都相交,且交点均为(15,0),说明这2013条直线任两条直线在椭圆内部均不可能相交,于是它们把椭圆可分成2014块．例3．作斜率为13的直线l 与椭圆C ：143622=+y x 交于,A B 两点（如图所示）,且)2,23(P 在直线l 的上方．（I ）证明：△PAB 的内切圆的圆心在一条定直线上；（II ）若︒=∠60APB ,求△PAB 的面积．解析（I ）分析：易计算出以点P 为切点的椭圆的切线的斜率为13-,由此可知以点P 关于x 轴的对称点为切点的椭圆的切线的斜率为13．可见斜率为13的直线l 在平移过程中与椭圆相切时恰好是上面的切线,由此可猜想直线PA 与直线PB 的斜率互为相反数,下面给予验证：设直线l 的方程为13y x b =+,点,A B 的坐标分别为11(,)x y 和22(,)x y ．把直线方程代入椭圆方程中可得22269360x bx b++-=,即得212129363,2bx x b x x-+=-=．因为PAk=PBk=两式相加=因为11221133y x b y x b=+=+,所以12121((3y x x b x-=+-12121(3x x b x b=+-,21211((3y x x b x-=+-12211(3x x b x b=+-,于是122112122((()3y x y x x x b x x b-+--=+-+-23123(0b b b b=----=．所以0PA PBk k+=．于是PAB∆的内切圆的圆心一定在直线x=（II）因为︒=∠60APB,所以直线PA,可得直线PA的方程为y x=-+代入椭圆方程中得2142340x x-+-=,由韦达定理可得点A．故由弦长公式可得|||1477PA-+=-==．同理可求得1)||7PB=．所以,△PAB的面积为111826||||sin602249PA PB⋅⋅︒=⋅=例4．在平面直角坐标系xOy中,椭圆的方程为22221(0)x ya ba b+=>>,12,A A分别为椭圆的左、右顶点,12,F F分别为椭圆的左、右焦点,P 为椭圆上不同于1A 和2A 的任意一点．若平面中两个点Q 、R 满足11221122,,,QA PA QA PA RF PF RF PF ⊥⊥⊥⊥,试确定线段QR 的长度与b 的大小关系,并给予证明．解析：如右图示,据题意可知12,,,P A Q A 四点共圆,又原点O 为该圆的弦12A A 的中点,则据圆的性质可得该圆的圆心在y 轴上；又PQ 为该圆的直径,所以线段PQ 的中点在y 轴上．同理,线段PR 的中点也在y 轴上．所以,点,Q R 的横坐标相等,且为点P 的横坐标的相反数．设点P 的坐标为00(,)x y ,则可设点,Q R 的坐标分别为01(,)x y -和02(,)x y -,且12||||QR y y =-．据题设,1212tan tan A PA AQA ∠=-∠,则据直线的到角公式有001100000011000011y y y yx a x a x a x ay y y y x a x a x a x a---+-+=+⋅+⋅-+-+,即012222220001y y x y a x y a =+-+-,整理得22010x a y y -=．同理可推得22020x c y y -=．于是222220021000||||||x c x a b y y y y y ---=-=．由于00||y b <≤,所以20||b b y ≥,即得线段QR 的长度不小于b ．又解：设点P 的坐标为00(,)x y ,则可得直线1A Q 的方程为00()x ay x a y +=-+；同理可得直线2A Q 的方程为00()x a y x a y -=--,两方程联立可得点Q 的坐标为22000(,)x a x y --．同理可得点R 的坐标为22000(,)x c x y --．于是得20||||b QR y =．因为00||y b <≤,所以20||||b QR b y =≥,可得线段QR 的长度不小于b ．二、向量条件下的曲线的弦问题（一）题型特点及解法思想：当直线与曲线相交但不相切,此时将产生曲线的一条弦,围绕着这条线弦展开的问题,我们把它称为曲线的“弦问题”．解决这类问题的基本思想是联立方程组,运用二次方程的有关知识加以解决．在曲线的“弦问题”中,时常把题中的条件通过向量的形式给出,或以向量为背景来设置问题．解决这种问题时,可以从两个方面来考虑向量知识的运用,一是运用向量的坐标表示形式解题,这与解析法一脉相承；二是运用向量的几何意义解题,即通过向量来揭示所研几何图像的几何性质,再运用数形结合的思想解题．（二）例题选讲：例5．点A 在直线y kx =上,点B 在直线y kx =-上(0)k >,且A 、B 两点在y 轴同侧,并满足2||||1OA OB k ⋅=+．（I ）求AB 中点M 的轨迹C ；（II ）若曲线C 与抛物线22(0)x py p =>相切于两点,求证这两个切点分别在定直线上,并求切线方程．解（I ）设点A 的坐标为11(,)t kt ,点B 的坐标为22(,)t kt -,则1||||OA t →=2||||OB t →=所以有12||1t t =,由于A 、B 两点在y 轴同侧,所以121t t =．设AB 的中点M 的坐标为(,)x y ,则12122()2t t x k t t y +⎧=⎪⎪⎨-⎪=⎪⎩,整理得22122y x t t k -=,即得2221y x k -=．所以点M 的轨迹C 的方程为2221y x k-=,可知轨迹C 是以直线y kx =和y kx =-为渐近线的双曲线．（II ）联立22x py =与2221y x k -=,得2221y py k-=,即22220y pk y k -+=,可知该关于y 的二次方程有两个相同的正根,即得242440p k k -=,即221p k =,即得1pk =．此时切点的纵坐标为2pk ,可得两切点坐标为2(,)pk ,即()k．由此可知两个切点分别在定直线x =x =当切点坐标为)k 时,切线的斜率为p,切线方程为y k x p -=,10py --=；当切点坐标为()k 时,切线的斜率为p -,切线方程为(y k x p-=-+,10py ++=．例6．设直线:l y kx m =+（其中,k m 为整数）与椭圆2211612x y +=交于不同两点,A B ,与双曲线221412x y -=交于不同两点,C D ,问是否存在直线l ,使得向量0AC BD +=,若存在,指出这样的直线有多少条？若不存在,请说明理由．解析设,A B 两点的坐标分别为11(,)x y 和22(,)x y ,,C D 两点的坐标分别为33(,)x y 和44(,)x y ,则由0AC BD +=可得1234x x x x +=+．把直线l 的方程代入椭圆方程中可得222(34)84480k x kmx m +++-=,于是122834kmx x k+=-+,且2212160k m +->．把直线l 的方程代入双曲线方程中可得222(3)2120k x kmx m ----=．因为k 为整数,所以230k -≠,于是34223km x x k+=-,且221240m k +->．由1234x x x x +=+可得2282343km kmk k -=+-,于是当0k =时,需2120m ->且2120m +>,即m -<<,这样的有序整数对(,)k m 共有7个,此时,共有7条满足题设的直线；当0m =,0k ≠时,需212160k +>,且21240k ->,即k <<这样的直线共有2条；当0m ≠且0k ≠时,2282343km kmk k -=+-即123-=,不能成立,此时没有满足题设的直线．综上,存在直线l ,这样的直线有9条．例7．已知椭圆1222=+y x ,过定点(1,0)C 两条互相垂直的动直线分别交椭圆于Q P ,两点．21,F F 分别为左右焦点,O 为坐标原点．（I ）求||21PF PF +的最小值；（II ）当向量21PF PF +与21QF QF +互相垂直时,求Q P ,两点所在直线的斜率．解析（I ）因为122PF PF PO +=,所以只需求||PO 的最小值．显然min ||1PO b ==,所以||21PF PF +的最小值为2．（II ）由21PF PF +与21QF QF +互相垂直可知OP OQ ⊥．又CP CQ ⊥,所以PQ 是两个直角三角形POQ 和PCQ 的公共斜边,即得线段PQ 的中点到,O C 两点的距离相等,即线段PQ 中点的横坐标为12．法1：设Q P ,两点所在直线的斜率k ,线段PQ 的中点坐标为01(,)2y ,则有2020014b x k a y y =-=-．故可设直线PQ 的方程为01()2y y k x -=-,即11()42y k x k +=-,代入椭圆方程中可得2212()2024k x kx k+---=,即2222213(12)(21)()0282k k x k x k +-+++-=．设1122(,),(,)P x y Q x y ,则42122241218(12)k k x x k k -+=+,而121x x +=,所以424221212122211412114()()()24248(12)16k k k k k y y k x x k x x k k k k-+-=-++++=++ 4222284116(12)k k k k -++=+．因为12120x x y y +=,所以424222224121284108(12)16(12)k k k k k k k k -+-+++=++,可得42202030k k --+=,即得2510k -+=,即k =法2：设直线PQ 的方程为y kx b =+,代入椭圆方程中得222(12)4220k x kbx b +++-=．设1122(,),(,)P x y Q x y ,则122412kb x x k+=-+．而121x x +=,所以2124k kb +=-——（1）另一方面,21222212b x x k -=+,于是222222121212222()12k b k y y k x x kb x x b kb b k -=+++=+++．因为12120x x y y +=,所以2222222222201212b k b k kb b k k--+++=++,即得 22322422320k b k b k b kb +-++-=——（2）由（1）（2）消去b 可得42202030k k --+=,于是k =法3：设直线PQ 的方程为y kx b =+,代入椭圆方程中得222(12)4220k x kbx b +++-=．设1122(,),(,)P x y Q x y ,则122412kbx x k+=-+,21222212b x x k -=+．一方面,由12120x x y y +=,因222212121222()12k b y y k x x kb x x b k -+=+++=+,故得2222222201212b k b k k--++=++即223220b k --=——（1）另一方面,由1122(1,)(1,)0x y x y -⋅-=可得121212()10x x x x y y -+++=,因此有222222224210121212b kb k b k k k--++++=+++即23410b kb +-=——（2）由（1）（2）消去b 可得42202030k k --+=,于是k =法4：设||,||OP m OQ n ==,则有2222111132m n a b +=+=,即得222232m n m n +=,可知原点O 到直线PO 的距离为3．故设直线PQ 的方程为cos sin 3x y θθ+=,代入椭圆方程可得22224(sin 2cos )cos 2sin 03x θθθθ++-=．设1122(,),(,)P x y Q x y ,则122243sin 2cos x x θθθ+=⋅+,而121x x +=,所以223sin 2cos θθθ=+,即23cos 30θθ-+=,解得cos θ=,于是得cot =,即斜率为k =三、曲线的切线问题（一）题型特点及解法思想：这里的曲线通常是二次曲线,其切线是指与曲线有两个相同的交点的直线,解题的基本思路是联立方程组,运用判别式等于0来体现切线特点．当然,还可以从导数的角度来分析切线,并运用导数工具研究切线．（二）例题选讲：例8．过直线l ：57700x y --=上点P 作椭圆221259x y +=的切线PM 、PN ,切点分别为M 、N ,联结MN ．（I ）当点P 在直线l 上运动时,证明：直线MN 经过定点Q ；（II ）当//MN l 时,证明：定点Q 平分线段MN ．解析（I ）设点P 的坐标为00(,)x y ,切点M 、N 的坐标分别为11(,)x y 和22(,)x y ,则两条切线的方程分别为111259x x y y +=和221259x x y y +=．因为点P 在这两条切线上,所以有 10101259x x y y +=且20201259x x y y+=．这说明过切点M 、N 的切点弦所在直线MN 的方程为001259x x y y+=．因为0057700x y --=,即007145x y =+,所以直线MN 的方程为0147()1x y x y ++=．令709125y x +=,则14125x =,解得2514x =,所以,直线MN 经过定点Q ,其坐标为25(,14（II ）若//MN l ,则直线MN 的方程为y 要证明此时定点Q 平分线段MN ,弦所在直线的方程就是9525()10714y x +=-此时可设,M N 两点的坐标分别为11(,x y 得1212121211()()()()0259x x x x y y y y -++-+=,因为1212,75x x y y +=+=-,所以 121211()()075x x y y ---=,即121257y y x x -=-,所以,此时直线MN 的斜率为57,其方程就是9525()10714y x +=-,这就是说,定点Q 平分线段MN ．例9．过点)3,2(作动直线l 交椭圆1422=+y x 于两个不同的点Q P ,,过Q P ,作椭圆的切线,两切线的交点为M ．（I ）求点M 的轨迹方程；（II ）设O 为坐标原点,当四边形POQM 的面积为4时,求直线l 的方程．解析（I ）设直线l 的方程为sin (2)cos (3)x y θθ-=-,即sin cos 3cos 2sin 0x y θθθθ-+-=．设交点M 的坐标为00(,)x y ,则直线PQ 的方程为0014x xy y +=,即00440x x y y +-=．于是有0044sin cos 3cos 2sin x y θθθθ-==--,即得动点M 的参数方程为（II 2(14)k +2sin α=．所以,四边形POQM 的面积为1||||sin 2S PQ OM α=⋅ 22|23|14k k =-+=．所以,4|23|k =-,解得1k =或11k =,得直线l 的方程为10x y -+=或114100x y --=．例10．已知111222(,),(,),A x y A x y 在的直线与抛物线22(0)x qy q =>证明：对不同的{},1,2,3i j ∈,i y y 证如图,不妨设边13A A 和23A A相切,切点分别为1T 和2T ．那么切点弦1T 2T 所在直线方程为33()x x q y y =+．设切点1T 和2T 的坐标分别为211(,)2t t q 和222(,)2t t q ,则切线13A A 的斜率为1t q ,于是有31131y y t x x q -=-,即1312t py y q=+．把切点1T 的坐标代入直线方程33()x x q y y =+中,可得21313()2t x t q y q =+,整理即223113()22y t t q y p q=+,再把1312t py y q=+中的1t 代入该式,可得22332313122[]2()y pq p q q y p y y y y ⋅=+++,即2233231312()y p q y y y y y =+++, 即213231312()y y p q y y y y -=++,即得21313()2y y y y p q +=-．同理,利用切点2T 可以推得22323()2y y y y p q +=-．上面两式相减可得123y y y +=-；上面两式相加可得2222312312()()4y y y y y y p q +++=-,即得 232312123[()2]4y y y y y y p q +--=-,即23233123(2)4y y y y y p q --=-,即得21232y y y p q =．所以21212123()2y y y y y y y p q +=-=-．综上,对不同的{},1,2,3i j ∈,()i j i j y y y y +为定值,定值为22p q -．四、焦点问题（一）题型特点及解法思想：此类题目总是围绕圆锥曲线的焦点展开,它紧扣圆锥曲线的定义,能更直接地揭示圆锥曲线的本质．解决这类问题时,一要抓住圆锥曲线的定义,包括椭圆、双曲线的第一、第二定义；二要抓住焦点与对应准线之间的关系；三要用好焦半径．（二）例题选讲：例11．如图,MN 为过椭圆22221(0)x y a b a b+=>>右焦点F 的弦,,A B 分别为椭圆的左、右顶点,直线AM 与BN 交于点P ,求点P 的横坐标.解析如图,设点,M N 的坐标分别为(cos ,sin )a b αα和(cos ,sin )a b ββ,设点P 的坐标为00(,)x y ,则一方面有00sin sin cos cos 1y b b x a a a a αααα==⋅+++, 00sin sin cos cos 1y b b x a a a a ββββ==⋅---, 两式相除可得00sin cos 1sin cos 1x a x a αββα--=⋅++ ————（1）另一方面,有sin sin cos cos b b a c a c αβαβ=--,即sin sin cos cos e eαβαβ=-- ————（2）由（1）得0[sin()sin sin ][sin()sin sin ]x a βααββαβα-++=++- ————（3）由（2）得sin()(sin sin )e αβαβ-=- ————（4）又（3）式左边为00[sin()sin sin ]2cos(sinsin)222x x βαβααββααβ--+-++=+04cossincos222x βαβα-=．（3）式右边为[sin()sin sin ]2cos(sinsin)222a a αβαββαβαβα++-++-=+4cossincos222a αββα+=．所以有0cos2cos2a x βαβα+=- ————（5）由（4）式可得2sin cos 2cos sin 2222e αβαβαβαβ--+-=,即cos cos22e αβαβ-+=,即cos12cos2e αβαβ+=-,代入（5）式中可得20a x c =．所以,点P 的横坐标为2a c ．例12．如图,在平面直角坐标系xOy 中,椭圆的左、右焦点分别为,．已知和都在椭圆上,其中e 为椭圆的离心率．（I ）求椭圆的方程；（II ）设是椭圆上位于轴上方的两点,且直线与直线平行,与交于点P ．求证：是定值．解析（I ）易求得椭圆方程为2212x y +=；（II ）设12||,||AF m BF n ==,则2||||m AP PF n =,1||||nBP PF m=．因为1212||||||||2AF AF BF BF a +=+=,所以21(1)||(1)||2m nm PF n PF a n m ++=++=, 即得2122||,||an mn am mn PF PF m n m n --==++,于是212||||2mnPF PF a m n+=-+．设12AF F θ∠=,则2BF x θ∠=,于是,1cos 1cos ep epm n e e θθ==+-,所以 2222222,1cos 1cos e p epmn m n e e θθ=+=--, 可得222mn c b b ep m n a c a==⋅=+．所以221||||22b PF PF a a +=-==,可见是定值．例13．已知椭圆Γ的方程为),0(12222>>=+b a b y a x 离心率12e =,1F 是椭圆Γ的左焦点,直线l 过点M（)0,2a -交椭圆Γ于A 、B 两点,且,121||1||111=+BF AF 当△1ABF 的面积最大时,求直线l 的方程． 22221(0)x y a b a b+=>>1(0)F c -，2(0)F c ，(1)e，e ⎛ ⎝⎭,A B x 1AF 2BF 2AF 1BF 12PF PF +12PF PF +解析如图,因为12e =,所以12c a =,可得2a c =．于是,2222a a a c a==,可知直线2x a =-是该椭圆的左准线,即得点M 落在左准线上．假设,A B 两点在x 轴的上方,并设它们的坐标分别为11221212(,),(,)(,)x y x y x x y y <<．则1212113(2)()()22ABF S a c y y c y y ∆=--=-．设直线AB 的方程为4x my c =-,代入椭圆方程2222434120c x c y c +-=中可得222(34)24360m y cmy c +-+=．所以21y y -==．令234m t +=,则21348m t ==≤+,于是212y y -≤,可知124ABF S c ∆≤,且当23432m +=即2283m =时等号成立．另一方面,分别过,A B 作左准线的垂线,垂线段长分别为12,d d ,则111211||,||22AF d BF d ==,而1122,y m d y m d ==,可得1212()y y m d d +=+．因为1222434cmy y m +=+,所以21222434cm d d m +=+．所以211122112||||()234cm AF BF d d m +=+=+．又因为21223634c y y m =+,即222121223634c m d d m y y m ==+,即221129||||34c m AF BF m =+．而条件有11111||||12AF BF +=,即111112(||||)||||AF BF AF BF +=,即得22222129123434cm c m m m ⋅=++,解得16c =,所以264a =．可得直线l的方程为64)14y x =±+．例14．在双曲线C ：22145x y -=中,12,F F 分别为双曲线C 的左右两个焦点,P 为双曲线上且在第一象限内的点,12PF F ∆的重心为G ,内心为（I ）是否存在一点P ,使得IG //（II ）已知A 为双曲线C 的左顶点,足1212k k +=-,求直线l 的方程．解析（I ）设点P 的坐标为00(,)(x y 面积为03y 001(6)2ex a ex a r ++-+,即0(ex +0(2)32x r +,即得00(2)332x ry +=,因为IG //12F F ,所以013r y =,可求得0y =．综上,存在一点P ,其坐标为,使得IG //12F F ．（II ）可设直线l 的方程为3x my =+,设,M N 两点的坐标为分别为11(,)x y 和22(,)x y ．把直线方程代入双曲线方程中,得22(54)30250m y my -++=．于是有1223045m y y m +=-,1222545y y m=-- ————（1）另一方面,因为121212,22y y k k x x ==++,而1212k k +=-,所以有12121222y y x x +=-++, 即得12121552y y my my +=-++,整理得21212(4)(105)()250m m y y m y y +++++=——（2）由（1）,（2）可得：2222530(4)(105)2504545m m m m m m -+⋅++⋅+=--,解得12m =-．所以,直线l 的方程为132x y =-+,即26y x =-+．五、曲线组问题（一）题型特点：这是一类典型的曲线性质探究问题,其曲线背景是由两条以上曲线组合而成,它使得问题更为复杂,体现出的综合性更强,更能突出曲线之间的自然联系．求解时,图形复杂,变量多,联系多,式子多,能很好地考查综合运用知识分析问题和解决问题的能力,更能考查思维素质．（二）例题选讲：例15．如图,曲线C 由上半椭圆1C ：22221(0,0)y x a b y a b+=>>≥和部分抛物线2C ：21(0)y x y =-+≤连接而成,12,C C 的公共点为,A B ,其中1C 的离心率为32．（I ）求,a b 的值；（II ）过点B 的直线l 与12,C C 分别交于,P Q （均异于点,A B ）,若AP AQ ⊥,求直线l 的方程．解析（I ）易知曲线12,C C 的结合点,A B 的坐标分别为(1,0)-和(1,0),于是可得1b =,再由1C 的离心率为32可得2a =．所以,2a =,1b =．（II ）显然直线l 的斜率存在,故设其方程为(1)y k x =-,将其代入曲线2C 的方程中可得210x kx k +--=,知该方程的一个根为1,由韦达定理可得点Q 的横坐标为1k --,于是点Q 的坐标为2(1,2)k k k ----；把直线l 的方程代入曲线1C 的方程中,可得2222(4)240k x k x k +-+-=,知该方程的一个根为1,由韦达定理可得点P 的横坐标为2244k k -+,于是点P 的坐标为22248(,)44k k k k --++．由AP AQ ⊥可得：4(2)1k k -⋅+=-,解得83k =-．所以,直线l 的方程为8(1)3y x =--,即8380x y +-=．例16．如图,设P 是抛物线1C ：2x y =上的动点．过点P 做圆2C 1)3(:22=++y x 的两条切线,交直线l ：3y =-于,A B 两点．（Ⅰ）求2C 的圆心M 到抛物线1C 准线的距离．（Ⅱ）是否存在点P ,使线段AB 被抛物线1C 在点P 处的切线平分,若存在,求出点P 的坐标；若不存在,请说明理由．解析（Ⅰ）抛物线1C 的准线方程为14y =-,所以2C 的圆心M 到抛物线 1C 准线的距离114．（Ⅱ）设点P 的坐标为200(,)x x ,切线方程可设为200()y x k x x -=-,则有2002|3|11kx x k--=+,即2234200000(1)(26)680x k x x k x x--++++=．于是3420000121222002668,11x x x xk k k kx x++++==--————（1）同时可得,A B两点的坐标分别为213(,3)xxk+--和223(,3)xxk+--,那么线段AB的中点坐标为22001233(,3)22x xxk k++---．以点P为切点的抛物线的切线方程为20002()y x x x x-=-,即2002y x x x=-,所以22200000123332()22x xx x xk k++-=---,整理得2120012(3)(1)0k kx xk k++-=,即1212k kxk k=+————（2）由（1）可得420012312006826x xk kk k x x++=++,代入到（2）中可得48x=,解得x=,此时点P的坐标为(,关于k的方程为21)3)160k k±++=,其判别式为23)1)(4640∆=-+=+>,可见这样的切线是存在的．综上,存在点P,其坐标为(．例17．设m R∈,在平面直角坐标系中,(,1)a mx y→=+,(,1)b x y→=-,a b→→⊥,动点(,)M x y的轨迹为E．（I）求轨迹E的方程,并说明该方程所表示的曲线的形状；（II）已知14m=,证明：存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA OB⊥（O为坐标原点）,并求该圆的方程；（III）已知14m=．设直线l与圆C：222(12)x y R R+=<<相切于A1,且l与轨迹E只有一个公共点B1．当R为何值时,|A1B1|取得最大值？并求最大值．解析（I）由a b→→⊥得221mx y+=,即为轨迹E的方程．当0m<时,方程表示焦点在y轴上的双曲线；当0m=时,方程表示两条互相平行的直线；当01m<<时,方程表示焦点在x轴上的椭圆；当1m=时,方程表示圆心在原点的单位圆；当1m>时,方程表示焦点在y轴上的椭圆．（II）此时方程为2214xy+=,如图．设|OA| = m,|OB| = n,则可设点A、B的坐标分别为(cos ,sin )m m θθ和(cos(),sin())22m m ππθθ++,代入椭圆方程中得 22222222cos sin 14sin cos 14m m n n θθθθ⎧+=⎪⎪⎨⎪+=⎪⎩,即 222222cos 1sin 4sin 1cos 4m n θθθθ⎧+=⎪⎪⎨⎪+=⎪⎩, 两式相加可得221115144n m +=+=．（注：形成公式22221111n m a b+=+）=O 到直线AB 的距离为d ,则据面积法有mn =所以d =．这说明存在圆2245x y +=,使得该圆的任意一条切线与轨迹E 恒有两个交点A,B,且OA OB ⊥（O 为坐标原点）．（III ）设点11,A B 的坐标分别为11(,)x y 和22(,)x y ．由于直线l 与圆O 和椭圆E 均相切,所以直线l 的方程既是211x x y y R +=,也是2214x xy y +=,所以有 211224x y R x y ==,即2212124,x R x y R y == ————（※）因为222111||||A B OB R =-,而222122||OB x y =+,又 222214x y +=,22211x y R +=,结合（※）有222222116R x R y +=, 可得222216(1)3R x R -=,222243R y R -=．所以2222122216(1)454||33R R R OB R R R---=+=, 得 22221122544||5()1R A B R R R R-=-=-+≤,且当R = 所以,当R =,|A 1B 1|取得最大值,最大值为1．五、综合问题例18．给定整数(2)n ≥,设000(,)M x y 是抛物线21y nx =-与直线y x =的一个交点,试证明：对于任意整数m ,必存在整数2k ≥,使得点00(,)m mx y 为抛物线21y kx =-与直线y x =的一个交点．解析据题设,有2001x nx =-,2001m mx kx =-,整理得001n x x =+,001mm k x x =+．注意到211000000211000000111111()()()()()m m m m m m m m m m x x x x n x x x x x x x x +++++++=++-+=+-+．当1m =时,001k x n x =+=显然是存在的；当2m =时,22001()222k x n x =+-=->显然也是存在的；假设,1()m s m s s N +==+∈时,k 存在,即001m mx x +和1101m m x x +++均为不小于2的整数,那么当2m s =+时,101011()()m mm m k n x x x x ++=+-+,其显然也是一个整数,又202012m m k x x ++=+≥,所以此时的k 为不小于2的整数．综上,对任意正整数m ,都存在不小于2的整数k ．若0m =,则2k =,显然存在；若m 为负整数,可令m p =-,那么001,pp k x p N x +=+∈,由上面证明可知依然存在不小于2的整数k ．综上,命题获证．六、练习题1．已知ABC ∆边上作匀速运动的点,,D E F ,在0t =时分别从,,A B C 出发,各以一定速度向,,B C A 前进,当时刻1t =时,分别到达,,B C A ．（1）证明：运动过程中DEF ∆的重心不变；（2）当DEF ∆面积取得最小值时,其值是ABC ∆面积的多少倍？2．已知抛物线x y 62=上的两个动点1122(,)(,)A x y B x y 和,其中21x x ≠且421=+x x ．线段AB 的垂直平分线与x 轴交于点C ,求ABC ∆面积的最大值．3．已知抛物线y 2 = 4px ( p > 0 ),过顶点O 作两条直线分别交抛物线于A 、B 两点,若OA ⊥OB,求O 在弦AB 上的射影M 的轨迹．4．已知梯形ABCD 中,AB = 2CD,点E 分有向线段→AC 所成的比为λ,双曲线过C 、D 、E 三点,且以A 、B 为焦点．当4332≤≤λ时,求双曲线离心率e 的取值范围． 5．是否存在无穷多条直线(1,2,,,)n l n m =形成的直线族,满足条件：（1）点（1,1）在直线(1,2,,,)n l n m =上；（2）1n n n k a b +=-,这里1n k +表示直线1(1,2,,,)n l n m +=的斜率,n a 、n b 分别表示直线(1,2,,,)n l n m =的横截距和纵截距；（3）10(1,2,,,)n n k k n m +>=．6．对于曲线C 1：3 ( x 2 + 2y 2 ) 2 = 2 ( x 2 + 4y 2 )上除原点外的每一点P,求证：存在过P 的直线与椭圆C 2：x 2 + 2y 2 = 2相交于两点A 、B,使∆AOP 与∆BOP 均为等腰三角形（O 为坐标原点）．七、练习题解答1．解析（1）如图,据题可令||||||||||||AD BE CF k AB BC CA ===, 则 ,,AD k AB BE k BC CF kCA ===．建立平面直角坐标系如图,设点B 的坐标为(,0)m ,点C 的坐标为(,)t s ,则点D 的坐标为(,0)km ,点E 的坐标为(,)m km kt ks -+,点F的坐标为(,)t kt s ks --．所以DEF ∆的重心坐标为(,)33m t s +,而ABC ∆的重心坐标也是(,)33m t s+,所以DEF ∆的重心不变．（2）因为(1)ADF ABC S k k S ∆∆=-,(1)BDE ABC S k k S ∆∆=-,(1)ECF ABC S k k S ∆∆=-,所以2[13(1)](331)DEF ABC ABC S k k S k k S ∆∆∆=--=-+,其最小值为14ABC S ∆,且当12k =时取到．所以,当DEF ∆面积取得最小值时,其值是ABC ∆面积的14倍． 2．解析：设AB 的中点D 的坐标为0(2,)y ,则由21122266y x y x ⎧=⎪⎨=⎪⎩可得1212126y y x x y y -=-+,即03AB k y =．设点C 的坐标为(,0)t ,则00312y t y ⋅=--,可得5t =,所以点C 的坐标为(5,0)．设直线AB 的方程为003(2)y y x y -=-,与抛物线x y 62=联立可得220022120y y y y -+-=,于是可得||AB ==而||CD =所以20(9)ABC S y ∆=+．因为20(9)y +=当且仅当22002429y y -=+,即205y =时,20(9)ABC S y ∆=+取到最大,．所以,ABC ∆此时直线AB的斜率为．3．解析设OA 直线方程为y = kx ,与抛物线方程y 2 = 4px 联立后得点A 的坐标为)442k pk p ，（．进而由OA ⊥OB 容易得到点B 的坐标（4pk 2,– 4pk ）．所以,直线AB 的方程为( 1 – k 2 ) y = k ( x – 4p ) -------- ( 1 )由此易得直线OM 的方程为)0(12≠-=k x kk y ------ ( 2 )由（1）（2）消参数k 后得：( x – 2p ) 2 + y 2 = 4p 2．经检验点M 不可能在原点,故x ≠0．所以,点M 的轨迹是以（2p ,0）为圆心,2 p 为半径的圆,还需除去原点．4．解析据双曲线的对称性可知梯形ABCD 为等腰梯形,且AD = BC ．以直线AB 为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系,如图．则可设双曲线的方程为22221(,0)x y a b a b-=>．由AB = 2CD可得|CD| = c ,可知点C 的横坐标为2c,代入双曲线方程中可得点C的纵坐标为2a ,即得C点坐标为(,22c a．由1AE AC λλ→→=+得点E的坐标为2(,12(1)cc a λλλλ-++,而E 点在双曲线上,所以有222222222(2)(4)14(1)4(1)c c a a a λλλλ---=++, 整理得 2222(2)a c c a λ+=-,同除2a 可得22(2)1e e λ+=-,即得2212e eλ-=+．因为4332≤≤λ,所以22213324e e -≤≤+,解得双曲线离心率e的取值范围是． 5．解析据题设可设直线(1,2,,,)n l n m =的方程为1(1)n y k x -=-,则11n n a k =-,1n n b k =-,可得11n n nk k k +=-．由于10(1,2,,,)n n k k n m +>=,所以所有的直线的斜率同号,不妨设0(1,2,,,)n k n m >=,则有110n n nk k k +-=-<,可知数列{}n k 是递减数列． XYOABM因为1112111()n n k k k k k +-=-+++,即1112111()n n k k k k k +=-+++,又因为121111n nk k k k +++>,所以111121111()n n n k k k k k k k +=-+++<-．令110n k k -<,得21n k >,故取21[]1N k >+,则1110N Nk k k +<-<,可知从第N+1项开始,数列{}n k 的每一项都是负值,与题设矛盾．同理,若0(1,2,,,)n k n m <=也矛盾．综上,不存在这样无穷多条直线．6．先分析：逆着思考这个问题,曲线C 1应该是点P 走出的轨迹,那么这样的点应该满足题中“使∆AOP 与∆BOP 均为等腰三角形”的条件．可以判断曲线C 1上的所有点都在椭圆的内部,所以点P 一定在椭圆的内部,如图．因此猜想当OA ⊥OB,且点P是弦AB 的中点时,可以使条件“使∆AOP 与∆BOP 均为等腰三角形”解析：变形方程3 ( x 2 + 2y 2 ) 2 = 2 ( x 2 + 4y 2 )得 22222223(2)6(2)4()0x y x y x y +-+++= 因为点P 不是坐标原点,所以x ,y 不可能同时为零,即得224()0x y +>,则有 222223(2)6(2)0x y x y +-+<,可得 22022x y <+<,即点P 在椭圆2222x y +=的内部．若OA ⊥OB,且点P 是弦AB 的中点,现求点P 的轨迹方程：如果直线AB 垂直于x 轴,则易求得点P 的坐标为(,0)3±,显然满足方程 222223(2)2(4)x y x y +=+；如果直线AB 不垂直于x 轴,可设其斜率为k ,A 、B 两点的坐标为11(,)x y 和22(,)x y ,线段AB 的中点P 的坐标为00(,)x y ．由点差法可得2002002b x xk a y y =-=- ————（1）设直线AB 的方程为00()y y k x x -=-,又设|OA| = m ,|OB| = n ,则2222111113122m n a b +=+=+=．因为点O 到直线AB ,故据直角三角形的等面积法有mn =,即222200111()k m n y kx ++=-．所以有220013()2ky kx+=-————（2）把（1）代入（2）中得22221432()2xyxyy+=+,整理得2200222002(4)3(2)x yx y+=+,即得 2222200003(2)2(4)x y x y+=+．综上,点P的轨迹方程为 222223(2)2(4)x y x y+=+．由于点P的轨迹方程 222223(2)2(4)x y x y+=+与点P满足的几何条件是充分必要的,所以满足方程 222223(2)2(4)x y x y+=+的点P,也一定能使“OA⊥OB,且点P是弦AB的中点”成立．那么,∆AOP与∆BOP 均为等腰三角形．2014年中国数学奥林匹克希望联盟夏令营讲义（二）函数与导数江苏南菁高级中学【知识要点概述】一、函数值域与最值问题：(1) 解决一切函数问题必须认真确定该函数的定义域,定义域含三种：①自然型：②限制型：③实际型：(2) 求函数的值域是比较困难的数学问题,求函数值域方法一般有：①配方法（将函数转化为二次函数）； ②判别式法（将函数转化为二次方程）； ③不等式法（运用不等式的各种性质）； ④函数法（运用基本函数性质,或抓住函数的单调性、函数图象等）；⑤换元法； ⑥反解法； ⑦几何法； ⑧导数法.(3) 恒成立问题：①不等式f (x )＞k 恒成立⇔f (x )min ＞k ；②不等式f (x )＜k 恒成立⇔f (x )max ＜k③f (x )≥g (x )恒成立⇔ f (x )−g (x )≥0恒成立⇔[f (x )−g (x )]min ≥0 (典型错误min max ()()f x g x ⇔≥) (4) 有解问题：①方程f (x )＝k 有解⇔k 的取值范围即为f (x )的值域；②不等式f (x )＞k 有解⇔f (x )max ＞k ；③不等式f (x )＜k 有解⇔f (x )min ＜k .(5) 最值存在定理：f (x )在闭区间[a , b ]内连续, 则f (x )必有最大值与最小值.二、函数基本性质：1．奇偶性定义：定义域关于原点对称, 且对∨−x ∈D ,f (−x )=f (x ) (偶函数) 或f (−x )=－f (x ) (奇函数) ①奇函数的图象关于原点对称；②偶函数的图象关于y 轴对称；③若奇函数的定义域包含0,则f (0)=0. 2．单调性定义：对∨−x 1, x 2∈I 且x 1＜x 2⇒ f (x 1)＜f (x 2) (增函数) 或f (x )＞f (x 2) (减函数). 3．研究函数的单调性,常用以下方法：（1）定义法：利用定义严格判断. 步骤为：①取值；②作差；③判断符号；④下结论.（2）直接利用已知基本初等函数的单调性. 例如若f (x )、g (x )为增函数,则 ①f (x )＋g (x )为函数；②1f (x )为函数（f (x )＞0）；③f (x )为函数（f (x )≥0）；④－f (x )为函数. （3）利用复合函数y = f [g (x )]的单调性(其中y =f (u ), u =g (x ))：判断的法则是“同增异减”具体步骤为：①求定义域；②找分界点,确定单调区间；③分析函数在每个区间上的单调性得出结论. （4）图象法：若一个函数的图象可画出来,则由图象可得单调区间.（5）利用奇偶函数的性质：①奇函数在对称区间上的单调性相同；②偶函数在对称区间上的单调性相反.（6）单调函数必存在反函数,且反函数的单调性与原函数的单调性相同.4．周期函数定义：若存在常数T (T ≠0),使得f (x +T )＝f (x )对定义域内任意x 恒成立,则称f (x )为周期函数,T 称为这个函数的周期,f (x+T )＝f (x )常常写作f (x ＋T 2)＝f (x －T2), 周期函数的定义域一定是无限集.①若T 是y =f (x )的周期,那么kT (k ∈N *)也是它的周期.②若y =f (x )是周期为T 的函数,则y =f (ax +b )(a ≠0)是周期为Ta的周期函数.③若u ＝g (x )是周期函数, f (u )是任意函数, 则f [g (x )]也是周期函数. 5．周期的常用结论：设a 为非零常数,若对f (x )定义域内的任意x 恒有下列条件之一成立, 则f (x )的周期为2a①()()f x a f x a +=-；②()()f x a f x +=-；③1()()f x a f x +=；④1()()f x a f x +=-；⑤()1()()1f x f x a f x ++=-；⑥1()()1()f x f x a f x -+=+. 上述结论可以通过反复运用已知条件来证明.另外：()1()()1f x f x a f x -+=+或1()()1()f x f x a f x ++=-,则f (x )的周期为4a .证明：由已知f (x ＋2a )＝()11()11()1()1()1()1()1f x f x a f x f x f x a f x f x --+-+===--++++, 于是f (x ＋4a )＝－1(2)f x a +＝f (x ) 6．周期性与对称性有如下关系：①若函数f (x )图象关于直线x =a 与x =b 对称,则它一定是周期函数,且2|a −b |是它的周期. ②若函数f (x )图象关于点(a , 0)和(b , 0)对称,则它一定是周期函数,且2|a −b |是它的周期. ③若函数f (x )图象关于直线x =a 及点(b , 0)对称,则它一定是周期函数,且4|a −b |是它的周期.证明①：不妨设a ＞b ,于是f [x ＋2(a －b )]＝f [2a －(2b －x )]＝f (2b －x )＝f (x ), ∴ 2(a －b )是f (x )的一个周期.已知函数f (x )对任意实数x , 都有f (m ＋x )＝f (m －x ),且f (x )是偶函数, 则f (x )的周期为_________ 已知函数f (x )对任意实数x , 都有f (m ＋x )＝f (m －x ),且f (x )是奇函数, 则f (x )的周期为_________ 三、基本初等函数：1. 指数函数及其性质：形如y =a x (a ＞0, a ≠1)的函数叫做指数函数,其性质有：①定义域为R ,值域为(0,+∞)； ②当0＜a ＜1时为减函数,当a ＞1时为增函数；③图象有两个特殊点：定点(0,1),不变点(1,a )； ④非奇非偶,但xy a =与xy a -=的图象关于y 轴对称；xy a =与xy a =-的图象关于x 轴对称；x y a =与log a y x =的图象关于直线y =x 对称；⑤对应关系为一一映射,从而存在反函数－－对数函数；⑥抽象性质：()(01)xf x a a a =>≠且⇒()()()(),()()f x f x y f x f y f x y f y +=⋅-=2. 对数函数及其性质：形如y =log a x (a ＞0, a ≠1)的函数叫做对数函数,其性质：①定义域为(0, +∞), 值域为R ；②图象有两个特殊点：定点(1,0), 不变点(a , 1)；③当0＜a ＜1时为减函数,当a ＞1时为增函数； ④非奇非偶,但-1log log a a y x y x ==与关于x 轴对称,log log ()a a y x y x ==-与图象关于y 轴对称,log x a y x y a ==与图象关于直线y x =对称；⑤对应关系为一一映射,因而有反函数——指数函数.3. 幂函数：形如y =x α的函数叫做幂函数,幂函数有如下性质：⑴它的图象都过(1,1)点,都不过第四象限,且除原点外与坐标轴都不相交；⑵定义域为R 或(−∞, 0)∪(0, +∞)的幂函数都具有奇偶性,定义域为(0, +∞)或[0, +∞)的幂函数都不具有奇偶性； ⑶幂函数y =x α都是无界函数；在第一象限中,当α＜0时为减函数,当α＞0时为增函数； ⑷任意两个幂函数的图象至少有一个公共点(1,1),至多有三个公共点；4. 画幂函数y ＝x α(α＝mn , m 、n 是互质的整数)草图的一般步骤是：(1)根据指数α的大小判断函数图象在第一象限的情形如图： (2)判断函数的奇偶性并确定函数图像在其他象限的情况：①m , n 均为奇数时,y =x α为奇函数,图象在一、三象限内关于原点中心对称. ②m 为偶数,n 为奇数时y =x α为偶函数,图象在一、二象限内关于y 轴对称. ③m 为奇数,n 为偶数时,y =x α既不是奇函数也不是偶函数,函数只在第一象限有图像.5．二次函数的图像和性质：二次函数是初等数学中遇到比较多的函数之一,它的图象简单,性质易于掌握,又与二次方程、二次不等式有联系,与之相关的理论如判别式,韦达定理,求根公式等又是中学教材的重点内容,因此有必要进一步认识二次函数的性质,研究与二次函数有关的解题规律、方法与技巧．(1) 二次函数的解析式：①一般式：2()(0)f x ax bx c a =++≠ ②顶点式：2()()f x a x h k =-+,顶点为(,)h k ③两根式：12()()()f x a x x x x =-- ④三点式：132312321313221231213()()()()()()()()()()()()()()()()x x x x x x x x x x x x f x f x f x f x x x x x x x x x x x x x ------=++------（2）2()(0)f x ax bx c a =++≠的图像是抛物线,顶点坐标24(,)24b ac b a a --,对称轴方程为2bx a=-,开口与。

2014年XXX高一新生分班考科学模拟试卷(含答案)

2014年XXX高一新生分班考科学模拟试卷(含答案)2014年杭州市学军中学高一新生适应性考试科学注意：1.本试卷满分180分，考试时间120分钟；2.所有答案必须写在答题卷上，写在试题卷上无效；3.本卷可能用到的相对原子质量：H-1 C-12 O-16 Na-23 Mg-24 Ca-40一、选择题：(本大题共72分，其中1-6题每小题4分，7-22题每小题3分)1.一个400N重的木箱放在大磅秤上，木箱内有一个质量为60kg的人站在小磅秤上，如图所示。

如果人用力推木箱顶板，则小磅秤和大磅秤上的示数FT1、FT2的变化情况是（）A。

FT1增大，FT2减小B。

FT1增大，FT2增大C。

FT1减小，FT2不变D。

FT1增大，FT2不变2.日前，加拿大科学家通过研究发现，将一定数量的银纳米粒子加入取自北极极地的土壤中后，会造成土壤中的许多种类的细菌数量减少，对此，下列说法正确的是A。

银纳米粒子对某些有害细菌伤害极大B。

银纳米粒子与土壤中的细菌是食物关系C。

银纳米粒子与土壤中的细菌不存在相互关系D。

银纳米粒子的影响可能破坏极地区域的生态系统3.如图所示甲、乙、丙、丁四种情况，光滑斜面的倾角都是θ，球的质量都是m，球都是用轻绳系住处于平衡状态，则()A。

球对斜面压力最大的是甲图所示情况B。

球对斜面压力最大的是乙图所示情况C。

球对斜面压力最小的是丙图所示情况D。

球对斜面压力最小的是XXX所示情况4.长途汽车经过长时间行驶后，驾驶员常常会停下车，拿根铁棒敲打车轮，凭借声音可以判断轮胎内的空气是否充足。

这主要是因为敲击的轮胎内空气充足时发出声音的A。

响度较大B。

音调较高C。

音调较低D。

响度较小5.蝴蝶飞行时能产生每秒振动5-6次的声波，蜜蜂飞行时能产生每秒振动300-400次的声波。

假如你的眼睛被蒙上，有蝴蝶和蜜蜂分别从你头顶附近飞过，那么A。

蝴蝶、蜜蜂都能被发觉B。

蝴蝶、蜜蜂都不能被发觉C。

蝴蝶能被发觉，蜜蜂不能被发觉D。

2014科学试题卷

2014年科学试题卷（本试卷满分120分，考试时间为60分钟，答案均涂或填在答题纸上）本卷可能用到的相对原子质量：H 1 C 12 O 16 Na 23 Fe 56 Zn 64一、选择题（每小题3分，共45分，每小题只有一个选项符合题意）1、下面是某同学以表格的形式所总结的一些知识点，其中完全正确的是（）2．甲型H1N1流感疑似病例和确诊病例,都要被送到专业医院的“负压病房”进行医学隔离观察和治疗,以防止病毒扩散．同学们对“负压”两字的含义有如下猜想．你认为猜想正确的是( )．A．病房内大气的压强大于病房外大气的压强B．病房内大气的压强小于病房外大气的压强C．因为病房是封闭的,所以病房内大气的压强可能大于也可能小于病房外大气的压强D．以上猜想都不正确3. 随着生活质量的提高,轿车进入了越来越多的城市家庭,我们的生活也与轿车产生了越来越紧密的关系．下面是关于轿车的一些说法,其中正确的是( )．A．轿车行驶时,只要不鸣喇叭,就不会产生噪声B．轿车静止时没有惯性,所以靠近静止的轿车是安全的C．轿车上凸下平近似流线型的设计,使它行驶时,底部比顶部受到的气流的压强小D．轿车发动机无论怎样先进,都不能把燃料燃烧时释放的内能全部转化为机械能4．如图所示的家庭电路中,有两个器件连接错误,它们是( )．A．闸刀开关和带开关的灯泡B．带开关的灯泡和带熔丝的两线插座C．带开关的灯泡和三线插座D．闸刀开关和三线插座5．天平、温度计、刻度尺、电压表是我们实验中常用的基本测量仪器．下面四副图表示的是一些同学对这四种仪器的操作和使用情况．其中不正确的是( )．6.如图是由相同的滑轮安装的滑轮组，甲乙两人分别用两装置在相等时间内将质量相等的重物匀速提升相同的高度，绳子自由端所受的拉力分别是F甲、F乙，若不计绳重和摩擦，下列说法正确的是（）A.甲的拉力是乙的拉力的3倍B.乙拉绳子的速度大小是甲拉绳子速度大小的2倍C.甲拉绳子的功率和乙拉绳子的功率不相等D.如果考虑滑轮质量，甲装置的机械效率比乙的低7.“卫星悬绳发电”是人类为寻找卫星的新型电力能源供应系统而进行的实验。

2014年省重点高中自主招生考试科学试卷及答案(DOC)

只有草履虫是无脊椎动物只有家兔才是真正的陆生动物其微观示意图如下（一种小球代表一种2014年省重点高中自主招生考试科学试卷1. 全卷满分为150分，考试时间为120分钟。

2. 本卷可能用到的相对原子质量： H:1 C:12 O:16 Cl:35.5 S:32 Cu:64 Ca:40 Zn:65一、选择题（本题共有20小题，每小题3分，共60分。

请选出每小题中一个符合题意的选项，不选、多选、错选，均不给分）1. 图中的四种操作行为符合安全用电规范的是A. 甲图中，有人触电无法切断电源时，立即用干木棍挑开电线B. 乙图中，用手握住测电笔的金属杆判断插座是否有电C. 丙图中，熔丝熔断后，用铜丝代替熔丝接入电路D. 丁图中，直接用潮湿的手去拔插头 2. 下列各项反射活动中，与“谈虎色变”这一反射类型相同的是A.酸橘入口，分泌唾液B .人的缩手反射C.精彩的哑剧引发观众哈哈大笑D •人熟睡时被蚊子叮咬会动一动 3•小明同学在课堂上测试了不同溶液的酸碱性如下表：物质柠檬汁食盐水肥皂水食醋 pH37102根据上表可知A. 柠檬汁的酸性比食醋强B. 上述溶液中只有肥皂水才能使紫色石蕊试液变色C. 上述溶液中不能使无色酚酞试液变色的一定是食盐水D. 将食盐水和食醋混合，混合液的酸性可能比柠檬汁强 4. 科学研究中常常需要对生物进行分类。

下列动物中A. 蝗虫属于鸟类B. C.只有家兔是恒温动物 D.5. 已知某两种物质在光照条件下能发生化学反应, 原子）：则下列说法正确的是A.参加反应的物质均为化合物B.C.该反应不符合质量守恒定律D.该反应属于复分解反应图示中共有4种物质的分子6. 右图是一个一次性加热杯的示意图。

当水袋破裂时，水与固体碎块混和，杯内食物温度逐渐上升。

制造此加热杯可选用的固体碎块是A.硝酸铵B.生石灰C .蔗糖D .食盐7. 将一玉米幼苗固定在支架上，支架固定在温度、湿度适宜且水坯底部有一透光孔的暗室内，从图所示状态开始，光源随暗室同步缓慢匀速旋转，几天后停止于起始位置，此时，幼苗的生成情况是A •根水平生长，茎向上弯曲B •根水平生长，茎向下弯曲C •根向下弯曲，茎向上弯曲D.根向下弯曲，茎向下弯曲8. 下列说法错误的是A. 近视镜片中间薄，边缘厚，是凹透镜B. 人眼中的晶状体与照相机的镜头（凸透镜）相似C. 近视眼不戴眼镜时成的像在视网膜的前面D. 远视眼应配戴对光有发散作用的透镜9. 下列有关实验仪器的说法中正确的是A •在测试溶液酸碱性可以用点滴板替代试管完成实验B •在配置一定质量分数的溶液时必须要使用托盘天平C •需要用高倍镜才能观察到鱼尾血液在毛细血管中流动D .在研究通电导体在磁场中的受力情况时必须要使用灵敏电流计10. 下列有关人体的新陈代谢的说法中，正确的是A. 红细胞和血小板都没有细胞核B. 人体呼出的气体中二氧化碳的含量大于氧气的含量C. 经过肾脏所形成的尿液中不含无机盐这一营养物质D. 蛋白质的消化产物在正常人体内将全部重新合成人体需要的蛋白质11. 右图为生态系统各个成分间的相互关系。

2014实验试题及评分标准 - 副本

实验试题及评分标准第一类基本操作一、配制250ml 0.1000mol.L-1NaCl 溶液。

评分标准：⑴所需NaCl质量计算2分⑵所用容量瓶、烧杯、玻璃棒的洗涤及容量瓶检验是否漏液 2分⑶溶液转移 3分⑷定容 2分⑸混匀 1分二、用0.1mol.L-1NaOH溶液滴定锥形瓶内HCl溶液，记录消耗体积。

评分标准：⑴滴定管洗涤、润洗、检验是否漏液及相应处理 3分⑵指示剂的选择 1分⑶滴定规范操作 4分⑷读数 2分三、从250ml容量瓶中移取25ml溶液至锥形瓶中。

评分标准：⑴移液管及锥形瓶的洗涤 2分⑵移液管的润洗 2分⑶吸取溶液 3分⑷放液 3分四、取25ml饱和硫酸铜溶液，用蒸发皿蒸发、浓缩评分标准：⑴正确选用量器（量筒：10ml、20ml、50ml；移液管25ml；滴定管50ml、刻度烧杯：50ml）1分⑵正确量取溶液 2分⑶正确选取蒸发皿 1分[4] 正确安装蒸发装置 1分[5] 正确蒸发操作 5分五、将乙酰苯胺重结晶：5g 乙酰苯胺重结晶、热过滤、减压过滤评分标准：⑴ 正确制备饱和溶液 2分热过滤准备滤纸漏斗选择操作4分2准备滤纸漏斗选择操作减压过滤4分[3]六、蒸馏装置的安装评分标准：⑴ 安装次序从下至上，从左至右（1分）⑵ 温度计的位置水银球上沿对着蒸馏头侧管下沿（1分）⑶ 冷凝水管的连接下进上出（2分）⑷ 安装部件加热器，蒸馏瓶，蒸馏头，冷凝管，接尾管，接收瓶（4分）⑸ 安装质量系统密闭性好，不漏气；装置安装端正、整齐（2分）七、带气体回收装置的回流装置的安装评分标准：⑴ 安装次序从下至上（2分）⑵ 安装部件加热器，石棉网，回流冷凝管，气体导管，玻璃漏斗，烧杯（内装吸收液）（3分）⑶ 冷凝水管的连接下进上出（2分）⑷ 漏斗与吸收液的相对位置漏斗上口（朝下）倾斜进入吸收液约三分之二（2分）⑸ 安装质量装置端正，接口不漏气（1分）八、二苯胺熔点（约53℃）测定装置的安装评分标准：⑴ 点管的制备折断毛细管，烧熔封闭管口（2分）⑵ 填样品蹾实，使样品进入熔点管底部（2分）⑶ 添加浴液加水于b 型管，液面略高于上支管（2分）⑷ 样品管与温度计的连接样品管贴于温度计表面，样品位于水银球中部，皮筋不得接触浴液（2分）⑸ 安装各部件酒精灯，b 型管（酒精灯火焰位于两支管交汇处），温度计（水银球位于两支管中部）（2分）九、丙酮（约56.2℃）沸点测定装置的安装评分标准：⑴熔点管内管的制备折断毛细管，烧熔封闭管口（2分）⑵加样品滴1—2滴样品于样品外管中（2分）⑶添加浴液加水于b型管，液面略高于上支管（2分）⑷安装内管倒插入外管样品中，样品管与温度计用皮筋套在一起，样品位于水银球中部，温度计插入b型管两支管之间，酒精灯火焰位于两支管交汇处，皮筋不得接触浴液（4分）十、索氏提取器的安装评分标准：⑴纸筒的制备直径略小于抽提筒，高度略高于虹吸管（2分）⑵加样品加样品于滤纸筒，样品低于虹吸管，将滤纸筒装入抽提筒，样品不得漏入抽提筒（3分）⑶安装次序从下至上（1分）⑷安装各部件加热器，蒸馏瓶，抽提筒，回流冷凝管（2分）[5] 冷凝水管的连接下进上出（2分）十一、混合物的分离[1] 制备氯化银沉淀（氯化钠+硝酸银）（2）[2] 离心分离（4）[3] 洗涤（3）[4] 仪器恢复（1）十二、萃取分离（1）分液漏斗的安装（3）（2）分离混合物（5）（3）仪器恢复（2）二、在510nm处测量一份溶液的吸光度。

csg2014年北大暑期体验营物理试题

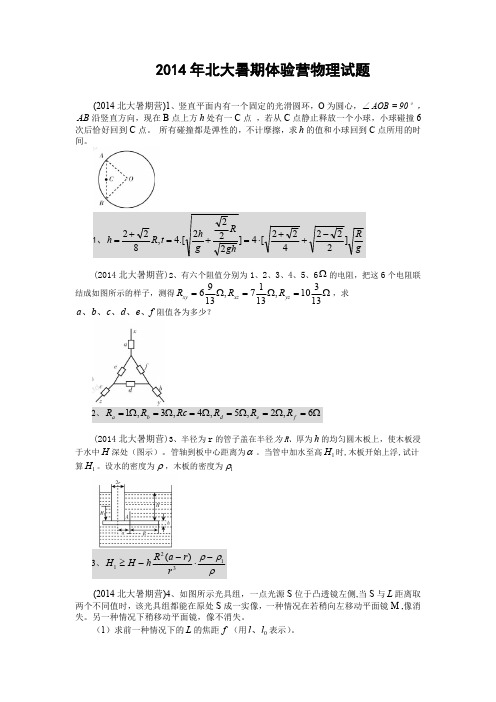
2014年北大暑期体验营物理试题(2014北大暑期营)1、竖直平面内有一个固定的光滑圆环，O 为圆心，∠AOB =90°，AB 沿竖直方向，现在B 点上方h 处有一C 点，若从C 点静止释放一个小球，小球碰撞6次后恰好回到C 点。

所有碰撞都是弹性的，不计摩擦，求h 的值和小球回到C 点所用的时间。

1、g R gh R g h t R h ]222422[4]2222.[4,822-++⋅=+=+=(2014北大暑期营)2、有六个阻值分别为1、2、3、4、5、6Ω的电阻，把这6个电阻联结成如图所示的样子，测得Ω=Ω=Ω=13310,1317,1396yz xz xy R R R ，求f e d c b a 、、、、、阻值各为多少？2、Ω=Ω=Ω=Ω=Ω=Ω=6,2,5,4,3,1f e d b a R R R Rc R R (2014北大暑期营)3、半径为r 的管子盖在半径为R、厚为h 的均匀圆木板上，使木板浸于水中H 深处（图示）。

管轴到板中心距离为α。

当管中加水至高1H 时,木板开始上浮,试计算1H 。

设水的密度为ρ，木板的密度为1ρ3、ρρρ1321)(-⋅--≥r r a R h H H (2014北大暑期营)4、如图所示光具组，一点光源S 位于凸透镜左侧,当S 与L 距离取两个不同值时，该光具组都能在原处S 成一实像，一种情况在若稍向左移动平面镜M ,像消失。

另一种情况下稍移动平面镜，像不消失。

（1）求前一种情况下的L 的焦距f （用0l l 、表示）。

（2）在（1）的情况下，将L 与M 的距离换为l l +02，现在距L 右侧0l 以外的某处放一个与L 相同的凸透镜，仍使S 能成像在原处，求放置的凸透镜L的距离。

(2014北大暑期营)5、在静止的实验室参照系中有两个飞船，实验室中测得它们的速度均为v ，在0=t 时它们位于原点并校准时间。

（1）实验系中当A 运动到距原点为l 处时原点发出一个光信号，求A 参照系中A 收到该信号的时刻。

关于2014北大物理科学营的情况介绍

关于2014北大物理科学营的情况介绍物理科学营从8月16日开始到8月20日结束，其中，16日报道，17日讲课，18日笔试，19日面试，20日宣布成绩并与部分学生签约。

全程不收取任何费用，并赠送北大85元的校园饭卡。

本次科学营与前几次不同，专门放在了9月份物理竞赛之前，目的是与清华竞争优秀生源，先于各种竞赛与优秀高中毕业生签约。

本次科学营的筛选方式是：向以往竞赛成绩优秀的地区和学校发送试题，由学校组织学生进行由北大命题的统一考试，考试分数达到一定标准方可进入该科学营（下称这次考试为“初试”）。

初试内容为140分的试卷，八道大题。

这次初试划定的分数线是110分。

北大在发送初试试题时，非常有地区侧重性。

有些偏远省份，北大根本没有给任何学校发试题，但一些竞赛大省，如浙江、湖北、湖南、北京、上海等所给名额比较多。

就16号的报名情况所了解的有这些：人大附中共13个学生进入科学营，杭州二中也有十多个学生，吉大附中有4个学生，浙江地区的学生达数十名。

因此从学生组成情况来看，这些学生的平均水平要比最终全国决赛的学生水平还要高。

17日上课内容主要有电介质、磁介质、阻尼振动、LCR振荡电路。

根据舒幼生老师（科学营的总顾问，未讲课，但领导出题与改卷）的介绍：“上课内容大约占第二天考试内容的1/4，主要考查学生是否有短时间之内学习新知识并使用新知识解决问题的能力，这也与国家队选拔和培训国际比赛的选手的方式相同。

”然而实际情况是，绝大多数学生这些内容都学习过了。

从濮心翼同学的笔记（课堂是不对外开放的，除了学生，其他人无法进入听课）来看，所讲授的内容难度并不是很大，主要是普物难度的东西。

18日笔试时间为下午1点30到5点30，共4小时。

全卷共8道题，160分满分。

考题的大致情况如下：第一题，力学碰撞问题。

第二题，球面镜成像，几何光学问题。

第三题，气态方程，热力学问题。

第四题，弹簧振子问题。

第五题，电流、静磁场的问题。

第六题，相对论，涉及到电磁问题。

2014夏令营考试题

华中师大一附中2014级夏令营摸底考试化学试题考试时间：120分钟总分：150分命题人：刘南可能用到的原子量：H: 1 N :14 C:12 O: 16 Na :23 K :39 Mg :24 P :31 S: 32 Ca :40 Fe: 56 Cl :35.5 Ba: 137 Br 80一、单项选择题（本题包括30小题，每小题3分，共90分）1．下列方法能鉴别空气、氧气和二氧化碳3 瓶气体的是A．闻气味B．将集气瓶倒扣在水中C．观察颜色D．将燃着的木条伸入集气瓶中2．下列物质必须密封保存的是A．木炭B．浓盐酸C．石灰石D．氯化钠3．下列不属于．．．新能源的是A．潮汐能B．太阳能C．风能D．石油4．下图表示的是碳及其化合物的相互转化关系：其中涉及的基本反应类型依次为 ( )A．置换、化合、分解、复分解 B．置换、化合、复分解、分解C．化合、置换、分解、复分解 D．化合、置换、复分解、分解5．下列图示的化学实验基本操作中，正确的是（）6. 下列各组物质发生的变化中，变化的本质均相同的一组是A. 少量酒精在空气中挥发不见了；少量酒精在空气中燃烧后消失B. 块状生石灰在空气中逐渐变成粉末；晶体碳酸钠在空气中逐渐变成粉末C. 木炭燃烧发光、发热；电灯发光发热D. 石灰水通入少量二氧化碳后变浑浊；室温下的饱和石灰水加热后变浑浊7. 如果将物质按单质、氧化物、酸、碱、盐、有机物分类，则甲、乙、丙是三类不同类别的物质，X能分别与甲、乙、丙发生化学反应，下列说法符合要求的是A. 当X为稀盐酸时，甲、乙、丙可以分别为铜、氢氧化铁、硝酸银B. 当X为氢氧化钙时，甲、乙、丙可以分别为二氧化碳、氯化铜、碳酸钠C. 当甲、乙、丙分别为酸、碱、盐时，X一定不可能为碳酸钠D. 当X 为氧气时，甲、乙、丙可以分别为氢气、一氧化碳、葡萄糖8. 下列除去物质中少量杂质（括号内为杂质）的方法中，不能达到目的的是A. CO 2气体(HCl):将气体通过足量的NaOH 溶液后干燥B. 铁粉(Fe 2O 3):通入足量的CO 气体加热后冷却C. CaO 固体(CaCO 3):将固体高温灼烧至质量不再减少不止D. NaCl 溶液(Na 2CO 3):逐滴滴加稀盐酸至不再产生气泡9．下列各组粒子，核外电子总数和质子总数均相同的是A ．S 2－和HS －B ．H 3O ＋和OH －C ．Na ＋和NH ＋4D ．K ＋和Ne10. 将过量CO 2逐渐通入NaOH 和Ca(OH)2的混合稀溶液中，生成沉淀的质量（m ）和通入CO 2的体积V 关系图，正确的是11．根据“绿色化学”的思想，某化学家设计了下列化学反应步骤：①CaBr 2+H 2O −−→−℃750CaO+2HBr ；②2HBr+Hg −−→−℃100HgBr 2+H 2↑；③HgBr 2+CaO −−→−℃750HgO+ CaBr 2； ④2HgO −−→−℃5002Hg+O 2↑。

乐清市2014年初中八年级科学竞赛试卷

乐清市2014年初中八年级科学知识与应用竞赛试题卷考生须知：1．本卷共4大题，29小题，考试时间120分钟，满分150分。

2．试卷分为试题卷(共8页)和答题卷(共4页)。

请在答题卷上写上学校、考生姓名、准考证号、座位号。

所有答案写在答题卷上，写在试题卷上无效。

3．可能用到的相对原子质量：H －1 C －12 O —16 Cl －35.5 K －39 Mn －55一、选择题（本大题有16题，每题3分，共48分，每题只有1个选项正确）1.两个敞口瓶，一个装满醋，一个装满花生油，放置在有阳光的窗台上。

几天后，观察到两个瓶中的液体都不满了。

从这个观察可以得到结论是（ ▲ ）A.醋蒸发得比花生油快B.花生油蒸发得比醋快C.醋和花生油都会蒸发D.只有含有水的液体才会蒸发2. 实验规范操作很重要。

下列实验操作符合规范要求的是（ ▲ ）A ．“配制一定溶质质量分数的溶液”实验中，多余的药品应放回原瓶B ．“高锰酸钾制取氧气”实验中，收集好气体后要及时停止加热，然后再将导管移出水槽C ．过滤时用蒸馏水洗涤滤纸上的硫酸钡沉淀，以除去其表面的可溶性杂质D ．使用滴瓶滴加试剂后，立即用蒸馏水洗净滴管并放回原瓶3. 如图所示的电路中，R X 为待测电阻，阻值约为5欧。

给你的器材有：滑动变阻器（2安，0～10欧）；电压表，有2个量程，分别为0～3伏、0～15伏；电流表，有2个量程，分别为0～0.6安、0～3安；电池组为新干电池3节串联。

两只电表的量程可采用以下4种选法，但为使测量时能较准确地读数，最后，两只电表的量程应采用（ ▲ ）A ．0～0.6安和0～3 伏B ．0～0.6安和0～15伏C ．0～3安和0～15伏D ．0～3安和0～3 伏4. 小梅家有一批盆栽的郁金香，过去一直开红色花，现在却开出了紫色的花，有人认为这是土壤中缺水引起的，但小梅经过一段时间补充水分后，还是开紫色的花。

这说明实验结果与原来的假设是不符合的，最好的处理方法是（ ▲ ）A ．实验不成功，停止探究B ．修改假设，重新实验C ．修改实验过程，使之与假设相符D ．修改结果，使之与假设相符5. 某科学家在20世纪70年代曾做过一次实验，将许多白色方块在草地上排成一长列，然后在1、2、4、6、8……方块上依次放上糖。

2014学年安洲中学八年级上科学选拔考试试卷正式卷

2014学年安洲中学八年级（上）应用科学竞赛试卷考生须知：1．本卷共二大题，30小题，考试时间60分钟，满分150分。

一、选择题（25* 4=100分。

每题只有一个选项是正确的）1、在煮饺子时，将饺子投入沸腾的水中，并用勺子轻轻在锅底推动沉下的饺子，等到水重新沸腾后，加上些凉水继续烧煮一会儿使水再次沸腾，这时煮热的饺子会浮出水面．熟饺子会浮起来的主要原因是（）A ．锅里的水量多了B ．饺子在水里经过烧煮变轻了C ．水温低时水对饺子的浮力小，水温高时水对饺子的浮力大D ．水沸腾后，饺子内的小部分水汽化后变成水蒸气，使饺子体积增大2、早晨，小明骑着自行车沿平直的公路驶向学校，强劲的北风迎面吹来，此时地面对车前轮的摩擦力为f 1，对车后轮的摩擦力为f 2。

则下列说法中正确的是（）A ．f 1与前进方向相反，f 1＜ f 2B ．f 2与前进方向相反，f 1＞f 2C ．f 1与前进方向相同，f 1 ＜f 2D ．f 2与前进方向相同，f 1＞f 23、、如图所示两个相同的光滑弧形槽，一个为凸形，一个为凹形，两个相同小球分别进入两弧形槽的速度都为V ，运动到槽末端的速度也都为V ，小球通过凸形槽的时间为1t ，通过凹形槽的时间为2t ，则1t 、2t 的关系为（）A 、12t t =B 、12t t >C 、12t t <D 、无法确定4、在图甲中，石料在钢绳拉力的作用下从水面上方以恒定的速度下降，直至全部没入水中。

图乙是钢绳拉力随时间t 变化的图像。

若不计水的摩擦力，则可算出该石料的密度为( )A.1.8×103千克/米3B.2.3×103千克/米3C.2.8×103千克/米 3D.3.2×103千克/米 35、雨滴在降落过程中，前段时间降落是加速的，后段时间是匀速的，它在前后两个阶段的受力情况分别是( )A.前段时间重力大于阻力，后段时间重力等于阻力B ．前段时间重力大于阻力，后段时间重力小于阻力C ．前段时间重力小于阻力，后段时间重力等于阻力D ．雨滴在整个下落过程中，都是重力大于阻力6、如图所示，一支试管口朝下插入水中，管内封闭有一定量的空气，在某一位置恰好悬浮在水中，当水的温度降低时，下列说法正确的是（）A．试管加速下沉 B．试管匀速下沉C．试管加速上浮 D．试管仍悬浮7、小明在一空玻璃杯中放入一块冰，并把它放在25℃的房间内，过一段时间后杯中仍有少量的冰没有熔化，则下列说法中正确的是（）A.冰的温度为0℃，剩余的冰继续熔化B.冰的温度为0℃，剩余的冰停止熔化C.冰的温度高于0℃，剩余的冰继续熔化D.冰的温度低于0℃，剩余的冰继续熔化8、若空间有一竖直放置的大凸透镜，在主光轴位置上拉一根钢丝，一个小杂技演员从很远的地方沿着钢丝向焦点处匀速走来。

2014浙江省宁波市中考科学真题及答案

2014浙江省宁波市中考科学真题及答案本卷可能用到的相对原子质量：H：1 C：12 O：16 Na：23 S:32 K：39 Cu：64试题卷 I一、选择题(本题共 20小题，第 l～10小题，每小题4分，第11～20小题．每小题3分，共70分。

请选出每小题中一个符合题意的选项，不选、错选均不给分)1．人类的生活和生产都离不开金属材料。

下列金属制品中，主要利用金属导热性的是（）2．今年“世界环境日”的主题是“提高你的呼声，而不是海平面”，海平面上升的主要原因是由于温室效应导致的全球气候变暖。

下列获取电能的途径会加剧温室效应的是（）A．火力发电 B．水力发电 C．风力发电 D．核能发电3．太阳为地球提供了光和热，同时太阳活动也会对地球产生不利影响。

下列现象肯定不是由太阳活动引起的是（）A．无线电通讯受干扰 B．地磁场发生磁暴C．昼夜长短规律性变化 D．气候发生明显变化4．小科对有关“人的生殖”知识作了右图归纳。

下列对图中①、②、③、④的判断，与事实不一致的是（）A．①----精子 B．②----卵巢C．③----受精卵 D．④----分娩5．如图是研究磁体周围磁场时的铁屑分布情况。

实验时， a、b、c三个位置所对应的磁极可能是（）A． N、N、N B． N、S、SC． N、N、S D． S、N、S6．2014年5月，德国亥姆霍兹重离子研究中心再次成功合成117号元素。

该元素已获正式名称“Ununseptium”，元素符号为Uus。

该原子的原子核内有ll7个质子，原子质量约是氢原子质量的291倍，是目前获得正式承认的最重的原子。

该原子的原子核外电子数为（）A ．1l7 B．174 C．291 D．4087．使用检索表对水稻、葫芦藓、肾蕨、松树和花生五种植物作如图所示分类，乙中除了水稻外，还有（）A．葫芦藓 B．肾蕨C．松树 D．花生8．在学习“物体运动状态改变的原因”时，老师做了如图的实验：具有一定速度的钢珠在水平面上能沿直线AB运动；如果在它的运动路径近旁放一磁铁，钢珠的运动路径将变成曲线AC。

2014年11月全国GIS应用水平考试参考答案(二级应用方向)

2014年11月全国GIS应用水平考试参考答案（二级应用方向）2014年11月全国GIS应用水平考试参考答案(二级应用方向)一、单选题:(本大题共50小题，每小题1分，共50分，每一小题只有一个正确答案，请把你认为正确的答案编号涂写到答题卡对应的位置上)。

1-5: B C A B C 6-10:B A B C D 11-15:C D A D A 16-20:D B D D C 21-25:A D D D D 26-30: B C B C C 31-35: D A A A C 36-40: B C C A B 41-45: B B D B C46-50: B C B B C二、多项选择题(本大题共5小题，每小题2分，共10分,每一小题有多个正确答案，请把你认为正确的答案编号填到对应的答题卡中，多选错选均不得分，少选一个扣1分)。

51: B C D 52: A C D 53: B C D 54: A B D 55: A B三、软件操作选择题(本大题共10小题，考生只能选择其中任意5题作答，每小题2分，满分10分，若作答超过5道题，将取考生所选前5道题评分;每一小题只有一个正确答案，请把你认为正确的答案选项涂写到答题卡对应的位置上)。

56-60: A D C B C 61-65: C B D C A四、名词解释: (本大题共5小题，每小题3分，共15分，请将答案填写在主观题目答题卡上)。

66、空间数据库引擎答:空间数据库引擎SDE采用客户/服务器体系结构，是高性能、面向目标的空间数据库管理系统，并提供一系列用于管理和访问大型分布式的地理数据的功能，SDE为系统开发者和集成商提供了一个高效能分布式和多用户的实时应用系统开发工具，它由一个多线程的空间数据库服务器和客户应用程序接口(API)组成。

67、监督与非监督分类答:监督分类 (supervised classification)又称训练场地法，是以建立统计识别函数为理论基础，依据典型样本训练方法进行分类的技术。