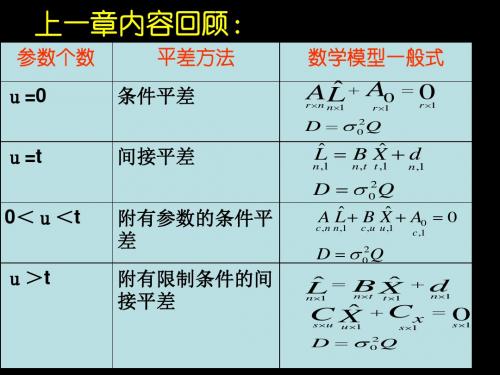
第三章 条件平差..

这些条件方程式（或改正数条件方程式），大体 上分为两类：其一是闭合路线情况，如条件方 程式中前四个条件方程式，可称为闭合条件方 程式；其二是附合路线情况，如条件方程式中 第五个，反应的是从A点出发后测得的B点的高 程值是否与 B 点的已知高程值相等的问题，可 称为附合条件方程式。
§3-3
平差值函数的协因数
T 1 QL ˆL ˆ Q QA N AQ
代入式得 Q f Q f f (Q QA N AQ) f 即 此式即为平差值函数式的协因数表达式。 该平差值函数的方差
FF T ˆL ˆ L T T 1
QFF f T Qf f T QAT N 1 AQf
测量平差
太原理工大学测绘科学与技术系
第三章
条件平差
第三章
§3-1
§3-2
条件平差
条件平差原理
高程网条件平差
§3-3
§3-4
导线网条件平差计算
三角网条件平差计算
§3-5
§3-6
附有参数的条件平差
条件平差估值的统计性质
§3-1
条件平差原理
n ,1 n ,n
n ,1
L 设在某个测量作业中，有n个观测值 ，均含有相互 V P 独立的偶然误差，相应的权阵为 ，改正数为 ， ˆ ，表示为 平差值为 nL ,1
§3-2
高程网条件平差
高程网包括水准网和三角高程网。对高 程网进行条件平差时，一般以已知高程 点的高程值作为起算数据，以各测段的 观测高差值作为独立观测值，写出其满 足的条件关系式，按照条件平差的原理 解算各高差值的改正数和平差值，然后 再计算出各待求点的高程平差值，并进 行精度评定。
高程网条件方程的个数及条件方程式
1 2 4
0 0 0 0
相对应的改正数条件方程式形式
v1 v 2 v 4 w1 0 v 2 v 3 v 5 w2 0 v 4 v 6 v 7 w3 0 v 5 v 7 v 8 w4 0 v 2 v 7 w5 0
V P 1 AT K P 1 AT (N 1 AL N 1 A0 ) P 1 AT N 1 AL P 1 AT N 1 A0
ˆ L V L (P 1 AT N 1 AL P 1 AT N 1 A ) (E P 1 AT N 1 A)L P 1 AT N 1 A L 0 0
p1 P n ,n
v1 v2 vn
p2
pn
ˆ L 1 ˆ ˆ L2 L n ,1 ˆ L n
条件平差原理
可以列出r个平差值线性条件方程
a1v1 a 2 v 2 a n v n wa 0 b1v1 b2 v 2 bn v n wb 0 r1v1 r2 v 2 rn v n wr 0
其中
高程网条件方程的个数及条件方程式
w1 (h1 h2 h4 ) w2 (h2 h3 h5 ) w3 (h4 h6 h7 ) w4 (h5 h7 h8 ) w5 (h2 h7 H A H B )
dV V 2 V 2V P 2 K A 0
V T P KT A 得 上式两端转置，得
P T V AT K
条件平差原理
由于P是主对角线阵，则 P = P T ，得 将上式两边左乘权逆阵P – 1，得
V P 1 AT K
PV AT K
此式称为改正数方程，其纯量形式为 1 v (a k b k r （ ik = )1，2，…，n） p 将上式代入，得
2 ˆ0 T
r
ˆ0
T
r
式中r为多余观测值个数，r = n – t。
协 因 数 阵
条件平差的基本向量L、W、K、V、都可以表达成 随机向量L的函数
LL
W AL A0
K N 1W N 1 ( AL A0 ) N 1 AL N 1 A0
协 因 数 阵
按协因数传播律，得Z的协因数阵为
ˆ L
QZZ
QLL QWL Q KL QVL Q ˆL L
QLW QWW Q KW QVW QL ˆW
Q LK QWK Q KK QVK QL ˆK
QLV QWV QKV QVV QL ˆV
Q LL ˆ Q QAT QWL ˆ AQ N N 1 AQ Q KL ˆ E T 1 T QA N AQ QA QVL ˆ Q QAT N 1 AQ 0 QL ˆL ˆ
2 ˆ0 DFF QFF
条件平差的计算步骤
（ 1）根据实际问题，确定出总观测值的个数n、必要观测 值的个数t及多余观测个数r = n - t，进一步列出最或是值 条件方程或改正数条件方程； （2）组成法方程式； （3）计算出联系数K； （4）计算出观测值改正数V；并计算出观测值的平差值； （5）计算单位权方差和单位权中误差； （6）列出平差值函数关系式，并对其全微分，求出其线 性函数的系数阵f，计算出平差值函数的协因数QFF ，计 算出平差值函数的协方差DFF。
QAT N 1 QAT N 1 AQ Q QAT N 1 AQ E AQ 0 1 1 N N AQ 0 QAT N 1 QAT N 1 AQ 0 T 1 0 0 Q QA N AQ
由上式可见，平差值与闭合差W、联系数K、改 正数V是不相关的统计量，又由于它们都是服 从正态分布的向量，所以与W、K、V也是相互 独立的向量。
)的
协因数QFF及其中误差 ˆ 的计算等。
计算单位权方差和中误差的估值
单位权中误差的计算公式为
ˆ0 [ p] r
在一般情况下，观测值的真误差△是不知 道的，也就不可能利用上式计算单位权 中误差。但在条件平差中，可以通过观 测值的改正数V来计算单位权方差和中误 差： V PV V PV
若取
a1 a 2 b b 2 A 1 r ,n r1 r2
an bn rn
a 0 b A0 0 r ,1 r0
wa w W b r ,1 wr
平差值函数的协因数
设有平差值函数
ˆ f (L ˆ ,L ˆ , , L ˆ ) F 1 2 n
对上式全微分得
ˆ f dL ˆ f dL ˆ f dF 1 2 L L L ˆ ˆ ˆ ˆ L ˆL 1 L 2 L n ˆ dL n ˆL L
高程网条件方程的个数及条件方程式
则多余观测个数r = n – t = 8 - 3 = 5，可以写出这5个 ˆ h ˆ h ˆ 0 h 条件方程式
ˆ h ˆ h ˆ h 2 3 5 ˆ h ˆ h ˆ h 4 6 7 ˆ h ˆ h ˆ h 5 7 8 ˆ h ˆ H H h 2 7 A B
进行条件平差时，首先要确定条件方程的个数。 从上节内容可知道，在一般情况下，条件方程式 的个数与多余观测的个数r相符。而要确定多余观 测个数就必须先确定必要观测个数t。 高程测量（包括三角高程测量和水准测量）的主 要目的是确定未知点的高程值。如图所示高程网 中，有2个已知高程点A、B，3个未知高程点C、D、 E和8个高差观测值。从图中可以看出，要确定3 个未知点的高程值，至少需要知道其中的3个高 差观测值（如h1、h2、h3，或h6 、h7 、h8 ，或h2、 h4 、h5 等多种选择），即必要观测个数t = 3。
上式两边左乘法方程系数阵N的逆阵N – 1，得 联系数K的唯一解： K N W 代入前式，可计算出V，再将V代入,即可计算出 ˆ L V 所求的观测值的最或然值。 L
1
精 度 评 定
2 ˆ0 精度评定包括单位权方差 和单位权中
误差
ˆ0
的计算、平差值函数(
F
ˆ) F f (L
L1 L L 2 n ,1 Ln
v1 v V 2 n ,1 v n
其中
在这n个观测值中，有t个必要观测数，多余观测 数为r。
ห้องสมุดไป่ตู้
ˆ L L1 1 ˆ L2 L2 ˆ L Ln n
式中，ai、bi、…、ri（i = 1,2,……n）为各平差值条件方 程式中的系数， a0、b0、…、r0 为各平差值条件方程式 中的常数项。相应的改正数条件方程式
ˆ a L ˆ a L ˆ a 0 a1 L 1 2 2 n n 0 ˆ b L ˆ b L ˆ b 0 b1 L 1 2 2 n n 0 ˆ r L ˆ r L ˆ r 0 r1 L 1 2 2 n n 0
i i a i b i r i
AP1 AT K W 0
此式称为联系数法方程（简称法方程）。
条件平差原理
取法方程的系数阵 AP-1AT = N，由上式易知N阵关 于主对角线对称，得法方程表达式
NK W 0
法方程数阵N的秩 即N是一个r阶的满秩方阵，且可逆。移项得
NK W
R( N ) R( AP1 AT ) r
将向量L、K、V、组成列向量，并以Z表示之
0 L E A W A 0 1 K N A0 N 1 A Z L 1 T 1 P A N A0 V P 1 AT N 1 A L 1 T 1 ˆ P A N A0 E P 1 AT N 1 A
上式可分别表达成矩阵形式如下