MATLAB图解精馏塔理论塔板数程序代码
MATLAB用二分法求解双组份精馏操作型计算

实用数值方法(Matlab) 小论文题目:用二分法求解双组份精馏操作型计算小组成员1.叙述问题在化工生产过程中,为了达到更好的生产效率,往往要进行设备的改良,改变其各项参数。
在这种情况下,为了对进行精馏的产品产物有一个直观的了解,往往需要先进行改变参数后结果的测算。
如以下情况:某精馏塔具有10块塔板,分离原料组成为摩尔分数0.25的苯-甲苯混合液,物系相对挥发度为2.47.已知在回流比为5,泡点进料时98.0'=D x ,085.0'=W x 。
今改用回流比8,塔顶采出率D/F及物料热状态均不变,求塔顶,塔底产品组成有何变化?2.分析问题此时的已知量为:全塔总板数N;相对挥发度或者相平衡曲线;原料组成F x 与热状态q ;回流比R;并规定塔顶馏出液的采出率D/F 。
待求的未知量为精馏操作的最终产果——产品组成D x ,W x 以及逐板的组成分布。
在这一题中,可以得到方程式()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--++=+++=-+=++提馏段操作线方程精馏段操作线方程相平衡方程____111____11____1111W n n D n n n n n x R D F x R D F R y R x x R R y x x y αα 在方程中,由于众多变量间的非线性关系,使操作型计算一般均通过试差法求解,即先假设一个塔顶(或塔底)组成,再用物料衡算及逐板计算予以校核的方法来解决。
3.建立模型根据方程组()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--++=+++=-+=++提馏段操作线方程精馏段操作线方程相平衡方程____111____11____1111W n n D n n n n n x R D F x R D F R y R x x R R y x x y αα可以得到一个关于预设值W x 与校核值W x 之间的关系式W W x x f =)(,将左边的式子右移,可以得到0)(=-W W x x f 。
基于MATLAB的精馏控制系统开发与仿真

过程控制三级项目说明书题目:精馏控制系统学院(系):电气工程学院年级专业: 13级仪表一班小组:第一组指导教师:摘要精馏塔是化工、石油化工、炼油生产过程中应用极为广泛的传质传热过程设备。
精馏过程的实质就是利用混合物中各组分具有不同的挥发度,实现各组分的分离。
精馏塔是一个多输入多输出的多变量过程,内在机理较复杂,动态响应迟缓,变量之间相互关联,在线测量困难,不同的塔工艺结构差别很大,而工艺对控制提出的要求又较高,所以确定精馆塔的控制方案是一个极为重要的课题。
此外,在全球金融危机的压力下,国内众多过程工业企业不仅面临着同行的竞争压力,同时也面临着来自国际间的市场挑战.在当前经济并不景气的大环境下,积极的开发和应用先进过程控制技术来提高企业的经济效益,增强企业自身的竞争力是过程工业迎接挑战的主要途径。
随着控制理论与计算机技术的发展,不仅为先进控制技术的应用奠定了理论基础,同样也提供了良好的软硬件平台。
近些年来,先进控制技术在实际工业过程中也取得了较好的成效,具有十分广泛的应用前景。
精馏过程因其大时滞、变量藕合、动态特性分析复杂、约束条件复杂且难以进行变量配对等特性成为过程控制界多年来理论研究和实践的热点。
本文针对工程训练任务书中给出的系统辨识函数,搭建了仿真框图,调整PID参数,最终使系统在较好的指标内达到稳定。
关键词:精馏塔仿真框图 PID参数目录1.精馏控制系统................................................3 1.1精馏工艺概述..............................................3 1.2精馏工艺的基本要求......................................4 2。
系统分析及方案选择..........................................43.控制对象的数学模型..........................................64.系统稳定性分析.......................................65.控制系统的参数整定..........................................8 6。
基于excel的精馏塔理论塔板数的图解法

基于excel的精馏塔理论塔板数的图解法精馏技术是炼油厂、石化厂和化工厂中最重要的过程之一,它是一种仅通过溶剂混合物中的分子亲和力而进行分离的技术。
其中,精馏塔理论塔板数(FBP)是精馏系统的重要参数,它直接关系到精馏系统的效率及能耗。
因此,开发一种准确计算FBP的方法非常重要,而基于Excel的精馏塔理论塔板数的图解法就是一种有效的计算FBP 的方法。
基于Excel的精馏塔理论塔板数的图解法是一种使用可视化方法计算精馏塔理论塔板数的一种方法。
它基于比蒙定律,即物质从差分压区移动时,温度和压力保持不变,唯一变化的参数是组分的构成。
根据该定律,我们可以使用FBP的曲线图来计算FBP的值,从而得出FBP的估算值。
图解法的算法如下:(1)首先,准备液体1和液体2的温度、压力和物质浓度数据;(2)把液体1和液体2转换成X-Y坐标;(3)绘制出X-Y坐标图表;(4)在图表上标出液体1和液体2的温度和压力;(5)在图表上从液体1到液体2的连线上作折线,折线来表示液体1和液体2物质浓度比的变化;(6)从折线上求出最低压力的坐标;(7)在最低压力的坐标位置标出精馏塔理论塔板数;(8)最终得出精馏塔理论塔板数的估算值。
此外,基于Excel的精馏塔理论塔板数的图解法还具有如下特点:(1)简单易操作,只需要准备液体1和液体2的数据;(2)准确性高,可以根据计算出来的折线图得出FBP;(3)具有良好的可视化效果,使我们能够很好地把握精馏塔理论塔板数的解。
综上所述,基于Excel的精馏塔理论塔板数的图解法是一种有效而可行的计算FBP的算法,它能够给出准确而准确的结果,在实际应用中具有重要意义。
未来,我们还可以改进这种方法,使其能够应用于更多的精馏塔系统,让精馏技术能够更好地发挥作用。
连续多组分三元精馏塔的模拟计算

function ConDistillclear allclcglobal F z1 z2 z3 R alpha1 alpha2 alpha3 M1 MN M Nt Nf V1 V D L L1 W F = 40; % 进料流量, kmol/hrR = 5; % 回流比z1 = 0.6; % 苯的进料组成(摩尔分率)z2 = 0.25; % 甲苯的进料组成(摩尔分率)z3 = 1-z1-z2; % 苯乙烯的进料组成(摩尔分率)M1 = 75; % 塔顶冷凝器中的滞液量(kmol)M = 10; % 塔板上的滞液量(kmol)MN = 150; % 塔釜中的滞液量(kmol)q = 1; % 饱和进料tf = 35;dt = 1;% 相对挥发度alpha1 = 2.75;alpha2 = 1;alpha3 = 0.4;Nt = 10; % 塔板总数Nf = 5; % 进料位置V1 = 150; % 从塔釜蒸发上来的蒸汽流量(kmol/hr)% 精馏段V = V1-(1-q)*F;D = V/(R+1); L = V-D;% 提馏段L1 = L+F;W = L1-V1;% 初始化x1和x2---开车时塔内所有板上的x1和x2分别与进料的z1和z2相同x1 = z1 * ones(1,Nt);x2 = z2 * ones(1,Nt);[t,y] = ode45(@DistMassBalances,[0:dt:tf],[x1 x2])% 输出结果x1 = y(:,1:Nt); % 苯的液相组成(摩尔分率)x2 = y(:,Nt+1:2*Nt); % 甲苯的液相组成(摩尔分率)x3 = 1-x1-x2; % 苯乙烯的液相组成(摩尔分率)plot(t,x1(:,1),'r-',t,x2(:,1),'k--',t,x3(:,1),'b:',t,x1(:,end),'r.-',t,x2(:,end),'k-.',t,x3(:,en d),'b.--')xlabel('Time (h)')ylabel('x_1_1, x_1_2, x_1_3, x_N_1, x_N_2, x_N_3')title('塔顶和塔釜产品从进料开始直至稳态的动态浓度曲线')legend('x_1_1','x_1_2','x_1_3','x_N_1','x_N_2','x_N_3')% 稳态图figureplate = 1:Nt;plot(plate,x1(end,:),'r.-',plate,x2(end,:),'k.--',plate,x3(end,:),'b.:')xlabel('塔板')ylabel('稳态时苯,甲苯,苯乙烯的组成')title('稳态时精馏塔的浓度曲线')legend('苯','甲苯','苯乙烯')% ------------------------------------------------------------------function dydt = DistMassBalances(t,y) % 物料平衡方程组global F z1 z2 z3 R alpha1 alpha2 alpha3 M1 MN M Nt Nf V1 V D L L1 W x1 = y(1:Nt); % 组分1(苯)x2 = y(Nt+1:2*Nt); % 组分2(甲苯)x3 = 1-x1-x2; % 组分3(苯乙烯)% 气相平衡denom = alpha1*x1+alpha2*x2+alpha3*x3;y1 = alpha1*x1./denom;y2 = alpha2*x2./denom;% 对塔顶冷凝器(i = 1)i = 1;dx1dt(i) = (V*y1(i+1)-(L+D)*x1(i))/M1;dx2dt(i) = (V*y2(i+1)-(L+D)*x2(i))/M1;% 精馏段(i = 2~Nf-1)for i=2:Nf-1dx1dt(i) = (L*(x1(i-1)-x1(i))+V*(y1(i+1)-y1(i)))/M;dx2dt(i) = (L*(x2(i-1)-x2(i))+V*(y2(i+1)-y2(i)))/M;end% 进料板(i = Nf)i = Nf;dx1dt(i) = (F*z1+L*x1(i-1)-L1*x1(i)+V1*y1(i+1)-V*y1(i))/M;dx2dt(i) = (F*z2+L*x2(i-1)-L1*x2(i)+V1*y2(i+1)-V*y2(i))/M;% 提馏段(Nf+1~Nt-1)for i=Nf+1:Nt-1dx1dt(i) = (L1*(x1(i-1)-x1(i))+V1*(y1(i+1)-y1(i)))/M;dx2dt(i) = (L1*(x2(i-1)-x2(i))+V1*(y2(i+1)-y2(i)))/M;end % 塔釜(i = Nt)i = Nt;dx1dt(i) = (L1*x1(i-1)-V1*y1(i)-W*x1(i))/MN;dx2dt(i) = (L1*x2(i-1)-V1*y2(i)-W*x2(i))/MN;function BatchDistill% 假设:% 1. 沸腾上升的蒸汽流量(V)恒定;% 2. 下降的液体摩尔流量(L)恒定;% 3. 塔板上的滞液量(M)恒定;% 4. 再沸器和塔顶冷凝器中的滞液量恒定。
图解法绘塔板图并求塔板数的matlab程序

plot(x_w*ones(1,1000),linspace(0,0.8,1000),'k:','LineWidth',0.75);hold on;
plot(x_d*ones(1,1000),linspace(0,0.8,1000),'k:','LineWidth',0.75);hold on;
functionnfunmaina1b1a2b2a1b1为精馏段方程ya1xb1a2b2为提馏段方程ya2xb2n为总塔板数不包括再沸器symsxyx0
function N=funmain(a1,b1,a2,b2)
%%a1,b1为精馏段方程y=a1x+b1
%%a2,b2为提馏段方程y=a2x+b2
%%N为总塔板数(不包括再沸器)
N2=length(find(A0~=0));
%t=0.0001;%%间距
M=[x_d;X0];
N=[Y0([1:length(X0)],1);B0(1,1)];
O=[B0;x_w];
for i=1:N1
p=linspace(M(i+1),M(i),1000);
q=Y0(i)*ones(1,length(p));
f=B0(j+1)*ones(1,length(e));
plot(e,f,'LineWidth',2);hold on;
g=linspace(O(j+1),O(j+2),1000);
h=A0(j+1)*ones(1,length(g));
plot(h,g,'LineWidth',2);hold on;
MATLAB图解精馏塔理论塔板数程序代码

MATLAB图解精馏塔理论塔板数程序代码function distillation %文件名“distillation”可以更改% 输入计算所需参数q=1;%输入进料热状况参数R=;%输入回流比xD=;%输入塔顶轻组分摩尔分数xW=;%输入塔底轻组分摩尔分数xF=;%输入进料轻组分摩尔分数%以下输入相平衡数据x0=[01]; y0=[01];Yr=@(x)R/(R+1).*x+xD/(R+1);%精馏段操作线fun=@(x)(q-1)*(R/(R+1).*x+xD/(R+1))-(q*(x-xF)+(q-1)*xF); xQ=fzero(fun,;%求操作点yQ=Yr(xQ);xOP=[xW,xQ,xD];yOP=[xW,yQ,xD];yfit=linspace(0,1,1001);xfit=interp1(y0,x0,yfit,'pchip');%%绘制图形hold onbox onplot([0 1],[0 1],'k');xlabel('x')ylabel('y')plot(x0,y0,'r')plot(xfit,yfit,'r-')plot(xF,xF,'b*')plot(xQ,yQ,'bo')plot(xOP,yOP,'b-')k=1;yn(1)=xD;xn(1)=interp1(y0,x0,yn(1),'pchip');plot([xD,xn(1)],[yn(1),yn(1)],'b-')text(xn(1),yn(1),num2str(1),...'HorizontalAlignment','center','VerticalAlignment','bottom') while xn(k)>xWyn(k+1)=interp1(xOP,yOP,xn(k));k=k+1;xn(k)=interp1(y0,x0,yn(k),'pchip');plot([xn(k-1),xn(k-1)],[yn(k-1),yn(k)],'b-')plot([xn(k-1),xn(k)],[yn(k),yn(k)],'b-')text(xn(k),yn(k),num2str(k),...'HorizontalAlignment','center','VerticalAlignment','bottom' ) endN=k;plot([xn(N),xn(N)],[yn(N),xn(N)],'b-')text(xn(N),yn(N),num2str(N),...'HorizontalAlignment','center','VerticalAlignment','bottom' )N_Feed=find(xn<xF);N_Feed=N_Feed(1);text,,{strcat('所需理论板:',num2str(N)),...strcat('进料板位置:',num2str(N_Feed))},...'HorizontalAlignment','left','VerticalAlignment','top')%以下代码是为了去掉顶端和右边坐标轴的刻度box offax2 = axes('Position',get(gca,'Position'),... 'XAxisLocation','top',... 'YAxisLocation','right',... 'Color','none',...'XColor','k','YColor','k'); set(ax2,'YTick', []);set(ax2,'XTick', []);box on运行结果如图1所示:图1 图解苯-甲苯精馏塔理论塔板数和进料位置 00.10.20.30.40.50.60.70.80.9100.10.20.30.40.50.60.70.80.91x y。
MATLAB辅助下化工原理精馏单元计算探讨

序, 同时 对典 型例题 进行 了求解 分析 , 得到 了 良好
的结果 .
1 双组 分 精 馏 的设 计 型 计算
设计 型计 算 的任 务 是 根 据规 定 的分 离 要求 , 选 择精 馏 的操 作条 件 , 算所 需要 的理论 板数 . 计 规
定 分离 要求是 对 塔 顶 、 塔底 产 品 的质量 和 数 量 提
例 2g 在一 常压 连续 精 馏 塔 中分 离 乙 醇水 [ ]
溶液 , 料液 组成 z 为 0 3 泡点进 料 . 求馏 出液 ., 要 组成 z 。为 0 8 , 液 组 成 3 .4釜 2 w为 0 2 取 回流 比 .. 为最小 回流 比的 1 5倍 . 图解 法 求 所 需理 论 板 . 用
论 知识 解决 实际 工程 问题 的能力 , 有概念 多 、 具 公 式 多 、 算过 程 复 杂 、 程 概 念 强 等特 点 Ⅲ. 主 计 工 其 要是 以化工 生产 中 的单 元操 作 为 内容 , 以动 量 传 递、 热量 传递 和 质量 传 递 和 研 究 方法 论 为 主 线 组
线.
具体 步 骤为 [ 从塔 顶 ( 可从 塔 底 ) 始进 行逐 板 也 开
计算 ] :
( ) 1 ( ) 2 ( ) 1
f通 过 w i . hl 环 语 句 连 续 绘 制 阶 梯 , 算 e循 计
理论 板数 . 同样 对 于上述 问题 求 出结果 见 图 2 .
XD —
feo ) zr ( 函数 , 过 whl 和 i语 句 简 洁快 速 的求 通 i e f 出结 果见 图 1 而且 我 们 设 计 的程 序 具 有 普 遍 性 . 的特 点 , 只要稍 加 修 改 就 能适 应所 有 这 类 题 算 结 果 的 可靠 性 . 们 在 我 实际 中遇 到 的物 系大 都 偏 离 理 想 体 系 , 出相 对 给 挥 发度 进 行求解 准确 度 不 高 , 以很 多 化工 原 理 所
精馏塔理论塔板数与c语言编程计算

# include <stdio.h># include <malloc.h># include <stdlib.h>void main (){long double *y=NULL,*x=NULL,a=0.0,R=0.0,R1=0.0,xf=0.0,xd=0.0,xw=0.0;int ii=0,ij=0,num=0,num1=0,a1=1;printf("估计需要多少塔板:");scanf ("%d",&num1);y=(long double *)malloc(sizeof(long double)*num1);x=(long double *)malloc(sizeof(long double)*num1);printf("输入相对挥发度α:");scanf ("%lf",&a);printf ("输入精馏段回流比R:");scanf("%lf",&R);printf ("输入精馏段回流比R1:");scanf("%lf",&R1);printf ("输入进料易挥发组分摩尔分数xf:");scanf("%lf",&xf);printf ("输入塔顶易挥发组分摩尔分数xd:");scanf("%lf",&xd);printf ("输入塔釜易挥发组分摩尔分数xw:");scanf("%lf",&xw);printf ("开始计算理论踏板\n");*y=xd;for (ii=0;ii<=num1;ii++){*(x+ii)=*(y+ii)/(a-(a-1)*(*(y+ii)));printf("根据相平衡关系式x%d=%lf\n",ii+1,*(x+ii));if (*(x+ii)<=xw){printf("理论踏板%d\n",num);break;}if (*(x+ii)>=xf){*(y+ii+1)=R/(R+1)*(*(x+ii))+xd/(R+1);printf ("根据精馏段操作线方程y%d=%lf\n",ii+2,*(y+ii+1));num++;printf("第%d块板\n",num);}else{while(a1){printf("\n第%d块板是最佳进料板\n\n",ii+1);a1=0;}*(y+ii+1)=(R1+1)/R1*(*(x+ii))+xw/R1;printf ("根据提馏段操作线方程y%d=%lf\n",ii+2,*(y+ii+1));num++;printf("第%d块板\n",num);}}}。
基于MATLAB_SIMULINK的间歇精馏模拟研究

第20卷 第2期 吉 林 化 工 学 院 学 报Vol.20No.2 2003年6月JOURNAL OF J IL IN INSTITU TE OF CHEMICAL TECHNOLOGYJ un. 2003收稿日期:2002-10-07作者简介:魏奇业(1964-),男,山东蓬莱人,在读博士,吉林化工学院副教授,主要从事化工系统工程方面的研究. 文章编号:100722853(2003)022*******基于MAT LAB/SI MU LI NK 的间歇精馏模拟研究魏奇业(吉林化工学院化学工程系,吉林吉林132022)摘要:建立了间歇精馏塔的数学模型,在MA TLAB/SIMUL IN K 中用S -函数编制了间歇精馏塔的模拟程序,相平衡计算采用严格的热力学模型,该方法为间歇精馏的设计及操作提供了参考.关 键 词:间歇精馏;模拟;MA TLAB/SIMUL IN K 中图分类号:TQ 018 TQ 028.1+1 文献标识码:A 间歇过程具有灵活多变的特性,可以用同一套多用途、多功能的设备生产多种类型的产品,主要用于食品、聚合物、药品、分子筛、增塑剂、抗氧剂、染料和涂料等产品的生产.由于间歇精馏是一种非稳态的传质过程,因此对间歇精馏的模拟要比连续精馏复杂得多,模型的研究报道也相应少得多.近年来,关于间歇精馏的研究受到国内外学者的普遍重视,取得了较大的进展[1~4].间歇精馏塔的计算实际上是求解非线性微分方程和代数方程的问题,MA TLAB 的出现为解决这类问题提供了有利的条件.MA TLAB 是Math 2Works 公司开发的一种面向科学和工程计算的高级语言,现已成为国际公认的最优秀的科技界应用软件,在世界范围内广为流行和使用[5].SIMUL IN K 以工具库的形式挂接在MA TLAB上,是一个进行动态系统建模、仿真和综合分析的集成软件包.在MA TLAB/SIMUL IN K中有三个用于求解非刚性微分方程组的求解器,适合各种非刚性问题的求解.所有求解困难的问题不一定都是刚性的,但所有刚性问题对于没有经过特殊设计的求解器来说是困难的.在MA TLAB/SIMUL IN K 中刚性问题求解器可以像其它求解器一样精确使用,而且可以为求解器提供问题的额外信息使求解效率显著提高,在MA TLAB/SIMUL IN K 中提供了四种刚性问题的求解器[6].1 间歇精馏塔的模拟1.1 间歇精馏塔的数学模型间歇精馏塔塔板的示意图见图1,塔内有N 22块塔板,自上而下,将冷凝器和塔顶贮罐作为第一块塔板,再沸器和塔釜作为第N 块塔板.推导模型需做如下简化假设:(1)每块塔板上液相充分混合,且温度分布均匀;(2)每块塔板上汽相滞留量忽略不计,液相滞留量不变(蒸馏釜除外);(3)塔板间汽、液相传递滞后忽略不计;(4)汽、液两相在塔板上达到平衡;(5)绝热操作.在此基础上进行了模型的推导并简化整理得到如下方程.蒸馏釜物料平衡方程:dd t ΛN=-D (1)组分物料平衡方程:d x i ,1d t=V 2y i ,2-V 1y i ,1-(L 1+D )x i ,1Λ1(2)i =1,…,Cd x ij d t V j+1y i,j+1+L j-1x i,j-1-V j y i,j-L j x i,jΛj(3) j=2,…,N-1 i=1,…,Cd x i,Nd t=L N-1x i,N-1+Dx i,N-V N y i,NΛN(4)i=1,…,C摩尔分率归一方程:6Ci=1x i,j=6C i=1y i,j=1.0(5) j=1,…,N i=1,…,C相平衡方程:y i,j=K i,j x i,j(6) j=1,…,N i=1,…,C汽液相流率计算式:V j+1=L j-1(h j-h j-1)+V j(H j-h j)H j+1-h j(7)j=2,…,N-1L j=V j+1-D(8) j=1,…,N-11.2 间歇精馏塔S2函数的建立在SIMUL IN K中进行间歇精馏塔的模拟计算,S2函数的建立是关键.建立S2函数时首先需确定过程的输入、输出和状态变量[7].在本文间歇精馏塔的模拟计算中,过程的输入变量为回流比,这是因为在计算时需调整回流比以便找出回流比与产品采出时间的关系.为了得到塔顶馏出物的液相组成随时间的变化曲线,设定S2函数的输出变量为塔顶馏出物的液相组成,S2函数的状态变量设为各塔板的液相组成.本文的相平衡采用PR 方程计算.2 应用实例一间歇精馏塔,有8块理论板,欲分离含4组分,摩尔组成分别为丙烷0.1,正丁烷0.3,正戊烷0.1,正己烷0.5的混合物,塔釜一次加料50 kmol,塔顶压力为102kPa,塔底压力为125kPa.精馏开始阶段采用全回流操作,计算时各塔板的液相组成初值设为与塔釜相同,当塔顶液相组成稳定后,在塔顶以2kmol/h的速率采出液相馏分,整个操作过程时间设为25h,该区间内塔顶液相组成的变化见图2.由该图可以看出,在1.5~3h时间段内塔顶采出的是丙烷含量99%以上的产物,采出累计量为3kmol;在6~11h时间段内塔顶采出的是正丁烷含量98%以上的产物,采出累计量为10kmol;18h以后采出的产物几乎全部是正己烷.图2 间歇精馏塔顶液相组成随时间的变化曲线3 结 论(1)在MA TLAB/SIMUL IN K中进行间歇精馏塔的模拟,编程时间短,程序运行易于收敛,也可用SIMUL IN K的控制模块进行控制规律的研究.(2)对间歇精馏过程的模拟,既可以为实际操作提供参考,也可以优化操作参数.(3)利用间歇精馏模拟得到的塔内汽液相流率及塔顶、塔釜热负荷,可进行设备的设计和核算.符 号 说 明C———组分数D———精馏塔顶馏出液的流量,kmol/hH———汽相焓值,kJ/kmolK———相平衡系数L———塔内液相流量,kmol/hN———精馏塔理论板数V———塔内汽相流量,kmol/hh———液相焓值,kJ/kmolt———时间,hx———液相组成y———汽相组成Λ———持液量,kmol下标2 吉 林 化 工 学 院 学 报2003年 i ———各组分j ———各理论板参考文献:[1] Rodriguez 2Donis I ,Pardillo 2Fontdevila E ,G erbaudV ,et al.Synthesis ,experiments and simulation of heterogeneous batch distillation processes [J ].Com 2puters and Chemical Engineering ,2001,25(4-6):799-806.[2] D üssel R ,Stichlmair J.Separation of azeotropic mix 2tures by batch distillation using an entrainer [J ].Computers and Chemical Engineering ,1995,19(Sup 2plement 1):113-118.[3] 陈俸荣,周荣琪,段占庭.间歇真空精馏过程的简捷设计[J ].石油化工,1997,26(10):687-690.[4] 李文秀,胡国良,张万忠.间歇精馏过渡馏分脉冲馏出规律研究[J ].化学工程,1999,27(1):11-14.[5] 魏奇业,华贲,高维平,等.醋酸生产的仿真研究(Ⅰ)———原料系统的仿真[J ].化工自动化及仪表,2002,29(4):17-20.[6] MathWorks Inc.MA TLAB The Language of Techni 2cal Computing[Z].US :Math works Inc ,1998.[7] MathWorks Inc.SIMUL IN K/Model 2Based and Sys 2tem 2Based Design[Z].US :Math works Inc ,1998.Simulation of batch distillation based on MAT LAB/SIMU L INKWEI Qi 2ye(Dept.of Chemical Engineering ,Jilin Institute of Chemical Technology ,Jilin City 132022,China )Abstract :Mathematical models of batch distillation column are presented.The S 2function in MA TLAB/SIMUL IN K is used to programming the simulation programs of batch distillation column ,and the rigorous thermodynamics model is used to calculate phase equilibrium.The method provides references for the design and operation of batch distillation.K ey w ords :batch distillation ;simulation ;MA TLAB/SIMUL IN K3 第2期魏奇业:基于MATLAB/SIMUL IN K 的间歇精馏模拟研究 。
01-MATLAB精馏塔塔板数计算

2 MATLAB
高效方便的矩阵和数组运算 编程效率高(库函数丰富) 方便的绘图工具 结构化、面向对象 用户使用方便 功能强大的工具箱
• 将MATLAB运用到精馏塔塔板数的计算中, 有利于简化计算。 • 本文将以MATLAB软件为平台,以双组份 物系为例,针对精馏塔理论塔板数的计算 问题进行探讨。
MATLAB精馏塔塔板数计算
1111
目录
引言 MATLAB 精馏操作
案例
解题思路 计算结果 结果讨论
1引 言
• 精馏塔是在化工生产过程中经常使用的分离设备, 广泛应用于石油化工中。 • 在精馏塔的设计中,塔板数的确定是非常重要的。 精馏塔塔板数的计算比较复杂和烦琐,计算过程中 囊括了精馏单元操作中几乎所有的基本原理和计算 方法。
以轻易得到所设计的精馏塔理论塔板数。
• 应用MATLAB求解二元精馏塔理论板数,方法简 单实用,可以方便快捷得到计算结果,并且可以 开发具有一定通用性的计算程序。
Thank you !
3 精馏操作
• 精馏塔是进行精 馏操作的一种塔 式气液接触装置。
4 案例
• 某双组份理想混合液用常压精馏塔进行分 离。进料组成含 A 81.5%, 含 B 18.5%( 摩尔百分数,下同) , 饱和液体进 料, 塔顶为全凝器, 塔釜为间接蒸气加热。 要求塔顶产品为含 A 95%, 塔釜为含B 95%, 此物系的相对挥发度为 2.0, 回流 比为 4.0。设计所需的理论板层数 NT。
5 解题思路
逐板计算
xD y1
x1 x2 x3
xn xF
y2பைடு நூலகம்y3 yn
相平衡方程 操作线方程
化工原理
yn1 ym
化原实验精馏实验报告

北京化工大学学生实验报告学院:化学工程学院姓名:学号:专业:化学工程与工艺班级:同组人员:课程名称:化工原理实验实验名称:精馏实验实验日期北京化工大学实验五精馏实验摘要:本实验通过测定稳定工作状态下塔顶、塔釜及任意两块塔板的液相折光度,得到该处液相浓度,根据数据绘出x-y图并用图解法求出理论塔板数,从而得到全回流时的全塔效率及单板效率。
通过实验,了解精馏塔工作原理。
关键词:精馏,图解法,理论板数,全塔效率,单板效率。
一、目的及任务①熟悉精馏的工艺流程,掌握精馏实验的操作方法。
②了解板式塔的结构,观察塔板上汽-液接触状况。
③测定全回流时的全塔效率及单塔效率。
④测定部分回流时的全塔效率。
⑤测定全塔的浓度(或温度)分布。
⑥测定塔釜再沸器的沸腾给热系数。
二、基本原理在板式精馏塔中,由塔釜产生的蒸汽沿塔逐板上升与来自塔顶逐板下降的回流液,在塔板上实现多次接触,进行传热与传质,使混合液达到一定程度的分离。
回流是精馏操作得以实现的基础。
塔顶的回流量与采出量之比,称为回流比。
回流比是精馏操作的重要参数之一,其大小影响着精馏操作的分离效果和能耗。
回流比存在两种极限情况:最小回流比和全回流。
若塔在最小回流比下操作,要完成分离任务,则需要无穷多塔板的精馏塔。
当然,这不符合工业实际,所以最小回流比只是一个操作限度。
若操作处于全回流时,既无任何产品采出,也无原料加入,塔顶的冷凝液全部返回塔中,这在生产中午实际意义。
但是由于此时所需理论板数最少,又易于达到稳定,故常在工业装置的开停车、排除故障及科学研究时采用。
实际回流比常取最小回流比的1.2~2.0倍。
在精馏操作中,若回流系统出现故障,操作情况会急剧恶化,分离效果也将变坏。
板效率是体现塔板性能及操作状况的主要参数,有以下两种定义方法。
(1)总板效率EE=N/Ne式中 E——总板效率;N——理论板数(不包括塔釜);Ne——实际板数。
(2)单板效率EmlEml =(xn-1-xn)/(xn-1-xn*)式中 Eml——以液相浓度表示的单板效率;xn ,xn-1——第n块板和第n-1块板的液相浓度;xn*——与第n块板气相浓度相平衡的液相浓度。
AutoCAD图解法求精馏塔理论塔板数

AutoCAD图解法求精馏塔理论塔板数精馏塔作为化工领域中常见的重要设备,其理论塔板数的确定对于塔的设计与性能评估具有关键意义。
本文将介绍一种基于AutoCAD图解法来求解精馏塔理论塔板数的方法。
1. 理论塔板数的定义与意义在精馏塔中,理论塔板数是指在保持给定塔顶与塔底温度差的情况下,需要多少个塔板才能将原料分离成所需的产品。
理论塔板数的确定可以帮助工程师评估塔的高度、直径和效率等关键参数,从而指导塔的设计和操作。
2. AutoCAD图解法的原理AutoCAD是一种功能强大的计算机辅助设计软件,可用于绘制平面、三维模型等。
在应用AutoCAD求解精馏塔理论塔板数时,我们可以利用该软件绘制塔的剖面图,并进行塔板的定位和标记,以便进行塔板的数值计算和分析。
3. 基于AutoCAD的求解步骤(1) 绘制塔的剖面图:利用AutoCAD绘制精馏塔的剖面图,包括塔的截面形状、塔底和塔顶位置等。
(2) 定位塔板:在剖面图中利用AutoCAD工具对塔板进行定位,并进行标记。
(3) 确定塔板高度:利用AutoCAD测量每个塔板的高度,并记录下来。
(4) 计算理论塔板数:根据已知的设计要求和分离效果,利用AutoCAD进行数值计算,得到理论塔板数。
4. 精馏塔理论塔板数求解实例为了更好地说明AutoCAD图解法的求解过程,假设我们需要设计一个精馏塔,并确定其理论塔板数。
利用AutoCAD进行如下操作:(1) 绘制塔的剖面图:绘制塔的剖面图,包括塔的截面形状、塔底和塔顶位置。
(2) 定位塔板:利用AutoCAD工具对塔板进行定位,并进行标记。
(3) 确定塔板高度:利用AutoCAD测量每个塔板的高度,并记录下来。
(4) 计算理论塔板数:根据设计要求和分离效果,利用AutoCAD进行数值计算,得到理论塔板数为10个。
5. 确定塔板数后的进一步分析一旦得到了理论塔板数,我们可以进一步分析塔的性能和参数。
(1) 塔的高度确定:根据理论塔板数,可以确定塔的总高度,从而指导塔的设计。
基于Excel的精馏塔理论塔板数的图解法

(4)
(3)提馏段操作线方程
y
RD qF FD x xW ( R 1) D (1 q) F ( R 1) D (1 q) F
(5)
(4)q 线方程
y q x x F q 1 q 1
(6)
2.2 有关计算和图表绘制
根据分离要求(塔顶、塔底和进料组成 xD,xW,xF)、进料状态 q 值和回流比 R 值,进行 以下计算: (1)根据精馏段操作线方程和 q 线方程,求出两条线的交点 d,坐标为(xd,yd)
Sub hong() Dim xcz(100) As Variant Dim ycz(100) As Variant Dim xph(100) As Variant Dim yph(100) As Variant Dim u(100) As Variant Dim v(100) As Variant For i=1 To 100 u(i)=ActiveSheet.Cells(i, 6) v(i)=ActiveSheet.Cells(i, 5) If u(1)=1 And u(i)=0 Then nph=i If u(1)=0 And u(i)=1 Then nph=i Next i xa=ActiveSheet.Cells(1, 15) ya=ActiveSheet.Cells(1, 15) xb=ActiveSheet.Cells(2, 15) yb=ActiveSheet.Cells(2, 15) q=ActiveSheet.Cells(3, 15) R=ActiveSheet.Cells(4, 15) xf=ActiveSheet.Cells(5, 15) xd=((xa/(R+1))+(xf/(q-1+1e-10))) / ((q/(q-1+1e-10))-(R/(R+1))) yd=q/(q-1+1e-10)*((xa/(R+1))+ (xf/(q-1+1e-10)))/((q/(q-1+1e-10)) -(R/(R+1)))-xf/(q-1+1e-10) ActiveSheet.Cells(6, 15)=xd ActiveSheet.Cells(6, 16)=yd xc=xa yc=ya For i=1 To 100 xcz(i)=xc ycz(i)=yc xc=chazhi(u, v, yc, nph) xph(i)=xc yph(i)=yc ActiveSheet.Cells(i, 1)=xph(i) ActiveSheet.Cells(i, 2)=yph(i) ActiveSheet.Cells(i*2-1, 11)=xcz(i) ActiveSheet.Cells(i*2-1, 12)=ycz(i) ActiveSheet.Cells(2*i, 11) =xph(i) ActiveSheet.Cells(2*i, 12) =yph(i) If xc<xd Then xab=xb yab=yb Else xab=xa yab=ya End If yc=(yab-yd)/(xab-xd)*(xc-xd)+yd If xph(i-1)>xd And xph(i)<xd Then ActiveSheet.Cells(5,8)=i-1+(xph(i-1)-xd)/ (xph(i-1)-xph(i)) ActiveSheet.Cells(4,8)=i-1+(xph(i-1)-xb)/ (xph(i-1)-xph(i)) If xc<xb Then End Next i End Sub Function chazhi(x, y, u, nph) n=nph For k=1 To n-1 If (u-x(k))*(u-x(k+1))<=0 Then GoTo 10 Next k If (u-x(1))*(u-x(n))<=0 Then k=1 Else k=n-1 10 G=(u-x(k))*(u-x(k+1)) If k=n-1 Or k<>1 And G Then k=k-1 v=0 For i=k To k+2 L=1 For j=k To k+2 If i<>j Then L=L*(u-x(j))/(x(i)-x(j)) Next j v=v+L*y(i) Next i chazhi=v End Function
化工原理实验——精馏实验

(8)
式中:
q
1kmol进料变为饱和蒸汽所需热量 1kmol料液的汽化潜热
1
C
pF
(t s rF
tF
)
ts — 进料液的泡点温度,℃; tF — 进料液的温度,℃;
(9)
CpF — 进料液在平均温度 (ts tF ) 下的比热,kJ/kg·K; 2
rF — 进料液组成下的汽化潜热,kJ/kg。 实验中根据进料液取样可得到 xF,并测量其进料温度 tF,再查附表可得 ts、CpF,rF,由式(9) 即可得到 q,代入式(8)即可得到 q 线方程。
(一)全回流操作时的全塔效率 ET 和单板效率 EmV(4)的测定
1.全塔效率(总板效率)ET
ET
NT
1 100%
NP
(1)
式中:NT — 为完成一定分离任务所需的理论板数,包括蒸馏釜; NP — 为完成一定分离任务所需的实际板数,本装置 NP=7 块。
在全回流操作时,操作线在 x—y 图上为对角线。根据实验中各所测定的塔顶组成 xD、 塔底组成 xW(均为摩尔百分数)在操作线和平衡线间作梯级,即可得到理论板数 NT。
tR
) ]
L0 — 回流转子流量计上的读数值,为 85ml/min; L — 实际回流量,ml/min;
tD — 塔顶液相温度,81℃; tR — 回流液温度,61℃;
CpD — 塔顶回流液在平均温度 (tD tR ) =71℃的比热,此时回流液浓度为 77.5%, 2
经查表得 CpD 为 3.34kJ/kg·K; rD — 塔顶回流液组成下的汽化潜热,经查表得,994.8kJ/kg。
图 1 筛板塔精馏操作及效率测定实验装置流程示意图
化工基础精馏实验理论塔板数的图解法计算
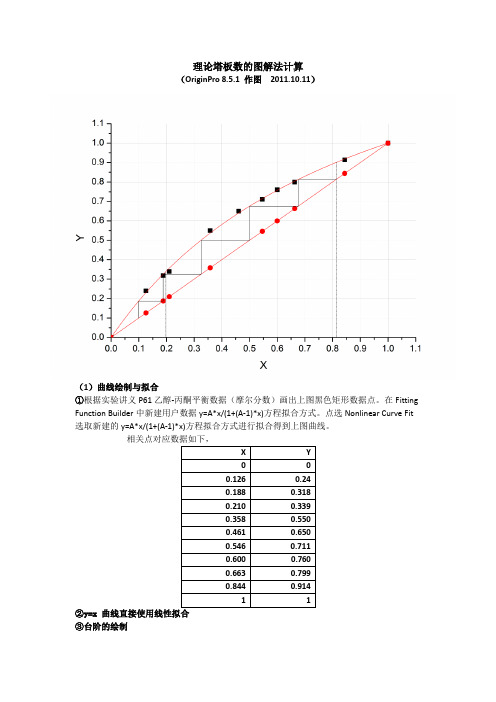
理论塔板数的图解法计算
(OriginPro 8.5.1 作图2011.10.11)
(1)曲线绘制与拟合
①根据实验讲义P61乙醇-丙酮平衡数据(摩尔分数)画出上图黑色矩形数据点。
在Fitting Function Builder中新建用户数据y=A*x/(1+(A-1)*x)方程拟合方式。
点选Nonlinear Curve Fit 选取新建的y=A*x/(1+(A-1)*x)方程拟合方式进行拟合得到上图曲线。
②y=x 曲线直接使用线性拟合
③台阶的绘制
根据塔顶的乙醇摩尔分数0.813,算出该y值下曲线上对应的x点,并依次求算下一个点的x值。
(根据OriginPro 8.5.1的拟合功能中的Find Special X from Y来实现)
用绘图中
④在图中标出塔顶和塔底的乙醇摩尔分数
塔顶 0.813
塔底 0.196
(2)理论塔板数
N完整=3
N不完整=(第三个台阶对应x值-塔底摩尔分数)/(第三个台阶对应x值第二个台阶对应x值)=(0.32493-0.196)/(0.32493-0.18773)= 0.12893 / 0.13720 ≈0.94 N理论=N完整+N不完整= 3 + 0.94 = 3.94 个
即根据2011.10.07日测定的数据处理后图解法求解的精馏塔的理论塔板数为3.94。
01-MATLAB精馏塔塔板数计算

MATLAB精馏塔塔板数计算一、引言精馏塔是在化工生产过程中经常使用的反应器,特别在石油化工中应用广泛。
在精馏塔的设计中,对不同的反应过程要确定不同的反应器,其中塔板数就是非常重要的参数之一。
精馏塔塔板计算是精馏计算比较复杂、烦琐的计算,计算过程中囊括了精馏单元操作中几乎所有的基本原理和计算方法,通过交替使用相平衡方程、精馏段操作线方程和提馏段操作线方程计算塔板组成。
在此过程中使用了几次相平衡方程即可得几块理论塔板数。
而在工程计算中MATLAB语言拥有大量的命令集和可用函数集可以完成各种计算和数据处理,方便快捷,计算精确,形式简单,易于掌握。
所以将MATLAB运用到精馏塔塔板数的计算中,有利于简化计算。
二、MATLABMATLAB是矩阵实验室(Matrix Laboratory)之意,基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解决问题要比用C、FORTRAN等语言完成相同的事情简捷得多。
有大量的指令可供调用,用户也可以将自己编写的实用程序导入MATLAB函数库中方便自己以后调用。
它拥有强大的函数库、工程运算和图形处理功能,程序命令简单,基本上是计算过程的呈现,是替代上述语言进行计算机辅助计算的一种良好工具。
用MATLAB来实现精馏过程的计算机辅助计算,不仅计算过程简单,而且可以利用图形直观地表达计算结果,是工程类学生学习课程的一种有效辅助手段。
本文将以MATLAB软件为平台,以双组份物系为例,针对精馏塔理论塔板的计算问题进行探讨。
三、精馏塔及操作原理精馏塔是进行精馏的一种塔式气液接触装置,又称蒸馏塔。
有板式塔和填料塔两种主要类型。
精馏操作是化工生产中应用最广的分离过程,精馏操作迫使混合物的气、液两相在精馏塔体中作逆向流动,在互相接触过程中,液相中的轻组分逐渐转入气相,而气相中的重组分则逐渐进入液相。
精馏过程本质上是一种传质过程,也伴随着传热。
四、案例某理想混合液用常压精馏塔进行分离。
MATLAB图解精馏塔理论塔板数程序代码

MATLAB图解精馏塔理论塔板数程序代码function distillation %文件名“distillation”可以更改% 输入计算所需参数q=1;%输入进料热状况参数R=1.5;%输入回流比xD=0.95;%输入塔顶轻组分摩尔分数xW=0.04;%输入塔底轻组分摩尔分数xF=0.52;%输入进料轻组分摩尔分数%以下输入相平衡数据x0=[00.01960780.03921560.05882350.07843130.09803920.11764710.13725490.15686270.17647060.19607840.21568630.23529410.2549020.27450980.29411760.31372550.33333330.35294120.3725490.39215690.4313725 0.4509804 0.4705882 0.4901961 0.5098039 0.5294118 0.5490196 0.5686275 0.5882353 0.6078431 0.627451 0.6470588 0.6666667 0.6862745 0.7058824 0.7254902 0.745098 0.7647059 0.7843137 0.8039216 0.8235294 0.8431373 0.8627451 0.8823529 0.9019608 0.9215686 0.9411765 0.96078430.98039221];y0=[0 0.04370290.1258286 0.1643911 0.2013788 0.2368595 0.2708994 0.303563 0.3349129 0.3650094 0.3939109 0.4216732 0.4483501 0.4739928 0.4986506 0.5223702 0.5451963 0.5671715 0.5883362 0.6087289 0.6283862 0.6473428 0.6656317 0.6832842 0.70033 0.7167974 0.7327131 0.7481026 0.76299 0.7773982 0.791349 0.8048631 0.8179601 0.83065870.85493130.86653820.8778130.88877020.8994240.90978740.91987340.92969390.93926070.94858470.95767680.9665470.97520520.98366080.99192281];Yr=@(x)R/(R+1).*x+xD/(R+1);%精馏段操作线fun=@(x)(q-1)*(R/(R+1).*x+xD/(R+1))-(q*(x-xF)+(q-1)*xF); xQ=fzero(fun,0.5);%求操作点yQ=Yr(xQ);xOP=[xW,xQ,xD];yOP=[xW,yQ,xD];yfit=linspace(0,1,1001);xfit=interp1(y0,x0,yfit,'pchip');%%绘制图形hold onbox onplot([0 1],[0 1],'k');xlabel('x')ylabel('y')plot(x0,y0,'r')plot(xfit,yfit,'r-')plot(xF,xF,'b*')plot(xQ,yQ,'bo')plot(xOP,yOP,'b-')k=1;yn(1)=xD;xn(1)=interp1(y0,x0,yn(1),'pchip');plot([xD,xn(1)],[yn(1),yn(1)],'b-')text(xn(1),yn(1),num2str(1),...'HorizontalAlignment','center','VerticalAlignment','bottom') while xn(k)>xWyn(k+1)=interp1(xOP,yOP,xn(k));k=k+1;xn(k)=interp1(y0,x0,yn(k),'pchip');plot([xn(k-1),xn(k-1)],[yn(k-1),yn(k)],'b-')plot([xn(k-1),xn(k)],[yn(k),yn(k)],'b-')text(xn(k),yn(k),num2str(k),...'HorizontalAlignment','center','VerticalAlignment','bottom' ) endN=k;plot([xn(N),xn(N)],[yn(N),xn(N)],'b-')text(xn(N),yn(N),num2str(N),...'HorizontalAlignment','center','VerticalAlignment','bottom' )N_Feed=find(xn<xF);N_Feed=N_Feed(1);text(0.5,0.5,{strcat('所需理论板:',num2str(N)),...strcat('进料板位置:',num2str(N_Feed))},...'HorizontalAlignment','left','VerticalAlignment','top')%以下代码是为了去掉顶端和右边坐标轴的刻度box offax2 = axes('Position',get(gca,'Position'),... 'XAxisLocation','top',... 'YAxisLocation','right',... 'Color','none',...'XColor','k','YColor','k'); set(ax2,'YTick', []);set(ax2,'XTick', []);box on运行结果如图1所示:图1 图解苯-甲苯精馏塔理论塔板数和进料位置00.10.20.30.40.50.60.70.80.9100.10.20.30.40.50.60.70.80.91x y。
用Matlab图解计算精馏塔理论级数黄建平

Graphical Method Based on Matlab for Calculating Theoretical Stage Number of Rectification Column
HUANG Jian-ping* ,ZHAO Ling
( Anyang Institute of Technology,Anyang 455000,China) Abstract: Matlab is a application software and it can be used to calculate the theoretical stage number of rectification column based on graphical method. A new,simple and accurate graphical method was exploited by Matlab 7. 0 software for the calculating theoretical stage number of rectification column. According to the proposed method,the theoretical stage numbers under different conditions can be calculated by inputing parameters as well as the process of graphic calculation can be output in visual way. Key words: Matlab; graphical method; rectification; theoretical stage number
信阳师范学院学报: 自然科学版 第 24 卷 第 4 期 2011 年 10 月
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB图解精馏塔理论塔板数程序代码
function distillation %文件名“distillation”可以更改
% 输入计算所需参数
q=1;%输入进料热状况参数
R=1.5;%输入回流比
xD=0.95;%输入塔顶轻组分摩尔分数
xW=0.04;%输入塔底轻组分摩尔分数
xF=0.52;%输入进料轻组分摩尔分数
%以下输入相平衡数据
x0=[0
0.0196078
0.0392156
0.0588235
0.0784313
0.0980392
0.1176471
0.1372549
0.1568627
0.1764706
0.1960784
0.2156863
0.2352941
0.254902
0.2745098
0.2941176
0.3137255
0.3333333
0.3529412
0.372549
0.3921569
0.4313725 0.4509804 0.4705882 0.4901961 0.5098039 0.5294118 0.5490196 0.5686275 0.5882353 0.6078431 0.627451 0.6470588 0.6666667 0.6862745 0.7058824 0.7254902 0.745098 0.7647059 0.7843137 0.8039216 0.8235294 0.8431373 0.8627451 0.8823529 0.9019608 0.9215686 0.9411765 0.9607843
0.9803922
1];
y0=[0 0.0437029
0.1258286 0.1643911 0.2013788 0.2368595 0.2708994 0.303563 0.3349129 0.3650094 0.3939109 0.4216732 0.4483501 0.4739928 0.4986506 0.5223702 0.5451963 0.5671715 0.5883362 0.6087289 0.6283862 0.6473428 0.6656317 0.6832842 0.70033 0.7167974 0.7327131 0.7481026 0.76299 0.7773982 0.791349 0.8048631 0.8179601 0.8306587
0.8549313
0.8665382
0.877813
0.8887702
0.899424
0.9097874
0.9198734
0.9296939
0.9392607
0.9485847
0.9576768
0.966547
0.9752052
0.9836608
0.9919228
1];
Yr=@(x)R/(R+1).*x+xD/(R+1);%精馏段操作线
fun=@(x)(q-1)*(R/(R+1).*x+xD/(R+1))-(q*(x-xF)+(q-1)*xF); xQ=fzero(fun,0.5);%求操作点
yQ=Yr(xQ);
xOP=[xW,xQ,xD];
yOP=[xW,yQ,xD];
yfit=linspace(0,1,1001);
xfit=interp1(y0,x0,yfit,'pchip');
%%绘制图形
hold on
box on
plot([0 1],[0 1],'k');
xlabel('x')
ylabel('y')
plot(x0,y0,'r')
plot(xfit,yfit,'r-')
plot(xF,xF,'b*')
plot(xQ,yQ,'bo')
plot(xOP,yOP,'b-')
k=1;
yn(1)=xD;
xn(1)=interp1(y0,x0,yn(1),'pchip');
plot([xD,xn(1)],[yn(1),yn(1)],'b-')
text(xn(1),yn(1),num2str(1),...
'HorizontalAlignment','center','VerticalAlignment','bottom') while xn(k)>xW
yn(k+1)=interp1(xOP,yOP,xn(k));
k=k+1;
xn(k)=interp1(y0,x0,yn(k),'pchip');
plot([xn(k-1),xn(k-1)],[yn(k-1),yn(k)],'b-')
plot([xn(k-1),xn(k)],[yn(k),yn(k)],'b-')
text(xn(k),yn(k),num2str(k),...
'HorizontalAlignment','center','VerticalAlignment','bottom' ) end
N=k;
plot([xn(N),xn(N)],[yn(N),xn(N)],'b-')
text(xn(N),yn(N),num2str(N),...
'HorizontalAlignment','center','VerticalAlignment','bottom' )
N_Feed=find(xn<xF);
N_Feed=N_Feed(1);
text(0.5,0.5,{strcat('所需理论板:',num2str(N)),...
strcat('进料板位置:',num2str(N_Feed))},...
'HorizontalAlignment','left','VerticalAlignment','top')
%以下代码是为了去掉顶端和右边坐标轴的刻度
box off
ax2 = axes('Position',get(gca,'Position'),... 'XAxisLocation','top',... 'YAxisLocation','right',... 'Color','none',...
'XColor','k','YColor','k'); set(ax2,'YTick', []);
set(ax2,'XTick', []);
box on
运行结果如图1所示:
图1 图解苯-甲苯精馏塔理论塔板数和进料位置
00.10.20.30.40.5
0.60.70.80.9100.10.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
x y。
