正矢计算公式

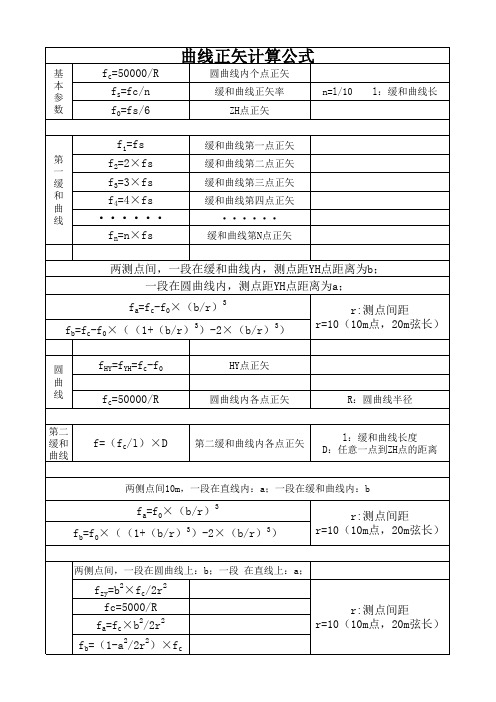
HY点正矢圆曲线内各点正矢
R：圆曲线半径
第二
缓和 f=（fc/l）×D
曲线
第二缓和曲线内各点正矢
l：缓和曲线长度 D：任意一点到ZH点的距离
两侧点间10m，一段在直线内：a；一段在缓和曲线内：b
fa=f0×（b/r）3 fb=f0×（（1+（b/r）3）-2×（b/r）3）
r:测点间距 r=10（10m点，20m弦长）
······ 缓和曲线第N点正矢
两测点间，一段在缓和曲线内，测点距YH点距离为b；一段在圆曲线内，测点距YH点距离为a；
fa=fc-f0×（b/r）3 fb=fc-f0×（（1+（b/r）3）-2×（b/r）3）
r:测点间距 r=10（10m点，20m弦长）
圆
fHY=fYH=fc-f0
曲
线
fc=50000/R
ቤተ መጻሕፍቲ ባይዱ
两侧点间，一段在圆曲线上：b；一段在直线上：a；
fzy=b2×fc/2r2 fc=5000/R
fa=fc×b2/2r2 fb=（1-a2/2r2）×fc
r:测点间距 r=10（10m点，20m弦长）
曲线正矢计算公式
基
fc=50000/R
本参
fs=fc/n
数
f0=fs/6
圆曲线内个点正矢缓和曲线正矢率
ZH点正矢
n=l/10 l：缓和曲线长
f1=fs
第一
f2=2×fs
缓
f3=3×fs
和曲
f4=4×fs
线
······
fn=n×fs
缓和曲线第一点正矢缓和曲线第二点正矢缓和曲线第三点正矢缓和曲线第四点正矢

正矢

一、曲线的分类：目前我段主要曲线类型有：1、由两端缓和曲线和圆曲线组成的曲线，如正线曲线。

容许行车速度高。

2、由圆曲线构成的曲线。

如道岔导曲线、附带曲线。

二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时，F C=50000/RF ZY=F YZ= F C/22、曲线头尾不在起终点桩上ZY前点：Fμ=（FC/2）*（δ/10）2ZY后点：Fη=FC-{（FC/2）*（τ/10）2}FC：圆曲线正矢δ：ZY点到后点的距离τ：ZY点到前点的距离三、缓和曲线上整点正矢的计算（起始点正好是测点）（1）缓和曲线头尾的计算：F0=F1/6（缓和曲线起点）F终= F C-F0（缓和曲线终点）（2）缓和曲线中间点正矢的计算：F1=F S= F C/N （N=L0/B：缓和曲线分段数）F2=2 F1 F3=3F1 F I=IF1（I为中间任意点）四、半点（5米桩）正矢的计算：a)ZH点后半点正矢的计算：F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM，其前半点很小（小于1MM）因此不作计算。

b)HY（YH）点前半点计划正矢的计算F前=1/2{[L03+（L0-15）3]/6R L0+[5L0+25]/2R}-（L0-5）3/6R L0c)HY（YH）点后半点计划正矢的计算F后=1/2{[ （L0-5）3 -L03]/6R L0+[5L0+175]/2R}d)中间点（5米桩）正矢的计算F中=（F前+F后）/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢Fμ=αυF S(直缓点外点) αυ=1/6(δ/B)3Fη=αηF S(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2) 缓圆点处相邻测点的计划正矢Fφ=F C-αυF S (缓圆点外点，缓和曲线之外)Fθ= F C-αηF S (缓圆点内点，缓和曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L0)L I（I为中间任意点）说明：B：半弦长δ：缓和曲线内点到ZH、HY（YH）距离L0：缓和曲线长F C：圆曲线正矢一、绳正法基本原理1、基本假定：（1）假定拨道前后两端切线方向不变，或起始点位置不变，即曲线终点拨量为零。

煤矿轨道正失计算公式

煤矿轨道正失计算公式煤矿窄轨铁道的作用：直接承担列车的载重，把机车和矿车的荷载通过车轮、钢轨、轨枕、道床传播，分散到地面和井下巷道底板上，引导列车沿铁道平稳高速运行。

我国的标准公称轨距是1435mm,大于标准轨距的叫宽轨轨距，小于标准轨距的叫窄轨轨距。

我国煤矿轨道线路按轨距类型分为900mm 762mm 600mm轨距。

轨道的铺设的步骤大致分为；1找中线、2摆放轨枕、3散布轨道、4串动轨道、5散布连接零部件、6连接钢轨、7钉道、8整道等步骤，保证列车平稳运行的主要技术指标是：轨距、水平、轨面前后高低、方向、钢轨内倾。

1. 轨道中心符合设计要求，偏差不大于设计值的±50mm。

双轨中心线的间距不大于设计值的20 mm，双轨的中心位置与设计位置的偏差不大于50 mm2.坡度与标高：轨面的实际标高与设计标高的偏差为±50mm，坡度误差50米内不超过±1‰，即50米内不超过±50mm（包括倾斜巷道的绞车道）铁道的坡度是指两端点的标高差与水平距离之比计算公式：H=H2-H1∕L = △H/L3.接头平整度：轨面及内侧错差不大于2mm，不应有硬弯对轨道的接头应如何养护（1）.轨枕材质尽可能一致，间距符合规定，更换轨枕时两根同时更换；保持道床丰满。

（2）.经常紧固螺丝，使接头作为一个整体来抵抗外力。

（3）.及时消除轨面前后高低不平，接头轨面及内错差不应大于2mm。

（4）.及时调整轨缝，保持轨缝均匀4.方向：主要运输线路：直线目视直顺，用10米弦量不超过10mm，曲线目视圆顺，用2米的弦量相邻正负差为半径50米以上不超过2mm，半径为50米以下时不超过3mm。

一般运输线路：直线目视直顺，用10米弦量不超过12mm，曲线用2米弦量相邻正失差不超过3mm。

方向不良对铁道的影响：线路方向不良超过允许范围，列车左右摇摆，作用在轨道上的横向力加大，钢轨受冲击，轨道损坏加速。

正矢：即在外股钢轨的内测轨顶面向下13mm处，两点拉一根弦线，弦线中点至钢轨工作边的距离即为正矢。

正矢计算公式教学文案

曲线正矢计算公式
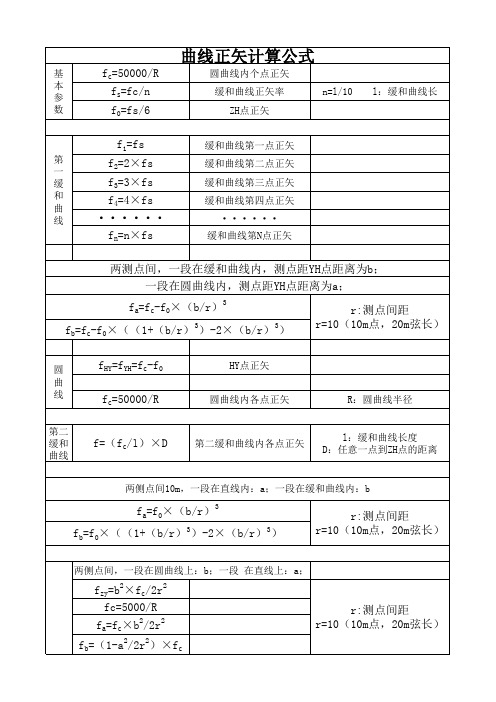
基
fc=50000/R
本参
fs=fc/n
数
f0=fs/6
圆曲线内个点正矢缓和曲线正矢率
ZH点正矢
n=l/10 l：缓和曲线长
பைடு நூலகம்
f1=fs
第一
f2=2×fs
缓
f3=3×fs
和曲
f4=4×fs
线
······
fn=n×fs
缓和曲线第一点正矢缓和曲线第二点正矢缓和曲线第三点正矢缓和曲线第四点正矢
HY点正矢圆曲线内各点正矢
R：圆曲线半径
第二
缓和 f=（fc/l）×D
曲线
第二缓和曲线内各点正矢
l：缓和曲线长度 D：任意一点到ZH点的距离
两侧点间10m，一段在直线内：a；一段在缓和曲线内：b
fa=f0×（b/r）3 fb=f0×（（1+（b/r）3）-2×（b/r）3）
r:测点间距 r=10（10m点，20m弦长）
两侧点间，一段在圆曲线上：b；一段在直线上：a；
fzy=b2×fc/2r2 fc=5000/R
fa=fc×b2/2r2 fb=（1-a2/2r2）×fc
r:测点间距 r=10（10m点，20m弦长）
······ 缓和曲线第N点正矢
两测点间，一段在缓和曲线内，测点距YH点距离为b；一段在圆曲线内，测点距YH点距离为a；
fa=fc-f0×（b/r）3 fb=fc-f0×（（1+（b/r）3）-2×（b/r）3）
r:测点间距 r=10（10m点，20m弦长）
圆
fHY=fYH=fc-f0
曲
线
fc=50000/R

曲线正矢计算

曲线正矢计算曲线半径、弦长、正矢之间的关系:2Lf,8R50000f, 当时， (mm) L,20mR12500 当时， (mm) f,L,10mRf式中—圆曲线正矢(mm)—圆曲线半径(m) R现场正线曲线取弦长为20 m计算正矢值。

现场站线曲线取弦长为10 m计算正矢值。

(一)圆曲线上各测点计划正矢50000f圆曲线计划正矢 (mm) ,cRfcf,圆曲线始终点的计划正矢 (mm) 始，终，2(二)缓和曲线正矢是从直线往圆曲线方向逐渐由小变大的，由直缓点向缓圆点方向变化的大小，叫缓和曲线的正矢递增率。

圆曲线计划正矢f，，c缓和曲线的正矢递增率f, ，，N，，一端缓和曲线分段数N1.缓和曲线始终点计划正矢，，缓和曲线正矢递增率fN，f，,缓和曲线始点正矢始6，，缓和曲线终点正矢，f，,f,缓和曲线始点正矢fc 终始2.缓和曲线中间各测点计划正矢f,Nf iiNfi,1，2？,N,1式中—缓和曲线中间各测点的计划正矢i ( );fN —测点距缓和曲线始点的段数 Ni—缓和曲线的正矢递增率【例题】已知曲线半径R=300m，缓和曲线长为70 m(如图3所示)求缓和曲线上各测点计划正矢值。

【解】5000050000mm f,,,167cR300圆曲线计划正矢f167，，cmm f,,,24N，，一端缓和曲线分段数N7 f24Nmm ，，直缓点ZH正矢，f，,,,4始87654663QZHYYH210ZHHZ mm ，，缓圆点HY正矢，f，,f,f,167,4,163c终始缓和曲线中间各测点的计划正矢为图2缓和曲线f,Nf,1，24,24mm 11Nmm f,Nf,2，24,4822Nmm f,Nf,3，24,7233Nmm f,Nf,4，24,9644Nmm f,Nf,5，24,12055Nmm f,Nf,6，24,14466N。

三角函数

常用的三角函数有6种(正弦，余弦，正切，余切，正割，余割).还有另外一些不常用的，有正矢、余矢、外正割、外余割、半正矢、半余矢等.比如：外余割就是余割的倒数；正矢：versinα=1-cosα，vercosinα=1+cosα；余矢：coversinα=1-sinα，covercosinα=1+sinα等.初中的三角函数都使用角度制.通用的是弧度制.弧度制的单位是弧度rad.360°=2πrad;60°=π/3 rad.弧度制就是将角度用构成这个角度的单位圆上的弧长来表示的方法.正弦与余弦的图像呈现单纯的波形，正因为正弦与余弦的这种波形的特质，它们也被用来研究一些波的问题.要改变y=asinbx的振幅，就要改变系数a，改变波长，就要改变b，a越大，振幅越大；b越大，波长越短.任何波都能够用“单纯的波”叠加起来表示.为了解析复杂的波是如何用单纯波叠加起来的，目前人们都使用一种叫做“傅里叶变换”的方法.那么接下来就要介绍三角函数的微分.微分是由牛顿，与德国数学家戈特弗里德·莱布尼茨发明的.正弦函数的斜率变化使用余弦函数来表示的.求微分即求某点的切线的斜率.以y=sinx为例，该函数在x从0~π/2变化时是递增的，斜率是减小的，在π/2处斜率为0；在π/2~3π/2时是递减的，斜率继续减小后增加，在3π/2处斜率也为0.如果把这些切线的斜率变化在新的坐标图上画出来，就是y=cosx.也就是说，对正弦函数求微分，得到的就是余弦函数.微分用d表示，d(sinx)=cosx.对余弦函数求微分，得到，d(cosx)=-sinx.接下来，我们就通过用计算的方法求三角函数的微分.再次以y=sinx为例，假如在这上面有一点A(x,sinx)，那么首先在沿x轴正方向，找一个与A相距h的B点，B点的坐标可求，为(x+h,sin(x+h)）.那么，连接A，B两点的直线，斜率就可以这样表示：sin(x+ℎ)−sinxℎ直线AB不是点A的切线.但如果B点沿着函数图像靠近A点的话，直线AB就接近A点的切线，如果h无限接近于0，也就是说，B点无限接近于A点，直线AB的斜率K，就会与A点的切线的斜率无限接近.所以，此处我们就引入极限的概念，点A切线的斜率可以表示为：K=limℎ→0sin(x+ℎ)−sin xℎ这也就是导数的概念。

铁路轨道曲线正矢计算(修正)

第一讲：曲线正矢计算一、曲线的分类：目前我段主要曲线类型有：1、由两端缓和曲线和圆曲线组成的曲线，如正线曲线。

容许行车速度高。

2、由圆曲线构成的曲线。

如道岔导曲线、附带曲线。

二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M 时，F c=50000/RF ZY=F YZ= F c/22、曲线头尾不在起终点桩上ZY 前点：= (FC/2) * ( S /10) 2ZY 后点：F n =FC-{ (FC/2) * ( T /10) 2}FC:圆曲线正矢S : ZY点到后点的距离T : ZY点到前点的距离三、缓和曲线上整点正矢的计算(起始点正好是测点)(1)缓和曲线头尾的计算：F o=F i/6 (缓和曲线起点) F终二F C-F Q (缓和曲线终点)(2)缓和曲线中间点正矢的计算：F I=F S=F C/N( N=L Q/B :缓和曲线分段数)F2=2 F I F3=3F I F I=IF I (I 为中间任意点)四、半点(5米桩)正矢的计算：a) ZH点后半点正矢的计算：F 后=25/48*F[因为ZH点正矢f o=f1/6,很小一般为1~2MM，其前半点很小(小于1MM ) 因此不作计算。

b) HY (YH)点前半点计划正矢的计算F 前=1/2{[L Q3+ (L o-15) 3]/6R L O+[5L°+25]/2R}- ( L Q-5)3/6R L°c) HY (YH)点后半点计划正矢的计算F 后=1/2{[ ( L Q-5)3 -L Q3]/6R L Q+[5L Q+175]/2R} d) 中间点(5米桩)正矢的计算F 中=(F 前+F 后) /2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢F产a u F S(直缓点外点) a u =1/6( S /B)3F n = a n F S (直缓点内点) a n =1/6[(1+ S/B)3-( S /B)3](2) 缓圆点处相邻测点的计划正矢F® =F C- a u F S(缓圆点外点，缓和曲线之外)F e = F C- a n F s (缓圆点内点，缓和曲线之内)(a u、a n查纵距率表《曲线设备与曲线整正》附表二)(3) 缓和曲线中间点各点计划正矢的计算F I=(F C/L°)L I(I为中间任意点)说明：B:半弦长S:缓和曲线内点到ZH、HY (YH)距离L o：缓和曲线长F c：圆曲线正矢第二讲：曲线拨道一、绳正法基本原理1、基本假定：(1)假定拨道前后两端切线方向不变，或起始点位置不变，即曲线终点拨量为零。

曲线正矢计算

第一讲:曲线正矢计算一、曲线得分类:目前我段主要曲线类型有:1、由两端缓与曲线与圆曲线组成得曲线,如正线曲线。

容许行车速度高。

2、由圆曲线构成得曲线。

如道岔导曲线、附带曲线。

二、圆曲线正矢得计算1、曲线头尾正好位于起终点桩上F C=L２/8ＲL=2０Ｍ时,ＦC=50００0/RF ZY=ＦYZ= F C/22、曲线头尾不在起终点桩上ＺY前点:Fμ=（ＦC/2) *（δ／１0)2ZY后点:Fη=FC－{（ＦC/２) *(τ/10)2}FC：圆曲线正矢δ：ZY点到后点得距离τ:ZＹ点到前点得距离三、缓与曲线上整点正矢得计算(起始点正好就是测点)（1）缓与曲线头尾得计算:Ｆ0＝F1/6（缓与曲线起点) F终=F C－F0 (缓与曲线终点）(2)缓与曲线中间点正矢得计算:Ｆ1=F S= F C/N (Ｎ＝L0/B:缓与曲线分段数)Ｆ２=２Ｆ１F3=3Ｆ1 ＦI=IF1(I为中间任意点)四、半点(5米桩)正矢得计算:a)ZH点后半点正矢得计算：F后＝25/４８*Ｆ1因为ＺH点正矢ｆ0＝f1／６,很小一般为1~２MM，其前半点很小(小于1ＭM)因此不作计算。

b)HY(YH)点前半点计划正矢得计算Ｆ前=１/2{[L03+(L0－１5)3]/６R L0+[5L０+2５］／2R}-(L0－５）3/６R L０c)HY(YH）点后半点计划正矢得计算F后＝1/２｛[(L０-５)3－L０３]/６R L０+［5L0+17５]/２R}d)中间点(５米桩）正矢得计算F中＝（Ｆ前+F后)/2五、测点不在曲线始终点时缓与曲线计划正矢得计算a)缓与曲线始点(ZH点)处相邻测点得计划正矢Fμ=αυF S(直缓点外点）αυ＝1/6（δ/Ｂ)３Fη=αηＦＳ(直缓点内点) αη＝1/6[(1+δ/B)３-(δ／B)3](2）缓圆点处相邻测点得计划正矢Fφ=ＦC－αυＦS (缓圆点外点,缓与曲线之外)Fθ=FＣ－αηF S (缓圆点内点,缓与曲线之内)（αυ、αη查纵距率表《曲线设备与曲线整正》附表二)（3)缓与曲线中间点各点计划正矢得计算F I=(F C／L0)L I(I为中间任意点)说明：B：半弦长δ:缓与曲线内点到ZH、ＨＹ(YH)距离L0:缓与曲线长F C:圆曲线正矢第二讲:曲线拨道一、绳正法基本原理１、基本假定:(1)假定拨道前后两端切线方向不变,或起始点位置不变,即曲线终点拨量为零。

铁路曲线正矢计算公式例题

铁路曲线正矢计算公式例题铁路曲线正矢计算公式例题在铁路设计中，曲线是一个重要的设计元素，目的是为了确保行车安全和行车速度。

曲线的设计参数包括半径、曲线长度和曲线正矢等。

本文将详细讨论曲线正矢的计算公式和应用例题。

1. 曲线正矢的定义曲线正矢是曲线的一个参数，是曲线下一条直线的长度，该直线与曲线的切线平行，在曲线上方。

曲线正矢是铁路曲线设计的重要指标之一，影响着铁路行车的安全和速度。

2. 曲线正矢的计算公式曲线正矢的计算公式可以根据铁路设计标准或手册给出，常用的计算公式有以下两种：（1）C=V²/127R式中，C为曲线正矢，单位为米（m）；V为轨道线速度，单位为千米/小时（km/h）；R为曲线半径，单位为米（m）。

该公式适用于直线轨道和大半径曲线，曲线半径大于1500米时，误差较小。

（2）C=137V²/(127R+9C)式中，C为曲线正矢，单位为米（m）；V为轨道线速度，单位为千米/小时（km/h）；R为曲线半径，单位为米（m）。

该公式适用于一般曲线和小半径曲线，曲线半径小于1500米时，误差较小。

3. 曲线正矢的应用例题下面举例说明曲线正矢的应用。

例题：一条半径为800米的曲线，设计速度为100km/h，求曲线正矢。

解：根据第一种计算公式，代入数据得：C=V²/127R=（100×100）/（127×800）=0.0982≈0.1(m)根据第二种计算公式，代入数据得：C=137V²/(127R+9C)=137×（100×100）/（127×800+9C）移项整理得：23C=127×800C=348.7≈350(m)因此，曲线正矢为0.1m和350m。

根据实际情况，如果曲线正矢过大，会影响行车速度；如果曲线正矢过小，则会影响行车安全。

因此，在设计曲线时，必须根据行车安全、行车速度和经济效益等因素进行合理的参数设计。

曲线正矢计算

曲线半径、弦长、正矢之间的关系:当时, (mm) 当时, (mm) 式中 —圆曲线正矢(mm)—圆曲线半径(m)现场正线曲线取弦长为20 m 计算正矢值。

现场站线曲线取弦长为10 m 计算正矢值。

(一)圆曲线上各测点计划正矢圆曲线计划正矢 (mm) 圆曲线始终点的计划正矢 (mm) (二)缓与曲线正矢就是从直线往圆曲线方向逐渐由小变大的,由直缓点向缓圆点方向变化的大小,叫缓与曲线的正矢递增率。

1、缓与曲线始终点计划正矢R L f 82=m L 20=Rf 50000=m L 10=Rf 12500=f R Rf c 50000=2c ）（f f =终始()()()N f f c N 一端缓和曲线分段数圆曲线计划正矢缓和曲线的正矢递增率=()6N f ）（f 缓和曲线正矢递增率缓和曲线始点正矢始=()始终缓和曲线始点正矢缓和曲线终点正矢f f ）（f c -=2、缓与曲线中间各测点计划正矢式中 —缓与曲线中间各测点的计划正矢( ); —测点距缓与曲线始点的段数—缓与曲线的正矢递增率【例题】已知曲线半径R=300m,缓与曲线长为70 m(如图3所示)求缓与曲线上各测点计划正矢值。

【解】mm mm mm mm 0缓与曲线中间各测点的计划正矢为图2缓与曲线mmmmmmmmmmmm Ni i f N f =i f 1,21-=N i，i N N f 1673005000050000≈==R f c ()()247167≈==N f f c N 一端缓和曲线分段数圆曲线计划正矢()46246===N f ）（f ZH 始正矢直缓点()1634167=-=-=始终正矢缓圆点f f ）（f HY c 2424111=⨯==N f N f 4824222=⨯==N f N f 7224333=⨯==N f N f 9624444=⨯==N f N f 12024555=⨯==N f N f 14424666=⨯==N f N f。

正矢计算公式

正矢计算公式正矢（Versine）这个概念在数学中相对比较冷门，可能很多同学在学习过程中都没怎么接触过。

但它其实在某些特定的数学和物理问题中有着独特的用处。

正矢的定义是：versinθ = 1 - cosθ 。

从这个公式咱们就能看出来，正矢其实就是用 1 减去余弦值得到的。

那正矢计算公式到底能用来干嘛呢？给大家举个例子。

有一次我去公园散步，看到一个摩天轮在缓缓转动。

我突然就想到了正矢公式。

假设摩天轮的半径是 r ，摩天轮转过的角度是θ ，那座舱距离摩天轮中心的水平距离就可以用 r ×versinθ 来计算。

咱们再深入研究一下这个公式。

如果θ 很小，那么cosθ 就接近于 1 ，这时候versinθ 就接近于 0 。

反过来，如果θ 接近 180 度，cosθ 就接近于 -1 ，versinθ 就接近于 2 。

在实际的数学解题中，正矢公式有时候能帮我们简化计算。

比如说，在求解某些几何图形中的线段长度或者角度关系时，如果能巧妙地运用正矢公式，可能会让原本复杂的问题变得清晰简单。

想象一下，如果要计算一个不规则扇形的面积，我们知道了扇形的圆心角和半径，常规方法可能会比较繁琐。

但如果我们先通过正矢公式求出一些关键的长度或者角度关系，再去计算面积，说不定就能少走很多弯路。

而且，正矢公式在物理学中的振动和波动问题中也有应用。

比如说，在研究弹簧振子的运动时，正矢公式就能帮助我们更准确地描述物体的位置和运动状态。

总之，正矢计算公式虽然不那么常见，但在一些特定的情况下，它就像是一把隐藏的钥匙，能帮我们打开解决问题的大门。

所以呀，同学们可别小看了这些看似冷门的数学知识，说不定哪天就能派上大用场呢！。

曲线正矢计算

二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求曲线各测点的计划正矢解：（1）圆曲线计划正矢： fc=L2/8R=20*20/8R=50000/R=50000/600=83.3mm，取84mm（2）缓和曲线正矢递增率： fs= fc/n=84/5=16.8mm（3）直缓（缓直）点正矢： f0=fs/6=16.8/6=2.8mm，取3mm（4）缓和曲线中间各点的正矢：缓和曲线第1点的正失 f1=fs=16.8mm，取17mm缓和曲线第2点的正失 f2=2fs=2*16.8=33.6mm，取34mm 缓和曲线第3点的正失 f3=3fs=3*16.8=50.4mm，取50mm 缓和曲线第4点的正失 f4=4fs=4*16.8=67.2mm，取67mm （5）缓圆（圆缓）点正矢： fhy=fc- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线l0=50m，圆曲线长304m,求各测点的计划正矢解：（1）第一缓和曲线和圆曲线的计划正矢算法同上；（2）第二缓和曲线各点计划正矢的计算：①第二缓和曲线始（HZ）点相邻测点的计划正矢因为圆曲线长L=304m，故第二缓和曲线始（HZ）点距缓和曲线和直线上相邻点（40点、41点）的距离分别为b≈4m，a≈6m，为测点间的距离，等于弦长的一半，a+b=则f40=1/6 fs[（1+b/）3-2（b/）3]=1/6*16.8*[（1+4/10）3-2*（4/10）3]=7.32mm，取7mm f41=1/6 fs（b/）3=1/6*16.8*（4/10）3=0.18mm，取0mm ②第二缓和曲线终点（YH）相邻测点的计划正矢第二缓和曲线终点（YH）距圆曲线和缓和曲线上相邻点（35点、36点）的距离分别为a≈4m，b≈6m，为测点间的距离，等于弦长的一半，a+b=则f35 = fc－1/6 fs（b/）3=84－1/6*16.8*（6/10）3=84－0.6=83.4mm，取84mm f36= fc－1/6 fs[（1+b/）3-2（b/）3]=84－1/6*16.8*[（1+6/10）3-2*（6/10）3]= 73.74mm，取74mm ③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢，可根据各点正矢与其距终点（HZ）距离成直线比例的关系，按下式求取：fi=fc/l0*li 则第37点、38点、39点的计划正矢分别为：f37=fc/l0*l37=84/50*34=57.12mm，取57mm f38=fc/l0*l38=84/50*24=40.32mm，取40mm f39=fc/l0*l39=84/50*14=23.52mm，取24mm 3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算（1）圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求缓和曲线辅助点的计划正矢解：辅助点与测点相距5m，即a=b=5m，①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为： f=1/6 fs[（1+b/）3-2（b/）3]=1/6*16.8*[（1+5/10）3-2*（5/10）3]=8.75mm，取9mm ②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为：f= fc－1/6 fs[（1+b/）3-2（b/）3]=84－1/6*16.8*[（1+5/10）3-2*（5/10）3 ]= 75.25mm，取75mm ③缓和曲线其他各中间辅助点的计划正矢：分别取li=15、25、35，按fi=fc/l0*li算得辅助点计划正矢分别为：25mm、42mm、59mm （2）圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m，缓和曲线长l0=50m，圆曲线长304m,求缓和曲线辅助点的计划正矢解：第一个缓和曲线辅助点的算法同上，第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算，即：①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为（B=4+5=9）： f=1/6 fs[（1+B/）3-2（B/）3]=1/6*16.8*[（1+9/10）3-2*（9/10）3]=15.12mm，取15mm ②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为（B=6-5=1）： f= fc －1/6 fs[（1+B/）3-2（B/）3]=84－1/6*16.8*[（1+1/10）3-2*（1/10）3]=80.3mm，取80mm ③缓和曲线其他各中间辅助点的计划正矢：分别取li=19、29、39，按fi=fc/l0*li算得辅助点计划正矢分别为：32mm、49mm、66mm。

铁路轨道曲线正矢计算(修正)

第一讲：曲线正矢计算一、曲线的分类：目前我段主要曲线类型有：1、由两端缓和曲线和圆曲线组成的曲线，如正线曲线。

容许行车速度高。

2、由圆曲线构成的曲线。

如道岔导曲线、附带曲线。

二、圆曲线正矢的计算1、曲线头尾正好位于起终点桩上F C=L2/8RL=20M时，F C=50000/RF ZY=F YZ= F C/22、曲线头尾不在起终点桩上ZY前点：Fμ=（FC/2）*（δ/10）2ZY后点：Fη=FC-{（FC/2）*（τ/10）2}FC：圆曲线正矢δ：ZY点到后点的距离τ：ZY点到前点的距离三、缓和曲线上整点正矢的计算（起始点正好是测点）（1）缓和曲线头尾的计算：F0=F1/6（缓和曲线起点）F终= F C-F0（缓和曲线终点）（2）缓和曲线中间点正矢的计算：F1=F S= F C/N （N=L0/B：缓和曲线分段数）F2=2 F1 F3=3F1 F I=IF1（I为中间任意点）四、半点（5米桩）正矢的计算：a)ZH点后半点正矢的计算：F后=25/48*F1因为ZH点正矢f0=f1/6,很小一般为1~2MM，其前半点很小（小于1MM）因此不作计算。

b)H Y（YH）点前半点计划正矢的计算F前=1/2{[L03+（L0-15）3]/6R L0+[5L0+25]/2R}-（L0-5）3/6R L0c)HY（YH）点后半点计划正矢的计算F后=1/2{[ （L0-5）3 -L03]/6R L0+[5L0+175]/2R}d)中间点（5米桩）正矢的计算F中=（F前+F后）/2五、测点不在曲线始终点时缓和曲线计划正矢的计算a)缓和曲线始点(ZH点)处相邻测点的计划正矢Fμ=αυF S(直缓点外点) αυ=1/6(δ/B)3Fη=αηF S(直缓点内点) αη=1/6[(1+δ/B)3-(δ/B)3](2) 缓圆点处相邻测点的计划正矢Fφ=F C-αυF S (缓圆点外点，缓和曲线之外)Fθ= F C-αηF S (缓圆点内点，缓和曲线之内)(αυ、αη查纵距率表《曲线设备与曲线整正》附表二)(3)缓和曲线中间点各点计划正矢的计算F I=(F C/L0)L I（I为中间任意点）说明：B：半弦长δ：缓和曲线内点到ZH、HY（YH）距离L0：缓和曲线长F C：圆曲线正矢第二讲：曲线拨道一、绳正法基本原理1、基本假定：（1）假定拨道前后两端切线方向不变，或起始点位置不变，即曲线终点拨量为零。

曲线计划正矢的计算

曲线计划正矢的计算一、计算方法1、圆曲线计划正矢的计算f c=L2/8R式中：L----弦长，一般为20m，当曲线状态不良为确保曲线圆顺，增加正矢点时，为10m；f c----圆曲线正矢（mm）；R----曲线半径（m）。

当L=20m时，f c=L2/8R=20*20/8R=50000/R；当L=10m时，f c=L2/8R=10*10/8R=12500/R；2、缓和曲线计划正矢的计算（1）缓和曲线正矢递增率f s= f c/n式中：f c----圆曲线正矢（mm）；n----缓和曲线的分段数，其值为l0/ , 其中l0为缓曲长，为测点间的距离，一般为10m。

（2）缓和曲线各点的计划正矢缓和曲线始点0点（ZH）点的正矢f0=f s/6缓和曲线第1点的正失f1=f s缓和曲线第2点的正失f2=2f s缓和曲线第3点的正失f3=3f s。

缓和曲线终点(HY)的正矢f hy=f c- f03、测点不在曲线始、终点时计划正矢的计算前述缓和曲线和圆曲线的长度都假定是10m的整数倍，但在实际工作中，缓和曲线的长度一般都设置成10m的整数倍，而圆曲线的长度一般都不是10m的整数倍，因此第二缓和曲线的始、终点就不可能恰好落在测点上。

这样缓和曲线始、终点左右相邻测点的计划正矢，都要作为一种特殊情况另行计算。

（1）第二缓和曲线始点（HZ）左右邻点计划正矢的计算HZ不在测点上，位于缓和曲线上的n点和直线上的n+1点之间，n点距HZ点的距离为b，n+1距HZ点的距离为a，相应的正矢分别为f n和f n+1，为测点间的距离，等于弦长的一半，a+b= ，则：f n=1/6 f s[（1+b/ ）3-2（b/ ）3]f n+1=1/6 f s（b/ ）3（2）第二缓和曲线终点（YH）左右邻点计划正矢的计算第二缓和曲线终点（YH）不在测点上，位于圆曲线上的n点和缓和曲线上的n+1点之间，n点距YH点的距离为a，n+1点距YH点的距离为b,相应的正矢分别为f n和f ，则：n+1f n = f c－1/6 f s（b/ ）3f n+1= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]（3）第二缓和曲线上其他各点计划正矢的计算第二缓和曲线上其他各点计划正矢，可根据各点正矢与其距终点HZ距离成直线比例的关系，按下式求取：f i= f c/ l0*l i式中：f i----缓和曲线上距HZ点为l i的测点正矢；二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求曲线各测点的计划正矢解：（1）圆曲线计划正矢：f c=L2/8R=20*20/8R=50000/R=50000/600=83.3mm，取84mm（2）缓和曲线正矢递增率：f s= f c/n=84/5=16.8mm（3）直缓（缓直）点正矢：f0=f s/6=16.8/6=2.8mm，取3mm（4）缓和曲线中间各点的正矢：缓和曲线第1点的正失f1=f s=16.8mm，取17mm缓和曲线第2点的正失f2=2f s=2*16.8=33.6mm，取34mm缓和曲线第3点的正失f3=3f s=3*16.8=50.4mm，取50mm缓和曲线第4点的正失f4=4f s=4*16.8=67.2mm，取67mm（5）缓圆（圆缓）点正矢：f hy=f c- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m，两端缓和曲线l0=50m，圆曲线长304m,求各测点的计划正矢解：（1）第一缓和曲线和圆曲线的计划正矢算法同上；（2）第二缓和曲线各点计划正矢的计算：①第二缓和曲线始（HZ）点相邻测点的计划正矢因为圆曲线长L=304m，故第二缓和曲线始（HZ）点距缓和曲线和直线上相邻点（40点、41点）的距离分别为b≈4m，a≈6m，为测点间的距离，等于弦长的一半，a+b= 则f40=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+4/10）3-2*（4/10）3]=7.32mm，取7mmf41=1/6 f s（b/ ）3=1/6*16.8*（4/10）3=0.18mm，取0mm②第二缓和曲线终点（YH）相邻测点的计划正矢第二缓和曲线终点（YH）距圆曲线和缓和曲线上相邻点（35点、36点）的距离分别为a≈4m，b≈6m，为测点间的距离，等于弦长的一半，a+b=则f35 = f c－1/6 f s（b/ ）3=84－1/6*16.8*（6/10）3=84－0.6=83.4mm，取84mmf36= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+6/10）3-2*（6/10）3]=73.74mm，取74mm③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢，可根据各点正矢与其距终点（HZ）距离成直线比例的关系，按下式求取：f i=f c/l0*l i则第37点、38点、39点的计划正矢分别为：f37=f c/l0*l37=84/50*34=57.12mm，取57mmf38=f c/l0*l38=84/50*24=40.32mm，取40mmf39=f c/l0*l39=84/50*14=23.52mm，取24mm3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算（1）圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m，两端缓和曲线长l0=50m，求缓和曲线辅助点的计划正矢解：辅助点与测点相距5m，即a=b=5m，①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为：f=1/6 f s[（1+b/ ）3-2（b/ ）3]=1/6*16.8*[（1+5/10）3-2*（5/10）3]=8.75mm，取9mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为：f= f c－1/6 f s[（1+b/ ）3-2（b/ ）3]=84－1/6*16.8*[（1+5/10）3-2*（5/10）3]=75.25mm，取75mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=15、25、35，按f i=f c/l0*l i算得辅助点计划正矢分别为：25mm、42mm、59mm（2）圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m，缓和曲线长l0=50m，圆曲线长304m,求缓和曲线辅助点的计划正矢解：第一个缓和曲线辅助点的算法同上，第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算，即：①缓和曲线上与始点（ZH、HZ）相邻辅助点计划正矢为（B=4+5=9）：f=1/6 f s[（1+B/ ）3-2（B/ ）3]=1/6*16.8*[（1+9/10）3-2*（9/10）3]=15.12mm，取15mm②缓和曲线上与终点（YH、HY）相邻辅助点计划正矢为（B=6-5=1）：f= f c－1/6 f s[（1+B/ ）3-2（B/ ）3]=84－1/6*16.8*[（1+1/10）3-2*（1/10）3]=80.3mm，取80mm③缓和曲线其他各中间辅助点的计划正矢：分别取l i=19、29、39，按f i=f c/l0*l i算得辅助点计划正矢分别为：32mm、49mm、66mm。

曲线正矢计算公式

曲线正矢计算公式
曲线正矢计算公式是在数学和物理学中用于计算曲线的弧长的公式。

在几何学中，曲线的弧长是指曲线上任意两点之间的距离。

曲线正矢是曲线上某一点处的切线方向与曲线的弧长比值，它可以帮助我们计算曲线上某点的速度、加速度等相关物理量。

对于一条曲线上的点P(x, y)，其曲线正矢记为S。

根据微积分中的定义，曲线正矢的计算公式为：
S = √(1 + (dy/dx)^2)
其中，dy/dx 是曲线在点P的斜率。

实际上，这个公式是利用了导数的概念来计算曲线正矢。

导数表示曲线在某一点的切线的斜率，而曲线正矢则将这个斜率与曲线的弧长联系起来。

曲线正矢计算公式的应用非常广泛。

在物理学中，它可用于计算质点沿曲线运动的速度和加速度。

在工程中，曲线正矢可用于曲线绘制和路径规划。

在计算机图形学中，曲线正矢可以帮助我们实现曲线的平滑绘制。

总之，曲线正矢计算公式是数学和物理学中一个重要的工具，它能够帮助我们计算曲线上某点处的切线方向与弧长的比值。

通过曲线正矢，我们可以了解曲线上的速度、加速度等重要物理量，并应用于各种实际问题的解决中。

sin、cos、tan公式

Sin a 、con a 、tan a 公式关系‎正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y以及两个不‎常用，已趋于被淘‎汰的函数：正矢函数 versi ‎n θ =1-cosθ余矢函数 verco ‎s θ =1-sinθ同角三角函‎数间的基本‎关系式：·平方关系：sin 2(α)+cos 2(α)=1 tan 2(α)+1=sec 2(α) cot 2(α)+1=csc 2(α)·积的关系：sinα=tanα*cosα cosα=cotα*sinα tanα=sinα*secα c otα=cosα*cscα secα=tanα*cscα cscα=secα*cotα·倒数关系：tanα·cotα=1 sinα·cscα=1 cosα·secα=1直角三角形‎A BC 中,角A 的正弦‎值就等于角‎A 的对边比‎斜边,余弦等于角‎A 的邻边比‎斜边正切等于对‎边比邻边,三角函数恒‎等变形公式‎·两角和与差‎的三角函数‎：cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβ sin(α±β)=sinα·cosβ±cosα·sinβ tan (α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan (α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式‎：Asin α‎+Bcos α‎=(A 2+B 2)^(1/2)sin(α+t)，其中 sint=B/(A^2+B^2)^(1/2) cost=A/(A^2+B^2)^(1/2) tant=B/A Asin α‎+Bcos α‎=(A 2+B 2)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sin α‎·cosα=2/(tanα+cotα) cos(2α)=cos 2(α)-sin 2(α)=2cos2‎(α)-1=1-2sin2‎(α) tan(2α)=2tan α‎/[1-tan 2(α)+·三倍角公式‎：sin(3α)=3sin α‎-4sin3‎(α) cos(3α)=4cos3‎(α)-3cos α‎·半角公式： sin(2a )=±21cona - cos(2a )=±21cona + tan(2a )=±cona cona +-11= conaa +1sin =a cona sin 1- ·降幂公式sin 2(α)=(1-cos(2α))/2=versi ‎n (2α)/2 cos 2(α)=(1+cos(2α))/2=verco ‎s (2α)/2tan 2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/*1+tan 2(α/2)+ cosα=*1-tan 2(α/2)+/*1+tan 2(α/2)+ tanα=2tan(α/2)/*1-tan 2(α/2)+ ·积化和差公‎式：sinα·cosβ=(1/2)*sin(α+β)+sin(α-β)+ cosα·sinβ=(1/2)*sin(α+β)-sin(α-β)+cos α·cosβ=(1/2)*cos(α+β)+cos(α-β)+ sinα·sinβ=-(1/2)*cos(α+β)-cos(α-β)+·和差化积公‎式：sinα+sinβ=2sin*(α+β)/2+cos*(α-β)/2+ sinα-sinβ=2cos*(α+β)/2+sin*(α-β)/2+cosα+cosβ=2cos*(α+β)/2+cos*(α-β)/2+cosα-cosβ=-2sin*(α+β)/2+sin*(α-β)/2+·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin*α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos*α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAt‎a nBta‎n(A+B)+tanA+tanB-tan(A+B)=0部分高等内‎容·高等代数中‎三角函数的‎指数表示(由泰勒级数‎易得)：sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有‎无穷级数，e^z=exp(z)＝1＋z/1！＋z^2/2！＋z^3/3！＋z^4/4！＋…＋z^n/n！＋… 此时三角函‎数定义域已‎推广至整个‎复数集。

曲线正矢计算公式的理论局限

第二章曲线正矢计算公式的理论局限由图中可知：AD＝f，即曲线正矢；BD＝L/2，即弦长的一半。

正矢计算公式为：f＝（L/2）2/（2R－f）＝L2/4（2R－f）。

在（2R－f）中，由于f与2R相比甚小，可忽略不计，则公式可近似写成为：f＝L2/8R弦长L现场一般取为20m ,当L＝20m时，有f＝50000/R而精确的的正矢数值应当为：f＝R（1－cos(α/2)）假定有一曲线，半径R＝500米，用近似公式求得的正矢为：f＝50000/R＝50000/500＝100mm精确的正矢值为：f＝R（1－cos(α/2)）＝500×（1－cos(10/500)）=99.99666mm二者相差不到0.1mm，所以利用简便公式不影响计算结果，该公式完全可以在日常生产中使用。

但以简便公式为基础推导出的公式是否也适用便值得商榷了，以一个近似的公式推导出的公式可能会使误差扩大，以致于影响到计算结果的正确，下面就我们常用的两个推导公式进行试算，以观察其结果的差异。

2.1 第一个推导公式是计算道岔导曲线支距的公式以50kg/m型9号道岔为例：自导曲线起点至终点全长15.793米，K＝2115mm，尖轨长6.25米，导曲线半径R＝180717.5mm。

如图二示，由尖轨跟端（导曲线起点）处作两条辅助线，一线与基本轨平行，一线为尖轨的延长线。

显然，各点支距都被截为三段，ｙ０、A、Ｂ。

用化简法将各点的ｙ０、A、Ｂ计算相加，即是其各点的支距。

计算公式为：Yｉ＝ｙ0+ Aｉ+ BｉAｉ＝ｕ×2000÷ｌ尖×ｉBｉ＝（2×支距点横距）2/(8R)=(2×2000×ｉ)2/(8R)=20002/(2R外)×ｉ2导曲线起点ｙ０＝ｕ导曲线终点ｙ终＝S－Ksinα≈S－K/ NS———轨距N———道岔号数K———导曲线终点到辙叉心轨理论尖端的直线段长度导曲线支距计算对照表表一ｙ终＝S－Ksinα＝1435－2115×sin6°20′25″＝1201.434ｙ终≈S－K/ N＝1435－2115÷9＝1435－235＝1200ｙ终的近似计算结果与实际值之间相差1.434mm从以上支距计算对照表(表一)可以看出，随着曲线长度的增加，利用近似计算法所得结果的误差也随着增大，当我们利用近似法计算所有2米点间的支距，而在辙叉前的导曲线终点却用另一个公式计算，这样便导致导曲线终点与其相邻点之间的圆顺程度相差3mm。